Statistical analysis of lung nodule volume measurements with CT in a large-scale phantom study

Abstract

Purpose

To determine inter-related factors that contribute substantially to measurement error of pulmonary nodule measurements with CT by assessing a large-scale dataset of phantom scans and to quantitatively validate the repeatability and reproducibility of a subset containing nodules and CT acquisitions consistent with the Quantitative Imaging Biomarker Alliance (QIBA) metrology recommendations.

Methods

The dataset has about 40 000 volume measurements of 48 nodules (5–20 mm, four shapes, three radiodensities) estimated by a matched-filter estimator from CT images involving 72 imaging protocols. Technical assessment was performed under a framework suggested by QIBA, which aimed to minimize the inconsistency of terminologies and techniques used in the literature. Accuracy and precision of lung nodule volume measurements were examined by analyzing the linearity, bias, variance, root mean square error (RMSE), repeatability, reproducibility, and significant and substantial factors that contribute to the measurement error. Statistical methodologies including linear regression, analysis of variance, and restricted maximum likelihood were applied to estimate the aforementioned metrics. The analysis was performed on both the whole dataset and a subset meeting the criteria proposed in the QIBA Profile document.

Results

Strong linearity was observed for all data. Size, slice thickness × collimation, and randomness in attachment to vessels or chest wall were the main sources of measurement error. Grouping the data by nodule size and slice thickness × collimation, the standard deviation (3.9%–28%), and RMSE (4.4%–68%) tended to increase with smaller nodule size and larger slice thickness. For 5, 8, 10, and 20 mm nodules with reconstruction slice thickness ≤0.8, 3, 3, and 5 mm, respectively, the measurements were almost unbiased (−3.0% to 3.0%). Repeatability coefficients (RCs) were from 6.2% to 40%. Pitch of 0.9, detail kernel, and smaller slice thicknesses yielded better (smaller) RCs than those from pitch of 1.2, medium kernel, and larger slice thicknesses. Exposure showed no impact on RC. The overall reproducibility coefficient (RDC) was 45%, and reduced to about 20%–30% when the slice thickness and collimation were fixed. For nodules and CT imaging complying with the QIBA Profile (QIBA Profile subset), the measurements were highly repeatable and reproducible in spite of variations in nodule characteristics and imaging protocols. The overall measurement error was small and mostly due to the randomness in attachment. The bias, standard deviation, and RMSE grouped by nodule size and slice thickness × collimation in the QIBA Profile subset were within ±3%, 4%, and 5%, respectively. RCs are within 11% and the overall RDC is equal to 11%.

Conclusions

The authors have performed a comprehensive technical assessment of lung nodule volumetry with a matched-filter estimator from CT scans of synthetic nodules and identified the main sources of measurement error among various nodule characteristics and imaging parameters. The results confirm that the QIBA Profile set is highly repeatable and reproducible. These phantom study results can serve as a bound on the clinical performance achievable with volumetric CT measurements of pulmonary nodules.

1. INTRODUCTION

The use of volumetric CT as a quantitative imaging biomarker (QIB) has been examined over the last decade, with the hope that it will provide a more accurate and consistent metric of lung nodule size and change in size. A number of inter-related factors can substantially impact the performance of pulmonary nodule volume measurements. These factors include but are not limited to nodule size, chest wall/vessel attachment, shape, density, texture (e.g., nonsolid nodules), CT acquisition parameters (pitch, exposure, collimation, and reconstruction method), the volume estimation tool, and the operator variability associated with their use.^1,2 Study findings examining the above factors have been summarized in a 2009 review by Gavrielides et al.,¹ and a 2014 update on the state of the science.² Those reviews addressed findings from clinical as well as phantom data. Clinical studies provide the most direct approach for evaluating lung volumetry but suffer from a lack of a reference standard in terms of true lesion size. In addition, they are limited to the range of parameters they can study due to the risk of patient radiation exposure. As such, clinical studies examining lesion sizing, when available, are typically limited to “coffee-break” or zero-change experiments where patients are scanned twice in a short period of time to allow for precision analysis but not bias analysis. Mozley et al. have reviewed literature findings regarding the use of volumetric CT in clinical studies and summarized their implications.³ Alternatively, phantom studies provide a framework where the true lesion size can be established and allow for the investigation of a wide range of imaging parameters without concerns for patient safety. This allows for a much more robust and systematic comparison of measurement error across a range of factors (CT acquisition and nodule characteristics) such that the interactions between these factors can be identified. These phantom study results can also be viewed as a bound on the expected clinical performance for any volumetric measurement tool and can offer valuable information related to expected differences between the uses of different imaging protocols.

Despite the numerous phantom studies that have been conducted to examine the effect of different imaging factors on the error associated with lung nodule volumetry, a number of underexamined issues remain. These include the effect of factors such as vessel attachment, low nodule density, and their interaction with other nodule characteristics and imaging parameters. Also, most studies so far have been conducted to target certain factors while keeping others constant, due to the high dimensionality of associated parameters, or the lack of complex objects (such as nodules varying in shape, size, and radiodensity). In addition, literature findings have not been reported consistently due to the use of different metrics and statistical analyses.⁴ Examples of this variability in the analyses of QIB performance for anthropomorphic phantom studies evaluating lung nodule sizing can be found in the literature.^5–8 Each of these studies used somewhat different performance metrics in assessing the accuracy and precision of the same QIB. The differences in analyses among studies make it difficult to consolidate results across the studies and limits the communities’ ability to use the reported results in the design of larger, more definitive studies. There has been a growing interest in developing meaningful methods for validating the technical performance of these potentially useful imaging biomarkers. In order to address this issue, the Radiological Society of North America and the Quantitative Imaging Biomarker Alliance (QIBA) developed a set of technical performance methods, metrics, and study design recommendations for QIBs that are consistent with widely accepted metrology standards.⁴ Reporting the results of phantom studies using common metrics and statistical methods will allow for meaningful comparisons between studies and allow for consensus development regarding imaging protocols to minimize measurement error and maximize the utility of volumetric CT.

The purpose of this study is to assess a much larger cross section of CT phantom data (~40 000 volume measurements) compared to previously reported phantom studies with the intent of more definitively determining the interactions between factors that contribute substantially to measurement error. These data were collected with a factorial data collection approach to systematically probe the large space of parameters associated with volumetric CT, including the use of different imaging protocols to measure synthetic nodules varying in size (5–20 mm), shape (from spherical to highly irregular), radiodensity (from −630 to 100 HU), and attachment (vessel and chest wall). Moreover, multiple acquisitions were conducted for each imaging protocol. This data collection serves another purpose, to create a shared database of CT scans with associated ground truth as a resource for thoracic CT researchers, as discussed in a paper by Gavrielides et al.⁹ As a result of this effort, imaging data are made public for research and commercial use as they become available. Currently, the scans include over 2600 image series. The full description of layouts and acquisition of the data is available through The Cancer Imaging Archive (TCIA).¹⁰ Previous analyses for subsets of these data were reported in several other publications.^7,8,10,11

To obtain volume measurements, we applied a model-based matched-filter estimator.¹² Although it might be less practical compared to segmentation based approaches, the use of such a tool greatly limits the variability from the estimation method such that the results more accurately characterize the ability of an imaging system to measure nodule volume. Minimizing the potential variance contributed by the estimation tool allows for the determination of substantial factors (imaging parameters and nodule characteristics) from the differential analyses. Hence, although the absolute values from the phantom study may not be directly applicable in clinical practice, our results can serve as a performance bound for the CT system and as a useful surrogate for clinical results. The trends we identify will provide useful information on how to set CT acquisition parameters for more consistent volume measurements of nodules with varying characteristics.

Our statistical assessment was based on the metrology recommendations outlined by the QIBA metrology working group,⁴ which included the analysis of linearity, bias, variance, reproducibility, and repeatability. One of our goals was to quantify volumetric error for nodules and CT acquisitions fitting the QIBA Profile, which defines standard working procedures for accurate and reproducible measurement of imaging biomarkers.¹³ In addition to assessing the QIBA Profile claim, we also aimed to understand how the proposed QIBA performance metrics (both aggregate and disaggregate) can be applied to the problem of determining conditions under which the measurements are highly repeatable and reproducible across the full range of nodule characteristics and imaging protocols identified.^4,14,15 A novel contribution of this paper is thus the investigation of CT nodule volumetry using recently recommended metrics when the range of acquisition, reconstruction, and nodule parameters are within the QIBA CT tumor volume change profile, as well as within a broader range of nodule and acquisition values. Our investigation was conducted using, to our knowledge, the largest public CT phantom dataset acquired for this purpose, to accommodate the range of factors described above.

2. MATERIALS, IMAGING AND VOLUME MEASUREMENTS

2.A. Anthropomorphic phantom and synthetic nodules

Multiple layouts of synthetic nodule combinations were placed within the vasculature insert of an anthropomorphic thorax phantom (Kyotokagaku Incorporated, Tokyo, Japan), as shown in Fig. 1. The set of synthetic nodules included 48 solid objects, independently manufactured by Kyotokagaku Incorporated and Computerized Imaging Reference Systems (CIRS, Norfolk, VA). The nodules included four shapes [spherical, elliptical, lobulated, and spiculated, Fig. 1(c)], four sizes (5, 8, 10, and 20 mm in equivalent diameter, defined as the diameter of a sphere with equivalent volume), and three radiodensities (−630, −10, and +100 HU). These nodules represent small and medium size solid lesions across a fairly wide range of radiodensities and shapes. Table I summarizes the properties of the nodule dataset. In most layouts, nodules were directly attached to the vasculature using radiographically lucent surgical suture material (prolene 5–0). In about 1/5 of layouts, efforts were made to avoid attachment of nodules to a local structure by placing them in radiographically lucent foam receptacles [Fig. 1(d)].

Fig. 1.

(a) and (b) Photograph of anthropomorphic phantom and vasculature insert. (c) Photograph of examples of synthetic nodules in different shapes. Clockwisely, spherical, elliptical, lobulated, and spiculated. (d) Synthetic nodules prepared for scanning. In this layout, nodules were held by radiographically lucent styrofoam buffer to avoid attachment.

Table I.

Description of the 48 synthetic nodules.

Diameter (mm)	Manufacturer	Shape	Radiodensity (HU)
5, 8, 10	Kyotokagaku	Spherical	+100, −630
5, 8, 10	CIRS	Spherical	−10
20	CIRS	Sphericala	+100, −10, −630
5, 8, 10, 20	CIRS	Elliptical, lobulated, spiculated	+100, −10, −630

^aThree 20 mm-spherical nodules were only scanned with half of the protocols as described in Table II (with pitch of 1.2 not 0.9).

2.B. Imaging protocols

The phantom along with each of the nodule layouts was scanned with a 16-detector row helical CT system (Mx8000 IDT, Philips Healthcare, Andover, MA). There were in total 72 imaging protocols: two levels of pitch, three levels of exposure, two reconstruction kernels, two collimation options coupled with three reconstruction slice thickness for each collimation (Table II). There were 61 nodules and 72 imaging protocols involved in our data collection efforts allowing for 41 217 volume measurements to be obtained using a model-based matched-filter estimator.¹⁶ Data from 13 nodules were excluded in this study because they were not examined by at least half of the imaging protocols, thus reducing the number of volume measurements in our analyses to 39 717. The vast majority of nodules (45 out of 48) were scanned ten times under each of the 72 different imaging conditions. In a few cases, there were only 8–9 repeats due to missing data during reconstruction and transfer of data. Three out of 48 nodules (spherical 20 mm with three radiodensities) were scanned with pitch of 1.2 only for a total of 36 imaging conditions. Note that some nodules were included in multiple layouts, resulting in 20 repeats. Detailed description of the synthetic nodules and imaging protocols is given in Tables I and II, respectively. Examples of CT slice data from the phantom are shown in Fig. 2. The reference standards of volumes for all synthetic nodules were obtained from high resolution microCT scans.¹⁷

Table II.

Description of imaging protocols.

Scanner	Philips 16-row CT scanner (Mx8000 IDT, Philips Healthcare, Andover, MA)
Pitch	0.9, 1.2
Exposure (dosea)	20 mAs (0.9–1.3), 100 mAs (4.4–6.6), 200 mAs (8.9–13.2)
Collimation	16 × 0.75 mm (thin), 16 × 1.5 mm (thick)
Reconstruction slice thickness	0.8, 1.5, 3 mm for thin collimation; 2, 3, 5 mm for thick collimation
Reconstruction kernel	Detail (b40f), medium (b30f)
Other	Filtered back-projection; in-plane resolution 0.78 mm; 50% reconstruction overlapping
Number of protocols	2 pitch × 3 exposure × 2 kernel × 2 collimation × 3 slice thickness per collimation=72

^aDose as CTDI_vol in mGy per 100 mAs for each exposure. The value varies due to different options in pitch and collimation.

Fig. 2.

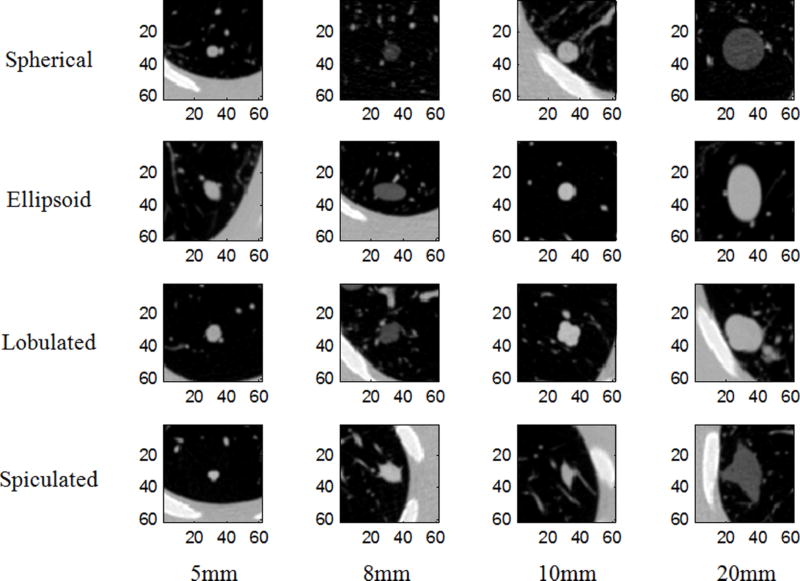
Randomly selected images for each shape and size. Each is approximately the central slice through the nodule. All images are shown using the same window: −1000 to 500 HU.

2.C. Volume measurements

Volume measurements for the nodules in each layout were derived from the reconstructed CT data using a previously developed matched filter (MF) estimator.¹⁶ Briefly, the MF estimator was informed of the nodule’s approximate centroid, and shape, and utilized templates of nodules with nominal diameters ranging from 75% to 125% of the actual value, with increments of 1%. Templates were moved within a 0.5 × 0.5 × 0.5 voxel neighborhood, and a squared absolute difference cost function was minimized to determine the best match. The volume of the best matching template was deemed the estimated volume for the particular measurement.

3. STATISTICAL ANALYSIS

3.A. Definitions and notations

General assessment terminology for QIB metrology concepts can be found in Kessler et al.¹⁴ The terminologies, concepts, and symbols that were used frequently in this paper are given below:

• Lung nodule volume measurement: y_ijk, i = 1, 2, …, n, j = 1, 2, …, m, k = 1, 2, …, r_ij stands for the kth repeated measurement of the ith nodule under the jth imaging protocol; the number of replicates (r_ij) may differ for each nodule and protocol.

• Measurand (true volume) of nodule i: x_i, i = 1, 2, …, n.

• Reference standard (best estimate of true nodule volume): z_i, i = 1, 2, …, n. In practice, this value may be different from the measurand due to error in the truthing method. For instance, the tolerance error of the scale when using a weight-density method or the readers’ bias when using the average of experts’ measurements as the reference standard size for clinical data could introduce differences between the reference standard and the true volume. In this work, our reference standard nodule volumes are based on volumes estimated from high resolution microCT scans of the individual synthetic nodules.

• QIBA CT tumor volume change profile:¹³ This QIBA Profile makes a specific claim about the confidence with which changes in tumor volumes can be measured under a set of defined image acquisition, processing, and analysis conditions. It includes specifications that may be adopted by users and developers to assure the ability to meet the targeted levels of clinical performance in identified settings. The specific claims made in this QIBA Profile are based on studies of varying scope. QIBA Profile includes restrictions on the lesion size (e.g., 10 mm ≤ diameter ≤ 100 mm), acquisition parameters (e.g., pitch ≤ 1.4), reconstruction parameters (e.g., slice thickness ≤ 2.5 mm), and image noise (standard deviation of ≤18 HU measured near the center of a 20 cm water phantom), to list a few. In our study, we consider all of the 10 and 20 mm nodules across all protocols where the reconstruction slice thickness was 0.8, 1.5, or 2 mm to be compliant with the QIBA Profile. We assumed that the other aspects of the profile such as in-plane spatial resolution requirements (≥6 lp/cm) were met in our experiments but we did not verify them. Our findings were based on the analyses of the following subsets of the whole dataset (39 717 measurements):

• Subset-F (38 537 measurements), fully crossed dataset: the 45 nodules scanned with all 72 protocols.

• Subset-Q (9181 measurements), measurements obtained from scans meeting the QIBA Profile: 10 and 20 mm nodules (24 nodules) with reconstruction slice thickness 0.8, 1.5, and 2 mm (36 protocols).

• Subset-QF (8771 measurements), subset-Q with the 20 mm spherical nodules excluded so that all nodules in this subset were scanned with all 36 protocols.

• Subset-SU (6480 measurements), measurements of spherical unattached nodules.

• Subset-SA (4290 measurements), measurements of spherical nodules with attachments.

3.B. Methods and metrics

3.B.1. Data transform

Prior to our analysis, all data were log-transformed (natural log) to reduce the heteroscedastic nature that was observed in our volumetric measurements.⁴ This transformation made the data better suited for subsequent analyses such as analysis of variance (ANOVA) which assumes homoscedasticity (equal variance across groups).

3.B.2. Linearity

The property of linearity between measurements and reference standard was examined based on point estimates of slope and intercept, along with their 95% confidence interval (CI), derived from least square linear regression. For a pooled group of measurements exhibiting linearity, a change in the reference standard was reflected as a proportional change in the measurement on average. A slope close to unity is the ideal relationship, and under such circumstances, the intercept provides an estimate of the overall bias. The R-squared was reported as a metric for goodness of fit, with value close to one indicating strong fits. Linear regression was performed on both the original and log-transformed scales to examine the impact of the transform on the linearity assessment.

3.B.3. Analysis of significant effects

N-way ANOVA without interaction and with two-factor interactions was performed to identify individual and interaction factors that contributed significantly to the overall measurement error.⁸ The individual factors included were nodule size, nodule shape, nodule radiodensity, reconstructed slice thickness × collimation, exposure, pitch, and reconstruction kernel. The factor slice thickness × collimation refers to slice thickness reconstructed from a certain detector collimation (thickness of 0.75, 1.5, and 3 mm derived from 16 × 0.75 mm collimation and 2, 3, and 5 mm derived from 16 × 1.5 mm) so that the reconstructed scans with 3 mm slice thickness derived from 16 × 0.75 mm would be distinguished from those derived using a 16 × 1.5 mm collimation. Eta-squared¹⁸ was used for ranking substantial contribution to overall error. The eta-squared is interpreted as the proportion of the total variance that is attributed to an explanatory variable. It is calculated as the ratio of the between-group sum of squares to the total sum of squares (SST). Note that since our data are unbalanced, the three ways of calculating the sums of squares (SS) in ANOVA, namely, type I, II, and III, lead to different results. No consensus has been established in general regarding which type of SS should be used. In our study, the dataset is large and reasonably balanced so that the results should not be greatly affected by the choice of SS type. The results reported in this study were based on type III SS. The analysis was done on the whole dataset, subset-Q, and subset-SU to better understand how the influence of factors may change for the different groups. Since there were six ANOVA performed (two types of ANOVA × three dataset), we applied a Bonferroni correction method to adjust the critical values.¹⁹ As a result, the adjusted critical value α* = 0.0083 (0.05/6) was used in our ANOVA. We used p < α* as the criterion for determining statistical significance.

3.B.4. Bias, variance, and mean square error (MSE)

QIB bias (δ(x)) is defined as the difference between the expected value of the measurements and the measurand (true value). Let Ω be the group we are interested in, which constrains the measuring interval.¹⁴ In our study, Ω defined the nodule set and group of imaging protocols. In our analyses, the measurand x_i was approximated using the reference standard value z_i which was based on measurements of nodule volumes from high resolution microCT scans. The bias on Ω is then estimated in log-transformed domain first as

$${\hat{\delta }}_{L,\mathrm{\Omega }}=\text{mean}{(\text{log }{y}_{\mathit{\text{ijk}}}-\text{log }{z}_i)}_{(i,j)\in \mathrm{\Omega }}.$$ (1)

For easier interpretation, the value was converted into percentage as

$${\hat{\delta }}_{P,\mathrm{\Omega }}=(\text{exp}({\hat{\delta }}_{L,\mathrm{\Omega }})-1)\times 100\%,$$ (2)

which means that for measurand x, the measurement y has a bias approximately equal to δ̂_P,Ω percent of its true value, if the measurand and imaging protocol are within the measuring interval Ω. Please refer to the Appendix regarding the relationship between Eqs. (1) and (2).

Similarly, the variance of measurements on Ω was estimated in the log-transformed domain as

$${\hat{\sigma }}_{L,\mathrm{\Omega }}^2=\frac{1}{N_{\mathrm{\Omega }}-1}\sum _{(i,j)\in \mathrm{\Omega }}{(\text{log }{y}_{\mathit{\text{ijk}}}-\mu )}^2,$$ (3)

where μ = mean(log y_ijk)_{(i,j)∈Ω,all k} and N_Ω equals the number of measurements in Ω. We could convert the value of the standard deviation σ̂_L,Ω to percentage in the same way as in Eq. (2).

The estimation of MSE (an aggregate performance metric) is obtained from the bias and variance as

$${\text{MSE}}_{L,\mathrm{\Omega }}={\hat{\delta }}_{L,\mathrm{\Omega }}^2+{\hat{\sigma }}_{L,\mathrm{\Omega }}^2.$$ (4)

The bias, variance, and MSE were evaluated as a function of nodule size and slice thickness (collimation) for the whole dataset, subset-Q, subset-SU, and subset-SA. Note that we reported the square root of the variance and MSE (the standard deviation and RMSE).

3.B.5. Repeatability

Repeatability represents the measurement precision under near identical imaging conditions. The repeatability coefficient (RC) is defined as the least significant difference between two repeated measurements taken under identical conditions at a two-sided significance of α = 0.05.⁴ Assume for a fixed imaging protocol, the transformed data satisfy the following:

$$\text{log }{y}_{\mathit{\text{ijk}}}={\mu }_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ijk}}},$$ (5)

where μ_ij is the expected value of the measurement in the log domain for the ith nodule by the jth imaging protocol, and the corresponding measurement error ${\epsilon }_{\mathit{\text{ijk}}}~𝒩(0,{\sigma }_w^2)$ with the assumption of equal variance among all nodules with this fixed imaging protocol. The within-subject variance ${\sigma }_w^2$ is estimated using

$${\hat{\sigma }}_w^2=\frac{1}{{\sum }_{i\in \mathrm{\Lambda }}{r}_{\mathit{\text{ij}}}}\sum _{i\in \mathrm{\Lambda }}\sum _{k=1}^{r_{\mathit{\text{ij}}}}{(\text{log }{y}_{\mathit{\text{ijk}}}-{\mu }_{\mathit{\text{ij}}})}^2,$$ (6)

where μ_ij = mean(log y_ijk)_{k=1, …, rij} and Λ are the indices for nodules scanned with the fixed imaging protocol. Equation (6) is the maximum-likelihood (ML) estimate of the variance. An approximate 95% CI of ${\hat{\sigma }}_w^2({\hat{\sigma }}_{w,L}^2,{\hat{\sigma }}_{w,U}^2)$, where ${\hat{\sigma }}_{w,L}^2$ and ${\hat{\sigma }}_{w,U}^2$ denote the lower and upper 95% bounds, respectively, could be established according to the well-known properties of the ML estimator (it is a consistent estimator of the true parameter and its distribution is asymptotically normal).

With the above assumptions, the difference of any two repeats for the ith nodule with the jth imaging protocol follows a normal distribution with zero mean and variance $2{\sigma }_w^2$. By definition, the RC and the estimate of RC are then given as

$$\text{RC}=1.96\sqrt{2{\sigma }_w^2},\widehat{\text{RC}}=1.96\sqrt{2{\hat{\sigma }}_w^2}.$$ (7)

The corresponding 95% CI of $\widehat{\text{RC}}$ is given by $({\widehat{\text{RC}}}_L,{\widehat{\text{RC}}}_U)=(2.77{\hat{\sigma }}_{w,L},2.77{\hat{\sigma }}_{w,U})$. The repeatability analysis was done on the whole dataset and subset-Q. The values were converted to percentage in the same way as Eq. (2).

3.B.6. Reproducibility

Reproducibility represents the measurement precision under a set of different conditions or reproducibility condition. The conditions might include different sites, operators, system parameters, and replicate measurements.⁴ For our study, we focused on imaging acquisition and reconstruction parameters and replicate measurements. The reproducibility coefficient (RDC) is a generalized RC for reproducibility condition. Assume the transformed data satisfy the following model:

$$\text{log }{y}_{\mathit{\text{ijk}}}=\mu +{\gamma }_i+{\varphi }_j+{(\gamma \varphi )}_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ijk}}},$$ (8)

with random effects ${\gamma }_i~N(0,{\sigma }_{\gamma }^2)$ for nodules, ${\varphi }_j~N(0,{\sigma }_{\varphi }^2)$ for imaging protocols, ${(\gamma \varphi )}_{\mathit{\text{ij}}}~N(0,{\sigma }_{\gamma \varphi }^2)$ for nodules by imaging protocol interactions, and ${\epsilon }_{\mathit{\text{ijk}}}~N(0,{\sigma }_{\epsilon }^2)$ for replicates within nodule and imaging protocol. Then, RDC and its estimate RDC̃ are given as

$$\text{RDC}=2.77\sqrt{{\sigma }_{\epsilon }^2+{\sigma }_{\varphi }^2+{\sigma }_{\gamma \varphi }^2},$$

$$\text{RD}\stackrel{\sim }{\mathrm{C}}=2.77\sqrt{{\hat{\sigma }}_{\epsilon }^2+{\hat{\sigma }}_{\varphi }^2+{\hat{\sigma }}_{\gamma \varphi }^2}.$$ (9)

Since the data we have are not balanced, we estimate the variance components using a restricted maximum-likelihood (REML) approach, which allows for an approximate estimate of the CI.^20,21 The RDCs were evaluated for only subset-F and subset-QF to avoid empty cells in the data table that could limit our ability to estimate RDCs (the cell is defined by the crossing of the imaging protocol factor and the nodule factor). Again, the values were converted to percentage in the same way as Eq. (2).

4. RESULTS

4.A. Linearity and data transform

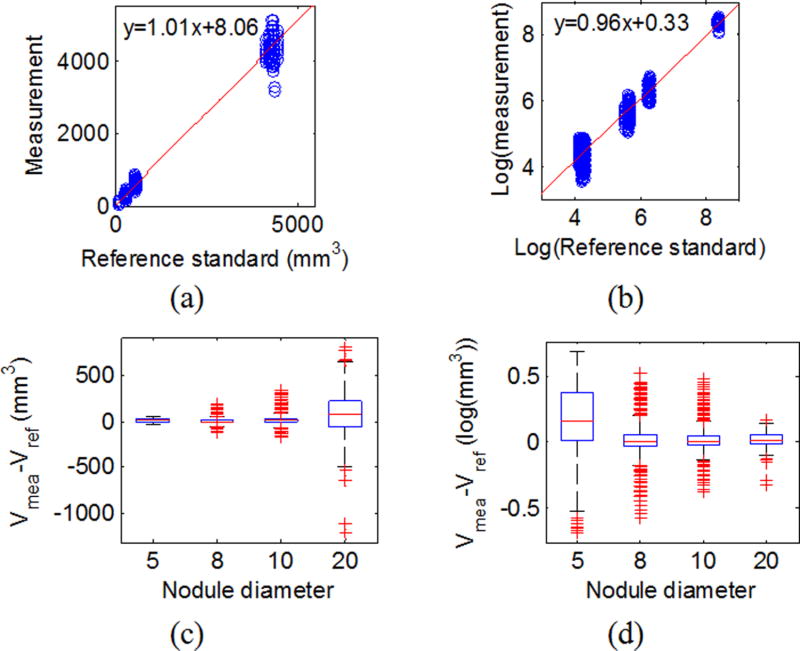
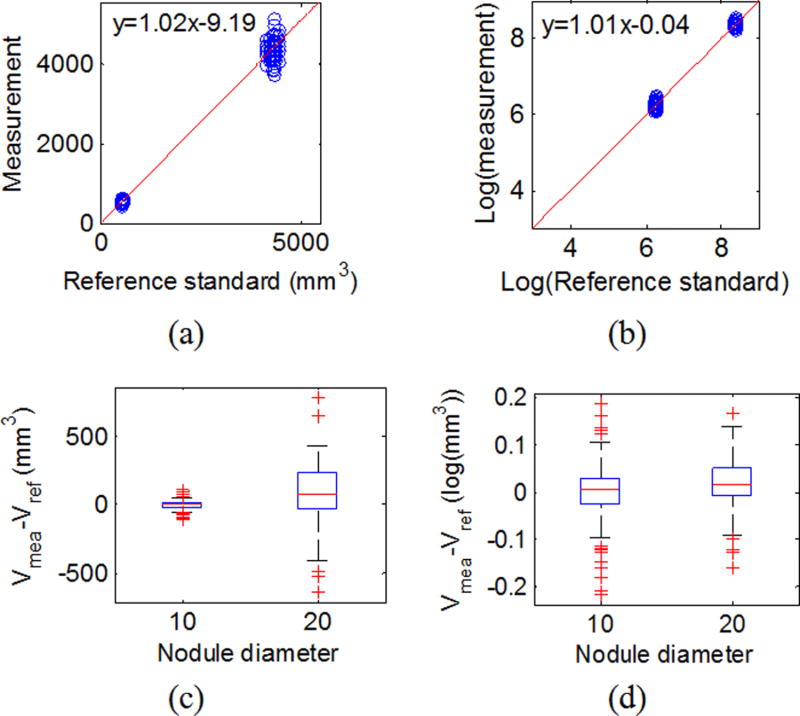
Table III summarizes the slope, intercept, and R-squared for the linear regression applied on all data, subset-Q on the original scale, and in the log-transformed domain. Results showed that for both all data and subset-Q, volume measurements were highly linear in relation to the reference standard, regardless of whether the original scale or log transformation was used. The R-squared values close to 1 indicated good fit of the linear regression model. The log transform produced more equally spaced data as shown in Fig. 3(b). The variances for the 8, 10, and 20 mm nodules were better stabilized after the log transform as shown in Fig. 3(d). For the QIBA Profile subset (subset-Q), the variance difference between the 10 and 20 mm nodules was basically removed using the log transformation, strongly suggesting that the log transformation was reasonable for the data even though the transformation led to an increased variance for the smaller 5 mm nodules.

Table III.

Linear regression results for measurement versus reference standard. The 95% CI of slope and intercept are given in parentheses.

	Slope	Intercept	R-square
All data	1.01 (1.01, 1.01)	8.06 (7.63, 9.91)	1.00
Log (all data)	0.957 (0.956, 0.958)	0.330 (0.323, 0.337)	0.98
QIBA data	1.02 (1.02, 1.02)	−9.19 (−12.4, −4.98)	1.00
Log (QIBA data)	1.01 (1.01,1.01)	−4.14 × 10−2(−4.77 × 10−2,−3.51 × 10−2)	1.00

Fig. 3.

Linearity for all data. (a) Scatter plot for reference standard and measurements with the red line being the linear regression line on the original scale. (c) Box-and-whisker plot of the difference between the measurement and the reference standard by size in the original scale. (b) and (d) are the same plots in the log-transformed domain.

As we pointed out earlier, when the slope is close to 1, the intercept is an estimate of the overall bias. From Figs. 3 and 4(c) and 4(d), the biases are not always constant across the different nodule sizes. Therefore, caution is needed when characterizing the biases. Instead of reporting the overall bias, we will report bias based on subgroups in Sec. 4.C.

Fig. 4.

Linearity for QIBA Profile subset (subset-Q). (a) Scatter plot for reference standard and measurements with the red line being the linear regression line on the original scale. (c) Box-and-whisker plot of the difference between the measurement and the reference standard by size in the original scale. (b) and (d) are the same plots in the log-transformed domain.

4.B. ANOVA

4.B.1. All data

Results of the ANOVA for this group are summarized in Table IV. Seven individual factors (size, shape, radiodensity, slice thickness × collimation, mAs, pitch, and kernel) were included as explanatory variables in ANOVA without interaction. All factors were found statistically significant at the p < 0.0083 level. This model’s R-squared was 0.46, indicating that the factors explained about 46% of the total error.

Table IV.

ANOVA results on all data. Interaction factors are denoted in parenthesis.

Factors: (1) size, (2) shape, (3) HU, (4) slice thickness × collimation, (5) mAs, (6) pitch, and (7) kernel
Model	Without interaction	With two-factor interactions
Variables	1–7	1–7 and interactions
R-squared	0.46	0.67
Nonsignificant variables (p > 0.0083)	N/A	(3,5), (5,7)

For ANOVA with two-factor interactions, all seven individual factors and their interactions were included as explanatory variables (resulting in 28 factors in total). The R-squared for this model increased to 0.67. This indicates that the interaction between factors significantly affects the overall error. Again, almost all explanatory variables were statistically significant (p < 0.0083). For all data, SST and degree of freedom (d.f.) were 1160.63 and 39 716, respectively. In other words, the mean of sum of squares (SST/d.f.) was about 2.9 × 10⁻².

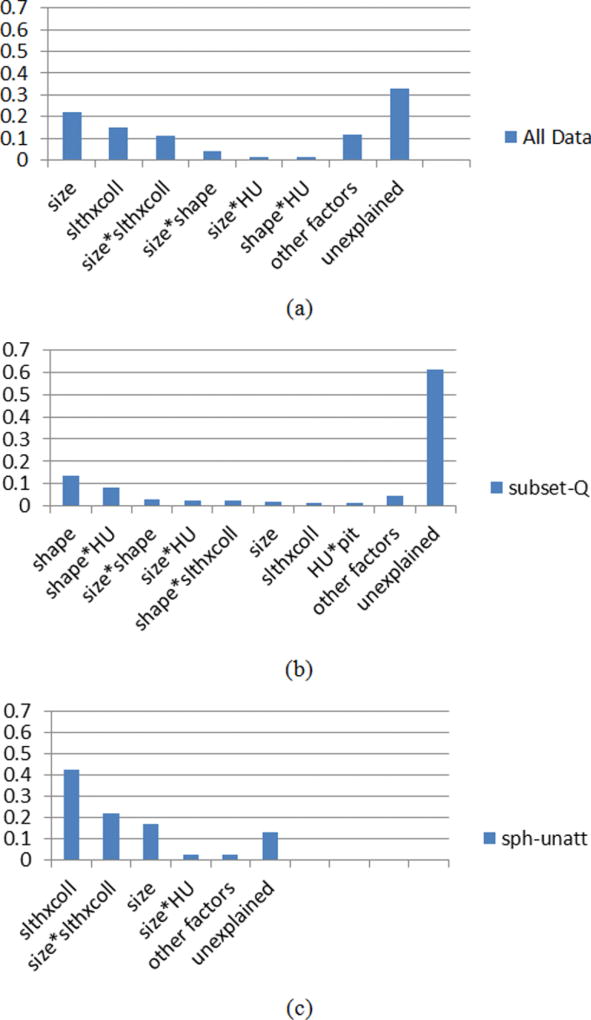
To determine which factors are substantial (significant and also explain a reasonable percentage of the total error), we ranked the explanatory variables by their eta-squared [Fig. 5(a)]. We found that nodule size, slice thickness × collimation, and their interaction contributed most to the total error (eta-squared > 0.1). The eta-squared of size*shape, size*HU, and shape*HU (* indicated interaction terms) were between 0.01 and 0.1. All the rest of the variables and the interaction terms (22 factors) in sum had an eta-squared of only about 0.12. The unexplained error was about 33% of SST. The unexplained error contains inherent test–retest variability and those contributed from factors that were not included in the model. The inherent test–retest variability could be interpreted as simply the residual random error that cannot be reduced substantially without tighter control of the CT imaging acquisition parameters. However, one important factor that was not included in the model is the nodule attachment to the vasculature. Results discussed in Sec. 4.B.3 (analysis of subset- SU) will shed light on how this additional factor may be a substantial contributor to the residual random error observed in this study.

Fig. 5.

Factors ranked according to eta-squared (from ANOVA with two-factor interactions) for (a) all data; (b) QIBA Profile set; (c) spherical unattached data. The bar named other factors includes those with <0.01 eta-squared. Total sum of squares equals 1160.63 (d.f. = 39 716), 18.35 (d.f. = 9180), and 95.95 (d.f. = 6479) for (a)–(c), respectively. Note the magnitude of unexplained error exceeds the sum of the other values in only (b).

4.B.2. Subset-Q

Results of the ANOVA for the QIBA Profile subset are summarized in Table V. In analysis with all factors but no interaction included, all factors except pitch and kernel were found to be significant (p < 0.0083 for all significant factors). The R-squared was very low (0.19).

Table V.

ANOVA results on the QIBA Profile set. Interaction factors are denoted in parenthesis.

Factors: (1) size, (2) shape, (3) HU, (4) Slice thickness × collimation, (5) mAs, (6) pitch, and (7) kernel
Model	Without interaction	With two-factor interactions
Variables	1–7	1–7 and interactions
R-squared	0.19	0.39
Nonsignificant variable (p > 0.0083)	6–7	6, 7, (1, 4), (1, 7), (2, 6), (2, 7), (4, 7), (5, 6), (5, 7), (6, 7)

With all interaction terms added, R-squared increased to 0.39, which is equivalent to say that about 60% of the error sources are not explained by the given factors. For this subgroup, SST and d.f. were 18.35 and 9180, respectively. Compared to the all-data group, the mean sum of squares was substantially reduced (SST/d.f. = 2 × 10⁻³). The majority of interaction factors were statistically significant at the p < 0.0083. Eight nonsignificant factors were listed in Table V. In addition, the ranking of eta-squared for the factors was quite different from the all-data case [Fig. 5(b)]. The first few factors were all related to nodule characteristics. The imaging parameters had only a very limited role for the QIBA Profile subset since scans were limited to <2.5 mm slice thickness, and therefore, the significant interaction between slice thickness and other parameters that were seen in the all-data ANOVA results was not observed here.

4.B.3. Subset-SU

Results of the ANOVA for the spherical unattached subset are shown in Table VI. This subset was considered the simplest task for volume estimation and therefore can be considered to provide a lower bound on estimation error. We carried out this analysis to see if the effects of factors would be substantially different compared with the whole dataset, which involved greater nodule complexity especially in terms of attachment. Results from Fig. 5(c) show that the dominant factors for this subset were the same as the whole set, namely, nodule size, slice thickness × collimation, and their interaction, although the order differed. Shape was not a factor since only spherical nodules were included in this subset. SST and d.f. were 95.95 and 6479, respectively (SST/d.f. = 1.5 × 10⁻²). The overall explained error increased to 87%. This is consistent with our hypothesis that much of the unexplained error for the whole dataset came from the added complexity associated with nodule attachment to the vasculature or chest wall. (Note that we did not apply ANOVA to the subset of attached spherical nodules since they were not scanned across all of the imaging protocols.)

Table VI.

ANOVA results on the unattached spherical subset. Interaction factors are denoted in parenthesis.

Factors: (1) size, (2) HU, (3) slice thickness × collimation, (4) mAs, (5) pitch, and (6) kernel
Model	Without interaction	With two-factor interactions
Variables	1–6	1–6 and interactions
R-squared	0.61	0.87
Nonsignificant variable (p > 0.0083)	4, 6	(1, 5), (2, 4), (2, 6), (4, 6), (5, 6)

4.C. Bias, variance, and MSE

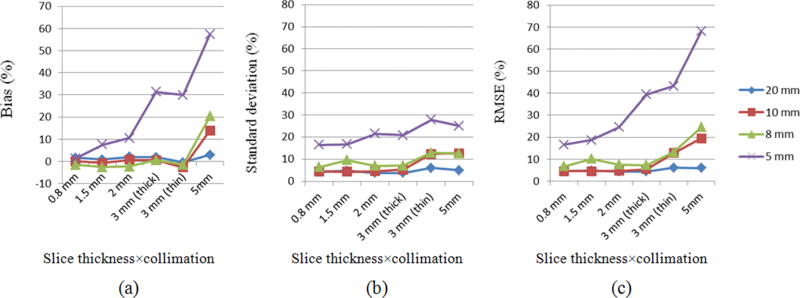
Based on the ANOVA results from Sec. 4.B, further analysis was conducted on data grouped by size and slice thickness × collimation which were the factors contributing most to the overall error. Thus, bias, standard deviation, and RMSE were evaluated for each size and slice thickness × collimation group. These metrics were all obtained in the log-transformed domain and then reported as percentages in the original scale.

Results are summarized in Table VII. The bias was overall low (−3% to 3%) for 5, 8, 10, and 20 mm nodules coupled with slice thickness ≤0.8, 3, 3, and 5 mm, respectively. Results showed a trend of increased bias with increasing slice thickness for 5 mm nodules. For variance (standard deviation), there was a clear trend toward increased variance with decreasing nodule size and increasing slice thickness. This trend was more profound for RMSE, which was the combination of bias and standard deviation (Fig. 6). Nevertheless, within certain subsets, both the bias and variance were small and stable. The QIBA Profile subset falls into this category. The bias, standard deviation, and RMSE for subset-Q were highlighted in bold in Table VII. One other observation to make from Table VII is that for the two subsets with 3 mm slice thickness, the one with thick collimation yielded significantly smaller (F-test at 5% significance level) standard deviation and RMSE than with thin collimation. In addition, we evaluated the biases in percentage using the original values and found the results were very close to those resulting from the log-transformed data, as given in Table VII. Thus, the use of log transform helped stabilize the variance without causing inconsistent results in terms of biases.

Table VII.

Basic statistics by nodule size and slice thickness (collimation).

	Slice thickness (collimation)
Nodule size (mm)	0.8 mm	1.5 mm	2 mm	3 mm (thick)	3 mm (thin)	5 mm
Number of measurements
5	1 766	1767	1770	1769	1769	1769
8	1 826	1827	1770	1769	1829	1769
10	1 821	1822	1770	1769	1824	1769
20	1 254	1254	1260	1260	1254	1260
Total	39 717
Bias in percentage (in italic if <3%, in bold for subset-Q)
5	1.35	7.59	10.6	31.38	29.88	58.91
8	−1.45	−2.51	−2.27	0.69	−1.53	20.34
10	0.13	−0.64	0.8	0.68	−2.62	14.02
20	1.65	0.83	2.13	1.91	−0.41	2.94
Standard deviation of measurement error in percentage (in bold for subset-Q)
5	16.54	16.76	21.55	20.91	27.90	25.16
8	6.57	9.75	7.09	7.23	13.04	12.54
10	4.51	4.46	4.66	5.35	12.49	12.71
20	4.42	4.78	3.91	3.92	6.13	5.14
RMSE of measurement error in percentage (in bold for subset-Q)
5	16.61	18.69	24.57	39.44	43.20	67.30
8	6.75	10.13	7.57	7.27	13.16	24.56
10	4.52	4.51	4.73	5.40	12.82	19.43
20	4.73	4.84	4.47	4.38	6.15	5.97

Fig. 6.

Plots of (a) bias, (b) standard deviation, and (c) RMSE in % for each subset grouped by slice thickness × collimation and nodule size. Lines with diamond, square, triangle, and cross marker correspond to nodule size of 20, 10, 8 and 5 mm, respectively.

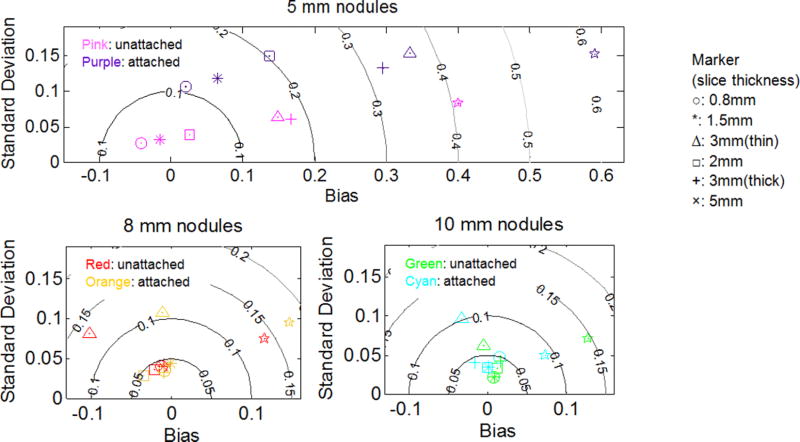
To further confirm the effects of nodule attachment, we evaluated the bias, standard deviation, and RMSE for subset-SU and subset-SA. These two subsets were selected due to comparable sample size. Results are shown in Fig. 7 as RMSE contour maps. We observed that the points on the contour maps for attached data scattered outward, indicating increased error with attachment. The influence of attachment was, however, much smaller for 8 and 10 mm nodules compared to that of 5 mm nodules. Note that all 20 mm spherical nodules were attached. Thus, the results are only shown for 5, 8, and 10 mm nodules. However, we expect that for nodules as large as 20 mm, the influence of attachment should be small in most scenarios.

Fig. 7.

RMSE contour map for subset-SU and subset-SA in the log domain (in percentage, MSE no longer equals to sum square of bias and standard deviation). A value of 0.05, 0.1, 0.15, and 0.2 in the log domain converts to 5.13%, 10.51%, 16.18%, and 22.14%, respectively.

4.D. Repeatability coefficient

In this section, we assess the repeatability of volume measurements. RCs were evaluated by Eqs. (6) and (7) in log-transformed domain and then converted to percentage.

4.D.1. All data

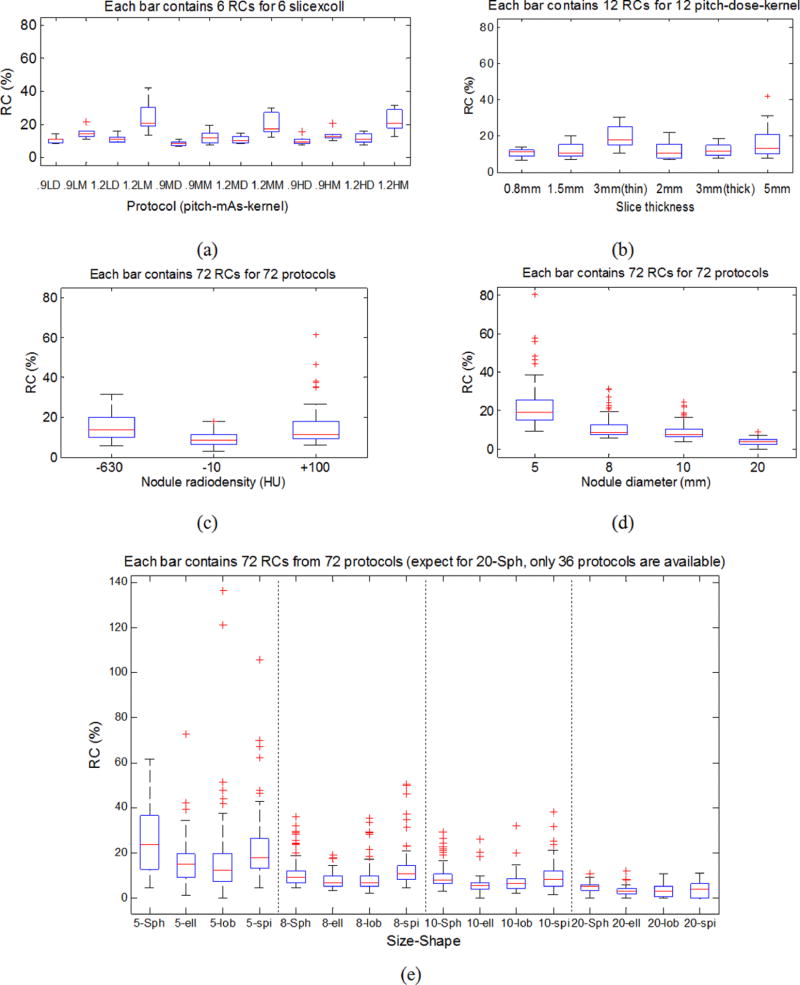
Results are reported in Table VIII and plotted in Figs. 8(a) and 8(b). Several conclusions can be reached from these results.

1. Measurements were more repeatable with smaller reconstruction slice thicknesses.

2. Collimation had an effect on the performance of this particular algorithm. Notice that for the two 3 mm slice thickness groups, the one with thin collimation had lower variance compared to the thicker collimation. This difference may be due to how the data are weighted to produce the slice projection data during the acquisition process. Additional studies are needed to investigate this more thoroughly.

3. Exposure did not impact repeatability. Moving from low to medium and to high exposure, the RCs were quite similar. In theory, low dose scanning produces higher noise in images which should impact the precision of the measurements for our model-based volume estimator. However, in practice, for solid lung nodules, the nodule-to-background contrast was relatively high (~[370, 1100] HU in this study) such that the variability associated with the imaging noise becomes negligible within the exposure levels we tested.

4. RCs increased when pitch moves from 0.9 to 1.2. Note that the number of subjects for pitches of 0.9 and 1.2 differed slightly due to lack of scans for three spherical 20 mm nodules with pitch of 0.9.

5. RCs increased when the reconstruction kernel changes from detail to medium.

Table VIII.

RCs for each imaging protocol (all data and subset-Q). In the first column, L/M/H for mAs stands for 20/100/200 mAs. D/M for kernel stands for detail/medium reconstruction kernel.

	All nodules						10 and 20 mm nodules
Pit-mAs-Kernel	0.8 mm	1.5 mm	2 mm	3 mm (thick)	3 mm (thin)	5 mm	0.8 mm	1.5 mm	2 mm
0.9-L-D	8.05	10.03	10.37	10.22	13.69	7.62	5.66	6.90	7.75
0.9-L-M	13.37	13.80	15.26	12.20	20.72	10.47	6.38	7.00	7.30
1.2-L-D	8.89	8.71	9.95	10.88	14.94	11.36	10.02	9.51	6.06
1.2-L-M	12.61	18.02	21.44	18.01	29.49	40.16	8.53	8.39	5.38
0.9-M-D	6.19	6.89	6.82	8.69	10.21	9.00	4.88	3.80	5.52
0.9-M-M	8.09	7.19	10.13	12.06	18.38	14.08	3.79	3.36	5.74
1.2-M-D	8.98	10.15	8.13	7.57	12.12	13.92	6.97	6.10	6.22
1.2-M-M	11.51	15.92	14.63	16.77	29.03	26.03	6.81	4.86	5.14
0.9-H-D	10.14	8.46	7.09	7.68	14.62	9.02	4.75	4.92	4.44
0.9-H-M	11.17	13.20	9.56	11.37	19.50	12.12	5.14	4.00	5.10
1.2-H-D	11.49	9.59	7.05	9.03	15.35	13.35	7.91	8.04	4.45
1.2-H-M	12.12	19.24	20.20	16.82	27.41	30.16	7.00	7.67	4.59

Fig. 8.

RC box-and-whisker plots. (a) RCs by imaging protocol with each box presenting 6 RCs for a fixed pitch-mAs-kernel condition. (b) RCs by imaging protocol with each box presenting 12 RCs for a fixed slice thickness and collimation. (c) RCs by nodule radiodensity. (d) RCs by nodule size. (e) RCs by nodule size and shape.

4.D.2. Subset-Q

There were 36 protocols satisfying the QIBA Profile and the subset of nodules was also restricted due to QIBA Profile claims. RC results for this subset are given in Table VIII. It can be seen that the RCs are dramatically smaller compared to those in the all-data group and the RCs were generally similar across all of the imaging protocols. The average RC was 5.96% [e.g., ~4 mm³ for a 5 mm nodule (65 mm³) and ~249 mm³ for a 20 mm nodule (4186 mm³)].

The 95% CI of each individual RC for all data and subset-Q were fairly consistent and tight across the groups. On average, the lower limit was about 94% of magnitude of the RC and the upper limit was about 106% of magnitude of the RC. Due to space considerations, the CIs are not reported for specific conditions in Table VIII.

4.D.3. RC by nodule characteristics

We report the repeatability by nodule radiodensity [Fig. 8(c)], nodule size [Fig. 8(d)], and nodule shape and size [Fig. 8(e)] using box-and-whisker plots. From Fig. 8(c), it can be seen that the RC was slightly smaller for −10 HU nodules. However, since only three levels of radiodensities were available and the differences of the RCs were relatively small, it is difficult to make a broader conclusion related to the impact of radiodensity. From Fig. 8(d), RCs were smaller for larger nodules as expected. For small nodules, vessel attachment seemed to introduce added variability in the volume estimates. As far as nodule shape is concerned, we observed a consistent pattern for each size group [Fig. 8(e)]. The mean RCs for each shape were in general similar relative to the magnitude of the variances. Note that our MF estimator was informed of the nodule shape, allowing it to account for the shape differences which likely accounts for the small impact observed across nodule shape. This result also suggests that nodule shape does not have to be a contributory factor to overall error if the CT imaging process is appropriately selected and the volume estimation tool is robust to shape differences. For spherical nodules, the RCs were not as small as we had anticipated compared to the other nodule shapes. This was possibly because that the portion of unattached cases in the spherical nodule subset was larger than for other shapes in our dataset. Although not systematically investigated in this work, the biases for unattached and attached nodules are likely to be intrinsically different, and as a result affected the RC.

4.E. Reproducibility coefficient

Reproducibility is reported for subset-F and subset-QF, which correspond to the whole dataset and subset-Q, excluding the three 20 mm spherical nodules from each dataset so that no empty cell would present. The RDCs were evaluated according to the approaches described in Sec. 3.B.6 using log-transformed data but converted to percentage for comparison purposes. Besides estimating the overall RDC, we also estimated RDC for fixed slice thickness and collimation.

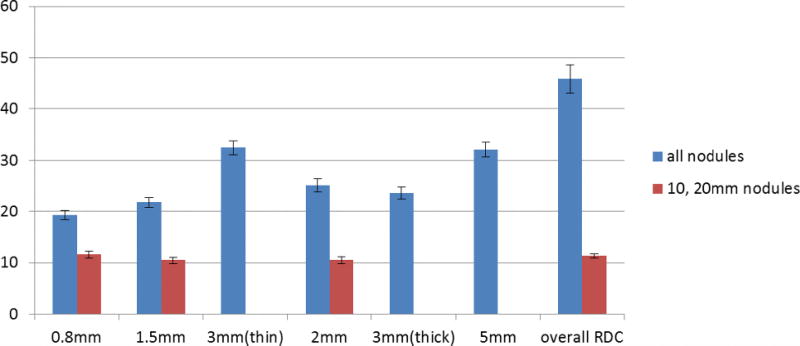
4.E.1. Subset-F

The results are given in Table IX. It can be seen that the RDCs increase with large slice thickness, from ~19% for the 0.8 mm to ~32% for the 5 mm slice thickness. The corresponding variance components are also summarized in Table IX with values in the log domain. The variance due to the interaction between protocol and nodule is the largest variance component. When the reproducibility condition contains all protocols, there is a considerable variance coming from the differing protocols. However, the variance component for protocol becomes negligible when the slice thickness is fixed.

Table IX.

RDC in % and variance component in the log domain for subset-F. Ptc and Nod stand for protocol and nodule, respectively.

			Variance component
Group	RDC (%)	95% CI of RDC (%)	Error	Protocol	Ptc, Nod interaction
All protocol	45.87	[43.02 48.64]	0.0029	0.0053	0.0103
0.8 mm	19.32	[18.41 20.20]	0.0015	0.0000	0.0026
1.5 mm	21.84	[20.89 22.78]	0.0021	0.0000	0.0030
3 mm-thin	32.49	[31.13 33.77]	0.0051	0.0000	0.0052
2 mm	25.15	[23.86 26.38]	0.0022	0.0002	0.0042
3 mm-thick	23.15	[22.50 24.76]	0.0021	0.0000	0.0038
5 mm	32.12	[30.65 33.55]	0.0047	0.0003	0.0051

4.E.2. Subset-QF

For the QIBA Profile fully crossed subgroup, RDCs were lower than the larger subset-F, with values ranging between 10.6% and 11.6% for the 0.8, 1.5, and 2 mm slice thickness subgroups, compared to a range of 19.3%–25.2% for the same slice thickness with subset-F. A direct comparison between subset-F and subset-QF can be found in Fig. 9. RDCs were not significantly different among the groups investigated in this analysis (Table X). This has great implication in practice: when nodules and scanning protocols are within the QIBA Profile, one can expect consistent performance across the appropriate range of imaging protocols and nodule sizes.

Fig. 9.

Plots of RDCs (in %) for subset-F and subset-QF.

Table X.

RDC in % and variance component in the log domain for subset-QF.

			Variance component
Group	RDC (%)	95% CI of RDC (%)	Error	Protocol	Ptc, Nod interaction
All protocol	11.34	[10.92 11.75]	0.0006	0.0000	0.0009
0.8 mm	11.63	[10.88 12.33]	0.0006	0.0000	0.0006
1.5 mm	10.52	[9.89 11.11]	0.0006	0.0000	0.0007
2 mm	10.57	[9.08 11.26]	0.0004	0.0000	0.0009

4.F. Summary of results

The results in the all-data group show a strong linear relationship with the reference standard. In terms of measurement error, all factors including nodule characteristics (size, shape, and radiodensity) and imaging parameters (pitch, kernel, mAs, and reconstruction slice thickness × collimation) and their two-factor interactions were found to be significant in our ANOVA testing. However, size, slice thickness × collimation, and randomness in attachment appear to be the main sources of measurement error. Grouping the data by nodule size and slice thickness × collimation, the variance (3.9%–28%), and RMSE (4.4%–68%) has an increasing trend for smaller nodules and larger slice thicknesses. Regarding accuracy, measurements were almost unbiased (range: −3% to 3%) for 5, 8, 10, and 20 mm nodules with reconstruction slice thickness ≤0.8, 3, 3, and 5 mm, respectively. In terms of repeatability, RCs are from 6.19% to 40.16%. Pitch of 0.9, the detail reconstruction kernel, and smaller slice thicknesses yielded better (smaller) RCs than those with pitch of 1.2, medium kernel, and larger slice thicknesses. Exposure shows no impact on RC. For reproducibility, the overall RDC is 45% and reduces to between 20% and 30% when the slice thickness and collimation are fixed instead of allowed to vary.

For the QIBA Profile subset, volumetric measurements were highly repeatable and reproducible in spite of differences in nodule characteristics (size of 10 and 20 mm, variable shapes, and radiodensities) and imaging protocols. The overall measurement error was quite small with bias, variance, and RMSE within ±3%, 4%, and 5%, respectively. The error that does exist could be associated with randomness in the nodule attachment to the vasculature. The grouped RCs were within 11% and the overall RDC was only 11% for the subset.

5. DISCUSSION

In this work, we performed technical assessment of lung nodule volume measurements extracted from CT scans in a large-scale phantom study, which resulted in about 40 000 measurements. We studied the accuracy and precision of lung nodule volume measurements under the statistical framework suggested by the QIBA metrology group, by analyzing the linearity, bias, variance, MSE, repeatability, reproducibility, and significant and substantial factors that contribute to the measurement error. The analysis focused on the whole dataset and the QIBA Profile subset.

From the analyses, we found that nodule size and thickness × collimation were the most important factors among all factors we examined. This finding from our large phantom dataset agreed and further supported results in the literature. In ANOVA, these two factors and their interaction explained most of the errors. These effects were greatly reduced when the range in nodule size and slice thickness were further constrained by the QIBA Profile requirements. For bias, variance, RMSE, and RC, these metrics increased with smaller nodule size and larger slice thickness yet fairly stable within QIBA Profile. In terms of RDC, for the entire dataset, it was observed that the variance component corresponding to protocol was primarily affected by the slice thickness × collimation factor. Again, within the QIBA Profile subset, the variance component was almost zero even with several slice thicknesses included. In addition, we consistently observed that the 3 mm slice thickness from thick collimation (16 × 1.5 mm) always performs better than the 3 mm slice thickness from thin collimation (16 × 0.75 mm) in terms of variance, repeatability, and reproducibility. The major difference behind these two slice thicknesses may be the dose efficiency in the raw data collection thanks to the adaptive array detector design: The 1.5 mm detector bin has a larger area to absorb incident photons compared to the area from binning two 0.75 mm detectors because of the unusable separation space between the two narrow detector bins.²² However, as will be discussed below, imaging dose does not appear to impact the volume estimates in this study. Thus, the reason behind this issue remains unclear and in need of further study.

The contribution to measurement error from pitch and kernel was quite small from our ANOVA. The eta-squared associated with these two factors was <0.01. However, they were found to have a clear impact on repeatability, with smaller pitch and detail kernel yielding more repeatable measurements [Fig. 8(a)] in the whole dataset. Note that in the ANOVA, nodule characteristics were included as factors to explain the observed variance. In the repeatability analyses, the data were divided into groups according to imaging protocols only. As a result, the impact from pitch and kernel in the repeatability analyses became less apparent in the ANOVA due to the involvement of nodule characteristics.

The effect of exposure (mAs), a major factor that controls imaging dose, was not consistently established in studies discussed in the 2009 review by Gavrielides et al.¹ However, in more recent years, some studies indicated that the volume of pulmonary nodules might be quasi-independent of the dose level.² In our study, exposure does not appear to be an important factor in solid lung nodule volume estimation. This is the reason we included the low dose imaging protocols in our QIBA Profile subset, although with the 20 mAs exposure scans, the noise requirement specified in the QIBA Profile could not be met.¹³ We also notice that the QIBA pixel noise requirement from the QIBA Profile is not organ specific. Therefore, for solid lung nodule volume estimation, where the contrast may be higher because of the low density lung parenchyma, the QIBA noise requirement may be overly stringent.

The conclusion for the other two factors, shape and radiodensity, remain unclear based on the study results because these two factors are associated with nodule characteristics and thus are expected to substantially interact with nodule attachment. Their impacts on measurement error and RCs may not be negligible. However, we do not think we are ready to comment on the strength of impact of these factors. We also could not rank, for instance, whether +100 HU nodules are less repeatable compared to −10 HU nodules simply from Fig. 9(c).

When interpreting the results, there are two points to keep in mind. First, the results are estimator specific. We expect that when switching from the matched-filter method to a segmentation-based method, the volume estimation performance will most likely be worse unless the segmentation-based method also incorporates prior information about the nodules such as nodule shape.²³ When the nodules have complicated shapes such as spiculations, segmentation methods tend to underestimate the volume when little attachment is present.²³ In addition, because of the fine detail in structures such as spiculations, the image resolution may impact the estimation accuracy to a greater extent. For the matched-filter estimator, the shape factor was found to only have minor impact because this estimator used the lesion shape as prior information. Unlike our results with the matched-filter approach, nodule shape has been found to be an important contributing factor to measurement error for segmentation-based approaches.^8,24 Second, our synthetic nodules are homogenous. Volume estimation for heterogeneous or semisolid nodules with complicated shapes is a much more challenging problem. However, the main criterion used for tumor monitoring in practice today, RECIST, only applies to solid nodules.²⁵ Meanwhile, the QIBA Profile is restricted to “measurable” nodules. Therefore, we believe that the solid nodules with shapes spanning from the simplest (spherical) to highly irregular (spiculated) embedded in vascular structures represent a reasonable range for measurable nodules. For nodules with nonuniform density, our results cannot be applied directly, although we believe that the ranges of CT acquisition parameters identified in this study would likely represent reasonable starting ranges for more complex nonuniform nodules. To test this, we initiated phantom studies of mixed-density nodules and our preliminary results were reported by Gavrielides et al.²⁶

As mentioned but not emphasized earlier, we transformed the data for the purpose of stabilizing/equalizing the variance. This step is in fact critical for most of the analyses we performed. The linear regression (results presented in Sec. 4.A), ANOVA test (Sec. 4.B) is all based on an assumption of constant variance across subgroups (homoscedasticity). Although these methods are not over sensitive to the violation of equal variance, results from the analyses might be misleading when the heteroscedasticity is pronounced. For the evaluation of RC (Sec. 4.D), we have assumed equal variance for different nodules with a fixed imaging protocol to reach Eq. (6). Equation (6) can be viewed as using the mean of all estimated variances of each nodule for the estimate of within-subject variance. If the equal variance assumption is strongly violated, in other words, ${\sigma }_w^2(x_i)$ depends on x_i, the average becomes meaningless and we may no longer obtain one uniform RC expression for all the nodules. In the case of such an unequal variance condition, the RC must be established based on each individual nodule or nodule set where the heteroscedasticity is minimal. This is true for the evaluation of RDC as well.

Besides the log transformation, we could use a more general Box–Cox transform (the log transform is actually just a special case of the Box–Cox transform). Using the log transform is convenient in terms of results interpretation. The difference in two log transformed data points is directly related the ratio between the two data points in the original domain, and as a result, we can easily interpret the results as percentages which is much easier to understand. However, we think there is still a need to gain a better understanding of data transformation. In some of our previous work, we used the percent error transformation. We choose to use log transform for this study since it is more generally applicable and we have showed that the two transformations yield similar results when the measurement error is relatively small. Details on the relationship between the log transformation and percent error transformation are given in the Appendix.

There are limitations in our work. First, only four fixed nodule sizes were evaluated. When narrowed down to just the QIBA Profile subset, only 10 and 20 mm were available. This makes our linearity analysis quite limited because it does not adequately span the QIBA size range. However, we expect bias to be smaller for larger sized single radiodensity synthetic lesions so this is unlikely a major limitation, at least for phantom analyses. Second, the complexity of the phantom still does not include all the properties of nodules and backgrounds encountered in clinical practice. For instance, our phantom does not simulate lung parenchyma (i.e., we have a simple flat air parenchyma background) and motion effects are not included in our data collection. The presence of parenchyma may influence the performance of nodule volume estimation due to a lower lesion-to-background contrast and increasing variation in background. For solid nodules, however, the lesion-to-background contrast is generally high even in the presence of real lung parenchyma so that this may not have strong impact on the estimation task. To further support this contention, we have not observed significant difference in performance between very low (−630 HU) and higher (100 HU) density nodules in our phantom experiments. This implies that the variability from the contrast difference is unlikely a substantial factor. As far as the variation in background is considered, additional experiments are needed to investigate this factor. Regarding motion, CT technology is greatly improved such that it minimizes motion artifact through a wider detector and fast gantry rotation. Thus, although the phantom is stationary, it is reasonable to suggest that the state-of-the-art CT systems will yield images of a moving object with negligible impact on estimates of nodule volumes. Finally, only the filter-back projection reconstruction algorithm was used due to the capability of the scanner we used. In the future, it is important to include iterative algorithms because of the growth of its use in practice.

6. CONCLUSION

In conclusion, we have performed a comprehensive technical assessment of solid lung nodule volumetry with a matched-filter estimator from CT scans and confirmed that the QIBA Profile set is highly repeatable and reproducible. Our statistical analysis follows the recommended framework from the QIBA Metrology group and in addition, we discussed methodologies dealing with unbalanced datasets. This work is a technical example of how to assess the technique performance of a QIB using a large complex dataset. The results of this work are of value for developing standardizing imaging protocols for minimizing the measurement error of CT lung nodule volumetry.

APPENDIX

PERCENT ERROR TRANSFORM AND LOG TRANSFORM

Another way to transform the data, when the reference standard is known, is to calculate the percent error for each measurement as PE_ijk = ((y_ijk − z_i)/z_i) × 100%. This approach has been used in some of our previous work.^8,11,16 In fact, the log transform and PE transform yield similar results for bias, variance, MSE, RC, and RDC, provided that the measurement error is small compared to the truth. To show this for bias, we assume that y_ijk = z_i + ε_ijk. As discussed before, the bias in the log transform domain can be estimated as δ̂_L,Ω = mean(log y_ijk−log z_i)_(i,j)∈Ω, where by Taylor expansion and with the assumption that (ε_ijk/z_i) < 1,

$$\text{log }{y}_{\mathit{\text{ijk}}}-\text{log }{z}_i=\text{log}\frac{y_{\mathit{\text{ijk}}}}{z_i}=\text{log}(1+\frac{{\epsilon }_{\mathit{\text{ijk}}}}{z_i})=\frac{{\epsilon }_{\mathit{\text{ijk}}}}{z_i}+𝒪\left(\frac{{\epsilon }_{\mathit{\text{ijk}}}^2}{z_i^2}\right).$$ (A1)

Substituting Eq. (A1) into Eq. (2) and keeping the first-order term in the Taylor expansion to Eq. (2), the bias in percentage from log-transformed data is

$${\hat{\delta }}_{P,\mathrm{\Omega }}=\text{mean}{(\frac{{\epsilon }_{\mathit{\text{ijk}}}}{z_i}+𝒪(\frac{{\epsilon }_{\mathit{\text{ijk}}}^2}{z_i^2}\left)\right)}_{(i,j)\in \mathrm{\Omega }}=\text{mean}{({\text{PE}}_{\mathit{\text{ijk}}}+𝒪(\frac{{\epsilon }_{\mathit{\text{ijk}}}^2}{z_i^2}\left)\right)}_{(i,j)\in \mathrm{\Omega }}.$$ (A2)

We can see that evaluating bias in the percent error domain is a first-order approximation to the bias in the log-transformed domain. This can be shown for the other metrics mentioned above in similar fashion.

In this work, the reference standard is available so that PE transform can be applied. We decided to use log transform since it can be applied without a reference standard (i.e., is more generally applicable) and provides similar results to PE.