Regularization Techniques to Overcome Overparameterization of Complex Biochemical Reaction Networks

Abstract

Models of biochemical reaction networks commonly contain a large number of parameters while at the same time there is only a limited amount of (noisy) data available for their estimation. As such, the values of many parameters are not well known as nominal parameter values have to be determined from the open scientific literature and a significant number of the values may have been derived in different cell types or organisms than that which is modeled. There clearly is a need to estimate at least some of the parameter values from experimental data, however, the small amount of available data and the large number of parameters commonly found in these types of models, require the use of regularization techniques to avoid over fitting. A tutorial of regularization techniques, including parameter set selection, precedes a case study of estimating parameters in a signal transduction network. Cross validation rather than fitting results are presented to further emphasize the need for models that generalize well to new data instead of simply fitting the current data.

I. Introduction

MODELS of biochemical reaction networks comprised of ordinary differential equations (ODEs) have been successfully employed for a variety of purposes, including summarizing experimental evidence [1], distinguishing between possible mechanisms [2], and reducing experimental burden [3]. Herein, the term “biochemical reaction networks” is used as a general term to incorporate all ODE models of biological systems, such as pharmacokinetic/dynamic models, signal transduction pathways, metabolic networks, and quantitative systems pharmacology models. These models typically contain a large number of uncertain parameters to adequately represent the underlying biology. When models such as these are first developed to describe a given data set, parameters are often sourced from the available literature. In practice, it is common to source parameters from different cell types/organisms or similar reaction networks when more relevant data are unavailable. This represents a clear need to estimate some or all of the parameters of these models to ensure that the model can fit and predict experimental data. While it would be desirable to have as much high quality data as possible, there are several challenges to this: measuring protein concentrations and other states inside of living cell is challenging, as the measurements can be noisy, and the cost and sometimes the destructive nature (or required offline analysis) of certain measurements leads to sparse data collection. Therefore, regularization techniques are typically employed to avoid over fitting the model to the experimental data.

The most common regularization techniques employed for the parameter estimation problem in biochemical reaction networks are parameter set selection, Tikhonov regularization, and ℒ₁ regularization. Herein, these three estimation techniques are presented together to allow the user to readily compare the objectives of each technique. A case study involving a representative example of a biochemical reaction network compares results obtained by each technique.

II. Problem Formulation

From here on, consider nonlinear dynamic models with n states, m inputs, ℓ parameters, and k outputs of the form

$$\dot{\hat{x}}=f(t,\hat{x},u,p),\hat{x}(t_0)={\hat{x}}_0\hat{y}=g(t,\hat{x},u,p)$$ (1)

where x̂ ∈ ℝⁿ is the state vector, u ∈ ℝ^m is the input vector, p ∈ ℝ^ℓ is the parameter vector, and ŷ ∈ ℝ^k is the output vector. In models of biochemical reaction networks, each output is often a single model state or proportionally related to a state. If the initial conditions are not precisely known, they may be included as additional parameters for estimation. Also, additional algebraic relations can be incorporated to form a systems of differential algebraic equations (DAEs) rather than ODEs.

Without regularization, the parameter estimation problem is usually posed as a least-squares problem and can be written as

$${\text{min}}_p\sum _{i=1}^j{(y(t_i)-\hat{y}(t_i))}^2$$ (2)

$$\mathrm{s}.\mathrm{t}.\dot{\hat{x}}=f(t,\hat{x},u,p),\hat{x}(t_0)={\hat{x}}_0$$

$$\hat{y}=g(t,\hat{x},u,p)$$

where y signifies the experimental measurements collected at various times. Systems of DAEs can be handled in the same way with additional equality constraints on the state variables. This objective can be modified (e.g. weights for different outputs, log scaling, etc.) to suit the needs of the modeler, but should be chosen to reduce the estimation error by manipulating the parameters. For additional parameter estimation techniques, the interested reader is referred to [4], [5].

Various solution strategies to solve ODE-constrained optimization problems have been developed (e.g. [6]–[8]) and are generally categorized into sequential or simultaneous approaches [9]. The sequential approach solves the system of ODEs at one level and an optimization algorithm updates the decision variables which requires multiple solutions of the ODEs at each iteration. While this approach is conceptually straightforward, a large number of decision variables will greatly increase the computational expense of the problem. The simultaneous approach instead discretizes the ODEs by some collocation method and includes the collocation equations as constraints in one large optimization problem.

When regularization is added, the objective function of the optimization problem becomes

$${\text{min}}_p\sum _{i=1}^j{(y(t_i)-\hat{y}(t_i))}^2+h(p,p_0)$$ (3)

where the regularization function h(p, p₀) is a function of both the estimated parameter values p and the nominal parameter values p₀. Path and terminal constraints can be added to provide regularization for the state and output trajectories, but they will be ignored here for simplicity.

A. Parameter Set Selection

Parameter set selection procedures regularize the parameter estimation problem by choosing a subset of parameters to estimate and setting the remaining parameters to their nominal values. A variety of methods for parameter set selection have been proposed in the literature (e.g. [10]–[12]), but all rely on local sensitivity analysis in some form to determine parameter effects on the outputs. Some, but not all of the available methods consider the correlations among parameters.

When the nominal values of most parameters are close to their true values, e.g., parameter estimation only results in small changes of the parameter values, then local sensitivity analysis at the nominal parameter values provides an acceptable approximation to the sensitivity of the system over the range of interest. However, this can only be determined after estimation has been performed. Also, as the uncertainty in the parameter values increases, a more detailed treatment of the systembs sensitivity over the entire region of feasible parameters may be warranted. Uncertainty, as measured by changes of the sensitivity vectors, can be incorporated at the parameter set selection stage through computation of sensitivity cones which envelop all sensitivity vectors derived for different nominal values of the parameters [9].

After a subset q ∈ p of parameters is chosen for estimation, the objective of the parameter estimation problem can be written in the form of 3 with

$$h(p,p_0)={\Vert p-p_0\Vert }_W^2$$ (4)

where the weight matrix is diagonal with

$$W_{\mathit{\text{ii}}}=\{\begin{array}{cc}\infty \hfill & i\cap q=\varnothing \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (5)

This formulation does not constrain parameters selected for estimation while it constrains the parameters not selected to such a degree that they remain at their nominal values. The choice of the norm is arbitrary. Although this formulation would never be numerically implemented as stated here, i.e., one would select a set of parameters to estimate using one of the existing parameter set selection approaches and then only estimate this subset of parameters, this formulation highlights that parameter set selection is one of the regularization techniques that can be used to deal with over-parameterized problems.

B. Tikhonov Regularization

Tikhonov regularization, also referred to as ridge regression, can be written in the form of 3 with the regularization function given by

$$h(p,p_0)=\lambda {\Vert L(p-p_0)\Vert }_2^2$$ (6)

where L is chosen to represent the relative scaling of the parameters and λ is a positive constant that balances the estimation error with the distance from the nominal parameter values. Tikhonov regularization is widely popular since it results in objective functions that are continuously differentiable, a requirement for many commonly available optimization packages.

C. ℒ₁ Regularization

Also known as the LASSO operator, the regularization function for penalizing the ℒ₁ norm can be written as

$$h(p,p_0)=\lambda {\Vert L(p-p_0)\Vert }_1$$ (7)

where L and λ have the same purpose as in Tikhonov regularization. Due to the sharp increase of the regularization function as p moves away from p₀, ℒ₁ regularization promotes sparsity in the parameter estimates, retaining more parameters at their nominal values than the Tikhonov approach.

D. Combination of Regularization Techniques

The above approaches can be combined for more sophisticated estimation strategies. Parameters set selection can remove unimportant parameters and directions from the full parameter set prior to, e.g., Tikhonov regularization. Tikhonov and ℒ₁ regularization can be combined to form an elastic net [13], a common methodology in empirical modeling.

It is important to point out that it is the authors belief that there is no one “best” regularization technique for all parameter estimation problems, but rather that (a) some form of regularization is almost always advantageous over no regularization when estimating parameters in complex biochemical reaction networks, (b) that each method can be tuned to achieve good outcomes, and (c) that each technique has its advantages and its own set of drawbacks.

III. Case Study: IL-6 Signaling

A model of interleukin–6 (IL–6) signaling developed previously [1] is used to illustrate the regularization approaches described above. The signal transduction model is described by 75 states and 128 parameters and measurements correspond to the transcription factor concentration STAT3 taken at different points in time.

A. Parameter Set Selection

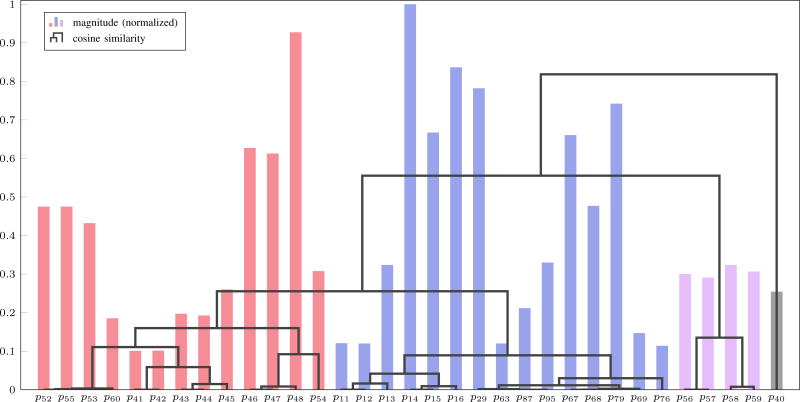
The method described in [12] is used to determine the parameters for estimation. Briefly, sensitivity vectors are obtained through local sensitivity analysis and scaled by the nominal parameter values. If a normalized sensitivity vector is small, the parameter can be removed from further analysis. Then the cosine distance between every pair of remaining sensitivity vectors is used to cluster parameters via agglomerative hierarchical clustering. The normalized sensitivity vectors are presented in a dendrogram as shown in Figure 1. In this example, a threshold of 0.1 is placed on the normalized sensitivity vector magnitude to remove parameters with small sensitivity from further consideration. This reduces the number of parameters from 128 to 33.

Fig. 1.

Sensitivity vector magnitude (normalized) and agglomerative hierarchical clustering based on the cosine similarity between sensitivity vectors. For a cosine similarity threshold of 0.2, the dendrogram shows separation of the parameters into four clusters, indicated by the four colors in the bar graph.

The dendrogram is used to view correlations between each pair of sensitivity vectors and each cluster of parameters below a user-defined cosine similarity threshold is said to be indistinguishable from other parameters in the same cluster. For example, a cosine similarity of 0.7 would divide the dendrogram into two clusters, namely {p₄₀} in one cluster and all other parameters in a separate cluster.

B. Tikhonov and ℒ₁ Regularization

Before Tikhonov and ℒ₁ regularization can be applied to this problem, an appropriate L matrix must be defined. If information on the uncertainty in the parameters is known, the covariance matrix can be used to normalize the parameters. In the absence of information about the covariance of the parameters, L can be chosen to simply normalize the parameter differences. Therefore, the L matrix is constructed as $(1/\sqrt{p_0})$ for Tikhonov regularization and L = diag(1/p₀) for ℒ₁ regularization.

C. Estimation Results

All parameter estimation problems were solved with a simultaneous optimization strategy with Legendre-Gauss-Radau collocation on finite elements. A variant step collocation method could be used since the system stiffness varies over time; however, this work uses a fixed-step, three-point Radau collocation.

Since regularization techniques aim to reduce over fitting of the model to data, cross validation is used to evaluate the effects of regularization on the parameter estimation problem. Five data sets of nuclear STAT3 fluorescence were collected following step changes in IL–6 administration. Table I presents cross validation results for different parameter sets obtained through parameter set selection as well as Tikhonov and ℒ₁ results at different values of λ.

TABLE I.

Cross-Validation Results

		MSE		Value of λ	MSE
Parameter Set Selection	{p14}*	70.4	Tikhonov Regularization	0.001	74.5
	{p48}	70.7		0.01	72.7
	{p58}	72.6		0.1	70.9
	{p40}	70.4		1	69.9
	{p14, p40}*	69.6		10	69.2
	{p14, p48}	70.0		100†	69.0
	{p48, p40}	69.5		1000	69.0
	{p14, p58, p40}*	69.8		10000	71.2
	{p14, p48, p40}	69.9		100000	78.1
	{p48, p58, p40}	70.7	ℒ1 Regularization	0.001	74.2
	10 largest	75.2		0.01	72.6
				0.1	71.0
				1	69.5
				10	69.3
				100	69.2
				1000†	69.2
				10000	74.6
				100000	78.1

^*Parameter sets of differing sizes obtained from the parameter set selection procedure.

^†Optimal value of λ

Parameter set selection indicates that estimating only a few parameters can achieve similar cross validation MSE as estimating all parameters with Tikhonov or ℒ₁ regularization. If parameter correlations are ignored, {p₁₄, p₄₈} would be selected for estimation. While this set is a decent choice in this example, it is not the best set as shown in Table I. The best set of parameters selected for estimation for this particular example is the set {p₄₀, p₄₈}; p₄₀ is in a cluster by itself while p₄₈ is the representative parameter from the remaining three clusters and in fact this parameter has one of the largest sensitivity values. The quality of choosing this parameter set for estimation can be judged by it resulting in the lowest cross validation mean-squared error (MSE) as shown in Table I. Furthermore, it can be seen from the results that including more than two parameters for estimation does not improve prediction accuracy as the lowest MSE for any set of three parameters is larger than the MSE achieved by estimating the parameter set {p₄₀, p₄₈}.

The cross validation results indicate that estimating only two parameters using parameter set selection gives similar performance to estimating all parameters with either Tikhonov or ℒ₁ regularization. Moreover, when the 10 largest parameters are estimated with only box constraints on the parameters to constrain the estimates to positive values, the cross validation error increases and it is clear that too many parameters were estimated in the model. The modest changes in mean-squared error seen in this example are a reflection of the good choice of initial nominal parameter values; more drastic results are seen when the nominal parameter values do not allow the model to predict the data as well.

IV. CONCLUSION

Due to the large number of uncertain parameters and small amounts of available data which, furthermore, tend to be noisy, the parameter estimation problem in biochemical reaction networks requires some form of regularization to avoid over fitting the model to the data. The choice of regularization depends on the modeler’s preference and the desired qualities of the estimated parameters. The three techniques presented here work equally well to regularize the parameter estimation problem presented in this work; however, while this is often the case based upon the authors’ experience on a number of biochemical reaction network, there is no guarantee that this will always hold and each particular example may lead to slightly different conclusions. Although parameter estimation explicitly minimizes the difference between the model outputs and experimental data, cross validation should be employed to ensure that the model can predict new data well rather than simply reflect the current data.