Wind causes Totten Ice Shelf melt and acceleration

Wind upwells warm water from the deep ocean off the East Antarctic coast, leading to ice-shelf melt and glacier acceleration.

Abstract

Totten Glacier in East Antarctica has the potential to raise global sea level by at least 3.5 m, but its sensitivity to climate change has not been well understood. The glacier is coupled to the ocean by the Totten Ice Shelf, which has exhibited variable speed, thickness, and grounding line position in recent years. To understand the drivers of this interannual variability, we compare ice velocity to oceanic wind stress and find a consistent pattern of ice-shelf acceleration 19 months after upwelling anomalies occur at the continental shelf break nearby. The sensitivity to climate forcing we observe is a response to wind-driven redistribution of oceanic heat and is independent of large-scale warming of the atmosphere or ocean. Our results establish a link between the stability of Totten Glacier and upwelling near the East Antarctic coast, where surface winds are projected to intensify over the next century as a result of increasing atmospheric greenhouse gas concentrations.

INTRODUCTION

Totten Glacier drains a 550,000-km² ice basin whose base lies primarily below sea level (1), indicating potential vulnerability to rapid collapse (2, 3). The grounding line where Totten Glacier goes afloat to form Totten Ice Shelf (TIS) has recently retreated (4) while the ice-shelf velocity and terminus position have been unstable (5–7). The TIS surface showed a marked lowering trend from 2002 to 2008 (8, 9), which continued through at least 2012 in the grounded part of the glacier (10), but longer records of TIS surface elevation suggest that subdecadal trends may only represent part of a longer-term variability (6, 11).

Observed changes in TIS are thought to be driven by a variable supply of warm, salty, modified circumpolar deep water (mCDW) (5, 7, 12), which can access the water cavity below TIS through a network of bathymetric troughs (13). Ship-based observations have repeatedly shown a presence of mCDW along the outer continental shelf (14–17), and a recent survey confirmed the ability of mCDW to traverse the continental shelf and fill the troughs near the TIS ice front (18, 19). Ocean models have linked interannual variability of the TIS melt rate to sea-ice production, which generates cold, dense water that has the potential to displace mCDW and quench melt (20, 21); however, no such cold, dense water was detected at the time of the only survey conducted on the continental shelf (18, 19, 22). Observations and models both suggest that the TIS melt rate is modulated by a variable supply of mCDW, but the mechanism driving mCDW exchange across the continental shelf break has not yet been explained, and until now, no links between forcing mechanisms and TIS response have been directly observed. Insights into the drivers of TIS variability may lie in West Antarctica, where similar behaviors observed at Pine Island Ice Shelf have been hypothesized as resulting from a variable supply of CDW, forced onto the continental shelf by wind processes at the shelf break (23–26).

We investigate the causes of recent TIS acceleration and deceleration by comparing a 14-year time series of ice-shelf velocity to oceanic surface wind stress. We use ice-surface velocity as a proxy for melt-driven ice thickness change and as a direct measure of the response of TIS to variable forcing. The TIS velocity time series is generated by a template-matching algorithm applied to 629 satellite image pairs obtained between February 2001 and September 2014. Zonal and meridional components of wind stress are calculated from surface wind and sea-ice reanalysis data. We focus on local regions of upwelling, which develop where wind causes surface waters to diverge. Because of the effects of Earth’s rotation, surface water is transported 90° to the left of the wind direction in the southern hemisphere, so surface-water divergence is given by the mathematical curl of wind stress. We define upwelling as the vertical water velocity at the bottom of the surface layer, which we estimate from the wind stress curl.

RESULTS

To assess the TIS response to interannual forcing from the ocean, we limit velocity analysis to a region of the ice shelf laterally bounded by shear margins, between 20 and 40 km from the ice front, where we expect minimal influence from pinning points, calving processes, or velocity anomalies associated with lateral motion near the ice front (Fig. 1). Here, we see a 5% increase in surface velocity from 2001 to 2006 followed by an immediate trend reversal, slowing 6% by 2013 (Fig. 2B). Minor velocity minima occurred in 2005 and 2009, and minor maxima occurred in 2010 and 2014.

Fig. 1. Ice flow regime of TIS, 2001 to 2014.

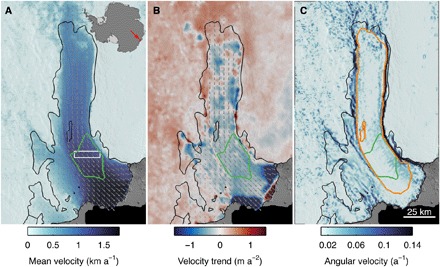
(A) Mean surface velocity from 2001 to 2014. A green polygon outlines the region of velocity measurements used in this analysis. A white box outlines the region used in a previous study by Roberts et al. (6). Inset map shows the location of TIS. (B) Linear trend of surface velocity indicates an overall slowdown of TIS from 2001 to 2014, whereas the surrounding grounded ice accelerated. Accelerations close to the ice front reflect calving processes. (C) The curl of the mean surface velocity is used to identify shear margins within TIS. The orange polygon outlines the region of surface velocities plotted in fig. S2B.

Fig. 2. Upwelling and ice-shelf velocity time series.

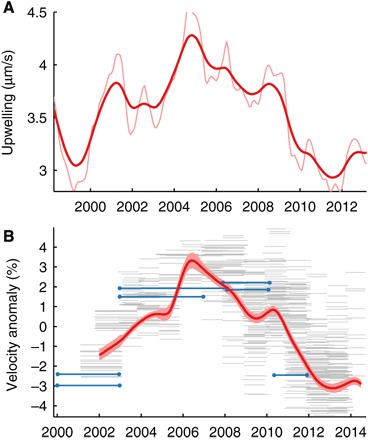
(A) Vertical water velocity at the bottom of the Ekman layer estimated from surface-water divergence caused by wind stress; plotted is the mean velocity within the gold polygon in Fig. 3D. Light and dark lines are low-pass–filtered to 12 and 24 months, respectively. (B) Dark red line is the ice velocity derived from 629 displacement measurements shown as thin gray lines bounded by the shaded region of estimated uncertainties (fig. S5). Blue lines are from displacement observations published in a previous study by Roberts et al. (6). The horizontal axis of (B) has been shifted relative to (A) to account for an observed 19-month lag.

With a 19-month lag, TIS velocity is negatively correlated with zonal wind throughout the domain (Fig. 3A), indicating that TIS accelerates in response to weakening of the eastward winds that drive the Antarctic Circumpolar Current or strengthening of the westward winds that drive the Antarctic Coastal Current. We assume that TIS velocity is linked to a variable supply of mCDW, and lag times are primarily due to the time required for melt-rate anomalies to integrate and cause sufficient thinning to produce an observable response in surface velocity (27). Over the deep ocean north of the continental shelf break, the negative correlation with zonal wind contrasts with the notion from classical Ekman dynamics that positive zonal wind anomalies should induce upwelling of warm deep water near 63°S. Over the continental shelf, westward winds are expected to induce southward transport of surface water, depress isotherms, and could therefore prevent mCDW from surmounting the continental shelf (28, 29), yet we provide evidence that competing processes prevail.

Fig. 3. Reanalysis fields and ice-shelf velocity.

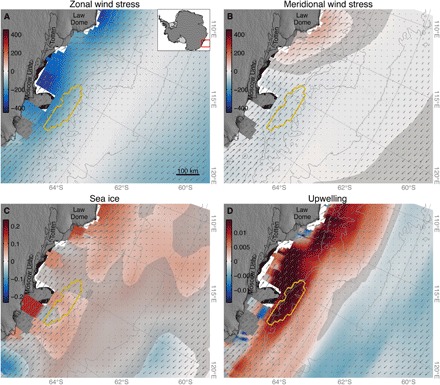
(A to D) Regression coefficients of linear least-squares fits of TIS velocity and zonal wind stress [μPa/(m a⁻¹)] (A), meridional wind stress [μPa/(m a⁻¹)] (B), sea-ice concentration [%/(m a⁻¹)] (C), and upwelling [(μm s⁻¹)/(m a⁻¹)] (D). All panels contain gray vectors representing mean wind velocity, gray 1-km bathymetric contours, and a gold polygon outlining the region of upwelling referred to in Fig. 2A. Gray shading denotes statistical insignificance at the 95% confidence level. Coefficients of determination are given in fig. S4.

Over the continental shelf, prevailing westward winds serve as the southern component of the wind stress curl, which causes upwelling along the continental slope. Thus, the negative correlation between TIS velocity and zonal wind over the continental shelf is associated with a positive correlation between TIS velocity and upwelling along the continental slope. Over the deep ocean, zonal winds maintain their negative correlation with TIS velocity, particularly where downwelling occurs in compensation for upwelling along the continental slope. These observations suggest that the meridional gradient of zonal wind stress contributes more to TIS velocity variability than do uniform zonal wind stress anomalies.

The mean coastal wind flow in the region is oriented such that its meridional component is small or nil with the exception of a northward flow diversion around Law Dome to the west of the TIS front. Throughout most of our region of study, where the meridional component of the mean velocity field is nearly zero, TIS velocity shows a weak but slightly negative relationship with meridional wind stress (Fig. 3B). Where coastal wind directs north around Law Dome, TIS shows a weak (r² < 0.2) positive correlation with meridional wind (fig. S4B). TIS velocity is positively correlated with sea-ice concentration throughout much of the domain, with small regions of negative correlation over the continental shelf and over the deep ocean (Fig. 3C). However, the relationship between sea-ice concentration and TIS velocity is quite weak (r² < 0.15) everywhere in the region (fig. S4C).

Linear regression of upwelling and TIS velocity reveals that TIS accelerates when upwelling is strong along the continental slope (Figs. 3D and 4). The relationship roughly follows bathymetric contours, indicating the role of seafloor topography in blocking mCDW intrusions when upwelling is weak. An upwelling zone bounded by a gold polygon in Fig. 3 lies upstream along the Antarctic Coastal Current and exhibits a particularly strong relationship with TIS velocity (r² > 0.85). This implies that TIS accelerates as a response to increased melt following strong upwelling anomalies along the continental slope. Correlation is maximized with a 19-month lag (fig. S3), indicating the time required for upwelled mCDW to traverse the continental shelf, enter the water cavity below TIS, induce melt, and lead to ice-shelf acceleration by reduced lateral shear stress.

Fig. 4. Schematic of mCDW upwelling along the Antarctica’s Sabrina Coast.

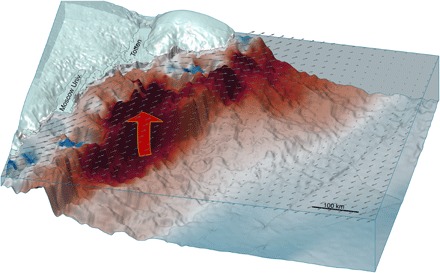
Around Antarctica, the warmest waters are found in the deep ocean north of the continental shelf break. Where wind stress (gray vectors) causes surface waters to part, warm deep water (red arrow) can upwell, surmount the continental shelf, and melt nearby ice shelves from below. Seafloor color depicts the covariance of TIS velocity and local upwelling as in Fig. 3D, indicating where wind-driven upwelling is closely linked to TIS velocity.

DISCUSSION

Oceanographic observations further implicate upwelling as the primary driver of mCDW variability on the continental shelf, where, between 450- and 650-m depth, temperature anomalies of 2°C or more can result from thermocline shoaling associated with upwelling along the nearby continental slope (fig. S1). The mean depth of the TIS base is 550 m in the region of our velocity time series observations, at which depth a +2°C temperature anomaly represents a sixfold increase in thermal driving potential relative to observed temperature minima of 0.4°C above the in situ freezing point. Models indicate that ice-shelf melt rates scale superlinearly to quadratically with thermal driving potential (30–32), suggesting that some areas of the TIS base can experience more than a 10-fold increase or decrease in melt rate depending on the availability of upwelled mCDW.

Profiling float and ship-based observations show a widespread presence of mCDW on the continental shelf, and the thickness of the mCDW layer is linked to upwelling along the continental slope. We posit that after mCDW surmounts the continental slope, the westward winds that drive the coastal current may enhance the delivery of mCDW to the water cavity below TIS, where the ice-shelf base is highly sensitive to small changes in thermal forcing (Fig. 4). Furthermore, a strengthened coastal current may flush cold meltwater from the cavity below TIS or intensify cavity circulation and increase melt (33).

Surface velocity averaged over the main trunk of TIS reached a maximum in early 2007, corresponding to a reported ice thickness minimum (6), when the lateral shear stress restraining TIS flow was minimized (fig. S2). The linear trend of TIS slowdown amidst ongoing acceleration of the surrounding grounded ice (Fig. 1B) is similar to a pattern seen at the Pine Island Glacier, whose ice shelf has shown a response to ocean forcing by accelerating approximately 9 months after thermal anomalies arrive at the ice front (27). The 19-month lag we observe from the time of upwelling along the continental slope to TIS acceleration includes the time required for mCDW to traverse the continental shelf. On average, TIS is much thicker than Pine Island Ice Shelf and is thus expected to respond more slowly to basal melt anomalies (27).

The region along the continental slope in which upwelling is highly covariant with TIS velocity is near a persistent eddy feature where dissolved silicate measurements have repeatedly revealed upwelling (14); warm, saline CDW has been detected (15, 16); and upwelling has been shown to be positively correlated with the Southern Annular Mode (SAM) (29). The SAM is the leading mode of climate variability in the southern hemisphere, it is seasonally influenced by various natural and anthropogenic drivers (34), and its positive mode is associated with an intensification of the eastward winds around Antarctica (35). In summer, the SAM has been trending toward its positive phase in recent decades primarily due to effects of ozone-depleting substances, but an increasing influence of atmospheric greenhouse gas is expected to dominate the SAM in the coming century and continue its positive bias as the ozone hole recovers (36, 37). Projections show an intensification of the wind-driven Antarctic Circumpolar Current and an increase in upwelling, particularly along the East Antarctic continental slope (36, 38, 39). It is possible that westward winds along the coast could weaken in conjunction with a southward migration of the divergence zone (39), in which case mCDW delivery to TIS could be tempered by a weakened coastal current; however, projections of coastal westward winds near TIS are few, and their relationships to SAM or atmospheric greenhouse gas have not been validated.

We have confirmed the role of wind-driven upwelling as a primary delivery mechanism for mCDW on the continental shelf of East Antarctica and have shown that mCDW upwelling is directly correlated with the melt-driven velocity of TIS. Wind patterns over the Southern Ocean are expected to evolve throughout the 21st century, and a shifting regime of upwelling could precipitate a marked response in Totten Glacier, unlocking the door to at least 3.5 m of eustatic sea-level potential (13) in the vast ice basin it drains.

MATERIALS AND METHODS

Ice velocity time series

The ice velocity time series was generated from displacement fields obtained for 363 MODIS (Moderate-resolution Imaging Spectroradiometer) band 2 image pairs (40) separated by 365 ± 29 days (referred to as M1 data herein) and 266 image pairs separated 730 ± 21 days (referred to as M2 data herein). Images were preprocessed with a Gaussian high-pass filter characterized by a 2-pixel SD and then supersampled by a factor of 2. Template matching was performed with ImGRAFT (41) for a 500-m resolution grid using a 10- × 10-pixel template and 20- × 20-pixel search box centered on displaced locations predicted by interferometric synthetic aperture radar–derived velocity fields (42). Displacement fields were postprocessed with a 3- × 3-pixel median filter, and the remaining grid cells with missing data were filled using a spring-metaphor inpainting technique (43).

M1 and M2 data were treated separately to allow direct comparison of velocity fields obtained over 1 and 2 years, respectively. M2 data provide lower uncertainty for slow-moving ice, whereas M1 data provide superior temporal resolution and perform best where ice moves fast, where motion is curvilinear, or where surface effects prevent matches separated by long periods of time.

An averaging technique was used to obtain velocities at monthly postings from 2001 to 2014. M1 and M2 data were treated separately, and for each monthly posting, an average velocity was calculated for all image pairs whose first image was obtained before the posting and whose second image was obtained after the posting. At least 14 image pairs contributed to M1 and M2 data at each monthly posting (fig. S5B). Velocity uncertainty σ at each monthly posting t was estimated as

$$\mathrm{\sigma }(\mathit{t})=\frac{{\mathrm{\sigma }}_{\mathit{N}}}{\sqrt{\mathit{N}}}$$ (1)

where σ_N is the SD of all N velocity measurements corresponding to time t, and N is the number of image pairs contributing to each monthly posting (44). The continuous ice velocity time series in this work was generated by the linear combination of low-pass–filtered M2 data and high-pass–filtered M1 data, where the crossover filtering period was 48 months for both data sets.

Ice-shelf thinning and acceleration

For a laterally bounded ice shelf under constant driving stress, small perturbations in ice thickness δH lead to changes in ice velocity δU by

$$\mathrm{\delta }\mathit{U}={\mathit{U}}_0[{\left(\frac{{\mathit{H}}_0}{{\mathit{H}}_0+\mathrm{\delta }\mathit{H}}\right)}^3-1]$$ (2)

where H₀ and U₀ are the nominal ice thickness and velocity, respectively (45). Figure S2 compares TIS velocity observations to predictions using Eq. 1, where U₀ is taken as the mean ice-shelf velocity within the orange polygon in Fig. 1C, H₀ = 1163 m is the mean ice thickness along the lateral shear margins of TIS (46), and δH is the time-varying ice thickness anomaly. We used an ice thickness time series derived from surface elevation measurements obtained by radar altimetry (6, 47) and followed an established procedure (8, 20) to remove the anomalies associated with accumulation (48) and firn densification (49). Surface elevation was converted to ice thickness assuming hydrostatic equilibrium, where the seawater density is 1028 kg/m³ and column-averaged ice density is 897 kg/m³, including a 22-m mean firn air thickness (49).

Profiling float data

Figure S1 shows a 15-month time series of the T = −0.4°C isotherm depth obtained by a profiling float. Geolocation of the profiling float was recorded for 29 surfacing events during data collection. Profile locations shown in fig. S1A (solid green line) indicate surfaced positions with a Global Positioning System fix. Linearly interpolated positions when the float was under ice between 5 April 2015 and 27 December 2015 were indicated by the green dashed line. Isotherm depth was determined by linear interpolation for each profile collected by the profiling float. The isotherm depth time series was linearly interpolated to daily postings, and then a first-order low-pass Butterworth filter was applied to account for the response of the lower layers to surface forcing. Filter cutoff periods of 45 and 90 days bracket expected response times (28), and both filtered time series agree well with upwelling time series filtered to the same periods.

Reanalysis data and upwelling estimation

This work used ERA-Interim monthly means of daily mean (50) sea-ice concentration and 10-m zonal and meridional wind components u₁₀ and v₁₀ generated at 0.75° resolution and regridded to 0.125° resolution. It has been shown that higher-resolution atmospheric models often produce stronger coastal winds (51, 52), but ERA-Interim matched observations well (53, 54) and was of sufficient resolution to capture the wind processes of interest to our analysis. Wind stress τ was calculated as

$$\mathrm{\tau }={\mathrm{\rho }}_{\text{air}}{\mathit{C}}_{\mathrm{D}}({\mathit{u}}_{10}^2+{\mathit{v}}_{10}^2)$$ (3)

where ρ_air = 1.225 kg/m³ is the density of air, and C_D = 1.25 × 10^{− 3} is the drag coefficient in the absence of sea ice (55) and is parameterized when sea ice is present (56). Seasonal cycles were removed, and time series of each grid cell were low-pass–filtered with a cutoff period of 24 months using a first-order Butterworth filter. Ekman pumping was calculated as the vertical velocity of water induced by surface-water divergence using the relation

$${\mathit{w}}_{\mathrm{E}}= \text{curl}\left(\frac{\mathrm{\tau }}{{\mathrm{\rho }}_{\mathrm{w}}\mathit{f}}\right)$$ (4)

where ρ_w = 1028 kg/m³ is the density of seawater, and f is the Coriolis frequency (57).

Mapping and figure generation

Data analysis was performed using Antarctic Mapping Tools for MATLAB (58), and graphics in this paper used cmocean (59) color maps. Background images in Figs. 1 and 3 and figs. S1 and S4 were from the MODIS Mosaic of Antarctica (60, 61), grounding lines were from MEaSUREs radar mapping (62), and bathymetric contours were from the IBCSO (International Bathymetric Chart of the Southern Ocean) (63).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/11/e1701681/DC1

fig. S1. Upwelling brings warm water onto the continental slope.

fig. S2. Ice-shelf thinning drives acceleration.

fig. S3. Regression of upwelling and TIS velocity.

fig. S4. Coefficients of determination.

fig. S5. Uncertainty estimates for TIS velocity time series.