Accurate Prediction of the Hydration Free Energies of 20 Salts through Adaptive Force Matching and the Proper Comparison with Experimental References

Abstract

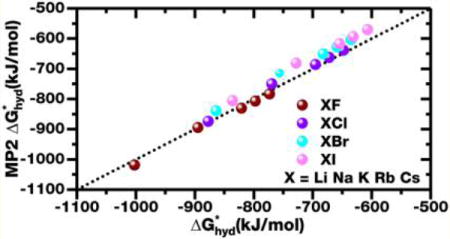
Simple pairwise potentials for five alkali ions and four halide ions were developed by only fitting to ab initio MP2 forces with the adaptive force matching (AFM) method. Without fitting to any experimental information, the AFM models predict the hydration free energies of all 10 fluoride and chloride salts formed by these ions within 1.5% of experimental references. The predicted hydration free energies for the 10 bromide and iodide salts are within 5–6% of experimental references with the larger error likely due to the neglect of explicit treatment of polarization and charge transfer. An inconsistency in the treatment of the gas phase entropy term between experimental and theoretical approaches is discussed. A new simplified hydration free energy for the ions is reported for use as a more appropriate experimental reference for further theoretical studies. The simulations show different dipole alignments for the hydration waters of cations and anions. While hydration waters of small cations tend to align their molecular dipole toward the ion, the dipole of one of the water OH bonds is aligned with the field of an anion.

Graphical Abstract

1. INTRODUCTION

Molecular modeling has increasingly established its value in a broad range of topics in physics, chemistry, and biology. Significant progress has been made in recent years both in methodology development and in available computational power, leading to the solution of many problems not previously amenable to modeling. Despite the numerous advances, some seemingly simple problems are still evasive to solve based purely on first-principles. One example is the prediction of the hydration free energies of simple ions and salts.^1–6

The importance of properly modeling ion hydration is well recognized.^7–12 Most proteins require a certain ionic strength to remain stable and perform their biological functions. Ligand binding and biological activities are frequently associated with the displacement of ions from the active site to the solution.¹³ Accurate modeling of the roles of the ions requires a potential that gives accurate hydration free energies.^14,15 In fact, the hydration free energies of ions are frequently fitted directly in the development of ion potentials.^16,17

It is important to note that fitting hydration free energies is not straightforward. Since single ion hydration free energies are not measurable in a condensed phase experiment, proper execution of such a fit requires the use of a number of correction terms. Even the sign of some of the correction terms is being debated.^18,19

Many groups have attempted to predict the ion hydration free energies from a first-principles based approach without experimental input.^6,20–22 One possible solution is with the adaptive force matching (AFM) method developed by our team.^23–26 Recently, with the AFM method, force fields have been developed for Na⁺, K⁺, F⁻, Cl⁻, and Br⁻, which correctly predicted the hydration free energies of the six different salts formed by these ions within a few percent of experimental values.^24,27,28 Since no experimental properties were used during the parametrization of the force fields, the good prediction of hydration free energies and other properties²⁴ is a good testament for the overall accuracy of the AFM based potentials.

Unlike most other potentials for ions, these AFM based models do not use the nominal charges of the ions as the ionic charge parameter. This is justified, since these potentials are not modeling the polarization effects explicitly.²⁹ As pointed out by Leontyev and Stuchebrukhov,³⁰ such an implicit consideration of polarization results in the optimal partial charges to be scaled by $\sqrt{1/{\epsilon }_{\mathrm{\infty }}}$, where ε_∞ is the high frequency dielectric constant of water as a result of electronic polarization. The ε_∞ of water is 1.78, which leads to an effective charge of 0.750 e for a monovalent ion. This is actually fairly close to the 0.804 e ionic charges determined by AFM in our previous investigations.²⁴

One way to understand this scaled charge is by recognizing that Coulombic interactions in a medium with a dielectric constant, ε_∞, can be written as

$$U=\frac{1}{4\pi {\epsilon }_0{\epsilon }_{\mathrm{\infty }}}\frac{q_1{q}_2}{r_{12}}=\frac{1}{4\pi {\epsilon }_0}\frac{q_1^e{q}_2^e}{r_{12}}{q}_1^e=\frac{q_1}{\sqrt{{\epsilon }_{\mathrm{\infty }}}}{q}_2^e=\frac{q_2}{\sqrt{{\epsilon }_{\mathrm{\infty }}}}$$ (1)

In an aqueous solution, ε_∞ is the high frequency contribution to the water dielectric constant as a result of electronic polarization, which for a nonpolarizable potential is better approximated as a dielectric continuum. When the contribution from ε_∞ is treated implicitly by a dielectric continuum, the MD code should divide the Coulombic energy by ε_∞, as shown in eq 1. However, most MD codes are not implemented in a way to explicitly consider the dielectric constant of the medium; thus, an alternative approach would be to scale all charges by $\sqrt{1/{\epsilon }_{\mathrm{\infty }}}$, which will effectively capture the same Coulombic energy using the dielectric of the vacuum.

The 0.804 e charge in the AFM models was determined as the average absolute charge of Na⁺, K⁺, Cl⁻, and Br⁻. Recently, we completed the development of the AFM models for the five alkali ions from Li⁺ to Cs⁺ and four halide ions from F⁻ and I⁻. The average absolute charge from these nine ions is 0.766 e in much better agreement with the proposed value of 0.75 e by Leontyev and Stuchebrukhov.³⁰

As we were working on the new potentials, we noticed a common mistake when a simulated hydration free energy is compared to experiments including our previous work. Most comparisons between experimental and simulated hydration free energies ignored the entropy term of the gas phase reference state, which was included in most published experimental hydration free energies.³¹ This leads to an error of around 35 kJ/mol for cations and around 15 kJ/mol for anions. Such an error is no longer negligible when quantitative prediction of hydration free energies can be accomplished with AFM models.

With the proper consideration of the entropy term and the 0.766 e charge, the AFM models are capable of predicting the hydration free energies of all 10 fluoride and chloride salts to 1.5%. For bromide and iodide salts, the average unsigned error in the prediction increases to approximately 4.6–5.6%, respectively. These later period anions have large polarizabilities and small electron affinities; it is thus anticipated a simple point charge based nonpolarizable potential as we developed may lead to larger discrepancies due to the implicit treatment of polarization and the complete neglect of charge transfer.

When the gas phase entropic term is properly accounted for, ion models with the previously determined 0.804 e charge also give a good agreement with experimental hydration free energies of the salts. However, the mean unsigned error for the 20 salts is slightly worse by about 0.7%. The previous better agreement for the two bromide salts was partly due to an accidental cancellation of errors when the gas phase entropic term was missing.

In this paper, we will discuss the gas phase entropy term in section 2, the AFM force field development procedure will be briefly reviewed in section 3, the calculation of the hydration free energy and the proper choices of correction terms will be briefly summarized in section 4, and the results and conclusion will be presented in section 5.

2. PROPER COMPARISON BETWEEN SIMULATED AND EXPERIMENTAL HYDRATION FREE ENERGIES

For an ion X, the free energy of hydration ΔG_hyd can be calculated from the free energies of formation ΔG_f through the formula

$$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}(\mathrm{X})=\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{aq})-\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{g})$$ (2)

In eq 1, the free energy of formation of the ion in the aqueous solution, $\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{aq})$, is available from thermodynamic tables, whereas standard thermodynamic tables typically do not provide the free energy of formation of the ions in the gas phase, $\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{g})$, and only list the gas phase enthalpy of formation, $\mathrm{\Delta }{H}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{g})$.

In order to obtain $\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{g})$, the entropy of the ion in the gaseous state has to be determined.³¹ For an ion X, the translational contribution to the single particle partition function is

$$q={\left(\frac{\sqrt{2\pi {\mathit{mk}}_{\mathrm{B}}T}}{h}\right)}^3\frac{\mathit{RT}}{P^{\mathrm{\ominus }}}$$ (3)

where m is the mass of the particle and the partition function is derived by integrating the number of states of a quantum mechanical particle in a box with the ideal gas volume under the standard temperature T and pressure p^⊖. Using the standard formula, the entropy for 1 mol of an ideal gas can be expressed as

$$S=\frac{5}{2}R+R\text{ln}\left(\frac{q}{N_{\mathrm{A}}}\right)$$ (4)

where N_A is Avogadro’s number arising from the indistinguishability of the particles.

If one chooses 298.15 K as the standard temperature and 1 bar as the standard pressure, it can be shown with eq 4 that the translational contribution to the entropy is

$$S_{\mathrm{trans}}^{\mathrm{\ominus }}=108.8553+12.4717\text{ln}\frac{m}{\mathrm{amu}}\mathrm{J}/(\mathrm{mol}\cdot \mathrm{K})$$ (5)

where amu is the atomic mass unit.

Since it is customary to define $\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}$, $\mathrm{\Delta }{H}_{\mathrm{f}}^{\mathrm{\ominus }}$, and S^⊖ for the H⁺ in an aqueous solution to be zero, it will not be appropriate to only use the translational entropy as the gas phase entropy of the ion when calculating $\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{g})$. Otherwise, it will lead to consistency issues.³²

To avoid consistency problems, the thermodynamic entropy for a proton in the gas phase becomes

$$S_{\mathrm{f}}^{\mathrm{\ominus }}({\mathrm{H}}^{+},\mathrm{g})=S_{\mathrm{trans}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})-\frac{1}{2}{S}^{\mathrm{\ominus }}({\mathrm{H}}_2)+S^{\mathrm{\ominus }}(\mathrm{e})$$ (6)

where S^⊖(H₂) is the entropy of H₂ gas in the standard state and the standard state entropy of the electron is

$$S^{\mathrm{\ominus }}(\mathrm{e})=108.8553+12.4717\text{ln}(5.4858\times {10}^{-4})+R\text{ln}2=20.9787\mathrm{J}/(\mathrm{mol}\cdot \mathrm{K})$$ (7)

The last term in S^⊖(e) is due to the spin degeneracy of the electron.

For a cation X⁺, the thermodynamic entropy becomes

$$S_{\mathrm{f}}^{\mathrm{\ominus }}({\mathrm{X}}^{+},\mathrm{g})=S_{\mathrm{trans}}^{\mathrm{\ominus }}({\mathrm{X}}^{+})-S^{\mathrm{\ominus }}(\mathrm{X})+S^{\mathrm{\ominus }}(\mathrm{e})$$ (8)

where S^⊖(X) is the standard state entropy of the corresponding metal. For anions, the corresponding standard state entropy becomes

$$S_{\mathrm{f}}^{\mathrm{\ominus }}({\mathrm{X}}^{-},\mathrm{g})=S_{\mathrm{trans}}^{\mathrm{\ominus }}({\mathrm{X}}^{-})-\frac{1}{2}{S}^{\mathrm{\ominus }}({\mathrm{X}}_2)-S^{\mathrm{\ominus }}(\mathrm{e})$$ (9)

where S^⊖(X₂) is the standard state entropy of the element in its most stable thermodynamic state, which ranges from gas to solid for the four anions studied in this paper.

When the hydration free energy is determined in an MD simulation, the typical approach would be to remove the ions from the solution and integrate the free energy change associated with such a process.^33,34 In this case, the quantum translational entropy of the gas is not included in the computational measurements. In addition, the contribution from the entropy of the elements and from the electron is not typically incorporated when theoretical estimates were obtained from simulations. When comparing the computational hydration free energies and those determined by experiments through eq 1, it is thus important to be consistent with regard to the treatment of the gas phase entropy term.

With a standard thermodynamic integration method, the simulation is effectively measuring

$$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }(\mathrm{X})=\mathrm{\Delta }{G}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{aq})-\mathrm{\Delta }{H}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{X},\mathrm{g})$$ (10)

which will be referred to as the simplified hydration free energy and will be distinguished from the thermodynamic hydration free energy, $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}(\mathrm{X})$, by a star.

Using the standard thermodynamics tables, such as those published by the CRC Press,³² the hydration free energies of the salts can be reliably obtained by simple summations of the hydration free energies of the ions. With the widely accepted thermodynamic table published by the CRC, the hydration free energy of the hydronium $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$ would be −1516.9 kJ/mol. However, due to challenges in determining single ion hydration free energies, there are vastly different estimates for $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$. For example, the commonly used reference values by Tissandier et al. put the $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$ at −1104.5 kJ/mol.³¹

To obtain ion hydration free energies consistent with the Tissandier $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$ reference, an offset

$$\mathrm{\Delta }{G}_{\mathrm{offset}}^{\mathrm{\ominus }}=n\cdot (-1104.05+1516.9)=412.4\cdot n\mathrm{kJ}/\mathrm{mol}$$ (11)

has to be added to all single ion hydration free energies obtained from CRC, where n is the nominal charge of the ion, with anions taking negative values.

Since the large experimental uncertainty is only present for single ions, the free energy offset, $\mathrm{\Delta }{G}_{\mathrm{offset}}^{\mathrm{\ominus }}$, has no effect on the hydration free energy of the salts. Table 1 summarizes the experimental hydration free energies, $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}$ and $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$ of the ions with the two different $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$ references, one from CRC and the other from the Tissandier work. The translational entropy and the thermodynamic entropy of the ions in the gas phase are also reported for convenience.

Table 1.

Translational and Thermodynamic Entropies (J/(mol·K)) for Nine Ions in the Gas Phase, along with the Corresponding Standard and Simplified Hydration Free Energies (kJ/mol) Calculated On the Basis of the CRC and Tissandier $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$ References

			based on CRC		based on Tissandier
ions	$\mathrm{\Delta }{S}_{\mathrm{trans}}^{\mathrm{\ominus }}$	$\mathrm{\Delta }{S}_{\mathrm{f}}^{\mathrm{\ominus }}(\mathrm{g})$	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}$	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}$	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$
Li+	133.02	124.88	−941.76	−978.99	−529.36	−566.59
Na+	147.96	117.72	−836.11	−871.21	−423.71	−458.81
K+	154.58	111.38	−764.28	−797.49	−351.88	−385.09
Rb+	164.33	108.53	−741.68	−774.04	−329.28	−361.64
Cs+	169.84	105.59	−718.46	−749.94	−306.06	−337.54
F−	145.58	23.21	−16.53	−23.44	−428.93	−435.84
Cl−	153.36	20.85	108.07	101.86	−304.33	−310.54
Br−	163.49	66.40	134.86	115.07	−277.54	−297.33
I−	169.26	90.22	169.88	142.99	−242.52	−269.41

The simplified hydration free energy, $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }(\mathrm{X})$, is the most convenient experimental reference to be used as benchmarks for theoretical calculations. This reference will eliminate the need to explicitly calculate the gas phase thermodynamic entropy, which has contribution from the entropy of the corresponding element. For comparison to the $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$ of the salts, $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$ calculated with either reference $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$ can be used. The appropriate offset term has to be included when comparing to the specific $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$ of the ions, which will be discussed in more detail in section 4.

3. DEVELOPMENT OF ION–WATER POTENTIALS WITH THE ADAPTIVE FORCE MATCHING METHOD

The adaptive force matching (AFM) method was used to develop force fields for all of the hydrated ions. The aqueous environment was modeled using the BLYPSP-4F water potential²³ also created with AFM by fitting to coupled-cluster quality forces obtained with the density functional theory-supplemental potential (DFT-SP) approach.^35,36 The water model was not reoptimized when developing the interaction terms for hydrated ions.

The AFM method refines a force field using an iterative approach to best mimic the condensed phase forces of the reference electronic structure method. Each iteration of AFM contains three steps, the sampling step, the quantum mechanics/molecular mechanics (QM/MM) step, and the force matching (FM) step. Details of the AFM method and the specifics for the development of the ion–water cross-terms have been reported previously.²⁴ Only a brief summary of key details is presented here.

For the development of the ion–water potentials, the sampling step was accomplished by a 5 ns MD simulation with a single ion in a cubic box containing 1000 water molecules. 100 configurations were obtained from the sampling step in each generation of AFM.

The sampling step creates a set of configurations that has the proper thermodynamic weight, thus maximizing the accuracy of the model for simulations under similar thermodynamic conditions. The iterative procedure enables the improved force fields to be used for sampling, thus minimizing biases that could be introduced if the initial sampling force field was not sufficiently accurate.

In the QM/MM step, the ion and part of its hydration structure were taken as the QM region, which was embedded in an MM region through Coulombic embedding. The inclusion of the large MM region ensures the QM particles feel a condensed phase environment, thus providing better approximations of the true condensed phase forces.

The procedure for the selection of the QM region has been reported previously. The Li⁺, Na⁺, and K⁺ were modeled with the aug-cc-pCVTZ basis set,^37–39 and Rb⁺ and Cs⁺ were modeled with the Def2-TZVPP basis set with the associated effective core potentials (ECP).⁴⁰ For anions, the aug-cc-pVTZ basis sets were used,⁴¹ except for I⁻. The I⁻ was modeled with the aug-cc-pVTZ-PP⁴² basis set and the associated ECP.

The energy expressions for the ion–water potential include a Buckingham term, U = Ae^−αr + C₆/r⁶, between the ion and the water oxygen, and an exponential repulsion term, U = Be^−βr, between the ion and the sites on water that carry the opposite charge. Thus, for cations, a repulsion term will be placed between the ion and the BLYPSP-4F M site, and for anions, a repulsion term will be placed between the ion and the water hydrogen atoms.

Whereas each generation of AFM only used 100 configurations, 7 generations of AFM were performed for each ion and the final 4 converged generations were fit together in a global fit. The parameters from the global fit are the final parameters of AFM.

It has been shown that, for alkali ions, the proper choices of basis sets and core–valence orbitals in the MP2 calculations are important to ensure the reference forces are of sufficient quality.²⁷ In addition, all ion–water C₆ parameters were determined using SAPT^43,44 by fitting to the gas phase E2 energy of the ion and an isolated water molecule with the aug-cc-pVTZ basis set.^37,41 The use of SAPT for the determination of C₆ is preferred, since a relatively small QM region was used during AFM and the dispersion showing strong higher order contributions at short distances as discussed previously.²⁴

Table 2 shows the parameters from AFM for the ions, Li⁺, Na⁺, K⁺, Rb⁺, Cs⁺, F⁻, Cl⁻, Br⁻, and I⁻. When performing AFM iterations, each ion was fit separately. This led to slightly different partial charges for the ions. The average of all nine single ion charges was 0.766 e. In order to ensure all of the ion potentials can be used together for salt simulations, the global fit for each ion is then performed with the charge value constrained to 0.766 e. Our previous study used a partial charge of 0.804 e, which was the average of the charges for Na⁺, K⁺, Cl⁻, and Br⁻. For all of the ions, parameters with a charge constraint of 0.804 e were also obtained. The objective of the 0.804 e fit is to show that the calculated hydration free energy has only a negligible dependence on the charge constraint, thus indicating that our use of the scaling term is properly justified. The parameters for all the ion–water terms with charge constraints of 0.766 and 0.804 e are reported in Tables 3 and 4. We recommend the models with a charge constraint of 0.766 e to be used for further studies. Twenty cross-terms between all cation and anion pairs with the 0.766 e partial charge are reported in Table 5.

Table 2.

Parameters of the Nine Ions from AFM

ion	qI (e)	A (kcal/mol)	C6 (Å6 kcal/mol)	α (Å−1)	B (kcal/mol)	β (Å−1)
Li+	0.8280	80081.0	−16.622	5.327	127575.8	5.419
Na+	0.8017	184008.6	−52.306	4.941	143703.6	4.816
K+	0.7840	292779.4	−555.769	4.414	187540.4	4.255
Rb+	0.7737	417099.7	−872.046	4.308	203649.3	4.045
Cs+	0.7945	295318.7	−1406.694	3.921	202737.3	3.826
F−	−0.7199	293042.1	−749.507	4.310	1282.7	3.764
Cl−	−0.7077	307900.0	−2038.906	3.768	4439.4	3.604
Br−	−0.7317	313163.8	−2750.986	3.630	3875.3	3.229
I−	−0.7539	199348.5	−4001.420	3.287	7788.2	3.225

Table 3.

Parameters of the Nine Ions from AFM with a 0.766 e Charge Constraint

ion	qI (e)	A (kcal/mol)	C6 (Å6 kcal/mol)	α (Å−1)	B (kcal/mol)	β (Å−1)
Li+	0.766	267969.8	−16.622	6.147	103715.6	5.264
Na+		281270.9	−52.306	5.191	133547.9	4.762
K+		371741.2	−555.769	4.531	186128.0	4.241
Rb+		478286.7	−872.046	4.369	229419.4	4.088
Cs+		398208.6	−1406.694	4.052	197937.1	3.800
F−	−0.766	402512.0	−749.507	4.478	976.7	3.386
Cl−		454494.9	−2038.906	3.936	2624.7	3.205
Br−		412658.7	−2750.986	3.741	2833.4	3.016
I−		214558.9	−4001.420	3.315	7084.5	3.169

Table 4.

Parameters of Nine Ions from AFM with a 0.804 e Charge Constraint

ion	qI (e)	A (kcal/mol)	C6 (Å6 kcal/mol)	α (Å−1)	B (kcal/mol)	β (Å−1)
Li+	0.804	128092.1	−16.622	5.648	113734.1	5.338
Na+		182800.2	−52.306	4.936	154550.0	4.854
K+		237099.0	−555.769	4.309	231065.1	4.356
Rb+		324467.5	−872.046	4.190	274512.2	4.178
Cs+		293130.8	−1406.694	3.914	230300.5	3.877
F−	−0.804	576290.0	−749.507	4.660	830.7	3.141
Cl−		659307.4	−2038.906	4.091	1961.5	2.976
Br−		623457.6	−2750.986	3.903	2050.0	2.793
I−		272777.7	−4001.420	3.410	4833.8	2.951

Table 5.

20 Cross-Terms between Ions to Be Used with the 0.766 e Model^a

ion	F−	Cl−	Br−	I−
Li+	41972.7	30540.7	27067.5	23068.0
	4.879	3.704	3.383	2.987
Na+	80571.1	68475.5	26224.8	54828.3
	4.465	3.625	3.063	3.086
K+	85585.8	144419.6	114780.2	83845.8
	3.938	3.520	3.261	2.937
Rb+	179949.6	102572.2	89063.7	83986.8
	4.062	3.179	2.950	2.739
Cs+	107859.5	547025.2	79182.1	238926.1
	3.655	4.188	2.778	3.024

^aThe two numbers in each cell are A (kcal/mol) (upper) and α (Å⁻¹) (lower) in the Buckingham potential. The C₆ term is always approximated to be zero due to the small cation polarizability.

4. CALCULATION OF THE HYDRATION FREE ENERGIES

In this work, the simplified hydration free energy, $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$, will be used as the experimental reference, thus eliminating the need to explicitly consider the gas phase entropy. As discussed previously,²⁴ the use of scaled ionic charges led to the gas phase enthalpy being different from those used as experimental references. For the determination of the experimental $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$, the gas reference state used for eq 1 is ions with the true valence charge, whereas the simulated hydration free energy corresponds to a dehydration to a gas state with the scaled charge. It has been shown that the simulated hydration free energy has to be scaled by

$$f=\frac{{q_{\mathrm{I}}}^2\cdot (1-1/{\epsilon }_{\mathrm{w}})}{{q_{\mathrm{I}\_\mathrm{m}}}^2\cdot (1-1/{\epsilon }_{\mathrm{w}\_\mathrm{m}})}$$ (12)

where the ε_w and ε_{w_m} are, respectively, the experimental and model dielectric constant of water. q₁ is the true ionic charge and q_{I_m} is the ionic charge of the model. With a q_{I_m} of 0.766 e, the scaling factor f calculated by eq 12 is 1.723. For the 0.804 e ionic charge, the scaling factor becomes 1.565.

With the scaling factor, the theoretical $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\ast }$ can be calculated with the formula

$$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\ast }=\mathrm{\Delta }{G}_{\mathrm{sim}}\cdot f+\mathrm{\Delta }{G}_{\mathrm{corr}}+\mathrm{\Delta }{G}_{\mathrm{offset}}$$ (13)

where ΔG_sim is the simulated hydration free energy. In this work, ΔG_sim was calculated with the Bennett acceptance ratio method as implemented in GROMACS.^45,46 The free energy integration was performed by removing a single ion from a box containing 2224 water molecules in 41 λ windows. The ion was converted to a neutral particle by removing its partial charges in 21 λ windows and then eliminated sterically in another 21 λ windows. Each λ window was simulated with 2 ns of MD under constant temperature and pressure.

The need for the correction term, ΔG_corr, has been well documented in the literature.^6,33,34,47 For neutral systems, such as salt solutions, the correction term, ΔG_corr, includes the concentration and pressure term, ΔG_cp, and the lattice sum term, ΔG_LS. The ΔG_cp term accounts for the fact that the concentration of the simulation box is not at 1 M and the gas phase particle removed is not at 1 bar according to the ideal gas law. Since both the ion concentration and gas phase pressure are inversely proportional to the volume, it can be shown that this term

$$\mathrm{\Delta }{G}_{\mathrm{cp}}=\mathit{RT}\text{ln}\frac{c_0}{c_l}+\mathit{RT}\text{ln}\frac{p_{\mathrm{g}}}{p_0}$$ (14)

reduces to 7.96 kJ/mol for all of the systems of interest.

The lattice sum term arises due to the interaction of a charged particle with its periodic images through Ewald summation. This term can be calculated as

$$\mathrm{\Delta }{G}_{\mathrm{LS}}=\frac{N_{\mathrm{A}}{q_{\mathrm{I}}}^2\xi }{8\pi {\epsilon }_{0}L}\cdot (1-\frac{1}{{\epsilon }_{\mathrm{s}}})$$ (15)

ξ is −2.837297 for a cubic box³³ as used in this work. The GROMACS code used to perform the thermodynamic integration already considers the contribution from the first term of eq 15; thus, only the second term is explicitly considered with a ε_s value of 42.9, which is that of BLYPSP-4F water.⁴⁸

For charged particles, additional correction terms are generally used in the literature. This includes the ΔG_ODL term, which corrects for another artifact of the Ewald summation,⁴⁹ and the ΔG_surf term, which accounts for the free energy for moving the charged ion from the solution to the gas phase through the liquid–vapor interface. In this work, we will only include the ΔG_ODL term, which is defined as

$$\mathrm{\Delta }{G}_{\mathrm{ODL}}=-q_{\mathrm{I}}\frac{1}{6{\epsilon }_0}{\rho }_{\mathrm{n}}\gamma$$ (16)

where γ and ρ_n are the quadruple moment and the number density of water, respectively.

With this term, the sum of ΔG_sim·f and ΔG_corr is generally referred to as the intrinsic hydration free energy.³⁴ We will not explicitly consider the ΔG_surf term; rather, we combine it with the uncertainty in the single ion hydration free energy, which can be accounted for by the ΔG_offset term.

As discussed previously, an offset term, ΔG_offset, can be used to compensate for the difference in the reference hydronium hydration free energies used in the literature. Since the ΔG_offset used for the cations is exactly the opposite of that used for the anions, it cancels exactly for the salts. For single ions, we will set a ΔG_offset so that for Li⁺ the $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$ from our calculation is identical to that reported in Table 1 based on the Tissandier estimate of $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus }}({\mathrm{H}}^{+})$.

We chose to use Li⁺ rather than developing a potential for hydronium due to complications in creating a good model for describing the hydration of a proton. This complication arises from the indistinguishability of the proton and the nucleus of the hydrogen atom in water. Several models, such as hydronium (H₃O⁺), eigen (H₉O₄⁺), or zundel (H₅O₂⁺), have been proposed and argued to best represent the proton hydration structure in aqueous solution.^50–53 Modeling these charge delocalized species is more complicated and will be postponed to our future work.

5. RESULTS AND DISCUSSION

The $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$ of the 20 salts are reported in Table 6 for the two models with different ionic charge constraints. With the 0.766 e ionic charge, the mean unsigned error (MUE) is 1.26% for all of the salts formed by the F⁻ and Cl⁻ ions, showing excellent agreement with the experimental reference. For the Br⁻ and I⁻ salts, the agreement is very good with MUE being 4.56 and 5.58%, respectively. The agreement with the 0.804 e charge is similarly good with MUE for the F⁻ and Cl⁻ salts being 1.50%, only slightly worse than the models with the 0.766 e charge. This is probably due to the fact that the repulsion term fitted with AFM compensates for the difference in Coulombic attraction between the ion and the partial charges on water. In addition, such a good agreement will not be possible unless our derivation of the scaling factor f is appropriate.

Table 6.

Hydration Free Energies (kJ/mol) of 20 Salts with Different Charge Models

		0.766 e			0.804 e
ion	$\mathrm{\Delta }{G}_{\exp }^{\mathrm{\ominus },\ast }$	ΔGsim	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$	Err %	ΔGsim	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$	Err %
LiF	−1002.43	−601.12	−1018.30	1.58	−649.97	−1000.04	−0.24
LiCl	−877.13	−517.14	−873.62	−0.40	−560.47	−859.94	−1.96
LiBr	−863.92	−496.85	−838.67	−2.92	−537.51	−824.01	−4.62
LiI	−836.00	−477.37	−805.12	−3.69	−516.72	−791.46	−5.33
NaF	−894.65	−529.11	−894.25	−0.05	−575.78	−883.91	−1.20
NaCl	−769.35	−445.13	−749.57	−2.57	−486.28	−743.82	−3.32
NaBr	−756.14	−424.84	−714.62	−5.49	−463.32	−707.88	−6.38
NaI	−728.22	−405.36	−681.07	−6.48	−442.53	−675.33	−7.26
KF	−820.93	−492.03	−830.37	1.15	−533.50	−817.73	−0.39
KCl	−695.63	−408.05	−685.70	−1.43	−444.00	−677.63	−2.59
KBr	−682.42	−387.76	−650.75	−4.64	−421.04	−641.69	−5.97
KI	−654.50	−368.28	−617.19	−5.70	−400.25	−609.14	−6.93
RbF	−797.48	−478.45	−806.97	1.19	−518.62	−794.44	−0.38
RbCl	−672.18	−394.47	−662.30	−1.47	−429.12	−654.34	−2.65
RbBr	−658.97	−374.18	−627.35	−4.80	−406.16	−618.40	−6.16
RbI	−631.05	−354.70	−593.79	−5.90	−385.37	−585.85	−7.16
CsF	−773.38	−464.56	−783.05	1.25	−505.41	−773.76	0.05
CsCl	−648.08	−380.58	−638.37	−1.50	−415.91	−633.66	−2.22
CsBr	−634.87	−360.29	−603.42	−4.95	−392.95	−597.72	−5.85
CsI	−606.95	−340.81	−569.86	−6.11	−372.16	−565.18	−6.88

Table 7 shows the single ion hydration free energies for both models. The ΔG_offset for the 0.766 e and the 0.804 e models were 55.28 and 55.33 kJ/mol, respectively. The perfect agreement for Li⁺ is by design. It is clear that, for all the cations and for F⁻ and Cl⁻, the AFM derived pairwise nonpolarizable potentials provide excellent predictions of the experimental hydration free energies with only MP2 forces as references. The agreement for Br⁻ and I⁻ is poorer with the 0.766 e model underestimating the experimental $\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$ by 25.3 and 30.9 kJ/mol, respectively.

Table 7.

Hydration Free Energies (kJ/mol) of Nine Ions with Different Charge Models^a

		0.766 e			0.804 e
ion	$\mathrm{\Delta }{G}_{\exp }^{\mathrm{\ominus },\ast }$	ΔGsim	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$	Err %	ΔGsim	$\mathrm{\Delta }{G}_{\mathrm{hyd}}^{\mathrm{\ominus },\ast }$	Err %
Li+	−566.59	−255.86	−566.59	−0.00	−279.11	−566.59	−0.00
Na+	−458.81	−183.85	−442.54	−3.55	−204.92	−450.46	−1.82
K+	−385.09	−146.77	−378.66	−1.67	−162.64	−384.27	−0.21
Rb+	−361.64	−133.19	−355.26	−1.76	−147.76	−360.98	−0.18
Cs+	−337.54	−119.30	−331.34	−1.84	−134.55	−340.31	0.82
F−	−435.84	−345.26	−451.71	3.64	−370.86	−433.45	−0.55
Cl−	−310.54	−261.28	−307.04	−1.13	−281.36	−293.36	−5.53
Br−	−297.33	−240.99	−272.08	−8.49	−258.40	−257.42	−13.42
I−	−269.41	−221.51	−238.53	−11.46	−237.61	−224.87	−16.53

^aThe experimental reference is from the Tissander work.³¹

Since the two ions, Br⁻ and I⁻, have significantly larger polarizabilities, it is likely that the implicit treatment of ion polarization leads to larger errors. In addition, charge transfer to solvent might be most significant for these anions with more diffuse electron distributions. Since polarization and charge transfer should provide additional stabilizations effect, it is not surprising the complete neglect of explicit treatment of these contributions leads to underestimation of hydration free energies.

Other than hydration free energies, all of the other ionic properties were calculated only with the 0.766 e model. The BLYPSP-4F water diffusion constant is 2.25 × 10⁻⁵ cm²/s,⁴⁸ comparing favorably to the experimental value of 2.3 × 10⁻⁵ cm²/s.⁵⁴ Table 8 reports the diffusion constants of the ions in BLYPSP-4F water, and the corresponding experimental diffusion constants are also reported for comparison.⁵⁴ All of the ion diffusion constants were obtained by three 30 ns simulations with one single ion in 343 water molecules. All models agree with experiments within approximately 10%, with I⁻ being the only exception. The I⁻ diffusion constant is 20% too small for the AFM based model.

Table 8.

Diffusion Constants (in 10⁻⁵ cm²/s) of Nine Ions with the 0.766 e Charge Model

ions	D	Dexp54
Li+	0.90 ± 0.06	1.029
Na+	1.40 ± 0.12	1.334
K+	1.94 ± 0.03	1.957
Rb+	2.15 ± 0.04	2.072
Cs+	1.78 ± 0.11	2.056
F−	1.27 ± 0.06	1.457
Cl−	2.27 ± 0.11	2.032
Br−	1.84 ± 0.09	2.080
I−	1.63 ± 0.08	2.045

Figure 1 reports the cation–water and anion–water radial distribution functions (RDFs). Since our AFM models provide accurate hydration free energies and diffusion constants without fitting to experiments, we believe that predictions from the AFM ion models for the hydration structures will be accurate. We note that a 343 water simulation box was used for these RDF calculations. This simulation box is much larger than most studies using DFT based MD techniques.^{21,53,55–57} The larger simulation box allows proper formation of several hydration shells around each ion.

Figure 1.

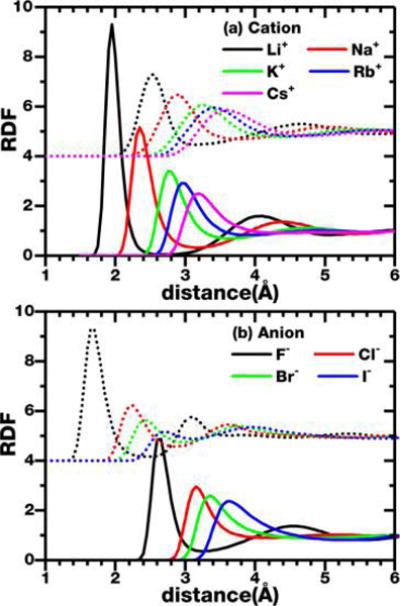
RDF of the nine ions with the O (solid line) and H (dotted line) atoms of water. (The ion-H RDF is shifted vertically by 4 to improve visibility.)

Not surprisingly, for cations, the water oxygens get closer to the ions than the hydrogens. The distance between the first O peak to the first H peak reflects the alignment between the water dipole moment and the field of the charge (Figure 2a). Table 9 summarizes the observed separation between the first ion-O and ion-H peak and that expected for the ion assuming a perfect alignment of the water dipole moment and the direction of the field of the ion. The better the agreement between the expected peak separation and the observed peak separation, the better the field alignment is. One can clearly see a progression from a higher degree of dipole alignment with the expected peak separation only 0.1 Å farther from the observed separation for the Li⁺ to a fairly poor alignment for Cs⁺ with the difference is as large as 0.23 Å.

Figure 2.

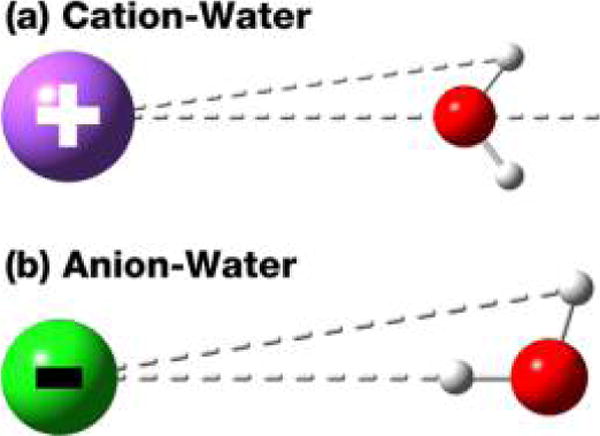
Schematic picture showing the preferred alignment of water dipole moment with the ions that are consistent with the observation of the ion–water RDFs.

Table 9.

Separation between the First Ion-O and Ion-H Peak for the Cations and Anions along with the Average Number of Hydrogen Bonds Formed by Each First Hydration Shell Water Molecule^a

ions	expected (Å)	observed (Å)	hydrogen bonds
Li+	0.68	0.58	2.43
Na+	0.67	0.55	2.60
K+	0.65	0.48	2.87
Rb+	0.65	0.47	2.98
Cs+	0.64	0.41	3.17
F−	0.95	0.96	2.75
Cl−	0.95	0.93	3.03
Br−	0.95	0.93	3.22
I−	0.95	0.93	3.36

^aFor cations, the ion-O peak is closer than the ion-H peak. For anions, the first ion-H peak is closer.

It is also clear from Figure 1 that, as the cations get larger, both the first O peak and especially the first H peak broadens, consistent with a significant reduction in dipole alignment as ions grow larger. Table 9 also shows the number of hydrogen bonds formed by each first hydration shell water molecule, which shows a significant increase from Li⁺ to Cs⁺. It has been proposed previously²⁴ that, as the ions grow in size, the dipole alignment reduces to maximize the number of first hydration shell hydrogen bonds that can be formed. The delicate balance between the field-dipole alignment and the stabilization from forming more hydrogen bonds thus explains the deviation from the expected peak separation and the broadening of the first O and H peaks in the RDF.

For all of the anions, two ion-H peaks can be resolved around the first ion-O peak. The distance between the first ion-H and the first ion-O peak does not show a large variation, with separations of 0.96 Å for F⁻ and 0.93 Å for Cl⁻, Br⁻, and I⁻. This is consistent with a good alignment of one of the OH bonds with the direction of the field (Figure 2b). However, Table 9 shows the number of hydrogen bonds formed by each first hydration shell water molecule for the anions. The number of hydrogen bonds also increases as ions get bigger.

For cations, the optimal dipole alignment of the water C_2v axis to the field leads to compromises in the number of hydrogen bonds that can be formed by each water. This has been argued due to the inability of water to form hydrogen bonds with other molecules also in the first hydration shell. For anions, the optimal dipole alignment is for one of the OH bonds to point toward the ion. Thus, the alignment is not hindering hydrogen bond formation. We believe the increase of the number of hydrogen bonds from F⁻ to I⁻ is mostly due to the increased size of the ion.

6. SUMMARY

In summary, ion–water potentials were developed for five alkali cations Li⁺ to Cs⁺ and four halide anions F⁻ to I⁻ by fitting only to MP2 forces calculated with a triple-ζ quality basis set. The hydration free energies for all 20 salts predicted by the potentials developed are in good agreement with experiments. For the 10 fluoride and chloride salts, the agreement is better than 2%. For the 10 bromide and iodide salts, the AFM models underestimate the experimental hydration free energies by around 5%. The slightly bigger error for the larger anions is likely due to the neglect of explicit treatment of polarization and charge transfer.

The diffusion constants of the ions predicted by the models are within 10% of the experimental values for all of the ions except iodide, for which the model underestimates the experiment by about 20%. Cations and anions show different dipole alignments for waters in their first hydration shell. For small cations, the water tends to align the total dipole to the field of the ion. This leads to a delicate competition between dipole alignment and the formation of hydrogen bonds. For anions, only one of the two OH bonds is aligned to the field of the anion. For both cation and anions, the average number of hydrogen bonds formed by first hydration shell water increases as the ion grows larger.

It is also pointed out that proper comparison of experimental and theoretical hydration free energies requires a consistent treatment of the gas phase entropy for the ions. The simplified hydration free energies for the ions are reported for further theoretical work to use as a more convenient experimental reference.

The work demonstrates the robustness of the adaptive force matching procedure in deriving predictive potentials with only ab initio reference without fitting to experiments. The simple potentials developed by AFM can be considered as a way to extend advanced electronic structure methods to much larger systems at a much greater time scale. On the other hand, especially for larger ions such as Br⁻ and I⁻, explicit treatment of many-body effects such as induction and charge transfer becomes more important. We are actively investigating the development of explicit polarizable potentials with AFM.