Abstract
Peptide-based supramolecular filaments, in particular filaments self-assembled by drug amphiphiles (DAs), possess great potential in the field of drug delivery. These filaments possess one hundred percent drug loading, with a release mechanism that can be tuned based on the dissociation of the supramolecular filaments and the degradation of the DAs [Cheetham et al., J. Am. Chem. Soc. 135 (8), 2907 (2013)]. Recently, much attention has been drawn to the competing intermolecular interactions that drive the self-assembly of peptide-based amphiphiles into supramolecular filaments. Recently, we reported on long-time atomistic molecular dynamics simulations to characterize the structure and growth of chiral filaments by the self-assembly of a DA containing the aromatic anti-cancer drug camptothecin [Kang et al., Macromolecules 49 (3), 994 (2016)]. We found that the π–π stacking of the aromatic drug governs the early stages of the self-assembly process, while also contributing towards the chirality of the self-assembled filament. Based on these all-atomistic simulations, we now build a chemically accurate coarse-grained model that can capture the structure and stability of these supramolecular filaments at long time-scales (microseconds). These coarse-grained models successfully recapitulate the growth of the molecular clusters (and their elongation trends) compared with previously reported atomistic simulations. Furthermore, the interfacial structure and the helicity of the filaments are conserved. Next, we focus on characterization of the disassembly process of a 0.675 μm DA filament at microsecond time-scales. These results provide very useful tools for the rational design of functional supramolecular filaments, in particular supramolecular filaments for drug delivery applications.
Graphical Abstract
1. Introduction
Peptide-amphiphiles (PAs) can self-assemble into a variety of architectures—ranging from the classic spherical micelles to ‘one-dimensional’ cylindrical filaments to twisted ribbons, nanotubes, or membranes1–5. The balance of intermolecular interactions, including hydrogen bonding in β-sheets and van der Waals interactions between the amphiphile tails, with respect to the strength of the electrostatic interactions determines the preferred morphology of the resulting nanostructure5–7. These structures possess numerous applications in the areas of biomimetic and biomedical materials8. Functional assemblies of aromatic components have been explored to obtain desired materials properties of these filaments/tubes.8–11 Supramolecular hydrogels formed by ‘π-gelators’ are a promising new field of functional materials.12, 13 In addition to the electronic properties of these materials, there are numerous biomedical applications of supramolecular self-assemblies of PAs, including bionanofabrication, biomimetic mineralization additives, sensing, tissue engineering, and drug delivery.14–19
Recent attempts to harness supramolecular assemblies composed by PAs for drug delivery have made much progress, including responsive vehicles and peptide-drug conjugates.20–26 There are many challenges in the design of an effective drug delivery vehicles, including a controlled and high drug loading capacity, extending the circulation time in blood-stream27, eliminating non-specific cell uptake28, the tunability of the vehicle morphology/shape at the nanoscale29, and ultimately the control of the drug vehicle interaction with the cellular membrane. Control can occur either through active targeting of cellular receptors and/or control of the membrane response via morphology30 and/or surface patterning31, 32. Peptide-based drug amphiphiles (DAs) as designed by the Cui laboratory20 are new candidates for drug delivery vehicles with the potential to address many of these issues.33–35 DAs possess one hundred percent loading capacity, as well as the ability to optimize the delivery of the drug via a biodegradable linker.36 This biodegradation is one of the key factors in the stability of the drug delivery vehicle, and resulting dissociation and delivery.
The disassembly of supramolecular nanostructures of PAs25, 37, as well as the transitions between micelle and fiber38 have been studied experimentally. Here we characterize the dissociation of filamentous drug delivery vehicles composed by DAs using large-scale molecular dynamics (MD) simulation techniques. The dynamic self-assembly and disassociation processes of PAs are guided by a delicate balance between the intermolecular forces between PAs. These intermolecular forces arise from the unique molecular character and the specific amino acid sequence of the PA. Specifically, the amphiphilic nature of the PA can be tailored by the degree of hydrogen bonding, hydrophobic interactions, and electrostatic interactions39–41. In addition, spontaneous chirality due to aromatic interactions42 or electrostatics43 can also add interesting ‘kicks’ to the assembled structures. Moreover, the molecular structure of the PA can be designed to respond to external stimuli such as light44, triggering dissociation. The cooperative interplay of these interactions may be shifted during the kinetic formation of intermediate supramolecular structures during the self-assembly as well as the dissociation processes, with different intermolecular forces dominating at different time-scales. This poses great challenges at the theoretical, computational, and experimental levels to probe the contributions of each specific intermolecular interaction at any stage of the formation/dissociation pathways.
Computational simulations, in particular molecular dynamics (MD) simulations, can provide insight into the intermolecular interactions that govern both the short (nanoseconds) and long-term (≫ microseconds) self-assembly and dissociation pathways of peptide-based amphiphiles. Results from MD simulations can also help characterize the balance of intra- and intermolecular forces that govern their disassembly mechanisms.42, 45 For example, in one of the first all-atomistic simulations of peptide-amphiphiles, Lee et al.45 characterized the structure of IKVAV-peptide amphiphiphile nanofibers using 40 ns all-atomistic MD simulations of pre-formed cylindrical fibers. They confirmed that the orientation of intermolecular hydrogen bonding followed the nanofiber axis, with a high population of β -sheets. These results were found to be consistent with Paramonov and colleagues’ experiments46. Subsequently, using the MARTINI model47 Lee et al.48 demonstrated the spontaneous formation of cylindrical nanofibers of PAs in multiple replicas of microseconds-long simulations. These studies also exemplified the versatility of coarse-grained (CGed) force fields such as the MARTINI model to demonstrate self-assembly. Furthermore, a comprehensive phase diagram showing the variation of micellar structures that can be formed when balancing the strength of hydrophobic and hydrogen-bonding interactions perpendicular to the PA axis was characterized by Velichko et al.49 In these studies, Velichko et al. used a united atom model with directional hydrogen-bonding to describe the peptide amphiphiles, and showed that the shape of self-assemblies can range from spherical micelles to single β-sheets to elongated cylindrical fibers.49, 50 Following, there have been a multitude of atomistic and coarse-grained MD simulations studies analysing the structure and self-assembly pathways of PA fibers5, 45, 48, 51–64.
Previously, we reported on the formation of chiral filaments by the self-assembly of DAs, using long-time all-atomistic molecular dynamics simulations.42 These DAs contain an the aromatic anticancer drug conjugated to a short β-sheet forming peptide.20 These all-atomistic simulations show that the aromatic π–π stacking interactions provide a critical role for the formation of the initial micellar nuclei, in addition to hydrophobic, electrostatic, and hydrogen-bonding interactions. Furthermore, the strong and directional π–π stacking interactions also contribute towards the chirality of DA filaments, which compares well with experimental results20. However, given the limitations in terms of the simulation time-scales (nanoseconds) and length-scales (Ångströms) with all-atomistic simulations, CGed molecular simulations can provide a more comprehensive view of the length-scales (micrometers) and time-scales (≫ microseconds) for self-assembly65. Herein, we utilize large-scale CGed MD simulations to characterize both the structure and stability of peptide-based drug amphiphile filaments at long time-scales (microseconds) using the Shinoda-DeVane-Klein (SDK) approach to CGed force field development66. These SDK CGed models successfully reproduce the growth of the molecular clusters and their elongation trends at extended microsecond time-scales, compared with previously reported atomistic simulations (100’s of ns). Moreover, the CGed models of the filament conserve the interfacial structure (density profile), as well the right-handed helicity. Furthermore, we characterize the disassembly process of the finite-length filaments (~0.675 μm) at elevated temperatures, demonstrating that the DA filament instability initiates from the end-cap of the drug delivery vehicle. These results provide very useful tools to elucidate the structure and stability of supramolecular filaments, in particular supramolecular filaments for applications in hydrophobic drug delivery.
2. Simulation methods
2.1 Coarse-grained model development
Within this study, we use large-scale MD simulations based on CGed force fields to overcome the limitation of atomistic MD simulations in terms of both time-scales and system size. CGed MD simulations have been utilized to characterize the self-assembly behaviour of polymers, proteins, and membranes66–72. Specifically, we develop CGed force field parameters for these DAs using the SDK approach.66, 73 The SDK approach to CGed MD force fields has been applied to simulate surfactants66, 68, phospholipid monolayers and bilayers,73 as well as proteins74 and polymers.75, 76 Here we study the structure and stability of a supramolecular filament composed by an aromatic hydrophobic anti-cancer drug conjugated to a short peptide sequence20, 42. More specifically we study the structure and stability of a supramolecular filaments composed by DAs, with the hydrophobic drug in the core of the filament and the peptide forming the corona of the filament. This DA is termed ‘mCPT-buSS-Tau’, which consists of the hydrophobic drug camptothecin (CPT), a DNA-topoisomerase I inhibitor, conjugated to a β -sheet-forming peptide sequence (CGVQIVYKK) derived from the Tau protein through a disulfylbutyrate (buSS) linker (Fig. 1A)20. The peptide sequence contains a short hexapeptide motif (VQIVYK)77 that forms β-sheet structures leading to Tau polymerization and, therefore, amyloid formation. In the SDK CGed model for the DA as shown in Fig. 1B, a single CGed bead represents two to four heavy atoms and their associated hydrogen atoms, as shown in Fig. 1. (see also Supporting Information for additional parameters). As shown in Fig. 1B, the hydrophobic anti-cancer drug camptothecin is represented with twelve CGed beads, in a nearly planar structure, conserving the flat pentacyclic structure. Peptide parameters utilize transferable SDK protein parameters74. In the SDK CGed water, each CGed water bead represents three water molecules.78 The total potential energy function, U, including intra and intermolecular CGed bead potentials, is defined as follows:
| (1) |
Fig. 1.
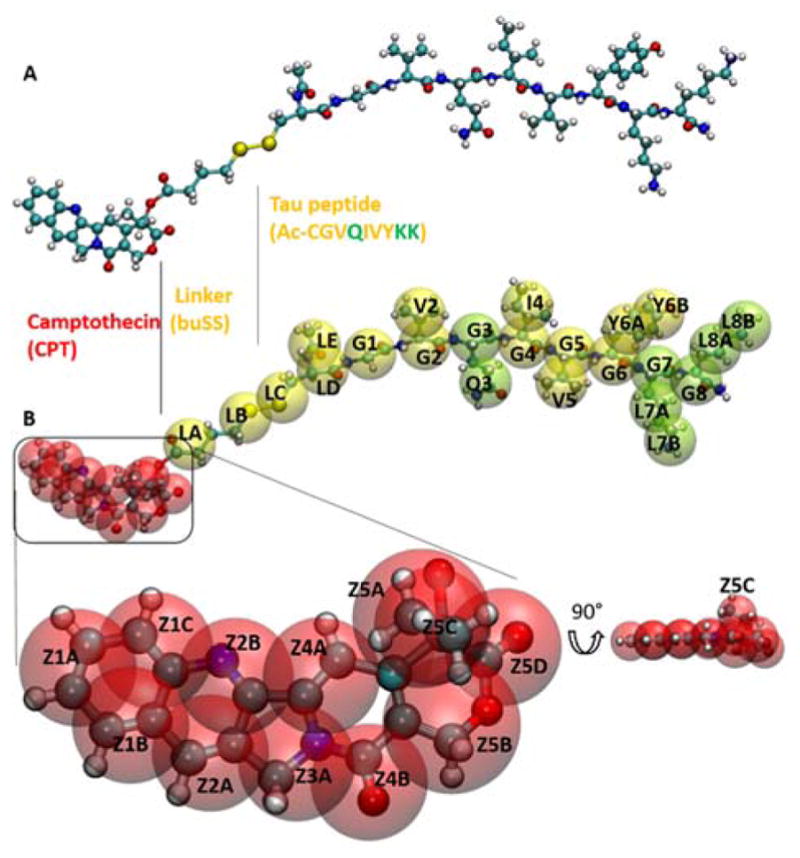
Coarse-grained and all-atomistic representations of the drug-amphiphile (DA) filaments. A. Atomistic model for ‘mCPT-buSS-Tau’, the DA in a CPK representation. B. CGed model for the DA shown as transparent VDW spheres, overlapping the atomistic model. The hydrophobic cancer drug camptothecin (CPT) is in red, the charged lysine and polar glutamine groups are shown in light green, while the rest residues are shown in yellow. CPT is expanded and rotated 90° to show the planar structure.
The bonded interactions consist of bond (Ubond), angle (Uangle ), and dihedral (Udihe ) interactions given in eq. 2, 3 and 4, respectively.
| (2) |
| (3) |
| (4) |
where kb, kϑ, and kφ are the bond, angle, and dihedral angle force constants, respectively; b, ϑ, and ϕ are the bond length, angle, and dihedral angle, respectively with the subscript zero representing the equilibrium values for the individual terms. n is the periodicity of the torsion and δ is the phase offset. For the total SDK model for the DA, all CGed beads except those for water interact via a Lennard-Jones (LJ) 9-6 potential given in eq. 5, while interactions with CGed beads for water are defined as a LJ 12-4 potential given in eq. 6:
| (5) |
| (6) |
where σ is the distance at the LJ minimum, ε is the LJ well depth, and r is the distance between CGed sites. In this model, the LJ parameters between pairs of non-identical CGed sites are generated using the combination rules, in which and σij = (σii + σjj)/2. A cutoff is set to 15 Å. The CGed sites are charged and this is also included in the electrostatic contribution given by eq.7.
| (7) |
where C is an energy-conversion constant, qi and qj are the charges on the beads i and j, and ε1 is the effective dielectric constant.
Bond, angle, and dihedral parameterization is based on Boltzmann inversion.79 The potential of mean force of any internal coordinate q and the probability distribution of q, P(q), is as follows:
| (8) |
Based on previous long-time all-atomistic MD simulations with the General Amber force field (GAFF),42 a CGed interaction site is defined as a center of mass of the selected atoms and the bonded interactions are parameterized by fitting eqs. 2, 3, and 4 using the last 10 ns of the atomistic trajectories of the preassembled filament. The charge of 0.1118 is assigned on the site of the side chain (L7B and L8B) of LYS (See Supplementary Table S2-1).74 Each system is neutralized with Chloride ions with a charge of −0.1118, such that the effective dielectric permittivity is uniform throughout the system with ε1=1. The long-range electrostatic interactions are calculated using the particle-particle particle-mesh (PPPM) method.80–82 Tables of atom parameters, bond parameters, angle parameters, dihedral parameters, and short range parameters are defined in Supplementary Tables S2-1-6.
2.2 Molecular dynamics simulations
Three types of simulations are explored in this study: 1) longtime CGed simulation of an infinite pre-assembled DA filament to compare with the previous all-atomistic studies to see if the structure of the filament is conserved as compared with all-atomistic simulations (as shown in Fig. 2), 2) long-time CGed MD simulations to evaluate self-assembly from random homogeneous distributions of the DA in a water box (as shown in the inset of Fig. 4A and Supplementary Fig. S1–4), and, 3) large-scale simulations of a finite length filament (0.675 μm in length) to evaluate the stability of the filaments at slightly elevated temperatures as shown in Fig. 7. Each system is neutralized with Chloride ions. Salt concentration effects on the assembly kinetics are not explored in this study, but can be explored in future studies. Simulation size, salt concentrations, and time-scales are summarized in Supplementary Table S1-1. The first type of simulation is conducted starting from a preassembled filament as shown in Supplementary Fig. S1–2. The starting configuration for the CGed DA filament is mapped directly from the previous all-atomistic DA filament, which was built with 9 layers with 6 DAs per layer and relaxed for 210 ns.42 This system is simulated for 1 μs, while the filamentous structure is allowed to relax. For this system, the cylindrical structure is infinite due to periodic boundary conditions. The second type of simulation includes two different concentrations of randomly distributed DA systems at 16 mM and 200 mM. In comparison, experimental concentrations are 50 μM and 1 mM. We chose the two concentrations to have better statistics with the given number of DAs in a simulation box. After neutralization of the systems with Chloride ions, the salt concentrations are 31 mM and 400 mM.
Fig. 2.
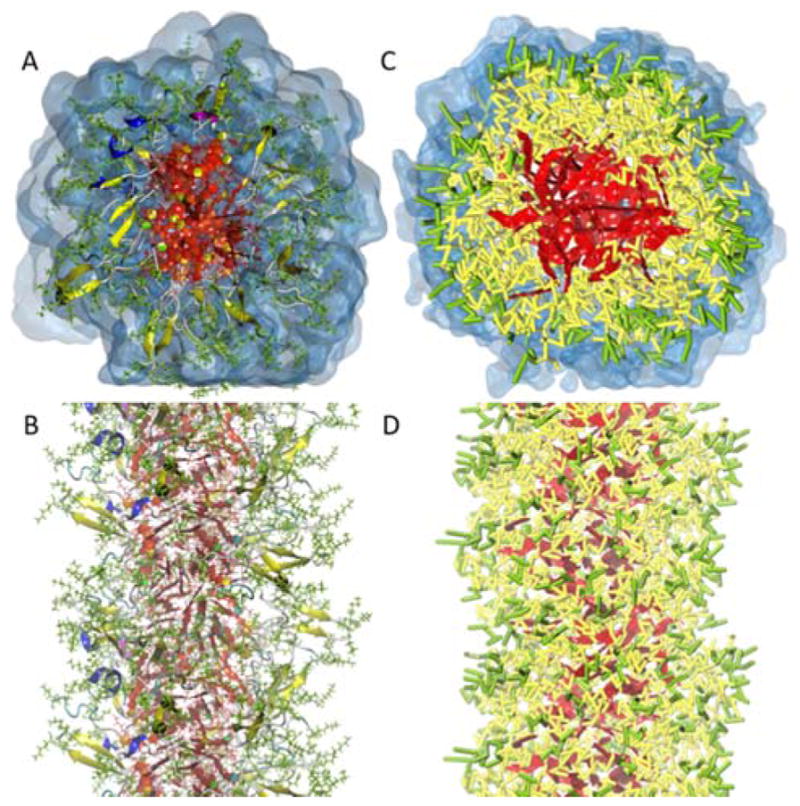
Coarse-grained and all-atomistic representations of the drug-amphiphile (DA) filaments. A and B. Top and side views of the atomistic preassembled filament of the DA from the results of reference 42 after 210 ns. In this representation, the atomistic CPT is also shown in red. In addition, β-sheets formed along the length of the filament are shown in yellow. C and D. The top and side views of the CGed preassembled filament of DAs after 1 μs simulation. The CGed DA is displayed in a licorice representation. The colors follow the same way as described in B. Water (transparent blue) is not shown for clarity in the side views.
Fig. 4.
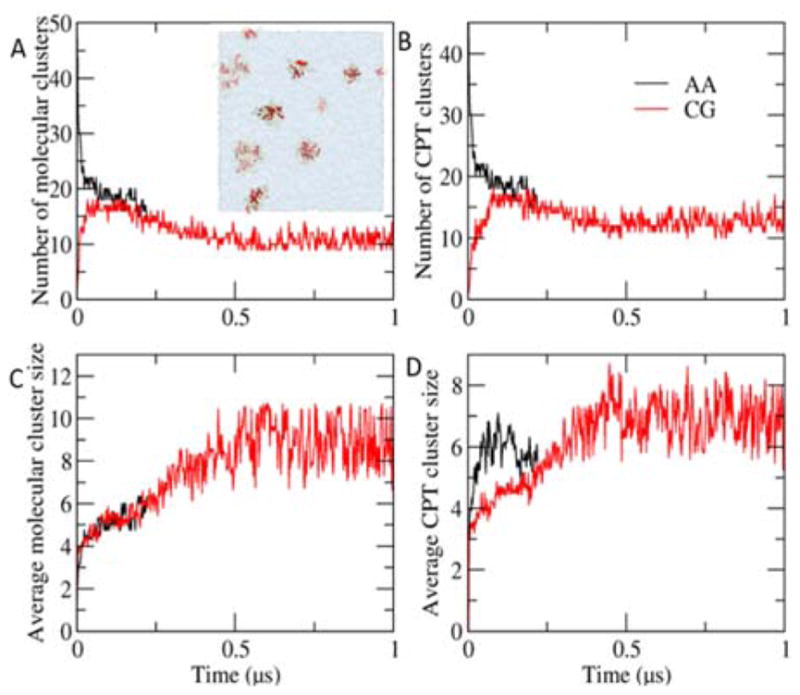
Cluster growth in a random system. A. A. The number of molecular clusters over time. The inset shows a snapshot of a random system of 16 mM at 1 μs. B. The number of CPT clusters over time. C. The average size of molecular clusters over time. D. The average size of CPT clusters over time. The results from the atomistic and the CGed models are in black, and red, respectively. The size of clusters increases, accompanying the gradual decrease of the number of molecular clusters. Compared with the atomistic results, the growth of molecular clusters of the CGed model matches well, while that of CPT clusters are slower in the CGed one.
Fig. 7.
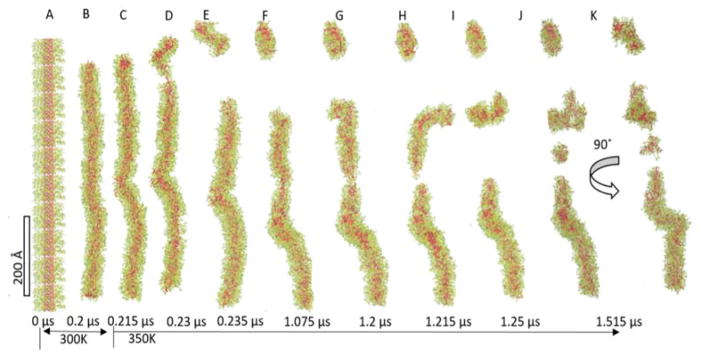
Dissociation of the finite-length DA filament. The 0.675 μm filament (A) is equilibrated at 300 K for 0.2 μs (0.576 μm, B), and then the temperature is elevated to 350 K. During the disassembly, kinking, thinning, and budding are observed.
All three types of MD simulations of the DA are performed utilizing LAMMPS.83 In order to increase the efficiency of both types of simulations, the planar CGed CPT is treated as a rigid body and the topology interactions are turned off between rigid atoms.84 The systems are simulated at the anisotropic pressure 1 atm and the temperature 300 K using a Nose-Hoover thermostat.85–87 With a two level rRESPA88 multi-time-scale integrator, the bond, angle, and dihedral angle potentials are evaluated with the inner time step of 0.5 fs and the non-bonded interactions are evaluated with the outer time step of 10 fs. Periodic boundary conditions are used in x,y, and z (Fig. S1–2A). Anisotropic conditions are used so that the z-direction of the fiber can relax. Each simulation is conducted for 1 μs in total. The third type of simulation of a pre-assembled finite-length filament of 0.675 μm is simulated for 200ns at 300 K and then for 1.315 μs at 350 K. In comparison, lengths of filaments are on the scale of a few micrometers.20 All systems are simulated on 1 node of a workstation with 4 GeForce GTX 680’s per node, with an efficiency of 5.4 ns/day for the largest system of the preassembled finite-length filament.
3. Results and Discussion
Simulations of CGed filament structure
Starting from Fig. 2, we compare resulting structures of all-atomistic and CGed preassembled filaments. The all-atomistic (AA) filaments as shown in Fig. 2A (top view) & B (side view) are compared with the exact same CGed system in the neighboring Fig. 2C (top view) & D (side view). CGed results are after 1 μs of relaxation, while the AA results as published in reference 42 are after 210 ns simulation. The CGed DA pre-assembled filament after 1 μs is displayed in a licorice representation (with the hydrophobic CPT in red) in Figs. 2C & D, with the neighboring water surrounding the filament shown in a transparent surface representation for the top view of Fig. 2C, but not for the side view of Fig. 2D. To compare, the same top and side view are shown for the results of AA simulations as published in reference 42 in Fig. 2A & B.
In this representation, the atomistic CPT is also shown in red. In addition, β-sheets formed along the length of the filament are shown in yellow. β-sheets formed from hydrogen-bonding are not shown explicitly in the CGed representation, since there is no explicit directional hydrogen-bonding term in this model. However, we are currently working on incorporating a directional hydrogen bonding term into the SDK force field for these DA molecules. To begin with, we first visually compare the structure of the AA and CGed simulations of the DA filaments as shown in Fig. 2.
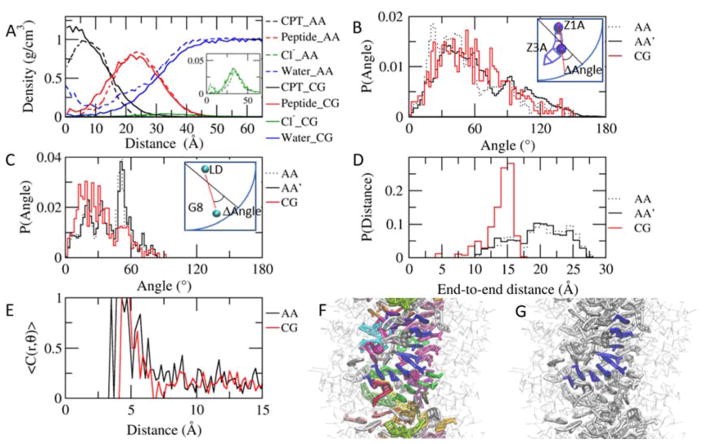
The structure of the AA simulations is conserved well in the CGed model simulations. The peptides wrap around the CPTs in the filament, as shown in Fig. 2C. The hydrophobic CPT (red in both representations) is in the hydrophobic core of the filament, hydrophobic residues in yellow form the interface between the hydrophobic drug and the charged Lysine and polar Glutamine groups (shown in light green). Next, we quantify the differences in the radial density of each component between AA and CGed simulations as shown in Fig. 3A. The interfacial density profiles for CPT, peptide, and water agree fairly well with each other. From the center outwards, the density profile confirms the CPT occupies the centremost region of the core, followed by the peptide, and then the water. The peak and width of the CPT and peptide density profile are extremely close, except for the density in the very center of the core. The reason behind this difference is the difference in simulation scales, specifically of water—the CGed water molecules are not present in the center of the hydrophobic core, whereas a finite density of waters is observed in AA simulation as shown in Fig. S1–3. In the corresponding AA simulation, the free volume cavities occupied by water in the hydrophobic core are small and randomly scattered, leading to a high density of water fitting in between stacks of CPTs as shown in Fig S1–3 A (top view) and B (side view). Since one water bead in the CGed model represents 3 AA water molecules, the CGed water bead is much bulkier. Furthermore, as the sizes of the beads increase in the CGed model, the thickness of the CPT planes also increase, which can fill the hydrophobic core of the filament more, leaving less open space accessible to the bulky CGed water as shown in Fig. S1–3 C (top view) and D (side view). The CGed water density recovers to bulk density outside of the peptide corona as shown in Fig. 3A. The distribution of Chloride ions in the CGed model matches well with that in the AA simulations, except the near-center region where no CGed water and, therefore, no Chloride ions are present.
Fig. 3.
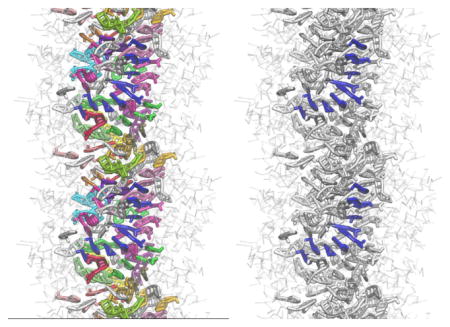
Structure of the preassembled system. A. Radial distributions in the preassembled system after 1 μs. The density is averaged for the last the last 100ns and 2 ns for the CGed and atomistic systems, respectively. The CPTs (black) remain buried in the core of the assembly, while the peptides (red) wrap around the core, forming the outer shell in both atomistic (dotted lines) and CGed (solid lines) models. In contrast to the water in the core in the atomistic model (blue dotted line), the CGed water (blue solid line) does not appear in the core of the assembly. The inset shows the density of the Cl− ions. B. Probability distribution of the angle formed between the CPT’s long axis (Z1A–Z3A) and the radial direction, from the center of the filament on the same xy plane as the center of CPT to the center of CPT. The atomistic (AA), the CG-matched atomistic (AA′) and the CGed (CG) results are in black dotted, black solid, and red solid, respectively, in B, C, and D. For the direct comparison, CG-matched atomistic (AA′) results are calculated based on the center of all atoms corresponding to each CGed bead: pairs used for AA, AA′, and CG are C24–N14, (C24, C25, H45 and H46)-(N14, C15, H41 and H42), and Z1A–Z3A, respectively. C. Probability distribution of the angle formed between the peptides’ longest axis (LD of CYS-G8 of LYS) and the radial vector. Pairs used for AA, AA′, and CG are Cα of CYS-Cα of LYS, (CA, N, C, O, H and HA of CYS)-(CA, N, C, O, H and HA of LYS), and LD-G8, respectively. D. Probability distribution of the end-to-end distances of peptides. E. Stacking probability as the function of the distance between CPT planes. A cutoff for angle is 30 °. C(r,ϑ) = 1 (|ϑ| < 30°), C(r,ϑ) = 0 (|ϑ| > 30°). The CPT planes are defined with C24, N20, and C17 in the AA model and Z1A, Z2A and Z2B in the CGed model. F. Near-parallel CPTs are grouped and color-coded to show their stacking in the center of a CGed pre-assembled filament after 1 μs simulation time. G. From F, one group of parallel CPTs is highlighted in blue to show right-handed helical stacking.
Next, we compare the angle that the CPT axis makes with respect to the radial direction in the filament. As seen in Fig. 3B, the long axis of CPT deviates approximately 30° from the radial vector that connects the center of mass of each CPT and the center of mass of the filament on the same xy plane. This is compared with the AA simulations, as well as AA simulations remapped to match the center of mass of the CGed beads (denoted by AA’ in Fig. 3B–D). All three distributions display a preferential angle at approximately 30°. This preferred angle of rotation around the core of the filament is consistent with the tilting of the CPTs, leading to the chiral helix-like packing of CPTs in the filament core. Thus, the CGed model of the filament preserves the chiral packing and orientation of CPTs in the core of the filament due to the planarity of the CGed CPT model. In a similar manner, in Fig. 3C we calculate the angle between a radial vector and the long axis of each peptide connecting the backbone beads of ending residues, i.e. LD of CYS and G8 of LYS. The CGed peptides are tilted at approximately 20°, while the corresponding angle deviation in the AA simulation has a peak at about 54° (Fig. 3C). Moreover, the end-to-end distances of the CGed peptides display a peak at approximately 15 Å, which falls short, compared to the peak at approximately 20 Å of the AA peptides (Fig. 3D). Interestingly, the combination of the smaller angle-deviation and the smaller end-to-end distance results in the almost perfect match of the density of the peptides in the preassembled filament (Fig. 3A). Specifically, the CGed peptides is shorter (Fig. 3D), but they deviate less from the radial vector (Fig. 3C), their ends span as much from the core of the nanofilament as those of the AA peptides. To reproduce the correct range of the end-to-end distance with the CGed peptides, we can tune the interaction between the peptides and water and implement a directional hydrogen bonding into a new version of our SDK CGed model for the DAs. Furthermore, we note that in order to utilize these CGed force-fields to calculate key properties of supramolecular assemblies, (structural and mechanical) anisotropic potentials can be developed and incorporated into the present models.
The CPT stackings form short right-handed helical strands, as shown in Fig. 3F & G. The probability of stacking angle as a function of the distance between CPT planes is calculated, using <C(r, ϑ)> with a cutoff angle of 30 °: C(r,ϑ) = 1 (|ϑ| < 30°), C(r,ϑ) = 0 (|ϑ| > 30°), where ϑ is the angle between the CPT planes, and r is the distance between the centers of Z2A and Z2B in the second CG ring of neighbouring CPTs. For comparison, the distance r in the AA model is measured between the centers of N20 and C17 in the second CPT ring. The CPT planes are defined with Z1A, Z2A, and Z2B in the CGed model and C24, N20, and C17 in the AA model. We found that the first stacking is very strong in both models and the fraction of stacking over the distance in the CGed model matches well with that in the AA model when the distance is longer than 4.4 Å. At shorter distances, the CGed model does not show stacking. This can be attributed to the slightly increased sphericity of the CGed model. The thickness of the CPT planes increase in the CGed model, as mentioned earlier. We next visually examine the stacking arrangements of the hydrophobic CPTs in the center of the core for the CGed filament in Fig. 3F & G. Near-parallel CPTs are grouped and color-coded to show their stacking in Fig. 3F. Within Fig. 3F, strands of similarly oriented CPTs are shown wrapping around the central DA filament axis in a right-handed fashion. From Fig. 3F, one unique group of parallel CPTs is highlighted in blue to show the right-handed helical stacking in Fig. 3G. The same visual results for the AA DA filament simulations are shown in Supplementary Figure S4 in reference42. The formation of single-handed helical assemblies regardless of the chirality of their building blocks has been reported in the self-assembly of perylene bisimide derivatives89.
Growth and elongation of clusters driven by π–π stacking
Since the stacking interaction between the CPTs in the filament is preserved between AA and CGed models, we next compare the self-assembly growth of filament nuclei from a random distribution of DAs. Previously, we found that the π-π interactions between the CPT planes guides filament nuclei formation into elongated micellar shapes as highlighted in Fig. 4A. In Fig. 4B–E, we quantify the growth of the clusters over time, comparing the CGed and AA models, using two different methodologies. To begin with, we quantify the growth of the number of filament nuclei in terms of the number of clusters as well as the average cluster size using an algorithm for the formation of ‘Molecular Clusters.’ In this algorithm, when any contact distance between DA molecules is less than 4.5 Å, we define it as a molecular cluster. As shown in Fig. 4B and D, the size of clusters increases in the 16 mM random system, accompanied by the gradual decrease of the number of molecular clusters. The growth of ‘Molecular Clusters’ in terms of the average cluster size of the CGed model matches well with that with AA results. We note that the 1 μs simulation time of this CGed model is not enough for the molecules to complete the self-assembling process into an intact filament at this concentration, but it can well reproduce the growth of molecular clusters in the early stage of the process. The π-π stacking between the planar CPTs is characteristic in filamentous self-assembly of DAs, which can serve as an anchor for the development for micellar nuclei in both AA and CGed simulations.
Next, in order to more carefully examine the contribution of π-π stacking in a similar fashion, we define a ‘CPT Cluster’ as opposed to a ‘Molecular Cluster’ when any contact distance between only the hydrophobic CPTs is less than 4.5 Å. However, in this case we find that the growth of CPT clusters is slower in the CGed simulations vs. AA simulations, suggesting that planar interactions between the CGed CPT models may be not as strong as those in the AA CPT molecular model.
Another indication on the weaker interactions between the CGed CPT planes as compared with the AA CPT model comes from comparison of the elongation of clusters, and their deviation from a spherical shape, as shown in Fig. 5. As shown schematically in Fig. 5A, we calculate ratio Rmin/Rmax where the Rmax is the maximum radius of gyration and Rmin is the minimum radius of gyration, for each of the ‘Molecular Clusters’ (Fig. 5B) and ‘CPT Clusters’ (Fig. 5C) as a function of cluster size for both the AA and CGed simulation studies. This data is collected over the 1 μs for the CGed simulations and the 200 ns for the AA simulations. In all four cases, we note that the larger the cluster sizes are, the more elongated they tend to be, or the more Rmin/Rmax deviates from 1. This holds true for both ‘Molecular Clusters’ and ‘CPT Clusters’. This supports the argument that there is a direct contribution of the π-π interactions towards the one-dimensional growth of the clusters. However, this elongation trend is slightly weaker in the CGed model. Overall, the CGed micellar clusters are more spherical, independent of the size of the cluster.
Fig. 5.
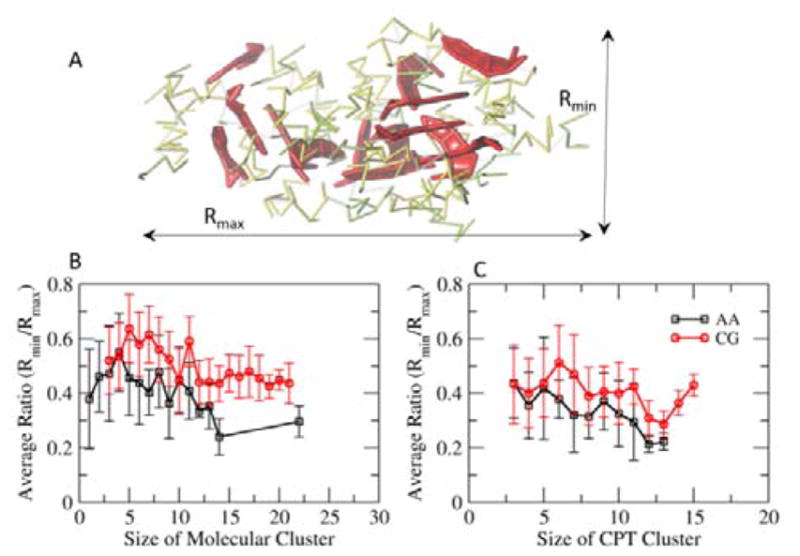
Elongation of clusters. A. A Cluster shows the shortest (Rmin) and longest (Rmax) axes. B. The average ratio of Rmin/Rmax of molecular clusters in the 16 mM random system. C. The average ratio of Rmin/Rmax of CPT clusters. The average ratio of Rmin/Rmax decreases as the size of clusters increases, indicating elongation of clusters over time. The elongation trend gets slightly weaker in the CGed model.
π-π Stacking of planar CPTs
The planar CPTs of the adjacent DAs form π-π stacking, as shown in Fig. 6A. Fig. 6B displays the distribution of angles between the CPT planes within 7 Å in the random system. Two distinctive peaks near 10° and 171° indicate their near-parallel packing within this distance. In the CGed model, the population of angles between these two angles increases, compared to those observed in the AA simulations. This weakened dependency on the angle between the planar CPTs in proximity is also observed in the preassembled system (Fig. 6C). In the preassembled system, the CPT-CPT angles show a peak at 20°, with a broader distribution.
Fig. 6.

π-π Stacking of CPTs. A. Clusters of DAs. The CPTs are highlighted in thicker red sticks. The rest parts of DAs and water are in yellow and transparent cyan, respectively. B. The distribution of angles between CPT planes within 7 Å in the random system. C. The distribution of angles between CPT planes within 7 Å in the preassembled system. The results from the AA and the CGed systems are displayed in black and red, respectively. The peaks near 0° and 180° indicate the near-parallel stackings of CPTs within 7 Å.
Along with the slower growth and elongation of the clusters, especially for ‘CPT Clusters’, this weaker angle-dependency of CPT-CPT packing indicates that the current version of the CGed model has a weaker π-π stacking interaction than the AA model. Given the suggested significant role of the π-π stacking, along with hydrogen bonding, the nonspecific hydrophobic interactions, as well as electrostatic interactions, it is important to improve this interaction in this SDK CGed model for DAs.
Disassembly of a finite-length filament at an elevated temperature
Next, we explore the stability of the DA through long-time CGed simulations of a finite length filament on the order of 0.675 μm by increasing the temperature from slightly above room temperature to 350K after 200 ns simulation at 300K (Fig. 7A–B). (Fig. 7). When gradually diluted in a short-term stability experiment, the self-assembled filament showed a dissociation tendency, which was decreasing with higher drug content.20 When exposed to mild sonication, dissociation was observed in the case of a similar DA called qCPT-Sub35 which has four CPT drugs conjugated to a Sub35 peptide.90–92 After relaxing the computational system for 200 ns at 300 K, the filament is 0.576 μm. When the temperature is elevated to 350 K, the disassembly process starts quickly with three distinct behaviours: kinking, thinning, and budding as shown in Fig. 7C–K. To begin with, the straight filament bends ~30° to form a kink in the middle at 0.215 μs (Fig. 7C). This bent conformation is not restored within 1.515 μs simulation time. In fact, one end of the filament buds out to an approximately 100 Å piece to form an elongated DA micelle at 0.23 μs (Fig. 7D). During this process, the peptide wraps around to minimize the exposure of CPT to the water. At 1.075 μs, thinning is observed in the longer filament, followed by budding off and pinching (Fig. 7F, G and H). The longest filament shows two kinks with about 90° (Fig. 7K). At the end of the 1.515 μs simulation, the filament breaks into 4 short pieces in total. The numbers of DAs in each fractioned micelle are 490, 197, 116, and 36. The ratios of longest and shortest principle axes of these pieces are 0.31, 0.37, 0.39, and 0.1, respectively. These low ratios indicate that micellar buds maintain elongated shapes, most likely due to the planarity of the CPTs.
Conclusions
Within this study, we present CGed MD results for the self-assembly, structure, and stability of supramolecular filaments composed by DAs. To begin with, we characterize the interfacial density profile and the helical stacking of CPTs within the core of the DA filament. We find that the SDK CGed models for the drug amphiphiles conserve mostly the interfacial structure of the filament, as well as the right-handed chirality governed by the stacking of CPT planes. Furthermore, we next show that the growth and elongated shape of micellar filament nuclei at the microsecond time-scale compares well with previous AA simulations. However, the slightly increased sphericity of the CGed CPT and molecular clusters indicates that the SDK CGed model for the DAs can be refined to incorporate an angle dependent potential for the interaction of the CPT planes. The CGed model can be further improved by tuning the interaction between the peptides and water and implementing a directional hydrogen bonding potential6 into a new version of our SDK CGed model for the DAs. Next, we examined the stability of a nearly half micron long isolated DA filament at slightly increased temperatures. We found that the DA filament begins its dissociation process at the end of the filament with an elongated micellar bud, similar to previous observations for the budding and break-up of diblock copolymer worm-like micelles.93 These results indicate that the dissociation of elongated supramolecular assemblies may occur via similar mechanisms. Thus, the CGed MD methodologies as discussed within this study are the ideal tools to investigate the stability of a range of similar drug delivery vehicles.
We also show with molecular simulation that aromatic groups in amphiphilic molecules that self-assemble into supramolecular systems play a key role in the initial stages of the self-assembly process. Moreover, the strength of the π-π stacking interactions between aromatic groups in competition with additional intermolecular forces such as hydrogen bonding and electrostatics may play a significant role in determining the chirality of supramolecular systems. The methodologies developed here can be applied to study the structure and stability of additional supramolecular assemblies governed by a competition of aromatic and hydrogen-bonding interactions94–96, as well as peptide-amphiphiles where electrostatic interactions play a key role.5
Supplementary Material
Acknowledgments
S.M.L. acknowledges support from the NIH (R15EB020343-01A1). In addition, this research was supported, in part, by the NSF through XSEDE resources under grant number TG-CHE130099 and a grant of computer time from the City University of New York High Performance Computing Center under NSF Grants CNS-0855217, CNS-0958379 and ACI-1126113. S.M.L. also acknowledges start-up funding received from College of Staten Island and City University of New York. M. K. also acknowledges partial support thanks to the Rosemary O’Halloran scholarship awarded to female chemists in the Chemistry department at College of Staten Island.
Footnotes
Electronic Supplementary Information (ESI) available: [details of any supplementary information available should be included here]. See DOI: 10.1039/x0xx00000x
References
- 1.Hartgerink JD, Beniash E, Stupp SI. Science. 2001;294:1684–1688. doi: 10.1126/science.1063187. [DOI] [PubMed] [Google Scholar]
- 2.Trent A, Marullo R, Lin B, Black M, Tirrell M. Soft Matter. 2011;7:9572–9572. [Google Scholar]
- 3.Kokkoli E, Mardilovich A, Wedekind A, Rexeisen EL, Garg A, Craig JA. Soft Matter. 2006;2:1015–1024. doi: 10.1039/b608929a. [DOI] [PubMed] [Google Scholar]
- 4.Cui H, Webber MJ, Stupp SI. Biopolymers. 2010;94:1–18. doi: 10.1002/bip.21328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gao C, Li H, Li Y, Kewalramani S, Palmer LC, Dravid VP, Stupp SI, Olvera de la Cruz M, Bedzyk MJ. J Phys Chem B. 2017;121:1623–1628. doi: 10.1021/acs.jpcb.6b11602. [DOI] [PubMed] [Google Scholar]
- 6.Velichko YS, Stupp SI, De La Cruz MO. J Physi Chem B. 2008;112:2326–2334. doi: 10.1021/jp074420n. [DOI] [PubMed] [Google Scholar]
- 7.Tantakitti F, Boekhoven J, Wang X, Kazantsev RV, Yu T, Li JH, Zhuang E, Zandi R, Ortony JH, Newcomb CJ, Palmer LC, Shekhawat GS, de la Cruz MO, Schatz GC, Stupp SI. Nat Mater. 2016;15:469–476. doi: 10.1038/nmat4538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Aida T, Meijer EW, Stupp SI. Science. 2012;335:813–817. doi: 10.1126/science.1205962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Takahashi R, Wang H, Lewis JP. J Phys Chem B. 2007;111:9093–9098. doi: 10.1021/jp0708446. [DOI] [PubMed] [Google Scholar]
- 10.Xu H, Das AK, Horie M, Shaik MS, Smith AM, Luo Y, Lu X, Collins R, Liem SY, Song A, Popelier PLA, Turner ML, Xiao P, Kinloch IA, Ulijn RV. Nanoscale. 2010;2:960–966. doi: 10.1039/b9nr00233b. [DOI] [PubMed] [Google Scholar]
- 11.Yang Z, Wang L, Wang J, Gao P, Xu B. J Mater Chem. 2010;20:2128–2132. [Google Scholar]
- 12.Babu SS, Praveen VK, Ajayaghosh A. Chem Rev. 2014;114:1973–2129. doi: 10.1021/cr400195e. [DOI] [PubMed] [Google Scholar]
- 13.Liyanage W, Ardoña HAM, Mao H-Q, Tovar JD. Bioconjugate Chem. 2017;28:751–759. doi: 10.1021/acs.bioconjchem.6b00593. [DOI] [PubMed] [Google Scholar]
- 14.Fleming S, Ulijn RV. Chem Soc Rev. 2014;43:8150–8177. doi: 10.1039/c4cs00247d. [DOI] [PubMed] [Google Scholar]
- 15.Cai C, Lin J, Lu Y, Zhang Q, Wang L. Chem Soc Rev. 2016;45:5985–6012. doi: 10.1039/c6cs00013d. [DOI] [PubMed] [Google Scholar]
- 16.De Santis E, Ryadnov MG. Chem Soc Rev. 2015;44:8288–8300. doi: 10.1039/c5cs00470e. [DOI] [PubMed] [Google Scholar]
- 17.Yan XZ, Wang F, Zheng B, Huang FH. Chem Soc Rev. 2012;41:6042–6065. doi: 10.1039/c2cs35091b. [DOI] [PubMed] [Google Scholar]
- 18.Soukasene S, Toft DJ, Moyer TJ, Lu H, Lee H-K, Standley SM, Cryns VL, Stupp SI. ACS Nano. 2011;5:9113–9121. doi: 10.1021/nn203343z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yoo SP, Pineda F, Barrett JC, Poon C, Tirrell M, Chung EJ. ACS Omega. 2016;1:996–1003. doi: 10.1021/acsomega.6b00210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cheetham AG, Zhang PC, Lin YA, Lock LL, Cui HG. J Am Chem Soc. 2013;135:2907–2910. doi: 10.1021/ja3115983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Andrew MacKay J, Chen M, McDaniel JR, Liu W, Simnick AJ, Chilkoti A. Nat Mater. 2009;8:993–999. doi: 10.1038/nmat2569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shen Y, Jin E, Zhang B, Murphy CJ, Sui M, Zhao J, Wang J, Tang J, Fan M, Van Kirk E, Murdoch WJ. J Am Chem Soc. 2010;132:4259–4265. doi: 10.1021/ja909475m. [DOI] [PubMed] [Google Scholar]
- 23.Denisov IG, Sligar SG. Biochimica et Biophysica Acta (BBA)-Proteins and Proteomics. 2011;1814:223–229. doi: 10.1016/j.bbapap.2010.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gao Y, Kuang Y, Guo Z-F, Guo Z, Krauss IJ, Xu B. J Am Chem Soc. 2009;131:13576–13577. doi: 10.1021/ja904411z. [DOI] [PubMed] [Google Scholar]
- 25.Xu X, Li Y, Li H, Liu R, Sheng M, He B, Gu Z. Small (Weinheim An Der Bergstrasse, Germany) 2014;10:1133–1140. doi: 10.1002/smll.201301885. [DOI] [PubMed] [Google Scholar]
- 26.Liu L, Xu K, Wang H, Jeremy Tan PK, Fan W, Venkatraman SS, Li L, Yang Y-Y. Nat Nano. 2009;4:457–463. doi: 10.1038/nnano.2009.153. [DOI] [PubMed] [Google Scholar]
- 27.Geng Y, Dalhaimer P, Cai S, Tsai R, Tewari M, Minko T, Discher DE. Nat Nanotechnol. 2007;2:249–255. doi: 10.1038/nnano.2007.70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rodriguez PL, Harada T, Christian DA, Pantano DA, Tsai RK, Discher DE. Science. 2013;339:971–975. doi: 10.1126/science.1229568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Mitragotri S, Lahann J. Nat Mater. 2009;8:15–23. doi: 10.1038/nmat2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Champion JA, Mitragotri S. Proc Natl Acad Sci U S A. 2006;103:4930–4934. doi: 10.1073/pnas.0600997103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Verma A, Uzun O, Hu Y, Hu Y, Han H-S, Watson N, Chen S, Irvine DJ, Stellacci F. Nat Mater. 2008;7:588–595. doi: 10.1038/nmat2202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Massignani M, LoPresti C, Blanazs A, Madsen J, Armes SP, Lewis AL, Battaglia G. Small. 2009;5:2424–2432. doi: 10.1002/smll.200900578. [DOI] [PubMed] [Google Scholar]
- 33.Wang Y, Cheetham AG, Angacian G, Su H, Xie L, Cui H. Adv Drug Deliver Rev. 2016 doi: 10.1016/j.addr.2016.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ma W, Cheetham AG, Cui H. Nano Today. 2016;11:13–30. doi: 10.1016/j.nantod.2015.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Su H, Koo JM, Cui H. J Control Release. 2015;219:383–395. doi: 10.1016/j.jconrel.2015.09.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Cheetham AG, Ou Y-C, Zhang P, Cui H. Chem Commun. 2014;50:6039–6042. doi: 10.1039/c3cc49453e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Löwik DWPM, Meijer JT, Minten IJ, van Kalkeren H, Heckenmüller L, Schulten I, Sliepen K, Smittenaar P, van Hest JCM. J Pept Sci. 2008;14:127–133. doi: 10.1002/psc.969. [DOI] [PubMed] [Google Scholar]
- 38.Sadownik JW, Leckie J, Ulijn RV. Chem Commun. 2011;47:728–730. doi: 10.1039/c0cc03796f. [DOI] [PubMed] [Google Scholar]
- 39.Toksöz S, Guler MO. Journal. 2009;4:458–469. [Google Scholar]
- 40.Paramonov SE, Jun HW, Hartgerink JD. Journal of the American Chemical Society. 2006;128:7291–7298. doi: 10.1021/ja060573x. [DOI] [PubMed] [Google Scholar]
- 41.Stendahl JC, Rao MS, Guler MO, Stupp SI. Advanced Functional Materials. 2006;16:499–508. [Google Scholar]
- 42.Kang M, Zhang P, Cui H, Loverde SM. Macromolecules. 2016;49:994–1001. doi: 10.1021/acs.macromol.5b02148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kohlstedt KL, Solis FJ, Vernizzi G, de la Cruz MO. Physical Review Letters. 2007:99. doi: 10.1103/PhysRevLett.99.030602. [DOI] [PubMed] [Google Scholar]
- 44.Muraoka T, Cui H, Stupp SI. Journal of the American Chemical Society. 2008;130:2946–2947. doi: 10.1021/ja711213s. [DOI] [PubMed] [Google Scholar]
- 45.Lee OS, Stupp SI, Schatz GC. J Am Chem Soc. 2011;133:3677–3683. doi: 10.1021/ja110966y. [DOI] [PubMed] [Google Scholar]
- 46.Paramonov SE, Jun H-W, Hartgerink JD. J Am Chem Soc. 2006;128:7291–7298. doi: 10.1021/ja060573x. [DOI] [PubMed] [Google Scholar]
- 47.Monticelli L, Kandasamy SK, Periole X, Larson RG, Tieleman DP, Marrink S-J. J Chem Theory Comput. 2008;4:819–834. doi: 10.1021/ct700324x. [DOI] [PubMed] [Google Scholar]
- 48.Lee O-S, Cho V, Schatz GC. Nano Lett. 2012;12:4907–4913. doi: 10.1021/nl302487m. [DOI] [PubMed] [Google Scholar]
- 49.Velichko YS, Stupp SI, de la Cruz MO. The Journal of Physical Chemistry B. 2008;112:2326–2334. doi: 10.1021/jp074420n. [DOI] [PubMed] [Google Scholar]
- 50.Palmer LC, Velichko YS, de la Cruz MO, Stupp SI. Philos T Roy Soc A. 2007;365:1417–1433. doi: 10.1098/rsta.2007.2024. [DOI] [PubMed] [Google Scholar]
- 51.Tsonchev S, Niece KL, Schatz GC, Ratner MA, Stupp SI. J Phys Chem B. 2008;112:441–447. doi: 10.1021/jp076273z. [DOI] [PubMed] [Google Scholar]
- 52.Tsonchev S, Schatz GC, Ratner MA. J Phys Chem B. 2004;108:8817–8822. [Google Scholar]
- 53.Tsonchev S, Schatz GC, Ratner MA. Nano Lett. 2003;3:623–626. [Google Scholar]
- 54.Tsonchev S, Troisi A, Schatz GC, Ratner MA. Nano Lett. 2004;4:427–431. [Google Scholar]
- 55.Lee OS, Liu Y, Schatz GC. J Nanopart Res. 2012;14:936–936. [Google Scholar]
- 56.Lee O-S, Stupp SI, Schatz GC. J Am Chem Soc. 2011;133:3677–3683. doi: 10.1021/ja110966y. [DOI] [PubMed] [Google Scholar]
- 57.Yu T, Lee OS, Schatz GC. J Phys Chem A. 2013;117:7453–7460. doi: 10.1021/jp401508w. [DOI] [PubMed] [Google Scholar]
- 58.Yu T, Lee OS, Schatz GC. J Phys Chem A. 2014;118:8553–8562. doi: 10.1021/jp502459r. [DOI] [PubMed] [Google Scholar]
- 59.Fu IW, Markegard CB, Chu BK, Nguyen HD. Adv Healthc Mater. 2013;2:1388–1400. doi: 10.1002/adhm.201200400. [DOI] [PubMed] [Google Scholar]
- 60.Fu IW, Markegard CB, Chu BK, Nguyen HD. Langmuir. 2014;30:7745–7754. doi: 10.1021/la5012988. [DOI] [PubMed] [Google Scholar]
- 61.Fu IW, Markegard CB, Nguyen HD. Langmuir. 2015;31:315–324. doi: 10.1021/la503399x. [DOI] [PubMed] [Google Scholar]
- 62.Fu IW, Nguyen HD. Biomacromolecules. 2015;16:2209–2219. doi: 10.1021/acs.biomac.5b00595. [DOI] [PubMed] [Google Scholar]
- 63.Ozkan AD, Tekinay AB, Guler MO, Tekin ED. RSC Adv. 2016;6:104201–104214. [Google Scholar]
- 64.Cote Y, Fu IW, Dobson ET, Goldberger JE, Nguyen HD, Shen JK. J Phys Chem C. 2014;118:16272–16278. doi: 10.1021/jp5048024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Klein ML, Shinoda W. Science. 2008;321:798–800. doi: 10.1126/science.1157834. [DOI] [PubMed] [Google Scholar]
- 66.Shinoda W, DeVane R, Klein ML. Mol Simulat. 2007;33:27–36. [Google Scholar]
- 67.Loverde SM, Klein ML, Discher DE. Adv Mater. 2012;24:3823–3830. doi: 10.1002/adma.201103192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Shinoda W, Discher DE, Klein ML, Loverde SM. Soft Matter. 2013;9:11549–11556. [Google Scholar]
- 69.Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, De Vries AH. J Phys Chem B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 70.Reynwar BJ, Illya G, Harmandaris VA, Muller MM, Kremer K, Deserno M. Nature. 2007;447:461–464. doi: 10.1038/nature05840. [DOI] [PubMed] [Google Scholar]
- 71.Allen EC, Rutledge GC. J Chem Phys. 2008;128:12. doi: 10.1063/1.2837651. [DOI] [PubMed] [Google Scholar]
- 72.Kamerlin SCL, Vicatos S, Dryga A, Warshel A. In: Annu Rev Phys Chem. Leone SR, Cremer PS, Groves JT, AJohnson M, editors. Vol. 62. 2011. pp. 41–64. [DOI] [PubMed] [Google Scholar]
- 73.Shinoda W, DeVane R, Klein ML. Soft Matter. 2008;4:2454–2462. [Google Scholar]
- 74.DeVane R, Shinoda W, Moore PB, Klein ML. J Chem Theory Comput. 2009;5:2115–2124. doi: 10.1021/ct800441u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Drenscko M, Loverde SM. Mol Simulat. 2017;43:234–241. [Google Scholar]
- 76.Loverde SM, Klein ML, Discher DE. Adv Mater. 2012;24:3823–3830. doi: 10.1002/adma.201103192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Goux WJ, Kopplin L, Nguyen AD, Leak K, Rutkofsky M, Shanmuganandam VD, Sharma D, Inouye H, Kirschner DA. J Biol Chem. 2004;279:26868–26875. doi: 10.1074/jbc.M402379200. [DOI] [PubMed] [Google Scholar]
- 78.He X, Shinoda W, DeVane R, Klein ML. Mol Phys. 2010;108:2007–2020. [Google Scholar]
- 79.Reith D, Pütz M, Müller-Plathe F. J Comput Chem. 2003;24:1624–1636. doi: 10.1002/jcc.10307. [DOI] [PubMed] [Google Scholar]
- 80.Hockney RW, Eastwood JW. Computer Simulation using Particles. IOP Publishing Ltd; Bristol, England: 1988. [Google Scholar]
- 81.Ballenegger V, Cerda JJ, Lenz O, Holm C. Journal of Chemical Physics. 2008:128. doi: 10.1063/1.2816570. [DOI] [PubMed] [Google Scholar]
- 82.de Joannis J, Arnold A, Holm C. Journal of Chemical Physics. 2002;117:2503–2512. [Google Scholar]
- 83.Plimpton S. J Comput Phys. 1995;117:1–19. [Google Scholar]
- 84.Kamberaj H, Low RJ, Neal MP. J Chem Phys. 2005;122:224114. doi: 10.1063/1.1906216. [DOI] [PubMed] [Google Scholar]
- 85.Hoover WG. Phys Rev A. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 86.Martyna GJ, Klein ML, Tuckerman M. J Chem Phys. 1992;97:2635–2643. [Google Scholar]
- 87.Martyna GJ, Tuckerman ME, Tobias DJ, Klein ML. Mol Phys. 1996;87:1117–1157. [Google Scholar]
- 88.Tuckerman ME, Alejandre J, López-Rendón R, Jochim AL, Martyna GJ. J Phys A-MathTheor. 2006;39:5629–5651. [Google Scholar]
- 89.Roche C, Sun H-J, Leowanawat P, Araoka F, Partridge BE, Peterca M, Wilson DA, Prendergast ME, Heiney PA, Graf R, Spiess HW, Zeng X, Ungar G, Percec V. Nat Chem. 2016;8:80–89. doi: 10.1038/nchem.2397. [DOI] [PubMed] [Google Scholar]
- 90.Cheetham AG, Lin Y-a, Lin R, Cui H. Acta Pharmacol Sin. 2017 doi: 10.1038/aps.2016.151. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Cheetham AG, Zhang P, Lin YA, Lin R, Cui H. J Mater Chem B. 2014;2:7316–7326. doi: 10.1039/C4TB01084A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Su H, Zhang P, Cheetham AG, Koo JM, Lin R, Masood A, Schiapparelli P, Quiñones-Hinojosa A, Cui H. Theranostics. 2016;6:1065–1074. doi: 10.7150/thno.15420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Loverde SM, Ortiz V, Kamien RD, Klein ML, Discher DE. Soft Matter. 2010;6:1419–1425. doi: 10.1039/b919581e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Rieth S, Li Z, Hinkle CE, Guzman CX, Lee JJ, Nehme SI, Braunschweig AB. J Phys Chem C. 2013;117:11347–11356. [Google Scholar]
- 95.Matmour R, De Cat I, George SJ, Adriaens W, Leclère P, Bomans PHH, Sommerdijk NAJM, Gielen JC, Christianen PCM, Heldens JT, van Hest JCM, Löwik DWPM, De Feyter S, Meijer EW, Schenning APHJ. J Am Chem Soc. 2008;130:14576–14583. doi: 10.1021/ja803026j. [DOI] [PubMed] [Google Scholar]
- 96.Huber V, SS, Würthner F. Chem Eur J. 2008;14:7791–7807. doi: 10.1002/chem.200800764. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.