Ergodic and localized regions in quantum spin glasses on the Bethe lattice

Abstract

By considering the quantum dynamics of a transverse-field Ising spin glass on the Bethe lattice, we find the existence of a many-body localized (MBL) region at small transverse field and low temperature. The region is located within the thermodynamic spin glass phase. Accordingly, we conjecture that quantum dynamics inside the glassy region is split into a small MBL region and a large delocalized (but not necessarily ergodic) region. This has implications for the analysis of the performance of quantum adiabatic algorithms.

This article is part of the themed issue ‘Breakdown of ergodicity in quantum systems: from solids to synthetic matter’.

1. Introduction

In recent years, the study of the different dynamical regimes of isolated quantum systems has received a lot of attention, due to improved experimental techniques [1,2] and theoretical progress. In the latter, one can identify two distinguished but not independent lines of research: the first is the study of how ergodicity is realized in isolated quantum systems, a mechanism that goes under the name of the eigenstate thermalization hypothesis (ETH) [3–5]; the second is the study of the most typical mechanism for failure of ergodicity in the presence of quenched disorder [6–10] (although some authors have suggested that disorder in the initial state suffices [11,12]) named many-body localization (MBL). While dynamical phases satisfying the ETH can be described by the usual tools of statistical mechanics and thermodynamics, MBL systems behave a lot like integrable systems [13] with local integrals of motions [9,14–17]: transport is suppressed [18,19], entanglement entropy grows slowly to its thermodynamic value [20] and some symmetry-breaking phases can exist, to which the Mermin–Wagner theorem does not apply, in low dimensions and at high temperature [21].

Soon after its inception, it was pointed out that MBL phases can be detrimental [22] for the performance of the adiabatic quantum computation protocol introduced in [23] (see also [24]). This has been contested in later works [25] and it remains a controversial claim. As this protocol has proved to be the most promising for the realization of a quantum computer [26], sorting out this question is of paramount importance for both theoretical discussions and technological implications.

In a series of recent works, which involve one of the present authors [27–29], the question of the appearance of an MBL phase in some models of quantum spin glasses has been addressed, with the result that, for realistic, mean-field glasses, MBL can exist only in finite-connectivity models, while in fully connected models only a weaker form, a remnant of the clustering phase existing in the phase space of the classical model [30], exists. These earlier works point to the necessity to examine a finite-connectivity quantum spin glass, in search of MBL.

In this work, we set out to do exactly this: we analyse the quantum dynamics of an isolated quantum spin glass, showing that there is an ETH phase at large transverse field, possibly extending all the way down to the spin glass phase, while, at all system sizes we were able to study, an MBL phase exists for small transverse field. Therefore, there should be an MBL–ETH dynamical transition in between.

2. Thermodynamics

The focus of the present paper is the transverse-field Ising spin glass model defined on a regular random graph (RRG) of degree d=3, whose Hamiltonian is defined by

2.1

where Γ>0 is the strength of the transverse field, the disordered interaction couplings J_ij take either of the two values in {±1} with equal probability and (for a=x,z) is a Pauli matrix acting on the ith spin of the system. The sum of the terms 〈i,j〉 is taken over the edges of a 3-RRG . Consequently, the Hamiltonian of equation (2.1) has two sources of disorder: the disordered interactions J_ij and the topology of the underlying RRG .

Here and in what follows, a d-regular¹ random graph (d-RRG) of size N is defined as a graph uniformly sampled from the set of all connected graphs with N vertices and fixed degree d. These graphs are related to the d-regular Bethe lattice, the unique (up to isomorphism) connected tree graph of fixed degree d with denumerably many vertices. The Bethe lattice was introduced in [31] to define models where the Bethe–Peierls approximation is exact. Regular graphs can be seen as finite-size approximations to the Bethe lattice in the sense that, even though they contain loops (and the Bethe lattice does not), the fraction of loops of any fixed length ℓ vanishes as the size N approaches infinity (i.e. almost all loops are of length greater than ℓ). Thus RRGs are ‘tree-like’ in the (finite-size) neighbourhood of any of their vertices, and are locally indistinguishable from the Bethe lattice (figure 1). For this reason, RRGs in the limit have been used to model the statistical properties of the Bethe lattice, and approximation schemes related to the Bethe–Peierls method (such as the cavity method and belief-propagation algorithms) are expected to perform well when applied to systems with local interactions that define an RRG structure.

Figure 1.

Locally, both the Bethe lattice (a) and an RRG (b) have a tree structure. The loops that are present in an RRG appear only at the global scale (c). (Online version in colour.)

The thermodynamical properties of the Hamiltonian of equation (2.1) were studied in a series of papers [32,33] that collectively reconstructed the equilibrium phase diagram shown in figure 2. For large values of the transverse field, or for high temperatures, the system lies in a paramagnetic phase where the z-component of each spin fluctuates randomly, so that the average z-magnetization is zero. In the region of small values of Γ and low temperatures T, each spin freezes independently in the z-direction and the system enters a phase where the Edwards–Anderson order parameter,

becomes strictly positive with a continuous transition [32,34].

Figure 2.

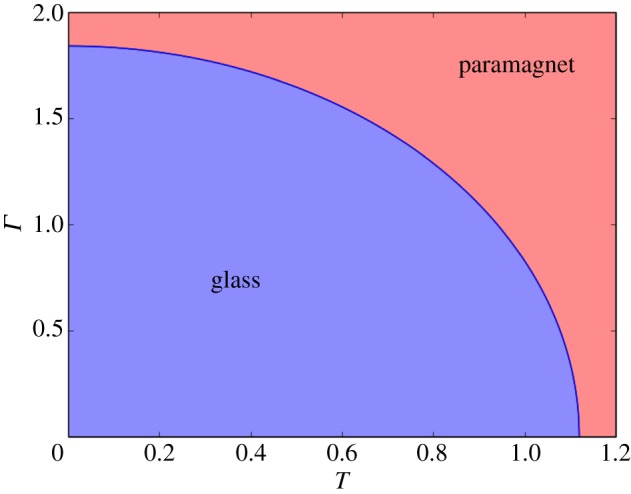
Phase diagram of the transverse-field Ising spin glass model of equation (2.1). The model transitions from a paramagnetic to a glassy phase for small values of the transverse field Γ and temperature T. (Online version in colour.)

The classical Γ=0 line of the phase diagram, where the transition is driven solely by the temperature, was studied in [35], where it was found that the critical temperature was given by the formula . The interior of the (T,Γ) plane was studied in [32]. The authors developed a quantum version of the cavity method to explore numerically the thermodynamic limit of the model and compute the critical line. The physics of the quantum T=0 line was studied by a series of papers [32,33] that gave various estimates of the critical point using cavity-like approximation schemes affected by the systematic error that these methods exhibit when applied to loopy graphs. It was conclusively studied numerically in [34] where the critical value of the transverse field was computed by path-integral Monte Carlo methods using several different physical quantities. All were found to agree on an estimated value of Γ_c=1.82±0.02 with a finite-size correction that disappears as 1/N for . Zero-temperature properties of the ground state were also studied in [34], where the ground state was found to have volumetric entanglement—as measured by the Rényi entropy of order two—in the entire part of the T=0 line which lies in the paramagnetic phase. The equal-time spin–spin connected correlation function in the z-direction,

was also studied in [34] in order to analyse the average and the extremal behaviour of the correlations across the transition. They considered the spatial maximal correlation , defined by picking the maximal value of C_ij among all spins j that are at fixed distance r from a given spin i (and averaging over i), and the mean correlation C_mean(r), defined by taking the average value of C_ij among all spins j that are at fixed distance r from i. Both were shown to follow a stretched exponential decay, and the correlation lengths extracted from them were found to converge to a finite value at the critical point of the transition in the thermodynamic limit.

3. Ergodic region at large transverse field

To develop some intuition about the phase transition, Mossi et al. [34] did a perturbative expansion by using the modulus of the interaction strength J=|J_ij| as the perturbative parameter. For ease of reference, we summarize here their results. The ‘free’ Hamiltonian is the transverse-field term . By shifting the ground-state energy E₀=−ΓN to zero, its spectrum is given by

Its unique ground state |0〉 (where we define ),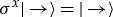

is taken as a pseudovacuum of quasiparticles. The operators 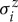create an excitation on top of the ground state

which is interpreted as a state containing a quasiparticle at site i. These form the N-fold degenerate eigenspace of H₀ with energy 2Γ. Additional applications of the operators either move the state upwards in the spectrum, creating states with two, three or more quasiparticles |i,j〉,|i,j,k〉,…, or downwards, by annihilating existing quasiparticles.

The perturbed Hamiltonian is

where V is the dimensionless spin glass term .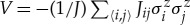

First-order perturbation theory gives a null correction to the ground-state energy

because . The degenerate band of one-particle states is split by the perturbation into distinct levels

3.1

for n=1,…,N, where JE_n are eigenvalues and {|ϕ_n〉} are the eigenvectors of the operator , which is the perturbation operator V restricted to the (unperturbed) one-particle subspace. The direct computation of the requires the diagonalization of an N by N matrix which, we will show, is a hopping matrix on the RRG.

Let us start by noting that the term 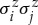applied to a quasiparticle state |i′,j′,k′,…〉 can affect it in one of three ways: (i) it can create a pair of adjacent quasiparticles provided sites i and j are devoid of them; (ii) it can move a quasiparticle from site i to site j provided site j is empty and site i is occupied (or vice versa, swapping the role of i and j); or (iii) it can annihilate a pair of adjacent quasiparticles sitting on sites i and j.

Note also that, in the one-particle subspace, annihilation processes cannot happen, while creation processes map a state into the three-particle subspace, which is orthogonal to the one-particle subspace. Therefore, only the hopping processes give a contribution to equation (3.1). For any state |ψ〉 in the one-particle subspace, the action of is then equivalent to that of H_hop, the Hamiltonian of a particle hopping on the same graph , with disordered hopping constants J_ij=±J:

For contrast, consider the Hamiltonian of a particle hopping on the graph with homogeneous hopping coefficients J>0. Even though solving for the spectrum of the latter Hamiltonian is difficult for any finite graph , in the thermodynamic limit, our RRG is the Bethe lattice and hence spectral properties of this model can be computed exactly using an iterative method (see [36,37] and figure 3). In particular, its spectral density is known to be supported on the set , where K is the constant connectivity of the graph. We give the proof here. One starts by writing down iteration equations for the diagonal Green’s function at the site i for generic complex E:

3.2

where the cavity Green’s function 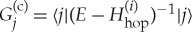is the Green’s function of the operator 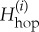obtained from the Hamiltonian H_hop by removing the hopping terms associated with the edges incident to site i. On the Bethe lattice the removal of these terms splits the system into K+1 isomorphic disconnected components that can be considered independently. Each component is an infinite rooted tree with a branching factor of K. These trees are isomorphic to each of their infinite descending subtrees rooted at any of their vertices. By writing the iteration equation (3.2) for , one gets

3.3

where G^(c′)_k is a second-step cavity Green’s function obtained from the G^(c)_j Hamiltonian by further removing the hopping terms associated with the edges incident to j. By solving (3.3) and plugging the result in (3.2), one recovers G_i and from G_i the spectral density

Figure 3.

(a) The diagonal Green’s function G_i at the point i=0 on a 3-regular Bethe lattice can be computed once the values G^(c)_j are known at the points j=1,2,3 (shown in darker red). is the Green’s function, computed at site j, of the operator obtained from the Hamiltonian H_hop by removing the hopping terms associated with the dashed edges of the graph. (b) Each disconnected component thus obtained is an infinite binary tree that is isomorphic to all its infinite descending binary subtrees (one such subtree is shown on the left in green). (Online version in colour.)

One can find P(ℑΣ_i) by and taking the limit ℑE→0. As we know from [6], the distribution of ℑΣ will tend to a delta function for delocalized states and to a long-tailed distribution for localized states. However, we can sidestep all this procedure by recognizing that, in all the equations, only appears and therefore the case J_ij=±J is identical to the case J_ij=J constant, which has only delocalized states. The latter statement follows from the observation that, given the constant connectivity of the graph and the constant value of the hopping J, the distribution of G^(c) must be a delta function centred on the solution of the deterministic equation (3.2):

3.4

which gives

3.5

By inserting (3.5) into (3.2), one gets

so

irrespective of i and therefore all the eigenstates are delocalized.

By extending this reasoning to any sector with n particles, as soon as n is finite when we can conclude that all such few-particle states are delocalized. When n/N becomes appreciable and the interaction between the particles can no longer be neglected, we shall conjecture that the introduction of a small interaction between the particles (which is of O(J²/Γ)), irrespective of its attractive or repulsive nature, does not localize excitations (this is true even in the presence of bound states) and the phase remains delocalized. We cannot predict the value of Γ/J where this breaks down without considering quantitatively the interaction between the particles.

Having showed that there is an ergodic region for large Γ/J, we will show in the following section that, starting from the opposite limit Γ/J≪1, we do have a localized region. Therefore, there must be at least one dynamical phase transition in between. We unfortunately are not able to answer the question whether this transition is unique or a crossover through a sequence of ergodicity-breaking transitions.

4. Many-body localization at small transverse field

(a). Localization and the forward approximation

Let us consider the Hamiltonian (2.1) for small values of Γ. Then H=H(Γ) can be treated as a small perturbation of the spin glass term with the transverse-field operator 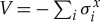acting as the perturbation:

Note that is diagonal in the N-fold σ^z product basis, whose elements we label by strings a∈{±1}^N through the usual identification |↑〉≡|1〉 and |↓〉≡|−1〉. Now and throughout this section, we use Latin letters a,b,c,…,x,y,z to label energies and eigenstates of the unperturbed Hamiltonian H₀, while Greek letters α,β,γ,… are reserved as labels for the energies and the eigenstates of the perturbed Hamiltonian, so that in the limit the perturbed Greek labels ‘converge’ to their corresponding Latin label,² e.g. for the energies and for the energy eigenstates .

The eigenstates |ψ(Γ)〉 of the Hamiltonian H(Γ) can be chosen to depend continuously on the parameter Γ, and will converge to the eigenstates of H₀ in the limit . Consequently, if we write the wavefunctions of the states |ψ(Γ)〉 in the unpertubed energy eigenbasis

we expect that these will converge to Kronecker delta functions as |ψ(Γ)〉 changes into the corresponding unperturbed eigenstate |a〉; this means that the state |ψ(Γ)〉 will be localized for small Γ. In the previous section, we saw that, in the large Γ limit, these states are delocalized, so we expect that there will be a value Γ_c where transition between these two behaviours occurs. In fact, if we write the Hamiltonian in the eigenbasis of H₀, we get

4.1

This is related to the Anderson model that describes a particle hopping on a lattice while under the effect of a disordered potential. This model is known to enter a localized phase when the disordered term dominates the hopping term. In equation (4.1), the unperturbed energies {E_a} are the equivalent of a disordered potential, while the values are the hopping coefficients for the particle. Note that here the underlying geometry of the hopping is defined by the matrix elements : sites a,a′ are adjacent (i.e. the particle can hop directly from one to the other) if and only if 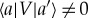. As the hopping is suppressed and the system is likely to enter a disorder-induced localized phase. In the transverse-field Ising spin glass Hamiltonian (2.1), the perturbation defines a hopping over the N-dimensional Boolean hypercube .

A disorder-driven localization/delocalization transition is usually studied as a function of two quantities: the energy density ϵ of the eigenstates considered and the strength W of the disorder in the Hamiltonian. One usually finds that states at a fixed energy density ϵ change from delocalized to localized as the disorder strength W is increased, with an energy-dependent critical value W_c(ϵ) that marks the boundary between these two behaviours. The set of critical points W_c(ϵ) for different values of ϵ define the ‘mobility edge’ of the system.

In our set-up, we keep the strength of the disordered interactions fixed so the relative strength of the disorder with respect to the ordering term is controlled by the parameter W/Γ=1/Γ. The mobility edge will consequently be defined by the critical values Γ_c(ϵ)≡1/W_c(ϵ).

Let us better define the kind of localization we will study. First, we fix a value ϵ for the energy density and Γ for the strength of the transverse field. For a given realization of disorder of the Hamiltonian H(Γ) (2.1) defined on a system of size N and a state |ψ〉 with localization centre |v〉 and energy density ϵ, we define

4.2

where the distance is taken over the Boolean hypercube. Note that in order to compute ψ_r from the amplitudes , one needs to know (or find out) the localization centre of the state |ψ〉. Next, for fixed and real numbers C,ξ>0 we define the quantity P(N,r,ξ) as the probability (taken over all disorder realizations of H(Γ) of size N and states of energy density ϵ) that the random variable satisfies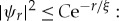

We say that a disordered system is localized if there exists a real number ξ>0 such that

This means that the probability distribution is under an exponentially decaying envelope, except possibly for a region of finite radius.

Note that we can write equivalently

so we can study the distribution of the values of the random variable . It was observed [38] that if the system is localized, then, in the limit the random variable Z_N is peaked around the value

4.3

which gives the value of Γ_c(ϵ). In practice, one can calculate ψ with Γ=1 and get Γ_c. By the way, the relation tells us the critical exponent for the ξ divergence is 1, because ξ∼1/|Γ−Γ_c|.

We have seen how one can study the localization properties of disordered systems by looking at the wave function values ψ(x). Of course this is not always a simple task, as it usually requires the diagonalization of a matrix whose size grows exponentially with the size of the system. However, in a perturbative set-up such as the one we described, we can use a technique known as the ‘forward approximation’ [6,38], namely, we neglect the renormalization of the free energy of the unperturbed eigenstates {|a〉}. This is known to give an underestimate of the critical hopping strength in both the many-body and Anderson localization; it is then useful for our purpose of proving the stability of the phase (basically the same strategy is used in [7,16]).

The forward approximation states that, for a perturbed energy eigenstate |ψ_α〉 that converges to |a〉 at Γ=0, the value of the wave function ψ_α(b)=〈b|ψ_α〉 can be approximated by a sum of contributions associated with the shortest paths connecting sites a and b in the Boolean hypercube:

4.4

where the set spaths(a,b) contains the shortest paths from a to b.

Note that the sum over paths of equation (4.4) can be computed numerically using a transfer matrix technique, in which case one computes iteratively the vector

4.5

with

4.6

4.7

4.8

4.9

where N is the distance between a and b in the Boolean hypercube. One can decrease memory requirements by noting that the vector v is very sparse during most of the computation, hence at each step most entries of the transfer matrix are irrelevant. This is because repeated applications of to the initial state define a diffusion process on the Boolean hypercube where, at each step t, one needs to propagate only the amplitudes of the vertices exactly at distance t from the initial vertex. This means that, in practice, one does not need to store in memory the entire transfer matrix , but instead a new transfer matrix is defined at each step that only propagates amplitudes from vertices actually relevant for that single step of propagation. This requires storing only non-zero entries instead of N2^N of the full transfer matrix . The vector v_t needs to store only entries.

(b). Numerical results

In this section, we apply the previously described methods to the transverse-field Ising spin glass Hamiltonian (2.1). Here, we immediately face an issue: the computation of the forward approximation is obstructed by the fact that the spin glass term has highly degenerate energy levels. This gives rise to diverging terms in equation (4.4) when E_a=E_i. To avoid this problem, we add a weak and random longitudinal field term H_long to the Hamiltonian H₀:

where each h_i is distributed uniformly in (−h,h) with h=0.001 (this has to be ≪1/N but ≫e^−aN). This has the effect of splitting the degeneracies while introducing only a negligible effect on the energies of the configurations (and therefore in the amplitudes ψ_α(b)) and on the amplitudes of transition between non-degenerate states.

We compute the many-body mobility edge for the system in the following way. For each system size N=18, 20, 22, 24, 26, we randomly generate a suitable number of realizations of disorder and, for each of these, we generate a set of initial states a=a₁,a₂,…,a_k, making sure that their energy densities ϵ_a=E_a/N are (approximately) uniformly distributed in the range allowed by the model. Each of these states a is then propagated to its -symmetric state b=−a (global spin flip) using the forward approximation algorithm with fixed Γ=1 in order to compute

Note that the configuration −a is the only configuration b∈{±1}^N to satisfy dist(a,b)=N; ergo for the state |ψ_α〉 we read from equation (4.2) that (after setting r=N)

The results are then binned according to the energy density of the initial state a and the average value of the random variable was taken for each bin, obtaining Z_N(ϵ)=〈Z_N〉.

Using the formula 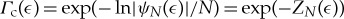from equation (4.3), we obtain a plot of the MBL critical point as a function of the energy density ϵ shown in figure 4. Note that this is the energy density of the unperturbed eigenstates |a〉, while usually one would write Γ_c as a function of the energy density of the perturbed eigenstates |ψ_α〉. However, the perturbed energies E_α=E_a+O(Γ²) coincide with the unperturbed ones up to second-order corrections in Γ, which we neglect.

Figure 4.

Finite-size estimates for Γ_c as a function of the unperturbed energy density ϵ, obtained using forward approximation together with a linear fit of the data at largest N. The ground-state energy density of the unperturbed model in the thermodynamic limit is ϵ₀≈−1.25, shown here as a black dashed line, while the critical energy density for the classical (Γ=0) glassy transition is ϵ_c≈−1.05, shown as a red dashed line. (Online version in colour.)

To plot the MBL critical line in the (T,Γ) phase diagram and compare it to the boundary of the glassy phase, we have to compute the relation T=T(ϵ) between temperature and (disorder-averaged) energy density. We used standard Monte Carlo methods to extract the (thermal) average energy density of different realizations of disorder at various temperatures and fixed Γ=0; then we took the average over the results.³ To better understand the low-energy regime, we studied the ground state of the unperturbed (i.e. Γ=0) model. For each size N=18,20,22,24,26, we generated a large number (1000 or more) of instances and extracted one of the ground states by performing a thermal annealing (whose results were checked against an exact solver for the smaller sizes). For each ground state we computed the Γ_c value using forward approximation. The disorder-averaged results are shown in figure 5. Extrapolations give a value of Γ_c=0.67 in the thermodynamic limit, which seems consistent with figure 4.

Figure 5.

Estimates of Γ_c for the ground state (T=0 case) for different system sizes N. As the disorder-averaged energy density of the ground state decreases towards the expected thermodynamic limit value of ϵ₀=−1.25. A linear interpolation of the Γ_c values obtained gives a thermodynamic limit value of Γ_c=0.67. (Online version in colour.)

Finally, we plotted a finite-size (N=26) estimate of the MBL critical line and the line of the glassy transition in the (T,Γ) phase diagram (figure 6). The MBL phase seems to be strictly contained in the glassy phase; therefore there is a region of the phase diagram where the system is both glassy and delocalized.

Figure 6.

Phase diagram of the Hamiltonian of the Ising spin glass in a transverse field (equation (2.1)). The MBL critical line obtained from the numerical data is shown as linked blue dots. The T=0 point was obtained from the thermodynamic-limit extrapolation of figure 5, while the finite-temperature points were derived from the Γ_c values for the largest size (N=26) of figure 4. With the possible exception of the small T>1.1 tail, the MBL phase seems to be a proper subset of the glassy phase. (Online version in colour.)

5. Conclusion

We studied the localization properties of the transverse-field Ising spin glass model on the 3-RRG in the limit where the transverse field is weak compared to the disordered interactions. This model is known to exhibit a transition from a paramagnetic to a glassy phase at low temperatures and a weak transverse field. The classical Ising spin glass model is widely believed to capture the complicated combinatorial structure of general NP-hard computational problems, while the zero-temperature, weak transverse-field regime describes the final stage of a quantum annealing protocol designed to find the ground-state energy of the Ising spin glass. MBL has been argued to be an obstacle to efficient quantum annealing due to the presence of exponentially closing gaps in the localized phase.

We computed numerically the many-body mobility edge of the system in the forward approximation, finding that the energy eigenstates of the system indeed localize for small values of the transverse field at finite system sizes. When plotted against the equilibrium phase diagram of the model, we discovered that the localized region does not coincide with the glassy phase. In particular, evidence points to the fact that the glassy phase is partitioned into a delocalized region and a localized one. We conjecture that the glassy, delocalized region will exhibit the same clustering of eigenstates observed in [29] for the p-spin model, where the eigenstates were found to form clusters inside of which the energies are distributed according to Wigner–Dyson, while the global distribution of the energy levels of the model is Poissonian.

Moreover, we expect that classical methods that exploit the fine-tuning of thermal relaxation (such as simulated annealing) will perform poorly in the entire glassy phase, while quantum annealers will perform poorly only once localization sets in. Therefore, we conjecture that, in the glassy, delocalized region of the phase space, quantum annealing algorithms can outperform any classical thermal annealing protocol.

A natural future direction outlined by our work would be to check whether the same localization/delocalization transition is present when the disordered term of the Hamiltonian encodes real-life computational problems such as 3-SAT (3-satisfiability). In the affirmative case, a detailed comparison of the performance of, for example, simulated annealing and quantum annealing (either simulated numerically or by an actual experiment) inside of the region that is both glassy and delocalized would help shed light on the realistic capabilities of quantum annealers over classical thermal annealing and other algorithms based on stochastic local optimization.

Data accessibility

All numerical data are accessible upon request to the corresponding author.

Authors' contributions

Both authors conceived and designed the study, G.M. carried out the numerical simulations. Both authors contributed in analysing the data and drafting the manuscript. Both authors gave their final approval for publication.

Competing interests

The authors declare that they have no competing interests.

Funding

A.S. acknowledges financial support in the form of a Google Faculty Research Award.