Skip to main content
NCBI home page
Philosophical transactions. Series A, Mathematical, physical, and engineering sciences logoLink to Philosophical transactions. Series A, Mathematical, physical, and engineering sciences
. 2017 Oct 30;375(2108):20160434. doi: 10.1098/rsta.2016.0434

Dynamical manifestations of quantum chaos: correlation hole and bulge

E J Torres-Herrera 1, Lea F Santos 2,✉
PMCID: PMC5665786  PMID: 29084885

Abstract

A main feature of a chaotic quantum system is a rigid spectrum where the levels do not cross. We discuss how the presence of level repulsion in lattice many-body quantum systems can be detected from the analysis of their time evolution instead of their energy spectra. This approach is advantageous to experiments that deal with dynamics, but have limited or no direct access to spectroscopy. Dynamical manifestations of avoided crossings occur at long times. They correspond to a drop, referred to as correlation hole, below the asymptotic value of the survival probability and to a bulge above the saturation point of the von Neumann entanglement entropy and the Shannon information entropy. By contrast, the evolution of these quantities at shorter times reflects the level of delocalization of the initial state, but not necessarily a rigid spectrum. The correlation hole is a general indicator of the integrable–chaos transition in disordered and clean models and as such can be used to detect the transition to the many-body localized phase in disordered interacting systems.

This article is part of the themed issue ‘Breakdown of ergodicity in quantum systems: from solids to synthetic matter’.

Keywords: correlation hole, level repulsion, quench dynamics

1. Introduction

Quantum chaos refers to specific properties of the spectrum and the eigenstates of a system, most notably to correlations between the eigenvalues that result in avoided crossings [1–5]. In the context of nuclear physics, the analysis of the statistical properties of nuclear spectra revealing level repulsion dates back to Wigner’s works [6,7] and was soon extended to other complex systems, such as atoms, molecules and condensed matter models. From a dynamical perspective, the onset of quantum chaos has been associated with very fast relaxation processes. Nevertheless, fast time evolution is found also in non-chaotic systems. This paper is devoted to the description of dynamical quantities that can unambiguously identify the presence of level repulsion in isolated finite lattice many-body quantum systems.

Strongly perturbed isolated finite many-body quantum systems equilibrate in a probabilistic sense. After a transient time, the dynamics saturates and the observables fluctuate around their infinite-time average, remaining very close to this average value for most of the time. In an attempt to distinguish quantum motion in chaotic and regular systems, Peres [8] argued that after the saturation of the evolution of the Loschmidt echo, the fluctuations in chaotic models should be smaller than in regular systems. More recently, however, it has been shown that after equilibration the amplitudes of the fluctuations of various observables decrease with system size in a very similar way for chaotic and also integrable systems with interactions [9–12]. In terms of the values reached by the observables after equilibration, comparisons between infinite-time averages and thermodynamic averages have been used to determine the onset of thermalization and by extension of quantum chaos [13,14], although the results are highly dependent on the initial state [15,16]. In contrast with these approaches, we focus here on evident manifestations of avoided crossings that emerge before the equilibration of the system.

Quantum chaos has been linked with the linear growth in time of the von Neumann entanglement entropy up to saturation [17]. This behaviour is analogous to what happens to the Shannon information entropy [18,19], which has the advantage of not requiring any partial trace of the system. However, the linear growth of these entropies is observed also in interacting integrable models [18–22]. Similarly, quantum chaos has been connected with the initial exponential decay of the survival probability and Loschmidt echo [23–26], but the same is verified in integrable models [27] and decays even faster are found in both regimes [28–33].

In one-dimensional interacting systems with onsite disorder, spatial localization due to large disorder occurs in parallel with the disappearance of level repulsion. Dynamical features at the vicinity of the delocalized–localized transition, which encompass the logarithmic growth of both entanglement and Shannon entropies [19,34–36] and the power-law decay of the survival probability with exponents smaller than 1 [19,37,38], may then be taken as signatures of the chaos–integrable transition. But this is a very particular example, where both transitions coincide. We seek for means to differentiate chaos from integrability in general scenarios, including also clean models and disordered systems in the proximity of spatially delocalized integrable points.

The power-law decay of the survival probability at long times is not exclusive to systems in the vicinity of the transition to the many-body localized phase. This behaviour is inevitable for any quantum system, but its source as well as the values of the power-law exponents vary [39,40]. One ever-present cause of the power-law decay is the unavoidable bounds in the energy spectrum of quantum systems [41,42]. In lattice many-body quantum systems with two-body interactions, the spectrum energy bound can lead to power-law exponents close to 2 [39,40]. Such large exponents indicate chaotic initial states [39,40], but they are still not explicit signatures of level repulsion.

Unambiguous dynamical manifestations of level repulsion occur at yet longer times, after the power-law decay and before equilibration. It shows up in the form of a drop in the value of the survival probability below its saturation point, a phenomenon known as correlation hole [43]. As we discuss here, it also leads to a minor bulge above the saturation values of the Shannon and entanglement entropies. The correlation hole reflects the correlations of the eigenvalues of complex systems. It is the dip of the spectral form factor discussed in [44]. It has also been investigated in molecules [43,45–49], random matrices [50–54], microwave billiards [55,56] and disordered spin models [19]. Here, we extend these studies to clean and disordered spin-Inline graphic models.

We stress that, in this work, we equate the term quantum chaos with level repulsion, more precisely with the Wigner–Dyson distribution of the spacings between neighbouring levels [1–3]. An alternative approach is to view quantum chaos as the emergence of chaotic eigenstates. The latter refers to states with a very large number of uncorrelated components, which may occur even in systems that do not show level repulsion [13]. This leads to generic dynamical behaviours that exhibit very fast relaxation processes. This second viewpoint is inspired by early works from Chirikov [57,58].

This paper is organized as follows. Section 2 presents the models and dynamical quantities studied. Section 3 compares the dynamics of integrable and chaotic models without random disorder, using for that the evolution of the entanglement entropy, the Shannon entropy and the survival probability. Section 4 shows how the correlation hole can be used to indicate the transition to a many-body localized phase. Section 5 presents the conclusions.

2. Spin-Inline graphic models and quantities analysed

We investigate a one-dimensional spin-Inline graphic system with an even number L of sites. The Hamiltonian is given by

2. 2.1

Above, Inline graphic and Inline graphic are spin operators acting on site k, Inline graphic being Pauli matrices. Three defects are created by applying three different local static magnetic fields in the z-direction on the first, last and middle sites. These fields lead, respectively, to the following Zeeman splittings: ε1J,εLJ and dJ. The Zeeman splittings hkJ correspond to onsite disorder caused by additional static magnetic fields; hk are random numbers from a uniform distribution in [−h,h]. Equation (2.1) contains couplings between nearest neighbour (NN) and next-nearest neighbour (NNN) sites. They include the flip-flop terms and Ising interactions. J is the exchange coupling, Δ is the anisotropy parameter, and λ is the ratio between the NN and NNN couplings. We set J=1. The sum for NN (NNN) couplings runs up to L−1 (L−2) for open boundary conditions and up to L for closed (periodic) boundary conditions.

Hamiltonian (2.1) conserves the total spin in the z-direction, Inline graphic, so Inline graphic. We deal with the sector that has L/2 up-spins and dimension Inline graphic.

The purpose of the defects on site 1 and site L is to reduce finite size effects and break symmetries, such as parity, conservation of total spin and spin reversal. We consider ε1,εL as small random numbers from a uniform distribution in the interval [−0.1,0.1].

(a). Spin models with and without random disorder

In §3, the results for three models without random onsite disorder (h=0), but with ε1,εL≠0, and open boundary conditions are compared. The models are as follows:

  • (i) For Δ≠0 and d,λ=0, equation (2.1) corresponds to the integrable XXZ model. Note that the integrability is not broken by the addition of border defects [59]. We choose Δ=0.48. The level spacing distribution in this case is Poisson, as typical of integrable models, where the eigenvalues are uncorrelated and crossings are not prohibited.

  • (ii) The system becomes chaotic and shows a Wigner–Dyson distribution when Inline graphic [60–62]. We fix d=0.9 and λ=0 and refer to it as the defect model.

  • (iii) Chaos also emerges when Inline graphic [62–65]. We choose λ=1 and d=0 and denote this case as the NNN model.

In §4, we study the disordered model of spins 1/2 with h≠0, Δ=1, ε1,εL,d,λ=0 and periodic boundary conditions. As h increases from zero to Inline graphic, the level spacing distribution changes from Poisson to Wigner–Dyson [60,66] and the eigenstates become even more delocalized in space [67]. As the disorder strength is further increased, the distribution transitions from Wigner–Dyson back to Poisson and the eigenstates become more localized in space [60,67,68].

(b). Basis and initial states

When studying localization in space, it is natural to choose the site-basis vectors, as we do in this work. They are also known in quantum information theory as computational-basis vectors. These states have on each site a spin that either points up or down in the z-direction, as for example |↓↑↓↑↓↑↓↑⋯ 〉z. We note, however, that further insights on the interplay between interaction and disorder may be gained by analysing the eigenstates also in other basis vectors, such as those corresponding to the eigenstates of the XXZ model [68].

The site-basis vectors are denoted by |ϕn〉. They are the initial states, |Ψ(0)〉=|ϕn=ini〉, that we use in the analysis of the system dynamics.

(c). Dynamical quantities

We study the evolution of the von Neumann entanglement, Shannon information entropy and survival probability.

(i). Entanglement entropy

The von Neumann entanglement entropy, SvN, is obtained by separating the system in subsystems A and B and then performing the partial trace of one of the two [69]. The entanglement entropy is the von Neumann entropy of the reduced density matrix ρA=TrB[ρ], where ρ is the density matrix of the total system. We divide the chain in two equal sizes, so the dimension of ρA is Inline graphic.

The system is initially in the product state ρ(0)=|Ψ(0)〉〈Ψ(0)|=|ϕini〉〈ϕini|, so SvN(0)=0. As time passes, the amount of entanglement grows as quantified by

(i). 2.2

(ii). Shannon entropy

The Shannon information entropy, SSh, is often used to measure the level of delocalization of the eigenstates in a chosen basis [4]. It can also be used to quantify the spreading in time of the initial state on a selected basis. For the site-basis vectors, it is written as

(ii). 2.3

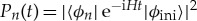where Inline graphic and Inline graphic is the dimension of the subspace considered.

We note that the Shannon entropy when written in the energy eigenbasis is now commonly referred to as diagonal entropy [70,71]. Comparisons between the diagonal entropy and entanglement entropy in the context of thermalization can be found in [72].

(iii). Survival probability and correlation hole

The survival probability, Inline graphic, is the probability for finding the system in its initial state later in time. For Inline graphic, it is given by

(iii). 2.4

where Inline graphic is the overlap between the initial state and the eigenstates Inline graphic of the Hamiltonian H that evolves |Ψ(0)〉, Eα are the eigenvalues of H and Inline graphic is the energy distribution weighted by the squared overlaps Inline graphic. This distribution is known as the local density of states (LDOS) or strength function.

The survival probability is the absolute square of the Fourier transform of the LDOS. If one has detailed information about the LDOS, one should be able to predict the evolution of Pini(t). Equivalently, Pini(t) is the Fourier transform of the spectral autocorrelation function, G(E), that is

(iii). 2.5

and

(iii). 2.6

It is clear from equations (2.5) and (2.6) that the dephasing of the initial state depends on both the initial state, through the overlaps Inline graphic, and the spacings between all energy levels.

The first term of G(E) leads to the infinite-time average of the survival probability Inline graphic. It is larger than zero in finite systems. The lowest values are reached by full random matrices (FRMs), which are matrices filled with random numbers whose sole constraint is to satisfy the symmetries of the system they represent [3]. For the FRMs of Gaussian orthogonal ensembles (GOEs), Inline graphic [4,18], where Inline graphic is the dimension of the random matrix.

The second term of G(E) determines the decay of Pini(t) and the fluctuations around the infinite-time average. In the case of FRM, it factorizes into a term depending only on the overlaps and one depending only on the eigenvalues, as

(iii). 2.7

Above, 〈.〉FRM denotes the average over an ensemble of FRMs.

The average over the distribution of level spacings leads to

(iii). 2.8

where R2(E1,E2) is the Dyson two-level correlation function [1]. R2(E1,E2) gives the probability for finding a level around the energies E1 and E2. This function can be written as R2(E1,E2)=R1(E1)R1(E2)−T2(E1,E2), where R1(E) is the density of states and T2(E1,E2) is the two-level cluster function [1].

The Fourier transform of T2(E1,E2) is non-zero only in systems that show level repulsion, being zero if the level spacing distribution is Poisson [3]. The Fourier transform of T2(E1,E2) is directly related to the level number variance [3,5], a quantity that measures the level of rigidity of the spectrum. Contrary to signatures of chaos associated with the spacings of neighbouring levels, the level number variance detects long-range correlations between the eigenvalues. Correlations between energy levels are the source of the drop of Pini(t) below Inline graphic, which is known as the correlation hole [43,45–56]. The correlation hole occurs at long times and disappears as we approach the Heisenberg time (the inverse of the mean level spacing [73]). In the particular case of FRMs from GOEs, the minimal value reached by Pini(t) due to the correlation hole is Inline graphic [52].

In FRMs, R1(E) and ρini(E) coincide, both having a semicircular form [30–32]. The similarity between density of states and LDOS holds also in realistic many-body models with two-body interactions when the initial state is very delocalized in the energy eigenbasis. However, in this case, the shape of both distributions is Gaussian [30–32]. The shape of the LDOS determines the behaviour of the survival probability at short times. The Fourier transform of a Gaussian envelope results in the Gaussian decay Inline graphic, where

(iii). 2.9

is the square of the width of the LDOS. Notice that this is not simply the quadratic decay that develops at very short times, 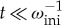Inline graphic, but a true Gaussian behaviour that can hold until the inevitable power-law decay develops [39,40].

3. Dynamical manifestation of level repulsion

We compare results for the integrable XXZ model with those for the chaotic defect and NNN models. To reduce finite size effects, we average the results over different realizations of random numbers representing the small border defects ε1 and εL. We also perform averages over initial states chosen at random among all site-basis vectors. As the density of states is Gaussian, the majority of these states have energy close to the middle of the spectrum. The results after performing all averages are denoted by 〈.〉.

(a). Growth in time of the entanglement and Shannon entropies

The main panels in figure 1 reinforce ideas presented in previous works. They show the evolution of the entanglement entropy (figure 1a,b,c) (equation (2.2)) and of the Shannon entropy (figure 1d,e,f) (equation (2.3)) for the XXZ (a,d), defect (b,e) and NNN (c,f) models. As described below, the behaviours are very similar for both entropies and for the integrable and chaotic models.

Figure 1.

Figure 1.

Open in a new tab

Evolution of the entanglement entropy (a,b,c) and Shannon entropy (d,e,f) for the XXZ (a,d), defect (b,e) and NNN (c, f) models. Dashed horizontal lines give the saturation values. The insets in (b) and (e) are zoom-ins of the plots at long times. The parameters are Δ=0.48, d=0.9, λ=1, h=0, L= 16, Inline graphic, Inline graphic=12 870, Inline graphicA=256; open boundaries. Average over 50 initial states corresponding to randomly selected site-basis vectors and average over 20 realizations of random border defects. (Online version in colour.)

For Inline graphic, the entropies grow quadratically [31], as expected by simply expanding the expressions in equations (2.2) and (2.3). Subsequently, the increase is nearly linear until saturation. The linear increase of the entropies reflects the large number of decay channels available for the initial state, not necessarily the presence of level repulsion. This was stressed in [18,21,22], where clean models were considered, and also in [19] for disordered systems. In [21,22], the Shannon entropy was studied for initial states corresponding to mean-field basis vectors. This allowed for the derivation of analytical expressions following the steps discussed in [74]. In [18], both entropies were considered, but only for two specific site-basis vectors, the Néel state and the domain wall state. Here, we average the results over 50 different site-basis vectors and also over 20 realizations of random border defects, so the curves are smoother.

The fact that both entropies lead to very similar behaviours suggests that any of the two can be equivalently used to study non-equilibrium quantum dynamics. In this context, entanglement does not appear to be an essential property [67,75]. The advantage of the Shannon entropy is to be computationally less expensive, because it does not require the partial trace of the system. It would be interesting, however, to identify which features of the dynamics of many-body quantum systems one entropy can detect that the other cannot.

At first sight, the results for the entropies in the main panels of figure 1 seem unable to differentiate integrable from chaotic models. However, the Shannon entropy explicitly contains the survival probability,

(a). 3.1

so one might expect that it could capture some signature of level repulsion. Specifically, in the time interval where the correlation hole takes place for the survival probability, equation (3.1) suggests that an increase beyond the saturation value for the Shannon entropy could happen. By substantially zooming in the results at long times, we indeed find such bulge. It is visible for both entropies in the chaotic defect model, as shown in the insets of figure 1b,e, but no sign of it appears in the integrable XXZ model. We note that the averages over initial states are necessary to smoothen the curves and reveal the correlation bulge. Averages over more states and for larger system sizes should further reduce the fluctuations.

(b). Emergence of the correlation hole

The survival probability is a very simple quantity that contains a lot of information about the system and its evolution at different timescales. When systems with two-body interactions are strongly perturbed out of equilibrium, as in the cases where site-basis vectors evolve under the XXZ, defect and NNN models, the envelope of the LDOS is Gaussian and the initial decay of the survival probability is also Gaussian [30–32]. This is illustrated in figure 2 for the three models: XXZ (a,d), defect (b,e) and NNN (c,f). This behaviour persists up to t∼2. Between t∼2 and t∼10, there are oscillations most likely associated with finite size effects and the energy bounds of the spectrum [39,40]. They can lead to values of 〈Pini(t)〉 below the saturation line, but they are not yet related to the correlation hole. In the examples of figure 2, these drops are more significant for the clean XXZ and NNN models than for the defect model.

Figure 2.

Figure 2.

Open in a new tab

Survival probability for the XXZ (a,d), defect (b,e) and NNN (c,f) models. The parameters are Δ=0.48, d=0.9, λ=1, h=0, L=16, Inline graphic, Inline graphic. Average over 50 initial states corresponding to randomly selected site-basis vectors and average over 20 realizations of random border defects. (Online version in colour.)

Owing to the energy bounds in the spectrum, the initial Gaussian decay gives place to a power-law decay at later times. For small system sizes, this behaviour is noticeable in disordered models [19,39,40], where averages over several disorder realizations and initial states are performed. The power-law decay is not visible in figure 2, probably because of large finite size effects. However, the small values of the survival probability, Inline graphic, for Inline graphic suggest an underlying power-law behaviour. In the vicinity of the point where the decay of the survival probability changes from Gaussian to power-law, there occurs an interference between the two contributions. This causes a phenomenon known as survival collapse [41,76,77] that often results in Inline graphic, as indeed confirmed for spin-Inline graphic systems in [40].

It is for times even longer, t>10, that the correlation hole finally develops, first for the NNN model, where the minimum occurs at t∼111 for the parameters of figure 2, and later for the defect model, where the minimum is at t∼564. This difference in time must be caused by the level of rigidity of the spectra of the two models. For the chosen parameters, the spectrum of the NNN model is more rigid than that for the defect model [61].

By comparing figure 2e and the inset of figure 1e, we note that the maximum value in the bulge of the Shannon entropy occurs at a time of the same order of magnitude as the time for the minimum of the correlation hole. After the correlation hole, the survival probability simply fluctuates around the saturation point, Inline graphic. The fluctuations tend to be smaller in chaotic models (compare figure 2d,e), but they decrease with system size in a similar way for chaotic and interacting integrable models [11].

4. Transition to the many-body localized phase

The characterization of the interacting disordered spin-Inline graphic model with h≠0 and λ=0 in terms of level statistics as well as delocalization and entanglement measures was first performed in 2004 [67]. As h increases from zero, 0≤h≤1, the system undergoes a transition from integrability to chaos followed in parallel by an increase in the level of delocalization of the eigenstates written in the site basis. As h further increases above 1, the system undergoes a second transition, now from chaos to integrability along with the spatial localization of the eigenstates. This section focuses on the two transition regions, with emphasis on the second one, between the chaotic phase and the spatially localized phase.

In this second transition region, the level statistics is intermediate between Wigner–Dyson and Poisson and the eigenstates are multifractal [37]. We deal in this case with extended non-ergodic eigenstates that become more correlated as h increases [19]. These correlations are responsible for the logarithmic growth of the entanglement [34,35] and Shannon entropies [19], and for the power-law decays of local observables [78,79], out-of-time order correlators [80] and survival probability with power-law exponents smaller than 1 [19,37]. It was shown in [19,37] that Inline graphic and Wini(t)∝t−D2, where D2 is the fractal dimension obtained from scaling analysis of the participation ratio of the initial state projected into the energy eigenbasis. D2 also agrees with the fractal dimension obtained from scaling analysis of the participation ratio of the eigenstates written in the site-basis vectors.

As the spatial delocalized–localized transition in disordered models with interactions happens in parallel with the transition from a Wigner–Dyson to a Poisson distribution [67], we can use the disappearance of level repulsion as a signature of the transition to the many-body localized phase. One way to do this is by computing the eigenvalues to directly study level statistics. The other is by analysing the evolution of the survival probability and how the correlation hole fades away as the disorder strength becomes large. The latter is the approach taken here. As explained in §2c(iii), the correlation hole exists only in systems that show level repulsion. There is a one-to-one correspondence between level statistics and the long-time behaviour of the survival probability.

Figure 3 shows the survival probability for various values of h smaller than the critical point for the transition to spatial localization. The decay is Gaussian at short times and subsequently becomes power-law. For disorder strengths in the intermediate region between the chaotic limit and the many-body localized phase, the Fourier transform of the autocorrelation function in equation (2.5), G(E)∝ED2−1, leads to the power-law decay with exponent D2<1. This exponent reflects the level of correlations of the eigenstates [19,37]. In the chaotic regime, the power-law exponent is larger than 1 and can no longer be explained in terms of the correlations between eigenstates. The power-law decay in this case is associated with the inevitable presence of energy bounds in the spectrum of quantum systems [39,40]. By taking these bounds into account when performing the Fourier transform of a Gaussian LDOS in equation (2.4), we find the maximum value 2 for the power-law exponent.

Figure 3.

Figure 3.

Open in a new tab

Survival probability up to saturation. The values of h are indicated in the figure; Δ=1, ε1,L,d,λ=0, L=16, Inline graphicz=0. The dashed lines in (a–h) indicate the infinite-time average, Inline graphic. Average performed over approximately 103 different initial states corresponding to site-basis vectors with energy in the middle of the spectrum and over 102 disorder realizations. (Online version in colour.)

At long times, beyond the power-law decay and before the saturation of 〈Pini(t)〉, the correlation hole emerges when the spectrum shows level repulsion. In figure 3a, where the disorder strength is very small and the system is close to the delocalized integrable XXZ model, one hardly sees the hole. It gets deeper as h increases from zero. The maximum level of chaoticity, in the sense of proximity to the GOE Wigner–Dyson distribution, happens at h∼0.5 for the system size considered here. At this point, the correlation hole is deepest (figure 3c). For even larger h, the hole starts shrinking once again. As the level of correlation between the eigenvalues decreases and the spectrum becomes less rigid, the correlation hole gets postponed to later times and fades away, as verified from figure 3c–h.

To quantify the depth of the correlation hole, we calculate

4. 4.1

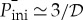where Inline graphic is the minimum value of 〈Pini(t)〉. Recall from the discussions in §2c(iii) that for FRMs of GOEs, Inline graphic and Inline graphic, so Inline graphic. Figure 4a,c shows κ as a function of the disorder strength; figure 4a is linear in h and figure 4b is logarithmic in h. The measure κ reaches the largest values in the chaotic region (h∼0.5), where it approaches κFRM. It decreases for h<0.5, as the system approaches the integrable point of the clean XXZ model, and for h>0.5, as the system approaches spatial localization. The depth of the correlation is therefore a general indicator of the integrable–chaos transition, which therefore captures also the spatial delocalized–localized transition.

Figure 4.

Figure 4.

Open in a new tab

The depth κ of the correlation hole (a,c) and the chaos indicator η (b,d) versus disorder strength. The system sizes are L=12 (circles), L=14 (diamonds) and L=16 (triangles); Δ=1, ε1,L,d,λ=0, Inline graphicz=0. The dashed lines in (a,c) indicate the maximum Inline graphic reached by FRM. Average performed over approximately 103 different initial states corresponding to site-basis vectors with energy in the middle of the spectrum and over 102 disorder realizations. (Online version in colour.)

Figure 4b,d shows results for the chaos indicator η computed with the eigenvalues and defined as

4. 4.2

where P(s) is the level spacing distribution, PP(s) denotes the Poisson distribution, PWD(s) is the Wigner–Dyson distribution, and s0 is the first point of intersection between PP(s) and PWD(s). When the distribution is Poisson, Inline graphic, and for the Wigner–Dyson, Inline graphic. The comparison between the left and right panels makes evident the correspondence between level statistics and the long-time behaviour of the survival probability. We note, however, that while P(s) detects the short-range correlations between the eigenvalues, the depth of the correlation hole detects also the long-range correlations [81], so κ and η are actually complementary.

The logarithmic scale of the x-axis in figure 4c,d draws attention to the first transition from delocalized integrable to chaos. One sees that the range of disorder strengths for which κ is large and η is small increases as the system size increases. This indicates that in the thermodynamic limit, this transition region may disappear and an infinitesimally small h may suffice to take the system into the chaotic regime [61,82]. Figure 4a,b makes more visible the second transition from chaos to spatial localization. Here also, one sees that the chaotic region gets extended, holding for larger values of h as L increases. This region may disappear in the thermodynamic limit, or it may reduce to a single critical point as in Anderson localization in higher dimensions, or yet it may remain a finite region. What will in fact happen to the two transition regions, integrable–chaos and chaos–localization, for Inline graphic as well as the differences and similarities between the two are open questions.

5. Conclusion

We analysed how the presence of level repulsion manifests itself in the dynamics of many-body quantum systems. We showed that it appears in the form of a correlation hole in the long-time evolution of the survival probability and as a minor bulge above the saturation values of the Shannon and entanglement entropies. The correlation hole detects integrable–chaos transitions in clean and disordered models, and by extension it is also an indicator of the spatial delocalized–localized transition in interacting systems with random onsite disorder. The correlation hole is not exclusive to the survival probability and is seen also in experimental observables, such as the density imbalance [83].

As the correlation hole reveals the statistical properties of the spectrum from the time domain, it is advantageous to experiments that have low energy resolution and to experiments that do not have direct access to the energy levels. The hole was observed in molecules. It requires long-time coherences to be seen in experiments with cold atoms and trapped ions, although these timescales are still shorter than those needed to reach equilibration. Another prerequisite for the observation of the correlation hole in relatively small systems is the performance of averages over initial states and disorder realizations that can smoothen the curves and thus reveal the hole.

It is worth emphasizing once again the similarities between the dynamical behaviour of the Shannon entropy and the entanglement entropy in clean and disordered systems. The entanglement entropy is not only computationally more involved, but also experimentally challenging. The Shannon entropy should be a more accessible quantity to current experiments that investigate non-equilibrium quantum dynamics.

Acknowledgements

E.J.T.-H. thanks the LNS-BUAP for allowing use of its supercomputing facility and the Aspen Center for Physics for its hospitality, where part of this work was done. L.F.S. thanks Antonio García-García for useful discussions.

Data accessibility

Codes are available at https://www.yu.edu/faculty-bios/santos/computer-codes.

Authors' contributions

E.J.T.-H was in charge of §4 and L.F.S. of §3.

Competing interests

The authors declare that there are no competing interests.

Funding

E.J.T.-H. acknowledges funding from PRODEP-SEP and Proyectos VIEP-BUAP, Mexico. L.F.S. was supported by NSF grant no. DMR-1603418.

References

  • 1.Mehta ML. 1991. Random matrices. Boston, MA: Academic Press. [Google Scholar]
  • 2.Brody TA, Flores J, French JB, Mello PA, Pandey A, Wong SSM. 1981. Random-matrix physics—spectrum and strength fluctuations. Rev. Mod. Phys. 53, 385 ( 10.1103/RevModPhys.53.385) [DOI] [Google Scholar]
  • 3.Guhr T, Mueller-Gröeling A, Weidenmüller HA. 1998. Random matrix theories in quantum physics: common concepts. Phys. Rep. 299, 189–425. ( 10.1016/S0370-1573(97)00088-4) [DOI] [Google Scholar]
  • 4.Zelevinsky V, Brown BA, Frazier N, Horoi M. 1996. The nuclear shell model as a testing ground for many-body quantum chaos. Phys. Rep. 276, 85–176. ( 10.1016/S0370-1573(96)00007-5) [DOI] [Google Scholar]
  • 5.Stöckmann H-J. 2006. Quantum chaos: an introduction. Cambridge, UK: Cambridge University Press. [Google Scholar]
  • 6.Wigner EP. 1951. On the statistical distribution of the widths and spacings of nuclear resonance levels. Proc. Cambridge Phil. Soc. 47, 790–798. ( 10.1017/S0305004100027237) [DOI] [Google Scholar]
  • 7.Wigner EP. 1958. On the distribution of the roots of certain symmetric matrices. Ann. Math. 67, 325–327. ( 10.2307/1970008) [DOI] [Google Scholar]
  • 8.Peres A. 1984. Stability of quantum motion in chaotic and regular systems. Phys. Rev. A 30, 1610–1615. ( 10.1103/PhysRevA.30.1610) [DOI] [Google Scholar]
  • 9.Reimann P. 2008. Foundation of statistical mechanics under experimentally realistic conditions. Phys. Rev. Lett. 101, 190403 ( 10.1103/PhysRevLett.101.190403) [DOI] [PubMed] [Google Scholar]
  • 10.Short AJ. 2011. Equilibration of quantum systems and subsystems. New J. Phys. 13, 053009 ( 10.1088/1367-2630/13/5/053009) [DOI] [Google Scholar]
  • 11.Zangara PR, Dente AD, Torres-Herrera EJ, Pastawski HM, Iucci A, Santos LF. 2013. Time fluctuations in isolated quantum systems of interacting particles. Phys. Rev. E 88, 032913 ( 10.1103/PhysRevE.88.032913) [DOI] [PubMed] [Google Scholar]
  • 12.Kiendl T, Marquardt F.2016. Many-particle dephasing after a quench. (http://arxiv.org/abs/1603.01071. )
  • 13.Borgonovi F, Izrailev FM, Santos LF, Zelevinsky VG. 2016. Quantum chaos and thermalization in isolated systems of interacting particles. Phys. Rep. 626, 1–58. ( 10.1016/j.physrep.2016.02.005) [DOI] [Google Scholar]
  • 14.D’Alessio L, Kafri Y, Polkovnikov A, Rigol M. 2016. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys. 65, 239–362. ( 10.1080/00018732.2016.1198134) [DOI] [Google Scholar]
  • 15.Rigol M, Srednicki M. 2012. Alternatives to eigenstate thermalization. Phys. Rev. Lett. 108, 110601 ( 10.1103/PhysRevLett.108.110601) [DOI] [PubMed] [Google Scholar]
  • 16.Torres-Herrera EJ, Santos LF. 2013. Effects of the interplay between initial state and Hamiltonian on the thermalization of isolated quantum many-body systems. Phys. Rev. E 88, 042121 ( 10.1103/PhysRevE.88.042121) [DOI] [PubMed] [Google Scholar]
  • 17.Eisert J, Cramer M, Plenio MB. 2010. Colloquium: area laws for the entanglement entropy. Rev. Mod. Phys. 82, 277–306. ( 10.1103/RevModPhys.82.277) [DOI] [Google Scholar]
  • 18.Torres-Herrera EJ, Karp J, Távora M, Santos LF. 2016. Realistic many-body quantum systems versus full random matrices: static and dynamical properties. Entropy 18, 359 ( 10.3390/e18100359) [DOI] [Google Scholar]
  • 19.Torres-Herrera EJ, Santos LF. 2017. Extended nonergodic states in disordered many-body quantum systems. Ann. Phys. (Berlin) 529, 1600284 ( 10.1002/andp.201600284) [DOI] [Google Scholar]
  • 20.Balachandran V, Benenti G, Casati G, Gong J. 2010. Phase-space characterization of complexity in quantum many-body dynamics. Phys. Rev. E 82, 046216 ( 10.1103/PhysRevE.82.046216) [DOI] [PubMed] [Google Scholar]
  • 21.Santos LF, Borgonovi F, Izrailev FM. 2012. Chaos and statistical relaxation in quantum systems of interacting particles. Phys. Rev. Lett. 108, 094102 ( 10.1103/PhysRevLett.108.094102) [DOI] [PubMed] [Google Scholar]
  • 22.Santos LF, Borgonovi F, Izrailev FM. 2012. Onset of chaos and relaxation in isolated systems of interacting spins-1 2: energy shell approach. Phys. Rev. E 85, 036209 ( 10.1103/PhysRevE.85.036209) [DOI] [PubMed] [Google Scholar]
  • 23.Jacquod P, Silvestrov P, Beenakker C. 2001. Golden rule decay versus Lyapunov decay of the quantum Loschmidt echo. Phys. Rev. E 64, 055203 ( 10.1103/PhysRevE.64.055203) [DOI] [PubMed] [Google Scholar]
  • 24.Cucchietti FM, Lewenkopf CH, Mucciolo ER, Pastawski HM, Vallejos RO. 2002. Measuring the Lyapunov exponent using quantum mechanics. Phys. Rev. E 65, 046209 ( 10.1103/PhysRevE.65.046209) [DOI] [PubMed] [Google Scholar]
  • 25.Prosen T. 2002. General relation between quantum ergodicity and fidelity of quantum dynamics. Phys. Rev. E 65, 036208 ( 10.1103/PhysRevE.65.036208) [DOI] [PubMed] [Google Scholar]
  • 26.Weinstein YS, Emerson J, Lloyd S, Cory D. 2003. Fidelity decay saturation level for initial eigenstates. Quant. Inf. Proc. 1, 439–448. ( 10.1023/A:1024018431394) [DOI] [Google Scholar]
  • 27.Torres-Herrera EJ, Santos LF. 2014. Isolated many-body quantum systems far from equilibrium: relaxation process and thermalization. AIP Conf. Proc. 1619, 171–180. ( 10.1063/1.4899233) [DOI] [Google Scholar]
  • 28.Flambaum VV, Izrailev FM. 2001. Unconventional decay law for excited states in closed many-body systems. Phys. Rev. E 64, 026124 ( 10.1103/PhysRevE.64.026124) [DOI] [PubMed] [Google Scholar]
  • 29.Kota VKB. 2014. Embedded random matrix ensembles in quantum physics. Lecture Notes in Physics, vol. 884. Heidelberg, Germany: Springer ( 10.1007/978-3-319-04567-2) [DOI]
  • 30.Torres-Herrera EJ, Santos LF. 2014. Quench dynamics of isolated many-body quantum systems. Phys. Rev. A 89, 043620 ( 10.1103/PhysRevA.89.043620) [DOI] [Google Scholar]
  • 31.Torres-Herrera EJ, Vyas M, Santos LF. 2014. General features of the relaxation dynamics of interacting quantum systems. New J. Phys. 16, 063010 ( 10.1088/1367-2630/16/6/063010) [DOI] [Google Scholar]
  • 32.Torres-Herrera EJ, Santos LF. 2014. Nonexponential fidelity decay in isolated interacting quantum systems. Phys. Rev. A 90, 033623 ( 10.1103/PhysRevA.90.033623) [DOI] [Google Scholar]
  • 33.Torres-Herrera EJ, Kollmar D, Santos LF. 2016. Relaxation and thermalization of isolated many-body quantum systems. Phys. Scr. T 165, 014018 ( 10.1088/0031-8949/2015/T165/014018) [DOI] [Google Scholar]
  • 34.Žnidarič M, Prosen T, Prelovšek P. 2008. Many-body localization in the Heisenberg XXZ magnet in a random field. Phys. Rev. B 77, 064426 ( 10.1103/PhysRevB.77.064426) [DOI] [Google Scholar]
  • 35.Bardarson JH, Pollmann F, Moore JE. 2012. Unbounded growth of entanglement in models of many-body localization. Phys. Rev. Lett. 109, 017202 ( 10.1103/PhysRevLett.109.017202) [DOI] [PubMed] [Google Scholar]
  • 36.Luitz DJ, Lev YB.2016. Anomalous thermalization in ergodic systems. (http://arxiv.org/abs/1607.01012. )
  • 37.Torres-Herrera EJ, Santos LF. 2015. Dynamics at the many-body localization transition. Phys. Rev. B 92, 014208 ( 10.1103/PhysRevB.92.014208) [DOI] [Google Scholar]
  • 38.Torres-Herrera EJ, Távora M, Santos LF. 2016. Survival probability of the Néel state in clean and disordered systems: an overview. Braz. J. Phys. 46, 239–247. ( 10.1007/s13538-015-0366-3) [DOI] [Google Scholar]
  • 39.Távora M, Torres-Herrera EJ, Santos LF. 2016. Inevitable power-law behavior of isolated many-body quantum systems and how it anticipates thermalization. Phys. Rev. A 94, 041603 ( 10.1103/PhysRevA.94.041603) [DOI] [Google Scholar]
  • 40.Távora M, Torres-Herrera EJ, Santos LF. 2017. Power-law decay exponents: a dynamical criterion for predicting thermalization. Phys. Rev. A 95, 013604 ( 10.1103/PhysRevA.95.013604) [DOI] [Google Scholar]
  • 41.Muga JG, Ruschhaupt A, del Campo A. 2009. Time in quantum mechanics, vol. 2 London, UK: Springer. [Google Scholar]
  • 42.del Campo A. 2016. Exact quantum decay of an interacting many-particle system: the Calogero-Sutherland model. New J. Phys. 18, 015014 ( 10.1088/1367-2630/18/1/015014) [DOI] [Google Scholar]
  • 43.Leviandier L, Lombardi M, Jost R, Pique JP. 1986. Fourier transform: a tool to measure statistical level properties in very complex spectra. Phys. Rev. Lett. 56, 2449–2452. ( 10.1103/PhysRevLett.56.2449) [DOI] [PubMed] [Google Scholar]
  • 44.Cotler JS, Gur-Ari G, Hanada M, Polchinski J, Saad P, Shenker SH, Stanford D, Streicher A, Tezuka M.2016. Black holes and random matrices. (http://arxiv.org/abs/1611.04650. )
  • 45.Pique JP, Chen Y, Field RW, Kinsey JL. 1987. Chaos and dynamics on 0.5–300 ps time scales in vibrationally excited acetylene: Fourier transform of stimulated-emission pumping spectrum. Phys. Rev. Lett. 58, 475–478. ( 10.1103/PhysRevLett.58.475) [DOI] [PubMed] [Google Scholar]
  • 46.Guhr T, Weidenmüller H. 1990. Correlations in anticrossing spectra and scattering theory. Analytical aspects. Chem. Phys. 146, 21–38. ( 10.1016/0301-0104(90)90003-R) [DOI] [Google Scholar]
  • 47.Lombardi M, Seligman TH. 1993. Universal and nonuniversal statistical properties of levels and intensities for chaotic Rydberg molecules. Phys. Rev. A 47, 3571–3586. ( 10.1103/PhysRevA.47.3571) [DOI] [PubMed] [Google Scholar]
  • 48.Michaille L, Pique J-P. 1999. Influence of experimental resolution on the spectral statistics used to show quantum chaos: the case of molecular vibrational chaos. Phys. Rev. Lett. 82, 2083–2086. ( 10.1103/PhysRevLett.82.2083) [DOI] [Google Scholar]
  • 49.Alhassid Y, Fyodorov YV, Gorin T, Ihra W, Mehlig B. 2006. Fano interference and cross-section fluctuations in molecular photodissociation. Phys. Rev. A 73, 042711 ( 10.1103/PhysRevA.73.042711) [DOI] [Google Scholar]
  • 50.Hartmann U, Weidenmüller H, Guhr T. 1991. Correlations in anticrossing spectra and scattering theory: numerical simulations. Chem. Phys. 150, 311–320. ( 10.1016/0301-0104(91)87105-5) [DOI] [Google Scholar]
  • 51.Delon A, Jost R, Lombardi M. 1991. NO2 jet cooled visible excitation spectrum: vibronic chaos induced by the X2 A1-A2 B2 interaction. J. Chem. Phys. 95, 5701–5718. ( 10.1063/1.461620) [DOI] [Google Scholar]
  • 52.Alhassid Y, Levine RD. 1992. Spectral autocorrelation function in the statistical theory of energy levels. Phys. Rev. A 46, 4650–4653. ( 10.1103/PhysRevA.46.4650) [DOI] [PubMed] [Google Scholar]
  • 53.Gorin T, Prosen T, Seligman TH. 2004. A random matrix formulation of fidelity decay. New J. Phys. 6, 20 ( 10.1088/1367-2630/6/1/020) [DOI] [Google Scholar]
  • 54.Leyvraz F, García A, Kohler H, Seligman TH. 2013. Fidelity under isospectral perturbations: a random matrix study. J. Phys. A 46, 275303 ( 10.1088/1751-8113/46/27/275303) [DOI] [Google Scholar]
  • 55.Kudrolli A, Sridhar S, Pandey A, Ramaswamy R. 1994. Signatures of chaos in quantum billiards: microwave experiments. Phys. Rev. E 49, R11–R14. ( 10.1103/PhysRevE.49.R11) [DOI] [PubMed] [Google Scholar]
  • 56.Alt H, Gräf H-D, Guhr T, Harney HL, Hofferbert R, Rehfeld H, Richter A, Schardt P. 1997. Correlation-hole method for the spectra of superconducting microwave billiards. Phys. Rev. E 55, 6674–6683. ( 10.1103/PhysRevE.55.6674) [DOI] [Google Scholar]
  • 57.Chirikov BV. 1985. An example of chaotic eigenstates in a complex atom. Phys. Lett. A 108, 68–70. ( 10.1016/0375-9601(85)90518-3) [DOI] [Google Scholar]
  • 58.Chirikov B. 1997. Linear and nonlinear dynamical chaos. Open Syst. Inform. Dyn. 4, 241–280. ( 10.1023/A:1009678102891) [DOI] [Google Scholar]
  • 59.Alcaraz FC, Barber MN, Batchelor MT, Baxter RJ, Quispel GRW. 1987. Surface exponents of the quantum XXZ, Ashkin-Teller and Potts models. J. Phys. A 20, 6397–6409. ( 10.1088/0305-4470/20/18/038) [DOI] [Google Scholar]
  • 60.Santos LF. 2004. Integrability of a disordered Heisenberg spin-1 2 chain. J. Phys. A 37, 4723–4729. ( 10.1088/0305-4470/37/17/004) [DOI] [Google Scholar]
  • 61.Torres-Herrera EJ, Santos LF. 2014. Local quenches with global effects in interacting quantum systems. Phys. Rev. E 89, 062110 ( 10.1103/PhysRevE.89.062110) [DOI] [PubMed] [Google Scholar]
  • 62.Gubin A, Santos LF. 2012. Quantum chaos: an introduction via chains of interacting spins 1_ 2. Am. J. Phys. 80, 246–251. ( 10.1119/1.3671068) [DOI] [Google Scholar]
  • 63.Hsu TC, d’Auriac JCA. 1993. Level repulsion in integrable and almost-integrable quantum spin models. Phys. Rev. B 47, 14 291–14 296. ( 10.1103/PhysRevB.47.14291) [DOI] [PubMed] [Google Scholar]
  • 64.Kudo K, Deguchi T. 2005. Level statistics of XXZ spin chains with discrete symmetries: analysis through finite-size effects. J. Phys. Soc. Jpn. 74, 1992–2000. ( 10.1143/JPSJ.74.1992) [DOI] [Google Scholar]
  • 65.Santos LF. 2009. Transport and control in one-dimensional systems. J. Math. Phys. 50, 095211 ( 10.1063/1.3181223) [DOI] [Google Scholar]
  • 66.Avishai Y, Richert J, Berkovitz R. 2002. Level statistics in a Heisenberg chain with random magnetic field. Phys. Rev. B 66, 052416 ( 10.1103/PhysRevB.66.052416) [DOI] [Google Scholar]
  • 67.Santos LF, Rigolin G, Escobar CO. 2004. Entanglement versus chaos in disordered spin systems. Phys. Rev. A 69, 042304 ( 10.1103/PhysRevA.69.042304) [DOI] [Google Scholar]
  • 68.Dukesz F, Zilbergerts M, Santos LF. 2009. Interplay between interaction and (un)correlated disorder in one-dimensional many-particle systems: delocalization and global entanglement. New J. Phys. 11, 043026 ( 10.1088/1367-2630/11/4/043026) [DOI] [Google Scholar]
  • 69.Amico L, Fazio R, Osterloh A, Vedral V. 2008. Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576. ( 10.1103/RevModPhys.80.517) [DOI] [Google Scholar]
  • 70.Polkovnikov A. 2011. Microscopic diagonal entropy and its connection to basic thermodynamic relations. Ann. Phys. (N.Y.) 326, 486–499. ( 10.1016/j.aop.2010.08.004) [DOI] [Google Scholar]
  • 71.Santos LF, Polkovnikov A, Rigol M. 2011. Entropy of isolated quantum systems after a quench. Phys. Rev. Lett. 107, 040601 ( 10.1103/PhysRevLett.107.040601) [DOI] [PubMed] [Google Scholar]
  • 72.Santos LF, Polkovnikov A, Rigol M. 2012. Weak and strong typicality in quantum systems. Phys. Rev. E 86, 010102(R) ( 10.1103/PhysRevE.86.010102) [DOI] [PubMed] [Google Scholar]
  • 73.García-García AM, Verbaarschot JJM. 2016. Spectral and thermodynamic properties of the Sachdev-Ye-Kitaev model. Phys. Rev. D 94, 126010 ( 10.1103/PhysRevD.94.126010) [DOI] [Google Scholar]
  • 74.Flambaum VV, Izrailev FM. 2001. Entropy production and wave packet dynamics in the fock space of closed chaotic many-body systems. Phys. Rev. E 64, 036220 ( 10.1103/PhysRevE.64.036220) [DOI] [PubMed] [Google Scholar]
  • 75.Brown WG, Santos LF, Starling D, Viola L. 2008. Quantum chaos, localization, and entanglement in disordered Heisenberg models. Phys. Rev. E 77, 021106 ( 10.1103/PhysRevE.77.021106) [DOI] [PubMed] [Google Scholar]
  • 76.Rufeil-Fiori E, Pastawski H. 2006. Non-Markovian decay beyond the Fermi golden rule: survival collapse of the polarization in spin chains. Chem. Phys. Lett. 420, 35–41. ( 10.1016/j.cplett.2005.12.025) [DOI] [Google Scholar]
  • 77.Rufeil-Fiori E, Pastawski H. 2009. Survival probability of a local excitation in a non-Markovian environment: survival collapse, Zeno and anti-Zeno effects. Physica B 404, 2812–2815. ( 10.1016/j.physb.2009.06.109) [DOI] [Google Scholar]
  • 78.Serbyn M. 2014. Quantum quenches in the many-body localized phase. Phys. Rev. B 90, 174302 ( 10.1103/PhysRevB.90.174302) [DOI] [Google Scholar]
  • 79.Luitz DJ, Laflorencie N, Alet F. 2016. Extended slow dynamical regime close to the many-body localization transition. Phys. Rev. B 93, 060201 ( 10.1103/PhysRevB.93.060201) [DOI] [Google Scholar]
  • 80.Fan R, Zhang P, Shen H, Zhai H.2016. Out-of-time-order correlation for many-body localization. (http://arxiv.org/abs/1608.01914. )
  • 81.Ma J-Z. 1995. Correlation hole of survival probability and level stastics. J. Phys. Soc. Jpn. 64, 4059–4063. ( 10.1143/JPSJ.64.4059) [DOI] [Google Scholar]
  • 82.Santos LF, Rigol M. 2010. Onset of quantum chaos in one-dimensional bosonic and fermionic systems and its relation to thermalization. Phys. Rev. E 81, 036206 ( 10.1103/PhysRevE.81.036206) [DOI] [PubMed] [Google Scholar]
  • 83.Torres-Herrera EJ, García-García AM, Santos LF. 2017 Generic dynamical features of quenched interacting quantum systems: survival probability, density imbalance and out-of-time-ordered correlator. (https://arxiv.org/abs/1704.06272. ) [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

Codes are available at https://www.yu.edu/faculty-bios/santos/computer-codes.

Articles from Philosophical transactions. Series A, Mathematical, physical, and engineering sciences are provided here courtesy of The Royal Society

RESOURCES