Skip to main content
PMC home page
Philosophical Transactions of the Royal Society B: Biological Sciences logoLink to Philosophical Transactions of the Royal Society B: Biological Sciences
. 2017 Oct 23;372(1735):20160416. doi: 10.1098/rstb.2016.0416

Information theory, evolutionary innovations and evolvability

Andreas Wagner 1,2,3,✉
PMCID: PMC5665804  PMID: 29061889

Abstract

How difficult is it to ‘discover’ an evolutionary adaptation or innovation? I here suggest that information theory, in combination with high-throughput DNA sequencing, can help answer this question by quantifying a new phenotype's information content. I apply this framework to compute the phenotypic information associated with novel gene regulation and with the ability to use novel carbon sources. The framework can also help quantify how DNA duplications affect evolvability, estimate the complexity of phenotypes and clarify the meaning of ‘progress’ in Darwinian evolution.

This article is part of the themed issue ‘Process and pattern in innovations from cells to societies’.

Keywords: evolvability, gene duplication, progress

1. Introduction

Evolutionary biologists have a long-standing interest in information theory, because it is ultimately information encoded in DNA that renders the survivors of natural selection well adapted to their environment [1–4]. Among the first researchers to explore the link between information and evolution was Motoo Kimura. He built on earlier work by J.B.S. Haldane to argue that adaptive evolution accumulates genetic information in proportion to the rate at which alleles are replaced by better-adapted alleles [5,6].

More recently, two independent lines of research have connected evolutionary biology and information theory. The first is centred on organisms and their phenotypes, which may harbour information about the environment [3,7–14]. For example, the growth rate of bacteria depends on information that cells sense about environmental nutrients [3,7,8,10,12,14,15]. The second line focuses on genotypes [2,16–19], where information-theoretic concepts such as Shannon's entropy [2,18] can help recast equations from classical population and quantitative genetics, in order to describe changes of genotypes, allele frequencies and fitness in information-theoretic terms. This line of research shows that natural selection can increase information encoded in the distribution of a population's allele frequencies [2,17].

Experimental evolution, be it through in vitro selection [20–23], through directed evolution of macromolecules [24–28] or through laboratory evolution of organisms [29], is a powerful tool to discover novel phenotypes, such as the ability to resist novel antibiotics, to regulate old genes in new ways and to thrive on novel sources of energy. A fundamental question about evolutionary adaptations and innovations—qualitatively new and beneficial phenotypes—is how difficult it is to acquire or ‘discover’ them. For example, it may be easier to acquire the ability to extract energy from some novel nutrient if this ability requires only one new enzyme (biochemical reaction) instead of two or more. I here suggest that basic concepts from information theory, together with data from high-throughput DNA sequencing technologies, may help us answer this and related questions quantitatively for different kinds of phenotypes.

In the next section, I will first introduce a suitable information-theoretic framework and illustrate its use to understand evolution by DNA or gene duplication. Second, I will apply the framework to two different kinds of phenotypes, the DNA-binding phenotypes of transcriptional regulators [30,31] and the metabolic phenotypes that allow an organism to procure energy and manufacture essential biomass molecules [32]. Third and finally, I will show how sequence data from experimental evolution could help quantify differences in the amount of information gained by different evolutionary adaptations.

2. Results

All evolutionary adaptations and innovations originate in some space of genotypes. Evolving populations of organisms or molecules explore genotype spaces through DNA mutation, genetic drift and selection. The relationship between genotypes and phenotypes—the genotype–phenotype map—has been studied for multiple different kinds of genotype spaces, either exhaustively (for small spaces) or through random sampling, using both computational and experimental techniques [20,21,33–38]. Such efforts show that, first, astronomically many genotypes usually form the same phenotype, and these genotypes are organized into one or more networks connected by point mutations. Second, the genotype networks of different phenotypes are interwoven in complex ways [35,38,39]. Third, some phenotypes have larger genotype networks than others. This observation is important to understand phenotypic evolvability, the ability of an organism with a specific phenotype to bring forth novel phenotypes through DNA mutations [40]. Both computational analyses and empirical data show that populations evolving on large genotype networks are—with possible exceptions [41,42]—more likely to ‘discover’ new and beneficial phenotypes, because such populations can explore a larger proportion of genotype spaces [38,40,43,44].

For any observed phenotype P, such as a protein's ability to bind or react with a specific molecule, I denote the set of genotypes with this phenotype as GP. For simplicity, I focus on discrete, qualitative phenotypes (e.g. binding or not) rather than on quantitative phenotypes (e.g. binding with a specific affinity), thus assuming that all genotypes with a particular phenotype are equivalent. Consider first a genotype space G, and the Shannon entropy of a random variable that assumes values g ∈ G with equal probability 1/|G|, where |G| denotes the number of genotypes in G. This entropy computes as 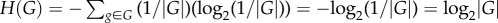Inline graphic [45]. The Shannon entropy for the same random variable defined on a subset GP of genotypes with a specific phenotype P (figure 1a) computes analogously as

2.

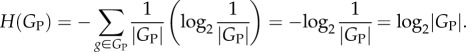Figure 1.

Figure 1.

Open in a new tab

Sets of genotypes with the same phenotype can have various topological relationships. Large rectangles symbolize genotype space, circles correspond to genotypes and straight lines connect 1-mutant neighbours, i.e. genotypes that differ by a small genetic change such as a single nucleotide change. Each set of genotypes is shown as a network, because such sets form networks in genotype space. (a) A hypothetical set (network) of genotypes with the same phenotype. The set is shown as a single genotype network, but I note that it could consist of multiple disconnected networks. (b) Two sets of genotypes: the first associated with an old phenotype (black and grey circles) and the second with a new phenotype (grey circles only, a subset of the first set). (c) Sets of genotypes with an old phenotype (black circles), a new phenotype (white circles) or with both an old and a new phenotype (grey circles). Unlike in (b), the genotype set of the new phenotype is not a subset of the genotype set with the old phenotype. (d) The sets of genotypes encoding different phenotypes can be non-overlapping.

These observations give rise to the following definition.

Definition 2.1:

the information content of phenotype P is given by

Definition 2.1: 2.1

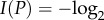
Equivalently, if Inline graphic, where fP indicates the fraction of genotype space occupied by GP, then Inline graphic Inline graphic. Analogous quantities have been called self-information, functional information, surprisal and (biological) complexity in other contexts [45–48]. The greater a phenotype's information content is, the more information is required to encode this phenotype. To compare data from genotype spaces of different dimensions (e.g. proteins of different length L), it can be useful to consider information content per monomer (I(P)/L).

Some empirical data on phenotypic information content are available for macromolecules. For example, in vitro selection experiments identifying ATP-binding proteins from a random library of proteins with 80 amino acids show that a fraction fP = 10−11 or Inline graphic proteins of this length can bind ATP [21]. The amount of information associated with this ATP-binding phenotype is Inline graphicInline graphic bits, which is much lower than the amount of information needed to specify a single amino acid sequence (Inline graphic bits), because many proteins can bind ATP.

Unlike in vitro selection, laboratory evolution experiments often do not start from random collections of genotypes, but from genotypes that already have a specific phenotype POld and acquire a novel phenotype PNew (figure 1b). For example, in a directed evolution experiment, TEM-1 β-lactamase molecules that convey resistance to ampicillin may acquire the ability to cleave the antibiotic cefotaxime. Denote as GOld the subset of genotypes with the old phenotype, and as GNew the subset of genotypes with the new phenotype.

Definition 2.2:

the information change associated with the acquisition of a new phenotype PNew starting from some phenotype POld is given by

Definition 2.2: 2.2

Here, one can distinguish two different scenarios. In the first, individuals with the new phenotype have also preserved the old phenotype (figure 1b), which implies that Inline graphic and ΔI ≥ 0. In this case, ΔI is equivalent to a Kullback–Leibler distance or relative entropy, an important quantity in information theory [45] (electronic supplementary material, Results S1). In the second scenario, GNew is not a proper subset of GOld (figure 1c). For example, consider β-lactamase enzymes that have evolved the ability to inactivate cefotaxime, but that may not have retained the old ability to inactivate ampicillin. In this case, ΔI can be negative, for example if more genotypes encode the ability to cleave cefotaxime than ampicillin.

To illustrate one potential use of this framework, consider DNA duplication, which has long been thought to increase evolvability [49–51]. To help quantify the advantage of duplicated DNA over single-copy DNA in exploring a genotype space, consider some phenotype, such as a regulatory region's ability to bind a transcription factor, or a protein's ability to catalyse a specific chemical reaction, and the set of genotypes GP associated with this phenotype. When the DNA encoding this phenotype becomes duplicated, both copies can undergo DNA mutation independently. Thus, they evolve in a larger genotype space, which comprises many more Inline graphic genotypes.

Such duplication can affect the information content of P, if only one of two copies of the duplicated DNA is sufficient to encode P. In this case, the difference between phenotypic information content after and before duplication is equal to

Definition 2.2: 2.3

per nucleotide or any other suitable unit, such as an amino acid monomer (see electronic supplementary material, Results S2, including for an analogous calculation of changes in absolute information content). Here, L is the dimension of G (e.g. the pre-duplication length of DNA). The approximation holds for Inline graphic. Importantly, this quantity is negative: duplication decreases a phenotype's information content per nucleotide, because the set of post-duplication genotypes with phenotype P occupies a larger fraction of the genotype space. This is important, because such a larger fraction of genotypes is associated with higher evolvability [38,40,43,44]. Thus, information theory can help link DNA duplication and evolvability. The set of genotypes associated with P expands after duplication by a factor Inline graphic (electronic supplementary material, Results S2). Because this expansion factor scales as Inline graphic, duplication will enhance evolvability to the greatest extent for phenotypes formed by few genotypes (small fP). In terms of the ATP-binding protein example above, where Inline graphic, fP = 10−11 and L = 80, duplication would reduce the phenotypic information content by Inline graphic bits per amino acid.

(a). Transcription factor binding phenotypes

Numerous evolutionary adaptations and innovations have been associated with the origin of new gene regulation mediated by new transcription factor binding sites on DNA, from changes in pathogen virulence to new body plans, such as the origin of two-winged insects [52–54]. I next analyse a genotype space of 48 = 65 536 DNA sequences of length eight nucleotides to illustrate the information change associated with new transcription factor binding sites. To this end, I take advantage of previously published protein binding microarray experiments that measured how strongly each of 187 mouse transcriptional regulators binds to all sequences in this space [30,31] (electronic supplementary material).

The phenotypes I analyse here are a DNA sequence's ability to bind specific regulators. For a de novo origin of transcription factor binding, the relevant phenotypic information content is that of a binding site (definition 2.1). Among the 187 regulators, this content varies widely (figure 2a; I(P) = 4.48–9.31 bits, median: 5.72 bits), because the fractional volume of genotype space bound varies among regulators. Binding sites with lower information content would be easier to acquire de novo [56,57]. The frequently made assumption that individual nucleotides contribute additively to phenotypic information [48,58,59] can lead to substantial underestimation of phenotypic information, i.e. by up to 8.22 bits (300-fold in terms of fP; electronic supplementary material, figure S1 and Results S3).

Figure 2.

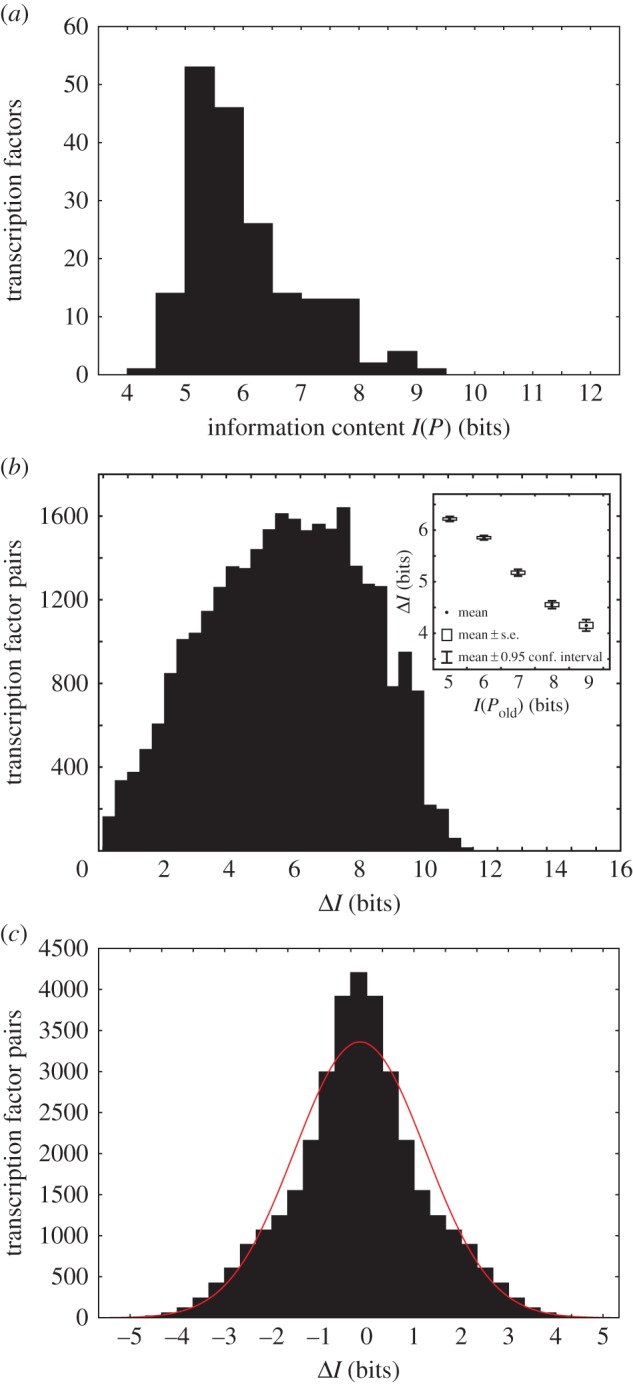
Figure 2.

Open in a new tab

Phenotypic information associated with new transcription factor binding. Data are based on experimentally measured binding of 187 mouse transcription factors to all possible DNA-binding sites of length eight [30,31,55]. (a) Histogram of the information content of the DNA-binding phenotype of each transcription factor (definition 2.1 and equation (2.1)). (b) The gain in information content associated with acquisition of a new DNA-binding phenotype, when an old phenotype is simultaneously preserved (equation (2.2)). The inset shows this gain in information content (vertical axis) as a function of the information content of the old phenotype (horizontal axis). Circles correspond to means, boxes to standard errors and whiskers indicate 95% confidence intervals. Data in (b) are based on all 29290 pairs of transcription factors whose sets of binding sites overlap. (c) The change in information content associated with acquisition of a new DNA-binding phenotype when the old phenotype need not be simultaneously preserved (equation (2.4)). The red line indicates the fit to a Gaussian distribution. Data in (c) are based on all 1872 pairs of transcription factors in the dataset.

If a site gets duplicated, such that the two duplicates evolve separately, and only one of them needs to preserve regulator binding, the change in phenotypic information content as a result of duplication lies between −0.34 and −0.64 bits per nucleotide (equation (2.3), with data from figure 2a, where 0.0016 < fP < 0.045), meaning that 44.4–1250 times more genotypes can be explored. In reality, duplication will confer an even greater advantage, because often entire regulatory regions and not just individual binding sites are duplicated.

When a binding site for a new regulator originates from one for an old regulator, and if binding of the old regulator is preserved (for example, because the old regulator directs essential gene expression in a different tissue), then phenotypic information increases (definition 2.2; figure 2b). For the 187 regulators considered here, the minimal increase is 0.04 bits when a binding site for factor Myb originates from one for factor Mybl1, because these regulators belong to the same gene family, and 97.2% of the 1969 sites bound by Mybl1 are also bound by Myb. The largest increase (11.5 bits) occurs when binding sites for transcription factor Mnt emerge from those for Sp110, because Sp110 binds to 2933 sites, but only one of them is also bound by Mnt. The complexity increase is generally lower if the old site had high information content (Spearman's r = −0.22; p < 10−17; n = 29 290; figure 2b, inset), which shows that phenotypic information changes can depend on ancestral phenotypes and are thus contingent on evolutionary history.

If binding to an old transcriptional regulator need not be preserved after a new binding phenotype originates, then the distribution of information change is symmetric (figure 2c), because for every value of information change X that occurs when binding is gained by some new regulator Y and lost by an old regulator Z, there is an opposite value –X when binding by Z is gained and binding by Y is lost. The maximal information loss or gain is 4.83 bits (Sp110-binding originating from Usf1-binding). Its minimum is zero for regulator pairs (e.g. Hbp1 and Rfx4) that bind the same number of sites.

(b). Metabolic genotypes and phenotypes

The metabolic genotype of an organism comprises all genes encoding metabolic enzymes. Systems biologists often represent this genotype more compactly, on the level of metabolic reactions these enzymes catalyse, by the presence or absence of specific reactions from a known ‘universe’ of such reactions [60,61] (electronic supplementary material, figure S3a). Such a genotype encodes a biochemical reaction network that transforms environmental nutrients into essential biomass molecules, such as amino acids and nucleotides. A metabolic genotype is viable only if it can produce all biomass molecules that an organism needs in a given nutrient environment. One can compute viability for any known genotype under some simplifying assumptions [60], and these predictions are often in good agreement with experimental observations [61–64].

The metabolic genotypes of free-living organism like Escherichia coli are members of a vast genotype space that can only be explored by sampling. I restrict myself here to a much smaller universe of 45 metabolic reactions from central carbon metabolism, which gives rise to a more tractable genotype space [39] (electronic supplementary material, figure S2). Given the right nutrients, the biochemical network encoded by these reactions can manufacture 13 essential biomass precursors, such as ribose 5-phosphate and oxaloacetate (electronic supplementary material, figure S2). The metabolic genotype space I explore is formed by all possible (245) subsets of these reactions. I consider 10 minimal chemical environments that differ only in the sole carbon source they contain (electronic supplementary material, figure S3b) and represent a metabolic phenotype as the combination of carbon sources on which a metabolism is viable (electronic supplementary material, figure S3b,c). Considering all possible combinations of 10 carbon sources on which a metabolism could be viable, this leads to 210 possible metabolic phenotypes.

In an earlier contribution, we have exhaustively computed these metabolic phenotypes for all 245 ≈ 1013 metabolic genotypes [39], which allows me to analyse their phenotypic information content. Some phenotypes contain much less information than others, e.g. viability on fructose and glucose requires 14.8 bits of information, whereas viability on all 10 carbon sources except glutamate and α-ketoglutarate requires 28.6 bits. Starting from a metabolic phenotype, viability on an additional carbon source requires an average of 0.75 additional bits (electronic supplementary material, figure S3d, inset). Neglecting non-additive interactions among reactions underestimates phenotypic information (electronic supplementary material, figures S3e and S4d), and duplication causes a substantial reduction in information by up to 29 bits (electronic supplementary material, Results S4). The distribution of information gain and information change are broad (electronic supplementary material, figure S3f,g and Results S4–S6). Gaining viability on given carbon sources can be informationally cheap (e.g. α-ketoglutarate) or expensive (acetate). Perhaps surprisingly, gaining viability on some carbon sources may lead to reduced phenotypic information, as a result of complex correlations between phenotypes (electronic supplementary material, Results S4).

(c). Inferring information content from sequence data

Tractable genotype spaces like those I have discussed so far are the exception. Usually, astronomically many genotypes encode the same phenotype, and because it is impossible to identify all of them, one cannot infer the information content of any one phenotype (definition 2.1). What is more, sequencing technology does not simply enumerate genotypes but samples them from an evolving population. I will argue next that it may nonetheless be possible to estimate the information change associated with a novel phenotype (definition 2.2). In doing so, I make simplifying assumptions whose relaxation will require future work. My main point is that quantifying phenotypic information change may be within reach of current technologies.

Consider two populations of which one is well adapted to some ancestral environment (with phenotype POld) and another one is adapted to a new environment, such as one that harbours a novel nutrient, an antibiotic or another stressor, and thus requires an altered phenotype PNew. I assume that both populations comprise asexually reproducing haploid individuals, that they are in mutation–selection–drift balance subject to Wright-Fisher dynamics [65] and that they have equal effective sizes Ne and mutation rates μ (per genome and generation). I also assume that both phenotypes POld and PNew are subject to strong truncation selection, that is, mutations that disrupt each phenotype are lethal. The two phenotypes may differ in their numbers of associated genotypes GOld and GNew, and thus also in their information content. The task is to estimate this difference (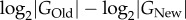Inline graphic) from two samples of n genotypes (DNA sequences), one from each of the populations. I model this difference as a difference in the average rate of strongly deleterious (lethal) mutations across all genotypes or, equivalently, in the average rate of neutral mutations. 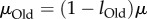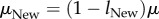If lOld and lNew denote the average proportion of all strongly deleterious (lethal) mutations in the two populations, then the average neutral mutation rate becomes Inline graphic and Inline graphic. 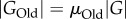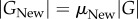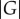Assuming further that mutations in all viable genotypes are equally likely to be strongly deleterious, one obtains the relationships Inline graphic and Inline graphic, where Inline graphic is the total size of genotype space. It is then easy to see that

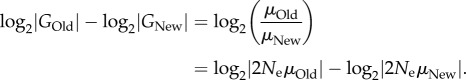(c). 2.4

Thus, estimating the difference in phenotypic information content requires estimating the quantities 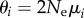Inline graphic, which are of broad importance in population genetics because they predict a population's amount of neutral polymorphisms [65,66]. If PNew harbours more information than 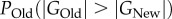Inline graphic, then 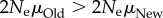Inline graphic, and the population with PNew would harbour more alleles. I emphasize that the derivation of equation (2.4) involves a strong tacit assumption, namely that the phenotypic effects of mutants are distributed as if mutations sampled genotypes at random from genotype space. This assumption is violated whenever mutant phenotypes are correlated with those of the wild type, or if some DNA sites are always neutral. It remains to be seen whether relaxation of this assumption leads to relationships as simple as that of (2.4).

A maximum-likelihood estimator of θi is the number of different genotypes ki in a random sample of n genotypes sequenced from the populations [67]. Importantly, the sampling distribution of ki is known, and it can help infer the minimal difference in information content detectable from a sample of n sequences (electronic supplementary material). Specifically, one can compute the probability of falsely rejecting the null hypothesis that phenotype PNew harbours more information than POld. Figure 3 shows the minimally detectable information difference (see legend), for multiple values of n and 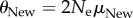Inline graphic. White regions in the plot indicate that the information content of two phenotypes is indistinguishable. 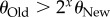In a region of the plot where the test can discriminate at least x bits, p < 0.05 for all values of θOld, such that Inline graphic.

Figure 3.

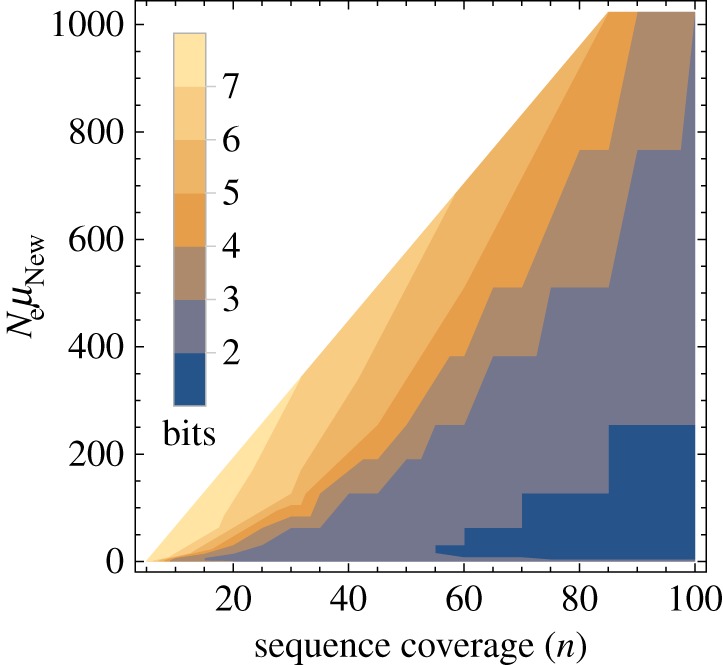
Figure 3.

Open in a new tab

High-throughput sequencing can help distinguish even modest differences in phenotypic information content. Minimally distinguishable information content of two phenotypes (in bits), colour-coded as indicated in the legend, for a given sequence coverage n (horizontal axis), and a given value of 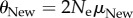Inline graphic. To create this plot, I chose multiple values of n and θNew and determined the minimal value of θOld, 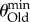Inline graphic, such that 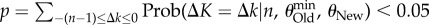Inline graphic (see electronic supplementary material, Methods S1) for each of these values. The minimally detectable information difference is then given by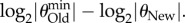 Inline graphic

In this analysis, I did not explore populations with 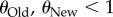Inline graphic, because such populations are monomorphic most of the time [66], which implies that even when sequencing multiple genotypes, most of the genotypes would be genetically identical. At the other extreme are values of 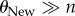Inline graphic (and thus also 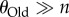Inline graphic), where one cannot discriminate the information content of two phenotypes (figure 3), because both populations are so highly polymorphic that all n sampled sequences may be different from each other. Thus, best discrimination between the information content of two phenotypes requires that 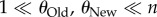Inline graphic (lower right corner of figure 3).

3. Discussion

The genotypes encoding a new phenotype may be difficult to access by an evolving population for two reasons. First, the phenotype may have high information content, implying that the few genotypes encoding it may be difficult to find through random search in a vast genotype space. Second, the population may be distant from these genotypes, requiring multiple genetic changes or inviable mutational intermediates to reach them. The information-theoretic framework eliminates the latter, historical factors from consideration, which is both an advantage and a limitation. In the data I analysed here, most phenotypes can be reached through few genetic changes (electronic supplementary material), but this may not hold in larger genotype spaces [68].

I have restricted myself here to qualitative or threshold phenotypes (binding/non-binding and viability/non-viability). They have proved useful in past experimental estimates of phenotypic information, such as that of RNA ligase ribozymes (L = 220) whose I(P) can be estimated at 43.2 bits [20]. Limited empirical data are also available about the information content of quantitative phenotypes. For example, a 10-fold increase in an RNA aptamer's binding affinity to guanosine triphosphate (GTP) requires 10 additional bits of information [47,59]. However, extending the concepts of this paper to quantitative phenotypes remains a task for future work (electronic supplementary material, Results S1).

Qualitative phenotypes are simplifications, but they also help separate properties intrinsic to a phenotype from properties of a population with this phenotype [48,69]. The latter depends not only on phenotypic information, but also on many factors affecting a population's dynamics, such as (effective) population size Ne and genomic mutation rate μ. For example, if 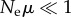Inline graphic, then all members of a population have identical genotypes most of the time [66]. A phenotype's information content estimated from such a monomorphic population would be 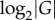Inline graphic, a highly misleading value, because the population does not harbour any of the myriad other genotypes that might encode the phenotype. Likewise, during adaptive evolution, apparent phenotypic information can rise dramatically and transiently before reaching a mutation–selection equilibrium, for example while an adaptive mutant genotype goes to fixation [48,69].

A typical experiment to estimate phenotypic information changes from an evolving population would start at the endpoint of a previous (laboratory) evolution experiment, in which a population has adapted evolutionarily to a novel environment, such as one containing a novel nutrient or antibiotic. The experiment would then establish two evolving populations, one derived from a single pre-evolution genotype and evolved in the ancestral environment (e.g. without antibiotic), and the second from a single post-evolution (adapted) genotype and evolved in the novel environment (e.g. with antibiotic). After each population has evolved sufficiently long to reach approximate mutation–selection balance, one would sequence n randomly chosen individuals from each population and infer ΔI from the number of different alleles (genomes) sampled. As I argued, to best discriminate between phenotypic information content in both populations, one needs 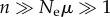Inline graphic. This is entirely feasible, even with multi-megabase genomes. For example, in E. coli, where μ ≈ 10−3 [70], a population of Ne = 104 individuals yields 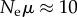Inline graphic. 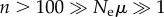Current technology permits sequencing of more than 100 clones isolated from such a population, such that Inline graphic.

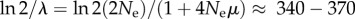My argument that today's sequencing technology can help distinguish even modest phenotypic information changes rests on simplifying assumptions, among them that a sampled population should not be far from mutation–selection balance. Such a balance is approached exponentially with decay parameter Inline graphic ([66], p. 204). For an evolving E. coli population of 104–107 individuals with μ ≈ 10−3 mutations per genome and generation [70], the half-life of this decay is given by Inline graphic generations, well within the time scale of a laboratory evolution experiment. Other assumptions, such as that of truncation selection, unbiased mutational sampling of GP, as well as a uniform deleterious mutation rate for all genotypes in GP, will need to be relaxed in more sophisticated modelling work, which will also be required for a rigorous sampling theory estimating quantities such as confidence intervals for phenotypic information changes.

The information-theoretic framework can speak to broad and fundamental questions in evolutionary biology. One of them is whether some organisms and phenotypes are more evolvable than others. Here, information theory unifies previous observations [38,40,43,44] to show that phenotypes with low information content are more evolvable (with possible exceptions where genotypes form highly fragmented sets in genotype space, figure 1d [44,71]). Relatedly, information theory can also help quantify the extent to which DNA or gene duplications increase evolvability (equation (2.3)). In addition, the framework can help solve the recalcitrant problem of how to define the complexity of phenotypes and organisms: more complex phenotypes are those with higher phenotypic information content. Relatedly, it can help answer under what circumstances evolution implies ‘progress’. This is controversial, partly because adaptive evolution can be regressive and lead to trait loss [72]. With a definition of phenotypic information in hand, evolutionary progress can be defined as an increase in phenotype information content in an evolving lineage.

Supplementary Material

Supplementary methods, results, and figures
rstb20160416supp1.docx (1,006.8KB, docx)

Acknowledgements

I thank Joshua Payne, José Aguilar Rodrigues and Rzgar Hosseini for valuable discussions on the data analysed here, as well as Troy Day and an anonymous reviewer for valuable comments.

Data accessibility

Transcriptional regulation data used here are publicly available data from refs 1 and 2 of the electronic supplementary material. Code to create simulated metabolism data is available at https://github.com/rzgar/EMETNET/tree/master/CCM.

Competing interests

I have no competing interests.

Funding

I acknowledge support by Swiss National Science Foundation grant 31003A_146137, by an EpiphysX RTD grant from SystemsX.ch, as well as by the University Priority Research Program in Evolutionary Biology at the University of Zurich.

References

  • 1.Maynard-Smith J. 2000. The concept of information in biology. Philos. Sci. 67, 177–194. ( 10.1086/392768) [DOI] [Google Scholar]
  • 2.Frank SA. 2012. Natural selection. V. How to read the fundamental equations of evolutionary change in terms of information theory. J. Evol. Biol. 25, 2377–2396. ( 10.1111/jeb.12010) [DOI] [PubMed] [Google Scholar]
  • 3.van Baalen M. 2013. Biological information: why we need a good measure and the challenges ahead. Interface Focus 3, 20130030 ( 10.1098/rsfs.2013.0030) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Wallace R, Wallace RG. 1998. Information theory, scaling laws and the thermodynamics of evolution. J. Theor. Biol. 192, 545–559. ( 10.1006/jtbi.1998.0680) [DOI] [PubMed] [Google Scholar]
  • 5.Kimura M. 1961. Natural selection as a process of accumulating genetic information in adaptive evolution. Genet. Res. 2, 127 ( 10.1017/S0016672300000616) [DOI] [Google Scholar]
  • 6.Haldane JBS. 1957. The cost of natural selection. Genetics 55, 511–524. ( 10.1007/BF02984069) [DOI] [Google Scholar]
  • 7.Hoffmann RJ. 1978. Environmental uncertainty and evolution of physiological adaptation in Colias butterflies. Am. Nat. 112, 999–1015. ( 10.1086/283343) [DOI] [Google Scholar]
  • 8.Donaldson-Matasci MC, Bergstrom CT, Lachmann M. 2010. The fitness value of information. Oikos 119, 219–230. ( 10.1111/j.1600-0706.2009.17781.x) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Donaldson-Matasci MC, Bergstrom CT, Lachmann M. 2013. When unreliable cues are good enough. Am. Nat. 182, 313–327. ( 10.1086/671161) [DOI] [PubMed] [Google Scholar]
  • 10.McNamara JM, Dall SRX. 2010. Information is a fitness enhancing resource. Oikos 119, 231–236. ( 10.1111/j.1600-0706.2009.17509.x) [DOI] [Google Scholar]
  • 11.Lachmann M, Bergstrom CT. 2004. The disadvantage of combinatorial communication. Proc. R. Soc. Lond. B 271, 2337–2343. ( 10.1098/rspb.2004.2844) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Rivoire O, Leibler S. 2011. The value of information for populations in varying environments. J. Stat. Phys. 142, 1124–1166. ( 10.1007/s10955-011-0166-2) [DOI] [Google Scholar]
  • 13.Tkacik G, Bialek W. 2016. Information processing in living systems. Annu. Rev. Condensed Matter Physics 7, 89–117. ( 10.1146/annurev-conmatphys-031214-014803) [DOI] [Google Scholar]
  • 14.Wagner A. 2007. From bit to it: the transformation of information into living matter by metabolic networks. BMC Syst. Biol. 1, 33 ( 10.1186/1752-0509-1-33) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Bergstrom CT, Lachmann M. 2004. Shannon information and biological fitness. In Proc. IEEE Information Theory Workshop 24–29 October 2004, San Antonio, TX, pp. 50–54. [Google Scholar]
  • 16.Frieden BR, Plastino A, Soffer BH. 2001. Population genetics from an information perspective. J. Theor. Biol. 208, 49–64. ( 10.1006/jtbi.2000.2199) [DOI] [PubMed] [Google Scholar]
  • 17.Weinberger ED. 2002. A theory of pragmatic information and its application to the quasi-species model of biological evolution. BioSystems 66, 105–119. ( 10.1016/s0303-2647(02)00038-2) [DOI] [PubMed] [Google Scholar]
  • 18.Iwasa Y. 1988. Free fitness that always increases in evolution. J. Theor. Biol. 135, 265–281. ( 10.1016/S0022-5193(88)80243-1) [DOI] [PubMed] [Google Scholar]
  • 19.Day T. 2015. Information entropy as a measure of genetic diversity and evolvability in colonization. Mol. Ecol. 24, 2073–2083. ( 10.1111/mec.13082) [DOI] [PubMed] [Google Scholar]
  • 20.Wilson DS, Szostak JW. 1999. In vitro selection of functional nucleic acids. Annu. Rev. Biochem. 68, 611–647. ( 10.1146/annurev.biochem.68.1.611) [DOI] [PubMed] [Google Scholar]
  • 21.Keefe AD, Szostak JW. 2001. Functional proteins from a random-sequence library. Nature 410, 715–718. ( 10.1038/35070613) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Curtis EA, Bartel DP. 2013. Synthetic shuffling and in vitro selection reveal the rugged adaptive fitness landscape of a kinase ribozyme. RNA 19, 1116–1128. ( 10.1261/rna.037572.112) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Jiménez JI, Xulvi-Brunet R, Campbell GW, Turk-MacLeod R, Chen IA. 2013. Comprehensive experimental fitness landscape and evolutionary network for small RNA. Proc. Natl Acad. Sci. USA 110, 14 984–14 989. ( 10.1073/pnas.1307604110) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Currin A, Swainston N, Day PJ, Kell DB. 2015. Synthetic biology for the directed evolution of protein biocatalysts: navigating sequence space intelligently. Chem. Soc. Rev. 44, 1172–1239. ( 10.1039/C4CS00351A) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Khersonsky O, Rosenblat M, Toker L, Yacobson S, Hugenmatter A, Silman I, Sussman JL, Aviram M, Tawfik DS. 2009. Directed evolution of serum paraoxonase PON3 by family shuffling and ancestor/consensus mutagenesis, and its biochemical characterization. Biochemistry 48, 6644–6654. ( 10.1021/bi900583y) [DOI] [PubMed] [Google Scholar]
  • 26.Romero PA, Arnold FH. 2009. Exploring protein fitness landscapes by directed evolution. Nat. Rev. Mol. Cell Biol. 10, 866–876. ( 10.1038/nrm2805) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Hayden EJ, Ferrada E, Wagner A. 2011. Cryptic genetic variation promotes rapid evolutionary adaptation in an RNA enzyme. Nature 474, 92–95. ( 10.1038/nature10083) [DOI] [PubMed] [Google Scholar]
  • 28.Szendro IG, Schenk MF, Franke J, Krug J, de Visser J. 2013. Quantitative analyses of empirical fitness landscapes. J. Stat. Mech.-Theory Exp. 2013, P01005 ( 10.1088/1742-5468/2013/01/p01005) [DOI] [Google Scholar]
  • 29.Buckling A, Maclean RC, Brockhurst MA, Colegrave N. 2009. The Beagle in a bottle. Nature 457, 824–829. ( 10.1038/nature07892) [DOI] [PubMed] [Google Scholar]
  • 30.Badis G, et al. 2009. Diversity and complexity in DNA recognition by transcription factors. Science 324, 1720–1723. ( 10.1126/science.1162327) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Weirauch MT, et al. 2014. Determination and inference of eukaryotic transcription factor sequence specificity. Cell 158, 1431–1443. ( 10.1016/j.cell.2014.08.009) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Feist AM, Herrgard MJ, Thiele I, Reed JL, Palsson BO. 2009. Reconstruction of biochemical networks in microorganisms. Nat. Rev. Microbiol. 7, 129–143. ( 10.1038/nrmicro1949) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Roscoe BP, Thayer KM, Zeldovich KB, Fushman D, Bolon DNA. 2013. Analyses of the effects of all ubiquitin point mutants on yeast growth rate. J. Mol. Biol. 425, 1363–1377. ( 10.1016/j.jmb.2013.01.032) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Araya CL, Fowler DM, Chen WT, Muniez I, Kelly JW, Fields S. 2012. A fundamental protein property, thermodynamic stability, revealed solely from large-scale measurements of protein function. Proc. Natl Acad. Sci. USA 109, 16 858–16 863. ( 10.1073/pnas.1209751109) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Schuster P, Fontana W, Stadler P, Hofacker I. 1994. From sequences to shapes and back—a case-study in RNA secondary structures. Proc. R. Soc. Lond. B 255, 279–284. ( 10.1098/rspb.1994.0040) [DOI] [PubMed] [Google Scholar]
  • 36.Lipman D, Wilbur W. 1991. Modeling neutral and selective evolution of protein folding. Proc. R. Soc. Lond. B 245, 7–11. ( 10.1098/rspb.1991.0081) [DOI] [PubMed] [Google Scholar]
  • 37.Rodrigues JFM, Wagner A. 2009. Evolutionary plasticity and innovations in complex metabolic reaction networks. PLoS Comput. Biol. 5, e1000613 ( 10.1371/journal.pcbi.1000613) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Payne JL, Wagner A. 2014. The robustness and evolvability of transcription factor binding sites. Science 343, 875–877. ( 10.1126/science.1249046) [DOI] [PubMed] [Google Scholar]
  • 39.Hosseini S-R, Barve A, Wagner A. 2015. Exhaustive analysis of a genotype space comprising 1015 central carbon metabolisms reveals an organization conducive to metabolic innovation. PLoS Comput. Biol. 11, e1004329 ( 10.1371/journal.pcbi.1004329) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Wagner A. 2008. Robustness and evolvability: a paradox resolved. Proc. R. Soc. B 275, 91–100. ( 10.1098/rspb.2007.1137) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Manrubia S, Cuesta JA.. 2015. Evolution on neutral networks accelerates the ticking rate of the molecular clock. J. R. Soc. Interface 12, 20141010 ( 10.1098/rsif.2014.1010) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Ancel LW, Fontana W. 2000. Plasticity, evolvability, and modularity in RNA. J. Exp. Zool. 288, 242–283. ( 10.1002/1097-010X(20001015)288:3%3C242::AID-JEZ5%3E3.0.CO;2-O) [DOI] [PubMed] [Google Scholar]
  • 43.Ferrada E, Wagner A. 2008. Protein robustness promotes evolutionary innovations on large evolutionary time scales. Proc. R. Soc. B 275, 1595–1602. ( 10.1098/rspb.2007.1617) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Greenbury SF, Johnston IG, Louis AA, Ahnert SE. 2014. A tractable genotype–phenotype map modelling the self-assembly of protein quaternary structure. J. R. Soc. Interface 11, 20140249 ( 10.1098/rsif.2014.0249) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Cover TM, Thomas JA. 2006. Elements of information theory, 2nd edn Hoboken, NJ: Wiley. [Google Scholar]
  • 46.Wootton JC. 1994. Non-globular domains in protein sequences: automated segmentation using complexity measures. Comput. Chem. 18, 269–285. ( 10.1016/0097-8485(94)85023-2) [DOI] [PubMed] [Google Scholar]
  • 47.Szostak JW. 2003. Molecular messages. Nature 423, 689 ( 10.1038/423689a) [DOI] [PubMed] [Google Scholar]
  • 48.Adami C, Ofria C, Collirer TC. 2000. Evolution of biological complexity. Proc. Natl Acad. Sci. USA 97, 4463–4468. ( 10.1073/pnas.97.9.4463) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Ohno S. 1970. Evolution by gene duplication. New York, NY: Springer. [Google Scholar]
  • 50.Theissen G. 2001. Development of floral organ identity: stories from the MADS house. Curr. Opin. Plant Biol. 4, 75–85. ( 10.1016/S1369-5266(00)00139-4) [DOI] [PubMed] [Google Scholar]
  • 51.Wagner A. 2008. Gene duplications, robustness and evolutionary innovations. BioEssays 30, 367–373. ( 10.1002/bies.20728) [DOI] [PubMed] [Google Scholar]
  • 52.Wray GA. 2007. The evolutionary significance of cis-regulatory mutations. Nat. Rev. Genet. 8, 206–216. ( 10.1038/nrg2063) [DOI] [PubMed] [Google Scholar]
  • 53.Prud'homme B, Gompel N, Carroll SB. 2007. Emerging principles of regulatory evolution. Proc. Natl Acad. Sci. USA 104, 8605–8612. ( 10.1073/pnas.0700488104) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Carroll SB, Grenier JK, Weatherbee SD. 2001. From DNA to diversity. Molecular genetics and the evolution of animal design. Malden, MA: Blackwell. [Google Scholar]
  • 55.Aguilar-Rodriguez JP, Payne JL, Wagner A.. 2017. 1000 empirical adaptive landscapes and their navigability. Nat. Ecol. Evol. 1, 0045 ( 10.1038/s41559-016-0045) [DOI] [PubMed] [Google Scholar]
  • 56.Tuğrul M, Paixão T, Barton NH, Tkačik G. 2015. Dynamics of transcription factor binding site evolution. PLoS Genet. 11, e1005639 ( 10.1371/journal.pgen.1005639) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 57.Berg J, Willmann S, Lässig M. 2004. Adaptive evolution of transcription factor binding sites. BMC Evol. Biol. 4, 1 ( 10.1186/1471-2148-4-1) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Weaver DC, Workman CT, Stormo GD. 1999. Modeling regulatory networks with weight matrices. Pac. Symp. Biocomput. 4, 112–123. [DOI] [PubMed] [Google Scholar]
  • 59.Carothers JM, Oestreich SC, Davis JH, Szostak JW. 2004. Informational complexity and functional activity of RNA structures. J. Am. Chem. Soc. 126, 5130–5137. ( 10.1021/ja031504a) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 60.Becker SA, Feist AM, Mo ML, Hannum G, Palsson BO, Herrgard MJ. 2007. Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox. Nat. Protoc. 2, 727–738. ( 10.1038/nprot.2007.99) [DOI] [PubMed] [Google Scholar]
  • 61.Edwards JS, Ibarra RU, Palsson BO. 2001. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nat. Biotechnol. 19, 125–130. ( 10.1038/84379) [DOI] [PubMed] [Google Scholar]
  • 62.Segre D, Vitkup D, Church G. 2002. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl Acad. Sci. USA 99, 15 112–15 117. ( 10.1073/pnas.232349399) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 63.Forster J, Famili I, Fu P, Palsson B, Nielsen J. 2003. Genome-scale reconstruction of the Saccharomyces cerevisiae metabolic network. Genome Res. 13, 244–253. ( 10.1101/gr.234503) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 64.Wang Z, Zhang JZ. 2009. Abundant indispensable redundancies in cellular metabolic networks. Genome Biol. Evol. 1, 23–33. ( 10.1093/gbe/evp002) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 65.Hartl DL, Clark AG. 2007. Principles of population genetics, 4th edn Sunderland, MA: Sinauer Associates. [Google Scholar]
  • 66.Kimura M. 1983. The neutral theory of molecular evolution. Cambridge, UK: Cambridge University Press. [Google Scholar]
  • 67.Ewens WJ. 2012. Mathematical population genetics 1: theoretical introduction. New York, NY: Springer Science & Business Media. [Google Scholar]
  • 68.Fontana W, Schuster P. 1998. Continuity in evolution: on the nature of transitions. Science 280, 1451–1455. ( 10.1126/science.280.5368.1451) [DOI] [PubMed] [Google Scholar]
  • 69.Strelioff CC, Lenski RE, Ofria C. 2010. Evolutionary dynamics, epistatic interactions, and biological information. J. Theor. Biol. 266, 584–594. ( 10.1016/j.jtbi.2010.07.025) [DOI] [PubMed] [Google Scholar]
  • 70.Lee H, Popodi E, Tang HX, Foster PL. 2012. Rate and molecular spectrum of spontaneous mutations in the bacterium Escherichia coli as determined by whole-genome sequencing. Proc. Natl Acad. Sci. USA 109, E2774–E2783. ( 10.1073/pnas.1210309109) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 71.Schaper S, Johnston IG, Louis AA. 2012. Epistasis can lead to fragmented neutral spaces and contingency in evolution. Proc. R. Soc. B 279, 1777–1783. ( 10.1098/rspb.2011.2183) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 72.Muller GB, Wagner GP.. 1991. Novelty in evolution: restructuring the concept. Annu. Rev. Ecol. Syst. 22, 229–256. ( 10.1146/annurev.es.22.110191.001305) [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary methods, results, and figures
rstb20160416supp1.docx (1,006.8KB, docx)

Data Availability Statement

Transcriptional regulation data used here are publicly available data from refs 1 and 2 of the electronic supplementary material. Code to create simulated metabolism data is available at https://github.com/rzgar/EMETNET/tree/master/CCM.

Articles from Philosophical Transactions of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES