Abstract
Network-based diffusion analysis (NBDA) is a statistical technique for detecting the social transmission of behavioural innovations in groups of animals, including humans. The strength of social transmission is inferred from the extent to which the diffusion (spread) of the innovation follows a social network. NBDA can have two goals: (a) to establish whether social transmission is occurring and how strong its effects are; and/or (b) to establish the typical pathways of information transfer. The technique has been used in a range of taxa, including primates, cetaceans, birds and fish, using a range of different types of network. Here I investigate the conceptual underpinnings of NBDA, in order to establish the meaning of results using different networks. I develop a model of the social transmission process where each individual observation of the target behaviour affects the rate at which the observer learns that behaviour. I then establish how NBDAs using different networks relate to this underlying process, and thus how we can interpret the results of each. My analysis shows that a different network or networks are appropriate depending on the specific goal or goals of the study, and establishes how the parameter estimates yielded from an NBDA can be interpreted for different networks.
This article is part of the themed issue ‘Process and pattern in innovations from cells to societies’.
Keywords: social learning, culture, social transmission, network-based diffusion analysis
1. Introduction
In recent years, there has been a substantial interest in better understanding how and why non-human animals use social information [1–3], and particularly understanding if novel behaviour (innovations) can diffuse through populations as a result of social transmission (learning from others) [4]. A capacity for social transmission has been demonstrated in many species using a traditional demonstrator–observer paradigm [5]. By contrast, recent studies have focused on studying the diffusion of innovations in freely interacting groups of animals in the field (e.g. [6,7]) or in captivity (e.g. [8,9]), aiming to assess the importance of social transmission in the spread of behaviour, and elucidate typical pathways of transmission. However, in many cases it can be challenging to determine whether the spread of innovations is caused by social transmission, or purely the product of asocial learning (see also [10]).
One approach to this problem is to use diffusion data: time-structured data on the spread of behaviour through a population or group. Network-based diffusion analysis (NBDA) is one such approach which infers social transmission if the spread of an innovation follows a social network [11,12]. For example, in 1980 a few humpback whales (Megaptera novaeangliae) were observed displaying a novel hunting behaviour, called ‘lobtail feeding’ whereby they would strike the water's surface with their tails before engaging in their usual bubble-feeding routine. This innovation diffused through the population over the course of the next 27 years. NBDA was used to show that the diffusion of the innovation followed a social network, providing evidence that it spread by social transmission [6]. In this case, and most applications of NBDA, the social network used is a pre-established association network (e.g. [6,13]) that is assumed to reflect opportunities for learning between each pair of individuals [12]. However, a number of different types of social network (e.g. based on different types of interactions between individuals) can be constructed and used in an NBDA [14] representing different hypothetical pathways about the pathways of social transmission. There are two main objectives a researcher might have in applying an NBDA: (a) to establish whether social transmission is occurring and how strong its effects are; and/or (b) to establish the typical pathways of social transmission in a population, group or context. However, it is not currently well established how an NBDA using each of the various kinds of networks relates to the underlying process of social learning. Such a conceptual foundation to NBDA is required if researchers are to (a) know what kinds of network can be validly used to validly accomplish each goal, and (b) interpret the results of an NBDA using a particular type of network. In this paper, I develop such a conceptual foundation, by presenting a simple, but realistic model of the social learning process, whereby observation of performance of the behaviour offers a naive individual the opportunity to learn that behaviour pattern for itself. I then use the model to assess the validity of different types of social network for each of the two goals, and establish how the results of an NBDA should be interpreted. I also use simulations to assess how error in the measured network impacts on the outputs of an NBDA, and assess whether error in a network influences the interpretation of the results.
2. Network-based diffusion analysis
The basic NBDA model states that at time t an individual, i, learns a target innovation at rate:
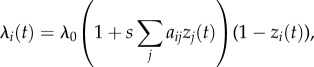 |
2.1 |
where λ0 is the baseline (asocial) rate of learning, aij is the social network connection from j to i, zi(t) is the status of individual i: informed = 1 (has learned the target behaviour), or naive = 0, and s is a parameter, fitted to the data, estimating the strength of social learning relative to asocial learning. The  term means that individuals learn at a rate proportional to their connection to informed individuals, and the
term means that individuals learn at a rate proportional to their connection to informed individuals, and the 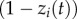 term means that only naive individuals can learn. If the diffusion follows the network closely, s is estimated to be large. The model can be fitted to data giving only the order in which individuals learn (order of acquisition diffusion analysis or OADA) or the times at which they learn, in continuous time, or in discrete time periods (continuous/discrete time of acquisition diffusion analysis or TADA) [11,12]. TADA has more statistical power, but OADA makes fewer assumptions about the time course of asocial learning [12]. In all cases the model is compared with a null model in which there is no social transmission (s = 0) to establish the strength of evidence for social transmission. Models can be fitted using maximum-likelihood [11,12] or Bayesian approaches [15,16]. In this paper, I use the former approach in simulations owing to its reduced computational complexity. Code for implementing NBDA in the R statistical environment [17], along with instructions, can be found at https://lalandlab.st-andrews.ac.uk/freeware/.
term means that only naive individuals can learn. If the diffusion follows the network closely, s is estimated to be large. The model can be fitted to data giving only the order in which individuals learn (order of acquisition diffusion analysis or OADA) or the times at which they learn, in continuous time, or in discrete time periods (continuous/discrete time of acquisition diffusion analysis or TADA) [11,12]. TADA has more statistical power, but OADA makes fewer assumptions about the time course of asocial learning [12]. In all cases the model is compared with a null model in which there is no social transmission (s = 0) to establish the strength of evidence for social transmission. Models can be fitted using maximum-likelihood [11,12] or Bayesian approaches [15,16]. In this paper, I use the former approach in simulations owing to its reduced computational complexity. Code for implementing NBDA in the R statistical environment [17], along with instructions, can be found at https://lalandlab.st-andrews.ac.uk/freeware/.
The basic NBDA model given in equation (2.1) has been expanded so that potentially confounding variables can be included and statistically controlled for [12] and so that it can account for a non-constant rate of asocial learning [18]. Franz & Nunn [19] have investigated the effect of inaccuracies in the times of acquisition data, and Whalen & Hoppitt [16] have shown that NBDA is robust to departures from the assumption of a linear relationship between λi(t) and aij. However, little work has been done on the effect of inaccuracies in the social network itself. Consequently, in this paper I assess the effect of various types of inaccuracies that might affect the recording of the social network aij. But first, I develop a model of social learning that is more realistic than the model underlying NBDA (equation (2.1)), at the mechanistic level, and use this to establish the conceptual foundations for NBDA.
3. A realistic model of social transmission
Here I develop a simple model of the social transmission process that is mechanistically realistic in groups of non-human animals, i.e. observation of performance of the behaviour offers a naive individual the opportunity to learn that behaviour pattern for itself. The model, and NBDA itself, may also be applicable to the diffusion of innovations in humans where the mechanism is relatively simple. However, the model is not intended to capture ‘complex contagions’ in which transmission relies on interactions with multiple contacts, and includes mechanisms such as judgement of credibility and legitimacy of innovations prior to adoption ([20], see also [21,22]). I start from the assumption that each time an individual i observes the target behaviour being performed by individual j there is a probability, 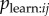 , that i learns the target behaviour. Therefore, the rate of transmission from j to i, Tij is given by:
, that i learns the target behaviour. Therefore, the rate of transmission from j to i, Tij is given by:
| 3.1 |
where Oij is the rate at which i observes j. We can further break the model down to:
| 3.2 |
where Bj is the rate at which j performs the behaviour, once it has learned it, and pobs,ij is the probability that a given performance of the behaviour by j is observed by i. Thus, the rate at which a naive individual acquires the novel behaviour to its repertoire, at a given time, t, will be:
| 3.3 |
where λ0 is the rate of asocial learning, and zj(t) gives the status of individual j at time t (1 = informed, 0 = naive). This corresponds closely to the basic NBDA model given in equation (2.1), where
| 3.4 |
s is fitted to the data and scales the rate of social transmission relative to the rate of asocial learning, λ0. This is because in equation (2.1) the rate of transmission from j to i is given by 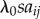 , whereas in equation (3.3) this is given by Tij, or, equivalently,
, whereas in equation (3.3) this is given by Tij, or, equivalently, 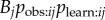 . Consequently, the more closely a social network, aij, approximates Tij, (scale aside) the better it will tend to predict the order and time of diffusion in an NBDA. However, the exact meaning of the s parameter, estimated by the NBDA, will depend on exactly what network aij is used (e.g. association versus interaction networks), as will the meaning of the model itself, when compared with models using alternative social networks. One of the key goals of this paper is to establish how an NBDA should be interpreted when different types of network are used.
. Consequently, the more closely a social network, aij, approximates Tij, (scale aside) the better it will tend to predict the order and time of diffusion in an NBDA. However, the exact meaning of the s parameter, estimated by the NBDA, will depend on exactly what network aij is used (e.g. association versus interaction networks), as will the meaning of the model itself, when compared with models using alternative social networks. One of the key goals of this paper is to establish how an NBDA should be interpreted when different types of network are used.
Thus far, I assume that social transmission occurs via observation, whereas instead it could occur when i encounters the products of j's behaviour, as has been observed in a number of cases of non-human social learning (e.g. [23]). In such cases the model might still apply: here instead Oij is the rate at which i encounters the products of j's behaviour, and pij is the probability of learning the behaviour from each encounter. In the remainder of the paper I refer to cases where social transmission occurs via observation, but analogous logic applies to cases where the transmission pathway does not operate via direct observation.
As noted above, there are two main objectives a researcher might have in applying an NBDA. Aim 1 is to establish whether social transmission is occurring and how strong its effects are. For this goal, a researcher ideally requires a social network that captures the opportunities for social transmission as directly as possible. Intuitively, the extent to which the diffusion follows such a network then reflects the importance of social transmission relative to asocial learning. Aim 2 is to determine the particular types of relationship that are important in providing the opportunity to observe and learn. Here, each network can be seen as a competing hypothesis, with the aim of NBDA being to establish which one best approximates the patterns of transmission among individuals (Tij). Given that part of this goal is to determine the types of relationship that determine opportunities to learn, a network that provides a direct quantification of such opportunities is not a useful predictor variable. In this paper, I will examine each aim in turn, and with reference to my simple model of the transmission process, look at the kind of networks that might be used to address each question.
I also assess the effects error in the measured social network has on estimates of the importance of social transmission (i.e. Aim 1). It is well known that sampling of animal interactions and associations can be incomplete, often because animals are missed during a given sampling period [24]. In some cases, incomplete sampling is likely to result in random noise applied to the network. However, of more concern is the possibility that individuals may be more likely or less likely to be missed when they are together than when they are apart, resulting in large network connections being under- or overestimated relative to smaller ones. Hoppitt & Farine [24] show that the indexes commonly believed to correct such bias (e.g. the half-weight index [25]) do so by an arbitrary amount, and are likely to either under-correct or over-correct the bias. It is possible to calculate corrected association indexes, but this requires calibration data to assess the degree of error to be corrected, which may not be possible to obtain in all studies [24]. Thus it is vital that researchers using association indexes know the effects that noise and bias might have on their findings. While work has been conducted on the effect error can have on inferences about network structure (e.g. [26]), it has not yet been established what effect noise and bias in the network have in an NBDA. In this paper, I conduct simulations to address this question.
4. NBDA Aim 1: detecting and quantifying social transmission
Here the goal is to assess the strength of evidence that social transmission is operating, and to estimate the effect social transmission has, with confidence intervals providing a plausible range. There are two main types of network that could be used, depending on how closely the diffusion process was observed and documented.
(a). Observation networks
In an ideal case, a researcher would know exactly when the innovation was performed, by whom, and who observed each performance. While such cases might seem rare, it is possible to attain data close to this level of resolution in cases where the target behaviour is only performed in a specific location that can be monitored closely. For example, Hobaiter et al. [7] applied NBDA to show evidence of social transmission of a tool using innovation, moss sponging, in a group of chimpanzees. Moss sponging is the use of pieces of moss as sponges to obtain water from holes in trees (differing from the usual use of folded leaves), and the initial spread was documented at a single water hole. A similar situation may be easy to achieve empirically using a novel artificial foraging task (e.g. [27]) that can be monitored closely by the researcher.
At first glance, one might attempt to fit a model in which 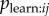 is modelled directly; however, this model deviates from the form of the standard NBDA. A standard NBDA assumes that transmission occurs at a rate that is proportional to a network connection between two individuals, whereas the model specified in §3 assumes there is a probability of learning from each discrete observation event. Furthermore, in order to fit a model in which
is modelled directly; however, this model deviates from the form of the standard NBDA. A standard NBDA assumes that transmission occurs at a rate that is proportional to a network connection between two individuals, whereas the model specified in §3 assumes there is a probability of learning from each discrete observation event. Furthermore, in order to fit a model in which 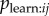 is estimated directly, we need to be able to ascertain whether learning has occurred as a result of a given observation event. The only way we have to infer this is by observing i perform the behaviour itself. Therefore, one has to address the question of how long after observing the behaviour i will perform it, given learning has occurred. A practical solution is to use an NBDA that approximates this process, by creating a dynamic observation network. I define a dynamic observation network, aij(t), as giving the number of times i has observed j performing the behaviour prior to time t. Hobaiter et al. [7] extend the NBDA model to allow use of a dynamic network. This model assumes that social transmission occurs at a rate that is proportional to the number of times the behaviour has been observed in the past. This model is perhaps less realistic than that specified above, because it seems improbable that an individual can continue to learn an innovation as a result at observing it at some time in the past, and that the effect of all such observations on the rate of learning would be cumulative. But the model might be used to approximate the case where
is estimated directly, we need to be able to ascertain whether learning has occurred as a result of a given observation event. The only way we have to infer this is by observing i perform the behaviour itself. Therefore, one has to address the question of how long after observing the behaviour i will perform it, given learning has occurred. A practical solution is to use an NBDA that approximates this process, by creating a dynamic observation network. I define a dynamic observation network, aij(t), as giving the number of times i has observed j performing the behaviour prior to time t. Hobaiter et al. [7] extend the NBDA model to allow use of a dynamic network. This model assumes that social transmission occurs at a rate that is proportional to the number of times the behaviour has been observed in the past. This model is perhaps less realistic than that specified above, because it seems improbable that an individual can continue to learn an innovation as a result at observing it at some time in the past, and that the effect of all such observations on the rate of learning would be cumulative. But the model might be used to approximate the case where 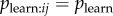 is constant across individuals.
is constant across individuals.
An alternative is to use a static network, where aij gives the number of times i observed j up until the point at which i learned the behaviour [7]. However, a static observation network does not fully allow for the time course of observations. For example, imagine a group of three individuals: A, B and C. A learns the behaviour first. Next, B observes A performing the behaviour three times and then learns the behaviour. Finally, C observes A performing the behaviour four times and subsequently learns the behaviour last. A static network would represent the network as having links of strength 3 from A to B and 4 to C, so an NBDA model based on this network would predict that C was more likely to learn second. In reality, we might expect B to be more likely to learn second, because B observed A performing the behaviour first. A dynamic network allows us to incorporate this information into the NBDA. Supporting this, Hobaiter et al. [7] found that an NBDA using a dynamic observation network had substantially more power than an NBDA using a static observation network.
Use of an observation network has the advantage that even when there is no social structure in the population, social transmission can be inferred if the chance order in which individuals observe the behaviour predicts the order of diffusion (this is illustrated in the simulation below). If plearn = 0, then we would not expect the diffusion to follow the observation network, and we would expect the s parameter in the NBDA not to be significantly greater than 0. Likewise, the greater plearn is, the greater our estimate of s will be, although s does not give an estimate of plearn. However, one can use the estimate of s to estimate the proportion of learning events that occurred by social transmission (as opposed to asocial learning), allowing an interpretable measure of social transmission to be obtained. For each acquisition event, e, at time te, one calculates the probability of social transmission as:
| 4.1 |
then takes the mean of 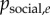 across acquisition events to estimate the proportion that occurred via social transmission (see [6] for more details).
across acquisition events to estimate the proportion that occurred via social transmission (see [6] for more details).
To test the performance of observation networks I simulated data from the model specified in equation 3.2 (see electronic supplementary material for details). I found that type 1 error rate was appropriate if slightly conservative, with the null hypothesis being rejected in 3.1% of cases when 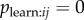 . Power increased rapidly as
. Power increased rapidly as 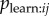 increased, showing that the dynamic network NBDA is able to detect social transmission occurring by the more realistic model even in the absence of any social structure (see electronic supplementary material, figure S1a; power is increased in the presence of underlying social structure, see electronic supplementary material, figure S2). However, the model did tend to slightly overestimate the proportion of events that occurred by social learning, with the true value lying above the 95% confidence intervals in more than 5% of simulations (see electronic supplementary material, figure S1b).
increased, showing that the dynamic network NBDA is able to detect social transmission occurring by the more realistic model even in the absence of any social structure (see electronic supplementary material, figure S1a; power is increased in the presence of underlying social structure, see electronic supplementary material, figure S2). However, the model did tend to slightly overestimate the proportion of events that occurred by social learning, with the true value lying above the 95% confidence intervals in more than 5% of simulations (see electronic supplementary material, figure S1b).
A concern with use of a dynamic observation network arises if the target behaviour is performed in a specific location or locations. For example, the moss sponging documented by Hobaiter et al. [7] was performed at a particular water hole. In these cases, a recorded observation for i may simply indicate that i was in the area appropriate for performing/learning the behaviour, and thus have been more likely to learn the target behaviour in the near future. Such an effect may look like social transmission in the NBDA. Hobaiter et al. [7] address this problem by including a variable giving each individual's exposure to the relevant location in the NBDA, and thus statistically controlling for it. Ideally exposure would be included as a time-varying variable (e.g. proportion of time spent in the target area each day) to allow for the possibility that patterns of changing exposure correlate with patterns of observation.
In conclusion, if detailed data are available on when the target behaviour is performed, by whom, and who observed each performance, use of a dynamic observation network is the most direct way to detect and quantify the effects of social transmission.
(b). Association networks
In most cases, researchers will not be able to document every performance and observation of the target innovation, but have a good idea of the order in which (and potentially times at which) individuals learned the target behaviour. In such cases, one can use an association network, where aij represents the proportion of time i spends associating with j (see [24,28,29] for reviews of techniques for estimating association networks). The assumption is that individuals can only learn from one another when they are associating; thus the rate of transmission from j to i, Tij, will be proportional to aij. For this logic to be valid, the criterion for i to be recorded as associating with j has to be specified at the appropriate spatial scale [30]. Individuals recorded as associating must be within a range at which observation can occur, whereas individuals not recorded as associating must tend to be at a distance at which observation is not possible. This is the case in Allen et al.'s [6] aforementioned humpback whale study, where the study was conducted over an area of approximately 1000 square miles. In contrast, other studies on captive groups of birds [8,31] have used a criterion for association based on proximity (e.g. nearest neighbour) within an enclosure of a few square metres—meaning that dyads not recorded as associating are still able to observe one another's behaviour. The discussion in this section pertains to the former kind of association network, whereas I return to the interpretation of the second kind, which I refer to as ‘small-scale association networks’ in §5b. Note that if patterns of association are known to change over the course of the diffusion, a dynamic association network aij(t) could be used.
In an NBDA using an appropriate association network, aij is an estimate of 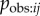 , with Bj = B and
, with Bj = B and 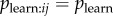 assumed to be approximately constant across individuals (though variation in learning rates can be modelled using individual covariates [8]). Therefore, from equation (3.4), the s parameter can be taken as an estimate of
assumed to be approximately constant across individuals (though variation in learning rates can be modelled using individual covariates [8]). Therefore, from equation (3.4), the s parameter can be taken as an estimate of 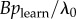 , the rate at which information is transmitted from an informed to a naive individual during periods when they are associating, relative to the rate of asocial learning.
, the rate at which information is transmitted from an informed to a naive individual during periods when they are associating, relative to the rate of asocial learning.
Alternatively, there may be variation in Bj, which is implicitly assumed to be constant in the standard NBDA. However, if data are available on the rate at which each individual performs the behaviour once they have learned it, this can be used to weight the association network and account for this variability [13]. Here, aij is replaced by Wjaij, where the transmission weight Wj is an estimate of Bj. This means that the meaning of the s parameter is now changed. From equation (3.3), in a weighted NBDA s now estimates 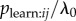 , i.e. the probability of learning each time i observes j perform the target behaviour, relative to the rate of asocial learning. However, the estimated proportion of events can still be calculated from equation (4.1) by replacing aij with Wjaij, allowing some comparison between weighted and un-weighted NBDAs. In the electronic supplementary material I present simulations showing both that inclusion of transmission weights can increase statistic power to detect social learning and that models with transmission weights fit the data better, as judged by Akaike's information criterion, AICc. This suggests that if transmission weights are available, they should be included in the analysis if they decrease AICc, as this indicates the model is more realistic and may result in better power to detect social transmission. However, these simulations also show that if transmission weights are not available, but a researcher suspects variation in Bj, he/she can still use an un-weighted NBDA as a valid means to detect and quantify social transmission. Note that transmission weights can be used with other types of networks too, where there is measured variation in performance rate (see §5d).
, i.e. the probability of learning each time i observes j perform the target behaviour, relative to the rate of asocial learning. However, the estimated proportion of events can still be calculated from equation (4.1) by replacing aij with Wjaij, allowing some comparison between weighted and un-weighted NBDAs. In the electronic supplementary material I present simulations showing both that inclusion of transmission weights can increase statistic power to detect social learning and that models with transmission weights fit the data better, as judged by Akaike's information criterion, AICc. This suggests that if transmission weights are available, they should be included in the analysis if they decrease AICc, as this indicates the model is more realistic and may result in better power to detect social transmission. However, these simulations also show that if transmission weights are not available, but a researcher suspects variation in Bj, he/she can still use an un-weighted NBDA as a valid means to detect and quantify social transmission. Note that transmission weights can be used with other types of networks too, where there is measured variation in performance rate (see §5d).
(c). Effects of error in the social network
Error could potentially arise in both dynamic observation networks and, as outlined above, in association networks. Here I conduct simulations to assess the effect of such error on the detection of social transmission and the estimates of its importance using NBDA. Full details of the simulations outlined below are provided in the electronic supplementary material. Note that the purpose of the simulations presented in this paper is not to draw general inferences about the power of NBDA for given values of s, or the relative power of OADA and TADA, which depend on sample size, network structure and whether asocial learning occurs at a constant rate [18]. Rather, the aim is to see how NBDA responds to errors in network structure.
When using an observation network researchers do not know for sure when an observation has occurred, because it is difficult to know what a subject is attending to (especially with non-human animals). In reality, some kind of proxy is used, such as: individuals within 1 m, with head orientated towards the performer and with an unobstructed view [7]. Potentially, individuals recorded as observers might not really have been observers, and some observers might have been missed (e.g. if they are outside the threshold distance). Critics of the use of observation networks might suggest that this uncertainty renders the results unreliable. I re-ran the simulations and analyses described in §4a, varying the degree of error in the network: i.e. the probability an individual recorded as an observer really was an observer (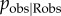 ). For all values of
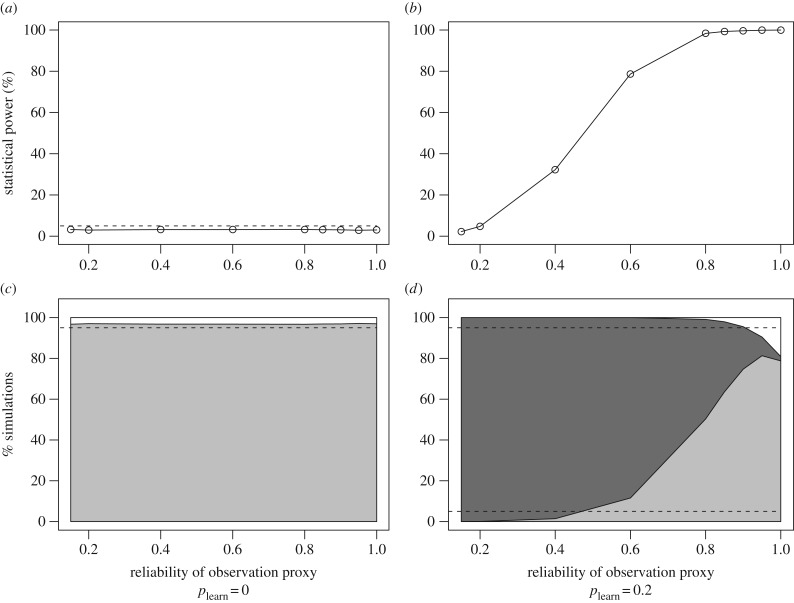
). For all values of 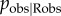 , the type 1 error rate remained approximately constant at 2.9–3.3%, showing that error in identifying observers does not increase the risk of a spurious social transmission effect (see figure 1a,c). Instead, power to detect social transmission was reduced as
, the type 1 error rate remained approximately constant at 2.9–3.3%, showing that error in identifying observers does not increase the risk of a spurious social transmission effect (see figure 1a,c). Instead, power to detect social transmission was reduced as 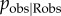 decreased (see figure 1b), accompanied by a tendency to underestimate the proportion of events occurring by social transmission (see figure 1d). This counteracts the tendency of the dynamic network NBDA to overestimate the importance of social transmission. Only when observers are identified with very high reliability (which is probably unachievable in practice) are overestimates produced. This means that researchers using a dynamic observation network should consider their estimates to be slightly conservative if good data on observers are available, and highly conservative if only a crude proxy for observation can be obtained.
decreased (see figure 1b), accompanied by a tendency to underestimate the proportion of events occurring by social transmission (see figure 1d). This counteracts the tendency of the dynamic network NBDA to overestimate the importance of social transmission. Only when observers are identified with very high reliability (which is probably unachievable in practice) are overestimates produced. This means that researchers using a dynamic observation network should consider their estimates to be slightly conservative if good data on observers are available, and highly conservative if only a crude proxy for observation can be obtained.
Figure 1.
Performance of NBDA (OADA variant) using a dynamic observation network, when there is error in identifying observers. (a) Type 1 error rate and (b) statistical power for plearn = 0.2 as a function of the reliability of the observation proxy. (c,d) The proportion of simulations for which the real proportion of social transmission events was within the 95% CI (light grey), underestimated (dark grey) or overestimated (white) for plearn = 0 (c) and plearn = 0.2 (d). Results were similar for the TADA variant of NBDA.
Next I investigate the robustness of an NBDA using an association network when aij is not a perfect estimate of 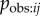 . First I assess how the method is affected when the aij has random noise, perhaps as a result of sampling error when collecting association data. Alternatively this could be due to variation in
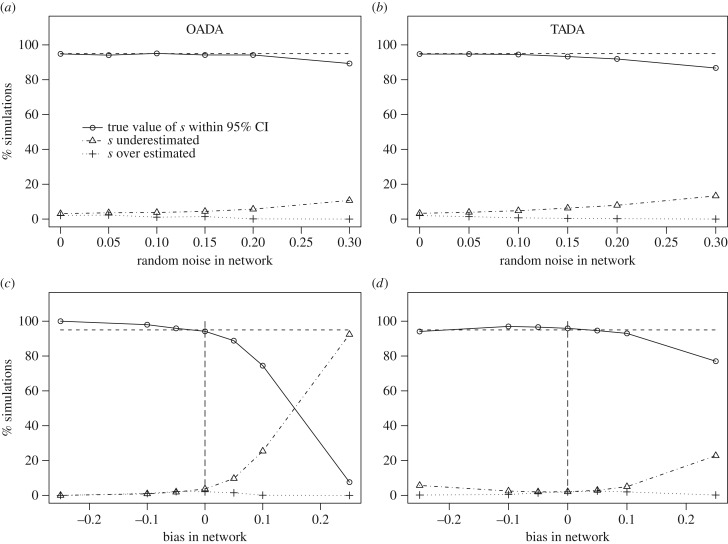
. First I assess how the method is affected when the aij has random noise, perhaps as a result of sampling error when collecting association data. Alternatively this could be due to variation in 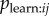 , causing Tij not to be directly proportional to aij. I simulated diffusion data from equation (3.4). I then simulated an association network as ‘recorded’ by the researcher, by adding random noise to the network before it was input into the NBDA (OADA and continuous TADA variants). For all levels of noise, the type 1 error rate remained less than 5%, showing that random noise in the network does not result in an increased risk of detecting a spurious social transmission effect. As expected, power increases with increasing values of s, and is greater for TADA than for OADA. In the OADA power was reduced as network noise increased; however this effect was not seen in the TADA (see electronic supplementary material, figure S3a,b). When no noise was present, 95% confidence intervals for s contained the true value 95–98% of the time, showing these to be appropriate or slightly too wide. However, as noise increased, both OADA and TADA showed a tendency to underestimate the true value of s (see figure 2a,b). Overall, this means that if a researcher suspects there is random noise in the association network: a positive result for social transmission can still be trusted, and 95% confidence intervals for s may be conservative (underestimate s). The same is true for the estimated proportion of events by social transmission (equation (4.1)) because this is calculated from s.
, causing Tij not to be directly proportional to aij. I simulated diffusion data from equation (3.4). I then simulated an association network as ‘recorded’ by the researcher, by adding random noise to the network before it was input into the NBDA (OADA and continuous TADA variants). For all levels of noise, the type 1 error rate remained less than 5%, showing that random noise in the network does not result in an increased risk of detecting a spurious social transmission effect. As expected, power increases with increasing values of s, and is greater for TADA than for OADA. In the OADA power was reduced as network noise increased; however this effect was not seen in the TADA (see electronic supplementary material, figure S3a,b). When no noise was present, 95% confidence intervals for s contained the true value 95–98% of the time, showing these to be appropriate or slightly too wide. However, as noise increased, both OADA and TADA showed a tendency to underestimate the true value of s (see figure 2a,b). Overall, this means that if a researcher suspects there is random noise in the association network: a positive result for social transmission can still be trusted, and 95% confidence intervals for s may be conservative (underestimate s). The same is true for the estimated proportion of events by social transmission (equation (4.1)) because this is calculated from s.
Figure 2.
Performance of NBDA using an association network when there was noise (a,b) or bias (c,d) in the network. The plots show the proportion of simulations in which the true value of the s parameter (giving the strength of social transmission) was within the 95% CI (circles), overestimated (crosses) or underestimated (triangles). The horizontal dashed line shows 95%: ideally the true value should be within the 95% CI 95% of the time. The left panels show the performance of the OADA variant of NBDA, and the right panels show the performance of the TADA variant. Positive bias means that large network connections are overestimated relative to smaller ones, whereas negative bias means small network connections are overestimated.
Another possibility is that there is systematic bias in the network. If all connections in the network are overestimated or underestimated by the same factor, this has little effect on the analysis, because it merely scales the network. If network connections are overestimated, s will be estimated as smaller than its true value and vice versa. However, the proportion of learning events estimated to have occurred by social transmission will be unchanged, as will the fit of the model to the data. A potentially more serious concern is when larger values of aij tend to be overestimated, and smaller values underestimated, or vice versa. This could occur if members of each dyad are more or less likely to be observed when they are together than when they are alone [24]. I investigate the effect of such bias by repeating the simulations described above but with systematic bias in the ‘recorded’ network instead of random noise. I did this by transforming each aij as aij = aij + (aij − 0.5) × bias, where bias < 0 means small network connections are overestimated relative to large ones and bias > 0 means large network connections are overestimated relative to small ones.
In all cases type 1 error rate remained less than 5%, showing that bias in the network does not result in an increased risk of detecting a spurious social transmission effect. There was little effect on statistical power in either the OADA or the TADA (see electronic supplementary material, figure S3c,d). When small network connections were overestimated relative to large ones (bias < 0), 95% confidence intervals contained the true value of s in >95% of cases, suggesting the 95% were too broad (underestimated the level of precision) (see figure 2c,d). In contrast, when large network connections tended to be overestimated relative to small ones (bias > 0) the 95% CIs tended to underestimate the true value of s, sometimes to a severe extent. For example, an OADA when s = 4 and bias = 0.25, in 92.4% of simulations the true value was below the 95% confidence interval. There is no indication that bias can result in confidence intervals that are too narrow, or a tendency to overestimate s. Overall, if a researcher suspects bias in the network it means the estimates of s are likely to be conservative, in terms of either the estimated precision (bias < 0) or the estimated value of s (bias > 0).
None of the sources of noise or bias considered here inflated the type 1 error rate, and statistical power was usually not badly reduced. In some cases, confidence intervals were found to be conservative in terms of precision (too broad) or because they tended to underestimate s. It is worth noting that if the aim is to compare rates of social transmission across diffusions (e.g. across species or contexts) it is important to ensure that association networks are quantified in a consistent manner, so any sources of noise and bias are consistent across diffusions and do not generate a spurious difference in social transmission rates.
5. NBDA Aim 2: establishing the typical pathways of information transfer
Another aim a researcher might have in an NBDA is to elucidate the typical pathways of diffusion, by comparing the fit of alternative NBDA models using different networks. The objective here may be to determine the particular types of relationship that are important in providing the opportunity to observe and learn. For example, in their study of common ravens (Corvus corax) Kulahci et al. [32] found that a social network based on affiliative interactions (e.g. allo-preening and food sharing) predicted the spread of novel foraging behaviour better than networks based on aggressive interactions and proximity. Alternatively, NBDA can be used to assess different hypotheses regarding social learning strategies (i.e. from whom do animals learn?) [2] or directed social learning [33]. The implicit aim is to identify the network that best approximates Tij. The logic is that the more closely the network approximates Tij, the more closely the diffusion will tend to follow the network, as quantified by AICc. (Alternatively, Whalen & Hoppitt [16] show that the Watanabe Akaike information criterion WAIC can be used in a Bayesian NBDA). This logic is supported by the simulations conducted in §4. For each set of simulations AICc tended to be lower (better) for the networks that more closely approximated Tij, with differences becoming more pronounced as the strength of social learning increased (see electronic supplementary material, figures S6 and S7).
A researcher might have the combined aim of detecting and quantifying social transmission, but also making inferences about the typical pathways of diffusion. If so, the researcher can include a model with no social transmission (s = 0) in the model comparison. If no network results in an AICc that is substantially lower than that yielded from the asocial model, there is little evidence for social transmission following any of the networks studied. If there is evidence for social transmission, the best fitting model can be used to generate estimates of the strength of social transmission, on the basis that this model is likely to best approximate the true Tij. There are a number of types of network that could be used the elucidate the typical pathways of information transfer; here I discuss them in turn.
(a). Observation networks
I showed above that a network giving the pattern of observations that occurred during the course of a diffusion is a direct and powerful way to detect and quantify social transmission. However, if the goal is to find a network that approximates Tij, then an observation network will usually be of little use when used as a predictor in an NBDA. Part of the goal here is to find a network that predicts the pattern of observations that is likely to occur during a diffusion (i.e. approximate 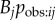 ). The pattern of observations that happened to occur in a specific diffusion, when used as a predictor, cannot tell us anything about what aspects of social structure influence patterns of observations in general. Therefore, it will usually make little sense to use an observation network in an NBDA for this purpose. Instead a researcher might ask if another network, N, is correlated with the observation network, and thus assess the case that the relationships quantified in N are important in determining opportunities for observation. If N is strongly correlated with the observation network, and has good predictive power (low AICc relative to other networks) in an NBDA, it suggests that N approximates the pathway of diffusion (Tij) well, and it does so at least in part because it predicts the pattern of observations (approximates
). The pattern of observations that happened to occur in a specific diffusion, when used as a predictor, cannot tell us anything about what aspects of social structure influence patterns of observations in general. Therefore, it will usually make little sense to use an observation network in an NBDA for this purpose. Instead a researcher might ask if another network, N, is correlated with the observation network, and thus assess the case that the relationships quantified in N are important in determining opportunities for observation. If N is strongly correlated with the observation network, and has good predictive power (low AICc relative to other networks) in an NBDA, it suggests that N approximates the pathway of diffusion (Tij) well, and it does so at least in part because it predicts the pattern of observations (approximates 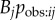 ). An exception occurs if a researcher wishes to test whether social transmission occurs via observation of the target innovation, as opposed to an alternative, mutually exclusive pathway, such as exposure to the products of behaviour. In this case, an NBDA model using an observation network could be compared to a model with a network representing that alternative pathway.
). An exception occurs if a researcher wishes to test whether social transmission occurs via observation of the target innovation, as opposed to an alternative, mutually exclusive pathway, such as exposure to the products of behaviour. In this case, an NBDA model using an observation network could be compared to a model with a network representing that alternative pathway.
(b). Association and proximity networks
Proximity networks are derived from data on the spatial relationships among individuals: members of a dyad who are commonly in close proximity have strong connections between them. These include association networks, which quantify the proportion of time members of a dyad spend together. In §4b above I argued that an association network based on data collected on an appropriate spatial scale is an estimate of 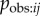 . This leads to an interpretation of s as the rate at which information is transmitted from an informed to a naive individual during periods when they are associating, relative to the rate of asocial learning. However, proximity networks are often collected on a small spatial scale, such that the individuals always remain in close proximity, such as groups housed in captivity (e.g. [8,32]), e.g. by quantifying which individuals tend to be nearest neighbours, or within five body lengths. In such cases, association or relative proximity is not a necessary condition for observation to occur, e.g. an animal could quite easily observe an individual that is not its nearest neighbour, or within five body lengths. Consequently, for such small-scale proximity networks, there is no logical guarantee that aij will estimate
. This leads to an interpretation of s as the rate at which information is transmitted from an informed to a naive individual during periods when they are associating, relative to the rate of asocial learning. However, proximity networks are often collected on a small spatial scale, such that the individuals always remain in close proximity, such as groups housed in captivity (e.g. [8,32]), e.g. by quantifying which individuals tend to be nearest neighbours, or within five body lengths. In such cases, association or relative proximity is not a necessary condition for observation to occur, e.g. an animal could quite easily observe an individual that is not its nearest neighbour, or within five body lengths. Consequently, for such small-scale proximity networks, there is no logical guarantee that aij will estimate 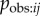 . Instead, use of a proximity network in an NBDA represents the hypothesis that individuals that are often in spatial proximity to one another will learn from one another more frequently than individuals that are usually spatially separated. It may be that another type of network (see below) may predict Tij better than a proximity network (e.g. [32]). Even in cases where a proximity or association network is a good estimate of
. Instead, use of a proximity network in an NBDA represents the hypothesis that individuals that are often in spatial proximity to one another will learn from one another more frequently than individuals that are usually spatially separated. It may be that another type of network (see below) may predict Tij better than a proximity network (e.g. [32]). Even in cases where a proximity or association network is a good estimate of 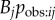 , another network may approximate Tij better if it better captures variation in
, another network may approximate Tij better if it better captures variation in 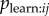 .
.
A question arises as to whether researchers should use association data that is collected during the course of the diffusion, or whether they should use data collected during a different period. For example, in their study on squirrel monkeys, Cladiere et al. [34] constructed an association network based on the amount of time dyads spent together in the area of the foraging task and thus were able to observe one another solving the task (though they did not use this for an NBDA, their aims were similar). Intuitively, such a ‘diffusion-specific network’ provides a better proxy for the observation network than association data collected during the weeks, months or years preceding the diffusion. For this reason, such data are likely to be more powerful for detecting and quantifying the effects of social transmission. However, for the same reasons as for the observation network, the diffusion-specific network is of little utility for an NBDA aiming to elucidate the general pathways of diffusion in the population. The diffusion-specific network will reflect the chance patterns of observation that happened to occur in the diffusion, and, therefore, cannot tell us anything about what aspects of social structure influence patterns of observations in general. Consequently, a diffusion-specific association network is suitable for detecting and quantifying social transmission, but not for establishing the typical pathways of information transfer.
(c). Interaction networks
Researchers often construct social networks based on the rate at which each dyad interacts, or show a particular type of interaction (e.g. grooming, fights) [14]. In animal social network analysis in general, this is often considered to be a more direct way of quantifying patterns of interactions among animals, with proximity/association networks providing an indirect proxy for interaction rate [14]. However, when used in an NBDA, interaction networks represent a hypothesis that a particular interaction type predicts the rate at which individuals learn from one another. As such there is no reason to think of interaction networks as being preferable to proximity networks a priori for an NBDA. Instead, alternative networks can be compared against one another as competing hypotheses using AICc. Once a supported model is found, a researcher may wish to use this to quantify the importance of social transmission. The s parameter obtained will estimate the rate of social transmission per unit connection relative to the rate of asocial learning. Thus, s will be dependent on the scale of the network, and potentially difficult to interpret. Therefore, I suggest researchers transform their estimate of s into an estimated proportion of events that occurred by social transmission using equation (4.1).
(d). Model networks
Instead of using social networks derived from association, proximity or interaction data, a researcher could construct a network representing a hypothesis about the pathway of diffusion that is theoretically derived. For example, a hypothesis that individuals only learn from high-prestige individuals [35] could be represented by a network, mij, that has mij = 1 when j is a high-prestige individual and mij = 0 otherwise (I use mij to represent a model network to distinguish it from the association network, aij, below). This model could be tested against a model with a homogeneous network (all mij = 1) to test for a prestige bias in learning, or against other theoretically derived networks. This allows NBDA to be used as a tool to test for evidence of evolved social learning strategies [2,36,37] in contexts and species where empirical tests (e.g. [38,39–41]) cannot be run.
In an NBDA, a copying bias could be manifested in Bj, 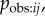
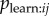 or some combination of the three. For illustration, imagine we have an evolved strategy ‘copy individuals of high prestige’. This may be implemented as a tendency to observe high-prestige individuals more often, resulting in large values of
or some combination of the three. For illustration, imagine we have an evolved strategy ‘copy individuals of high prestige’. This may be implemented as a tendency to observe high-prestige individuals more often, resulting in large values of 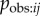 when j has high prestige. Alternatively, or in addition, individuals may be more likely to copy behaviour after they observe it being performed by a high-prestige individual, resulting in large values of
when j has high prestige. Alternatively, or in addition, individuals may be more likely to copy behaviour after they observe it being performed by a high-prestige individual, resulting in large values of 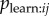 when j has high prestige. A similar copying bias might result if high-prestige individuals tend to perform the behaviour more once they have learned it (high Bj). This is unlikely to be a result of an evolved social learning strategy, but nonetheless would result in a similar bias in favour of learning from high-prestige individuals—i.e. high values of Tij when j has high prestige.
when j has high prestige. A similar copying bias might result if high-prestige individuals tend to perform the behaviour more once they have learned it (high Bj). This is unlikely to be a result of an evolved social learning strategy, but nonetheless would result in a similar bias in favour of learning from high-prestige individuals—i.e. high values of Tij when j has high prestige.
Therefore, if a researcher uses a binary network representing a particular copying bias, and finds it is supported, this provides evidence of a bias in Tij, which could be a result of bias in any combination of Bj, 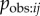 and
and 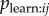 . The s parameter obtained will provide an estimate of the rate of transmission averaged across all relevant dyads (i.e. average
. The s parameter obtained will provide an estimate of the rate of transmission averaged across all relevant dyads (i.e. average 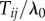 given mij = 1). However, the analysis could be broken down further to investigate where the bias lies. If a researcher has transmission weights Wj providing a good estimate of Bj (see §4b), he/she can test whether Wj tends to be higher for the target class (e.g. high prestige) of individuals, to assess whether there is bias resulting from performance rate. They can then include Wj in the NBDA: if copying bias still remains, it suggests there is bias in
given mij = 1). However, the analysis could be broken down further to investigate where the bias lies. If a researcher has transmission weights Wj providing a good estimate of Bj (see §4b), he/she can test whether Wj tends to be higher for the target class (e.g. high prestige) of individuals, to assess whether there is bias resulting from performance rate. They can then include Wj in the NBDA: if copying bias still remains, it suggests there is bias in 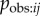 and/or
and/or 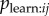 . The s parameter now estimates the average of
. The s parameter now estimates the average of 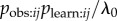 given mij = 1. If the researcher has an association network, he/she can test whether aij is correlated with the binary model network, e.g. whether aij tends to be higher when j has high prestige, thus testing for a bias in
given mij = 1. If the researcher has an association network, he/she can test whether aij is correlated with the binary model network, e.g. whether aij tends to be higher when j has high prestige, thus testing for a bias in 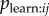 . The researcher can then include aij in the NBDA. A social network with connections of strength aijmij with transmission weights Wj represents the hypothesis that there is (strong) copying bias in
. The researcher can then include aij in the NBDA. A social network with connections of strength aijmij with transmission weights Wj represents the hypothesis that there is (strong) copying bias in 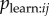 . This can be compared with a weighted model using the unaltered association matrix aij, representing the hypothesis of no copying bias in
. This can be compared with a weighted model using the unaltered association matrix aij, representing the hypothesis of no copying bias in 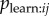 . The s parameter obtained from an NBDA using the network aijmij with transmission weights estimates
. The s parameter obtained from an NBDA using the network aijmij with transmission weights estimates 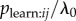 given mij = 1. As yet there are no studies using this approach to detecting and breaking down biases in Tij (but see [42] for a similar approach).
given mij = 1. As yet there are no studies using this approach to detecting and breaking down biases in Tij (but see [42] for a similar approach).
(e). Multiple networks
The approaches described above allow researchers to test which of a specified set of social networks best approximates Tij. An alternative approach is to acknowledge that social transmission might follow more than one pathway, but do so at different rates. To this end, one can input multiple networks into an NBDA, each with a separate s parameter estimated for each network [43]. The NBDA model then becomes:
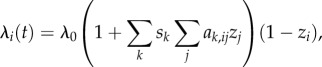 |
5.1 |
where ak,ij is the kth social network, and sk estimates the rate of social transmission through that network. This model can be compared with one in which s parameters are constrained, e.g. s1 = s2, to test for evidence of a difference in transmission rate between different pathways. It can also be compared with models in which there is no transmission along a specific pathway, e.g. s1 = 0, to test for evidence of social transmission along that pathway.
It is important to note that there are two ways a researcher might then quantify and compare the importance of social transmission in the different networks. The sk parameters estimate the relative strength of social transmission per unit of network connection. The exact interpretation of sk depends on the type of network, as shown above. In addition, a researcher can estimate the proportion of events occurring by social transmission through each network, N, by modifying equation (4.1) as follows:
| 5.2 |
and taking the mean across all acquisition events. Unlike sk, this figure will also take into account the strength and number of connections in each network, in estimating the influence of each network on the diffusion. See [43] for further discussion of how to quantify the influence of each network in a multi-network NBDA.
Multi-network NBDA might also provide an improved approach for detecting biases in social transmission. For instance, in the example given in §5d, the hypothetical prestige bias model states that only high-prestige individuals socially transmit the target behaviour. It is perhaps more realistic to assume that all individuals socially transmit the behaviour, and test whether high-prestige individuals do so at a higher rate. One network, m1,ij would contain binary connections only from high-prestige individuals, whereas another network m2,ij would contain binary connections from all other individuals. If a model with s1 > s2 is favoured over a model with s1 = s2, then it provides evidence of a prestige bias in Tij. The source of this bias could then be investigated in an analogous manner to that described in §5d.
Farine et al. [44] used multi-network NBDA to analyse the pathways by which juvenile zebra finches (Taeniopygia guttata) socially learn foraging skills. Half of the juveniles had been exposed to the avian stress hormone corticosterone (CORT) earlier in life, mimicking the effects of developmental stress. Farine et al. hypothesized that different social learning strategies would be used by finches that had experienced developmental stress (CORT) from those that had not. They constructed eight different association networks representing transmission from (1) adults to adults, (2) juveniles to adults, (3) parents to CORT offspring, (4) adults to unrelated CORT juveniles, (5) all juveniles to CORT juveniles, (6) parents to non-CORT offspring, (7) adults to unrelated non-CORT juveniles, and (8) all juveniles to control juveniles. They then compared the predictive power of models combining different combinations of these networks. The results suggested that all individuals learned exclusively from adults. Furthermore, they found evidence of a different social learning strategy between non-CORT-treated juveniles and CORT-treated juveniles. The former category relied more on social transmission from their parents (bigger estimate of s for network 6 than network 7) whereas the latter relied more (almost exclusively) on social transmission from unrelated adults (bigger s for network 4 than network 3). This case study illustrates the potential of multi-network NBDA to quantify the relative importance of different pathways of information transmission.
(f). Other approaches
Given its potential role as a tool for testing for transmission biases and social learning strategies, NBDA can be compared with experience-weighted attraction models. McElreath et al. [45] adapted these models to infer specific social learning strategies given data on the choices individuals make, and the choices they observe others making. This approach is similar to an NBDA, as it is used in §5, insofar as both use time series of data to make inferences about pathways of learning. However, NBDA is solely concerned with the acquisition of novel behaviour (innovations) to the repertoire. In contrast, experience-weighted attraction models are concerned with the choices made by individuals when faced with a number of different behavioural options (e.g. a number of ways to solve a foraging task), and whether they adopt particular social learning strategies in making these choices. Thus the approaches answer subtly different, and potentially complementary questions. Some combination of the two methods might also be useful: an experience-weighted attraction model might incorporate network data to account for who is likely to have observed each performance of the target behaviours. It seems likely that experience-weighted attraction models will have more power than NBDA to detect social learning strategies from detailed data (accurate dynamic observation networks), because they take into account the repeated behaviour of individuals, rather than the first time they perform a novel behavioural trait. However, NBDA may be applicable to sparser datasets (e.g. using only association data).
6. Conclusion
In summary, an NBDA can have two goals: (1) to detect and quantify social transmission from diffusion data, and/or (2) to make inferences about the typical pathways of diffusion and information transfer in a given species or context. Some types of social network are only generally appropriate for the first of these goals. In this paper, I have attempted to establish the conceptual foundations of NBDA, by showing how an NBDA using each type of network links to the underlying process of learning. I showed that the precise meaning of the estimate of the key parameter, s, depends on the type of network that is used. However, I suggested that quantifying the proportion of learning events that occurred by social transmission can be used as an additional measure that transfers more easily across analyses using different networks. I showed that observation networks and association networks are robust to violations of the assumptions implicit in the NBDA model, and that such violations are not a cause to suspect a spurious positive result for social transmission. However, under some circumstances, biases can arise in estimates of the importance of social transmission, which social learning researchers should be aware of when interpreting their results. Finally, I suggested how NBDA might be used to detect social transmission biases and social learning strategies using diffusion data. Thus, NBDA might prove a valuable addition to social learning researchers' toolkit, in elucidating the taxonomic distribution of such strategies, and their relationship to the emergence of traditions and culture in natural settings.
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Supplementary Material
Acknowledgements
I am grateful to Sonja Wild, Damien Farine and Elli Leadbeater for valuable discussions about the practical applications of NBDA and the effects of error in social networks.
Data accessibility
This article has no additional data.
Competing interests
I have no competing interests.
Funding
The work was funded by the ERC grant BeeDanceGap (638873).
References
- 1.Heyes CM. 1994. Social-learning in animals: categories and mechanisms. Biol. Rev. 69, 207–231. ( 10.1111/j.1469-185X.1994.tb01506.x) [DOI] [PubMed] [Google Scholar]
- 2.Laland KN. 2004. Social learning strategies. Learn. Behav. 32, 4–14. ( 10.3758/BF03196002) [DOI] [PubMed] [Google Scholar]
- 3.Laland KN, Galef BG (eds). 2009. The question of animal culture. Cambridge, MA: Harvard University Press. [Google Scholar]
- 4.Reader SM. 2004. Distinguishing social and asocial learning using diffusion dynamics. Learn. Behav. 32, 90–104. ( 10.3758/BF03196010) [DOI] [PubMed] [Google Scholar]
- 5.Hoppitt W, Laland KN. 2013. Social learning: an introduction to mechanisms, methods and models. Princeton, NJ: Princeton Univeristy Press. [Google Scholar]
- 6.Allen J, Weinrich M, Hoppitt W, Rendell L. 2013. Network-based diffusion analysis reveals cultural transmission of lobtail feeding in humpback whales. Science 340, 485–488. ( 10.1126/science.1231976) [DOI] [PubMed] [Google Scholar]
- 7.Hobaiter C, Poisot T, Zuberbuehler K, Hoppitt W, Gruber T. 2014. Social network analysis shows direct evidence for social transmission of tool use in wild chimpanzees. PLoS Biol. 12, e1001960 ( 10.1371/journal.pbio.1001960) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boogert NJ, Reader SM, Hoppitt W, Laland KN. 2008. The origin and spread of innovations in starlings. Anim. Behav. 75, 1509–1518. ( 10.1016/j.anbehav.2007.09.033) [DOI] [Google Scholar]
- 9.Atton N, Hoppitt W, Webster MM, Galef BG, Laland KN. 2012. Information flow through threespine stickleback networks without social transmission. Proc. R. Soc. B 279, 4272–4278. ( 10.1098/rspb.2012.1462) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Duboscq J, Romano V, MacIntosh A, Sueur C. 2016. Social information transmission in animals: lessons from studies of diffusion. Front. Psychol. 7, 1147 ( 10.3389/fpsyg.2016.01147) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Franz M, Nunn CL. 2009. Network-based diffusion analysis: a new method for detecting social learning. Proc. R. Soc. B 276, 1829–1836. ( 10.1098/rspb.2008.1824) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hoppitt W, Boogert NJ, Laland KN. 2010. Detecting social transmission in networks. J. Theor. Biol. 263, 544–555. ( 10.1016/j.jtbi.2010.01.004) [DOI] [PubMed] [Google Scholar]
- 13.Aplin LM, Farine DR, Morand-Ferron J, Sheldon BC. 2012. Social networks predict patch discovery in a wild population of songbirds. Proc. R. Soc. B 279, 4199–4205. ( 10.1098/rspb.2012.1591) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Croft DP, James R, Krause J. 2008. Exploring animal social networks. Princeton, NJ: Princeton University Press. [Google Scholar]
- 15.Nightingale G, et al. 2015. Quantifying diffusion in social networks: a Bayesian approach. In Animal social networks (eds J Krause et al.), pp. 38–52. Oxford, UK: Oxford University Press. [Google Scholar]
- 16.Whalen A, Hoppitt WJE. 2016. Bayesian model selection with network based diffusion analysis. Front. Psychol. 7, 267 ( 10.3389/fpsyg.2016.00409) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.R Core Team. 2017. R: a language and environment for statistical computing. 2.10.1 edn. Vienna, Austria: R Foundation for Statistical Computing; http://www.R-project.org [Google Scholar]
- 18.Hoppitt W, Kandler A, Kendal J, Laland K. 2010. The effect of task structure on diffusion dynamics: implications for diffusion curve and network-based analyses. Learn. Behav. 38, 243–251. ( 10.3758/LB.38.3.243) [DOI] [PubMed] [Google Scholar]
- 19.Franz M, Nunn CL. 2010. Investigating the impact of observation errors on the statistical performance of network-based diffusion analysis. Learn. Behav. 38, 235–242. ( 10.3758/LB.38.3.235) [DOI] [PubMed] [Google Scholar]
- 20.Centola D, Macy M. 2007. Complex contagions and the weakness of long ties. Am. J. Sociol. 113, 702–734. ( 10.1086/521848) [DOI] [Google Scholar]
- 21.McGuigan N, Burdett E, Burgess V, Dean L, Lucas A, Vale G, Whiten A. 2017. Innovation and social transmission in experimental micro-societies: exploring the scope of cumulative culture in young children. Phil. Trans. R. Soc. B 372, 20160425 ( 10.1098/rstb.2016.0425) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Weinberger VP, Quiñinao C, Marquet PA. 2017. Innovation and the growth of human population. Phil. Trans. R. Soc. B 372, 20160415 ( 10.1098/rstb.2016.0415) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Terkel J. 1995. Cultural transmission in the black rat: pine-cone feeding. Adv. Stud. Behav. 24, 119–154. ( 10.1016/S0065-3454(08)60393-9) [DOI] [Google Scholar]
- 24.Hoppitt W, Farine DR. In press. Association indices for quantifying social relationships: how to deal with missing observations of individuals or groups. Anim. Behav. ( 10.1016/j.anbehav.2017.08.029) [DOI]
- 25.Cairns SJ, Schwager SJ. 1987. A comparison of association indexes. Anim. Behav. 35, 1454–1469. ( 10.1016/S0003-3472(87)80018-0) [DOI] [Google Scholar]
- 26.Lusseau D, Whitehead H, Gero S. 2008. Incorporating uncertainty into the study of animal social networks. Anim. Behav. 75, 1809–1815. ( 10.1016/j.anbehav.2007.10.029) [DOI] [Google Scholar]
- 27.van de Waal E, Renevey N, Favre CM, Bshary R. 2010. Selective attention to philopatric models causes directed social learning in wild vervet monkeys. Proc. R. Soc. B 277, 2105–2111. ( 10.1098/rspb.2009.2260) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Whitehead H. 2008. Analyzing animal societies: quantitative methods for vertebrate social analysis. London, UK: University of Chicago Press. [Google Scholar]
- 29.Farine DR, Whitehead H. 2015. Constructing, conducting and interpreting animal social network analysis. J. Anim. Ecol. 84, 1144–1163. ( 10.1111/1365-2656.12418) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Farine DR. 2015. Proximity as a proxy for interactions: issues of scale in social network analysis. Anim. Behav. 104, E1–E5. ( 10.1016/j.anbehav.2014.11.019) [DOI] [Google Scholar]
- 31.Boogert NJ, Nightingale GF, Hoppitt W, Laland KN. 2014. Perching but not foraging networks predict the spread of novel foraging skills in starlings. Behav. Process. 109, 135–144. ( 10.1016/j.beproc.2014.08.016) [DOI] [PubMed] [Google Scholar]
- 32.Kulahci IG, Rubenstein DI, Bugnyar T, Hoppitt W, Mikus N, Schwab C. 2016. Social networks predict selective observation and information spread in ravens. R. Soc. Open Sci. 3, 160256 ( 10.1098/rsos.160256) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Coussi-Korbel S, Fragaszy D. 1995. On the relation between social dynamics and social learning. Anim. Behav. 50, 1441–1453. ( 10.1016/0003-3472(95)80001-8) [DOI] [Google Scholar]
- 34.Claidiere N, Messer EJE, Hoppitt W, Whiten A. 2013. Diffusion dynamics of socially learned foraging techniques in squirrel monkeys. Curr. Biol. 23, 1251–1255. ( 10.1016/j.cub.2013.05.036) [DOI] [PubMed] [Google Scholar]
- 35.Henrich J, Gil-White FJ. 2001. The evolution of prestige: freely conferred deference as a mechanism for enhancing the benefits of cultural transmission. Evol. Hum. Behav. 22, 165–196. ( 10.1016/S1090-5138(00)00071-4) [DOI] [PubMed] [Google Scholar]
- 36.Rendell L, Fogarty L, Hoppitt WJE, Morgan TJH, Webster MM, Laland KN. 2011. Cognitive culture: theoretical and empirical insights into social learning strategies. Trends Cogn. Sci. 15, 68–76. ( 10.1016/j.tics.2010.12.002) [DOI] [PubMed] [Google Scholar]
- 37.Henrich J, McElreath R. 2003. The evolution of cultural evolution. Evol. Anthropol. 12, 123–135. ( 10.1002/evan.10110) [DOI] [Google Scholar]
- 38.Webster MM, Laland KN. 2008. Social learning strategies and predation risk: minnows copy only when using private information would be costly. Proc. R. Soc. B 275, 2869–2876. ( 10.1098/rspb.2008.0817) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pike TW, Kendal JR, Rendell LE, Laland KN. 2010. Learning by proportional observation in a species of fish. Behav. Ecol. 21, 570–575. ( 10.1093/beheco/arq025) [DOI] [Google Scholar]
- 40.Pike TW, Laland KN. 2010. Conformist learning in nine-spined sticklebacks’ foraging decisions. Biol. Lett. 6, 466–468. ( 10.1098/rsbl.2009.1014) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Morgan TJH, Rendell LE, Ehn M, Hoppitt W, Laland KN. 2012. The evolutionary basis of human social learning. Proc. R. Soc. B 279, 653–662. ( 10.1098/rspb.2011.1172) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kendal R. 2015. Chimpanzees copy dominant and knowledgeable individuals: implications for cultural diversity. Evol. Hum. Behav. 36, 65–72. ( 10.1016/j.evolhumbehav.2014.09.002) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Farine DR, Aplin LM, Sheldon BC, Hoppitt W. 2015. Interspecific social networks promote information transmission in wild songbirds. Proc. R. Soc. B 282, 20142804 ( 10.1098/rspb.2014.2804) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Farine DR, Spencer KA, Boogert NJ. 2015. Early-life stress triggers juvenile zebra finches to switch social learning strategies. Curr. Biol. 25, 2184–2188. ( 10.1016/j.cub.2015.06.071) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.McElreath R, Bell A, Efferson C, Lubell M, Richerson P, Waring T. 2008. Beyond existence and aiming outside the laboratory: estimating frequency-dependent and pay-off-biased social learning strategies. Phil. Trans. R. Soc. B 363, 3515–3528. ( 10.1098/rstb.2008.0131) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
This article has no additional data.