Tissue loading and microstructure regulate the deformation of embedded nerve fibres: predictions from single-scale and multiscale simulations

Abstract

Excessive deformation of nerve fibres (axons) in the spinal facet capsular ligaments (FCLs) can be a cause of pain. The axons are embedded in the fibrous extracellular matrix (ECM) of FCLs, so understanding how local fibre organization and micromechanics modulate their mechanical behaviour is essential. We constructed a computational discrete-fibre model of an axon embedded in a collagen fibre network attached to the axon by distinct fibre–axon connections. This model was used to relate the axonal deformation to the fibre alignment and collagen volume concentration of the surrounding network during transverse, axial and shear deformations. Our results showed that fibre alignment affects axonal deformation only during transverse and axial loading, but higher collagen volume concentration results in larger overall axonal strains for all loading cases. Furthermore, axial loading leads to the largest stretch of axonal microtubules and induces the largest forces on axon's surface in most cases. Comparison between this model and a multiscale continuum model for a representative case showed that although both models predicted similar averaged axonal strains, strain was more heterogeneous in the discrete-fibre model.

1. Introduction

Low back and neck pain are major health issues, and despite much effort across many different fields of study, their aetiology is still poorly defined [1,2]. One common cause of spine pain and disability is excessive nerve fibre deformation during joint overuse and/or trauma [3]. The facet capsular ligaments (FCLs), which enclose the bilateral facet joints throughout the spine (figure 1), are highly innervated and are increasingly recognized as sources of lower back and neck pain [4–7]. Nerve fibres embedded in the FCL can be activated by its deformation during repeated physiological or injurious motions, leading to pain [7–9]. On the macroscale, spinal motion causes heterogeneous and localized deformation of the FCLs [10–12]. Even uniform displacement of the FCL's boundaries during simple ex vivo mechanical tests results in heterogeneous deformation, attributable to the non-uniform fibre structure of their extracellular matrix (ECM) [13–15]. On the microscale, the ECM fibres in these ligaments rotate, deform, and transmit local forces and deformations to the embedded sensory components, which can trigger their neural response.

Figure 1.

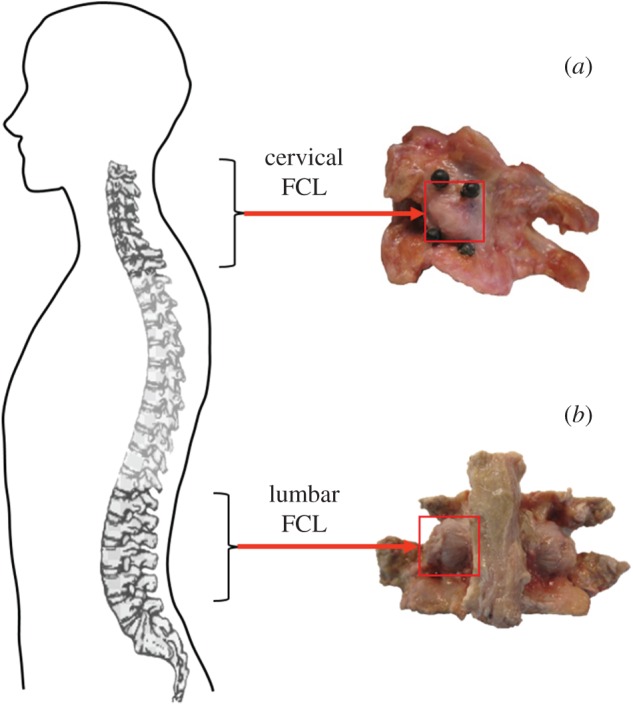
The anatomy of (a) cervical and (b) lumbar facet capsular ligaments (FCLs) and their relative locations on the spine. The cervical FCL is roughly oriented in superior-inferior direction, whereas the lumbar FCL runs in the lateral-medial direction. (Online version in colour.)

The axonal cytoskeleton is composed of axial stiff microtubules laterally reinforced by microfilaments and neurofilaments, and the axon physically connects to its environment via adhesive foci, such as focal adhesions [16]. These adhesions transmit forces and deformations from ECM to neurons, and could serve as regions where strains and stresses are concentrated [17]. Localized neuron deformation can open stretch-gated membrane channels [18] and directly or indirectly, result in the generation of pain signals. In addition, the localized mechanical response can induce stresses and strains higher than those applied to the tissue as a whole, increasing the vulnerability of certain regions.

Type I collagen fibres, with irregularly arranged and aligned regions, are the main ECM components in the FCLs and provide mechanical strength [14,19]. Nerve fibres embedded in this complex three-dimensional (3D) ECM, respond to external loads depending on the local deformation and architecture of the surrounding ECM components. Assessing how the collagen fibres organization, as well as the local mechanics, modulate the neuron's mechanical response is necessary. There have been several studies investigating mechanical and neural behaviours of neurons in ECM substrates [20–22]. Although the collagen composition and mechanical properties of these substrates are different from those of FCL tissues [11,13,20,23,24], such constructs can be valuable tissue analogues. For instance, constructs can be made with isotropic or aligned fibre organization to mimic patterns in native tissues [20]. Zhang et al. [20] measured the deformation of embedded neurons in response to collagen gel stretch, but they were unable to examine regional variations in cell membrane deformation. In parallel with mechanical stretch of the neuron–collagen co-gel, we constructed a discrete fibre network simulation to predict fibre-level strains during gel loading [25]. That model did not, however, include a neuronal component. Thus, the objective of this work was to employ computational tools to analyse the transmission of force from ECM to an embedded idealized neuron. Although this work is motivated by neuron mechanics, the principles would apply to any mechanosensitive cell in a fibrous matrix.

2. Methods

Two different structural models were examined. First, we developed a structural-mechanical finite-element (FE) model of an isolated neuronal extension (axon) embedded in a collagen fibre network within a microscopic space. This discrete-fibre model was based on key mechanical/structural characteristics of the axon and the fibre network. The axon was physically connected to the surrounding fibre network by distinct fibre–axon connections. As a comparative study, motivated by tissue structures too large to allow a discrete-fibre model, a multiscale model of an axon embedded in a continuous fibrous ECM was created, and the results were compared with those for the discrete-fibre model.

2.1. Discrete-fibre model

We constructed a 3D FE model with a cylindrical nerve fibre segment (axon) embedded in a fibre network to simulate innervated fibrous tissue (e.g. FCL) (figure 2). The model contained no non-fibrillar matrix, which was assumed to be of negligible stiffness. We simulated fibre networks with a range of structures and loading conditions (figure 2a–c). First, 3D Delaunay fibre networks¹ with different alignment and volume concentration were created for each loading scenario. Networks contained 2-node nonlinear springs (properties given below), representing the ECM's collagen fibres, connected to each other by pin joints. Each network was generated in Matlab (Mathworks, USA, R2015b) by 3D random node generation, Delaunay tessellation, artificial stretch in X, Y and Z to acquire an alignment, and finally by clipping the network and keeping only the fibres within the desired computational space. The number of initially generated random nodes (range: 2000–20 000 nodes) and the amount of artificial stretch (range: 0–400%) were adjusted to give the desired fibre volume concentration and fibre alignment. Networks were either isotropic or transversely isotropic with alignment primarily along the computational Z direction. Aligned networks had longer fibres and hence lower fibre node density.

Figure 2.

A schematic of embedded axon in the fibre network and the boundary displacement applied on the network for (a) transverse, (b) axial and (c) shear loadings. The walls highlighted in blue are fixed (at least one degree of freedom). (d) A schematic of all the components in the discrete-fibre model. Collagen fibres (white) are connected to the axon at pin joint connections. Local adhesions are modelled as nonlinear springs (yellow) at the connection site. The axon is made of a linear axial spring (red) that models the microtubules and an elastic ground substance (blue) that models all the other constituents.

A cylindrical space with diameter D = 1 µm and length L = 3 µm along the Z direction was removed from the network to make space for a cylindrical axon. The diameter of the cylinder was based on histological studies of the free nerve endings of nociceptive nerve fibres embedded in the lumbar and cervical FCLs [26], and the length was chosen to model only a small portion of the nerve fibre. The axon was oriented in parallel to the aligned fibres, following experimental observations [4]. For transverse-to-axon loading, the network domain size was 5 × 5 × 3 µm³, so that the axon spanned the whole length of the network along Z direction (figure 2a). To allow non-affine deformation of the axon in the network, and to avoid applying the boundary displacement directly on the axon's end surface, for axial and shear loadings, the network size was set to 5 × 5 × 6 µm³, where the axon occupied only half of the network length in Z (figure 2b,c). The axon's end surface was held rigid for numerical stability. The ECM fibre structure was assumed to be similar throughout our model's length scale, as supported previously by Ban et al. [27], who found that fibre alignment remains relatively uniform over an approximately 500 µm length scale, which is two orders of magnitude larger than the network size in our model. When fibres intersected the cylinder, they were attached to the cylinder at pin joint insertion points, and any fibre inside the cylinder was removed. Nonlinear springs with assumed stiffness equal to half of that of the collagen fibres were constructed between each insertion point and the adjacent finite-element nodes on the axon surface (distance <0.05 µm) to model focal adhesions. In addition to fibres in the ECM network, collagen fibres were added circumferential to the axon to ensure complete wrapping of the axon. Three loading cases—transverse, axial and shear—were considered (figure 2a–c).

Collagen fibres were modelled with the phenomenological constitutive equation [28]

2.1

where F, A, S, B and λ represent fibre force, stiffness, cross-section area, nonlinearity and stretch ratio, respectively. The fibre radius R and properties A and B were set to 50 nm, 43.3 MPa and 2.5, respectively, based on previous studies [24].

The axon was modelled as a fibre composite with a linear elastic ground substance and linear axial fibre reinforcements (figure 2d). The elastic part models the microfilaments, neurofilaments, axoplasm and other non-microtubular constituents of the nerve fibre. The mechanical properties of that material are yet to be measured experimentally for different loading cases, so we performed a parametric study. The stiffness was set to 0.1 A, 0.01 A and 0.001 A, where A is the stiffness parameter for the collagen fibres in equation (2.1). Microtubules—the stiffest component of the axon [29]—were modelled by embedded linear elastic fibres. The microtubule's axial spring constant was measured as 9.42 N m⁻¹ [30]. Histological studies [31] showed that an approximately 1 µm diameter axon contains 15–45 microtubules. In our model, the microtubules pass through all 299 nodes in each cross section, so we reduced the spring constant by 10× to compensate. Material properties are listed in table 1.

Table 1.

Material properties used in the simulations.

component	material type	parameter	value	references
collagen fibres		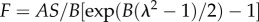A	43.3 MPa	Lai [24]
		B	2.5
		S	7854 nm2
focal adhesion fibres		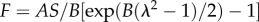A	21.65 MPa	—
		B	2.5
		S	7854 nm2
microtubule	linear fibres	spring constant	0.94 N m−1	Pampaloni [30] Fadić [31]
non-microtubule part of axon	linear elastic	Young's modulus	0.1 A, 0.01 A, 0.001 A	—

Displacement control models are more relevant for ligamentous tissues where tissue deformation is governed by the insertion sites connected to bones. Therefore, for each loading case, network boundaries were displaced to create 40% stretch (48% Green strain), a typical strain that produces painful condition in cervical FCL [8,32]. For transverse loading, the network walls normal to X direction were pulled by 40% stretch (figure 2a), while the other faces stretched affinely to ensure minimal forces from the lateral faces along the stretch direction. To allow lateral contraction in Y, the fibres close (distance <0.5 µm) to the Y-facing surfaces were made hypercompliant compared to other fibres in the network (stiffness 100× lower). To eliminate edge effects, nodes located on the Z-facing surfaces were free to move in X and Y. For axial loading, the network was held fixed at one end and pulled on the other end up to 40% stretch, while the X-facing and Y-facing faces underwent affine stretch (figure 2b). Fibres close to the X-facing and Y-facing surfaces were made hypercompliant, while nodes on the Z-facing faces were free to move in X and Y. Finally for shear loading (figure 2c), the bottom face was fixed while the other boundary nodes were moved in X linearly, with the maximum displacement of 2.4 µm (40% shear strain). These boundary conditions were specified to represent loading of a small segment of a long axon and the ECM surrounding it.

We generated networks with different strengths of fibre alignment (with respect to the axon's long-axis) and fibre volume concentration. For each network, the degree of anisotropy (strength of alignment) was described by the orientation tensor [14] defined as

2.2

where L^k, a^k and L^T are each fibre's length, each fibre's orientation vector, and the total length of all fibres. For a transversely isotropic network, the difference between the largest eigenvalue and the other eigenvalues of T_ij represents the degree of anisotropy (δ). For our A-aligned networks

2.3

δ changes from 0 (isotropic) to 1 (completely aligned). Three degrees of anisotropy (δ)—0 (isotropic), 0.4 (mildly aligned), 0.8 (strongly aligned)—were simulated for each loading scenario (transverse, axial, shear). Our choice of δ values was based on our previous imaging of cervical and lumbar FCL, [11,14] which suggested a wide range of orientation states, with nearly isotropic regions and highly aligned regions. As the fibre alignment rises, the fibre lengths increase, and the density of ECM-axon connection points drops.

Fibre volume concentration was calculated by dividing the total volume occupied by the fibres by the total volume of the domain excluding the axon. Volume concentrations of 0.1, 0.3 and 0.5 were tested for the aforementioned loading conditions, again to cover a range of possible values [33,34].

We used eight different network realizations for each case. A total of 438 simulations were run on ABAQUS/Standard (Dassault systemes, France, 6.11-2) in static analysis. Linear brick elements (C3D8, 13 600 elements) and 2-node connective elements (CONN3D2) were used for the axon and the fibres (collagen, microtubules, etc.), respectively. Mesh convergence was assessed by simulating an axon subjected to a traction force on its end surface. Simulations were repeated with 2880 and 5320 elements, and it was found that there the change in the displacement of the end surface's midpoint was less than 1% for simulations involving at least 2880 elements. The average simulation time using 1 core was 30–45 min. A template of the ABAQUS input file is provided as electronic supplementary material.

The maximum principal Green strain,² as well as the microtubule stretch for each segment, were calculated and visualized for each simulation. In addition, forces exerted on the axon surface by the surrounding fibres were calculated.

2.2. Multiscale continuum model

For comparison, we also constructed a multiscale FE model of the axon with the surrounding continuous matrix. This multiscale scheme has been explained in detail previously [35,36], so only a brief summary is presented here.

The method connects the (macroscopic) tissue level (ECM around the axon in this case) to underlying (microscopic) representative volume elements (RVEs) (figure 3a). The macroscale stresses are calculated based on the deformation of the microscopic RVEs, each located at a Gauss point. RVEs are analysed in a 1 × 1 × 1 computational space and contain a fibre network (representing the fibrous structure) and a neo-Hookean ground substance, which deforms independent of the fibres. Both the network fibres and the neo-Hookean ground substance contributed to the macroscopic stresses

2.4

where S^total, S^fib and S^neo are total macroscopic Cauchy stress, macroscopic Cauchy stress due to fibres and macroscopic Cauchy stress due to the neo-Hookean matrix, respectively. The averaged macroscopic equilibrium equation is

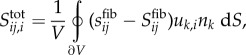2.5

where s^fib is the microscopic Cauchy stress tensor of the network fibres. Also, u_k, n_k, and V are the displacement of the RVE boundaries, the surface normal vectors for the RVE, and the RVE volume, respectively. The integral is calculated over the RVE boundary. The additional term on the right-hand side accounts for correlations between stress and deformation along the RVE boundaries contributing to the gradient of the averaged stress.

Figure 3.

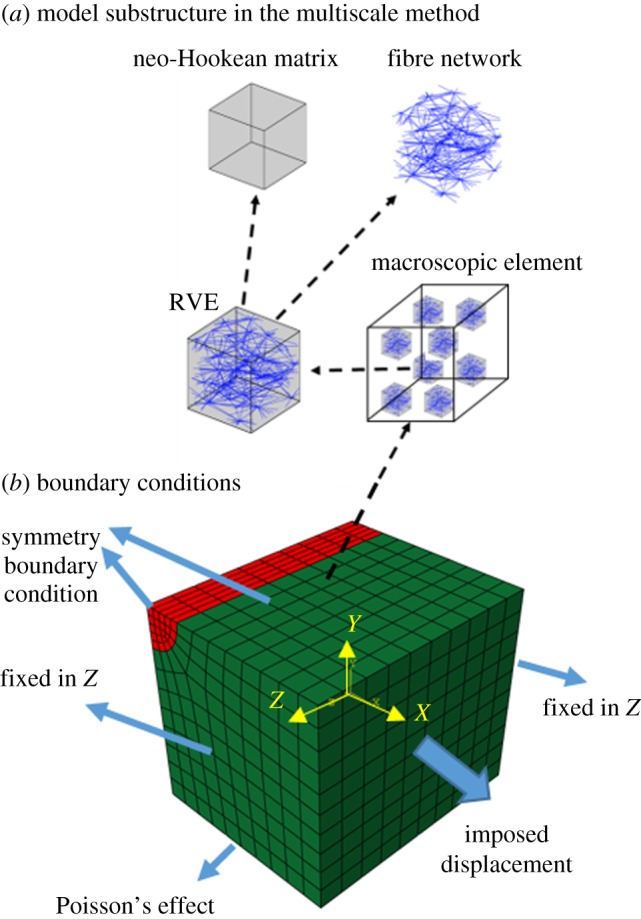
(a) Model substructure in the multiscale method. Eight RVEs are embedded on each Gauss point of the macroscopic finite elements. Each RVE is composed of a fibre network and a neo-Hookean matrix. (b) Model geometry of an embedded axon in a continuous ECM, along with boundary conditions for transverse loading case. In comparison with the corresponding discrete-fibre model, only one quarter of the axon and ECM is modelled. (Online version in colour.)

The average fibre Cauchy stress tensor is obtained from network fibre forces, according to volume averaging theory and under the assumption of negligible fibre cross-section

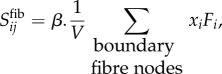2.6

where x is the position of a node located on the RVE boundaries and F is the force acting on that node per equation (2.1). The parameter β converts between the micro- and macro-scale

2.7

where ϕ, L and S are the network's fibre volume fraction, total length of fibres in the non-dimensional 1 × 1 × 1 RVE and fibre cross-sectional area. The stress due to the non-fibrillar neo-Hookean ground substance was assumed to vary only macroscopically and thus did not need such conversion.

The case with an axon of stiffness 0.001 A embedded in an isotropic network with fibre volume fraction 0.1 loaded transverse to the axon was selected as a representative case to compare the two models. We constructed the multiscale model using identical geometrical, structural and mechanical specifications to those of the corresponding discrete-fibre model, except that due to symmetry only one quarter of the geometry was modelled in the multiscale method (figure 3b). Thus, a 2.5 × 2.5 × 3 µm box with an embedded 0.5 µm radius cylinder was created in ABAQUS (figure 3b). That mesh was then imported into the multiscale modelling program (written in C), and Delaunay networks with isotropic fibre organization for the ECM and strongly aligned (δ > 0.8) fibres for the long axis of the cylinder (Z) were used. The Poisson's ratio for the non-fibrillar material (ν ∼ 0.48) was chosen to be nearly incompressible. We assumed that both the axon and the ECM maintain their volume due to their fluid content in vivo. Although the discrete-fibre model has no non-fibrous ECM component, we added a slight neo-Hookean contribution (with 0.01% of the collagen fibre stiffness) to the multiscale model for numerical stability. The fibres inside the ECM networks followed the same constitutive equation as in equation (2.1), while those inside the axon were linear elastic. The boundary conditions were similar to the discrete-fibre model, except that the lateral Y-facing surface (far from the axon) was free to move in Y, surfaces which were fixed in the discrete-fibre model to avoid numerical problems.

This simulation was run on 128 processors, with running time of approximately 5 h. The maximum principal Green strain of the cylinder was calculated after simulation and compared with the results of the discrete-fibre model.

3. Results

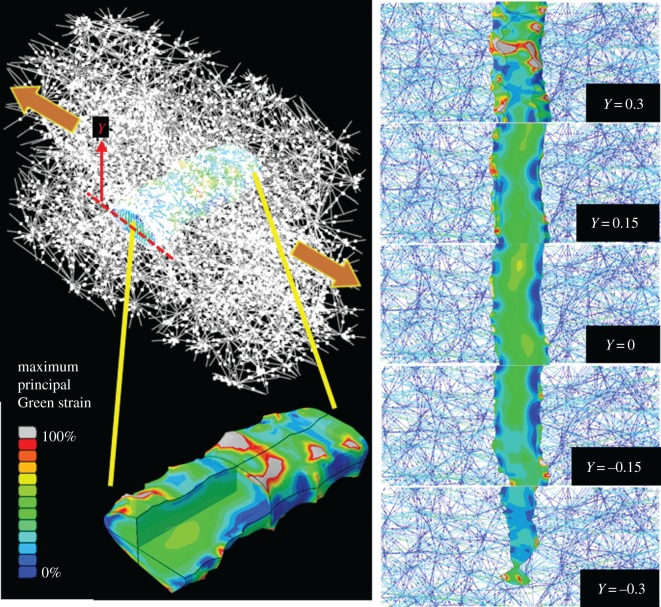
The discrete-fibre model produced a heterogeneous strain field on the axon (figure 4). High-strain regions formed on the axon surface near fibre insertion sites, whereas the interior underwent smaller deformations. For the isotropic-network, transversely loaded case, the axon's maximum principal Green strain field varied from values as low as approximately 0%, to extremely large values (approx. 300%) at a few regions (figure 4), with the average over all elements was around approximately 30%. The fibre–axon connection points act as stress concentrators and would be natural sites for the axon to sense network strain. Strain distribution over the axon during axial and shear loading for a representative axon are shown as the electronic supplementary material, figure S1.

Figure 4.

Maximum principal Green strain field on a representative axon in an initially isotropic fibre network (fibre volume concentration = 0.3) pulled transversely. Although the axon's shape follows the gross transverse displacement, the strain field is highly localized. The grey regions have strains out of the range of the colour bar. The panels on the right show the 2D slices viewed from the top. In the 2D images, the collagen fibres are colour coded based on their Green strain value.

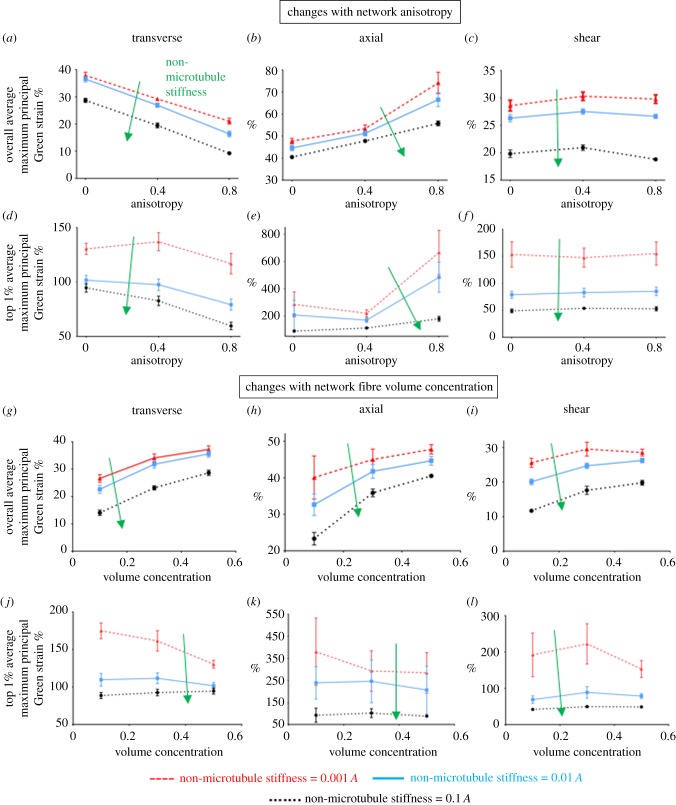
Fibre architecture and volume concentration differentially modulated axonal deformations for the three loading conditions. As degree of alignment (anisotropy) increased, for transverse loading, both the overall (figure 5a) and the top-1% (figure 5d) average maximum principal Green strain dropped by 20–60%; In contrast, the strains increased by at least 50% with increasing anisotropy during axial loading (figure 5b,e). The overall average strains are calculated based on the entire axon, whereas the top 1% average is for elements that were in the top 1% by maximum principal Green strain. Strains during shear loading showed only a small change with ECM anisotropy (figure 5c,f). In general, both strain measures (overall average and top 1% average) had similar trends for each individual case, but the top-1% values were 3–9 times larger than the overall average. Axonal strains varied similarly with collagen concentration during transverse, axial and shear loading (figure 5). Generally, as the volume concentration of fibres increased, the number of collagen insertion points rose, which provided the network with more regions to transmit the macroscopic load. As a result, overall average axonal strain increased with the fibre volume concentration (figure 5g–i). The top 1% values, however, had opposite trends (figure 5j–l), as the values tended to decrease or remain unchanged with increasing collagen concentration. Axons with different non-microtubule stiffness underwent similar changes. As the non-microtubule stiffness increased, the effect of volume concentration on top-1% values was mitigated, such that for non-microtubule stiffness of 0.1 A and 0.01 A, the top 1% values were largely unchanged with volume concentration.

Figure 5.

Correlation of fibres' anisotropy (a–f) and volume concentration (g–l) with axonal strains during transverse (a, d, g and j), axial (b, e, h and k), and shear loading (c, f, I and l) of the fibre networks. Results are for different stiffness (0.1 A, 0.01 A and 0.001 A where A is the stiffness of the collagen fibres) of the non-microtubule part of the axon model. Lines show the mean values (n = 8), and error bars are the 95% CI. At some data points, error bars are small and they are covered under the symbol.

The local stretch of the axon's microtubule segments depended on the loading mode and network structure. For microtubule segments within the top 1% of stretch magnitudes, the average stretch was compared across different loading cases and network types (figure 6), for a non-microtubule stiffness of 0.001A. Since each individual microtubule running across the axon's whole length was composed of several connecting segments constructed between adjacent mesh nodes, local microtubule stretch could be measured. During transverse loading, the non-uniform deformation of the axon led to increased microtubule stretch, an effect that declined as the network anisotropy increased. Similar to the axonal maximum principal Green strain values, the microtubule stretch showed minimal dependence on network alignment for shear loading. Furthermore, transverse and shear loading lead to similar values of microtubule stretch, which were substantially lower than those during axial loading (figure 6a). For all loading cases, microtubule stretch increased with fibre volume fraction, as shown for isotropic networks (figure 6b).

Figure 6.

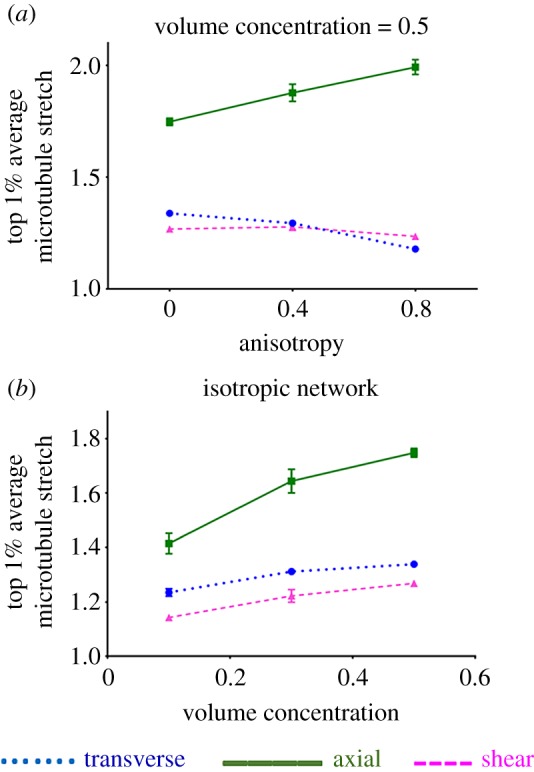
The correlation of microtubules stretch with fibres’ (a) anisotropy and (b) volume concentration, for transverse, axial and shear loading. MTSR_TOP is the average of microtubule stretch in the top 1% high-stretched microtubule segments. Lines show the mean values (n = 8), and error bars are 95% CI. At some data points, error bars are small and they are covered under the symbol.

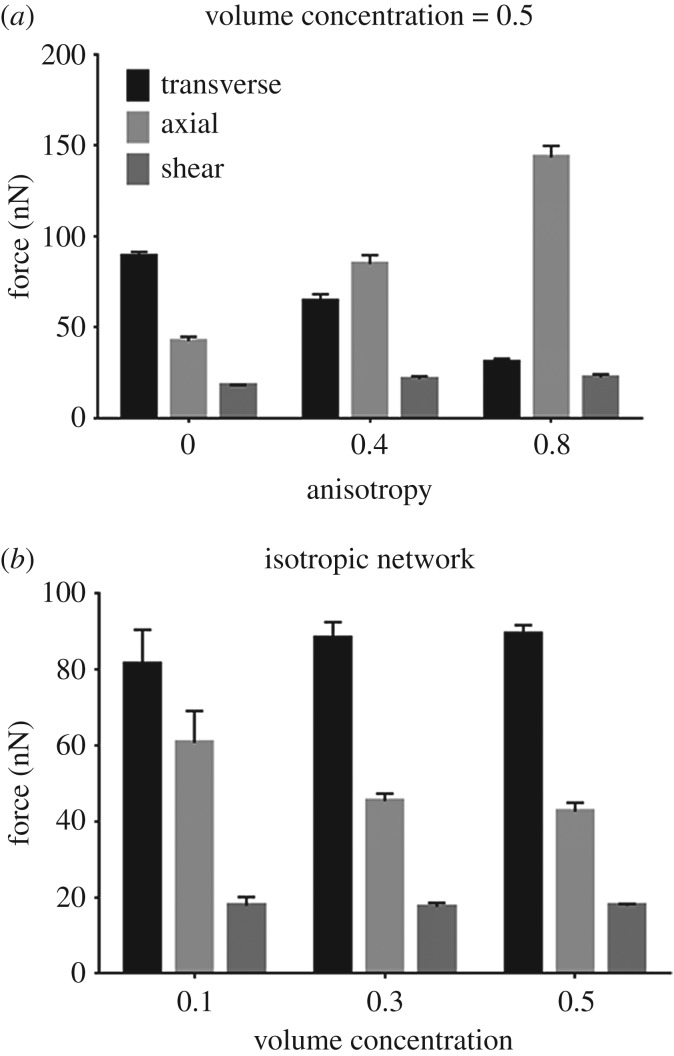
The forces exerted on the axon's surface by its surrounding collagen fibres strongly depended on the type of loading (figure 7). Stiffer networks, under each loading, resulted in more concentrated forces on the axon's surface. We calculated these concentrated forces at each insertion point by calculating the connecting fibre's stretch ratio and employing its constitutive equation (equation (2.1)). Except for isotropic networks, the axial loading resulted in average forces of around 1.5–7 times larger than those generated during shear and transverse loading. For isotropic networks, transverse loading induced the largest forces on the axon's surface, with the shear loading resulting in approximately four times lower forces. Of note, these concentrated forces act in the direction of connecting fibres, and therefore averaging the force values does not yield the resultant force, but instead constitutes a simple measure of the force on the axon. These forces follow similar changes with network anisotropy to those observed for overall average axonal strain in figure 5a–c. As the networks' fibre volume concentration increased, the force values remain unchanged during shear and transverse loading, but decreased in axial loading. The axon's load sharing fraction, defined as the ratio of the total force exerted on the axon over the total force acting on the network, is shown for different cases in electronic supplementary material, figure S2.

Figure 7.

Correlation between fibres' (a) anisotropy and (b) volume concentration with the average of forces exerted on the axon's surface due to the surrounding collagen fibres for different loading conditions. Columns show the mean values (n = 8) and error bars are 95% CI.

The multiscale model predicted much smoother strains on the axon compared to the discrete-fibre model (figure 8). Strain localization can be quantified by measuring and comparing the average and peak strains. Although on average the axon underwent similar amounts of deformation for each model (approx. 7% difference in strain), the peak (average of top 1% values for discrete-fibre model versus maximum value for the continuum model) strains in the discrete-fibre model are approximately seven times higher (figure 8b).

Figure 8.

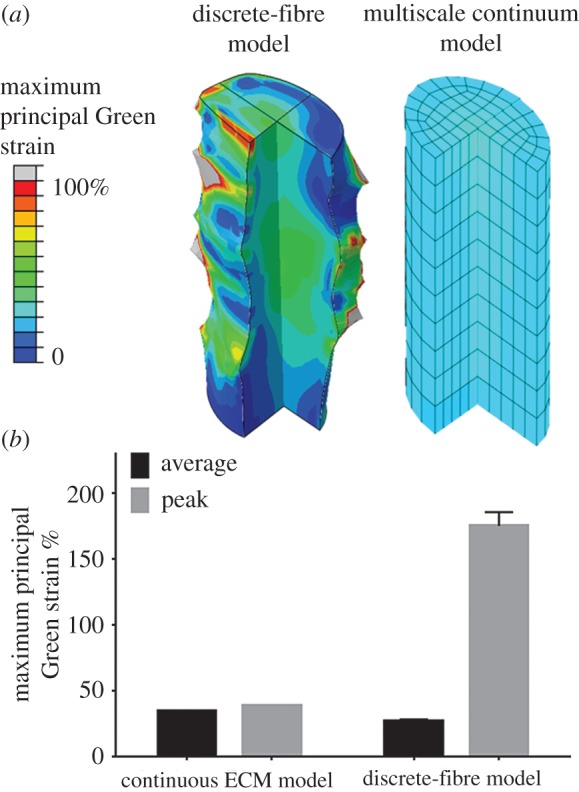
(a) Comparison between the axon's deformed shape and maximum principal Green strain (MPGS) in the discrete fibres model (left) and continuum (continuous ECM) model (right) during transverse loading. The ECM network (not shown here) was initially isotropic and had fibre volume concentration of 0.1. The grey regions in the discrete-fibre model have strains out of the range of the colour bar. (b) Average and peak MPGS values for the discrete-fibre and continuum model. The peak MPGS for the discrete-fibre model is the average of MPGS in the top 1% high-strain elements. For the discrete-fibre model columns, the values are mean (n = 8) and error bars are the 95% CI. For the average column, the error bar is very small. For continuous ECM model, n = 1.

4. Discussion

In this work, we created a structural-mechanical discrete-fibre model of an individual axon embedded in a network of collagen fibres and attached to the network by distinct fibre-axon connections. This model was used to assess the axon's mechanical behaviour in networks with varied fibre alignment and collagen volume concentration under transverse, axial, and shear deformations. For transverse and axial loading, the fibre alignment modulates the mechanical behaviour of the axon (figure 5). In contrast, the axon's strain during simple shear does not appear to depend on network alignment (figure 5). Fibre volume concentration correlates positively with averaged axonal strains, but increased fibre concentration distributes the load more evenly and thus reduces the peak strains (figure 5). Owing to strain localization on the axon, axonal average and maximum Green strains can reach values well above the applied stretch. Axial loading leads to largest strains in microtubules (figure 6) per unit macroscopic strain, and results in highest forces on the axon's surface in aligned networks (figure 7). The results of this model were also compared with those of a multiscale model of a continuous fibrous ECM around the axon (figure 8). Although the axon experiences similar averaged strains in each model, the strain is much more uniform in the continuous model. This difference is attributable to the nature of each model; in the discrete-fibre model, connective fibres are the bridges between the axon surface and the ECM, where in the continuum model, strain gets transmitted uniformly over the axon–ECM interface. The consistency of the results on average, suggests that a two-step process could be used for studies of larger tissue segments or more complicated axon geometries; specifically, the multiscale model could be used first to get a coarse-grained representation of local deformations, and the discrete-fibre model could be used to get finer-scale estimates of the forces acting on the axon.

Our choice of the ratio between the axon length and the network length during axial and shear loading was to assure that axon is long enough to undergo considerable deformation, and short enough to minimize edge effects. The average fibre length was less than 30% of the portion of the network with no axon. Since such effects do not occur during transverse loading, we considered a smaller domain with the axon running throughout its length to reduce computational cost. In addition, the connection between the axon's end surface and the ECM is significant during axial loading. Having no or low connection density at the end surface for example, would result in smaller axonal stretches. Therefore, for networks with lower volume concentration, since the variability of connection points is relatively higher (coefficient of variation ∼ 0.45), larger error bars in the strain graphs resulted during axial loading. The fibre connection density on the axon's end surface was similar to that on the circumferential surfaces.

Microtubules are the main load-bearing components of the axon. Their breakage caused by stretch injury, could lead to disrupted axonal transport, morphological abnormalities and, eventually, axonal degeneration [37]. Therefore, microtubule stretch in the simulation may indicate axonal injury [37,38]. Continuing this line of thought, the ability to identify injurious loading conditions for a fibrous tissue could help predict high-risk physiological motions. Since microtubules align with the axon's long axis, they were expected to experience higher stretches during axial loading, especially in strongly aligned tissues. Therefore, tension can be identified as the most harmful loading mode, although the extent of the imposed stretches would also matter—a 40% transverse stretch, for example, would likely be more damaging than a 1% axial stretch. Based on these results, supraphysiological motion that stretch tissue along the local fibre direction, such as spinal torsion for lumbar FCL or neck flexion/extension for cervical FCL, may be suspected to be most injurious to neurons. Previous studies [7,39] showed that excessive tensile stretch of the FCL can cause damage to the axon and/or induce pain. Although failure is not implemented in our model, due to the excessively large strains in some cases, local failure may occur and could affect the stress/strain distribution. For instance, Janmey et al. [40] found that microtubules undergo rupture once they reach a stretch ratio of approximately 1.6. Our model predicted that at the highest strains studied, the microtubule stretch ratio could exceed that threshold. Therefore, under these critical conditions, local microtubule (or collagen or focal adhesion) failure could change the force distribution throughout the tissue.

Forces exerted on the axon's surface could trigger neural responses. For example, stretch-gated ion channels, located on the surface of the axon, may undergo conformational changes due to the imposed deformation, which in turn might lead to altered ionic balance and eventually generate an electrical signal [18,41]. Although the magnitude of stretch/force that would open an individual stretch-gated ion channel has not been quantified experimentally, our results provide a controlled comparison to identify the loading modes more likely to open these channels. Based on our results, axial deformation applies the largest forces to the axon's surface in aligned ECM networks (figure 7). Force values in figure 7 are per ECM-axon connection point. Therefore, our results correlating this force with fibre volume concentration suggest that although the total force on the axon varies linearly with number of ECM-axon connection points during transverse and shear loading, during axial loading, however, the force does not rise as much when the number of connection points increases. The average force values ranged from approximately 15 nN to approximately 150 nN, comparable to forces reported previously for cells/axons in stretchable substrates (range from 0 to 40 nN) [42,43]. These results are particularly significant for the cervical FCL, which undergoes large axial deformation in the joint direction during neck flexion/extension. The lumbar FCL contains collagen fibres mainly aligned in the facet joint direction, and it undergoes axial tension during spine motion [44] (e.g. torsion) as well.

Owing to heterogeneous fibre structure and loading in the spinal FCLs, accurately determining how fibres are loaded requires experimental observations or realistic structure-based models. In the cervical FCL, for example, there is a wide range of fibre orientation with various degrees of anisotropy [11]. Therefore, even gross axial loading during neck flexion might lead to shear or transverse loadings of some fibres (with respect to their direction), and other modes of neck motion, such as torsion, might also lead to axial loading of some fibres. In the case of lumbar FCL, however, since the fibres are primarily oriented in the joint direction [14], estimating the loading of fibres during different physiological motions is easier.

Comparison between our discrete-fibre and multiscale continuum models reveals the inherent capabilities and limitations of each. On one hand, the multiscale model cannot predict heterogenous axonal deformation due to non-continuous connections between the axon and its surrounding fibres. The multiscale model can, however, perform more robustly, in terms of numerical stability, for more complicated geometries and loadings or for very large problems, a feature that could be a concern for the discrete-fibre model. Therefore, these methods are complementary and must be used together.

There are several methodological considerations regarding our discrete-fibre model. First, the axon was simplified as a cylinder with axial linear microtubules in a linearly elastic ground substance. The modelled microtubules spanned the entire cross section of the axon, and they also elongated through the entire length of our axon segment. In vivo, however, the axon has a more complicated structure with multiple interconnected constituents. For instance, axonal microtubules have been shown to have an average length of 4 µm and to be arranged in polarized arrays in each cross section [45,46]. We homogenized the axon structure in our model by having more microtubules with lower stiffness than the real axon does. In addition, lumping all of the non-microtubule constituents of the axon into a linear elastic material may have oversimplified the axon's complex internal structure. Owing to the lack of experimental data on the properties of non-microtubule components of the axon, especially during transverse loading where microtubules are not loaded, we considered a range stiffness values. This sensitivity analysis does not ensure the accuracy of the simulation. In fact, our results from the continuum model for a transversely loaded isotropic network suggest that the ECM may experience higher strains than the axon, which is not consistent with the fact that neurons have higher compliance compared to the surrounding ECM [24,47]. Owing to low cost for fibre reorientation and the fibres' inability to bear moments, as well as possible inconsistency of material properties between axon and ECM since they are from different sources, this inconsistency is not entirely unexpected. Improved models with more detailed axon structure could be used to study the regulation of axonal cytoskeleton in response to tissue loading.

The collagen fibre network structure and the axon-fibre connections are also idealizations. Focal adhesions are complicated structures with many components [16]. In our model, however, we modelled them as simple nonlinear springs that distributed the collagen fibre forces on insertion points between the axon and the fibre network. These nonlinear springs were assumed to behave similar to collagen fibres, with half of the stiffness. This assumption is not supported by any experimental observation and was chosen merely to provide a bridge between collagen fibres and the axon. Focal adhesion springs distribute the fibre forces between adjacent nodes at the connection site, so having more compliant focal adhesions would result in sharper strain transmission. Also, increasing the length of these springs would enlarge the axon–ECM interacting area and result in more uniform axonal strains. Reportedly, the size of focal adhesions correlates with ECM stiffness [48], so relating the adhesion stiffness to the ECM stiffness might be necessary. Further experimental observations, such as high-resolution imaging, are necessitated to validate our assumption of focal adhesion's size and properties. Lastly, the non-fibrous components of the ECM may also contribute, depending on the tissue and the loading configuration. Since these components contain water content, they might be significant during rapid compressive loading. Also, a non-fibrous component could facilitate strain transmission to the axon and reduce strain localization. Although, this component might elevate the overall stiffness of the matrix, by limiting the extent of the fibre reorientation. The mechanical behaviour of fibrous tissues is modulated by fibre reorientations in response to external loading. It is thus essential to recruit detailed material models that effectively incorporate fibre architecture [49,50]. Efficient structural models enable robust computational simulations of complex geometries [51–54] and altered tissue states [55].

A complementary study with experimental validation of the discussed computational models would be very useful. Fine tuning the material properties, geometries and structures requires comparison with a set of experimental observations at the axon's scale. For instance, tracking individual axon deformations during their displacement would provide greater insight into mechanical properties of axons, structure of binding sites, etc.

Regardless of these limitations, the discrete-fibre model can serve as a tool to study the relationships between a fibrous tissue's microstructure and the mechanical responses of the innervating nerves. The model shows how different local ECM loading could be critical in modulating the mechanical behaviour of the nerve endings. Innervated fibrous tissues, such as the facet capsular ligament, undergo complex deformations during daily activities [10,44]. Complicated macroscopic deformation patterns within the tissues, along with their non-uniform microstructure, impose complex loading on the nerve fibres. Our model could help identify vulnerable regions in heterogeneous fibrous tissues and injurious loading conditions in vivo, which are otherwise difficult to probe experimentally. Our results suggest that this utility requires realistic characterization of nerve–ECM connection if one considers vulnerability in terms of local behaviour of the nerve. Our two models show two likely different limits of nerve–ECM interaction, and the actual connection is potentially somewhere between these two approaches. The discrete-fibre and multiscale continuum models, each and/or together, can serve as tools to bridge between gross tissue motion and the sensory response. At one end of the bridge, tying this model to local fibre architecture and also local macroscale tissue deformation—obtained experimentally [13,44] or by modelling approaches [10,14]—during supraphysiological motions could provide us with a better estimate of the how damaging loads are transmitted to the nerves. At the other end, using the mechanical response of the nerves to predict their electrical response could yield insights on how different body motions could induce injury or pain.

Data accessibility

Data have been uploaded as ESM.

Authors' contributions

V.Z., S.Z., B.A.W. and V.H.B. designed this study and contributed to writing of the manuscript. V.Z. conducted the research implementation, computer modelling and data analysis. S.Z. contributed with model set-up. B.A.W. and V.H.B. supervised the whole work and contributed to interpretation of results.

Competing interests

The authors declare no competing interests.

Funding

This work was supported by the National Institutes of Health (U01EB016638) (V.H.B. and B.A.W.), AMTI Force and Motion Scholarship (S.Z.), and a National Science Foundation training grant (#1548571) (S.Z.).