Suction effects in cratered surfaces

Abstract

It has been shown experimentally that cratered surfaces may have better adhesion properties than flat ones. However, the suction effect produced by the craters, which may be chiefly responsible for the improved adhesion, has not been properly modelled. This paper combines experimental, numerical simulation and analytical approaches towards developing a framework for quantifying the suction effect produced by isolated craters and cratered surfaces. The modelling approach emphasizes the essential role of large elastic deformation, while the airflow dynamics, microscopic mechanisms, like surface tension and air permeation, and rate-dependence are neglected. This approach is validated using experimental data for isolated hemi-spherical craters. The modelling approach is further applied to spherical cap (not necessarily hemi-spherical) craters with the objective of identifying optimal geometric and material properties, as well as the minimum preload necessary for attaining the maximum suction force. It is determined that stiff polymers with deep craters are capable of producing large suction forces. For soft materials, central to biomedical applications, large suction forces can be attained by reinforcing deep craters with thin stiff layers. Parametric optimization studies of reinforced craters reveal that some of them perform beyond common expectations. However, those high-performance reinforced craters are prone to surface instabilities, and therefore the practical use of such craters may be problematic.

1. Introduction

Removable adhesives are designed to form temporary bonds, and ideally can be removed without damaging or leaving any residue on the adherend. Commonly used adhesives include Post-it^® notes and medical tapes. Removable adhesives, which are also reusable and capable of strong bonding, are particularly attractive for such applications as wall mounts, wafer handlers [1–3], foot pads for climbing robots [4,5] and bio-integrated electronics [6,7].

Many reusable adhesives can be found in nature. For example, geckos are capable of running upside down because they are endowed with anatomic features functioning as reusable adhesives that, on the one hand, can support a large weight, and, on the other hand, allow for a quick and easy release. Experimental observations reveal that toe pads of geckos feature intricate hierarchical fibrillary structures. These structures result in adhesive strength close to 100 kPa [8,9], which is comparable to that of a 3M scotch tape (200 kPa). A lot of progress has been made towards the fundamental understanding of the gecko fibrillary structure [10–12] and its artificial reproduction [13–15].

While commercial use of engineered hierarchical fibrillary structures is in its infancy, low-cost fixtures in the form of suction cups have been widely used in numerous applications, such as wall/window-mounting suction hooks (figure 1a) and skin-mounting suction electrodes. Suction cups are attractive because they can combine high strength and quick release. Adhesion of suction cups is enabled by a vacuum generated inside the cup upon applying and releasing a compressive load. We refer to the peak compressive load as the preload. The basic mechanics of thin-walled suction cups has been elucidated in [16,17].

Figure 1.

(a) A thin-walled suction cup fixture. (b) A 3D schematic of a cratered surface. (c) SEM images of closely packed sub-micron-sized surface dimples on UV resin (adopted from Chang et al. [2] with permission from Copyright (2017) American Chemical Society). (d) AFM images of 1 μm diameter craters on the surface of polydimethylsiloxane (PDMS) (adopted from Choi et al. [6] with permission from Copyright Wiley-VCH Verlag GmbH & Co. KGaA).

The suction effect has been exploited for reusable adhesives by using fibrillary structures with concave tips [18–20]. A simple alternative to such reusable adhesives is cratered surfaces [2,3,6,21]. Unlike suction cups, usually formed by thin-walled structures [16,17] (figure 1a), craters are surface dimples on engineered surfaces which can be easily moulded over large areas (figure 1b). Chang et al. produced closely packed sub-micron-sized surface dimples on UV resin (figure 1c) and reported the adhesive shear strength of 750 kPa [2]. Choi et al. fabricated 1 μm diameter craters on the surface of polydimethylsiloxane (PDMS) (figure 1d) and measured the adhesive shear strength of 1.6 kPa, which exceeds the adhesive strength of the same PDMS with both flat surfaces and surface pillars [6]. Both Chang et al. and Choi et al. attributed the enhanced adhesion of cratered polymeric surfaces to the suction effect. Chang et al. did not provide any analysis of the suction effect, while Choi et al. analysed it on the basis of linear elasticity theory. In the next section, we will show that this approach, based on the assumption of small deformations, is insufficient for characterizing the suction effect, as it requires one to consider large deformations. Also, Akerboom et al. observed enhanced adhesion for PDMS with 100 nm diameter craters and found that the pull-off force depends on the crater geometry and preload [21]. Akerboom et al. explained the increase in adhesion of dimpled PDMS surface by energy-dissipating mechanisms during detachment but did not take suction effect into account. Recently, Baik et al. [22] fabricated removable adhesives enabled by craters, and obtained a closed-form solution for the adhesion strengths that agrees well with experimental measurements. However, we were not able to reproduce that solutions based on details provided in [22]. Furthermore, the analysis in [22] is based on the prior work of Afferrante et al. [23] and Tramacere et al. [24], which is applicable to membrane-like structures rather than craters.

Our point of departure is that, at this stage, modelling of the suction effect produced by cratered surfaces is at its infancy, and therefore we focus on the basic problem involving an isolated crater. By definition, dimensions of an isolated crater are much smaller than all other specimen dimensions, so that the specimen can be regarded as a semi-infinite solid. As a result, the response of an isolated crater is unaffected by structural length scales other than those of the crater itself. Further, we assume that the crater is macroscopic, that is its dimensions are much larger than material length scales associated with microscopic mechanisms like surface tension, air permeation, and others, and therefore the crater response can be described using scale-independent continuum models. Finally, we assume that the suction is induced so that the rate effects associated with the airflow, deformation and adhesion are negligible. Some of these assumptions can be validated either by comparing modelling predictions with experimental data or basic dimensional analysis. Other assumptions are hard to evaluate. For example, the interfacial surface roughness may affect the airflow and adhesion, and these effects are difficult to characterize in terms of both modelling and experimentation. In summary, the modelling approach emphasizes the essential role of large elastic deformation as the primary engine for creating the suction effect.

In an attempt to maximize the suction effect we consider two types of craters. First, we study spherical-cap-shaped (SCS) craters, establish the suction-preload dependence, and identify optimal geometric and material properties, as well as the minimum preload necessary to attain the maximum suction force. As a result we learn that materials suitable for many applications are too soft for optimal SCS craters. Therefore, we consider SCS craters reinforced with thin stiff layers, and discover that such craters perform beyond our expectations.

This paper is organized as follows. In §2, we focus on the suction force produced by hemi-spherical craters. We study such craters based on experimental, numerical simulation and analytical approaches. We establish a good agreement between experimental and simulation data, and therefore adopt the simulation approach for characterizing more general SCS craters. In §3, we study isolated SCS craters, for which we establish optimal geometric and material parameters, and the minimum preload necessary for maximizing the suction force. In §4, we focus on reinforced SCS craters, and identify optimal reinforcement parameters. Section 5 presents a discussion of several related topics and adopted assumptions. Section 6 provides a brief summary of key results.

2. Hemi-spherical craters

In this section, we use experimental, computational and analytical approaches to study isolated hemi-spherical macroscopic craters. The computational framework established in this section will be applicable to more general classes of isolated macroscopic craters.

2.1. Modelling set-up

Consider a specimen containing a hemi-spherical crater with radius a (figure 2a). The specimen rests on a flat rigid substrate. We suppose that the specimen is made of rubber, that is it is capable of sustaining large elastic strains. The air inside the crater is the same as in the ambient environment, and it is characterized by the pressure p₀, volume V₀ and N₀ molecules (figure 2a). The suction effect is realized in two stages:

• (1) The specimen is compressed, so that the air is squeezed out of the crater; at the end of this stage, the remaining air in the crater is characterized by the triplet (p₁, V₁, N₁) (figure 2b).

• (2) The specimen is unloaded, so that the crater springs back. This action results in a pressure drop associated with the suction effect. At the end of this stage, the air in the crater is characterized by the triplet (p₂, V₂, N₂) (figure 2c). Accordingly, the pressure drop is

  

and the suction force is

2.1

where A₂ is the projected area of the crater at the end of Stage 2.

Figure 2.

A loading–unloading cycle that produces the suction effect: (a) A specimen with an isolated hemi-spherical crater of radius a resting on a flat plate (blue). (b) The specimen is preloaded in compression and the air is squeezed out of the crater. (c) The preload is released, and the springback induces vacuum in the crater. The symbols p, V and N denote the pressure, volume and number of molecules of air inside the crater at each state.

A complete analysis of the two-stage process requires one to model the airflow dynamics. In this paper, we avoid this task by adopting the following assumptions:

• 1. The air flows freely out of the crater upon loading, so that p₁ = p₀.

• 2. No air exchange takes place upon unloading, so that N₁ = N₂.

• 3. The entire process is isothermal and the air is an ideal gas, so that p₁V₁ = p₂V₂.

As a result, the expression for the suction force becomes

2.2

With the adopted assumptions, the dynamics of airflow is regarded as a sequence of static equilibrium states. Consequently, it becomes sufficient to analyse the two-stage process in the context of solid mechanics, as it is explained in §2.3.

In the remainder of this section, we describe an experimental set-up designed to conform with the adopted assumptions. Further, we show that the experimental results can be accurately predicted using nonlinear elasticity theory alone. That is neglecting the airflow dynamics appears to be a good assumption.

2.2. Experimental set-up

The experimental set-up was designed so that it realizes the two-stage process under conditions that well represent the adopted assumptions. First, polydimethylsiloxane (PDMS, Sylgard 184 Dow Corning) with the base-to-curing-agent mass ratio equal to 30 : 1 was cured at 70°C for 12 h to mould four specimens. The first specimen was a pure rectangular prism whose dimensions were 25 × 25 × 40 mm³. The other three specimens were prisms with the same dimensions, but each prism was endowed with a hemi-spherical crater of diameter 12.7 mm, placed at the centre of a square (25 × 25 mm²) face. PDMS is an ideal material for our purposes, as it is a quintessential rubber with negligible rate-dependence in the time-temperature range in our experiments [25]. Further, it is clear that specimen dimensions in the centimetre range are much larger than any length scale associated with microscopic mechanisms. The pure rectangular prism was used for identifying material properties. To this end, we conducted a uniaxial compression test using a Dynamic Mechanical Analyzer (DMA) (RSA-G2, TA Instruments). The top and bottom surfaces of the specimen were lubricated by performance oil (Fellowes Powershred Performance Shredder Oil) such that the specimen was under uniaxial stress. The loading velocity was set at 3 mm min⁻¹, which corresponds to a nominal strain rate of 1.25 × 10⁻³ s⁻¹, so that the deformation was dominated by rubber elasticity. The axial load-displacement data were converted into the nominal stress σ versus the principal stretch λ data and fitted by the incompressible neo-Hookean model

2.3

where the shear modulus μ is the fitting parameter. As shown in figure 3, this model fits the experimental data very well for μ = 47.3 kPa.

Figure 3.

Nominal stress σ versus the principal stretch λ. The data were obtained using pure rectangular specimens subjected to uniaxial compression, and fitted based on the incompressible neo-Hookean model (equation (2.3)) for μ = 47.3 kPa. (Online version in colour.)

Direct measurements of the suction force are difficult. Therefore, we performed the loading–unloading experiments on all four specimens and in each case measured the pull-off force rather than suction force. These data will be used for calculating the suction force as explained in §2.4.

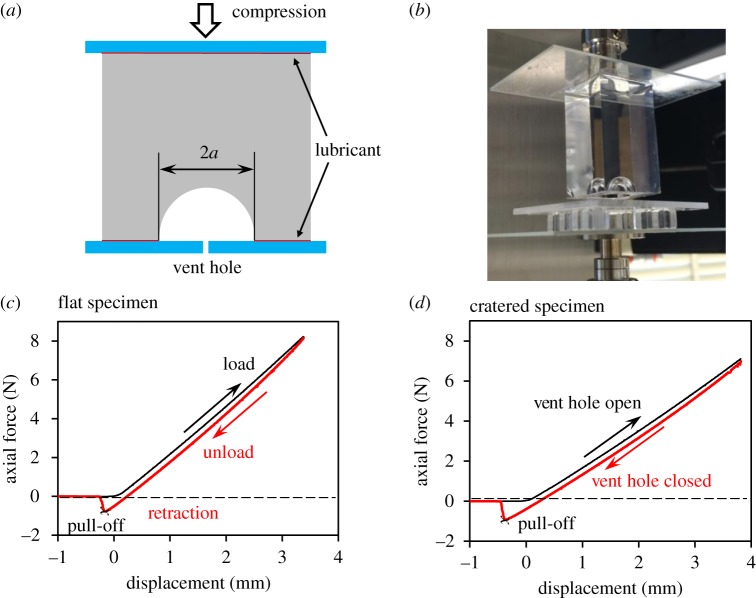
To realize experimental conditions that well represent the adopted assumptions, we built a special platform as illustrated by a schematic in figure 4a and a photograph in figure 4b. The cratered specimen was compressed against a stiff acrylic platform. At the platform centre, we drilled a ventilation hole with diameter of 0.8 mm, which was used for releasing and trapping the air in the crater. During the first stage, consistent with the first assumption, the hole was opened. During the second stage, consistent with the second assumption, the hole was sealed. Both stages were realized using a 3 mm min⁻¹ loading velocity. Similar to the pure rectangular prism, the top and bottom surfaces of the cratered specimens were lubricated. To measure the pull-off force, the second stage involved not only unloading but also retraction. That is, during the second stage, the specimen was stretched beyond the unloading point, until the cratered surface was pulled off the platform. The load-displacement data for both pure prismatic and cratered specimens are shown in figure 4c,d. There we identify the loading, unloading, and retraction stages, and the pull-off force. Note that the two sets of data are qualitatively similar. Nevertheless, quantitative differences are significant enough to identify the suction effect. Experimental results will be further discussed in §2.4.

Figure 4.

A schematic drawing (a) and a photograph (b) of the experimental platform. The small ventilation hole drilled in the bottom plate is open during loading and closed during unloading. Load-displacement curves for pure prismatic (c) and cratered (d) specimens under peak compressive strain of approximately 10%, with loading, unloading, retraction stages, and the pull-off points identified.

2.3. Simulations

Following experimental data for the pure prismatic specimens, we assumed that the constitutive behaviour of the cratered specimens is described by the incompressible neo-Hookean constitutive model with μ = 47.3 kPa. Further, to simplify the analysis, we assumed that the specimen dimensions were large in comparison to the crater size. This allowed us to model the specimens as axisymmetric rather than prismatic. The specimen/substrate interface was assumed to be frictionless (figure 5a).

Figure 5.

(a) A finite-element mesh for an axisymmetric model. (b) Raw experimental data of pull-off forces for pure prismatic (blue markers) and cratered (red markers) specimens. (c) Comparisons of suction forces between experimental data (markers) and modelling/simulation results (curves).

Following the third assumption, the gas inside the crater was assumed to be ideal, and its pressure during the second stage was controlled by the crater volume. Since the solid is assumed to be incompressible, one can define the reference state for the solid as the one in which the specimen is uniformly compressed with the ambient pressure p₀.

We used finite-element simulations to compute the relationship between the suction force (equation (2.2)) and the peak macroscopic axial strain, defined as

where L is the specimen length. All simulations were conducted using ABAQUS v. 6.14. The finite-element mesh formed by CAX4H elements is shown in figure 5a; this mesh was selected using basic convergence tests. We used the option *FLUID CAVITY, which is ideal for modelling both stages of the gas-solid interactions.

2.4. Results

In this section, we establish a relationship between the suction and pull-off forces, and compare experimental and simulation results. In addition, we present results of linear analysis of the problem based on Eshelby's formalism [26].

The experimental data provide us with two pull-off forces F′ and F″ corresponding to the cratered and pure prismatic specimens (figure 5b), respectively. One way to determine the suction force F is by calculating the difference

2.4

However, this approach does not take into account that the adhesion areas of the cratered and pure prismatic specimens are different. Accordingly, we modify the formula as

2.5

where ϕ is the area fraction of the crater defined in the reference configuration. Although this formula is imperfect, figure 5c clearly shows that the correction 1 − ϕ does not affect the value of F significantly. Therefore, further refinements of equation (2.5) were not pursued.

Comparisons of experimental (red markers) and simulation (red curve) results, based on equations (2.5) and (2.2), respectively, are shown in figure 5c where the suction force is plotted versus Θ. Note that the simulation results were obtained for 0 ≤ Θ ≤ 0.5, whereas the experimental results were limited to 0 ≤ Θ ≤ 0.25. This limitation is not of a fundamental nature, as it is associated with the allowable load of the DMA used in the experiments. At any rate, in the range of 0 ≤ Θ ≤ 0.25, experimental and simulation results are in good agreement. This justifies the use of the modelling assumptions and simulations for characterizing more general situations.

In addition to finite-element simulation results, we calculated the suction force using linear (infinitesimal strain) analysis based on Eshelby's formalism [26]. This approach is possible because of the assumptions that the specimen is large, the interface is frictionless, and the surface tension effects are negligible. Details of this analysis are presented in appendix A, and the results (green curve) are shown in figure 5c. It is clear that the linear analysis is acceptable for small strains, but its validity is limited, so that it should not be used for, say, Θ > 0.2.

To optimize the suction force, the loading stage should result in a complete closure of the crater. In this regard, it is useful to identify the minimum value of Θ corresponding to a complete closure of the crater; we denote that minimum Θ by Θ_m. For hemi-spherical craters, we computed Θ ≈0.48, independent of the specimen stiffness. It is clear that the suction forces will not increase for Θ > Θ_m.

3. Spherical-cap-shaped craters

In this section, we extend the simulation approach developed for hemi-spherical craters to spherical-cap-shaped (SCS) craters. Our focus is on maximizing the suction force by optimizing the crater shape and specimen mechanical properties. Since our analysis is limited to large specimens, the only dimensionless geometric parameter involved is

where a is crater base radius and b is the crater height (figure 6a). The dimensionless stiffness parameter is defined as

In the previous section, these parameters were fixed at α = 1 and β = 0.47. Further, in the previous section, the preloading parameter Θ was varied. In contrast, in this section, this parameter is set to be Θ_m, so that the crater attains a full closure and realizes complete vacuum. With this provision V₁ = 0, and the suction force is computed from equation (2.2) as

3.1

A contour plot for the normalized suction force

3.2

as a function of α and β is presented in figure 6b. This plot was generated using finite-element simulations; the raw data are provided in electronic supplementary material, table S1. The plot clearly demonstrates that large 's are realized by specimens with large α and β. But the dependence of on α and β is not monotonic. Further, for sufficiently stiff specimens, the dependence on α is relatively weak. We identify ‘good’ specimens as those for which ; the rest of the specimens are regarded as ‘bad’. This (arbitrary) classification is represented by the black curve on figure 6b. In figure 6c we present Θ_m as a function of α; apparently Θ_m is independent of β. As expected, deep craters require large Θ_m.

Figure 6.

(a) A schematic of the spherical-cap-shaped (SCS) crater. (b) A contour plot for the normalized achievable suction force as a function of α and β. (c) Minimum preload strain for closure Θ_m as a function of α.

To gain further insight into simulation results in figure 6b, we present the deformed shape of twelve specimens upon full unloading corresponding to α = 0.25, 0.5, 0.75, 1 and β = 0.5, 1, 10 (figure 7). The dashed lines show the initial craters. It is clear from figure 7 that stiff specimens with deep craters are capable of recovering in a way that A₂ ≈A₀ and therefore for such specimens . In contrast, soft specimens with shallow craters result in 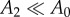and therefore very small . Electronic supplementary material, movies S1 and S2 allow one to visualize the deformation during the loading–unloading cycle. Electronic supplementary material, movie S1 shows specimens with the same crater shape but different stiffness, while electronic supplementary material, movie S2 shows specimens with the same stiffness but with different crater shapes. The colour-map in both movies is for the von Mises stress normalized by the shear modulus.

Figure 7.

(a–d) Deformed (solid lines) and undeformed (dashed lines) shapes of craters. The deformed shapes correspond to complete unload.

4. Reinforced craters

While stiff specimens with deep craters result in large suction forces, many biomedical applications involve soft polymers for which β ≈1. According to figure 6b, such specimens are classified as bad ones. To address this issue we consider soft specimens with craters reinforced by thin stiff layers (figure 8a), with the expectation that such layers would result in the recovered base area A₂ ≈A₀. Such layers are straightforward to manufacture. For example, PDMS with the base-to-curing-agent mass ratio equal to 10 : 1 has shear modulus around 1 MPa, and, thus, can be used to reinforce a cratered specimen made of Ecoflex^® 0300 (Smooth-On, Inc.) whose shear modulus is about 27 kPa [27]. In what follows, the stiff layers added to the surface of the craters are called reinforcement layers, which should not be confused with the bulk reinforcement.

Figure 8.

(a) A schematic of a hemi-spherical crater reinforced by a thin stiff layer (red). (b) A three-colour map in the α′−β′ parametric space for specimens with α = β = 1. The green zone is for craters exhibiting instabilities upon both loading and unloading, the red zone is for craters exhibiting instabilities upon unloading only, and the blue zone is for stable craters. The interior of the yellow line is for craters with . (c) Comparison of the reinforced and unreinforced craters.

We considered reinforcement layers made of incompressible neo-Hookean materials, so that the layers were characterized by the dimensionless parameters

where t and μ_l are the layer thickness and shear modulus, respectively. To reduce the size of the parametric space, we limited our studies to β = 1. As a result, the optimal search involved three parameters only: α, α′ and β′; as in the simulations for unreinforced craters the preload was equal to Θ_m.

First, we set α = 1 and examined the α ′− β′ parametric space (electronic supplementary material, table S2). We determined that the best craters were characterized by 0.015 < α′ < 0.045 and 10 < β′ < 50. In this parametric domain, the normalized suction force was . It is remarkable that one can achieve 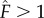. Upon further inspection of simulation results, we determined that all cases resulting in involved crater surface instabilities. In most cases, was associated with instabilities upon unloading only. In some cases, we observed instabilities both upon loading and unloading. To visualize relationships between instabilities and the normalized suction force, we present a three-colour map in the α′ − β′ parametric space (figure 8b). The green colour corresponds to craters that exhibit instabilities upon both loading and unloading, the red colour corresponds to craters that exhibit instabilities upon unloading only, and the blue colour corresponds to stable craters. The yellow box is the boundary of the domain inside which . This map was constructed on the basis of a coarse grid in the α′−β′ parametric space, and therefore the map boundaries are somewhat approximate. In the discussion section, we present several examples of instabilities occurring in reinforced craters.

Next, we set α′ = 0.03 and β′ = 30, and examined the dependence of 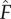on α; note that the chosen α′ and β′ are the centres of the respective optimal parametric intervals identified in the previous set of simulations. Simulation results for versus α are shown in figure 8c. The peak force of is achieved for α = 0.85. This value exceeds the force for the unreinforced specimen with α = 0.85 by a factor of 1.17/0.80 ≈1.46. Note that the optimal unreinforced crater is characterized by α = 0.7 rather than α = 0.85; in this case and the amplification factor is 1.17/0.84 ≈1.39.

A comparison of deformation histories for reinforced (α = β = 1, α′ = 0.03, β′ = 30) and unreinforced (α = β = 1) craters is shown in electronic supplementary material, movie S3.

5. Discussion

In this paper, we analysed suction-enabled reusable adhesives in the form of cratered surfaces. We restricted our attention to isolated macroscopic SCS craters, for which microscopic and rate effects were assumed to be negligible. The restriction to SCS craters is dictated by manufacturing considerations, but of course one can consider other shapes. In particular, we analysed hemi-spheroidal craters, as they appear to be similar in shape to SCS craters. Simulation results revealed that hemi-spheroidal and SCS unreinforced craters with the same aspect ratio α may have significantly different mechanical responses. Furthermore, the differences between reinforced hemi-spheroidal and SCS craters could be even more pronounced. Detailed results for suction forces of hemi-spheroidal craters are summarized in electronic supplementary material. Further, in general, it is difficult to decide a priori which shape would result in a better performance. Thus one should be careful in extending results of this work to craters with other shapes.

Both experimental and simulation results focused on specimens resting on frictionless substrates. Clearly, friction weakens the suction effect as it resists the crater volume loss during the loading step. Herein, it requires large force to close the crater, and therefore reducing friction should be desirable for all practical purposes.

Optimization studies considered in this paper involved preloads which completely close the crater. In practice, such preloads may be impossible to apply, and therefore the optimization procedure may be different. For example, if the preloading device can exert a maximum force insufficient for attaining Θ_m, as it was the case in our experiments, then the optimization procedure must include this condition as a constraint. That is, the optimal parameters must be determined under the constraint that the preloading force cannot exceed a prescribed value dictated by the preloading device.

While the main focus of this work is on identifying craters that maximize the suction force, it is important to appreciate that mechanical behaviour of those craters is rather complex. At this stage, we do not have a good understanding of relationships between the suction force and the underlying deformation mechanisms for reinforced craters. In what follows, we present four representative cases of reinforced craters that exhibit a broad range of deformation mechanisms (figure 9). In all cases, the craters are characterized by α = β = 1, that is, all craters are hemi-spherical with μ = p₀.

Figure 9.

Four representative reinforced craters with (α = β = 1): (a) no instability during either loading or unloading, (b) long-wavelength instabilities during both loading and unloading, (c) short-wavelength instabilities during both loading and unloading, and (d) short-wavelength instabilities during unloading only. For each case, the frames at Θ = 0, 0.2 and Θ_m represent the loading stage, and the frames at Θ = 0.2, 0.1 and 0 represent the unloading stage.

The crater in figure 9a can be described as weakly reinforced because the reinforcement layer is thin (α′ = 0.015) and not very stiff (β′ = 2). This weak reinforcement is inadequate, as it results in only. The six figures in the first row are instances of the loading–unloading cycle. The first and last figures in this sequence are the initial and final configurations, respectively. The third figure corresponds to full closure, and the rest are intermediate states. Note that in the final configuration, the projected area is significantly smaller than the initial one, which explains the low value of . It is clear that the deformation of this crater does not involve surface instabilities.

In contrast to the first case, the crater in figure 9b involves a strong reinforcement with α′ = 0.055 and β′ = 40. This strong reinforcement results in , which is an improvement over the weakly reinforced crater, but still suboptimal, as far as reinforced craters are concerned. The corresponding six figures (the second row) show that the loading–unloading cycle involves long-wavelength instabilities, which disappear upon unloading.

The third case involves a thin (α′ = 0.015) but very stiff (β′ = 80) reinforcement layer (figure 9c). This is an excellent reinforcement resulting in . The loading–unloading cycle is prone to short-wavelength instabilities which do not disappear upon complete unloading. Note that instabilities form upon loading, near the equator, and disappear at full closure. Instabilities re-emerge at the equator upon unloading, and propagate towards the pole. This pattern of instabilities suggests that design of optimal reinforced craters could be challenging.

The fourth case with α′ = 0.03 and β′ = 6 (figure 9d) involves a moderate reinforcement which results in 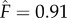. We included this case to demonstrate that, in contrast to the third case, instabilities arising upon loading and unloading can be quite different. In particular, the loading stage involves long-wavelength instabilities, if at all, whereas the unloading stage is characterized by short-wavelength instabilities.

The deformation histories of the four reinforced craters are also summarized in electronic supplementary material, movie S4.

This work can be extended in two complementary directions. First, it is straightforward to apply our approach to cratered surfaces rather than isolated craters. To this end, one has to analyse periodic three-dimensional rather than quasi-two-dimensional axisymmetric problems and expand the parametric space by including various periodic patterns (square, hexagonal, etc.) and cratered area fractions. The second, and much more challenging, direction involves modelling of microscopic rather than macroscopic craters. To this end, it may be prudent first to consider mesoscopic craters, whose modelling must involve surface tension [28] and permeation but not atomistic details necessary for modelling adhesion. We note that for our experiments the surface tension effect is indeed negligible, as the dimensionless number comparing the surface tension versus elastic effects is very small:

5.1

Here γ is the surface tension of PDMS [29]. In contrast, the air permeation through the crater surface is not entirely insignificant. Using a well-established quantifying approach for this effect [30], and the data necessary to estimate it for our specimens [31–33], we estimated that the permeation effect can lead to the air volume changes of the order of 5%. Details can be found in appendix B. While this estimate does not negate our overall approach, it implies that the permeation effect must be taken into account for microscopic and mesoscopic craters.

6. Summary

In this work, we focused on isolated macroscopic craters capable of generating large suction forces. Our key findings are summarized as follows:

• — In stiff materials, one can realize large suction forces by optimizing the crater shape.

• — In soft materials, typical of many biomedical applications, large suction forces require crater reinforcement.

• — The optimal performance of reinforced craters is realized by moderately stiff layers whose shear modules is about 30 times larger than the base modulus. Similarly, optimal layers should not be too thick or too thin—the optimal thickness is about 3% of the crater radius.

• — We were able to identify craters with the normalized suction force as large as 1.17. This was somewhat surprising because, prior to this work, we believed that the normalized force cannot exceed 1.

• — Reinforced craters capable of realizing large suction forces often function in the presence of instabilities, which are not well understood at the moment.

Appendix A

In this appendix, we derive an analytical solution of classical linear elasticity theory for the suction force of an isolated hemi-spherical crater in a semi-infinite specimen. We take advantage of the assumption that the contact between the specimen and the substrate is frictionless. This allows us to replace the problem for semi-infinite specimen containing a hemi-spherical crater with an infinite specimen containing a spherical cavity. This problem is straightforward to analyse using Eshelby's formulism [26].

According to equation (2.2), we need to calculate V₁, V₂ and A₂. Note that according to classical linear elasticity, the quantities ΔV₁ = V₁ − V₀, ΔV₂ = V₂ − V₀ and ΔA₂ = A₂ − A₀ are infinitesimal. This allows us to replace A₂ with A₀. However, computing ΔV₁ and ΔV₂ is essential for meaningful calculation of the suction force.

To compute ΔV₁, we subject the infinite specimen to remote uniaxial compressive strain Θ. For this case, Eshelby's formulism yields

A 1

where ν is the Poisson's ratio of the specimen material.

To compute ΔV₂, we subject the cavity to the surface traction

where n is the outward normal. As far as ΔV₂ is concerned, this problem is equivalent to the superposition of two problems. In the first problem, the specimen is uniformly loaded by −Δp on both cavity and remote surfaces. In the second problem, the cavity surface is traction-free and the remote surface is subjected to Δp. As a result, we obtain

A 2

where

A 3

Combing equations (A 1), (A 2) and (A 3), one obtains the suction force

A 4

Appendix B

Gas permeation is important in structures made of PDMS, especially for ones in micro size whose area-to-volume ratios are high. For bulk PDMS specimens, the solution-diffusion model is usually applied [30], in which the Henry permeability, P_Henry = DS, characterizes the gas permeability, where D is the diffusion coefficient and S is the solubility. In a loading–unloading cycle, gas permeation only occurs in the unloading step driven by the pressure drop Δp inside the crater. Note that Δp is negative. The relative gas leakage is expressed as the following:

where J is the air flux volume, V₀ is the initial volume of the crater, A is the area of air/PDMS interface in, T is the environment temperature, T₀ = 273.15 K, Δp(t) is the pressure drop inside the crater that depends on time t, and t₀ is the time period of unloading. l represents the PDMS membrane thickness in common permeation tests. For cratered specimen, we choose l = 6 mm which is the shortest distance from crater surface to outer PDMS surface. In the experiments, we have T = 20°C, A = 2πa², V₀ = 2πa³/3, a = 0.635 mm, max(−Δp) ≈ 0.2 atm and max(t₀) ≈ 200 s. According to [31],

for CO₂/PDMS is used for estimation, which is usually higher than that of N₂/PDMS and O₂/PDMS based on the study of PDMS membranes in [32], and thus, can be used to estimate the upper bound of the relative gas leakage. However, this permeability is for PDMS with base-to-curing-agent mass ratio equal to 10 : 1. Considering the effect of curing agent ratio characterized in [33], we multiply P_Henry by a factor of 3 to approximate the gas permeability for PDMS with base-to-curing-agent mass ratio equal to 30 : 1. Herein, the estimated relative air flux is

and therefore, the effect of gas permeation on suction force in our experiments is considered as negligible.

Data accessibility

The raw finite-element results have been included in the electronic supplementary material.

Authors' contributions

S.Q. carried out the finite-element simulations, analytical analysis, and helped draft the manuscript. L.W. participated in finite-element simulations, discussions and manuscript writing. H.J. and S.Q. designed the experiments. H.J. prepared all the specimens for S.Q. who carried out the pull-off force measurements. N.L. and G.J.R. conceived and led the project; they also directed writing of the manuscript. All authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This work was supported by the National Science Foundation (NSF) Division of Civil, Mechanical and Manufacturing Innovation (CMMI) award under Grant no. 1663551 and the Office of Naval Research (ONR) Young Investigator Program (YIP) Award under Grant No. N00014-16-1-2044.