simcausal R Package: Conducting Transparent and Reproducible Simulation Studies of Causal Effect Estimation with Complex Longitudinal Data

Abstract

The simcausal R package is a tool for specification and simulation of complex longitudinal data structures that are based on non-parametric structural equation models. The package aims to provide a flexible tool for simplifying the conduct of transparent and reproducible simulation studies, with a particular emphasis on the types of data and interventions frequently encountered in real-world causal inference problems, such as, observational data with time-dependent confounding, selection bias, and random monitoring processes. The package interface allows for concise expression of complex functional dependencies between a large number of nodes, where each node may represent a measurement at a specific time point. The package allows for specification and simulation of counterfactual data under various user-specified interventions (e.g., static, dynamic, deterministic, or stochastic). In particular, the interventions may represent exposures to treatment regimens, the occurrence or non-occurrence of right-censoring events, or of clinical monitoring events. Finally, the package enables the computation of a selected set of user-specified features of the distribution of the counterfactual data that represent common causal quantities of interest, such as, treatment-specific means, the average treatment effects and coefficients from working marginal structural models. The applicability of simcausal is demonstrated by replicating the results of two published simulation studies.

1. Introduction

1.1. Motivation for simcausal

This article describes the simcausal package (Sofrygin et al. 2015), a comprehensive set of tools for the specification and simulation of complex longitudinal data structures to study causal inference methodologies. The package is developed using the R system for statistical computing (R Core Team 2015) and is available from the Comprehensive R Archive Network (CRAN) at http://CRAN.R-project.org/package=simcausal. Our package is intended to provide a flexible tool to facilitate the process of conducting transparent and reproducible simulation studies, with a particular emphasis on the types of data and interventions frequently encountered in real-world causal inference problems. For example, our package simplifies the simulation of observational data based on random clinical monitoring to evaluate the effect of time-varying interventions in the presence of time-dependent confounding and sources of selection bias (e.g., informative right censoring). The package provides a novel user-interface that allows concise and intuitive expression of complex functional dependencies between a large number of nodes that may represent time-varying random variables (e.g., repeated measurements over time of the same subject-matter attribute, such as, blood pressure).

Statisticians often rely on simulation studies for assessing the appropriateness and accuracy of different statistical methods (Burton et al. 2006). These studies generally help evaluate and uncover potential problems with a method because the statistician knows and controls the true data generating distribution, which remains unknown in a real data study (Hill and Reiter 2006). Hence, a simulation study provides statisticians with a gold standard for evaluating and comparing the performance of different statistical methods. The artificial population data is usually drawn according to the specified model and the statistical procedure is then applied to such data many times. For example, simulations have been applied to evaluate the bias of an estimator (Porter et al. 2011; Brookhart et al. 2006), study its asymptotic behavior (Mynbaev and Martins-Filho 2015), diagnose its sensitivity towards different modeling assumptions (Petersen et al. 2012; Brookhart et al. 2006), and determine the power of hypothesis tests (Væth and Skovlund 2004). Moreover, it may not only be of value to find out that the statistical method works when its postulated assumptions are true, but also to evaluate its robustness towards departures from the required causal and statistical assumptions (Demirtas 2007). These are some of the common reasons why simulation studies are increasingly being used in the medical literature (Burton et al. 2006; Kristman et al. 2004; Væth and Skovlund 2004; Collins et al. 2001). We also note that careful consideration should be given to a simulation study design (Burton et al. 2006). Indeed, simulations are of most value when there is some hope that they are capable of capturing the complexities one might expect to see in real-world data-generating processes. We also argue that careful attention should be paid to the structure and clarity of the simulation code itself, not only to simplify the conduct and presentation of extensive and complex simulation studies, but also to avoid coding errors which may lead to incorrect conclusions and difficulty with reproducing the findings of such a simulation study.

In this package, data can be simulated using a broad range of parametric distributions, such that the resulting user-specified data generating distribution always falls into some non-parametric structural equation model (NPSEM) (Pearl 1995, 2009, 2010a). An NPSEM consists of a set of structural equations, which describe the causal mechanisms for generating independent observations of a user-specified data structure. Each structural equation is used to describe a single variable (call it ‘X’), which may be latent or observed. Specifically, the structural equation for X postulates a mechanism in which Nature could have generated X, as a consequence of other endogenous variables’ values and a random disturbance (representing the effect of exogenous variables). Thus, defining X in this manner avoids having to make a commitment to a particular parametric family of distributions or specific functional form in which X may relate to other variables. As a result, an NPSEM enforces the separation of the notion of a causal “effect” from its algebraic representation in a particular parametric family (i.e., a coefficient in a linear causal model), and redefines an effect as a ‘general capacity to transmit changes among variables’ (Pearl 2010b, 2012). In particular, the NPSEM framework allows the extension of the capabilities of traditional SEM methods to problems that involve discrete variables, nonlinear dependencies, and heterogeneous treatment effects (Elwert 2013). The interventions can then be defined by replacing some of the equations in NPSEM with their intervened values, which then defines the counterfactual data.

Our package was developed based on the principles of the NPSEM framework and thus aims to provide the user with a toolkit for specifying and simulating data based on a very large collection of parametric distributions with often nonlinear relationships between the variables. Moreover, simcausal is built around the language and the logic of counterfactuals: What would happen if a subject received a different treatment? In other words, simcausal also allows for specification and simulation of counterfactual data under various user-specified interventions (e.g., static, dynamic, deterministic, or stochastic), which are referred to as “actions”. These actions may represent exposure to treatment regimens, the occurrence or non-occurrence of right-censoring events, or of clinical monitoring events (e.g., laboratory measurements based on which treatment decisions may be made). Finally, the package enables the computation of a selected set of “effects” (defined as user-specified features of the distribution of some counterfactual data) that represent common causal quantities of interest, referred to as causal target parameters. For instance, treatment-specific means, the average treatment effects (ATE) (on the multiplicative or additive scale) and coefficients from working marginal structural model (MSM) (Robins 1998; Neugebauer and van der Laan 2007) are a few of the causal target parameters that can be evaluated by the package. The computed value of a particular causal parameter can then serve as the gold standard for evaluating and comparing different estimation methods, e.g., evaluating finite sample bias of an estimator. We note that our package also provides a valuable tool for incorporating and changing various causal independence assumptions and then testing the sensitivity or robustness of the studied statistical methods towards departures from those assumptions.

One of the possible examples of applying simcausal in practice includes simulating the types of data collected on subjects in the fields of medicine and public health, e.g., electronic healthrecords data. Specifically, when one is interested in evaluating the utility and appropriateness of a statistical procedure towards answering causal policy questions about the effects of different interventions on the exposures of interest (e.g., the average effect of a treatment for lowering blood pressure vs. placebo). In addition, our package provides tools for converting simulated and real data between various formats, simplifying the data processing as it may be required by different estimation R packages (e.g., converting longitudinal data from wide to long formats, performing forward imputation on right-censored data). Finally, we note that the simcausal package can be a useful instructional tool, since it can elucidate understanding of complex causal concepts (Hodgson and Burke 2000), for example, using a simulated setting to demonstrate the validity of complex causal identifiability results, showing bias due to unmeasured confounding (Fewell et al. 2007), selection bias (Elwert and Winship 2014), and bias due to positivity violations (Petersen et al. 2012). In summary, these are just a few of the possible practical applications of simcausal: (a) Evaluating and comparing the performance of statistical methods and their sensitivity towards departures from specific modeling assumptions; (b) Modeling simulations after real data sets and technically validating an implementation of a novel statistical procedure; (c) Identifying possible issues with statistical algorithms that were not or could not be predicted from theory; and (d) Serving as an instructional tool for understanding complex causal theory in practical simulated settings.

1.2. Comparison to other simulation packages

The CRAN system contains several R packages for conducting data simulations with various statistical applications. We reference some of these packages below. Our review is not intended to be exhaustive and we focus on two key aspects in which simcausal differ from these other simulation tools.

First, simulations in the simcausal package are based on data generating distributions that can be specified via general structural equation models. By allowing the specification of a broad range of structural equations, the set of possible distributions available to the analyst for simulating data is meant to be not overly restrictive. For instance, any sampling distribution that is currently available in R or that can be user-defined in the R programming environment can be used for defining the conditional distribution of a node given its parents. Some of the other R packages rely on alternative approaches for specifying and simulating data. For example, the package gems (Blaser et al. 2015) is based on the generalized multistate models, and the package survsim (Moriña and Navarro 2014) is based on the Weibull, log-logistic or log-normal models. Finally, the following R simulation packages rely on linear structural equation models: lavaan (Rosseel 2012), lavaan.survey (Oberski 2014), sem (Fox 2006; Fox et al. 2014), semPLS (Monecke and Leisch 2012), OpenMx (Boker et al. 2011, 2014) and simsem (Pornprasertmanit et al. 2015). The latter group of R packages is traditionally described as being based on the LISREL model (Bollen 1989). We note that the purpose and formulation of LISREL framework differs from the NPSEM framework that we adopt in simcausal, and we use the example in Section 3 to help highlight some of the differences. However, describing all the technical details of these two modeling approaches is beyond the scope of this article and we refer the reader to the following sources for the additional details: Glynn and Quinn (2007); Pearl (2010b); Matsueda (2012); Pearl (2012); Bollen and Pearl (2013); Shpitser and Pearl (2009).

Second, unlike the simFrame package, which is meant as a general object-oriented tool for designing simulation studies, the simcausal package is instead tailored to study causal inference methodologies and is particularly suited to investigate problems based on complex longitudinal data structures (Robins 1998). Indeed, simcausal provides a single pipeline for performing the following common steps frequently encountered in simulation studies from the causal inference literature and described in details later in this article: defining the observed data distribution, defining intervention/counterfactual distributions, defining causal parameters, simulating observed and counterfactual data, and evaluating the true value of causal parameters. In addition, the package introduces an intuitive user-interface for specifying complex data-generating distributions to emulate realistic real-world longitudinal data studies characterized by a large number of repeated measurements of the same subject-matter attributes over time. In particular, the simcausal package was designed to facilitate the study of causal inference methods for investigating the effects of complex intervention regimens such as dynamic and stochastic interventions (not just the common static and deterministic intervention regimens), and summary measures of these effects defined by (working) marginal structural models. We note, however, that while the package was initially developed for this particular methodological research purpose, its utility can be extended to a broader range of causal inference research, e.g., to perform simulation-based power calculations for informing the design of real-world studies.

1.3. Organization of this article

The rest of this article is organized as follows. In Section 2, we provide an overview of the technical details for a typical use of the simcausal package. In Section 3, we describe a template workflow for a simple simulation study with single time point interventions, while also drawing parallels with the traditional linear SEM framework. In Section 4, we describe the use of the package for a more realistic and complex simulation study example based on survival data with repeated measures and dynamic interventions at multiple time points. In Section 4, we also apply the simcausal package to replicate some of the results of a previously published simulation study by Neugebauer et al. (2014, 2015). In Section 5, we apply the simcausal package to replicate results of another published simulation study by Lefebvre et al. (2008). We conclude with a discussion in Section 6.

2. Technical details

2.1. NPSEM, causal parameter and causal graph

For the sake of clarity, we limit ourselves to describing a non-parametric structural equation model [NPSEM, Pearl (2009)] for the observed data collected from a simple single-time point intervention study (no repeated measures on subjects over time) and we note that this NPSEM can be easily extended to longitudinal settings with repeated measures. Suppose that we collect data on baseline covariates, denoted as W, an exposure, denoted as A (e.g. treatment variable), and an outcome of interest, denoted as Y. An NPSEM is a causal model that describes how these variables could be generated from a system of equations, such as: W = f_W(U_W), A = f_A(W, U_A) and Y = f_Y(W, A, U_Y). We note that an NPSEM is defined by unspecified (non-random) functions f_W, f_A, f_Y, and a model on the probability distribution P_U of random “disturbances” U = (U_W, U_A, U_Y). These equations are non-parametric in the sense that they make no specific statement about the functional form of f_W, f_A, f_Y. We define the observed data¹ as O = (W, A, Y), and we note that the allowed set of probability distributions for O is referred to as the the statistical model and it is implied by the causal model encoded by the above NPSEM (i.e., by the choice of f and the choice of the distribution P_U). We also note that every parametric data-generating distribution defined in the simcausal package can be described as an instance of a distribution in some NPSEM. Such NPSEM encodes the independence assumptions between the endogenous variables. For instance, the NPSEM described above assumes that the exposure A can depend on all baseline variables W. As another example, suppose that (W, A, Y) were collected from a clinical trial in which the exposure A was assigned at random. In this case, A is independent of W, an assumption that can be encoded in the above NPSEM by removing W from the above equation f_A as follows: A = f_A(U_A).

The NPSEM also implicitly encodes the definition of counterfactual variables, i.e., variables which would result from some particular interventions on a set of endogenous variables. For example, the NPSEM can be modified as follows: W = f_W(U_W), A = a, Y_a = f_Y(W, a, U_Y), where the equation for W was kept unchanged, A was set to a known constant a and Y_a denotes the counterfactual outcome under an intervention that sets A = a. In this article, we will refer to (W, a, Y_a) as counterfactual data and we define our target causal parameter as a function of such counterfactual data distribution, resulting from one or more exposure intervention “a”. For example, the average treatment effect (ATE) can be expressed as E [Y₁ − Y₀]. The fundamental feature of the causal parameter defined in this manner is that it remains a well-defined quantity under any probability distribution P_U for the disturbances and any choice of functions f, a notion which we also highlight with examples in Section 3.

Furthermore, suppose our goal is to evaluate the effect of the exposure with more than two levels (e.g., categorical or time-varying A), in which case we could evaluate the above ATE for any two possible combinations of different exposure levels. We could also undertake an equivalent approach and characterize all such contrast with a saturated model for the mean counterfactual outcome (E(Y_a)), as indexed by the exposure levels a of interest. For example, for an exposure with levels a ∈ {0, 1, 2}, we may use the following saturated MSM with three parameters: E(Y_a) = α₀ + α₁I(a = 1) + α₂I(a = 2). This model then implies that each possible contrast (ATE) can be recovered as a function of α = (α₀, α₁, α₂), e.g., E(Y₁ − Y₀) = α₁. However, this approach becomes problematic when dealing with small sample datasets and high dimensional or continuous exposures. That is, suppose our goal is to characterize the entire causal function of a given by {E(Y_a) : a ∈ 𝒜}, where 𝒜 represents the support of a highly dimensional or continuous A. An alternative approach is to approximate the true causal function {E(Y_a) : a ∈ 𝒜} with some low-dimensional working marginal structural model m(a|α). For example, one may define the working MSM as the following linear model: m(a|α) = α₀ + α₁a + α₂a². Note, however, that the term “working MSM” implies that we are not assuming E(Y_a) = m(a|α), but instead we are defining our causal parameter (α) as the best parametric approximation of the true function E(Y_a) with m(a|α). That is, such a working MSM made no assumptions about the true functional form of E(Y_a) and thus made no additional assumptions about the distribution of U and the functions f, beyond those already implied by the NPSEM (e.g., independence of (U_W, U_A, U_Y)). We also refer to Neugebauer and van der Laan (2007) for additional details and examples of working MSMs. Also note that the concept of such working MSMs is easily extended to arbitrary functions, e.g., we could define m(a|α) as an expit function when the outcome Y is binary.

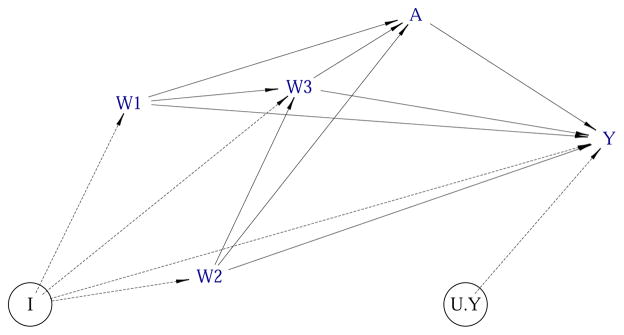
We note that the above NPSEM can be equivalently represented as a Directed Acyclic Graph (DAG) (Pearl 1995), such as the one in Figure 1 (left), by drawing arrows from causes to their effects. Links in this DAG can be of two kinds: those that involve unmeasured quantities are represented by dashed arrows and those that only involve measured quantities by solid arrows. We note that each endogenous node in Figure 1 represents a single equation in the above NPSEM. The causal assumptions in such a DAG are conveyed by the missing arrows, i.e., in our second example of the NPSEM, the absence of a variable W from the right-hand side of the equation for A = f_A(U_A) would correspond with no direct arrow between W and A. The disturbances U (also referred to as ‘errors’) are enclosed in circles in the diagram on the left because they represent unobserved (latent) factors that the modeler decides to keep unexplained. When the error terms (U_W, U_A, U_Y) are assumed to be independent, the often-used convention is to remove them from the causal DAG (Pearl 2012), as shown in Figure 1 (right), with the implication that each of the remaining variables is subject to the influence of its own independent error. This is also precisely how the function plotDAG of the simcausal package will plot the diagram of the user-specified SEM, that is, omitting the implied independent errors that influence each user-defined latent and endogenous node. We also refer to the examples in Section 3 for illustrations of this functionality of simcausal.

Figure 1.

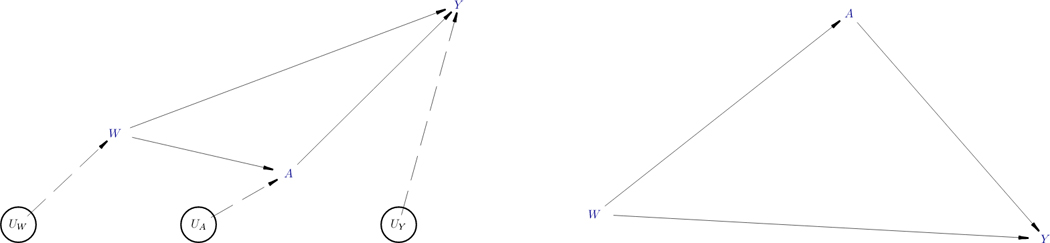
Two alternative ways to graphically represent the same structural equation model (SEM) using directed acyclic graphs (DAGs). The left figure shows the independent (latent) errors, while the right figure doesn’t.

We note that simcausal was designed to facilitate simulations from NPSEM with mutually independent disturbances. However, we also note that one can use simcausal to simulate dependent errors (U) with an arbitrary correlation structure using one of the following methods: a) Sample U jointly using a user-specified multivariate distribution with a specific correlation structure, e.g., multivariate normal or copula (see the documentation and examples for the node function); b) Create a common (also latent) parent that has a direct effect of all three variables in U (see the example in Section 3; or c) Perform Cholesky decomposition of the covariance matrix Σ for a multivariate normal N(μ, Σ), then generate correlated (U_W, U_A, U_Y) distributed as N(μ, Σ) based on the previously sampled independent standard normal variables (see the example in Appendix A).

2.2. The workflow

Data structures

The following most common types of output are produced by the package.

• parameterized causal DAG model - object that specifies the structural equation model, along with interventions and the causal target parameter of interest.

• observed data - data simulated from the (pre-intervention) distribution specified by the structural equation model.

• counterfactual data - data simulated from one or more post-intervention distributions defined by actions on the structural equation model.

• causal target parameter - the true value of the causal target parameter evaluated with counterfactual data.

Routines

The following routines, also outlined in Figure 2, will be generally invoked by a user, in the same order as presented below.

Figure 2.

Schematic of simcausal routines and the order in which one would usually call such routines in a typical simulation study.

• DAG.empty initiates an empty DAG object that contains no nodes.

• node defines a node in the structural equation model and its conditional distribution, i.e., the outcome of one equation in the structural equation model and the formula that links the outcome value to that of earlier covariates, referred to as parent nodes. A call to node can specify either a single node or multiple nodes at once, with name and distr being the only required arguments. To specify multiple nodes with a single node call, one must also provide an indexing vector of integers as an argument t. In this case, each node shares the same name, but is indexed by distinct values in t. The simultaneous specification of multiple nodes is particularly relevant for providing a shorthand syntax for defining a time-varying covariate, i.e., for defining repeated measurements over time of the same subject-matter attribute, as shown in the example in Section 4.1.

• add.nodes or D + node provide two equivalent ways of growing the structural equation model by adding new nodes and their conditional distributions. Informally, these routines are intended to be used to sequentially populate a DAG object with all the structural equations that make up the causal model of interest. See Sections 3.1 and 4.1 for examples.

• set.DAG locks the DAG object in the sense that no additional nodes can be subsequently added to the structural equation model. In addition, this routine performs several consistency checks of the user-populated DAG object. In particular, the routine attempts to simulate observations to verify that all conditional distributions in the DAG object are well-defined.

• sim simulates independent and identically distributed (iid) observations of the complete node sequence defined by a DAG object. The output dataset is stored as a data.frame and is referred to as the observed data. It can be structured in one of two formats, as discussed in Section 4.5.

• add.action or D + action provides two equivalent ways to define one or more actions. An action modifies the conditional distribution of one or more nodes of the structural equation model. The resulting data generating distribution is referred to as the postintervention distribution. It is saved in the DAG object alongside the original structural equation model. See Sections 3.3 and 4.3 for examples.

• sim(…, actions = …) can also be used for simulating independent observations from one or more post-intervention distributions, as specified by the actions argument. The resulting output is a named list of data.frame objects, collectively referred to as the counterfactual data. The number of data.frame objects in this list is equal to the number of post-intervention distributions specified in the actions argument, where each data.frame object is an iid sample from a particular post-intervention distribution.

• set.targetE and set.targetMSM define two distinct types of target causal parameters. The output from these routines is the input DAG object with the definition of the target causal parameter saved alongside the interventions. See Sections 3.5 and 4.6 for examples defining various target parameters.

• eval.target evaluates the causal parameter of interest using simulated counterfactual data. As input, it can take previously simulated counterfactual data (i.e., the output of a call to the sim(…, actions = …) function) or, alternatively, the user can specify the sample size n, based on which counterfactual data will be simulated first.

2.3. Specifying a structural equation model

The simcausal package encodes a structural equation model using a DAG object. The DAG object is a collection of nodes, each node represented by a DAG.node object that captures a single equation of the structural equation model. DAG.node objects are created by calling the node function. When the node function is used to simultaneously define multiple nodes, these nodes share the same name, but must be indexed by distinct user-specified integer values of the time variable t, as shown in the example in Section 4.1. We will refer to a collection of nodes defined simultaneously in this manner as a time-varying node and we will refer to each node of such a collection as a measurement at a specific time point.

Each node is usually added to a growing DAG object by using either the add.nodes function or equivalently the ’+’ function, as shown in the example in Sections 3.1 and 4.1. Each new node added to a DAG object must be uniquely identified by its name or the combination of a name and a value for the time variable argument t.

The user may explicitly specify the temporal ordering of each node using the order argument of the node()function. However, if this argument is omitted, the add.nodes function assigns the temporal ordering to a node by using the actual order in which this node was added to the DAG object and, if applicable, the value of the time variable that indexes this node (earlier added nodes receive a lower order value, compared to those that are added later; nodes with a lower value for the t argument receive a lower order value, compared to those with a higher value of t).

The node function also defines the conditional distribution of a node, given its parents, with a combination of the sampling distribution specified by the distr argument and the distributional parameters specified as additional named arguments to the node()function. This distr argument can be set to the name of any R function that accepts an integer argument named n and returns a vector of size n. Examples of such distribution functions are provided in Section 3.6.

The distributional parameters are specified as additional named arguments of the node()function and can be either constants or some summary measures of the parent nodes. Their values can be set to any evaluable R expressions that may reference any standard or user-specified R function, and also, may invoke a novel and intuitive shorthand syntax for referencing specific measurements of time-varying parent nodes, i.e., nodes identified by the combination of a node name and a time point value t. The syntax for identifying specific measurements of time-varying nodes is based on a re-purposed R square-bracket vector subsetting function ’[’: e.g., writing the expression sum(A[0:5]) , where A is the name of a previously defined time-varying node, defines the summary measure that is the sum of the node values over time points t = 0,…, 5. This syntax may also be invoked to simultaneously define the conditional distribution of the measurements of a time-varying node over multiple time points t at once. For example, defining the conditional distribution of a time-varying node with the R expression sum(A[max(0, t - 5):t]) + t will resolve to different node formulas for each measurement of the time-varying node, depending on the value of t:

1. A[0] at t = 0;

2. sum(A[0:1]) + 1 at t = 1, …, sum(A[0:5]) + 5 at t = 5;

3. sum(A[1:6]) + 6 at t = 6, …, sum(A[5:10]) + 10 at t = 10.

Concrete applications of this syntax are described in Section 4.1, as well as in the documentation of the node()function ( ?node).

Note that the user can also define a causal model with one or more nodes that represent the occurrence of end of follow-up (EFU) events (e.g., right-censoring events or failure events of interest). Such nodes are defined by calling the node()function with the EFU argument being set to TRUE. The EFU nodes encode binary random variables whose value of 1 indicates that, by default, all of the subsequent nodes (i.e., nodes with a higher temporal order value) are to be replaced with a constant NA (missing) value. As an alternative, the user may choose to impute missing values for the time-varying node that represents the failure event of interest using the last time point value carried forward (LTCF) imputation method. This imputation procedure consists in replacing missing values for measurements of a time-varying node at time points t after an end of follow-up event with its last known measurement value prior to the occurrence of an end of follow-up event. Additional details about this imputation procedure are provided in the simcausal package vignette Section 4.6 (Sofrygin et al. 2015).

Finally, we note that the package includes pre-written wrapper functions for random sampling from some commonly employed distributions. These routines can be passed directly to the distr argument of the node function with the relevant distributional parameters on which they depend. These built-in functions can be listed at any time by calling distr.list(). In particular, the routines “rbern”, “rconst”, and “rcat.b1” can be used for specifying a Bernoulli distribution, a degenerate distribution (constant at a given value), and a categorical distribution, respectively. One can also use any of the standard random generating R functions, e.g., “rnorm” for sampling from the normal distribution and “runif” for sampling from the uniform distribution, as demonstrated in Sections 3.1 and 3.6.

2.4. Specifying interventions

An intervention regimen (also referred to as action regimen) is defined as a sequence of conditional distributions that replace the original distributions of a subset of nodes in a DAG object. To specify an intervention regimen, the user must identify the set of nodes to be intervened upon and provide new node distributions for them. The user may define a static, dynamic, deterministic or stochastic intervention on any given node, depending on the type of distributions specified. A deterministic static intervention is characterized by replacing a node distribution with a degenerate distribution such that the node takes on a constant value. A deterministic dynamic intervention is characterized by a conditional degenerate distribution such that the node takes on a value that is only a function of the values of its parents (i.e., a decision rule). A stochastic intervention is characterized by a non-degenerate conditional distribution. A stochastic intervention is dynamic if it is characterized by a non-degenerate conditional distribution that is defined as a function of the parent nodes and it is static otherwise. Note that a particular intervention may span different types of nodes and consist of different types of distributions, e.g., an intervention on a monitoring node can be static, while the intervention on a treatment node from the same structural equation model may be dynamic.

To define an intervention the user must call D + action(A, nodes = B) (or equivalently add.action(D, A, nodes = B)), where D is a DAG object, A is a unique character string that represents the intervention name, and B is a list of DAG.node objects defining the intervention regimen. To construct B the user must first aggregate the output from one or more calls to node (using c(…, …)), with the name argument of the node function call set to node names that already exist in the locked DAG object D. The example in Section 4.3 demonstrates this functionality. Alternatively, repeated calls to add.action or D+action with the same intervention name, e.g., A = “A1”, allow the incremental definition of an intervention regimen by passing each time a different node object, enabling iterative build-up of the collection B of the intervened nodes that define the intervention regimen. Note, however, that by calling D + action or add.action(D, …) with a new action name, e.g., action(“A2”, …), the user initiates the definition of a new intervention regimen.

2.5. Specifying a target causal parameter

The causal parameter of interest (possibly a vector) is defined by either calling the function set.targetE or set.targetMSM. The function set.targetE defines causal parameters as the expected value(s) of DAG node(s) under one post-intervention distribution or the contrast of such expected value(s) from two post-intervention distributions. The function set.targetMSM defines causal parameters based on a working marginal structural model (Neugebauer and van der Laan 2007). In both cases, the true value of the causal parameter is defined by one or several post-intervention distributions and can thus be approximated using counterfactual data.

The following types of causal parameters can be defined with the function set.targetE:

• The expectation of an outcome node under an intervention regimen denoted by d, where the outcome under d is denoted by Y_d. This parameter can be naturally generalized to a vector of measurements of a time-varying node, i.e., the collection of nodes Y_d(t) sharing the same name, but indexed by distinct time points t that represents a sequence of repeated measurements of the same attribute (e.g., a CD4 count or the indicator of past occurrence of a given failure event):

  $$E(Y_d)\text{or}{(E(Y_d(t)))}_{t=0,1,\dots }.$$
• The difference between two expectations of an outcome node under two interventions, d₁ and d₀. This parameter can also be naturally generalized to a vector of measurements of a time-varying node:

  $$E(Y_{d_1})-E(Y_{d_0})\text{or}{(E(Y_{d_1}(t))-E(Y_{d_0}(t)))}_{t=0,1,\dots }.$$
• The ratio of two expectations of an outcome node under two interventions. This parameter can also be naturally generalized to a vector of measurements of a time-varying node:

  $$\frac{E(Y_{d_1})}{E(Y_{d_0})}\text{or}{\left(\frac{E(Y_{d_1}(t))}{E(Y_{d_0}(t))}\right)}_{t=0,1,\dots }.$$

Note that if the DAG object contains nodes of type EFU = TRUE other than the outcome nodes of interest Y_d(t), the target parameter must be defined by intervention regimens that set all such nodes that precede all outcomes of interest Y_d(t) to 0. Also note that with such intervention regimens, if the outcome node is time-varying of type EFU = TRUE then the nodes Y_d(t) remain well defined (equal to 1) even after the time point when the simulated value for the outcome jumps to 1 for the first time. The nodes Y_d(t) can then be interpreted as indicators of past failures in the absence of right-censoring events. The specification of these target parameters is covered with examples in Sections 3.5.1 and 4.6.1.

When the definition of the target parameter is based on a working marginal structural model, the vector of coefficients (denoted by α) of the working model defines the target parameter. The definition of these coefficients relies on the specification of a particular weighting function when the working model is not a correct model (see Neugebauer and van der Laan (2007) for details). This weighting function is set to the constant function of 1 in this package. The corresponding true value of the coefficients α can then be approximated by running a standard (unweighted) regression routines applied to simulated counterfactual data observations. The following types of working models, denoted by m(), can be defined with the function set.targetMSM:

• The working linear or logistic model for the expectation of one outcome node under intervention d, possibly conditional on baseline node(s) V, where a baseline node is any node preceding the earliest node that is intervened upon, i.e., E(Y_d | V):

  $$m(d,V\mid \alpha ).$$

  Such a working model can, for example, be used to evaluate the effects of HIV treatment regimens on the mean CD4 count measured at one point in time.

• The working linear or logistic model for the expectation vector of measurements of a time-varying outcome node, possibly conditional on baseline node(s) V, i.e., E(Y_d(t) | V):

  $$m(t,d,V\mid \alpha ),\text{for}t=0,1,\dots .$$

  Such a working model can, for example, be used to evaluate the effects of HIV treatment regimens on survival probabilities over time.

• The logistic working model for discrete-time hazards, i.e., for the probabilities that a measurement of a time-varying outcome node of type EFU=TRUE is equal to 1 under intervention d, given that the previous measurement of the time-varying outcome node under intervention d is equal to 0, possibly conditional on baseline node(s) V, i.e., E(Y_d(t) | Y_d(t − 1) = 0, V):

  $$m(t,d,V),\text{for}t=0,1,\dots .$$

  Such a working model can, for example, be used to evaluate the effects of HIV treatment regimens on discrete-time hazards of death over time.

Examples of the specification of the above target parameters are provided in Sections 3.5.2 and 4.6.2. As shown above, the working MSM formula m() can be a function of t, V and d, where d is a unique identifier of each intervention regimen. In Sections 3.5.2 and 4.6.2 we describe in detail how to specify such identifiers for d as part of the action function call. Also note that the working MSM formula, m, may reference time-varying nodes using the square-bracket syntax introduced in Section 2.3, as long as all such instances are embedded within the syntax S(…). Example use of this syntax is provided in Section 4.6.2 (Example 2 of set.targetMSM).

2.6. Simulating data and evaluating the target causal parameter

The simcausal package can simulate two types of data: 1) observed data, sampled from the (pre-intervention) distribution specified by the structural equation model and 2) counterfactual data, sampled from one or more post-intervention distributions defined by actions on the structural equation model. Both types of data are simulated by invoking the sim function and the user can set the seed for the random number generator using the argument rndseed. The examples showing how to simulate observed data are provided in Sections 3.2 and 4.2, whereas the examples showing how to simulate counterfactual data are provided in Sections 3.4 and 4.4.

We note that two types of structural equation models can be encoded with the DAG object: 1) models where some or all nodes are defined by specifying the “time” argument t to the node function, or 2) models where the argument t is not used for any of the nodes. For the first type of structural equation models, the simulated data can be structured in either long or wide formats. A dataset is considered to be in wide format when each simulated observation of the complete sequence of nodes is represented by only one row of data, with each time-varying node represented by columns spanning distinct values of t. In contrast, for a dataset in long format, each simulated observation is typically represented by multiple rows of data indexed by distinct values of t and each time-varying node represented by a single column. The format of the output data is controlled by setting the argument wide of the sim function to TRUE or FALSE. The default setting for sim is to simulate data in wide format, i.e., wide = TRUE. An example describing these two formats is provided in Section 4.5.

In addition, as previously described, for nodes representing the occurrence of end of follow-up events (i.e., censoring or outcome nodes declared with EFU = TRUE), the value of 1 indicates that, during data simulation, by default, all values of subsequent nodes (including the outcome nodes) are set to missing ( NA). To instead impute these missing values after a particular end of follow-up event occurs (typically the outcome event) with the last time point value carried forward (LTCF) method, the user must set the argument LTCF of the sim function to the name of the EFU-type node that represents the end of follow-up event of interest. This will result in carrying forward the last observed measurement value for all time-varying nodes, after the value of the EFU node whose name is specified by the LTCF argument is observed to be 1. For additional details see the package documentation for the function sim.

In the last step of a typical workflow, the function eval.target is generally invoked for estimation of the true value of a previously defined target causal parameter. The true value is estimated using counterfactual data simulated from post-intervention distributions. The function eval.target can be called with either previously simulated counterfactual data, specified by the argument data or a sample size value, specified by the argument n. In the latter case, counterfactual data with the user-specified sample size will be simulated first.

3. Simulation study with single time point interventions

The following examples describe a typical workflow for specifying a structural equation model, defining various interventions, simulating observed and counterfactual data, and calculating various causal target parameters. The structural equation model chosen here illustrates a common point treatment problem in which one is interested in evaluating the effect of an intervention on one treatment node on a single outcome node using observational data with confounding by baseline covariates. In addition, these examples demonstrate the plotting functionality of the simcausal package that builds upon the igraph R package (Csardi and Nepusz 2006) to visualize the Directed Acyclic Graph (DAG) (Pearl 1995, 2009, 2010a) implied by the structural equation model encoded in the DAG object.

We also undertake an approach similar to the one described in (Elwert 2013) and use the following examples to highlight some of the differences between the non-parametric structural equation models (Pearl 2009) and the traditional linear structural equation models based on the LISREL framework (Bollen 1989). Many traditional applications of structural equation modeling are devoted to addressing the problem of the measurement in the exposure, and more precisely, to address problems in which the true exposure of interest is a latent variable, such as talent, motivation or political climate that cannot be observed directly, but that is instead measured via some noisy and correlated proxies. Hence, the LISREL framework is frequently applied to formally assess the causal effects of such latent variables. However, the primary intended goal of simcausal is not to simulate such measurement error data, even though one could adapt simcausal for that purpose. Instead, our package specifically focuses on data simulation for the purpose of evaluating estimation methods for assessing the effect of exposures that can be observed directly. Additionally, one may also use simcausal to simulate data problems with latent variables that might impact the observed exposures of interest.

3.1. Specifying parametric structural equation models in simcausal

Suppose that we want to simulate data that could be generated in a hypothetical study evaluating the effect of receiving school vouchers on mean test scores based on a sample of students. We start by assuming that a latent covariate I represents the level of subject’s true and unobserved intelligence, where I is categorical and its distribution is defined by the node named “I” in the code example below. We also assume that I directly influences the values of the three observed baseline covariates W = (W₁, W₂, W₃) (nodes “W1”, “W2” and “W3” below) and we define the distribution of each W conditional on I. That is, the observed baseline covariates in W will be correlated, since all three depend on a common and latent parent I. We now let A (node “A” below) define the observed binary exposure (receiving school vouchers), where the probability of success for A is defined as the following logit-linear function² of W:

$$\mathit{logit}(P(A=1\mid W))={\alpha }_0+{\gamma }_{A}W,$$

for W = (W₁, W₂, W₃)^t, α₀ = 4.2 and γ_A = (−0.5, 0.1, 0.2).

That is, the above model assumes that A is directly influenced by the observed variable W, while the latent I has no direct influence on A. We also emphasize that we want to study the effect of intervening on the observed variable(s), such as A, whereas in the traditional measurement error model the focus might have been on modeling the effect of the latent varible I on some observed outcome(s). The following example code defines the distributions of (I, W, A). Specifically, we use the pre-defined R functions rcat.b1, rnorm, runif and rbern to define the latent categorical node I, normal node W1, uniform node W2 and Bernoulli nodes W3 and A, respectively³. We also note that implicit in the specification of these nodes is the specification of independent exogenous errors (disturbances), whose distributions are defined by the distr arguments as shown below.

R> library(“simcausal”)
R> D <- DAG.empty()
R> D <- D +
+   node(“I”, distr = “rcat.b1”,
+     probs = c(0.1, 0.2, 0.2, 0.2, 0.1, 0.1, 0.1)) +
+   node(“W1”, distr = “rnorm”,
+     mean = ifelse(I == 1, 0, ifelse(I == 2, 3, 10)) + 0.6 * I, sd = 1) +
+   node(“W2”, distr = “runif”,
+     min = 0.025*I, max = 0.7*I) +
+   node(“W3”, distr = “rbern”,
+     prob = plogis(-0.5 + 0.7*W1 + 0.3*W2 - 0.2*I)) +
+   node(“A”, distr = “rbern”,
+     prob = plogis(+4.2 - 0.5*W1 + 0.1*W2 + 0.2*W3))

Similarly, we assume that the outcome Y is influenced by an independent latent error U_Y ~ N(0, 1), and we use the following code example to show how one might explicitly define U_Y using a node named “U.Y”⁴:

R> D <- D + node(“U.Y”, distr = “rnorm”, mean = 0, sd = 1)

The following example defines the outcome Y (node named “Y”) by using the following linear structural equation:

$$Y={\beta }_0+{\beta }_{1}A+{\beta }_{2}I+{\gamma }_{Y}W+U_Y,$$

where β₀ = −0.5, β₁ = 1.2, β₂ = 0.2 and γ_Y = (0.1, 0.3, 0.2).

Note that in this example, we are assuming that the effect of exposure A on Y is the same for every strata of W and I (i.e., homogeneous treatment effect). We also note that the distribution of the node Y is defined below as degenerate ( distr = “rconst”), since we explicitly define its error term with the above node U.Y. That is, the following example uses a predefined R function rconst, which puts mass one on the value of the node function argument const:

R> D <- D + node(“Y”, distr = “rconst”,
+      const = -0.5 + 1.2*A + 0.2*I + 0.1*W1 + 0.3*W2 + 0.2*W3 + U.Y)

Note that the names of all user-defined endogenous latent nodes must be specified within the set.DAG function via the argument latent.v, as shown in this example:

R> Dset1 <- set.DAG(D, latent.v = c(“I”, “U.Y”))

Running the code above results in implicitly assigning a sampling order (temporal order) to each node - based on the order in which the nodes were added to the DAG object D. Alternatively, one can use the optional node()argument order to explicitly specify the integer value of the sampling order of each node, as described in more detail in the documentation for the node function. The resulting internal representation of the structural equation model encoded by the DAG object Dset1 can be examined as follows:

R> str(Dset1)

In the example above, we are interested in the causal target parameter defined as the average treatment effect (ATE) of school vouchers on mean test scores, which is generally defined in the NPSEM framework as E(Y₁ − Y₀). Analytically, one can show that in the simple SEM defined above, the ATE is equal to the coefficient β₁ (Pearl 2012).

Our example so far illustrates a scenario typical of the linear SEM literature in which the effect of interest corresponds with a coefficient from one of the structural equations. We now illustrate other more complex scenarios in which the effect of interest (ATE) is not equal to one particular structural equation coefficient. In the following example, we modify the above SEM for Y and allow for the effect of treatment on Y to vary by strata of W₃:

$$Y={\beta }_0+{\beta }_{1}A+{\beta }_1^{\ast }(A{W}_3)+{\beta }_{2}I+{\gamma }_{Y}W+U_Y,$$

where β₀ = −0.5, β₁ = 1.2, ${\beta }_1^{\ast }=-0.5$, β₂ = 0.2 and γ_Y = (0.2, 0.2, 0.2). Note that in this example we moved away from the classical linear structural model for Y, specifically, we allowed for the causal effect of A on Y to vary by subject depending on their value of W₃. Finally, we note that whenever the node named “Y” is added again to the same DAG object D, simcausal automatically overwrites the previously defined distribution of Y with the one given by the new node function call, as demonstrated below.

R> D <- D + node(“Y”, distr = “rconst”, +      const = -0.5 + 1.2*A - 0.5*(A * W3) + 0.2*I + 0.2*(W1 + W2 + W3) + U.Y) R> Dset2 <- set.DAG(D, latent.v = c(“I”, “U.Y”))

Note that for the above data generating distribution specified by the object Dset2, the ATE (E(Y₁ − Y₀)) is no longer equal to β₁, but is rather equal to ${\beta }_1+{\beta }_1^{\ast }E(W_3)$ (proof not shown, but easily derived by following the same logic as in the previous example).

For our final example shown below, we re-define Y as a nonlinear function of the same parent nodes used in the previous two examples:

$$Y={\beta }_{1}A+{\beta }_2(W_1^2+W_2^3/10+W_3)+{\beta }_3\mid U_Y\mid +{\beta }_1{I}^2+{\beta }_5\mid \frac{1}{sin(U_Y{W}_2+A)}\mid h_Y(U_Y,W)+{\beta }_6(1-h_Y(U_Y,W)),$$

where h_Y(U_Y, W) = I(|1/sin(U_YW₂)| ≤ 10), β₁ = 1.2, β₂ = 0.05, β₃ = 0.7, β₄ = 0.002, β₅ = 0.02 and β₆ = 5. Note that in this model for the outcome Y, the analytic derivation of the ATE becomes intractable. However, one can use simcausal to find a Monte-Carlo approximation of the ATE from simulated counterfactual data, as shown in Section 3.5.

R> D <- D + node(“Y”, distr = “rconst”,
+      const =
+       +1.2*A + 0.05*(W1ˆ2 + W2ˆ3 / 10 + W3) + 0.7*abs(U.Y) + 0.002*Iˆ2 +
+       +0.02*abs(1 / sin(U.Y * W2 + A)) * (abs(1/sin(U.Y * W2)) <= 10) +
+       +5*(abs(1/sin(U.Y * W2)) > 10))
R> Dset3 <- set.DAG(D, latent.v = c(“I”, “U.Y”))

We note that all three of the above structural equations for Y depend on exactly the same variables, namely, (A, W, I). Therefore, the three parameterizations of the SEM specified by the above objects Dset1, Dset2 and Dset3 are all represented by the same NPSEM and the same DAG in Figure 3. The DAG in Figure 3 was automatically generated by calling the function plotDAG. The plotting is accomplished by using the visualization functionality from the igraph package (Csardi and Nepusz 2006). The directional arrows (solid and dashed) represent the functional dependencies in the structural equation model. Specifically, the node of origin of each arrow is an extracted node name from the node formula(s). The user-specified latent nodes are surrounded by circles, and each functional dependency that originates at a latent node is displayed via a dashed directional arrow⁵.

Figure 3.

Graphical representation of the structural equation model using a DAG, where the latent nodes I and U.Y are enclosed in circles.

The above alternative examples for specifying the outcome variable Y also demonstrate how simcausal can be applied for defining a variety of functional and distributional relationships between the model variables, including those that can be specified by the traditional linear structural equation models. We have also demonstrated that our package can be used for defining the SEM with endogenous latent variables. The above examples also highlight the merit of defining the target causal parameters in a way that remains meaningful for any parametric specification of the SEM. As we demonstrate in Section 3.3 below, our package provides exactly this type of functionality, allowing the user to define and evaluate various causal target parameters as functions of the counterfactual data distribution.

3.2. Simulating observed data ( sim)

Simulating observed data is accomplished by calling the function sim and specifying its arguments DAG and n that indicate the causal model and sample size of interest. Below is an example of how to simulate an observed dataset with 10,000 observations using the causal model defined in the previous section. The output is a data.frame object.

R> Odat <- sim(DAG = Dset3, n = 10000, rndseed = 123)

The format of the output dataset is easily understood by examining the first row of the data.frame returned by the sim function. Note that the latent variables ‘ I’ and ‘ U.Y’ are absent from the simulated data, as shown below.

R> Odat[1,]

   ID      W1       W2 W3 A       Y
1   1 3.705826 0.1686546   1 1 7.080206

3.3. Specifying interventions ( + action)

The example below defines two actions on the treatment node. The first action named “A1” consists in replacing the distribution of the treatment node A with the degenerate distribution at value 1. The second action named “A0” consists in replacing the distribution of the treatment node A with the degenerate distribution at value 0. As shown below, these interventions are defined by invoking the + action syntax on the existing DAG object. This syntax automatically adds and saves the new intervention object within the original DAG object, without overwriting it.

R> A1 <- node(“A”, distr = “rbern”, prob = 1)
R> Dset3 <- Dset3 + action(“A1”, nodes = A1)
R> A0 <- node(“A”, distr = “rbern”, prob = 0)
R> Dset3 <- Dset3 + action(“A0”, nodes = A0)

The added actions can be examined by looking at the result of the call A(Dset) . Note that A(Dset) returns a list of DAG.action objects, with each DAG.action encoding a particular post-intervention distribution, i.e., it is a modified copy of the original DAG object, where the original distribution of the node A is replaced with the degenerate distribution at value 0 or 1, for actions “A0” and “A1”, respectively.

R> names(A(Dset3))
R> class(A(Dset3)[[“A0”]])

3.4. Simulating counterfactual data ( sim)

Simulating counterfactual data is accomplished by calling the function sim and specifying its arguments DAG, actions and n to indicate the causal model, interventions, and sample size of interest. Counterfactual data can be simulated for all actions stored in the DAG object or a subset by setting the actions argument to the vector of the desired action names.

The example below shows how to use the sim function to simulate 100,000 observations for each of the two actions, “A1” and “A0”. These actions were defined as part of the DAG object Dset above. The call to sim below produces a list of two named data.frame objects, where each data.frame object contains observations simulated from the same post-intervention distribution defined by one particular action only.

R> Xdat1 <- sim(DAG = Dset3, actions = c(“A1”, “A0”), n = 100000, rndseed = 123)
R> names(Xdat1)
R> nrow(Xdat1[[“A1”]])
R> nrow(Xdat1[[“A0”]])

The format of the output list is easily understood by examining the first row of each data.frame object:

R> Xdat1[[“A1”]][1, ]
R> Xdat1[[“A0”]][1, ]

3.5. Defining and evaluating various causal target parameters

Causal parameters defined with set.targetE

The first example below defines the causal quantity of interest as the expectation of node Y under action “A1”, i.e., E(Y₁):

R> Dset3 <- set.targetE(Dset3, outcome = “Y”, param = “A1”)

The true value of the above causal parameter is now evaluated by calling the function eval.target and passing the previously simulated counterfactual data object Xdat1.

R> eval.target(Dset3, data = Xdat1)$res

Alternatively, eval.target can be called without the simulated counterfactual data, specifying the sample size argument n instead. In this case a counterfactual dataset with the user-specified sample size is simulated first.

R> eval.target(Dset3, n = 100000, rndseed = 123)$res

The example below defines the causal target parameter as the ATE on the additive scale, i.e., the expectation of Y under action “A1” minus its expectation under action “A0”, given by E(Y₁ − Y₀):

R> Dset3 <- set.targetE(Dset3, outcome = “Y”, param = “A1-A0”)
R> eval.target(Dset3, data = Xdat1)$res

  Diff_Y
1.281203

Similarly, the ATE on the multiplicative scale given by E(Y₁)/E(Y₀) can be evaluated as follows:

R> Dset3 <- set.targetE(Dset3, outcome = “Y”, param = “A1/A0”)
R> eval.target(Dset3, data = Xdat1)$res

Causal parameters defined with set.targetMSM

To specify MSM target causal parameter, the user must provide the following arguments to set.targetMSM: (1) the DAG object that contains all and only the actions of interest; (2) outcome, the name of the outcome node (possibly time-varying); (3) for a time-varying outcome node, the vector of time points t that index the outcome measurements of interest; (4) form, the regression formula defining the working MSM; (5) family, the working model family that is passed on to glm, e.g., family = “binomial” or family = “gaussian” for a logistic or a linear working model; and (6) for time-to-event outcomes, the logical flag hazard that indicates whether the working MSM describes discrete-time hazards ( hazard = TRUE) or survival probabilities ( hazard = FALSE).

In the examples above, the two actions “A1” and “A0” are defined as deterministic static interventions on the node A, setting it to either constant 0 or 1. Thus, each of these two interventions is uniquely indexed by the post-intervention value of the node A itself. In the following example, we instead introduce the variable d ∈ {0, 1} to explicitly index each of the two post-intervention distributions when defining the two actions of interest. We then define the target causal parameter as the coefficients of the following linear marginal structural model m(d | α) = α₀ +α₁d. As expected, the estimated true value for α₁ obtained below corresponds exactly with the estimated value for the ATE on the additive scale obtained above by running set.targetE with the parameter param = “A1-A0”.

As just described, we now redefine the actions “A1” and “A0” by indexing the intervention node formula (the distributional parameter prob) with parameter d before setting its values to 0 or 1 by introducing an additional new argument named d into the action function call. This creates an action-specific attribute variable d whose value uniquely identifies each of the two actions and that will be included as an additional column variable to the simulating counterfactual data sets.

R> newA <- node(“A”, distr = “rbern”, prob = d)
R> Dset3 <- Dset3 + action(“A1”, nodes = newA, d = 1)
R> Dset3 <- Dset3 + action(“A0”, nodes = newA, d = 0)

Creating such an action-specific attribute d allows it to be referenced in the MSM regression formula as shown below:

R> msm.form <- “Y ∼ d”
R> Dset3 <- set.targetMSM(Dset3, outcome = “Y”, form = msm.form,
+                     family = “gaussian”)
R> msm.res <- eval.target(Dset3, n = 100000, rndseed = 123)
R> msm.res$coef

(Intercept)          d
 7.385276   1.281203

3.6. Defining node distributions

To facilitate the comprehension of this subsection, we note that, in the simcausal package, simulation of observed or counterfactual data follows the temporal ordering of the nodes that define the DAG object and is vectorized. More specifically, the simulation of a dataset with sample size n is carried out by first sampling the vector of all n observations of the first node, before sampling the vector of all n observations of the second node and so on, where the node ranking is defined by the temporal ordering that was explicitly or implicitly specified by the user during the creation of the DAG object (see Section 2.3 for a discussion of temporal ordering).

The distribution of a particular node is specified by passing the name of an evaluable R function to the distr argument of the function node. Such a distribution function must implement the mapping of n independent realizations of the parent nodes into n independent realizations of this node. In general, any node with a lower temporal ordering can be defined as a parent. Thus, such a distribution function requires an argument n, but will also typically rely on additional input arguments referred to as distributional parameters. In addition, the output of the distribution function must also be a vector of length n. Distributional parameters must be either scalars or vectors of n realizations of summary measures of the parent nodes. The latter types of distributional arguments are referred to as the node formula(s) because they are specified by evaluable R expressions. Distributional parameters are passed as named arguments to the node function so they can be mapped uniquely to the relevant argument of the function that is user-specified by the distr argument of the node function call. The node formula(s) of any given node may invoke the name(s) of any other node(s) with a lower temporal order value. The parents of a particular node are thus defined as the collection of nodes that are referenced by its node formula(s). Note that unlike the values of distributional parameters, the value of the argument n of the distr function is internally determined during data simulation and is set to the sample size value passed to the sim function by the user.

For example, as shown below, the pre-written wrapper function for the Bernoulli distribution rbern is defined with two arguments, n and prob. When defining a node with the distr argument set to “rbern”, only the second argument must be explicitly user-specified by a distributional parameter named prob in the call to the node function, e.g., node(“N1”, distr=“rbern”, prob = 0.5). The argument prob can be either a numeric constant as in the previous example or an evaluable R expression. When prob is a numeric constant, the distribution function rbern returns n iid realizations of the Bernoulli random variable with probability prob. When prob is an R expression (e.g., see the definition of node W3 in Section 3.1) that involves parent nodes, the prob argument passed to the rbern function becomes a vector of length n. The value of each of its component is determined by the R expression evaluated using one of the n iid realizations of the parent nodes simulated previously. Thus, the resulting simulated independent observations of the child node (e.g., W3 in Section 3.1) are not necessarily identically distributed if the vector prob contains distinct values. We note that the R expression in the prob argument is evaluated in the environment containing the simulated observations of all previous nodes (i.e., nodes with a lower temporal order value).

To see the names of all pre-written distribution wrapper functions that are specifically optimized for use as distr functions in the simcausal package, invoke distr.list(), as shown below:

R> distr.list()

[1]  “rbern”      “rcat.b0”       “rcat.b1”       “rcat.factor”
[5]  “rcategor”    “rcategor.int”   “rconst”       “rdistr.template”

For a template on how to write a custom distribution function, see the documentation ?rdistr.template and rdistr.template, as well as any of the pre-written distribution functions above. For example, the rbern function below simply wraps around the standard R function rbinom to define the Bernoulli random variable generator:

R> rbern

function (n, prob)
{
    rbinom(n = n, prob = prob, size = 1)
}
<environment: namespace:simcausal>

Another example on how to write a custom distribution function to define a custom left-truncated normal distribution function based on the standard R function rnorm with arguments mean and sd is demonstrated below. The truncation level is specified by an additional distributional parameter minval, with default value set to 0.

R> rnorm_trunc <- function(n, mean, sd, minval = 0) {
+   out <- rnorm(n = n, mean = mean, sd = sd)
+   minval <- minval[1]
+   out[out < minval] <- minval
+   out
+ }

The example below makes use of this function to define the outcome node Y with positive values only:

R> Dmin0 <- DAG.empty()
R> Dmin0 <- Dmin0 +
+    node(“W”, distr = “rbern”,
+      prob = plogis(-0.5)) +
+    node(“A”, distr = “rbern”,
+      prob = plogis(-0.5 - 0.3 * W)) +
+    node(“Y”, distr = “rnorm_trunc”,
+      mean = -0.1 + 1.2 * A + 0.3 * W,
+      sd = 10)
R> Dmin0set <- set.DAG(Dmin0)

In the next example, we overwrite the previous definition of node Y to demonstrate how alternative values for the truncation parameter minval may be passed by the user as part of the node function call:

R> Dmin0 <- Dmin0 +
+    node(“Y”, distr = “rnorm_trunc”,
+      mean = -0.1 + 1.2 * A + 0.3 * W,
+      sd = 10,
+      minval = 10)
R> Dmin10set <- set.DAG(Dmin0)

Finally, we illustrate how the minval argument can also be defined as a function of parent node realizations:

R> Dmin0 <- Dmin0 +
+    node(“Y”, distr = “rnorm_trunc”,
+      mean = -0.1 + 1.2 * A + 0.3 * W,
+      sd = 10,
+      minval = ifelse(A == 0, 5, 10))
R> Dminset <- set.DAG(Dmin0)

As just described, the distributional parameters defining a particular node distribution can be evaluable R expressions, referred to as node formulas. These expressions can contain any built-in or user-defined R functions. By default, any user-defined function inside such an R expression is assumed non-vectorized, except for functions on the simcausal built-in list of known vectorized functions (this list can be printed by calling vecfun.all.print()). We note that the simulation time can often be significantly improved by using vectorized user-defined node formula functions. For example, to register a new user-defined vectorized function “funname”, which is not part of the built-in vectorized function list, the user may call vecfun.add(“funname”). We refer to the package vignette (Sofrygin et al. 2015) for additional details and examples on how to write custom vectorized node formula functions. We also refer to the same vignette for a simulation demonstrating the performance gains as a result of vectorization.

4. Simulation study with multiple time point interventions

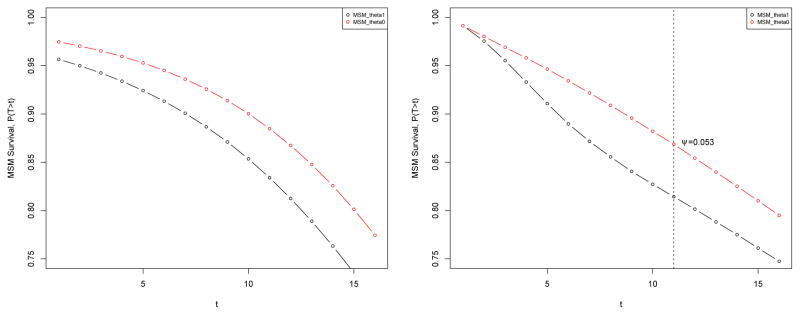
In this example we replicate results from the longitudinal data simulation protocol used in two published manuscripts Neugebauer et al. (2014, 2015). We first describe the structural equation model that implies the data generating distribution of the observed data, with time-to-event outcome, as reported in Section 5.1 of Neugebauer et al. (2015). We then show how to specify this model using the simcausal R interface, simulate observed data, define static and dynamic intervention, simulate counterfactual data, and calculate various causal parameters based on these interventions. In particular, we replicate estimates of true counterfactual risk differences under the dynamic interventions reported in Neugebauer et al. (2014), as shown in Section 4.6 (Example 1 for set.targetE and Example 1 for set.targetMSM).

4.1. Specifying the structural equation model

In this section, we demonstrate how to specify the structural equation model described by the following longitudinal data simulation protocol (Section 5.1 of Neugebauer et al. (2015)):

1. L₂(0) ~ ℬ(0.05) where ℬ denotes the Bernoulli distribution (e.g., L₂(0) represents a baseline value of a time-dependent variable such as low versus high A1c)

2. If L₂(0) = 1 then L₁(0) ~ ℬ(0.5), else L₁(0) ~ ℬ(0.1) (e.g., L₁(0) represents a time-independent variable such as history of cardiovascular disease at baseline)

3. If (L₁(0), L₂(0)) = (1, 0) then A₁(0) ~ ℬ(0.5), else if (L₁(0), L₂(0)) = (0, 0) then A₁(0) ~ ℬ(0.1), else if (L₁(0), L₂(0)) = (1, 1) then A₁(0) ~ ℬ(0.9), else if (L₁(0), L₂(0)) = (0, 1) then A₁(0) ~ ℬ(0.5) (e.g., A₁(0) represents the binary exposure to an intensified type 2 diabetes pharmacotherapy)

4. for t = 1, …, 16 and as long as Y (t − 1) = 0 (by convention, Y (0) = 0):

   1. $Y(t)~\mathcal{B}(\frac{1}{1+exp(-(-6.5+L_1(0)+4L_2(t-1)+0.05\ast {\sum }_{j=0}^{t-1}I(L_2(j)=0)))})$ (e.g., Y(t) represents the indicator of failure such as onset or progression of albuminuria)

   2. If A₁(t − 1) = 1 then L₂(t) ~ ℬ(0.1), else if L₂(t − 1) = 1 then L₂(t) ~ ℬ(0.9), else L₂(t) ~ ℬ(min(1, 0.1 + t/16))

   3. If A₁(t − 1) = 1 then A₁(t) = 1, else if (L₁(0), L₂(t)) = (1, 0) then A₁(t) ~ ℬ(0.3), else if (L₁(0), L₂(t)) = (0, 0) then A₁(t) ~ ℬ(0.1), else if (L₁(0), L₂(t)) = (1, 1) then A₁(t) ~ ℬ(0.7), else if (L₁(0), L₂(t)) = (0, 1) then A₁(t) ~ ℬ(0.5).

First, the example below shows how to define the nodes L2, L1 and A1 at time point t = 0 as Bernoulli random variables, using the distribution function “rbern”:

R> library(“simcausal”)
R> D <- DAG.empty()
R> D <- D +
+   node(“L2”, t = 0, distr = “rbern”,
+     prob = 0.05) +
+   node(“L1”, t = 0, distr = “rbern”,
+     prob = ifelse(L2[0] == 1, 0.5, 0.1)) +
+   node(“A1”, t = 0, distr = “rbern”,
+     prob =
+      ifelse(L1[0] == 1 & L2[0] == 0, 0.5,
+      ifelse(L1[0] == 0 & L2[0] == 0, 0.1,
+      ifelse(L1[0] == 1 & L2[0] == 1, 0.9, 0.5))))

Second, the example below shows how one may use the node function with node formulas based on the square bracket function ’[’ to easily define the time-varying nodes Y, L1 and A1 simultaneously for all subsequent time points t ranging from 1 to 16:

R> t.end <- 16
R> D <- D +
+   node(“Y”, t = 1:t.end, distr = “rbern”,
+     prob =
+      plogis(-6.5 + L1[0] + 4 * L2[t-1] +
+        0.05 * sum(I(L2[0:(t-1)] == rep(0, t)))),
+     EFU = TRUE) +
+   node(“L2”, t = 1:t.end, distr = “rbern”,
+     prob =
+      ifelse(A1[t-1] == 1, 0.1,
+      ifelse(L2[t-1] == 1, 0.9, min(1, 0.1 + t / 16)))) +
+   node(“A1”, t = 1:t.end, distr = “rbern”,
+     prob =
+      ifelse(A1[t-1] == 1, 1,
+      ifelse(L1[0] == 1 & L2[t] == 0, 0.3,
+      ifelse(L1[0] == 0 & L2[t] == 0, 0.1,
+      ifelse(L1[0] == 1 & L2[t] == 1, 0.7, 0.5)))))
R> lDAG <- set.DAG(D)

Note that the node formulas specified with the prob argument above use the generic time variable t both outside and inside the square-bracket vector syntax. For example, the conditional distribution of the time-varying node Y is defined by an R expression that contains the syntax sum(I(L2[0:(t - 1)] == rep(0, t))) , which evaluates to different R expressions, as t ranges from 0 to 16:

1. sum(I(L2[0] == 0)) , for t = 1; and

2. sum(I(L2[0:1] == c(0, 0))) , for t = 2, …, sum(I(L2[0:16] == c(0, …, 0))) , for t = 16.

For more details on the specification of node formulas, see Section 3.6.

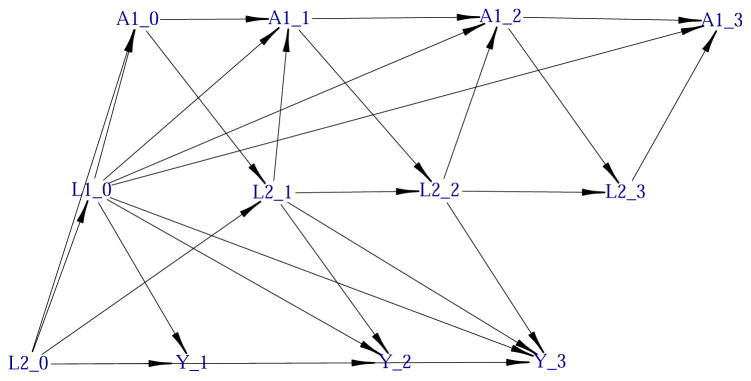
One can visualize the observed data generating distribution defined in the lDAG object as shown in Figures 4 by calling plotDAG. Note that the appearance of the resulting diagram can be customized with additional arguments, as demonstrated in the package vignette (Sofrygin et al. 2015).

Figure 4.

Graphical representation of a portion of the structural equation model using a DAG. Only the nodes indexed by time points lower than or equal to 3 are represented.

4.2. Simulating observed data ( sim)

Simulating observed data is accomplished by calling the function sim and specifying its arguments DAG and n that indicate the causal model and sample size of interest. Below is an example of how to simulate an observed dataset with 10, 000 observations using the causal model defined previously. The output is a data.frame object.

R> Odat <- sim(DAG = lDAG, n = 10000, rndseed = 123)
R> Odat[1,]

4.3. Specifying interventions ( + action)

Dynamic interventions

The following two dynamic interventions on the time-varying node A1 of the structural equation model encoded by the previously defined lDAG object were studied in Neugebauer et al. (2014): ‘Initiate treatment A₁ the first time t that the covariate L₂ is greater than or equal to θ and continue treatment thereafter (i.e., Ā₁(t − 1) = 0 and A(t) = 1, A(t + 1) = 1, …)’, for θ = 0, 1. The example below demonstrates how to specify these two dynamic interventions.

First, we define the list of intervention nodes and their post-intervention distributions. Note that these distributions are indexed by the attribute theta, whose value is not yet defined:

R> act_theta <-c(
+   node(“A1”, t = 0, distr = “rbern”,
+     prob = ifelse(L2[0] >= theta, 1, 0)),
+   node(“A1”, t = 1:(t.end), distr = “rbern”,
+     prob = ifelse(A1[t-1] == 1, 1, ifelse(L2[t] >= theta, 1, 0))))

Second, we add the two dynamic interventions to the lDAG object while defining the value of theta for each intervention:

R> Ddyn <- lDAG
R> Ddyn <- Ddyn + action(“A1_th0”, nodes = act_theta, theta = 0)
R> Ddyn <- Ddyn + action(“A1_th1”, nodes = act_theta, theta = 1)

We refer to the argument theta passed to the +action function as an action attribute.

One can select and inspect particular actions saved in a DAG object by invoking the function A():

R> class(A(Ddyn)[[“A1_th0”]])
R> A(Ddyn)[[“A1_th0”]]

The distribution of some or all of the the intervention nodes that define an action saved within a DAG object can be modified by adding a new intervention object with the same action name to the DAG object. The new intervention object can involve actions on only a subset of the original intervention nodes for a partial modification of the original action definition. For example, the code below demonstrates how the existing action “A1_th0” with the previously defined dynamic and deterministic intervention on the node A1[0] is partially modified by replacing the intervention distribution for the node A1[0] with a deterministic and static intervention defined by a degenerate distribution at value 1. Note that the other intervention nodes previously defined as part of the action “A1_th0” remain unchanged.

R> A(Ddyn)[[“A1_th0”]]$A1_0
R> Ddyntry <- Ddyn +
+    action(“A1_th0”, nodes = node(“A1”, t = 0, distr = “rbern”, prob = 0))
R> A(Ddyntry)[[“A1_th0”]]$A1_0

Similarly, some or all of the action attributes that define an action saved within a DAG object can be modified by adding a new intervention object with the same action name but a different attribute value to the DAG object. This functionality is demonstrated with the example below in which the previous value 0 of the action attribute theta that defines the action named “A1_th0” is replaced with the value 1 and in which a new attribute newparam is simultaneously added to the previously defined action “A1_th0”:

R> A(Ddyntry)[[“A1_th0”]]
R> Ddyntry <- Ddyntry +
+    action(“A1_th0”, nodes = act_theta, theta = 1, newparam = 100)
R> A(Ddyntry)[[“A1_th0”]]

Static interventions

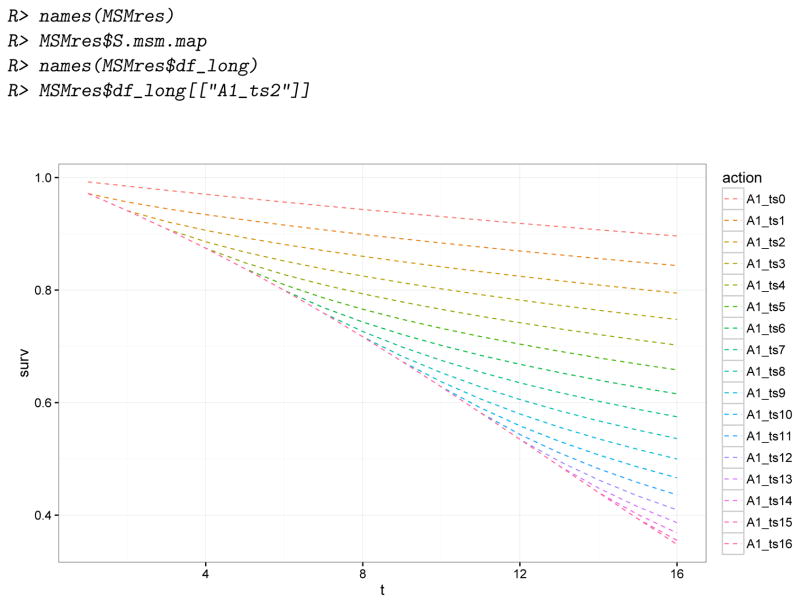
Here we diverge from the replication of simulation results presented in Neugebauer et al. (2014). Instead, we build on the structural equation model introduced in that paper to illustrate the specification of static interventions on the treatment nodes A1. These static interventions are defined by more or less early treatment initiation during follow-up followed by subsequent treatment continuation. Each of these static interventions is thus uniquely identified by the time when the measurements of the time-varying node A1 switch from value 0 to 1. The time of this value switch is represented by the parameter tswitch in the code below. Note that the value tswitch = 16 identifies the static intervention corresponding with no treatment initiation during follow-up in our example while the values 0 through 15 represent 16 distinct interventions representing increasingly delayed treatment initiation during follow-up.

First, we define the list of intervention nodes and their post-intervention distributions. Note that these distributions are indexed by the attribute tswitch, whose value is not yet defined:

R> ‘%+%’ <- function(a, b) paste0(a, b)
R> Dstat <- lDAG
R> act_A1_tswitch <- node(“A1”,t = 0:(t.end), distr = “rbern”,
+                     prob = ifelse(t >= tswitch, 1, 0))

Second, we add the 17 static interventions to the lDAG object while defining the value of tswitch for each intervention:

R> tswitch_vec <- (0:t.end)
R> for (tswitch_i in tswitch_vec) {
+   abar <- rep(0, length(tswitch_vec))
+   abar[which(tswitch_vec >= tswitch_i)] <- 1
+   Dstat <- Dstat + action(“A1_ts”%+%tswitch_i,
+                      nodes = act_A1_tswitch,
+                      tswitch = tswitch_i,
+                      abar = abar)
+  }

Note that in addition to the action attribute tswitch, each intervention is also indexed by an additional action attribute abar that also uniquely identifies the intervention and that represents the actual sequence of treatment decisions that defines the intervention, i.e., ā(tswitch − 1) = 0, a(tswitch) = 1, …:

R> A(Dstat)[[“A1_ts3”]]

The purpose of this additional action attribute abar will become clear when we illustrate the definition of target parameters defined by working MSMs based on these 17 static interventions in Section 4.6.2 (Example 2 of set.targetMSM).

4.4. Simulating counterfactual data ( sim)

Simulating counterfactual data is accomplished by calling the function sim and specifying its arguments DAG, actions and n to indicate the causal model, interventions, and sample size of interest. The counterfactual data can be simulated for all actions stored in the DAG object or a subset by setting the actions argument to the vector of the desired-action names.

The example below shows how to use the sim function to simulate 200,000 observations for each of the two dynamic actions, “A1_th0” and “A1_th1”, defined in Section 4.3.1. The call to sim below produces a list of two named data.frame objects, where each data.frame object contains observations simulated from the same post-intervention distribution defined by one particular action only.

R> Xdyn <- sim(Ddyn, actions = c(“A1_th0”, “A1_th1”),
+           n = 200000, rndseed = 123)

The default format of the output list generated by the sim function is easily understood by examining the first row of each data.frame object:

R> Xdyn[[“A1_th0”]][1, ]
R> Xdyn[[“A1_th1”]][1, ]

4.5. Converting a dataset from wide to long format ( DF.to.long)

The specification of structural equation models based on time-varying nodes such as the one described in Section 4.1 allows for simulated (observed or counterfactual) data to be structured in either long or wide formats. Below, we illustrate these two alternatives. We note that, by default, simulated (observed or counterfactual) data from the sim function are stored in wide format. The data output format from the sim function can, however, be changed to the long format by setting the wide argument of the sim function to FALSE or, equivalently, by applying the function DF.to.long to an existing simulated dataset in wide format.

The following code demonstrates the default data formatting behavior of the sim function and how this behavior can be modified to generate data in the long format:

R> Odat.wide <- sim(DAG = lDAG, n = 1000, wide = TRUE, rndseed = 123)
R> Odat.wide[1:2, 1:16]

  ID L2_0 L1_0 A1_0 Y_1 L2_1 A1_1 Y_2 L2_2 A1_2 Y_3 L2_3 A1_3 Y_4 L2_4 A1_4
1 1     0     0     0    0    0     0    0     0     0   0     1     0    1   NA   NA
2 2     0     0     0    0    0     0    0     0     0   0     0     0    0     0    0

R> Odat.long <- sim(DAG = lDAG, n = 1000, wide = FALSE, rndseed = 123)
R> Odat.long[1:7, ]

   ID L1  t  L2  A1  Y
1  1  0  0   0   0 NA
2  1  0  1   0   0   0
3  1  0  2   0   0   0
4  1  0  3   1   0   0
5  1  0  4 NA NA   1
6  2  0  0   0   0 NA
7  2  0  1   0   0   0

Note that the first observation in Odat.wide contains NAs following Y_4. As described in Section 2.3, this is due to the fact that the node Y was defined earlier as an end of follow-up (EFU) event (using argument EFU=TRUE). That is, Y_4=1 indicates that the first subject has reached the end of the follow-up at time point t = 4 (i.e., was right-censored), therefore, all of the subsequent columns following Y_4 are replaced with NA (missing) value. This is also the reason why we only see 5 rows of data on subject with ID=1 in the above long format dataset Odat.long. Also note that in Odat.long, the value of Y is always NA (missing) for t=0, since the node Y was only defined for time-points t > 0.

4.6. Defining and evaluating various causal target parameters

Causal parameters defined with set.targetE

Example 1

In the example below, we first define two causal target parameters as two vectors, each containing the expectations of the node Y[t] , for time points t=1, …, 16, under the post-intervention distribution defined by one of the two dynamic interventions “A1_th0” and “A1_th1” defined in Section 4.3.1. Second, we evaluate these target parameters using the counterfactual data simulated previously in Section 4.4 and we map the resulting estimates of cumulative risks into estimates of survival probabilities. We also plot the corresponding two counterfactual survival curves using the simcausal routine plotSurvEst as shown in Figure 5. Finally, we note that Figure 5 replicates the simulation study results reported in Figure 4 of Neugebauer et al. (2014).

Figure 5.

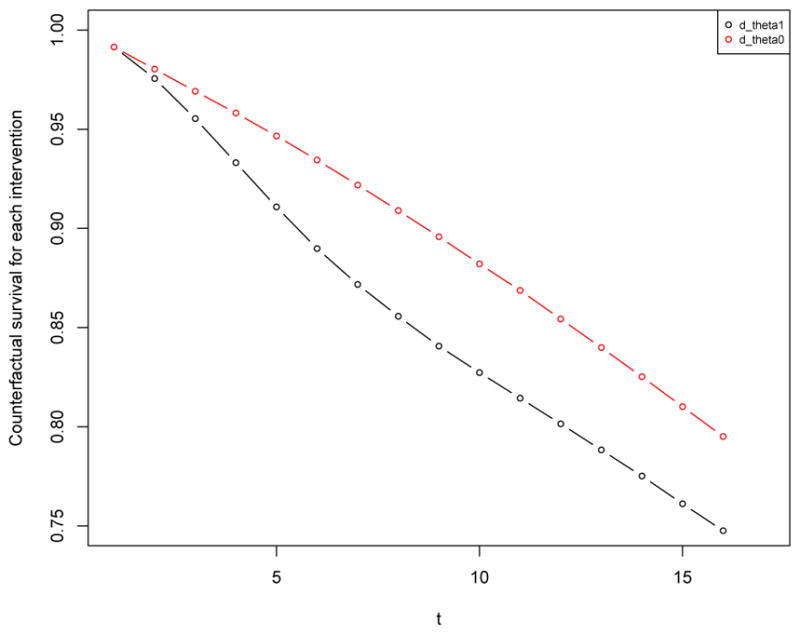
Estimates of the true survival curves under the two dynamic interventions.

R> Ddyn <- set.targetE(Ddyn, outcome = “Y”, t = 1:16, param = “A1_th1”)
R> surv_th1 <- 1 - eval.target(Ddyn, data = Xdyn)$res
R> Ddyn <- set.targetE(Ddyn, outcome = “Y”, t = 1:16, param = “A1_th0”);
R> surv_th0 <- 1 - eval.target(Ddyn, data = Xdyn)$res
R> plotSurvEst(surv = list(d_theta1 = surv_th1, d_theta0 = surv_th0),
+            xindx = 1:17,
+            ylab = “Counterfactual survival for each intervention”,
+            ylim = c(0.75, 1.0))

Example 2

In the example below, we first define the causal target parameter as the ATE on the additive scale (cumulative risk differences) for the two dynamic interventions ( “A1_th1” and “A1_th0”) defined in Section 4.3.1 at time point t = 12. Second, we evaluate this target parameter using the previously simulated counterfactual data from Section 4.4.

ATE on the additive scale:

R> Ddyn <- set.targetE(Ddyn, outcome = “Y”, t = 12, param = “A1_th1-A1_th0”)
R> (psi <- round(eval.target(Ddyn, data = Xdyn)$res, 3))

Diff_Y_12
    0.053

We also note that the above result for the ATE (0.053) replicates the simulation result reported for ψ in Section 5.1 and Figure 4 of Neugebauer et al. (2014), where ψ was defined as the difference between the cumulative risks of failure at t₀ = 12 for the two dynamic interventions d₁ and d₀.

Causal parameters defined with set.targetMSM

In Section 3.5.2, we described the arguments of the function set.targetMSM that the user must specify to define MSM target causal parameters. They include the specification of the argument form which encodes the working MSM formula. This formula can only be a function of the time index t, action attributes that uniquely identify each intervention of interest, and baseline nodes (defined as nodes that precede the earliest intervention node). Both baseline nodes that are measurements of time-varying nodes and time-varying action attributes must be referenced in the R expression passed to the form argument within the wrapping syntax S(…)as illustrated in several examples below.

Example 1. Working dynamic MSM for survival probabilities over time

Here, we illustrate the evaluation of the counterfactual survival curves E(Y_dθ(t)) for t = 1, …, 16 under the dynamic interventions d_θ for θ = 0, 1 introduced in Section 4.3.1 using the following pooled working logistic MSM (MSM 1):

$$\text{expit}({\alpha }_0+{\alpha }_1\theta +{\alpha }_{2}t+{\alpha }_{3}t\theta ),$$

where the true values of the coefficients (α_i, i = 0, …, 3) define the target parameters of interest. First, we define these target parameters:

R> msm.form <- “Y ∼ theta + t + I(theta*t)”
R> Ddyn <- set.targetMSM(Ddyn, outcome = “Y”, t = 1:16, form = msm.form,
+                     family = “binomial”, hazard = FALSE)

Note that when the outcome is a time-varying node of type EFU, the argument hazard = FALSE indicates that the working MSM of interest is a model for survival probabilities. The argument family = “binomial” indicates that the working model is a logistic model. Second, we evaluate the coefficients of the working model:

R> MSMres1 <- eval.target(Ddyn, n = 10000, rndseed = 123)
R> MSMres1$coef

We also note that no previously simulated counterfactual data were passed as argument to the function eval.target above. Instead, the sample size argument n was specified and the routine will thus first sample n = 10,000 observations from each of the two post-intervention distributions before fitting the working MSM with these counterfactual data to derive estimates of the true coefficient values. Alternatively, the user could have passed the previously simulated counterfactual data. Note however that in this case, the user must either simulate counterfactual data by calling the sim function with the argument LTCF = “Y” or convert the previously simulated counterfactual data with the last time point value carried forward imputation function doLTCF. Both approaches are described in the simcausal package vignette Section 4.7 (Sofrygin et al. 2015).

The resulting coefficient estimates for MSM 1 can be mapped into estimates of the two counterfactual survival curves and plotted as shown on the left in Figure 6 using the simcausal plotSurvEst function.

Figure 6.

Survival curve estimates evaluated based on working MSM 1 (left) and saturated MSM 2 (right).

Next, we modify the previous working model formula by specifying a saturated MSM to directly replicate the results reported in Figure 4 of Neugebauer et al. (2014) that are based on a non-parametric MSM approach (MSM 2):

R> msm.form <- “Y ∼ theta + as.factor(t) + as.factor(t):theta”
R> Ddyn <- set.targetMSM(Ddyn, outcome = “Y”, t = 1:16, formula = msm.form,
+                     family = “binomial”, hazard = FALSE)
R> MSMres2 <- eval.target(Ddyn, n = 200000, rndseed = 123)
R> MSMres2$coef

Finally, we plot the resulting survival curves obtained from MSM 2 as shown on the right in Figure 6. The resulting estimates of the survival curves replicate those reported in Figure 4 of Neugebauer et al. (2014).

Example 2. Working static MSM for discrete-time hazards over time

Here, we illustrate the evaluation of discrete-time hazards E(Y_ā(t))|Y_ā(t−1) = 0), for t = 1, …, 16 under the 17 static interventions introduced in Section 4.3.2 using the following pooled working logistic MSM:

$$\mathit{expit}({\alpha }_0+{\alpha }_{1}t+{\alpha }_2\frac{1}{t}\sum _{j=0}^{t-1}a(j)+{\alpha }_3\sum _{j=0}^{t-1}a(j)),$$

where we use the notation ā = (a(0), a(1), …, a(16)) to denote the 17 static intervention regimens on the time-varying treatment node A1. Note that the time-varying action attribute abar introduced in Section 4.3.2 directly encodes the 17 treatment regimens values ā referenced in the MSM working model above. To evaluate the target parameters α_j above, for j = 0, …, 3, we first simulate counterfactual data for the 17 static interventions of interest as follows:

R> Xts <- sim(Dstat, actions = names(A(Dstat)), n = 1000, rndseed = 123)

Second, we define the target parameters and estimate them using the counterfactual data just simulated as follows:

R> msm.form_1 <- “Y ∼ t +
+               S(mean(abar[0:(t-1)])) + I(t*S(mean(abar[0:(t-1)])))”
R> Dstat <- set.targetMSM(Dstat, outcome = “Y”, t = 1:16, form = msm.form_1,
+                     family = “binomial”, hazard = TRUE)
R> MSMres <- eval.target(Dstat, data = Xts)
R> MSMres$coef

Note that the working MSMformulas can reference arbitrary summary measures (functions) of time-varying action attributes such as abar. The square-bracket ’[’ syntax can then be used to identify specific elements of the time-varying action attributes in the same way it can be used in node formulas to reference particular measurements of time-varying nodes. For example, the term sum(abar[0:t]) indicates a summation over the elements of the action attribute abar indexed by time points lower than or equal to value t and the syntax S(abar[max(0, t - 2)]) creates a summary measure representing time-lagged values of abar that are equal to abar[0] if t< 2 and to abar[t-2] if t≥ 2. Note also that references to time-varying action attributes in the working MSM formula must be wrapped within a call to the S(…)function, e.g., Y~t + S(mean(abar[0:t])) .

The eval.target function returns a list with the following named attributes: the working MSM fit returned by a glm function call ( msm), the coefficient estimates ( coef), the mapping ( S.msm.map) of the formula terms defined by expressions enclosed within the S(…)function into the corresponding variable names in the design matrix that was used to implement the regression, and the design matrix ( df_long) stored as a list of data.table objects from the R package data.table (Dowle et al. 2014). Each of these data.table objects contains counterfactual data indexed by a particular intervention. These counterfactual data are stored in long format with possibly additional new columns representing terms in the working MSM formula defined by expressions enclosed with the S()function. The design matrix can be derived by row binding these data.table objects.

R> names(MSMres)
R> MSMres$S.msm.map
R> names(MSMres$df_long)
R> MSMres$df_long[[“A1_ts2”]]

Finally, we plot the resulting counterfactual survival curve estimates using the function survbyMSMterm (source code provided in a supplementary R script), as shown in Figure 7:

Figure 7.

Survival curve estimates evaluated based on working MSM 2.

R> survMSMh_wS <- survbyMSMterm(MSMres = MSMres, t_vec = 1:16,
+                               MSMtermName = “mean(abar[0:(t - 1)])”)
R> print(plotsurvbyMSMterm(survMSMh_wS))

Additional examples of working MSMs are available in the package vignette (Sofrygin et al. 2015), which includes the examples of dynamic MSM for discrete-time hazards and dynamic MSMs that evaluate effect modification by a baseline covariate.

5. Replication study of the impact of misspecification of propensity score models

In this section, we use the simcausal package for replicating a simulation study from Lefebvre et al. (2008). Specifically, we replicate the results reported in Tables II and IV of that paper. We first specify the observed data generating distribution using the two structural equation models corresponding with Scenarios 1 and 3 described in Lefebvre et al. (2008). Second, for each scenario, we evaluate the true values of the coefficients of the MSM using counterfactual data and compare them to those reported by Lefebvre et al. (2008). Finally, for each scenario, we implement the same inverse probability weighting (IPW) estimators of these MSM coefficients and evaluate their performances using the same two metrics (bias and mean squared error) as in Lefebvre et al. (2008). We refer to Appendix A for the description of the details on how the simcausal package was used to conduct this replication study. The R code that fully reproduces the tables presented in this section is provided as a supplementary R script.

Our replication results for Scenarios 1 and 3 are reported in Table 1 and Table 3, respectively. The simulation results, as they were originally reported by Lefebvre et al. (2008), are presented in Table 2 and Table 4. We note that our results closely match those originally reported in Lefebvre et al. (2008).

Table 1.

Replication of the simulation results from Lefebvre et al. (2008) for Scenario 1.

Covariates in P(A|L)	N	A(0) Bias*10	A(0) MSE*10	A(1) Bias*10	A(1) MSE*10
Confounder(s) only	300	0.576	1.803	0.752	1.690
	1000	0.278	0.725	0.374	0.688
	10000	0.062	0.139	0.069	0.147
Confounder(s) & risk factors	300	0.572	1.714	0.785	1.489
	1000	0.250	0.764	0.304	0.665
	10000	0.071	0.121	0.077	0.120

Table 3.

Replication of the simulation results from Lefebvre et al. (2008) for Scenario 3.

Covariates in P(A|L)	N	A(0) Bias*10	A(0) MSE*10	A(1) Bias*10	A(1) MSE*10
Confounder(s) only	300	−0.179	1.238	0.157	1.102
	1000	−0.341	0.413	−0.137	0.363
	10000	−0.347	0.054	−0.177	0.046
Confounder(s) & risk factors	300	−0.151	1.156	0.110	0.890
	1000	−0.266	0.348	−0.093	0.271
	10000	−0.354	0.050	−0.190	0.034
Confounder(s) & IVs	300	1.397	3.966	2.014	3.854
	1000	0.919	2.016	1.200	1.989
	10000	0.438	0.605	0.457	0.595
Confounder(s), IVs & risk factors	300	1.304	4.010	1.966	3.841
	1000	0.936	2.082	1.208	2.027
	10000	0.375	0.644	0.422	0.626
Mis-specified	300	2.742	3.203	5.542	5.437
	1000	2.598	1.737	5.188	3.739
	10000	2.407	0.809	5.009	2.730
Full Model	300	1.383	4.028	2.109	3.924
	1000	0.934	2.020	1.285	1.926
	10000	0.417	0.607	0.435	0.609

Table 2.

Simulation results for Scenario 1 as reported in Table II of Lefebvre et al. (2008).

Covariates in P(A|L)	N	A(0) Bias*10	A(0) MSE*10	A(1) Bias*10	A(1) MSE*10
Lefebvre et al.: Confounder(s) only	300	0.768	1.761	0.889	1.728
	1000	0.265	0.761	0.312	0.723
	10000	0.057	0.146	0.086	0.120
Lefebvre et al.: Confounder(s) & risk factors	300	0.757	1.642	0.836	1.505
	1000	0.283	0.718	0.330	0.638
	10000	0.056	0.139	0.081	0.114

Table 4.

Simulation results for Scenario 3 as reported in Table IV of Lefebvreet al. (2008).

Covariates in P(A|L)	N	A(0) Bias*10	A(0) MSE*10	A(1) Bias*10	A(1) MSE*10
Lefebvre et al.: Confounder(s) only	300	−0.080	1.170	0.099	1.155
	1000	−0.371	0.385	−0.035	0.331
	10000	−0.368	0.056	−0.203	0.043
Lefebvre et al.: Confounder(s) & risk factors	300	−0.110	1.092	0.112	0.865
	1000	−0.330	0.340	−0.108	0.245
	10000	−0.378	0.051	−0.207	0.037
Lefebvre et al.: Confounder(s) & IVs	300	1.611	3.538	2.069	3.841
	1000	0.824	2.063	1.245	2.188
	10000	0.241	0.684	0.379	0.622
Lefebvre et al.: Confounder(s), IVs & risk factors	300	1.600	3.477	2.143	3.598
	1000	0.867	2.053	1.170	2.043
	10000	0.235	0.676	0.372	0.625
Lefebvre et al.: Mis-specified	300	3.146	3.326	5.591	5.494
	1000	2.460	1.700	5.258	3.851
	10000	2.364	0.832	4.943	2.705
Lefebvre et al.: Full Model	300	1.524	3.648	2.221	3.907
	1000	0.878	2.099	1.185	2.099
	10000	0.240	0.679	0.377	0.630

6. Discussion

In this article we described how our simulation package can be used for creating a wide range of artificial datasets often encountered in medical and public health applications of causal inference methods. Specifically, we demonstrated that the simcausal R package is a flexible tool that facilitates the conduct of transparent and reproducible simulation studies. The package allows the user to simulate complex longitudinal data structures based on structural equation models using a novel interface which allows concise and intuitive expression of complex functional dependencies for a large number of nodes. We also argued that such complex simulations are often necessary when one tries to conduct a realistic simulation study that attempts to replicate a large variety of scenarios one might expect to see from a true data-generating process. The package allows the user to specify and simulate counterfactual data under various interventions (e.g., static, dynamic, deterministic, or stochastic). These interventions may represent exposures to treatment regimens, the occurrence or non-occurrence of right-censoring events, or of specific monitoring events. The package also enables the computation of a selected set of user-specified features of the distribution of the counterfactual data that represent common causal target parameters (the gold standards), such as, treatment-specific means, average treatment effects and coefficients from working marginal structural models. In addition, the package provides a flexible graphical component that produces plots of directed acyclic graphs (DAGs) for observed (or post-intervention) data generating distributions.

We note that one of the distinguishing features of simcausal is that it allows the user to define and evaluate a causal target parameter, such as the ATE, that can then serve as the model-free gold standard. That is, the causal parameter is always the same functional of the counterfactual data distribution, regardless of the user-selected parameterization of the SEM. For example, the gold standard defined in this manner provides an objective measure of bias that does not depend on the modeling assumptions of a specific statistical method. Furthermore, coupled with a wide variety of possible data generating distributions that may be specified in simcausal, this package provides statisticians with a powerful tool for testing the validity and accuracy of various statistical methods. For example, one may use our package for validating an implementation of a novel statistical method, using the simulated data with the known truth (the true value of the causal parameter), prior to applying such an algorithm to real data, in which this truth is unknown. As another example, one may use simcausal to simulate data from a large variety of data-generating distributions and conduct a simulation study comparing the properties of different statistical procedures (e.g., bias, mean-squared error (MSE), asymptotic confidence interval coverage), using the user-selected causal parameter as the gold standard.

We also demonstrated the functionality of the package with a single time point intervention simulation study in Section 3 and a complex multiple time point simulation study in Section 4. Moreover, we also showed two real-world applications of the simcausal package in Sections 4 and 5, by replicating some of results of the two previously published simulation studies (Neugebauer et al. 2014, 2015; Lefebvre et al. 2008). The first simulation study by Neugebauer et al. (2014) was initially conducted as a complement to a real data analysis in order to validate the claimed theoretical benefits of a new estimator in a simulated setting that was designed to resemble the data structure collected and used in the real-world study. The second simulation study by Lefebvre et al. (2008) evaluated the impact of the model misspecification of the treatment mechanism on the MSE for the inverse probability-weighting (IPW) estimator, where the coefficients of the marginal structural model were used as the tar- get causal quantity. We note that in both of these instances, we were able to use simcausal to specify the desired data-generating distribution, then simulate repeated observed data samples, and finally, specify and evaluate the different causal parameters that were used in these simulation studies. We also note that the simcausal package vignette (Sofrygin et al. 2015) contains additional replication results of the simulation study described by Neugebauer et al. (2014) that evaluated the comparative performance of targeted minimum loss based estimation (TMLE) and IPW estimation of a causal risk difference between two dynamic treatment regimens.

Finally, we note that the simcausal package is being actively developed and contains several new features that are beyond the scope of this paper. In particular, recently implemented functionality allows one to simulate dependent observations using networks (Eckles et al. 2014). We refer to the forthcoming simcausal network vignette for details describing this new feature. We also note that the implementation of additional functionalities in future releases of the simcausal package should further expand its utility for methods research. Among such possible improvements is the evaluation of additional causal parameters, e.g., the average treatment effect on the treated (Holland 1986; Imbens 2004; Shpitser and Pearl 2009), survivorship causal effects (Joffe et al. 2007; Greene et al. 2013) and direct/indirect effects (Pearl 2001; Petersen et al. 2006; VanderWeele 2009; VanderWeele and Vansteelandt 2014; Hafeman and VanderWeele 2011).

Appendix A: Replicating the simulation study by Lefebvre et al. (2008)

A number of IPW estimators were considered in this simulation study, each estimator defined by a distinct model for the propensity scores P(A(0)|L(0)) and P(A(1)|A(0), L(1)). To estimate these propensity scores we used the same models presented in Table I of Lefebvre et al. (2008) for Scenarios 1 and 3. We considered three sample sizes N = 300; 1, 000; and 10, 000, and we report the bias of each IPW estimator, multiplied by 10 (Bias*10) and the mean-squared error, also multiplied by 10 (MSE*10) in Tables 1 and 3.

Replicating Scenario 1

To carry out the simulation study, we first define a new distribution function rbivNorm for simulating observations from a bivariate normal distribution with a user-specified mean vector (specified by the argument mu) and a user-specified covariance matrix (specified by the arguments var1, var2, and rho to represent the diagonal and off-diagonal scalars, respectively). This new distribution function is based on Cholesky decomposition of the covariance matrix and independent observations simulated from the standard normal distribution which are provided by the input argument norms. The argument whichbiv indicates whether the function should return independent observations from the first or second element of the bivariate normal vector.

R> rbivNorm <- function(n, whichbiv, norms, mu, var1 = 1, var2 = 1, rho = 0.7) {
+   whichbiv <- whichbiv[1]; var1 <- var1[1]; var2 <- var2[1]; rho <- rho[1]
+   sigma <- matrix(c(var1, rho, rho, var2), nrow = 2)
+   Scol <- chol(sigma)[, whichbiv]
+   bivX <- (Scol[1] * norms[, 1] + Scol[2] * norms[, 2]) + mu
+   bivX
+  }

Second, using this distribution function, we define the structural equation model specified for data simulation according to Scenario 1 in Lefebvre et al. (2008).

R> ‘%+%’<- function(a, b) paste0(a, b)
R> Lnames <- c(“LO1”, “LO2”, “LO3”, “LC1”)
R> D <- DAG.empty()
R> for (Lname in Lnames) {
+   D <- D +
+     node(Lname%+%“.norm1”, distr = “rnorm”, mean = 0, sd = 1) +
+       node(Lname%+%“.norm2”, distr = “rnorm”, mean = 0, sd = 1)
+  }
R> D <- D +
+    node(“LO1”, t = 0:1, distr = “rbivNorm”, whichbiv = t + 1,
+     norms = c(LO1.norm1, LO1.norm2),
+     mu = 0) +
+    node(“LO2”, t = 0:1, distr = “rbivNorm”, whichbiv = t + 1,
+     norms = c(LO2.norm1, LO2.norm2),
+     mu = 0) +
+    node(“LO3”, t = 0:1, distr = “rbivNorm”, whichbiv = t + 1,
+     norms = c(LO3.norm1, LO3.norm2),
+     mu = 0) +
+    node(“LC1”, t = 0:1, distr = “rbivNorm”, whichbiv = t + 1,
+     norms = c(LC1.norm1, LC1.norm2),
+     mu = {if (t == 0) {0} else {-0.30 * A[t-1]}}) +
+    node(“alpha”, t = 0:1, distr = “rconst”,
+     const = {if(t == 0) {log(0.6)} else {log(1.0)}}) +
+    node(“A”, t = 0:1, distr = “rbern”,
+     prob =
+       plogis(alpha[t] +
+       log(5)*LC1[t] + {if(t == 0) {0} else {log(5)*A[t-1]}})) +
+    node(“Y”, t = 1, distr = “rnorm”,
+     mean = (0.98 * LO1[t] + 0.58 * LO2[t] + 0.33 * LO3[t] +
+            0.98 * LC1[t] - 0.37 * A[t]),
+     sd = 1)
R> DAGO.sc1 <- set.DAG(D)

Third, we define the target parameter as the coefficients β₁ and β₂ of the following correctly specified marginal structural model:

$$E[Y_{a(0),a(1)}]={\beta }_0+{\beta }_{1}a(0)+{\beta }_{2}a(1),$$

defined by the following four possible static and deterministic interventions (a(0), a(1)) on the treatment process (A(0), A(1)): (0, 0), (1, 0), (0, 1), and (1, 1).

R> defAct <- function (Dact) {
+    act.At <- node(“A”, t = 0:1, distr = “rbern”, prob = abar[t])
+    Dact <- Dact +
+      action(“A00”, nodes = act.At, abar = c(0, 0)) +
+      action(“A10”, nodes = act.At, abar = c(1, 0)) +
+      action(“A01”, nodes = act.At, abar = c(0, 1)) +
+      action(“A11”, nodes = act.At, abar = c(1, 1))
+    return(Dact)
+  }
R> Dact.sc1 <- defAct(DAGO.sc1)
R> msm.form <- “Y ∼ S(abar[0]) + S(abar[1])”
R> Dact.sc1 <- set.targetMSM(Dact.sc1, outcome = “Y”, t = 1,
+                         form = msm.form, family = “gaussian”)

Fourth, we evaluate the true values of these MSM coefficients using the eval.target function and note that our results closely match the true value of the MSM coefficients reported in Table II of Lefebvre et al. (2008):

R> repstudy2.sc1.truetarget <- function() {
+   trueMSMreps.sc1 <- NULL
+   reptrue <- 50
+   for (i in (1:reptrue)) {
+     res.sc1.i <- eval.target(Dact.sc1, n = 500000)$coef
+     trueMSMreps.sc1 <- rbind(trueMSMreps.sc1, res.sc1.i)
+   }
+   return(trueMSMreps.sc1)
+  }
R> f1name <- “replication_dat/trueMSMreps.sc1.Rdata”
R> if (file.exists(f1name)) {
+   load(f1name)
+  } else {
+   trueMSMreps.sc1 <- repstudy2.sc3.truetarget()
+   save(list = “trueMSMreps.sc1”, file = f1name)
+  }
R> trueMSM.sc1 <- apply(trueMSMreps.sc1, 2, mean)
R> print(trueMSM.sc1)

   (Intercept)     S(abar[0])     S(abar[1])
0.0001540635 -0.2941187264 -0.3700397969

Note that the true values of the MSM coefficients above were obtained from the averages of coefficient estimates obtained from several simulated counterfactual data sets. This approach was implemented to avoid the memory limitation that can be encountered when trying to simulate a single very large counterfactual data set. Finally, using the R code provided as a supplementary script file, we replicate the IPW estimation results for Scenario 1 as presented originally in Table II of Lefebvre et al. (2008).

Replicating Scenario 3

Next, using the same approach described above, we replicate the simulation results for Scenario 3 reported in Table IV of Lefebvre et al. (2008). We start by defining the structural equation model specified for data simulation according to Scenario 3 in Lefebvre et al. (2008) as follows:

R> ‘%+%’<- function(a, b) paste0(a, b)
R> Lnames <- c(“LO1”, “LO2”, “LO3”, “LE1”, “LE2”, “LE3”, “LC1”, “LC2”, “LC3”)
R> D <- DAG.empty()
R> for (Lname in Lnames) {
+   D <- D +
+     node(Lname%+%“.norm1”, distr = “rnorm”) +
+     node(Lname%+%“.norm2”, distr = “rnorm”)
+  }
R> coefAi <- c(-0.10, -0.20, -0.30)
R> sdLNi <- c(sqrt(1), sqrt(5), sqrt(10))
R> for (i in (1:3)) {
+   D <- D +
+     node(“LO”%+%i, t = 0:1, distr = “rbivNorm”, whichbiv = t + 1,
+      mu = 0,
+      params = list(norms = “c(LO”%+%i%+%“.norm1, LO”%+%i%+%“.norm2)”)) +
+     node(“LE”%+%i, t = 0:1, distr = “rbivNorm”, whichbiv = t + 1,
+      mu = 0, var1 = 1, var2 = 1, rho = 0.7,
+      params = list(norms = “c(LE”%+%i%+%“.norm1, LE”%+%i%+%“.norm2)”)) +
+     node(“LC”%+%i, t = 0:1, distr = “rbivNorm”, whichbiv = t + 1,
+      mu = {if (t == 0) {0} else {.(coefAi[i]) * A[t-1]}},
+      params = list(norms = “c(LC”%+%i%+%“.norm1, LC”%+%i%+%“.norm2)”)) +
+     node(“LN”%+%i, t = 0:1, distr = “rnorm”,
+      mean = 0, sd = .(sdLNi[i]))
+  }
R> D <- D +
+    node(“alpha”, t = 0:1, distr = “rconst”,
+      const = {if(t == 0) {log(0.6)} else {log(1.0)}}) +
+    node(“A”, t = 0:1, distr = “rbern”,
+      prob = plogis(alpha[t] +
+                 log(5) * LC1[t] + log(2) * LC2[t] + log(1.5) * LC3[t] +
+                 log(5) * LE1[t] + log(2) * LE2[t] + log(1.5) * LE3[t] +
+                 {if (t == 0) {0} else {log(5) * A[t-1]}})) +
+    node(“Y”, t = 1, distr = “rnorm”,
+      mean = 0.98 * LO1[t] + 0.58 * LO2[t] + 0.33 * LO3[t] +
+             0.98 * LC1[t] + 0.58 * LC2[t] + 0.33 * LC3[t] - 0.39 * A[t],
+      sd = 1)
R> DAGO.sc3 <- set.DAG(D)

Similar to Scenario 1, we then define the same four actions on the new DAG object before defining and evaluating the causal target parameter of interest. We note that our results match the true value of the MSM coefficients reported in Table IV of Lefebvre et al. (2008). Finally, using the R code provided as a supplementary script file, we replicate the IPW estimation results for Scenario 3 as presented originally in Table IV of Lefebvre et al. (2008).

R> Dact.sc3 <- defAct(DAGO.sc3)
R> msm.form <- “Y ∼ S(abar[0]) + S(abar[1])”
R> Dact.sc3 <- set.targetMSM(Dact.sc3, outcome = “Y”, t = 1,
+                         form = msm.form, family = “gaussian”)
R> repstudy2.sc3.truetarget <- function() {
+   trueMSMreps.sc3 <- NULL
+   reptrue <- 50
+   for (i in (1:reptrue)) {
+    res.sc3.i <- eval.target(Dact.sc3, n = 500000)$coef
+    trueMSMreps.sc3 <- rbind(trueMSMreps.sc3, res.sc3.i)
+   }
+   return(trueMSMreps.sc3)
+  }
R> f2name <- “replication_dat/trueMSMreps.sc3.Rdata”
R> if (file.exists(f2name)) {
+   load(f2name)
+  } else {
+   trueMSMreps.sc3 <- repstudy2.sc3.truetarget()
+   save(list = “trueMSMreps.sc3”, file = f2name)
+  }
R> trueMSM.sc3 <- apply(trueMSMreps.sc3, 2, mean)
R> print(trueMSM.sc3)

   (Intercept)     S(abar[0])     S(abar[1])
0.0001690372 -0.3134283871 -0.3901595327