Quantile regression in linear mixed models: a stochastic approximation EM approach

Abstract

This paper develops a likelihood-based approach to analyze quantile regression (QR) models for continuous longitudinal data via the asymmetric Laplace distribution (ALD). Compared to the conventional mean regression approach, QR can characterize the entire conditional distribution of the outcome variable and is more robust to the presence of outliers and misspecification of the error distribution. Exploiting the nice hierarchical representation of the ALD, our classical approach follows a Stochastic Approximation of the EM (SAEM) algorithm in deriving exact maximum likelihood estimates of the fixed-effects and variance components. We evaluate the finite sample performance of the algorithm and the asymptotic properties of the ML estimates through empirical experiments and applications to two real life datasets. Our empirical results clearly indicate that the SAEM estimates outperforms the estimates obtained via the combination of Gaussian quadrature and non-smooth optimization routines of the Geraci and Bottai (2014) approach in terms of standard errors and mean square error. The proposed SAEM algorithm is implemented in the R package qrLMM().

1. INTRODUCTION

Linear mixed models (LMM) are frequently used to analyze grouped/clustered data (such as longitudinal data, repeated measures, and multilevel data) because of their ability to handle within-subject correlations that characterizes grouped data [30]. Majority of these LMMs estimate covariate effects on the response through a mean regression, controlling for between-cluster heterogeneity via normally-distributed cluster-specific random effects and random errors. However, this centrality-based inferential framework is often inadequate when the conditional distribution of the response (conditional on the random terms) is skewed, multimodal, or affected by atypical observations. In contrast, conditional quantile regression (QR) methods [15, 16] quantifying the entire conditional distribution of the outcome variable were developed that can provide assessment of covariate effects at any arbitrary quantiles of the outcome. In addition, QR methods do not impose any distributional assumption on the error terms, except that the error term has a zero conditional quantile. Because of its popularity and the flexibility it provides, standard QR methods are implementable via available software packages, such as, the R package quantreg.

Although QR was initially developed under a univariate framework, the abundance of clustered data in recent times led to its extensions to mixed modeling framework (classical, or Bayesian), via either the distribution-free route [25, 9, 10, 7], or the traditional likelihood-based route, mostly using the asymmetric Laplace distribution (ALD) [12, 40, 13]. Among the ALD-based models, [12] proposed a Monte Carlo EM (MCEM)-based conditional QR model for continuous responses with a subject-specific random (univariate) intercept to account for within-subject dependence in the context of longitudinal data. However, due to the limitations of a simple random intercept model to account for the between-cluster heterogeneity, [13] extended it to a general quantile regression linear mixed model (QR-LMM) with multiple random effects (both intercepts and slopes). However, instead of going the MCEM route, the estimation of the fixed effects and the covariance components were implemented using an efficient combination of Gaussian quadrature approximations and non-smooth optimization algorithms.

The literature on QR-LMM is now extensive. However, there are no studies conducting exact inferences for QR-LMM from a likelihood-based perspective. In this paper, we proceed to achieve that via a robust parametric ALD-based QR-LMM specification, where the full likelihood-based implementation follows a stochastic version of the EM algorithm (SAEM). The SAEM was initially proposed by [5] using maximum likelihood (ML) techniques as a powerful alternative to the EM when the E-step is intractable. The SAEM algorithm has been proved to be more computationally efficient than the classical MCEM algorithm due to the recycling of simulations from one iteration to the next in the smoothing phase of the algorithm. Moreover, as pointed out in [29], the SAEM algorithm, unlike the MCEM, converges even in a typically small simulation size. However, since the unobserved data cannot be simulated exactly under the conditional distributions for a variety of models, [19, 20] coupled a MCMC procedure to the SAEM algorithm, and studied the general conditions for its convergence. We adapt this strategy for inference in the context of QR-LMM, and compare and contrast this to the approximate method proposed by Geraci and Bottai [13]. Furthermore, application of our method to two longitudinal datasets is illustrated via the R package qrLMM().

The rest of the paper proceeds as follows. Section 2 presents some preliminaries, in particular the connection between QR and ALD, and an outline of the EM and SAEM algorithms. Section 3 develops the MCEM and the SAEM algorithms for a general LMM, while Section 4 outlines the likelihood estimation and standard errors. Section 5 presents simulation studies to compare the finite sample performance of our proposed methods with the competing method of geraci and Bottai [13]. Application of the SAEM method to two longitudinal datasets, one examining cholesterol level and the other on orthodontic distance growth are presented in Section 6. Finally, Section 7 concludes, sketching some future research directions.

2. PRELIMINARIES

In this section, we provide some useful results on the ALD and QR, and outline the EM and SAEM algorithms for ML estimation.

2.1 Connection between QR and ALD

Let y_i denote the response of interest and x_i the corresponding covariate vector of dimension k × 1 for subject i, i = 1, …, n. Then, the pth (0 < p < 1) QR model takes the form

$$Q_p({\mathbf{y}}_i)={\mathbf{x}}_i^{\top }{\mathit{\beta }}_p,i=1,\dots ,n,$$

where Q_p(y_i) is the quantile function (or the inverse cumulative distribution function) of y_i given x_i evaluated at p, and β_p is a vector of regression parameters corresponding to the pth quantile. The regression vector β_p is estimated by minimizing

$$\sum _{i=1}^n{\rho }_p(y_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p),$$ (1)

where ρ_p(·) is the check (or loss) function defined by ρ_p(u) = u(p − 𝕀{u < 0}), with 𝕀{·} the usual indicator function.

Next, we define the ALD. A random variable Y is distributed as an ALD [39] with location parameter μ, scale parameter σ > 0 and skewness parameter p ∈ (0, 1), if its probability density function (pdf) given by

$$f(y\mid \mu ,\sigma ,p)=\frac{p(1-p)}{\sigma }exp\left\{-{\rho }_p\left(\frac{y-\mu }{\sigma }\right)\right\}.$$ (2)

The ALD is an asymmetric distribution with a straightforward skewness parametrization, and the check function ρ_p(·) is closely related to the ALD [17, 39]. Note that minimizing the loss function in (1) is equivalent to maximizing the ALD likelihood function. This is in tune to the result from simple linear regression, where the ordinary least square (OLS) estimator of the regression parameter minimizing the error sum of squares is equivalent to the maximum likelihood (ML) estimator of the corresponding Gaussian likelihood.

It is easy to see that ${\rho }_p\left(\frac{Y-\mu }{\sigma }\right)$ follows an exponential(1) distribution. Figure 1 plots the ALD, illustrating how the skewness changes with p. For example, when p = 0.1, most of the mass is concentrated around the right tail, while for p = 0.5, both tails of the ALD have equal mass and the distribution resemble the more common double exponential distribution. In contrast to the normal distribution with a quadratic term in the exponent, the ALD is linear in the exponent. This results in a more peaked mode, together with thicker tails. On the contrary, the normal distribution has heavier shoulders compared to the ALD. The ALD abides by the following stochastic representation [18, 21]. Let U ~ exp(σ) and Z ~ N(0, 1) be two independent random variables. Then, Y ~ ALD(μ, σ, p) can be represented as

Figure 1.

Standard asymmetric Laplace density.

$$Y\stackrel{d}{=}\mu +{\vartheta }_{p}U+{\tau }_p\sqrt{\sigma U}Z,$$ (3)

where ${\vartheta }_p=\frac{1-2p}{p(1-p)}$ and ${\tau }_p^2=\frac{2}{p(1-p)}$, and $\stackrel{d}{=}$ denotes equality in distribution. This representation is useful in obtaining the moment generating function (mgf), and formulating the estimation algorithm. From (3), the hierarchical representation of the ALD follows

$$\begin{array}{lll}\hfill Y\mid U=u& ~\hfill & N(\mu +{\vartheta }_{p}u,{\tau }_p^2\sigma u),\hfill \\ \hfill U& ~\hfill & exp(\sigma ).\hfill \end{array}$$ (4)

This representation will be useful for the implementation of the EM algorithm. Moreover, since $Y\mid U=u~N(\mu +{\vartheta }_{p}u,{\tau }_p^2\sigma u)$, one can easily derive the pdf of Y, given by

$$f(y\mid \mu ,\sigma ,p)=\frac{1}{\sqrt{2\pi }}\frac{1}{{\tau }_p{\sigma }^{\frac{3}{2}}}exp\left(\frac{\delta (y)}{\gamma }\right)A(y),$$ (5)

where $\delta (y)=\frac{\mid y-\mu \mid }{{\tau }_p\sqrt{\sigma }},\gamma =\sqrt{\frac{1}{\sigma }\left(2+\frac{{\vartheta }_p^2}{{\tau }_p^2}\right)}=\frac{{\tau }_p}{2\sqrt{\sigma }}$ and $A(y)=2{\left(\frac{\delta (y)}{\gamma }\right)}^{1/2}{K}_{1/2}\left(\delta (y)\gamma \right)$, with K_v(.), the modified Bessel function of the third kind. It is easy to observe that the conditional distribution of U, given Y = y, is $U\mid (Y=y)~\mathit{GIG}(\frac{1}{2},\delta ,\gamma )$, where GIG(v, a, b) is the Generalized Inverse Gaussian (GIG) distribution [2] with the pdf

$$h(u\mid \nu ,a,b)=\frac{{(b/a)}^{\nu }}{2K_{\nu }(ab)}{u}^{\nu -1}exp\left\{-\frac{1}{2}(a^2/u+b^{2}u)\right\};u>0,\nu \in ℝ,a,b>0$$

The moments of U can be expressed as

$$E[U^k]={\left(\frac{a}{b}\right)}^k\frac{K_{\nu +k}(ab)}{K_{\nu }(ab)},k\in ℝ.$$ (6)

2.2 The EM and SAEM algorithms

In models with missing data, the EM algorithm [6] has established itself as the centerpiece for ML estimation of model parameters, mostly when the maximization of the observed log-likelihood function denoted by ℓ(θ; y_obs) = log f(y_obs; θ) is complicated. Let y_obs and q represent observed and missing data, respectively, such that the complete data can be written as y_com = (y_obs, q)^⊤. This iterative algorithm maximizes the complete log-likelihood function ℓ_c(θ; y_com) = logf(y_obs, q; θ) at each step, converging to a stationary point of the observed likelihood ℓ(θ; y_obs) under mild regularity conditions [38, 35]. The EM algorithm proceeds in two simple steps:

E-Step

Replace the observed likelihood by the complete likelihood and compute its conditional expectation Q(θ|θ̂^(k)) = E{ℓ_c(θ; y_com)|θ̂^(k), y_obs}, where θ̂^(k) is the estimate of θ at the k-th iteration;

M-Step

Maximize Q(θ|θ̂^(k)) with respect to θ to obtain θ̂^(k+1).

However, in some applications of the EM algorithm, the E-step cannot be obtained analytically and has to be calculated using simulations. The Monte Carlo EM (MCEM) algorithm was proposed in [36], where the E-step is replaced by a Monte Carlo approximation based on a large number of independent simulations of the missing data. This simple solution is infact computationally expensive, given the need to generate a large number of independent simulations of the missing data for a good approximation. Thus, in order to reduce the amount of required simulations compared to the MCEM algorithm, the SAEM algorithm proposed by [5] replaces the E-step of the EM algorithm by a stochastic approximation procedure, while the Maximization step remains unchanged. Besides having good theoretical properties, the SAEM estimates the population parameters accurately, converging to the global maxima of the ML estimates under quite general conditions [1, 5, 19]. At each iteration, the SAEM algorithm successively simulates missing data with the conditional distribution, and updates the unknown parameters of the model. At iteration k, the SAEM proceeds as follows:

E-Step

• Simulation: Draw (q^(ℓ,k)), ℓ = 1, …, m from the conditional distribution of the missing data f(q|θ^(k−1), y_obs).

• Stochastic Approximation: Update the Q(θ|θ̂^(k)) function as

  $$Q(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k)})\approx Q(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k-1)})+{\delta }_k\left[\frac{1}{m}\sum _{\ell =1}^{m}logf({\mathbf{y}}_{\text{obs}},{\mathbf{q}}^{(\ell ,k)};\mathit{\theta })-Q(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k-1)})\right]$$ (7)

M-Step

• Maximization: Update θ̂^(k) as ${\widehat{\mathit{\theta }}}^{(k+1)}=\underset{\theta }{argmax}Q(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k)})$,

where δ_k is a smoothness parameter [19], i.e., a decreasing sequence of positive numbers such that ${\sum }_{k=1}^{\infty }{\delta }_k=\infty$ and ${\sum }_{k=1}^{\infty }{\delta }_k^2<\infty$. Note that, for the SAEM algorithm, the E-Step coincides with the MCEM algorithm, however a small number of simulations m (suggested to be m ≤ 20) is necessary. This is possible because unlike the traditional EM algorithm and its variants, the SAEM algorithm uses not only the current simulation of the missing data at the iteration k denoted by (q^(ℓ,k)), ℓ = 1, …, m but some or all previous simulations, where this ‘memory’ property is set by the smoothing parameter δ_k.

Note, in equation (7), if the smoothing parameter δ_k is equal to 1 for all k, the SAEM algorithm will have ‘no memory’, and will be equivalent to the MCEM algorithm. The SAEM with no memory will converge quickly (convergence in distribution) to a solution neighbourhood, however the algorithm with memory will converge slowly (almost sure convergence) to the ML solution. We suggested the following choice of the smoothing parameter:

$${\delta }_k=\{\begin{array}{lll}1,\hfill & \text{for}\hfill & \hfill 1\le k\le cW\\ \frac{1}{k-cW},\hfill & \text{for}\hfill & \hfill cW+1\le k\le W\end{array}$$

where W is the maximum number of Monte-Carlo iterations, and c a cut point (0 ≤ c ≤ 1) which determines the percentage of initial iterations with no memory. For example, if c = 0, the algorithm will have memory for all iterations, and hence will converge slowly to the ML estimates. If c = 1, the algorithm will have no memory, and so will converge quickly to a solution neighbourhood. For the first case, W would need to be large in order to achieve the ML estimates. For the second, the algorithm will output a Markov Chain where after applying a burn in and thin, the mean of the chain observations can be a reasonable estimate.

A number between 0 and 1 (0 < c < 1) will assure an initial convergence in distribution to a solution neighbourhood for the first cW iterations and an almost sure convergence for the rest of the iterations. Hence, this combination will lead us to a fast algorithm with good estimates. To implement SAEM, the user must fix several constants matching the number of total iterations W and the cut point c that defines the starting of the smoothing step of the SAEM algorithm, however, those parameters will vary depending of the model and the data. As suggested in [23], to determine those constants, a graphical approach is recommended to monitor the convergence of the estimates for all the parameters, and, if possible, to monitor the difference (relative difference) between two successive evaluations of the log-likelihood ℓ(θ|y_obs), given by ||ℓ(θ^(k+1)|y_obs)−ℓ(θ^(k)|y_obs)|| or ||ℓ(θ^(k+1)|y_obs)/ℓ(θ^(k)|y_obs) − 1||, respectively.

3. QR FOR LINEAR MIXED MODELS AND ALGORITHMS

We consider the following general LMM $y_{ij}={\mathbf{x}}_{ij}^{\top }\mathit{\beta }+{\mathbf{z}}_{ij}{\mathbf{b}}_i+{\epsilon }_{ij}$, i = 1, …, n, j = 1, …, n_i, where y_ij is the jth measurement of a continuous random variable for the ith subject, ${\mathbf{x}}_{ij}^{\top }$ are row vectors of a known design matrix of dimension N × k corresponding to the k × 1 vector of population-averaged fixed effects β, z_ij is a q × 1 design matrix corresponding to the q×1 vector of random effects b_i, and ε_ij the independent and identically distributed random errors. We define pth quantile function of the response y_ij as

$$Q_p(y_{ij}\mid {\mathbf{x}}_{ij},{\mathbf{b}}_i)={\mathbf{x}}_{ij}^{\top }{\mathit{\beta }}_p+{\mathbf{z}}_{ij}{\mathbf{b}}_i.$$ (8)

where Q_p denotes the inverse of the unknown distribution function F, β_p is the regression coefficient corresponding to the pth quantile, the random effects b_i are distributed as ${\mathbf{b}}_i\stackrel{\text{iid}}{\sim }{\mathrm{N}}_q(\mathbf{0},\mathbf{\Psi })$, where the dispersion matrix Ψ = Ψ(α) depends on unknown and reduced parameters α, and the errors ε_ij ~ ALD(0, σ). Then, y_ij |b_i independently follows as ALD with the density given by

$$f(y_{ij}\mid {\mathit{\beta }}_p,{\mathbf{b}}_i,\sigma )=\frac{p(1-p)}{\sigma }exp\left\{-{\rho }_p\left(\frac{y_{ij}-{\mathbf{x}}_{ij}^{\top }{\mathit{\beta }}_p-{\mathbf{z}}_{ij}{\mathbf{b}}_i}{\sigma }\right)\right\},$$ (9)

Using an MCEM algorithm, a QR-LMM with random intercepts (q = 1) was proposed by [12]. More recently, [13] extended that setup to accommodate multiple random effects where the estimation of fixed effects and covariance matrix of the random effects were accomplished via a combination of Gaussian quadrature approximations and non-smooth optimization algorithms. Here, we consider a more general correlated random effects framework with general dispersion matrix Ψ = Ψ(α).

3.1 An MCEM algorithm

First, we develop an MCEM algorithm for ML estimation of the parameters in the QR-LMM. From (4), the QR-LMM defined in (8)–(9) can be represented in a hierarchical form as:

$$\begin{array}{lll}\hfill {\mathbf{y}}_i\mid {\mathbf{b}}_i,{\mathbf{u}}_i& ~\hfill & N_{n_i}\left({\mathbf{x}}_i^{\top }{\mathit{\beta }}_p+{\mathbf{z}}_i{\mathbf{b}}_i+{\vartheta }_p{\mathbf{u}}_i,\sigma {\tau }_p^2{\mathbf{D}}_i\right),\hfill \\ \hfill {\mathbf{b}}_i& ~\hfill & N_q(\mathbf{0},\mathbf{\Psi }),\hfill \\ \hfill {\mathbf{u}}_i& ~\hfill & \prod _{j=1}^{n_i}exp(\sigma ),\hfill \end{array}$$ (10)

for i = 1, …, n, where ϑ_p and ${\tau }_p^2$ are as in (3); D_i represents a diagonal matrix that contains the vector of missing values u_i = (u_i1, …, u_ini )^⊤ and exp(σ) denotes the exponential distribution with mean σ. Let ${\mathbf{y}}_{i_c}={({\mathbf{y}}_i^{\top },{\mathbf{b}}_i^{\top },{\mathbf{u}}_i^{\top })}^{\top }$, with y_i = (y_i1, …, y_ini )^⊤, b_i = (b_i1, …, b_iq)_⊤, u_i = (u_i1, …, u_ini )^⊤ and let ${\theta }^{(k)}={({\mathit{\beta }}_p^{(k)\top },{\sigma }^{(k)},{\mathit{\alpha }}^{(k)\top })}^{\top }$, the estimate of θ at the k-th iteration. Since b_i and u_i are independent for all i = 1, …, n, it follows from (4) that the complete-data log-likelihood function is of the form ${\ell }_c(\mathit{\theta };{\mathbf{y}}_c)={\sum }_{i=1}^n{\ell }_c(\mathit{\theta };{\mathbf{y}}_{i_c})$, where

$$\begin{array}{l}{\ell }_c(\mathit{\theta };{\mathbf{y}}_{i_c})=\text{constant}-\frac{3}{2}{n}_i\mathit{log}\sigma -\frac{1}{2}\mathit{log}\mid \mathbf{\Psi }\mid -\frac{1}{2}{\mathbf{b}}_i^{\top }{\mathbf{\Psi }}^{-1}{\mathbf{b}}_i\\ -\frac{1}{\sigma }{\mathbf{u}}_i^{\top }{\mathbf{1}}_{n_i}-\frac{1}{2\sigma {\tau }_p^2}{({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p-{\mathbf{z}}_i{\mathbf{b}}_i-{\vartheta }_p{\mathbf{u}}_i)}^{\top }\\ \times {\mathbf{D}}_i^{-1}({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p-{\mathbf{z}}_i{\mathbf{b}}_i-{\vartheta }_p{\mathbf{u}}_i).\end{array}$$

Given the current estimate θ = θ^(k), the E-step calculates the function $Q(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k)})={\sum }_{i=1}^n{Q}_i(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k)})$, where

$$\begin{array}{l}{Q}_i(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k)})\\ =\mathrm{E}\left\{{\ell }_c(\mathit{\theta };{\mathbf{y}}_{i_c})\mid {\mathit{\theta }}^{(k)},\mathbf{y}\right\}\\ \propto -\frac{3}{2}{n}_i\text{log}\sigma -\frac{1}{2\sigma {\tau }_p^2}[{({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p)}^{\top }{\widehat{{\mathbf{D}}_i^{-1}}}^{(k)}({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p)\\ -2({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p){{(\widehat{{\mathbf{D}}_i^{-1}\mathbf{zb}})}_i}^{(k)}+\text{tr}\left\{{\mathbf{z}}_i{{(\mathbf{b}\widehat{{\mathbf{b}}^{\top }\mathbf{z}{\mathbf{D}}_i^{-1}})}_i}^{(k)}\right\}\\ -2{\vartheta }_p{({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p)}^{\top }{\mathbf{1}}_{n_i}+2{\vartheta }_p{(\mathbf{z}{\widehat{\mathbf{b}}}^{(k)})}_i^{\top }{\mathbf{1}}_{n_i}\\ +\frac{{\tau }_p^4}{4}{\widehat{{\mathbf{u}}_i}}^{(k)\top }{\mathbf{1}}_{n_i}]-\frac{1}{2}\mathit{log}\mid \mathbf{\Psi }\mid -\frac{1}{2}\text{tr}\left\{{\widehat{{(\mathbf{b}{\mathbf{b}}^{\top })}_i}}^{(k)}{\mathbf{\Psi }}^{-1}\right\},\end{array}$$ (11)

where tr(A) indicates the trace of matrix A and 1_p is the vector of ones of dimension p. The calculation of these functions require expressions for

$$\begin{array}{ll}\hfill {\widehat{{\mathbf{b}}_i}}^{(k)}& =\mathrm{E}\{{\mathbf{b}}_i\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\},\hfill \\ \hfill {\widehat{{\left(\mathbf{b}{\mathbf{b}}^{\top }\right)}_i}}^{(k)}& =\mathrm{E}\{{\mathbf{b}}_i{\mathbf{b}}_i^{\top }\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\},\hfill \\ \hfill {{(\widehat{\mathbf{b}{\mathbf{b}}^{\top }{\mathbf{zD}}^{-\mathrm{i}}})}_i}^{(k)}& =\mathrm{E}\{{\mathbf{b}}_i{\mathbf{b}}_i^{\top }{\mathbf{z}}_i^{\top }{\mathbf{D}}_i^{-1}\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\},\hfill \\ \hfill {\widehat{{\mathbf{u}}_i}}^{(k)}& =\mathrm{E}\{{\mathbf{u}}_i\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\},\hfill \\ \hfill {\widehat{{\mathbf{D}}_i^{-1}}}^{(k)}& =\mathrm{E}\{{\mathbf{D}}_i^{-1}\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\},\hfill \\ \hfill {{(\widehat{{\mathbf{D}}^{-1}\mathbf{zb}})}_i}^{(k)}& =\mathrm{E}\{{\mathbf{D}}_i^{-1}{\mathbf{z}}_i{\mathbf{b}}_i\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\},\hfill \end{array}$$

which do not have closed forms. Since the joint distribution of the missing data ( ${\mathbf{b}}_i^{(k)},{\mathbf{u}}_i^{(k)}$) is unknown and the conditional expectations cannot be computed analytically for any function g(.), the MCEM algorithm approximates the conditional expectations above by their Monte Carlo approximations

$$\mathrm{E}[g({\mathbf{b}}_i,{\mathbf{u}}_i)\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i]\approx \frac{1}{m}\sum _{\ell =1}^{m}g({\mathbf{b}}_i^{(\ell ,k)},{\mathbf{u}}_i^{(\ell ,k)}),$$ (12)

which depend on the simulations of the two latent (missing) variables ${\mathbf{b}}_i^{(k)}$ and ${\mathbf{u}}_i^{(k)}$from the conditional joint density f(b_i, u_i|θ^(k), y_i). A Gibbs sampler can be easily implemented (see Supplementary Material, http://intlpress.com/site/pub/pages/journals/items/sii/content/vols/0010/0003/s003) given that the two full conditional distributions f(b_i|θ^(k), u_i, y_i) and f(u_i|θ^(k), b_i, y_i) are known. However, using known properties of conditional expectations, the expected value in (12) can be more accurately approximated as

$$\begin{array}{l}{\mathrm{E}}_{{\mathbf{b}}_i,{\mathbf{u}}_i}[g({\mathbf{b}}_i,{\mathbf{u}}_i)\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i]={\mathrm{E}}_{{\mathbf{b}}_i}[{\mathrm{E}}_{{\mathbf{u}}_i}[g({\mathbf{b}}_i,{\mathbf{u}}_i)\mid {\mathit{\theta }}^{(k)},{\mathbf{b}}_i,{\mathbf{y}}_i]\mid {\mathbf{y}}_i]\\ \approx \frac{1}{m}\sum _{\ell =1}^m{\mathrm{E}}_{u_i}[g({\mathbf{b}}_i^{(\ell ,k)},{\mathbf{u}}_i)\mid {\mathit{\theta }}^{(k)},{\mathbf{b}}_i^{(\ell ,k)},{\mathbf{y}}_i],\end{array}$$ (13)

where b^(ℓ,k) is a sample from the conditional density f(b_i|θ^(k), y_i).

Now, to drawn random samples from the full conditional distribution f(u_i|y_i, b_i), first note that the vector u_i|y_i, b_i can be written as u_i|y_i, b_i = [u_i1|y_i1, b_i, u_i2|y_i2, b_i, · · ·, u_ini |y_ini, b_i]^⊤, since u_ij | y_ij, b_i is independent of u_ik| y_ik, b_i, for all j, k = 1, 2, …, n_i and j ≠ k. Thus, the distribution of f(u_ij |y_ij, b_i) is proportional to

$$f(u_{ij}\mid y_{ij},{\mathbf{b}}_i)\propto \varphi (y_{ij}\mid {\mathbf{x}}_{ij}^{\top }{\mathit{\beta }}_p+{\mathbf{z}}_{ij}^{\top }{\mathbf{b}}_i+{\vartheta }_p{u}_{ij},\sigma {\tau }_p^2{u}_{ij})\times exp(\sigma ),$$

which, from Subsection 2.1, leads to u_ij |y_ij, ${\mathbf{b}}_i~\mathit{GIG}(\frac{1}{2},{\chi }_{ij},\psi )$, where χ_ij and ψ are given by

$${\chi }_{ij}=\frac{\mid y_{ij}-{\mathbf{x}}_{ij}^{\top }{\mathit{\beta }}_p-{\mathbf{z}}_{ij}^{\top }{\mathbf{b}}_i\mid }{{\tau }_p\sqrt{\sigma }}\text{and}\psi =\frac{{\tau }_p}{2\sqrt{\sigma }}$$ (14)

From (6), and after generating samples from f(b_i|θ^(k), y_i) (see Subsection 3.3), the conditional expectation E_ui [·|θ, b_i, y_i] in (13) can be computed analytically. Finally, the proposed MCEM algorithm for estimating the parameters of the QR-LMM can be summarized as follows:

MC E-step

Given θ = θ^(k), for i = 1, …, n;

• Simulation Step: For ℓ = 1, …, m, draw ${\mathbf{b}}_i^{(\ell ,k)}$ from f(b_i|θ^(k), y_i), as described later in Subsection 3.3.

• Monte Carlo approximation: Using (6) and the simulated sample above, evaluate

  $$\mathrm{E}[g({\mathbf{b}}_i,{\mathbf{u}}_i)\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i]\approx \frac{1}{m}\sum _{\ell =1}^m{\mathrm{E}}_{{\mathbf{u}}_i}[g({\mathbf{b}}_i^{(\ell ,k)},{\mathbf{u}}_i)\mid {\mathit{\theta }}^{(k)},{\mathbf{b}}_i^{(\ell ,k)},{\mathbf{y}}_i].$$

M-step

Update θ̂^(k) by maximizing $Q(\mathit{\theta }\mid {\widehat{\mathit{\theta }}}^{(k)})\approx \frac{1}{m}{\sum }_{l=1}^m{\sum }_{i=1}^n{\ell }_c(\theta ;{\mathbf{y}}_i,{\mathbf{b}}_i^{(l,k)},{\mathbf{u}}_i)$ over θ̂^(k), which leads to the following estimates:

$$\begin{array}{ll}\hfill {{\widehat{\mathit{\beta }}}_p}^{(k+1)}=& {\left[\sum _{i=1}^n\left\{\frac{1}{m}\sum _{\ell =1}^m{\mathbf{x}}_i\mathcal{E}{({\mathbf{D}}_i^{-1})}^{(\ell ,k)}{\mathbf{x}}_i^{\top }\right\}\right]}^{-1}\hfill \\ \hfill & \times \left[\sum _{i=1}^n\left\{\frac{1}{m}\sum _{\ell =1}^m[{\mathbf{x}}_i\mathcal{E}{({\mathbf{D}}_i^{-1})}^{(\ell ,k)}[{\mathbf{y}}_i-{\mathbf{z}}_i^{\top }{\mathbf{b}}_i^{(\ell ,k)}-{\vartheta }_p\mathcal{E}{({\mathbf{u}}_i)}^{(\ell ,k)}]]\right\}\right],\hfill \\ \hfill {\widehat{\sigma }}^{(k+1)}=& \frac{1}{3N{\tau }_p^2}\sum _{i=1}^n\{\frac{1}{m}\sum _{\ell =1}^m[{({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p^{(k+1)}-{\mathbf{z}}_i{\mathbf{b}}_i^{(\ell ,k)})}^{\top }\hfill \\ \hfill & \times \mathcal{E}{({\mathbf{D}}^{-1})}^{(\ell ,k)}({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p^{(k+1)}-{\mathbf{z}}_i{\mathbf{b}}_i^{(\ell ,k)})\hfill \\ \hfill & -2{\vartheta }_p{({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p^{(k+1)}-{\mathbf{z}}_i{\mathbf{b}}_i^{(\ell ,k)})}^{\top }{\mathbf{1}}_{n_i}\hfill \\ \hfill & +\frac{{\tau }_p^4}{4}\mathcal{E}{({\mathbf{u}}_i)}^{(\ell ,k)\top }{\mathbf{1}}_{n_i}]\},\hfill \\ \hfill {\widehat{\mathbf{\Psi }}}^{(k+1)}=& \frac{1}{n}\sum _{i=1}^n\left[\frac{1}{m}\sum _{\ell =1}^m{\mathbf{b}}_i^{(\ell ,k)}{{\mathbf{b}}_i^{(\ell ,k)}}^{\top }\right],\hfill \end{array}$$

where $N={\sum }_{i=1}^n{n}_i$ and expressions ℰ(u_i)^(ℓ,k) and $\mathcal{E}{({\mathbf{D}}_i^{-1})}^{(\ell ,k)}$ are defined in Appendix A.2 of the Supplementary Material. Note that for the MC E-step, we need to draw samples ${\mathbf{b}}_i^{(\ell ,k)}$, ℓ = 1, …, m, from f(b_i|θ^(k), y_i), where m is the number of Monte Carlo simulations to be used, a number suggested to be large enough. A simulation method to draw samples from f(b_i|θ^(k), y_i), is described in Subsection 3.3.

3.2 A SAEM algorithm

As mentioned in Subsection 2.2, the SAEM circumvents the cumbersome problem of simulating a large number of missing values at every iteration, leading to a faster and efficient solution than the MCEM. In summary, the SAEM algorithm proceeds as follows:

E-step

Given θ = θ^(k) for i = 1, …, n;

• Simulation step: Draw ${\mathbf{b}}_i^{(\ell ,k)}$, ℓ = 1, …, m, from f(b_i|θ^(k), y_i), for m ≤ 20.

• Stochastic approximation: Update the MC approximations for the conditional expectations by their stochastic approximations, given by

  $$\begin{array}{ll}{S}_{1,i}^{(k)}=\hfill & S_{1,i}^{(k-1)}+{\delta }_k\left[\frac{1}{m}\sum _{\ell =1}^m[{\mathbf{x}}_i\mathcal{E}{({\mathbf{D}}_i^{-1})}^{(\ell ,k)}{\mathbf{x}}_i^{\top }]-S_{1,i}^{(k-1)}\right],\hfill \\ S_{2,i}^{(k)}=\hfill & S_{2,i}^{(k-1)}+{\delta }_k[\frac{1}{m}\sum _{\ell =1}^m[{\mathbf{x}}_i\mathcal{E}{({\mathbf{D}}_i^{-1})}^{(\ell ,k)}[{\mathbf{y}}_i-{\mathbf{z}}_i^{\top }{\mathbf{b}}_i^{(\ell ,k)}\hfill \\ \hfill & -{\vartheta }_p\mathcal{E}{({\mathbf{u}}_i)}^{(\ell ,k)}]]-S_{2,i}^{(k-1)}],\hfill \\ S_{3,i}^{(k)}=\hfill & S_{3,i}^{(k-1)}+{\delta }_k[\frac{1}{m}\sum _{\ell =1}^m[{({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p^{(k+1)}-{\mathbf{z}}_i{\mathbf{b}}_i^{(\ell ,k)})}^{\top }\hfill \\ \hfill & \times \mathcal{E}{({\mathbf{D}}^{-1})}^{(\ell ,k)}({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p^{(k+1)}-{\mathbf{z}}_i{\mathbf{b}}_i^{(\ell .k)})\hfill \\ \hfill & -2{\vartheta }_p{({\mathbf{y}}_i-{\mathbf{x}}_i^{\top }{\mathit{\beta }}_p^{(k+1)}-{\mathbf{z}}_i{\mathbf{b}}_i^{(\ell ,k)})}^{\top }{\mathbf{1}}_{n_i}\hfill \\ \hfill & +\frac{{\tau }_p^4}{4}\mathcal{E}{({\mathbf{u}}_i)}^{(\ell ,k)\top }{\mathbf{1}}_{n_i}]-S_{3,i}^{(k-1)}],\hfill \\ S_{4,i}^{(k)}=\hfill & S_{4,i}^{(k-1)}+{\delta }_k\left[\frac{1}{m}\sum _{\ell =1}^m[{\mathbf{b}}_i^{(\ell ,k)}{{\mathbf{b}}_i^{(\ell ,k)}}^{\top }]-S_{4,i}^{(k-1)}\right].\hfill \end{array}$$

M-step

Update θ̂^(k) by maximizing Q(θ|θ̂^(k)) over θ̂^(k), which leads to the following expressions:

$$\begin{array}{lll}{\widehat{{\mathit{\beta }}_p}}^{(k+1)}\hfill & =\hfill & {\left[\sum _{i=1}^n{S}_{1,i}^{(k)}\right]}^{-1}\sum _{i=1}^n{S}_{2,i}^{(k)},\hfill \\ {\widehat{\sigma }}^{(k+1)}\hfill & =\hfill & \frac{1}{3N{\tau }_p^2}\sum _{i=1}^n{S}_{3,i}^{(k)},\hfill \\ {\widehat{\mathrm{\Psi }}}^{(k+1)}\hfill & =\hfill & \frac{1}{n}\sum _{i=1}^n{S}_{4,i}^{(k)}.\hfill \end{array}$$ (15)

Given a set of suitable initial values θ̂⁽⁰⁾ (see Appendix A.1 of the Supplementary Material), the SAEM iterates till convergence at iteration k, if ${max}_i\left\{\frac{\mid {\widehat{\theta }}_i^{(k+1)}-{\widehat{\theta }}_i^{(k)}\mid }{\mid {\widehat{\theta }}_i^{(k)}\mid +{\delta }_1}\right\}<{\delta }_2$, the stopping criterion, is satisfied for three consecutive times, where δ₁ and δ₂ are pre-established small values. This consecutive evaluation avoids a fake convergence produced by an unlucky Monte Carlo simulation. As suggested by [34] (page. 269), we use δ₁ = 0.001 and δ₂ = 0.0001. This proposed criterion will need an extremely large number of iterations (more than usual) in order to detect parameter convergence that are close to the boundary of the parametric space. In this case for variance components, a parameter value close to zero will inflate the ratio in above and the convergence will not be attained even though the likelihood was maximized with few iterations. As proposed by [4], we also use a second convergence criteria defined by ${max}_i\left\{\frac{\mid {\widehat{\theta }}_i^{(k+1)}-{\widehat{\theta }}_i^{(k)}\mid }{\sqrt{\widehat{var}({\theta }_i^{(k)})+{\delta }_1}}\right\}<{\delta }_2$, where the parameter estimates change relative to their standard errors leading to a convergence detection even for bounded parameters. Once again, δ₁ and δ₂ are some small pre-assigned values, not necessarily equal to the ones in the previous criterion. Based on simulation results, we fix δ₁ = 0.0001 and δ₂ = 0.0002. This stopping criteria is similar to the one proposed by [3] for non-linear least squares.

3.3 Missing data simulation method

In order to draw samples from f(b_i|y_i,θ), we utilize the Metropolis-Hastings (MH) algorithm [28, 14], a MCMC algorithm for obtaining a sequence of random samples from a probability distribution for which direct sampling is not possible. The MH algorithm proceeds as follows:

Given θ = θ^(k), for i = 1, …, n;

1. Start with an initial value ${\mathbf{b}}_i^{(0,k)}$.

2. Draw ${\mathbf{b}}_i^{\ast }~h({\mathbf{b}}_i^{\ast }\mid {\mathbf{b}}_i^{(\ell -1,k)})$ from a proposal distribution with the same support as the objective distribution f(b_i|θ^(k), y_i).

   Generate U ~ U(0, 1).

3. If $U>min\left\{1,\frac{f\left({\mathbf{b}}_i^{\ast }\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\right)h\left({\mathbf{b}}_i^{(0,k)}\mid {\mathbf{b}}_i^{\ast }\right)}{f\left({\mathbf{b}}_i^{(0,k)}\mid {\mathit{\theta }}^{(k)},{\mathbf{y}}_i\right)h\left({\mathbf{b}}_i^{\ast }\mid {\mathbf{b}}_i^{(0,k)}\right)}\right\}$, return to the step 2, else ${\mathbf{b}}_i^{(\ell ,k)}={\mathbf{b}}_i^{\ast }$.

4. Repeat steps 2–4 until m samples ( ${\mathbf{b}}_i^{(1,k)},{\mathbf{b}}_i^{(2,k)},\dots ,{\mathbf{b}}_i^{(m,k)}$) are drawn from b_i|θ^(k), y_i.

Note that the marginal distribution f (b_i|y_i,θ) (omitting θ) can be represented as

$$f({\mathbf{b}}_i\mid {\mathbf{y}}_i)\propto f({\mathbf{y}}_i\mid {\mathbf{b}}_i)\times f({\mathbf{b}}_i),$$

where b_i ~ N_q(0,Ψ) and $f({\mathbf{y}}_i\mid {\mathbf{b}}_i)={\prod }_{j=1}^{n_i}f(y_{ij}\mid {\mathbf{b}}_i)$, with $y_{ij}\mid {\mathbf{b}}_i~\mathit{ALD}({\mathbf{x}}_{ij}^{\top }{\mathit{\beta }}_p+{\mathbf{z}}_{ij}{\mathbf{b}}_i,\sigma ,p)$. Since the objective function is a product of two distributions (with both support lying in ℝ), a suitable choice for the proposal density is a multivariate normal distribution with the mean and variance-covariance matrix that are the stochastic approximations of the conditional expectation $\mathrm{E}({\mathbf{b}}_i^{(k-1)}\mid {\mathbf{y}}_i)$ and the conditional variance $\text{Var}({\mathbf{b}}_i^{(k-1)}\mid {\mathbf{y}}_i)$ respectively, obtained from the last iteration of the SAEM algorithm. This candidate (with possible information about the shape of the target distribution) leads to better acceptance rate, and consequently a faster algorithm. The resulting chain ${\mathbf{b}}_i^{(1,k)},{\mathbf{b}}_i^{(2,k)},\dots ,{\mathbf{b}}_i^{(m,k)}$ is a MCMC sample from the marginal conditional distribution f(b_i|θ^(k), y_i). Due the dependent nature of these MCMC samples, at least 10 MC simulations are suggested.

4. ESTIMATION

4.1 Likelihood estimation

Given the observed data, the likelihood function ℓ_o(θ|y) of the model defined in (8)–(9) is given by

$${\ell }_o(\mathit{\theta }\mid \mathbf{y})=\sum _{i=1}^{n}logf({\mathbf{y}}_i\mid \mathit{\theta }))=\sum _{i=1}^{n}log{\int }_{{ℝ}^q}f({\mathbf{y}}_i\mid {\mathbf{b}}_i;\mathit{\theta })f({\mathbf{b}}_i;\mathit{\theta })d{\mathbf{b}}_i,$$ (16)

where the integral can be expressed as an expectation with respect to b_i, i.e., E_bi [f(y_i|b_i; θ)]. The evaluation of this integral is not available analytically and is often replaced by its MC approximation involving a large number of simulations. However, alternative importance sampling (IS) procedures might require a smaller number of simulations than the typical MC procedure. Following [29], we can compute this integral using an IS scheme for any continuous distribution f̂(b_i; θ) of b_i having the same support as f(b_i; θ). Re-writing (16) as

$${\ell }_o(\mathit{\theta }\mid \mathbf{y})=\sum _{i=1}^{n}log{\int }_{{ℝ}^q}f({\mathbf{y}}_i\mid {\mathbf{b}}_i;\mathit{\theta })\frac{f({\mathbf{b}}_i;\mathit{\theta })}{\widehat{f}({\mathbf{b}}_i;\mathit{\theta })}\widehat{f}({\mathbf{b}}_i;\mathit{\theta })d{\mathbf{b}}_i,$$

we can express it as an expectation with respect to ${\mathbf{b}}_i^{\ast }$, where ${\mathbf{b}}_i^{\ast }~\widehat{f}({\mathbf{b}}_i^{\ast };\theta )$. Thus, the likelihood function can now be expressed as

$${\ell }_o(\mathit{\theta }\mid \mathbf{y})\approx \sum _{i=1}^{n}log\left\{\frac{1}{m}\sum _{\ell =1}^m\left[\prod _{j=1}^{n_i}[f(y_{ij}\mid {\mathbf{b}}_i^{\ast (\ell )};\mathit{\theta })]\frac{f({\mathbf{b}}_i^{\ast (\ell )};\mathit{\theta })}{\widehat{f}({\mathbf{b}}_i^{\ast (\ell )};\mathit{\theta })}\right]\right\},$$ (17)

where { ${\mathbf{b}}_i^{\ast (\ell )}$}, l = 1, …, m, is a MC sample from $\widehat{f}({\mathbf{b}}_i^{\ast };\mathit{\theta })$, and $f({\mathbf{y}}_i\mid {\mathbf{b}}_i^{\ast (\ell )};\mathit{\theta })$ is expressed as ${\prod }_{j=1}^{n_i}f(y_{ij}\mid {\mathbf{b}}_i^{\ast (\ell )};\mathit{\theta })$ due to independence. An efficient choice for $\widehat{f}({\mathbf{b}}_i^{\ast (\ell )};\theta )$ is f(b_i|y_i). Therefore, we use the same proposal distribution discussed in Subsection 3.3, and generate samples ${\mathbf{b}}_i^{\ast (\ell )}~N_q({\widehat{\mathit{\mu }}}_{{\mathbf{b}}_i},{\widehat{\mathbf{\sum }}}_{{\mathbf{b}}_i})$, where ${\widehat{\mathit{\mu }}}_{{\mathbf{b}}_i}=\mathrm{E}({\mathbf{b}}_i^{(w)}\mid {\mathbf{y}}_i)$ and Σ̂_bi = Var(b_i|y_i), which are estimated empirically during the last few iterations of the SAEM at convergence.

4.2 Standard error approximation

Louis’ missing information principle [26] relates the score function of the incomplete data log-likelihood with the complete data log-likelihood through the conditional expectation ∇_o(θ) = E_θ[∇_c(θ;Y_com|Y_obs)], where ∇_o(θ) = ∂ℓ_o(θ;Y_obs)/∂θ and ∇_c(θ) = ∂ℓ_c(θ;Y_com)/∂θ are the score functions for the incomplete and complete data, respectively. As defined in [27], the empirical information matrix can be computed as

$${\mathbf{I}}_e(\mathit{\theta }\mid \mathbf{y})=\sum _{i=1}^n\mathbf{s}({\mathbf{y}}_i\mid \mathit{\theta }){\mathbf{s}}^{\top }({\mathbf{y}}_i\mid \widehat{\mathit{\theta }})-\frac{1}{n}\mathbf{S}(\mathbf{y}\mid \mathit{\theta }){\mathbf{S}}^{\top }(\mathbf{y}\mid \mathit{\theta }),$$ (18)

where $\mathbf{S}(\mathbf{y}\mid \mathit{\theta })={\sum }_{i=1}^n\mathbf{s}({\mathbf{y}}_i\mid \mathit{\theta })$, with s(y_i|θ) the empirical score function for the i-th individual. Replacing θ by its ML estimator θ̂ and considering ∇_o(θ̂) = 0, equation (18) takes the simple form

$${\mathbf{I}}_e(\widehat{\mathit{\theta }}\mid \mathbf{y})=\sum _{i=1}^n\mathbf{s}({\mathbf{y}}_i\mid \widehat{\mathit{\theta }}){\mathbf{s}}^{\top }({\mathbf{y}}_i\mid \widehat{\mathit{\theta }}).$$ (19)

At the kth iteration, the empirical score function for the i-th subject can be computed as

$$\mathrm{s}{({\mathbf{y}}_i\mid \mathit{\theta })}^{(k)}=\mathbf{s}{({\mathbf{y}}_i\mid \mathit{\theta })}^{(k-1)}+{\delta }_k\left[\frac{1}{m}\sum _{\ell =1}^m\mathbf{s}({\mathbf{y}}_i,{\mathbf{q}}^{(\ell ,k)};{\mathit{\theta }}^{(k)})-\mathbf{s}{({\mathbf{y}}_i\mid \mathit{\theta })}^{(k-1)}\right],$$ (20)

where q^(ℓ,k), ℓ = 1, …, m, are the simulated missing values drawn from the conditional distribution f(·|θ^(k−1), y_i). Thus, at iteration k, the observed information matrix can be approximated as ${\mathbf{I}}_e{(\mathit{\theta }\mid \mathbf{y})}^{(k)}={\sum }_{i=1}^n\mathbf{s}{({\mathbf{y}}_i\mid \mathit{\theta })}^{(k)}{\mathbf{s}}^{\top }{({\mathbf{y}}_i\mid \mathit{\theta })}^{(k)}$, such that at convergence, ${\mathbf{I}}_e^{-1}(\widehat{\mathit{\theta }}\mid \mathbf{y})={({\mathbf{I}}_e(\mathit{\theta }{\mid \mathbf{y})\mid }_{\mathit{\theta }=\widehat{\mathit{\theta }}})}^{-1}$ is an estimate of the covariance matrix of the parameter estimates. Expressions for the elements of the score vector with respect to θ are given in Appendix A.3 of the Supplementary Material.

5. SIMULATION STUDIES

In this section, the finite sample performance of the proposed algorithm and its performance comparison with the method of [13] is evaluated via simulation studies. These computational procedures were implemented using the R software [33]. In particular, we consider the following linear mixed model:

$$y_{ij}={\mathbf{x}}_{ij}^{\top }\mathit{\beta }+{\mathbf{z}}_{ij}\mathbf{b}+{\epsilon }_{ij},i=1,\dots ,n,j=1,\dots ,3,$$ (21)

where the goal is to estimate the fixed effects parameters β for a grid of percentiles p = {0.05, 0.10, 0.50, 0.90, 0.95}. We simulated a 3 × 3 design matrix ${\mathbf{x}}_{ij}^{\top }$ for the fixed effects β, where the first column corresponds to the intercept and the other columns generated from a N₂(0, I₂) density, for all i = 1, …, n. We also simulated a 3×2 design matrix associated with the random effects, with the columns distributed as N₂(0, I₂). The fixed effects parameters were chosen as β₁ = 0.8, β₂ = 0.5 and β₃ = 1, σ = 0.20, and the matrix Ψ with elements Ψ₁₁ = 0.8, Ψ₁₂ = 0.5 and Ψ₂₂ = 1. The error terms ε_ij are generated independently from an ALD(0, σ, p), where p stands for respective percentile to be estimated. For varying sample sizes of n = 50, 100, 200 and 300, we generate 100 data samples for each scenario. In addition, we also choose m = 20, W = 500 (the number of Monte-Carlo simulations corresponding to each data sample) and c = 0.2. Note, the choice of c depends on the dataset, and also the underlying model. We set c = 0.2, given that an initial run of 100 iterations (which is 20% of W) for the 0.05th quantile led to convergence to the neighborhood solution.

For all scenarios, we compute the square root of the mean square error (RMSE), the bias (Bias) and the Monte carlo standard deviation (MC-Sd) for each parameter over the 100 replicates. They are defined as $\text{MC-Sd}(\widehat{{\theta }_i})=\sqrt{\frac{1}{99}{\sum }_{j=1}^{100}{\left({\widehat{{\theta }_i}}^{(j)}-\overline{\widehat{{\theta }_i}}\right)}^2},\text{Bias}(\widehat{{\theta }_i})=\overline{\widehat{{\theta }_i}}-{\theta }_i$, and $\text{RMSE}(\widehat{{\theta }_i})=\sqrt{\text{MC-}{\text{Sd}}^2(\widehat{{\theta }_i})+{\text{Bias}}^2(\widehat{{\theta }_i})}$, where $\overline{\widehat{{\theta }_i}}=\frac{1}{100}{\sum }_{j=1}^{100}{\widehat{{\theta }_i}}^{(j)}$ and θ_i ^(j) is the estimate of θ_i from the j-th sample, j = 1…100. In addition, we also computed the average of the standard deviations (IM-Sd) obtained via the observed information matrix derived in Subsection 4.2 and the 95% coverage probability (MC-CP) as $\text{CP}({\widehat{\theta }}_i)=\frac{1}{100}{\sum }_{j=1}^{100}I({\theta }_i\in [{\widehat{\theta }}_{i,\mathit{LCL}},{\widehat{\theta }}_{i,\mathit{UCL}}])$, where I is the indicator function such that θ_i lies in the interval [θ̂_i,LCL, θ̂_i,UCL], with θ̂_i,LCL and θ̂_i,UCL as the estimated lower and upper bounds of the 95% CIs, respectively.

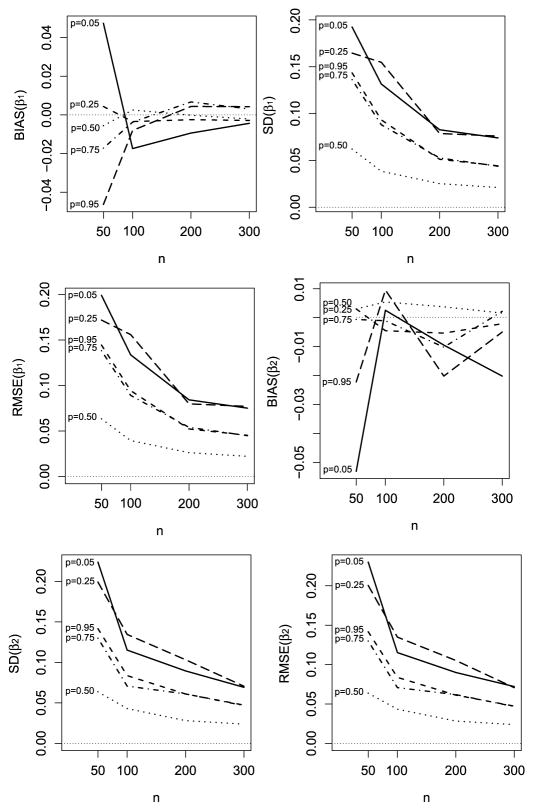
The results are summarized in Figure 2. We observe that the Bias, SD and RMSE for the regression parameters β₁ and β₂ tends to approach zero with increasing sample size (n), revealing that the ML estimates obtained via the proposed SAEM algorithm are conformable to the expected asymptotic properties. In addition, Table 1 presents the IM Sd, MC-Sd and MC-CP for β₁ and β₂ across various quantiles. The estimates of MC-Sd and IM-Sd are very close, hence we can infer that the asymptotic approximation of the parameter standard errors are reliable. Furthermore, as expected, we observe that the MC-CP remains lower for extreme quantiles.

Figure 2.

Bias, Standard Deviation and RMSE for β₁ (upper panel) and β₂ (lower panel) for varying sample sizes over the quantiles p = 0.05, 0.10, 0.50, 0.90, 0.95.

Table 1.

Monte Carlo standard deviation (MC-Sd), mean standard deviation (IM-Sd) and Monte Carlo coverage probability (MC-CP) estimates of the fixed effects β₁ and β₂ from fitting the QR-LMM under various quantiles for sample size n = 100

	β1			β2
Quantile (%)	MC-Sd	IM-Sd	MC-CP	MC-Sd	IM-Sd	MC-CP
5	0.073	0.060	90	0.067	0.059	90
10	0.045	0.044	95	0.047	0.044	96
50	0.022	0.024	97	0.024	0.025	96
90	0.045	0.045	92	0.047	0.044	96
95	0.060	0.056	88	0.071	0.056	83

Finally, we compare the performance of SAEM algorithm with the approximate method proposed by [11]. The Geraci’s algorithm can be implemented using the R package lqmm(). The results are presented in Table 2 and Figure B.1 (Supplementary Material). We observe that the RMSE from the proposed SAEM algorithm are lower than Geraci method across all scenarios, with the differences considerably higher for the extreme quantiles. Finally, Figure B.2 (Supplementary Material) that compares the differences in SD between the two methods for fixed effects β₁ and β₂ at specified quantiles reveals that the SD are mostly smaller for the SAEM method. Thus, we conclude that the SAEM algorithm produces more precise estimates.

Table 2.

Simulation 1: Root Mean Squared Error (RMSE) for the fixed effects β₀, β₁, β₂ and the nuisance parameter σ, obtained after fitting our QR-LMM and the Geraci’s model [11] to simulated data under various settings of quantiles and sample sizes

RMSE
		β0		β1		β2		σ
Quantile (%)	n	SAEM	Geraci	SAEM	Geraci	SAEM	Geraci	SAEM	Geraci
5	50	0.249	0.622	0.199	0.311	0.230	0.296	0.024	0.046
	100	0.209	0.496	0.134	0.180	0.115	0.165	0.017	0.037
	200	0.195	0.303	0.084	0.099	0.090	0.137	0.017	0.029
	300	0.163	0.345	0.075	0.100	0.072	0.101	0.012	0.031
10	50	0.159	0.382	0.144	0.187	0.142	0.201	0.023	0.048
	100	0.112	0.355	0.094	0.117	0.084	0.130	0.019	0.048
	200	0.082	0.231	0.052	0.087	0.061	0.081	0.017	0.036
	300	0.073	0.223	0.045	0.072	0.047	0.076	0.011	0.034
50	50	0.063	0.107	0.063	0.090	0.064	0.102	0.025	0.174
	100	0.042	0.052	0.040	0.056	0.043	0.070	0.021	0.196
	200	0.027	0.053	0.026	0.048	0.028	0.039	0.016	0.164
	300	0.024	0.034	0.022	0.022	0.024	0.040	0.012	0.180
90	50	0.160	0.389	0.138	0.159	0.130	0.177	0.025	0.050
	100	0.102	0.394	0.089	0.100	0.071	0.126	0.019	0.051
	200	0.085	0.240	0.054	0.097	0.062	0.078	0.014	0.038
	300	0.065	0.276	0.045	0.066	0.047	0.064	0.011	0.038
95	50	0.255	0.552	0.172	0.255	0.200	0.243	0.020	0.040
	100	0.233	0.470	0.156	0.169	0.135	0.161	0.020	0.036
	200	0.146	0.423	0.080	0.160	0.105	0.106	0.015	0.038
	300	0.157	0.468	0.077	0.113	0.071	0.061	0.014	0.036

6. APPLICATIONS

In this section, we illustrate the application of our method to two interesting longitudinal datasets from the literature via our developed R package qrLMM, currently available for free download from the R CRAN (Comprehensive R Archive Network).

6.1 Cholesterol data

The Framingham cholesterol study generated a benchmark dataset [41] for longitudinal analysis to examine the role of serum cholesterol as a risk factor for the evolution of cardiovascular disease. We analyze this dataset with the aim of explaining the full conditional distribution of the serum cholesterol as a function of a set of covariates of interest via modelling a grid of response quantiles. We fit a LMM model to the data as specified by

$$Y_{ij}={\beta }_0+{\beta }_1{\text{gender}}_i+{\beta }_2{\text{age}}_i+b_{0i}+b_{1i}{t}_{ij}+{\epsilon }_{ij},$$ (22)

where Y_ij is the cholesterol level (divided by 100) at the jth time point for the ith subject, t_ij = (τ − 5)/10 where τ is the time measured in years from the start of the study, age denotes the subject’s baseline age, gender is the dichotomous gender (0=female, 1=male), b_0i and b_1i the random intercept and slope, respectively, for subject i, and ε_ij the measurement error term, for 200 randomly selected subjects.

We fit the proposed SAEM algorithm and the approximate method of Geraci [11] over the grid p = {0.05, 0.10, …, 0.95} to the cholesterol dataset. Figure 3 plots the standard errors (SE) of the fixed effects parameters β₀ − β₂, and the AIC from both models. We observe that our SAEM method leads to mostly smaller SEs and AIC compared to the Geraci method. The SEs corresponding to the extreme quantiles are substantially lower. This supports the simulation findings. Interestingly, for the extremes quantiles, some warnings messages on convergence were displayed while fitting Geraci’s method, even after increasing the number of iterations and reducing the tolerance, as suggested in the lqmm manual. However, the mean estimation time per quantile for the SAEM method was about 7 hours compared to 1 hour for Geraci’s method. Hence, although the SAEM algorithm is relatively slow, the substantial gain in the AIC criterion and the SEs establish that our SAEM approach provides a much better fit to the dataset.

Figure 3.

Standard errors for the fixed effects β₀, β₁ and β₂ and AIC over the quantiles p = {0.05, 0.10, …, 0.95} from fitting the proposed QR-LMM model and Geraci’s method to the Cholesterol data.

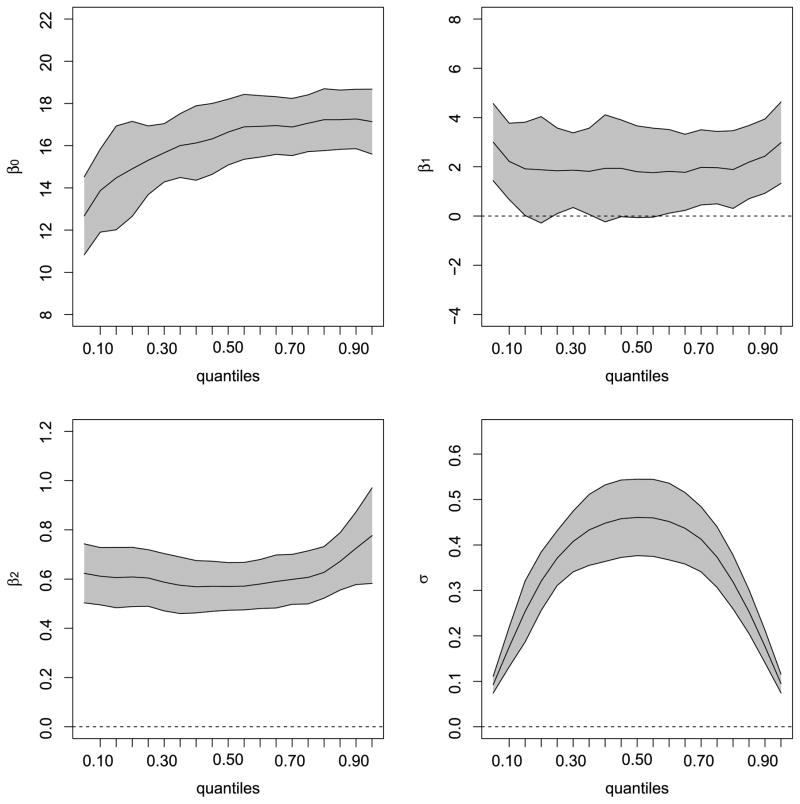
Figure 4 presents graphical summaries (confidence bands) for the fixed effects parameters β₀, …, β₂, and the nuisance parameter σ. The solid lines represent the 2.5th, 50th and, 97.5th percentiles across various quantiles, obtained from the estimated standard errors defined in Subsection 4.2. The figures reveal that the effect of gender and age become more prominent with increasing conditional quantiles. In addition, although age exhibits a positive influence on the cholesterol level across all quantiles, the confidence band for gender includes 0 across all quantiles, and hence its effect is nonsignificant. The estimated nuisance parameter σ is symmetric about p = 0.5, taking its maximum value at that point and decreasing for the extreme quantiles. Figure B.3 (Supplementary Material) plots the fitted regression lines for the quantiles 0.10, 0.25, 0.50 (the mean), 0.75 and 0.90 by gender. From this figure, it is clear how the extreme quantiles capture the full data variability and detect some atypical observations. The intercept of the quantile functions look very similar for both panels due to the non-significant gender.

Figure 4.

Point estimates (center solid line) and 95% confidence intervals across various quantiles for model parameters after fitting the proposed QR-LMM model to the Cholesterol data using the qrLMM package. The interpolated curves are spline-smoothed.

6.2 Orthodontic distance growth data

A second application was developed using a data set form a longitudinal orthodontic study [32, 31] performed at the University of North Carolina Dental School. Here, researchers measured the distance between the pituitary and the pterygomaxillary fissure (two points that are easily identified on x-ray exposures of the side of the head) for 27 children (16 boys and 11 girls) every two years from age 8 until age 14. Similar to Application 1, we fit the following LMM to the data:

$$Y_{ij}={\beta }_0+{\beta }_1{\text{gender}}_i+{\beta }_2{t}_{ij}+b_{0i}+b_{1i}{t}_{ij}+{\epsilon }_{ij},$$ (23)

where Y_ij is the distance between the pituitary and the pterygomaxillary fissure (in mm) at the jth time for the ith child, t_ij is the child’s age at time j taking values 8, 10, 12, and 14 years, gender is a dichotomous variable (0=female, 1=male) for child i and ε_ij the random measurement error term. Initial exploratory plots for 10 random children in the left panel of Figure B.4 (Supplementary Material) suggest an increasing distance with respect to age. The individual profiles by gender (right panel) show differences between distances for boys and girls (distance for boys greater than those for girls), and hence we could expect a significant gender effect. Once again, after fitting the QR-LMM over the grid p = {0.05, 0.10, …, 0.95}, the point estimates and associated 95% confidence bands for model parameters are presented in Figure 5. From the figure, we infer that the effect of gender and age are significant across all quantiles, with their effect increasing for higher conditional quantiles. Effect of Age is always positive across all quantiles, with a higher effect at the two extremes. σ behaves the same as in Application 1. Figure B.5 (Supplementary Material) plots the fitted regression lines for the quantiles 0.10, 0.25, 0.50, 0.75 and 0.90, overlayed with the individual profiles (gray solid lines), by gender. These fits capture the variability of the individual profiles, and also differ by gender due to its significance in the model. The R package also produces graphical summaries of point estimates and confidence intervals (95% by default) across various quantiles, as presented in Figures 4 and 5. Trace plots showing convergence of these estimates are presented in Figure B.6 (Supplementary Material). For example, for the 75th quantile, we can confirm that the convergence parameters for the SAEM algorithm (M = 10, c = 0.25 and W = 300) has been set adequately leading to a quick convergence in distribution within the first 75 iterations, and then converging almost surely to a local maxima in a total of 300 iterations. Sample output from the qrLMM package is provided in Appendix C of the Supplementary Material.

Figure 5.

Point estimates (center solid line) and 95% confidence intervals for model parameters across various quantiles from fitting the QR-LMM using the qrLMM package to the orthodontic growth distance data. The interpolated curves are spline-smoothed.

7. CONCLUSIONS

In this paper, we developed likelihood-based inference for QR-LMM, where the likelihood function is based on the ALD. The ALD presents a convenient framework for the implementation of the SAEM algorithm leading to the exact ML estimation of the parameters. The methodology is illustrated via application to two longitudinal clinical datasets. We believe this paper is the first attempt for exact ML estimation in the context of QR-LMMs, and provide improvement over the methods proposed by Geraci and his co-authors [13, 11]. The methods developed here are readily implementable via the R package qrLMM(). Our proposition is parametric. Although nonparametric considerations [24] are available for the standard linear QR problem, adapting those to the LMM framework can lead to non-trivial computational bottlenecks. This is possibly a research direction to pursue.

Certainly, other distributions can be used as alternatives to the ALD. Recently, [37] presented a generalized class of skew density for QR that provides competing solutions to the ALD-based formulation. However, their exploration is limited to the simple linear QR framework. Also, due to the lack of a relevant stochastic representation, the corresponding EM-type implementation can lead to difficulties. Recently, [8] presented an R package for a linear QR using a new family of skew distributions that includes the ones formulated in [37] as special cases. This family includes the skewed version of Normal, Student-t, Laplace, Contaminated Normal and Slash distribution, all with the zero quantile property for the error term, and with a convenient stochastic representation. Undoubtedly, incorporating this skewed class into our LMM proposition can enhance flexibility, and potentially improve our inference. Furthermore, for QR-LMM, its robustness against outliers can be seriously affected in presence of skewness and thick-tails. Not long ago, [22] proposed a parametric remedy using scale mixtures of skew-normal distributions in the random effects. We conjecture that this methodology can be transferred to the QR-LMM framework, and should yield satisfactory results at the expense of additional complexity in implementation. An in-depth investigation of these propositions are beyond the scope of the present paper, and will be considered elsewhere.