Tracking excited–state charge and spin dynamics in iron coordination complexes

Abstract

Crucial to many light-driven processes in transition metal complexes is the absorption and dissipation of energy by 3d electrons^1–4. But a detailed understanding of such non-equilibrium excited-state dynamics and their interplay with structural changes is challenging: a multitude of excited states and possible transitions result in phenomena too complex to unravel when faced with the indirect sensitivity of optical spectroscopy to spin dynamics⁵ and the flux limitations of ultrafast X-ray sources^6,7. Such a situation exists for archetypal polypyridyl iron complexes, such as [Fe(2,2′-bipyridine)₃]²⁺, where the excited-state charge and spin dynamics involved in the transition from a low- to a high-spin state (spin crossover) have long been a source of interest and controversy^6–15. Here we demonstrate that femtosecond resolution X-ray fluorescence spectroscopy, with its sensitivity to spin state, can elucidate the spin crossover dynamics of [Fe(2,2′-bipyridine)₃]²⁺ on photoinduced metal-to-ligand charge transfer excitation. We are able to track the charge and spin dynamics, and establish the critical role of intermediate spin states in the crossover mechanism. We anticipate that these capabilities will make our method a valuable tool for mapping in unprecedented detail the fundamental electronic excited-state dynamics that underpin many useful light-triggered molecular phenomena involving 3d transition metal complexes.

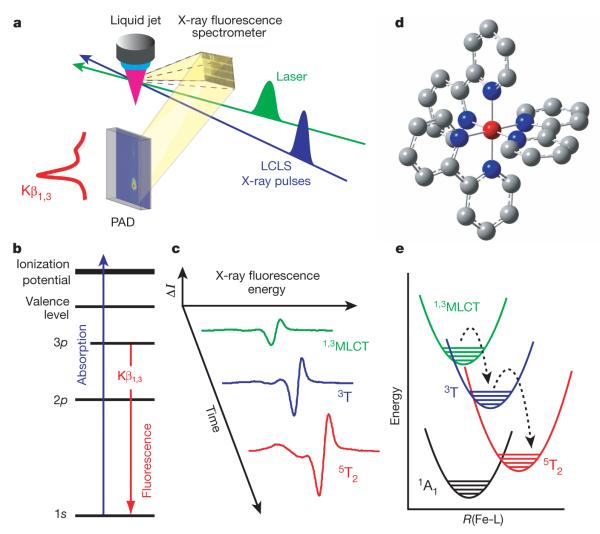
The femtosecond duration of the intense hard X-ray pulses generated by the LCLS (Linac Coherent Light Source) X-ray free-electron laser^16,17 creates the opportunity to study spin dynamics with iron 3p–1s (Kβ) X-ray fluorescence spectroscopy^18,19. Figure 1 shows diagrams of the measurement technique and relevant energy levels (Fig. 1–c), a ‘ball-and-stick’ representation of the [Fe(2,2′-bipyridine)₃]²⁺ complex (Fig. 1d), and the dependence of photoexcited spin crossover dynamics on the Fe–ligand distance (Fig. 1e). Given the roughly 100 femtosecond (fs) time resolution of the measurement¹⁷, the subfemtosecond lifetime of the iron 1s core hole makes X-ray fluorescence an effectively instantaneous probe²⁰. A variety of distinct electronic excited states, including singlet and triplet metal-to-ligand charge transfer states (^1,3MLCT), triplet ligand field excited states (³T) and quintet ligand field excited states (⁵T₂) have been proposed to participate in the spin crossover mechanism^{6,8,10,11,21,22} (Fig. 1e). Distinguishing electronic excited states with different charge and spin density, such as the ^1,3MLCT, ³T and ⁵T₂ states listed above, represents a critical step in characterizing the spin crossover mechanism.

Figure 1. Schematic depiction of ultrafast X-ray fluorescence detection of spin crossover dynamics.

a, Experimental set-up involving liquid jet for sample replenishment, optical laser pump, and 8-keV X-ray beam for generating X-ray fluorescence measured with a dispersive crystal spectrometer. b, Energy level diagram for Kβ fluorescence involving photo-ionization of a 1s electron and X-ray fluorescence originating from the transition of a 3p electron to the 1s hole. c, Schematic diagram of how the spin crossover dynamics influence the time-dependent Kβ fluorescence difference spectra. d, Molecular structure of [Fe(2,2′-bipyridine)₃]²⁺ (red, Fe atom; blue, N; grey, C; H not shown). e, A schematic drawing of the potential energy surfaces involved in the spin crossover dynamics.

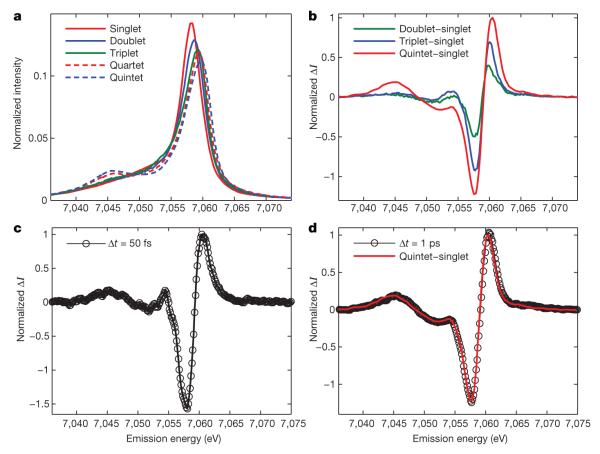
Figure 2a shows the sensitivity of the iron Kβ fluorescence spectrum to the 3d spin moment, a sensitivity that results from the exchange interaction between the 3p and 3d electrons^{18,19,23–25}. Equally important, the ground-state spectra of iron coordination complexes with different ligation, but the same iron spin moment, exhibit similar Kβ fluorescence spectra. This insensitivity of Kβ fluorescence spectroscopy to the details of the coordinating ligands and the local symmetry of the complex has previously been used to characterize the electronic ground-state spin moment of a variety of molecular systems^19,25. We note that the insensitivity of the Kβ fluorescence spectrum to the electronic properties of the ligand means that the spectrum cannot be used to distinguish between singlet and triplet MLCT states. We utilize these spectra of distinct spin configurations to model transient difference spectra—that is, the time and energy dependence of the fluorescent amplitude difference between excited-state and ground-state spectra. Figure 2b shows the model complex difference spectra generated from the ground-state spectra of the relevant excited-state spin configurations and the singlet ground state. These model complex difference spectra confirm that each excited-state spin moment generates a distinct difference spectrum that cannot be reproduced by a linear combination of the other difference spectra (see Fig. 2, Extended Data Fig. 1 and Methods for details).

Figure 2. Spin-dependent iron Kβ fluorescence spectra.

a, The Kβ fluorescence spectra of ground-state iron complexes with different spin moments: singlet ([Fe(2,2′-bipyridine)₃]²⁺, red), doublet ([Fe(2,2′-bipyridine)₃]³⁺, blue), triplet (iron(II) phthalocyanine, green), quartet (iron(III) phthalocyanine chloride, red dashed), and quintet ([Fe(phenanthroline)₂(NCS)₂], blue dashed). b, Model complex difference spectra for the ^1,3MLCT, ³T and ⁵T₂ excited states constructed by subtracting the singlet model complex spectrum from the doublet, triplet and quintet model complex spectra shown in a. c, Kβ transient difference spectra obtained at 50-fs time delay for [Fe(2,2′-bipyridine)₃]²⁺ (black circles). The best fit of this difference spectra can be found in Extended Data Fig. 4. d, Kβ transient difference spectra obtained at 1-ps time delay for [Fe(2,2′-bipyridine)₃]²⁺ (black circles), which closely matches the model complex difference spectra (red) obtained when subtracting the singlet from the quintet spectra shown in a.

The time-resolved Kβ fluorescence spectra provide the sensitivity to spin dynamics needed to answer a critical question regarding the spin crossover mechanism: does the ⁵T₂ state form directly from the ^1,3MLCT state^6,13,26, or does spin crossover involve a ³T transient^8,10? Ultraviolet–visible transient absorption^13,14, time-resolved luminescence¹³, and time-resolved iron K-edge XANES⁶ have been used to characterize the spin crossover dynamics of [Fe(2,2′-bipyridine)₃]²⁺, and the similar rates measured for ³MLCT decay and ⁵T₂ formation were attributed to the ³MLCT excited state converting directly to the ⁵T₂ excited state, although a conversion including transient triplet states was also considered⁶. Potential energy surfaces calculated for this system allow either mechanism to proceed with minimal reaction barriers^21,22, but cannot explain why the ^1,3MLCT and ⁵T₂ states should be strongly coupled: the leading order spin–orbit interaction cannot couple the ^1,3MLCT and ⁵T₂ states because a transition between these states requires the excitation of two electrons on two distinct centres, whereas spin–orbit coupling is predominantly a single-centre, one-electron operator²².

Figure 2c, d shows the transient difference spectra for [Fe(2,2′-bipyridine)₃]²⁺ measured for a 50-fs and a 1-ps (picosecond) time delay. The spectrum in Fig. 2d clearly demonstrates the ease of identifying the ⁵T₂ state with the Kβ fluorescence spectrum. Determining whether spin crossover from the ^1,3MLCT to the ⁵T₂ proceeds through a transient ³T state proves more challenging because the relaxation dynamics do not lead to a time regime where the majority of the excited molecules reside in the ³T excited state. The significant difference between the spectra in Fig. 2c and d, however, clearly demonstrates the presence of excited-state species other than the ⁵T₂ state. With statistically rigorous kinetic modelling, ^1,3MLCT, ³T and ⁵T₂ states can be clearly distinguished in the relaxation dynamics probed with Kβ fluorescence.

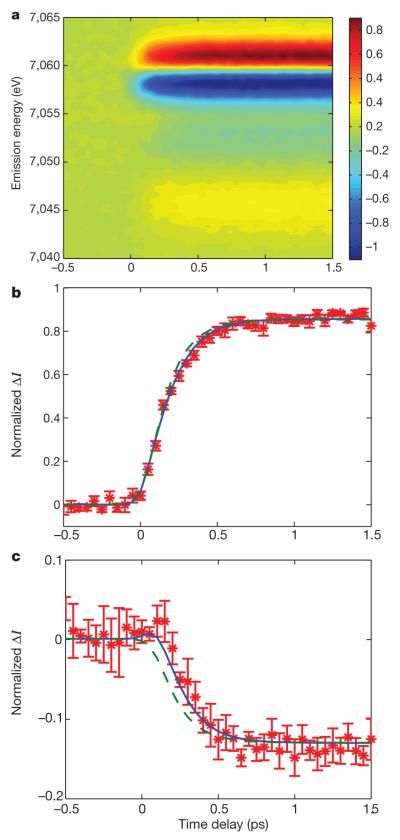
The ability to spectroscopically distinguish between ^1,3MLCT, ³T and ⁵T₂ electronic excited states allows the spin crossover mechanism to be determined from the time evolution of the iron Kβ fluorescence spectrum. The time-resolved difference spectra, model fits of the difference spectra, and the parameters extracted from the fit can be found in Fig. 3, Extended Data Figs 2–4 and Extended Data Table 1. We have fitted the difference spectra to two distinct models: one where the ^1,3MLCT decays directly to a ⁵T₂ excited state and one where the ^1,3MLCT relaxes to the ⁵T₂ state via a ³T transient. Figure 3b, c shows the time-dependent difference signal measured at two X-ray fluorescence energies: 7,061 eV, where the difference signal is largest, and 7,054 eV, where the triplet model complex has a spectral signature clearly distinct from the ^1,3MLCT and ⁵T₂ states as shown in Fig. 2b. The fits in Fig. 3b, c have been determined from a global analysis of the full time-dependent spectra. The statistical significance of the more complex kinetic model involving the triplet transient can be determined from an F-test comparison of the two models (described in Methods). The reduction in residuals achieved with the model containing the triplet transient is sufficient to reject the direct ^1,3MLCT→⁵T₂ model with greater than 95% confidence. Note that the successful use of a kinetic model to describe subpicosecond dynamics implies that the Kβ spectra do not depend significantly on the time-evolving nuclear structure, consistent with the insensitivity of the ground-state Kβ spectra to the ligand details.

Figure 3. Time-dependent photo-induced iron Kβ difference spectra and kinetic modelling of spin crossover dynamics.

a, Time-dependent optically induced two-dimensional Kβ fluorescence difference spectra for [Fe(2,2′-bipyridine)₃]²⁺. b, c, The difference signal measured at a Kβ fluorescence energy of 7,061 eV (b) and 7,054 eV (c) for [Fe(2,2′-bipyridine)₃]²⁺ (red stars), as well as the best fit achieved for kinetic models with (blue) or without (green dashed) a ³T_1,2 transient. The error bars in b and c reflect the standard error for the difference signal determined from six independent measurements.

The successful analysis of the experimental data relies on two constraints presented by the model spectra shown in Fig. 2b and two constraints derived from the kinetic models. We force (1) the shape and (2) the relative amplitudes of the difference signals for the ^1,3MLCT, ³T and ⁵T₂ electronic excited states to match the shape and relative amplitudes of the model complex difference spectra. We also require (3) allX-ray fluorescence energies to be fitted with a single time zero and (4) all MLCT excited states to undergo spin crossover, consistent with previous measurements of the spin crossover quantum yield¹³. The ultrafast rise of the difference signal shown in Fig. 3b greatly constrains the value of time zero and the final ⁵T₂ state population. For the fit to the direct spin crossover mechanism shown in Fig. 3b, the fast rise in signal at 7,061 eV requires a fast rise in ⁵T₂ population. As shown in Fig. 3c, the fast rise in the direct mechanism fit at 7,061 eV also leads to a fast drop in signal at 7,054 eV, because the ⁵T₂ state has a negative difference signal at 7,054 eV. For the fit to the sequential spin crossover mechanism also shown in Fig. 3b, the fast rise in signal at 7,061 eV can be accommodated initially by a rise in ³T population. Because the ³T state does not have a negative difference signal at 7,054 eV, the fast rise in ³T population does not lead to a fast drop at 7,054 eV. The stepwise transition through the ³T leads to a delayed onset of the drop in fluorescence amplitude at 7,054 eV relative to the rise in signal at 7,061 eV, consistent with the experimental data. For the direct model, a shift in time zero to fit the data in Fig. 3c would lead to a poor fit of the data in Fig. 3b.

Relaxation to the ⁵T₂ excited state via a ³T transient provides a more satisfying explanation for the relaxation dynamics. We speculate that the sequential relaxation occurs more promptly than the direct crossover from the ^1,3MCLT to the ⁵T₂ excited state because the sequential transition involves single electronic transitions coupled by a spin–orbit operator, whereas the direct transition involves the simultaneous transition of two distinct electrons on two centres and cannot occur with the first-order spin–orbit operator. The sequential relaxation, like the direct transition, provides an energetically feasible pathway with minimal reaction barriers between states that can be coupled with standard spin–orbit interactions²². The spin–orbit matrix elements in conjunction with the calculated potential energies of a variety of electronic excited states of [Fe(2,2′-bipyridine)₃]²⁺ as a function of the metal–ligand bond distance provide an approximate explanation for the fast intersystem crossing and the extremely short lifetime of the ³T excited state. A diagram of these potential energy surfaces can be found in Fig. 1e. In principle, the triplet ligand field excited state could be either a ³T₁ or a ³T₂ state. Computations indicate a crossing of the ³T₂ state in the Franck–Condon region of the ^1,3MLCT excited state and that the ^1,3MLCT→³T₂→⁵T₂ pathway dominates²⁷; however, relaxation trajectories involving the ³T₁ ligand field excited state remain plausible, and more definite conclusions will require a more complete calculation of the multidimensional potential energy surfaces, including the potentially important role of metal–ligand torsional motion²⁸. The sequential model fit in Fig. 3 gives a 150 ± 50 fs time constant for ^1,3MLCT decay to the ³T state and a 70 ± 30 fs time constant for ³T decay to the ⁵T₂ state. Although the mechanistic conclusions we have drawn from our measurements differ from the earlier interpretation²⁶, our experimental findings do not contradict the earlier results, but rather expand on them. The extracted decay time for the ^1,3MLCT excited state and the effective rise time for the ⁵T₂ excited state agree with the time constants observed previously within experimental error²⁶. The similarity of the ^1,3MLCT decay time and the ⁵T₂ rise time results from the rate of ³T decay being greater than that of ³T formation. This inhibits the build-up of molecules in the ³T excited state and challenges the temporal differentiation of the distinct electronic states involved in spin crossover (see Extended Data Fig. 2d). Only with a technique highly sensitive to the iron spin multiplicity can the presence of the ³T transient excited state in the relaxation dynamics be robustly resolved.

The complex excited-state electronic structure of molecules containing transition metals has inhibited the unambiguous interpretation of experimental measurements and the development of excited-state quantum dynamics simulations. We have demonstrated here that ultrafast X-ray fluorescence spectroscopy enables robust measurements of the charge and spin dynamics integral to excited-state relaxation in 3d transition-metal coordination complexes, which represents an important step towards an incisive mechanistic understanding of excited-state dynamics in 3d transition metal complexes.

METHODS

Experimental procedures

We performed femtosecond hard X-ray fluorescence measurements on a 50 mM solution of [Fe(2,2′-bipyridine)₃]²⁺ in water at the X-ray pump-probe (XPP) instrument at the Linac Coherent Light Source (LCLS). The experiment used a 0.1 mm thick planar liquid jet oriented at an angle of 45° with respect to the direction of the incident X-ray beam. We measured the ultra-violet–visible absorption spectrum of the solution before and after the measurement to ensure no appreciable sample damage had occurred. The sample solution was collinearly excited with a 70 fs FWHM 520 nm laser beam (120 mJ cm⁻²) generated by optical parametric amplification of the 800 nm output of a Ti:sapphire regenerative amplifier laser system (Coherent, Legend). With 520 nm light, we excited [Fe(2,2′-bipyridine)₃]²⁺ at the peak of the MLCT band (Extended Data Fig. 5a). We set the pump laser fluence to maximize excitation yield, while avoiding other deleterious photophysical phenomena. Previous time-resolved hard X-ray spectroscopy measurements of iron spin crossover compounds have used higher, often significantly higher, optical laser fluence^29–31. We used an excitation laser fluence where the transient optical signal changes linearly with pump fluence, as shown in Extended Data Fig. 5b. The 8 keV X-ray laser pulses, with an average bandwidth of 0.3%, were focused using Be compound refractive lenses to a 50 μm diameter spot size at the sample position. Shot-to-shot fluctuations in the X-ray incidence energy and band width do not influence the X-ray fluorescence spectrum when the X-ray energy is well above the core ionization threshold. For iron, with a 1s ionization threshold of 7.112 keV, the 8 keV X-ray energy used in the experiment achieves this goal.

The incoming X-ray pulse energy was measured using non-invasive diagnostics before the sample³². A high-resolution energy dispersive X-ray emission spectrometer³³, based on the von Hamos geometry, was used to capture the iron 3p–1s (Kβ) fluorescence. The spectrometer was equipped with 4 cylindrically bent (0.5 m radius) Ge(620) crystal analysers and set to cover a Bragg angle range from 78.0° to 80.4°. The CSPAD 2D pixel array detector (388 × 370 pixels)³⁴ intersected the X-rays diffracted from the crystal analysers in an energy range from 7,033 to 7,084 eV.

The detector response calibration involved a pixel dependent dark current (pedestal) subtraction, a common mode offset, and an experimentally determined gain map. The gain map was built from histograms of each pixel response extracted from multiple images (after dark current and common mode offset corrections) collected over many minutes. Gaussians were fitted to the zero and one photon peaks of the histograms, enabling fine-tuned dark and gain corrections to the histograms directly from the data. The zero photon peaks were centred at zero analogue-to-digital units and the separation between the zero and one photon peaks were scaled to unity for all pixels. The counts for each pixel in a given time-step were obtained by averaging the analogue-to-digital values above a threshold of 2.5σ of the zero-photon peak and scaling to the incident X-ray intensity. The final 1D spectrum for each time-step was obtained by integrating the signal in the non-dispersive direction³³.

The shot-to-shot X-ray–optical relative time of arrival fluctuations were measured for every X-ray–optical pulse pair with a timing diagnostic tool based on optical detection of X-ray generated carriers in a Si₃N₄ thin film. A description of the time diagnostic tool and the demonstrated performance of the tool can be found elsewhere^17,35. This experimental measure of the relative timing can be used to sort each experimental shot by the relative time of arrival. Although the timing tool provides an accurate measure of the shot-to-shot variation in there lative time of arrival between the X-ray and optical laser pulses, it does not provide an accurate measure of the instrument response function. The timing tool uses changes in the Si₃N₄ dielectric function to modify the transmission of a chirped white light pulse through the Si₃N₄ thin film. These changes in the dielectric function result from the increase in free carriers generated by X-ray ionization, Auger relaxation and impact ionization. The temporal response is the convolution of these complex dynamics with the cross-correlation of the X-ray and optical laser pulses. Without a detailed model of the carrier generation, the cross-correlation cannot be extracted from the timing tool. At present, no experimental means of cross-correlating the hard X-ray and optical pulses has been demonstrated.

The final time resolution of the experiment results from the convolution of the optical and X-ray pulse durations, the group velocity walk-off of the X-ray and optical pulses in the sample and the error in the relative time of arrival measurement. These factors would predict a cross-correlation of roughly 150 fs FWHM. In the data analysis, the instrument response function FWHM and time zero (coincident arrival of the X-ray and optical pulses) are fit parameters.

Kβ fluorescence spectra for model complexes

The 3p–1s X-ray (Kβ) fluorescence spectra of model complexes play an important role in our analysis of the time-dependent data. The Kβ fluorescence spectra of 3d transition-metal ions reflect the 3p–3d exchange interaction, which makes the line shapes sensitive to the spin state of the transition metal atom^{19,23,24,36,37}. Kβ fluorescence provides a powerful technique for spin state studies, particularly when there are advantages of working with penetrating hard X-rays. When a sample contains multiple spin states, the spin state distribution can be readily and precisely calculated from the line shape variations¹⁹.

We measured the Kβ fluorescence spectra of a series of iron complexes with different spin states at beamline 6-2 of the Stanford Synchrotron Radiation Light-source (SSRL). All the samples were cooled to 10 K to reduce the influence of X-ray damage. The static spectra, collected with a multi-crystal high-resolution X-ray emission spectrometer, are shown in Fig. 2a.

We use the model complex difference spectra generated from molecules that have different spin multiplicities in their electronic ground state to model the time-dependent populations of electron excited states with different spin multiplicities. We verify the validity of using the model complex difference spectra generated from the quintet [Fe(phenanthroline)₂(NCS)₂] and the singlet [Fe(2,2′-bipyridine)₃]²⁺ model compounds for the quintet excited state by comparing it with the transient difference spectra of [Fe(2,2′-bipyridine)₃]²⁺ after a 1-ps time delay (see Fig. 2d). The validity of model complex difference spectra for the ^1,3MLCT and ³T excited states proves more challenging to demonstrate because we do not isolate these excited states at any time delay in our pump probe measurements (the fit to the 50-fs time delay spectra shown in Fig. 2c indicates a population ratio of 5:1.3:1 for the ^1,3MLCT:³T:⁵T₂ excited states).

Despite this limitation, the model for the ^1,3MLCT excited generated from doublet [Fe(2,2′-bipyridine)₃]³⁺ and singlet [Fe(2,2′-bipyridine)₃]²⁺ compounds should be robust since the only distinction is the presence of the electron on the 2,2′-bipyridine ligand which should have minimal impact on the Kβ fluorescence spectrum. For the ³T transient, no long-lived triplet excited state can be used to extract an excited state Kβ fluorescence difference spectrum as an internal reference. Instead, we use the ground state model complex difference spectrum obtained from triplet Fe(II) phtha locyanine (FePc) and singlet [Fe(2,2′-bipyridine)₃]²⁺ Kβ spectra as our reference difference spectra. We used the four-coordinate FePc, rather than an octahedral model complex, because octahedral Fe(II) complexes cannot have a triplet ground state. While de Beer et al. have shown that tetrahedral, octahedral, and square planar molecules in the same quintet or sextet spin state have very similar Kβ spectra²⁵, this cannot be demonstrated experimentally for intermediate spin states. Instead, we use theoretical calculations to demonstrate this point. We theoretically calculated the Kβ fluorescence spectra of a four-coordinate square planar and a six-coordinate octahedral ferrous complex using atomic multiplet theory³⁸. This theory is the standard method for calculating and interpreting hard X-ray fluorescence spectra³⁸. For all calculations, the Slater–Condon parameters were reduced to 80% of their atomic value and the 3d orbital and spin angular momentum (LS) coupling was switched off for simplicity. The Kβ spectra were calculated as a 3p→1s fluorescence following 1s ionization. For FePc, we use the previously published crystal field parameters (10Dq = 2.7 eV, Ds = 0.86 and Dt = 0.247) in our calculations³⁹. For the six-coordinate octahedral complex calculation, we used a 10Dq = 1.5 eV, consistent with the experimental 10Dq ≈ 1.5 eV measured for [Fe(2,2′-bipyridine)₃]²⁺ (ref. 9). This value also ensures a low spin (S = 0) ground state, a high spin (S = 2) first excited state and an intermediate spin (S = 1) second excited state.

Extended Data Fig. 1a shows the calculated Kβ fluorescence spectra for both the four- and six-coordinate complexes. The square planar and octahedral symmetries have similar triplet state Kβ fluorescence spectra, consistent with prior experimental and theoretical findings for high spin complexes^19,25. The accuracy of the calculations can also be assessed by comparing calculated and experimental difference spectra. In Extended Data Fig. 1b we show a comparison between the calculated difference spectrum generated when subtracting an octahedral crystal field singlet state from the square planar triplet ground state and the experimental difference spectrum generated by subtracting singlet [Fe(2,2′-bipyridine)₃]²⁺ spectrum from the triplet FePc spectrum. The calculated difference spectrum reproduces the qualitative features of the experimental difference spectrum. The insensitivity of the calculated spectra to the coordination geometry and the ability of the calculations to reproduce the main features of the experimental difference spectrum validate the use of the FePc fluorescence spectrum as a model for the triplet excited state of [Fe(2,2′-bipyridine)₃]²⁺.

Using model complex difference spectra has proven more fruitful for the kinetic modelling than singular value decomposition (SVD). The model complex difference spectra demonstrate that differentiation of the ^1,3MLCT and the ³T excited states depends upon both the shape of the difference spectra and the relative amplitudes of the difference spectra. To first order, the integrated area of the Kβ fluorescence spectra do not change with spin state. The integral of the absolute value of the difference spectrum, however, depends linearly on the magnitude of the spin change³⁹. This robust and reproducible aspect of Kβ fluorescence spectroscopy makes the relative amplitudes of the difference spectra an important distinction. SVD, however, struggles to differentiate species when a difference in relative amplitude is a key distinguishing feature of the difference spectra. For this reason, we have used model complex difference spectra, rather than SVD to model the time resolved data.

Kinetic modelling of the [Fe(2,2′-bipyridine)₃]²⁺ experimental population dynamics

We have used two distinct kinetic models to analyse the time-dependent electron dynamics in [Fe(2,2′-bipyridine)₃]²⁺. For the direct transition between ^1,3MLCT and ⁵T₂, without a ³T transient state, the relaxation mechanism can be expressed as follows:

$${}^{1,3}\mathrm{MLCT}\stackrel{k_1}{\to }{}^5\mathrm{T}_2\stackrel{k_3}{\to }{}^1\mathrm{A}_1$$

where ^1,3MLCT corresponds to the electronic excited state populated by optical excitation, ⁵T₂ corresponds to the quintet ligand field state, and ¹A₁ represents the electronic ground state. The differential rate equations for each species are given by the following mass balance simultaneous equations,

$$\begin{array}{cc}\hfill \frac{\mathrm{d}[{}^{1,3}\mathrm{MLCT}]}{\mathrm{d}t}=& -k_1\left[{}^{1,3}\mathrm{MLCT}\right]\hfill \\ \hfill \frac{\mathrm{d}\left[{}^5\mathrm{T}_2\right]}{\mathrm{d}t}=& k_1\left[{}^{1,3}\mathrm{MLCT}\right]-k_3\left[{}^5\mathrm{T}_2\right]\hfill \\ \hfill \frac{\mathrm{d}\left[{}^1\mathrm{A}_1\right]}{\mathrm{d}t}=& k_3\left[{}^5\mathrm{T}_2\right]\hfill \end{array}$$

The integrated rate equations provide the following time-dependent populations for the three species,

$$\begin{array}{cc}\hfill \left[{}^{1,3}\mathrm{MLCT}\right]=& \left[{}^{1,3}\mathrm{MLCT}\right]{{}_0}^{e^{-k_{1}t}}\hfill \\ \hfill \left[{}^5\mathrm{T}_2\right]=& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0\frac{k_1}{k_3-k_1}(e^{-k_{1}t}-e^{-k_{3}t})\hfill \\ \hfill \left[{}^1\mathrm{A}_1\right]=& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0-\left[{}^{1,3}\mathrm{MLCT}\right]-\left[{}^5\mathrm{T}_2\right]\hfill \end{array}$$

From prior ultrafast measurements, we know that the lifetime of the ⁵T₂ excited state is roughly 660 ps (refs 6, 13, 15). The long lifetime of the ⁵T₂ excited state allows us to set k₃ ≈ 0 when we model the kinetics in the first couple of picoseconds. The integrated rate equations can be reduced to:

$$\begin{array}{cc}\hfill \left[{}^{1,3}\mathrm{MLCT}\right]=& {{\left[{}^{1,3}\mathrm{MLCT}\right]}_0}^{e^{-k_{1}t}}\hfill \\ \hfill \left[{}^5\mathrm{T}_2\right]=& {\left[{}^{1,3}\mathrm{MLTC}\right]}_0(1-e^{-k_{1}t})\hfill \end{array}$$

For the sequential kinetic model with a ³T transient state, the relaxation mechanism can be expressed as follows:

$${}^{1,3}\mathrm{MLCT}\stackrel{k_1}{\to }{}^3\mathrm{T}\stackrel{k_2}{\to }{}^5\mathrm{T}_2\stackrel{k_3}{\to }{}^1\mathrm{A}_1$$

where ^1,3MLCT corresponds to the electronic excited state populated by optical excitation, ³T corresponds to the triplet ligand field excited state, and ⁵T₂ corresponds to the quintet ligand field excited state, and ¹A₁ represents the electronic ground state. The differential rate equations for each species are given by the following mass balance simultaneous equations:

$$\begin{array}{cc}\hfill \frac{\mathrm{d}\left[{}^{1,3}\mathrm{MLCT}\right]}{\mathrm{d}t}=& -k_1\left[{}^{1,3}\mathrm{MLCT}\right]\hfill \\ \hfill \frac{\mathrm{d}\left[{}^3\mathrm{T}\right]}{\mathrm{d}t}=& k_1\left[{}^{1,3}\mathrm{MLCT}\right]-k_2\left[{}^3\mathrm{T}\right]\hfill \\ \hfill \frac{\mathrm{d}\left[{}^5\mathrm{T}_2\right]}{\mathrm{d}t}=& k_2\left[{}^3\mathrm{T}\right]-k_3\left[{}^5\mathrm{T}_2\right]\hfill \\ \hfill \frac{\mathrm{d}\left[{}^1\mathrm{A}_1\right]}{\mathrm{d}t}=& k_3\left[{}^5\mathrm{T}_2\right]\hfill \end{array}$$

The integrated rate equations provide the following time-dependent populations for the four species:

$$\begin{array}{cc}\hfill \left[{}^{1,3}\mathrm{MLCT}\right]=& {{\left[{}^{1,3}\mathrm{MLCT}\right]}_0}^{e^{-k_{1}t}}\hfill \\ \hfill \left[{}^3\mathrm{T}\right]=& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0\frac{k_1}{k_2-k_1}(e^{-k_{1}t}-e^{-k_{2}t})\hfill \\ \hfill \left[{}^5\mathrm{T}_2\right]=& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0\frac{k_1{k}_2\left[\right(k_3-k_2)e^{-k_{1}t}-(k_3-k_1)e^{-k_{2}t}+(k_2-k_1\left)e^{-k_{3}t}\right]}{(k_2-k_1)(k_3-k_2)(k_3-k_1)}\hfill \\ \hfill =& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0\frac{k_1{k}_2\left[k_3\right(e^{-k_{1}t}-e^{-k_{2}t})+k_2(e^{-k_{3}t}-e^{-k_{1}t})+k_1(e^{-k_{2}t}-e^{-k_{3}t}\left)\right]}{(k_2-k_1)(k_3-k_2)(k_3-k_1)}\hfill \\ \hfill \left[{}^1\mathrm{A}_1\right]=& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0-\left[{}^{1,3}\mathrm{MLCT}\right]-\left[{}^3\mathrm{T}\right]-\left[{}^5\mathrm{T}_2\right]\hfill \end{array}$$

The long lifetime of the ⁵T₂ excited state allows us to set k₃ ≈ 0 when we model the kinetics in the first couple of picoseconds. The integrated rate equations can be reduced to:

$$\begin{array}{cc}\hfill \left[{}^{1,3}\mathrm{MLCT}\right]=& {{\left[{}^{1,3}\mathrm{MLCT}\right]}_0}^{e^{-k_{1}t}}\hfill \\ \hfill \left[{}^3\mathrm{T}\right]=& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0\frac{k_1}{k_2-k_1}(e^{-k_{1}t}-e^{-k_{2}t})\hfill \\ \hfill \left[{}^5\mathrm{T}_2\right]=& {\left[{}^{1,3}\mathrm{MLCT}\right]}_0(1-\frac{k_2{e}^{-k_{1}t}-k_1{e}^{-k_{2}t}}{k_2-k_1})\hfill \end{array}$$

To fit the experimental data to a kinetic model, we must convolve the kinetic model with the instrument response function which we describe with a Gaussian function. Taking the example of [^1,3MLCT] = [^1,3MLCT]₀e^−k₁t, which is an exponential decay starting at time zero (t₀), it will be expressed as

$$\left[{}^{1,3}\mathrm{MLCT}\right]={\left[{}^{1,3}\mathrm{MLCT}\right]}_0{\int }_{-\infty }^{\infty }\frac{1}{\sigma \sqrt{2\pi }}{e}^{-y^2∕2{\sigma }^2}\mathrm{H}(t-t_0-y)e^{-k_1(t-t_0-y)}\mathrm{dy}$$

where H is the Heaviside step function and σ is the temporal width of the instrument response function.

Statistical determination of the correct kinetic model

Given two distinct kinetic models, we must determine which model best represents the experimental data. Choosing the model with smaller residual sum of squares (RSS) is not sufficient because the two models do not have the same number of fit parameters. We have used the statistical F-test to determine whether the model with or without a ³T transient provides the best fit of the experimental data⁴⁰.

The F-test provides a statistically robust method for comparing the quality of two models with a different number of fit parameters when the simpler model 1 can be ‘nested’ within the more complex model 2. Model 1 has p₁ parameters, and model 2 has p₂ parameters, where p₂ > p₁. For any choice of parameters in model 1, the model 2 should always be able to fit the data at least as well as the model 1. Thus, model 2 typically will have a lower RSS than model 1. The F-test allows us to determine the statistical significance of this variance in RSS. The F statistic can be calculated by

$$\begin{array}{cc}\hfill & \frac{{\mathrm{RSS}}_1-{\mathrm{RSS}}_2}{}\hfill \\ \hfill F=& \frac{p_2-p_1}{{\mathrm{RSS}}_2}=\frac{({\mathrm{RSS}}_1-{\mathrm{Rss}}_2)(n-p_2)}{{\mathrm{RSS}}_2(p_2-p_1)}\hfill \\ \hfill & \frac{}{n-p_2}\hfill \end{array}$$

where n is the number of data points (time delays) fitted by the two models. For the null hypothesis that model 2 does not provide a fit statistically superior to that provided by model 1, the F will have an F distribution defined by the degrees of freedom, (p₂ – p₁) and (n – p₂). To reject the null hypothesis, F must exceed a critical value that depends upon the degrees of freedom and the level of confidence⁴⁰.

[Fe(2,2′-bipyridine)₃]²⁺ experimental data modelling

Using the reference difference spectra with the kinetic model, we fit the time-dependent difference Kβ fluorescence spectra for optically excited [Fe(2,2′-bipyridine)₃]²⁺ in water. The parameters extracted from the fit of the two kinetic models can be found in Extended Data Table 1. We compute the time constants and uncertainties reported in Extended Data Table 1 by fitting multiple runs of the same experiment and then calculating the mean and the standard deviation. The experimental two-dimensional transient difference spectra, fit spectra, residuals, and excited electronic state populations extracted from the best fit for each model can be found in Extended Data Figs 2 and 3. Given the very short lifetime of the ³T excited state, the deviations between the fits of the two models predominantly occur within the first 500 fs. The two-dimensional plots of the residuals in Extended Data Figs 2c and 3c highlight the regions where the ^1,3MLCT→³T→⁵T₂ model provides a fit superior to that of the ^1,3MLCT→⁵T₂ model. Unsurprisingly, this corresponds to time delays with larger ³T populations and spectral regions with the largest difference between the ³T and ⁵T₂ spectra (7,053–7,056 eV).

The residual sum of squares quantifies the variable quality in the fits. The residual sum of squares for each model is: RSS₁ = 3.77 and RSS₂ = 3.21. In this situation, we have p₁ = 5, p₂ = 6 and n = 45. To be 95% confident that the complex model is better than the nested model, the calculated F value must be larger than the F distribution value that captures 95% of the distribution for F(p₂ – p₁, n – p₂) which is 4.09. The calculated F value is 6.71 which exceeded 4.09. So with 95% confidence we conclude that the model containing the ³T transient provides a better description of the experimental data.

Influence of instrument response function parameters on the data analysis

We utilize the instrument response function (IRF) as a variable since the technology does not yet exist to measure the instrument response time accurately. This leads to an increase in the number of parameters in the data analysis. This increase in fit parameters makes statistically differentiating the robustness of alternative kinetic models more difficult, rather than easier.

To ensure that the statistical superiority of the kinetic model possessing the ³T transient does not result from our uncertainty about the instrument response function parameters, we have investigated how variation of time zero and FWHM values differentially influence the RSS for the direct ^1,3MLCT→⁵T₂ model and the ^1,3MLCT→³T→⁵T₂ model. For the range of time zero and FWHM values reported in Extended Data Table 1 that adequately fit the experimental data with either model, the model containing the ³T transient always provides a significantly superior fit to the experimental data. We have used the instrument response function values that minimize the RSS for the ^1,3MLCT→⁵T₂ model to fit the data with the ^1,3MLCT→³T→⁵T₂ model. Using this sub-optimal instrument response function only increases the RSS₂ from 3.21 to 3.27, both significantly less than the direct model RSS₁ = 3.77. Using the definition for F given above and p₁ = 5, p₂ = 6 and n = 45, we calculate F = 5.98, in excess of the 4.09 value needed to conclude with 95% confidence that the complex model provides a better representation of the experimental data than the nested model.

Experimental time resolution can also influence the ability to identify a distinct excited state. For the case of the triplet transient, the temporal resolution of 150 fs has little impact on the characterization of the triplet excited state dynamics. To demonstrate that the roughly 150 fs FWHM IRF does not inhibit our ability to characterize the triplet population dynamics, we have simulated the ^1,3MLCT→³T→⁵T₂ population kinetics using the time constants extracted from the best fit to the experimental data listed in Extended Data Table 1 with an IRF possessing a 150 fs FWHM and a 5 fs FWHM. The initial time dependence of the ^1,3MLCT state signal depends significantly on the time resolution (though the decays for time delays longer than 200 fs look similar), but the shape and amplitude of the triplet population is similar. The convolution of the IRF and the lifetime of the ^1,3MLCT excited state determine the time dependence of the ³T transient state formation observed experimentally. The low transient population of the triplet state results primarily from the fact that the decay rate of the ³T state exceeds that of the ^1,3MLCT state by a factor of two.

Supplementary Material

01

Extended Data Figure 1 | Experimental and calculated Kβ fluorescence spectra for triplet spin states. a, The calculated Kβ fluorescence spectra of iron complexes: triplet Fe(II) in square planar crystal field (red) (calculation parameters based on Fe(II)phthalocyanine), and triplet excited state in an octahedral crystal field (blue) (calculation parameters based on [Fe(2,2′-bipyridine)₃]²⁺). b, The experimental Kβ fluorescence difference spectrum (red) obtained by subtracting the singlet [Fe(2,2′-bipyridine)₃]²⁺ spectrum from the triplet Fe(II)phthalocyanine spectrum, and the calculated Kβ fluorescence difference spectrum (blue) generated by subtracting the spectrum of the singlet state in an octahedral crystal field from the triplet state in a square planar crystal field.

Extended Data Figure 2 | Time-dependent Kβ fluorescence spectra and fit using the sequential kinetic model with a triplet transient. a, Experimental transient fluorescent amplitude difference spectra plotted with arbitrary units, and b, fit using the sequential kinetic model with a triplet transient. c, Residuals for the best fit, with the colour-scale maximum and minimum set to one-fifth of the value used in a and b. d, The excited state populations extracted from the best fit.

Extended Data Figure 3 | Time-dependent Kβ fluorescence spectra and fit using the direct kinetic model without a triplet transient. a, Experimental transient fluorescent amplitude difference spectra plotted with arbitrary units, and b, fit using the direct kinetic model without a triplet transient. c, Residuals for the best fit with the colour scale maximum and minimum set to one-fifth of the value used in a and b. d, The excited state populations extracted from the best fit.

Extended Data Figure 4 | The 50 fs time delay normalized Kβ fluorescent amplitude difference spectrum (ΔI) and kinetic model fit plotted as a function of X-ray emission energy. The measured data (black circles and line), along with the best global fit from the sequential kinetic model with a transient triplet state (red line).

Extended Data Figure 5 | Absorption spectrum and pump power dependence measurements. a, The ultraviolet–visible absorption spectrum of [Fe(2,2′-bipyridine)₃]²⁺ in water. b, Power (fluence) dependence of the change in probe transmission measured at 520 nm, following excitation of an aqueous solution of [Fe(2,2′-bipyridine)₃]Cl₂ with a 520 nm pump pulse. The figure shows the change in transmission (ΔT) measured at a 10 ps time delay, a time long compared to the spin crossover and vibrational cooling timescales, but short compared to the lifetime of the high-spin excited state.

Extended Data Table 1 | Fitted model parameters