Gating of Connexin Channels by transjunctional-voltage: Conformations and models of open and closed states

Abstract

Voltage is an important physiologic regulator of channels formed by the connexin gene family. Connexins are unique among ion channels in that both plasma membrane inserted hemichannels (undocked hemichannels) and intercellular channels (aggregates of which form gap junctions) have important physiological roles. The hemichannel is the fundamental unit of gap junction voltage-gating. Each hemichannel displays two distinct voltage-gating mechanisms that are primarily sensitive to a voltage gradient formed along the length of the channel pore (the transjunctional voltage) rather than sensitivity to the absolute membrane potential (V_m or V_i-o). These transjunctional voltage dependent processes have been termed V_j- or fast-gating and loop- or slow-gating. Understanding the mechanism of voltage-gating, defined as the sequence of voltage-driven transitions that connect open and closed states, first and foremost requires atomic resolution models of the end states. Although ion channels formed by connexins were among the first to be characterized structurally by electron microscopy and x-ray diffraction in the early 1980’s, subsequent progress has been slow. Much of the current understanding of the structure-function relations of connexin channels is based on two crystal structures of Cx26 gap junction channels. Refinement of crystal structure by all-atom molecular dynamics and incorporation of charge changing protein modifications has resulted in an atomic model of the open state that arguably corresponds to the physiologic open state. Obtaining validated atomic models of voltage-dependent closed states is more challenging, as there are currently no methods to solve protein structure while a stable voltage gradient is applied across the length of an oriented channel. It is widely believed that the best approach to solve the atomic structure of a voltage-gated closed ion channel is to apply different but complementary experimental and computational methods and to use the resulting information to derive a consensus atomic structure that is then subjected to rigorous validation. In this paper, we summarize our efforts to obtain and validate atomic models of the open and voltage-driven closed states of undocked connexin hemichannels.

Introduction

Connexins are channel forming, tetraspan membrane proteins with intracellular N- and C- termini. In humans, connexin proteins are encoded by a twenty-one-member gene family divided into 5 phylogenetic subclasses that differ substantially in their primary amino acid sequences [1]. Six connexin subunits assemble to form hemichannels (also termed connexons), which in turn form intercellular channels by the head to head docking of two hemichannels located in closely apposed plasma membranes. Intercellular channels assemble to form morphologically distinct plaques, first termed the “nexus” [2] and subsequently, the “gap junction” [3, 4]. Connexin channels are large pore channels that provide a direct pathway for intercellular electrical and chemical signaling in nearly all tissues. Connexin channels are unique in that plasma membrane inserted undocked hemichannels are also operational and have important physiologic and pathologic roles.

The role of gap junctions in development and organ system physiology has been established by studies of mouse knockouts of connexin genes primarily by Klaus Willecke and co-workers (e.g. [5–8]), and by investigations of inherited connexin diseases. At present, mutations mapping to 10 connexin genes are known to cause at least 13 human diseases [9, 10]. Structure-function studies of Cx26 and Cx32 disease mutations have been particularly informative, in part due to the large numbers of mutations identified in affected individuals. More than 300 different missense Cx32 mutations causing X-linked Charcot-Marie-Tooth (CMTX) and more than 200 Cx26 mutations that cause non-syndromic deafness and syndromic deafness associated with skin disease have been described. Given the large number of mutations, it is perhaps not surprising these mutations cover a significant percentage of the coding region; indeed missense mutations have been recovered at most Cx32 residues [11]. Most of these connexin mutations cause disease by “loss of function”, which can occur by diverse mechanisms including; assembly defects, failure to traffic to the plasma membrane, failure to dock, altered functional properties including decreased or absence of permeability to second messengers and other signaling molecules. Shifts in voltage-dependence cause loss of function when the channel is closed at voltages where it should be open [10].

Many undocked connexin hemichannels also operate as voltage-gated, moderately cation selective channels in the plasma membrane, although some have low open probability and do not appear to contribute substantially to total membrane currents [12]. The operation of undocked hemichannels is often inferred by the intracellular accumulation of membrane impermeant dyes (e.g. ethidium bromide) measured over the course of minutes [13]. Despite their low open probability, it has become widely accepted that undocked hemichannels have important physiological and pathological roles [14], including autocrine/paracrine signaling mediated by ATP release [15]. Regulated opening of undocked hemichannels in excitable cells can alter membrane potential to modulate excitability and electrical signaling [16–20]. Closure of undocked hemichannels is strongly favored at the resting potential of most cells by the so-called loop- or slow-gating mechanism. Although the loop-gating mechanism is not dependent on the presence of divalent cations (voltage-gating transitions are observed in divalent cation free solutions), it is modulated physiologically by Ca²⁺ and Mg²⁺ [21, 22]. Channel opening is favored with low concentrations of Ca²⁺ and voltage-dependence is shifted rightward with increased Ca²⁺ [21]. Consequently, undocked hemichannels have the potential to function as calcium sensors, analogous to the function of the phylogenetically related neuronal CALHM1 (Calcium Homeostasis Modulator 1) channel where channel open probability also increases with decreases in extracellular Ca²⁺ [23, 24]. The resulting depolarization will move the resting membrane potential closer to threshold, increasing excitability.

Syndromic Cx26 mutations (deafness with associated skin disease often lethal) are classified as dominant gain of function mutations. They appear to result from dysregulation of Cx26 undocked hemichannels by voltage and/or in combination with extracellular calcium [25–30]. In these mutations, undocked hemichannels are open in the plasma membrane when they should be gated closed by the normal resting membrane potential and/or with physiologic extracellular calcium. Maintaining the closed state of undocked hemichannels in plasma membranes prior to intercellular channel formation appears to be a critical role for voltage-gating. For example, the Cx32S85C CMT-X mutation has altered voltage-dependence such that undocked hemichannels have increased open probability. It has been proposed that this defect leads to loss of Schwann cells and development of Charcot-Marie-Tooth disease [31].

It has long been known that gap junctions form electrical synapses in the central nervous system and heart. Indeed, much of the interest in gap junctions in early years was driven by study of electrical synapses [32, 33]. Today it is known that Cx36 (and it homologs, Cx35 and Cx34.7) form the majority of neuronal electrical synapses in vertebrates, while Cx43 forms the major population of cardiac gap junctions that function to synchronize contraction. Electrical synapses among neurons in conjunction with extensively gap junction coupled glial networks participate in the development, emergent properties and dynamic regulation of neuronal networks [22, 34–42]. A recent Hodgkin-Huxley based computational study of network dynamics has shown that the voltage-dependence of electrical synapses can contribute to the dynamic properties of circuits, specifically the property of reverberation, which may be important for the development of short-term memory and its consolidation into long-term memory [39]. While electrical synapses formed by Cx36 are only weakly voltage-dependent, their voltage-dependence increases markedly with increased concentrations of intracellular Mg²⁺ [22]. It has been suggested that Mg²⁺ favors channel entry into a “deep-closed” state and that entry into this state may also be responsible for the observed low percentage of activatable channels in an electrical synapse. Changes in the proportion of activatable channels in response to Mg²⁺ may contribute to the reported activity dependent plasticity in synaptic strength of electrical synapses [22, 43–45]. Others have proposed that phosphorylation [46] or channel turnover may be responsible [44]. A low percentage of “functioning” channels has been reported for other gap junctions [47], leading to the possibility that this property may be a common feature of all connexins channels.

To summarize, voltage-dependent closure of connexin channels is not only required to maintain cellular integrity prior to docking of plasma membrane inserted hemichannels to form intercellular channels, but voltage-gating and its modulation by divalent cations also appears to play a fundamental role in creating dynamic biological processes. The voltage-dependence of intercellular channels can dynamically regulate the strength of electrical and chemical coupling in response to changes in transjunctional voltage and can in principle play a role in the dynamics of electrical signaling in neuronal networks. The regulation of undocked hemichannel open probability by voltage can contribute to the regulation of autocrine/paracrine signaling. Similarly, changes in open probability of undocked hemichannels can modulate resting membrane potential and hence has the potential to alter excitability.

Voltage regulation of connexin channel conductance – biophysical considerations

Connexin channels display two fundamentally different voltage-dependent mechanisms, 1) rectification of ionic currents through fully open channels and 2) voltage-dependent gating that determines open probability as a function of voltage.

Current rectification is a single channel property in which channel conductance is a non-linear function of voltage. For example, the heterotypic Cx26/Cx32 intercellular channel forms a P-N junction (electrical diode) rather than an ohmic resistor, in which single channel current is a linear function of voltage. The rectification is a consequence of asymmetry in the magnitude and distribution of fixed charge along the length of the channel pore [48].

In contrast, voltage-dependent gating is a voltage-driven change in channel conformation that regulates current by changing open probability. In the simplest case, the channel is an on-off switch, i.e. an open and closed state. The critical point is that voltage performs work on the channel, typically by changing the position of charged amino acids (the voltage sensor) in response to changes in voltage, which in turn is coupled to other structural changes that open or close the channel pore. Stated differently, the voltage sensor transduces electrical energy (potential energy) into kinetic energy to effect a conformational change in the channel molecule.

Some of the key features of connexin channel voltage-dependence that underpin our understanding of structure-function relations and mechanisms of voltage-gating are founded on the early papers of Harris, Spray and Bennett [49, 50].

1. Intercellular connexin channels are typically sensitive to the relative voltage difference between coupled cells, the transjunctional voltage, V_j, and most are insensitive to the absolute membrane potential, V_m or V_i-o (see [51] for a full explanation). Sensitivity to only V_j has an immediate structure-function consequence: the voltage-sensor must reside within the channel pore, as only in this position can it sense only the voltage drop along the length of the channel pore and not the voltage drop across the plasma membrane. Furthermore, when the channel is fully closed, most of the voltage drop will occur across the permeability barrier, which blocks the channel pore. Consequently, charged residues residing within the permeability barrier will be most sensitive to changes in V_j and these will most likely serve as voltage sensors to confer voltage-dependence to channel opening. In the case of undocked hemichannels, membrane potential is effectively equivalent to V_j, so the voltage-dependence measured in undocked hemichannels will be at least qualitatively identical to that of hemichannels that comprises the intercellular channels (Because undocked hemichannels are half the length of intercellular channels, the voltage drop will differ). In contrast to connexin channels, an innexin channel expressed in Drosophila salivary glands displays strong dependence on V_i-o in addition to V_j. The interaction of the two gates and their structural implications is discussed in [52, 53]. While some intercellular connexin channels are sensitive to V_i-o (V_m), sensitivity is substantially weaker than that of some intercellular innexin channels. V_m dependence has been examined for Cx45 intercellular channels by Barrio and coworkers and they conclude that the molecular determinants are contained in each hemichannel [54]. The initial currents of Cx26 intercellular channels also display weak V_i-o sensitivity in macroscopic recordings from paired oocytes [48, 55]. While in most cases, rectification of initial currents reflects single channel properties, the single channel I/V relation of Cx26 expressed in pairs of transfected cells is unexpectedly linear, suggesting that the rectification of Cx26 initial currents may have a different molecular basis.

2. Because hemichannels dock as mirror images, transjunctional voltage that favors closure of gates in one hemichannel of a homotypic intercellular channel will favor opening of gates in the apposed hemichannel [56]. This feature, leads to a property called “contingent gating” in which gates fully closed by voltage in one hemichannel must open prior to closure of gates in the apposed hemichannel when the polarity of applied V_j is reversed (see [51]). This indicates that the hemichannel is the fundamental unit of voltage-gating, with each hemichannel containing a voltage-sensor and gate. This does not mean that pairing of hemichannels cannot modulate the expression of voltage-dependence, but rather that docking of hemichannels does not “create” the voltage-dependent mechanism per se.

3. Subsequent studies showed that each hemichannel has two distinct V_j-sensitive voltage-gating mechanisms, termed loop-gating (or slow-gating) and V_j-gating (or fast-gating) [57] and that both processes operate in intercellular channels [10] as well as undocked hemichannels. In single channel records (Fig. 1), V_j-gating events correspond to fast transitions between the open and at least 3 different sub-conductance states (substates); loop-gating, as a series of small amplitude transitions between multiple intermediate states that together give the appearance of an event with a slow time course that fully closes the channel [57, 58]. In all connexin channels examined to date, loop-gate closure is favored at inside negative voltages. In contrast, closure of V_j-gates is connexin specific. In Cx32 hemichannels, closure of V_j-gates is favored when the cytoplasmic entrance to the hemichannel is negative, in Cx26, closure of V_j-gates is favored when the cytoplasmic entrance is positive. In a heterotypic intercellular channel formed by pairing Cx26 and Cx32 hemichannels, V_j-gates in both hemichannels close when the Cx32 side is negative (because the Cx26 side will be positive). When the Cx32 side is positive both V_j-gates open. In general, V_j-gates are more sensitive to voltage than loop-gates, i.e. closure of V_j (fast)-gates is favored at smaller V_j (transjunctional voltage) than loop-gates. That explains why there is little or no current relaxations observed in heterotypic Cx26/Cx32 intercellular channels at voltages where the cytoplasmic side of either hemichannel is negative. Operation of loop-gates can be inferred in the conductance-voltage relations of some intercellular at large V_j’s (e.g. Cx32KE intercellular channel in [56]). Note that because V_j-gating does not fully close a hemichannel, the applied voltage gradient can be “sensed” by loop-gates even when V_j-gates are closed. Thus, loop-gates can open and close when V_j-gates are closed. When loop-gates are closed, opening of V_j-gates appears to be favored. This suggests that the V_j-gate voltage sensor resides outside (towards the intracellular entrance of the loop-gate permeability barrier in an intercellular channel), as closure of the loop-gate collapses the voltage-gradient across the V_j-gate favoring opening of this gate.

4. The presence of two gates in each hemichannel, complicates study of voltage-gating in intercellular channels. Fortunately, several connexins form conductive undocked hemichannels allowing unequivocal separation of the two gating processes. These include rat Cx46, Cx50 and human Cx26. We utilize a chimeric construct, Cx32*43E1, first described by Dahl [59] in which the first extracellular loop (E1) of Cx32, residues 41–70, is replaced with that of Cx43. This undocked hemichannel recapitulates the essential features of wild-type Cx32 voltage-dependence [58] and indeed most of our understanding of the molecular determinants and mechanisms of voltage-gating are derived from its study [60]. Of particular significance is the ability to manipulate V_j-gating polarity to allow unambiguous separation of V_j-gating from loop-gating. Substitution of negatively charged residues at N2, T4, or G5 reverses V_j-gating polarity [56, 58, 61] to favor closure at inside positive voltages while loop-gate closure at inside negative potentials is unchanged [58, 61, 62]. Unlike other channels, negative charge substitutions at these positions reverse V_j-gating polarity without causing large shifts in channel voltage-dependence including that of loop-gating (e.g. Cx26D2N [48]). Thus, the open and closed states of N2E hemichannels should be comparable to those of wild-type. It should be noted that study of Cx32*43E1 intercellular channels in paired oocytes is technically challenging as a consequence of gating of undocked hemichannels in the non-junctional membrane during recording (see [58]). Remarkably, Cx32*43E1 intercellular channels may have some dependence on V_m, but this may be due to the activity of undocked hemichannels as discussed in [58] rather than an intrinsic property of the intercellular channel.

Figure 1.

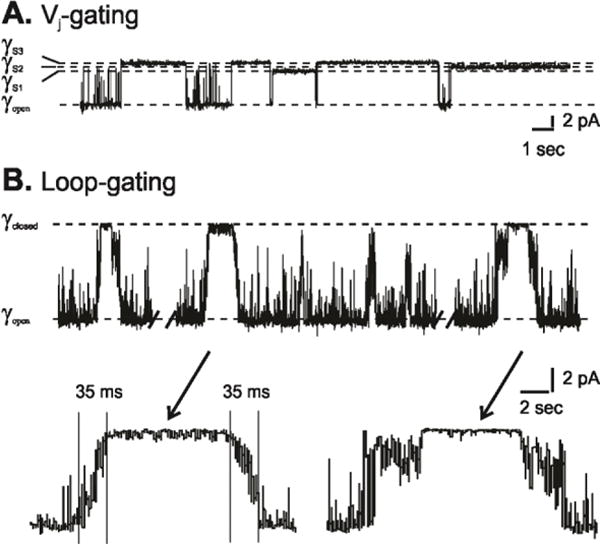
Single channel records illustrating two different voltage-dependent gating processes in Cx32*43E1 undocked hemichannels following expression in Xenopus oocytes. (A). Segment of a record of an outside-out patch containing a single channel illustrating Vj-gating transitions to three substates at a holding potential of −100 mV. (B). Cell attached recording of a single wild type channel at a holding potential of −70 mV illustrating loop-gating transitions. Note the slow time course of the gating transitions and that not all events lead to full channel closure. The records were obtained in presence of EDTA and EGTA, indicating that the two gating mechanisms do not depend on the presence of divalent cations. Reproduced from the Journal of General Physiology.

The major advance in understanding the structure-function relations of connexin channels followed the solution of the atomic structure of Cx26 hemichannels by Maeda et al, [63] and more recently by Bennett et al. [64]. Knowledge of atomic structure guides interpretation of studies of connexin mutations, many of which cause disease, and allows application of computational methods to probe structure-function relations in silico. The challenge with the later approach is to design experimental tests of function that test the mechanisms and relations predicted by computation.

Understanding the sequence of voltage-driven molecular conformation linking open and closed states requires validated atomic models of the end states. Validation that an atomic model corresponds to that of the physiologic native channel state is challenging, and requires application of experimental and computational methods. An advantage of ion channel research is that methods have been and continue to be developed that allow computation of channel properties from atomic structure. These include gating charge, changes in ΔΔG (FEP/MD) [65–69] and ion permeation, at least for large pore ion channels [70, 71]. In the following sections, we summarize attempts to obtain and validate open and loop-gate closed atomic models.

Open state atomic models: Cx26 Undocked hemichannels

Current atomic models of the open state of connexin channels are based on the X-ray crystallographic structure of Cx26 intercellular channels; PDB ID: 2ZW3 at 3.5 Å [63]. A more recent structure, PDB ID: 5ERA at 3.8 Å [64] has not been used to date, but will be of value, as it provides another initial structure for refinement and analyses by all atom MD simulations comparable to those described below for 2ZW3.

Maeda et al., [63] suggested that although incomplete, the structure of 2ZW3 represented the open state of the Cx26 intercellular channel, as a continuous large diameter aqueous pore was evident. Furthermore, the close correspondence among residues that lined the Cx26 channel pore in the crystal with that of ratCx46 and Cx32*43E1 hemichannels inferred from accessibility of substituted cysteines to thiol modifying reagents [72–75] supported the view that the Cx26 crystal structure corresponded to the open state. However, the crystal structure did not include the coordinates of the N-terminal methionine (Met1), whose inclusion would reduce the pore diameter, nor of the side chains of residues K15, S17, and S19 contained in the N terminus (NT) and residues forming the cytoplasmic loop (CL; residues 110–124) and C terminus (residues 218–226) domains. While the undefined region of the CL is not pore lining, its proximity to the pore entrance could influence ion permeation by its effects on surface charge.

We tested whether the crystal structure represented that of the physiologic open state by application of grand canonical Monte Carlo Brownian Dynamics (GCMC/BD). The system is illustrated in Fig. 2G. This method provides a means to compute the expected current-voltage relation of the atomic structure of the undocked hemichannel and compare it to experimental data obtained under identical ionic conditions. The GCMC/BD algorithm was developed by Roux, Im, and co-workers for study of permeation in large pore diameter ion channels [70, 71, 76] and validated by demonstrating correspondence of ionic permeation calculated by GCMC/BD and long duration MD simulation of atomic models of VDAC and other channels to experimental values [77, 78]. Ion flux through large pore ion channels has been determined accurately by GCMC/BD computation [76, 78, 79]. Protein-ion interactions are explicitly defined in GCMC/BD. Ion mobilities within the channel pore, which are critical to obtaining correct values of conductance, are determined either ab initio by methods detailed in Noskov et al [79] or by all atom MD simulation for small segments of the channels pore as described in [77]. There is no “curve-fitting” by adjusting ion mobility to obtain correct conductance. A significant advantage of GCMC/BD is that the method is rapid, current-voltage relations are obtained within days rather than weeks or longer with all-atom MD. GCMC/BD has several intrinsic limitations, including a rigid channel, and an implicit solvent and membrane bilayer and is not applicable to determine ion permeation through small pore ion channels such as K⁺ channels, which require close range interactions between the ion and channel pore to create the remarkable ability to discriminate among small metal cations.

Figure 2.

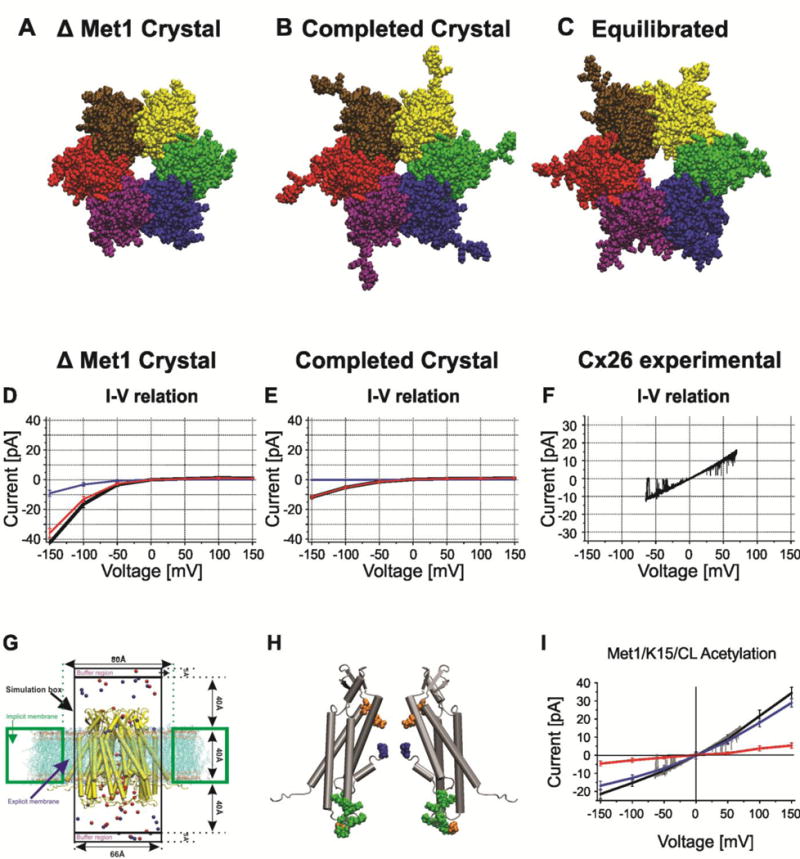
Structural models of Cx26 undocked hemichannels and corresponding computed currents-voltage relations with GCMC/BD. A–C. End on views of atomic models (A). The Cx26 crystal structure PDB ID:2ZW3. The larger pore diameter reflects the absence Met1 in the crystal structure. (B). The completed crystal structure in which all missing atoms were added to the crystal structure. The decreased pore diameter is a consequence of presence of Met1. (C). The structure of the average equilibrated atomic model following all-atom MD simulation in a fully hydrated POPC membrane. The large pore diameter is a consequence of the relaxation of the crystal structure. (D). I/V relation of the completed crystal structure with Met1 removed computed with GCMC/BD. Blue line is K⁺ current, red line is Cl⁻ current, black line is total current. (E). I/V relation of the completed crystal structure with Met1 included computed with GCMC/BD. Blue line is K⁺ current, red line is Cl⁻ current, black line is total current. (F) Single channel I/V relation of an excised (outside-out) undocked Cx26 hemichannel in symmetric 100mM KCl elicited by a ± 70 mV voltage ramp. (G). Schematic of the GCMC/BD simulation system. The connexin channel (yellow) embedded in explicit POPC lipid is inserted into an implicit membrane containing a circular hole. The explicit membrane prevents any leak current passing between the channel and implicit membrane. The upper compartment (extracellular part of the channel) was defined as the ground in voltage applications. 20 replicate 450-ns simulations were performed at each of seven voltages, ±150, ±100, ±50, and 0 mV, to plot the I/V relations. Blue circles, K⁺; red circles, Cl⁻. (H) Positions of modified residues identified by Locke et al. (2009) that would alter the distribution of charge in the Cx26 channel pore, shown in a side view of two opposite subunits of the completed crystal structure. The positions of acetylated residues are colored as follows: blue, Met1; red, K15; green, K102, K103, K105, K108, K112, and K116 in CL/TM2; orange, γ-carboxyglutamated residues E42, E47, and E114. (I) The I/V relation of the MD equilibrated channel with Met/K15 6 cytoplasmic loop lysine residues acetylated. Blue line is K⁺ current, red line is Cl⁻ current, black line is total current. The experimental current trace depicted in gray is the current trace in panel F. Computed and experimental currents superimpose closely. Reproduced from the Journal of General Physiology.

Prior to computing I/V relations with GCMC/BD, it was necessary to complete the crystal structure to include all missing and incomplete residues in order to determine all possible amino acid – ion interactions. A main concern was the absence of Met1 in the crystal structure, as this residue is expected to have a major impact on pore diameter (Fig. 2A–C). We first computed current/voltage relations with GCMC/BD for two atomic models that included or excluded the Met1 (Fig. 2D and E) and compared these to experimental traces. Significantly, the current-voltage relations of Cx26 undocked hemichannel models computed with and without Met1 deviated substantially from those observed experimentally. The physiologic current-voltage relation of human Cx26 undocked hemichannels typically displays a slight outward rectification, with a slope conductance of ~ 210 pS when single channel recordings are performed in symmetric 100 mM KCl (Fig. 2F) [80]. The conductance is reported to be somewhat larger, ~ 340 pS in 140 mM KCl [27]. Both computed current-voltage relations displayed marked inward rectification, such that the channels were impermeant at small inside negative potentials and at all positive potentials (Fig. 2D and E). The observed steep inward rectification of ionic currents is characteristic of an electrical diode or P-N junction, where positive and negative charges are segregated across the length of the channel. The 2ZW3 crystal structure shows this feature: the intracellular entrance of Cx26 channel crystal has a net positive potential ≥ 40 kT/e, whereas the extracellular half of the pore has a net negative potential ≤ 40 kT/e. Thus, the formation of inward rectifying P/N junction is expected for the crystal structure based on this separation of charge.

GCMC/BD also predicts that the modeled channels would be ideally anion selective in 100 mM symmetric KCl (determined from the ratio of predicted K⁺ and Cl⁻ current). This differs substantially from experimental reports of slight cation selectivity for Cx26 intercellular channels, P_K/P_Cl ~ 2.6 based on permeability ratios [81]. Undocked Cx26 hemichannels, in the inside-out recording configuration and a 140:10 mM salt gradient, have a P_K/P_Cl ~ 3.8 (Tang and Bargiello, unpublished). Note that ion selectivity of a P/N junction depends on the experimental method employed to measure it, particularly the orientation of the ionic gradient with respect to the orientation of fixed charged; a consequence of differential charge screening [73, 82].

The discrepancies in I/V relations, conductance and charge selectivity strongly suggest that the crystal structure does not correspond to the physiologic open state. Consequently, we first refined the completed structure by all-atom MD simulations in an explicit solvent and POPC membrane system. Briefly, the completed undocked hemichannel structure was equilibrated in NAMD at 310 K using NP_nAT dynamics. All system trajectories, which included total energy, surface tension, membrane thickness and channel RMSD reached equilibrium within 140 ns. Order parameters indicated that POPC remained in the disordered liquid state throughout the simulation. Following equilibration, four independent replica production stage MD simulations, each 20 ns in duration, were performed to increase the probability that the simulation represented the conformational space of the system. Trajectories were calculated from protein structures obtained every 2-fs. The positions of atoms in each time step in the four production stage simulations were averaged and the atomic structure with the smallest RMSD from this average was identified and selected for investigation with GCMC/BD. The structure was termed the “average equilibrated structure” and represents the average of all structures sampled during the four 20-ns production-phase simulations. As expected, the MD equilibration relaxed the crystal structure, eliminating the constriction at Met1, which reduced pore diameter to ~ 6 Å in the completed crystal (Fig. 2C). The extracellular half of the channel becomes narrowest region of the channel pore with a diameter of 12–14 Å. Packing of the TM helices was relaxed, but their overall topology and orientation was unchanged with equilibration. There was little change in predicted pore lining residues (supplementary information in [80]).

However, ion permeation computed with GCMC/BD for the average equilibrated structure continued to deviate from experimental, with I/V relations displaying inward rather than slight outward rectification, reduced slope conductance at 0 mV, and moderate anion rather than cation selectivity in 100 mM symmetric KCl [80].

The observed inward rectification and anion selectivity indicate that distribution of fixed charge on the channel surface and within the pore was incorrect both in the crystal and average equilibrated structure. A potential solution to the problem came from studies of Locke et al. [83] who showed, with tandem mass spectroscopy (MS/MS), that human Cx26 expressed in transfected HeLa cells was subject to several charge-changing co- and post-translational modifications. Amino acid modifications included neutralization of the positive charge of Met1 by N-terminal acetylation and acetylation of positively charged lysine residues at the cytoplasmic entrance, including the 15th, 102nd, 103rd, 105th, 108th, 112th, and 116th loci. These residues contribute to the positive potential observed in the intracellular half of the 2ZW3 crystal structure and their neutralization should change the degree of current rectification and reduce anion selectivity. Locke et al. also reported that glutamic acid residues, E42 and E47 may be modified by γ-carboxyglutamation. This would add negative charge near the center of the channel, which would increase the magnitude of charge separation in the P/N junction if positive charges at the intracellular entrance were not neutralized. The addition of negative charge would increase rectification (causing further deviation from experimental) and decrease anion selectivity (as required for it to agree with experimental).

However, it is important to keep in mind that carboxyglutamation was not confirmed by tandem MS and the fraction of Cx26 peptides modified was not determined. Furthermore, it is not clear given the location of these residues in the central region of the channel pore, (which would coincide with the central region of a transmembrane domain immediately following connexin insertion the ER prior to channel assembly), whether these glutamic acid residues would be accessible to modification by γ-glutamyl carboxylase; a polytypic ER membrane protein. In contrast, N-terminal acetylation is co-translational and would occur prior to translocation from the translocon into the ER. Similarly, most cytoplasmic lysines are expected to be accessible to enzymatic modification following incorporation into the ER, downstream compartments and in the plasma membrane. The positions of modified residues in the structure of the completed crystal structure channel are shown in Fig. 2H.

In Kwon et al. 2012 [80], we presented an extensive study of the effect of these charge modifications, individually and in combination on ion permeation. We reported that the I/V relation of the average equilibrated structure computed with GCMC/BD perfectly matched experimental results when the N-terminal Met1 residue and lysine residues were neutralized. Neutralization of Met 1 appeared to be key, as neutralization of lysines alone resulted in channels displaying inward rectification and anion selectivity. The perfect correspondence of channels with neutralized positive charges is shown in Fig. 2I. Notably, there is close agreement between predicted charge selectivity (P_K/P_Cl ~ 4.6) computed with GCMC/BD and that observed experimentally (P_K/P_Cl ~ 3.8). Note, the difference in experimental conditions from computational is expected to contribute to the observed difference. Experimental charge selectivity was determined by measurement of reversal potential of an excised inside-out patch in a 10:140 mM KCl gradient, whereas computed charge selectivity by the ratio of cation to anion flux in symmetric 100 mM KCl. Differences in ion concentration would change the degree of charge screening. Charges exposed to low ionic strength solutions will have larger effects on reversal potential than charges exposed to high ionic strength solutions as shown by Oh et al., [73] for Cx32*43E1 undocked hemichannels with and without negative charge substitutions at the 2^nd, 5^th, and 8^th positions in the N-terminus.

While combinations of positive charge neutralizations and increased negative charge by carboxyglutamations produced I/V relations similar to some experimental I/V relations of Cx26 undocked hemichannels, these channels were predicted to be almost perfectly cation selective, deviating markedly from experimental determinations. Carboxyglutamation alone resulted in channels predicted to be cation selective with inward rectifying I/V relations. Consequently, we conclude that carboxyglutamation is unlikely to be a significant physiologically relevant post-translation modification.

Significantly, no charge modifications of crystal or completed crystal structure produced I/V relations that bore any resemblance to experiment (Kwon et al., supplemental information [84]). We concluded that the average equilibrated structure obtained after MD simulations more closely represents the open Cx26 hemichannel structure than does the crystal structure, and that co- and post-translational modifications of Cx26 hemichannels are likely to play an important physiological role by defining the conductance and ion selectivity of Cx26 channels. We subsequently (Kwon and Bargiello, unpublished) redid the Cx26 MD simulation with acetylated residues defined explicitly by their CHARMM parameters. The resulting equilibrated structure did not differ substantially from that reported in Kwon et al. [80].

Open state models of Cx32*43E1 hemichannels

Because much of our understanding of the mechanisms of connexin voltage-gating is based on studies of the Cx32*43E1 hemichannel, it was important to obtain and validate and atomic model of its open state. Fortunately, Cx32*43E1 shares 83% sequence homology and 65% sequence identity with human Cx26 (excluding their C-termini). The high degree of sequence homology increases the likelihood that homology modeling of Cx32*43E1 based on Cx26 crystal structure will provide a reasonably accurate initial structure that following refinement by all-atom MD will closely correspond to the physiologic open state. (It should be noted that this may not be true for all connexins, as some, for example Cx36, have little sequence homology to Cx26. Consequently, direct solutions of Cx36 and other connexin channels are required rather than reliance on homology modelling to guide and interpret structure-function relations).

An open state model of the N2E Cx32*43E1 ΔCT hemichannel was constructed with MODELLER [85–87] using the Cx26 crystal structure (PDB ID: 2ZW3) as template. Recall that, the N2E substitution reverses the polarity of V_j-gating, from closure favored at inside negative to inside positive potentials, and thereby allowing distinction of V_j-gating and loop-gating in single channel and macroscopic recordings. As discussed below, this hemichannel uniquely provides the means to establish state-dependence of metal bridging studies to define the loop-gate closed state, and consequently we chose to model this hemichannel. The C-terminus was truncated at residue 220. We reported that this truncation did not alter the expression of either V_j-gating or loop-gating in Cx32*43E1 undocked hemichannels, and by extension Cx32 channels [88]. The lowest energy model (the lowest DOPE score, i.e. Discrete Optimized Protein Energy), of 500 models returned by MODELLER, was selected and following equilibration, sampled by a 400 ns all-atom MD production stage simulation in an explicit fully hydrated (100 mM KCl) POPC membrane using the specialized computer ANTON [89, 90].

The pore lining sequence of the modeled hemichannel agrees well with demonstrated accessibility of cysteine substitutions at positions 56, 50, 45, 38, 4, 8, 108 and 109 to modification with thiol reactive reagents. The I/V relation of the average equilibrated N2E Cx32*43E1 structure computed with GCMC/BD matches the experimentally determined I/V relation in symmetric 100 mM KCl [73]. As with the Cx26 hemichannel, the near perfect correspondence required N-acetylation of Met 1 and acetylation of two pore lining lysine residues (K103 and K104). Initial MS studies of affinity purified His-tagged Cx32 expressed in insect cells demonstrated that Met 1 is modified by N-terminal acetylation (Bargiello, unpublished). The final equilibrated model was obtained from MD simulation with the acetylated state of these residues explicitly defined according to their CHARMM parameters. The perfect correspondence of computed and experimental I/V relations results strongly support the view that the equilibrated structure corresponds to that of the physiological open hemichannel. Similarly, there is close correspondence between the computationally derived and experimental P_K/P_Cl although as explained for Cx26 the values are not directly comparable. The P_K/P_Cl for inside-out patch recordings in a 100:10 KCl gradient, ~ 13 [73], is almost identical to the P_K/P_Cl ~ 14.6 calculated from the ratio of K⁺ and Cl currents computed with GCMC/BD in 100 mM symmetric KCl. We conclude that the close correspondence of conductance, shape of the I/V relation and charge selectivity indicates that the atomic model closely corresponds to the native physiologic state of the N2E Cx32*43E1 undocked hemichannel.

Stabilization of the open state

Given the close correspondence between experimental and computed ion permeation, we reasoned that atomic models of the open state were reasonable approximations of the native, physiologic open state and that these open state structures may provide insight into changes in conformation underlying voltage-gating. It is well established that inside-negative voltage initiates loop-gate closure by destabilizing the open state [51, 60]. In the absence of applied voltage, most if not all connexin channels reside exclusively in the open state, thus, voltage must destabilize the open conformation. As reviewed in following sections, we demonstrated that the loop-gate permeability barrier was formed by a large conformational change of a segment of the channel pore, residues 41–50, termed the 3₁₀ helix [63] or parahelix [80, 91] that reduces pore diameter from 15–20 Å to ≤ 4 Å in Cx32*43E1 and Cx50 undocked hemichannels [60, 74, 92]. Surprisingly, the parahelix is the most stable region of the Cx26 channel pore [80].

To understand where and how voltage acts to destabilize the parahelix in the open state, we identified amino acid interactions that originate from the parahelix, as these are expected to stabilize that region of the channel pore. Identified interactions included a large intra-subunit van der Waals network and a dynamically correlated electrostatic network that extends across subunits, such that the electrostatic interactions in one subunit are linked to the parahelix in the adjacent subunit. These interactions are summarized in Fig. 3.

Figure 3.

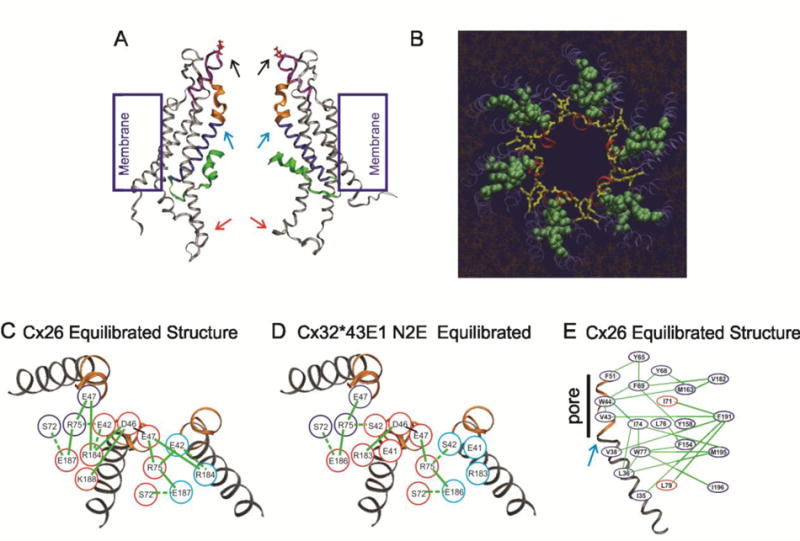
Electrostatic and van der Waals networks stabilize the open state of Cx26 and N2E Cx32*43E1 undocked hemichannels. (A). Side view of the equilibrated Cx26 hemichannel. The parahelix (3₁₀ helix in Maeda et al.) which form the loop-gate permeability barrier in Cx32*43E1 and Cx50 hemichannels is depicted by the purple ribbon. The first transmembrane domain in blue. The TM1/E1 bend angle is marked by the turquoise arrow (it is in fact the TM1/parahelix bend angle). The first extracellular loop is colored blue. The N-terminus is colored green. The cytoplasmic entrance to the channel pore (109C) indicated by the red arrow. The extracellular entrance (residue 56) by the black arrow. (B) End on view from the extracellular entrance of the Cx26 hemichannel. Red ribbons are the parahelix, yellow rods are the electrostatic network, green spheres are the van der Waals network. (C). Schematic representation of the electrostatic network in the Cx26 equilibrated structure. (D). Schematic representation of the electrostatic network in the equilibrated N2E Cx32*43E1 hemichannel. (E). Schematic representation of the van der Waals network in the equilibrated atomic model of Cx26. Panels B–E are reproduced from Biophysical Journal.

Briefly, the major van der Waals network emanating from parahelical residues, V43 and W44 in Cx26 include primary interactions with A39, F69, I74, M163 and F191; secondary interactions of these 5 residues with I35, L36, V38, A40, Y65, Y68, I71, W77, L79, Y158, V182, and M195 (Fig 3E). Maeda et al. [63] were first to identify this network, but in many cases contacts between residues resulted in highly unfavorable interaction energies (Lennard-Jones potentials) in the crystal structure [93]. The MD simulation adjusted the position of residues contained within the network, decreasing the free energy of the network in the crystal structure from 1.6 kcal/mol/subunit to −26.9 kcal/mol/subunit. A significant feature of the van der Waals network is that it extends across the bend at TM1/E1 border. A change in the bend angle of TM1/E1 (Fig. 3A) is likely required to allow narrowing of the intracellular entrance to the channel pore as implicated by metal bridging at 108C, 109C and 40C (see below).

We used the same conceptual approach, to trace electrostatic interactions from charged amino acids, contained within the parahelix. These include the conserved residues, D46 and E47 as well as D50 and E42 although the latter are not highly conserved among connexins. Two separate electrostatic networks were identified, but the one extending directly from D46 and E47 was most interesting. It included salt-bridge and hydrogen-bond formation among subsets of residues in the group R75, R184, K188, E42, E187, and S72 (Fig. 3 B and C). (A comparable electrostatic network is present in the atomic model of the N2E Cx32*43E1 hemichannel (Fig. 3D)). Specific pairs of interactions of these residues, were shown to undergo large fluctuations in properties over the course of production state simulations (Fig. 4). The significant feature of Cx26 network was uncovered by a multifactorial correlation analyses of the trajectories of: 1) All the electrostatic and vdW interactions described in the interaction lists provided in Kwon et al. [80] for the entire Cx26 hemichannel. 2) The pitch, dihedral angles (Ψ/Φ), and side-chain bond torsion angles of the parahelix. 3) The solvent accessibility and pore-lining probability of all residues. 4) The TM1/E1 bend angle. 5) The tilt angle (with respect to the membrane-normal) of the four transmembrane helices. Significantly, the correlation analysis revealed that changes in the strength of electrostatic interactions between specific residues in one subunit causes changes in the interactions that determine the structure of the parahelix and TM1/ E1 bend angle in the adjacent subunit (Fig. 4). Furthermore, changes in the dynamics of the electrostatic network were shown to be coupled to the van der Waals network by demonstration that mutation of the 2 amino acids (V43A and I74V) in the van der Waals network altered the dynamics of interactions in the electrostatic network [93].

Figure 4.

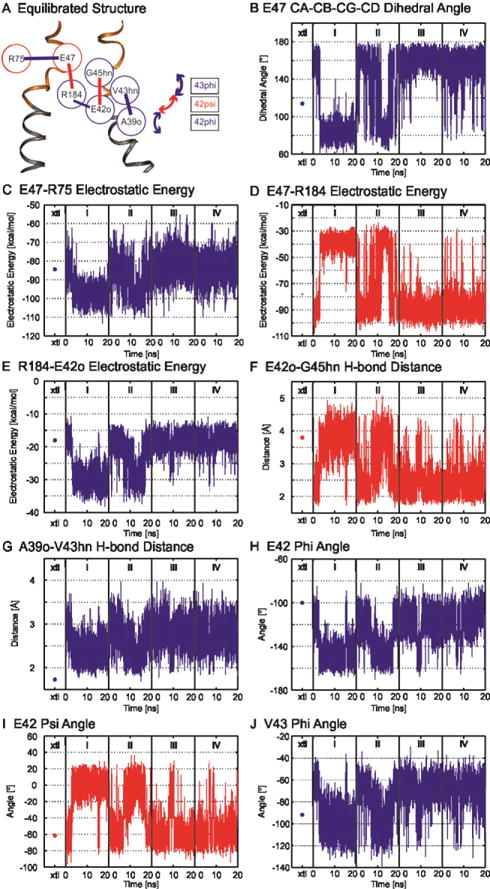
Correlation map of the electrostatic network derived from correlated time series of electrostatic interactions present between two adjacent subunits. (A) Correlation map of electrostatic interactions. (Red and blue circles) Residues located in adjacent subunits. (B–J) Time series properties of specified interactions. (Blue) All interactions positively correlated with that of E47-R75; (red) those that are negatively correlated. Dots in column xtl are the energies of the interactions determined for the unequilibrated crystal structure. Additional details are provided in Kwon et al. [93]. Reproduced from Biophysical Journal.

The direct coupling of dynamic interactions across subunits suggests that loop-gating is concerted and cooperative. We propose that together the electrostatic and van der Waals networks form the connexin voltage sensing domain (VSD). We hypothesize that voltage initiates loop-gating by driving the reorganization of the electrostatic network (Fig. 3C and D). Thus, gating charge will reflect breakage, reformation and repositioning of charge interactions in a changing electric field. This differentiates the connexin loop-gate voltage sensor from the canonical voltage sensor, exemplified by K⁺ channels, where directional movement of four highly conserved arginines through the electric field accounts for most of the ~12–14 elementary gating charges. The MD simulations also show how reorganization of VSD may also change the TM1/E1 bend angle to explain the observed changes in conformation at the intracellular entrance. It remains to be seen if the diameter of the channel entrance is strongly coupled to the conformation of the parahelix. The slow gating transition, caused by sequential transitions through a series of substates, may correspond to “ratcheting” of the parahelix through a series of quasi-stable intermediate conformations.

Conformation and atomic modelling of the loop-gate closed state with distance constraints

A major challenge to the elucidation of the molecular mechanism of connexin voltage-gating is obtaining and validating atomic models of the closed state. Currently, there are no methods that allow direct structural solution of a wild-type channel residing in a native voltage-gated closed state, as this would require application of a stable voltage-gradient across a purified, correctly oriented channel in a lipid membrane during crystallization or electron microscopy. While it may become possible to capture wild type channels in a voltage-closed state by rapid freezing of channels reconstituted in liposomes in the presence of an ionic gradient, the resulting atomic structure would still need to be validated to show that it does in fact correspond to the physiologic, native closed state.

As an alternative to direct solution of the channel in a voltage induced closed state, it may be possible to take advantage of the possible similarity between the structure of channels closed by voltage and chemical agents. It has been proposed that the closed state induced by Ca²⁺ and other divalent cations is equivalent to that of the closed state of voltage-dependent loop-gating [94]. If correct, this would simplify solving the atomic structure of the voltage-dependent closed state. Bennett et al. [64] solved the crystal structure of Cx26 gap junctions in the presence and absence of 20 mM Ca²⁺ (PDB ID:5ER7). Remarkably, the Ca²⁺ bound structure displayed no major changes in pore diameter and overall channel conformation. Rather, Ca²⁺ was coordinated in the channel pore by formation of intersubunit salt bridges involving residues E47, E42 and G45. Molecular dynamics simulations showed that bound Ca²⁺ formed an electrostatic barrier that significantly reduced permeability to cations but not anions [64]. In contrast, Cd²⁺-thiolate metal bridging indicates that pore diameter of Cx32*43E1 and Cx50 undocked hemichannels narrows from 15–20 to ≤ 4 Å in the same region of the channel where Ca²⁺ binds. This result suggests that the closed conformation of voltage-dependent loop-gate closed state differs from that resulting from Ca²⁺ binding. However, further study of the loop-gate closed state is required because high Ca²⁺ fully abolishes conductance. A recent study by Contreras and colleagues [28] implicates Ca²⁺ in the destabilization of the Cx26 hemichannel open state by interfering with D50-K61 salt bridge formation, which in turn appears to alter interactions among components of the electrostatic network described above. One cannot dismiss the possibility that purified isolated Cx26 channels did not respond to Ca²⁺ in a manner identical to the native conformation or that crystallization prevented relaxation of channel structure to the physiological Ca²⁺- closed state. It should also be noted that the intracellular entrance of the channel, including the region of the pore formed by the N-terminus was not resolved in the crystal structure. Consequently, one cannot rule out the possibility that Ca²⁺ binding did not change the conformation of these regions. Solution of the Cx26 intercellular channel structure in the presence and absence of Ca²⁺ using single particle cyro-EM may provide additional insight, given that the method is more likely to maintain channels in a native conformation than crystallization. In any case, other approaches will be required to assess the relation between that the Ca²⁺-gated and voltage-gated closed states, before one concludes that the voltage and chemical gates differ fundamentally.

It is generally accepted that the best strategy to create and validate an atomic model of a voltage-gated closed state is to apply different but complementary experimental and computational methods and to use the resulting information to derive a consensus atomic structure. Vargas et al. used this approach to obtain an atomic model of the resting state of voltage-gated K⁺ and Na⁺ channels [95, 96] from structural and computational data and experimental distance constraints. The consensus approach recognizes that all methods, both structural, experimental and computational have different intrinsic limitations, in part reflecting underlying assumptions as well as intrinsic technical limitations. Convergence of structures obtained by different methods increases confidence that the structure obtained represents the native, physiologically relevant closed structure.

Conformation of the loop-gate closed state determined by metal-bridging and disulfide bond formation

A powerful experimental approach to define protein conformation is the use of chemical crosslinking as a “molecular ruler” to define the distance between specific amino acid residues when the protein resides in different functional states. The chemistry of cysteine residues is often exploited in this approach, both in use of specific cross-linkers of known length and the ability of cysteine residues to coordinate Cd²⁺ and other heavy metals with well-defined stoichiometry and structure. Correct application of the approach requires that channels can be identified where substituted cysteines do not alter the structure of open and closed states. This condition is indicated when the equilibrium and kinetic properties of voltage-dependence of cysteine substituted channels are identical to wild-type. It increases the likelihood that inferences drawn from studies of cysteine mutants will represent the structure of native wild-type channels.

Distance constraints obtained from Cd²⁺-thiolate bridging and disulfide bonding between substituted cysteines played a significant role in the development and testing of consensus atomic models of the resting state of the K⁺ and Na⁺ channel VSDs [95–102] and BK channel gating [103] and in defining the loop-gate closed conformation of connexin channels [74, 92, 104]. Large intrinsic variability in protein conformation for any given state can make the approach unreliable. For example, the approach was less successful in defining conformational changes in ionotropic GABA and ACh receptors, apparently because the large intrinsic flexibility of these channels allows disulfide bonding between substituted cysteines at residues that subsequent structural solutions showed were separated by 15–17 Å [105–107]. Whenever possible, the rate of modification should be determined. Determination of modification rates informs how long any specific distance was maintained during measurement, i.e. the length of time that the channel resides in a given conformation.

Connexin hemichannels are well-suited to application of these methods to define closed conformation because the channel pore appears to be overall very stable. Stability is indicated by temperature factors of crystallographic solution [63] and root mean square fluctuations (RMSF) of all-atom MD simulations [80]. The extracellular half of the channel is stabilized by three pairs of disulfide bonds within and between extracellular loops of each subunit and by an extensive network of electrostatic and van der Waals interactions – the hypothesized VSD. The RMSF of the parahelix is ~3 Å in the open state [80]. Although there are fewer stabilizing interactions at intracellular channel entrance, the RMSF in this region is still quite small, ~4.5 Å [80]

The chemistry of Cd²⁺-cysteine complexation is well-defined and underpins structural inferences derived from studies of Cd²⁺-thiolate bridging. Briefly, the electron configuration of Cd²⁺ ([Kr] 4d¹⁰5s²) allows accommodation of up to 8 additional electrons, so that up to 4 cysteines can coordinate a single Cd²⁺ (tetradendate coordination). The 2 electrons contributed by each cysteine sulfur atom form a “dative covalent bond” with Cd²⁺. In free solution, the tetradendate complex preferentially adopts a tetrahedral geometry, with a Cd²⁺ stability constant, logK ~40. Cd²⁺ can be coordinated by two cysteines (bidentate coordination) at lower affinity, logK ~20 [108–110]. In peptides, bidentate coordination is significantly less stable (K_d ~50–500 μM) [111–113]. This decrease in affinity presumably reflects steric hindrance that prevents optimal coordination geometry.

We define high affinity coordination to occur when bound Cd²⁺ can only be dissociated from the cysteine coordination site by chelation with TPEN or DTT. (Cd²⁺-TPEN and -DTT logK stability constants are 16.3 and 10.8 respectively [114, 115]). When such an effect is specific to the loop-closed state, we consider that the substituted cysteines form a tetradendate coordination site that locks the channel closed. We define a low affinity site coordination site as one at which Cd²⁺ binding is readily reversed by wash with Cd²⁺-free solutions. In this case, we can use comparative kinetic measurements to determine if Cd²⁺ binding stabilizes the closed state. We consider this to indicate bidentate coordination. The average distance between Cα (from atomic structures deposited in the RCSB protein structure database) is 6.53 ± 0.01 Å in tetradendate coordination and 8.20 ± 0.01 Å in bidentate coordination. We preferentially use high affinity sites to model channel states as the interpretation of the experimental data indicating state-dependent lock is straightforward.

To date, we have investigated cysteine substitutions at 16 of 27 loci spanning the length of the Cx32*43E1 hemichannel pore expressed voltage-dependent currents as undocked hemichannels. Cysteine substitutions of a number pore exposed loci, (based on open state models) produced functional channels. These included, from the intracellular to extracellular entrances: L108C, E109C, I33C, L36C, V38C, A40C, A43C, G45C, A50C, and Q56C, all of which form channels with voltage dependencies very similar to or indistinguishable from wild type. This suggests that the conformation of open and closed states and intervening transition states of these mutant channels, are comparable, if not identical, to native wild-type channels. Thus, state-dependent metal bridging in such cysteine substituted channels should report the conformation of the physiologic, native channel. Others cysteine substitutions, including T4C, G5C and T8C caused large rightward shifts in the P_open/voltage relation, making it difficult to establish the relationship between open and closed state in the mutant and wild type channels. Several cysteine substitutions failed to express membrane currents reliably in Xenopus oocytes. These included: T55C, Q48C, E47C, D46C, W44C, S42C, E41C, N2C, L106C, R107C. The failure of N2C, E41C and S42C to express currents in Cx32 and Cx32*43E1 backgrounds was surprising as these loci tolerated substitution of other amino acids.

Conformational changes in the parahelix

The results of Cd²⁺ studies are summarized in Fig. 5A. Briefly, cysteine substitutions at 3 loci in the parahelix, two of which A43C and A50C form high affinity state-dependent Cd²⁺-thiolate bridges, while the third G45C forms a site with lower affinity. The electrophysiological behavior of A43C illustrates several aspects of state-dependent high affinity metal bridge formation. A representative trace for Cx32*43E1 A43C is shown in Fig. 5B.

Figure 5.

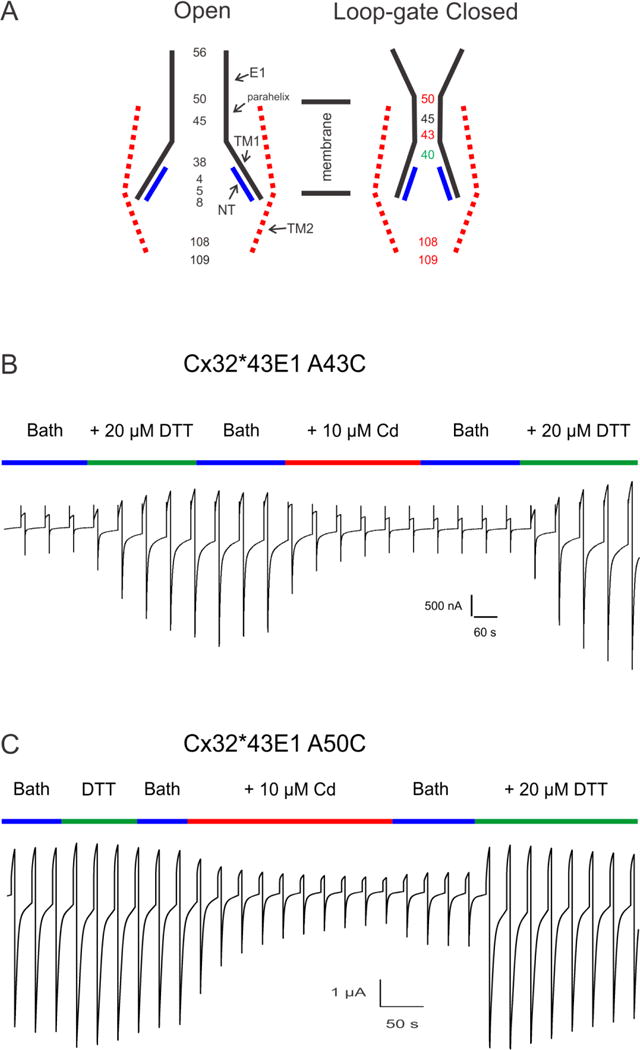
(A). Schematic illustration of the Cx32*43E1 channel pore in the open and loop-gate closed state. Cysteine substitutions of the loci depicted in the open state were shown to be accessible to modification with thiol reagents. In the loop-gate closed state, cysteine substitutions at 43 and 50 form “high affinity” state-dependent Cd²⁺-thiolate metal bridges as does the double mutation 108C+109C. In contrast, the effect of Cd²⁺ on channels formed by individual mutations, 108C and 109C, is reversed by wash out of Cd²⁺. We attribute this effect to formation of low affinity bridges. Similarly, cysteine substitution at 40, are not accessible to MTS modification in the open state, and form “low affinity” metal bridges in the loop-gate closed state. Cysteine substitutions of G45C, interact with Cd²⁺ to lock the channel in the loop-gate closed state, but much of the effect can be reversed by wash-out of Cd²⁺ (incomplete reversal). Current relaxations of channels containing Q56C are unchanged by Cd²⁺. (B) High affinity Cd²⁺-thiolate bridge formation at 43C (see text). Activation of A43C currents requires application of either TPEN or DTT, as does restoration of currents following application of 1–10 μM Cd^2+. (C) Currents from A50C channels differ from A43C in two ways, i) activation of currents does not require chelation, and ii) currents are partially restored by wash out of Cd²⁺, but full restoration requires application of metal chelators.

Typically, A43C and N2EA43C undocked hemichannels (on the Cx32*43E1 background) do not express membrane currents above background levels in Xenopus oocytes. Bath application of low concentrations (1–20 μM) of either DTT or TPEN cause a large increase in membrane current attributable to activation of A43C channels. Because DTT and TPEN are both strong chelators of heavy metal divalent cations, the simplest explanation is that inhibition of currents is a consequence of presence of low concentrations of contaminating heavy metals that lock A43C channels in a closed state. Subsequent application of 1–20 μM Cd²⁺ causes a very rapid and complete reduction in A43C current, which can only be reversed by reapplication of DTT or TPEN. Furthermore, we demonstrated that the “high affinity” metal bridging requires a minimum of four A43C residues [74] to lock the channel closed. These results are consistent with tetradendate Cd²⁺ coordination. In support, we showed that some fraction of subunits of A43C channels are cross-linked by disulfide bonds, although it is not clear what fraction of channels are crosslinked. A contributing factor may be the difference in the distance between adjacent Cα to form Cd²⁺ – thiolate coordination site ~ 6.5 to 8.2 Å as compared to ~ 5.6 Å for disulfide bonds [116]. Similarly, Cx32*43E1 A50C undocked hemichannels are locked in the loop-gate closed state by Cd²⁺. The interaction can only be fully reversed by metal chelation with DTT or TPEN (Fig 5 C).

Based on Cd²⁺-thiolate bridge formation, we infer that pore diameter at the parahelix is reduced from 15–20 Å in the open state to < 4 Å in the loop-gate closed state. A pore of this diameter, containing positively and negatively charged residues, will prevent flux of K⁺ and Cl⁻ [74]. A similar conclusion was reached for Cx50 undocked hemichannels, based on analogous behavior of F43C (S42 in Cx32*43E1). In contrast, high affinity metal bridging was reported at Cx50 F43C and G46C (G45 in Cx32*43E1) and lower affinity at D51C (D50 in Cx32*43E1) [92]. Notably, Cd²⁺ coordination at G45C has lower affinity than at either A43C or A50C in Cx32*43E1. In most cases, lock of the channel in the loop-gate closed state can be almost fully reversed by wash out of applied Cd²⁺. However, because of the proximity of G45 to A43 and A50, it is most likely that the pore diameter of the closed channel will be uniform along this segment. We suggest that the difference in affinity results from steric hindrance that prevents G45C to coordinate Cd²⁺ in an optimal low energy geometry.

We also showed that the Cx32*43E1 parahelix is reorganized with loop-gate closure [74]. A43C, which is not pore-lining in the open state, becomes pore-lining in the loop-gate closed state, while G45C and D50C line the channel pore in both. A40C lines the channel pore only with loop-gate closure, where it forms a low affinity Cd²⁺-thiolate bridge, suggesting that pore diameter at this locus narrows less than at loci within the parahelix. The simplest explanation is that the narrowing at A40 is caused by straightening the TM1/E1 bend angle, which would also narrow the intracellular entrance to the channel pore. Notably, because A40C does not appear to be pore lining (i.e. was not modified by MTS reagents in long-duration single channel recordings [74]), it should also be inaccessible to Cd²⁺ binding in the open state, Consequently, it is unlikely that the observed reductions in current at A40C are due to introduction of positive charge by Cd²⁺ binding to A40C residues in the open state. The introduction of positive charge could potentially shift voltage-dependence, by altering the electric field across charged residues in the parahelix, which are believed to form part of the loop-gate voltage sensor. Notably, Cx50 A41C (A40C in Cx32*43E1) did not interact with Cd²⁺ in the open and the loop-gate closed state, suggesting that the intracellular entrance of Cx50 undocked hemichannels may not narrow.

The ability to reverse V_j-gating polarity independently of loop-gating and without causing large shits in open probability of Cx32*43E1 along the voltage axis provided the means to establish state-dependence of Cd²⁺-thiolate bridge formation. For example, Cx32*43E1 A43C channels reside in the open state at all membrane potentials more positive than −30 mV. Thus, application of Cd²⁺ at positive potentials provides a means to determine if: 1) channels can be locked in the open state. If they are locked open, then subsequent steps to negative potentials will fail to produce current relaxations. 2) If Cd²⁺ acts to destabilize the open state, then currents elicited at positive holding potentials will relax resulting in decreased steady-state values. In contrast to Cx32*43E1 A43C, current relaxations elicited by steps to inside negative potentials will correspond only to the closure of loop-gate in N2ECx32*43E1 hemichannels. Current relaxations elicited by steps to positive voltages will reflect closure of V_j-gates. We observed that there was no effect of Cd²⁺ when applied at positive potentials, Metal bridge formation only occurs at inside negative potentials, when N2E Cx32*43E1 A43C undocked hemichannels preferentially reside in the loop-gate closed state. Channels were not locked when they resided in the open state. These data led to the conclusion that loop-gate closure results from a conformational change that narrows the channel pore.

Conformational changes at the channel entrances

The apparent formation of a low affinity Cd²⁺-thiolate metal bridge at A40C implicates straightening of the TM1/E1 bend angle with loop-gate closure, which in turn is expected to narrow the intracellular entrance to the channel pore demarcated by residues L108 and E109 (Fig. 5). We examined this possibility by determining whether substituted cysteines at these loci would form state-dependent Cd²⁺-thiolate metal bridges that would lock or stabilize the channel in the loop-gate closed state. We reported that both L108C and E109C appeared to form low-affinity Cd²⁺-thiolate metal bridges, which we attributed to bidentate coordination. These conclusions were based on the following observations:

1. Bath applied Cd²⁺ reduced membrane currents of N2ECx32*43E1 E109C undocked hemichannels in a concentration dependent manner, varying from ~ 50% reduction with 10 μM to > 90% with 60 μM Cd²⁺ using a train of voltage steps alternating between from −10 to −70 mV. This voltage paradigm elicits opening (at −10 mV) and closing of loop-gates (at −70 mV).

2. Current inhibition was reversed by simple wash-out of Cd²⁺ without addition of metal chelators (DTT or TPEN).

3. 20 μM Cd²⁺ had no effect on the operation of V_j-gates, as evidenced by no change in current levels or kinetics of current relaxation in steps from 10 mV to 50 mV applied to N2ECx32*43E1 E109C.

4. No change in currents were observed in Cx32*43E1 E109C channels elicited by alternating voltage steps between 10 and 50 mV. Because the channel resides exclusively in the open state at these potentials, Cd²⁺ does not destabilize the open state at these potentials.

5. The time constant of current relaxation elicited by steps from −70 mV (loop-gate closed state favored) to −10 mV (loop-gate open state favored) was significantly lengthened by application of 10 μM Cd²⁺. Because N2ECx32*43E1 E109C undocked channels are fully open at −10 mV, the time constant of current relaxation at this voltage corresponds to the rate constant of channel opening. Lengthening of this rate constant corresponds to a reduction in the number of transitions from the loop-gate closed state to the open state, consistent with the stabilization of the loop-gate closed state by Cd²⁺. Surprisingly, the time constant of current relaxations elicited by steps to −70 mV (where P_open is ~ 0.5) from −10 mV is shortened by Cd²⁺. This suggests that Cd²⁺ may destabilize the open state sufficiently at −70 mV to increase the number of transitions from the open to closed state. But open state destabilization is not supported by electrophysiological recordings showing that Cd²⁺ had no effect on the open state. Previously, we misinterpreted the shortening of this rate constant to indicate that Cd²⁺ had stabilized the loop-gate closed state. We suggest that Cd²⁺ may destabilize an intermediate partially closed loop-gate state.

6. We demonstrated that E109C was accessible to modification by MTSEA (2-aminoethyl methanethiosulfonate); a positively charged MTS reagent. Modification of E109C blocks the effect of Cd²⁺ at this locus, indicating that the effects of Cd²⁺ are due to interactions with the thiol group of the substituted cysteine. Notably, the addition of positive charge following MTSEA modification has markedly different effects than does Cd²⁺: The amplitude of macroscopic currents elicited by steps to −70 mV are doubled, the time constant of current relaxations elicited by steps from −70 to −10 mV are markedly shortened, as are the time constants of current relaxations corresponding to loop-gate closure driven by polarization to −70 mV. Together, these results indicate that simple addition of positive charge to E109C subunits cannot explain the effect of Cd²⁺, which would also likely add positive charge to individual substituted cysteines by monodentate interactions (i.e. if and when cysteines were not correctly positioned to coordinate Cd²⁺). The simplest interpretation to explain the lock in the loop-gate closed state, is that Cd²⁺ interacts with multiple E109C subunits when the channel resides in the closed state. Given the apparent low affinity of binding, bidentate coordination seems most likely. If correct, the diameter of the loop-gate closed channel at the intracellular entrance would entrance narrows from 15 Å to ~ 10 Å with loop-gate closure, a diameter that might restrict but not prevent ion permeation. Although studied in less detail, L108C behaved similarly to E109C [117].

Reliance on low affinity Cd²⁺-thiolate binding to infer a change in the conformation of the intracellular channel entrance was nevertheless a concern. Consequently, we constructed the double mutation, L108C+E109C to further probe conformational changes of the cytoplasmic entrance. We reasoned that steric constraints may contribute to the low affinity metal bridging observed in individual mutations, as formation of a stable coordination site might require opposite rotations of adjacent subunits. Significantly, the voltage dependence of the double mutation (like each single mutation) is indistinguishable from wild type chimeric hemichannel. This indicates that open and closed states of the mutant should be identical to that of wild type and consequently that any conformational change reported by metal-bridging will likely represent that of the native channel.

We found that the L108C+E109C double mutant on the N2ECx32*43E1 (we abbreviate this to N2E 108C+109C) background forms a high affinity Cd²⁺-thiolate bridge at the intracellular entrance that locks the channel in the loop-closed state (Fig. 6A). N2E 108C+109C membrane currents are only observed following application of 20 μM DTT or TPEN and are completely inhibited by 1–20 μM Cd²⁺ at voltages that close loop-gates. This inhibition can be reversed only by heavy metal chelation with 20 μM DTT or TPEN, behavior identical to that of A43C, A50C and Cx50F43C and Cx50G46C [60, 74, 92]. Significantly, the voltage-dependence of N2E 108C+109C hemichannels is indistinguishable from “wild type” – N2E Cx32*43E1 (Fig. 6B and C). This supports the view that the open and closed states of the double mutation are identical to wild type and that Cd²⁺ locks the channel in a physiologically relevant closed conformation. Interestingly, western blots of the double mutation after electrophysiological study reveal formation of dimers and trimers crosslinked by disulfide bonds (not shown), indicating that the thiolates of at least some adjacent cysteines approach to within 2 Å and perhaps accounting for the failure of complete current restoration by chelation of Cd²⁺ by DTT or TPEN. The absence of any appreciable “leak” current indicates that these disulfide bonds and metal bridges form only when the channel is closed. However, in contrast to E109C, 20 μM Cd²⁺ reduces current through open channels of the double mutation with comparable voltage paradigms (i.e. steps from 10 to 50 mV as well as application of Cd²⁺ to oocytes at 0 mV holding potential), indicating that Cd²⁺ also destabilizes the open state. We suggest that Cd²⁺ binding to individual 108C+109C subunits “drives” open channels into the loop-gate closed state and the closed state is subsequently locked by high affinity Cd²⁺ bridging. It appears that the double mutation may have created a connexin channel that is gated by both μM Cd²⁺ and voltage.

Figure 6.

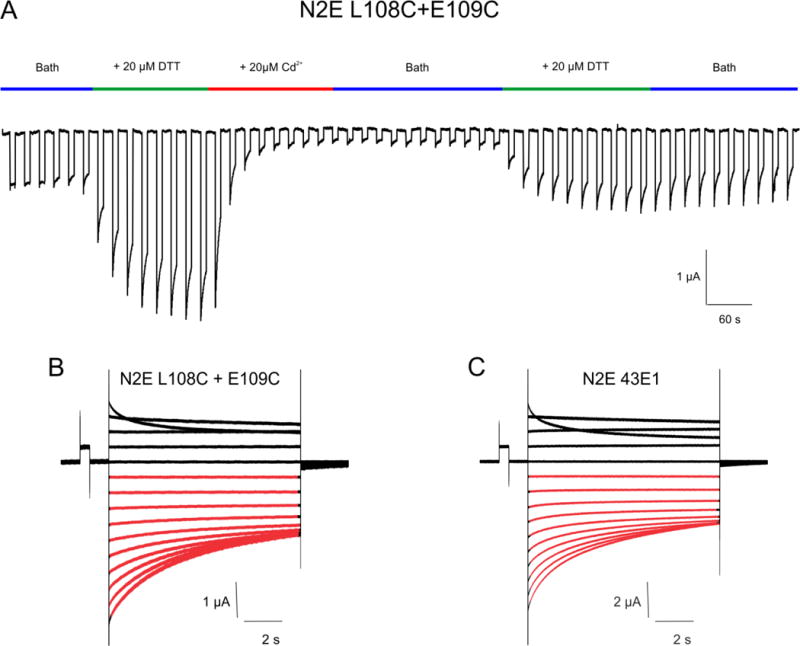
N2E Cx32*43E1 L108C +E109C undocked hemichannels are locked in loop-gate closed state by Cd²⁺. Currents were elicited by a train of voltage steps alternating between −10 and −70 mV, the time of reagent application is shown in the colored bars above the current trace. Low levels of initial currents are markedly increased by bath application of 20 μM DTT. Currents are decreased by application of 1–20 μM Cd²⁺ and are only partially restored by subsequent chelation of Cd²⁺ with 20 μM DTT. The result is consistent with formation of a high affinity Cd²⁺ site by substituted cysteines when the channel resides in the loop-gate closed state. (B and C). Currents from the N2E L108C+109C and “wild-type” N2E 43E1 (N2ECx32*43E1) hemichannels elicited by sequential voltage steps from +40 to −120 mV from a holding potential of 0mV. Closure of loop-gates at inside negative potentials corresponds to current relaxations shown in red. Closure of V_j-gates at inside positive potentials corresponds to current relaxations shown in black.

We conclude that it is likely that the intracellular entrance to the channel pore is coupled to conformation of the parahelix and that the coupling is mediated by changes in the TM1/E1 bend angle. An unanswered question is how tightly the two domains are coupled. Will for example, lock of the intracellular channel entrance in the loop-gate closed conformation, also prevent the parahelix from opening at voltages that favor this transition. If this proves to be the case, then the intracellular channel entrance may be a viable target for development of therapeutic drugs to modulate connexin channel activity.

In contrast, the extracellular entrance, demarcated by Q56, did not appear to undergo large conformational changes with either voltage-gating process [104]. Thus, it appears that the loop-gate permeability is essentially focal, being largely restricted to conformational changes in the parahelix. The large conformational narrowing in the parahelix can only account for full channel closure.

Atomic modelling of the N2ECx32*43E1 loop-gate closed state

Recently, we constructed an atomic model of the N2ECx32*43E1 undocked hemichannel in the loop-gate closed state by incorporating distance constraints corresponding to high affinity metal bridging at A43C, G45C and A50C in the parahelix, low affinity at A40C, and at L108C and at E109C. The appropriate distance constraints (tetradendate Cα – 6.5 Å; bidentate Cα – 8.2 Å) were incorporated into MODELLER using the N2ECx32*43E1 sequence and the Cx26 crystal structure (PDB ID:2ZW3) as template. The resulting closed-state model with the lowest DOPE score was equilibrated by all-atom MD in a fully hydrated POPC membrane with voltage (−200 mV) that strongly favors residency in the loop-gate closed state. Harmonic distance constraints derived from metal bridging studies were gradually removed during 3 sequential equilibration simulations and finally four replicate 50 ns production stage simulations with no constraints were performed and “average equilibrated structure” obtained. While we have shown with GCMC/BD that the model is non-conductive, it is premature to present details here other than to outline approaches to test the model’s validity.

The first is an experimental approach to test the formation of unique interactions that are specific to the closed state atomic model. These novel interactions are being investigated by experimental methods, which include both biochemical and functional tests. Biochemical tests, such as formation of disulfide linkages between substituted cysteines of residues predicted to interact, are rapid and straightforward. However, these initial screens must be followed by functional tests, such as additional metal bridging studies (which are restricted to cysteine substitutions that are accessible to Cd²⁺), and mutant cycling approaches exemplified by studies in Cx26 hemichannels that are based on open state atomic models [29, 118]. Notably, these mutant cycling studies provided additional validation of the structural models that were derived from the Cx26 crystal.

The second utilizes computational methods to compare gating charge computed for open and closed state atomic models with experimentally calculated gating charge. Computational methods have been developed to calculate gating charge from atomic structure for ion channels exemplified by the superfamily family of K⁺, Na⁺ and Ca²⁺ [65] and these have been used to evaluate atomic models. Connexin channels pose a significant and interesting theoretical problem because the voltage sensor resides in the pore. Application of voltage to the open state results in net ion flux, which as a non-equilibrium condition disqualifies equilibrium computational methods, such as the Poisson-Boltzmann equation, to compute the voltage field that affects the voltage sensors. The gating charge of the N2E Cx32*43E1 ΔCT undocked hemichannel is ~ 0.4 [119], ranging from 0.34 to 0.43 in 0 Mg²⁺. It is likely that the high dielectric of the channel pore contributes to the low gating charge as charged components of the sensor reside in the pore. Calculated gating charge should increase if measured in low ionic strength solutions, and may provide increased sensitivity to measurement.

The third method utilizes direct structural solutions of mutant channels that are locked in the loop-gate closed state (for example 108C+109C) or display large rightward shifts in voltage-dependence such that they are closed in the absence of applied potential. Several mutations that map into the electrostatic and van der Waals networks have been described [10, 120]. The loop-gate closed state of mutations that favor residency in the closed state by destabilizing the open state without changing the stability of the closed state, provide the best means of directly solving the structure of the loop-gate closed state. Recent advances in single particle cryo-EM have led to the solution of atomic resolution models of ion channels. For example, the 440 kDa anthrax protective antigen pore at 2.9 Å [121], the 300 kDa TrpV1 ion channel at 3.4 Å [122] the 560 kDa Slo2.2 channel at 4.5 Å [123], and the 400 kDa innexin6 hemichannel and 800 kDa intercellular channel at 3.3 and 3.6 Å respectively [124]. These successes support the view that the solution of the structure of mutant channels that preferentially reside or are locked in the closed state in the absence of applied voltage is possible. Integration of the results obtained by application of these three diverse approaches should lead to the solution of the atomic structure of the voltage-dependent loop-gate closed state.

The N-terminus and V_j-gating

Structure-function studies identified the first 8 amino acids of the helical region (the NTH) formed by the N-terminus to be key in establishing the polarity of V_j-gating in Cx32 and Cx32*43E1 intercellular and undocked hemichannels [48, 56, 58, 61, 62]. Negative charge substitutions at the 2^nd, 4^th and 5^th residues of Cx32, reversed gating polarity from closure favored at inside negative potentials to closure favored at inside positive potentials, while those at the 8^th residue produced channels with bi-polar gating. (Bi-polar gating is defined as channel closure at both inside positive and inside negative potentials, and when the channels are fully open in the absence of applied voltage). Significantly, analyses of heteromeric channels containing different numbers of N2E and wild type subunits demonstrated that a single subunit was sufficient to produce channels with bi-polar V_j-gating. We interpreted this finding to indicate that V_j-gating was a property of an individual channel subunit rather than a concerted hemichannel property. Cx26 has not been examined extensively, only polarity reversal by neutralization of the negative charge at D2 has been reported and to our knowledge no additional studies have been undertaken. Notably, substitution of the first 11 residues Cx26 into Cx32, additionally required the presence of the Cx26 cytoplasmic loop domain to produce functional channels (Oh et al 1999), suggesting additional interactions of the Cx26 NT with other regions of the channel. The same was not true for Cx32 substitutions into Cx26; exchanging the NT of Cx32 alone did not interfere with Cx26 channel function. The molecular bases of this difference is unknown, but it should be noted that NMR studies of N-terminal mutations in Cx26 and Cx32 peptides indicate that the “rules” underlying the folding and structure of the N-terminus differ in the two connexins [125] (see below).

Taken together, the simplest interpretation of these results is that charges in the pore lining region of N-terminus form at least part of the V_j-gating voltage sensor, with V_j-gate closure being initiated by the inward (toward the cytoplasm) movement of voltage-sensing residues. The structural implication of these results, was that the NTH must reside in the channel pore, as only in this position could it sense changes in V_j. The proposed structure was supported by solution of peptides corresponding to the entire N-terminus (residue 1–21) of Cx26 and Cx32 by NMR. These studies showed that N-terminal peptides were characterized by formation of an open turn in the vicinity of the conserved G12 residue in these connexins. The turn and its intrinsic flexibility allows positioning of the NTH into the channel pore [126, 127]. This interpretation was supported by correlations between mutations that failed to form functional channels and their NMR structure [126, 128]. Mutations, such as G12S, which fail to form channels, prevent turn formation. Interestingly, the mutation G12R adopts a different structure and has a different functional effect than in the NT of Cx32 than it does in Cx26, suggesting that the rules of underpinning the structure of the N-terminus differ in the two connexins [125]. In spite of the intrinsic limitations of inferring protein structure form that of small peptides, the NT of Cx26 gap junction crystal structure 2ZW3 was remarkably similar to that of the NMR. Unfortunately, the N-terminus was not resolved in either of Bennett et al. more recent Cx26 structures [64].

Despite these initial advances, little is known how and where the permeability barrier for the V_j-gate is formed. Explanation of the structural basis of V_j-gating faces several challenges, including the existence of at least 3 distinct sub-conductance states. Presumably, these substates represent different “quasi-stable” channel conformations. Of potential significance is the observation that heteromeric channels containing a single N2E subunit continue to display V_j-gating to 3 substates [58]. This finding suggests that entry into substates reflects a change in the conformation of an individual subunit and not necessarily the sequential entry of more than one subunit into the channel pore.

Oh et al., [48] reported that the direction of single channel current rectification observed for intercellular Cx32 channels, is consistent positioning greater amount of positive charge into the pore and consequently with narrowing of the intracellular entrance [48]. However, the location of the constriction and positive charge was not established. Bukauskas and co-workers [129] reported that Cx43 V_j-substates also result from channel narrowing and increase anion charge selectivity (consistent with an increase in the effect of positive charge in determining ion selectivity in a narrow versus wide diameter pore).

Maeda et al. [63] proposed that the V_j-gate is formed by narrowing of the channel pore formed by the N-terminal helix (NTH) to form a “gating plug”. In their crystal structure, the position of the NTH in the pore of the open channel is stabilized primarily by two interactions; 1) an inter-subunit hydrogen bond between the side chain of D2 and the backbone amide of T4 and 2) inter-subunit van der Waals interaction between W3 and M34, a pore lining residue located in TM1. The inter-subunit hydrogen bond would be a major determinant of pore diameter at this region of the NTH, while the inter-subunit van der Waals interaction would determine how deep into the channel pore the tip of the NTH resides. Breaking these interactions by voltage is predicted to allow the 6 NTH’s to form the gating plug. The model is based on structure-function studies of a N-terminal deletion and the Cx26 M34A mutations [130–132]. The Cx26 M34A channel has low conductance and displays a density in the channel pore in cryo-EM studies. However, the residual electrical conductance is reported to display normal voltage-gating [132] suggesting that M34A may have caused a structural change that bears little or no relation to the physiologic voltage-driven closed state. Although interesting in their own right, the challenges faced by structural studies of mutations is to demonstrate that the solved structures represent that of the physiologic native state so that one can deduce gating mechanisms from structure.

Given our apparent success in identifying electrostatic and van der Waals networks that stabilize the open state and insights into the loop-gating mechanism that these studies provided, we explored whether the same approach would provide insight into the mechanism of V_j-gating. Unfortunately, MD simulations did not provide information that could be interpreted to inform the mechanism of V_j-gating. The difficulties were as follows.

As noted above, Maeda et al. proposed that the position of the NTH in the channel pore of the crystal structure is stabilized an inter-subunit hydrogen bond between the side chain of D2 and the backbone amide of T4 and a van der Waals interaction between W3 and M34. In our MD simulations of Cx26 both interactions were more labile than could be inferred by consideration of the crystal structure. The hydrogen bond between the side chain of D2 and T4hn was broken within the first 5 ns of the 140 ns equilibration phase of the MD simulation and did not reform for the duration of the production stage simulations (4 replicate 20 ns simulations). While the van der Waals interaction between W3 and M34 continues in some subunits, it is often lost and replaced by intra-subunit interactions involving W3 and Met1 with other residues in TM1 and by other interactions between adjacent NTH. The remarkable feature of the MD simulations is the substantial dynamic variability in the position of the NTH. This dynamic variability makes it difficult to derive any insight as to the mechanism by which voltage destabilizes the open state and drives the open channel into one of at least three quasi-stable sub-conductance (closed) states or to derive any significance to the ones that form. It is possible that the dynamic variability observed in the MD simulations is because the initial structure of the N-terminus (2ZW3) used in MD simulations does not represent the native structure. Consequently, the variability of NT structures observed would be a consequence of the failure to start MD simulations with the correct initial structure.

Summary and Perspectives

A full understanding of the mechanism of connexin voltage-dependent gating requires validated atomic models of open and closed states. We utilized a Cx26 crystal structure (PDB ID:2ZW3) to obtain what appears to be a valid physiologic model of the open state of the undocked hemichannel, following refinement of the crystal structure by all-atom molecular dynamics and incorporation of charge changing protein modifications to reduce positive charge within the cytoplasmic half of the channel. We demonstrated, by application of GCMC/BD that the computed single channel current-voltage relation matched that of single channel recording of Cx26 undocked hemichannels expressed in Xenopus oocytes, and also that the computed charge selectivity agreed with experimental values. Similarly, we used the Cx26 coordinates to model the open state of N2ECx32*43E1 undocked hemichannels, and showed with GCMC/BD that the atomic model corresponds to the physiologic open state following equilibration with all-atom MD. Application of GCMC/BD, illustrates a major advantage in ion channel structure-function research, namely the development of computational methods to derive functional parameters from atomic structure. This coupled with experimental investigations provides a powerful means to test the validity of atomic structures.

Analyses of the trajectories of MD simulations provided insight into the one of two voltage-dependent gating processes characteristic of all connexin channels: namely voltage-dependent loop-gating or slow-gating. We showed that in the open state, the loop-gate permeability barrier was stabilized by a large dynamic electrostatic network and associated van der Waals network. The dynamics of this electrostatic network interactions demonstrated that interconnections between all six channel subunits, whereby conformational changes in charged residues in one subunit were coupled to the conformation of the parahelix in the adjacent subunit. This result suggests that loop-gating is a cooperative concerted process, such that closure of loop-gates involves sequential conformational changes in all six subunits. This differs from voltage-dependent V_j-gating (also termed fast-gating) where the gating transition appears to be initiated by a single subunit.

Obtaining valid models of voltage-driven closed states is a more difficult and challenging problem, as there are no methods currently available to solve structure while an isolated ion channel is properly oriented in a stable electric field. It is widely agreed that the best way to obtain accurate models of these closed states is to apply different but complementary experimental and computational methods and to use the resulting information to derive a consensus atomic structure. Vargas et al. [96] used this approach to solve the resting state of voltage-gated K⁺ and Na⁺ channels from structural and computational data and experimental distance constraints, an approach we are following. The consensus approach recognizes that all methods have different intrinsic limitations, in part reflecting underlying assumptions and technical limitations. Hence convergence of different methods to the same closed-state structure increases confidence in the final outcome.

A major objective of our past and ongoing studies has been to define the conformation of the loop-gate closed state by biochemical and functional studies of cysteine substituted channels. State-dependent Cd²⁺-thiolate bridge formation to lock channels in defined conformations provides a “molecular ruler” to measure the distance among substituted cysteines in channel subunits. The distances can be used to create atomic models of the closed state, which following refinement by all-atom molecular dynamics provide a set of testable intersubunit interactions that are predicted to form uniquely in the closed state. The results provide an iterative means to refine this class of atomic models. A subsequent approach to validate atomic models is to compute the gating charge from the models of the open and closed state and to compare these values to those determined experimentally. Connexin channels pose an interesting biophysical problem in that the voltage-sensor(s) must reside in the channel pore. Flow of current in the open state results in a non-equilibrium condition disqualifying the use of equilibrium methods (e.g. Poisson-Boltzmann equation) to calculate gating charge.

Recent developments in single particle cryo-EM provide another strategy to solve the atomic structure of channels. These include structural solutions that are locked in the closed state by disulfide bridging or metal bridges and structural solutions of mutations that cause large shifts in voltage-dependence by destabilization of the open state (for example, those mapping to the parahelix and its interacting network [10, 120]. Such channels will reside in a loop-gate closed state that is likely to be similar to the structure of the native closed state in the absence of applied voltage. Remarkably, Cx32 channels were among the first to be purified and to be examined by cryo-EM in the early 1990’s by Unwin and Gilula and co-workers [133]. These studies set the stage for structural solution of other connexin channels by single particle cryo-EM. Structural solutions of other connexin channels by cryo-EM should greatly expand our understanding of structure-function relations, physiological roles and the etiology of connexin disease mutations.

Highlights.

• Connexin channels have two distinct voltage-gating mechanisms: loop- and V_j-gating.

• Understanding voltage-gating requires atomic models of end states.

• Atomic models of the physiological open state have been created and validated.

• Metal bridging has defined the conformation of the loop-gate closed state.

• The distance constraints provide closed state atomic models.

• Strategies to further refine and validate atomic models are discussed.