Flexible decision stopping rules confer control over decision processes. Using an auditory change detection task, we found that alterations of decision stopping rules did not result in systematic changes in the temporal weighting of sensory information. We also found that post-error alterations of decision stopping rules depended on the type of mistake subjects make. These results provide guidance for understanding the neural mechanisms that control decision stopping rules, one of the critical components of decision making and behavioral flexibility.
Keywords: adaptive behavior, change detection, decision commitment, decision making, executive control
Abstract
A critical component of decision making is determining when to commit to a choice. This involves stopping rules that specify the requirements for decision commitment. Flexibility of decision stopping rules provides an important means of control over decision-making processes. In many situations, these stopping rules establish a balance between premature decisions and late decisions. In this study we use a novel change detection paradigm to examine how subjects control this balance when invoking different decision stopping rules. The task design allows us to estimate the temporal weighting of sensory information for the decisions, and we find that different stopping rules did not result in systematic differences in that weighting. We also find bidirectional post-error alterations of decision strategy that depend on the type of error and effectively reduce the probability of making consecutive mistakes of the same type. This is a generalization to change detection tasks of the widespread observation of unidirectional post-error slowing in forced-choice tasks. On the basis of these results, we suggest change detection tasks as a promising paradigm to study the neural mechanisms that support flexible control of decision rules.
NEW & NOTEWORTHY Flexible decision stopping rules confer control over decision processes. Using an auditory change detection task, we found that alterations of decision stopping rules did not result in systematic changes in the temporal weighting of sensory information. We also found that post-error alterations of decision stopping rules depended on the type of mistake subjects make. These results provide guidance for understanding the neural mechanisms that control decision stopping rules, one of the critical components of decision making and behavioral flexibility.
adaptive behavior requires responses that can vary depending on context rather than remaining rigid and inflexible. In the domain of decision making, this involves executive control over decision rules that determine how and when to commit to a choice. For example, consider a zebra grazing in a savanna also inhabited by predators such as lions. If the zebra initiates an escape response at the slightest hint of distant movement, then it will use a substantial amount of energy on unnecessary responses. However, if the zebra instead reacts too slowly or not at all to an approaching lion, it risks getting caught. Thus the zebra may either give priority to faster responses at the expense of wasted energy, or it may give priority to energy savings at the risk of falling victim to a predator. The balance between the two is established by a stopping rule that determines how much evidence is required to trigger commitment to the decision to escape.
Control over decision stopping rules has been studied most extensively in the context of the tradeoff between the speed and accuracy of decisions. Most commonly, this has been done in free-response (reaction time) decision tasks that involve a forced choice (Luce 1986). In these tasks, subjects must make a choice based on the categorical classification along a particular sensory dimension and report their choice when ready. In these situations, longer decision times promote higher accuracy (Green and Luce 1973; Wickelgren 1977). Furthermore, the balance between speed and accuracy has been consistently explained as a change in a criterion level of evidence needed to commit to a choice (Bogacz et al. 2010; Hanks et al. 2014; Heitz and Schall 2012; Palmer et al. 2005; Reddi et al. 2003).
In theory, in addition to changes in decision bounds, control over decision stopping rules may also operate by altering when information bears on a choice (Teichert et al. 2016)—that is, the temporal weighting of incoming information. How information for a decision is weighted can be studied using the technique of psychophysical reverse correlation (Beard and Ahumada 1998; Churchland and Kiani 2016; Neri et al. 1999). In short, psychophysical reverse correlation relies on stochastic fluctuations in stimuli that convey information for a decision to measure how much leverage these fluctuations have on decisions above and beyond the nonrandom signals driving the choice. This method has been used in forced-choice decision tasks for a variety of purposes, including to delineate the relative weighting of early vs. late information for a decision (Brunton et al. 2013; Kiani et al. 2008; Raposo et al. 2012) and to determine a subject’s task strategy (Nienborg and Cumming 2007). In the first part of this report, we use this method to determine whether subjects alter the weighting of information when invoking different decision stopping rules.
Decision stopping rules are subject to feedback that allows strategies to change when actions fail to produce positive outcomes. In the types of forced-choice tasks described above, this is frequently observed as post-error slowing, in which subjects who make an error take longer to report a choice for subsequent decisions (Laming 1979). Recent work has begun to reveal the neural mechanisms responsible for post-error slowing (Purcell and Kiani 2016). Importantly, in the forced-choice decisions where this phenomenon occurs, all errors are of the same type and in theory could be mitigated by slowing. However, there exist many situations where errors come in different varieties, and often, the optimal corrective action depends on the type of error. In the second part of this work, we ask whether post-error changes in decision strategy depend on the type of error in these types of situations.
For these studies, we employ a change detection task that requires subjects to determine when the underlying statistics of a noisy stream of evidence have changed. Unlike simple reaction time tasks with highly salient cues (Luce 1986; Teichner 1954; Woodrow 1914), the fluctuating nature of our stimulus results in behavior that involves a sizeable fraction of both premature false alarms and tardy misses. Thus, rather than establishing a tradeoff between speed and accuracy, the decision stopping rule in our task establishes a tradeoff between false alarms and misses. This also differs from the standard “yes-no” procedure detection tasks that invoke a tradeoff between false alarms and misses but do not require explicit judgment of the timing of the stimulus to detect (Green and Swets 1966). Instead, our task shares closer similarity to reaction-time detection tasks using near-threshold stimuli (Cook and Maunsell 2002; Green and Luce 1971; Luce and Green 1970). Importantly, our change detection task allows one to examine how different decision stopping rule policies alter the decision process up to the moment of decision commitment.
METHODS
Subjects.
Subjects were all undergraduate students at University of California, Davis. Ages ranged from 20 to 22 yr. Six subjects were female and two were male. All subjects were given instructions explaining how to complete the task but were not informed of the specific details being studied. No previous knowledge of protocol, apparatus, or technical systems used for this study was known by the individuals before becoming a subject. The study’s procedures were approved by the UC Davis Institutional Review Board, and all subjects gave their informed consent.
The subjects were compensated for their time with a $10 Amazon gift card for every hour they completed of the study. On average, subjects completed 5 h. Neither the payment nor the study’s outcomes were based on any measure of performance of subjects during their sessions.
A total of eight subjects were recruited, but data from only seven were analyzed in the comparison between false alarm prone and false alarm averse conditions. The excluded subject (subject AS) did not change behavior after receiving instructions to do so (see below).
Each subject was asked if they could commit to coming in 5 separate days to complete 5 full sessions (1 practice, 4 analyzed). In each session, the subject would perform the change detection task (described below) for three 15-min trial blocks with a short break in between each block of trials.
Apparatus.
The software control was written in MATLAB and carried out in conjunction with Bpod, a real-time control system for behavioral measurement, and Pulse Pal, an open source pulse train generator. A cone-shaped port was used as a trigger for a human finger to respond to the stimulus. Subjects sat in front of a small speaker and port that is triggered when an infrared light beam is obstructed by the subject’s finger.
Change detection task.
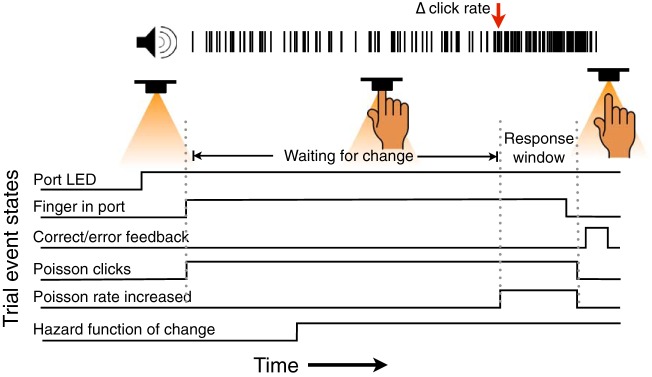
The subjects were asked to identify when they heard a change in the underlying rate of a series of clicks generated by a random Poisson process. An LED light within the port was illuminated to indicate that the trial was ready to begin. This cued subjects to insert their finger into the port, which in turn triggered the onset of the auditory click sequence to play through the speaker. Subjects were required to keep their finger in the port while they waited for the change in the stimulus. The click rate started at a baseline frequency of 50 Hz. For all trials, either the click train randomly terminated with no change (catch trial), or it changed to a higher frequency with equal probability of 60, 80, or 100 Hz, yielding a delta click rate of 10, 30, or 50 Hz. Ten percent of all trials were catch trials. The change in frequency occurred randomly for each new trial, giving a varying fore period. This fore period had a minimum duration of 0.5 s, followed by a wait time drawn from a truncated exponential distribution with a mean of 2.5 s and a maximum of 6.5 s. Times exceeding the maximum were resampled from the exponential to avoid edge effects. An exponential distribution results in flat hazard rate of the stimulus change, so the probability of a change in the next moment of time does not increase or decrease during the course of a trial. Catch trials also ended with the same timing as non-catch trials.
When the subject decided to report a detected change, they were to remove their finger from the port. There were two types of errors possible on non-catch trials. False alarms were defined as trials where the subject reported a change before it had occurred. Note that in traditional “go-no go” (or “yes-no”) tasks, false alarms correspond to “go” responses on “no-go” trials. Our definition extends false alarms to “go” responses that occur before the “go” signal, in line with previous change detection studies (Boubenec et al. 2017; Cook and Maunsell 2002). When the subjects removed their finger from the port, the LED light would turn off and the click sequence would continue to its programmed conclusion. Misses were defined as trials where the subject failed to report a change within 0.8 s after its onset. If the subjects detected no change, they were to leave their finger in the port until the sound stopped playing. In all cases, auditory feedback was provided to indicate correct or error responses. After an intertrial interval with a duration of 0.1 s plus an additional 1.0 s for error trials, the port LED was illuminated again to initiate the next trial. Accuracy was calculated as the number of correct trials as a fraction of the total number of trials, including both catch and non-catch trial types. Thus, errors on all trial types contribute to the measure of accuracy.
Decision policy manipulation.
In the initial sessions of data collection, we allowed subjects to establish their own tradeoff between false alarms and misses without any instructions on how to balance the two. We call these “baseline” sessions. After two full sessions of three trial blocks of data collection in the baseline case, we sought to change the subjects’ decision stopping rule policies that would control the balance between false alarms and misses. To maximize the chances that subjects would be able to do this successfully, we assessed each on a case-by-case basis to determine whether they had more room to decrease their miss rate or false alarm rate. Accordingly, we categorized subjects on the basis of whether their average false alarm rate was greater or less than 20% in the baseline sessions. If it was greater than 20%, we categorized the subject as “false alarm prone,” and if it was less than 20%, we categorized the subject as “false alarm averse.” Four subjects were categorized as false alarm prone in the baseline sessions (KE, BB, GC, and MH), and four subjects were categorized as false alarm averse in the baseline sessions (AS, BA, EJ, and HP).
To change the subjects’ balance between misses and false alarms, we provided explicit instructions to either reduce “early withdrawal” mistakes for false alarm prone subjects or reduce “late response” mistakes for false alarm averse subjects, even if it caused more of the other type of error. Because we used explicit instructions, we call these the “instructed” sessions. Furthermore, the error that the subjects were supposed to avoid in the instructed sessions was given a higher pitched tone feedback sound than the feedback sound for the other error. In all other ways, the trials proceeded exactly as in the baseline sessions. Similarly to the baseline sessions, we collected two full sessions of three trial blocks of data collection in the instructed case. For seven of eight subjects, this resulted in changes in both miss rates and false alarm rates consistent with the instructions. For one subject, behavior did not change, so that subject was excluded from analyses aimed at understanding the nature of the change between the two conditions. For the other subjects, data for the false alarm prone condition thus involve a combination of baseline data from subjects naturally prone to false alarms and instructed data from subjects naturally averse to false alarms. Likewise, data for the false alarm averse condition involve a combination of baseline data from subjects naturally averse to false alarms and instructed data from subjects naturally prone to false alarms.
Data analysis and statistics.
Psychometric functions were generated to measure how hit rate, miss rate, and reaction time (RT) depended on the magnitude of the stimulus change. Hit rate was defined as the proportion of hits out of all non-catch trials. Miss rate was defined as the proportion of misses out of all trials with a stimulus change present. Thus the denominator for miss rate excluded catch trials and false alarm trials. This was intended to avoid a confounding influence of higher false alarm rates necessarily resulting in lower miss rates due to fewer opportunities for a miss. RT was calculated only for correct hit responses to capture the amount of time after a change in the stimulus until the subjects correctly reported the change. False alarm rate was calculated as the proportion of false alarms out of all trials, excluding catch trials. False alarms occur before the change in the stimulus, so its rate necessarily cannot depend on the magnitude of the stimulus change. Correct rejection rate was calculated as the proportion of correct rejections out of all catch trials.
Standard linear regression was used to measure the effects of stimulus strength on RT. Logistic regression was used to measure the effects of stimulus strength on hit rate and miss rate. This is equivalent to a generalized linear model with a binomial distribution and a logit link function. For all analyses, similar results were obtained with a probit link function, as well. For both linear and logistic regressions, statistical significance was determined on the basis of P values for the effect of stimulus strength, calculated using a two-tailed t-test on the stimulus strength regressor term.
To compare RT and miss rates between conditions (decision policy conditions or previous trial outcome “conditions”), an additional regressor was added to act as a dummy variable for condition. The changes in miss rates reported in Fig. 3A and Fig. 6A are based on an inverse logit transformation of the regressor to units of probability. Statistical significance of the effect of condition was determined on the basis of P values for the condition regressor, calculated using a two-tailed t-test. Comparisons of false alarm and correct rejection rates between conditions did not require regression because neither depended on stimulus strength. Instead, a standard two-tailed t-test was performed on these binomial variables. P values are reported for all statistical comparisons.
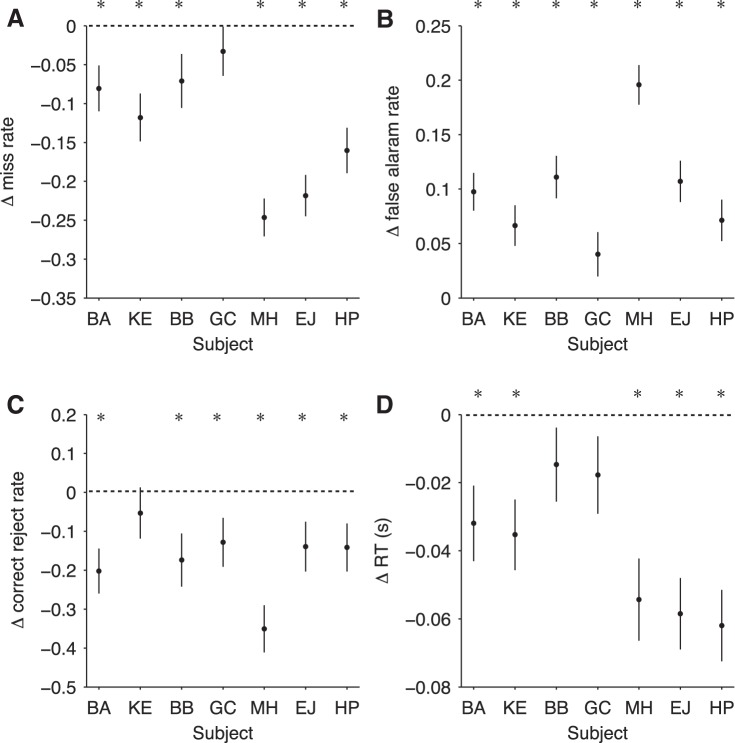
Fig. 3.
Changes in behavior for individual subjects and comparison of the 2 decision policy conditions. A: change in miss rate for each individual subject. Negative values indicate lower miss rate in false alarm prone condition compared with the false alarm averse condition, and vice versa for positive values (subject BA: t = −2.65, P < 0.01, n = 1,540; subject KE: t = −3.64, P < 0.001, n = 1,540; subject BB: t = −2.00, P < 0.05, n = 1,297; subject GC: t = −1.03, P = 0.30, n = 1,381; subject MH: t = −8.10, P < 0.001, n = 1,400; subject EJ: t = −6.90, P < 0.001, n = 1,476; and subject HP: t = −4.99, P < 0.001, n = 1,469, where n refers to total number of possible miss trials, that is, trials with a change present). B: change in false alarm rate on non-catch trials for each individual subject. Positive values indicate higher false alarm rate in false alarm prone condition compared with the false alarm averse condition, and vice versa for negative values (subject BA: t = 5.69, P < 0.001, n = 1,843; subject KE: t = 3.56, P < 0.001, n = 1,936; subject BB: t = 5.66, P < 0.001, n = 1,613; subject GC: t = 1.98, P < 0.05, n = 1,863; subject MH: t = 10.68, P < 0.001, n = 1,732; subject EJ: t = 5.64 P < 0.001, n = 1,907; and subject HP: t = 3.73, P < 0.001, n = 1,893, where n refers to total number of non-catch trials). C: change in correct rejection rate for each individual subject. Negative values indicate lower correct rejection rate in false alarm prone condition compared with the false alarm averse condition, and vice versa for positive values (subject BA: t = −3.50, P < 0.001, n = 208; subject KE: t = −0.81, P = 0.42, n = 196; subject BB: t = −2.50, P < 0.05, n = 174; subject GC: t = −2.11, P < 0.05, n = 215; subject MH: t = −5.80, P < 0.001, n = 211; subject EJ: t = −2.21, P < 0.05, n = 228; and subject HP: t = −2.29, P < 0.05, n = 224, where n refers to total number of catch trials). D: change in RT for each individual subject. Negative values indicate shorter RTs in false alarm prone condition compared with the false alarm averse condition, and vice versa for positive values (subject BA: t = −2.88, P < 0.01, n = 866; subject KE: t = −3.41, P < 0.001, n = 960; subject BB: t = −1.36, P = 0.18, n = 841; subject GC: t = −1.56, P = 0.12, n = 848; subject MH: t = −4.52, P < 0.001, n = 763; subject EJ: t = −5.58, P < 0.001, n = 974; and subject HP: t = −5.92, P < 0.001, n = 951, where n refers to total number of hit trials). Error bars indicate SE. *P < 0.05. Subjects BA, HP, and EJ were categorized as false alarm averse in the baseline sessions and false alarm prone in the instructed sessions. Subjects KE, BB, GC, and MH were categorized as false alarm prone in the baseline sessions and false alarm averse in the instructed sessions.
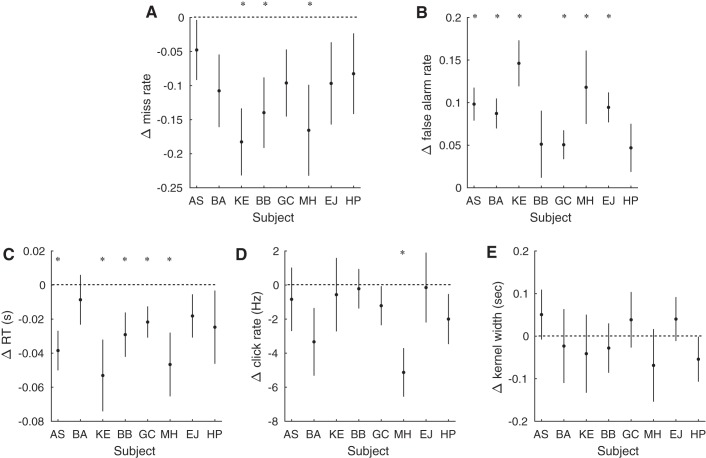
Fig. 6.
Changes in behavior and psychophysical reverse correlation kernel for individual subjects dependent on previous trial outcome. A: change in miss rate for each individual subject. Negative values indicate lower miss rate after miss trials than after false alarm trials, and vice versa for positive values (subject AS: t = −1.08, P = 0.30; subject BA: t = −2.02, P = 0.7; subject KE: t = −3.71, P < 0.01; subject BB: t = −2.70, P < 0.05; subject GC: t = −1.95, P = 0.08; subject MH: t = −2.48, P < 0.05; subject EJ: t = −1.60, P = 0.14; and subject HP: t = −1.39, P = 0.19; n = 12 blocks of trials for each subject). B: change in false alarm rate for each individual subject. Positive values indicate higher false alarm rate after miss trials than after false alarm trials, and vice versa for negative values (subject AS: t = 5.07, P < 0.001; subject BA: t = 4.96, P < 0.001; subject KE: t = 5.42, P < 0.001; subject BB: t = 1.30, P = 0.22; subject GC: t = 2.98, P < 0.05; subject MH: t = 2.74, P < 0.05; subject EJ: t = 5.36, P < 0.001; and subject HP: t = 1.66, P = 0.13; n = 12 blocks of trials for each subject). C: change in RT for each individual subject. Negative values indicate shorter RTs after miss trials than false alarm trials, and vice versa for positive values (subject AS: t = −3.31, P < 0.01; subject BA: t = −0.59, P = 0.57; subject KE: t = −2.52, P < 0.05; subject BB: t = −2.23, P < 0.05; subject GC: t = −2.36, P < 0.05; subject MH: t = −2.50, P < 0.05; subject EJ: t = −1.43, P = 0.18; and subject HP: t = −1.15, P = 0.27; n = 12 blocks of trials for each subject). D: change in click rate preceding a false alarm response for each individual subject. Click rate was calculated in the window from 0.5 to 0.15 s before the choice response. Negative values indicate lower click rate after miss trials than after false alarm trials, and vice versa for positive values (subject AS: t = −0.45, P = 0.66; subject BA: t = −1.68, P = 0.13; subject KE: t = −0.26, P = 0.80; subject BB: t = −0.19, P = 0.86; subject GC: t = −1.06, P = 0.31; subject MH: t = −3.60, P < 0.01; subject EJ: t = −0.07, P = 0.94; and subject HP: t = −1.36, P = 0.20; n = 12 blocks of trials for each subject). E: change in width of “kernel” derived from reverse correlation preceding a false alarm response for each individual subject. The width is the portion of the reverse correlation kernel that exceeds the background rate and thus quantifies the temporal weighting of the sensory information preceding a response. Positive values indicate a wider kernel after miss trials than after false alarm trials, and vice versa for negative values (subject AS: t = 0.86, P = 0.41; subject BA: t = −0.27, P = 0.80; subject KE: t = −0.45, P = 0.66; subject BB: t = −0.48, P = 0.64; subject GC: t = 0.59, P = 0.57; subject MH: t = −0.81, P = 0.44; subject EJ: t = 0.78, P = 0.45; and subject HP: t = −1.03, P = 0.33; n = 12 blocks of trials for each subject). Error bars indicate SE. *P < 0.05.
For all analyses based on previous trial outcome, comparisons were made only within individual 15-min trial blocks. Thus, in reporting the effects of trial outcome for individual subjects, means and SE were calculated across trial blocks. This within-block calculation was intended to mitigate the confounding effect of longer timescale changes in decision policy on this analysis. Any such longer timescale changes would reduce the ability of our analysis to detect the trial-by-trial modifications we observed. The intuition for this becomes more obvious if one considers two blocks, one with a high decision bound and one with a low decision bound. The block with a high decision bound will have fewer false alarms and more misses, and vice versa for the block with a low decision bound. If analyzed together, this would result in higher miss rates after misses and higher false alarm rates after false alarms due to anticorrelation of these two types of mistakes in this scenario. More generally, any longer timescale changes in decision bounds that are independent of trial outcome would yield results exactly opposite to what we found. Thus, to the extent such slow modulations of the decision bound exist, it would reduce the effect sizes we measured for changes in decision bound based on trial outcome.
The psychophysical reverse correlation analysis was performed on false alarm trials. On these trials, subjects responded even though the generative mean of the Poisson click sequence had not yet changed. Therefore, if these false alarms were unrelated to the stimulus, the average rate preceding them would equal the baseline rate of 50 Hz. However, if false alarms were triggered by consistent Poisson fluctuations in the stimulus, then the average rate preceding a false alarm response would deviate from this baseline. We note that if subjects were required to report both increases and decreases in stimulus rate without indicating the sign, then false alarms triggered by increases and decreases would to some extent cancel in the average. For calculating the average, we first smoothed the click sequences using a Gaussian filter with a width of 25 ms. We refer to the false alarm triggered average stimulus as the stimulus “kernel.” The kernel width was calculated by fitting the kernel with a square-wave function with free parameters for wave onset, offset, and height. Kernel width was defined as the difference between onset and offset of this square-wave fit. The change in click rate from baseline in the reverse correlation kernel was calculated by counting the average number of clicks that occurred between 0.5 and 0.15 s preceding the false alarm responses. These boundaries were taken on the basis of the average kernel profiles. Statistical comparisons of these metrics were based on P values calculated using t-tests.
RESULTS
We trained naive human subjects to perform an auditory change detection task (Fig. 1). In this task, subjects were supposed to report with a hand movement when the underlying statistics of a noisy auditory stimulus changed. Trials were initiated when subjects placed their right index finger into a detection port. The stimulus consisted of a sequence of clicks that was generated by a Poisson process. At a random point in time taken with an unpredictable flat hazard function, the Poisson rate increased. The baseline Poisson rate was fixed at 50 Hz, and the magnitude of the increase was randomly varied on a trial-by-trial basis from the set [10, 30, 50] Hz. After a change occurred, subjects were allowed up to 800 ms to respond by removing their finger from the detector. If subjects responded within this window, they were given a positive feedback sound after their response, and the trial was categorized as a hit. If the subjects responded before the change, they were given a negative feedback sound while the stimulus concurrently continued until the end, and the trial was categorized as a false alarm. If the subjects did not respond in time, they were given a negative feedback sound after the stimulus was terminated, and the trial was categorized as a miss. In addition, on 10% of the trials, there was no change, and we call these catch trials. If the subjects withheld a response for the entire duration of these trials, they were given a positive feedback sound, and the trial was categorized as a correct reject.
Fig. 1.
Auditory change detection task design showing sequence of events for each trial. Trials begin with the illumination of an LED in a port cuing subjects to place their finger in the port. After they do, a stream of auditory clicks is played from a speaker above the port. The clicks are generated by a Poisson process with an initial generative rate of 50 Hz. This baseline is maintained for at least 500 ms. After that time, the click rate can increase at a random time by either 10, 30, or 50 Hz. The time of the change (shown in this example by the red arrow) is dictated by a flat hazard function, so subjects cannot predict its timing. Subjects are supposed to remove their finger from the port when they detect the change. They are allowed a response window of 800 ms after the change to remove their finger. Subjects receive feedback in the form of an auditory tone to indicate whether they responded correctly or in error.
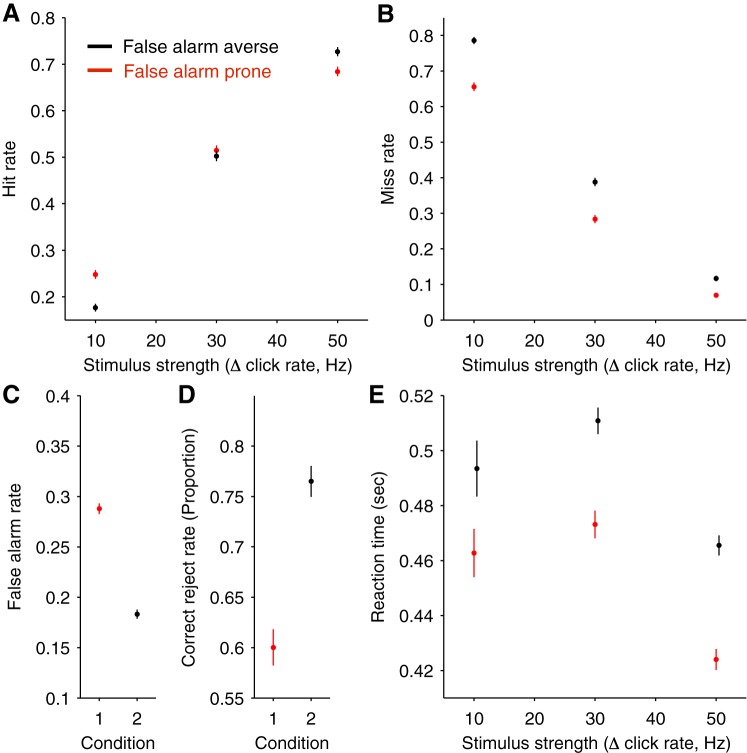
Subjects performed the change detection task under two different decision policy conditions. The first conditions involved baseline sessions where subjects were not given instructions about their balance of misses and false alarms. The second condition involved instructed sessions where subjects naturally prone to false alarms were encouraged to reduce false alarms and those naturally averse to false alarms were encouraged to reduce misses. Four of seven subjects were categorized as naturally prone to false alarms, and three of seven subjects were categorized as naturally averse to false alarms. Thus the false alarm prone condition includes baseline session data from subjects naturally prone to false alarms and instructed session data from subjects naturally averse to false alarms. Likewise, the false alarm averse condition includes baseline session data from subjects naturally averse to false alarms and instructed session data from subjects naturally prone to false alarms. For both situations, performance of the subjects depended on the magnitude of the change in Poisson rate. Not surprisingly, large changes were associated with higher hit rates, on average, than were small changes (regression coefficient: 0.056 ± 0.001, P < 0.001, t = 44.1, n = 12,787 trials; Fig. 2A). The non-hit trials can be classified in two types: misses and false alarms. Complementary to the effect on hit rate, lower miss rates ensued for larger changes in the stimulus than for small changes (regression coefficient: −0.082 ± 0.002, P < 0.001, t = −47.7, n = 10,082 possible miss trials; Fig. 2B). Because false alarms on non-catch trials occur before a stimulus change, they naturally do not depend on the magnitude of the stimulus change, so we summarize them with a single quantity for each condition (Fig. 2C). We also quantify the percentage of catch trials where subjects successfully withheld a response, what we describe as correct rejections (Fig. 2D). Finally, we found that RTs on hit trials also depended on the stimulus strength, with faster RTs for larger magnitude changes (regression coefficient: −1.21 ± 0.14, P < 0.001, t = −8.4, n = 6,203 hit trials; Fig. 2E).
Fig. 2.
Aggregate behavioral performance across subjects. For A–E, performance is shown for 2 conditions. Black data points correspond to the false alarm averse condition, and red data points correspond to the false alarm prone condition. Note that subjects varied in whether they were false alarm prone or averse at baseline, so the categories correspond to a mixture of data from the baseline and instructed sessions. A: the proportion of hit trials plotted as a function of the change (Δ) in stimulus click rate. Non-hit trials consist of both false alarms and misses. B: miss rate plotted as a function of the change in stimulus click rate. Miss rate is defined as the proportion of trials where a stimulus change was present but failed to be detected. Importantly, this does not include false alarm trials in the denominator of the calculation, so changes in miss rate are not confounded with changes in false alarm rate. These definitions explain why miss rate does not equal 1 minus hit rate, and why the sum of hit, miss, and false alarm rates does not equal 1. C: false alarm rate plotted for each condition. False alarms occur before the stimulus change, so they cannot depend on its magnitude. D: correct reject rate for catch trials interleaved in each of the 2 conditions. E: RTs on correct (hit) trials plotted as a function of the change in the stimulus click rate. Larger click rate changes are associated with faster RTs. Error bars indicate SE; n = 7 subjects, 14,243 trials.
There were multiple changes in behavior associated with the two different decision policy conditions. Because subjects were given explicit instructions to change the balance of miss and false alarm errors, the changes in miss rate, false alarm rate, and correct rejection rate (Fig. 3, A–C; Tables 1–3) are readily explained as the subjects following these instructions. The changes in miss and false alarm rates offset each other so that the overall accuracy did not change significantly between conditions for all but one subject (Table 4). In addition, because trials were matched for duration, this implies a similar lack of change in reward rate. More interestingly, despite having been given no explicit instructions about RTs, subjects responded more quickly on hit trials when they were in the false alarm prone decision policy condition (Fig. 3D; Table 5). Thus a policy balanced toward more early response errors also results in faster responses on correct trials.
Table 1.
Statistical comparisons of changes to miss rate between decision policy conditions
| Subject | t Value | P Value | No. of (Possible Miss) Trials |
|---|---|---|---|
| BA | −2.65 | <0.01 | 1,540 |
| KE | −3.64 | <0.001 | 1,519 |
| BB | −2.00 | <0.05 | 1,297 |
| GC | −1.03 | 0.30 | 1,381 |
| MH | −8.10 | <0.001 | 1,400 |
| EJ | −6.90 | <0.001 | 1,476 |
| HP | −4.99 | <0.001 | 1,469 |
Table 3.
Statistical comparisons of changes to correct rejection rate between decision policy conditions
| Subject | t Value | P Value | No. of (Catch) Trials |
|---|---|---|---|
| BA | −3.50 | <0.001 | 208 |
| KE | −0.81 | 0.42 | 196 |
| BB | −2.50 | <0.05 | 174 |
| GC | −2.11 | <0.05 | 215 |
| MH | −5.80 | <0.001 | 211 |
| EJ | −2.21 | <0.05 | 228 |
| HP | −2.29 | <0.05 | 224 |
Table 4.
Statistical comparisons of changes to accuracy between decision policy conditions
| Subject | t Value | P Value | No. of (Total) Trials |
|---|---|---|---|
| BA | −0.95 | 0.34 | 2,051 |
| KE | −0.04 | 0.97 | 2,132 |
| BB | −2.24 | <0.05 | 1,787 |
| GC | −1.35 | 0.18 | 2,078 |
| MH | 0.31 | 0.76 | 1,943 |
| EJ | 1.05 | 0.29 | 2,135 |
| HP | 1.20 | 0.23 | 2,117 |
Table 5.
Statistical comparisons of changes to reaction time decision policy conditions
| Subject | t Value | P Value | No. of (Hit) Trials |
|---|---|---|---|
| BA | −2.88 | <0.01 | 866 |
| KE | −3.41 | <0.001 | 960 |
| BB | −1.36 | 0.18 | 841 |
| GC | −1.56 | 0.12 | 848 |
| MH | −4.52 | <0.001 | 763 |
| EJ | −5.58 | <0.001 | 974 |
| HP | −5.92 | <0.001 | 951 |
Table 2.
Statistical comparisons of changes to false alarm rate on non-catch trials between decision policy conditions
| Subject | t Value | P Value | No. of (Non-Catch) Trials |
|---|---|---|---|
| BA | 5.69 | <0.001 | 1,843 |
| KE | 3.56 | <0.001 | 1,936 |
| BB | 5.66 | <0.001 | 1,613 |
| GC | 1.98 | <0.05 | 1,863 |
| MH | 10.68 | <0.001 | 1,732 |
| EJ | 5.64 | <0.001 | 1,907 |
| HP | 3.73 | <0.001 | 1,893 |
Although numerous other studies have examined the relationship between choice behavior and RT as subjects change their decision stopping rules (Bogacz et al. 2010; Hanks et al. 2014; Heitz and Schall 2012; Palmer et al. 2005; Reddi et al. 2003), few have explicitly measured whether such changes are associated with alterations in the weighting of information that bears on a decision. The fluctuating nature of the sensory stimulus in our task allows us to measure this directly. In particular, even before the generative click rate increases, the Poisson-generated sequence of clicks results in random fluctuations in the local click rate evenly distributed around the mean. We can exploit these fluctuations to determine the average stimulus that triggers a response even in the absence of a change in the generative rate. False alarm trials correspond to exactly this condition. Thus we calculated the choice-triggered average stimulus that preceded false alarm responses. If false alarm responses were guesses that were not informed by stimulus fluctuations, then the choice-triggered average would be independent of the choice and mirror the statistics of stimulus generation. In contrast, if false alarm responses were informed by stimulus fluctuations, then the choice-triggered average for false alarms should show an increase at points in time where the stimulus has leverage on the choice. Thus the choice-triggered average for false alarm responses reveals how subjects weight sensory evidence for their choices.
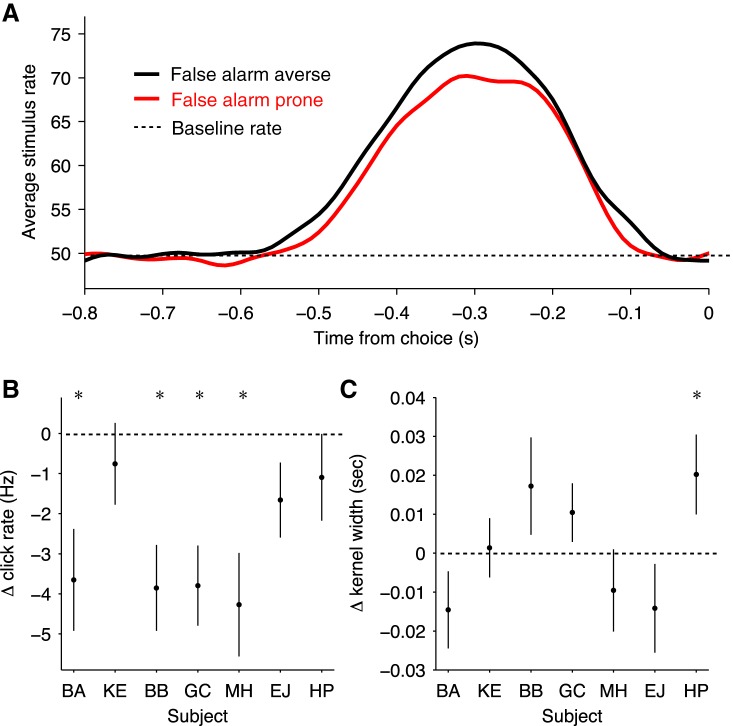
Using this psychophysical reverse correlation approach, we found that false alarm responses were indeed preceded, on average, by increases in the local click rate (Fig. 4A). When subjects were more averse to false alarms, larger magnitude deflections of click rate preceded the choices (Fig. 4B; Table 6). However, the span of times that had leverage on the choice—that is, the width of the choice-triggered average—had small and inconsistent changes associated with different decision stopping rule conditions across subjects (Fig. 4C; Table 7). This suggests that subjects change their decision stopping rule primarily through alterations of a decision bound rather than changes to the temporal weighting of sensory evidence.
Fig. 4.
Psychophysical reverse correlation of temporal weighting of incoming information on the decision. A: average stimulus preceding false alarm responses for false alarm averse condition in black and miss averse condition in red. Stimulus rate was calculated by smoothing with a Gaussian filter having a width of 0.025 s. B: change in click rate preceding a false alarm response for each individual subject. Click rate was calculated in the window from 0.5 to 0.15 s before the choice response. Negative values indicate lower click rate in false alarm prone condition compared with the false alarm averse condition, and vice versa for positive values (subject BA: t = −2.89, P < 0.01, n = 347; subject KE: t = −0.74, P = 0.46, n = 403; subject BB: t = −3.60, P < 0.001, n = 360; subject GC: t = −3.80, P < 0.001, n = 502; subject MH: t = −3.31, P < 0.001, n = 390; subject EJ: t = −1.77, P = 0.08, n = 505; and subject HP: t = −1.01, P = 0.31, n = 481, where n refers to total number of false alarm trials). C: width of “kernel” derived from reverse correlation for each individual subject. The width is the portion of the reverse correlation kernel that exceeds the background rate and thus quantifies the temporal weighting of the sensory information preceding a response. Positive values indicate a wider kernel in false alarm prone condition compared with the false alarm averse condition, and vice versa for negative values (subject BA: t = −1.47, P = 0.14, n = 347; subject KE: t = 0.18, P = 0.86, n = 403; subject BB: t = 1.38, P = 0.17, n = 360; subject GC: t = 1.39, P = 0.17, n = 502; subject MH: t = −0.90, P = 0.37, n = 390; subject EJ: t = −1.25, P = 0.21, n = 505; and subject HP: t = 1.97, P < 0.05, n = 481, where n refers to total number of false alarm trials). Error bars indicate SE. *P < 0.05. Subjects BA, HP, and EJ were categorized as false alarm averse in the baseline sessions and false alarm prone in the instructed sessions. Subjects KE, BB, GC, and MH were categorized as false alarm prone in the baseline sessions and false alarm averse in the instructed sessions.
Table 6.
Statistical comparisons of changes to false alarm-triggered click rate between decision policy conditions
| Subject | t Value | P Value | No. of (False Alarm) Trials |
|---|---|---|---|
| BA | −2.89 | <0.01 | 347 |
| KE | −0.74 | 0.46 | 403 |
| BB | −3.60 | <0.001 | 360 |
| GC | −3.80 | <0.001 | 502 |
| MH | −3.32 | <0.001 | 390 |
| EJ | −1.77 | 0.08 | 505 |
| HP | −1.01 | 0.31 | 481 |
Table 7.
Statistical comparisons of changes to false alarm-triggered kernel width between decision policy conditions
| Subject | t Value | P Value | No. of (False Alarm) Trials |
|---|---|---|---|
| BA | −1.47 | 0.14 | 347 |
| KE | 0.18 | 0.86 | 403 |
| BB | 1.38 | 0.17 | 360 |
| GC | 1.39 | 0.17 | 502 |
| MH | −0.90 | 0.37 | 390 |
| EJ | −1.25 | 0.21 | 505 |
| HP | 1.97 | <0.05 | 481 |
Up to now, we have focused on changes in decision stopping rules that occurred between experimental sessions and were brought about by explicit instructions to the subjects. However, we also wanted to examine whether subjects varied their decision rules on shorter timescales based on the outcome of previous trials. The intuition for this is as follows. Mechanisms that support behavioral optimization may lead to adaptive changes between decisions to reduce errors (Botvinick et al. 2001). Thus, if subjects have a false alarm error, they may adjust to avoid that. However, the tradeoff between false alarms and misses would then cause an increase in the probability of a miss. Similarly, if subjects have a miss error, they may move the tradeoff back toward a position that reduces misses at the expense of false alarms.
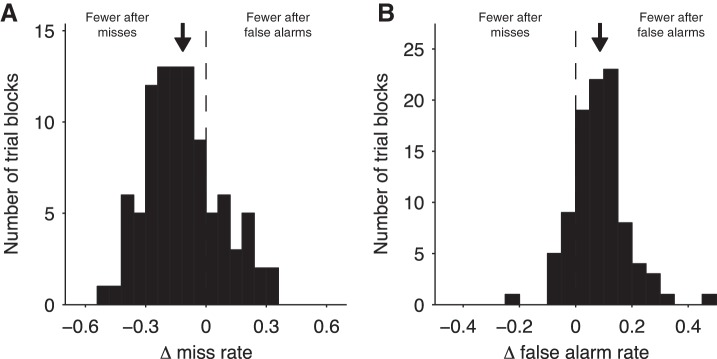
To test this idea, we measured within individual blocks of trials whether the miss rate differed between trials that followed misses compared with those that followed false alarms. We quantified this so that negative values indicated a higher miss rate after false alarms. We found negative values of this index for most trial blocks (regression coefficient: −0.11 ± 0.02, P < 0.001, t = −6.0, n = 96 blocks of trials; Fig. 5A). Similarly, we measured whether the false alarm rate differed between trials that followed misses compared with those that followed false alarms, again with negative values indicating a higher false alarm rate after false alarms. In this case, we found positive values for most trial blocks (mean: 0.087 ± 0.010, P < 0.001, t = 8.6, n = 96 blocks of trials; Fig. 5B). Thus, for both analyses, we found a relative reduction in the rate of repeating an error of the same type. Furthermore, these changes were fairly consistent across subjects (Fig. 6, A and B; Tables 8 and 9).
Fig. 5.
Changes in behavior dependent on previous trial outcome for each individual trial block. A: distribution across all trial blocks of the difference between the miss rate following misses compared with the miss rate following false alarms trials. Positive values indicate higher miss rate after miss trials, and negative values indicated a higher miss rate after false alarms. B: distribution across all trial blocks of the difference between the false alarm rate following misses compared with the false alarm rate following false alarms trials. Positive values indicate higher false alarm rate after miss trials, and negative values indicated a higher false alarm rate after false alarms. Arrow indicates the mean effect (miss: −0.11, 95% CI: −0.15 to −0.08; false alarm: 0.087, 95% CI: 0.067 to 0.11); n = 8 subjects, 96 trial blocks.
Table 8.
Statistical comparisons of changes to miss rate based on trial outcome
| Subject | t Value | P Value | No. of Trial Blocks |
|---|---|---|---|
| AS | −1.08 | 0.30 | 12 |
| BA | −2.02 | 0.07 | 12 |
| KE | −3.71 | <0.01 | 12 |
| BB | −2.70 | <0.05 | 12 |
| GC | −1.95 | 0.08 | 12 |
| MH | −2.48 | <0.05 | 12 |
| EJ | −1.60 | 0.14 | 12 |
| HP | −1.39 | 0.19 | 12 |
Table 9.
Statistical comparisons of changes to false alarm rate based on trial outcome
| Subject | t Value | P Value | No. of Trial Blocks |
|---|---|---|---|
| AS | 5.07 | <0.001 | 12 |
| BA | 4.96 | <0.001 | 12 |
| KE | 5.42 | <0.001 | 12 |
| BB | 1.30 | 0.22 | 12 |
| GC | 2.98 | <0.05 | 12 |
| MH | 2.74 | <0.05 | 12 |
| EJ | 5.36 | <0.001 | 12 |
| HP | 1.66 | 0.13 | 12 |
These results suggest that subjects adjust their decision bound dynamically on the basis of individual trial outcomes. In particular, it is consistent with the idea that subjects reduce their decision bound after misses and increase it after false alarms. This makes the prediction that RTs on correct hit trials should be faster after misses than false alarms, and indeed, that was the case (Fig. 6C; Table 10). To further test this, we applied the choice-triggered average analysis contingent on previous type of error. Because this analysis relies on the relatively rare case of a false alarm response that follows another error, we had limited power. The magnitude of the choice-triggered average stimulus following misses compared with that following false alarms lacked significance in all but one individual subject (Table 11), and the changes to its width were not significant for any individual subject (Table 12). Nonetheless, for all subjects we still found a consistent reduction of the magnitude of the choice-triggered average stimulus (Fig. 6D), as compared with inconsistent changes to its width (Fig. 6E).
Table 10.
Statistical comparisons of changes to reaction time based on trial outcome
| Subject | t Value | P Value | No. of Trial Blocks |
|---|---|---|---|
| AS | −3.31 | <0.01 | 12 |
| BA | −0.59 | 0.57 | 12 |
| KE | −2.52 | <0.05 | 12 |
| BB | −2.23 | <0.05 | 12 |
| GC | −2.36 | <0.05 | 12 |
| MH | −2.50 | <0.05 | 12 |
| EJ | −1.43 | 0.18 | 12 |
| HP | −1.15 | 0.27 | 12 |
Table 11.
Statistical comparisons of changes to false alarm-triggered stimulus magnitude based on trial outcome
| Subject | t Value | P Value | No. of Trial Blocks |
|---|---|---|---|
| AS | −0.45 | 0.66 | 12 |
| BA | −1.68 | 0.13 | 12 |
| KE | −0.26 | 0.80 | 12 |
| BB | −0.19 | 0.86 | 12 |
| GC | −1.06 | 0.31 | 12 |
| MH | −3.60 | <0.01 | 12 |
| EJ | −0.07 | 0.94 | 12 |
| HP | −1.36 | 0.20 | 12 |
Table 12.
Statistical comparisons of changes to false alarm-triggered stimulus average width based on trial outcome
| Subject | t Value | P Value | No. of Trial Blocks |
|---|---|---|---|
| AS | 0.86 | 0.41 | 12 |
| BA | −0.27 | 0.80 | 12 |
| KE | −0.45 | 0.66 | 12 |
| BB | −0.48 | 0.64 | 12 |
| GC | 0.59 | 0.57 | 12 |
| MH | −0.81 | 0.44 | 12 |
| EJ | 0.78 | 0.45 | 12 |
| HP | −1.03 | 0.33 | 12 |
DISCUSSION
We developed a new change detection task based on a stream of auditory clicks generated by a Poisson process. This allowed us to measure the temporal weighting of sensory evidence when subjects employ different decision stopping rules. It also allowed us to determine whether and how subjects adaptively alter their decision policy in the face of different types of mistakes: early false alarms and tardy misses.
We found that changes in decision stopping rules did not alter the temporal weighting of sensory evidence on the decision in a systematic way. Instead, it altered the magnitude of evidence needed to trigger a choice. This is consistent with a lengthy literature suggesting that bounds on evidence control flexible decision stopping rules without recourse to other mechanisms (Bogacz et al. 2010; Hanks et al. 2014; Heitz and Schall 2012; Palmer et al. 2005; Reddi et al. 2003). Although this result is admittedly not surprising, it provides reassurance that existing theories have not improperly neglected changes to the temporal weighting of sensory evidence as an obligatory part of altering decision stopping rules. For example, it would in theory be possible to decrease misses at the expense of more false alarms by using a decision rule that requires a similar change in local click rate over a shorter period of time. Nonetheless, we find support lacking for this type of mechanism.
We also found that subjects adaptively altered their decision policy on the basis of feedback on individual trials even though they were not instructed to have this behavior. Models of decision making often assume that decision bounds and other parameters that affect the decision process are either stable or vary randomly between trials, so our results bolster the point that many types of decisions will likely be better explained by also taking into account sequential effects based on previous choices and outcomes (Bertelson 1961; Goldfarb et al. 2012; Mendonca 2015; Remington 1969). We cannot rule out the possibility that other changes accompany altered bounds, such as changes to sensitivity as observed with post-error slowing (Purcell and Kiani 2016). A full account of all changes associated with altered decision stopping rules will likely benefit from future work involving neural recordings. We think it is an intriguing question to consider the extent to which these adaptive modifications share a common neural mechanism with changes in decision policies deriving from other sources that operate on longer timescales.
Our finding of post-error modifications of decision policy is reminiscent of the post-error slowing that has been observed in a wide variety of discrimination tasks (Laming 1979; Purcell and Kiani 2016). In contrast to the unidirectional effect of post-error slowing, post-error modifications in our task were bidirectional, resulting in slowing or speeding depending on the type of mistake. This follows intuitively from the idea that modifications are brought about by an optimization process that serves to reduce future errors of the same type (Botvinick et al. 2001). False alarms can be reduced by increasing one’s decision bound, and misses can be reduced by decreasing one’s decision bound. In this way, our results generalize the finding of post-error slowing to situations where different types of errors demand different modifications.
This generalization also leads to the suggestion that alteration of decision bound in our change detection task may involve similar neural circuits and mechanisms that are involved in discrimination tasks. Models that trigger choices with bounds on neural responses can explain behavior in both change detection (Boubenec et al. 2017; Cook and Maunsell 2002) and discrimination tasks (Gold and Shadlen 2007; Hanks and Summerfield 2017). Candidate neural responses involved in this bound-crossing process span a wide range of brain regions, including parietal cortex, frontal cortex, and subcortical structures (Brody and Hanks 2016; Gold and Shadlen 2007). Changes to decision bounds that control the tradeoff between speed and accuracy appear to be implemented through alterations of the dynamics of associated neural responses rather than the final level of activity before the choice (Hanks et al. 2014; Heitz and Schall 2012; Thura and Cisek 2016; van Veen et al. 2008). Furthermore, changes to dynamics of neural responses in the posterior parietal cortex were found to explain post-error slowing effects in a visual discrimination task (Purcell and Kiani 2016). Even though our task invoked a tradeoff between misses and false alarms rather than between speed and accuracy, both involve changes to decision bounds.
What is the source of post-error signals that in turn alter the bound-crossing process? Neurons in the medial frontal cortex of rats have been found to respond after errors in a simple reaction time task, and inactivation of that brain region reduces post-error slowing in the task (Narayanan and Laubach 2008). A common mechanism for this post-error slowing has also been suggested to be at play in both rats and humans (Narayanan et al. 2013). Whether similar mechanisms extend to the bidirectional post-errors alterations we observed in our change detection task will be an interesting question for further study.
We think that the increased richness of post-error modifications provided by our task will aid in providing a more complete picture of the neural mechanisms that support flexible decision making. We also note that the naturally occurring adaptive modifications of decision rules that we describe in this article allow for investigation of their neural mechanism without requiring explicit training of subjects to change their decision rules. This will be especially useful for experiments involving nonhuman subjects.
GRANTS
T. D. Hanks is funded by a National Alliance for Research on Schizophrenia and Depression Young Investigator Award and a Whitehall Foundation Grant.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
B.J., M.S., and T.D.H. conceived and designed research; B.J., R.V., and T.D.H. performed experiments; T.D.H. analyzed data; B.J., R.V., and T.D.H. interpreted results of experiments; T.D.H. prepared figures; B.J. and T.D.H. drafted manuscript; B.J., R.V., M.S., and T.D.H. edited and revised manuscript; B.J., R.V., M.S., and T.D.H. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Jochen Ditterich, Rashed Harun, and Adam Goldring for comments on the manuscript. We thank Adil Abbuthalha for assistance with building equipment.
REFERENCES
- Beard BL, Ahumada AJ Jr. Technique to extract relevant image features for visual tasks. Proc. SPIE 3299, Human Vision and Electronic Imaging III, 1998, p. 79–85. doi: 10.1117/12.320099. [DOI] [Google Scholar]
- Bertelson P. Sequential redundancy and speed in a serial two-choice responding task. Q J Exp Psychol 13: 90–102, 1961. doi: 10.1080/17470216108416478. [DOI] [Google Scholar]
- Bogacz R, Wagenmakers EJ, Forstmann BU, Nieuwenhuis S. The neural basis of the speed-accuracy tradeoff. Trends Neurosci 33: 10–16, 2010. doi: 10.1016/j.tins.2009.09.002. [DOI] [PubMed] [Google Scholar]
- Botvinick MM, Braver TS, Barch DM, Carter CS, Cohen JD. Conflict monitoring and cognitive control. Psychol Rev 108: 624–652, 2001. doi: 10.1037/0033-295X.108.3.624. [DOI] [PubMed] [Google Scholar]
- Boubenec Y, Lawlor J, Górska U, Shamma S, Englitz B. Detecting changes in dynamic and complex acoustic environments. eLife 6: e24910, 2017. doi: 10.7554/eLife.24910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brody CD, Hanks TD. Neural underpinnings of the evidence accumulator. Curr Opin Neurobiol 37: 149–157, 2016. doi: 10.1016/j.conb.2016.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunton BW, Botvinick MM, Brody CD. Rats and humans can optimally accumulate evidence for decision-making. Science 340: 95–98, 2013. doi: 10.1126/science.1233912. [DOI] [PubMed] [Google Scholar]
- Churchland AK, Kiani R. Three challenges for connecting model to mechanism in decision-making. Curr Opin Behav Sci 11: 74–80, 2016. doi: 10.1016/j.cobeha.2016.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook EP, Maunsell JH. Dynamics of neuronal responses in macaque MT and VIP during motion detection. Nat Neurosci 5: 985–994, 2002. doi: 10.1038/nn924. [DOI] [PubMed] [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci 30: 535–574, 2007. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- Goldfarb S, Wong-Lin K, Schwemmer M, Leonard NE, Holmes P. Can post-error dynamics explain sequential reaction time patterns? Front Psychol 3: 213, 2012. doi: 10.3389/fpsyg.2012.00213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green DM, Luce RD. Detection of auditory signals presented at random times: III. Atten Percept Psychophys 9: 257–268, 1971. doi: 10.3758/BF03212645. [DOI] [Google Scholar]
- Green DM, Luce RD. Speed-accuracy trade off in auditory detection. In: Attention and Performance IV, edited by Kornblum S. New York: Academic, 1973. [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York: Wiley, 1966. [Google Scholar]
- Hanks T, Kiani R, Shadlen MN. A neural mechanism of speed-accuracy tradeoff in macaque area LIP. eLife 3: e02260, 2014. doi: 10.7554/eLife.02260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanks TD, Summerfield C. Perceptual decision making in rodents, monkeys, and humans. Neuron 93: 15–31, 2017. doi: 10.1016/j.neuron.2016.12.003. [DOI] [PubMed] [Google Scholar]
- Heitz RP, Schall JD. Neural mechanisms of speed-accuracy tradeoff. Neuron 76: 616–628, 2012. doi: 10.1016/j.neuron.2012.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Hanks TD, Shadlen MN. Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J Neurosci 28: 3017–3029, 2008. doi: 10.1523/JNEUROSCI.4761-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laming D. Choice reaction performance following an error. Acta Psychol (Amst) 43: 199–224, 1979. doi: 10.1016/0001-6918(79)90026-X. [DOI] [PubMed] [Google Scholar]
- Luce RD. Response Times: Their Role in Inferring Elementary Mental Organization. New York: Oxford University Press, 1986. [Google Scholar]
- Luce RD, Green DM. Detection of auditory signals presented at random times, II. Atten Percept Psychophys 7: 1–14, 1970. doi: 10.3758/BF03210123. [DOI] [Google Scholar]
- Mendonca A. The Role of Reinforcement Learning in Perceptual Decision-Making (PhD thesis). Lisbon, Portugal: Instituto de Tecnologia Química e Biológica António Xavier, Universidade Nova de Lisboa, 2015. [Google Scholar]
- Narayanan NS, Cavanagh JF, Frank MJ, Laubach M. Common medial frontal mechanisms of adaptive control in humans and rodents. Nat Neurosci 16: 1888–1895, 2013. doi: 10.1038/nn.3549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narayanan NS, Laubach M. Neuronal correlates of post-error slowing in the rat dorsomedial prefrontal cortex. J Neurophysiol 100: 520–525, 2008. doi: 10.1152/jn.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neri P, Parker AJ, Blakemore C. Probing the human stereoscopic system with reverse correlation. Nature 401: 695–698, 1999. doi: 10.1038/44409. [DOI] [PubMed] [Google Scholar]
- Nienborg H, Cumming BG. Psychophysically measured task strategy for disparity discrimination is reflected in V2 neurons. Nat Neurosci 10: 1608–1614, 2007. doi: 10.1038/nn1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer J, Huk AC, Shadlen MN. The effect of stimulus strength on the speed and accuracy of a perceptual decision. J Vis 5: 376–404, 2005. doi: 10.1167/5.5.1. [DOI] [PubMed] [Google Scholar]
- Purcell BA, Kiani R. Neural mechanisms of post-error adjustments of decision policy in parietal cortex. Neuron 89: 658–671, 2016. doi: 10.1016/j.neuron.2015.12.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raposo D, Sheppard JP, Schrater PR, Churchland AK. Multisensory decision-making in rats and humans. J Neurosci 32: 3726–3735, 2012. doi: 10.1523/JNEUROSCI.4998-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddi BA, Asrress KN, Carpenter RH. Accuracy, information, and response time in a saccadic decision task. J Neurophysiol 90: 3538–3546, 2003. doi: 10.1152/jn.00689.2002. [DOI] [PubMed] [Google Scholar]
- Remington RJ. Analysis of sequential effects in choice reaction times. J Exp Psychol 82: 250–257, 1969. doi: 10.1037/h0028122. [DOI] [PubMed] [Google Scholar]
- Teichert T, Grinband J, Ferrera V. The importance of decision onset. J Neurophysiol 115: 643–661, 2016. doi: 10.1152/jn.00274.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teichner WH. Recent studies of simple reaction time. Psychol Bull 51: 128–149, 1954. doi: 10.1037/h0060900. [DOI] [PubMed] [Google Scholar]
- Thura D, Cisek P. Modulation of premotor and primary motor cortical activity during volitional adjustments of speed-accuracy trade-offs. J Neurosci 36: 938–956, 2016. doi: 10.1523/JNEUROSCI.2230-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Veen V, Krug MK, Carter CS. The neural and computational basis of controlled speed-accuracy tradeoff during task performance. J Cogn Neurosci 20: 1952–1965, 2008. doi: 10.1162/jocn.2008.20146. [DOI] [PubMed] [Google Scholar]
- Wickelgren WA. Speed-accuracy tradeoff and information processing dynamics. Acta Psychol (Amst) 41: 67–85, 1977. doi: 10.1016/0001-6918(77)90012-9. [DOI] [Google Scholar]
- Woodrow H. The measurement of attention. Psychol Monogr 17: i–158, 1914. doi: 10.1037/h0093087. [DOI] [Google Scholar]