Efficient and optimized identification of generalized Maxwell viscoelastic relaxation spectra

Abstract

Viscoelastic relaxation spectra are essential for predicting and interpreting the mechanical responses of materials and structures. For biological tissues, these spectra must usually be estimated from viscoelastic relaxation tests. Interpreting viscoelastic relaxation tests is challenging because the inverse problem is expensive computationally. We present here an efficient algorithm that enables rapid identification of viscoelastic relaxation spectra. The algorithm was tested against trial data to characterize its robustness and identify its limitations and strengths. The algorithm was then applied to identify the viscoelastic response of reconstituted collagen, revealing an extensive distribution of viscoelastic time constants.

1. Introduction

The mechanical responses of nearly all materials and structures are viscoelastic, differing to some degree based upon the rate and duration of loading (Osaki, 1973; Frost & Ashby, 1982; Baschnagel, 2000; Hillman et al., 2005; Stadler et al., 2005). Characterizing viscoelasticity is important because viscoelasticity affects the transmission, storage, and dissipation of force and energy, and because variations in viscoelastic response as a function of loading duration or frequency can provide clues about micromechanical deformation, resilience mechanisms and molecular structure. Because cells and collagen-rich extracellular matrix (ECM) show strong viscoelastic behavior at physiological loading rates (Guilak et al., 2000; Pryse et al., 2003; Xu et al., 2013; Antoine et al., 2014), viscoelasticity is a factor in almost all biological tissues and organs. Indeed, viscoelastic responses have been studied as metrics of tissue function and health of arteries (Corman et al., 1998), brain parenchyma (Schregel et al., 2012), liver tissues (Chen et al., 2013), the prostate (Salcudean et al., 2006), skin (Clancy et al., 2010), breasts (Carp et al., 2008), articular cartilage (Edelsten et al., 2010), ligaments (Abramowitch et al., 2004), and tendon (Fang et al., 2014) and its attachments to bone (Thomopoulos et al., 2003).

For engineering polymers, the characterization test of choice is often rotational rheometry, which can provide information about the frequencies and timescales of loading over which a material absorbs energy most effectively. However, rotational rheometry is often unsuitable for the characterization of biological tissues because of issues of gripping, orienting, and aligning specimens (Arbogast & Margulies, 1998). Instead, other viscoelastic protocols such as relaxation tests are typically used. These involve ramping uniaxial stretch to a prescribed level, then monitoring the isometric force needed to sustain that level of stretch.

However, estimating the viscoelastic spectrum from the time variation of this isometric force response requires solving a difficult and ill-posed inverse problem (Provencher, 1982a,b). Here we present an algorithm that is fast enough to yield a discrete spectrum of time constants sufficient to fit a measured relaxation spectrum with an accuracy insensitive to further refine-ment. The algorithm fits a discrete spectral generalized Maxwell (Maxwell-Wiechert) model to results from a stress-relaxation test. The algorithm is analogous to the inverse fast Fourier transformation (FFT), except that the algorithm dissects the time domain relaxation data into a spectrum of viscoelastic time constants,each defined as a viscous coefficient η divided by an elastic modulus E (Fig. 1). Several idealized, noisy, and incomplete data sets were analyzed to establish the strengths and limitations of the approach. Thereafter, the approach was applied to study the viscoelastic relaxation of reconstituted collagen.

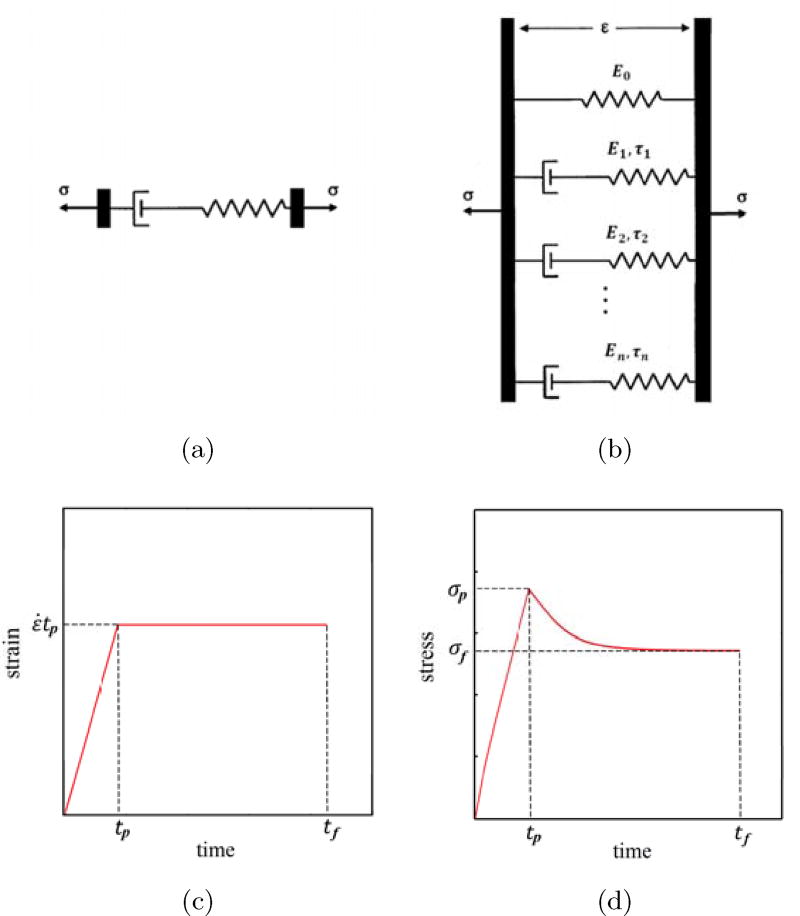
Figure 1.

Schematics of the Maxwell model (a) and generalized Maxwell (Maxwell-Wiechert) model (b). The strain profile of a stress-relaxation test showing a linear ramp to an isometric value of strain (c), and the associated stress response, showing a peak at the end of the ramp and a relaxation to a strain-dependent steady state.

1.1. Background: the generalized Maxwell (Maxwell-Wiechert) constitutive model

The Maxwell model (Fig. 1(a)) is composed of a linear dashpot connected in series with a linear spring. A feature of this model is that it has a single relaxation time constant, τ = η/E. However, this does not wholly simulate the viscoelastic behavior of most materials. For this reason, the generalized Maxwell (or Maxwell-Wiechert) model with multiple springs and dashpots is commonly applied (Fig. 1(b)). This model is composed of a spring of elastic modulus E₀ in parallel with M Maxwell elements, with the i^th Maxwell element having time constant τ_i and a spring of elastic modulus E_i. Since the components of the generalized Maxwell model are connected in parallel, all branches have the same strain ε(t) at all times t, and the overall stress of the system is the sum of the stresses in each branch. The response of a fully relaxed generalized Maxwell material to a strain history ε(t) is typically studied following convolution integral:

$$\sigma (t)=s_0+\sum _{i=1}^M{s}_i(t)={\int }_0^t(E_0+\sum _{i=1}^M{E}_i{e}^{-(t-u)/{\tau }_i})\dot{\epsilon }\mathit{\text{du}}$$ (1.1)

where σ(t) is the generalized Maxwell prediction of the overall stress in a material sample, M is the number of Maxwell branches, s₀ is stress in the single spring and s_i(t) is the stress within the i^th Maxwell element.

When calibrating the generalized Maxwell model to a particular material, the objective is to find the strain-independent material properties E_i and τ_i and number of branches M.

Although Eq. (1.1) is particularly simple when the ε(t) represents a stepwise change in strain, approximating such a strain course experimentally is fraught with difficulty because inertial effects can cause overshoot in the loading frame and wave motion in the specimen that can in turn cause substantial error in parameter fitting (Nekouzadeh et al., 2005). Instead, strain is typically increased at some constant rate ε̇ over a time interval 0 ≤ t ≤ t_p, and then held over the time interval t_p ≤ t ≤ t_f (Fig. 1(c)). At discrete times t_j, the predicted stress response is (Fig. 1(d)):

$$\sigma (t_j)=\{\begin{array}{cc}{E}_0\dot{\epsilon }{t}_j+\sum _{i=1}^M{E}_i{\tau }_i\dot{\epsilon }(1-e^{-t_j/{\tau }_i})\hfill & j=1,2,\dots ,p\hfill \\ E_0\dot{\epsilon }{t}_p+\sum _{i=1}^M{E}_i{\tau }_i\dot{\epsilon }(1-e^{-t_p/{\tau }_i})\left(e^{-(t_j-t_p)/{\tau }_i}\right)\hfill & j=p,p+1,\dots ,f\hfill \end{array}$$ (1.2)

where p and f are the number of data points in ramp and relaxation intervals, respectively. Note that the response to a very fast ramp (t_p → 0, ε̇ → ∞) to a defined strain level ε_p has the simple form:

$$\sigma (t_j)=(E_0+\sum _{i=1}^M{E}_i{e}^{-t_j/{\tau }_i}){\epsilon }_{p}j=1,2,\dots ,f$$ (1.3)

where the substitution t = ε/ε̇ was made into Eq. (1.2), and $\underset{\dot{\epsilon }\to \infty }{\text{lim}}\dot{\epsilon }(1-e^{-\epsilon /\dot{\epsilon }{\tau }_i})=\epsilon /{\tau }_i$ was used.

2. Methods

2.1. Fitting of generalized Maxwell data

Two classes of approaches were used to fit a generalized Maxwell model to stress data σ̄(t_j) recorded at discrete times t_j as a material responds to a straining history ε(t_j): an ad hoc approach and a discrete spectral approach. We present here both approaches.

ad hoc approach

The first approach was a simple and widely used ad hoc approach, requiring an ad hoc function to compute E_i and τ_i. Thus, the number M of Maxwell elements was guessed in advance, and the time constants τ_i and associated values of E_i were unknown. The values of τ_i and E_i could be estimated by minimizing the least squares error to fit a set of f observations with a relation for 2M unknown parameters (f > 2M). The approach started with a vector of initial guesses for E_i and τ_i and refined the estimates iteratively by minimizing the mean squared error:

$$\mathit{\text{MSE}}=\frac{1}{f}\sum _{j=1}^f{(s_0+\sum _{i=1}^M{s}_i(t)-\overline{\sigma }(t_j))}^2$$ (2.1)

where s₀ and s_i(t) were defined in Eq. (1.1) and σ̄(t) is the recorded stress history. We found that the ad hoc approach could fit most experimental stress-relaxation data with M = 2 or 3. This can be advantageous because a fit to subsequent analogous loadings could be obtained with little effort or complexity. However, this could be disadvantageous because such fitting may provide little information relevant to the characterization of intrinsic deformation mechanisms. Further, if one analyzes a single set of experimental data with three different arbitrary exponential terms, e.g. M=1,2 or 3, the results of these analyses are not comparable easily: the derived parameters such as τ_i and E_i are usually affected by the arbitrarily chosen M. In the following sections we present a simple, fast, and robust algorithm for overcoming this limitation.

Discrete spectral approach

In the second approach, the time constants τ_i of Maxwell elements were chosen in advance, with τ_i spaced sufficiently closely to be approximately continuous on a logarithmic scale. For analysis of collagen, on the order of M = 1000–10000 time constants were distributed equidistantly in logarithmic space over an interval of 10⁻³ to 10⁵ s, an interval broader than any previously reported time constants of biological materials. The corresponding values of E_i were determined by fitting a generalized Maxwell model to relaxation data σ̄(t_j).

The problem of determining a low-rank solution is ill-posed. A range of methods exist for this problem, but they are relatively slow and are thus difficult to optimize (Provencher, 1982a; Stadler & Bailly, 2009; Honerkamp, 1989). Our contribution is a relatively fast algorithm that enables a well converged (although not necessarily optimal) approximation to experimental data. We converted (1.2) to a system of linear equations in matrix form that could be solved rapidly as:

$$\left[\begin{array}{c}\hfill {\sigma }_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\sigma }_p\hfill \\ \hfill {\sigma }_p\hfill \\ \hfill ⋮\hfill \\ \hfill {\sigma }_f\hfill \end{array}\right]=\{\begin{array}{cc}\hfill \left[\begin{array}{ccc}\hfill \dot{\epsilon }{t}_1\hfill & \hfill a_{11}\cdots \hfill & \hfill a_{M1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \dot{\epsilon }{t}_p\hfill & \hfill a_{1p}\cdots \hfill & \hfill a_{\mathit{\text{Mp}}}\hfill \end{array}\right]\hfill & \hfill \left[\begin{array}{c}\hfill E_0\hfill \\ \hfill E_1\hfill \\ \hfill ⋮\hfill \\ \hfill E_M\hfill \end{array}\right]\hfill \\ \hfill \left[\begin{array}{ccc}\hfill \dot{\epsilon }{t}_p\hfill & \hfill b_{1p}\cdots \hfill & \hfill b_{\mathit{\text{Mp}}}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill \dot{\epsilon }{t}_p\hfill & \hfill b_{1f}\cdots \hfill & \hfill b_{\mathit{\text{Mf}}}\hfill \end{array}\right]\hfill & \hfill \left[\begin{array}{c}\hfill E_0\hfill \\ \hfill E_1\hfill \\ \hfill ⋮\hfill \\ \hfill E_M\hfill \end{array}\right]\hfill \end{array}$$ (2.2)

where a_ij = τ_iε̇ (1 − e^−t_j/τ_i) for i = 1,2, …, M and for j = 1,2, …, p; and b_ij = τ_iε̇ (1 − e^−t_p/τ_i) e^{−(t_j−t_p)/τ_i} for i = 1,2, …, M and for j = p, p + 1, …, f.

The matrix form of (1.3) was written:

$$\left[\begin{array}{c}\hfill {\sigma }_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\sigma }_f\hfill \end{array}\right]=\{\begin{array}{c}\hfill \left[\begin{array}{ccc}\hfill {\epsilon }_p\hfill & \hfill c_{11}\cdots \hfill & \hfill c_{M1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill {\epsilon }_p\hfill & \hfill c_{1f}\cdots \hfill & \hfill c_{Mf}\hfill \end{array}\right]\left[\begin{array}{c}\hfill E_0\hfill \\ \hfill E_1\hfill \\ \hfill ⋮\hfill \\ \hfill E_M\hfill \end{array}\right]\hfill \end{array}$$ (2.3)

where c_ij = ε_pe^−t_i/τ_j for i = 1,2, …, M & j = 1,2, …, p.

A non-negative least squares regression (Lawson & Hanson, 1974; Bro & De Jong, 1997) was used to determine the values E_i from the stress-relaxation data. For a large dataset, corresponding to a large-scale matrix, solving the above equations was computationally expensive. Our approach was to use a singular value decomposition method (Demmel, 1997; Klema & Laub, 1980) to decrease the rank of the matrices and speed up the solution procedure. The procedure was repeated with increasingly large numbers M of Maxwell elements to ensure that approximations converged to those that would arise from infinitely large matrices. For all cases studied, spectra estimated using M = 1000 did not differ from those estimated using M = 10000. We therefore used M = 1000, and the algorithm calculated dominant time constants and moduli of relaxation data sets precisely, without needing to guess the requisite number of time constants in advance.

Convergence was achieved in 6.4 s when the algorithm was implemented in uncompiled Matlab (The Mathworks, Natick, MA) on a laptop running with an Intel Core i7-4710 CPU at 2.50 GHz and 8 GB of RAM for f=25,000 data points and M=1000 time constants.

2.2. Calibration

Fitting to idealized and incomplete data

Simulated stress-relaxation data were generated using the generalized Maxwell model and a strain history involving a ramp to 10% strain at a constant rate of 100%/s, followed by 500 s with the strain level held constant at the fixed level of 10%. The generalized Maxwell model had M = 3 Maxwell elements in parallel with a linear spring. The elastic modulus of the parallel spring was E₀ = 100 MPa; the time constants of Maxwell branches were {τ₁, τ₂, τ₃} = {1 s, 10 s, 100 s}; the elastic moduli of the springs within the Maxwell branches were {E₁, E₂, E₃} = {18 MPa, 25 MPa, 9 MPa}. Data were generated at 50 data points per second.

Several permutations were studied, including fitting the generated data with a generalized Maxwell model having M=1, 2, 3 and 4 time constants, and fitting of truncated datasets. The latter studies aimed to assess the robustness of the procedure when data are acquired over time intervals that are not long compared to the longest time constant.

Sensitivity to noise

To study the stability of both ad hoc and discrete spectral fittings with respect to noise, random noise was added to the simulated stress-relaxation data. We superimposed upon the data noise chosen from the Gaussian distribution with amplitudes of 0%, 1%, 2%, 3% and 4% of the steady state stress. These noise amplitudes were in the range of experimental levels of noise. In this way, 50 noisy data sets were generated (10 sets for each noise percentage). For these new data sets, the time constants of the system were estimated. The sensitivity to noise level was then quantified by relative error of the predicted parameters compared to the underlying input ones.

2.3. Estimation of the viscoelastic relaxation spectrum of reconstituted collagen

Viscoelastic relaxation spectra of reconstituted collagen gels were estimated from the data of Pryse et al. (2003) using both the ad hoc and discrete spectral approaches. Briefly, type I rat tail collagen (Upstate Biotechnologies), was diluted to 2.5 mg/ml in Dulbecco’s Modified Eagle Medium (DMEM) brought to pH 7 with sodium hydroxide. One milliliter of the collagen solution was pipetted into Teflon casting molds composed of an outer cylinder and an inner mandrel, and centrifuged gently and incubated at 37 °C to form ring-shaped specimens of 9.5 mm inner diameter, 2 mm thickness, and 10 mm height. Specimens were kept in molds at 37 °C for 15–18 hours before force measurements were performed. Ring gel specimens were then removed from the casting mold and mounted on a loading frame. Specimens were stretched to a strain of 6.7% in 20 ms and held isometrically while the force was monitored for 30 min at 5 Hz.

3. Results and Discussion

Because the generalized Maxwell model only approximates dominant elastic moduli and time constants of a real material, validation of the fitting method began with application to a fictional material whose mechanical response followed the generalized Maxwell model exactly. In this way, we checked the reproducibility of the approximations to further understand how the approximations deviate from the optimum. Then, viscoelastic response of collagen gel (Pryse et al., 2003) was reinterpreted by using the discrete spectral approach.

3.1. Characterization of relaxation spectra from idealized generalized Maxwell data

Ad hoc analysis

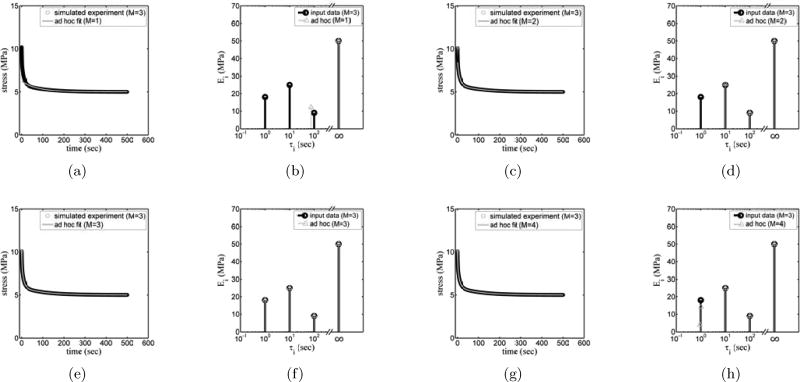
We began by evaluating what happens when data generated via the generalized Maxwell model with M=3 were interpreted using the ad hoc approach with M=1, 2, 3, or 4. When data from a model with M = 3 Maxwell elements were fitted using a generalized Maxwell model with M=1 elements (i.e., a system including a spring and dashpot in series, in parallel with a single spring), the longest relaxation was estimated while two fast relaxation time constants were missed (Fig. 2(b)). The data were fitted based on their weights (with MSE regression); thus, the model estimated the time constants which had the highest weight in the data, which is τ=100 s. Correspondingly, the fitting (Fig. 2(a)) was good for longer times, but noticeably poor at shorter times. Different weighting functions could be applied to change this, but optimization based upon approach always captured the longest time constants.

Figure 2.

Stress relaxation data for an idealized generalized Maxwell material with M=3 time constants, fit with M=1 ((a) and (e)), M=2 ((b) and (f)), M=3 ((c) and (g)), and M=4 ((d) and (h)) time constants.

For M=2, the two longer time constants were well estimated (Fig. 2(c)–(d)), and the fit to the data was much improved. For M=3 all three time constants were identified correctly (Fig. 2(e)–(f)).

When the process was repeated for M=4, in which the number of the viscoelastic terms was overestimated, a counterfeit peak appeared with a relatively small amplitude in the vicinity of the fastest time constant of the material’s viscoelastic relaxation (Figs. 2(g)–(h)). This small counterfeit peak disrupted estimation of the fastest time constant. With a sufficiently tight convergence criterion and no experimental noise, this peak would presumably disappear with a well-tailored algorithm and sufficient iteration. However, the peak was sustained to convergence criteria far tighter than are practical with experimental data. In each case, the value of R² for the fitting was very close to 1, even for the case of a fitting with M=1 (Table 1). We noted that the MSE of the fittings was a far more sensitive metric of goodness of fit (Table 1) and applied it in all subsequent analyses.

Table 1.

Both the ad hoc and discrete spectral approaches were used to fit simulated, noise-free stress-relaxation data generated using M=3 Maxwell branches. R² and mean squared error (MSE) for each fitting were calculated. The results for M=1, 2, 3, and 4 correspond to Fig. 2 (ad hoc approach) while the results for M=1000 correspond to Fig. 3 (discrete spectral approach). The approaches required comparable CPU time (f=25000 data points, 1000 iterations).

M	1	2	3	4	1000
R2	0.9957	0.9999	0.9999	0.9999	0.9999
MSE	0.6 × 10−2	3.7 × 10−3	1.6 × 10−9	2.1 × 10−9	1.8 × 10−9
CPU time (s)	7.0	6.1	3.7	5.6	6.4

Discrete spectral analysis

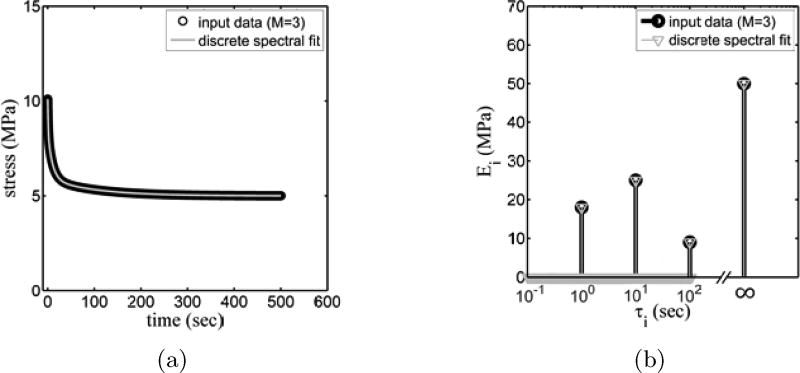
With a sufficiently large number M of fixed time constants in the discrete spectrum, the number, elastic moduli, and time constants of Maxwell branches were well predicted using discrete spectral analysis (Fig. 3). Counterfeit peaks did not arise in the discrete spectrum as they did in the ad hoc spectrum.

Figure 3.

Stress relaxation data for an idealized generalized Maxwell material with M=3 time constants, fit using the discrete spectral approach with 1000 time constants distributed equidistantly in log space over the interval 10^{− 1}s ≤ τ ≤ 10³s.

Effects of noise

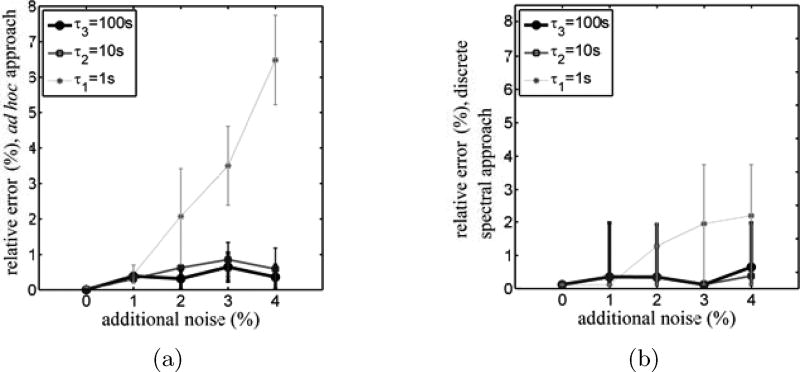
Random noise added to the stress-relaxation data affected estimation time constants that were not long compared to the frequency of the noise. The effect increased with the amplitude of noise added (Fig. 4). Although estimates of the time constants were affected, the noise did not introduce new, artifactual time constants into the viscoelastic relaxation spectrum.

Figure 4.

50 sets of Gaussian noise were generated (10 sets for each of 5 noise amplitudes) and added to ideal simulated stress-relaxation data. The simulated noisy stress relaxation data were then analyzed using the (a) ad hoc and (b) discrete spectral approaches.

To study the effect of noise estimates derived using the ad hoc approach, a best case scenario was assumed in which the correct number of Maxwell branches (M = 3) was known in advance. In this best-case scenario, the fastest time constant of the system, τ₁, for 4% noise, was estimated with less than 8% error, while the other time constants were estimated with less than 1.5% error. For comparison, the time constants were estimated correctly to within floating point precision for the ideal case of no noise. The errors associated with interpreting these data using the discrete spectral approach were smaller still (Fig. 4). For 4% noise, the fastest time constant was estimated with less than 4% error while the other time constants were estimated with less than 2% error. These results suggest that for the interpretation of noisy data from a generalized Maxwell material, the discrete spectral approach is at least as accurate as the ad hoc approach, and has the additional advantages of being fast computationally and of avoiding the need to guess the number M of time constants a priori.

3.2. Interpretation of incomplete relaxation data

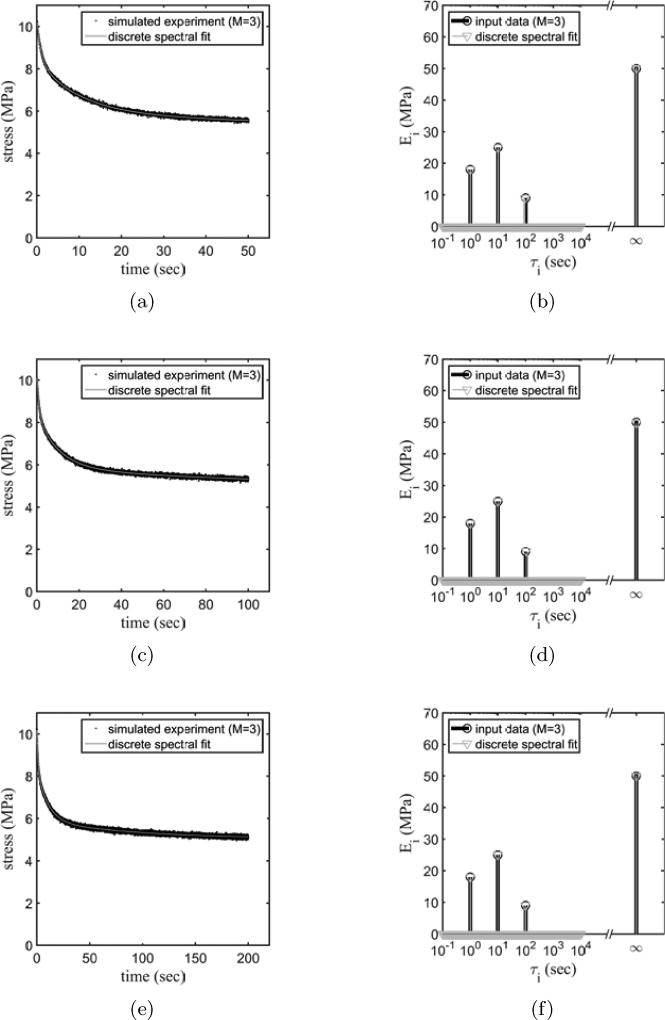
With the efficacy of the discrete spectral approach established, we evaluated its performance against incomplete data. This is useful because biological systems often preclude the possibility of holding a specimen sufficiently long for complete relaxation to occur. For example, in biological tissue constructs consisting of living cells in a reconstituted collagen matrix, relaxation has been shown to persist to times sufficient for cellular remodeling to occur (Lee et al., 2012); in such a case, the tissue construct as a whole becomes a different material before relaxation is complete, and only partial data can be used.

For the stress relaxation data studied in Fig. 2, the first test involved analyzing the first 50 s of stress relaxation data (Fig. 5(a)), a time interval that is only 50% of the slowest finite viscoelastic time constant in the input data. The interpretation of the spectrum succeeded in identifying the three time constants and the infinite time constant (Fig. 5(b)). The first, second and infinite time constants had accurate positions, but the third time constant estimation deviated about 7% from input time constant. When 100 s of the stress relaxation data were studied (Fig. 5(c)), a time interval equal to the longest time constant of the input data, the interpretation succeeded in capturing the first two fast time constants (Fig. 5(d)), but the interpretation again captured the third peak with about 7% error. With 200 s of stress-relaxation data, the interpretation succeeded in capturing the peaks at the all three time constants and also the correct amplitude of the infinite time constant (Fig. 5(e)–(f)). Here, we considered an estimate of the time constant with less than 2% error as successful.

Figure 5.

Discrete spectral analyses of noisy data following 50 s ((a) and (b)), 100 s ((c) and (d)), or 200 s ((e) and (f)) of relaxation.

The guidelines demonstrated in this simple test are that a predicted time constant can be trusted as being represented in the actual spectrum of a tested material if it is infinite or if it is less than half the duration of the viscoelastic relaxation data. Error was on the order of 10% or less for a time constant that is twice the duration of the viscoelastic relaxation data.

3.3. The viscoelastic relaxation response of reconstituted collagen

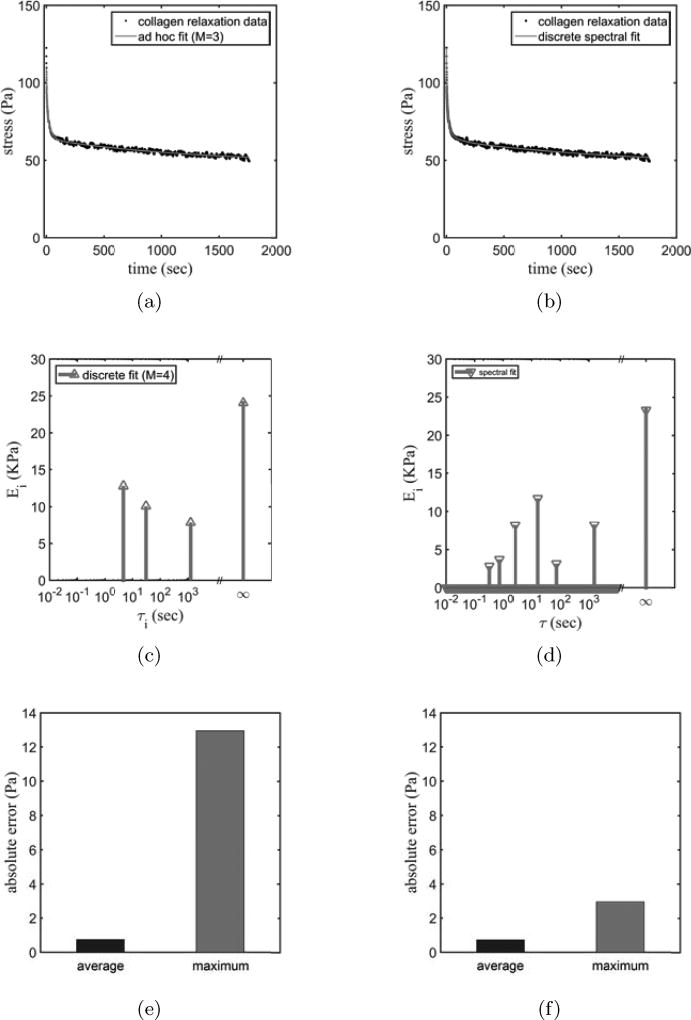
We reinterpreted the experimental data studied by Pryse et al. (2003) using the ad hoc and discrete spectral approaches (Figs. 6, columns 1 and 2, receptively). For the fitting of these data collagen gel data, the highest absolute error was associated with the ad hoc approach, but the mean errors were comparable (Fig. 6(e)–(f)).

Figure 6.

Fittings for stress-relaxation data acquired from a collagen gel stretched 20% strain under a fast strain rate (100 %/s) fitted by (a,c,e) the ad hoc and (b,d,f) discrete spectral approaches. (c) Three time constants were estimated at 4.63 s, 30.6 s and 1250 s using the ad hoc approach. Using the discrete spectral approach the spectrum shows that relaxation of the collagen has six main time constants at about 0.3 s, 0.7 s, 2.6 s, 16.1 s, 72.7 s and 1520 s.

Consistent with the analyses of Pryse et al. (2003), ad hoc analysis estimated that collagen gel has three relaxation mechanisms that manifest themselves as viscoelastic relaxation time constants of 4.6 s, 30.6 s and 1250 s (Fig. 6(c)). However, the discrete spectral approach revealed a region with relatively fast time constants (Fig. 6(d)). The studies described in the previous sections suggest that these time constants are not artifacts arising from noise or from the duration of the test. The spectrum suggested six main relaxation time constants of about 0.3 s, 0.7 s, 2.6 s, 16.1 s, 72.7 s, and 1520 s (Fig. 6(d)). Because the time constants found were either infinite or less than twice the 1800 s duration of the isometric stretch, they can be expected to have an error of less than 10%. In addition to being consistent with the analysis of Pryse et al. (2003), they are further consistent with some of the slower time constants identified by Gupta et al. (2010) and Xu et al. (2013). The faster time constants might have been absent in the work of Gupta et al. (2010) because their study was of tendons rather than of reconstituted collagen. Alternatively, it is possible that, either because their approach was analogous to the ad hoc approach or because that study used a data acquisition rate whose inverse was slow compared to the fastest time constants observed here, they were able to obtain an excellent fit in the absence of the contributions of faster time constants. The slowest time constant of 1500 s was not present in the work of Gupta et al. (2010), possibly reflecting once more a difference between collagen within reconstituted tissues and collagen within the fibers and fibrils of a tendon.

3.4. Prospects for application to collagenous tissues

A central theme of this study is the potential of a viscoelastic spectrum as a tool for assessing the health and function of a biological tissue. We envision that this potential will be strong for assessing pathologies such as hypertrophic cardiomyopathy, in which relaxation is central to the progression of pathology (Babaei et al., 2015). However, several important factors need to be considered when extending our application of the method to living tissues, especially collagenous tissues such as tendon. First, viscoelastic time constants of collagenous tissues are well known to depend upon the degree of hydration of the tissue. This is known from studies at the molecular (Gautieri et al., 2012), fibril (Shen et al., 2011), and tissue (Venkatasubramanian et al., 2010) levels, for both unmineralized and mineralized tissues (Liu et al., 2014). Therefore, the viscoelastic spectra estimated by our approaches will likely be sensitive to the nature of the medium in which tendons are tested.

Second, such tissues are highly nonlinear and anisotropic. Although these two material factors are well understood from the perspective of linear elasticity, the nature of the viscoelastic nonlinearity and anisotropy is not yet certain (Puso & Weiss, 1998; Stylianopoulos & Barocas, 2007; Nguyen et al., 2008). While we expect that the tools presented in this article will be of value in defining these effects, we note that characterization and comparison of viscoelastic spectra may be sensitive to the details of strain state and direction of loading.

Third, we expect viscoelastic spectra to be sensitive to the details of the composition of tissues. A key motivation for our group is understanding viscoelastic responses at interfaces between tendon and bone, where composition is known to vary in a graded fashion. Understanding such spatial variations will be complicated by the nature and media-sensitivity of glycosaminoglycans and by the spatial disposition of mineral. Although outstanding models exist for the viscoelastic responses of proteoglycan rich tissues, the extension of these to spectral representations will be a challenge.

4. Conclusions

We presented a fast and general discrete spectral approach to estimating viscoelastic relaxation spectra from force or stress relaxation data, and compared it to an ad hoc approach. When using an ad hoc approach with a fixed number M of variable viscoelastic time constants, the fitting process was sensitive to M: by underestimating M, faster relaxation mechanisms were missed; by overestimating M, artifactual fast time constants were introduced. These problems were not clearly evident when comparing goodness of fit using R², because R² was near 1 for all of the fittings. The precision of fittings was more distinguishable by considering MSEs.

The discrete spectral approach predicted the number of time constants and corresponding elastic moduli with very low MSE, only slightly higher than when the correct number of viscoelastic time constants was known a priori. The discrete spectral approach was less sensitive to noise, but for ideal data, without any noise, the ad hoc method was more efficient.

Application of the discrete spectral approach to reconstituted collagen gels revealed six time constants, with the slower time constants analogous to those captured by ad hoc analyses in the literature. As with the work of others, the discrete spectra that arise are of value in relating viscoelastic responses to micro-mechanical phenomena that occur across length scales (Xu et al., 2015; Ashrafi & Shariyat, 2010; Graham et al., 2011). Results suggest that the discrete spectral approach is a computationally efficient and informative approach to analyzing viscoelastic relaxation data.