Abstract
The treatment of cancer using targeted radionuclide therapy is of interest to nuclear medicine and radiation oncology because of its potential for killing tumor cells while minimizing dose-limiting toxicities to normal tissue. The ionizing radiations emitted by radiopharmaceuticals deliver radiation absorbed doses over protracted periods of time with continuously varying dose rates. As targeted radionuclide therapy becomes a more prominent part of cancer therapy, accurate models for estimating the biologically effective dose (BED) or equieffective dose (EQD2α/β) will become essential for treatment planning. This study examines the radiobiological impact of the dose rate increase half-time during the uptake phase of the radiopharmaceutical. MDA-MB-231 human breast cancer cells and V79 Chinese hamster lung fibroblasts were irradiated chronically with 662 keV γ rays delivered with time-varying dose rates that are clinically relevant. The temporal dose-rate patterns were: 1. acute, 2. exponential decrease with a half-time of 64 h (Td = 64 h), 3. initial exponential increase to a maximum (half time Ti = 2, 8 or 24 h) followed by exponential decrease (Td = 64 h). Cell survival assays were conducted and surviving fractions were determined. There was a marked reduction in biological effect when Ti was increased. Cell survival data were tested against existing dose-response models to assess their capacity to predict response. Currently accepted models that are used in radiation oncology overestimated BED and EQD2α/β at low-dose rates and underestimated them at high-dose rates. This appears to be caused by an adaptive response arising as a consequence of the initial low-dose-rate phase of exposure. An adaptive response function was derived that yields more accurate BED and EQD2α/β values over the spectrum of dose rates and absorbed doses delivered. Our experimental data demonstrate a marked increase in cell survival when the dose-rate-increase half-time is increased, thereby suggesting an adaptive response arising as a consequence of this phase of exposure. We have modified conventional radiobiological models used in the clinic for brachytherapy and external beams of radiation to account for this phenomenon and facilitate their use for treatment planning in targeted radionuclide therapy.
INTRODUCTION
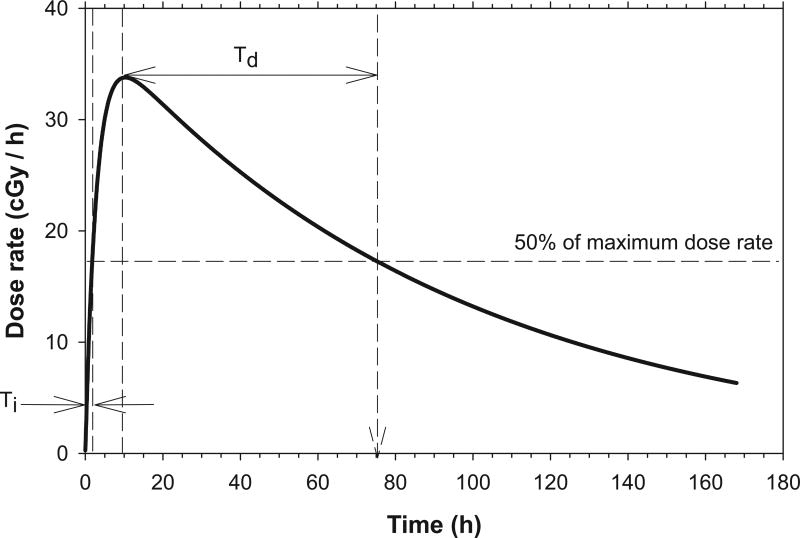
Radiopharmaceuticals deliver absorbed radiation doses to various organs and tissues over protracted times. The temporal variation in dose rate during irradiation is dependent upon the biological uptake and clearance half-times of the radiopharmaceutical in the tissue, and the physical half-life of the radionuclide. The dose-rate patterns that emerge are continuously variable and uniquely different than those encountered in other diagnostic and therapeutic modalities that usually involve either single or fractionated acute exposures. These dose-rate patterns are often characterized by an initial exponential increase to a maximum value followed by an exponential decrease. The dose rate increase half-time Ti is the approximate time required for the dose rate to increase to one-half of its maximum value. Whereas, the dose rate decrease half-time Td is the approximate time required for dose rate to decrease to one-half of its maximum value (Fig. 1).
FIG. 1.
Dose-rate pattern characterized by an initial exponential increase in dose rate, followed by an exponential decrease in dose rate. The dose rate increase half-time Ti is the time required for dose rate to increase to about one-half of its maximum value. The dose rate decrease half-time Td is the time required for dose rate to decrease to about one-half of its maximum value.
There is a wealth of literature regarding the biological effects of single or fractionated acute-exposure patterns, as well as for chronic irradiation at constant dose rate (1, 2). Research has shown that responses to continuous irradiation are markedly different from responses to an acute exposure (3, 4). Depending on the tissue irradiated, the underlying reasons behind these differences have been attributed to a multitude of factors such as cell cycle dependence of radiosensitivity, proliferation, cell signaling, inflammatory responses, adaptive responses, compensatory responses and many other factors such as linear energy transfer (LET) (1). The relative importance of these factors depends on the dose rate and total absorbed dose. There is also considerable experimental data published on the effects of exponentially decreasing dose rates (3, 5, 6). Yet, there is a paucity of experimental data available regarding how the initial exponential increase in dose rate to a maximum, followed by an exponential decrease in dose rate, affects biological response under conditions that are not influenced by the spatial nonuniformities of absorbed dose that are often inherent in nuclear medicine. Behr et al. showed that slow effective uptake of the radiopharmaceutical by tumors was less effective than fast effective uptake at retarding the growth of subcutaneous human xenografts in mice (7). This is relevant not only for targeted radionuclide therapies, but also for diagnostic nuclear medicine (8). More data concerning biologic responses to the dose-rate patterns associated with these modalities could lend insight into the effectiveness and toxicity of new and existing procedures.
Moreover, modeling the biological response to ionizing radiation in the context of radiation therapy is also vital to plan and adjust treatment schedules. Dose-response models have been developed for single and multiple fractionated acute exposures (9, 10). Dose-response models that were developed for fractionated therapy have also been adapted for brachytherapy and targeted radionuclide therapy (10–21). However, the majority of these dose-response models do not consider the impact of increasing dose rates, that occur during the uptake phase of the radiopharmaceutical, on biological response. Dose-response models have been developed to account for this phase of irradiation, however they are theoretical in nature and not based on experimental data (11, 14, 22). The accuracy of these models has yet to be tested thoroughly. This experimental and modeling study examines the radiobiological impact of the dose rate increase half-time (Ti) during the uptake phase of the radiopharmaceutical, and then develops new approaches for calculating the biologically effective dose (BED) and EQD2α/β for the multicomponent exponential dose-rate profiles encountered in nuclear medicine. Finally, suggestions are made as to how these models can improve treatment planning for radiopharmaceutical therapies. Table 1 contains a summary of all symbols used in the models, along with their corresponding units and references.
TABLE 1.
Quantities and Parameters
| Units | Definition | Ref. | |
|---|---|---|---|
| A | - | Adaptive response correction factor. | Eq. (12) |
| BED | Gy | Biologically effective dose. | (9) |
| D | Gy | Absorbed dose. | (58) |
| EQD2α/β | Gy | Total absorbed dose delivered with 2 Gy fractions of reference radiation that yields the same biologic effect as the test radiation treatment plan, where α/β is the numeric value used for the calculations. | (33) |
| G | - | Lea-Catcheside G factor. | (59) |
| LQ model | - | Linear quadratic model. | (9) |
| RE | - | Relative effectiveness. | (31) |
| r | Gy h−1 | Absorbed dose rate. | (58) |
| r0 | Gy h−1 | Extrapolated initial dose rate. (see Fig. 3) | (11) |
| r0,ref | Gy h−1 | Intercept of a linear fit of r0 versus Ti. | Eq. (12) |
| sref | Gy h−2 | Slope of a linear fit of r0 versus Ti. | Eq. (12) |
| SF | - | Surviving fraction of single cells seeded into flask. | Eq. (3) |
| SFref | - | Reference surviving fraction at which r0,ref and sref are determined. | Eq. (12) |
| Ti | h | Dose rate increase half-time. (see Fig. 2) | (24, 60) |
| Approximate time required for dose rate to increase to one-half of its maximum value. | |||
| Td | h | Dose rate decrease half-time. (see Fig. 2) | (24, 60) |
| Approximate time required for dose rate to decrease to one-half of its maximum value. | |||
| Tp | h | Physical half-life of radionuclide | |
| μ | Rate constant for exponential sublethal DNA damage repair with first order kinetics. | (24, 60) | |
| Tμ | h | Repair half-time for exponential sublethal DNA damage repair with first order kinetics | (24, 60) |
| α | Gy−1 | Linear parameter in LQ model. | Eq. (3) |
| β | Gy−2 | Quadratic parameter in LQ model. | Eq. (3) |
| α/β | Gy | Ratio of alpha over beta. | Eqs. (5)–(11) |
| λd | h−1 | Rate constant for exponentially decreasing dose rate. | (14) |
| λi | h−1 | Rate constant for exponentially increasing dose rate. | (14) |
MATERIALS AND METHODS
Cell Cultures
Triple-negative human breast cancer MDA-MB-231 cells and Chinese hamster V79 cells were maintained as monolayers in 75 cm2 culture flasks (Corning Life Sciences, New York) at 37°C and 5% CO2/95% air. The latter cell line was used to establish the approach with a cell line for which there are extensive data on dose-rate effects (chronic constant and exponentially decreasing) in the literature, including from our laboratory (5, 23). Both cell lines were cultured in minimum essential medium (Cellgro). The medium was supplemented with heat-inactivated 10% fetal calf serum (Life Technologies), 2 mM l-glutamine (Cellgro), 50 units/mL of penicillin per milliliter, 50 µg/mL streptomycin (Cellgro) and 5 mL nonessential amino acid concentrate (Cellgro) per 500 mL medium (MDA-MB-231). Cells were used for experiments at passages 3–7 and at 70–90% confluence.
Irradiation Procedure and Colony Forming Assay
Corning 25 cm2 culture flasks containing 5 mL of culture medium were seeded in triplicate with either 3.0 × 102, 3.0 × 103 or 3.0 × 104 cells from a single-cell suspension and incubated at 37°C, 5% CO2/95% air, for 4 h to allow cells to attach to flasks. Flasks were then capped tightly and transferred to a custom 137Cs gamma irradiator maintained at 37°C as described in Pasternack et al. (24). Triplicate flasks were placed at different distances from the 137Cs source (Fig. 2) and irradiated chronically with 662 keV γ rays with different dose-rates patterns (Fig. 3); the irradiation was terminated after 168 h. Dose-rate profiles for the position closest to the source are given in Fig. 3, and dose-rate profiles for all positions are given in Supplementary Fig. S1 (http://dx.doi.org/10.1667/RR14766.1.S1). The dose rates received by the cells were calibrated as described below. After the 168 h irradiation period, the cell colonies were washed with phosphate buffered saline, fixed with ethanol, stained with crystal violet, and counted (colonies consist of >50 cells). The surviving fractions relative to controls were then calculated. Due to the longer doubling time of the human MDA-MB-231 cells, the irradiated flasks were placed in a 37°C incubator for an additional 168 h to allow for further growth of the colonies. Additional flasks were similarly prepared with cells and irradiated for cell cycle analysis studies as described below.
FIG. 2.
Photograph of the cabinet 137Cs irradiator showing the position of the cell culture flasks that were irradiated with exponentially increasing and decreasing dose rates. The desired dose-rate pattern is achieved by varying the level of mercury in the attenuator (24). Each layer of flasks receives successively lower extrapolated initial dose rates as the distance from the 137Cs source increases, however the dose rate increase and decrease half times are the same at each position.
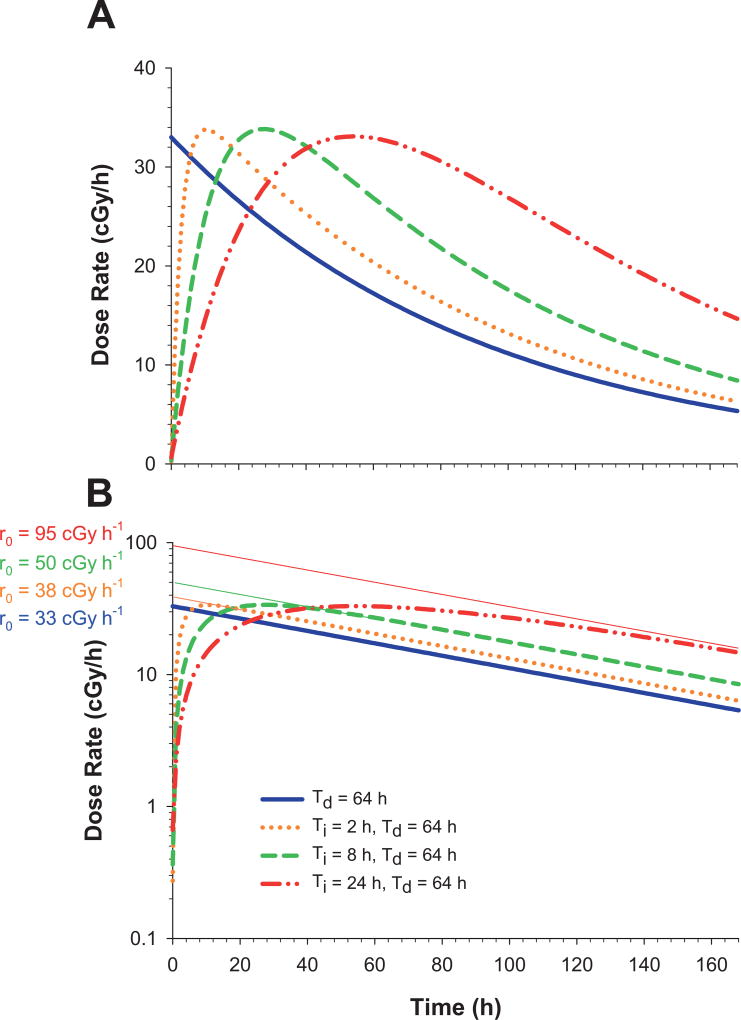
FIG. 3.
Panel A: Experimental dose-rate patterns used to irradiate the cells. Different dose rate increase half-times (Ti = 0, 2, 8 and 24 h) and a fixed dose rate decrease half-time (Td = 64 h) were used. These profiles correspond to those delivered to the flasks in the top position for each Ti; the maximum dose rate achieved decreases with increasing distance of the flask from the 137Cs γ-ray source (see Supplemental Fig. S1; http://dx.doi.org/10.1667/RR14766.1.S1). Panel B: Extrapolated initial dose rates (r0) are depicted by replotting panel A with the abscissa on a log scale; the r0 values correspond to those in shown in Table 2.
In separate experiments using acute irradiation, flasks were similarly seeded with cells, incubated for 4 h, capped tightly and irradiated at a constant dose rate (2.6 Gy/min) for several minutes with 0–12 Gy γ rays (JL Shepherd Mark I irradiator, San Fernando, CA). The flasks with V79 and MDA-MB-231 cells were then incubated for 168 and 336 h, respectively.
It should be noted that the relative biological effectiveness of the 662 keV γ rays delivered by the 137Cs irradiators may differ somewhat from the energetic beta particles emitted by radionuclides relevant to therapeutic nuclear medicine (e.g., 90Y, 131I 32P, 186Re). However, these differences are expected to be very small provided that the radionuclide is not incorporated into nuclear DNA (25, 26).
Dose-Rate Profiles
The dose rate was varied in a manner commensurate with the temporal pattern that would arise as a consequence of an organ or tissue that receives a self-dose from a radiopharmaceutical. In this scenario, the dose rate increase half-time and dose rate decrease half-time are equal to the effective uptake half-time and effective clearance half-time of the radiopharmaceutical. As described by Howell et al. (11), these in turn are dictated by the biological uptake and clearance half-times of the radiopharmaceutical and the physical half-life of the radionuclide. Accordingly, dose-rate profiles in the present experiments were varied by changing the extrapolated initial dose rate (ro), dose rate increase half-time (Ti), and dose rate decrease half-time (Td) (11, 14). The extrapolated initial dose rates depended on where the flasks were placed below the source, whereas Ti and Td were the same for all positions. Extrapolated initial dose rates corresponding to the position closest to the source are depicted in Fig. 3B. The dose rate r(t) and the absorbed dose D(t) delivered at time t after initiating irradiation are described elsewhere (11, 14):
| (1) |
| (2) |
where 0 ≤ a ≤ 1 and 0 ≤ b ≤ 1, r0 is the initial dose rate (when b = 0) or extrapolated initial dose rate (when b ≠ 0), Td is the dose rate decrease half-time, and Ti is the dose rate increase half-time. A monoexponentially decreasing dose rate was achieved by setting a = 1, b = 0, Ti = 0 and Td = 64 h. The Td = 64 h is equal to the physical half-life of the beta-particle emitter 90Y and therefore this scenario could represent instantaneous uptake of an 90Y-labeled drug that is not cleared biologically (e.g., Theraspheres®). The Td = 64 h can also represent the 50–100 h effective clearance half-times in tumors of patients administered 131I-tositumomab [(27) and personal communication with the authors]. Exponentially increasing dose rates followed by exponentially decreasing dose rates were achieved by setting a = 1, b = 0.993, Ti = 2, 8 or 24 h and Td = 64 h. The coefficient b = 0.993 is required because of the nonzero dose rate at t = 0 which arises due to the finite thickness of the variable attenuator in the irradiator (24). These dose rate increase half-times are representative of effective uptake half-times measured in the tumors of patients administered 131I-labeled antibodies (27–30). Thus, our use of Ti = 0–24 h represents much of the range of half-times that could be observed clinically.
Calibration of Extrapolated Initial Dose Rates
The RadNuc irradiator software was designed to irradiate a single sample and therefore only provides a calibrated extrapolated initial dose rate (ro) value for a single position in the irradiator (24). Details of the calibration of this software/irradiator are provided elsewhere (24). It was necessary to determine r0 for all positions at which cell culture flasks were placed from the top of the irradiator chamber. The r0 for each position was then obtained using a trial and error approach wherein the dose rate increase and decrease half-times were entered into the RadNuc software, and then the r0 was changed until the desired distance values were found. This is because the RadNuc software provides calibrated r0 values when no flasks are present (24). Accordingly, attenuation corrections for the presence of flasks are necessary to know the precise extrapolated initial dose rate and absorbed dose at each position.
Attenuation corrections were determined by first placing several pieces of pre-calibrated GAFchromic film on the bottom of each flask that was loaded with 5 mL of culture medium. The flasks were irradiated at constant dose rate for 24 h and the absorbed doses were recorded by the GAFchromic films at several flask positions. Replicate measurements were averaged and the ratios of the absorbed doses at each flask position relative to the absorbed dose received by the top flask positioned closest to the 137Cs source (102 mm from top of irradiator chamber) were determined. These ratios, derived from GAFchromic film measurements, are a consequence of attenuation by the flasks and distance from the source. To isolate the attenuation correction from the effect of distance on the extrapolated initial dose rate, the ratio of the measured GAF chromic doses divided by the ratio of the calibrated extrapolated initial dose rates from RADNuc (r0,calibrated) was calculated for each flask position:
where x is the distance from the top of the irradiator chamber (x = 102 mm refers to the top flask which receives the highest r0). A plot of the attenuation ratio versus the number of flasks was generated to determine μflask, the attenuation constant for a flask containing 5 mL of cell growth medium (Supplementary Fig. S2; http://dx.doi.org/10.1667/RR14766.1.S1). The constant μflask was found to be 0.013 flasks−1. The corrected absorbed dose and extrapolated initial dose rate were found at each position for each dosing pattern (Supplementary Materials; http://dx.doi.org/10.1667/RR14766.1.S2)
Radiobiological Models
Linear quadratic model
The linear-quadratic (LQ) model is commonly used to describe the radiobiological response of irradiated cell populations. The surviving fraction (SF) of cells as a function of absorbed dose (D) is given by
| (3) |
where α and β are the LQ parameters.
Biologically effective dose
The BED is defined as
| (4) |
where RE is the relative effectiveness of the irradiation regimen. In the case of acute irradiation with a single fraction, RE is given by:
| (5) |
The RE for incomplete decay (i.e., less than 10 half-times) derived by Dale to account for DNA repair, was used to calculate BED for the exponentially decreasing dose rates corresponding to the cell survival data for Ti = 0, Td = 64 h (13).
| (6) |
where r0 is the initial dose rate, μ is the rate constant for exponential sublethal DNA damage repair with first order kinetics (0.46 h−1 for V-79 cells and 0.23 h−1 for MDA-MB-231 cells) (15, 31, 32), and λd (Td = ln(2)/λd) is the rate constant for an exponentially decreasing dose rate, and t is the time over which irradiation takes place. Using Eq. (6) and t =168 h, the RE and BED were calculated for each datum of the Td = 64 h data set using their respective initial dose rates r0. Similarly, the RE and BED were calculated for each datum point obtained for the acutely irradiated cells.
Howell et al. derived the RE for an exponentially increasing dose rate followed by an exponentially decreasing dose rate (14),
| (7) |
where , and Tμ is equal to the DNA repair half-time for monoexponential repair kinetics. Konijnenberg, Baechler et al. and Hobbs et al. have written RE in terms of the Lea-Catcheside G-factor (17–19):
| (8) |
By substituting Eq. (7) into Eq. (8) we solve for G at time t for the regimen with exponentially increasing and decreasing dose rates:
| (9) |
where D(t) is the absorbed dose accumulated over the exposure time t. In the present experiments, t = 168 h, the time period that the cells were irradiated.
Equieffective dose
The International Commission on Radiation Units and Measurements has defined the equieffective dose, EQDX, as “the total absorbed dose delivered by the reference treatment plan (fraction size X) that leads to the same biological effect as a test treatment plan that is conducted with absorbed dose per fraction d and total absorbed dose D according to a relation adapted from the Withers formula” (33). The equieffective dose for an acute irradiation where the absorbed dose is delivered in a single fraction and if the reference treatment is taken as 2 Gy fractions is given by:
| (10) |
As described elsewhere (1) and by Hobbs et al. (3), EQD2α/β for regimens involving low-dose rates can be written as:
| (11) |
EQD2α/β was calculated for each datum point using Eqs. (10) and (11).
Proliferation
BED models have also been developed that include a proliferation term. Proliferation is a critical consideration when considering the effectiveness of targeted radionuclide therapy. For a tumor to be eradicated, cells must lose their reproductive integrity. This can occur via mitotic death or apoptosis (34). If the dose-rate is so low that the rate of cell killing is lower than the rate of clonogenic potential, then any dose delivered at this dose rate, irrespective of its magnitude, is ineffective. This could have occurred with the dose-rate profiles used in the present experiments. Dale and Ling created models to account for proliferation of the cell population (35, 36). These are summarized in the accompanying Supplementary Materials (http://dx.doi.org/10.1667/RR14766.1.S2). Clonogenic production is relevant for every dosing pattern, however it is especially relevant for Ti = 24 h, Td = 64 h considering the doubling time of V79 cells is 12–14 h and MDA-MB-231 is about 24 h.
Integration of dose rate to obtain absorbed dose
It is important to note that most BED and EQD2α/β equations for exponential dose rates are given in the literature for the limiting case where time is integrated to infinity, signifying complete decay of the source. While this does occur in the case of targeted radionuclide therapy, the current study was stopped after 168 h. At this time, approximately 80% of the absorbed dose for complete decay was delivered. The BED and EQD2α/β [Eqs. (4), (6), (7), (9) and (11)] are for incomplete decay as is appropriate for the present study. Factors that were considered in this choice were time to complete experiments, cell doubling time and growth of control colonies. Therefore, the calculations were done for a time course of 168 h.
Cell Cycle Analysis
Additional flasks were prepared with 4.0 × 104 V79 cells and irradiated chronically with exponentially increasing and decreasing dose rates (r0 = 50.5 cGy/h, Ti = 8 h, Td = 64 h; r0 = 95.0 cGy/h, Ti = 24 h, Td = 64 h). Flasks were removed during the chronic irradiation process at t = 0, 8, 24 and 48 h after the beginning of irradiation, along with its corresponding unirradiated control. The total doses received by cells would have been 33.2 and 41.0 Gy for the Ti = 8 h and Ti = 24 h irradiation protocols, respectively, if irradiation was allowed to continue for 168 h. Cells were harvested with 0.75 mL trypsin and washed with cold PBS. Cells were fixed with 95% alcohol that was added drop wise while vortexing the cells, rested at −20°C for 5 h and stained with propidium iodide. Cells were subjected to flow cytometry (LSR II, Becton Dickinson) and analyzed for DNA content with manual analysis within ModFitLT V3.1 PMac (Verity House Software).
RESULTS
Cell Cycle Analysis and Cell Survival
Cell cycle analysis
The percentage of V79 cells in each phase of the cell cycle at different time points while being irradiated with Ti = 8 or 24 h and Td = 64 h, along with their corresponding controls, can be found in Supplementary Fig. S3 (http://dx.doi.org/10.1667/RR14766.1.S1). The irradiated populations demonstrated an increased proportion of cells in G2 relative to controls, and a decreased proportion of cells in G1 relative to controls, as a function of time after initiating the irradiation protocols. It is worth noting that the proportion of cells in S phase fluctuates over time in all cases, however the percentages for irradiated cells and unirradiated controls remains similar.
Surviving fraction vs. absorbed dose
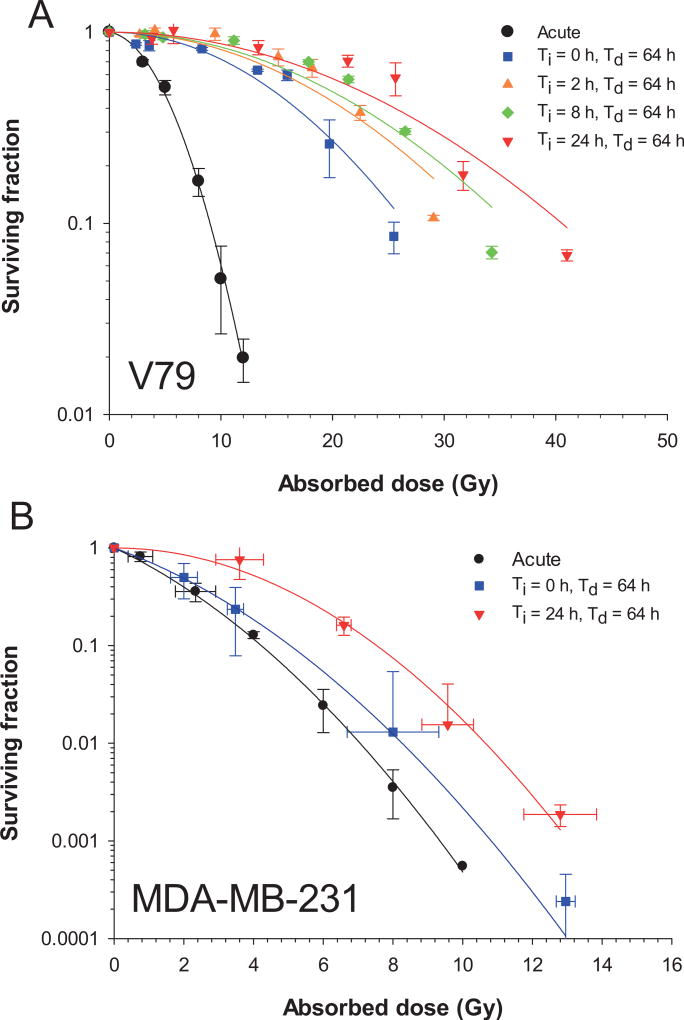
The surviving fractions of cells after irradiation with various dose-rate profiles are plotted as a function of absorbed dose in Fig. 4A for V79 cells and Fig. 4B for MDA-MB-231 cells. Data were nonlinearly least squares fitted to the LQ model [Eq. (3)] using the Levenberg-Marquardt fitting algorithm in SigmaPlot V12.5. The data points were weighted to 1/SF to obtain the best fit. The parameters used to deliver the experimental dose-rate patterns and the fitted LQ parameters for the survival curves that result from the irradiations are provided in Table 2. The α/β ratios for acute irradiation were 1.78 and 10.2 Gy for V79 and MDA-MB-231 cells, respectively, and were used for all subsequent radiobiological modeling.
FIG. 4.
Panel A: Surviving fraction of Chinese hamster V79 lung cells as a function of absorbed dose after irradiation with 662 keV γ rays. Error bars represent the standard deviation of the surviving fraction based on the average of two experiments each for acute irradiation and irradiation with exponentially increasing (Ti = 0, 2, 8, or 24 h) followed by exponentially decreasing dose rates (Td = 64 h). Solid lines represent least squares fitting to the data to the linear-quadratic model (Table 2). Panel B: Cell survival curves for irradiated MDA-MB-231 human breast cancer cells. Flask positions were changed between successive experiments to achieve the desired number of logs of kill thereby resulting in somewhat different absorbed doses. Accordingly, data clusters on a graph of SF versus absorbed dose were averaged, and standard deviations were calculated for both SF and absorbed dose. Curves represent least squares fitting to the data to the linear-quadratic model.
TABLE 2.
Irradiation Variables (r0, Ti, Td) and Fitted Linear-Quadratic Parameters (α, β) for Surviving Fraction of V79 and MDA-MB-231 Cells Irradiated with 137Cs γ Rays
| Dose-rate pattern | acute | exponential | chronic | chronic | chronic |
|---|---|---|---|---|---|
| Ti (h)* | 0 | 2 | 8 | 24 | |
| Td (h)† | 64 | 64 | 64 | 64 | |
| V79 Cells | |||||
| Maximum r0 (cGy h−1)‡ | 33 | 38 | 50.5 | 95 | |
| α (Gy−1) | 0.0396 | 0 | 0 | 0 | 0 |
| β (Gy−2) | 0.0222 | 0.0033 | 0.0021 | 0.0018 | 0.0014 |
| α/β (Gy) | 1.78 | ||||
| MDA-MB-231 Cells | |||||
| Maximum r0 (cGy h−1)‡ | 16.8 | 29.6 | |||
| α (Gy−1) | 0.386 | 0.2962 | 0 | ||
| β (Gy−2) | 0.0378 | 0.0316 | 0.0406 | ||
| α/β (Gy) | 10.2 | ||||
Ti = Dose rate increase half time.
Td = Dose rate decrease half time.
Maximum extrapolated initial dose rate corresponding to position closest to 137Cs source. Dose-rate profiles for the lower positions in the irradiator are given in Supplemental Fig. 1 (http://dx.doi.org/10.1667/RR14766.1.S1).
Modeling the Radiobiological Effect
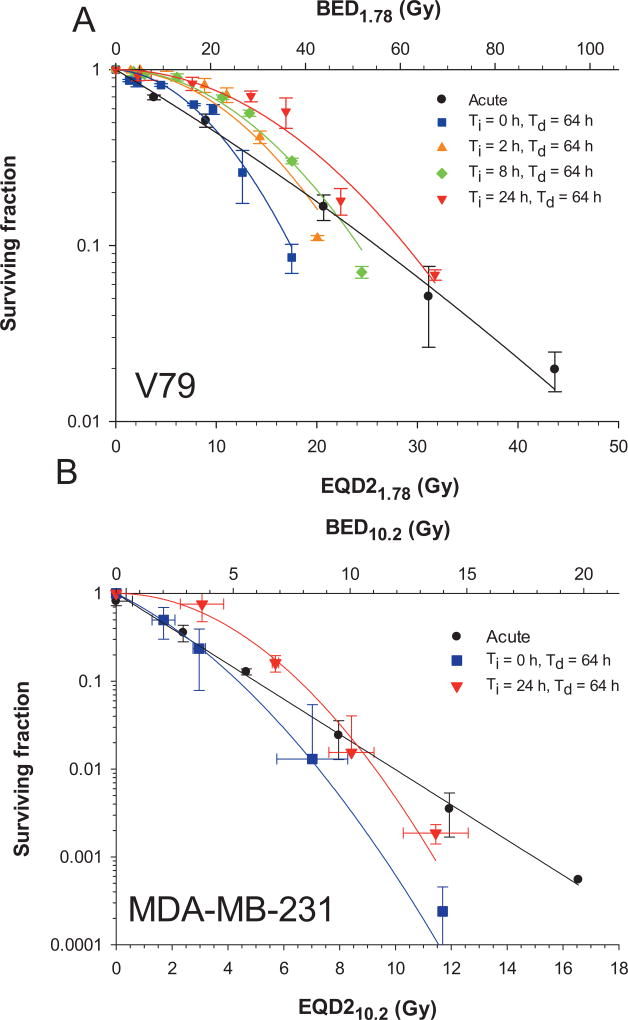
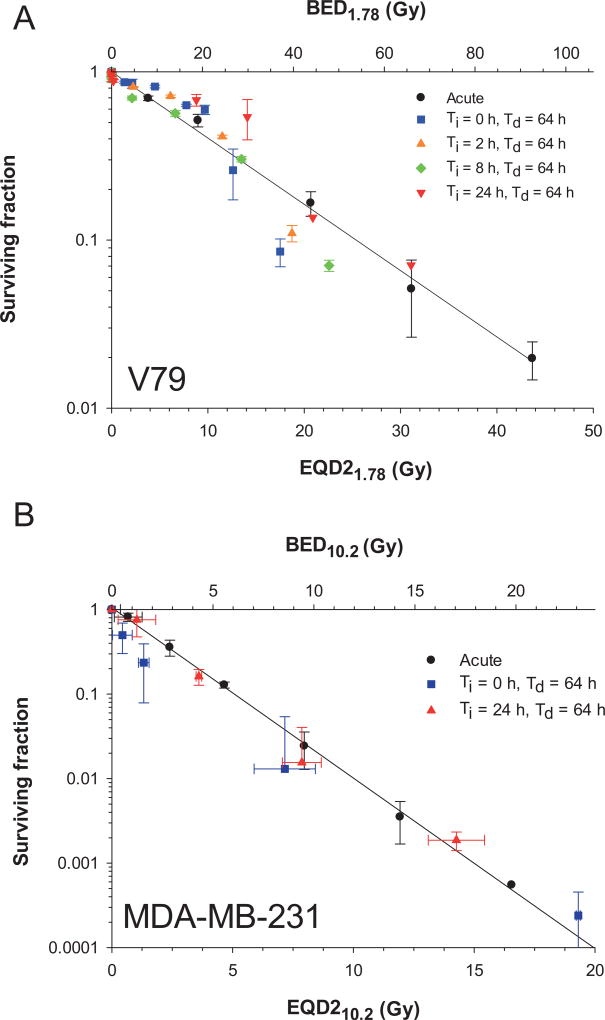
The mean absorbed dose for each datum point in Fig. 4 was used to calculate the corresponding EQD2α/β; the EQD2α/β values for acute irradiation were calculated using Eq. (10), whereas Eqs. (9) and (11) were used for exponential dose-rate patterns. BED was calculated using Eqs. (4) and (5) for acute irradiation, and Eqs. (4) and (7) for exponentially increasing and decreasing dose rates. The surviving fractions for both cell lines are plotted as a function of EQD2α/β and BED in Fig. 5.
FIG. 5.
Panel A: Surviving fraction of V79 cells as a function of EQD21.78 (lower ordinate) and BED1.78 (upper ordinate) after irradiation with 662 keV γ rays. Error bars represent the standard deviation of the surviving fraction based on the average of two or three experiments each for acute irradiation, and irradiation with exponentially increasing (Ti = 0, 2, 8 or 24 h) followed by exponentially decreasing dose rates (Td = 64 h). Panel B: Surviving fraction versus EQD210.2 (lower ordinate) and BED10.2 (upper ordinate) for MDA-MB-231 cells. The EQD2 values were calculated using Eq. (10) for acute irradiation (black line) and Eqs. (9) and (11) for the variable dose-rate patterns considered by Dale (13) and Howell et al. (14). The BED was calculated according to Eq. (7) for exponentially increasing and decreasing dose rates and Eq. (5) for acute irradiation (black line). Note that the data corresponding to the variable dose-rate conditions do not lie on the acute curves (black lines), therefore the Dale and Howell models do not adequately predict the response.
DISCUSSION
Dose-rate effects have long been a topic of importance to radiobiology (37). The published experimental studies on dose-rate effects have largely focused on constant or monoexponentially decreasing dose rates. However, the effect of more complex dose-rate patterns of relevance to those encountered in nuclear medicine is understudied (7). The current experiments demonstrate that exponentially increasing dose rates, which occur when radiopharmaceuticals are being taken up by organs and tissues, can have a profound effect on the radiotoxicity of subsequent exponentially decreasing dose rates, which occur after the maximum uptake of the radiopharmaceutical has taken place (Fig. 4). Specifically, our experimental data demonstrates that the dose rate increase half-time, Ti, plays a key role in reducing the lethal effects of the radiation insult and corroborates the theoretical considerations of Howell et al. (11) and Sefl et al. (22). As Ti increases, the shoulder of the survival curve flattens (i.e., α → 0) and, correspondingly, α/β → 0 (Fig. 4 and Table 2). As shown, absorbed dose does not adequately predict surviving fraction and other approaches must be considered to predict the lethality of the complex dose-rate patterns considered herein.
The quantities EQDXα/β and BED were developed with the goal of providing a means to correlate biological response to fractionated and other protracted irradiation protocols with a dose-related quantity. As described in the methods, the EQD2α/β and BED values were calculated for the present cell culture data using different published approaches depending on the irradiation conditions. In the case of acute irradiation with a single fraction, which serves as our standard, the calculated EQD21.78 values linearize the V79 cell survival data (Fig. 5A vs. Fig. 4A) (3). However, it is apparent that the calculated EQD21.78 values do not produce the expected straight-line dependence when the doses are delivered using complex dose-rate patterns including monoexponentially decreasing dose rate (Fig. 5A). The EQD21.78 values are overestimated for nearly all of the data points in a manner that depends on Ti and D. Whereas, in the case of high doses of exponentially decreasing dose rates the EQD21.78 values are underestimated (i.e., Fig. 5A, Ti = 0, Td = 64 h, EQD21.78 = 19 Gy). The same patterns emerge when the surviving fraction is plotted as a function of BED (Fig. 5A, upper ordinate). Furthermore, similar patterns emerge for MDA-MB-231 cells, albeit less dramatic (Fig. 5B).
It is apparent that the EQDX and BED calculations that use the approach of Dale for exponentially decreasing dose rates (13), and the approach of Howell et al. for more complex dose-rate patterns (14), do not produce equivalent EQD2α/β curves (Fig. 5). This is most apparent for the case of the MDA-MB-231 cells with the exponentially decreasing dose-rate pattern (Ti = 0, Td = 64 h). In other words, the approaches do not yield the same EQD2α/β for the same biological effect. Modifications to the EQD2α/β and BED equations are needed to correct for variables that are unaccounted for in the current model. Proliferation is an important consideration, but the BED proliferation model presented in the Supplementary Materials (http://dx.doi.org/10.1667/RR14766.1.S2) grossly overestimated the repopulation factors for V79 cells (RF = 210–245 Gy) and consequently yielded negative BED values. A problem with the repopulation model for the present application is that the subtractive term is constant across all r0 and Ti values. This is in keeping with a suggestion by Dale (13) that the repopulation factor may be an over-simplification. Similar problems arise when using other models (22, 36). Therefore, considerations other than proliferation are warranted.
There is ample data in the literature to suggest that adaptive responses may be playing a role in the cells’ resistance to the complex dose-rate profiles studied herein (Fig. 3). The survival curve shown in Fig. 4 appears to demonstrate some form of adaptive protection to the exponentially increasing dose rates as there was marked reduction in biological effect when the dose rate increase half-time was increased. Adaptive responses were originally shown in studies by Olivieri et al. by proving that low-level chronically irradiated human lymphocytes show fewer chromosome aberrations when followed by an acute insult of X rays (38). Adaptive responses were also demonstrated by Azzam et al. who investigated the phenomenon in the context of DNA damage and transformation related to the carcinogenic effects of X rays (39). Subsequently, adaptive responses for exponentially increasing dose rates have been demonstrated by de Toledo et al. in quiescent normal human fibroblasts exposed to γ rays (40). Buonanno et al. showed that pre-exposure of AG1522 cells to a low dose of low-LET protons protects against DNA damage caused by a subsequent exposure to high-LET energetic iron particles (41). In addition, protective effects against high-LET iron ions are propagated to neighboring nonirradiated cells. Thus, exponentially increasing dose rates of γ rays can initiate a cascade of intracellular and extracellular changes that make the tissue more resistant to subsequent exposure to radiation.
In light of the evidence for adaptive responses, one approach to converging the BED and EQD2α/β plots for the different dose-rate profiles is to develop an adaptive response function. After noting a hinge region shown in Fig. 5 where the curve fits for Ti ≠ 0 cross the curve fit for acute irradiation, we attempted a simple adaptive correction by taking the ratio of r0 over the maximum r0 for each Ti data set and found it to be remarkably good. Further analysis using the LQ fit parameters shown in Table 2 revealed that the r0 required to achieve a given surviving fraction depends linearly on Ti. Accordingly, we tested an empirical adaptive response correction factor to BED and EQD2α/β that is a ratio of r0 values wherein the denominator is the linear relationship:
| (12) |
where sref and r0,ref are the slope and intercept, respectfully of a linear fit of r0 vs. Ti at a reference surviving fraction (SFref).
| (13) |
| (14) |
The values of sref, r0,ref and SFref were obtained by an iterative process. First, the data shown in Table 2 were entered into a spreadsheet. A value of SFref was guessed and the corresponding values of D and r0 required to achieve that SFref were calculated for each Ti using the LQ model with the corresponding LQ parameters in Table 2. The calculated r0 values were then plotted as a function of Ti, fitted to a linear function, and the slope sref and intercept r0,ref determined. The values of sref and r0,ref were then substituted into Eq. (12). EQD2α/β was then calculated with Eq. (14) for each experimental data point shown in Fig. 4. The squares of the differences between the EQD2α/β values calculated with Eq. (14) and the EQD2α/β values calculated for the standard acute irradiation data were then summed. This entire process was automated using an Excel spreadsheet and repeated for different values of SFref until the sum was minimized. Minimization for the V79 data occurred at SFref = 0.21 which yielded sref = 0.020 Gy h−2 and r0,ref = 0.30 Gy h−1. In the case of MDA-MD-231 minimization was achieved at SFref = 0.014, which yielded sref = 0.0057 Gy h−2 and r0,ref = 0.10 Gy h−1. The resulting plots of SF vs. EQD2α/β and BED are shown in Fig. 6. This empirical adaptive response function accounts for the reduced biological effect at low-dose rates from the exponentially increasing dose rates that are followed by exponentially decreasing dose rates. Figure 6A and B show a dramatic improvement in linearization of the data for V79 cells and MDA-MB-231 cells, respectively. The difference in the slope sref for V79 and MDA-MB-231 cells suggests that the inherent ability of cells to adapt to exponentially increasing dose rate of γ rays depends on cell type. It is likely that there will be tumor cell lines that demonstrate a variety of adaptive behaviors, which is a reflection of individual variability in tumor response to ionizing radiation.
FIG. 6.
Panel A: Surviving fraction of V79 cells versus EQD21.78 (lower ordinate) and BED1.78 (upper ordinate) with the adaptive response function [Eq. (12)]. Error bars represent the standard deviation of the average surviving fraction obtained for two experiments of Ti = 24 h and Td = 64 h, Ti = 8 h and Td = 64 h, Ti = 2 h and Td = 64 h and Td = 64 h and acute dose. Panel B: Surviving fraction of MDA-MB-231 cells versus EQD210.2 (lower ordinate) and BED10.2 (upper ordinate) with the adaptive response function. The correction for adaptive response aligns the data for chronic irradiation more closely with the solid black line which represents the response to acute irradiation.
Admittedly, the mechanisms responsible for our observations are not elucidated in the current study. Gaining knowledge regarding the underlying molecular mechanisms responsible for adaptive responses seen in V79 and MDA-MB-231 cells may facilitate predicting a given cell population’s response to these dose-rate patterns. Wolff reviewed some of the mechanisms that have been proposed such as induction of new DNA repair enzymes, loss of a repressor in the irradiated cells, DNA DSB with either blunt or staggered ends as lesions that induce the adaptive response, etc. (42). The studies of Zhang et al. suggest that upregulation of the translationally controlled tumor protein (TCTP) may play a role in the observed adaptive responses (43). Further exploration of this phenomenon is warranted in other cell lines and animal models to determine whether it can be exploited in offering protection in the context of diagnostic nuclear medicine, or development of interventions in the context of therapeutic nuclear medicine. Among the considerations that should be explored are dose-rate patterns encountered with repeated administrations of radiopharmaceuticals and whether prior administrations affect the efficacy of subsequent administrations. In addition, these findings warrant further exploration of optimizing the physical half-life of the radionuclide to minimize normal tissue toxicity while maintaining therapeutic efficacy (11, 14).
Another consideration is the possibility that the observed resistance conferred by exponentially increasing dose rates is simply due to cell cycle redistribution within the irradiated cell population. It is generally accepted that cells in S-phase cell cycle are more radioresistant than in G1 and G2/M phases, with cells in G2/M phase being the most radiosensitive. Preferential accumulation of irradiated cells in a more resistant phase could explain increased survival seen in cells irradiated with Ti = 24 h compared to Ti = 8 h, 2 h and 0 h. According to Supplemental Fig. S3 (http://dx.doi.org/10.1667/RR14766.1.S1), the percentage of cells in S phase changes in time, but is always about the same for the Ti = 8 h and Ti = 24 h irradiation protocols. However, at t = 8 h after initiating irradiation, the Ti = 8 h population has about twice the percentage of cells in G2/M and half the percentage of cells in G1 compared to the Ti = 24 h population. The trend remains the same at t = 24 h, albeit to a smaller degree and they coalesce by t = 48 h. This increased prevalence of G2/M cells in the Ti = 8 h population compared to the Ti = 24 h population suggests that cell cycle effects may play some role in the differential response between the Ti = 8 h and Ti =24 h populations. It is interesting to note that the percentage of cells in G2/M is low among the unirradiated control population; this is the same distribution that is present when the cells were irradiated acutely.
Our calculations to this point have assumed exponential sublethal DNA damage repair with first order kinetics and rate constant μ of 0.46 h−1 for V-79 cells and 0.23 h−1 for MDA-MB-231 cells. To ascertain whether the inability of the LQ model (without adaptive correction) to predict the experimental data (Fig. 5) is simply related to uncertainty in μ, we recalculated EQD2 with μ values ranging from 0.1 to 5 h−1. In each case, the squares of the differences between the EQD2α/β values calculated with Eqs. (4) and (7) and the EQD2α/β values calculated for the standard acute irradiation data were summed. The difference was minimized when μ = 0.57 h−1 for V-79 cells, a value close to our assumed value of 0.46 h−1. However, no significant improvement was realized in the process. It is possible that use of more complex DNA repair models may improve the fit (44, 45).
Because of the chronic nature of the radiation, the present clonal cell survival studies are conducted by seeding flasks at low density with sufficient cells to form a countable number of colonies. Similar conditions were undertaken by Mitchell et al. who studied the effects of low-dose rates on V79 cells (23). Their clonal cell survival studies demonstrated pronounced dose-rate effects. They found that when cells were irradiated at constant dose rates of 55 cGy h−1, repair and cell division were the major factors affecting the surviving fraction. At 154 cGy h−1 cell division was blocked and cell cycle redistribution and repair dominated. Comparisons with the present data are complicated given that we delivered complex dose-rate patterns at dose rates even lower than 55 cGy h−1 (Fig. 2 and Supplemental Fig. S1; http://dx.doi.org/10.1667/RR14766.1.S1). Our experimental data and modeling suggest that repair and cell cycle redistribution may be involved but may not explain our observations entirely. Interestingly, fractionated high-dose-rate studies with 2 Gy/day halted mitotic entry in basal skin cells by day 3, whereas this is overcome weeks later after sufficient cell depletion and despite ongoing exposures of the same fraction size (46). These complexities point to the need for studying such effects in vivo over long terms. The current study only looks at shorter term effects in vitro and the increment in dose rate particularly, how the cell kinetic distribution can change and adaptive responses emerge. These may be quite different according to the cell type (normal or neoplastic) with and without check point control losses. In fact, if normal tissue responses are affected by dose rate increase half-time more substantially than neoplastic tissues, this could support the use of longer lived radionuclides in targeted therapies (11, 12, 14).
Adaptive responses have also been reported for high-LET radiations (47, 48) and modeling by Leonard (49) suggests that the alpha-particle data of Brooks supports adaptive behavior (50, 51). On the other hand, recent work indicates that alpha particles emitted by internalized 226Ra do not elicit an adaptive response (52). Therefore, more work is needed to determine whether the dose-rate patterns used in the current work elicit adaptive responses in the context of targeted radionuclide therapy with alpha-particle emitters.
Finally, it should be noted that there are other radiobiological dose-response models that have been advanced over the years. For example, the time dose fractionation (TDF) model was advanced and then modified for use in the context of nuclear medicine (53–55). It may be possible that these and other models (56) may be able to be adjusted to fit the needs of the complex dose-rate patterns encountered in nuclear medicine. Essential to the clinical implementation of these models is information regarding the uptake and clearance half-times in the tumor and normal tissues. Such data can be garnered on a patient-specific basis from imaging studies derived from SPECT/CT studies with the therapeutic ligand labeled with 111In or other suitable radionuclides, such as in the case of Zevalin® (57). These data, coupled with radiobiological models such as those presented here, could be used to guide the therapeutic administration.
CONCLUSIONS
The goal of targeted radionuclide therapy is to provide clinicians with the ability to deliver high radiation doses to micrometastatic disease while sparing normal tissues. It is critical to understand the radiobiological effects of the doses being delivered to the targeted and nontargeted tissues to ensure that optimal treatment plans are created. The current work characterizes the response of cells to complex dose-rate patterns encountered in nuclear medicine and demonstrates that the initial phase of the dose-rate pattern of low-LET radiation can have a profound impact on the biological effect of given radiation absorbed dose. Current models for calculating BED and EQD2α/β account for DNA repair but do not account for this apparent adaptive response. Here, an adaptive response function is advanced to more accurately calculate BED and EQD2α/β values for the exponentially increasing and decreasing dose rates of low-LET radiation encountered in targeted radionuclide therapies.
Supplementary Material
Acknowledgments
We would like to thank Yuni Dewaraja and Paul Roberson for providing tumor uptake and clearance half-times for patients. This work was supported in part by NCI grant no. R01 CA198073. Thanks to Harvey Ozer and Gwendolyn Mahon for supporting JS in the Cancer Summer Student Research Program, supported by NCI 5R25CA019536-32. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health (NIH).
References
- 1.Joiner M, Kogel Avd. Basic clinical radiobiology. 4. London: Hodder Arnold; 2009. p. 375. [Google Scholar]
- 2.Hall EJ, Brenner DJ. The dose-rate effect revisited: Radiobiological considerations of importance to radiotherapy. Int J Radiat Oncol Biol Phys. 1991;21:1403–14. doi: 10.1016/0360-3016(91)90314-t. [DOI] [PubMed] [Google Scholar]
- 3.Hobbs RF, Howell RW, Song H, Baechler S, Sgouros G. Redefining relative biological effectiveness in the context of the EQDX formalism: implications for alpha-particle emitter therapy. Radiat Res. 2014;181:90–8. doi: 10.1667/RR13483.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mazeron JJ, Scalliet P, Van Limbergen E, Lartigau E. Radiobiology of brachytherapy and the dose-rate effect. In: Gerbaulet A, Pötter R, Mazeron JJ, Meertens H, Van Limbergen E, editors. The GEC-ESTRO handbook of brachytherapy. Brussels: ESTRO; 2002. pp. 95–121. [Google Scholar]
- 5.Howell RW, Rao DV, Hou D-Y, Narra VR, Sastry KSR. The question of relative biological effectiveness and quality factor for Auger emitters incorporated into proliferating mammalian cells. Radiat Res. 1991;128:282–92. [PubMed] [Google Scholar]
- 6.Wong JYC, Williams LE, Demidecki AJ, Wessels BW, Yan XW. Radiobiologic studies comparing yttrium-90 irradiation and external beam irradiation in vitro. Int J Radiat Oncol Biol Phys. 1991;20:715–22. doi: 10.1016/0360-3016(91)90014-u. [DOI] [PubMed] [Google Scholar]
- 7.Behr TM, Memtsoudis S, Sharkey RM, Blumenthal RD, Dunn RM, Gratz S, et al. Experimental studies on the role of antibody fragments in cancer radio-immunotherapy: Influence of radiation dose and dose rate on toxicity and anti-tumor efficacy. Int J Cancer. 1998;77:787–95. doi: 10.1002/(sici)1097-0215(19980831)77:5<787::aid-ijc19>3.0.co;2-z. [DOI] [PubMed] [Google Scholar]
- 8.Rajon D, Bolch WE, Howell RW. Survival of tumor and normal cells upon targeting with electron-emitting radionuclides. Med Phys. 2013;40(1):014101. doi: 10.1118/1.4769409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Barendsen GW. Dose fractionation, dose rate and iso-effect relationships for normal tissue responses. Int J Radiat Oncol Biol Phys. 1982;8(11):1981–97. doi: 10.1016/0360-3016(82)90459-x. [DOI] [PubMed] [Google Scholar]
- 10.Fowler JF. The linear-quadratic formula and progress in fractionated radiotherapy. Br J Radiol. 1989;62:679–94. doi: 10.1259/0007-1285-62-740-679. [DOI] [PubMed] [Google Scholar]
- 11.Howell RW, Goddu SM, Rao DV. Application of the linear-quadratic model to radioimmunotherapy: Further support for the advantage of longer-lived radionuclides. J Nucl Med. 1994;35:1861–9. [PubMed] [Google Scholar]
- 12.Rao DV, Howell RW. Time dose fractionation in radioimmunotherapy: Implications for selecting radionuclides. J Nucl Med. 1993;34:1801–10. [PubMed] [Google Scholar]
- 13.Dale RG. Dose-rate effects in targeted radiotherapy. Phys Med Biol. 1996;41:1871–84. doi: 10.1088/0031-9155/41/10/001. [DOI] [PubMed] [Google Scholar]
- 14.Howell RW, Goddu SM, Rao DV. Proliferation and the advantage of longer-lived radionuclides in radioimmunotherapy. Med Phys. 1998;25:37–42. doi: 10.1118/1.598171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fowler JF. Radiobiological aspects of low dose rates in radioimmunotherapy. Int J Radiat Oncol Biol Phys. 1990;18:1261–9. doi: 10.1016/0360-3016(90)90467-x. [DOI] [PubMed] [Google Scholar]
- 16.O’Donoghue JA. Isoeffect relationships for fractionated biologically targeted radiotherapy. Radiother Oncol. 1990;19:257–65. doi: 10.1016/0167-8140(90)90152-m. [DOI] [PubMed] [Google Scholar]
- 17.Konijnenberg MW. Is the renal dosimetry for [90Y-DOTA0, Tyr3]octreotide accurate enough to predict thresholds for individual patients? Cancer Biother Radiopharm. 2003;18:619–25. doi: 10.1089/108497803322287718. [DOI] [PubMed] [Google Scholar]
- 18.Baechler S, Hobbs RF, Prideaux AR, Wahl RL, Sgouros G. Extension of the biological effective dose to the MIRD schema and possible implications in radionuclide therapy dosimetry. Med Phys. 2008;35:1123–34. doi: 10.1118/1.2836421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hobbs RF, Sgouros G. Calculation of the biological effective dose for piecewise defined dose-rate fits. Med Phys. 2009;36:904–7. doi: 10.1118/1.3070587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jones B, Dale RG. Mathematical models of tumour and normal tissue response. Acta Oncologica. 1999;38:883–93. doi: 10.1080/028418699432572. [DOI] [PubMed] [Google Scholar]
- 21.O’Donoghue JA. The impact of tumor cell proliferation in radioimmunotherapy. Cancer (Suppl) 1994;73(3):974–80. doi: 10.1002/1097-0142(19940201)73:3+<974::aid-cncr2820731333>3.0.co;2-i. [DOI] [PubMed] [Google Scholar]
- 22.Sefl M, Kyriakou I, Emfietzoglou D. Technical Note: Impact of cell repopulation and radionuclide uptake phase on cell survival. Med Phys. 2016;43(6):2715. doi: 10.1118/1.4948504. [DOI] [PubMed] [Google Scholar]
- 23.Mitchell JB, Bedord JS, Bailey SM. Dose-rate effects on the cell cycle and survival of S3 HeLa and V79 cells. Radiat Res. 1979;79:520–36. [PubMed] [Google Scholar]
- 24.Pasternack JB, Howell RW. RadNuc: a graphical user interface to deliver dose rate patterns encountered in nuclear medicine with a 137Cs irradiator. Nucl Med Biol. 2013;40:304–11. doi: 10.1016/j.nucmedbio.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Barendsen GW, Beusker TLJ, Vergroesen AJ, Budke L. Effects of different ionizing radiations on human cells in tissue culture II. Biological experiments. Radiat Res. 1960;13:841–9. [PubMed] [Google Scholar]
- 26.Neti PV, Howell RW. Isolating effects of microscopic nonuniform distributions of 131I on labeled and unlabeled cells. J Nucl Med. 2004;45:1050–8. [PMC free article] [PubMed] [Google Scholar]
- 27.Dewaraja YK, Schipper MJ, Roberson PL, Wilderman SJ, Amro H, Regan DD, et al. 131I-tositumomab radioimmunotherapy: initial tumor dose-response results using 3-dimensional dosimetry including radiobiologic modeling. J Nucl Med. 2010;51:1155–62. doi: 10.2967/jnumed.110.075176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Order SE, Klein JL, Ettinger D, Alderson P, Siegelman S, Leichner P. Phase I-II study of radiolabelled antibody integrated in the treatment of primary hepatic malignancies. Int J Radiat Oncol Biol Phys. 1980;6:703–10. doi: 10.1016/0360-3016(80)90226-6. [DOI] [PubMed] [Google Scholar]
- 29.Schipper MJ, Koral KF, Avram AM, Kaminski MS, Dewaraja YK. Prediction of therapy tumor-absorbed dose estimates in I-131 radioimmunotherapy using tracer data via a mixed-model fit to time activity. Cancer Biother Radiopharm. 2012;27:403–11. doi: 10.1089/cbr.2011.1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dewaraja YK, Ljungberg M, Green AJ, Zanzonico PB, Frey EC, Committee SM, et al. MIRD pamphlet No. 24: Guidelines for quantitative 131I SPECT in dosimetry applications. J Nucl Med. 2013;54:2182–8. doi: 10.2967/jnumed.113.122390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dale RG. The application of the linear-quadratic dose-effect equation to fractionated and protracted radiotherapy. Br J Radiol. 1985;58:515–28. doi: 10.1259/0007-1285-58-690-515. [DOI] [PubMed] [Google Scholar]
- 32.Salem SD, Abou-Tarboush FM, Saeed NM, Al-Qadasi WD, Farah MA, Al-Buhairi M, et al. Involvement of p53 in gemcitabine mediated cytotoxicity and radiosensitivity in breast cancer cell lines. Gene. 2012;498:300–7. doi: 10.1016/j.gene.2012.01.099. [DOI] [PubMed] [Google Scholar]
- 33.Bentzen SM, Dorr W, Gahbauer R, Howell RW, Joiner MC, Jones B, et al. Bioeffect modeling and equieffective dose concepts in radiation oncology - Terminology, quantities and units. Radiother Oncol. 2012;105:266–8. doi: 10.1016/j.radonc.2012.10.006. [DOI] [PubMed] [Google Scholar]
- 34.Hall EJ. Radiobiology for the Radiologist. 5. Philadelphia: JB: Lippincott Co.; 2000. [Google Scholar]
- 35.Dale RG. Radiobiological assessment of permanent implants using tumour repopulation factors in the linear-quadratic model. Br J Radiol. 1989;62:241–4. doi: 10.1259/0007-1285-62-735-241. [DOI] [PubMed] [Google Scholar]
- 36.Ling CC. Permanent implants using Au-198, Pd-103 and I-125: Radiobiological considerations based on the linear quadratic model. Int J Radiat Oncol Biol Phys. 1992;23:81–7. doi: 10.1016/0360-3016(92)90546-t. [DOI] [PubMed] [Google Scholar]
- 37.NCRP. Influence of Dose and its Distribution in Time on Dose-response Relationships for Low-LET Radiations. Bethesda: National Council on Radiation Protection and Measurements; 1980. Apr 1, 1980. Report No. 64. [Google Scholar]
- 38.Olivieri G, Bodycote J, Wolff S. Adaptive response of human lymphocytes to low concentrations of radioactive thymidine. Science. 1984;223:594–7. doi: 10.1126/science.6695170. [DOI] [PubMed] [Google Scholar]
- 39.Azzam EI, Raaphorst GP, Mitchel RE. Radiation-induced adaptive response for protection against micronucleus formation and neoplastic transformation in C3H 10T1/2 mouse embryo cells. Radiat Res. 1994;138:S28–31. [PubMed] [Google Scholar]
- 40.de Toledo SM, Asaad N, Venkatachalam P, Li L, Howell RW, Spitz DR, et al. Adaptive responses to low-dose/low-dose-rate gamma rays in normal human fibroblasts: the role of growth architecture and oxidative metabolism. Radiat Res. 2006;166:849–57. doi: 10.1667/RR0640.1. [DOI] [PubMed] [Google Scholar]
- 41.Buonanno M, De Toledo SM, Howell RW, Azzam EI. Low-dose energetic protons induce adaptive and bystander effects that protect human cells against DNA damage caused by a subsequent exposure to energetic iron ions. J Radiat Res (Tokyo) 2015;56:502–8. doi: 10.1093/jrr/rrv005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wolff S. The adaptive response in radiobiology: evolving insights and implications. Environmental Health Perspectives. 1998;106:277–83. doi: 10.1289/ehp.98106s1277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhang J, de Toledo SM, Pandey BN, Guo G, Pain D, Li H, et al. Role of the translationally controlled tumor protein in DNA damage sensing and repair. Proc Natl Acad Sci U S A. 2012;109:E926–33. doi: 10.1073/pnas.1106300109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Thames HD. An ’incomplete-repair’ model for survival after fractionated and continuous irradiations. Int J Radiat Biol. 1985;47:319–39. doi: 10.1080/09553008514550461. [DOI] [PubMed] [Google Scholar]
- 45.Millar WT. Application of the linear-quadratic model with incomplete repair to radionuclide directed therapy. Br J Radiol. 64:242–51. doi: 10.1259/0007-1285-64-759-242. 199. [DOI] [PubMed] [Google Scholar]
- 46.Hopewell JW. The skin: its structure and response to ionizing radiation. Int J Radiat Biol. 1990;57:751–73. doi: 10.1080/09553009014550911. [DOI] [PubMed] [Google Scholar]
- 47.Marples B, Skov KA. Small doses of high-linear energy transfer radiation increase the radioresistance of Chinese hamster V79 cells to subsequent X irradiation. Radiat Res. 1996;146:382–7. [PubMed] [Google Scholar]
- 48.Vares G, Wang B, Tanaka K, Kakimoto A, Eguchi-Kasai K, Nenoi M. Mutagenic adaptive response to high-LET radiation in human lymphoblastoid cells exposed to X-rays. Mutation Res. 2011;706:46–52. doi: 10.1016/j.mrfmmm.2010.10.009. [DOI] [PubMed] [Google Scholar]
- 49.Leonard BE. A composite microdose Adaptive Response (AR) and Bystander Effect (BE) model-application to low LET and high LET AR and BE data. Int J Radiat Biol. 2008;84:681–701. doi: 10.1080/09553000802241820. [DOI] [PubMed] [Google Scholar]
- 50.Brooks AL, Khan MA, Duncan A, Buschbom RL, Jostes RF, Cross FT. Effectiveness of radon relative to acute 60Co gamma-rays for induction of micronuclei in vitro and in vivo. Int J Radiat Biol. 1994;66:801–8. [PubMed] [Google Scholar]
- 51.Brooks AL, Newton GJ, Shyr LJ, Seiler FA, Scott BR. The combined effects of alpha-particles and X-rays on cell killing and micronuclei induction in lung epithelial cells. Int J Radiat Biol. 1990;58:799–811. doi: 10.1080/09553009014552181. [DOI] [PubMed] [Google Scholar]
- 52.Shi X, Mothersill C, Seymour C. No adaptive response is induced by chronic low-dose radiation from Ra-226 in the CHSE/F fish embryonic cell line and the HaCaT human epithelial cell line. Environmental Res. 2016;151:537–46. doi: 10.1016/j.envres.2016.08.026. [DOI] [PubMed] [Google Scholar]
- 53.Bigler RE. Dosimetry for evaluation of the biologic effects of radiation treatment using internally deposited radionuclides and labeled compounds. In: Cloutier RJ, Coffey JL, Snyder WS, editors. Radiopharmaceutical Dosimetry Symposium. Rockville, MD: HEW Publication (FDA) 76-8044; 1976. pp. 221–9. [Google Scholar]
- 54.Rao DV, Howell RW. On the modeling of the tumor uptake to determine the time-dose-fractionation (TDF) effect in radioimmunotherapy (reply to letter) J Nucl Med. 1994;35:1562–4. [PubMed] [Google Scholar]
- 55.Siegel JA, Stabin MG, Sharkey RM. Renal dosimetry: ready for biological effective dose? Cancer Biother Radiopharm. 2010;25:589–91. doi: 10.1089/cbr.2010.0851. [DOI] [PubMed] [Google Scholar]
- 56.Roberson PL, Wilderman SJ, Avram AM, Kaminski MS, Schipper MJ, Dewaraja YK. Biological-effect modeling of radioimmunotherapy for non-hodgkins lymphoma: determination of model parameters. Cancer Biother Radiopharm. 2014;29:26–33. doi: 10.1089/cbr.2012.1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Wiseman GA, White CA, Sparks RB, Erwin WD, Podoloff DA, Lamonica D, et al. Biodistribution and dosimetry results from a phase III prospectively randomized controlled trial of Zevalin radioimmunotherapy for low-grade, follicular, or transformed Bcell non-Hodgkin’s lymphoma. Crit Rev Oncol/Hematol. 2001;39:181–94. doi: 10.1016/s1040-8428(01)00107-x. [DOI] [PubMed] [Google Scholar]
- 58.ICRU. ICRU Report No. 85. Fundamental quantities and units for ionizing radiation. J ICRU. 2011;11:1–30. doi: 10.1093/jicru/ndr011. [DOI] [PubMed] [Google Scholar]
- 59.Lea DE, Catcheside DG. The mechanism of the induction by radiation of chromosome aberrations in tradescantia. J Genet. 1942;44:216–45. [Google Scholar]
- 60.Howell RW, Goddu SM, Rao DV. Design and performance characteristics of an experimental Cs-137 irradiator to simulate internal radionuclide dose rate patterns. J Nucl Med. 1997;38:727–31. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.