Geometrical frustration yields fiber formation in self-assembly

Abstract

Controlling the self-assembly of supramolecular structures is vital for living cells, and a central challenge for engineering at the nano- and microscales [1, 2]. Nevertheless, even particles without optimized shapes can robustly form well-defined morphologies. This is the case in numerous medical conditions where normally soluble proteins aggregate into fibers [3, 4]. Beyond the diversity of molecular mechanisms involved [5, 6], we propose that fibers generically arise from the aggregation of irregular particles with short-range interactions. Using a minimal model of ill-fitting, sticky particles, we demonstrate robust fiber formation for a variety of particle shapes and aggregation conditions. Geometrical frustration plays a crucial role in this process, and accounts for the range of parameters in which fibers form as well as for their metastable character.

Identical cubes can pack into dense space-filling aggregates, but most shapes do not. As a result, the aggregates formed by these shapes tend to be frustrated, giving rise to arrested, glassy states [7, 8]. In protein aggregates, this frustration can arise from, e.g., deformed or partially denatured protein domains, the juxtaposition of residues with unfavorable interactions or sterically hindered hydrogen bonding. The global morphology of compact packings of these objects thus involves a competition between geometrical constraints, which hinder the formation of compact aggregates, and the particles’ overall attractive interactions.

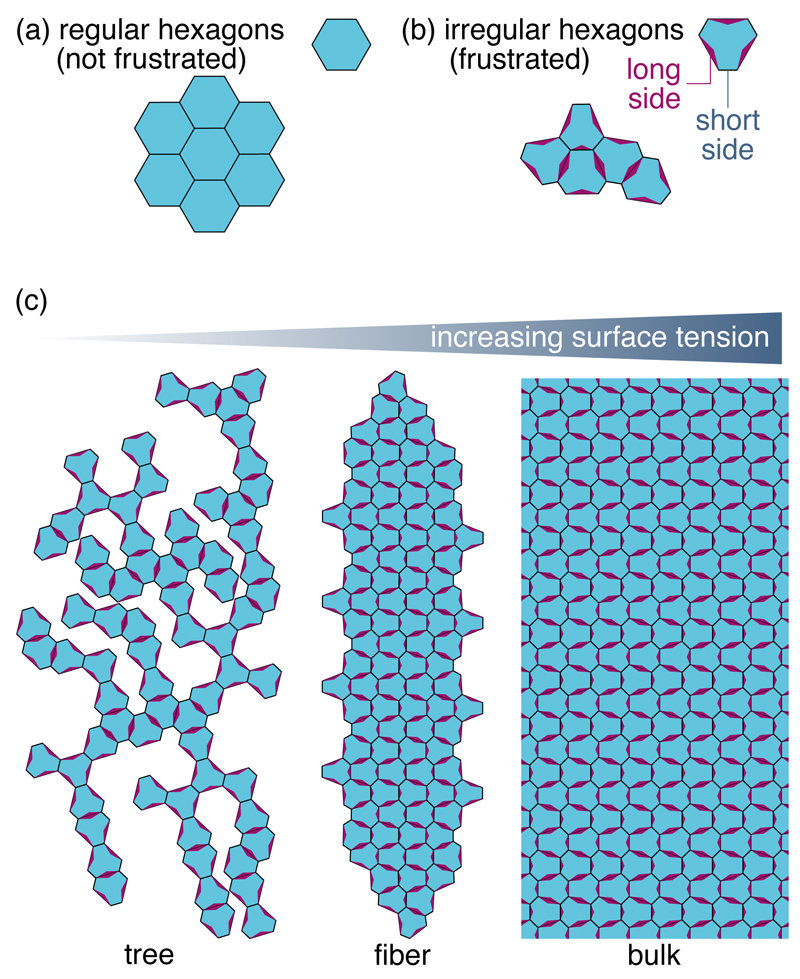
To explore this competition in its simplest form, we consider two-dimensional, deformable polygons driven to aggregate by zero-range attractive interactions [Fig. 1(a-b)]. We parametrize the magnitude of this attraction by a surface tension whose value controls the aggregate morphology [Fig. 1(c)]. A low surface tension thus favors thin tree-like aggregates composed of undeformed particles with very little elastic frustration, reminiscent of so-called empty liquids [9]. Conversely, a large surface tension leads to space-filling aggregates in which all particles are substantially deformed. In this paper, we demonstrate that fibers form at intermediate values of the tension, where the characteristic energies associated with particle attraction and deformation are comparable. We quantitatively account for these values based on the role of frustration, and show that fibers are very robust to changes in microscopic parameters, aggregation protocol and seeding conditions. Finally, we show that despite this robustness fibers do not constitute the ground state of our aggregates. Instead, they are kinetically trapped metastable states, consistent with their inherent frustration and with the well-documented irreversible character of protein fiber assembly in vivo.

Figure 1. Frustration and adhesion compete to determine the morphology of aggregates of mismatched particles.

(a) Polygonal particles with well-matched shapes (here regular hexagons) readily aggregate into space-filling two-dimensional aggregates. (b) Generic particles (e.g., irregular hexagons with long and short sides) must be distorted to form a compact aggregate, resulting in geometrical frustration. (c) At low surface tensions, frustration precludes the formation of compact polygon packings, yielding tree-like aggregates. Conversely, a large surface tension results in a bulk. Fibers constitute a compromise between these two extremes.

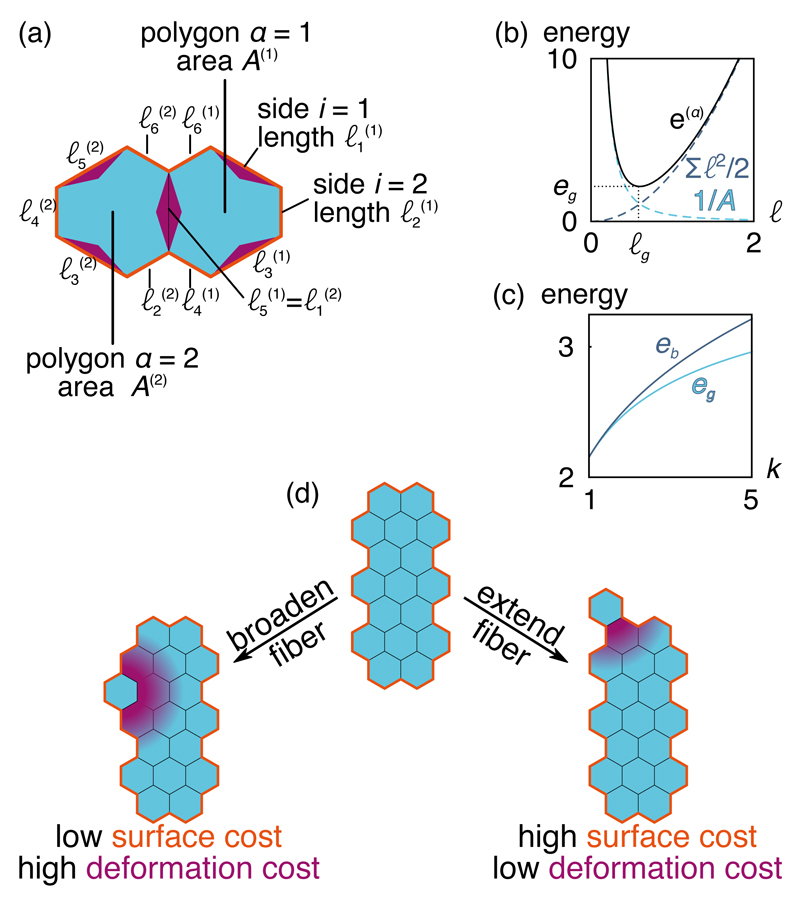
We consider n-sided polygons, and use a deformation energy e^(α) for the αth polygon that is a function of its area A^(α) and of the lengths ${\left\{l_i^{(\alpha )}\right\}}_{i=1\dots n}$ of its sides [Fig. 2(a)]. In the following we use both regular and irregular polygons [as in Fig. 1(b)], and characterize the latter by an asymmetry parameter k ≥ 1, where k → 1 is the regular polygon limit while k → +∞ yields short sides with vanishing rest length (see Methods). Minimizing the energy e^(α) with respect to the positions of the polygon’s vertices yields a rigid elastic ground state of energy e_g [Fig. 2(b)]. Aggregates are formed by connecting multiple polygons through the joining of one or several of their sides. Two joined sides are treated as a single object, implying that they share the same two end-vertices [Fig. 2(a)]. Side joining is favored by the adhesion energy between particles, modeled by an energy penalty σ > 0 for each unjoined side regardless of its actual length. Thus σ parametrizes the surface tension introduced in Fig. 1(c). However, side-joining also involves a distortion of the mismatched polygons, and thus increases their deformation energy above e_g.

Figure 2. Polygon model of aggregation.

Here we present hexagons with sides of alternating length characterized by an asymmetry parameter k > 1. (a) Two-hexagon aggregate with two joined sides and 10 unjoined sides outlined in orange. (b) Magnitude of the total energy e^(α) of a k = 1 regular hexagon of side ℓ. We also plot separately each of its two terms as defined in the Methods. The equilibrium side length ℓ_g and ground-state deformation energy e_g are shown. (c) Hexagons with alternating sides become increasingly frustrated as their asymmetry is increased (k ≠ 1), as evidenced by the increasing gap between the energies of the ground state (e_g) and the bulk [e_b, corresponding to the bulk topology of Fig. 1(c)]. This frustration eventually decreases at high k as the hexagon bulk goes to a triangular lattice (see Supplementary information). (d) Two contrasting additions to an anisotropic aggregate: left, to a side flank that broadens the fiber, right, to the end of the fiber to extend it. The different energy costs are noted below each case, and illustrated on the figure by the orange line and the purple shading, respectively.

A tree such as the one of Fig. 1(c) is always in its elastic ground state. Its average energy per particle is entirely due to surface tension, and reads e ∼ (n − 2)σ in the large-system limit (see Methods). A large bulk, on the other hand, has a negligible surface energy but a finite deformation energy e ∼ e_b − e_g, where e_b denotes the minimal deformation energy for a polygon constrained by the bulk topology [Fig. 2(c)]. Rescaling the elastic energy and tension through ẽ(α) = [e^(α) − e_g]/(e_b − e_g) and σ̃ = (n − 2)σ/(e_b − e_g), we obtain ẽ = σ̃ for a tree and ẽ = 1 for a bulk. These rescaled energies make it clear that adhesion overcomes frustrations and trees become less stable than bulks at high tensions, with a transition at σ̃ = 1. As a result, if fibers indeed form as a result of the competition between these two effects, we expect them to appear for a dimensionless tension of order one.

To test this hypothesis, we simulate irreversible aggregation starting from a single polygon. Our algorithm mimics irreversible protein aggregation, where a particle binding to an existing aggregate does so in the most energetically favorable location without substantial rearrangements of the preexisting aggregate topology. Throughout this process the aggregate energy is always minimized with respect to all vertex positions, imposing force balance before the aggregate energy is assessed (see Methods). We first grow aggregates of 150 irregular hexagons. The unfrustrated k = 1 case simply yields the bulk of Fig. 1(a) up to very large values of σ. Next considering substantially frustrated hexagons with k = 2, we observe bulks at high tensions (σ̃ ≥ 2.4), while low tensions (σ̃ ≤ 2.0) yield irregular tree-like aggregates [Fig. 3(a)]. By contrast, periodic fibers form at intermediate tensions, and maintain perfect regularity to indefinitely large lengths (see Movie S1). While these fibers appear for σ̃ of order unity, they form closer to σ̃ = 2 than the expected σ̃ = 1, suggesting that fiber formation is not completely captured by the tentative equilibrium reasoning used to define σ̃. To confirm this, we extrapolate the specific energy of our periodic fibers to infinite lengths and compare them to that of the hexagon bulk shown in Figs. 1(c) and 4(a). As shown in Fig. 4(b), the fiber energy exceeds that of the bulk, implying that fibers are indeed out of equilibrium.

Figure 3. Aggregates resulting from our growth algorithm.

For all conditions probed (shown on figure), periodic fibers form at intermediate rescaled surface tension σ̃. Orange polygons represent the initial topology used to initiate the growth algorithm. Older polygons are colored in dark blue, while light blue denotes the most recent additions. The orange line outlines unjoined sides. Trees form at low tension, but superficially appear much more compact than the illustration of Fig. 1(c): this is because their many branches overlap each other, as can be seen from the convoluted, re-entrant orange aggregate boundary. Such self-overlaps are not penalized in our algorithm. Bulks form at high tensions. High-resolution images and movies of the growth process are shown in the Supplementary information.

Figure 4. Fiber energy and structure.

(a) Hexagon, pentagon and octagon bulk structures used to compute the bulk energy e_b—and thus the rescaled tension σ̃—with unit cells outlined in orange (see Methods). Their structures are inspired by aggregates grown under high tensions. The two octagon bulks have identical energies per particle; note that while their polygons superficially appear to have only six sides on the figure, they are actually octagons with two pairs of perfectly aligned sides appearing as longer sides. (b) The energy per particle of infinite fibers based on those shown in Fig. 3 is higher that of the bulk, implying that they are nonequilibrium structures. (c) Defects, i.e., four-coordinated and two-coordinated vertices, are apparent upon closer inspection of some fibers from Fig. 3 (arrows).

We rationalize fiber formation by contrasting the marginal cost of adding a polygon to the side or to the tip of a preexisting anisotropic aggregate [Fig. 2(d)]. Upon a side-addition, the new polygon is tucked into the existing structure, minimizing the surface energy cost associated with the addition. A tip-addition, on the other hand, hardly deforms the existing aggregate and thus implies a lower deformation cost. This difference in deformation cost is more dramatic for thicker aggregates, where a side-addition deforms a larger number of particles. As a result, for moderate surface tensions side-additions may be favorable for thinner aggregates but not for thicker ones, leading to the formation of finite-width fibers. As this argument specifically deals with marginal addition energies in sequential growth, it does not imply that fibers are global energy minima for the aggregate morphologies.

To confirm that our fibers are metastable aggregates, we next establish that they are unaffected by small perturbations in the growth pathway but change morphology if nucleated from a more stable phase. To test the first point, we modify our algorithm to successively add two polygons, then remove one. Similar to polygon addition, our polygon removal procedure minimizes the aggregate energy in a short-sighted fashion, allowing the relaxation of built-up stresses and thus lowering the aggregate energy. The whole procedure is then iterated until an aggregate of the desired size is obtained. As expected, fibers are essentially unaffected by this local change in protocol [Fig. 3(b)]. We next grow an aggregate from a nucleus of the bulk, inducing significant morphological changes as predicted [Fig. 3(c)]. The one-dimensional, periodic growth is however preserved, attesting to the robustness of the fiber-forming mechanism. Furthermore, seeding aggregates with fiber fragment results in morphologies identical to those of Fig. 3(a) (see Supplementary information).

Moving beyond the k = 2 hexagons considered above, Fig. 3(d-e) demonstrates that our description is valid for a broad range of k corresponding to variations of the frustration energy e_b − e_g by several orders of magnitude, from ≃ 7 × 10⁻⁶ for k = 1.01 to ≃ 2 × 10⁻¹ for k = 4. Despite these very substantial differences, the rescaled parameter σ̃ remains an excellent predictor of fiber formation. Finally, we move away from hexagons altogether in Fig. 3(f-g) and demonstrate fiber formation in regular pentagons and octagons, two further shapes that do not tile the plane and thus generate intrinsically frustrated aggregates. Despite very diverse internal fiber structures, the onset of fiber formation is again very well predicted by the criterion σ̃ ≃ 2.

Our results demonstrate that inherently frustrated aggregates of mismatched particles assume a richer range of morphologies than is found in well-matched objects. They moreover robustly form fibers when particle adhesion is commensurate with frustration, in strong contrast with the three-dimensional morphologies resulting from, e.g., the flocculation of simple spherical colloids. Our analysis suggests that slender aggregates result from a compromise between, on the one hand, the elastic incentive to place all particles in the vicinity of the boundary of the aggregate to relax their frustrated shapes, and on the other hand the tendency to form a compact aggregate that maximizes adhesion. This simple principle should also apply to three-dimensional objects, where the deformation cost illustrated in Fig. 2(d) is augmented by chirality effects, which favor one-dimensional twisted ribbons morphologies in colloidal assemblies [10]. Chirality moreover penalizes bulk aggregates in 3D [11, 12], which can lead to the formation of either fibers or sheets.

The currently dominant paradigm for frustration in soft matter equates shape incompatibility with a mismatch between an intrinsically curved Riemanian metric favored by the object and the flat metric of the embedding space [13–16]. At equilibrium, this mismatch is accommodated by introducing defects in the system [17] or by forming slender morphologies if defects are strongly penalized [12, 18–21]. While slender morphologies and topological defects both arise in our aggregates [see Fig. 4(c)], our fibers are distinctively out of equilibrium structures. They moreover arise irrespective of whether the intrinsic Gaussian curvature of their constitutive polygons is positive (for pentagons), negative (octagons), or zero (irregular hexagons), in contrast with existing Riemanian metric models.

Turning to pathological fiber formation, our results suggest that the distinctive fibrous morphologies of protein aggregates need not be due to a mere coincidental convergence of molecular mechanisms, but could instead result from generic physical principles. Indeed, while the formation of cross-β spines is often discussed as the defining feature of one important class of such fibers, namely amyloids [4], deviations from this specific molecular organization have been observed [22] and secondary interactions contribute significantly to their mechanics [23] and morphologies [24]. While our simple model does not incorporate important effects such as the stochasticity due to thermal agitation or the entropic stabilization of fibers through their vibrational modes, these basic features are still consistent with the diverse morphologies we obtain upon small variations of our parameters, and could apply to protein fibers with radically different structures [3]. Beyond biological materials, fiber formation upon aggregation could become a hallmark of self-assembled, frustrated matter, leading to new design principles taking advantage of increasingly sophisticated artificial asymmetrical building blocks at the nano- and micro-scale [25, 26].

Methods

Expression of the aggregate energy

The deformation energy for the αth polygon is a function of its area A^(α) and of the lengths ${\left\{l_i^{(\alpha )}\right\}}_{i=1\dots n}$ of its sides through

$$e^{(\alpha )}=\frac{1}{A^{(\alpha )}}+{\displaystyle \sum _{i=1}^n\frac{k_i}{2}{\left[l_i^{(\alpha )}\right]}^2,}$$ (1)

where n is the number of sides of the polygon. In this expression, the tendency to extend the area of the polygon due to the first term is counteracted by the harmonic restoring forces due to the second term [Fig. 2(b)]. The elastic ground state of energy e_g discussed in the text is obtained by minimizing e^(α) with respect to the positions of the polygon’s vertices. Ground state polygons are rigid, i.e., devoid of internal soft modes due to the prestress inherent to Eq. (1) [27]. The irregularity of this ground state can be continuously tuned through the choice of the spring constants k_i, and regular polygons are obtained when they are all identical. The alternating-side polygons presented in Figs. 1(b) and 2(a) and used throughout have k₁ = k₃ = k₅ = 1 (long sides, marked by pink tabs) and k₂ = k₄ = k₆ = k > 1 (short sides, unmarked), which defines the asymmetry parameter k. Throughout this work we concentrate on the domain k ≥ 1 without loss of generality. Indeed our problem is invariant under the transformation k → 1/k by way of a proper rescaling of lengths and energies, and thus the aggregation process at any k ∈ (0, 1) can be inferred from the appropriate k ∈ (1, ∞). While the specific form of the energy Eq. (1) is chosen for numerical convenience, its precise expression does not strongly influence our results.

Multiple polygons can be connected through the joining of one or several of their sides. Two joined sides are treated as a single object, implying that they share the same two endvertices [Fig. 2(a)]. We refer to the specification of all such junctions as the topology $\mathit{𝒯}$ of the aggregate. The specification of a $\mathit{𝒯}$ constrains the aggregate shape, and thus tends to increase the deformation energy e^(α) of each polygon above e_g. In this paper, we consider aggregates whose energies are minimal with respect to the position of their vertices for a given $\mathit{𝒯}$, and denote by $e_{𝒯}^{(\alpha )}$ the deformation energy of particle α in this state of mechanical force balance. We denote by N_u($\mathit{𝒯}$) the number of unjoined sides in topology $\mathit{𝒯}$ ; for instance N_u = 10 in Fig. 2(a), as indicated by the orange lines. Imposing the surface tension energy penalty σ > 0 to each unjoined side regardless of its actual length, the total energy of an aggregate comprising N polygons thus reads

$$E\left(\left\{k_i\right\},\sigma ,𝒯\right)={\displaystyle \sum _{\alpha =1}^N\left[e_{𝒯}^{(\alpha )}-e_g\right]}+N_u\left(𝒯\right)\sigma .$$ (2)

The first term of the right-hand side of Eq. (2) describes the total deformation energy in excess of the ground state energy Ne_g, while the second term is the surface energy. Overall, E depends on the structure of the aggregate only through its topology $\mathit{𝒯}$. The average energy per particle discussed in the text is defined as e = E/N.

Surface energy for trees and bulks

We compute the surface energy of a tree comprising N polygons by noting that it has N_u = 2 + N (n − 2) unjoined sides. We demonstrate this by recursion over N, noting that N_u = n for N = 1. Each additional polygon adds n sides to the existing aggregate, n−1 of which are unjoined. The existing aggregate moreover loses one unjoined side to the connection with the new polygon. Thus N_u is incremented by n − 2 each time a new polygon is added to the tree, which proves our statement. The number of unjoined sides in a tree is thus proportional to its total number of polygons. As the number of unjoined sides in a two-dimensional bulk is proportional to $\sqrt{N},$ in the N → ∞ limit its surface energy is negligible compared to its nonzero elastic energy per particle.

Deformation energy for trees and bulks

The deformation energy of trees and bulks are computed by minimizing the energy Eq. (1) respectively with free boundary conditions or assuming the lattice structures illustrated in Fig. 4(a) for regular pentagons:

$$\begin{array}{cc}{e}_g=2\sqrt{2}{\left(5-2\sqrt{5}\right)}^{1/4},& e_b=\sqrt{6},\end{array}$$ (3)

regular octagons:

$$\begin{array}{cc}{e}_g=2\sqrt{2(\sqrt{2}-1)},& e_b=\frac{2^{3/2}}{5^{1/4}},\end{array}$$ (4)

and irregular hexagons:

$$\begin{array}{l}{e}_g=\frac{2\sqrt{2}}{3b+\sqrt{3a}}\{\sqrt{3}(k-2)a^2+2\sqrt{3}(k+1)a\\ {-3b\left[2a+\sqrt{3}kb-2(k+1)\right]\}}^{1/2},\\ e_b=\frac{2^{3/2}{k}^{1/4}}{3^{1/4}},\end{array}$$ (5)

with $a=\left(3-3k+\sqrt{1+14k+k^2}\right)/\left(4+4k\right)$ and $b=\sqrt{1-a^2}.$

Sequential aggregation algorithm

We use a deterministic algorithm that considers all possible options for the addition of a polygon onto an existing aggregate, some of which are illustrated in Supplementary Fig. S4. After minimizing the total energy of the whole aggregate with respect to the coordinates of all its vertices for each option (which induces the polygon distortions seen in the figure), it selects the option associated with the lowest total energy E and uses the result as the basis of the next polygon addition. Similar to kinetic, irreversible protein aggregation in vivo, this procedure thus does not necessarily achieve the most energetically favorable aggregate topology globally. Instead, our algorithm locally guarantees the best energetic choice at each addition step, allowing the formation of metastable aggregates characteristic of our frustrated interactions.