Ultrafast magnetization reversal by picosecond electrical pulses

Magnetic switching is induced in 10 ps by electrical current pulses.

Abstract

The field of spintronics involves the study of both spin and charge transport in solid-state devices. Ultrafast magnetism involves the use of femtosecond laser pulses to manipulate magnetic order on subpicosecond time scales. We unite these phenomena by using picosecond charge current pulses to rapidly excite conduction electrons in magnetic metals. We observe deterministic, repeatable ultrafast reversal of the magnetization of a GdFeCo thin film with a single sub–10-ps electrical pulse. The magnetization reverses in ~10 ps, which is more than one order of magnitude faster than any other electrically controlled magnetic switching, and demonstrates a fundamentally new electrical switching mechanism that does not require spin-polarized currents or spin-transfer/orbit torques. The energy density required for switching is low, projecting to only 4 fJ needed to switch a (20 nm)³ cell. This discovery introduces a new field of research into ultrafast charge current–driven spintronic phenomena and devices.

INTRODUCTION

Spintronic devices are promising candidates for future low-energy electronics that take advantage of the nonvolatility of nanoscale magnets (1). For example, magnetic random access memory (MRAM) is emerging as a universal integrated on-chip memory (2). Investigations into spintronic logic devices are also underway due to their potential for low-power computing (3–6). A significant obstacle that impedes the widespread adoption of spintronic devices is their speed. Spintronic mechanisms, such as spin-transfer torque (STT) or spin-orbit torque (SOT), can theoretically transfer angular momentum in the low-picosecond time scale and induce fast magnetization dynamics (7, 8). However, so far, the record switching time of spintronic devices is still on the order of hundreds of picoseconds (9–12). For comparison, silicon field-effect transistors have switching delays less than 5 ps (13). For spintronic technologies to challenge charge-based devices in information technologies, increases in the speed of operation are necessary.

Research over the past two decades in the field of ultrafast magnetism demonstrates that precessional speed limits for manipulating magnetic order can be broken if the electrons are excited on time scales that are faster than the electron-phonon relaxation time, that is, excited on picosecond or subpicosecond time scales (14). For example, the magnetization of a ferromagnetic thin film can be quenched within 300 fs upon irradiation by a 60 fs laser pulse (15). Furthermore, multiple studies have demonstrated the ability of single 100-fs laser pulses to deterministically and repetitively switch the magnetization of the ferrimagnetic metal GdFeCo on subpicosecond time scales (16–19), a phenomenon known as all-optical switching (AOS).

Although a unified description of AOS remains elusive (20–23), multiple theoretical and experimental studies suggest that ultrafast heating of the electronic system is the driving force for AOS in GdFeCo ferromagnetic materials (17–19). GdFeCo contains two distinct spin sublattices aligned antiparallel to each other with uncompensated magnetic moments. Both experiment (17) and theory (18) indicate that the distinct dynamics of the Gd and the FeCo sublattices enable ultrafast switching following ultrafast heating of the electrons. First, the magnetic sublattices undergo demagnetization at different rates after laser excitation. Then, angular momentum exchange between sublattices induces a transient ferromagnetic alignment of the two sublattices by flipping the FeCo spins. Last, reversal is achieved when the Gd sublattice flips, driven by the antiparallel exchange interaction with the FeCo sublattice (17).

Here, we take advantage of the physics responsible for AOS in GdFeCo to demonstrate a new regime of purely electrical ultrafast spintronics. Instead of optically exciting electrons, we use picosecond charge current pulses to excite the conduction electrons of a GdFeCo metal film. We observe repeatable ultrafast magnetization reversal in the GdFeCo film with single sub–10-ps electrical pulse excitation.

RESULTS

To generate picosecond electrical pulses, we fabricated picosecond photoconductive switches (24), in a gold coplanar stripline (CPS) geometry, on a “low temperature (LT)–grown” GaAs substrate (25). Figure 1A shows a schematic of the CPS device. The CPS is tapered from 50 to 5 μm, contacting on top of both sides of a patterned GdFeCo film, leaving a 4-μm by 5-μm uncovered GdFeCo section. By irradiating the dc-biased photoconductive switch with 60-fs laser pulses [full width at half maximum (FWHM)] at a wavelength of 810 nm, we can generate current pulses that have a duration of ~9 ps at FWHM and a current density as high as 10⁹ A/cm² through the GdFeCo section (Fig. 1B). Additional information on the sample fabrication and current pulse characterization is provided in Materials and Methods.

Fig. 1. Schematic of the CPS device and characterization of electrical pulse.

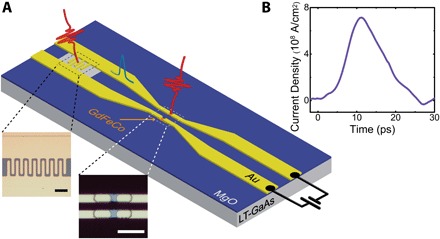
(A) Schematic of electrical switching experiment. The photoswitch is illuminated with laser pulses while being biased with a dc source. Magnetization dynamics of GdFeCo is monitored with time-resolved MOKE. Left: Optical image of the photoswitch. During laser illumination, photoexcited carriers in low-temperature GaAs conduct current across the gap, generating a transient electrical pulse propagating in both directions. Right: Optical image of the GdFeCo section of CPS. Scale bars, 20 μm. (B) Calculated temporal current density profile through the GdFeCo section, based on the temporal current profile measured with a Protemics Spike probe positioned 1 mm before the GdFeCo section.

In our experiments, we studied the magnetic response of a Ta (5 nm)/Gd₃₀Fe₆₃Co₇ (20 nm)/Pt (5 nm) multilayer. The film presented perpendicular magnetic anisotropy with a coercivity of 80 Oe at room temperature. The compensation temperature for this sample, that is, the temperature where the net moment is minimized in ferrimagnets, is ~270 K (fig. S1). Consistent with previous studies (17–19), as shown in the differential magneto-optic Kerr effect (MOKE) images of Fig. 2A, upon irradiation by a sequence of single laser pulses, the magnetization of the GdFeCo film toggles after each pulse. We checked the AOS ability at different laser pulse durations and found that the GdFeCo film switches with laser pulse durations between 60 fs (FWHM) and 10 ps, consistent with our previous work (19).

Fig. 2. Single-shot optical and electrical switching of GdFeCo.

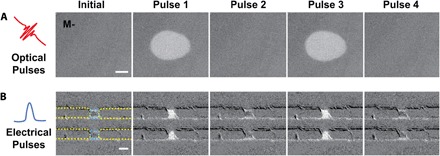
(A) Differential MOKE images of bare GdFeCo film after sequential 6.4-ps optical pulse irradiation. Absorbed fluence is 1.8 mJ/cm². After each optical pulse, the magnetization of GdFeCo toggles to the opposite direction. The contrast indicates change in magnetization. (B) Differential MOKE images of GdFeCo CPS section after sequential 9-ps electrical pulse excitation. After each electrical pulse, the magnetization of GdFeCo toggles. Yellow and blue dashed lines indicate gold CPS and GdFeCo sections, respectively. Scale bars, 5 μm.

We examined the response of the GdFeCo film to electrical pulses. Figure 2B shows the differential MOKE images of the device after a sequence of individual 9-ps electrical pulses with a peak current density of ~7 × 10⁸ A/cm² through the GdFeCo section. The magnetization of the GdFeCo section toggles after each electrical pulse, just as in the optical experiments.

We performed time-resolved MOKE measurements to temporally resolve the switching dynamics following the arrival of an electrical pulse. Figure 3 shows the magnetic dynamics that result from electrical pulses of different amplitude. For electrical pulses with an absorbed energy density less than 0.8 mJ/cm² in the GdFeCo section (with reference to the surface area), the MOKE signal (primarily indicative of the FeCo sublattice magnetization; see Materials and Methods) shows demagnetization within 20 ps, followed by a recovery to the initial magnetization state on longer time scales. With increased current pulse amplitude, the FeCo demagnetization is larger. For the electrical pulses with an absorbed energy density greater than 1.3 mJ/cm², the magnetic moment of the FeCo sublattice reverses within ~10 ps of the electrical pulse arrival at the GdFeCo film. Following reversal, the FeCo magnetization recovers rapidly toward the opposite direction. It reaches 70% of saturation within just 30 ps. We attribute the nonmonotonic evolution of the magnetization (for example, the decreasing of magnetization at ~40 ps) to the arrival of several low-amplitude electrical pulses that arise from reflections of the initial pulse from various electrical discontinuities in the CPS structure.

Fig. 3. Magnetization dynamics of GdFeCo after electrical excitations.

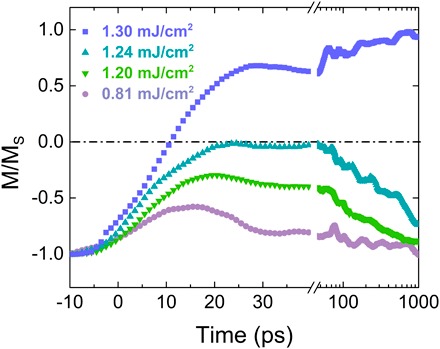
Electrical demagnetization and switching of GdFeCo. All fluences are calculated absorbed fluences. With increasing electrical pulse amplitude, the GdFeCo demagnetization amplitude increases and eventually switches around 10 ps.

DISCUSSION

The ability to induce magnetization reversal in GdFeCo by picosecond electrical heating demonstrates that exciting a nonthermal electron distribution is not necessary for magnetization reversal, consistent with previous studies (19, 26, 27). Electrical heating results in a large population of excited electrons with average energies less than 10 meV, whereas optical heating initially excites a much smaller number of electrons with electron volt–scale energies (28). The electrons always follow a Fermi-Dirac distribution under electrical heating and are considered “thermal.” On the other hand, upon optical excitation, there is a short period of time (~80 to 400 fs) when electrons do not follow a Fermi-Dirac distribution and are thus “nonthermal” (29). In both optical and electrical cases, electrons will thermalize with the lattice due to electron-phonon scattering, but the thermalization time will depend on the thermal versus nonthermal nature of the excitation (28, 30).

In addition to ultrafast heating, the electrical pulse will induce magnetization dynamics in two other ways: via the associated oersted field and via SOTs due to strong spin-orbit coupling in the Pt layer (31). The current density flowing through the Pt layer is estimated to be 2 × 10¹³ A/m² (Materials and Methods). If we assume that there is no magnetic anisotropy, then the fastest the magnetization can precess around the in-plane oersted field and cross M_z = 0 is within a quarter of a precession period (9). Using Ampere’s law, we estimate the oersted field to be of only 70 mT, corresponding to a quarter period of ~125 ps. Assuming that the precessional period does not change as the sample is heated, then, our 9-ps electrical pulses are too short to switch the magnetization.

Spin-orbit coupling in Pt leads to two different types of SOTs on the GdFeCo magnetization (32). These torques have orthogonal directions and are known as damping-like and field-like torques (32). We performed simulations (described in Materials and Methods) with the Landau-Lifshitz-Gilbert equation, including the SOT terms, where the Gd and FeCo macrospin moments are coupled via an exchange interaction. We modeled three different scenarios: The SOT is applied on the FeCo macrospin uniquely, on the Gd uniquely, or on both simultaneously. Our results show that the maximum change in the out-of-plane component of the magnetization due to SOT is less than 10%. From these calculations, we conclude that the toggling behavior of the GdFeCo magnetization is principally due to ultrafast heating of the electronic system and driven by physics similar to that responsible for AOS (17–19). Future work will further investigate the effects of ultrafast spin injection on the magnetization dynamics.

The ability to switch a magnetic metal, such as GdFeCo, with a single short electrical pulse has significant potential technological impact. For experimental convenience, we used an optoelectronic switch to generate picosecond electrical pulses; however, this is not necessary. It is currently possible to generate and deliver sub–10-ps current pulses on-chip in conventional complementary metal-oxide semiconductor (CMOS) electronics. For example, a 5-ps gate delay has been demonstrated with 45-nm CMOS technology (13). Therefore, it may be possible to implement GdFeCo-based ultrafast on-chip memory and logic devices. A memory device would also require an electrical readout. The addition of an oxide tunnel junction to the GdFeCo stack would enable an electrical readout of the magnetic state (33).

A nonvolatile ultrafast embedded MRAM technology based on ultrafast electrical excitation of the GdFeCo electrons would not only allow low static power dissipation due to the nonvolatility of GdFeCo but also require low dynamic energy consumption. The energy density required to switch the magnetization in our device is 13 aJ/nm². For a cell size of (20 nm)³, which is typical for memory devices (34), switching should be possible with a current pulse with a peak current of 3 mA that delivers ~4 fJ of energy. The energy required for switching remains low despite the high current density required because the electrical pulse duration is short. We conclude that picosecond electrical switching of GdFeCo can be as energy efficient as STT and SOT schemes (10–12, 35, 36) yet more than one order of magnitude faster.

An important merit of MRAM over other memory devices is the nearly unlimited cycling endurance (2). Electrical heating of GdFeCo shows strong potential for high endurance in our experiments. We observe no degradation of electrical or magnetic properties in our devices after more than 10 hours of pump-probe experiments, which were performed with a laser repetition rate of 252 kHz. Ten hours of experiments corresponds to more than 10¹⁰ switching cycles. Although the peak current density during switching is high (~7 × 10⁸ A cm⁻²), the average current density is only ~2 × 10³ A cm⁻²; therefore, we do not expect electromigration to be an issue in device durability. A lifetime in excess of 10¹⁰ cycles is many orders of magnitude higher than most resistive RAM, phase-change memory, or conductive bridging RAM (37).

Thus far, the peak current requirements for switching that we observe represent significant technological challenges for practical implementation. Further device and structure optimization may allow for significant reductions in the peak current and energy required for electrical switching. For example, switching energy per unit area could be significantly lowered by reducing the thickness of the GdFeCo stack from the 30 nm used here. Further optimization of the magnetic stack to reduce the peak switching current requirement is a subject of ongoing research. New memory circuit architectures that support these short electrical pulses may also be needed.

In summary, we demonstrate that picosecond heating by electrical current pulses can reverse magnetic order efficiently. The observed switching is an order of magnitude faster than previous methods for electrical switching based on spin-polarized currents or spin torques. Our discovery bridges the gap between the fields of spintronics and ultrafast magnetism, which will open a new frontier for ultrafast spintronics science and related devices.

MATERIALS AND METHODS

Sample fabrication

The LT GaAs substrate, (PAM-Xiamen), consisted of a 1-μm-thick GaAs layer grown at low temperature by molecular beam epitaxy on a GaAs substrate. Time-domain thermal reflectance measurements show a carrier lifetime of around 1.4 ps. The device fabrication process consisted of three photolithography, material deposition, and lift-off steps. First, a 100-nm-thick MgO layer was deposited by radiofrequency sputtering and patterned by a standard lift-off process. The substrate was fully covered with MgO, except for several windows (100 μm by 60 μm) where the photoconductive switches are placed to electrically isolate the CPS from the substrate. As a second step, the magnetic layer [Ta (5 nm)/Gd₃₀Fe₆₃Co₇ (20 nm)/Pt (5 nm)] was sputtered and patterned using the same methods as for the MgO layer. This defined a GdFeCo island with a size of 5 μm by 20 μm within the MgO window. As a third and final step, a CPS consisting of 20-nm-thick Ti and 250-nm-thick Au was deposited by electron-beam evaporation and patterned by a standard lift-off process. The CPS design contained a tapered region on each side of the GdFeCo island that narrowed down the width of the lines to increase the current density at the GdFeCo section. The narrow part of the CPS on each side overlapped with the edges of the GdFeCo island, allowing for electrical pulses to flow through it.

Electrical pulse generation and characterization

When the CPS was dc-biased, a 60-fs (FWHM) laser pulse discharges the CPS by irradiating the photoswitch, hence generating an ultrafast electrical pulse propagating along the line. We used a terahertz probe (Protemics Teraspike) to characterize the temporal profile of the electric field on the CPS device. The probe consisted of a 2-μm-wide LT GaAs photoswitch that was positioned on the end of a flexible polyethylene terephthalate cantilever. We positioned the probe tip between the two lines of the CPS at the region of interest of the sample (fig. S2). A probe laser beam illuminated the photoswitch on the tip. A linear delay stage controlled the optical delay between the probe beam and the pump beam exciting the photoswitch on the sample. During probe beam illumination, the Protemics probe output a photocurrent proportional to the strength of the electric field between the lines of the CPS. By monitoring the average photocurrent from the Protemics probe as a function of the optical delay between the pump and probe lasers, we mapped the temporal profile of the electric field at that location on the CPS. We used the average photocurrent generated by the photoswitch on the CPS, as measured by a dc voltage source (Keithley 2410 SourceMeter) to estimate the total charge contained in each electrical pulse. Using the measured temporal profile, we can determine the peak current amplitude of the electrical pulse, assuming that all the charges are contained in the pulse.

Single-shot AOS of GdFeCo

We used an external magnetic field to homogeneously polarize the magnetization in the out-of-plane direction. Then, we irradiated the GdFeCo with a single linearly polarized 810-nm-wavelength laser pulse. We used differential MOKE microscopy to image the magnetization direction before and after laser irradiation.

Time-resolved MOKE measurement

An amplified Ti-Sapphire laser with a 252-kHz repetition rate was used for time-resolved measurements. The 60-fs laser pulse, with 810-nm center wavelength, was split into the pump and probe beams. The probe was used to measure the magnetization of the sample via MOKE. The pump beam reflected off a retroreflector on a linear delay stage. By scanning the position of the delay stage, the probe beam arrived at various time delays on the sample with respect to the pump beam so that the temporal magnetization information of the sample could be measured. To measure the small polarization rotation in the probe induced by MOKE, a photoelastic modulator (PEM) and lock-in detection were used. The PEM modulated the polarization of the probe beam at 50 kHz. After the reflection off the sample, the probe beam went through an analyzer, converting polarization changes into intensity changes. The intensity of the probe beam was then measured with a Si photodetector (Thorlabs PDB 450A-AC). By sending this intensity signal into a lock-in amplifier referenced to twice the PEM frequency (100 kHz), the polarization rotation caused by the magnetization can be obtained. All time-resolved MOKE scans were measured with an external magnetic field set in each of two opposite directions. Then, the difference of the two scans was plotted to cancel any nonmagnetic contribution. At the optical wavelength of 810 nm, our measurement was only sensitive to the magnetization of the FeCo sublattice (38). An external magnetic field of 200 Oe was applied during measurements to reset the magnetization between electrical pulses. Because the compensation temperature of GdFeCo was below room temperature, no transition across compensation occurred during optical or electrical heating. This means that the external magnetic field will always tend to align the magnetic moments back to the original direction, excluding the possibility of the external field assisting the switching (39).

Electrical pulse absorption calculation

We determined the electrical energy absorbed in the GdFeCo section using two steps. First, we calculated the attenuation of the electrical pulse when propagating on the CPS to the GdFeCo section. We take the Fourier transform of the electrical pulse (voltage) V(t) in time domain to get the frequency domain spectrum $\tilde{\mathit{V}}(\mathrm{\omega })$. The energy spectral density is then proportional to ${|\tilde{\mathit{V}}(\mathrm{\omega })|}^2$ (fig. S4). The voltage on the CPS for an individual frequency ω signal at a given position x₀ away from the photoswitch is given by

$$\tilde{\mathit{V}}(\mathrm{\omega },{\mathit{x}}_0)= \text{exp}(-{\displaystyle {\int }_0^{{\mathit{x}}_0}}\mathrm{\gamma }\mathit{d}\mathit{x})*\tilde{\mathit{V}}(\mathrm{\omega },0)$$

where γ is the propagation constant defined as follows

$$\mathrm{\gamma }=\sqrt{(\mathit{R}+\mathit{j}\mathrm{\omega }\mathit{L})(\mathit{G}+\mathit{j}\mathrm{\omega }\mathit{C})}$$

R, L, G, and C are the resistance, inductance, conductance, and capacitance per unit length for the CPS, respectively. R is estimated to be 10⁴ and 10³ ohm/m for 5-μm-wide and 50-μm-wide CPS regions, respectively. G is estimated to be 0.14 and 0.014 S/m for 5-μm-wide and 50-μm-wide CPS regions, respectively. L and C can be calculated with the equations given by Chen and Chou (40). Because of nonperfect lithography, the impedance of the 5-μm-wide and 50-μm-wide CPS was slightly different. We assume a gradual linear change of γ across the taper region. The energy attenuation for a single frequency ω is then given by

$${\mathrm{\alpha }}_1(\mathrm{\omega })= \text{exp}(-2\mathit{R}\mathit{e}({\displaystyle {\int }_0^{{\mathit{x}}_0}}\mathrm{\gamma }\mathit{d}\mathit{x}\left)\right)*{\mathit{Z}}_1(\mathrm{\omega })/{\mathit{Z}}_2(\mathrm{\omega })$$

where Z_i is the frequency-dependent impedance for 50-μm-wide CPS (Z₁) and 5-μm-wide CPS (Z₂), defined as

$$\mathit{Z}=\sqrt{(\mathit{R}+\mathit{j}\mathrm{\omega }\mathit{L})/(\mathit{G}+\mathit{j}\mathrm{\omega }\mathit{C})}$$

The frequency-dependent attenuation before the GdFeCo load α₁(ω) is plotted in fig. S5A.

As a second step, we calculated the absorption of the electrical pulse in the GdFeCo load. We used a multilayer absorption calculation, using the same method as in the optical absorption calculation in (19). Here, we assumed that the electromagnetic wave traveled from the gold CPS into a thin layer (4 μm) of GdFeCo CPS and then exited back into the gold CPS line. The effective complex refractive index is given by

$$\mathit{n}(\mathrm{\omega })= \text{Conjugate}\left(\frac{\mathrm{\gamma }*\mathit{c}}{\mathrm{\omega }*\mathit{j}}\right)$$

where c is the speed of light. The difference of complex refractive indices of the GdFeCo section and gold CPS section came from the difference in R. For the GdFeCo CPS section, R was estimated to be 2.48 × 10⁷ ohm/m instead of 10⁴ ohm/m for the 5-μm-wide gold section. The absorption α₂(ω), reflection, and transmission across the GdFeCo load are plotted in fig. S5B.

Finally, the total absorption in the GdFeCo load can be calculated as follows

$$\mathrm{\alpha }=\frac{{\displaystyle \int }{|\tilde{\mathit{V}}(\mathrm{\omega })|}^2*{\mathrm{\alpha }}_1(\mathrm{\omega })*{\mathrm{\alpha }}_2(\mathrm{\omega })\mathit{d}\mathrm{\omega }}{{\displaystyle \int }{|\tilde{\mathit{V}}(\mathrm{\omega })|}^2\mathit{d}\mathrm{\omega }}$$

We calculated the total absorption of electrical pulse energy in the Ta/GdFeCo/Pt stack to be 13%. The total energy carried by the initial electrical pulse is estimated by ∫I(t)² * Zdt = 4.3 nJ, where Z = 75 ohm is the impedance of the 50-μm CPS. The temporal profile of the current I(t) is determined as described in the Electrical pulse generation and characterization section. This means that we deliver about 560 pJ of electrical energy into the Ta/GdFeCo/Pt load to switch the magnetization.

Modeling of magnetization dynamics induced by SOTs

We modeled the GdFeCo in the macrospin approximation, with a normalized Gd macrospin m_Gd and a normalized FeCo macrospin m_Fe coupled via the exchange interaction. For simplicity, we assumed no magnetic anisotropy and a constant temperature of 300 K. The Landau-Lifshitz-Gilbert equation with the SOTs for each sublattice is

$$\frac{\partial {\mathit{m}}_{\text{Fe}}}{\partial \mathit{t}}=-{\mathrm{\gamma }}_{\text{Fe}}{\mathit{m}}_{\text{Fe}}\times {\mathit{H}}_{\text{eff},\text{Fe}}+{\mathrm{\alpha }}_{\text{Fe}}{\mathit{m}}_{\text{Fe}}\times \frac{\partial {\mathit{m}}_{\text{Fe}}}{\partial \mathit{t}}$$

$$\frac{\partial {\mathit{m}}_{\text{Gd}}}{\partial \mathit{t}}=-{\mathrm{\gamma }}_{\text{Gd}}{\mathit{m}}_{\text{Gd}}\times {\mathit{H}}_{\text{eff},\text{Gd}}+{\mathrm{\alpha }}_{\text{Gd}}{\mathit{m}}_{\text{Gd}}\times \frac{\partial {\mathit{m}}_{\text{Gd}}}{\partial \mathit{t}}$$

where γ_Fe and γ_Gd are the gyromagnetic ratios for the FeCo and Gd sublattice, and α_Fe and α_Gd are the damping constant of each sublattice and are the effective field applied on the sublattice. We set γ_Fe = γ_Gd = 1.7 × 10¹¹ rad/(T·s) and α_Fe = α_Gd = 0.1. The effective magnetic fields, in the mean-field approximation, include the exchange field (41, 42), the damping-like spin-orbit field (32), and the field-like spin-orbit field (32). The effective fields are thus

$${\mathit{H}}_{\text{eff},\text{Fe}}=\frac{{\mathit{J}}_{\text{Fe}-\text{Gd}}}{{\mathrm{\mu }}_{\text{Fe}}}{\mathit{m}}_{\text{Gd}}+(\mathit{m}\times \frac{{\mathrm{\theta }}_{\mathit{D}{\mathit{L}}_{\text{Fe}}}{\mathit{J}}_{\mathit{e}}}{\mathit{e}{\mathit{M}}_{\text{Fe}}\mathit{t}}{\mathit{S}}_{\mathit{y}})+\frac{{\mathrm{\theta }}_{\mathit{F}{\mathit{L}}_{\text{Fe}}}{\mathit{J}}_{\mathit{e}}}{\mathit{e}{\mathit{M}}_{\text{Fe}}\mathit{h}}{\mathit{S}}_{\mathit{y}}$$

$${\mathit{H}}_{\text{eff},\text{Gd}}=\frac{{\mathit{J}}_{\text{Gd}-\text{Fe}}}{{\mathrm{\mu }}_{\text{Gd}}}{\mathit{m}}_{\text{Fe}}+(\mathit{m}\times \frac{{\mathrm{\theta }}_{\mathit{D}{\mathit{L}}_{\text{Gd}}}{\mathit{J}}_{\mathit{e}}}{\mathit{e}{\mathit{M}}_{\text{Gd}}\mathit{t}}{\mathit{S}}_{\mathit{y}})+\frac{{\mathrm{\theta }}_{\mathit{F}{\mathit{L}}_{\text{Gd}}}{\mathit{J}}_{\mathit{e}}}{\mathit{e}{\mathit{M}}_{\text{Gd}}\mathit{h}}{\mathit{S}}_{\mathit{y}}$$

where J_Fe−Gd = xJ_ex and J_Gd−Fe = (1 − x)J_ex, with x being the Gd concentration and J_ex = −1.09 × 10⁻²¹ J being the antiferromagnetic exchange energy (41, 42). The atomic magnetic moments are μ_Fe = 2.217 ∙ μ_B and μ_Gd = 7.63 ∙ μ_B, with μ_B being the Bohr magneton. ${\mathrm{\theta }}_{{\mathit{D}\mathit{L}}_{\text{Fe}}}$, ${\mathrm{\theta }}_{{\mathit{F}\mathit{L}}_{\text{Fe}}}$, ${\mathrm{\theta }}_{{\mathit{D}\mathit{L}}_{\text{Gd}}}$, and ${\mathrm{\theta }}_{{\mathit{F}\mathit{L}}_{\text{Gd}}}$ are the damping-like and field-like torque efficiencies (or spin Hall angles) acting on the FeCo and Gd sublattices, respectively. We chose a rather large spin Hall angle of 0.18, as measured for a similar Pt/GdFeCo system (31). Assuming a Pt resistivity of 6 × 10⁻⁷ ohm/m, we calculated the square resistance of the Pt layer to be 120 ohm. Using four-point measurement, we measured the square resistance of the Ta/GdFeCo/Pt stack to be ~60 ohm. Thus, half of the current was flowing through the Pt layer. We calculated the current density in the Pt layer to be ~ 2 × 10¹³ A/m², which was about three times higher than average current density. In our simulations, we used 9-ps-wide (FWHM) Gaussian electrical current pulses of peak current densities of J_e = 2 × 10¹³A/m² along the x direction, as in our experiments. We define e as the electron charge, h = 20 nm as the thickness of the ferrimagnet, M_Fe = 0.7M_{pure_Fe} = 1190 kA/m and M_Gd = 1160 kA/m as the saturation magnetization of the Fe sublattice (taken as 70% of pure Fe) and Gd sublattice (taken as the Fe magnetization minus the net magnetization of the ferrimagnet M_S = 30 kA/m), respectively, and S_y = ℏ/2y as the spin along the y direction.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/11/e1603117/DC1

Supplementary Text

fig. S1. Magnetic properties of the GdFeCo stack.

fig. S2. Schematic of the experimental setup for measuring the temporal profile of the electrical pulse.

fig. S3. Temporal current density profiles in CPS.

fig. S4. Energy spectral density of the electrical pulse, calculated as the square of the Fourier transform of the electrical pulse in the time domain.

fig. S5. Frequency-dependent absorption calculation on CPS.

fig. S6. Evolution of the out-of-plane component of the magnetization after arrival of a 9-ps electrical pulse due to SOTs.

Reference (43)