A Careful Accounting of Extrinsic Noise in Protein Expression Reveals Correlations Among its Sources

Abstract

In order to grow and replicate, living cells must express a diverse array of proteins, but the process by which proteins are made includes a great deal of inherent randomness. Understanding this randomness—whether it arises from the discrete stochastic nature of chemical reactivity (“intrinsic” noise), or from cell-to-cell variability in the concentrations of molecules involved in gene expression or the timings of important cell-cycle events like DNA replication or cell division (“extrinsic” noise)—remains a challenge. In this article we analyze a model of gene expression that accounts for several extrinsic sources of noise, including those associated with chromosomal replication, cell division, and variability in the numbers of RNA polymerase, ribonuclease E, and ribosomes. We then attempt to fit our model to a large proteomics and transcriptomics data set, and find that only through the introduction of a few key correlations among the extrinsic noise sources can we accurately recapitulate the experimental data. These include significant correlations between the rate of mRNA degradation (mediated by ribonuclease E) and the rates of both transcription (RNA polymerase) and translation (ribosomes), and strikingly, an anticorrelation between the transcription and translation rates themselves.

I. INTRODUCTION

Over the last 15 years, experiments have repeatedly shown that seemingly identical cells (e.g. cells belonging to a clonal population grown in a well-stirred environment) can differ significantly in their gene expression states [1–3]. How stochastic gene expression (SGE) impacts the fitness of a cell remains a fertile area of research, and as a result stochastic modeling has grown into a cornerstone of biological physics. SGE can impart some advantages; it has been shown, for example, that in E. coli SGE gives rise to a diverse array of behavioral phenotypes [4–9], and can enable populations to quickly adapt to environmental niches [10, 11]. Nevertheless, SGE has also been shown to decrease overall growth rates and natural selection efficacy [12]. Various models of the different ways in which gene expression noise arises and how cells have evolved to control it (either amplifying or attenuating it) have been explored [13–17].

With the notable exception of a 2002 article by Swain, Elowitz and Siggia [18], little attention has been paid until recently to the effect that DNA replication has on gene expression variability [19]. During replication, as the DNA polymerases progress along the chromosome, every gene is systematically copied. Because of this, depending on their stage in the cell cycle, cells can have a different number of copies of a given gene, and this cell-to-cell variation in copy number can impact gene expression stochasticity in important ways. Jones et al. [20] showed that the noise associated with gene replication represents a major component of the total mRNA variability. Building on this work, Peterson et al. [21] showed that the messenger degradation rate, which defines the timescale at which the mean messenger count “relaxes” from its low state before to its high state after gene replication, plays an critical role in accurately describing messenger noise. Earlier analytical models of gene expression either neglect DNA replication entirely, or fail to account for the mRNA relaxation by either tacitly ignoring it or significantly overestimating the messenger degradation rate (which in turn effectively ignores the relaxation).

In this article we investigate several extrinsic sources of protein expression noise (defined as Var[p]/E[p]²). We begin by deriving expressions for the protein mean and variance assuming a simple constitutive model of gene expression that explicitly accounts for gene replication, and show that these expressions agree with simulations that exactly sample the chemical master equation (CME) for the modeled system. We then extend our considerations to account for other extrinsic sources of noise, including variability in transcription, translation, and messenger degradation rates, as well as variability in the timing of gene replication and the cell cycle duration. We find that the contribution of gene replication-associated noise to the total protein noise is significant, by itself accounting for roughly as much noise as any other extrinsic source. More importantly, we find that measurements of mRNA and protein expression in E. coli (specifically the famed Taniguchi et al. data set [2]) preclude versions of our model in which the extrinsic noise sources are assumed to act independently. In such cases, the predicted protein noise is far greater than that measured, especially among highly expressed genes. Only through the inclusion of correlations among the extrinsic noise sources is our model able to accurately describe the experimental data. We sample the space of possible correlations and find that the sets that best recover the experimentally measured protein statistics tend to include significant correlations between the mRNA degradation rate (k_d) and both the transcription (k_t) and translation (k_r) rates, as well as anticorrelations between the transcription and translation rates themselves—a finding corroborated by an recent investigation of the correlations observed between protein and mRNA expression in E. coli [22]. We use our model to estimate transcription, translation, and messenger degradation rates for 585 E. coli genes, and show that the use of an earlier model of gene expression that does not account for gene replication and the other extrinsic noise sources leads to median relative errors of ∼ 23%, ∼ 21% and ∼ 36% in the predicted transcription, translation, and mRNA degradation rates. Finally we show that the our model tends to predict larger mRNA copy numbers than appear in the Taniguchi data set, which we attribute to a widely-used but likely underestimated literature value for the total mRNA content of E. coli.

II. MODEL

We begin by considering the simplest model of constitutive gene expression (see Figure 1). We assume mRNA (denoted m) is transcribed at rate k_t from a gene (denoted D), and that the mRNA can either degrade at rate k_d or be translated at rate k_r to form a protein (denoted p):

$$D(t)\stackrel{k_t}{\to }D(t)+m$$

$$m\stackrel{k_r}{\to }m+p$$ (1)

$$m\stackrel{k_d}{\to }ø$$

Importantly, in the above equation we have expressly noted the time-dependence of the gene copy number. For our purposes, D(t) can either take the value 1 for t less than the gene replication time t_r, or 2 after the gene has been copied. This system can be described by a chemical master equation (CME, see Equation A2), which describes the time evolution of the probability that a cell is in a given chemical state. In this description, the cell can transition between states in discrete jumps; it may, for example, go from having m messengers to m − 1 as the result of an mRNA degradation event, or p proteins to p + 1 through a translation event. From the CME we can derive ODEs for the instantaneous mRNA and protein means, and variances, and the instantaneous mRNA and protein covariance (see Appendix A for details):

$$\frac{d\overline{m}(t)}{dt}=k_{t}D(t)-k_d\overline{m}(t)$$

$$\frac{d{\sigma }_m^2(t)}{dt}=k_{t}D(t)+k_d\overline{m}(t)-2k_d{\sigma }_m^2(t)$$

$$\frac{d\overline{p}(t)}{dt}=k_r\overline{m}(t)$$ (2)

$$\frac{d{\sigma }_p^2(t)}{dt}=k_r\overline{m}(t)+2k_r\mathrm{Cov}[m,p](t)$$

$$\frac{d\mathrm{Cov}[m,p](t)}{dt}=k_r{\sigma }_m^2(t)-k_d\mathrm{Cov}[m,p](t)$$

FIG. 1.

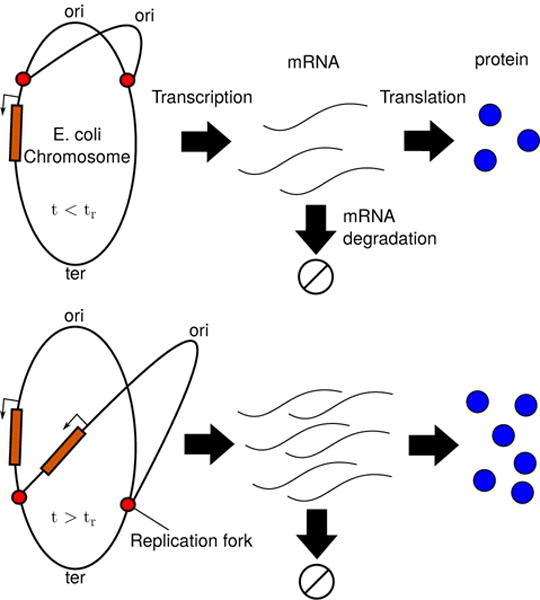
The central dogma of molecular biology for a replicating chromosome. Replication forks form at the origin of replication and proceed along both sides of the chromosome until they meet at the terminus. Each gene, depending on its location, gets copied at its own gene replication time t_r; prior to t_r an single copy exists, and afterward two copies exist. The gene can be transcribed into mRNA, which in turn can be translated to form proteins.

Worth noting is that this model does not explicitly assume a protein degradation rate. Because proteins generally degrade on time-scales longer than the cell cycle, we expect that the main avenue by which protein concentrations are attenuated is through dilution as the cells grow and divide. We therefore posit that at the cell division time, t_D, the existing proteins and mRNA are distributed to daughter cells with equal probabilities according to the binomial distribution. This assumption yields the constraints (see Equations A38 and A39):

$$\overline{m}(0)=\frac{1}{2}\overline{m}(t_D)$$

$${\sigma }_m^2(0)=\frac{1}{4}\left[\overline{m}(t_D)+{\sigma }_m^2(t_D)\right]$$

$$\overline{p}(0)=\frac{1}{2}\overline{p}(t_D)$$ (3)

$${\sigma }_p^2(0)=\frac{1}{4}\left[\overline{p}(t_D)+{\sigma }_p^2(t_D)\right]$$

$$\mathrm{Cov}[m,p](0)=\frac{1}{4}\mathrm{Cov}[m,p](t_D)$$

For constitutively expressed genes, the solutions for the messenger mean and variance are known [21], allowing for the simultaneous solution of Equations 2 and 3 (see Equations A12 and A41). Normalizing by cell size and time-averaging over the cell cycle (accounting for the fact that log-phase cells are known to have exponentially distributed ages [23, 24], and grow exponentially during the cell cycle [25]) then yields closed form solutions for the messenger and protein means and variances, E[m], Var[m], E[p], and Var[p], that depend on k_t, k_r, k_d, t_r, and t_D. The expressions are cumbersome and will not be reproduced here (although E[m] and E[p] appear in Equation A48), but they can easily be computed using Mathematica [26, 27]. We note that all five model parameters should be considered stochastic variables—cells can, after all, have different numbers of RNA polymerases, ribosomes, or ribonucleases, as examples, which can affect their respective transcription, translation, or mRNA degradation rates. Accounting for these types of extrinsic variability is accomplished in Section III.

In order to get a feel for how DNA replication impacts gene expression variability, we can consider an idealized “median gene”—that is, a gene with median values for its messenger and protein copy numbers (approximately 0.064 and 18.2 per cell, respectively [2]), a median mRNA half life (approximately 2.4 minutes [2]), and a gene loci situated half-way between the origin and terminus of replication. We note that the cells used in the Taniguchi study had doubling times in the vicinity of 120 minutes (although some strain-to-strain variability, ranging between approximately 110 and 150 minutes, have been reported [4, 28]). E. coli with similar doubling times have recently been measured to have a B-period (the portion of the cell cycle prior to replication initiation) of around 42.2 minutes, and a C-period (the portion of the cell cycle during which the chromosome is being replicated) around 42.4 minutes [29], although other studies have reported slightly shorter and longer B- and C-periods, respectively [30, 31]. These values lead to a median gene replication time of t_r = 42.2 + 0.5 × 42.4 = 63.4 minutes). We can then solve for estimates of the transcription and translation rates for our median gene (k_t = 0.014 and k_r = 1.6) and compute the protein copy number variance we should expect it to have. The result is a value of Var[p] = 115.3, corresponding to a noise level of Var[p]/E[p]² = 0.35. Fixing all other parameters and scanning over gene loci (denoted χ, the fraction of the gene’s position along the chromosome measured from origin to terminus, which we assume affects the gene replication time as t_r = 42.2+χ×42.4) shows that the noise level of our median gene can vary between 0.31 and 0.39—a relative difference of as much as 20%. Explicit stochastic simulations (using the stochastic simulation algorithm (SSA) of Gillespie [32, 33]) show outstanding agreement with these results (see Figure 2).

FIG. 2.

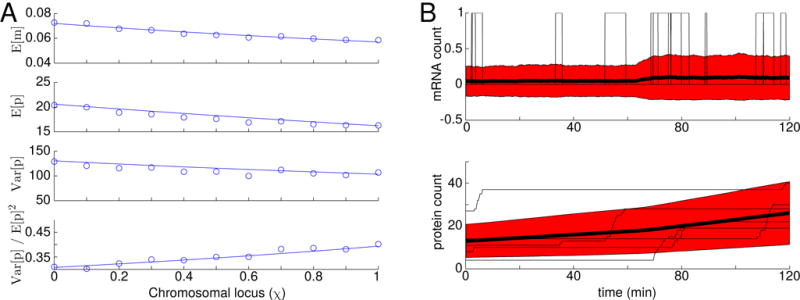
(A) Analytical and simulated mRNA and protein statistics for a “median” E. coli gene as a function of gene loci. Circles represent statistics calculated from 5,000 simulated cell cycles. At the start of each cycle, the mRNA and protein copy numbers were drawn from a binomial distribution based on the final counts in the previous cycle. The simulated counts were normalized to account for cell growth, and the fact that cell ages are exponentially distributed. The lines represent analytical results evaluated according to Equations A47. (B) Simulated mRNA and protein traces with χ = 0.5. The thin black lines indicate 5 individual cell cycles, while the heavy black lines indicate the mean of 5,000 cell cycles. The red areas indicates ± 1 standard deviation.

Despite the agreement between our simulations and analysis, the noise level we have computed, 0.35, should make us somewhat wary—we have not included any extrinsic sources of gene expression noise other than DNA replication and already our model appears to account for more than the entirety of the noise-floor observed in the Taniguchi study (approximately 0.09 for proteins expressed at levels above 10 [2]). If we do account for the other extrinsic noise sources, will our model be able to accurately describe the protein data?

III. ACCOUNTING FOR EXTRINSIC NOISE SOURCES

We can extend our model to include extrinsic sources of noise, such as variability in RNA polymerase (RNAP), ribosome, or ribonuclease E (Rne) copy numbers (which can affect the transcription, translation, and messenger degradation rates, respectively), or variability in the cell cycle duration, t_D, or the timing of gene replication, t_r. In each case, the effect of randomness in a given parameter can be estimated by Taylor expanding about the mean parameter value (see Equation B1).

We can (at least roughly) estimate the variance in each parameter in our model. By noting that the rates of transcription, translation, and mRNA degradation are proportional to the concentrations of RNAP, ribosomes, and Rne, and that these macromolecules tend to be highly expressed (and therefore likely to have noise levels of around 0.1) we can estimate Var[k_t], Var[k_r], and Var[k_d] as $0.1\times k_t^2$, $0.1\times k_r^2$, and $0.1\times k_d^2$, respectively (where we now understand k_t, k_r, and k_d to represent the mean transcription, translation, and mRNA degradation rates). Variability in the cell cycle duration is estimated to be around 10% [29], and so we might expect Var[t_D] ≈ 12² min² (assuming a 120 minute cell doubling time). Finally, using published values of the variability in the B- and C-periods of the cell cycle (52% [29], and 16% [30], respectively), we can estimate the variance in a gene’s replication time as Var[t_r] ≈ (0.52 × 42.2)² + χ²(0.16 × 42.4)² min².

It is fairly common in models of this type to assume that the extrinsic noise sources act independently (i.e. the matrix ρ that describes the correlations among the extrinsic noise sources in Equation B1 is the identity matrix, 𝟙). Under this assumption, Figure 3A shows the total protein noise broken down into contributions from each of its contributing sources for the same “median” gene modeled previously. For the sake of comparison, we have distinguished the extrinsic noise associated with gene replication (denoted “DNA rep”) from the intrinsic noise associated with the biochemical network (denoted Γ) by subtracting from our expressions the noise predicted by a model that does not include gene duplication [2, 5, 34]. We find that gene replication contributes a comparable amount of gene expression noise (~0.1) as variability in any of k_t, k_r, or k_d, while variability in the timing of DNA replication and cell division, conversely, contribute very little noise (~0.02). Importantly, the total noise we find, 0.69, is significantly larger than the noise measured by Taniguchi et al. [2] for the majority of proteins with mean expression levels around 18. We can forge ahead and try to fit every point in the Taniguchi data set (see Figure 4A, and Appendix C for details on the fitting procedure) but this only confirms our fears—when (independent) extrinsic noise sources are accounted for, our model overestimates protein expression variability, and simply can not describe most of the data.

FIG. 3.

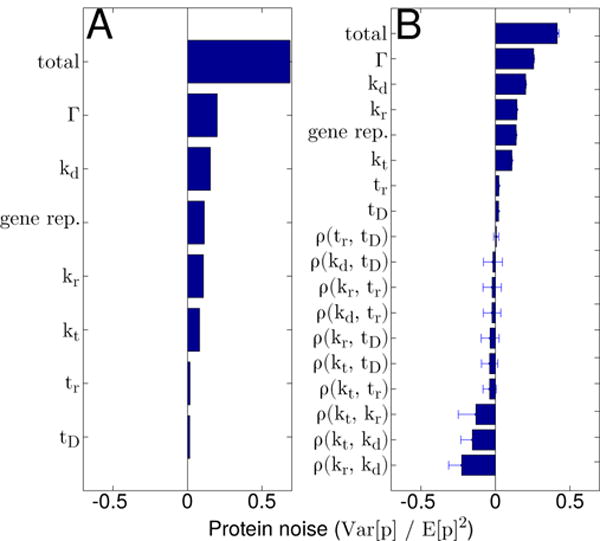
Protein noise broken down by contributing source for the “median” gene assuming either (A) all extrinsic noise sources act independently, or (B) extrinsic noise sources exhibit correlations among themselves. Note that in (B), bars indicate the median noise contributions calculated using the top 0.5% of sampled correlation matrices, while the error bars indicate their respective median absolute deviations (see Section IV for details)

FIG. 4.

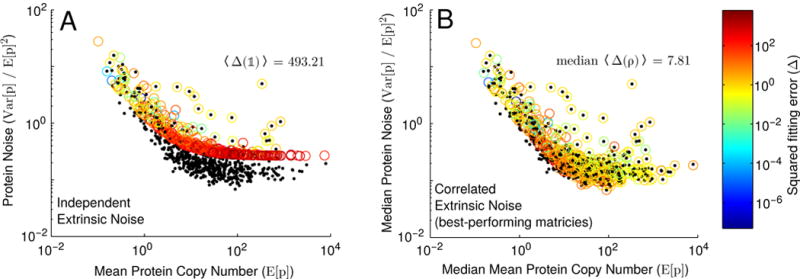
Fitting our model to the Taniguchi et al. dataset assuming either (A) all extrinsic noise sources act independently (i.e. ρ = 𝟙), or (B) extrinsic noise sources exhibit correlations among themselves (see Section IV). Black points represent experimental data from [2], while circles represent best fits from our model (colored by the squared fitting error, Δ(ρ), see Equation C1). Note that in (B), circles represent median values of E[p], V ar[p]/E[p]² and Δ(ρ), calculated using the top 0.5% of sampled correlation matrices (see Section IV for details). Also noted is the mean squared fitting error, 〈Δ(𝟙)〉, when extrinsic noise sources are assumed to act independently, as well as the median mean squared fitting error for the best-performing matrices.

There have been a number of different mechanisms proposed by which gene-expression noise may be attenuated, including negative feedback, near-saturated signaling cascades, and forms of post-transcriptional regulation [13, 16, 17]. While undoubtedly some fraction of the genes in the Taniguchi data set are controlled through these mechanisms, the problem we face is that significant noise attenuation is required for our model to fit most of the data, and so we wish to find an explanation that applies to most—if not all—E. coli proteins. One possibility is that extrinsic noise sources should not in general be assumed to be independent. Taniguchi et al. found that the fluctuations of highly-expressed proteins (both RNAP and Rne are expressed in thousands per cell) can have correlation coefficients of as much as 0.66 [2]. Similarly, the timing of DNA replication has long been believed to be correlated with the cell cycle duration [35], and a recent study found a correlation coefficient of as high as 0.79 between the B-period and the doubling time of E. coli [30]. We can investigate the effect that extrinsic noise correlations have on our model’s ability to match the Taniguchi data by simply including the cross terms in our Taylor expansions that depend on the covariance of the model parameters.

IV. FINDING EXTRINSIC NOISE CORRELATIONS THAT FIT EXPERIMENTAL PROTEIN AND MRNA STATISTICS

Because our model overestimates protein noise when extrinsic sources are treated independently, finding correlations coefficients that lead to noise attenuation is an important part of fitting our model to the Taniguchi data. In general, the noise will be attenuated by the negative cross terms in our Taylor expansion of Var[p] (Equation B1). These arise when either: 1) the correlation coefficient between two extrinsic noise sources is negative and the partial derivatives of Var[p] with respect to these sources have the same sign; or 2) the correlation between the sources is positive and the partial derivatives with respect to them have opposite signs. An example of the former might be if the transcription and translation rates were anticorrelated (since the derivatives with respect to k_t and k_r are both positive), while an example of the latter might be if the transcription and mRNA degradation rates were positively correlated (because the derivative with respect to k_d is negative). Importantly, finding noise-attenuating correlations can not be done arbitrarily. Any matrix ρ that describes the possible correlations among k_t, k_r, k_d, t_r, and t_D must be both positive definite (which bars cases in which, for example, noise sources A and B are strongly correlated, and A and C are strongly correlated, but B and C are strongly anti-correlated) and have ones on diagonal. Such a matrix can be constructed as ρ = LL^T, where L is a lower triangular matrix with diagonal values greater than 0 and whose squared row elements sum to 1 (i.e. ${\displaystyle {\sum }_j{L}_{i,j}^2}=1$ for each row i).

Although it may be tempting to try to search for correlation matrix that minimizes the mean squared fitting error (denoted 〈Δ(ρ)〉), nonlinear fits of this type—especially those involving large parameter spaces—are notoriously difficult [36]. Moreover, even if an optimal ρ could be found, without knowledge of the shape of 〈Δ(ρ)〉, it’s difficult to say with confidence that other—possibly very different—correlation matrices could not yield fitting errors of comparable size. Here we take a more circumspect approach, opting for questions like “what correlation coefficients are likely to occur in matrices consistent with the gene expression data?” To that end, we constructed a set of 50,000 random correlation matrices with approximately uniformly-distributed off-diagonal elements (see Appendix D for details). These matrices’ associated mean squared fitting errors ranged between 5.76 and 1125.90. Focusing on the top 0.5 percentile (the set of 250 matrices with the lowest associated errors, ranging up to 8.78, and denoted {ρ*}), a number of clear trends emerged (see Figure 5A).

FIG. 5.

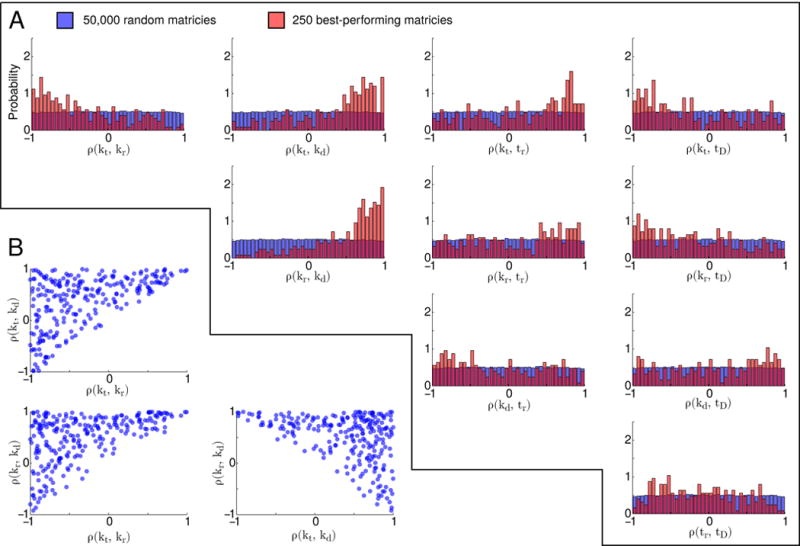
(A) Marginal distributions of off-diagonal terms in sampled correlation matrices. Blue indicates the distributions of all 50,000 matrices, while red indicated the distributions of the best-performing matrices (those among the 0.5% with lowest associated 〈Δ(ρ)〉 values). (B) Scatter plots of ρ(k_t, k_r), ρ(k_t, k_d), and ρ(k_r, k_d) with respect to each other for the best-performing matrices

The median values of the correlation coefficients in our best-performing matrices, with their associated median absolute deviations (MAD), are represented in Equation 4. These matrices tend to include significant positive correlations between the mRNA degradation rates and both the transcription and translation rates, as well as significant anticorrelations between the transcription and translation rates themselves. While some matrices defy one or another of these general trends (approximately 23% of {ρ*} include negative correlations between k_d and k_t, 16% include negative correlations between k_d and k_r, and 28% include positive correlations between k_t and k_r), none defy two or more of them simultaneously.

Based on these results, we can say the true extrinsic noise correlation matrix—whatever it may be—likely includes correlations between the mRNA degradation rate and the transcription and translation rates. This is in keeping with what is known about highly-expressed cellular components. Rne, RNAP, and ribosomes all occur in large concentrations within the cell, and as such some correlation among their numbers should naturally arise [2]. Indeed, one can easily imagine how cells with relatively high transcription rates (due to high copy numbers of RNAP) or high translation rates (high copy numbers of ribosomes) would express high numbers of Rne, and in turn have relatively high mRNA degradation rates. These two correlations are extremely important for the overall fitting of the model to the data, and represent the largest two sources of noise attenuation among our {ρ*} matrices (see Figure 3B).

The tendency of our best-performing matrices to include anticorrelations between the transcription and translation rates is less intuitive, but considerably more interesting. Naively one would expect that a cell with greater numbers of RNAP would transcribe more ribosomes, and similarly, a cell with greater numbers of ribosomes would translate more RNAP, together giving rise to a positive correlation between the cell’s transcription and translation rates; but the correlation matrices that elicit the best fits to the data actually predict the opposite. A skeptic might attribute these results to the necessity of our matrices to include noise-attenuating terms (ρ(k_t, k_r) represents the third-largest overall source of noise attenuation, see Figure 3B), but there are compelling reasons to believe that this anticorrelation might be real. It has been shown that translation of the rpoB. These three correlation coefficients tend to compensate for each other; matrices with higher transcription-translation correlations, for example, also have correspondingly higher mRNA degradation-transcription and mRNA degradation-translation correlations (see Figure 5B). Other statistical enhancements are somewhat less pronounced. The transcription rate tends to be positively correlated with the timing of gene replication, and both the transcription and translation rates tend to be negatively correlated with the timing of cell division. Finally, we note that the distributions of ρ(k_r, t_r), ρ(k_d, t_r), ρ(k_d, t_D), and ρ(t_r, t_D) show only weak biases, and are relatively widely dispersed.

$$\text{median}\{{\rho }_{i,j}^{\ast }\}=\left(\begin{array}{ccccc}{k}_t& k_r& k_d& t_r& t_D\\ 1& -0.44\pm 0.37& 0.56\pm 0.27& 0.37\pm 0.43& -0.34\pm 0.48\\ .& 1& 0.67\pm 0.24& 0.18\pm 0.53& -0.27\pm 0.47\\ .& .& 1& -0.20\pm 0.53& 0.14\pm 0.53\\ .& .& .& 1& -0.14\pm 0.43\\ .& .& .& .& 1\end{array}\right)\begin{array}{c}{k}_t\\ k_r\\ k_d\\ t_r\\ t_D\end{array}$$ (4)

mRNA (encoding the β-subunit of RNAP) is inhibited by the 50S ribosomal protein L1 [37–39]. This means that cells with high ribosomal protein copy numbers should exhibit low RNAP translation rates, and in turn suppressed transcription rates. Given the current context, it is possible that this regulatory mechanism may have evolved in order to suppress overall protein noise. Moreover, an elegant recent article by Hilfinger, Norman, and Paulsson [22] analyzed the space of all possible gene-expression models and found that only models in which the transcription and translation rates were anticorrelated could give rise to the negligible mRNA-protein correlation coefficients seen experimentally [2, 22].

The enhancements in anticorrelations between the timing of cell division and both the transcription and translation rates observed among our {ρ*} matrices are consistent with the current leading models of bacterial cell size control and division. Although it remains an active area of research, a number of theories have been posited to understand how cell division timing is regulated. These include “accumulation” models involving the buildup of a critical number of initiator molecules (such as FtsZ [40]) before division is triggered, “adder” models in which cells attempt to add a fixed volume before dividing, mixtures thereof (including the particularly compelling “multiple origins accumulation” model [24]), as well as the earlier “sizer” models (in which cells divide at a critical size) and “timer” models (wherein cells attempt to maintain fixed cell-cycle intervals). In our context, cells with high transcription or translation rates (or both) should be expected to grow faster and accumulate greater numbers of initiator molecules at earlier times. As a result—at least according to the accumulation, adder, and sizer models—these cells should divide sooner and exhibit the types of k_t–t_D and k_r–t_D anticorrelations seen in our data.

In contrast, the bias in {ρ*} toward positive correlations between the transcription rate and the timing of gene replication is considerably stronger than was expected based on the biochemical literature. Its known, for example, that accumulation of DnaA to the origin of replication plays an integral role in replication initiation. One might surmise, then, that cells with relatively high transcription rates would produce DnaA at correspondingly faster rates, leading to earlier replication times (and small or negative correlations). Similarly, its been shown that high transcriptional activity also gives rise to net negative chromosomal supercoiling, especially near the origin of replication where several highly-expressed rRNA genes reside. This supercoiling should facilitate DNA melting, again leading to earlier replication times [41]. In light of these considerations, we anticipated lower ρ(k_t, t_r) values than were in fact observed among our best-performing matrices.

Finally, we note that although positive correlations between the timing of DNA replication and cell division have been measured [30], no enhancement among positive values was observed in {ρ*}. We attribute this to the fact that variability in neither t_r nor t_d contribute significantly to the overall protein noise, and as a result, correlations among them contribute correspondingly small amounts (see Figure 3). This means that the matrices that are most consistent with the experimental data—those that enable the greatest noise attenuation—show little bias in their t_r–t_D correlation coefficients.

V. FAILURE TO ACCOUNT FOR EXTRINSIC NOISE LEADS TO UNDERESTIMATION OF THE TRANSCRIPTION AND MRNA DEGRADATION RATES

We can compare the transcription, translation, and mRNA degradation rates fit using the theory developed here (using our set of best-performing correlation matrices) with those fit using the gamma distribution [2, 5, 34]. As before, we simultaneously fit k_t, k_r, and k_d to the measured mRNA means, protein means and variances, and mRNA degradation rates from the Taniguchi data set using the expressions:

$$E{[m]}_{\mathrm{\Gamma }}=\frac{k_t}{k_d}$$

$$E{[p]}_{\mathrm{\Gamma }}=\frac{k_t{t}_D}{ln(2)}\frac{k_r}{k_d}$$ (5)

$$\mathit{Var}{[p]}_{\mathrm{\Gamma }}=\frac{k_t{t}_D}{ln(2)}{\left(\frac{k_r}{k_d}\right)}^2$$

where we have substituted ln(2)/t_D for the dilution rate that would normally appear. We find that for the majority of genes in the data set, the transcription and mRNA degradation rates extracted using our model are significantly higher than those extracted using the gamma distribution (with median fold-changes, calculated over all genes and {ρ*} matrices, of approximately 1.23 for k_t and 1.36 for k_d, see Figure 6A & C). For many genes the effect can be dramatic, resulting in order of magnitude or more differences in the predicted k_t and k_d rates. In contrast, the translation rates predicted by our model tended to be lower (approximately 0.79-fold) than those predicted by the gamma distribution (see Figure 6B). These observations highlight the necessity of a careful accounting of extrinsic noise sources when fitting rates using gene expression variability data.

FIG. 6.

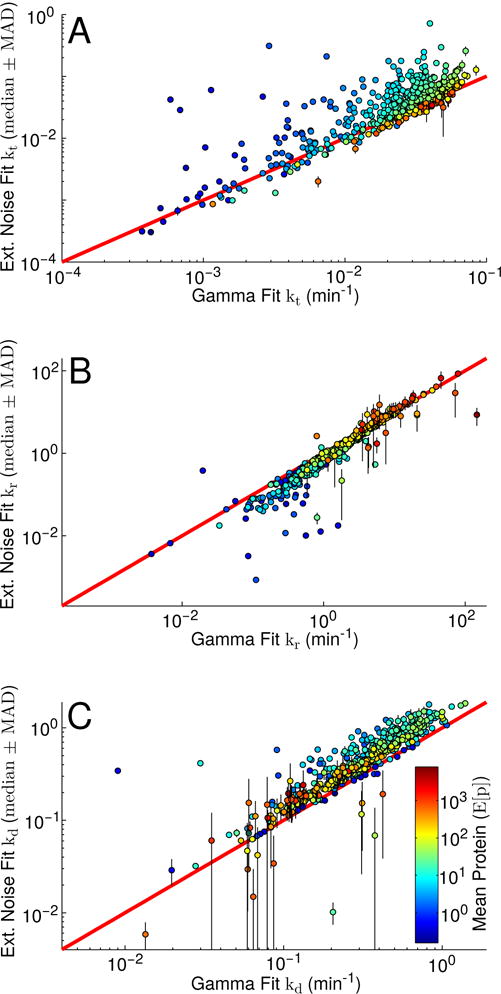
Comparison of fit kinetic parameters using our model versus the earlier Gamma distribution model [34]. (A) Comparison of fit transcription rates. (B) Comparison of fit translation rates. (C) Comparison of fit mRNA degradation rates. Points are colored by mean protein expression level. The red diagonal lines indicate perfect agreement. In all cases, the plotted Ext. Noise Fit values represent each gene’s median transcription, translation, and mRNA degradation values obtained by performing the fits described in Equation C1 using each of our best-performing correlation matrices, with the respective median absolute deviation shown as vertical black lines. The plotted Gamma Fit values represent the analogous fits performed using Equation 5 rather than our ρ-dependent extrinsic noise model.

VI. THE TANIGUCHI DATASET APPEARS TO UNDERESTIMATE MRNA COPY NUMBERS

We compared the mean mRNA copy numbers extracted by fitting our model (again using our best-performing correlation matrices) with those reported in the Taniguchi data set. For most (over 75%) of the genes considered, our fit median E[m]_{ext. nse}. was larger than the measured value (by a median fold-change, over all genes and {ρ*} matrices, of approximately 1.68, see Figure 7). As has been fairly common with quantifying copy numbers using RNA-seq, Taniguchi et al. scaled their relative measurements such that the total mRNA per cell was 1, 350, a value that derives from [42] and is based in part on total mRNA mass. More recent studies employ “spiked” samples with additional calibration mRNA added in known quantities prior to RNA-seq which serve to more directly measure the concentrations of the cellular transcripts. These studies have yielded estimates of the total mRNA content of an E. coli cell in glucose minimal medium to be approximately 2, 400 transcripts [43, 44]. Had the Taniguchi mRNA data been normalized to this value, it would have increased each mRNA count by 1.78-fold, and brought their measurements and our fits into very close agreement.

FIG. 7.

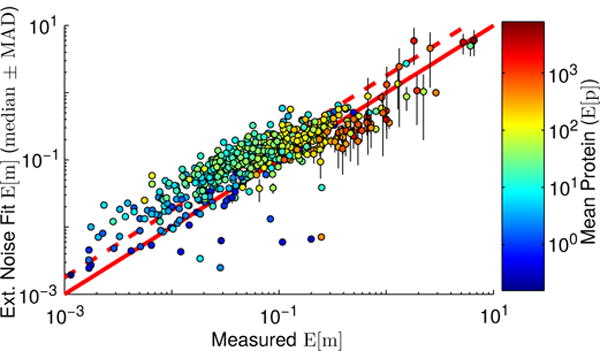
Comparison of experimental [2] and fit mean mRNA copy numbers. Points are colored by mean protein expression level, and represent the median mean mRNA copy numbers computed over our best-performing matrices, with their associated median absolute deviations shown with black vertical lines. The solid red line indicates the line of perfect agreement, while the dashed red line indicates the line of perfect agreement if the Taniguchi mRNA counts had been scaled to 2,400 total mRNA per cell.

VII. CONCLUSIONS

Building on prior work by us and other authors [18, 20, 21], we have derived expressions for mRNA and protein statistics assuming a simple constitutive model of gene expression that accounts for chromosome replication. We are not the first to consider this effect [19], but to our knowledge we are the first to carefully understand it in the context of other sources of extrinsic noise, and more importantly, critically compare our model with experimental results. While we did find that the noise contribution associated with gene replication was of comparable size to those associated with variability in RNAP, Rne, and ribosome copy numbers, it turned out that this was only part of the story. As is so often the case, much more interesting results emerged when our model failed to match experimental data. Under the assumption of independent extrinsic variability (a fairly routine approximation in models of this kind) we vastly overestimated the protein noise. This in turn led to an investigation of how the extrinsic noise sources might be correlated, and ultimately to several important results. These included 1) mRNA degradation rates likely correlate with both the transcription and translation rates, perhaps through the natural correlations that emerge among highly-expressed cellular components like Rne, RNAP, and ribosomes; 2) transcription and translation rates in E. coli likely anticorrelate, possibly through the suppression of rpoB translation by the large ribosomal protein L1, although other explanations have been posited [22]; 3) accounting for extrinsic noise when extracting kinetic parameters from gene expression data consistently (and often significantly) impacts the results; and 4) the total mRNA content of E. coli appears to be greater than previously assumed literature values estimate.

Ultimately, the determination of the true extrinsic noise correlation coefficients must be an empirical exercise. As such, we note that some relatively straightforward experiments can be conducted to directly test our predictions. For example, researchers have already counted RNAP and ribosome copy numbers individually [45, 46]; by measuring both simultaneously in a two-color experiment, the anticorrelation we predict between the transcription and translation rates could be observed.

Appendix A: Derivation of the protein copy number Mean and Variance

Here we derive expressions for the protein copy number mean and variance. Due to the potentially broad applicability of our results, including to researchers outside the traditional physics community, we have made a concerted effort not to “skip steps.” As a result, this derivation likely includes details that may seem obvious to the more seasoned reader.

We consider the system:

$$D(t)\stackrel{k_t}{\to }D(t)+m$$

$$m\stackrel{k_r}{\to }m+p$$ (A1)

$$m\stackrel{k_d}{\to }ø$$

where D(t) is the time-dependent gene copy number, either one before the gene replication time, t_r, or two after it. Assuming that after replication both copies can be transcribed independently and with equal rates, we can write the master equation for this system as:

$$\frac{d}{dt}P(m,p|t)=k_t(t)P(m-1,p|t)-k_t(t)P(m,p,|t)+k_d(m+1)P(m+1,p,|t)-k_{d}mP(m,p,|t)+k_{r}mP(m,p-1|t)-k_{r}mP(m,p|t)$$ (A2)

where:

$$k_t(t)=\{\begin{array}{cc}{k}_t& t<t_r\\ 2k_t& t>t_r\end{array}$$ (A3)

From this we can derive differential equation for the mean and variance of the mRNA count (see [21]), and the protein count. We consider the mean protein count, $\overline{p}(t)$ first:

$$\frac{d}{dt}\overline{p}(t)=\frac{d}{dt}{\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }pP(m,p|t)}}={\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p\frac{d}{dt}P(m,p|t)}}$$ (A4)

We can insert the RHS of our master equation (Equation A2) for $\frac{d}{dt}P(m,p|t)$ and evaluate term-by-term. The first term is:

$${\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(m-1,p|t)}}={\displaystyle \sum _{n=-1}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(n,p|t)}}={\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(-1,p|t)}+{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(n,p|t)}}={\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)\times 0}+{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(n,p|t)}={\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(p|t)}}=\overline{p}(t)k_t(t)$$ (A5)

where we have used the fact that cells can not have negative mRNA (or protein) copy numbers, and so the probability of being in a state with m = −1 is 0. The second term gives:

$${\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(m,p|t)}}={\displaystyle \sum _{p=0}^{\infty }p{k}_t(t)P(p|t)}=\overline{p}(t)k_t(t)$$ (A6)

The third term gives:

$${\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_d(m+1)P(m+1,p,|t)}}={\displaystyle \sum _{n=1}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_{d}nP(n,p,|t)}}={\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_{d}nP(n,p,|t)}}-{\displaystyle \sum _{p=0}^{\infty }p{k}_d\times 0\times P(0,p|t)}=k_d\overline{p}(t)\overline{n}(t)=k_d\overline{p}(t)\overline{m}(t)$$ (A7)

The fourth term gives:

$${\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_{d}mP(m,p,|t)}}=k_d\overline{p}(t)\overline{m}(t)$$ (A8)

The fifth term gives:

$${\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_{r}mP(m,p-1|t)}}={\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{y=-1}^{\infty }(y+1)k_{r}mP(m,y|t)}}={\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{y=0}^{\infty }(y+1)k_{r}mP(m,y|t)}}+{\displaystyle \sum _{m=0}^{\infty }0\times k_{r}mP(m,-1|t)}=k_r\langle m(p+1)\rangle (t)=k_r\langle m_p\rangle (t)+k_r\overline{m}(t)$$ (A9)

where $\overline{m}(t)$ represents the time-dependent mean mRNA count. Finally, the sixth term gives:

$${\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{p=0}^{\infty }p{k}_{r}mP(m,p|t)}=k_r}\langle mp\rangle (t)$$ (A10)

Now, simply pulling this all together with appropriate signs leaves us with the expression:

$$\frac{d}{dt}\overline{p}(t)=k_r\overline{m}(t)$$ (A11)

Now, inserting Equation 2 from [21] into Equation A11 and requiring $\overline{p}(0)=\frac{1}{2}\overline{p}(t_D)$ yields the solution:

$$\overline{p}(t)=\frac{k_r{k}_t}{k_d}[\frac{e^{-k_d{t}_D}-e^{-k_d{t}_r}}{k_d}+2t_D-t_r]+\eta (t)$$ (A12)

where

$$\eta (t)=\{\begin{array}{l}\frac{k_r{k}_t}{k_d}t\\ \frac{k_r{k}_t}{k_d}[\frac{e^{-k_{d}t}-e^{-k_d{t}_r}}{k_d}+2t-t_r]\end{array}\begin{array}{l}\text{for}0<t<t_r\hfill \\ \text{for}{t}_r<t<t_D\hfill \end{array}$$ (A13)

We can now begin to consider the differential equation for the variance of the protein count:

$$\frac{d}{dt}{\sigma }_p^2(t)=\left({\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{m=0}^{\infty }\frac{d}{dt}P(m,p|t)}\right)-2\overline{p}(t)\frac{d}{dt}\overline{p}(t)$$ (A14)

As before, we can insert the RHS of Equation A2 into Equation A14 and evaluate it term by term. The first term gives:

$${\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_t(t)P(m-1,p|t)}={\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{n=-1}^{\infty }{k}_t(t)P(n,p|t)}={\displaystyle \sum _{p=0}^{\infty }{p}^2}\left(k_t(t)P(-1,p|t)+{\displaystyle \sum _{n=0}^{\infty }{k}_t(t)P(n,p|t)}\right)={\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{n=0}^{\infty }{k}_t(t)P(n,p|t)}=k_t(t)\langle p^2\rangle (t)$$ (A15)

The second term gives:

$${\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_t(t)P(m,p|t)}=k_t(t)\langle p^2\rangle (t)$$ (A16)

The third term gives:

$${\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_d(m+1)P(m+1,p,|t)}={\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{n=1}^{\infty }{k}_{d}nP(n,p,|t)}={\displaystyle \sum _{p=0}^{\infty }{p}^2}\left({\displaystyle \sum _{n=0}^{\infty }{k}_{d}nP(n,p,|t)-k_d\times 0\times P(0,p|t)}\right)=k_d\langle m{p}^2\rangle (t)$$ (A17)

The fourth term gives:

$${\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_{d}mP(m,p,|t)}=k_d\langle m{p}^2\rangle (t)$$ (A18)

The fifth term gives:

$${\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_{r}mP(m,p-1|t)}={\displaystyle \sum _{y=-1}^{\infty }{\left(y+1\right)}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_{r}mP(m,y,|t)}={\displaystyle \sum _{y=0}^{\infty }{\left(y+1\right)}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_{r}mP(m,y,|t)}+0^2\times {\displaystyle \sum _{m=0}^{\infty }{k}_{r}mP(m,-1|t)}=k_r\langle m(p^2+2p+1)\rangle (t)=k_r\langle m{p}^2\rangle (t)+2k_r\langle mp\rangle (t)+k_r\overline{m}(t)$$ (A19)

And finally the sixth term gives:

$${\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{m=0}^{\infty }{k}_{r}mP(m,p,|t)}=k_r\langle m{p}^2\rangle (t)$$ (A20)

The final term on the RHS of Equation A14 can be evaluated by inserting Equation A11:

$$2\overline{p}(t)\frac{d}{dt}\overline{p}(t)=2\overline{p}(t)k_r\overline{m}(t)$$ (A21)

Now, putting these all together (with appropriate signs) yields:

$$\frac{d}{dt}{\sigma }_p^2(t)=k_r\overline{m}(t)+2k_r\left[\langle mp\rangle -\overline{m}(t)\overline{p}(t)\right]=k_r\overline{m}(t)+2k_r\mathrm{Cov}[m,p](t)$$ (A22)

Evidently we need an equation for the mRNA and protein covariance. This can be easily written down:

$$\frac{d}{dt}\mathrm{Cov}[m,p](t)={\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{m=0}^{\infty }m\frac{d}{dt}P(m,p|t)}-\overline{m}(t)\frac{d}{dt}\overline{p}(t)-\overline{p}(t)\frac{d}{dt}\overline{m}(t)$$ (A23)

Again, we insert the RHS of Equation A2, and evaluate term by term. The first term gives:

$${\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{m=0}^{\infty }m{k}_{t}P(m-1,p|t)}=k_t\langle (m+1)p\rangle =k_t\langle mp\rangle (t)+k_t\overline{p}(t)$$ (A24)

The second term gives:

$${\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{m=0}^{\infty }m{k}_{t}P(m,p|t)}=k_t\langle mp\rangle (t)$$ (A25)

The third term gives:

$${\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{m=0}^{\infty }m{k}_d(m+1)P(m+1,p,|t)}={\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{n=1}^{\infty }(n-1)k_{d}nP(n,p,|t)}={\displaystyle \sum _{p=0}^{\infty }p\left(-1\times k_d\times 0\times P(0,p|t)+{\displaystyle \sum _{n=1}^{\infty }(n-1)k_{d}nP(n,p,|t)}\right)}={\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{n=0}^{\infty }(n-1)k_{d}nP(n,p,|t)}=k_d\langle m(m-1)p\rangle (t)=k_d\langle m^{2}p\rangle (t)-k_d\langle mp\rangle (t)$$ (A26)

The fourth term gives:

$${\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{m=0}^{\infty }m{k}_{d}mP(m,p,|t)}=k_d\langle m^{2}p\rangle$$ (A27)

The fifth term gives

$${\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{m=0}^{\infty }m{k}_{r}mP(m,p-1|t)}={\displaystyle \sum _{q=-1}^{\infty }(q+1)}{\displaystyle \sum _{m=0}^{\infty }m{k}_{r}mP(m,q|t)}=k_r\langle m^2(p+1)\rangle (t)=k_r\langle m^{2}p\rangle (t)+k_r\langle m^2\rangle (t)$$ (A28)

And finally the sixth term gives

$${\displaystyle \sum _{p=0}^{\infty }p}{\displaystyle \sum _{m=0}^{\infty }m{k}_{r}mP(m,p|t)}=k_r\langle m^{2}p\rangle$$ (A29)

The final two terms on the RHS of Equation A23 give:

$$\overline{m}(t)\frac{d}{dt}\overline{p}(t)=k_r{\overline{m}}^2(t)$$ (A30)

and:

$$\overline{p}(t)\frac{d}{dt}\overline{m}(t)=\overline{p}(t)[k_t-k_d\overline{m}(t)]$$ (A31)

so, finally, pulling this all together yields:

$$\frac{d}{dt}\mathrm{Cov}[m,p](t)=-k_d\langle mp\rangle (t)+k_r\langle m^2\rangle (t)-k_r{\overline{m}}^2(t)+k_d\overline{m}(t)\overline{p}(t)=k_r\left[\langle m^2\rangle (t)-{\overline{m}}^2(t)\right]-k_d\left[\langle mp\rangle (t)-\overline{m}(t)\overline{p}(t)\right]=k_r{\sigma }_m^2(t)-k_d\mathrm{Cov}[m,p](t)=k_r\overline{m}(t)-k_d\mathrm{Cov}[m,p](t)$$ (A32)

where the last line follows from Equation 2 in [21].

We can solve Equation A22 for Cov[m, p](t) and insert it and Equation A11 into Equation A32 to yield:

$$\frac{d}{dt}\mathrm{Cov}[m,p](t)=\frac{d}{dt}\overline{p}(t)-\frac{k_d}{2k_r}\frac{d}{dt}\left[{\sigma }_p^2(t)-\overline{p}(t)\right]=\frac{d}{dt}\left[(1+\frac{k_d}{2k_r})\overline{p}(t)-\frac{k_d}{2k_r}{\sigma }_p^2(t)\right]$$ (A33)

which immediately gives:

$$\mathrm{Cov}[m,p](t)=c_0+\left[(1+\frac{k_d}{2k_r})\overline{p}(t)-\frac{k_d}{2k_r}{\sigma }_p^2(t)\right]$$ (A34)

where c₀ is an arbitrary integration constant that will be determined shortly. Inserting this into Equation A22 gives:

$$\frac{d}{dt}{\sigma }_p^2(t)=k_r\overline{m}(t)+2k_r\left(c_0+\left[(1+\frac{k_d}{2k_r})\overline{p}(t)-\frac{k_d}{2k_r}{\sigma }_p^2(t)\right]\right)=k_r\overline{m}(t)+2k_r{c}_0+(2k_r+k_d)\overline{p}(t)-k_d{\sigma }_p^2(t)$$ (A35)

For which the general solution is:

$${\sigma }_p^2(t)=c_1{e}^{-k_{d}t}+e^{-k_{d}t}{\displaystyle {\int }_0^{t}d{t}^{\prime }{e}^{k_d{t}^{\prime }}}\left[k_r\overline{m}(t^{\prime })+2c_0{k}_r+(2k_r+k_d)\overline{p}(t^{\prime })\right]$$ (A36)

The expressions for $\overline{p}(t)$ and $\overline{m}(t)$ can be inserted (see Equation A12 and Equation 2 of [21], respectively), and the integral can be evaluated in closed form. We require a few more constraints, however, in order to set c₀ and c₁. We assume that at cell division the contents (messengers and proteins) of the mother cell is distributed among the two daughters randomly but with equal probability. We can then write:

$$P_{\text{daughter}}(p)={\displaystyle \sum _{q=0}^{\infty }{P}_{\text{binom}}(p|q)P_{\text{mother}}(q)}$$ (A37)

Where P_binom(p|q) represents the probability that p proteins are distributed to a daughter cell given that the mother cell contains q proteins at division time. This is obviously just the binomial distribution with the probability of a successful Bernoulli trial equal to 0.5. P_mother(q) in the above equation represents the probability that the mother contains q proteins.

From this we can compute the relationship between the protein variance immediately before and immediately after cell division:

$${\sigma }_p^2(0)=\left[{\displaystyle \sum _{p=0}^{\infty }{p}^2}{\displaystyle \sum _{q=0}^{\infty }{P}_{\text{binom}}(p|q)P_{\text{mother}}(q)}\right]-{\overline{p}}^2(0)=\left[{\displaystyle \sum _{q=0}^{\infty }{P}_{\text{mother}}(q)}{\displaystyle \sum _{p=0}^{\infty }{p}^2{P}_{\text{binom}}(p|q)}\right]-{\overline{p}}^2(0)=\left[{\displaystyle \sum _{q=0}^{\infty }{P}_{\text{mother}}(q)}\left({\mathrm{Var}}_{\text{binom}}[p|q]+E_{\text{binom}}{[p|q]}^2\right)\right]-{\overline{p}}^2(0)=\left[{\displaystyle \sum _{q=0}^{\infty }{P}_{\text{mother}}(q)\left(\frac{1}{2}(1-\frac{1}{2})q+{(\frac{q}{2})}^2\right)}\right]-{\overline{p}}^2(0)=\frac{1}{4}\langle q\rangle +\frac{1}{4}\langle q^2\rangle -{\overline{p}}^2(0)=\frac{1}{4}[\langle q\rangle +\langle q^2\rangle -{\langle q\rangle }^2]=\frac{1}{4}[\langle q\rangle +\mathrm{Var}[q]]=\frac{1}{4}[\overline{p}(t_D)+{\sigma }_p^2(t_D)]$$ (A38)

where Var_binom[p|q] and E_binom[p|q] represent the variance and mean of the number of successful Bernoulli trials, p, given q attempts. We can also compute:

$$\mathrm{Cov}[m,p](0)=\left[{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{q=0}^{\infty }{\displaystyle \sum _{m=0}^{\infty }m}{\displaystyle \sum _{p=0}^{\infty }p}{P}_{\text{binom}}(m|n)}}{P}_{\text{binom}}(p|q)P_{\text{mother}}(n,q)\right]-\overline{m}(0)\overline{p}(0)=\left[{\displaystyle \sum _{n=0}^{\infty }{\displaystyle \sum _{q=0}^{\infty }{P}_{\text{mother}}(n,q)}\frac{n}{2}\frac{q}{2}}\right]-\overline{m}(0)\overline{p}(0)=\frac{1}{4}\langle nq\rangle (t_D)-\frac{\overline{m}(t_D)}{2}\frac{\overline{p}(t_D)}{2}=\frac{1}{4}\mathrm{Cov}[m,p](t_D)$$ (A39)

We can insert Equations A12, A38, and A39 into Equation A34 in order to solve for c₀; this yields:

$$c_0=-\frac{1}{3}\overline{p}(t_D)=-\frac{2}{3}\overline{p}(0)=-\frac{2}{3}\frac{k_r{k}_t}{k_d}\left[\frac{e^{-k_d{t}_D}-e^{-k_d{t}_r}}{k_d}+2t_D-t_r\right]$$ (A40)

which, along with Equation A38, allows us to write:

$$\begin{gathered} {\sigma }_p^2(0<t<t_r)=\frac{k_r{k}_t{e}^{-k_{d}t}}{3k_d^3}[(3k_d+2k_r)(e^{k_d{t}_r}-e^{k_d{t}_D})+3(t_r-2t_D)k_d^2+k_r(6-4k_d{t}_D+2k_d{t}_r)+e^{-k_d(t_r+t_D-t)} \\ \times \left((3k_d+2k_r)(e^{k_d{t}_r}-e^{k_d{t}_D})+e^{k_d(t_r+t_D)}[3k_d^2(2t_D-t_r+t)+k_r(6k_{d}t+4k_d{t}_D-2k_d{t}_r-6)]\right) \\ +\frac{e^{-3k_d(t_r+t_D)}}{4e^{k_d{t}_D}-1}\times ((3k_d+2k_r)\times [e^{3k_d{t}_D+2k_d{t}_r}-e^{2k_d{t}_D+3k_d{t}_r}-4e^{2k_d(2t_D+t_r)}]+e^{3k_d{t}_D+4k_d{t}_r}[6k_r+3k_d^2(t_r-t_D)] \\ +4e^{4k_d{t}_D+3k_d{t}_r}[3k_d^2(2t_D-t_r)]+k_r(4k_d{t}_D-2k_d{t}_r-3)]+e^{3k_d(t_D+t_r)}[14k_r+2k_d(6+k_r{t}_D-2k_r{t}_r)-3k_d^2{t}_D])] \end{gathered}$$

$$\begin{gathered} {\sigma }_p^2(t_r<t<t_D)=\frac{k_r{k}_t}{3k_d^3}\frac{e^{-k_d(t+3(t_r+t_D))}}{4e^{k_d{t}_D}-1}\times [-(3k_d+2k_r)e^{k_d(t+2t_D+3t_r)}-8(3k_d+4k_r)e^{k_d(t+4t_D+2t_r)}+2(3k_d+4k_r)e^{k_d(t+3t_D+2t_r)}-3k_d^2(t_D-t)e^{3k_d{t}_D+4k_d{t}_r} \\ +3(k_d+2k_r)(k_d(t_D-t)-1)e^{3k_d(t_D+t_r)}+8[2k_r(k_d(3t+t_D-2t_r)-3)+3k_d^2(t+t_D-t_r)]e^{k_d(t+4t_D+3t_r)}-2[2k_d(k_r(3t+t_D-2t_r)-3)+3k_d^2(t+t_D-t_r)-10k_r]e^{k_d(t+3(t_D+t_r))} \\ +12[2k_r+k_d^2(t_r-t)]e^{4k_d(t_D+t_r)}-12[k_d(2k_r{t}_r-2k_{r}t-1)+k_d^2(t_r-t)-3k_r]e^{4k_d{t}_D+3k_d{t}_r}] \end{gathered}$$ (A41)

Now, deriving the population mean and variance is simply a matter of integrating out the time variable according to the prescription of [21] (see equations S23 and S25 therein). It is well established that populations of log-phase cells have exponentially distributed ages [23, 24]:

$$P_{\text{age}}(t)=\frac{2\ln (2)}{t_D}{2}^{-t/t_D}$$ (A42)

and so we can write:

$$E[p]={\displaystyle {\int }_0^{t_D}\overline{p}}(t)\frac{2\ln (2)}{t_D}{2}^{-t/t_D}dt$$

$$\mathrm{Var}[p]={\displaystyle {\int }_0^{t_D}{\sigma }_p^2}(t)\frac{2\ln (2)}{t_D}{2}^{-t/t_D}dt+{\displaystyle {\int }_0^{t_D}{\overline{p}}^2}(t)\frac{2\ln (2)}{t_D}{2}^{-t/t_D}dt-E{[p]}^2$$ (A43)

The resulting expression for the population mean is relatively simple:

$$E[p]=\frac{2^{-t_r/t_D}{e}^{-k_d(t_D+t_r)}{k}_r{k}_t{t}_D}{t_D{k}_d^2\ln (2)+k_d{\ln }^2(2)}\times \left[\ln (2)2^{t_r/t_D}{e}^{k_d{t}_r}-\ln (4)e^{k_d{t}_D}+\left(2k_d{t}_D+4{\ln }^2(2)+\ln (4)-{\ln }^2(4)\right)e^{k_d(t_r+t_D)}\right]$$ (A44)

while the expression for the population variance is quite long and cumbersome (and as such, will not be reproduced here) although it can be expressed in closed form.

It it fairly common in single cell proteomics measurements to report size-normalized protein distributions [2, 3]. Deriving the size-normalized protein statistics can be accomplished with only a minor revision to our formulae. Assuming cells grow exponentially during the cell cycle, we can write the a cell’s size, s, as:

$$s(t)=s_0{2}^{t/t_D}$$ (A45)

Now we can compute the average cell size, $\overline{s}$, as:

$$\overline{s}={\displaystyle {\int }_0^{t_D}{s}_0{2}^{t/t_D}\frac{2\ln (2)}{t_D}}{2}^{-t/t_D}dt=2\ln (2)s_0$$ (A46)

Then solving for s₀ such that $\overline{s}$ is 1 average cell gives s₀ = 1/(2ln(2)). We can use this to write the size-normalized messenger mean and protein mean simply by dividing $\overline{m}(t)$ (as computed in [21]) and $\overline{p}(t)$ by the instantaneous cell size, and we can also write the protein variance by dividing ${\sigma }_p^2(t)$ by the squared instantaneous cell size:

$$E{[m]}_{\text{norm}}={\displaystyle {\int }_0^{t_D}\overline{m}(t)\frac{4{\ln }^2(2)}{t_D}}{2}^{-2t/t_D}dt$$

$$E{[p]}_{\text{norm}}={\displaystyle {\int }_0^{t_D}\overline{p}(t)\frac{4{\ln }^2(2)}{t_D}}{2}^{-2t/t_D}dt$$

$$\mathrm{Var}{[p]}_{\text{norm}}={\displaystyle {\int }_0^{t_D}{\sigma }_p^2(t)\frac{8{\ln }^3(2)}{t_D}}{2}^{-3t/t_D}dt+{\displaystyle {\int }_0^{t_D}{\overline{p}}^2(t)\frac{8{\ln }^3(2)}{t_D}}{2}^{-3t/t_D}dt-E{[p]}_{\text{norm}}^2$$ (A47)

Again omitting the expression for the protein variance (we have included a Mathematica workbook that includes it as part of the Supplemental Material [47]), we find:

$$E{[m]}_{\text{norm}}=\frac{k_t}{k_d}\left[\ln (2)\left(4^{1-t_r/t_D}-1\right)+\ln (4)\left(1-4^{-t_r/t_D}\right)-\frac{\ln {(2)}^2}{k_d{t}_D+\ln (4)}\left(4^{1-t_r/t_D}-e^{k_d(t_r-t_D)}\right)\right]$$

$$E{[p]}_{\text{norm}}=\frac{k_r{k}_t{2^{-1-2}}^{t_r/t_D}{e}^{-k_d(t_r+t_D)}}{k_d^2(k_d{t}_D+\ln (4))}\times \left[4^{t_r/t_D}{e}^{k_d{t}_r}(-2\ln {(2)}^2-\ln (2)\ln (4)+k_d{t}_D\ln (8)+\ln (4)\ln (16))+e^{k_d{t}_D}\left(8\ln {(2)}^2-k_d{t}_D(4^{t_r/t_D}\ln (4)+\ln (16))-\ln (4)(4^{t_r/t_D}\ln (4)+\ln (16))\right)+e^{k_d(t_r+t_D)}{k}_d(k_d{t}_D+\ln (4))\left(-4^{t_r/t_D}{t}_r\ln (4)+t_D(2+4^{t_r/t_D}+4^{t_r/t_D}\ln (16))\right)\right]$$ (A48)

Finally, we note that a time-dependent expression for the protein messenger covariance was derived en route to the protein mean and variance (see Equations A34 and A40). We can use this to compute the size-normalized time-averaged mRNA-protein covariance and Pearson correlation coefficient:

$$\mathrm{Cov}{[m,p]}_{\text{norm}}={\displaystyle {\int }_0^{t_D}\mathrm{Cov}[m,p](t)\frac{8{\ln }^3(2)}{t_D}}{2}^{-3t/t_D}dt+{\displaystyle {\int }_0^{t_D}\overline{m}(t)\overline{p}(t)\frac{8{\ln }^3(2)}{t_D}}{2}^{-3t/t_D}dt-E{[m]}_{\text{norm}}E{[p]}_{\text{norm}}$$

$${{\rho }_m}_{,p,\text{norm}}=\frac{\mathrm{Cov}{[m,p]}_{\text{norm}}}{\sqrt{\mathrm{Var}{[m]}_{\text{norm}}\mathrm{Var}{[p]}_{\text{norm}}}}$$ (A49)

Appendix B: Correcting for extrinsic noise

We can consider the effects of extrinsic noise in the parameters in our model. Following the prescription of [21] we can Taylor expand about the mean values of each parameter:

$$E_{\text{ext}.\text{nse}.}[m]\approx E[m|{\overline{x}}_1,\dots {\overline{x}}_n]+\frac{1}{2}{\displaystyle \sum _i{\left(\frac{{\partial }^{2}E[m|x_1,\dots x_n]}{\partial x_i^2}\right)}_{{\overline{x}}_1,\dots {\overline{x}}_n}\mathrm{Var}[x_i]}+{\displaystyle \sum _{i<j}{\left(\frac{{\partial }^{2}E[m|x_1,\dots x_n]}{\partial x_i\partial x_j}\right)}_{{\overline{x}}_1,\dots {\overline{x}}_n}\mathrm{Cov}[x_i,x_j]}$$

$$\begin{gathered} E_{\text{ext}.\text{nse}.}[p]\approx E[p|{\overline{x}}_1,\dots {\overline{x}}_n] \\ +\frac{1}{2}{\displaystyle \sum _i{\left(\frac{{\partial }^{2}E[p|x_1,\dots x_n]}{\partial x_i^2}\right)}_{{\overline{x}}_1,\dots {\overline{x}}_n} \\ \mathrm{Var}[x_i]}+{\displaystyle \sum _{i<j}{\left(\frac{{\partial }^{2}E[p|x_1,\dots x_n]}{\partial x_i\partial x_j}\right)}_{{\overline{x}}_1,\dots {\overline{x}}_n} \\ \mathrm{Cov}[x_i,x_j]} \end{gathered}$$

$${\mathrm{Var}}_{\text{ext}.\text{nse}.}[p]\approx \mathrm{Var}[p|{\overline{x}}_1,\dots {\overline{x}}_n]+E{[p|{\overline{x}}_1,\dots {\overline{x}}_n]}^2+\frac{1}{2}{\displaystyle \sum _i{\left(\frac{{\partial }^2\mathrm{Var}[p|x_1,\dots x_n]}{\partial x_i^2}\right)}_{{\overline{x}}_1,\dots {\overline{x}}_n}\mathrm{Var}[x_i]}+{\displaystyle \sum _{i<j}{\left(\frac{{\partial }^2\mathrm{Var}[p|x_1,\dots x_n]}{\partial x_i\partial x_j}\right)}_{{\overline{x}}_1,\dots {\overline{x}}_n}\mathrm{Cov}[x_i,x_j]}+\frac{1}{2}{{\displaystyle \sum _i\left(\frac{{\partial }^{2}E{[p|x_1,\dots x_n]}^2}{\partial x_i^2}\right)}}_{{\overline{x}}_1,\dots {\overline{x}}_n}\mathrm{Var}[x_i]+{{\displaystyle \sum _{i<j}\left(\frac{{\partial }^{2}E{[p|x_1,\dots x_n]}^2}{\partial x_i\partial x_j}\right)}}_{{\overline{x}}_1,\dots {\overline{x}}_n}\mathrm{Cov}[x_i,x_j]-E_{\text{ext}.\text{nse}.}{[p]}^2$$ (B1)

where E[p|x₁, …x_n], for example, represents the expression for the mean protein count (e.g. Equation A47), evaluated with parameters x₁, …x_n. An analogous expression can also be written down for Cov[m, p] in order to compute the effect of extrinsic noise on the mRNA-protein covariance and Pearson correlation.

Appendix C: Fitting Our Model to the Taniguchi Data Set

We attempted to find the transcription, translation, and mRNA degradation rates that minimize the squared error (denoted Δ_i) when fitting our model to the experimental data in [2]. The data includes measured protein variances and means (represented below as ${\sigma }_i^2$ and ${\overline{p}}_i$ for each protein i), their respective error estimates ( ${\epsilon }_{{\sigma }_i^2}$ and ${\epsilon }_{{\overline{p}}_i}$), mRNA means ( ${\overline{m}}_i$), and mRNA lifetimes (the inverse of the mRNA degradation rates, denoted below as $k_{d,i}^{\exp }$) for 585 E. coli genes.

We pose the set of optimization problems:

$${\mathrm{\Delta }}_i(\rho )=\underset{\{k_{t,i},k_{r,i},k_{d,i}\}>0}{min}\left[{\left(\frac{{\mathrm{Var}}_{\text{ext}.\text{nse}.}[p_i](k_{t,i},k_{r,i},k_{d,i};\rho )-{\sigma }_i^2}{{\epsilon }_{{\sigma }_i^2}}\right)}^2+{\left(\frac{E_{\text{ext}.\text{nse}.}[p_i](k_{t,i},k_{r,i},k_{d,i};\rho )-{\overline{p}}_i}{{\epsilon }_{{\overline{p}}_i}}\right)}^2+{\left(\frac{E_{\text{ext}.\text{nse}.}[m_i](k_{t,i},k_{d,i};\rho )-{\overline{m}}_i}{{\epsilon }_{{\overline{m}}_i}}\right)}^2+{\left(\frac{k_{d,i}-k_{d,i}^{\exp }}{{\epsilon }_{k_{d,i}}}\right)}^2\right]$$ (C1)

where Var_{ext. nse.}[p_i](k_t,i, k_r,i, k_d,i; ρ), E_{ext. nse.}[p_i](k_t,i, k_r,i, k_d,i; ρ), and E_{ext. nse.}[m_i](k_t,i, k_d,i; ρ) represent our theoretical expressions for the protein variance, protein mean, and mRNA mean, respectively (Equations B1). Here, ρ represents a matrix describing correlations among the various extrinsic noise sources; when they are assumed to be independent, ρ = 𝟙. Because [2] does not report errors for the messenger mean and degradation rates, ${\epsilon }_{{\overline{m}}_i}$ and ${\epsilon }_{k_{d,i}}$ were set equal to ${\overline{m}}_i$, and $k_{d,i}^{\exp }$ (the third and fourth terms in Δ_i therefore represent squared relative deviations). Its important to note that each Δ_i is a fit of our model to four measured values by allowing only three to vary (k_t,i, k_r,i, k_d,i); enabling more parameters to vary, or fitting to three or two measured values leaves the system underconstrained, and is not a meaningful test of the model’s ability to recapitulate the data. Also of note, the dependence Var_{ext. nse.}[p_i], E_{ext. nse.}[p_i], and E_{ext. nse.}[m_i] on t_r and t_D have been suppressed above. We assume during the fitting that cells have average doubling times of t_D = 120 minutes and each gene, i, has its own average replication time that depends on it location along the chromosome as t_r,i = 42.2 + χ_i × 42.4 minutes. Each χ_i was computed as the fraction of the given gene’s locus along the E. coli chromosome as measured from origin to terminus [27, 48].

We performed the 585 optimizations using the SUBPLEX [49] method as implemented in the freely available nlopt software package [50].

Appendix D: Sampling Correlation matrices with Approximately Uniformly-Distributed Off-Diagonal Elements

We constructed 50,000 random correlation matrices with approximately uniformly-distributed off-diagonal terms by first constructing a large set of random matrices and then pruning the ones from over-represented regions of the correlation matrix space.

The random matrices were constructed by sampling the elements of a lower triangular matrix, L, such that the squared elements of each row sum to 1 and the diagonal terms are non-negative. The elements of each row, i, live on an i-dimensional half-sphere of radius 1; we can evenly sample the surface of each of these half-spheres by sampling the elements in L from a standard normal distribution, or from the positive half of the standard normal distribution if the element is on-diagonal, and then normalizing each row element by $\sqrt{{\displaystyle {\sum }_j{L}_{i,j}^2}}$. The product, ρ = LL^T, is then positive definite with ones on diagonal (as all correlation matrices must be). In practice, this will lead to a set of correlation matrices with very-different distributions of off-diagonal terms. Randomly permuting the indices of the rows and columns of these matrices yields off-diagonal distributions of similar shape, but they remain non-uniform.

In order to ensure approximate uniformity in the off-diagonal terms, we generated 100,000 random matrices, and assigned to each a score, S, representing the degree to which its off-diagonal terms are over- or under-represented. This was accomplished by first histogramming (with a bin width of 0.001) the 100,000 occurrences of each off-diagonal term and using the results as “frequency” functions, f_i,j(ρ), that represent the number of random matrices with i, j elements within the same bin as the given matrix, ρ. Using these, a score was computed for each matrix as:

$$S(\rho )={\displaystyle \sum _{i,j<i}{f}_{i,j}{(\rho )}^{-2}}$$ (D1)

This score tends to be larger for ρ matrices in which most terms are under-represented in our set of 100,000 random matrices, and smaller for ρs in which most terms are over-represented. Taking the 50,000 matrices with the largest scores yielded approximately uniformly-distributed off-diagonal terms (see Figure 5A, blue histograms).