Understanding genetic architecture of hybrid performances is important for species showing heterosis. Giraud et al. evaluated an...
Keywords: hybrids, QTL detection, additivity, dominance, silage maize, multiparental populations, MPP
Abstract
Several plant and animal species of agricultural importance are commercialized as hybrids to take advantage of the heterosis phenomenon. Understanding the genetic architecture of hybrid performances is therefore of key importance. We developed two multiparental maize (Zea mays L.) populations, each corresponding to an important heterotic group (dent or flint) and comprised of six connected biparental segregating populations of inbred lines (802 and 822 lines for each group, respectively) issued from four founder lines. Instead of using “testers” to evaluate their hybrid values, segregating lines were crossed according to an incomplete factorial design to produce 951 dent–flint hybrids, evaluated for four biomass production traits in eight environments. QTL detection was carried out for the general-combining-ability (GCA) and specific-combining-ability (SCA) components of hybrid value, considering allelic effects transmitted from each founder line. In total, 42 QTL were detected across traits. We detected mostly QTL affecting GCA, 31% (41% for dry matter yield) of which also had mild effects on SCA. The small impact of dominant effects is consistent with the known differentiation between the dent and flint heterotic groups and the small percentage of hybrid variance due to SCA observed in our design (∼20% for the different traits). Furthermore, most (80%) of GCA QTL were segregating in only one of the two heterotic groups. Relative to tester-based designs, use of hybrids between two multiparental populations appears highly cost efficient to detect QTL in two heterotic groups simultaneously. This presents new prospects for selecting superior hybrid combinations with markers.
ALLOGAMOUS crops such as maize generally display high heterosis and strong inbreeding depression for yield-related traits. This phenomenon has prompted the invention of hybrid varieties (East 1908; Shull 1908). The definition of heterotic groups has played a major role in advancing and exploiting heterosis in maize breeding. Heterotic groups are developed to maximize the performance of hybrids. Selection is performed within one group relative to its performance when crossed with lines of the reciprocal group. In the U.S. Corn Belt, hybrid breeding has shaped two main heterotic groups: the “stiff stalks” and the “nonstiff stalks.” In Northern Europe the two main heterotic groups are “dent” and “flint.” Hybrid breeding has been adopted in sunflower, rapeseed, and rye (Bernardo 2010), but also recently in numerous autogamous species such as tomato, barley, wheat, and rice (Bai and Lindhout 2007; Longin et al. 2012; Mühleisen et al. 2013). The definition of heterotic groups remains a major research objective in species recently subjected to hybrid breeding methods (cf. Zhao et al. 2015). Hybrids between animals from different breeds are also used in pigs and poultry, and there is a growing interest in considering crossbred performances instead of purebred performances for improving hybrid value (see for instance Zeng et al. 2013; Vitezica et al. 2014).
Understanding the genetic basis of hybrid performance between two genetic groups is therefore a key issue in defining efficient hybrid breeding strategies. Hybrid value is traditionally decomposed into two parts: general combining ability (GCA) and specific combining ability (SCA). GCA is an estimate of the average hybrid performance of the parent. In hybrid breeding, the GCA of a line is a reflection of its average performance when crossed with lines from the complementary group. SCA is the difference between the value of the hybrid and its prediction based on the GCAs of the parents (Sprague and Tatum 1942). GCAs reflect the statistically additive allelic effects. They involve additive, dominance, and epistatic gene action effects. SCA only involves dominant and epistatic gene action effects (cf. Reif et al. 2007). The relative magnitudes of the GCA and SCA variation determine optimal strategies for hybrid breeding schemes. In crop species such as maize, selection for yield is generally carried out in two stages. In the first stage, new inbred lines of each group are selected based on their “test-cross hybrid value,” i.e., the performance of a hybrid(s) with a limited number of lines representative of the complementary group, called the tester(s). In the second stage, an incomplete factorial design is implemented to identify the best hybrid combinations between inbred lines selected in each group. Test-cross hybrid value of a line is a combination of its GCA and its SCA with the (few) tester(s) considered. As the magnitude of SCA increases relative to GCA, the second stage requires more resources and the choice of tester in the first stage is critical. In maize, GCA has a larger contribution to the test-cross hybrid value than SCA [see for instance Schrag et al. (2006) or Fischer et al. (2008) for grain yield; Geiger et al. (1986), Argillier et al. (2000), or Grieder et al. (2012) for whole plant biomass yield]. However, SCA is large enough to warrant the use of several testers during the first stage and/or devoting substantial resources to the second stage. For species where heterotic groups were defined recently, a higher ratio of SCA to GCA is expected (as shown theoretically by Reif et al. 2007).
Identification of the QTL underpinning hybrid values and their GCA and SCA components would improve the efficiency of hybrid breeding, and lead to increased understanding of heterosis. Most of the QTL detection experiments on maize yield-related traits have been based on biparental populations evaluated with a single tester (reviewed in Truntzler et al. 2010; Manicacci et al. 2011). Such designs limit the evaluation of heterosis and by definition are unable to detect SCA effects. QTL detection in multiparental populations has proved efficient for exploring a larger part of the diversity and for increasing power in comparison to biparental populations (Blanc et al. 2006; Kump et al. 2011; Bardol et al. 2013; Giraud et al. 2014; Foiada et al. 2015). A few studies have investigated multiparental populations and estimated additivity (GCA) and dominance (SCA). One approach has been to consider all or some parental lines as testers (Rebaï et al. 1997; Larièpe et al. 2012). Larièpe et al. (2012) found QTL with apparent overdominance for heterotic traits, such as yield, due to the presence of hybrids between related lines in the studied design.
Other multiparental QTL studies were conducted on hybrids between sets of lines selected in complementary genetic groups (factorial mating designs corresponding to the second stage of hybrid breeding programs). This was carried out first with a limited number of SSR markers by Parisseaux and Bernardo (2004), then by van Eeuwijk et al. (2010) with SNP markers. Both studies identified QTL for GCA that were specific to each heterotic group. SCA effects were considered negligible in these studies. Technow et al. (2014) used a factorial design between two heterotic groups corresponding to the last stages of a breeding program for genomic prediction. The use of a Bayes B model led to the identification of a few markers with sizable effects on GCA and SCA.
Compared to tester-based designs, factorial designs between two complementary heterotic groups enable the simultaneous detection of GCA QTL in both groups. Each hybrid involves a pair of recombinant lines, which reflect the allelic segregations in their respective groups and therefore both are informative for QTL mapping. Conversely, tester designs involve a single recombinant line per hybrid. As a consequence, for the same number of recombinant lines to be evaluated in each group, factorials potentially require phenotyping fewer hybrids than tester-based designs. Depending on how the design is constructed, factorials have the potential to address QTL involved in the SCA of intergroup hybrids, which is of direct interest for breeding. However, to date the factorial populations examined comprised inbred lines displaying a complex pedigree structure within each group. These mapping lines had undergone a first cycle of selection based on their test-cross value and did not contribute equally to the hybrid population. An unselected hybrid population with known family structure would a priori be preferable for detecting QTL for GCA and SCA. Kadam et al. (2016) recently developed such a factorial design by crossing segregating populations from two complementary heterotic groups and showed its interest for genomic selection. However, the segregating populations had different sizes, resulting in very unbalanced contributions of founder lines to the hybrids.
A QTL mapping strategy based on the performances of hybrids between segregating lines created with a balanced mating design in each heterotic group, without a first step of selection, has the potential to transform maize breeding. To evaluate this strategy, two multiparental populations were developed, one in the flint and one in the dent heterotic groups. Segregating lines from the two groups were crossed according to an incomplete balanced factorial design to produce dent–flint hybrids that were phenotypically evaluated for silage performances. This approach leads to an original design to decompose hybrid value in its GCA and SCA QTL components using an extension of the joint linkage mapping model proposed so far for multiple parental designs. After estimating group-specific GCA and SCA variance components in our design, we demonstrate the effectiveness of this strategy to detect QTL for silage-related traits in maize. We discuss its broader application to better understand the basis of hybrid performance and monitor favorable alleles in hybrid breeding programs.
Materials and Methods
Genetic material
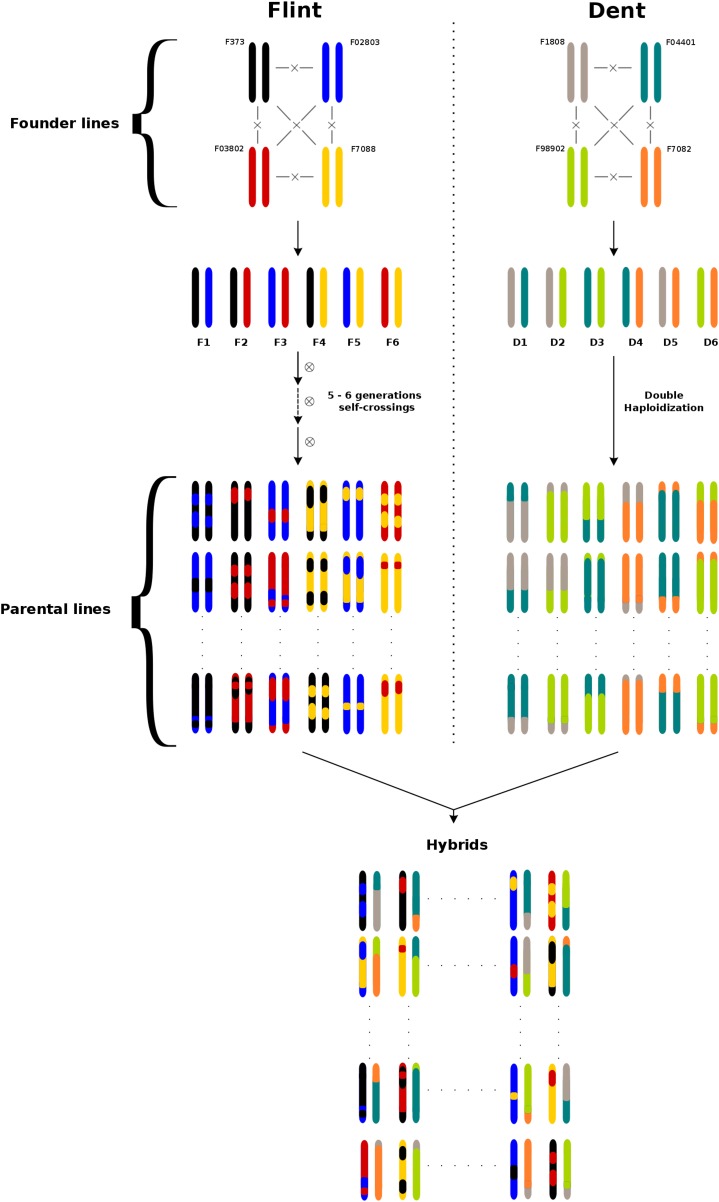
The experimental material consists of dent–flint hybrids obtained by crossing recombinant inbred lines (Figure 1). Four founder inbred lines within each heterotic group (dent and flint) were crossed according to a half-diallel mating design to produce six different F1’s. From these six F1’s, six biparental populations were derived (called D1–D6 for the dent and F1–F6 for the flint populations). The dent lines were obtained by doubled haploidization and the flint lines were obtained by selfing independent F2 individuals for five or six generations, depending on the biparental population. A total of 931 dent lines and 913 flint lines were obtained. From these “parental lines,” 863 dent lines and 879 flint lines were crossed in an incomplete factorial design to produce 1044 experimental hybrids. Each biparental population of one group was crossed with all of the biparental populations of the other group, with the objective of balancing the contributions of all founders. To increase the power of our QTL detection approach, we decided to maximize the number of different inbred lines from each group at the expense of our ability to separate GCA and SCA. Therefore, the majority of lines (699 in the dent group and 732 in the flint group) contributed to only one hybrid, but some lines contributed twice (163 in the dent group and 146 in the flint group) or even three (one dent parental line) or four times (one flint parental line). All founder lines of one group were crossed with the founder lines of the other group to create 16 hybrids which were used as checks.
Figure 1.
Schematic representation of the experimental design. Circled crosses indicate self-crossing generations and the dashed arrow indicates several generations of self-crossing.
Genotyping data
The founder lines and the parental lines were genotyped with an Affymetrix array designed by Limagrain which includes a subset of 18,480 SNPs of the Illumina 50K SNP Maize array (Ganal et al. 2011). To avoid ascertainment bias, we only considered the markers identified in the Panzea project (Ganal et al. 2011) which were polymorphic among the founder lines. After quality controls based on missing data, heterozygosity, and minor allele frequency, 9643 markers were retained for further analyses (see details in Giraud et al. 2017).
After checking for genotype consistency between founder lines and parental lines, off-type lines were excluded as well as inbred lines showing a high level of heterozygosity. A total of 875 dent lines and 883 flint lines were retained and used to build 12 genetic maps, 1 for each of the 12 biparental populations, as well as 1 dent–flint consensus map [see Giraud et al. (2017) for a description of the methods and individual population maps]. The dent–flint consensus map comprised 9548 markers. This map had a total length of 1578.6 cM and contains 5216 unique positions (cf. Supplemental Material, File S1 for the consensus map and File S2 for the genotypes of the inbred lines).
Field trial design and analysis
Hybrids were evaluated in eight different environments (four locations in 2013 and four in 2014) in the north of France and in Germany. Four traits were measured: silage yield [dry matter yield (DMY) in tons of dry matter per ha], dry matter content (DMC) at harvest (in percentage of fresh weight), plant height (PH) (six environments) (measured in centimeters), and female flowering [silking date (DtSILK) in days after January 1, scored as the date at which 50% of the plants of the elementary plot exhibited stigmas, referred to as “silks” in maize]. Trials were conducted according to common agricultural practices of the region. The field experiments were laid out as an augmented partially replicated design (Williams et al. 2011) where 17% of the experimental hybrids and all of the checks were evaluated twice. Trials were constituted of 1088 elementary plots, laid out in 68 incomplete blocks (see Giraud et al. 2017 for more details). Outlying observations (identified from visual inspection of the data and notes taken during field trial visits) were deleted. For silage yield, data from one of eight environments were excluded as they were not correlated with the other environments. Among the hybrids evaluated, 951 were considered for further analyses (950 for PH and DMY), corresponding to hybrids for which both parents had genotypic data consistent with their pedigree (822 flint parental lines and 802 dent parental lines). They belong to all of the 36 hybrid populations corresponding to the crosses between the six flint and the six dent line populations. The number of hybrids per population ranged from 15 to 32 (Table 1).
Table 1. Distribution of the 951 hybrids considered for QTL detection in the 36 populations according to the populations of origin of their parental lines.
| Parental line populations | F1: F373 × F02803 | F2: F373 × F03802 | F3: F02803 × F03802 | F4: F373 × F7088 | F5: F02803 × F7088 | F6: F03802 × F7088 | Total no. of hybrids | Total no. of lines |
|---|---|---|---|---|---|---|---|---|
| D1: F1808 × F04401 | 31 | 27 | 22 | 30 | 25 | 27 | 162 | 139 |
| D2: F1808 × F98902 | 34 | 27 | 22 | 30 | 23 | 32 | 168 | 144 |
| D3: F04401 × F98902 | 28 | 29 | 23 | 30 | 26 | 27 | 163 | 140 |
| D4: F1808 × F7082 | 28 | 28 | 25 | 30 | 27 | 27 | 165 | 138 |
| D5: F04401 × F7082 | 33 | 29 | 23 | 28 | 24 | 30 | 167 | 142 |
| D6: F98902 × F7082 | 24 | 23 | 15 | 25 | 21 | 18 | 126 | 99 |
| Total no. of hybrids | 178 | 163 | 130 | 173 | 146 | 161 | 951 | 802a |
| Total no. of lines | 162 | 139 | 111 | 154 | 118 | 138 | 822b | 1624 |
Dent populations are named D1–D6 and flint populations are named F1–F6, followed by the names of the two founder lines. The number of hybrids derived from each parental population is indicated (“Total no. of hybrids”) as well as the number of lines that contributed to hybrids (“Total no. of lines”).
Total number of flint lines contributing to hybrids.
Total number of dent lines contributing to hybrids.
Variance component analysis
Genetic variance decomposition was done on elementary plot values. The objectives were to estimate trait heritabilities, evaluate the relative importance of the GCA and SCA components in the hybrid variance, and the proportion of this variation due to the population structure. The general model is
| (1) |
where is the phenotypic value of the hth hybrid evaluated in the lth environment at the plot located at row column y, and in block . In this model, is the intercept, is the fixed effect of the environment To distinguish between the checks and the experimental hybrids, we used the parameter is set to 1 for check hybrids and to 0 for experimental hybrids. is the fixed genetic effect of the check hybrid derived from the cross between the dent founder line and the flint founder line is the genetic value of the hybrid issued from the cross between the flint parental line and the dent parental line Two models were used for (see below). To correct for spatial heterogeneities, we included in the model either a random block effect or random row and column effects, depending on the environment and trait. The choice between the two models was done by analyzing each environment independently and by choosing the best correction model based on the likelihood. is set to 1 for the environment if the spatial effects are modeled by block effects, 0 otherwise. These effects are assumed to be independent and normally distributed with variances specific to each environment. is the residual effect associated with the model with with a unique variance within each environment. In this model, the hybrid effect was decomposed into its GCA and SCA components, either considering or ignoring the population structure of the hybrid design.
Thus, in model (1.1), is decomposed into
| (1.1) |
where (respectively ) is the random GCA effect of the line () from the flint (dent) group. These effects are assumed to follow normal distributions with zero mean and two group-specific variances: is the random SCA effect of the interaction between the inbred lines and with
In model (1.2), the hybrid value is decomposed into the population structure and the within-population GCA and SCA components. Thus is decomposed into
| (1.2) |
where () is the fixed effect of the flint (dent) population of origin of the flint (dent) parental line () derived from the cross between founder lines i and j (i′ and j′), is the fixed effect corresponding to the interaction between the flint and dent populations of origin of the parental lines. and are the within-population equivalents of and These effects are assumed to follow the same distribution for all hybrid populations considered, i.e., and
From model (1.1) we derived the heritability at the whole design level as where is the genetic variance of the hybrids, computed as the sum of the GCA and SCA variance components; is the average number of times an experimental hybrid was evaluated in the whole design; and is the average residual variance of the model over all environments. The within-population heritability of the design was calculated with a similar formula but considering the within-population genetic variance computed from model (1.2). In the two models, the significance of the GCA and SCA effects was tested with a likelihood ratio test and we computed the percentages of SCA in the hybrid genetic variance and the within-population hybrid genetic variance.
The joint analysis of the hybrids between founder lines (considered as fixed effects) and the experimental hybrids (considered as random effects) allowed an efficient use of all field plots for estimating spatial field effects and partitioning variance into its genetic/nongenetic components. We tried to fit specific variances for each hybrid population, but as it did not significantly improve the adjustment of the models (P-value of likelihood ratio test >5%) whatever the trait considered, we fit homogeneous variances among populations in the final analyses. We also did not include interaction effects between hybrids and environments, which are thus part of the residuals of the models. Evaluation of genotype by environment interactions was not an objective of this study. Models were fit using the ASReml-R package (Butler et al. 2007; R Core Team 2013).
Computation of adjusted means and correlations between traits
QTL detection was based on the least-square means (ls-means) of each hybrid over the environments. To obtain these ls-means, we first corrected single-plot values by the best linear unbiased predictions of the spatial field effects obtained with model (1.2). Then for each trait, the corrected data of all hybrids were used to compute ls-means of hybrids using a model including a hybrid effect and an environment effect, both considered as fixed. Correlations between the different traits were calculated based on these ls-means. The R scripts used to estimate variance components and ls-means are included in File S3.
QTL detection
The QTL detection model considers the founder alleles transmitted to the hybrids and makes the assumption that each of the eight founder lines carries a different allele. The population structure of the design was taken into account in the model. We included random genetic effects corresponding to the parents of the hybrids to account for the fact that some parental inbred lines were involved in several hybrids.
| (2) |
where is an N × 1 vector of the ls-means of the experimental hybrids phenotyped for the considered trait, is the intercept, and is an N × 1 vector of 1. The term α (β) is a 6 × 1 vector of the fixed effects of the dent (flint) populations of origin of the dent (flint) parental line, (αβ) is a 36 × 1 vector of the fixed interaction effects between the dent and flint populations of parental lines. A, B, and C are the corresponding design matrices. () is an × 1 ( × 1) vector of the random effects of the dent ( flint) parents, with and are the corresponding design matrices. and are similar to the GCA effects of model (1.2) and correspond in this model to the GCA residuals not accounted for by the QTL. e is an N × 1 vector of the residuals of the model with The QTL effect is decomposed into three terms: and The first term, (), is the 4 × 1 vector of the allelic effects at the marker associated with each dent (flint) founder line. These effects correspond to the GCA effects of the QTL. For each marker, () is an N × 4 matrix of the probabilities that the hybrid received its dent (flint) allele from each of the four dent (flint) founder lines. is the 16 × 1 vector of the interactions, or SCAs, between the founder alleles; and is an N × 16 matrix corresponding to the element-wise product between each column of and each column of As the sum of probabilities for each allele equals 1, this model has 3 d.f. for the additive effects of the founder alleles (GCAs) in each group and 9 d.f. for the interaction effects (SCA). Probabilities that a hybrid received one of the four dent (flint) founder alleles were inferred for each position of the 9548 mapped markers based on the genotypes of its parental lines at the closest informative markers. These probabilities were computed with PlantImpute (Hickey et al. 2015) using 10 iterations.
QTL detection was performed with ASReml-R (Butler et al. 2007) considering the level of significance of the Wald test for the QTL effects. We considered a 5% genome-wide significance threshold based on the number of effective markers (Gao et al. 2008). The total effect at each marker position was tested using the “group” function of the ASReml-R package (Butler et al. 2007). After the first initial single-marker scan along the genome, a multimarker procedure was implemented using a forward and backward marker selection process. In the forward stage, the genome was scanned with a model including markers identified in previous steps and the most significant marker was added to the model. The process stopped when no more markers had significant effects at the 5% genome-wide risk level (in total, or for the GCA or SCA component). Finally, in the backward stage, all effects included in the model at the end of the forward process were jointly tested. Markers with no significant effect were removed step by step. The R scripts used to perform QTL detection are included in File S3.
The percentage of phenotypic variance explained by the population effects was calculated according to Nakagawa and Schielzeth (2013): where is the variance of the predicted values based on the population effects of the model when no QTL are included in the model, and and are the estimated variance components of the same model. Similarly, we estimated the percentage of variance explained by the population structure and the QTL effects () as where corresponds to the variance of the predicted performances based on the population and QTL effects, and and are the variance components in the corresponding model. To estimate the percentage of variance explained by the detected QTL (), we adapted the presented by Nakagawa and Schielzeth (2013) as where is the variance of predictions based on QTL effects, orthogonalized by the population effects. From these parameters, we estimated the percentage of within-population phenotypic variance explained by the QTL as We also estimated the individual R2 of each QTL after orthogonalizing predictions by the population effects and the effects of the other QTL.
To evaluate the quality of prediction of the QTL models, we also performed a cross-validation approach. A total of 80% of the data (training set) was sampled and used to identify QTL, estimate the population and QTL effects, and predict the values of the hybrids on the remaining 20% (test set). Sampling was stratified by population and was repeated 100 times. We observed that a full de novo QTL detection for each sampling would have led to excessive computing time. Therefore, for each sampling the significance of the QTL detected in the whole data set was tested in the training set and, following a backward procedure, only significant QTL were considered in the prediction model. The percentages of variance explained were estimated by the squared correlation between the predicted and observed hybrid values of the test set. This procedure was conducted (i) without taking into account SCA QTL effects; and (ii) taking them into account for QTL for which they were significant at a 5% individual risk level. We also considered a model including only the population effects.
Data availability
Raw phenotypic data, adjusted means of hybrid performances, genetic map, and genotypic data are available in File S4, File S5, File S1, and File S2, respectively. The pedigree of the segregating populations is described in File S6. The R scripts used for data analysis are available in File S3. File S7 contains the P-values of each marker in the single-marker QTL detection model. The markers with significant effects in the final multi-marker models are shown in Table S1. All the supplemental files are described in the File S8.
Results
Adjusted means and correlations between traits
The adjusted means of the experimental hybrids had greater variation than the hybrids between founder lines for all traits (Table 2). Adjusted means of hybrids between founder lines were on average slightly higher than the average values of the experimental hybrids (Table 2). DMY was positively correlated to PH (0.64) and DtSILK (0.57), and negatively correlated to DMC (−0.28). DMC was also negatively correlated to PH (−0.28) and DtSILK (−0.55). These correlations are consistent with those usually observed for these traits.
Table 2. Average performances across environments for the hybrids and variance components.
| Average performancesa | Variance components | ||||
|---|---|---|---|---|---|
| Trait | Hybrids between founder lines | Experimental hybrids | Effects | Globalb | Within-populationb |
| DMC | 33.5 (30.2–36.1) | 33.0 (25.7–41.3) | Flint GCA | 2.31 (0.26)*** | 0.98 (0.23)*** |
| (% of fresh weight) | Dent GCA | 0.92 (0.27)*** | 0.96 (0.23)*** | ||
| SCA | 0.43 (0.27)ns | 0.53 (0.25)* | |||
| Residual | 1.45–6.13c | 1.52–6.04c | |||
| H | 0.89 | 0.85 | |||
| %SCA | 11.7 | 21.5 | |||
| DMY | 16.5 (14.8–18.4) | 16.0 (11.8–20.2) | Flint GCA | 0.28 (0.10)*** | 0.30 (0.10)*** |
| (t.ha−1) | Dent GCA | 0.74 (0.10)*** | 0.44 (0.09)*** | ||
| SCA | 0.22 (0.11)* | 0.20 (0.10)* | |||
| Residual | 1.00–3.53c | 1.02–3.56c | |||
| H | 0.81 | 0.77 | |||
| %SCA | 17.4 | 21.0 | |||
| DtSILK | 211.6 (209.2–213.6) | 211.5 (206.7–217.9) | Flint GCA | 0.74 (0.19)*** | 0.51 (0.19)*** |
| (days after January 1) | Dent GCA | 1.26 (0.18)*** | 1.09 (0.17)*** | ||
| SCA | 0.39 (0.19)* | 0.47 (0.19)** | |||
| Residual | 0.96–6.13c | 0.96–6.12c | |||
| H | 0.89 | 0.88 | |||
| %SCA | 16.3 | 22.6 | |||
| PH | 251 (229–275) | 248 (204–283) | Flint GCA | 42.9 (11.7)*** | 38.4 (8.9)*** |
| (cm) | Dent GCA | 92.8 (11.0)*** | 45.1 (8.2)*** | ||
| SCA | 19.3 (11.8)ns | 13.4 (8.8)ns | |||
| Residual | 50.0–243.6c | 46.7–243.2c | |||
| H | 0.88 | 0.82 | |||
| %SCA | 12.4 | 13.8 | |||
Shown are the average performances across environments for the hybrids between founder lines and the experimental hybrids and variance components estimated using two models ignoring (global) or including (within-population) the population structure of the design, for DMC, DMY, female flowering time (DtSILK), and PH. Variance components were used to compute trait heritability and the percentage of hybrid variance due to SCA (in bold). ns, nonsignificant; H, heritability; %SCA, percentage of hybrid variance due to SCA. * P < 5%, ** P < 1%, *** P < 0.1%.
For each category of hybrids, range of variation (minimal and maximum values) is indicated between brackets.
SD of the GCA and SCA variance components is shown between brackets along with the level of significance of the random effect.
Minimum and maximum environmental residual variances.
Genetic variance analysis
We observed large and significant hybrid variances for all traits (Table 2). Broad-sense heritabilities at the design level were high for all traits: between 0.81 (DMY) and 0.89 (DMC and DtSILK). For all the traits except DMC, the dent and flint population effects were both significant at P < 5%, whereas their interaction was not. For DMC, the effect of the dent population was not significant (results not shown), in agreement with the small variation of DMC performances among the dent founder lines. Considering population effects in the model reduced the genetic variances but did not affect the inferences. In particular, GCA was significant for all traits and within-population heritabilities remained high (Table 2).
The decomposition of the hybrid variance into GCA and SCA showed that most of the hybrid variation was due to GCA. For the model which did not take into account the population structure, SCA was only significant (P < 5%) for DMY and DtSILK. It represented between 11.7% (DMC) and 17.4% (DMY) of the hybrid genetic variance. When considering the population structure in the model, the SCA variance component was significant for all traits but PH. The proportion of SCA represented ∼20% of the within-population genetic variance for all traits but PH, for which it was lower. The SD for SCA variances were large, which was expected from the design because of the small number of inbred lines that contributed to more than one hybrid.
QTL detection
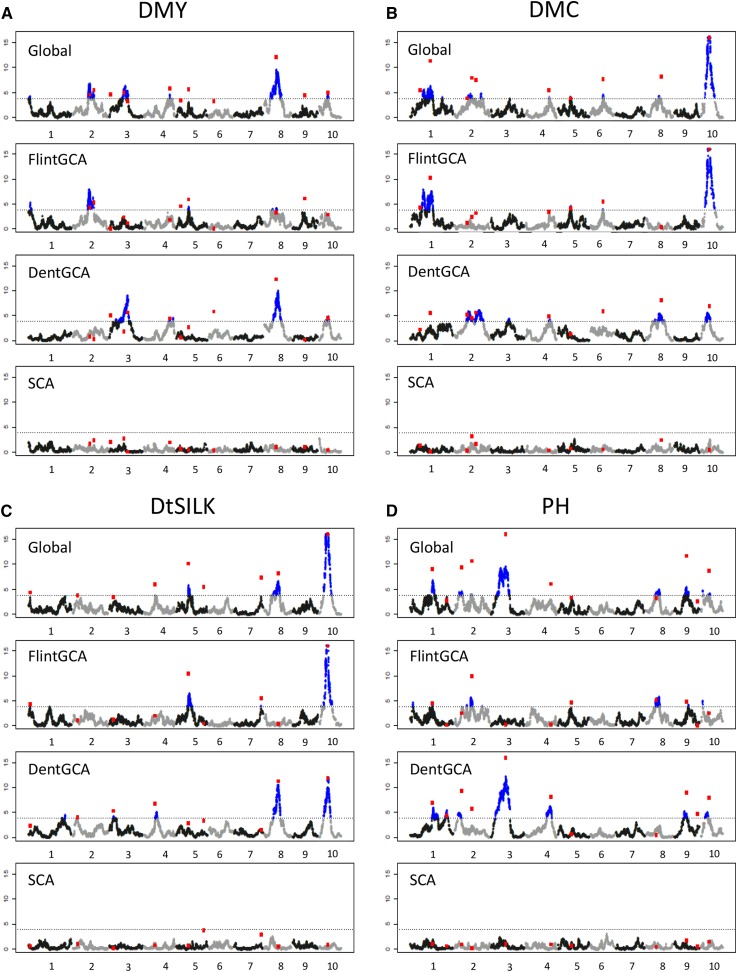
The thresholds at a 5% genome-wide level used for QTL detection were determined as −log(P-value) equal to 3.84. In total 42 QTL were detected for the four studied traits (Table 3): between 9 for DtSILK and 12 for DMY.
Table 3. QTL detection results for the different traits.
| Without SCA | With SCA | |||||||
|---|---|---|---|---|---|---|---|---|
| Trait | No. | R2pop | R2pop+QTL | R2QTL | R2*QTL | R2pop+QTL | R2QTL | R2*QTL |
| DMC | 10 (4) | 32.4 | 60.1 | 27.6 | 40.9 | 63.8 | 32.4 | 47.9 |
| DMY | 12 (5) | 21.9 | 49.5 | 27.7 | 35.5 | 55.1 | 34.2 | 43.9 |
| DtSILK | 9 (2) | 15.0 | 46.6 | 31.4 | 36.9 | 51.5 | 36.7 | 43.2 |
| PH | 11(2) | 33.8 | 60.0 | 26.6 | 40.2 | 63.0 | 30.7 | 46.4 |
Shown are the QTL detection results for the different traits: DMC, DMY, female flowering time (DtSILK), and PH. For each trait we indicated the number of QTL detected (No.) and between brackets the number of these QTL showing significant SCA effects at a 5% individual risk level, the proportion of the phenotypic variance (R2QTL, in %), and of the within-population phenotypic variance (R2*QTL, in %) explained by the detected QTL (with and without including SCA effects in the model). The percentage of variance explained by the population effect is also indicated (R2pop).
The majority of the QTL explained <5% of the variation (see Table S1). The only notable exception was a QTL detected on chromosome 10 at 44.5 cM, which explained ∼8% of the variance for DMC and 12% of the variance for DtSILK. This QTL region was also detected but with a smaller effect for DMY and PH. Other QTL regions also showed pleiotropic effects on different traits (Figure 2 and Table S1).
Figure 2.
QTL detected for the different traits: (A) DMY, (B) DMC, (C) DtSILK, and (D) PH. The chromosome number is indicated on the x-axis. For each trait, graphics correspond to the test of the global effect (“Global”) or of one component (“Flint GCA,” “Dent GCA,” and “SCA” effects). The blue (black) dots correspond to positions that were above (below) the threshold in the single-marker analysis (see File S7 for detailed results). The red ▪’s correspond to the −log(P-value) of the QTL that were included in the final multilocus model, with tests conditioned by the other QTL effects of the model. Note that values of −log(P-value) >16 were set to 16.
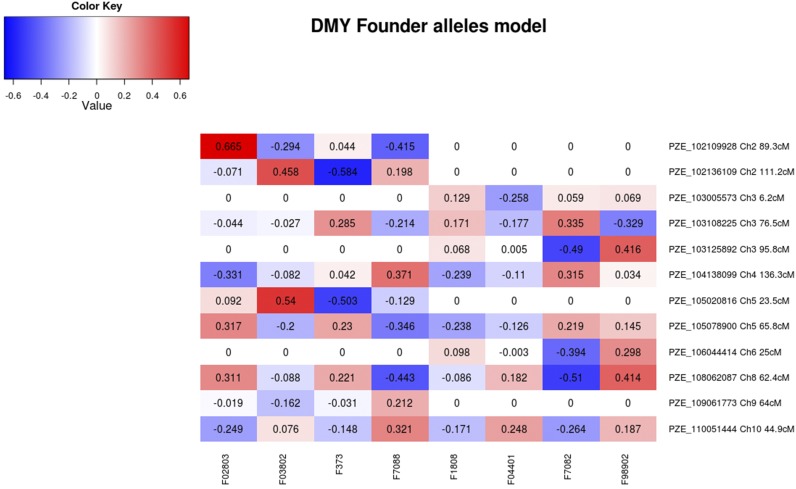
We tested the level of significance of GCA/SCA components for all QTL that were detected (Figure 2 and Table S1). A majority of QTL appeared specific to one group: 7 QTL were significant for both GCA effects, 21 only for the dent GCA effect, and 12 only for the flint GCA effect (Figure 2 and Table S1). The other QTL correspond to QTL with significant global effect but no significant individual GCA component. Interestingly, no founder line presented favorable alleles at all detected QTL. For instance, considering the dent and flint GCA effects for DMY, all founder lines presented positive and negative allelic effects at the QTL (Figure 3). This is consistent with the transgressive segregation observed in the experimental hybrid populations compared to the founder hybrids. None of the detected QTL showed a significant SCA effect at a 5% genome-wide level. However, 13 QTL were significant for SCA with an individual risk at 5%. QTL with significant SCA effects were located all over the genome.
Figure 3.
GCA effects for the founder lines for the QTL detected for DMY (in t.ha−1). Allelic effects are centered on zero for the dent founder lines (F1808, F04401, F7082, and F98902) and for the flint founder lines (F02803, F03802, F373, and F7088). QTL presenting a dent (flint) GCA effect not significant at a 5% individual risk level had their dent (flint) effects set to zero.
The detected QTL explained jointly from 30.7% (PH) to 36.7% (DtSILK) of the total phenotypic variance, and between 43.2 and 47.9% of the within-population phenotypic variance (for DtSILK and DMC, respectively). The increase in the percentage of phenotypic variance explained when taking into account SCA was moderate (between +6 and +7% for all traits) (Table 3).
These R2 values (Table 3) were computed on the data also used to estimate QTL effects, potentially giving an unfair advantage to models with a high number of parameters (i.e., models including SCA effects). Cross-validations were performed to eliminate this potential bias. They also provide an evaluation of the quality of predictions of our QTL models for new hybrids derived from the same populations. We observed a strong reduction of the R2 obtained by cross-validation compared to the R2 evaluated on the whole data set (R2pop+QTL column of Table 3). For instance, for DMY the R2pop+QTL decreased from 55% for the model including SCA to 27% (Table 4). The number of QTL found significant when considering only four-fifths of the data were lower than the number of QTL detected using the whole data set (results not shown). Taking into account the SCA effects that were significant at a 5% individual risk always had a small negative impact on the R2 of the models in the cross-validation process (Table 4).
Table 4. Cross-validation estimates of the quality of prediction of different models (average R2 and its SD) including population effects or population effects and QTL effects.
| Model | DMC | DMY | DtSILK | PH |
|---|---|---|---|---|
| Population effects | 28.4 ± 4.18 (SD) | 17.1 ± 4.16 (SD) | 10.4 ± 2.97 (SD) | 29.2 ± 4.35 (SD) |
| Pop+QTL GCA | 48.2 ± 4.48 (SD) | 29.0 ± 5.32 (SD) | 32.9 ± 4.60 (SD) | 49.8 ± 4.82 (SD) |
| Pop+QTL GCA and SCA | 47.4 ± 4.58 (SD) | 27.3 ± 5.13 (SD) | 32.1 ± 4.81 (SD) | 48.3 ± 4.78 (SD) |
For the models including QTL, for each sampling, QTL detected in the whole data set had their effects in the training set tested following a backward procedure and only the significant QTL were considered in the prediction model. Predictions were based on GCA effects only or on models considering also SCA effects significant at a 5% individual risk level. Pop, population.
Discussion
Genetic variance components
We observed significant variation among hybrids for all traits, with transgressive segregation evident in the hybrids. Experimental hybrids showed on average a slight decrease in performance compared to hybrids between founder lines. This suggests that recombination may have broken some favorable epistatic interactions between founder alleles. However, these effects seem limited and we cannot exclude that these differences were also partly explained by the small imbalance of our design or by segregation distortions (although no strong distortion was observed, cf. Giraud et al. 2017). The fact that some of the parental inbred lines contributed to more than one hybrid allowed us to estimate SCA/GCA variance components. Although the SCA variance component estimate was not very accurate, our results showed that most of the hybrid variance was due to GCA, with ∼20% of the within-population genetic variance due to SCA. This proportion was smaller for PH (14%). To our knowledge, few studies estimated SCA variances on European silage maize, limiting the number of possible comparisons. In a factorial between 11 dent and 11 flint lines, Geiger et al. (1986) found that SCA explained 8% of the hybrid variance for PH and DMC, and 15% for DMY. Significant but small SCA effects were found by Argillier et al. (2000) and Grieder et al. (2012) for DMC and DMY. Estimations of GCA/SCA components obtained for hybrid designs evaluated for grain yield considering dent–flint hybrids (Schrag et al. 2006, 2009, 2010; Fischer et al. 2008; and more recently Technow et al. 2014) or other heterotic patterns (Parisseaux and Bernardo 2004) consistently showed that SCA usually explained <10% of the hybrid variation for the traits considered. Most studies cited above were based on factorials derived from inbred lines that passed through a selection stage based on their test-cross values on the tester(s). This selection is expected to have reduced the magnitude of GCA but may also have retained lines with similar SCAs with the tester(s). This may have affected the relative proportions of the GCA and SCA components, potentially explaining the lower proportion of SCA observed compared to our study. In our design, the parental lines are derived without selection from the founder lines. They thus represent the whole allelic diversity available in each population, allowing us to estimate unbiased GCA and SCA components of the hybrid values of candidate lines.
The predominance of GCA over SCA is expected for hybrids obtained by crossing two divergent populations (Reif et al. 2007). In our study, founder lines derive from two heterotic groups created from populations that diverged >500 years ago (Tenaillon and Charcosset 2011). These two groups have undergone several cycles of reciprocal selection since the 1950s, which is expected to increase differentiation at loci showing dominance effects. If one QTL is fixed in one group but still segregates in the other group, dominance effects become confounded with additive effects (Technow et al. 2014). This results in a decrease of the SCA variance compared to the GCA variances over time. Even if the proportion of SCA is limited compared to GCA (20 vs. 40% for each GCA in our study), it might be sufficient to hinder an accurate estimation of GCA when using only a small number (one or two) of tester lines from the opposite group, as it is usually done in breeding programs.
QTL detection reveals complex allelic series and a predominance of group-specific GCA QTL
One advantage of our new genetic design is the known pedigree relationships between hybrids and a clear population structure, which can easily be accounted for in the QTL detection models to control for spurious association between markers and QTL. The structure of biparental populations allowed us to trace founder alleles down to the hybrids and thus to perform a QTL detection based on linkage information. This QTL detection model can be seen as an extension of the models used to detect QTL in multiparental population(s) crossed to the tester(s) (as done in Rebaï et al. 1997; Blanc et al. 2006; Giraud et al. 2014) or evaluated per se (Buckler et al. 2009).
Most QTL detected in our design are group-specific GCA QTL. This is in agreement with Giraud et al. (2014) who found different QTL in the dent and flint heterotic group. Among those group-specific QTL, we detected a QTL for DtSILK on chromosome 8 that is specific to the dent group. This QTL is located in a region where two flowering time QTL have been cloned [Vgt1 and Vgt2 (Salvi et al. 2007; Bouchet et al. 2013)]. Association mapping showed that for both QTL the early alleles are almost fixed in the flint group whereas they still segregate in the dent pool, consistent with Bouchet et al. (2013). We also observed a major QTL for DtSILK on chromosome 10. This QTL is significant in both the dent and flint group but has a larger effect in the flint group. This QTL likely corresponds to the QTL detected with a similar pattern in Giraud et al. (2014), close to the ZmCCT gene, which was fine mapped as a major flowering time QTL by Ducrocq et al. (2009) and validated by Coles et al. (2011). The predominance of group-specific GCA QTL was also observed by van Eeuwijk et al. (2010), when analyzing a maize factorial between two other heterotic groups for ear height, and by Parisseaux and Bernardo (2004), when considering intergroup hybrids obtained by crossing pairs of lines issued from a total of nine different heterotic groups. Group-specific GCA QTL may be due to actual differences in QTL allelic variability but may also result from epistatic effects differing between heterotic groups.
SCA represented ∼20% of the within-population genetic variance (except for PH), but we did not detect QTL with SCA effects significant at a 5% genome-wide risk level. We nevertheless detected dominance and/or SCA effects significant at a 5% individual risk level for some QTL. Cross-validation results showed that adding SCA QTL effects to the models slightly decreased the quality of prediction of hybrid values, suggesting that these moderate QTL SCA effects may not be well estimated in training sets. These results contrast strongly with those of Lu et al. (2003), Frascaroli et al. (2007, 2009), Schön et al. (2010), and Larièpe et al. (2012) who found a majority of QTL with large dominance effects for grain yield. An important feature of these studies is that they involve hybrids with a high level of inbreeding due to the use of parental lines as testers, contrary to our present study in which all hybrids evaluated are created from unrelated parents. This suggests that, in the absence of inbreeding, SCA is likely due to numerous small effects that are hardly detectable and/or that SCA is due to epistatic effects not included in our detection models. Similar effects may explain the differences in the QTL detected in biparental populations when comparing results obtained with different testers unrelated to the mapping population (Schön et al. 1994; Lübberstedt et al. 1997; Melchinger et al. 1998; Austin et al. 2000).
Also, Larièpe et al. (2012) and Schön et al. (2010) detected a large proportion of QTL with (pseudo-)overdominance in the pericentromeric regions, consistent with the observation of McMullen et al. (2009) that these regions show delayed fixation when developing recombinant inbred lines. In our design, the QTL presenting significant effects for SCA at a 5% individual risk level were not specifically mapped in the pericentromeric regions. A similar observation was reported by Technow et al. (2014) for hybrids between two heterotic groups. Altogether these observations support the hypothesis that reciprocal selection of heterotic groups has fixed complementary haplotypes in low recombinant centromeric regions involving linked dominant QTL. Such regions appear with large effects in populations that recombine different groups (e.g., Schön et al. 2010; Larièpe et al. 2012) and not in studies that only evaluate hybrids between groups (Technow et al. 2014; our present study).
Hence, all results show that performance of hybrids between lines from different heterotic groups is mostly affected by GCA QTL that are located at different positions in the two groups of interest. This is a combined consequence of (i) initial foundation of heterotic groups to prevent inbreeding by maximizing their differentiation; and (ii) later reciprocal selection (see above) that reinforced differentiation. A smaller fraction of QTL segregates in both groups and/or present SCA effects. In a reciprocal selection process these QTL are expected to evolve toward the first category (group-specific GCA QTL), or the absence of effect in any of the two groups when one favorable dominant allele becomes fixed in one of the two groups.
Possible adaptation of the QTL detection model
One of the main drawbacks of the linkage-based QTL detection model used in this study is that it requires the estimation of many parameters (35 d.f. for the combinations between the dent and flint populations plus 6 d.f. for the GCA and 9 d.f. for the SCA per QTL) which makes it necessary to develop large segregating populations to get enough power and accurate QTL effect estimates in practice. This certainly explains the strong reduction of R2 observed in cross-validation results. For this reason, it might become difficult to apply it to designs involving a larger number of founder lines and populations. Several alternative approaches can be explored to improve the power of the QTL detection model. One option for more complex cases would be to cluster the parental alleles based on their local similarities [as proposed by Leroux et al. (2014), and applied to experimental data by Bardol et al. (2013), Giraud et al. (2014), and Han et al. (2016)]. A simple option could be to consider, as done in genome-wide association study models, the SNP alleles received by each parental line or even the hybrid SNP genotypes directly. This is beyond the scope of this study but is addressed in a companion article (Giraud et al. 2017).
Interest of hybrids between recombinant materials vs. tester designs
One important feature of the design we implemented is that each hybrid is informative about both heterotic groups, which allowed us to reduce the number of tested hybrids by a factor of two in comparison to a test-cross evaluation based on a single tester from the opposite group and the same number of segregating lines in each group. The use of a factorial makes it necessary to produce hybrids using handmade crosses, whereas tester-based hybrids can be more easily produced in isolation blocks. As a first rough estimation (C. Bauland, personal communication), for planting 10 maize elementary plots for phenotyping, the additional cost of producing seeds by hand crosses rather than with an isolation block is <50%. This is less than the cost of phenotyping a single plot. It would nevertheless be interesting to compare the cost efficiency of different factorial and tester designs, for different species, experimentally or using simulations. Although not a direct experimental comparison due to different founders, it can be noted that in the joint analysis of two nested association mapping (NAM) designs (one flint and one dent) evaluated each for silage test-cross performances, Giraud et al. (2014) detected equal or slightly higher (up to six for PH) numbers of QTL than in our study. These differences are small in regards to the fact that these NAM designs involved almost two times more hybrids (∼1650 hybrids).
Also, our design certainly leads to better estimations of GCA QTL effects than designs based on few testers and gives the possibility to detect QTL involved in SCA (even if, as in our case, only small SCA effects were found). The factorial design we studied was obtained by crossing two multiparental designs, each comprised of connected biparental populations. Such multiparental designs are close to the type of populations routinely produced by breeders. One can also consider developing factorials from other types of multiparental designs such as multiparent advanced generation inter-cross (MAGIC) populations (Huang et al. 2015). Our QTL detection model can be extended easily to this case by simply removing the population structure effects.
The QTL detected in this study open the way to the implementation of a marker-assisted selection of new lines, taking into account complementarities of favorable alleles in each group (based on GCA and also on SCA), to produce the next generation of superior hybrids. Our results are encouraging but the QTL that were detected only partly explain the hybrid variability. It would thus be interesting to compare these predictions based on detected QTL with genomic predictions [as performed recently by Kadam et al. (2016) on a similar design], and to evaluate how to combine both sources of information. This issue is beyond the scope of this article but will be addressed in another study.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300305/-/DC1.
Acknowledgments
We thank T. Mary-Huard for helpful discussions and advice for the estimation of R2. We are grateful to anonymous reviewers and editors Jim Holland, Lauren Mc Intyre, and D. J. de Koning for very helpful comments. H.G. was funded by Université Paris–Sud through a scholarship from the Ministry of Research given by the Doctoral School ABIES (Agriculture Food Biology Environment Health). We thank Caussade Semences, Euralis Semences, Limagrain Europe, Maïsadour Semences, Pioneer Genetics, R2n, and Syngenta Seeds grouped in the frame of the ProMais SAM-MCR program for the funding, inbred lines development, hybrid production, and phenotyping. We are also grateful to scientists from these companies for helpful discussions on the results. We thank the Institut National de la Recherche Agronomique metaprogram SelGen and specifically the X-Gen and SelDir projects coordinated by Andrés Legarra and Hélène Gilbert, respectively, for partial funding and scientific feedback on the results.
Footnotes
Communicating editor: L. McIntyre
Literature Cited
- Argillier O., Méchin V., Barrière Y., 2000. Inbred line evaluation and breeding for digestibility-related traits in forage maize. Crop Sci. 40: 1596–1600. [Google Scholar]
- Austin D. F., Lee M., Veldboom L. R., Hallauer A. R., 2000. Genetic mapping in maize with hybrid progeny across testers and generations: grain yield and grain moisture. Crop Sci. 40: 30–39. [Google Scholar]
- Bai Y., Lindhout P., 2007. Domestication and breeding of tomatoes: what have we gained and what can we gain in the future? Ann. Bot. 100: 1085–1094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bardol N., Ventelon M., Mangin B., Jasson S., Loywick V., et al. , 2013. Combined linkage and linkage disequilibrium QTL mapping in multiple families of maize (Zea mays L.) line crosses highlights complementarities between models based on parental haplotype and single locus polymorphism. Theor. Appl. Genet. 126: 2717–2736. [DOI] [PubMed] [Google Scholar]
- Bernardo, R., 2010 Heterosis and hybrid prediction, pp. 301–322 in Breeding for Quantitative Traits in Plants, Ed. 2. Stemma Press, Woodbury, MN. [Google Scholar]
- Blanc G., Charcosset A., Mangin B., Gallais A., Moreau L., 2006. Connected populations for detecting quantitative trait loci and testing for epistasis: an application in maize. Theor. Appl. Genet. 113: 206–224. [DOI] [PubMed] [Google Scholar]
- Bouchet S., Servin B., Bertin P., Madur D., Combes V., et al. , 2013. Adaptation of maize to temperate climates: mid-density genome-wide association genetics and diversity patterns reveal key genomic regions, with a major contribution of the Vgt2 (ZCN8) locus. PLoS One 8: e71377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckler E. S., Holland J. B., Bradbury P. J., Acharya C. B., Brown P. J., et al. , 2009. The genetic architecture of maize flowering time. Science 325: 714–718. [DOI] [PubMed] [Google Scholar]
- Butler D., Cullis B. R., Gilmour A. R., Gogel B. J., 2007. ASReml-R Reference Manual. State of Queensland Department of Primary Industries and Fisheries, Brisbane, Australia. [Google Scholar]
- Coles N. D., Zila C. T., Holland J. B., 2011. Allelic effect variation at key photoperiod response quantitative trait loci in maize. Crop Sci. 51: 1036–1049. [Google Scholar]
- Ducrocq S., Giauffret C., Madur D., Combes V., Dumas F., et al. , 2009. Fine mapping and haplotype structure analysis of a major flowering time quantitative trait locus on maize chromosome 10. Genetics 183: 1555–1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- East E. M., 1908. Inbreeding in corn, pp. 419–428 in Reports of the Connecticut Agricultural Experimental Station for Years 1907–1908. Connecticut Agricultural Experiment Station, New Haven, CT. [Google Scholar]
- Fischer S., Mohring J., Schön C. C., Piepho H.-P., Klein D., et al. , 2008. Trends in genetic variance components during 30 years of hybrid maize breeding at the University of Hohenheim. Plant Breed. 127: 446–451. [Google Scholar]
- Foiada F., Westermeier P., Kessel B., Ouzunova M., Wimmer V., et al. , 2015. Improving resistance to the European corn borer: a comprehensive study in elite maize using QTL mapping and genome-wide prediction. Theor. Appl. Genet. 128: 875–891. [DOI] [PubMed] [Google Scholar]
- Frascaroli E., Canè M. A., Landi P., Pea G., Gianfranceschi L., et al. , 2007. Classical genetic and quantitative trait loci analyses of heterosis in a maize hybrid between two elite inbred lines. Genetics 176: 625–644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frascaroli E., Canè M. A., Pè M. E., Pea G., Morgante M., et al. , 2009. QTL detection in maize testcross progenies as affected by related and unrelated testers. Theor. Appl. Genet. 118: 993–1004. [DOI] [PubMed] [Google Scholar]
- Ganal M. W., Durstewitz G., Polley A., Bérard A., Buckler E. S., et al. , 2011. A large maize (Zea mays L.) SNP genotyping array: development and germplasm genotyping, and genetic mapping to compare with the B73 reference genome. PLoS One 6: e28334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao X., Starmer J., Martin E. R., 2008. A multiple testing correction method for genetic association studies using correlated single nucleotide polymorphisms. Genet. Epidemiol. 32: 361–369. [DOI] [PubMed] [Google Scholar]
- Geiger H. H., Melchinger A. E., Schmidt G. A., 1986. Analysis of factorial crosses between flint and dent maize inbred lines for forage performance and quality traits, pp. 147–154 in Breeding of Silage Maize. Proceedings of the 13th Congress of the Maize and Sorghum Section of EUCARPIA, edited by Dolstra O., Miedema P. Pudoc, Wageningen, The Netherlands. [Google Scholar]
- Giraud H., Lehermeier C., Bauer E., Falque M., Segura V., et al. , 2014. Linkage disequilibrium with linkage analysis of multiline crosses reveals different multiallelic QTL for hybrid performance in the flint and dent heterotic groups of maize. Genetics 198: 1717–1734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giraud H., Bauland C., Falque M., Madur D., Combes V., et al. , 2017. Linkage analysis and association mapping QTL detection models for hybrids between multiparental populations from two heterotic groups: application to biomass production in maize (Zea mays L.). G3 (Bethesda) DOI: 10.1534/g3.117.300121. [DOI] [PMC free article] [PubMed]
- Grieder C., Dhillon B. S., Schipprack W., Melchinger A. E., 2012. Breeding maize as biogas substrate in Central Europe: I. Quantitative-genetic parameters for testcross performance. Theor. Appl. Genet. 124: 971–980. [DOI] [PubMed] [Google Scholar]
- Han S., Utz H. F., Liu W., Schrag T. A., Stange M., et al. , 2016. Choice of models for QTL mapping with multiple families and design of the training set for prediction of Fusarium resistance traits in maize. Theor. Appl. Genet. 129: 431–444. [DOI] [PubMed] [Google Scholar]
- Hickey J. M., Gorjanc G., Varshney R. K., Nettelblad C., 2015. Imputation of single nucleotide polymorphism genotypes in biparental, backcross, and topcross populations with a hidden Markov model. Crop Sci. 55: 1934–1946. [Google Scholar]
- Huang B. E., Verbyla K. L., Verbyla A. P., Raghavan C., Singh V. K., et al. , 2015. MAGIC populations in crops: current status and future prospects. Theor. Appl. Genet. 128: 999–1017. [DOI] [PubMed] [Google Scholar]
- Kadam D. C., Potts S. M., Bohn M. O., Lipka A. E., Lorenz A. J., 2016. Genomic prediction of single crosses in the early stages of a maize hybrid breeding pipeline. G3 (Bethesda) 6: 3443–3453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kump K. L., Bradbury P. J., Wisser R. J., Buckler E. S., Belcher A. R., et al. , 2011. Genome-wide association study of quantitative resistance to southern leaf blight in the maize nested association mapping population. Nat. Genet. 43: 163–168. [DOI] [PubMed] [Google Scholar]
- Larièpe A., Mangin B., Jasson S., Combes V., Dumas F., et al. , 2012. The genetic basis of heterosis: multiparental quantitative trait loci mapping reveals contrasted levels of apparent overdominance among traits of agronomical interest in maize (Zea mays L.). Genetics 190: 795–811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leroux D., Rahmani A., Jasson S., Ventelon M., Louis F., et al. , 2014. Clusthaplo: a plug-in for MCQTL to enhance QTL detection using ancestral alleles in multi-cross design. Theor. Appl. Genet. 127: 921–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longin C. F. H., Mühleisen J., Maurer H. P., Zhang H., Gowda M., et al. , 2012. Hybrid breeding in autogamous cereals. Theor. Appl. Genet. 125: 1087–1096. [DOI] [PubMed] [Google Scholar]
- Lu H., Romero-Severson J., Bernardo R., 2003. Genetic basis of heterosis explored by simple sequence repeat markers in a random-mated maize population. Theor. Appl. Genet. 107: 494–502. [DOI] [PubMed] [Google Scholar]
- Lübberstedt T., Melchinger A. E., Klein D., Degenhardt H., Paul C., 1997. QTL mapping in test crosses of European flint lines of maize: II. Comparisons of different testers for forage quality traits. Crop Sci. 37: 1913–1922. [Google Scholar]
- Manicacci, D., L. Moreau, and A. Charcosset, 2011 Quantitative trait loci cartography, meta-analysis and association genetics, pp. 37–66 in Advances in Maize (Essential Reviews in Experimental Biology), Vol. 3. Society for Experimental Biology, London. [Google Scholar]
- McMullen M. D., Kresovich S., Villeda H. S., Bradbury P., Li H., et al. , 2009. Genetic properties of the maize nested association mapping population. Science 325: 737–740. [DOI] [PubMed] [Google Scholar]
- Melchinger A. E., Utz H. F., Schön C. C., 1998. Quantitative trait locus (QTL) mapping using different testers and independent population samples in maize reveals low power of QTL detection and large bias in estimates of QTL. Genetics 149: 383–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mühleisen J., Maurer H. P., Stiewe G., Bury P., Reif J. C., 2013. Hybrid breeding in barley. Crop Sci. 53: 819–824. [Google Scholar]
- Nakagawa S., Schielzeth H., 2013. A general and simple method for obtaining R2 from generalized linear mixed-effects models. Methods Ecol. Evol. 4: 133–142. [Google Scholar]
- Parisseaux B., Bernardo R., 2004. In silico mapping of quantitative trait loci in maize. Theor. Appl. Genet. 109: 508–514. [DOI] [PubMed] [Google Scholar]
- R Core Team , 2013. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. [Google Scholar]
- Rebaï A., Blanchard P., Perret D., Vincourt P., 1997. Mapping quantitative trait loci controlling silking date in a diallel cross among four lines of maize. Theor. Appl. Genet. 95: 451–459. [Google Scholar]
- Reif J. C., Gumpert F.-M., Fischer S., Melchinger A. E., 2007. Impact of interpopulation divergence on additive and dominance variance in hybrid populations. Genetics 176: 1931–1934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvi S., Sponza G., Morgante M., Tomes D., Niu X., et al. , 2007. Conserved noncoding genomic sequences associated with a flowering-time quantitative trait locus in maize. Proc. Natl. Acad. Sci. USA 104: 11376–11381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schön C. C., Melchinger A. E., Boppenmaier J., Brunklaus-Jung E., Herrmann R. G., et al. , 1994. RFLP mapping in maize: quantitative trait loci affecting the testcross performance of elite European flint lines. Crop Sci. 34: 378–389. [Google Scholar]
- Schön C. C., Dhillon B. S., Utz H. F., Melchinger A. E., 2010. High congruency of QTL positions for heterosis of grain yield in three crosses of maize. Theor. Appl. Genet. 120: 321–332. [DOI] [PubMed] [Google Scholar]
- Schrag T. A., Melchinger A. E., Sørensen A. P., Frisch M., 2006. Prediction of single-cross hybrid performance for grain yield and grain dry matter content in maize using AFLP markers associated with QTL. Theor. Appl. Genet. 113: 1037–1047. [DOI] [PubMed] [Google Scholar]
- Schrag T. A., Möhring J., Maurer H. P., Dilhon B. S., Melchinger A. E., et al. , 2009. Molecular marker-based prediction of hybrid performance in maize using unbalanced data from multiple experiments with factorial crosses. Theor. Appl. Genet. 118: 741–751. [DOI] [PubMed] [Google Scholar]
- Schrag T. A., Möhring J., Melchinger A. E., Kusterer B., Dhillon B. S., et al. , 2010. Prediction of hybrid performance in maize using molecular markers and joint analyses of hybrids and parental inbreds. Theor. Appl. Genet. 120: 451–461. [DOI] [PubMed] [Google Scholar]
- Shull G. H., 1908. The composition of a field of maize. Am. Breed. Assoc. Rep. 5: 51–59. [Google Scholar]
- Sprague G. F., Tatum L. A., 1942. General vs. specific combining ability in single crosses of corn. J. Am. Soc. Agron. 34: 923–932. [Google Scholar]
- Technow F., Schrag T. A., Schipprack W., Bauer E., Simianer H., et al. , 2014. Genome properties and prospects of genomic prediction of hybrid performance in a breeding program of maize. Genetics 197: 1343–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenaillon M. I., Charcosset A., 2011. A European perspective on maize history. C. R. Biol. 334: 221–228. [DOI] [PubMed] [Google Scholar]
- Truntzler M., Barrière Y., Sawkins M. C., Lespinasse D., Bertran J., et al. , 2010. Meta-analysis of QTL involved in silage quality of maize and comparison with the position of candidate genes. Theor. Appl. Genet. 121: 1465–1482. [DOI] [PubMed] [Google Scholar]
- van Eeuwijk F. A., Boer M., Totir L. R., Bink M., Wright D., et al. , 2010. Mixed model approaches for the identification of QTLs within a maize hybrid breeding program. Theor. Appl. Genet. 120: 429–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vitezica Z. G., Varona L., Legarra A., 2014. On the additive and dominant variance and covariance of individuals within the genomic selection scope. Genetics 195: 1223–1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams E., Piepho H.-P., Whitaker D., 2011. Augmented p-rep designs. Biom. J. 53: 19–27. [DOI] [PubMed] [Google Scholar]
- Zeng J., Toosi A., Fernando R. L., Dekkers J. C., Garrick D. J., 2013. Genomic selection of purebred animals for crossbred performance in the presence of dominant gene action. Genet. Sel. Evol. 45: 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., Li Z., Liu G., Jiang Y., Maurer H. P., et al. , 2015. Genome-based establishment of a high-yielding heterotic pattern for hybrid wheat breeding. Proc. Natl. Acad. Sci. USA 112: 15624–15629. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Raw phenotypic data, adjusted means of hybrid performances, genetic map, and genotypic data are available in File S4, File S5, File S1, and File S2, respectively. The pedigree of the segregating populations is described in File S6. The R scripts used for data analysis are available in File S3. File S7 contains the P-values of each marker in the single-marker QTL detection model. The markers with significant effects in the final multi-marker models are shown in Table S1. All the supplemental files are described in the File S8.