In Vivo Non-Invasive Measurement of Young’s Modulus of Elasticity in Human Eyes: A Feasibility Study

Abstract

Purpose

Abnormal ocular biomechanical properties may be important for understanding the risk of glaucoma. However, there are no clinical methods for measuring standard material properties in patients. In this feasibility study we demonstrated proof-of-principle for a novel method, ultrasound surface wave elastography (USWE), to determine the in vivo Young’s modulus of elasticity of corneas in normal human eyes.

Methods

Twenty eyes of 10 healthy subjects (mean age 51.4 ± 7.2; ± SD, range 43–64 years) were studied. A spherical-tipped probe (3-mm diameter) was placed on closed eyelids and generated a gentle harmonic vibration at 100 Hz for 0.1 second. Wave speed propagation in the cornea was measured by USWE, and Young’s modulus was calculated from the wave speed. Associations between Young’s modulus and intraocular pressure (IOP), age, central corneal thickness, and axial length were explored by Pearson correlation. Statistical significance was determined by using generalized estimating equation models to account for possible correlation between fellow eyes.

Results

Mean IOP was 12.8 ± 2.7 mmHg. Mean wave speed in the cornea was 1.82 ± 0.10 m/s. Young’s modulus of elasticity was 696 ± 113 kPa and was correlated with IOP (r=0.57; p=0.004), but none of the other variables (p>0.1).

Conclusions

USWE is a novel non-invasive technique for measuring ocular biomechanical properties. Corneal Young’s modulus in normal eyes is associated with IOP, consistent with measurements in cadaver eyes. Further work is needed to determine elasticity in other ocular tissues, particularly the sclera, and if elasticity is altered in glaucoma patients.

INTRODUCTION

Glaucoma is the second leading cause of blindness worldwide and the only proven treatment is reduction of intraocular pressure (IOP). Despite reduction of IOP, a significant number of glaucoma patients develop progressive vision loss and blindness.^1,2 Conversely, most patients with elevated IOP do not develop glaucoma.³ These incongruities may be related to abnormal biomechanical properties that predispose the eye towards glaucoma. Elevated IOP can distend the sclera and lamina cribrosa,^4,5 which may lead to strain and damage of the axons of the optic nerve.⁶ Strain can also thin the lamina cribrosa and increase the trans-laminar pressure gradient between the intraocular environment and the intracranial environment, which may impair retrograde transport of neurotrophic factors from the lateral geniculate nucleus to the retinal ganglion cells.⁷ Stiffer ocular tissues would resist distortion, but may have less damping and cause greater IOP variability, a factor that has also been identified as increasing the risk for glaucoma.^8–10

There is currently no non-invasive technique for in vivo clinical measurement of ocular tissue elasticity. Two instruments, the Ocular Response Analyzer (ORA, Reichert, Depew, NY) and the Corvis ST (Oculus, Wetzlar, Germany), measure the ease of corneal deformation, but these measurements currently cannot be related to standard measurements of tissue elasticity, such as Young’s modulus. Consequently, in vivo measurements of elasticity in eyes of glaucoma patients have not been compared to those in eyes of normal subjects.

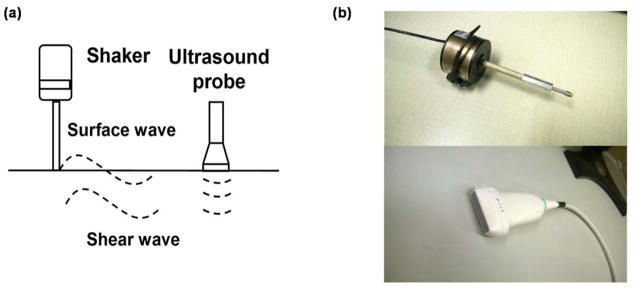
Viscoelastic properties of non-ocular tissues, such as lung,¹¹ skin,¹² abdominal muscle,¹³ and tendon,¹⁴ have been measured by a novel method called ultrasound surface wave elastography (USWE), but this method has not been used in the eye. With this technique, a small handheld probe (Fig. 1) gently vibrates on the skin and induces waves that propagate through the underlying tissue as slight tissue displacements. These displacements are measured by using an ultrasound probe and surface wave and shear wave propagation analyses are used to examine superficial tissues and deeper tissues respectively.

Figure 1. Ultrasound surface wave elastography (USWE) system.

(a) Generation and measurement of surface and shear waves. For this study, propagation of shear waves in the central cornea was analyzed; (b) Handheld shaker (top) and linear array ultrasound probe (bottom) of the USWE system.

In this feasibility study, we applied USWE to determine ocular biomechanical properties of the eye. As a proof-of-principle, we have measured wave propagation in eyes of normal subjects and demonstrated the ability to determine Young’s modulus of elasticity in the cornea.

METHODS

Participants

Twenty eyes of 10 participants were recruited from local area residents, patients, and employees of Mayo Clinic. An ophthalmic history was collected and a complete dilated eye exam was performed to ensure that all participants had normal eyes. Both males and females were included and both eyes were studied. All participants gave written consent to participate after discussion of the possible benefits and consequences of the study. This study was approved by the Institutional Review Board at Mayo Clinic and conformed to the tenets of the Declaration of Helsinki.

Ultrasound Surface Wave Elastography

A handheld electromagnetic shaker (Model: FG-142, Labworks Inc., Costa Mesa, CA 92626) with a 3-mm diameter probe was used to apply a local harmonic vibration to the eyelid of the closed eye. Propagation of the tissue displacement wave into the ocular tissues was recorded through a linear array ultrasound probe with a central frequency of 6.4 MHz (L11-4V, Verasonics, Inc, Kirkland, WA), which images the entire globe in a single measurement. Wave propagation through and across different tissue layers of the eye can therefore be imaged simultaneously. For ocular tissues, wave propagation in the longitudinal (circumferential) direction was imaged and analyzed. The stimulus signal for the mechanical probe was generated by a function generator (Model FG33120A, Hewlett Packard, Palo Alto, CA 94301) and was synchronized to the ultrasound system to enable detection of wave phase based on tissue displacement (Fig. 2).

Figure 2. Implementation of USWE.

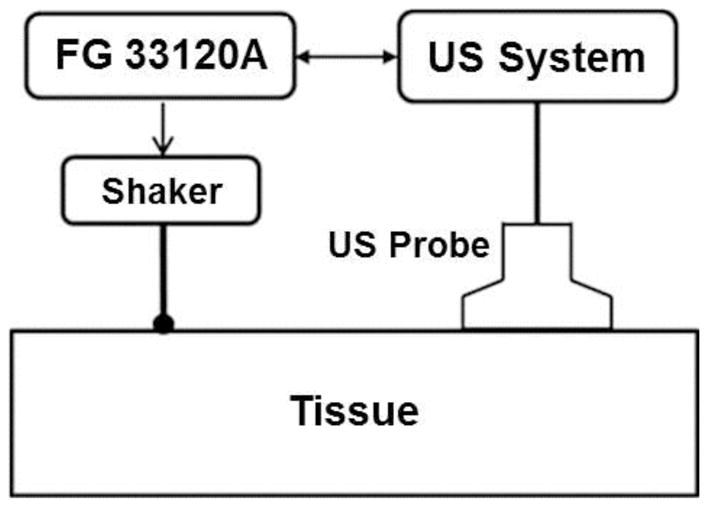
The harmonic oscillation of the shaker is initiated by the function generator (FG 33120A) and synchronized with the ultrasound (US) probe, which detects propagation of the induced wave in the tissue.

The handheld shaker produced a harmonic vibration at 100 Hz for 0.1 seconds (10 cycles). The wave speed, c_s(ω), was measured by the phase gradient method:

$$c_s(\omega )=\frac{\omega \mathrm{\Delta }r}{\mathrm{\Delta }\phi }$$ (1)

where Δr is the distance between 2 detection locations, Δφ is the phase change over that distance, and ω is the angular frequency. To improve the estimation of wave speed over the measurement region and minimize noise associated with single pair of points, the parameters used in equation 1 were estimated by linear regression analysis of the phase change measured over multiple locations:

$$\mathrm{\Delta }\widehat{\phi }=\alpha \mathrm{\Delta }r+\beta$$ (2)

where Δφ̂ denotes the regression value for phase change at distance Δr, α is the slope, and β is the regression constant. The quality of wave speed was considered acceptable if the coefficient of determination for the linear regression (R²) was greater than 0.8. For this study, wave speed propagation between locations in the central 6 mm of the mid-stromal cornea was calculated.

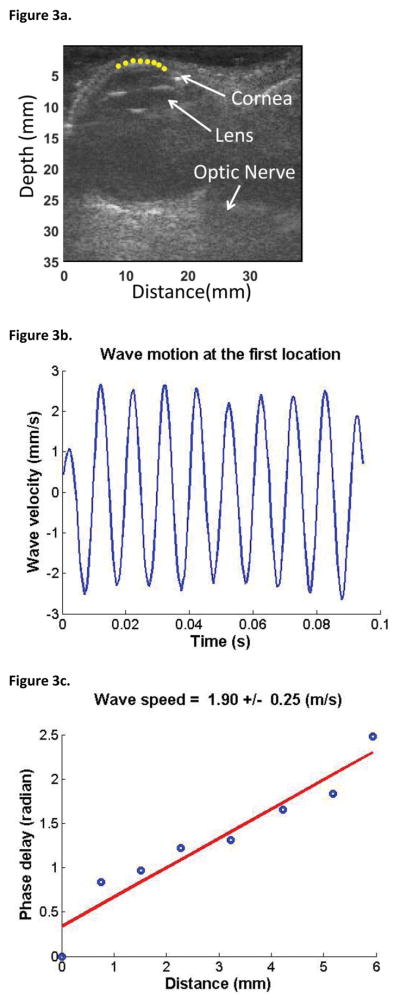
Analysis of wave propagation in the cornea was guided by ultrasound imaging; a typical analysis of wave speed is shown in Figure 3. Ultrasound images were recorded at a frame rate of 2000 frames/second during a continuous 0.1-second wave vibration at 100 Hz frequency. The cornea was then identified in the ultrasound images and eight positions in the central 6 mm of the corneal mid-stroma were selected (yellow dots in Figure 3a). Tissue motion at the selected locations in the cornea were analyzed by cross-correlation analysis of ultrasound tracking beams.¹⁵ Typical corneal tissue velocity was approximately 3 mm/s, with an amplitude of approximately 30 μm. With our technique, a tissue displacement of 1 μm can be detected. Wave motion at the first selected location for one eye is shown in Figure 3b. Wave speed was then measured by determining the change in wave phase at each location relative to the first location (Fig. 3c) using several ultrasound tracking beams.^11,16,17 In the example in Figure 3, the wave speed was determined to be 1.85 ± 0.15 m/s based on the best-fit line of phase change at all the locations. Because the wave speed in the cornea is determined by analyzing ultrasound data directly from the cornea, the wave speed measurement is local and independent of the source of excitation. As well, since the device captures all ultrasound data from the full depth of penetration, different tissue layers can be analyzed using the same data set, but selecting different analysis points. However, we limited the scope of this feasibility study to analysis of corneal properties.

Figure 3. Measurement of Wave Speed Using USWE.

(a) Points in the cornea were selected to measure the wave propagation by using ultrasound tracking. Yellow dots indicate the points selected for measurement. The anterior surface of the cornea is clearly visible, without any indentation from the ultrasound probe. (b) Wave motion at the first location. (c) The wave phase change with position, in response to a 0.1-second excitation at 100 Hz, was used to measure the wave speed. A linear regression model of the phase delay at multiple points on the cornea was used to improve accuracy.

Young’s modulus of elasticity for tissue, E, is directly related to the wave speed, c_s:¹⁸

$$E=9\frac{\rho {c_s}^4}{{(\omega h)}^2}$$ (3)

where ρ is tissue density (assumed to be equal to water, 1.0 g/mL), ω is the angular frequency, h is the thickness of the tissue, and the cornea is modelled as a thin plate.

Feasibility Study Protocol

Central corneal thickness was measured by ultrasound pachymetry (Pachmate, DGH Technology Inc., Exton, PA) and mean corneal thickness over the central 6 mm of cornea was measured by using Scheimpflug imaging (Pentacam, Oculus, Wetzlar, Germany). Axial length was measured by A-scan ultrasonography (Sonomed, New Hyde Park, NY) and IOP was measured by Goldmann applanation tonometry. At least 20 minutes elapsed from the time of any contact measurements until the USWE measurements, allowing IOP to return to baseline.

Wave speed was then determined with the participant in the supine position. Ultrasound gel was placed over the closed eyelid of the eye to be assessed. The ultrasound probe was placed over the eye and used to image the globe in a nasal-temporal direction. The probe contacted only the gel, and did not indent or displace the globe. The tip of the shaker was then gently placed on the eyelid adjacent to the probe, near the medial canthus, without adding pressure to the eye, and images were captured. Three measurements were performed in each eye within 10 minutes. This procedure was then repeated for the contralateral eye.

Statistical analysis

Young’s modulus of elasticity was determined for each measurement of wave speed by using Equation 3 and the mean of the three estimates was accepted as the Young’s modulus for the cornea. Relationships between Young’s modulus and IOP, age, central corneal thickness, and axial length were explored by using Pearson correlations. Significance was determined by using generalized estimating equation models to account for possible correlation between fellow eyes; p<0.05 was accepted as significant.

Repeatability analysis

Measurement of wave speed and calculation of Young’s modulus of the cornea depends on the selection of analysis points within the tissue of interest. Inter-rater variability was assessed in order to determine the repeatability of USWE measurement when different analysis points are selected. Ten analyses of wave speed in 10 eyes were performed in one session. In a second session, this was repeated using a new set of analysis points selected independently. Inter-rater repeatability was evaluated by using intra-class correlations (ICC). ICC was analyzed by the Pearson correlation of the two data sets. Repeatability was considered as good for 0.60 ≤ ICC ≤ 0.74, and excellent for 0.75 ≤ ICC ≤ 1.00.¹⁹

RESULTS

The mean age of the participants was 51.4 ± 7.2 years (mean ± standard deviation, range 43–64 years). The vibration induced by the shaker on the eyelids and underlying ocular tissues was gentle and there were no complaints of discomfort from any of the participants. Mean IOP in our sample of 20 eyes was 12.6 ± 2.7 mmHg. Scheimpflug imaging was not obtained, and Young’s modulus was not calculated, for two subjects. Mean central corneal thickness was 541 ± 37 μm by ultrasound pachymetry (n=20), and 549 ± 38 μm by Scheimpflug imaging (n=16). The mean thickness averaged over the central 6 mm of cornea was 598 ± 43 μm (n=16). Mean axial length was 23.7 ± 0.8 mm.

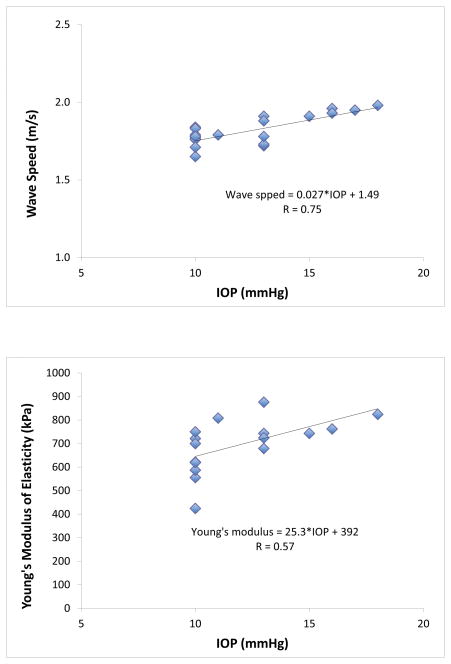
Mean speed of wave propagation in the cornea was 1.82 ± 0.10 m/s at 100 Hz and Young’s modulus of elasticity was 696 ± 113 kPa. Wave speed was strongly correlated with IOP (r=0.74, p<0.001, n=20; Fig. 4) while Young’s modulus was moderately correlated with IOP (r=0.57, P=0.004, n=16). There was no significant correlation between Young’s modulus and age (r=0.02, p=0.88), central corneal thickness (r=−0.23, p=0.43), or axial length (r=0.18, p=0.30; Table).

Figure 4. Relationship Between Wave Speed and Young’s Modulus, and IOP.

Relationship between wave speed and IOP (top) and Young’s modulus and IOP (bottom). Both wave speed and Young’s modulus increased as IOP increased (p<0.01).

Table.

Relationship between Young’s modulus of elasticity and ocular parameters and age. Young’s modulus was correlated with IOP but not central corneal thickness, axial length, or age.

	Mean ± SD	r (Pearson correlation)	p (GEE)
Young’s modulus of elasticity	696 ± 113 kPa
IOP (GAT1)	12.6 ± 2.7 mmHg	0.57	0.004
Age	51.4 ± 7.2 yrs	0.023	0.88
CCT (pachymeter)	541 ± 37 μm	−0.14	0.65
CCT (pentacam)	549 ± 38 μm	−0.23	0.43
CCT (6mm)	598 ± 43 μm	−0.23	0.43
Axial length	23.7 ± 0.8 mm	0.18	0.30

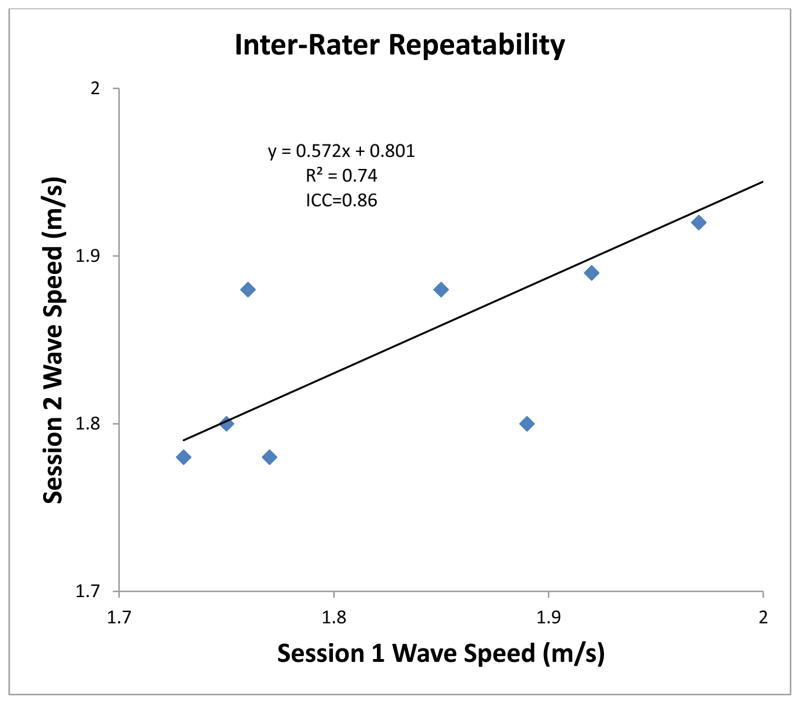
Inter-rater repeatability (Fig. 5) was excellent with an ICC of 0.86. As well, there was a strong correlation between the measurements in Session 1 and Session 2 (R² = 0.74).

Figure 5. Inter-Rater Repeatability Analysis of Wave Speed Calculation.

Comparison of wave speed calculated in session 1 compared with wave speed calculated using different analysis points in session 2.

DISCUSSION

The long-term goal of this study is to help understand the role of ocular tissue properties in glaucoma. While the tissues of greatest interest are likely the parapapillary sclera and lamina cribrosa, the cornea serves as an excellent tissue for proof-of-principle of this novel technique, given the extensive past research into corneal biomechanics.

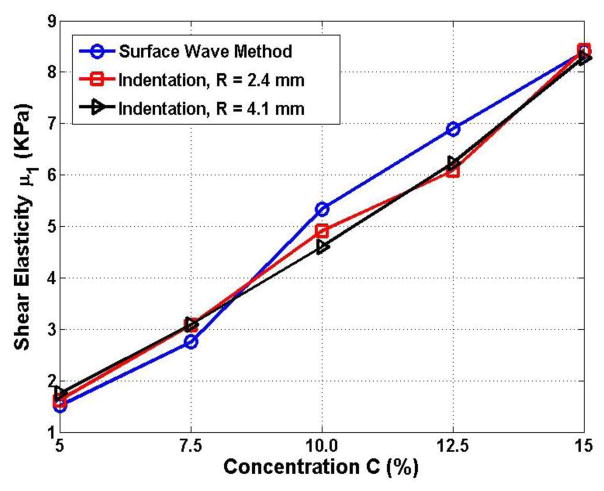
The lack of a gold standard for measurement of corneal elasticity makes validation of the USWE measurements in our study challenging. Although our study did not compare in vivo USWE measurements of corneal tissue with ex vivo measurements, we have previously validated the technique in other tissues using the indentation technique.^17,20 The indentation technique measures the elasticity of a medium by analyzing the relationship between the indentation displacement and the resulting force, and is consistent with finite element models. In a previous study¹⁷, we compared the elasticity of five gelatin phantoms prepared with different concentrations (5%–15%) of porcine skin gelatin powder. The results (Fig. 6) demonstrated good agreement between the two techniques. The largest difference between the USWE and indentation techniques was 16% in the 5% gel, which has an elasticity similar to that of young rat brains. In contrast, the difference with the 15% gel, which has an elasticity similar to that of human skin, was less than 1.5%. While the elasticity of corneal tissue is significantly higher than skin, and was not assessed in those experiments, the techniques do appear to show good agreement across a wide range of elasticity.

Figure 6. Comparison of USWE with the Indentation Method.

Shear elasticity determined by using the ultrasound surface wave elastography (USWE) method and the indentation method for different concentrations of gel. Adapted from Zhang et al. ¹⁷.

Other investigators have directly assessed corneal biomechanical properties in cadaver tissue. Strip extensometry is a straight forward technique in which the stress-strain relationship is determined by testing a tissue strip on a tensometer. However, this technique has a number of limitations related to tissue anisotropy, and inflation testing of anterior segments or whole globes may provide better estimates of in vivo elasticity.^21,22 Elsheikh et al.²³ mounted cadaver human and porcine corneas on a pressure chamber, measured the displacement of the cornea as IOP was varied, and explored the stress-strain behavior of the intact cornea. They found that Young’s modulus of elasticity was related to the age of the donor as well as to the pressure. For a similar age group and IOP of our population, the reported Young’s modulus in their study was approximately 200–250 kPA, considerably lower than our mean of 696 ± 113 kPa. Dias and Ziebarth²⁴ used atomic force microscopy and reported that anterior stroma had a mean value of 281 ± 214 kPa, while posterior stroma had a mean value of 89.5 ± 46.1 kPa, which was again considerably lower than the results from our study. In contrast, Lombardo et al.²⁵ also used atomic force microscopy and found that mean values for Young’s modulus of the anterior stroma ranged from 1.14 to 2.63 MPa in 4 samples, which was considerably higher than our results. Indeed, other previous studies have reported highly disparate values for Young’s modulus of elasticity, ranging from 0.159 MPa to 57 MPa as reviewed by Glass et al.²⁶ There are likely many reasons for the large range in values from studies that typically use cadaver tissue, including age of the tissue tested, speed of tissue deflection, corneal layer and region tested, post-mortem time, and storage medium. Therefore, these results may not reflect in vivo properties of the cornea.

In a study with living human subjects, Lam et al. used an indentation device to estimate the tangent modulus of elasticity of corneas.²⁷ With this device, a 2 mm flat surface cylinder is mounted on a slit-lamp biomicroscope. The cylinder is advanced at a rate of 12 mm/s to a depth of 1 mm. Young’s modulus was then calculated based on the force and displacement. The authors reported a mean modulus of elasticity of 755 ± 159 kPa, which is very similar to the results from our current study. However, unlike the USWE technique used the current study, indentation techniques require direct tissue contact, rendering assessment of posterior ocular tissues impractical.

Imaging-based techniques to assess ocular biomechanical properties avoid many of the limitations of tissue deformation techniques. Dupps et al. reported a technique for measuring corneal tissue properties called surface wave elastometry.²⁸ Similar to USWE, this technique involves measurement of wave speed in tissue; however, fundamental differences exist. First, the tissue waves with their technique were generated by using a transducer that produced a 4–5 kHz oscillatory force over approximately 1 millisecond. The frequency is in the acoustic range, and wave speed is calculated based on time to propagate over a fixed 4.5 mm distance between two transducers. The wave is assumed to reach the receiving transducer when the amplitude crosses a threshold. The high frequency and short duration impulse results in rapid signal decay. In contrast, USWE used in our current study employs a macroscopic vibration at 100 Hz. This allows tissue displacement to be easily imaged with an ultrasound probe, and wave speed to be determined by phase change without the need to capture time-of-flight based on an amplitude threshold. The wave speed measured by Dupps et al. was also approximately 2 orders of magnitude greater than the wave speed in our study. This was due to the well-described wave speed increase with frequency that occurs in tissues, a phenomenon called the wave speed dispersion with frequency.^29,30 Another advantage of USWE is that wave speed measurements are not limited to a specific region between two fixed points based on transducer placement. Instead, wave speed can be determined for any part of the tissue through which the vibration propagates and can be imaged with the ultrasound probe. This could enable in vivo assessment of different tissue layers, as well as posterior portions of the eye which are not accessible to a probe such as that described by Dupps et al.

Another imaging-based technique to measure corneal biomechanical properties ex vivo was recently reported by Scarcelli et al.^31–33. These investigators used Brillouin microscopy, a method based on scattering that arises from the interaction between incident light and a medium of interest, to determine the elasticity of the medium. A frequency shift in the light was detected by using a confocal microscope and spectrometer, and was related to the longitudinal modulus of the tissue. One advantage of this technique is the high resolution possible with cadaveric cornea specimens, sufficient to allow comparison of mechanical properties between different tissue layers. Scarcelli et al.^31–33 used this technique to characterize the longitudinal modulus of elasticity in normal and collagen cross-linked cadaver corneas and found that the elastic modulus was greatest in the central region of the cornea, lower in the anterior region, and least in the posterior region. However, it is unclear if this technique can be adapted to measure elastic moduli in optically opaque tissues, such as sclera, which would be critical for application to glaucoma.

Corneal biomechanical properties have also recently been assessed by using shear wave imaging optical coherence tomography (SWI-OCT).³⁴ A focused air-jet briefly deforms the cornea and the resulting elastic wave propagation through the cornea is measured by using a phase-sensitive spectral-domain OCT. A surrogate measure of elasticity, the frequency-dependent phase velocity of the propagated wave (Lamb wave), can be calculated from tissue displacement, and is related to the modulus of elasticity of the cornea. While this technique can produce high resolution measurements, it is currently limited to tissues that can be imaged with OCT.

Surrogate measures of ocular biomechanics have been proposed as potential biomarkers for glaucoma in humans. The Ocular Hypertension Treatment Study reported that among patients with elevated IOP, those with thin corneas were more likely than those with thick corneas to develop glaucoma.³ Some have suggested that falsely low IOP on applanation tonometry in patients with thin corneas can explain this relationship, but adjustment of IOP based on corneal thickness does not alter the relationship.³⁵ Corneal thickness may also be a marker for ocular biomechanical properties and thin corneas may be associated with disadvantageous characteristics. However, thickness is likely only a crude predictor of other ocular biomechanical properties and does not reflect the inherent material properties of the tissue.

Investigators have attempted to study biomechanical properties of the eye by using the Ocular Response Analyzer (ORA, Reichert, Depew, NY), a commercially available device that measures deformation of the cornea in response to an air-jet pulse. The air-jet pressure that applanates the cornea during the corneal rebound is lower than it is than during the initial compression and this hysteresis likely reflects the viscous damping of the tissue and the globe; in a purely elastic eye, the cornea would applanate at the same pressure on rebound. Based on the difference between the two applanation pressures, two variables have been defined: corneal hysteresis (CH) and the corneal resistance factor (CRF). Some studies have indicated that CH and CRF are correlated with IOP, and CH may be decreased in glaucoma patients.^36,37 However, the relationship between these variables and standard biomechanical properties, such as modulus of elasticity, is unknown.

Our feasibility study demonstrated a relationship between IOP and the modulus of elasticity, consistent with other investigators.^23,38 One possible explanation is that this is due to the dependence of corneal modulus of elasticity on the magnitude of tissue strain, but since our study was cross-sectional, we cannot determine causation. Unlike previous studies of cadaver eyes,^23,39 we did not find a relationship between Young’s modulus and subject age, likely because of our small sample size and clustering of our subjects in a fairly narrow age range (mean 51.4 ± 7.2 years; range 43–64 years). We also did not find a relationship between the modulus of elasticity and central corneal thickness or axial length. This suggests that, in our study population, tissue dimensions (thickness or length) are not related to the intrinsic elastic properties of the tissue. While this would be expected in a healthy population, it is also possible that our sample size was simply too small to detect such a relationship. As well, all of our subjects had healthy eyes, and in certain disease states (e.g., pathologic myopia) tissue elasticity may be altered, potentially resulting in pathological alteration of ocular dimensions.

One potential concern about USWE is that measurements are performed through closed eyelids, and overlying tissues may influence the measurements of wave speed and subsequent calculation of Young’s modulus. The presence of overlying tissue would not have any direct effect on wave speed since wave propagation can be directly imaged in different tissue layers and locations by using the ultrasound probe. Selecting the cornea for this study was straight forward based on our ultrasound images (Fig. 3). However, it is possible that eyelid tension could affect IOP, which would consequently affect wave speed. Future studies will be needed to fully evaluate this variable. In addition, future studies will compare corneal biomechanical properties with the biomechanical properties of other ocular tissues.

Another concern about USWE is the effect of measurement on IOP. Although care was taken not to apply pressure to the globe during measurements, any compression of the eye could elevate IOP. As well, the supine position was required for USWE measurements and this has a well-characterized effect on IOP.⁴⁰ Because wave speed and Young’s modulus are both correlated with IOP, inadvertent pressure elevations could alter the measurement. However, if external pressure were applied to the eye during measurements, it is unlikely that a consistent elevation would occur, and a strong correlation with IOP would likely be masked.

Our current USWE implementation is limited by the measurement of wave propagation along one direction, while ocular tissues demonstrate significant anisotropy. As well, ocular tissues, such as the cornea, do not have uniform properties throughout the structure. With the current ultrasound probe, resolution is insufficient to differentiate between layers of the cornea and resolution of smaller structures, such as the lamina cribrosa, is beyond our current system. Future iterations, with higher frequency ultrasound probes, may provide the necessary resolution to further characterize ocular tissues.

The assumption of the cornea as a thin plate limits the calculation of Young’s modulus of elasticity. While this may be a reasonable rough approximation of a 6-mm region of the central cornea, there is clearly opportunity to refine this model. Unlike our model, a real cornea is a curved tissue with non-uniform thickness. As well, the cornea is anisotropic and properties vary across layers of tissue.⁴¹ Corneal properties also vary depending on hydration. Although beyond the scope of this feasibility project, additional parameters to be included in a more refined model are the aspherical curvature, variable thickness, and multiple tissue layers of the cornea. The limitations of the thin plate model may introduce additional sources of error, explaining the stronger correlation between wave speed and IOP than between Young’s modulus and IOP in our study.

Despite the limitations of a small feasibility project, our current study demonstrated proof-of-principle for measuring wave speed in ocular tissues and demonstrated the ability to assess the Young’s modulus of the cornea in eyes of healthy participants by using ultrasound surface wave elastography. However, our sample size was small and was not designed to definitively determine the parameters that affect elasticity. As well, full characterization of the technique, including repeatability, and variations across a normal population are beyond the scope of this study. Future studies are needed to characterize the population norms, as well as evaluate changes of elasticity in glaucoma and other ocular diseases, such as keratoconus and pathologic myopia, which may be influenced by biomechanical properties of the eye. The development of this non-invasive technique for in vivo measurement of ocular tissue elasticity provides a new approach to understanding the pathophysiology of these conditions.