Affinity and path of binding xylopyranose unto E. coli xylose permease

Abstract

Glucose transporters (GLUTs), expressed in all types of human cells, are responsible for the uptake of sugars as the primary energy source for the normal functions of good cells and for the abnormal growth of cancer cells. The E. coli xylose permease (XylE), a homologue of human GLUTs, has been investigated more thoroughly than other major facilitator proteins in the current literature. In this paper, we present a molecular dynamics (MD) study of an all-atom model system to elucidate the atomistic details and the free-energy landscape along the path of binding a xylopyranose (XYP) from the extracellular space to the inside of the transporter protein XylE. From the MD simulations, the Gibbs free energy of binding was found to be −4.4 kcal/mol in agreement with the experimental value of −4.7 kcal/mol. The accuracy of our study is further shown in the computed hydration energy of XYP of −14.6 kcal/mol in comparison with the experimental data of −15.0 kcal/mol. Along the binding path, the Gibbs free energy of the XYP-XylE complex first rises from zero in the dissociated state to approximately 4 kcal/mol in the transition state (when XylE slightly increases its opening toward the extracellular side to accommodate XYP) before dropping down to −9.0 kcal/mol in the bound state. These quantitative insights indicate the fast equilibration between the bound and the unbound states of XylE and XYP. They also serve as an atomistic-dynamic corroboration of the experimental conclusion that XylE is a high-affinity sugar transporter.

1. INTRODUCTION

Glucose transporters (GLUTs) are membrane proteins in the family of sugar porters [1] that belongs to the major facilitator superfamily (MFS)[2]. GLUTs, ubiquitously present in all living organisms, are responsible for transporting sugar across the cell membrane[3]. In humans, GLUTs are responsible for up taking sugar into cells where it is used as a primary source of energy[1, 4, 5]. Mis-regulation or mutation of GLUTs have been correlated to diseases including diabetes, hyper- and hypo-glycemia and heart disease[1]. Over expressions of GLUTs have been identified in cancer cells for increased glucose uptake necessitated by the uncontrolled cellular proliferation of cancers[6, 7]. In bacteria, the Escherichia coli xylose permease (XylE), one of the GLUT homologues, co-transports a proton down its gradient and a β-D-xylose (XYP) against its concentration gradient from the extracellular side to the intracellular side of the cell membrane [8, 9].

XylE is the first well-studied member of the MFS[8–17]. Multiple crystal structures of XylE [13–15] have been obtained in both the outward-facing and the inward-facing conformations. Extensive molecular dynamics (MD) simulations[15, 16] have been carried to elucidate how XylE transforms from the outward-facing conformation to the inward-facing conformation to carry an XYP from the extracellular side to the intracellular side along with changes in the protonation states of relevant residues. Similar MD studies have been done on GLUT 1[16, 18, 19]. In the current literature, an essential part of the XYP-XylE interaction still remains to be elucidated, namely, the atomistic details about how an XYP binds to XylE from the extracellular side. What characteristics are in the free-energy landscape along the XYP-XylE binding path? Relatedly, can theoretical-computational studies based on the current force-field parameters give quantitatively accurate representation of this transporter protein? In this paper, we answer these questions and present a quantitative study of the binding affinity and the binding path of XYP unto XylE from the extracellular side based on MD simulations of an all-atom model system. As a validation of our method, we also compute the hydration energy of XYP as a problem of binding XYP from vacuum to inside a bulk of water. The accuracy of our approach is further indicated in the close agreement between our computed hydration energy and the experimental data.

2. METHODS

2.1. All-atom model systems

For the sugar hydration problem, an XYP is placed inside a 60 Å × 60 Å × 60 Å cubic box of water. The sugar is centered at the origin of the Cartesian coordinates which is 10 Å beneath the top side of the water box (the plane of z = 10 Å in parallel to the xy-plane). Reflective boundary conditions are implemented for water molecules (but not for XYP) on the planes of z = 10 Å and z = −50Å, which keep the waters inside the system box when XYP becomes dehydrated—moves out of the water box into the vacuum above the plane of z = 10 Å. This all-atom model system consists of 20,440 atoms.

For the sugar-protein binding problem, we take the crystal structure of Sun et al.[13] (PDB code: 4GBZ), translate and rotate the protein complex so that its center is located at the origin of the Cartesian coordinates and its orientation is such that the protein opens toward the z-axis (Fig. 1) for computational convenience, solvate the protein complex with a cubic box of water whose dimensions are 80 Å × 80 Å × 120 Å, and then add sodium and chloride ions to neutralize the net charges of the protein and to salinate the system to the physiological concentration of 150 mM NaCl. The all-atom model system of XylE-XYP so constructed consists of 71,997 atoms.

Fig. 1.

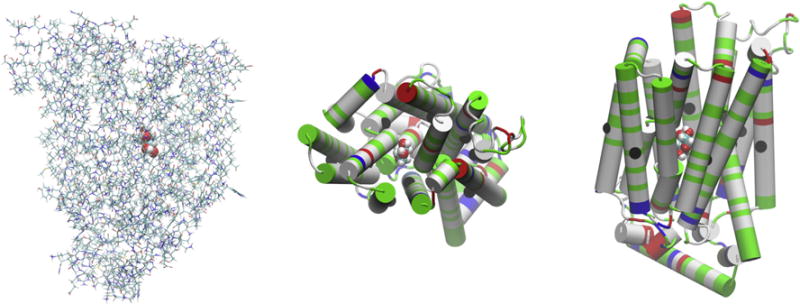
The XylE-XYP complex. The coordinates are from the last frame of 50 ns MD run of the all-atom model system. In the left panel is the side view of the complex where the protein is represented in licorices and the sugar in large spheres all colored by atoms (H, white; C, cyan; O, red; N, blue; S, yellow). The top side is the extracellular side. The central panel gives the top view and the right panel gives the side view of the complex where the protein is represented in cartoons colored by residue types (polar, green; hydrophobic, white; positively charged, blue; negatively charged, red). The 12 Cα atoms on the 12 transmembrane helices (Leu23Cα, Leu65 Cα, Phe95Cα, Gly136Cα, Ile172Cα, Pro209Cα, Gln289Cα, Leu326Cα, Gly351Cα, Phe383Cα, Ala418Cα, Cys450Cα) are shown as large black spheres in the central and the right panels. All molecular graphics were rendered with VMD[28].

Simulation parameters

In all the MD runs, the CHARMM36 force field parameters[20, 21] were used for all the intra- and inter-molecular interactions. The Langevin stochastic dynamics was implemented with NAMD[22] to simulate the systems at constant temperature of 298 K and constant pressure of 1 bar. The time step was 1 fs for the short-range and 2 fs for the long-range interactions. The damping constant was 5/ps. Explicit solvent (water) was represented with the TIP3P model. Full electrostatics was implemented via particle mesh Ewald at the level of 128 × 128 × 128 for the binding problem.

Absolute binding free energy from PMF in 3nD

Following the standard literature (e.g., [23]), one can relate the standard (absolute) free energy of binding to the PMF difference in 3n dimensions (3nD) and the two partial partitions as follows:

$$\mathrm{\Delta }{G}_{\mathit{bind}}=\mathrm{\Delta }\text{PMF}-k_B\mathit{Tln}(Z_0{c}_0/Z_{\infty })$$ (1)

Here c₀ is the standard concentration of 1M. k_B is the Boltzmann constant. T is the absolute temperature. Z₀ is the partial partition of the sugar in the bound state which can be computed by sampling the fluctuations in 3n degrees of freedom of the sugar and invoking the Gaussian approximation for the fluctuations in the bound state [24, 25]. Z_∞ is the partial partition of the sugar in the unbound state for the 3(n-1) degrees of freedom of the sugar when three degrees of freedom are fixed so that the sugar rotates and fluctuates in the aqueous bulk far away from the protein. In this study, we choose n = 1 and use the coordinates of the sugar’s C5 atom to represent its position. The partial partition of the unbound state Z_∞ = 1. The PMF is 3D and Z₀ contains the 3D fluctuations of the sugar in the bound state. To simulate how the cell membrane anchors the protein, we fix the z-coordinate of one Cα atom on each of the 12 transmembrane helices near the center (Fig. 1). The x- and y-coordinates of these 12 Cα atoms are freely subject to the stochastic dynamics of the system without any constraints. Therefore, the 12 transmembrane helices can freely move in the lateral dimensions (in parallel to the cell membrane) and they can pivot around their centers.

Hydration energy from PMF in 3nD

The problem of hydrating a sugar molecule is simply a problem of binding a sugar to a large bulk of water. The bound state is when the sugar is completely inside the water bulk and the unbound state is when it is in the vacuum far away from the water-vacuum boundary. Eq. (1) can be easily adapted into the following form for the hydration energy:

$$\mathrm{\Delta }{G}_{\mathit{hydr}.}=\mathrm{\Delta }\text{PMF}-k_B\mathit{Tln}\left(Z^{aq.}/Z^{\mathit{vac}.}\right)$$ (2)

Here Z^aq. and Z^vac. are the partial partition of the sugar in the hydrated and in the dehydrated states respectively. In this study, we use n = 2 for the hydration problem for computing efficiency. The C3 and O5 atoms are chosen as the two centers to represent the position and the orientation of the sugar. The PMF is in 6D and the partial partition of the sugar is 3D involving rotation of one center around the other center (two degrees of freedom) and the vibration between the two centers (one degree of freedom)[26].

RESULTS AND DISCUSSION

Interaction with water is fundamental to all biological systems. In this section, we first present the problem of XYP hydration, which serves to verify the accuracy of the CHARMM36 force field parameters used in this study of the sugar-protein complex and the algorithm of approach. We then give quantitative characterization of the affinity and the most probable path of binding xylopyranose to E. coli xylose permease.

Hydration of XYP

In Fig. 2, we plot the PMF of moving the sugar molecule from vacuum to inside a bulk of water by steering two centers (the C3 and O5 atoms of XYP). The dehydration path, i.e., the reverse of the hydration path, is illustrated in the Supplemental Information (SI) (movie S1). The fluctuations of the two steering centers in vacuum and in water are shown in the bottom panel of Fig. 2. Combination of the PMF difference, ΔPMF = −14.8 kcal/mol, and the two partitions of XYP in water and in vacuum, we obtain the hydration energy of XYP, ΔG_hydr = −14.6 kcal/mol. From the vapor pressure (85.3 μPa) and the solubility (555 g/l) of xylopyranose[27], one can find the experimental value of XYP hydration energy, −15.0 kcal/mol, which is in close agreement with our computation. This confirms the accuracy of the parameters employed in this work.

Fig. 2.

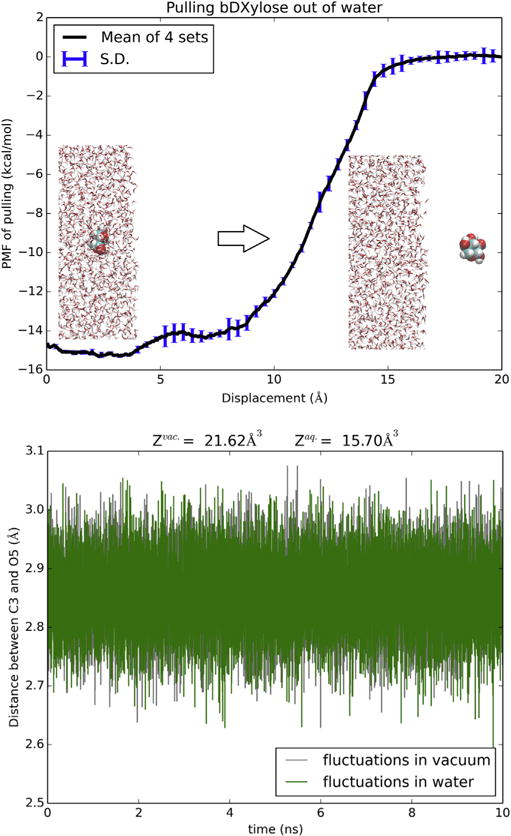
Hydration of XYP. Shown in the top panel is the 6D PMF along a dehydration path of pulling XYP out of water by its C3 and O5 atoms. Shown in the bottom panel are the fluctuations of the two atoms in water and in vacuum from which the molecule’s partitions in water and in vacuum were computed respectively.

Supplementary video related to this article can be found at https://doi.org/10.1016/j.bbrc.2017.10.053.

Comparing the partial partitions of XYP in water and in vacuum, the slightly larger fluctuations in vacuum than in water gives a contribution of 0.19 kcal/mol to the total free energy of hydration (−14.6 kcal/mol). When fully hydrated, XYP can form 8 to 10 hydrogen bonds with waters in its hydration shell (SI, Fig. S1). These hydrogen bonds slightly rigidify the sugar and reduce its partial partition.

The steepest part of the hydration PMF curve is when the sugar is outside and near the water-vacuum interface (z = 10 Å, Fig. 2). In that range, the van der Waals attractions between the sugar and the waters is the strongest and multiple hydrogen bonds are involved between them as well (SI, Fig. S1). When the sugar is deeper inside the water box, it breaks more hydrogen bonds between waters while forming more hydrogen bonds with waters. All these together give rise to the non-monotonous behavior of the PMF from z = 10 Å to z = 0, indicating possibility of higher sugar concentration near the surface than deep inside the bulk of water.

The standard binding free energy of XYP-XylE

In Fig. 3, we plot the 3D PMF along the most probable path of binding xylopyranose to inside the protein and the fluctuations of the sugar in the bound state inside the protein. The free energy of binding can be computed from the combination of the PMF difference, ΔPMF = −9.0 kcal/mol, the partial partition in the bound state (Z₀ = 1.38ų), and the partial partition in the unbound state (Z_∞ = 1): ΔG_bind = −4.4 kcal/mol. From the experimental data of the dissociation constant, k_D = 0.35 mM [13], we obtain the free energy of binding to be $k_B\mathit{Tln}\left(\frac{k_D}{c_0}\right)=-4.7\text{kcal/mol}$. The difference between the experimental data and our computed binding free energy is less than k_BT, indicating that chemical accuracy can be achieved in all-atom simulations when the statistical mechanics of the many particle system is adequately implemented. The current force field parameters (in this study, CHARMM 36) are sufficiently optimized for quantifying protein-sugar interactions with chemical accuracy.

Fig. 3.

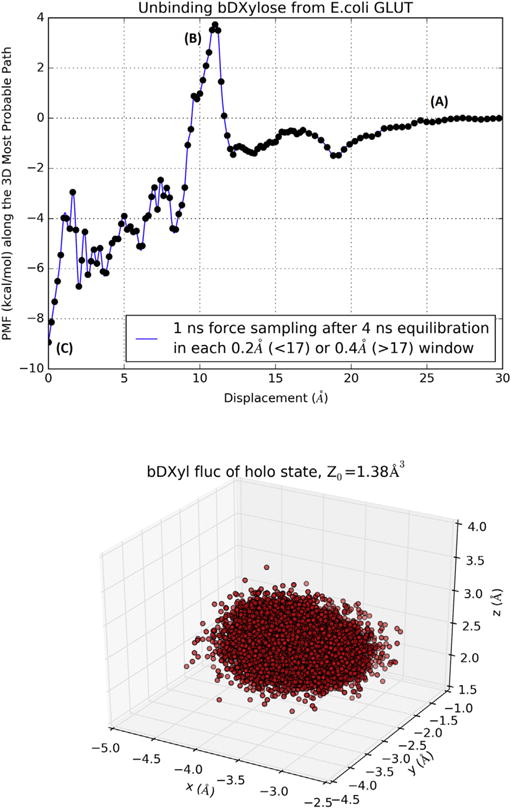
Binding XYP to XylE. Top panel, PMF along the binding path (most probably path) of XylE-XYP (inverse of the unbinding path). Bottom panel, fluctuation of XYP in the bound state.

The path of binding

The path of binding is assumed to be the inverse of the most probable path of unbinding which was sampled by steering the sugar away from the binding site toward the extracellular at a speed of 2.5Å/ns along the z-axis while the x- and y-degrees of freedom were free to fluctuate. This assumption is valid when the steering speed is sufficiently slow to allow relaxation of the x- and y-degrees of freedom at every step of advancing the z-coordinate by 2.5 × 10⁻⁶Å. The agreement between our computed affinity and the experimental data indeed validates our approach. Along the path of binding (illustrated in SI, movie S2), three representative states, (A), (B), and (C), are marked on the PMF curve in Fig. 3. Fig. 4 shows the conformations of the transporter protein and the positions of the sugar in those three states. When the sugar is away from the transporter (Fig. 4(A)), the protein is partly open to the extracellular side (top side). By thermodynamic fluctuation, the transporter can become fully open with an energetic cost of 4 kcal/mol for the sugar to move over the threshold (Fig. 4(B)). From there to the binding site (Fig. 4(C)), the free energy of the sugar-protein complex goes down by 13 kcal/mol. All this well agrees with experimental evidences that XylE is a high-affinity xylose transporter[8, 9, 13].

Fig. 4.

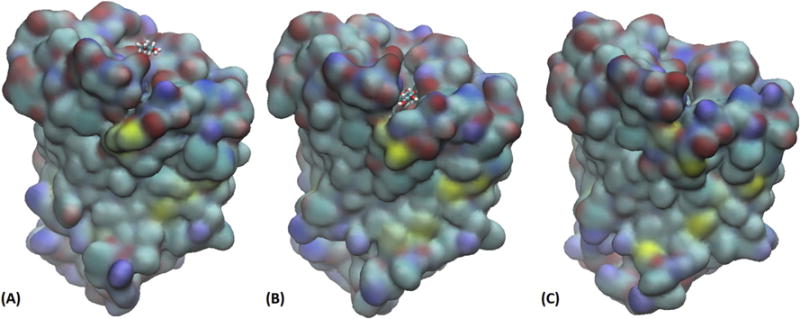
Three snapshots along the path of binding xylopyranose to E. coli xylose permease. The protein is shown as surfaces and the sugar as licorices, all colored by atom names (H, white; C, cyan; N, blue; O, red; S, yellow). (A) The sugar is away from the protein on the extracellular side and the protein is partially open. (B) The sugar is in the transition state/midway along the binding path and the protein is open wide. (C) The sugar is inside the protein and protein is partially closed to the extracellular side. All three snapshots were taken from the same viewing angle on the same scale. The locations along the binding path of these snapshots are marked in Fig. 3 as (A), (B), and (C) accordingly.

ABBREVIATIONS

3nD

3n dimensions

MD

molecular dynamics

PMF

potential of mean force

TI

thermodynamic integration

XylE

Escherichia coli xylose permease, xylose-proton symporter

XYP

β-D-xylose, xylopyranose

Appendix A. Supplementary data

Supplementary data related to this article can be found at https://doi.org/10.1016/j.bbrc.2017.10.053.