We found that choice confidence data show dynamics consistent with evidence accumulation for a forced-choice subjective visual vertical task. We also found that the evidence accumulation appeared unbounded when judging confidence, which suggests that the brain utilizes mechanisms consistent with signal detection theory to determine choice confidence.
Keywords: choice confidence, drift-diffusion model, perceptual decision making, signal detection theory, subjective visual vertical
Abstract
Humans can subjectively yet quantitatively assess choice confidence based on perceptual precision even when a perceptual decision is made without an immediate reward or feedback. However, surprisingly little is known about choice confidence. Here we investigate the dynamics of choice confidence by merging two parallel conceptual frameworks of decision making, signal detection theory and sequential analyses (i.e., drift-diffusion modeling). Specifically, to capture end-point statistics of binary choice and confidence, we built on a previous study that defined choice confidence in terms of psychophysics derived from signal detection theory. At the same time, we augmented this mathematical model to include accumulator dynamics of a drift-diffusion model to characterize the time dependence of the choice behaviors in a standard forced-choice paradigm in which stimulus duration is controlled by the operator. Human subjects performed a subjective visual vertical task, simultaneously reporting binary orientation choice and probabilistic confidence. Both binary choice and confidence experimental data displayed statistics and dynamics consistent with both signal detection theory and evidence accumulation, respectively. Specifically, the computational simulations showed that the unbounded evidence accumulator model fits the confidence data better than the classical bounded model, while bounded and unbounded models were indistinguishable for binary choice data. These results suggest that the brain can utilize mechanisms consistent with signal detection theory—especially when judging confidence without time pressure.
NEW & NOTEWORTHY We found that choice confidence data show dynamics consistent with evidence accumulation for a forced-choice subjective visual vertical task. We also found that the evidence accumulation appeared unbounded when judging confidence, which suggests that the brain utilizes mechanisms consistent with signal detection theory to determine choice confidence.
decision making spans scientific disciplines ranging from neuroscience to experimental psychology to neuroeconomics and is a fundamental component of cognition. Perceptual decision making is commonly used as a tool to investigate both cognitive decision making and perception. To advance our understanding of both human perception and human cognitive decision making, we performed studies in which human subjects performed a standard and easily reproduced forced-choice decision making task that utilized subjective visual vertical (SVV) stimuli (Baccini et al. 2014). We specifically chose an SVV direction-recognition task because SVV may be the best-studied visual-vestibular perception in humans (Baccini et al. 2014; Barnett-Cowan et al. 2010b; Clemens et al. 2011; De Vrijer et al. 2009; Dyde et al. 2006; Howard and Templeton 1966; Schöne and De Haes 1968; Vingerhoets et al. 2009), including possible clinical utility (Barnett-Cowan et al. 2010a; Böhmer and Rickenmann 1995; Cohen and Sangi-Haghpeykar 2012; Dieterich et al. 1993; Dieterich and Brandt 1992; Vibert et al. 1999; Vibert and Häusler 2000; Zwergal et al. 2009). Furthermore, decisions based on vertical perception are fundamentally important; most of us regularly make life-or-death decisions (e.g., while driving, biking, and/or reaching on a ladder) related to vertical perception.
As noted in an influential review (Gold and Shadlen 2007) two conceptual frameworks—signal detection theory (SDT) and sequential analysis—are commonly used to study perceptual decision making. Sequential analysis (Wald 1947), which is sometimes called drift-diffusion modeling (DDM) (Bogacz et al. 2006; Ratcliff 1978; Stone 1960), is commonly used to model response-time tasks in which subjects are provided a stimulus and tasked to respond as soon as they make their decision. Such DDMs are commonly recognized as mechanistic hypotheses for how the brain accumulates information to make decisions (Kiani et al. 2008; O’Connell et al. 2012; Ratcliff 1978; Ratcliff and McKoon 2008). This sequential analysis approach has been so successful that a family of such models has evolved in the literature—including collapsing bounds models (Bowman et al. 2012; Milica et al. 2010; Ratcliff and Frank 2012), urgency signal models (Churchland et al. 2008; Cisek et al. 2009; Thura et al. 2012), and models with high-pass dynamics (Bogacz et al. 2006; Busemeyer and Townsend 1993; Merfeld et al. 2016; Tsetsos et al. 2012; Usher and McClelland 2001). Models that form this DDM family integrate noisy information over time to yield a decision variable that represents accumulated information; these models “make” a decision when the decision variable crosses a decision bound (Ratcliff and Rouder 1998).
SDT (Green and Swets 1966; Macmillan and Creelman 2005) is a second framework used to study decision making and is certainly among the most widely used and most successful formalisms used to study perception and psychophysics. SDT is commonly applied during the analysis of data obtained with forced-choice tasks in which the operator controls all aspects of stimulus presentation (e.g., amplitude, duration) and the subject must provide a response after the stimulus presentation is over. Unlike evidence accumulation models that model hypothesized neural mechanisms, SDT is a statistical model that does not explicitly model an underlying neural mechanism for evidence accumulation. In fact, many studies using forced-choice signal-detection tasks do not posit an explicit mechanistic model of the decision making process, but some have applied sequential analyses (Ratcliff and McKoon 2008)—in large part because such sequential analyses have been so successful in their ability to model response-time data.
When sequential analyses have been applied to forced-choice signal-detection tasks, several models assumed that the same decision bounds successfully used for response-time tasks were applicable. For example, previous studies terminated the accumulation process whenever a decision bound was crossed (Ratcliff 2006; Ratcliff and McKoon 2008), which precisely replicates how these models work for response-time tasks. This bounded DDM has been referred to as having “absorbing” bounds (Diederich 1997). Such a DDM with absorbing bounds was later combined with SDT to address forced-choice tasks. Specifically, a “partial information model” (Ratcliff 2006) allowed part of the binary choice to be made when accumulated evidence crossed bounds, with the remaining portion of the choice determined by SDT using the end-point statistics. Moreover, a leak mechanism replacing the bound mechanism was proposed (Busemeyer and Townsend 1993) in order to better capture the decision dynamics and the speed-accuracy trade-off in forced-choice paradigms (Bogacz et al. 2006; Usher and McClelland 2001). To compare decision dynamics of the leaky integrator model and DDM in forced-choice paradigms, decision bounds were removed from DDM—making drift variance the key parameter determining the dynamics of the stochastic information accumulation (Usher and McClelland 2001). This study showed that both an unbounded DDM and an unbounded leaky integrator fit the time-accuracy data better than fits provided by bounded models (Usher and McClelland 2001). As for the speed-accuracy trade-off, it was shown that the DDM bounds are modulated in forced-choice paradigms to maximize the reward rate when reward is provided (Bogacz et al. 2006).
Since forced-choice signal-detection tasks, without rewards or feedback, are ubiquitous and because no mechanistic model has been established for such tasks, our goal was to determine the pertinent decision making mechanism for forced-choice signal-detection tasks. More specifically, using forced-choice tasks in which observation duration is constrained but response time is not, we investigated 1) whether perceptual choice and confidence mechanisms include evidence accumulation and 2) whether such evidence accumulation is terminated by decision bounds. In short, two accumulator models, bounded DDM with “absorbing” bounds (Ratcliff and McKoon 2008) and unbounded DDM without decision bounds, were augmented to include confidence probability judgments (Yi and Merfeld 2016), and then these models were compared with empiric SVV binary choice (i.e., is the visual scene tilted left or right?) and confidence (i.e., what is the probability that the choice is correct?) data obtained from 12 human subjects who performed a forced-choice signal-detection direction-recognition task while simultaneously reporting their choice confidence.
We report that forced-choice SVV choice confidence data were not matched by the bounded DDMs. Data were well matched by the unbounded DDM having a mechanism that continually accumulates information throughout stimulus presentation (i.e., decision boundaries do not interfere with continual evidence accumulation). This establishes the DDM having no bounds as a mechanistic confidence model for this forced-choice SVV direction-recognition task. While we focus our analysis on a simple DDM, we show that other DDM variants (e.g., collapsing bounds, urgency signal, high-pass filtering) yield the same conclusion regarding the contribution of boundaries, which highlights the robustness of our primary finding that decision boundaries have little, if any, impact on confidence for our forced-choice signal-detection SVV task.
METHODS
Human Studies
The Massachusetts Eye and Ear Infirmary Human Studies Committee and the MIT Committee on the Use of Humans as Experimental Subjects approved the study, and informed consent was obtained. Twelve normal volunteers (7 women, 5 men; mean age 31 yr, range 20–55 yr) participated in the study. Each subject answered health questionnaires, including vestibular function history. All 12 subjects had normal vision after correction; 3 required correction via contact lenses.
The task was to report the perceived orientation of a visual object displayed on a computer monitor. In each trial, a stationary Gabor patch (Baccini et al. 2014) was displayed at the center, and subjects indicated whether the Gabor appeared tilted left (counterclockwise) or right (clockwise) of subjective vertical (upright) after the Gabor turned off. Subjects reported simultaneously the binary orientation choice (left or right) and choice confidence by tapping on an iPad screen (Fig. 1). Subjects were informed that confidence is defined as the probability that their choice is correct. The confidence ranged between 50% and 100% with 1% resolution, with 100% being the highest confidence and 50% indicating a random guess.
Fig. 1.
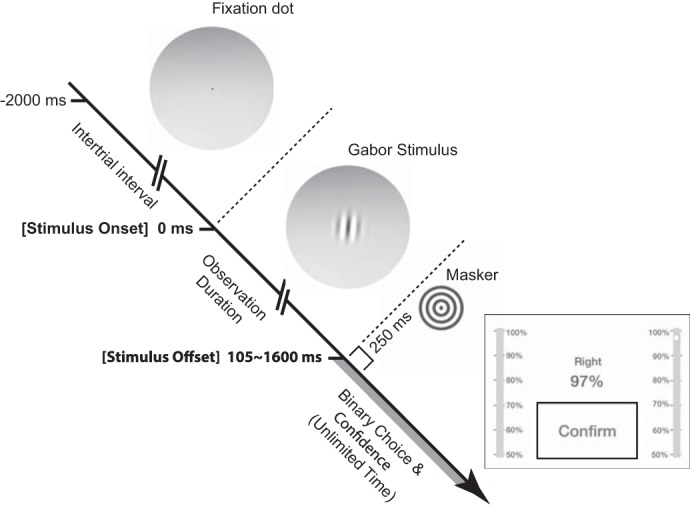
Experimental procedure. Subjects simultaneously reported both orientation choice and confidence after the Gabor stimulus turned off. The observation duration was controlled by the experimenter, pseudorandomly selected among the 5 stimulus durations (i.e., between 105 ms and 1,600 ms). Stimuli were presented on a computer monitor through a round window, and the subject response was obtained via iPad.
The stimulus was applied with five durations (105, 200, 400, 800, and 1,600 ms) in order to investigate the time dependence of binary choice accuracy and choice confidence. Also, to obtain a psychometric function for each duration, a fixed-interval nonadaptive procedure was used. In other words, stimuli were provided at seven tilt magnitudes (0.3°, 0.5°, 0.8°, 1.3°, 2.1°, 3.3°, and 5.5°) regardless of the perceptual thresholds of individual subjects. When combined with the two tilt directions (left and right), this yielded 14 tilt amplitudes between −5.5° and +5.5°. The experiment consisted of 900 trials in total per subject, carried out in 5 blocks of 180 trials. Five durations and 14 amplitudes were randomly interleaved within a block. Before the main data collection, a short practice session consisting of ~10 trials was performed to familiarize our subjects with the task.
A visual fixation point was displayed during intertrial intervals of 2,000 ms, and each Gabor stimulus was followed by a visual masker without orientation cues (i.e., a bull’s-eye target of the same size as the Gabor) to disrupt the influence of any Gabor afterimage that may have been present (Fig. 1). The iPad turned on only after the Gabor turned off, and then the iPad turned off after the subject submitted a response. The visual scene was displayed on a computer monitor (Asus VG248QE) and was generated with Psychtoolbox (Brainard 1997) at a refresh rate of 144 Hz. The Gabor patch had a visual angle of 7° diameter (Lopez et al. 2011) with 2 cycle/° and 80% contrast (Baccini et al. 2014). Subjects viewed the display through a round window having a 20° viewing angle at a distance of 85 cm from the eyes inside a dark chamber. Subjects rested their chin on a chin bar to hold their head in a steady position throughout the experiment.
Computational Models
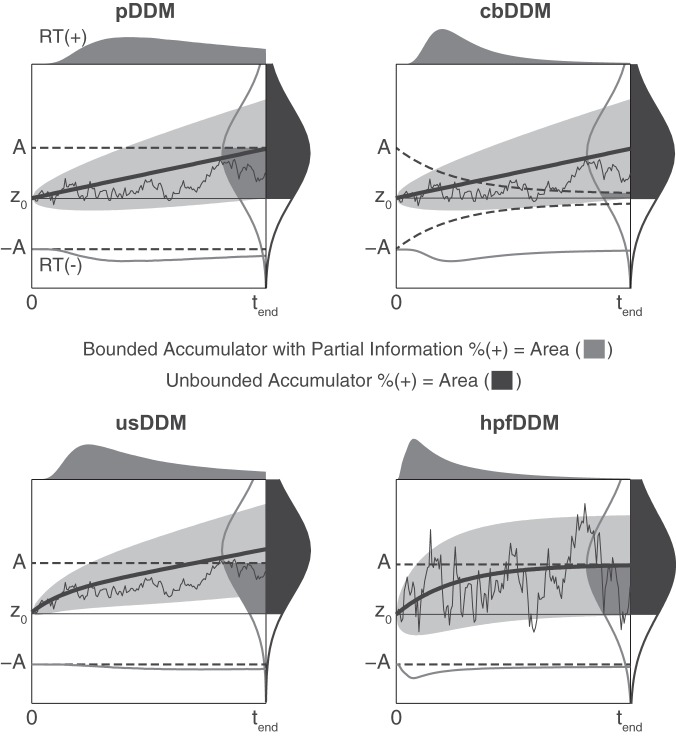
In this study, we compare four DDMs that differ in the dynamical features of evidence accumulation and decision bounds. These four models include a pure DDM (pDDM), a collapsing bound DDM (cbDDM), an urgency signal DDM (usDDM), and a high-pass filter DDM (hpfDDM). Figure 2 illustrates the dynamics of the four DDMs, and a list of the model parameters is provided in Table 1. Here, pDDM is the simplest model, consisting of an integrator that accumulates sensory evidence until the evidence crosses a fixed decision bound (Fig. 2, top left). In cbDDM, the dynamics of evidence accumulation is identical to pDDM, but the decision bounds collapse over time instead of being constant (Fig. 2, top right). In usDDM, a signless urgency signal is added to the accumulated evidence to boost the signal to cross the bounds earlier (Fig. 2, bottom left). Finally, in hpfDDM, older information leaks away to weigh more recent information when accumulating the sensory evidence (Fig. 2, bottom right). Figure 2 also illustrates how the decision bounds affect the binary response statistics, such as choice accuracy (i.e., % choosing a positive choice when given positive stimulus) in a forced-choice paradigm. For instance, in bounded DDMs, the probability of choosing a positive choice %(+) is determined by applying the partial information model (Ratcliff 2006). In the partial information model, part of the choice is determined when accumulated evidence crosses a bound, and the remaining portion of the choice is determined by the position of the accumulated evidence. Figure 2 shows sensory evidence accumulation in response to positive stimulus. In Fig. 2, the probability of accumulated evidence crossing a positive bound A at any time during stimulus presentation is depicted by the gray curve labeled RT(+), which shows a response time (RT) distribution. Then by tend, the total percentage crossing a bound equals the area under the distribution curve [e.g., gray area under RT(+) curve]. For the remaining proportion that did not cross a bound by tend, the total probability of the accumulated evidence positioned between the mean neutral point (z0) and the positive bound A (e.g., gray area under vertical bell curve) contributes to positive choice. Hence, for bounded DDMs, the total choice accuracy when given a positive stimulus is the sum of two gray areas in Fig. 2. In contrast, in the unbounded DDMs the choice is determined only by the position of the accumulated evidence at tend. In Fig. 2, the vertical black bell curve illustrates the probability of the accumulated evidence positioned at tend, and the total %(+) equals the black area under the distribution curve.
Fig. 2.
Four drift-diffusion model variants—each including both signal detection theory and partial information variants for a total of 8 models. Each panel shows 1 of 4 individual models, pDDM, cbDDM, hpfDDM, and usDDM. See extended text sections describing the details of each of these 4 models. Each panel also shows 2 variants representing signal detection theory and partial information models. As the mean accumulated evidence (thick solid black curve) increases over time, the variance (light gray shading showing the standard deviation) increases as well. An example decision variable (i.e., accumulated evidence) for a single trial is shown as the jagged thin black line, which starts at mean decision bias z0. For the partial information model, a decision is made whenever the decision variable crosses 1 of the decision bounds (dashed black line starting at A or −A). The probability of hitting a bound, which defines the decision time distribution, is shown as dark gray curves above each plot. The probability of crossing the positive (+) bound is drawn on the top of each panel, and the probability of crossing the negative (–) bound is drawn below the negative bound, inverted. If a stimulus ends before crossing a decision bound, signal detection theory is applied (dark gray curve in a vertical orientation at tend). In a partial information model, the probability responding positive [% (+)] is the sum of a decision variable’s 1) probability of crossing (+) bound up until the end of the stimulus at tend and 2) the probability positioned between z0 and A at tend, which corresponds to the sum of the gray areas. On the other hand, if the binary decision is determined purely based on end-point statistics (consistent with signal detection theory), only the position of the decision variable at the end of the stimulus tend contributes to the decision. The distribution of decision variables at tend is shown as a black bell curve in a vertical orientation. In such case, the %(+) corresponds to the area colored black.
Table 1.
Free parameters for each accumulator model
| Parameter | pDDM | cbDDM | usDDM | hpfDDM | Definition |
|---|---|---|---|---|---|
| σ | ○ | ○ | ○ | ○ | Diffusion noise |
| η | ○ | ○ | ○ | Sensory noise | |
| τ | ○ | Leak time constant | |||
| μ | ○ | ○ | ○ | ○ | Sensory bias |
| z0 | ○ | ○ | ○ | ○ | Mean decision bias |
| z | ○ | ○ | ○ | ○ | Decision bias range |
| λ∞ | ○ | Maximum urgency signal | |||
| τA | ○ | Urgency signal time constant | |||
| a | △ | △ | △ | △ | Decision bound |
| τa | △ | Decision bound time constant | |||
| Total no. of parameters | 5 | 5 | 7 | 5 | Unbounded models |
| 6 | 7 | 8 | 6 | Bounded models |
○, Parameters in both unbounded and bounded models; △, parameters in only the bounded models.
Pure DDM.
Consistent with Ratcliff’s model (Ratcliff 2006), pDDM is modeled as a simple integrator (∫) to accumulate the noisy sensory cue x over time to yield a decision variable y such that
The noisy sensory cue x is normally distributed around the noiseless stimulus level (= drift rate in Ratcliff 2006) v with a variance η2 and a bias μ, such that x ∼ N(v − μ,η2). In addition to sensory noise, another source of noise in Ratcliff’s model is the initial offset parameter that is uniformly distributed, . During the accumulation process, diffusion noise w˙ ∼ N(0, σ2) is added, yielding y˙ = x + w˙. Consistent with earlier formulations (Bitzer et al. 2014; Ratcliff 2006), this process is a Weiner diffusion process (Gardiner 1985).
When a constant stimulus with a magnitude of v is assumed, solving for the continuous time solution yields
| (1a) |
| (1b) |
Discrete time solutions are provided in the appendix. In Eq. 1a, xt is noisy sensory information that is accumulated over time, W(t) is diffusion noise associated with the decision (nonsensory) process, and y0 is the starting point of the accumulator. The variance of y0 is . Therefore, the expected value and the variance of y(t) are
| (2a) |
| (2b) |
Collapsing bound DDM.
cbDDM equations range widely in terms of complexity (Bowman et al. 2012; Milica et al. 2010; Ratcliff and Frank 2012), but here we consider cbDDM in its simplest form having the fewest free parameters (Milica et al. 2010). As in pDDM, the accumulation process remains the same (Eqs. 1a and 2), but the decision bounds decay exponentially toward 0 such that
| (3) |
Urgency signal DDM.
usDDM has an even wider range of complexity (Churchland et al. 2008; Cisek et al. 2009; Thura et al. 2012), but as with cbDDM we consider the simplest mechanism (Churchland et al. 2008). In usDDM, an urgency signal λ is added to accumulated sensory evidence to make the decision variable rise faster,
λ usually takes the form of exponentially saturating function (Churchland et al. 2008; Cisek et al. 2009; Thura et al. 2012). One of the simpler versions of λ was introduced by Churchland (Churchland et al. 2008), who characterized the urgency signal as a half-life formula. However, since this formula is nonlinear when expressed in discrete formulation, we here define λ as an exponential decay. Meanwhile, decision bounds stay constant in usDDM. Hence, the continuous time solutions for usDDM are
| (4a) |
| (4b) |
| (4c) |
Here, τus characterizes the decay rate of the urgency signal and λ∞ characterizes the maximum urgency signal. The expected value and the variance of y(t) are then
| (5a) |
| (5b) |
High-pass filter DDM.
For the hpfDDM, it is assumed that the brain considers only the more recent information while discarding older information (Merfeld et al. 2016; Tsetsos et al. 2012; Usher and McClelland 2001). This mechanism of putting a time window around incoming sensory input can be modeled as a high-pass filter (HPF), and this HPF is applied sequentially with a DDM. For the linear model considered here, the order of these processes (HPF before DDM or DDM before HPF) does not matter. The width of the time window is characterized by a time constant τ, which can be represented by the following expression:
Unlike previous models, the diffusion noise σ for an hpfDDM is assumed to originate from the sensory noise (i.e., η = σ). Also, now the diffusion process is also affected by the leak (HPF), resulting in a Langevin process (Langevin 1908) rather than being a pure diffusion (Weiner) process. Applying Langevin’s equation (Langevin 1908) yields a continuous time solution with the following noise variance:
| (6a) |
| (6b) |
The expected value and the variance of y(t) are then
| (7a) |
| (7b) |
An important dynamic characteristic of an hpfDDM is that both the expected value and the variance of the decision variable reach a steady state [(v − μ)τ and , respectively] as t → +∞. In contrast, E[y(t)] and Var[y(t)] in the other three models diverge toward +∞ as t → +∞. These differences play a crucial role in the assumption about the internal representation of the decision variable noise distribution. In other words, because the steady-state decision variable variance converges to a finite value beyond the time constant, the neural network is not required to track the variance in real time. This means that the neurons now can establish a stationary representation of decision noise, contrary to the other models that require nonstationary, time-dependent noise representations. Here, we assume such steady-state stationary decision noise with variance (Var):
| (7c) |
The procedures for finding thresholds based on these four DDMs are outlined in Eqs. 13–18.
Psychophysics, confidence, and DDM.
There is a general consensus that confidence reflects the state of the decision variables, although it is still debated whether decision and confidence involve a single- or double-stage process (Murphy et al. 2015; Navajas et al. 2016; Pleskac and Busemeyer 2010; Rahnev et al. 2015; van den Berg et al. 2016; Yu et al. 2015). Yi and Merfeld recently proposed a psychophysical model explaining the correlations between confidence and perceptual precision (Yi and Merfeld 2016). Here we combine this earlier confidence model with a DDM. Perceptual precision is effectively modeled as a sigmoidal psychometric function based on SDT (Green and Swets 1966; Merfeld 2011; Wichmann and Hill 2001). This function represents perceptual noise, and thresholds are defined in terms of the spread parameter σ of such distribution. Unlike in Yi and Merfeld (2016), which developed the model in the stimulus domain, here we define confidence in terms of the decision variable (i.e., define confidence in terms of y instead of v).
The direction-recognition psychometric function is typically modeled as the probability of choosing a positive choice given a stimulus in the form of cumulative Gaussian function,
| (8a) |
where E[y(v,T)] indicates the expected decision variable driven by the stimulus v with a duration t. Then each individual y(v,t) is a random variable from each trial such that y(v,t) ∼ N{E[y(v,t)], Var[y(t)]}. Therefore the probability density of y(v,t) is a Gaussian function
| (8b) |
Confidence is an internal probabilistic representation of choice accuracy given the decision variable that is driven by the stimulus. Taking Yi’s mapping of confidence from the psychophysics, confidence on a single-trial basis can be obtained from
| (9) |
where K(t) is a confidence factor at time t, K < 1 indicating overconfidence and K > 1 indicating underconfidence (Yi and Merfeld 2016). Here, as an empiric model required to match data, K(t) is modeled as an exponentially decaying function such that
| (10) |
since K showed time dependence (Fig. 3L). The probability density of confidence can be obtained through a coordinate conversion from the stimulus domain in Eq. 9 to the confidence domain by substituting y(v,t) = Φ−1{conf; 0,K·Var[y(t)]} from Eq. 9 into Eq. 8b,
Fig. 3.
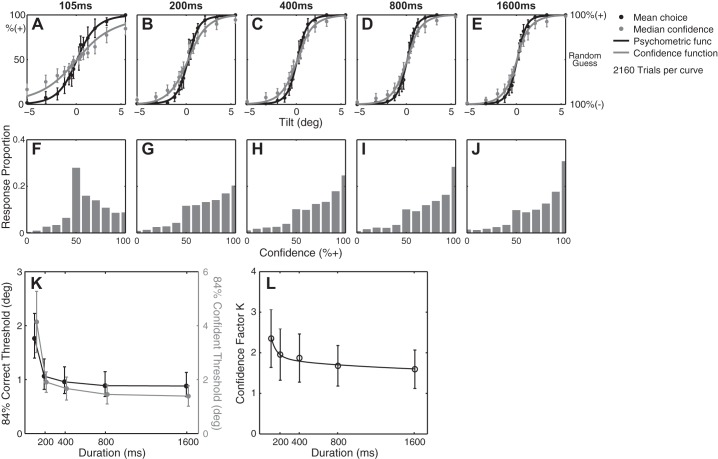
Perceptual binary choice and confidence data summary from 12 subjects. A–E: a Gaussian psychometric function (solid black curve) was fitted to binary choice data (black circles), and a Gaussian confidence function (solid gray curve) was fitted to confidence data (gray circles) at individual stimulus durations. x-Axis is stimulus level in tilt. Left y-axis is % responding + for the binary responses and % confidence that the stimulus is + for confidence responses. Right y-axis shows the confidence interpreted by subjects (% correct). F–J: confidence histograms with 11 confidence bins. K: choice threshold (solid black) and confidence threshold (solid gray) in terms of stimulus duration. L: confidence factor as a function of stimulus duration. Error bars show 95% confidence interval.
| (11) |
When expressed as a discrete probability density, Eq. 11 becomes equivalent to the confidence density equation (Equation 2) in Yi and Merfeld (2016).
| (12) |
In Eq. 12, Δc is the resolution allowed for the confidence response. In this study, subjects reported confidence with a 1% resolution (Δc = 1%).
Perceptual threshold in unbounded DDMs.
In unbounded DDMs, as illustrated in Fig. 2, the final position of the decision variable determines the categorical response. This is consistent with SDT that assumes no decision bounds, in which the end-point statistics determine the probability correct. In binary forced-choice paradigms where there are only two choice categories (positive or negative as in Fig. 2) a decision variable greater than 0 (or z0) yields a positive response. In the direction-recognition paradigm that was utilized in several studies investigating the precision of vestibular perception (Grabherr et al. 2008; Karmali et al. 2014; Lim et al. 2017; Valko et al. 2012), the threshold is defined at the stimulus level that would yield 84% (1σ) correct direction choice. In DDMs, this corresponds to the stimulus level v at which . Then solving for v gives the direction-recognition threshold Tm,SDT(t) as a function of stimulus duration t for pDDM. Subscript m indicates the DDM variant (p, cb, us, or hpf). Hence the threshold expressions for the four models are
| (13) |
| (14) |
| (15) |
For cbDDM, because SDT assumes no decision boundary, Tcb,SDT(t) = Tp,SDT(t) as in Eq. 13. In Eqs. 13 and 14, even though the accumulated evidence approaches infinity with increasing time, the threshold approaches a nonzero asymptote because the variance also increases at a comparable rate. Therefore, the steady-state threshold asymptotes to η + μ as t → ∞ for pDDM, cbDDM, and usDDM. hpfDDM threshold also asymptotes but to a different steady-state as t → ∞.
Perceptual threshold in bounded DDM.
In the past, response time (RT) and choice accuracy (Hawkins et al. 2015; Ratcliff 2006; Ratcliff and Rouder 1998; Usher and McClelland 2001) were used to verify DDM. Although the experimental design here does not allow RT measurement, the mathematical expression for choice accuracy can still be derived while assuming absorbing decision bounds. For instance, the decision process terminates when a decision variable hits a bound at any time before the stimulus ends, and the choice accuracy corresponds to the cumulative probability of hitting the correct bound plus the remaining decision variables on the correct side (Ratcliff 2006). This concept of applying SDT to only the decision variables that did not reach a decision bound was proposed as “partial information theory” (Ratcliff 2006). Since this study investigated direction-recognition decision processes, two decision bounds A and −A are assumed. At time t, the probability of a decision variable yt hitting either A or −A is denoted as . This is the union of the probability of Pr(yt > A) and Pr(yt < −A):
| (16) |
Then the probability of a decision variable yt hitting one particular bound is the joint probability between the proportion that remains after the previous time t − Δt and the probability of the current yt distance being greater than the distance to the bound:
| (17a) |
| (17b) |
The probability density of the correct RT given positive stimulus (e.g., response in the positive direction given the positive stimulus) is provided in Eq. 17a, while the incorrect RT (e.g., response in the negative direction given the positive stimulus) is provided in Eq. 17b. Based on these, the choice accuracy is the sum of all the correct RT probability up until t and the remaining decision variables that are closer to the correct bound (equivalently above z0 given positive stimulus) at t. For defined as the total choice accuracy, is the sum of probability correct when given positive stimulus and when given negative stimulus .
| (18a) |
| (18b) |
| (18c) |
Solving for yields the threshold prediction as a function of time. Because of the iterative nature of Eq. 18, an analytical threshold expression was not derived. Rather, these equations were solved numerically via DDM modeling.
Fitting
Fitting a psychometric function to binary responses.
The models were fit with maximum-likelihood methods. First, the likelihood function L for the models based on SDT (Eq. 8) was defined as the joint probability of all of the responses R(− or +) happening given the stimulus and duration arrays V and T, respectively, while assuming a set of free parameters for an unbounded fit model () or a different set of parameters for a bounded () fit model.
| (19a) |
As one example, as shown in Table 1, pDDM has free parameter set .
Taking a natural log of yields the log-likelihood
| (19b) |
The likelihood for the bounded DDM takes a more complicated form but is similar in principle to Eq. 19a,
| (20a) |
The free parameter set here includes the bound parameter as well such that for pDDM (see Table 1). Consequently, the log-likelihood of Eq. 20a becomes
| (20b) |
The DDM parameters, and , that yielded a minimum negative log-likelihood (NLL = −lnL) were found with fmincon in MATLAB.
Fitting a confidence function to confidence responses.
Similar to the method used to fit binary data, the confidence models were fitted with maximum-likelihood methods (Yi and Merfeld 2016) when sufficient measurements were available to calculate the likelihood. This time, instead of binary responses, the likelihood is defined as the joint probability of all of the confidence responses C ∈ [0 100] happening given the stimulus and duration arrays V and T, as well as the underlying perceptual parameters, or , found from the binary data fit while assuming confidence function parameters K = {K0, K∞, τc}.
| (21a) |
Then the log-likelihood is
| (21b) |
Equations 21a and 21b require the time at which the confidence is calculated, since confidence at time t is measured against Var[y(t)]. Within SDT, the confidence is calculated always at the end of the stimulus at t = T. However, in the bounded DDMs, the time at which a y(t) crosses a bound depends on the random noise driving y(t) at each trial. Such information on timing is not available in the present experimental data, where the observation duration was controlled by the experimenter by design. Therefore, to fit the bounded DDMs, the root-mean-squared error (RMSE) was calculated between the predicted confidence histogram and the observed confidence histogram for each subject. To generate the model predictions, each DDM was simulated with 90,000 trials at each duration for each subject with the estimated DDM parameters. The histogram (with response proportion instead of count) was then obtained by binning the simulated confidence with the same binning used for the observed data. The confidence parameters that yielded a minimum RMSE were found via fmincon in MATLAB.
Goodness of fit assessment.
In this study, each subject provides two related data sets, binary choice and confidence vectors—one value for each per stimulus. The goodness of fit was evaluated separately for the binary choice and confidence data. For binary choice data, the Bayesian information criterion (BIC) was calculated from the negative log-likelihood (NLL) since the responses are in binary form.
| (22a) |
Here, n is the number of trials, which equals the length of binary response vector, and k is the number of free parameters. For confidence data, BIC was calculated from RMSE such that
| (22b) |
where m is the number of confidence bins. When comparing two models A and B, ΔBIC was calculated such that ΔBICA − B = BICA − BICB, in which a positive value indicates that the model B fit is better than the model A fit. When comparing multiple models, notation ΔBICA − B,C is used to summarize ΔBICA − B and ΔBICA − C. For example, ΔBICA − B,C > 0 indicates that model A scored worse than models B and C.
Given the study design, as is not uncommon, the DDMs face an overfitting problem—even though there are 900 trials per subject—given that there are only five durations to fit five free parameters in Eq. 10 and six free parameters in Eq. 11. To assess overfitting, log-likelihood ratio (LLR) tests with χ2-statistics were performed (Huelsenbeck and Crandall 1997; Wilks 1938). In other words, the LLR was calculated for each model with subsets of nonzero parameters to identify free parameters that can be eliminated.
To compare the unbounded and bounded model fits to the confidence data, binomial test and χ2-test were used to compare the model fit performances between the unbounded and bounded models. Also, pairwise two-sided multiple comparisons between the confidence data and each of the models were performed with the Dwass-Steel-Critchlow-Fligner method.
RESULTS
Overview
Both perceptual choice accuracy and confidence increased with increasing stimulus duration (Fig. 3) when stimulus duration was operator controlled and the response was constrained to occur after stimulus presentation was complete. To investigate these dynamics, 1) two different decision bound mechanisms for 2) four variants of accumulator models were simulated and fitted to the experimental data. Goodness of fit analysis of confidence response showed that each of the four models performed significantly better when sensory accumulation was unbounded. On the other hand, both bounded and unbounded models did similarly well in describing the binary response data. Also, goodness of fit analysis showed that unbounded pDDM (cbDDM) and hpfDDM are indistinguishable for the stimuli used in this study but each performed significantly better than unbounded usDDM. Before model fits, a parametric study was performed in order to identify the free parameters that significantly contribute to model fit improvement. Nested model analysis of the data from 12 subjects eliminated three free parameters, sensory bias, decision bias, and decision bias range.
Perceptual Decision Accuracy and Confidence Data
Figure 3 summarizes the behavioral responses from 12 subjects. Figure 3, A–E, show psychometric functions fitted to binary choice and confidence responses. Continuous cumulative Gaussian functions describe mean accuracy as well as median confidence. Median confidence is used because the distribution of confidence responses is not Gaussian (Fig. 3, F–J). Both choice accuracy and confidence can be expressed as thresholds, which are, respectively, defined as the stimulus levels at which % correct and % confidence are 84%. These binary choice and confidence thresholds are plotted against stimulus duration to visualize the dynamic characteristics (Fig. 3K); thresholds show an exponential-like decay that attains nonzero asymptotes for both binary choice and confidence. In addition, the mean confidence factor K(t) shows time dependence (Fig. 3L). Here, K(t) in Fig. 3L is equivalent to the ratio of the confidence threshold to the binary choice threshold curves in Fig. 3K. However, K(t) was calculated for individual subjects since the data showed that each subject has a different tendency to be more or less confident for given choice accuracy. Even after such normalization of the confidence by the choice accuracy, the time dependence of K(t) remained. In short, the time dependence of K(t) was characterized for each subject by fitting a function that decays exponentially to a nonzero asymptote (Eq. 10).
Parametric Study—Nested Model Analysis
Before final fits of the experimental data to the models, a parametric evaluation was performed to prevent overfitting. Nested model hierarchical analysis using binary choice data from 12 subjects showed that at least three free parameters can be excluded from the models. Tables 2 and 3 show the resulting free parameters and LLR for all four accumulator models, both unbounded (Table 2) and bounded (Table 3) conditions. If adding more free parameters improves fitting, the LLR with a greater number of free parameters should be greater than 0. A negative LLR indicates that the model fit worsened compared with the baseline model. indicates the baseline parameter set for the unbounded models, and indicates the i number of parameters added to the baseline set in Table 2. Similarly, indicates the baseline parameter set for the bounded models, and indicates the i number of parameters added to the baseline set in Table 3.
Table 2.
Unbounded models: nested model hierarchical analysis
| NLL |
LLR |
||||||
|---|---|---|---|---|---|---|---|
| Resulting Model Parameters | |||||||
| pDDM, cbDDM | 313 [309, 387] | 303*** [291, 376] | 12** [9.0, 14] | −412 [−485, −308] | −31 [−48, −1.4] | 1.5* [0.2, 2.1] | |
| usDDM | 433*** [387, 483] | 501 [460, 571] | −65 [−120, 2.7] | ||||
| hpfDDM§ | 302*** [290, 375] | −459 [−783, −276] | −212 [−251, −164] | 0.00 [−0.00, 0.00] | |||
Values are medians [quartiles].
Marginally significant improvement (0.05 > P > 0.01) for 4 subjects.
Significant improvement (P < 0.01, ) for 11 subjects. For the remaining 1 subject, additional free parameter did not alter the fit (χ2 = 0).
(Bold) High statistical significance (P < 0.01, ) for all 12 subjects.
For hpfDDM, threshold expression Eq. 15 is undefined when τ = 0.
Table 3.
Bounded models: nested model hierarchical analysis
| NLL |
LLR |
||||||
|---|---|---|---|---|---|---|---|
| Resulting Model Parameters | |||||||
| pDDM | 340 [251, 434]7 | 295** [291, 379]11 | 0.00 [−0.00, 0.05]6 | 0.02 [−1.7, 0.06]11 | —§§ | 0.00 [−0.01, 0.00]11 | |
| cbDDM | 340 [251, 434]7 | 295** [291, 379]11 | 0.00 [−0.00, 0.05]6 | 0.02 [−1.7, 0.06]11 | —§§ | 0.00 [−0.01, 0.00]11 | |
| usDDM | 317 [292, 417]8 | 295** [291, 379]11 | 0.07 [0.06, 0.37]7 | 0.4 [−0.04, 1.5]11 | —§§ | 0.00 [−0.00, 0.00]11 | |
| hpfDDM§ | 295** [289, 380]11 | 0.2 [−1.3, 1.5]8 | —§§ | 0.00 [−0.00, 0.00]11 | |||
Values are medians [quartiles]. Subscripts to right of quartiles indicate the number of subjects that yielded converging model fits.
(Bold) Best median NLL with highest model fit convergence rate.
For hpfDDM, threshold expression Eq. 15 is undefined when τ = 0.
Model fits did not converge for more than half of the subjects.
For unbounded model fits, the fits converged for all 12 subjects. For bounded model fits, the fits did not converge for a few subjects; numbers varied depending on the free parameter sets. The number of converging fits is indicated by the subscripts in Table 3. The best NLL scores with high statistical significance (P < 0.01, ) are highlighted with bold triple asterisks in Table 2, and the parameter sets with these best NLL scores are used in all analyses that follow.
The nested model hierarchical analyses of unbounded models indicated that sensory bias μ and decision bias z0 do not significantly improve model fits. Decision bias range z marginally improves the model fit for pDDM only partially (4 of 12 subjects). Based on these, only sensory noise η and diffusion noise σ remained for pDDM and cbDDM; only diffusion noise σ and urgency signal parameters λ∞ and τλ remained for usDDM; and only a diffusion noise σ and a leak time constant τ remained for hpfDDM for the unbounded models (Table 2).
Similarly, the nested model hierarchical analyses of bounded models indicated that decision bias z0 and decision bias range z did not significantly improve the model fit for any of the four DDMs and that sensory bias μ improved the model fits for only one or two subjects. Based on these, only sensory noise η and diffusion noise σ remained for pDDM, cbDDM, and usDDM, and only a diffusion noise σ and a leak time constant τ remained for hpfDDM in addition to bound parameters for the bounded models (Table 3).
Model Dynamics Comparisons
In this study, two questions were investigated through computational modeling: 1) What is the role of decision bounds when the task does not constrain response time? 2) What is the additional feature of the decision dynamics—is it a simple accumulator or does it require additional dynamic components such as a leak mechanism or urgency signal? Table 4, Fig. 4, and Fig. 5 summarize the model fit results relevant to these two questions. In short, goodness-of-fit scores consistently show that, with one exception described below, unbounded models fit both binary choice and confidence data better than bounded models for all four accumulator model variants. On the other hand, pure accumulator and leaky accumulator model fits are indistinguishable, while the urgency signal model scored worse than all other models. Detailed results are presented in Unbounded vs. bounded evidence accumulation and Evidence accumulation dynamics.
Table 4.
Model fit results: goodness-of-fit score comparisons between Unbounded and Bounded models
| ΔBICBounded −
Unbounded |
||||
|---|---|---|---|---|
| pDDM | cbDDM | usDDM | hpfDDM | |
| Binary choice | 1.9* [−0.5, 4.5]6 | 8.7** [6.3, 11]10 | −160 [−365, −19]2 | 6.6** [6.4, 6.8]10 |
| Confidence | 114*** [87, 133]11 | 115*** [99, 147]11 | 130*** [92, 150]10 | 12*** [4.5, 47]9 |
Values are medians [quartiles]; n = 11. Subscripts indicate the number of subjects that yielded ΔBIC > 2.
Positive evidence for unbounded models (ΔBIC > 2).
Strong evidence for unbounded models (ΔBIC > 6).
(Bold) Very strong evidence for unbounded models (ΔBIC > 10) (Kass and Raftery 1995).
Fig. 4.
Model comparisons: unbounded and bounded pure accumulator models (pDDM). A: binary choice threshold estimates as a function of stimulus duration. Unbounded pDDM, bounded pDDM, and signal detection theory (SDT) threshold predictions were averaged across 11 subjects. Gray shading shows 95% CI for SDT estimates. B: probability of hitting a bound as a function of stimulus duration in bounded pDDM. C: mean goodness-of-fit scores at individual stimulus duration for binary responses (top) and confidence responses (bottom). D: marginal goodness-of-fit scores across all durations for binary responses (top) and confidence responses (bottom). Horizontal bars: *positive evidence (ΔBICBounded − Unbounded > 2), ***very strong support (ΔBICBounded − Unbounded > 10) for unbounded pDDM. Error bars show lower and upper quartiles. E–I: confidence histograms aggregated across all stimulus levels for 11 subjects. Solid black curves, unbounded pDDM; dashed black curves, bounded pDDM.
Fig. 5.
Unbounded model comparisons: 4 variants of accumulator dynamics. A: binary choice threshold estimates as a function of stimulus duration. pDDM and cbDDM, usDDM, hpfDDM, and signal detection theory (SDT) threshold predictions were averaged across 12 subjects. Gray shading shows 95% CI for SDT estimates. B: mean goodness-of-fit scores at individual stimulus duration for binary responses (top) and confidence responses (bottom). C: marginal goodness-of-fit scores across all durations for binary responses (top) and confidence responses (bottom). Horizontal bars: *positive evidence that hpfDDM performs better than pDDM; ***very strong evidence against usDDM. Error bars show lower and upper quartiles. > Symbol indicates that BICpDDM > BIChpfDDM. D–H: confidence histograms aggregated across all stimulus levels for 12 subjects. Same conventions as A for curves. Differences between pDDM and hpfDDM are barely evident in D–H; the most pronounced difference is observed in D for confidence near 100%.
Unbounded vs. bounded evidence accumulation.
To quantitatively compare between unbounded and bounded conditions, ΔBICBounded − Unbounded (= BICBounded − BICUnbounded) was calculated, taking the number of free parameters into account. Here, 11 subjects with converging fits for both unbounded and bounded models were compared. Because BIC is smaller for better model fits, positive ΔBICBounded − Unbounded indicates that the unbounded model fits the data better than the bounded model.
Table 4 shows that three of four unbounded models fit binary data better than bounded models. There is strong evidence (median ΔBIC > 6; ΔBIC > 2 for 10 of 11 subjects) that unbounded cbDDM and hpfDDM performed better than bounded cbDDM and hpfDDM, but the improvement offered by unbounded pDDM over bounded pDDM was less strong (ΔBIC > 2 for 6 of 11 subjects). In contrast, the bounded usDDM performs better, with very strong evidence (ΔBIC > 2 for 9 of 11 subjects), than its unbounded version.
Focusing on confidence, each of the four unbounded models fits confidence data substantially better than the bounded model, with very strong evidence (median ΔBIC > 6; ΔBIC > 2 for 9 or more of 11 subjects). Examples of detailed analyses are presented in Fig. 4. Because the pure accumulator model (pDDM) is the simplest model that scored well in the goodness of fit assessments (Tables 2 and 3) without assistance of an additional dynamic component, only the pDDM fit results are presented in Fig. 4 for simplicity.
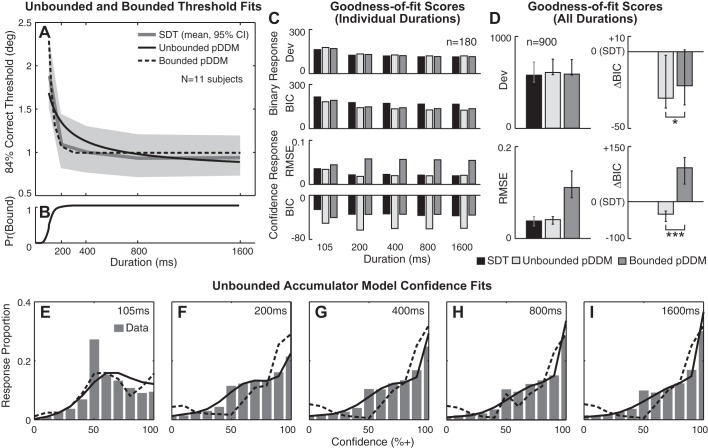
Figure 4A shows the SVV orientation direction-recognition binary choice thresholds estimated by three different models: 1) SDT that does not include any dynamics, 2) unbounded pDDM, and 3) bounded pDDM. Here, binary choice thresholds are defined as the stimulus levels at which 84% correct response is achieved. The curves are the mean estimates across 11 subjects, since 1 subject’s data did not yield a converging fit for the bounded pDDM. The light gray shading shows 95% CI from SDT fits. All three threshold estimates show similar time dependence: thresholds decrease to a nonzero plateau. For binary choice thresholds, SDT yields 2 free parameters per duration, totaling 10 free parameters across five durations. Unbounded and bounded pDDMs have two and three free parameters, respectively. When comparing the model fits, SDT estimates were chosen as the baseline because the biggest number of free parameters should guarantee the smallest fitting errors (smallest Dev in Fig. 4, C and D) in addition to the historical explanation that SDT has been the standard means to calculate thresholds under the forced-choice experimental paradigm used. See Table 2 for the values of Dev (= 2 × NLL).
Before adjusting for the number of free parameters, all three models score similarly in explaining the binary response (Dev in Fig. 4, C and D). After the adjustment, unbounded and bounded models provide substantially better explanations of the binary response data than SDT in isolation (ΔBICUnbounded − SDT < −10 for 8 of 11 subjects and ΔBICBounded − SDT < −10 for 7 of 11 subjects) (Kass and Raftery 1995). Between unbounded and bounded pDDM, the median ΔBIC (Table 4) indicates positive support for unbounded pDDM (Fig. 4D).
The confidence response is explained significantly better by the unbounded pDDM than the bounded pDDM stimulus durations between 200 ms and 1,600 ms (binomial test P < 0.0001, χ2-test P = 0.03). Such quantitative analyses are visualized as RMSE and ΔBIC scores at each duration in Fig. 4C, bottom, and the sum across all durations in Fig. 4D, bottom. For instance, RMSE for both SDT and unbounded pDDM was approximately three times better than bounded pDDM. Also, BIC scores showed very strong support for unbounded pDDM (ΔBICBounded − SDT,Unbounded > 10 in Fig. 4D) (Kass and Raftery 1995) compared with the other models. Between unbounded and bounded pDDM, the median ΔBIC (Table 4) indicates very strong support for unbounded pDDM (Fig. 4D) when describing the confidence data.
These quantitative analyses are visually matched by confidence fit quality (Fig. 4, E–I), such that unbounded pDDM outlines the confidence data better than bounded pDDM between 200 ms and 1,600 ms. In support of this result, statistical analyses show that there is no difference between unbounded pDDM and the confidence data (multiple comparisons P = 0.95) whereas there is a significant difference between bounded pDDM and the confidence data (multiple comparisons P < 0.0001). At 105 ms, the confidence fits are statistically indistinguishable between the bounded and unbounded pDDMs (multiple comparisons P ≥ 0.35) because a large proportion of the decision variables do not cross bounds within such a short accumulation time. Figure 4B shows the proportion of the decision variables that cross one of the two bounds as a function of stimulus duration. The proportion is the mean calculated given the stimulus vector. As can be seen, nearly all decision variables hit a bound by 200 ms. In other words, when the stimulus duration is short, the majority of trials do not yield a decision boundary crossing, even when a decision boundary is present, hence yielding choice confidence dictated by SDT. On the contrary, when the stimulus duration is long, the majority of the trials yield a decision boundary crossing when a decision boundary is present, yielding choice confidence determined by the position of the decision bounds.
Evidence accumulation dynamics.
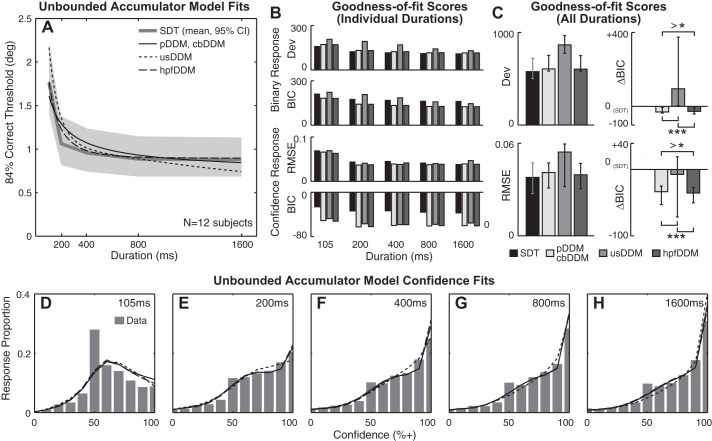
Because several previous studies performed extensive model comparisons using binary response data (Bogacz et al. 2006; Hawkins et al. 2015; Tsetsos et al. 2012; Usher and McClelland 2001), this study focused on confidence data. Since the comparisons between unbounded and bounded models showed that the confidence response is better explained by unbounded models (e.g., Fig. 4), only the unbounded accumulator models are compared here. Moreover, among the four dynamic variants of unbounded accumulator models, pDDM and cbDDM yield identical theoretical binary choice thresholds (Eq. 13); therefore, one curve for each of three accumulator models (pDDM, usDDM, hpfDDM) in addition to one curve based on SDT are compared in Fig. 5A. All unbounded models showed thresholds that decay to a nonzero asymptote. Among three accumulator models, pDDM and hpfDDM performed similarly well in fitting both binary and confidence data (Fig. 5, B and C). However, the hpfDDM BIC scored marginally better than pDDM as inferred by the median ΔBICpDDM − hpfDDM = 3.11 (ΔBICpDDM − hpfDDM > 2 for 7 of 12 subjects). usDDM performed substantially worse than the other accumulators in describing binary choice data (ΔBICusDDM − pDDM,hpfDDM > 10 for 11 of 12 subjects).
Furthermore, median RMSE and BIC for the usDDM fit of the confidence data were also worse than for the other accumulator models (ΔBICusDDM − pDDM,hpfDDM > 10 for 6 of 12 subjects in Fig. 5, B and C). In theory, the urgency component boosts the decision variable, resulting in lower thresholds and higher confidence. These behaviors are illustrated in Fig. 5, A and D–H: usDDM estimates achieve lower thresholds (Fig. 5A) and higher confidence (Fig. 5, D–H). On the other hand, hpfDDM was only marginally better than pDDM (cbDDM) in fitting the confidence data (ΔBICpDDM − hpfDDM > 2 for 6 of 12 subjects; Table 2 and Fig. 5, B and C), which is consistent with the results from the binary data. Such quantitative similarity between pDDM and hpfDDM is especially pronounced in the confidence prediction. In Fig. 5, D–H, pDDM and hpfDDM nearly overlap.
DISCUSSION
Summary
Both SVV perceptual threshold and confidence data displayed a dependence on stimulus duration. Perceptual thresholds decreased exponentially to a nonzero asymptote and confidence increased as stimulus duration increased. Computational simulations showed that such dynamics of perceptual choice and confidence are consistent with an evidence accumulator mechanism. More importantly, human perceptual choice confidence was found to be consistent with a SDT model that assumed unbounded evidence accumulation. These results indicate that the sensory evidence accumulates without bounds when judging perceptual choice confidence for tasks that constrain the response time to occur after completion of stimulus presentation. The model comparisons also showed that the models cannot be distinguished with only the binary choice response for these data.
Binary Choice Behavior in Unbounded and Bounded Evidence Accumulators
For binary choice data, there are numerous decision making studies that present choice accuracy and response time data supporting bounded accumulator models (Hawkins et al. 2015; Ratcliff 2006; Ratcliff and Rouder 1998; Usher and McClelland 2001). In these studies, a response-time task was used in which response time is signaled by the subjects. At the same time, there are equally numerous perceptual psychophysical studies that present choice accuracy data supporting SDT (Green and Swets 1966; Wichmann and Hill 2001). In these studies, a forced-choice task was used, in which stimulus duration is controlled by operators but decision time is not signaled. Considering that these two theories successfully explain the binary choice behavior, it is not surprising that both unbounded and bounded models perform comparably in fitting binary choice data. In fact, the bounded accumulator equation (Eq. 18) converges with SDT (psychometric function in Eq. 8a) when bound A is sufficiently large. This is consistent with an earlier study that showed A approaching infinity when neither stimulus duration nor response time was constrained (Bogacz et al. 2006). However, as shown in Table A1 (in appendix), the fitted A is finite and A ≪ ∞ such that the bound is only 1 standard deviation (of the decision variables) away at t = 450 ms. Hence, the alternative explanation is that there are two solutions for the bounded model: one with finite bounds yielding a bounded model fit and another one with infinite bounds, which converges with an unbounded model fit.
To verify that both of these two solutions are valid, simulated data sets were generated using the fitted parameters of each of our 12 subjects, and then the models were fitted to the simulated data sets. Figures 6 and 7 show simulated data generated by unbounded and bounded accumulation models, respectively. Each of these simulated data sets was fit with both bounded and unbounded fit models. For simplicity, only pDDM was considered for both the model generating and the model fitting the simulated data. The same number of virtual subjects was simulated using the model parameters fitted to each subject. For unbounded model simulations 11 of 12 simulated subjects yielded converging fits, and for bounded model simulations 10 of 11 simulated subjects yielded converging fits.
Fig. 6.
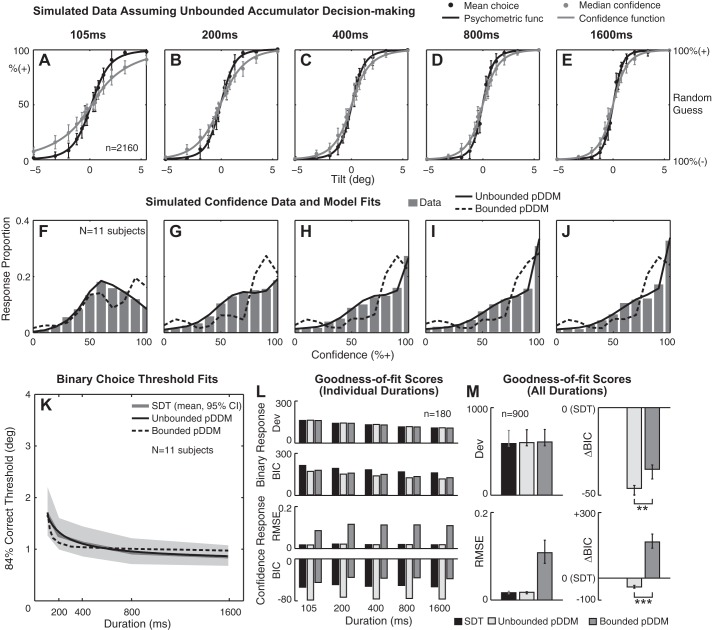
Simulated data set generated by an unbounded pDDM. A–E: a Gaussian psychometric function (solid black curve) was fitted to simulated binary choice data (black circles), and a Gaussian confidence function (solid gray curve) was fitted to simulated confidence data (gray circles) at individual stimulus durations. Twelve virtual subjects were simulated, yielding 2,160 data points per duration. x-Axis is stimulus level in tilt. Left y-axis is % responding + in case of binary response and % confidence that the stimulus is + in case of confidence response. Right y-axis shows the confidence interpreted by subjects (% correct). F–J: confidence histograms aggregated across all stimulus levels for 11 simulated subjects that yielded converging fits for both unbounded and bounded models. K: binary choice threshold estimates as a function of stimulus duration. Unbounded pDDM, bounded pDDM, and signal detection theory (SDT) threshold predictions were averaged across 11 simulated subjects. Gray shading shows 95% CI for SDT fit. L: mean goodness-of-fit scores at individual stimulus duration for binary responses (top) and confidence responses (bottom). M: marginal goodness-of-fit scores across all durations for binary responses (top) and confidence responses (bottom). Horizontal bars: **strong (ΔBICBounded − Unbounded > 6) support, ***very strong support (ΔBICBounded − Unbounded > 10) for unbounded pDDM. Error bars show lower and upper quartiles.
Fig. 7.
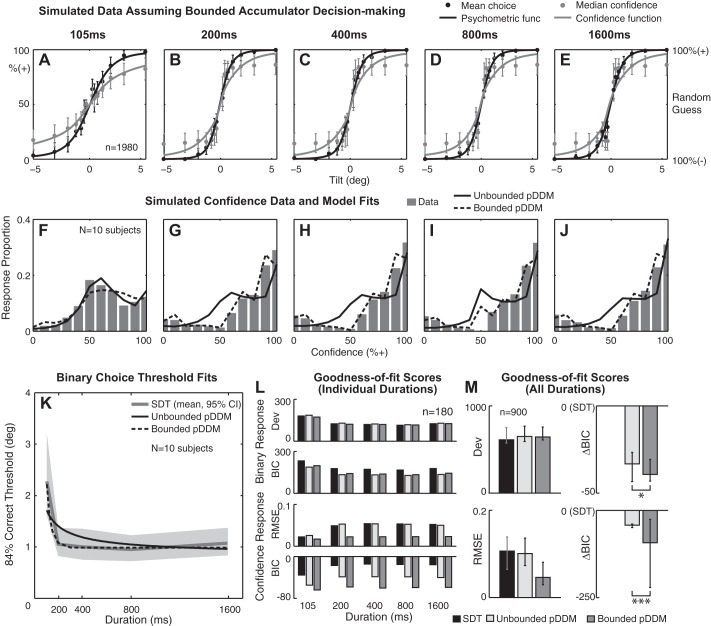
Simulated data set generated by a bounded pDDM. A–E: a Gaussian psychometric function (solid black curve) was fitted to simulated binary choice data (black circles), and a Gaussian confidence function (solid gray curve) was fitted to simulated confidence data (gray circles) at individual stimulus durations. Eleven virtual subjects with converging bounded model fits were simulated, yielding 1,980 data points per duration. x-Axis is stimulus level in tilt. Left y-axis is % responding + in case of binary response and % confidence that the stimulus is + in case of confidence response. Right y-axis shows the confidence interpreted by subjects (%correct). F–J: confidence histograms aggregated across all stimulus levels for 10 simulated subjects that yielded converging fits for both unbounded and bounded models. K: binary choice threshold estimates as a function of stimulus duration. Unbounded pDDM, bounded pDDM, and signal detection theory (SDT) threshold predictions were averaged across 10 simulated subjects. Gray shading shows 95% CI for SDT fit. L: mean goodness-of-fit scores at individual stimulus duration for binary responses (top) and confidence responses (bottom). M: marginal goodness-of-fit scores across all durations for binary responses (top) and confidence responses (bottom). Horizontal bars: *positive evidence (ΔBICBounded − Unbounded > 2), ***very strong evidence (ΔBICBounded − Unbounded > 10) for bounded pDDM. These results are the opposite of the analysis from the real experimental data. Error bars show lower and upper quartiles.
The simulated binary choice resulted in choice accuracy and psychometric functions shown in Fig. 6, A–E, and Fig. 7, A–E, for unbounded and bounded simulation models, respectively. Both Figs. 6 and 7 are plotted with a format identical to that shown in Fig. 4 for the human data. Figure 6K and Fig. 7K show thresholds as a function of stimulus duration. Deviance (Dev) scores (Fig. 6, L and M, Fig. 7, L and M) are similar for all three models—SDT and unbounded and bounded accumulators—indicating that bound mechanisms are difficult to distinguish based only on binary choice response. Although the present experimental design is not able to provide strong evidence to clarify the bound mechanisms for binary decision making, the computational modeling and simulations in this study provide insights into why SDT provides effective summary statistics while a bounded accumulator provides an effective mechanism for choice behavior at the same time.
Confidence Judgment in Unbounded and Bounded Evidence Accumulator
The model comparisons between unbounded and bounded data-generating models showed that binary response fits are equally well fit by both boundary models. This matched our human findings (Figs. 4 and 5). For comparison, the human confidence data were explained substantially better by unbounded accumulators. Both of these effects were reproduced in the simulated data set. In other words, the simulated confidence responses assuming different bound conditions display strikingly different behavior unlike the simulated binary choice.
Figure 6, A–E, and Fig. 7, A–E, show confidence functions fitted to median confidence assuming unbounded and bounded accumulators, respectively. Circles are the mean and error bars are 95% confidence interval calculated across all simulated subjects. When a bounded mechanism is assumed, the accumulation process ends when the decision variable crosses a bound, so a decision variable cannot never be greater than the position of the decision bounds. This bounded behavior causes the confidence to saturate below 100% even when the stimulus is big, which is apparent in Fig. 7, A–E. This magnitude-dependent confidence saturation is not consistent with the experimental data (Fig. 3, A–E) that do not display such a saturation. Moreover, simulated confidence histograms in Fig. 6, F–J, match the empirical data in Fig. 3, F–J, better than those in Fig. 7, F–J. For instance, only unbounded simulated data were significantly better fit by the unbounded pDDM than by the bounded pDDM (median ΔBICBounded − Unbounded > 10) whereas bounded simulated data were better fit by the bounded pDDM than the unbounded pDDM.
Simulated confidence data were also fitted by both unbounded and bounded models. The model that matched that used to generate the simulated data always yielded a lower RMSE than the other model (Fig. 6, L and M and Fig. 7, L and M). For instance, when unbounded pDDM was assumed, unbounded accumulator and SDT scored better RMSE than a bounded accumulator pDDM. Similarly, when a bounded pDDM was assumed, the bounded pDDM scored the best. When these goodness-of-fit scores of the simulated data (Figs. 6 and 7) are compared with the empirical data analyses (Fig. 4), it can be seen that unbounded model simulations reproduce the RMSE and BIC score patterns. In other words, for both empirical and simulated confidence, assuming unbounded pDDM yields better RMSE and BIC and, inversely, bounded pDDM yields worse RMSE and BIC. These results indicate that 1) choice confidence shows dynamics consistent with an integration mechanism and 2) choice confidence utilizes unbounded evidence accumulation.
Additional Components of Accumulator Models
To infer the effect of the model parameters on choice accuracy (i.e., threshold), we start with threshold Eqs. 13–15 obtained assuming an unbounded mechanism. There are two justifications for this inference. First, we showed that decision boundary conditions cannot be distinguished with forced-choice tasks that utilize static (i.e., constant) sensory stimuli. Second, Eqs. 13–15 are analytical solutions, in which the contribution of the parameters on the threshold dynamics is explicit. For instance, threshold equations of an unbounded pDDM and usDDM (Eqs. 13 and 14) show that decision bias parameters (z0 and z) and diffusion noise (σ) contribute to the rate at which the threshold decreases with increasing stimulus duration. On the other hand, sensory noise parameters (η and μ) contribute to the threshold asymptote. Similarly, an unbounded hpfDDM’s threshold Eq. 15 shows that decision bias parameters (z0 and z) and leak time constant (τ) contribute to the the threshold decay rate while sensory noise parameters (σ and μ) contribute to the threshold asymptote. Although the decision making models presented here do not explicitly include sensory models, threshold predictions can be extrapolated based on the known behaviors of sensory noise (e.g., η and μ in pDDM). For example, in the case of SVV perception, subjects performing the SVV task with the head tilted are known to show systematic biases (μ) (De Vrijer et al. 2008) and changes in precision (inversely related to η) (De Vrijer et al. 2009). According to Eqs. 13–15, increase in SVV sensory bias and decrease in SVV sensory precision result in the elevation of the threshold asymptote, shifting the threshold curve as a whole without affecting the threshold decay rate.
Decoupling the effects of z0, z, and σ requires extensive sampling for t less than ∼300 ms where the threshold is changing, and even then separating z0 and z is impossible since both contribute inversely to . Similarly, η and μ cannot be separated. Therefore, only σ survived as the threshold rate parameter and η survived as the asymptote parameter in the nested model analysis. Such parameter overlaps are more pronounced for usDDM (Eq. 14). As a result, in the unbounded usDDM the component having the strongest temporal effect, the urgency signal component , takes over as the threshold rate parameter. As a consequence, σ has a median four times greater than for the other models and serves as the asymptote parameter within the given stimulus duration range (t < 1,600 ms). On the other hand, in unbounded hpfDDM (Eq. 15) τ is the only dynamic term, and the rest contribute to the threshold asymptote. In the end, all models resulted in one threshold change rate parameter and one asymptote parameter.
Similarly, for the bounded models, in addition to the decision bound parameter(s) all models resulted in one threshold change rate parameter and one asymptote parameter. The values of σ and η of bounded models were comparable among pDDM, cbDDM, and usDDM (see Table A1 in APPENDIX), and the values of a were comparable among all four bounded DDMs. Additional dynamic components in cbDDM and usDDM had little effect. For instance, the time constant for the collapsing bound in cbDDM (τa) was greater than ~1,000 ms (median 3,450 ms), indicating that the bounds remained near constant within the stimulus duration range (≤1,600 ms). Also, the time constant for the urgency signal was near 0, rendering the overall effect of the urgency signal near 0 as well. Such similarity of necessitating only three effective free parameters with comparable values is consistent with nearly identical goodness-of-fit performance observed in NLL scores (Table 3) of the three models. For bounded hpfDDM, σ and τ had values nearly identical to unbounded hpfDDM, which is consistent with similar NLL scores between the unbounded and bounded hpfDDMs (Table 2 and Table 3).
Accumulation Dynamics—Effective Time Window of Evidence Accumulation
As presented in Fig. 5A, the general shape of the threshold prediction is similar across all four models. On the basis of this observation, the width of the time window relevant for accumulating evidence can be calculated for pDDM that does not have specified time window. For hpfDDM, the width of the time window is defined in terms of τ, at which the threshold is 1.58 times the asymptote threshold Thpf,∞ (i.e., ). By applying the same criterion, the time constant that satisfies can be calculated, which in turn yields
| (23) |
Then the median τp is 227 ms, which is comparable to the median τhpf of 141 ms. This implies that even without an explicit time window, pDDM requires only the initial ~200 ms to achieve near-optimal choice accuracy. Although it is not apparent in Eq. 23 whether such a time window is located near the stimulus onset or near the stimulus offset (equivalent to near the response time), the threshold equation for pDDM (Eq. 13) indicates that it is the initial segment of information that is most relevant in pDDM for static (i.e., constant) stimuli. Such an effect is consistent with the previously reported primacy effect (Kiani et al. 2008).
In addition, Eq. 23 shows that diffusion noise and decision bias range each widen the time window while sensory noise shortens the time window. Going back to the pDDM threshold equation (Eq. 13), sensory noise determines the lowest threshold whereas diffusion noise from the accumulation process increases the threshold for short stimulus duration. When summing these two, in pDDM, the accumulation process actually hurts choice accuracy since a better threshold can be achieved based solely on the sensory noise. In turn, the role of the accumulator in pDDM penalizes the earlier decision in order to prevent premature decision. This contrasts with hpfDDM, in which the accumulation process rewards waiting. An hpfDDM does not add additional noise, since diffusion noise arises from sensory noise. However, the leak mechanism discards older information, keeping only the recent information. Hence, in pDDM the threshold is determined by the amount of the most recent information contained within the time window, and such an effect was previously reported as a recency effect (Tsetsos et al. 2012). While previous debates about pure, urgency signal, and leaky accumulator models focused on dynamic characteristics (Thura 2016) like primacy vs. recency effects, the analytical solutions for a forced-choice task highlight a fundamental difference in the neural implementation: penalizing a premature decision vs. rewarding a delayed decision.
Confidence Model—Additional Dynamics
This study focused on a narrow definition of confidence and its dynamics: how does choice confidence change in a forced-choice paradigm, in which observation duration was set by the operator? Therefore, our experimental design presented here cannot clear all of the hurdles identified by previous choice confidence research (Moran et al. 2015). However, our findings are consistent with earlier studies showing that 1) “confidence decreases as the difficulty level increases,” 2) confidence increases as the response time increases, 3) confidence increases as choice accuracy increases, and 4) confidence decreases for correct choices as the difficulty level increases (Moran et al. 2015; Pleskac and Busemeyer 2010). The latter finding (4) is particularly relevant to help explain the observation that the confidence data appeared to show that there is another time constant τk associated with confidence that may not impact binary choice (Fig. 3L).
In addition, modeling results led to stronger boundary condition (bounded vs. unbounded) conclusions for confidence responses than for binary data. Because of this, although binary choice and confidence data point to a conclusion that both behaviors display accumulation dynamics, it is not conclusive whether the two choice behaviors share the same accumulation process. At this point, it is worth recapitulating the assumption underlying the confidence model. Instead of viewing binary choice and confidence as two separate processes, we assumed that the state of a decision variable is mapped onto confidence judgment and that the same state is used to determine the binary decision, which is consistent with one-stage theory of choice and confidence (Kiani and Shadlen 2009; Ratcliff and Starns 2013; Sanders et al. 2016). Within this framework, confidence is determined on a single-trial basis given the prior knowledge of the decision variable distribution. The distribution may be accessible through population coding that provides a time-varying representation of the distribution or through stored neural circuitry that provides a representation that is stationary (i.e., nonvarying) in time. Nonetheless, holding this one-stage assumption leads to another assumption when additional dynamics K(t) attributing to confidence were allowed in order to account for overrepresentation of low confidence. Interestingly, while the confidence model including K(t) described both low- and high-confidence data, the overrepresentation of 50% confidence (random guess) was still not fully ameliorated. This implies there may be an additional nonlinear process contributing to confidence judgment. Although it could not be determined whether these additional dynamic elements were mediated by parallel or postdecisional processing under the present experimental design, K(t) is consistent with a two-stage theory of choice and confidence (Kvam et al. 2015; Moran et al. 2015; Pleskac and Busemeyer 2010; Yu et al. 2015). Investigating such a question requires the measurement of all three choice behaviors, choice accuracy, binary choice response time, confidence, and confidence judgment time. An equally important measurement would be provided by functional neuroimaging with high enough temporal resolution to make connections among the three choice behaviors in terms of timing—i.e., is confidence a postdecisional process? Also, uncovering the neuroanatomy of choice behaviors is essential to determine whether confidence builds on the variables available to decision making or whether confidence estimation requires a separate, parallel process separate from the processes governing binary choice.
GRANTS
This work was funded by National Institute on Deafness and Other Communication Disorders (NIDCD) Grant 5R01 DC-014924-02 (K. Lim), Med-El (Medical Electronics) (K. Lim), SHBT Fellowship Support (1539610, K. Lim), NIDCD Grant 5R01 DC-014924-02 (W. Wang), and NIDCD Grant 5R01 DC-014924-02 (D. M. Merfeld).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
K.L. and D.M.M. conceived and designed research; K.L. performed experiments; K.L. and W.W. analyzed data; K.L., W.W., and D.M.M. interpreted results of experiments; K.L. prepared figures; K.L. and D.M.M. drafted manuscript; K.L., W.W., and D.M.M. edited and revised manuscript; K.L., W.W., and D.M.M. approved final version of manuscript.
APPENDIX
Pure DDM
When Weiner’s diffusion process y˙ = x + w˙ is expressed in discrete time,
| (A1) |
where xΔt ∼ [(v − μ)Δt, η2Δt2] and Δw ∼ N(0, σ2Δt). At time t, the decision variable is updated from the previous state by Δy, such that yt = yt − Δt + Δy while the decision bound stays constant,
| (A2a) |
| (A2b) |
Collapsing Bound DDM
The discrete time solution for the decision bounds is
| (A3) |
Urgency Signal DDM
The discrete time solutions for usDDM are
| (A4a) |
| (A4b) |
| (A4c) |
High-Pass Filter DDM
The discrete time solutions for hpfDDM are
| (A5a) |
| (A5b) |
Model parameter values and comparisons between unbounded and bounded conditions for pDDM, cbDDM, usDDM, and hpfDDM are shown in Table A1.
Table A1.
Model parameter values and comparisons between unbounded and bounded conditions
| Parameter | pDDM | cbDDM | usDDM | hpfDDM |
|---|---|---|---|---|
| Unbounded (n = 12) | ||||
| Accumulator model | ||||
| σ, °s1/2 | 0.40 (0.32, 0.56) | 1.36 (0.97, 1.86) | ||
| η, ° | 0.71 (0.49, 0.92) | |||
| τ, ms | 141 (128, 160) | |||
| λ∞, °s | 0.21 (0.19, 2.54) | |||
| τλ, ms | 230 (0, 870) | |||
| No. of parameters | 2 | 3 | 2 | |
| Confidence model | ||||
| κ0 | 3.63 (2.05, 12.21) | 3.63 (1.52, 12.21) | 3.76 (2.10, 12.21) | |
| κ∞ | 0.84 (0.44, 1.48) | 0.92 (0.42, 1.78) | 0.86 (0.44, 1.47) | |
| τκ, ms | 41 (11, 103) | 41 (11, 100) | 41 (11, 108) | |
| Bounded (n = 11) | ||||
| Accumulator model | ||||
| σ, °s1/2 | 0.32 (0.00, 1.09) | 0.63 (0.01, 2.41) | 0.23 (0.01, 0.75) | 0.43 (0.32, 0.62) |
| η, ° | 1.98 (0.01, 2.43) | 1.73 (0.00, 2.41) | 2.25 (0.87, 3.22) | |
| τ, ms | 139 (123, 160) | |||
| λ∞, °s | 2.69 (0.10, 5.29) | |||
| τλ, ms | 0 (0, 34) | |||
| a, °s | 0.84 (0.61, 1.04) | 0.80 (0.64, 1.09) | 0.76 (0.61, 1.05) | 0.91 (0.60, 1.98) |
| τa, ms | 3.45 × 103 (1,000, 7.91 × 106) | |||
| No. of parameters | 3 | 4 | 5 | 3 |
| Confidence model | ||||
| κ0 | 3.50 (1.92, 6.67) | 2.90 (1.63, 11.88) | 3.92 (1.69, 5.66) | 3.65 (2.36, 4.77) |
| κ∞ | 0.92 (0.46, 1.45) | 1.00 (0.41, 1.94) | 0.92 (0.28, 1.13) | 0.99 (0.67, 1.35) |
| τκ, ms | 52 (14, 211) | 52 (11, 116) | 51 (11, 152) | 61 (11, 1,114) |
Values are medians (25%, 75%).
REFERENCES
- Baccini M, Paci M, Del Colletto M, Ravenni M, Baldassi S. The assessment of subjective visual vertical: comparison of two psychophysical paradigms and age-related performance. Atten Percept Psychophys 76: 112–122, 2014. doi: 10.3758/s13414-013-0551-9. [DOI] [PubMed] [Google Scholar]
- Barnett-Cowan M, Dyde RT, Fox SH, Moro E, Hutchison WD, Harris LR. Multisensory determinants of orientation perception in Parkinson’s disease. Neuroscience 167: 1138–1150, 2010a. doi: 10.1016/j.neuroscience.2010.02.065. [DOI] [PubMed] [Google Scholar]
- Barnett-Cowan M, Dyde RT, Thompson C, Harris LR. Multisensory determinants of orientation perception: task-specific sex differences. Eur J Neurosci 31: 1899–1907, 2010b. doi: 10.1111/j.1460-9568.2010.07199.x. [DOI] [PubMed] [Google Scholar]
- Bitzer S, Park H, Blankenburg F, Kiebel SJ. Perceptual decision making: drift-diffusion model is equivalent to a Bayesian model. Front Hum Neurosci 8: 102, 2014. doi: 10.3389/fnhum.2014.00102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bogacz R, Brown E, Moehlis J, Holmes P, Cohen JD. The physics of optimal decision making: a formal analysis of models of performance in two-alternative forced-choice tasks. Psychol Rev 113: 700–765, 2006. doi: 10.1037/0033-295X.113.4.700. [DOI] [PubMed] [Google Scholar]
- Böhmer A, Rickenmann J. The subjective visual vertical as a clinical parameter of vestibular function in peripheral vestibular diseases. J Vestib Res 5: 35–45, 1995. doi: 10.1016/0957-4271(94)00021-S. [DOI] [PubMed] [Google Scholar]
- Bowman NE, Kording KP, Gottfried JA. Temporal integration of olfactory perceptual evidence in human orbitofrontal cortex. Neuron 75: 916–927, 2012. doi: 10.1016/j.neuron.2012.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis 10: 433–436, 1997. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Busemeyer JR, Townsend JT. Decision field theory: a dynamic-cognitive approach to decision making in an uncertain environment. Psychol Rev 100: 432–459, 1993. doi: 10.1037/0033-295X.100.3.432. [DOI] [PubMed] [Google Scholar]
- Churchland AK, Kiani R, Shadlen MN. Decision-making with multiple alternatives. Nat Neurosci 11: 693–702, 2008. doi: 10.1038/nn.2123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cisek P, Puskas GA, El-Murr S. Decisions in changing conditions: the urgency-gating model. J Neurosci 29: 11560–11571, 2009. doi: 10.1523/JNEUROSCI.1844-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemens IA, De Vrijer M, Selen LP, Van Gisbergen JA, Medendorp WP. Multisensory processing in spatial orientation: an inverse probabilistic approach. J Neurosci 31: 5365–5377, 2011. doi: 10.1523/JNEUROSCI.6472-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen HS, Sangi-Haghpeykar H. Subjective visual vertical in vestibular disorders measured with the bucket test. Acta Otolaryngol 132: 850–854, 2012. doi: 10.3109/00016489.2012.6687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Vrijer M, Medendorp WP, Van Gisbergen JA. Shared computational mechanism for tilt compensation accounts for biased verticality percepts in motion and pattern vision. J Neurophysiol 99: 915–930, 2008. doi: 10.1152/jn.00921.2007. [DOI] [PubMed] [Google Scholar]
- De Vrijer M, Medendorp WP, Van Gisbergen JA. Accuracy-precision trade-off in visual orientation constancy. J Vis 9: 9, 2009. doi: 10.1167/9.2.9. [DOI] [PubMed] [Google Scholar]
- Diederich A. Dynamic stochastic models for decision making under time constraints. J Math Psychol 41: 260–274, 1997. doi: 10.1006/jmps.1997.1167. [DOI] [PubMed] [Google Scholar]
- Dieterich M, Brandt T. Wallenberg’s syndrome: lateropulsion, cyclorotation, and subjective visual vertical in thirty-six patients. Ann Neurol 31: 399–408, 1992. doi: 10.1002/ana.410310409. [DOI] [PubMed] [Google Scholar]
- Dieterich M, Pöllmann W, Pfaffenrath V. Cervicogenic headache: electronystagmography, perception of verticality and posturography in patients before and after C2-blockade. Cephalalgia 13: 285–288, 1993. doi: 10.1046/j.1468-2982.1993.1304285.x. [DOI] [PubMed] [Google Scholar]
- Dyde RT, Jenkin MR, Harris LR. The subjective visual vertical and the perceptual upright. Exp Brain Res 173: 612–622, 2006. doi: 10.1007/s00221-006-0405-y. [DOI] [PubMed] [Google Scholar]
- Gardiner CW. Stochastic Methods. Berlin: Springer, 1985. [Google Scholar]
- Gold JI, Shadlen MN. The neural basis of decision making. Annu Rev Neurosci 30: 535–574, 2007. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
- Grabherr L, Nicoucar K, Mast FW, Merfeld DM. Vestibular thresholds for yaw rotation about an earth-vertical axis as a function of frequency. Exp Brain Res 186: 677–681, 2008. doi: 10.1007/s00221-008-1350-8. [DOI] [PubMed] [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York: Wiley, 1966, p. xi. [Google Scholar]
- Hawkins GE, Forstmann BU, Wagenmakers EJ, Ratcliff R, Brown SD. Revisiting the evidence for collapsing boundaries and urgency signals in perceptual decision-making. J Neurosci 35: 2476–2484, 2015. doi: 10.1523/JNEUROSCI.2410-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard IP, Templeton WB. Human Spatial Orientation. New York: Wiley, 1966. [Google Scholar]
- Huelsenbeck JP, Crandall KA. Phylogeny estimation and hypothesis testing using maximum likelihood. Annu Rev Ecol Syst 28: 437–466, 1997. doi: 10.1146/annurev.ecolsys.28.1.437. [DOI] [Google Scholar]
- Karmali F, Lim K, Merfeld DM. Visual and vestibular perceptual thresholds each demonstrate better precision at specific frequencies and also exhibit optimal integration. J Neurophysiol 111: 2393–2403, 2014. doi: 10.1152/jn.00332.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kass RE, Raftery AE. Bayes factors. J Am Stat Assoc 90: 773–795, 1995. doi: 10.1080/01621459.1995.10476572. [DOI] [Google Scholar]
- Kiani R, Hanks TD, Shadlen MN. Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. J Neurosci 28: 3017–3029, 2008. doi: 10.1523/JNEUROSCI.4761-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science 324: 759–764, 2009. doi: 10.1126/science.1169405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kvam PD, Pleskac TJ, Yu S, Busemeyer JR. Interference effects of choice on confidence: quantum characteristics of evidence accumulation. Proc Natl Acad Sci USA 112: 10645–10650, 2015. doi: 10.1073/pnas.1500688112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langevin P. Sur la théorie du mouvement brownien. CR Acad Sci Paris 146: 530–533, 1908. [Google Scholar]
- Lim K, Karmali F, Nicoucar K, Merfeld DM. Perceptual precision of passive body tilt is consistent with statistically optimal cue integration. J Neurophysiol 117: 2037–2052, 2017. doi: 10.1152/jn.00073.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez C, Mercier MR, Halje P, Blanke O. Spatiotemporal dynamics of visual vertical judgments: early and late brain mechanisms as revealed by high-density electrical neuroimaging. Neuroscience 181: 134–149, 2011. doi: 10.1016/j.neuroscience.2011.02.009. [DOI] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection Theory: A User’s Guide. Mahwah, NJ: Erlbaum, 2005. [Google Scholar]
- Merfeld DM. Signal detection theory and vestibular thresholds: I. Basic theory and practical considerations. Exp Brain Res 210: 389–405, 2011. doi: 10.1007/s00221-011-2557-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merfeld DM, Clark TK, Lu YM, Karmali F. Dynamics of individual perceptual decisions. J Neurophysiol 115: 39–59, 2016. doi: 10.1152/jn.00225.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milica M, Jonathan M, Alexander H, Christof K, Antonio R. The Drift Diffusion Model can account for the accuracy and reaction time of value-based choices under high and low time pressure. Judgm Decis Mak 5: 437–449, 2010. [Google Scholar]
- Moran R, Teodorescu AR, Usher M. Post choice information integration as a causal determinant of confidence: novel data and a computational account. Cognit Psychol 78: 99–147, 2015. doi: 10.1016/j.cogpsych.2015.01.002. [DOI] [PubMed] [Google Scholar]
- Murphy PR, Robertson IH, Harty S, O’Connell RG. Neural evidence accumulation persists after choice to inform metacognitive judgments. eLife 4: e11946, 2015. doi: 10.7554/eLife.11946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Navajas J, Bahrami B, Latham PE. Post-decisional accounts of biases in confidence. Curr Opin Behav Sci 11: 55–60, 2016. doi: 10.1016/j.cobeha.2016.05.005. [DOI] [Google Scholar]
- O’Connell RG, Dockree PM, Kelly SP. A supramodal accumulation-to-bound signal that determines perceptual decisions in humans. Nat Neurosci 15: 1729–1735, 2012. doi: 10.1038/nn.3248. [DOI] [PubMed] [Google Scholar]
- Pleskac TJ, Busemeyer JR. Two-stage dynamic signal detection: a theory of choice, decision time, and confidence. Psychol Rev 117: 864–901, 2010. doi: 10.1037/a0019737. [DOI] [PubMed] [Google Scholar]
- Rahnev D, Koizumi A, McCurdy LY, D’Esposito M, Lau H. Confidence leak in perceptual decision making. Psychol Sci 26: 1664–1680, 2015. doi: 10.1177/0956797615595037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R. A theory of memory retrieval. Psychol Rev 85: 59–108, 1978. doi: 10.1037/0033-295X.85.2.59. [DOI] [Google Scholar]
- Ratcliff R. Modeling response signal and response time data. Cognit Psychol 53: 195–237, 2006. doi: 10.1016/j.cogpsych.2005.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Frank MJ. Reinforcement-based decision making in corticostriatal circuits: mutual constraints by neurocomputational and diffusion models. Neural Comput 24: 1186–1229, 2012. doi: 10.1162/NECO_a_00270. [DOI] [PubMed] [Google Scholar]
- Ratcliff R, McKoon G. The diffusion decision model: theory and data for two-choice decision tasks. Neural Comput 20: 873–922, 2008. doi: 10.1162/neco.2008.12-06-420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratcliff R, Rouder JN. Modeling response times for two-choice decisions. Psychol Sci 9: 347–356, 1998. doi: 10.1111/1467-9280.00067. [DOI] [Google Scholar]
- Ratcliff R, Starns JJ. Modeling confidence judgments, response times, and multiple choices in decision making: recognition memory and motion discrimination. Psychol Rev 120: 697–719, 2013. doi: 10.1037/a0033152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders JI, Hangya B, Kepecs A. Signatures of a statistical computation in the human sense of confidence. Neuron 90: 499–506, 2016. doi: 10.1016/j.neuron.2016.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schöne H, De Haes HU. Perception of gravity-vertical as a function of head and trunk position. Z Vgl Physiol 60: 440–444, 1968. doi: 10.1007/BF00297938. [DOI] [Google Scholar]
- Stone M. Models for choice-reaction time. Psychometrika 25: 251–260, 1960. doi: 10.1007/BF02289729. [DOI] [Google Scholar]
- Thura D. How to discriminate conclusively among different models of decision making? J Neurophysiol 115: 2251–2254, 2016. doi: 10.1152/jn.00911.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thura D, Beauregard-Racine J, Fradet CW, Cisek P. Decision making by urgency gating: theory and experimental support. J Neurophysiol 108: 2912–2930, 2012. doi: 10.1152/jn.01071.2011. [DOI] [PubMed] [Google Scholar]
- Tsetsos K, Gao J, McClelland JL, Usher M. Using time-varying evidence to test models of decision dynamics: bounded diffusion vs. the leaky competing accumulator model. Front Neurosci 6: 79, 2012. doi: 10.3389/fnins.2012.00079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychol Rev 108: 550–592, 2001. doi: 10.1037/0033-295X.108.3.550. [DOI] [PubMed] [Google Scholar]
- Valko Y, Lewis RF, Priesol AJ, Merfeld DM. Vestibular labyrinth contributions to human whole-body motion discrimination. J Neurosci 32: 13537–13542, 2012. doi: 10.1523/JNEUROSCI.2157-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Berg R, Anandalingam K, Zylberberg A, Kiani R, Shadlen MN, Wolpert DM. A common mechanism underlies changes of mind about decisions and confidence. eLife 5: e12192, 2016. doi: 10.7554/eLife.12192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vibert D, Häusler R. Long-term evolution of subjective visual vertical after vestibular neurectomy and labyrinthectomy. Acta Otolaryngol 120: 620–622, 2000. doi: 10.1080/000164800750000432. [DOI] [PubMed] [Google Scholar]
- Vibert D, Häusler R, Safran AB. Subjective visual vertical in peripheral unilateral vestibular diseases. J Vestib Res 9: 145–152, 1999. [PubMed] [Google Scholar]
- Vingerhoets RA, De Vrijer M, Van Gisbergen JA, Medendorp WP. Fusion of visual and vestibular tilt cues in the perception of visual vertical. J Neurophysiol 101: 1321–1333, 2009. doi: 10.1152/jn.90725.2008. [DOI] [PubMed] [Google Scholar]
- Wald A. Sequential Analysis. New York: Wiley, 1947. [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Percept Psychophys 63: 1293–1313, 2001. doi: 10.3758/BF03194544. [DOI] [PubMed] [Google Scholar]
- Wilks SS. The large-sample distribution of the likelihood ratio for testing composite hypotheses. Ann Math Stat 9: 60–62, 1938. doi: 10.1214/aoms/1177732360. [DOI] [Google Scholar]
- Yi Y, Merfeld DM. A quantitative confidence signal detection model: 1. Fitting psychometric functions. J Neurophysiol 115: 1932–1945, 2016. doi: 10.1152/jn.00318.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu S, Pleskac TJ, Zeigenfuse MD. Dynamics of postdecisional processing of confidence. J Exp Psychol Gen 144: 489–510, 2015. doi: 10.1037/xge0000062. [DOI] [PubMed] [Google Scholar]
- Zwergal A, Rettinger N, Frenzel C, Dieterich M, Brandt T, Strupp M. A bucket of static vestibular function. Neurology 72: 1689–1692, 2009. doi: 10.1212/WNL.0b013e3181a55ecf. [DOI] [PubMed] [Google Scholar]