Extending the Nonbonded Cationic Dummy Model to Account for Ion-Induced Dipole Interactions

Abstract

Modeling metalloproteins often requires classical molecular dynamics (MD) simulations in order to capture their relevant motions, which in turn necessitates reliable descriptions of the metal centers involved. One of the most successful approaches to date is provided by the “cationic dummy model”, where the positive charge of the metal ion is transferred toward dummy particles that are bonded to the central metal ion in a predefined coordination geometry. While this approach allows for ligand exchange, and captures the correct electrostatics as demonstrated for different divalent metal ions, current dummy models neglect ion-induced dipole interactions. In the present work, we resolve this weakness by taking advantage of the recently introduced 12–6–4 type Lennard-Jones potential to include ion-induced dipole interactions. We revise our previous dummy model for Mg²⁺ and demonstrate that the resulting model can simultaneously reproduce the experimental solvation free energy and metal–ligand distances without the need for artificial restraints or bonds. As ion-induced dipole interactions become particularly important for highly charged metal ions, we develop dummy models for the biologically relevant ions Al³⁺, Fe³⁺, and Cr³⁺. Finally, the effectiveness of our new models is demonstrated in MD simulations of several diverse (and highly challenging to simulate) metalloproteins.

Metalloproteins are ubiquitous in nature¹ and have been proposed to play functional roles in around one-quarter to one-third of all proteins.² While divalent ions such as Mg²⁺ are extremely common in biological catalysts,¹ even highly charged metal ions, such as Fe³⁺ and Cr³⁺, play crucial biological roles, such as the transport and transfer of oxygen,³ redox chemistry,⁴ and metabolism of carbohydrates, fats, proteins, and nucleic acids.⁵ In addition, Al³⁺ has been used as part of metal–fluoride transition state analogues to probe the mechanisms of phosphoryl transfer in a variety of phosphatases.⁶⁻⁸ Therefore, obtaining a more comprehensive understanding of the role of metals in biology is a topic of great interest to both theory and experiment. However, while classical (force field based) approaches provide a significant advantage over quantum chemical approaches in terms of computational cost, obtaining reliable classical descriptions of metal centers that capture key physicochemical properties such as correct coordination geometries, solvation free energies and time scales for ligand exchange remains a major simulation challenge, particularly when addressing more “exotic” metal centers such as Al³⁺ or Cr³⁺.⁹ Here, the biggest problem is that ligand field effects lead to more complex patterns of solvation free energies than would be expected for alkaline-earth metals with the same ionic radius, and thus a simple Lennard-Jones sphere cannot simultaneously capture the ionic radii and the solvation free energies,¹⁰⁻¹² and more specialized models are needed.

Due to the importance of this problem to molecular simulations, various approaches have been developed to address this issue (for a recent review, see ref (13)). Nonbonded models typically describe the metal center as a simple Lennard-Jones sphere with an integer charge, in which only electrostatic and van der Waals (vdW) terms are used to describe the interaction between the metal ion and its surroundings. Li and Merz have published different parameter sets to describe monovalent,¹⁴ divalent,^12,15 and highly charged metal ions,¹¹ using different water models. Moreover, polarizable nonbonded models have also been published for Cu²⁺, Zn²⁺, and Fe²⁺ in recent years.¹⁶⁻¹⁸ However, as described above, such models struggle to simultaneously reproduce the structural and electrostatic features of the metal centers involved,¹⁰⁻¹² or maintain correct coordination geometries,¹⁹ often requiring the use of large restraints on the metal center to maintain system stability. This issue can, to some extent, be addressed by bonded models, which use predefined covalent bonds between the metal ion and its coordinating residues, and thus the interactions between the metal center and its ligands are represented via bond, angle, dihedral, electrostatic, and vdW terms. While clearly very useful for modeling systems in which the metal ion is primarily playing a structural role, the use of predefined bonds makes such models unable to account for ligand exchange, which is clearly important when modeling chemical reactivity involving catalytic metal centers.²⁰ In addition, such models tend to be very heavily parametrized for the specific system of interest, limiting their transferability.¹⁹

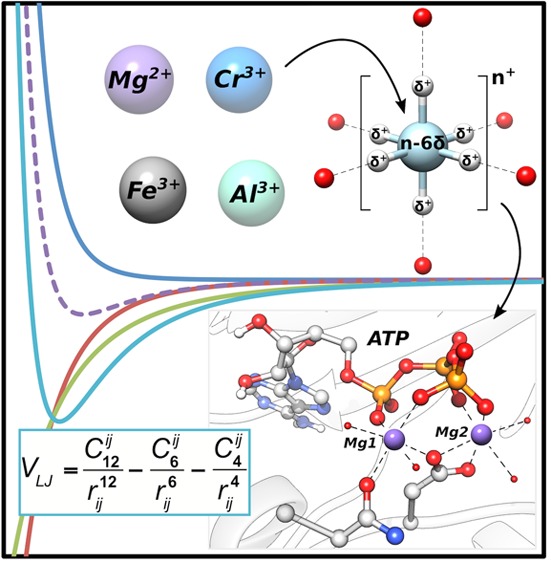
An alternative approach, originally developed by Åqvist and Warshel,^10,21 is a “cationic dummy model” (Figure 1), which places cationic dummy particles around the central metal ion in a predefined coordination geometry (tetrahedral,²² octahedral,²³⁻²⁷ and pentagonal bipyramidal²³ geometries have all been used to date). These dummy particles are bonded to the central atom such that the complex forms a rigid frame, but there are no bonds between the dummy atoms and the ligands, and thus the model is free to move around its frame, change coordination geometry, and exchange ligands, while simultaneously capturing correct electrostatics and coordination geometries without the need for artificial restraints or bonds to the ligands.

Figure 1.

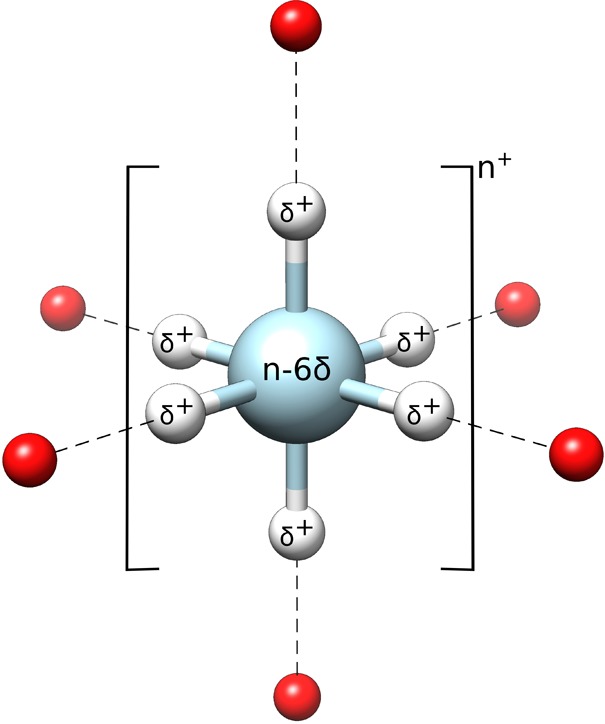
Schematic illustration of the octahedral dummy model used in this work. Instead of a simple sphere, the point charge of the metal ion is distributed to the six dummy atoms with a partial charge of δ⁺. The coordinating water molecules are represented as red spheres.

In a typical cationic dummy model, the central atom will be described by a standard 12–6 Lennard-Jones potential as a vdW sphere that carries mass but little or no charge (n⁺), whereas the dummy models will be described as particles that carry partial charges but no mass or vdW parameters.^10,21 The dummy particles are then each given a partial positive charge, δ⁺, relative to the central metal ion which carries a charge n – xδ, where x refers to the number of dummy particles (note that nonsymmetrical charge distributions have also been used²⁵). In this way, the total charge of the metal ion is retained over the entire complex. Distributing the charge of the central metal center over dummy particles in this way allows for a simplified representation of the partially covalent and partially electrostatic nature of the coordinative bond, as it splits up the space between the transition metal atom and the ligand into a covalent bond between the metal atom and the cationic dummy atom, and an electrostatic interaction between the cationic dummy atom and the surrounding ligands. Such a charge distribution is particularly advantageous in binuclear metal sites,^24,25 as it allows for smaller artificial repulsion between the metal ions by distributing the positive charge of each metal center over the individual cationic dummy atoms.

The cationic dummy model has been used to describe a broad range of metal centers,^{10,21,25,27−30} including Ca²⁺, Mg²⁺, Mn²⁺, Zn²⁺, Co²⁺, Ni²⁺, Fe²⁺, and Cu²⁺, and has been applied to understanding a range of biological problems, in which the metal centers have played both structural and/or catalytic roles (e.g., refs (10, 22, 24, 26, 31, and 32) among others). However, while the 12–6 Lennard-Jones potential used to describe these cationic dummy models is widely used in computer simulations due to its simple form, computational efficiency, and easy transferability,³³⁻³⁵ it fails to reproduce several key experimental properties of a series of divalent metal ions due to its neglect of ion-induced dipole interactions,^11,15 which should not be ignored, especially for highly charged metal ions. Recently, Li and Merz developed a new type of Lennard-Jones potential by adding an additional r^–4 term to describe the ion-induced dipole interactions.¹⁵ This new 12–6–4-type Lennard-Jones (LJ) potential was successfully used to develop nonbonded models for a series of monovalent,¹⁴ divalent,¹⁵ and highly charged¹¹ metal ions, which could simultaneously reproduce both the experimental solvation free energy and radial distribution functions of these ions (which is typically a major challenge for such models^10,11).

In the present work, we have taken advantage of this new 12–6–4 potential to extend the cationic dummy model to describe Al³⁺, Fe³⁺, and Cr³⁺, as they are important metal ions for the study of biochemical systems, and our procedure can be used as a baseline for further parametrization of dummy models for other highly charged systems. In addition, due to its ubiquitousness in biology,¹ we have revisited our previous model for Mg²⁺ now using a 12–6–4 potential (see eq 4 in the Supporting Information). We demonstrate that this new model can simultaneously reproduce the experimental solvation free energy and metal–ligand distances without the need for artificial restraints or bonds, while exploring the impact of the magnitude of the C₄ term on the obtained physicochemical parameters.

Full details of the parametrization strategy used to generate our models are provided in the Supporting Information. As our starting point, we used the new form of the LJ function to derive an updated version of our previous Mg²⁺ model. The initial geometry and LJ parameters for this model were taken from Duarte et al.,²⁸ while the initial C₄ term was taken from Li and Merz.¹⁵ Then, the LJ parameters describing R_min/2, ε and C₄ between Mg²⁺ and the water oxygen were systematically optimized, in order to reproduce both the experimental Mg²⁺–O distance and the hydration free energy (ΔG_hydr) for Mg²⁺ in water. It is not clear how large the contribution of the C₄ term is to the hydration free energy in Li and Merz’s studies,^11,14,15 as it was calculated together with the electrostatic contribution. Therefore, in order to assess the C₄ contribution, the calculation of the hydration free energy was divided into three steps, including the step of calculating the contribution of the C₄ term, as shown in Figure S1. Here, we derived three different parameter sets for the Mg²⁺ model in order to investigate the effects of the C₄ term, as shown in Tables 1 and 2 and Figure S2. All three parameter sets can reproduce both the hydration free energy and the Mg²⁺–O distances, as shown in Table 2, with the relative magnitudes of the contributions from the R_min/2, ε, and C₄ terms depending on how large the C₄ term was chosen to be (we parametrized all three terms so as to balance each other out in order to avoid the Lennard-Jones contribution to ΔG_hydr becoming too large; see also Table S1 for the relative contributions to the calculated ΔG_hydr).

Table 1. Force Field Parameters for the Metal Dummy Models Presented in This Work.

Bonded Parameters
		b0 (Å)
bond typea	Kb (kcal mol–1 Å–2)	MG	AL	FE	CR
M-Di	800.0	0.90	1.10	1.10	1.10

angle typeb	Kθ (kcal mol–1 rad–2)	θ (degrees)
Di-M-Di	125.0		180.0
Di-M-Dj	125.0		90.0

Nonbonded Parameters
atom typec	mass	charge	Rmin/2 (Å)	ε (kcal mol–1)	C4 (kcal mol–1 Å–4)
MG (minC4)	6.305	–1.0	0.579	118.3569	1.0
MG (midC4)	6.305	–1.0	0.706	26.8375	67.0
MG (maxC4)	6.305	–1.0	1.045	0.9768	149.0
AL	8.982	–1.2	0.725	12.4578	214.0
FE	37.845	–1.2	0.796	32.4579	324.0
CR	33.996	–1.2	0.670	57.3268	180.0
D (Mg2+)	3.00	0.5	0	0	0
D (Al3+)	3.00	0.7	0	0	0
D (Fe3+)	3.00	0.7	0	0	0
D (Cr3+)	3.00	0.7	0	0	0

^aU_b = K_b(b – b₀)², where K_b is the force constant and b₀ is the equilibrium bond length.

^bU_θ = K_θ(θ – θ₀)², where K_θ is the force constant and θ₀ is the equilibrium angle. M and D denote the central metal ion and the dummy atom, respectively. The subscripts i and j on the dummy atoms distinguish between dummy atoms that are collinear or perpendicular to each other.

^cMG, AL, FE, and CR denote the central Mg²⁺, Al³⁺, Fe³⁺, Cr³⁺ ions, respectively. The three different Mg²⁺ models, minC₄, midC₄, and maxC₄, mainly differ in the magnitude of the C₄ term, with min, mid, and max denoting the relevant magnitude of the C₄ terms (R_min and ε were then adjusted accordingly to the C₄ term used).

Table 2. Comparison of Calculated and Experimental Thermodynamic and Geometric Parameters for the Metal Models Presented in This Work^a.

		calculatedc			experimentald
ions		ΔGhydr	metal–O	CN	ΔGhydr	metal–O	CN
Mg2+b	minC4	–454.2 ± 0.5	2.09 ± 0.01	6.0	–454.2	2.09	6.0
	midC4	–453.6 ± 0.3	2.09 ± 0.01	6.0
	maxC4	–454.6 ± 0.5	2.09 ± 0.01	6.0
Al3+		–1101.2 ± 0.8	1.89 ± 0.003	6.0	–1100.3	1.89	6.0
Fe3+		–1032.5 ± 0.4	2.03 ± 0.003	6.0	–1033.0	2.03	6.0
Cr3+		–1037.0 ± 0.3	1.98 ± 0.006	6.0	–1037.0	1.96	6.0

^aΔG_hydr, metal–O, and CN denote the hydration free energies (kcal mol^–1), metal–oxygen distances in aqueous solution (Å) and coordination numbers of each metal ion, respectively.

^bFor a definition of the parameter sets that describe the three Mg²⁺ models, see Table 1, and for the radial distribution functions see Figure S7.

^cThe calculated hydration free energies are a sum of ΔG_LJ126, ΔG_C4 and ΔG_elec, respectively, as listed in Table S1 for all the models.

^dAll the experimental hydration free energy values were obtained from Noyes,³⁶ as described in the main text, while the experimental metal–oxygen distances and the coordination numbers were taken from Marcus’ review.³⁷

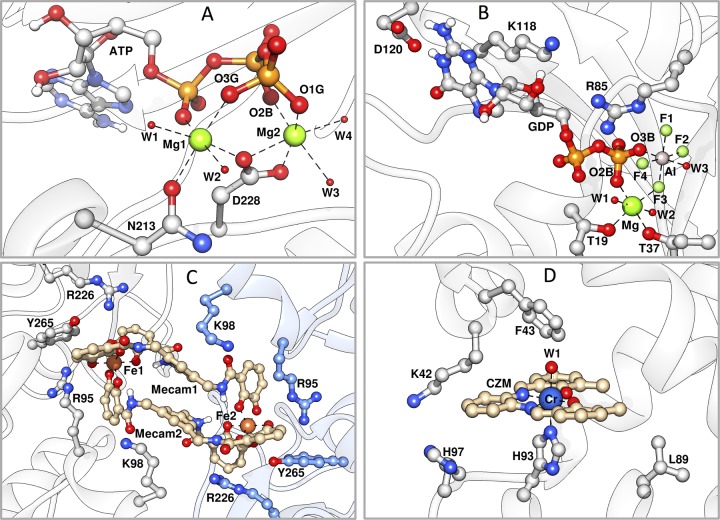
To further validate our Mg²⁺ models, we performed 50 ns molecular dynamics (MD) simulations of N-acetylhexosamine 1-kinase (NahK), in complex with adenosine triphosphate (ATP, PDB ID: 4WH3(38,39)), together with two Mg²⁺ dummy models in the active site (Figure 2A) for each model. As can be seen from Tables 3 and S2, all three models produced equivalently stable NahK and ATP, with very similar root-mean-square deviations (RMSD) for ATP between the three models. However, the midC₄ model had the highest RMSD (1.38 Å) among the three models. All three models also produced a slightly smaller intermetal distance (d(Mg–Mg)) than the crystal structure (3.82 Å), as shown in Figures S3A and Table S2. It appears that the higher the C₄ term is, the closer d(Mg–Mg) is to the original crystal structure, although the differences are very small. Jiang et al.²⁹ have reparametrized our Mg²⁺ dummy model,²⁸ and tested it in similar protein systems, GSK-3β (PDB ID: 1PYX(39,40)) and glutathione synthase (PDB ID: 1M0W(39,41)) in complex with ATP together with two Mg²⁺ ions, obtaining 26.1% and 11.2% higher d(Mg–Mg) than in the crystal structures, respectively. These are again much higher differences than those we obtained for our newly developed Mg²⁺ models (5.5% for minC₄, 4.5% for midC₄, and 3.1% for maxC₄). After we fully validated the Mg²⁺ model with the new LJ potential, the same strategy was then used to develop the dummy models of highly charged metal ions, Al³⁺, Fe³⁺, and Cr³⁺ (Figures S4 – S6).

Figure 2.

Representative structures of the most populated conformations of the metal binding sites of different metal ions in different proteins after 3 × 50 ns MD simulations of each system. Shown here are representative final snapshots from individual MD trajectories of (A) N-acetylhexosamine 1-kinase (NahK) in complex with ATP and two Mg²⁺ ions (PBD ID 4WH3^38,39), (B) RhoA GTPase in complex with guanine diphosphate (GDP), AlF₄^–, Mg²⁺, and rhoGAP (PDB entry 1TX4(39,42)), and (C) CeuE in complex with an [Fe(Mecam)]₂^6– bridge (PDB ID 2CHU(39,43)). Residues and backbone from Chain A are highlighted in gray, and residues and backbone from Chain B are highlighted in blue. (D) An artificial metalloprotein built from myoglobin in complex with 3,3′-Me₂-salophen (CZM) and Cr³⁺ (PDB entry 1J3F(39,44)). Colors: green for Mg²⁺, gray for Al³⁺, orange for Fe³⁺, and blue for Cr³⁺, green for fluoride and red for water. W1–W4 denote individual water molecules in different structures, and F1–F4 denote the F atoms of AlF₄^–. Note that our dummy models have been shown here as Lennard-Jones spheres for clarity. The pictures were generated using Chimera.⁴⁵

Table 3. Time Averages of the Root Mean Square Deviations (RMSD, Å) of the Protein Backbone Atoms, of the Ligands, and of the Metal Ions of All Systems Tested in This Work^a.

system		protein backbone	ligandb	metal 1c	metal 2d
NahK/Mg2+(minC4)		1.17 ± 0.23	0.90 ± 0.27	0.80 ± 0.20	0.38 ± 0.12
NahK/Mg2+(midC4)		1.38 ± 0.31	1.17 ± 0.33	0.73 ± 0.22	0.37 ± 0.12
NahK/Mg2+(maxC4)		1.21 ± 0.32	0.99 ± 0.31	0.68 ± 0.15	0.36 ± 0.13
RhoA/Mg2+-AlF4–/RhoGAP		1.35 ± 0.15	1.11 ± 0.27	0.74 ± 0.26	0.66 ± 0.20
CeuE/Fe3+	A	1.34 ± 0.27	2.22 ± 0.72	0.38 ± 0.13	0.38 ± 0.15
	B	0.98 ± 0.08
	A and B	3.28 ± 0.86
artificial myoglobin/Cr3+		1.38 ± 0.20	5.22 ± 0.69e	0.21 ± 0.11	--

^aFor a more detailed description of each system and the identity of the different metal ions, see the main text and the caption to Figure 2.

^bRMSD of ligands were calculated excluding hydrogen atoms after the alignment of the protein backbone.

^cRMSD of the metal ions were calculated after the alignment of the ligands excluding hydrogen atoms.

^dSecond metal ion, when more than one metal ion is present in the active site.

^eThe high RMSD for the ligand in the artificial myoglobin/Cr³⁺ complex corresponds to a slight movement of the noncovalently bound 3,3′-Me₂-salophen compared to the initial structure. Despite this high ligand RMSD, the coordination of the metal ion observed in the crystal is reproduced with high accuracy.

We note here a number of limitations with our reference experimental data set. (1) A key issue with correctly assigning hydration free energies for metal ions is the value assigned to the reference hydrogen potential. The data set used in this work, Noyes’ data set,³⁶ assigns zero values to the free energy, enthalpy, and entropy of the hydrated proton. We have used this data set for consistency with our previous work,^25,28 however, as we noted also in ref (28), it is important to bear in mind that considering the very large absolute hydration free energies of these metal ions, the differences between the data sets available amount to only a very small percentage difference in the actual hydration free energies. (2) To be fully rigorous, one should take into account the intrinsic single ion standard hydration free energies of the metal ions considered in the present work, as pointed out in ref (46). However, we point out that, as also discussed in ref (47), there is currently no approach commonly accepted by the field for performing this correction (and indeed, as discussed in ref (48) and references cited therein, the assumptions often made to address this experimentally unverifiable assumption can be highly problematic). Therefore, to be able to conclusively address this issue would be a substantial contribution to the field in its own right, which is far beyond the scope of the present work. Finally, (3) in principle, one should also correct for artifacts introduced by using a lattice sum method under periodic boundary conditions with a finite box-size. This is more trivial to address with spherical boundary conditions, where a standard Born correction can be applied, as in our previous work;²⁸ however, once again, this problem is much more complex using periodic boundary conditions, and there is currently no solution that is generally accepted and broadly used in the field. One possibility is the correction in eq 32 of ref (49). Using this equation, we obtain corrections of −44.3 kcal mol^–1 for Mg²⁺, and −98.8 kcal mol^–1 for Al³⁺, Fe³⁺, and Cr³⁺, when considering the ∼40 Å box length used in this work. While these numbers may seem large, we remind the reader that they are both within 10% of the absolute hydration free energies presented by Noyes,³⁶ and also in the same range as the experimental uncertainty between the data sets presented by Noyes³⁶ and Marcus.⁵⁰ Therefore, when taking into account these points and also the fact that there is currently not a consensus in the field with regard to how this correction should be implemented, we have followed the example of refs (11, 15, and 23) and not applied this correction in the present work. However, we discuss these points here so the reader is aware of the limitations of the reference model used for the hydration free energies. With these caveats in mind, the parameters of the three newly developed models are presented in Table 1, and all three models can again reproduce both experimental hydration free energies and metal-water distances simultaneously within the experimental uncertainty, as shown in Table 2.

Finally, to validate all systems, we performed MD simulations of the new metal ions presented here in complex with relevant proteins, which, together with the simulation setups, are described in more detail in the Supporting Information. The simulations of NahK in complex with ATP (Figure 2A) have already been described above. We performed additional simulations of Rho GTPase in complex with GDP and an AlF₄^– transition state analogue (TSA, Figure 2B), CeuE in complex with an [Fe(Mecam)]₂^6– bridge (Figure 2C), and an artificial metalloprotein built from myoglobin in complex with 3,3′-Me₂-salophen (CZM) and Cr³⁺ (Figure 2D). These systems were chosen in part for their (bio)chemical relevance, but most importantly because they are extremely challenging systems to model: compounds such as the CZM complex shown in Figure 2D would typically be modeled using a complex bonded model that requires several system-specific parameters,¹⁹ the AlF₄^– TSA in Rho GTPase is formed by primarily electrostatic interactions between the central metal ion and the surrounding fluoride ions, and finally, the ferric enterobactin binding protein from Campylobacter jejuni (CeuE) is a dimeric protein kept together by an [Fe(Mecam)]₂^6– bridge, as shown in Figure S8. Despite the fact that these are very challenging systems, as can be seen from Figure S3 and Tables 3 and S2 to S5, in all cases, we have stable protein/ligand/metal ion RMSD values, and both metal–metal and metal–ligand distances are in reasonable agreement with experiment, without the need for any additional artificial bonds or restraints. Finally, in the case of Rho GTPase, the distance between the Al³⁺ and F^– in the AlF₄^– transition state analogue, as well as the F–Al–F angles, agree quite well with the ones from the crystal structure, as shown in Table S3. Therefore, our model is valuable for the computational modeling of the aluminum fluoride TSAs so often used to study the enzymes that catalyze phosphoryl transfer.^6,8

We note as an aside that, for comparison, we have also performed 20 ns of molecular dynamics simulations using the same protocol as described in the Supporting Information for the multisite model, but with soft-sphere model presented in refs (11 and 15). In the case of N-acetylhexosamine 1-kinase, the system remained stable over the simulation time and in this particular case there was no added advantage of inclusion of a multisite model. In the case of the other three systems, however, either we obtained poorer agreement between the calculated and experimental metal–ligand distances (for example, in the case of Rho GTPase, where the soft-sphere model gave Al–F distances of 1.88 ± 0.05 Å (1.86 ± 0.04 Å, 1.84 ± 0.03 Å, 1.87 ± 0.04 Å, 1.93 ± 0.05 Å for the four Al–F distances, respectively), compared to 1.77 ± 0.02 Å in our calculations, and 1.76–1.79 Å in the crystal structure), or, in the even more challenging cases of the [Fe(Mecam)]₂^6– supramolecular bridge in CeuE, or the planar complex between 3,3′-Me₂-salophen and Cr³⁺ in the artificial metalloenzyme shown in Figure 2D, the metal site lost crystallographic coordination in at least one out of three replicas within the first 10–20 ns of simulation time. This is of course not a critique of the models presented in refs (11 and 15), but rather illustrates that, when moving to highly challenging systems, a soft-sphere model is not sufficient, and the added complexity presented by a multisite model is necessary. This is, therefore, a big advantage for the multisite models presented here, as we demonstrate that once suitably parametrized in aqueous solution, they are transferable also to highly complex biological systems, without the need for extensive system-specific additional parametrization.

In summary, we have presented here an updated parametrization of our nonbonded Mg²⁺ model, now using a 12–6–4 Lennard-Jones potential, and demonstrated that the inclusion of ion-induced dipole interactions provides a far more physical Mg²⁺ model, in agreement with ref (15). This model was used as a starting point to parametrize new nonbonded dummy models for highly charged metal ions (Al³⁺, Fe³⁺, Cr³⁺), and these models were then successfully applied to simulating particularly challenging metalloproteins. Taken together, we believe the models presented herein provide a valuable resource to the simulation community, and are of use to computational chemists and biologists alike for the simulation of metalloproteins and related compounds.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b02358.

• Detailed computational methods, simulation validation, and structural and thermodynamic parameters from the simulations (PDF)

The authors declare no competing financial interest.