Standard Reticle Slide To Objectively Evaluate Spatial Resolution and Instrument Performance in Imaging Mass Spectrometry

Abstract

Spatial resolution is a key parameter in imaging mass spectrometry (IMS). Aside from being a primary determinant in overall image quality, spatial resolution has important consequences on the acquisition time of the IMS experiment and the resulting file size. Hardware and software modifications during instrumentation development can dramatically affect the spatial resolution achievable using a given imaging mass spectrometer. As such, an accurate and objective method to determine the working spatial resolution is needed to guide instrument development and ensure quality IMS results. We have used lithographic and self-assembly techniques to fabricate a pattern of crystal violet as a standard reticle slide for assessing spatial resolution in matrix-assisted laser desorption/ionization (MALDI) IMS experiments. The reticle is used to evaluate spatial resolution under user-defined instrumental conditions. Edgespread analysis measures the beam diameter for a Gaussian profile and line scans measure an “effective” spatial resolution that is a convolution of beam optics and sampling frequency. The patterned crystal violet reticle was also used to diagnose issues with IMS instrumentation such as intermittent losses of pixel data.

Graphical Abstract

Matrix-assisted laser desorption/ionization (MALDI) imaging mass spectrometry (IMS) is an enabling tool for medical and biological research. Since the first publication in 1997,¹ the technology has been applied to study the distribution of wide variety of analyte classes including metabolites, lipids, peptides, and proteins in biological samples.^2–4 In a typical MALDI IMS experiment, a frozen or fixed tissue is sectioned and thaw-mounted onto a target. The resulting tissue section is coated with a MALDI matrix usually by sublimation or spray-based methods. The matrix-coated tissue sample is then analyzed by a serial raster of the laser across the tissue section, acquiring a mass spectrum at each defined x, y coordinate. Following acquisition, the spectral ion intensity is plotted for ions of interest providing two-dimensional maps of specific molecular distributions.

Instrumental conditions in IMS experiments offer trade-offs in various aspects of performance. For example, higher spatial resolution IMS generates a greater number of pixels in a given area compared to the same area sampled at a lower spatial resolution. Consequently, higher spatial resolution images allow the visualization of finer structural detail; however, the file size for such images will be greater and their acquisition time will be longer. Depending on the experimental task or question to be answered, instrument parameters are typically selected to achieve particular image characteristics. Beam optics, laser energy, the number of laser shots, and stage step size can be independently tuned for each experiment. For example, to achieve high spatial resolution, Gaussian laser beams have successfully been focused to small diameters, whereas smartbeam (Bruker Daltonics) lasers have been developed to yield high sensitivity.⁵ Spatial resolution is also limited by sample stage positioning, with most commercial instruments offering 1–10 μm stage accuracy. As vendors and investigators actively refine instrumentation, objective methods are needed to test for and correct hardware inaccuracies (e.g., inaccuracies in data acquisition and stage positioning) that can diminish spatial resolution. Monitoring the consequences of instrumental parameters and catching potential errors effecting spatial resolution is vitally important to maintaining high quality IMS data.

Several investigators have reported methods for evaluating spatial resolution in secondary ion mass spectrometry (SIMS). Senoner et al.⁶ fabricated a multilayer structure comprising alternating epitaxially grown layers of GaAs, AlGaAs, and InGaAs using metal organic chemical vapor deposition. They used this target in cross-section to evaluate spatial resolution in SIMS across 16 laboratories in 10 countries.⁷ They scanned the beam across a narrow strip (0.5–50 nm) of Al_0.65Ga_0.35As and used the intensity profile to estimate the beam width. They also imaged a series of parallel lines to estimate spatial resolution using the Rayleigh criterion.⁸ Passarelli and Ewing fabricated a reticle with gratings of liposomes and PEG that they used to measure spatial resolution in TOF-SIMS and in MALDI-TOF, obtaining fwhm values of ~2–4 and ~184 μm, respectively.⁹ The high value of fwhm observed in the case of MALDI-TOF was because of secondary steps required in sample preparation, including the use of a solvent-based matrix spray that caused delocalization of the liposomes and PEG. This confounding factor prevented the intrinsic measurement of MALDI instrument spatial resolution. Fagerer et al.¹⁰ used a tungsten grid placed on top of the coatings of the matrix compounds 9AA and CHCA to evaluate spatial resolution in a MALDI TOF instrument with continuous stage motion. While the use of a grid as a physical mask with defined openings provided a simple approach, the laser beam was distorted upon transmission through the grid.

In the present work, we developed a method to directly measure the spatial resolution of a given instrumental setup of an imaging mass spectrometer. Our approach employs a device that consists of a crystal violet pattern on a conductive substrate; crystal violet was selected because it readily desorbs and ionizes upon laser ablation. Imaging this crystal violet pattern enables a direct measurement of beam size and spatial resolution without the delocalizing effect of matrix application or the distorting effect of a masking grid as encountered for other methods. The developed reticle provides a reliable standard for measuring and comparing spatial resolution across different MALDI imaging platforms. With the reticle, the measurements of spatial resolution could be automated. We also present results using this approach to evaluate the effects of the laser energy and focus setting on spatial resolution. The reticle described here includes patterned features with dimensions ranging from 30 to 200 μm that are typical in current MALDI imaging experiments. The lithographic techniques used in the fabrication of the reticle can be scaled down to smaller dimensions when needed for evaluating spatial resolutions below 30 μm.¹¹

MATERIALS AND METHODS

Materials

Crystal violet, n-hexadecanethiol, and ethanol were purchased from Sigma-Aldrich (St. Louis, MO) and used as received. Glass slides coated with a 50 nm layer of gold were purchased from Deposition Research Laboratory (St. Charles, MO). Polydimethylsiloxane (PDMS) Sylgard 184 was purchased from Essex Brownell (Memphis, Tennessee). SU-8 3025 photoresist and SU-8 developer were obtained from MicroChem Corp (Westborough, MA). Reticle patterns were designed using the CAD freeware program DraftSight (Dassault Systèmes, Velizy-Villacoublay, France) and printed as photomasks by CAD/Art Services, Inc. (Bandon, OR).

Fabrication of the Reticle

Soft lithography techniques as described by Whitesides et al.^12,13 were adapted for generating patterned substrates used to produce the reticle. Specific conditions are detailed below.

Photomask

The pattern for the reticle was drawn using DraftSight (Dassault Systèmes, Velizy-Villacoublay, France). It consisted of a series of parallel lines of varying widths separated by gaps ranging from 30 to 200 μm. This pattern was replicated 16 times within a field measuring 1 x 1 (see Figure S1 in Supporting Information). A photomask of the pattern was produced on a transparency sheet using a high resolution laser printer (Orbotech LP9008, Orbotech, Yavne, Israel).

SU-8 Master

A 3D relief structure of the pattern was generated in SU-8 3025.¹⁴ The SU-8 was spin-coated onto a silicon wafer at 3000 rpm to generate a layer ~25 μm in thickness.¹⁵ The SU-8 coated wafer was heated for 10 min at 95 °C. The photoresist layer was illuminated for 25 s with a UV curing flood lamp equipped with a metal halide bulb that emits UVA longwave (Dymax 5000-EC Series, Dymax, Torrington, CT) through a 0.4 OD 3 sq. absorptive neutral density filter from Edmund Optics (Barrington NJ) and the photomask.. The exposed photoresist was heated for 3 min at 95 °C to cross-link the exposed regions (Figure 1a). The film was immersed in the SU-8 developer solution for 5 min to produce a patterned relief structure.

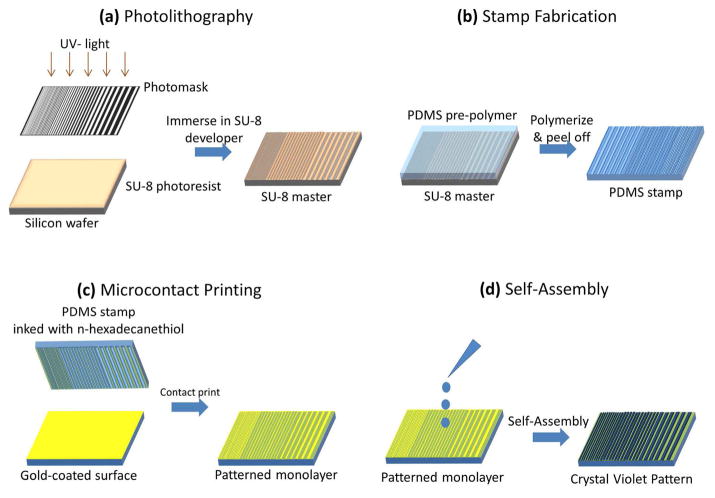
Figure 1.

Schematic process for generating a surface patterned with crystal violet. (a) Photolithography was used to produce the SU-8 master. (b) A PDMS stamp was fabricated as a negative replica of the SU-8 master. (c) PDMS inked with n-hexadecanethiol and contact printed onto a gold-coated surface. (d) Self-assembly of crystal violet into patterned lines.

PDMS Stamp

Sylgard 184 silicone monomer and cross-linking agent were mixed together in a 10:1 ratio, and poured onto the SU-8 master as a layer ~0.7 cm in thickness. After incubation in an oven for 2 h at 85 °C, the cross-linked PDMS was peeled from the SU-8 master, yielding the PDMS stamp (Figure 1b).

Microcontact Printing

A gold-coated slide was cleaned by immersion in “base piranha” (a mixture of saturated KOH and 30% H₂O₂ (aq) in a 1:2 ratio by volume) for 90 s, rinsed with deionized water, and blown dry with a stream of nitrogen. The PDMS stamp was inked with a 2 mM solution of n-hexadecanethiol in ethanol and then brought into contact with the gold surface to yield a patterned self-assembled monolayer (Figure 1c).

Self-Assembly of Crystal Violet Pattern

Crystal violet was dissolved in ethanol at a concentration of 10 mg/mL, sonicated, and filtered (0.2 μm pore size). A 200 μL aliquot of this solution was pipetted onto a patterned gold slide measuring 1 x 1 to completely cover its surface. The slide was rotated at 3000 rpm for 1 min within a spin coater to produce a pattern of crystal violet (Figure 1d).

Surface Characterization

A stylus contact profilometer (Veeco Dektak 150, Bruker, Billerica, MA) and Dimension Icon atomic force microscope (Bruker, Billerica, MA) were used to measure the thickness of the crystal violet features.

Mass Spectrometry Instrumentation

The reticle was used to evaluate the performance of three mass spectrometers: a Bruker UltrafleXtreme MALDI TOF/TOF (Billerica, MA), a Bruker Rapiflex MALDI Tissuetyper (Billerica, MA), and a SimulTOF 300 Tandem MALDI TOF/TOF (SimulTOF Systems, Sudbury, MA). The Bruker Ultraflextreme was equipped with a smartbeam (355 nm, frequency-tripled Nd:YAG laser) and operated in positive ion reflector mode at 20 kV. A laser step size of 5 μm was used in both the x- and y-directions. The laser focus setting was set to different settings including “ultra”, “medium”, and “small”. Laser power was individually adjusted for each focus setting to enable comparable ion current for crystal violet. Laser power was measured for each setting using a pyroelectric energy sensor (PE9 Ophir Optics, North Andover, MA) at the location where sample would be placed in the source. Each pixel represents signal accumulated from 100 laser shots.

The Rapiflex was also equipped with smartbeam (355 nm, frequency-tripled Nd:YAG laser) and operated in positive ion reflector mode at 20 kV. A laser step size of 5 μm was used in the x-direction; a step size of 30–70 μm was used in the y-direction, as stated in the text. The laser focus setting was set to “single”, “mod 5”, and “mod 5 defocus”. The laser power was individually adjusted for each focus setting. Each pixel represents signal accumulated from 50 laser shots.

The SimulTOF 300 Tandem was operated in positive ion reflector mode at 8 kV. This system is equipped with a 349 nm, diode-pumped, frequency-tripled Nd:YLF laser (Spectra-Physics, Santa Clara, CA) capable of laser repetition rates up to 5 kHz. The laser energy was controlled by adjusting the current applied to the diode and was maintained at 14.5 μJ/ pulse for all experiments (as measured prior to attenuation, which was kept constant). The instrument utilizes continuous laser raster sampling. All images were acquired under instrument conditions set for 50 μm spatial resolution (50 μm spatial resolution in the x-direction, as defined by the laser repetition rate, stage speed, and number of hardware averages, and 50 μm spatial resolution in the y-direction, as defined by the motor step size between continuously rastered rows). Laser repetition rate, stage speed, and number of hardware averages were altered systematically, as noted in the text to maintain a lateral spatial resolution of 50 μm.

For all three instruments, the reticle was simply mounted on the target holder provided by the vendor and was fixed to the target holder using conductive copper tape. The reticle could be mounted on the target holder along with a tissue sample to ensure similar operating conditions for both the sample and the reticle.

Data Analysis

Image data for edgespread and point spread methods were acquired on the UltrafleXtreme using Bruker FlexImaging 3.0 and were imported into MATLAB using a conversion tool created within this lab. Subsequent numerical analysis was conducted in MATLAB; the relevant code is provided in Supporting Information (see SI-1). The curve fitting toolbox was used to model experimental results and 18–20 rows of data were averaged together to determine beam sizes. Data for determining spatial resolution using line gratings were acquired on the Rapiflex using Bruker FlexImaging 5.0. The data were converted into Analyze 7.5 format, and further analysis was conducted in MATLAB (see Supporting Information, SI-2). For linescan determination of spatial resolution, 10 rows were averaged together. Image data from the reticle acquired on the SimulTOF instrument were analyzed using the SimulTOF Viewer.

RESULTS AND DISCUSSION

Figure 1 provides an overview of the process for reticle fabrication. Photolithography was used to generate a patterned SU-8 master. The pattern consisted of parallel lines with gaps ranging from 30 to 200 μm (Figure 1a). A PDMS stamp was produced using a replica molding process (Figure 1b). The stamp was inked with n-hexadecanethiol and placed onto a gold-coated slide to transfer the pattern (Figure 1c). A crystal violet solution was pipetted onto the functionalized gold surface, the slide was spun at 3000 rpm, and the dye self-assembled into discrete areas (Figure 1d). The crystal violet formed a pattern in the regions not functionalized with the n-hexadecanethiol. The process to form the crystal violet pattern is rapid, with the SU-8 master and PDMS stamps allowing reuse. For example, a single SU-8 master was used to produce tens of PDMS stamps, and each stamp was used more than 20 times for functionalizing gold surfaces. The overall process of contact printing and self-assembly required less than 5 min.

Characterization of the Reticle

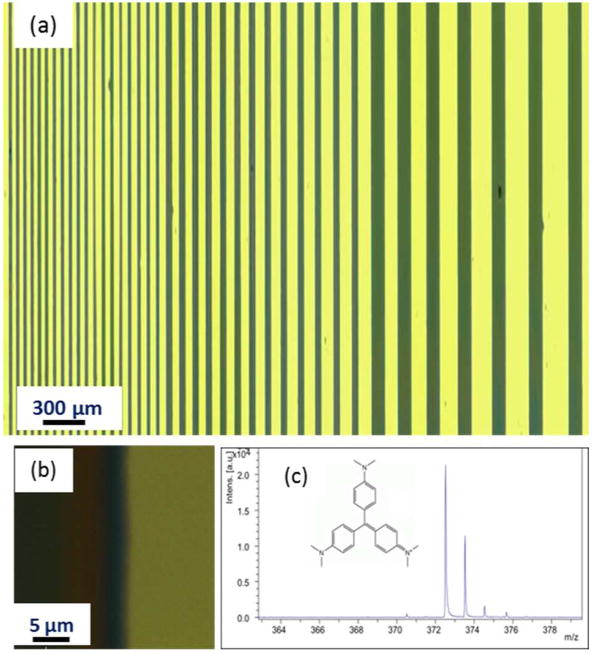
Figure 2 shows a representative optical image for a reticle prepared in a traditional wet chemical laboratory environment. The image shows a series of parallel lines of crystal violet (dark regions) separated by changing distances between them. The crystal violet lines ranged in thickness from 300 to 800 nm, as measured using contact profilometry and atomic force microscopy. In general, the narrower lines were thinner than the wider lines. In comparing the reticle pattern with that of our photomask, the measured widths of the crystal violet lines and the gaps between them were both ~2% smaller than those in the mask. We attribute this difference to shrinkage of the PDMS stamp as no we found no size differences between the features in the photomask pattern and those in our SU-8 master. Figure 2b shows a magnified view for one of the 100 μm wide crystal violet lines from the reticle. In this image, both sides of the crystal violet line show an edge sharpness of better than 1 μm, which was routinely achieved across all line sizes by the fabrication method.

Figure 2.

(a) Optical microscopy image of the reticle. The widths of the crystal violet lines are 100, 50, and 25 μm from left to right. The gaps between the crystal violet lines range from 200 to 30 μm. (b) Magnified view of a 100 μm crystal violet line. (c) Mass spectrum obtained from the reticle showing a monoisotopic peak at m/z 372.5 that represents crystal violet after loss of its chlorine ion. Direct laser ablation was sufficient to detect this peak for crystal violet without the use of a matrix.

Mass spectral signals from the crystal violet pattern were readily obtained by direct laser ablation without the use of matrix. Figure 2c displays a representative mass spectrum from the reticle, showing a monoisotopic peak at m/z 372.5 that corresponds to crystal violet (M) after the loss of chlorine ion, [M – Cl]⁺. The ease of generating of the peak at m/z 372.5 and measuring its intensity provided the basis for mapping variations in its locational intensity from the reticle and using these variations for determining spatial resolution.

Measurement of Beam Size by Imaging a Sharp Edge

A routine method for measuring the beam size of an irradiated spot on a target within an IMS instrument would be useful for characterizing instrument performance and assessing the effects of alterations made during instrument development on instrument resolution. The “knife edge” method is a common approach for characterizing beam size, where the beam intensity is measured as a sharp edge is translated perpendicular to its path.^16,17 To assess the size of a beam on a target, an analogous approach can be used where the beam is translated across a sharp edge of a patterned feature, and the obtained line profile is evaluated. The steepness of the edge profile can then be used to characterize the sharpness of the image.¹⁶ This measurement of signal intensity across the sharp edge of a pattern is attractive because it is simple, it characterizes the beam size at the site of interest, and it can yield similar profiles even for very different beam shapes.

With a suitable target, the edge-spread profile approach can be adapted for MALDI IMS and provides a measurement of the beam size responsible for generating detectable signals. This measured “effective” beam size would be the region of the laser beam with intensity above the threshold needed for ablating material and generating ionized molecular species for detection. The actual size of the laser beam on the target would be larger than that obtained by this approach; however, as this measurement only reflects the region of the incident beam that generates MS signal, it would provide more suitable information for asssessing spatial resolution for MALDI IMS.

We employed this edge-spread profile approach with the reticle to characterize the spot sizes provided by a Bruker Ultraflextreme mass spectrometer under three different focus settings: ultra, medium, and small. At each setting, the power was set just above the ionization threshold in order to prevent excessive ablation of crystal violet from the reticle during the scan (see Figure S2 in the Supporting Information). In the experiment, the laser beam was scanned toward the edge of a crystal violet feature on the reticle in 5 μm steps, as illustrated in Figure 3a. The crystal violet pattern consisted of parallel lines, each having edge resolutions of better than 1 μm as estimated from microscopy images at high magnification (Figure 2b). Figure 3b–d shows the signal intensity for crystal violet at these three focus settings as the position of the crystal violet edge was translated across the incident laser. Typically, multiple adjacent nonoverlapping linescans were combined for analysis. In Figure 3b–d, all three scans exhibited a transition from no to full signal as the edge moved across the beam. At each setting, we separated the scans of signal intensity with stage position into three regions: a background signal from bare substrate, a rising signal across the edge, and a maximum signal from the crystal violet area. We fit horizontal lines to the background and maximum signals, and applied a polynomial fit to the rising signal between these values. To compare these profiles, we determined values of Δ_12–88%, the lateral distance over which the signal intensity changed from 12 to 88% of the signal difference across the edge, as this distance corresponds to the full-width half-maximum (fwhm) for a Gaussian profile. For fwhm values greater than 30 μm, the profiles exhibited well-defined shapes for this analysis. In contrast, smaller spot sizes (<20 μm) were more sensitive to local differences in the amounts of crystal violet on the surface, leading to greater difficulties in fitting the region of maximum intensity by a horizontal line. Despite this challenge, we estimate the uncertainty in Δ_12–88% to be a few micrometers.

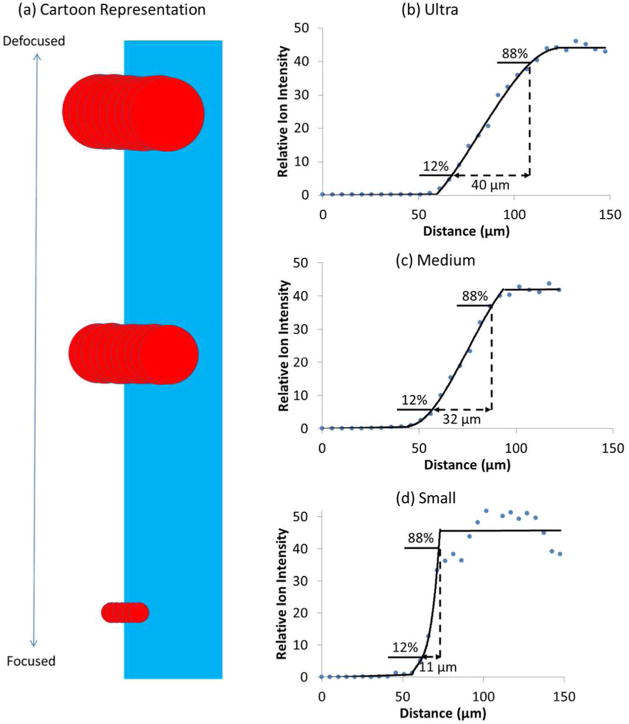
Figure 3.

Edge-spread profile analysis obtained by scanning a smartbeam laser across a crystal violet edge. (a) Schematic illustration of laser pulses traversing the crystal violet edge as the stage is moved in 5 μm steps. (b–d) Average ion intensity for crytal violet vs distance (μm) at three different laser focus settings: “ultra”, “medium”, and “small”. Effective beam sizes were measured to be 40, 32, and 11 μm, respectively. The signal intensities in each panel with position are the average from ~20 adjacent scans.

Table 1 summarizes the averaged results from three independent edge-spread profile measurements using the reticle at each of three focus settings. The data were obtained under acquisition conditions where the average signal intensities were of similar levels to minimize differences in ablation levels. The measured fwhm values showed good reproducibility at each setting and clearly distinguished the differences in lateral size for the different beam settings.

Table 1.

Results from Edge-Spread Profile Analysis of a Smartbeam Laser at Various Focus Settings; The ± Values Represent Standard Deviations from Three Measurements^a

laser focus setting	laser power (μJ)	average signal/pixel (×104)	Δ12–88% (μm)
ultra	4.66 ± 0.17	9.6	45 ± 4
medium	10.0 ± 0.3	7.5	31.9 ± 0.3
small	4.69 ± 0.13	7.1	11.2 ± 0.8

^aData were collected using a Bruker Ultraflex. The laser power as percentages were 82.0, 83.2, and 84.8% for the ultra, medium, and small focus settings, respectively.

Measurement of Gaussian Beam Size Using the Convolution of PSF with the Object Pattern

The edge-spread profile method described above involves imaging a single sharp edge or a step function. Its precision is limited by the available step size for the scan, particularly for smaller beams. As shown above, variations in the signal intensity in a region where its value should be a maximum can introduce uncertainties for defining the position of the edge. To overcome this issue, we extended the edge-spread profile method to the characterization of a pattern of step edges separated by known distances. The separation distances between the crystal violet features on the reticle and their widths were defined by the photomask used to generate the reticle (Figure 1) and verified by optical microscopy. In cross-section, the pattern provides a series of rising and falling edges with known distances between them, thereby reducing the uncertainty in the position of any one edge profile in a scan. By this approach, the results across multiple edges can be evaluated simultaneously for measurement of the effective beam size on the target.

To describe the signal intensity expected from the beam moving in a direction perpendicular to the parallel lines of crystal violet on the reticle, we employed a general two-dimensional point spread function (PSF) that would describe the beam profile (i.e., shape, size, and power distribution). The PSF can be considered as an impulse reponse of the incident laser beam on the target that is responsible for producing a blurred image of the actual pattern. The PSF profile for the incident beam may have a Gaussian, Tophat, Lorentzian, or other shape depending on the optical set up. When used to image a pattern, the intensity of each pixel i(x′,y′) in the resulting image represents a convolution between the pattern provided by the target being imaged and its blurring by the PSF. The mathematical representation for this convolution is presented in detail in the Supporting Information (see SI-3) along with the development of general mathematical expressions to describe the expected variations in signal intensity for imaging a pattern of parallel lines. For a Gaussian-shaped beam, the signal intensity obtained by scanning across four parallel lines in the perpendicular direction with widths and separation distances for the pattern shown in Figure 4a can described by the equation:

$$\begin{gathered} i(x^{\prime },y^{\prime })=A_{min}+A_1\left[\text{erf}\left(\frac{x-b}{\sqrt{2}\sigma }\right)-\text{erf}\left(\frac{x-b-100}{\sqrt{2}\sigma }\right)\right] \\ +A_2\left[\text{erf}\left(\frac{x-b-260}{\sqrt{2}\sigma }\right)-\text{erf}\left(\frac{x-b-360}{\sqrt{2}\sigma }\right)\right] \\ +A_3\left[\text{erf}\left(\frac{x-b-540}{\sqrt{2}\sigma }\right)-\text{erf}\left(\frac{x-b-640}{\sqrt{2}\sigma }\right)\right] \\ +A_4\left[\text{erf}\left(\frac{x-b-840}{\sqrt{2}\sigma }\right)-\text{erf}\left(\frac{x-b-940}{\sqrt{2}\sigma }\right)\right] \end{gathered}$$ (1)

where x′ and y′ are the center positions of the incident beam, σ is a parameter describing the width of the beam in the x direction, b represents the position along the x-axis of the first rising edge (i.e., the edge of the first line), A_min represents a background signal level, and A₁, A₂, A₃, and A₄ represent the maximum signal amplitudes obtained on each line. The different values for these maximum signal amplitudes allow accommodation of local intensity variations in the maxima from each feature should they occur.

Figure 4.

Edge-profile analysis across multiple rising and falling edge profiles of known spacings. (a) Crystal violet pattern prior to laser ablation. Each crystal violet line is 100 μm wide; the gaps between the lines are 160, 180, and 200 μm from left to right. Beam focus and power settings were adjusted manually for each of the three experiments. (b) Beam focus = “ultra”; σ = 16.4 μm. (c) Beam focus = “medium”; σ = 13.1 μm. (d) Beam focus = “small”; σ = 5.4 μm. Fits are to eq 1 to provide measurements of σ.

Figure 4b shows experimental data of the signal intensity obtained from line scans performed on the test pattern shown in Figure 4a along with a best fit by eq 1. The experimental data were obtained at a step size of 5 μm, an acquisition setting of 100 shots/pixel, an “ultra” focus setting, and a power setting of 82.0%. The signal intensity exhibits four rising and four falling transitions, with the maximum signal intensity obtained from each line showing some variations. The data are fit well by eq 1 assuming a Gaussian beam profile, yielding a 95% confidence range of 16.4 ± 0.8 μm for the characteristic beam width, σ, at this acquisition setting. A second set of experimental data obtained under the same operating conditions yielded a 95% confidence range for σ of 16.8 ± 1.0 μm, showing good reproducibility for the method. The strong agreement between the model and the experimental data (R² > 0.99) suggests that the imaging results generated by a smartbeam profile can be modeled well by a Gaussian distribution for typical focus settings. For cases where the beam shape of the laser differs greatly from a Gaussian distribution (such as for the ‘Mod 5” setting described in a later section), an alternative approach using the linescan method detailed later in this paper is instead recommended for measuring spatial resolution (vide infra).

Related experimental data sets of signal intensity as a function of laser focus position and power setting were obtained on the pattern of four lines to examine their effects on the characteristic beam width. Figure 4c shows that using a “medium” focus setting and a power setting of 83.2% resulted in a smaller characteristic beam width, σ, of 13.1 ± 0.7 μm. As the “medium” instrumental setting provided a more focused beam than the “ultra” setting, the σ value was expected to be reduced as was observed. For this data set, the best fit exhibited flatter tops than those in Figure 4b, resulting from greater sharpness in the rising and falling transitions. Figure 4d shows the results for the “small” focus setting at a power setting of 84.8%. Under these conditions, the fit to eq 1 produced a 95% confidence range for σ of 5.4 ± 0.9 μm. Flatter tops are even more apparent in the fit for the “small” focus setting, consistent with the greater sharpness in the rising and falling transition regions. Table 2 summarizes the results from these and related experiments showing the reliability of the determined values of σ. As the focus is changed from “ultra” to “medium” to “small”, the fwhm of the beam decreased from 40 ± 2 μm to 30.8 ± 1.6 μm to 13 ± 2 μm.

Table 2.

Beam Width Values Obtained from Edgespread Analysis Across Multiple Rising and Falling Edge Profiles of Known Spacings under Different Focus and Power Settings^a

laser focus setting	laser power (μJ)	average signal/ pixel (×104)	σ (μm)	fwhm (μm)
ultra	4.66 ± 0.17	9.0	16.8 ± 1.0	40 ± 2
	4.66 ± 0.17	9.6	16.4 ± 0.8	38.6 ± 1.9
medium	10.0 ± 0.3	7.5	13.1 ± 0.7	30.8 ± 1.6
	9.9 ± 0.3	0.3	12.2 ± 2.7	29 ± 6
small	4.69 ± 0.13	7.1	5.4 ± 0.9	13 ± 2
	4.69 ± 0.13	8.0	5.5 ± 0.8	13.0 ± 1.9

^aData were collected using a Bruker Ultraflex. The laser power as percentages were 82.0, 83.2, and 84.8% for ultra, medium, and small focus settings, respectively.

Across these three different focus settings, a consistent 95% confidence range of ±1.0 μm or less on the value of σ was obtained, corresponding to a fwhm range of ±2.0 μm or less, when a sufficient laser power setting was used. In all cases, the model fit the transition regions well, with the greatest departures being in the regions of maximum signal intensity, possibly reflecting local variations in crystal violet amounts within the patterned lines. These differences likely affect little the measurement of σ as its primary influence on eq 1 is the sharpness of the fitting curve in the rising and falling transition regions. The known locations of and the distances between these transition regions in the pattern allow the determination of σ by a fully objective curve fitting algorithm, providing a notable advantage over the analysis method performed over a single step edge (Figure 3) where the exact position of the edge in a scan is not known. Further, the fitting approach using eq 1 is amenable to being conducted under automated control and being performed on other related patterned structures with different separation distances and line widths for determining σ with greater confidence by a global fitting strategy.

In Table 2, the fwhm values obtained at each focus setting were consistent with each other, with small differences in laser intensity causing small variations in the uncertainty values. Laser power settings that yielded much weaker signal intensities produced fits having the greatest uncertainty in the fitted fwhm values; however, the 95% confidence intervals on the fwhm values measured at the lower laser power settings were consistent with those obtained at that focus setting and a higher laser power setting.

At each of the focus settings in Table 2, the step size (5 μm) was smaller than the calculated fwhm values for the beam. As a result, adjacent laser spots overlapped with one another during a scan raising the concern whether oversampling could be occurring that could affect signal intensity. In preparing the reticle, the crystal violet features were fabricated to be sufficiently thick (>300 nm) to ensure that they would not be completely ablated during a scan when typical laser power settings were used. An optical image of the crystal violet pattern after imaging is provided in the Supporting Information (Figure S2a) showing that most of the crystal violet is retained. We tested to ensure that such changes to the crystal violet film did not dramatically affect signal intensity. Under the normal laser power settings, we found that the signals provided from previously investigated homogeneous areas of crystal violet were roughly 90% or more of those obtained previously unexamined areas and the measured fwhm values were unchanged. At higher power settings, it was possible to ablate greater amounts of crystal violet (as shown in Figure S2b in the Supporting Information) and produce results compatible with oversampling. For example, in scanning a previously investigated region at a “large” (i.e., intermediate beween “medium” and “ultra”) focus setting, a FWHM value of 21.9 ± 1.4 μm was obtained that was roughly 10 μm smaller than was obtained for this setting in a first scan. The lower value of FWHM is consistent with an oversampling type of experiment in which the signal intensity would rise more quickly and reach a plateau faster across a pattern. By proper control of conditions, oversampling could be avoided. By such repeated scans, the reticle provided the ability to evaluate whether its measurements of spatial resolution were uncompromised by over-sampling effects.

Use of Line Gratings to Determine Spatial Resolution

Spatial resolution is defined as the smallest spacing in an image that can be recognized as distinct and separate within a specified threshold. The effective beam sizes determined by the edgespread and PSF methods detailed above provide a measurement related to spatial resolution but are themselves not a direct measure of spatial resolution. The ability to resolve a small region with attributes different from those adjacent to it underlies most determinations of spatial resolution. Various criteria have been suggested for assessing spatial resolution, such as those reported by Rayleigh and Sparrow that have been primarily used for optical measurements. The Rayleigh criterion measures the separation between two equal point sources such that the central maximum in the signal originating from one source overlays with the minimum signal from the other. An empirical estimate of spatial resolution is made based on the observation of an intensity level from a region that has a value that is 19% lower in intensity from that of two nearby maxima, as expected for two equal point sources with this separation.⁸ The Sparrow criterion defines the minimum possible spatial resolution by the observation of a dip in the obtained signal from separated equal point source.⁸ A drawback of these methods is that neither of these criteria include experimental uncertainties such as noise in their theoretical assignment of spatial resolution. The reliance of the Rayleigh and Sparrow criteria on the ability to discern modest differences in signal from those that may be due to noise severely limits the application of these criteria for IMS. Instead, we employed a threshold level where the ability to distinguish separated sources of no signal intensity was used to provide a measurement of spatial resolution. Specifically, we defined a threshold level of 10%, so that if the signal intensity dipped to a value less than 10% of that of maximum as the laser beam is scanned across a striped pattern, the features are said to be resolved.

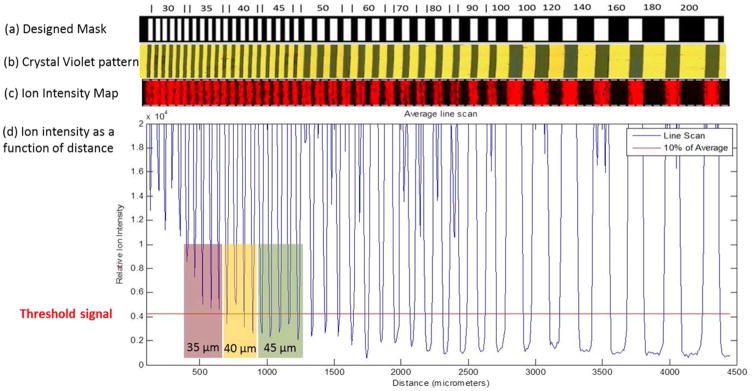
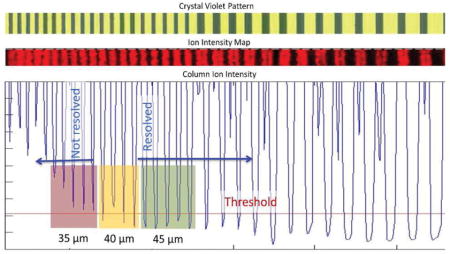
For determination of spatial resolution in IMS, we designed a pattern that would provide a series of parallel stripes that differed in their separation distances between them. Figure 5a shows an illustration of the line grating design used to produce the photomask that yielded the reticle pattern. The numerical values in Figure 5a represent the separation distances (the black regions) in microns between adjacent stripes (the white regions) of the reticle pattern. The white regions in the photomask correspond to those areas on the reticle that contain crystal violet and the black regions define their separation. Figure 5b shows an optical image of a crystal violet pattern obtained using the photomask by the procedure summarized in Figure 1. The crystal violet areas appear black against the gold background for the uncovered areas. Figure 5c shows the ion image collected at m/z of 372.5 ± 0.2 Da corresponding to the positively charged hexamethyl pararosanilium ion from crystal violet. The image was acquired at a 10 μm step size, a 70% focus setting, and 84% power. The image data were converted to a graphical view shown in Figure 5d by averaging ion intensities from 10 sequential scans. The signal switches from high to low intensity values across the pattern, with the minimum values increasing in intensity from regions with smaller separation distances between the crystal violet regions. The red line in Figure 5d shows the cutoff used for establishing spatial resolution from the pattern and was set to 10% of the maximum intensity. If the ion intensity from a region with a particular separation distance fell below this cutoff value, the instrumental conditions are said to resolve that feature size. Relatedly, the instrumental conditions were unable to resolve a particular feature size if the ion intensity from a region with that separation distance did not fall below this cutoff value. The data in Figure 5d exhibit a progession of behaviors. In Figure 5d, the smallest separation distance resolved consistently was 45 μm, as the linescan in this region (highlighted in green) consistently yielded signals below the 10% cutoff value. At a smaller separation distance of 40 μm between the striped regions, the yellow region notes a limiting resolution as the linescan dips below the cutoff inconsistently (three out of the four times). The red region (35 μm separation distances) highlights results obtained below the limit of resolution as the linescan intensity was consistently above the 10% cutoff value across this striped region. We note that this general method would be applicable to irregularly shaped beams and not just limited to Gaussian, Lorentzian, or Top-hat beam profiles.

Figure 5.

(a) Photomask pattern as designed in CAD software with specified dimensions in microns. The white rectangular regions represent transparent areas and the surrounding black regions are opaque. (b) Resulting crystal violet pattern fabricated using the photomask, soft lithography, and surface patterning techniques. (c) Ion image acquired by MALDI IMS of the distribution of m/z 372.5 Da corresponding to signal from crystal violet after the loss of chlorine. (d) Linescan of ion intensity for crystal violet across the pattern. The threshold signal (red line) is calculated as 10% of the obtained signal from regions with crystal violet.

We applied the method detailed in Figure 5 using the 10% threshold to measure the spatial resolutions across various operating conditions. To illustrate the broad utility of this method particularly for irregularly shaped beam profiles, we obtained data using the single and multiple spot settings provided by a Bruker Rapiflex. Table 3 summarizes the results from experiments performed at three different laser focus setting: “single”, “mod 5”, and “mod 5 defocused”. At each focus setting, three different power settings were tested. For each experiment, we also compared the spatial resolution measurements obtained from the linescan analysis with the size of ablation craters produced in homogeneous coatings of crystal violet under the same instrumental conditions. For the “single” laser focus setting, the intensity values dipped below the 10% threshold value between each stripe for all power settings, demonstrating a spatial resolution below 30 μm. For the “mod 5” laser focus setting, the smallest resolved separation was 50 μm at a laser power setting of 39.4% and was 60 μm at laser power settings of 43.4 and 47.4%. For the “mod 5 defocused” laser focus setting, the resolved separation spacing was below 30 μm for 62.8% power, while at laser power settings of 66 and 70%, the smallest resolved separation increased to 35 and 70 μm, respectively. Across all laser focus settings, the smallest resolved separation beween features increased in size with increasing power, suggesting a greater sampling area by the beam at higher power levels.

Table 3.

Measurements of Spatial Resolution Using Line Gratings across Various Instrument Settings^a

laser focus setting	laser power (%)	smallest resolved separation (μm)
single	19.0	<30
	21.0	<30
	23.0	<30
Mod 5	39.4	50
	43.4	60
	47.4	60
Mod 5 defocused	62.8	<30
	66.0	35
	70.0	70

^aData were collected using a Bruker Rapiflex.

For comparison with the obtained spatial resolution measurements, we exposed homogeneous coatings of crystal violet to repeated laser pulses at the above instrument conditions and measured the size of the resulting ablation craters. We note that the number of laser pulses required to generate visible ablation craters in the crystal violet coating were ~20× that used to obtain the data in Figure 5c. Images of the resulting ablation craters are provided in Figure S3. For comparison, each image includes an overlay with dimensions of the smallest resolved separation obtained using the line grating at that instrumental condition from Table 3.

Application of the Reticle to Diagnose Instrumentation Errors

In addition to determining spatial resolution, the developed synthetic pattern can be used to diagnose instrumentation errors including improper laser alignment, irregular stage movement and faulty data acquisition. In particular, we highlight the application of the reticle in diagnosing pixel striping in high-throughput MS instrumentation (SI-7). The pixel striping manifested itself by the appearance of elongated pixels, that is, pixels that were longer than the defined instrumental spatial resolution of the experiment (Figure S4). Through a series of investigations, we determined that the data acquisition step was responsible for the pixel elongations. Specifically, by varying the mass bin size at constant pixel acquisition speeds, we were able to alter the degree of pixel striping in the image. More details are provided in Supporting Information, SI-7.

CONCLUSIONS

A developed reticle consisting of patterned lines of crystal violet on a gold-coated slide provides a convenient method for measuring the beam diameter and spatial resolution for MALDI IMS. The reticle is readily prepared using a combination of soft lithography to define and control feature sizes and selective dewetting to form a patterned coating of crystal violet on a conductive substrate. Crystal violet provides a suitable material for assessing spatial resolution in IMS as it is readily ionized and easily detected under conditions employed in MALDI IMS without requiring the presence of a supplemental matrix coating. The direct imaging of the crystal violet pattern avoids delocalizing effects that could affect the pattern upon matrix application.

Various methods are presented that can be used with the reticle for measurement of spatial resolution in IMS in an objective manner. The edgespread method enables determination of the effective Gaussian-based full-width half-maximum of the incident beam by measuring the change in signal intensity from 12 to 88% across the edge of the crystal violet pattern. This approach has been generalized for use across a series of edges by convoluting the pattern of the object with a point spread function (PSF) to describe the beam profile. The line grating approach provides a direct measurement of spatial resolution. Both approaches rely on the use of defined thresholds or mathematical fitting to provide objective measurements of spatial resolution that could be developed to allow automated operation. Their implementation requires no post analysis of the reticle outside the mass spectrometer, in comparison with approaches that determine the size of ablated features by microscopy, which are often subjective. In contrast to such methods, the determined spatial resolution using the reticle relies on the analysis of obtained signal rather than on secondary factors such as beam size or ablation patterns that play a role in spatial resolution but are not direct measures of spatial resolution.

The reticle has been used to obtain measurements of spatial resolution under a variety of defined experimental conditions including different laser focus and power settings. We note that while the spatial resolution measurements using the reticle may not be directly transferrable to the spatial resolution on tissue or other specimens (due to differences in ionization efficiency, the presence of matrix, etc.), the methods described here can provide an accurate evaluation of instrument setup They further allow assessment of differences in instrument performance over time and across platforms. The determination of how the relative spatial resolution is affected as instrumental hardware and software conditions are varied can be extremely important. This has been exemplified by its use to diagnose instrumental conditions that cause unsatisfactory “pixel striping” on a MALDI TOF mass spectrometer. By providing an objective evaluation of spatial resolution, the reticle will be exceedingly useful in the development of future IMS instruments and benchmarking their performance. Future directions for this work include having feature sizes below 25 μm as needed for anticipated higher resolution IMS instruments under development.