Abstract
When estimating the effect of an exposure on a time-to-event type of outcome, one can focus on the baseline exposure or the time-updated exposures. Cox regression models can be used in both situations. When time-dependent confounding exists, the Cox model with time-updated covariates may produce biased effect estimates. Marginal structural models, estimated through inverse-probability weighting, were developed to appropriately adjust for time-dependent confounding. We review the concept of time-dependent confounding and illustrate the process of inverse-probability weighting. We fit a marginal structural model to estimate the effect of time-updated systolic BP on the time to renal events such as ESRD in the Chronic Renal Insufficiency Cohort. We compare the Cox regression model and the marginal structural model on several attributes (effects estimated, result interpretation, and assumptions) and give recommendations for when to use each method.
Keywords: Causal inference, marginal structural models, survival analysis, time-varying Cox model, time-dependent confounding, inverse-probability treatment weight, inverse-probability censoring weight, blood pressure, Cohort Studies, Kidney Failure, Chronic, Probability, Proportional Hazards Models, Renal Insufficiency, Chronic, chronic kidney disease
Introduction
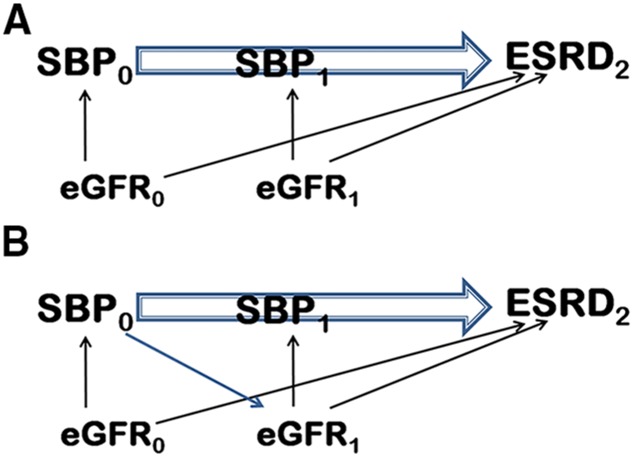
In cohort studies an exposure often changes over time. Such an exposure is called “time-dependent,” “time-varying,” or “time-updated.” It is often of interest to study the effect of a time-updated exposure on an event-type outcome. When confounders also change over time, there is a circular relationship between the exposure and confounder, with the confounder affecting the exposure and the exposure affecting subsequent values of the confounder, a situation referred to as time-dependent confounding. An example is illustrated in Figure 1, in which the effect of systolic BP (SBP) (the exposure) on ESRD is confounded by eGFR in a time-dependent fashion.
Figure 1.
Time Dependent Confounding illustrated. (A) Time-dependent confounding is absent. (B) Time-dependent confounding is present. The difference between (A) and (B) is that there is an additional arrow from SBP0 to eGFR1 in (B). It means that SBP0 is also associated with eGFR1. In other words, eGFR1 is on the causal pathway between SBP0 and ESRD2. This kind of confounding is called time-dependent confounding. For simplicity, we omitted the arrow from eGFR0 to eGFR1 and from eGFR0 to SBP1. eGFR0, eGFR at time 0; eGFR1, eGFR at time 1; ESRD2, ESRD status at time 2; SBP0, SBP at time 0; SBP1, SBP at time 1.
When time-dependent confounding exists, the estimated effects of the time-updated exposure on outcome in a Cox regression model with time-updated covariates may be biased. This is because the regression model controls for variables that are, in part, affected by earlier exposures. Thus, some of the effect is being controlled for, rather than estimated. Marginal structural models (MSMs) are designed to correctly estimate the effect of a time-updated exposure in the presence of time-dependent confounding; this is accomplished through inverse-probability weighting (IPW). This article will review the Cox regression model and the MSM model with the focus on the latter. We will compare the Cox regression model and the MSM model on several aspects, such as the effects these models are estimating, the interpretation of the results, and the key assumptions. We will also provide recommendations regarding situations in which one would use MSM versus Cox models.
Motivating Example: Time-Updated SBP and the Progression of CKD
The Chronic Renal Insufficiency Cohort (CRIC) study is a multicenter cohort study of individuals with CKD. The study enrolled 3939 individuals from seven clinical centers in the United States between 2003 and 2008. The details of the study design and participant characteristics and findings are reported elsewhere (1–3).
In the CRIC study, one of the main outcomes of interest is ESRD, for which hypertension is a common comorbidity—80% of the participants were hypertensive at baseline. To estimate the effects of SBP on ESRD, CRIC study investigators published a paper (4) in which both Cox regression model and the MSM approach were used. The paper also provided details of the rationale behind the research question.
Participants were followed up through annual clinic visits at which SBPs were measured. Other annually updated variables included eGFR, urine protein-to-creatinine ratio, diabetes mellitus, hypertension awareness, history of cardiovascular disease, body mass index, number of antihypertensive medication classes received, and angiotensin-converting enzyme inhibitor/angiotensin-receptor blocker use. The detailed definition of these variables can be found in the paper mentioned above (4).
Cox Regression Model and the MSM
The Cox regression model can be used to study the association between baseline or time-updated SBP and ESRD. The setup for the Cox regression model makes it easy to handle time-updated covariates. When baseline and time-updated exposures are included, Cox regression produces different estimates for their effects. When including only baseline exposure in the model, Cox regression is estimating the “long-term” effect. “Long term” means that we are estimating the effect of baseline exposure using all of the events across the whole length of follow-up. By contrast, the effect of time-updated exposure on the event estimated by the Cox model with time-updated exposure is “short-term,” where “short term” is defined as the interval between successive updates of exposures. For example, in the CRIC study, in which SBP was updated annually, the short term would be about 1 year. The estimation of the short-term effect is accomplished as follows: a separate Cox regression model is run for each interval, the beginning of which is defined as the point in time when the exposure was updated. The final estimate of the hazard ratio (HR) generated by the model is a weighted average of the individual HRs for each interval. Interested readers can refer to Dekker et al. (5) for more discussion on long- and short-term effects and figures to illustrate the difference between them.
The MSM differs from the Cox regression model in at least two ways. First, instead of modeling separately the effects of baseline and time-updated exposures on outcome, it models the effect of the entire history of exposure. For example, if we measure SBP at two time points (e.g., at baseline and year 1 visits) and SBP is categorized into two levels (low/high), then the history of SBP can be summarized by the four possible combinations defining four groups of patients: group 1: SBP=low at both time points; group 2: SBP=low at baseline and high at year 1; group 3: SBP=high at baseline and low at year 1; and group 4: SBP=high at both time points. The MSM is able to estimate HRs comparing any two of these groups. For example, if we treat group 1 as the reference, we can obtain three HRs comparing groups 2, 3, and 4 to group 1.
Second, the MSM correctly estimates the effects when there is time-dependent confounding. To explain how the effects estimated by the MSM differ from those estimated by the Cox regression model, we will first discuss confounding and time-dependent confounding.
Confounding and IPW
In observational studies, exposures are not randomized and there is typically confounding. We can account for the confounding by adjusting for or stratifying by those measured confounders. Alternatively, we can use the IPW approach to adjust for those confounders.
The IPW approach weights each subject by the inverse of the probability of that subject’s observed exposure. To understand this, consider an exposure that can be expressed as a yes/no variable (e.g., 1=hypertension, 0=no hypertension). The IPW approach starts by estimating the probability of having an exposure value of what is observed. The inverse of the probability is the weight assigned to each subject. For example, if a subject’s observed exposure X is 1, the weight given to the subject will be the inverse of the probability that X=1, on the basis of the subject’s confounder measurements. Similarly, if a subject’s observed exposure X is 0, the weight will be the inverse of the probability that X=0, on the basis of the subject’s confounder measurements.
Illustration of IPW When There Is Only One Confounder and One Time Point
To illustrate the IPW approach, we give an example with hypothetic data. In this example, hypertension (two levels: Yes/No) is the main exposure, ESRD (two levels: Yes/No) the outcome, and eGFR level (two levels: High/Low) the only confounder. Table 1 shows a hypothetic distribution of participants with and without ESRD, stratified by both eGFR and hypertension; Tables 2–4 depict the same data, but stratified by only one of the variables.
Table 1.
Hypothetic distribution for hypertension and ESRD stratified by eGFR level
| Confounder | Exposure: Hypertension (n, row %) | Outcome: ESRD | Total | |
|---|---|---|---|---|
| Yes | No | |||
| eGFR=High | Yes | 250 | 1000 | 1250 |
| 20% | 80% | |||
| No | 750 | 3000 | 3750 | |
| 20% | 80% | |||
| Total | 1000 | 4000 | 5000 | |
| 20% | 80% | |||
| eGFR=Low | Yes | 1250 | 1250 | 2500 |
| 50% | 50% | |||
| No | 1250 | 1250 | 2500 | |
| 50% | 50% | |||
| Total | 2500 | 2500 | 5000 | |
| 50% | 50% | |||
Table 2.
Hypothetic distribution for hypertension and ESRD without stratifying by eGFR level
| Exposure: Hypertension | Outcome: ESRD | Total | |
|---|---|---|---|
| Yes | No | ||
| Yes | 1500 | 2250 | 3750 |
| 40% | 60% | ||
| No | 2000 | 4250 | 6250 |
| 32% | 68% | ||
| Total | 3500 | 6500 | 10,000 |
| 35% | 65% | ||
Table 4.
Hypothetic distribution for eGFR and ESRD
| Confounder: eGFR | Outcome: ESRD | Total | |
|---|---|---|---|
| Yes | No | ||
| High | 1000 | 4000 | 5000 |
| 20% | 80% | ||
| Low | 2500 | 2500 | 5000 |
| 50% | 50% | ||
| Total | 3500 | 6500 | 10,000 |
| 35% | 65% | ||
From these tables, we can see that: eGFR is a confounder, as it is associated with the exposure (Table 3) and the outcome (Table 4); hypertension is not associated with ESRD when we stratify by eGFR (Table 1); and hypertension seems to be associated with ESRD if we do not control for the confounding of eGFR (Table 2).
Table 3.
Hypothetic distribution for eGFR and hypertension
| Confounder: eGFR | Exposure: Hypertension | Total | |
|---|---|---|---|
| Yes | No | ||
| High | 1250 | 3750 | 5000 |
| 25% | 75% | ||
| Low | 2500 | 2500 | 5000 |
| 50% | 50% | ||
| Total | 3750 | 6250 | 10,000 |
| 37.5% | 62.5% | ||
Now we will show how to use the IPW approach to adjust for confounding. Table 3 gives the probability that hypertension=Yes or No within each stratum of eGFR. Note that these are conditional probabilities, as they are conditional on the value of eGFR. IPW is then defined as the inverse of these conditional probabilities (Table 5).
Table 5.
Illustration of definition of inverse-probability weight
| Confounder: eGFR | Exposure: Hypertension | |
|---|---|---|
| Yes | No | |
| High | P(hypertension=Yes when eGFR=High)=25% | P(hypertension=No when eGFR=High)=75% |
| IPW=1/25%=4 | IPW=1/75%=4/3 | |
| Low | P(hypertension=Yes when eGFR=Low)=50% | P(hypertension=No when eGFR=Low)=50% |
| IPW=1/50%=2 | IPW=1/50%=2 | |
P, probability of; IPW, inverse probability weight.
We can then apply these weights to each subject according to their hypertension and eGFR values. The results are shown in Tables 6 and 7, which correspond to the upper and lower halves of Table 1 respectively—the number of subjects in each cell of Table 1 is multiplied by the weight assigned to the subjects in that cell. We can then collapse Tables 6 and 7 to get Table 8, which shows the marginal association between hypertension and ESRD after weighting. We can see that the IPW approach concludes that there is no association between hypertension and ESRD. This is consistent with the stratified results shown in Table 1.
Table 6.
Hypothetic distribution for hypertension and ESRD when eGFR level is high after applying inverse-probability weighting
| Confounder: eGFR=High | Exposure: Hypertension (n, row %) | Outcome: ESRD | Total | |
|---|---|---|---|---|
| Yes | No | |||
| Yes | 250×4=1000 | 1000×4=4000 | 5000 | |
| 20% | 80% | |||
| No | 750×(4/3)=1000 | 3000×(4/3)=4000 | 5000 | |
| 20% | 80% | |||
| Total | 2000 | 8000 | 10,000 | |
| 20% | 80% | |||
Table 7.
Hypothetic distribution for hypertension and ESRD when eGFR level is low after applying inverse-probability weighting
| Confounder: eGFR=Low | Exposure: Hypertension (n, row %) | Outcome: ESRD | Total | |
|---|---|---|---|---|
| Yes | No | |||
| Yes | 1250×2=2500 | 1250×2=2500 | 5000 | |
| 50% | 50% | |||
| No | 1250×2=2500 | 1250×2=2500 | 5000 | |
| 50% | 50% | |||
| Total | 5000 | 5000 | 10,000 | |
| 50% | 50% | |||
Table 8.
Hypothetic distribution for hypertension and ESRD after applying inverse-probability weighting
| Exposure: Hypertension | Outcome: ESRD | Total | |
|---|---|---|---|
| Yes | No | ||
| Yes | 3500 | 6500 | 10,000 |
| 35% | 65% | ||
| No | 3500 | 6500 | 10,000 |
| 35% | 65% | ||
| Total | 7000 | 13,000 | 20,000 |
| 35% | 65% | ||
Stabilized and Unstabilized Weights
We can stabilize (or equivalently, reduce) the variance in the weights derived above (called the unstabilized weights) by multiplying the unstabilized weight by the probability of observed exposure without conditioning on the confounders. Specifically, the stabilized weight is the ratio of the unconditional probability (the numerator) to the conditional probability (the denominator).
We illustrate the calculation of stabilized weights by going back to the example in Tables 1–4. The bottom row of Table 3 gives the unconditional probabilities of exposure, which are P (hypertension=yes) =37.5% and P (hypertension=No) =62.5%. Table 9 shows how to calculate the stabilized weights. We can see that the stabilized weights are distributed around 1 and have a smaller variance than the unstabilized weights.
Table 9.
Illustration of definition of stabilized inverse-probability weighting
| Confounder: eGFR | Exposure: Hypertension | |
|---|---|---|
| Yes | No | |
| High | P(hypertension=Yes when eGFR=High)=25% | P(hypertension=No when eGFR=High)=75% |
| Unstabilized IPW=1/25%=4 | Unstabilized IPW=1/75%=4/3 | |
| P(hypertension=Yes)=37.5% | P(hypertension=No)=62.5% | |
| Stabilized IPW=4×37.5%=1.5 | Stabilized IPW=(4/3)×62.5%=0.83 | |
| Low | P(hypertension=Yes when eGFR=Low)=50% | P(hypertension=No when eGFR=Low)=50% |
| Unstabilized IPW=1/50%=2 | Unstabilized IPW=1/50%=2 | |
| P(hypertension=Yes)=37.5% | P(hypertension=No)=62.5% | |
| Stabilized IPW=2×37.5%=0.75 | Stabilized IPW=2×62.5%=1.25 | |
P, probability of; IPW, inverse probability weight.
Time-Dependent Confounding
In the example given above, both the exposure and the confounder were measured at only one time point. When both exposure and confounders are time-updated, situations can arise in which we have not only the confounders affecting exposure, but also exposure affecting later confounders. In other words, the later confounders are in the causal pathway between the previous exposure and the outcome. When this happens, we say there is time-dependent confounding.
In Figure 1, we use the data from the motivating example to illustrate the concept of time-dependent confounding. Suppose here that SBP is the main exposure, eGFR is a confounder, and ESRD is the outcome. SBP at baseline (SBP0) is associated with ESRD at time 2 (ESRD2). Because eGFR at baseline (eGFR0) is a confounder, we see two arrows from it indicating that eGFR0 is associated with SBP0 and ESRD2. At time 1, we have the same situation—eGFR1 is a confounder, which means that it is associated with SBP1 and ESRD2. The difference between Figure 1, (A) and (B) is that there is an additional arrow from SBP0 to eGFR1 in Figure 1B. It means that SBP0 is also associated with eGFR1. In other words, eGFR1 is on the causal pathway between SBP0 and ESRD2. This kind of confounding is called time-dependent confounding. When there is time-dependent confounding, and we are interested in the causal effect of time-updated exposure on a time-to-event outcome, Robins et al. (6) showed that the Cox regression model with time-updated covariates may be biased.
MSMs
When time-dependent confounding exists, MSMs can be used to estimate the causal effect of a time-updated exposure on a time-to-event outcome. This model is also called the marginal structural Cox proportional hazards model (6). As this name implies, the MSM is essentially a Cox model. The main difference between MSM and the Cox regression model described earlier is that MSM is a weighted model in which time-dependent confounding is controlled via IPW.
IPW When There Are Multiple Confounders and One Time Point
In our earlier illustration of the derivation of IPWs, there was only a single binary confounder, allowing us to derive weights easily from simple crosstabulations. When there are many confounders, IPWs can be estimated via regression models. Specifically, logistic or multinomial logistic regression can be used when the exposure is binary or multilevel. When the exposure is a continuous variable, there are some difficulties in deriving the IPWs (5–7). To avoid these difficulties, one can categorize the continuous exposure. In our motivating example, we divided SBP into four categories and used multinomial logistic regression for the weight estimation.
IPW When There Are Multiple Time Points
When exposures and confounders are measured at multiple time points, IPWs are calculated at each time point, and are the inverse of the probability of observed exposure history given the confounder history. To understand this, let us extend our previous illustration such that the exposure (hypertension) and confounder (eGFR) are measured at two time points, and consider a subject with values of 1 on hypertension at both points. The IPW at time 1 for this subject is derived in the same fashion as previously described. At time 2, however, the IPW is on the basis of the probability that the subject has a value of 1 on hypertension at both time 1 and time 2 (the subject’s observed exposure history), given their values on eGFR at time 1 and time 2 (the observed confounder history). This is equivalent to the product of two probabilities: (1) the probability that the subject has a value of 1 on hypertension at time 1, given their value on eGFR at time 1; and (2) the probability that the subject has a value of 1 on hypertension at time 2, given their values on eGFR at time 1 and 2 and their value on hypertension at time 1. These conditional probability terms can be estimated via appropriate regression models.
Inverse Probability Censoring Weight and Inverse Probability Treatment Weight
When we are interested in a time-to-event outcome, typically there is censoring because of study dropout or reaching the administrative end of follow-up. Censoring can also be handled using IPW. Similar to the IPW to adjust for confounders (to avoid confusion, we now call that weight the “inverse probability treatment weight [IPTW]”), the weight adjusting for censoring (called the “inverse probability censoring weight [IPCW]”) also has unstabilized and stabilized versions.
The unstabilized IPCW is defined as the probability of staying in the study up to the current time point given the past exposure and confounder history. Similar to IPTW, we can decompose this probability into the product of conditional probability terms.
To obtain the stabilized IPCW, we multiply the unstabilized IPCW by the probability of staying in the study up to the current time point given the past exposure history. Therefore, the stabilized IPCW is also defined as a ratio. Both the numerator and the denominator are the product of a series of conditional probability terms. The numerator conditions on exposure history, whereas the denominator conditions on exposure history and confounder history. These conditional probability terms can also be estimated via appropriate regression models. Table 10 illustrates the definitions of stabilized IPTW and IPCW at multiple time points. (Table 10 also shows the unstabilized versions of these weights, because, as indicated above, they are the denominators of the stabilized versions.) The final weight at each time point is then defined as IPTW×IPCW. Weight truncation (6) can be considered when we finalize the weights.
Table 10.
Illustration of stabilized IPTW and IPCW definitions with multiple time points
| Stabilized Weights | Time 1 | Time 2 | Time 3 | |
|---|---|---|---|---|
| IPTW | Numeratora | P(X1=a1) | P(X2=a2|X1=a1) ×P(X1=a1) | P(X3=a3|X1=a1, X2=a2) ×P(X2=a2|X1=a1) ×P(X1=a1) |
| Denominatora | P(X1=a1|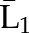 ) ) |
P(X2=a2|X1=a1, 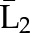 ) ×P(X1=a1| ) ×P(X1=a1|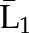 ) ) |
P(X3=a3|X1=a1, X2=a2,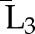 ) ×P(X2=a2|X1=a1, ) ×P(X2=a2|X1=a1, 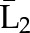 ) ×P(X1=a1| ) ×P(X1=a1|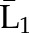 ) ) |
|
| IPCW | Numeratora | P(C1=0|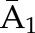 ) ) |
P(C2=0|C1=0, 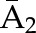 ) ×P(C1=0| ) ×P(C1=0|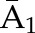 ) ) |
P(C3=0| C1=0, C2=0, 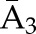 ) × P(C2=0| C1=0, ) × P(C2=0| C1=0, 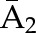 ) ×P(C1=0| ) ×P(C1=0|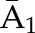 ) ) |
| Denominatora | P(C1=0|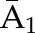 , , 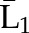 ) ) |
P(C2=0|C1=0, 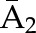 , , 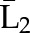 ) ×P(C1=0| ) ×P(C1=0|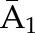 , , 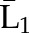 ) ) |
P(C3=0| C1=0, C2=0, 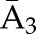 , , 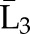 ) × P(C2=0| C1=0, ) × P(C2=0| C1=0, 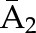 , , 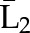 ) ×P(C1=0| ) ×P(C1=0|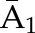 , , 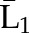 ) ) |
|
X1, X2, and X3 are the exposure; a1, a2, and a3 are the values of exposure; and the confounder history (i.e., confounder values since baseline to this time point) is 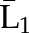 ,
,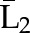 , and
, and 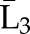 at time points 1, 2, and 3. C1, C2, and C3 are the censoring indicators at time points 1, 2, and 3 for one subject. They are defined as 1 if right-censored by that time point, and 0 otherwise.
at time points 1, 2, and 3. C1, C2, and C3 are the censoring indicators at time points 1, 2, and 3 for one subject. They are defined as 1 if right-censored by that time point, and 0 otherwise. 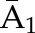 ,
,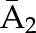 , and
, and 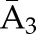 are the exposure history at time points 1, 2, and 3. IPTW, inverse probability treatment weight; P, probability of; IPCW, inverse probability censoring weight.
are the exposure history at time points 1, 2, and 3. IPTW, inverse probability treatment weight; P, probability of; IPCW, inverse probability censoring weight.
We can adjust for baseline covariates 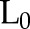 in all models.
in all models.
Discrete Failure Time Model
As illustrated previously, IPW may vary over time for each subject if we have multiple time points. No standard software for Cox regression can handle time-updated weights. One solution is to use the discrete failure time model to replace the Cox model; this is the typical practice for MSMs. Note that although the MSM is also called the marginal structural Cox proportional hazards model, in practice the Cox proportional hazards model is often replaced by the discrete failure time model which can produce equivalent estimates.
The discrete failure time model is actually a pooled logistic regression model. The first step is to divide time into small intervals. Within each small interval, we can define the values for exposure, confounders, and outcome for each subject. The time-to-event outcome is defined as a binary outcome within each interval. That is, if a subject experiences the outcome within a given interval, that subject’s outcome for that interval is defined as “Yes” and otherwise “No.” Each subject contributes either one record, or multiple records, to the analysis, depending on the number of intervals during which the subject is followed up. We then “pool” all of the records from all subjects together to fit a logistic regression model. A generalized estimating equation procedure (for example, option “repeated” in PROC GENMOD in SAS) can then be used to account for the within-subject correlation.
If we fit a logistic regression for the discrete failure time model, the odds ratios from the logistic regression model approximate the HRs from the Cox regression model more closely as the intervals used become shorter and shorter.
The discrete failure time model can naturally incorporate time-updated exposures and confounders. Time-updated weights can also be incorporated easily (e.g., using option SCWGT in PROC GENMOD in SAS).
Assumptions for Cox Regression Models and MSMs
Assumptions for Cox Regression Models
For Cox regression models, an implicit assumption is noninformative censoring. In other words, the design of the underlying study must ensure that the mechanisms giving rise to censoring of individual subjects are not related to the probability of an outcome event occurring.
For Cox regression models for baseline exposures, the second often-made assumption is the proportional hazards assumption. It means that the HR is assumed to remain unchanged over the whole length of follow-up. The Cox regression models with time-updated exposure often assume the same assumptions.
Assumptions for MSMs
MSMs share the same assumptions with the Cox regression. In addition, MSMs make additional assumptions including exchangeability, positivity, and correct specification of the weight models. Note that MSMs can explicitly handle noninformative censoring through IPCW.
The exchangeability assumption is equivalent to assuming that there is no unmeasured confounding in observational studies. By definition, this assumption is not easy to test explicitly (i.e., we cannot assess the effect of a variable we have not measured); therefore, we typically just assume that it holds.
The positivity assumption was checked in our motivating example. Specific to the example, it requires that there are observed individuals in all four SBP categories for any stratum corresponding to a particular combination of the baseline covariates. We evaluated the assumption on the basis of the large sample size and the distribution of the final weights.
For the correct specification of weight model, Cole and Hernan (7) discussed strategies in model building in more detail. In summary, the goal of model building is to achieve a balance between bias and variance. If we control for too many confounders, it might lead to violation of the positivity assumption and the variance in the final estimates might increase. If we control for too few confounders, then the estimates will be biased. Cole and Hernan (7) fitted six different weight models. For each weight model, they showed the estimate and the variance in the final model. They selected their weight model on the basis of the bias and the variance of the final estimates. Detailed discussions can be found in other papers (8).
Implementation of Cox Regression Model and MSM Approach Using CRIC Data
The details of implementing the Cox regression model and the MSM model in the motivating example are given in the Supplemental Appendix. We choose several key points to mention here.
First, we categorized the continuous exposure (SBP) into four categories (<120, 120–129, 130–139, and ≥140 mmHg) and used multinomial logistic regression models to estimate the treatment weights. These cutoff points were chosen because of clinical relevance.
Second, for the models of numerators for the IPTW and IPCW, we chose to include some baseline covariates to further reduce the variability of the weights. As a result, the causal effect estimated was not in fact unconditional (marginal), but, rather, conditional on the included covariates (7). This affects the interpretation of the model estimates from the MSM.
Third, ideally we want to draw causal conclusions for each scenario of the exposure history. In our previous illustration, we had two time points, at each of which SBP could take one of two values, high and low. It would be ideal if we can estimate three HRs from the MSM, comparing the risk of event for groups 2, 3, and 4 to the reference group (group 1). This kind of MSM, in which the number of parameters is the number of unique exposure history scenarios minus 1, is called the saturated MSM.
If the exposure is a categoric variable with k levels and we have m time points, then there are km possible exposure scenarios. In our motivating example, the exposure had four levels and there were eight time points, which means there are 48=65,536 scenarios for exposure history. Needless to say, we did not have enough observations to estimate 65,535 parameters.
When the saturated MSM is not possible, it is important to summarize the exposure history. For a binary exposure, the summary could be the exposure level at the last time point (9) or the average exposure over the follow-up period. A categoric exposure can be represented by several dummy variables. The summary could also be several variables, e.g., the average of those dummy variables. In our motivating example, we adopted this summarizing approach for a categoric exposure.
Analyses of the CRIC Data in the Motivating Example
For the data used by Anderson et al. (4), the median (25th, 75th percentiles) duration of follow-up was 5.7 (4.6, 6.7) years. The within-participant mean SBP over time ranged from 74 to 218 mmHg (mean [SD]: 128.6 [19.1]). A total of 33.1%, 19.2%, and 10.6% of the participants, respectively, had SBP at or above 120, 130, and 140 mmHg at all of their study visits. Over follow-up, 699 participants developed ESRD, corresponding to an event rate of 38.0 per 1000 person-years.
For the analysis, we fitted Cox regression models with baseline SBP and marginal structural Cox regression models. Note that the HRs from the two models had different interpretations. From the Cox regression model with baseline SBP, after multivariable adjustment, participants with baseline SBP>130 mmHg had significantly increased risk for ESRD across the whole length of follow-up compared with those whose baseline SBP was <120 mmHg. The results from the Cox regression model with time-updated covariates were not reported because that is not the appropriate approach. From the MSMs, we chose to adjust for baseline covariates which led to further reduction in the variability of the weights. The risk of ESRD for participants who had a time-updated SBP between 130 and 139 or ≥140 mmHg at all time points was 2.25–3.30 times the risk for those with a time-updated SBP always <120 mmHg (reference group; Table 11) given the adjusted baseline covariates.
Table 11.
Multivariable associations of baseline and time-updated systolic BP with renal endpoints in the Chronic Renal Insufficiency Cohort Study
| Renal Endpoint: ESRD Categoric SBP (Reference: SBP <120) | Models of Baseline SBP Hazard Ratio (95% CI) | Models of Time-Updated SBPa Hazard Ratio (95% CI) |
|---|---|---|
| SBP 120–129 | 1.06 (0.82 to 1.37) | 0.92 (0.54 to 1.57) |
| SBP 130–139 | 1.46 (1.14 to 1.89) | 2.25 (1.41 to 3.60) |
| SBP≥140 | 1.48 (1.18 to 1.85) | 3.30 (2.21 to 4.94) |
All models are stratified by clinical center, and adjusted for age, sex, race/ethnicity, education, hypertension awareness, history of cardiovascular disease, body mass index, number of antihypertensive medication classes, angiotensin-converting enzyme inhibitor/angiotensin-receptor blocker use, diabetes status, eGFR, and urine protein-to-creatinine ratio. SBP, systolic BP; 95% CI, 95% confidence interval.
Using MSMs with adjustment for all covariates listed above and study time (all time-updated with the exception of sex, race/ethnicity, education level, and hypertension awareness); HR estimates depicted using MSMs and using categorical SBP reflect the risk of the renal endpoint for selected scenarios in which SBP at all study visits consistently fell into that BP category.
When to Use Each Approach?
When one is interested in the “long-term” effect of the baseline exposure, or equivalently, wants to associate the baseline exposure with the outcomes occurring throughout the follow-up period, one can use the Cox model with baseline exposure (Table 12), adjusting for baseline covariates only.
Table 12.
Comparisons among the approaches
| Variable | Cox Regression with Baseline Exposure | Cox Regression with Time-Varying Exposure | MSM |
|---|---|---|---|
| Effects estimated | “Long-term” effects | “Short-term” effects | Effects of the whole exposure history |
| Correctly estimate effects of time-updated exposure when time-dependent confounding is present | N/A | No | Yes |
| Assumptions | Noninformative censoring, proportional hazard | Noninformative censoring, proportional hazard | Noninformative censoring, proportional hazard, exchangeability, positivity, and correct specification of weight models |
| Programming | Easy | Easy | Tedious |
MSM, marginal structural model; N/A, not applicable.
When one is interested in studying the effects of time-updated exposure on an outcome, the MSM approach is the right choice with proper adjustment of time-dependent confounding. However, if the interest is only the short-term effect of the most recent exposure on an outcome, then the Cox regression model for time-updated exposure adjusting for time-updated covariates is a reasonable approach to consider.
Discussion
In this article, we compared several approaches for analyzing time-to-event outcomes. The approaches include the Cox regression model with baseline exposure, the Cox regression model with time-updated exposure, and MSM.
We discussed the situations in which each approach is appropriate. Note that the questions that each approach can answer are different. In other words, the three approaches are estimating different effects. It is possible to compare the “long-term” and “short-term” effects from the Cox regression models with baseline exposure and those with time-updated exposure. However, the effects of time-updated exposure from the MSM are not so comparable to the Cox regression estimates. The comparison on the scale of the effects is not meaningful and the direction of the effects might be the only aspect that can be compared.
There are several limitations for MSMs. For example, MSMs cannot examine effect modification by variables measured after baseline. In addition, MSMs cannot be used when the positivity assumption is violated. Other methods, e.g., structural nested models (10,11), can be used but are more difficult to implement in practice.
There are many cohort studies collecting data on patients with CKD, and many of the exposures of interest are time-updated. Cox regression models with baseline or updated exposure are easy to implement in standard statistical packages and thus represent a convenient choice. However, the issue of time-dependent confounding must be considered when estimating the effect of whole exposure history.
MSM can estimate the effects of the whole history of exposure and can properly handle time-dependent confounding through IPW. Therefore, it should be considered in the analysis of CKD cohort studies. MSM can also be used to analyze health record data where people are seen at variable intervals. The implementation is the same as in the cohort studies in principle.
There are some difficulties in implementing MSM. First, it takes some time for the clinical audience to understand the approach and the interpretation of the estimates. Second, the programming of the MSMs can be very tedious (Table 12). To overcome these difficulties, in recent years the National Institute of Diabetes and Digestive and Kidney Diseases has sponsored the CRIC study to provide an annual research workshop (12) to the wider community of CKD researchers, and the MSM was one of the topics covered in those workshops. We hope that the CKD research community can benefit from these efforts to have a better understanding of these approaches and use appropriate methods for the analysis of CKD studies.
Disclosures
None.
Supplementary Material
Acknowledgements
Funding for the Chronic Renal Insufficiency Cohort Study was obtained under a cooperative agreement from the National Institute of Diabetes and Digestive and Kidney Diseases (U01DK060990, U01DK060984, U01DK061022, U01DK061021, U01DK061028, U01DK60980, U01DK060963, and U01DK060902). Additional funding was provided by U01DK85649 (CKD Biocon).
Footnotes
Published online ahead of print. Publication date available at www.cjasn.org.
This article contains supplemental material online at http://cjasn.asnjournals.org/lookup/suppl/doi:10.2215/CJN.00650117/-/DCSupplemental.
References
- 1.Feldman HI, Appel LJ, Chertow GM, Cifelli D, Cizman B, Daugirdas J, Fink JC, Franklin-Becker ED, Go AS, Hamm LL, He J, Hostetter T, Hsu CY, Jamerson K, Joffe M, Kusek JW, Landis JR, Lash JP, Miller ER, Mohler ER 3rd, Muntner P, Ojo AO, Rahman M, Townsend RR, Wright JT; Chronic Renal Insufficiency Cohort (CRIC) Study Investigators: The Chronic Renal Insufficiency Cohort (CRIC) Study: Design and methods. J Am Soc Nephrol 14[Suppl 2]: S148–S153, 2003 [DOI] [PubMed] [Google Scholar]
- 2.Lash JP, Go AS, Appel LJ, He J, Ojo A, Rahman M, Townsend RR, Xie D, Cifelli D, Cohan J, Fink JC, Fischer MJ, Gadegbeku C, Hamm LL, Kusek JW, Landis JR, Narva A, Robinson N, Teal V, Feldman HI; Chronic Renal Insufficiency Cohort (CRIC) Study Group: Chronic Renal Insufficiency Cohort (CRIC) Study: Baseline characteristics and associations with kidney function. Clin J Am Soc Nephrol 4: 1302–1311, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Denker M, Boyle S, Anderson AH, Appel LJ, Chen J, Fink JC, Flack J, Go AS, Horwitz E, Hsu CY, Kusek JW, Lash JP, Navaneethan S, Ojo AO, Rahman M, Steigerwalt SP, Townsend RR, Feldman HI; Chronic Renal Insufficiency Cohort Study Investigators: Chronic Renal Insufficiency Cohort Study (CRIC): Overview and summary of selected findings. Clin J Am Soc Nephrol 10: 2073–2083, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Anderson AH, Yang W, Townsend RR, Pan Q, Chertow GM, Kusek JW, Charleston J, He J, Kallem R, Lash JP, Miller ER 3rd, Rahman M, Steigerwalt S, Weir M, Wright JT Jr, Feldman HI; Chronic Renal Insufficiency Cohort Study Investigators: Time-updated systolic blood pressure and the progression of chronic kidney disease: A cohort study. Ann Intern Med 162: 258–265, 2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Dekker FW, de Mutsert R, van Dijk PC, Zoccali C, Jager KJ: Survival analysis: Time-dependent effects and time-varying risk factors. Kidney Int 74: 994–997, 2008 [DOI] [PubMed] [Google Scholar]
- 6.Robins J: Marginal structural models versus structural nested models as tools for causal inference. In: Statistical Models in Epidemiology: The Environment and Clinical Trials, edited by Halloran E, Berry D, New York, Springer-Verlag, 1999, pp 95–134 [Google Scholar]
- 7.Cole SR, Hernán MA: Constructing inverse probability weights for marginal structural models. Am J Epidemiol 168: 656–664, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cole SR, Frangakis CE: The consistency statement in causal inference: A definition or an assumption? Epidemiology 20: 3–5, 2009 [DOI] [PubMed] [Google Scholar]
- 9.Hernán MÁ, Brumback B, Robins JM: Marginal structural models to estimate the causal effect of zidovudine on the survival of HIV-positive men. Epidemiology 11: 561–570, 2000 [DOI] [PubMed] [Google Scholar]
- 10.Robins J, Tsiatis AA: Semiparametric estimation of an accelerated failure time model with time- dependent covariates. Biometrika 79: 311–319, 1992 [Google Scholar]
- 11.Vansteelandt S, Joffe M: Structural nested models and G-estimation: The partially realized promise. Stat Sci 29: 707–731, 2014 [Google Scholar]
- 12.University of Pennsylvania: CRIC Study Research Workshop, 2017. Available at: http://www.med.upenn.edu/cric/. Accessed May 22, 2017
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.