Divided pulse soliton self-frequency shift: a multi-color, dual-polarization, power-scalable, broadly tunable optical source

Abstract

A versatile, broadly tunable, power scalable, multi-line, ultrafast source is presented, the operation of which is based on combining principles of pulse division with the phenomenon of the soliton self-frequency shift (SSFS). Interferometric pulse recombination is demonstrated showing that the source can decouple the generally limiting relationship between the output power and the center wavelength in SSFS-based optical sources. Broadly tunable two- and four-color soliton self-frequency shifted pulses are experimentally demonstrated. Simultaneous dual-polarization second-harmonic generation was performed with the source, demonstrating one novel imaging methodology that the source can enable. It is expected that this source architecture will be useful for advancing current nonlinear optical imaging methodologies.

The tunability of an ultrafast source and the characteristics of the pulses it can generate (e.g., power, wavelength, temporal width) play an important role in determining its viability for use in a myriad of applications such as nonlinear imaging, materials characterization and processing, and fundamental studies involving frequency comb metrology and basic research exploring ultrafast dynamics, which rely on such sources. The phenomenon of the soliton self-frequency shift (SSFS) in optical fibers, where the center wavelength of a soliton pulse undergoes a continuous redshift via intrapulse stimulated Raman scattering, has been one method that has been extensively explored for realizing a broadly tunable ultrafast excitation source [1–8]. However, although traditional SSFS-based sources have been successful in demonstrating multi-color outputs that are widely tunable, restrictions in the achievable number of pulse outputs, and difficulty in ensuring that these pulse outputs are independently tunable, can limit application. Further, these systems suffer from a one-to-one mapping between the pulse peak power and the center wavelength, which limits the ability to scale SSFS-based sources to higher output powers. Yet, developing a broadly tunable ultrafast excitation source outputting multi-colors in a power scalable design that accounts for practical considerations such as usability, price, and size is critical for nonlinear imaging applications, materials characterizations, and general ultrafast nonlinear optical instrumentation.

To fulfill these characteristics, this Letter proposes a divided pulse soliton self-frequency shift (DPS) source and presents preliminary experimental studies demonstrating its feasibility. Such a source enables multi-color, dual-polarization, power-scalable optical outputs that are broadly tunable. Furthermore, the implementation of the DPS architecture is compact and lends itself to an ease of alignment and experimentation.

The incorporation of techniques of pulse division within the field of nonlinear optics has been a beneficial one [9–13]. Beginning with the divided pulse amplifier [14,15] and, later, the divided pulse laser [16], these techniques have provided a means for managing otherwise excessive nonlinear phase accumulations, enabling pulses to be amplified to greater powers than otherwise possible without degradation to pulse quality. Here we apply techniques of the pulse division to the SSFS. By dividing a parent pulse into N copies and coupling these copies into a suitable length of optical fiber that can support soliton formation, each pulse copy is shifted in wavelength according to its input peak power [17]. In making use of the one-to-one mapping of the input peak power to the output wavelength, the ability to quickly generate a multiple pulse output from a single parent pulse (controlled by the number of pulse divisions N), as well as the ability to broadly tune the wavelengths of these pulses (by adjusting their input peak powers), is achievable.

A schematic of the DPS architecture is shown in Fig. 1. The output from a Ti:sapphire laser (KMLabs, 30 fs, central wavelength ~845 nm, average output power ~670 mW, repetition rate 87 MHz) is used as a pump source. A pair of SF11 prisms pre-compensates for the group delay dispersion of the pulse division setup, consisting of a series of broadband-coated polarizing beam splitter (PBS) cubes arranged in a Mach-Zender-like configuration. Each division stage creates two pulses for each pulse input. These two pulses possess orthogonal polarization states and are separated by the path difference between the interferometric arms of the division stage. The relative amplitudes between the divided pulses can be controlled by adjusting the orientation of the half-wave plate preceding the division stage. The PBS cubes are chosen instead of birefringent crystals for division and recombination as they allow the overall temporal separation between pulses to be determined by the path length through air (rather than a dielectric material), ensuring that the path length between pulses is wavelength independent.

Fig. 1.

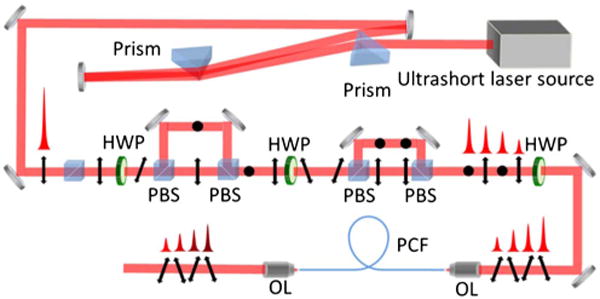
Schematic of the DPS architecture. HWP, half-wave plate; PBS, polarizing beam splitter; OL, objective lens; PCF, photonic crystal fiber.

An exemplary pulse divider for generating four pulse copies is illustrated in Fig. 1. The difference in path length between the first division stage is 100 mm, creating two pulse copies with orthogonal polarization states separated by 333 ps. In Fig. 1, the pulses with vertical or out-of-plane polarization are depicted by dots; the pulses with horizontal or in plane polarization are depicted with vertical arrows; and the pulses with a 45 deg polarization state relative to these two are represented by tilted arrows. A preceding half-wave plate controls the power ratio between the first two pulses, while the following half-wave plate rotates the polarization state of each of these two pulses before entering the second division stage, which introduces a 50 mm path length difference. As a result of passing through the entire division system, four pulse copies separated in time by 167 ps with alternating vertical and horizontal polarization states are generated. The energy of the individual pulses can be controlled through the proper adjustment of the tandem half-wave plates. The system is scalable, and further pulse copies can be added by incorporating additional PBS cube pairs. The resultant pulse train is subsequently coupled into a 1.8 m long highly nonlinear photonic crystal fiber (PCF) [NL-PM-750 with a zero-dispersion wavelength of 750 nm] for an SSFS with a 40× objective. A similar strength objective is used for collimating the fiber output.

We benchmarked the source by recording the relationship between single-pulse soliton energy and the frequency shift of the resultant output pulse [1–6]. An Andor spectrometer (SR-500i-A-R) with an InGaAs IR camera (iDus InGaAs 490A-1.7) was used to measure the output pulse spectrum. A wavelength shift from 850 to 1250 nm was achieved by varying the input pulse energy with further tuning limited by the second zero-dispersion wavelength (~1270 nm) of the PCF. The polarization of the output pulses was maintained from fiber birefringence. The average power of the first-order soliton at 1100 nm with a 28 nm bandwidth (corresponding to a 40 fs pulse) was measured at ~3 mW. The one-to-one mapping between the input pulse energy and the output wavelength presents a significant limitation on the achievable peak power and the average power at a particular wavelength for conventional SSFS architectures.

For the DPS architecture, we first generated two pulses by blocking one arm of the division system in Fig. 1. A broadly tunable two-color output was achieved by varying the input pulse energy by rotating the wave plate controlling the ratio of the pulse splitting in the second pair of PBS cubes. Figure 2(a) shows the center wavelengths of the two pulse copies as a function of the wave plate rotation angle, showing continuous tuning of the wavelength in opposite directions over a range of 300 nm spanning from 850 to 1150 nm. Independent tuning of each pulse wavelength is also possible (e.g., with a variable density neutral density filter in each polarization arm).

Fig. 2.

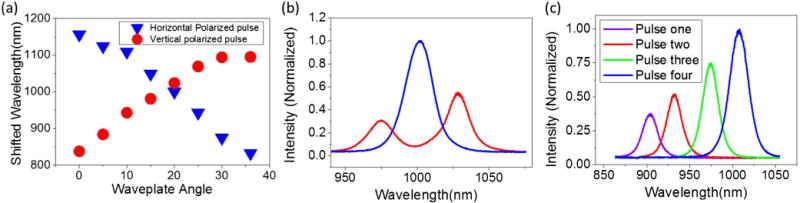
(a) Wavelength tuning of two pulse copies while changing the half-wave plate angle to modify the power ratio between two pulse copies. (b) Red line, two pulse copies with different wavelength tuning; blue line, two pulse copies with identical wavelength. (c) Four pulse copies with different wavelengths.

A typical spectrum of the two-color DPS source is shown in Fig. 2(b), depicting two ultrashort pulses centered at 975 and 1030 nm, respectively. In addition, the input pulse energy can be tuned (by adjusting the wave plate) so that the two pulse copies have identical center wavelengths [shown in Fig. 2(b)], but with twice the power as a single-pulse SSFS at the same wavelength. The temporal recombination of these two pulses is shown later in this Letter.

Four pulses were also generated by adjusting the splitting ratios in the first and second division stages. Figure 2(c) shows representative pulse spectra obtained in the multi-color DPS source with shifted center wavelengths of 905, 932, 974, and 1004 nm. The tuning of center wavelengths beyond 1 μm for the four-pulse system is limited by the power of the pump laser. It is expected that a DPS source constructed from a higher-power pump source with a longer center wavelength (enabling the use of a PCF with a larger mode area) will extend the DPS source capabilities demonstrated here even further (e.g., higher average power, four or more colors, even broader tunability).

The DPS source also provides the unique ability for power scaling pulses undergoing intraband Raman scattering. Generally, fixed experimental parameters such as the peak power and the spectral width of an input pulse, as well as the length of the fiber available in an experiment, will create a fixed relationship between the achievable output power and the wavelength of a SSFS pulse. The DPS uses pulse division and recombination techniques to effectively decouple the achievable wavelength shift from the final average and peak power achievable from a SSFS pulse.

The ability to generate a larger number of pulses is practically limited only by the available power of the pump source. Although the division technique is itself theoretically lossless, the availability of a PCF with a net anomalous dispersion of near 800 nm necessitates a smaller fiber core to provide large waveguide dispersion which translates to coupling efficiencies on the order of 30%. For this reason, along with available pump power, recombination studies were restricted to a two-pulse DPS system in order to best demonstrate source capabilities with the expectation that results will scale. A schematic of the recombination stage is shown by Fig. 3. The two pulses were shifted to a center wavelength of 1100 nm, while a 1050 nm long pass filter was employed to block higherorder solitons, supercontinuum generation, and residual pump light.

Fig. 3.

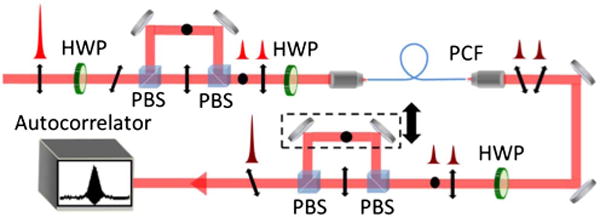
Schematic of pulse recombination setup. HWP, half-wave plate; PBS, polarizing beam splitter; PCF, photonic crystal fiber.

An autocorrelation and a spectrum of the recombined pulse are shown in Fig. 4. Figures 4(a) and 4(b) show that the deconvolved single-pulse width is 66 fs, and the recombined pulse width is 87 fs. The pulse broadening of an original 40 to 66 fs pulse is well explained by dispersive elements. The broadening between single-pulse and recombined pulse autocorrelations might be attributed to timing fluctuations between the two pulse copies. For example, a 0.3% change in soliton peak power (e.g., due to the variation in coupling efficiencies between the two pulse copies) could result in approximately a 0.5 nm change in center wavelengths and, thus, an effective time delay of 45 fs between pulse copies. This timing jitter contributed to the observed temporally broader recombined pulse width, and we anticipate that active stabilization techniques will be required for more efficient pulse recombination.

Fig. 4.

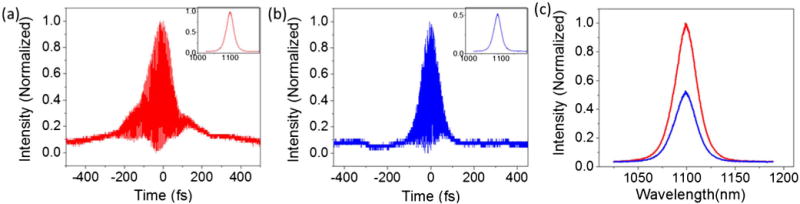
(a) Autocorrelation and spectrum of recombined pulse. (b) Autocorrelation and spectrum of individual pulse. (c) Spectrum of recombined pulse and individual pulse.

For a PM-fiber, the wavelength dependence of fiber birefringence makes power scalability realistic with only one SSFS wavelength. However, for a non-PM fiber, the DPS architecture theoretically supports power scaling for multiple colors simultaneously. In both cases, with the proper design of the division stage, after compensating for fiber birefringence (if necessary), and after rotating the polarization state of the SSFS shifted pulses to an orthogonal state, the pulses can be passed through the original division stage and picked off with a turning mirror at the desired location.

The dual-polarization, multi-color, tunable characteristics of the DPS source are here applied for polarization multiplexed imaging, in which the different polarization states are encoded by two different wavelengths. In the following, the authors present a demonstration of simultaneous dual-polarization second-harmonic generation (SHG) microscopy. It is anticipated that this method may be useful for the imaging of polarization-sensitive dynamic processes. SHG imaging probes the spatial distribution of the second-order nonlinear susceptibility tensor χ² [18,19]. Polarized SHG imaging is often necessary to reveal the rich tensorial properties of χ², which contain useful information about molecular orientation or domain structure [20–24]. As an example, a tetragonal barium titanate (BaTiO₃) crystal consisting of alternating domains is imaged [25]. A two-color DPS excitation source was used, with orthogonally polarized pulses at center wavelengths of 908 and 970 nm. Dual-polarization SHG imaging was performed by raster scanning of the sample using a focused excitation beam. By examining the SHG signal at 454 and 485 nm, polarized SHG images at both polarization states was obtained simultaneously in one scan, as shown in Figs. 5(a) and 5(b). As expected, the results reveal that the observation of a particular domain is dependent on the polarization state of the excitation beam.

Fig. 5.

SHG images of BaTiO₃ crystal domain at (a) 454 and (b) 485 nm. Images are 36 by 36 pixels with each pixel separated by 1.7 μm. The SHG signals were integrated over the respective spectra with the background subtracted.

In summary, this Letter has discussed and demonstrated the optical architecture of a multi-color, broadly tunable ultrafast optical source based on the DPS. The power scalable design of the DPS source decouples the center wavelength and the output pulse power, making it an appealing excitation source for many applications and, specifically, for nonlinear optical imaging methodologies [6,26–32]. The ability of the optical imaging instrumentation to penetrate deeper into biological tissue and to provide greater sample selectivity provide two capabilities that have enabled significant growth in the biological and biomedical fields. The DPS architecture provides a source option for meeting these aims by generating multicolor and broadly tunable pulses in a way that inherently lends itself to an ease of alignment, tunability, design, and power scalability.