Model-based functional neuroimaging using dynamic neural fields: An integrative cognitive neuroscience approach

Abstract

A fundamental challenge in cognitive neuroscience is to develop theoretical frameworks that effectively span the gap between brain and behavior, between neuroscience and psychology. Here, we attempt to bridge this divide by formalizing an integrative cognitive neuroscience approach using dynamic field theory (DFT). We begin by providing an overview of how DFT seeks to understand the neural population dynamics that underlie cognitive processes through previous applications and comparisons to other modeling approaches. We then use previously published behavioral and neural data from a response selection Go/Nogo task as a case study for model simulations. Results from this study served as the ‘standard’ for comparisons with a model-based fMRI approach using dynamic neural fields (DNF). The tutorial explains the rationale and hypotheses involved in the process of creating the DNF architecture and fitting model parameters. Two DNF models, with similar structure and parameter sets, are then compared. Both models effectively simulated reaction times from the task as we varied the number of stimulus-response mappings and the proportion of Go trials. Next, we directly simulated hemodynamic predictions from the neural activation patterns from each model. These predictions were tested using general linear models (GLMs). Results showed that the DNF model that was created by tuning parameters to capture simultaneously trends in neural activation and behavioral data quantitatively outperformed a Standard GLM analysis of the same dataset. Further, by using the GLM results to assign functional roles to particular clusters in the brain, we illustrate how DNF models shed new light on the neural populations’ dynamics within particular brain regions. Thus, the present study illustrates how an interactive cognitive neuroscience model can be used in practice to bridge the gap between brain and behavior.

1. Introduction

Although great strides have been made in understanding the brain using data-driven methods (Smith et al., 2009) to understand the brain’s complexity, human neuroscience will need sophisticated theories (Gerstner, Sprekeler, & Deco, 2012). But what would a good theory of brain function look like? Addressing this question requires theories that bridge the disparate scientific languages of neuroscience and psychology.

Turner et al. (2016) described three categories of approaches to this issue using model-based cognitive neuroscience that bridge the gap between brain and behavior by bringing together fMRI data and cognitive models (Turner, Forstmann, Love, Palmeri, & Van Maanen, 2016). The first approach uses neural data to guide and inform a behavioral model, that is, a model that mimics features of responses such as reaction times and accuracy. One example of this approach is the Leaky Competing Accumulator model by Usher and McClelland (Usher & McClelland, 2001). This is a mechanistic model for evidence accumulation, which incorporates well-known properties of neuronal ensembles such as leakage and lateral inhibition. The model provides a good fit for a range of behavioral data, for example, time-accuracy curves and the effects of the number of alternatives on choice response times. Unfortunately, as remarked by Turner et al., this mechanistic approach stops short of establishing any direct connection to the dynamics of particular neural circuits or brain areas.

The second type of approach uses a behavioral model and applies it to the prediction of neural data. One example of this approach is Rescorla and Wagner’s (1972) model of learning conditioned responses. In this model, the value of a conditioned stimulus is updated over successive trials according to a learning rate parameter. The model produces trial-by-trial estimates of the error between the conditioned and unconditioned stimuli. This measure can then be used in general linear models to detect patterns matching the model predictions within fMRI data. The method potentially allows one to identify neural processes that are not directly measureable through behavioral results (Davis, Love, & Preston, 2012; Mack, Preston, & Love, 2013; Palmeri, Schall, & Logan, 2015). However, a drawback of this model-based fMRI approach is that it does not explain cognitive states encoded by patterns of activation distributed over multiple voxels in the brain.

The last, and most difficult approach is an integrative cognitive neuroscience approach where a model simultaneously predicts behavioral and neural data. That is, the model explains what the brain is doing in real-time to generate specific patterns of fMRI and behavioral data. Turner et al. acknowledge that there are relatively few examples in this category. For instance, they highlight recent papers that use cognitive architectures such as ACT-R (‘Adaptive Control of Thought – Rational’) to capture simultaneously fMRI and behavioral data (Anderson, Matessa, & Lebiere, 1997; Borst & Anderson, 2013; Borst, Nijboer, Taatgen, Van Rijn, & Anderson, 2015). Although we agree that this approach has immense potential, this is a relatively limited example of an integrative cognitive neuroscience approach because ACT-R is not a neural process model. Thus, ACT-R does not capitalize on constraints regarding how real brains actually work.

An alternative approach that does capitalize on neural constraints was proposed by Deco et al (Deco, Rolls, & Horwitz, 2004). These researchers used integrate-and-fire attractor networks to simulate neural activity from a ‘where-and-what’ task. The model includes several populations of simulated neurons to reflect networks tuned to specific objects, positions, or combinations thereof. The authors then define a local field potential (LFP) measure from each neural population by averaging the synaptic flow at each time step. To generate a BOLD response, they convolved the LFP measure with an impulse response function. Although one version of the model was able to approximate single neuron recordings from a prior study, as well as a measured fMRI pattern in dorsolateral prefrontal cortex, other fMRI patterns from the ventrolateral prefrontal cortex were not modeled. Moreover, comparisons to fMRI data were made qualitatively via visual inspection. No attempt was made to quantitatively relate the measures. Finally, behavioral data from this study were not a central focus. Such issues are relatively common when modeling relies on biophysical neural networks due to the immense computational challenges of simulating such networks. Appropriate partitioning of the parameter space and estimation of model parameters are, in general, difficult steps of this approach (see Anderson, 2012; Turner et al., 2016).

Inspired by this work, Buss, Wifall, Hazeltine, and Spencer (2014) adapted this approach to simultaneously model behavioral and fMRI data from a dual-task paradigm (Buss, Wifall, Hazeltine, & Spencer, 2013). They first constructed a dynamic neural field (DNF) model of the dual-task paradigm reported by Dux and colleagues (Dux et al., 2009). The model quantitatively fit a complex pattern of reaction time changes over learning, including the reduction of dual-task costs over learning to single task levels. These researchers then generated a LFP measure from each component of the neural model and convolved the LFPs with an impulse response function to generate BOLD responses from the model. The DNF model captured key fMRI results from Dux et al., including the reduction of the amplitude of the hemodynamic response in inferior frontal junction in dual-task conditions over learning. Moreover, Buss et al. contrasted competing predictions of the DNF model and ACT-R, showing that changes in hemodynamics over learning predicted by the DNF model matched fMRI results from Dux et al., while predictions from ACT-R did not.

It is important to highlight several key points achieved by Buss et al. (2013). First, the DNF model simulated neural dynamics in real time. The dynamics created robust ‘peaks’ of activation that were directly linked to behavioral responses by the model, and these responses quantitatively captured a complex pattern of reaction times over learning. Second, the same neural dynamics that quantitatively fit behavior also simulated observed hemodynamics measured with fMRI. Finally, Buss et al. demonstrated the specificity of these findings by contrasted predictions of two theories. Thus, their work constitutes a notable example of an integrative cognitive neuroscience approach using a neural process model that capitalizes on constraints regarding how brains work.

The current paper builds on the above example, by formalizing an integrative cognitive neuroscience approach using dynamic neural fields. Our paper is tutorial in nature, walking the reader through each step of this model-based cognitive neuroscience framework. We extend the work of Buss et al. (2013) by (1) formalizing several steps regarding the calculation of LFPs from dynamic neural fields and the generation of BOLD predictions; (2) adding new methods to quantitatively evaluate BOLD predictions from dynamic neural field models using general linear models (GLM), inspired by other model-based fMRI approaches; and (3) adding new methods to identify model-based functional networks from group-level GLM results. These methods allow for effectively identifying where particular neural patterns live in the brain, as well as specifying their functional roles.

The paper proceeds as follows. We begin with a brief introduction to dynamic field theory. This places our model-based approach within a broader context for readers who might be less familiar with this theoretical approach. Next, we introduce the particular case study we will use throughout the paper, that is, the particular behavioral and fMRI data set that serves as the basis for the tutorial. We then discuss the DNF model that we used to capture simultaneously behavioral and neural data from this study, explaining where this model comes from and how we approached the simulation case study. The presentation will highlight key issues that theoreticians face when adopting an integrative cognitive neuroscience approach. Next, we present behavioral fits of the data and discuss strengths and limitations of the DNF model at this level of analysis.

After considering the behavioral data, we introduce a step-by-step guide to generating hemodynamic predictions from dynamic neural field models. We then discuss how to evaluate these predictions using general linear modeling (GLM). We first evaluate the model predictions at the individual level. We then move to the group level, showing how our approach can be used to identify model-based functional networks. To evaluate these networks, we compare our approach to standard fMRI analyses, highlighting examples where the DNF model sheds interesting light on the functional roles of particular brain regions. The tutorial concludes with a general evaluation of our model-based approach, highlighting strengths, weaknesses, and future directions.

2. Overview of Dynamic Field Theory

The present report introduces a tutorial on an integrative model-based fMRI approach using Dynamic Field Theory (DFT). Thus, for clarity, before explaining the integrative cognitive neuroscience approach, we start by giving a brief introduction to DFT. Readers are referred to the DFT Research Group (2015) for a thorough treatment of these ideas.

DFT grew out of the principles and concepts of dynamical systems (Gregor Schöner et al., 2015) theory initially explored in the ‘motor approach’ pioneered by Gregor Schöner, Esther Thelen, Scott Kelso, and Michael Turvey (Kelso, Scholz, & Schoner, 1988; Schöner & Kelso, 1988; Turvey, 1995). The goal was to develop a formal, neurally-grounded theory that could bring the concepts of dynamical systems theory to bear on issues in cognition and cognitive development (for discussion, see Spencer & Schoner, 2003). DFT was initially applied to issues closely aligned with the cognitive aspects of motor systems such as motor planning for arm and eye movements (Erlhagen & Schöner, 2002; Kopecz & Schöner, 1995). Subsequent work extended DFT, capturing a wide array of phenomena in the area of spatially-grounded cognition, from infant perseverative reaching (Smith, Thelen, Titzer, & McLin, 1999; Thelen, Schöner, Scheier, & Smith, 2001) to spatial category biases to changes in the metric precision of spatial working memory from childhood to adulthood (Schutte, Spencer, & Schöner, 2003; Simmering, Peterson, Darling, & Spencer, 2008). In the last decade, DFT has been extended into a host of other domains including visual working memory [VWM] (Johnson, Hollingworth, & Luck, 2008; Johnson, Spencer, Luck, & Schöner, 2009; Schneegans, Spencer, Schöner, Hwang, & Hollingworth, 2014), retinal remapping (Schneegans & Schöner, 2012), preferential looking and visual habituation ( Perone, Spencer, & Schöner, 2007; Perone & Spencer, 2008), spatial language (Lipinski, Spencer, & Samuelson, 2010), word learning (Samuelson, Jenkins, & Spencer, 2015), executive function (Buss & Spencer, 2008), and autonomous behavioral organization in cognitive robotics (Sandamirskaya & Schöner, 2010).

The dynamic field framework was initially developed to understand brain function at the level of neural population dynamics. Evidence suggests that local neural populations move into and out of attractor states, reliable patterns of activation that the neural population maintains in the context of particular inputs. For instance, when presented with visual input, neural populations in visual cortex create stable ‘peaks’ of activation that indicate that something is on the left side of the retina (Erlhagen, Bastian, Jancke, Riehle, & Schöner, 1999; Markounikau & Jancke, 2008). These local decisions—peaks—then share activation with other neural populations—other peaks—creating a macro-scale brain state. Thinking, according to DFT, is the movement into and out of these states. Behaving is the connection of these states to sensorimotor systems. Learning is the refinement of these patterns via the construction of localized memory traces and connectivity between fields. Development is the shaping of neural activation patterns step-by-step through hours, days, weeks, and years of generalized experience.

Formally, dynamic neural field models are in a class of bi-stable neural networks first developed by Amari (Amari, 1977), and then studied theoretically and computationally by many research groups over last two decades (Bressloff, 2001; Coombes & Owen, 2005; Curtu & Ermentrout, 2001; Ermentrout & Kleinfeld, 2001; Jirsa & Haken, 1997; Laing & Chow, 2001; Wilson & Cowan, 1973; Wong & Wang, 2006). Activation in these networks--called ‘cortical fields’--is distributed over continuous dimensions—space, movement direction, color, and so on. Importantly, patterns of activation can live in different “attractor” states: a resting state; an input-driven state where input forms stabilized “peaks” of activation within a cortical field, but peaks go away when input is removed; and a self-sustaining or working memory state where activation peaks remain stable even in the absence of input. Movement into and out of these states is assembled in real-time depending on a variety of factors including inputs to a field. Critically, though, activation patterns can “rise above” the current input pattern via recurrent interactions: activation can be in a stable “on” state where subsequent inputs are suppressed. That said, the “on” state is still open to change: in the presence of continued input, the network might “update” its decision to focus on one item over another. This points toward flexibility—how activation patterns can go smoothly and autonomously from one stable state to another.

To date, several strengths of DFT are evident. First, DFT provides a predictive language to understand both brain and behavior. DFT has been used to test specific predictions about early visual processing, attention, working memory, response selection, and spatial cognition at behavioral and brain levels using multiple neuroscience technologies (Johnson, Spencer, Luck, & Schöner, 2009; Valentin Markounikau, Igel, Grinvald, & Jancke, 2010; Schneegans et al., 2014; Schutte et al., 2003). Second, DFT scales up. Across several papers, we have demonstrated, for instance, that ‘local’ theories of attention, working memory, and response selection can be integrated in a large-scale neural model that explains and predicts how humans represent objects in a visual scene - see Schoner, Spencer & the DFT Research Group, 2015. Third, DFT is well positioned to bridge the gap between brain and behavior, simultaneously generating real-time neural population dynamics and responses that mimic behavior, often in quantitative detail (Buss et al., 2013; Erlhagen & Schöner, 2002).

The neural grounding of DFT has been investigated using both multi-unit neurophysiology (Bastian, Riehle, Erlhagen, & Schöner, 1998; Erlhagen et al., 1999) and voltage-sensitive dye imaging (Markounikau, Igel, Grinvald, & Jancke, 2010). Data from these studies demonstrate that DFT can capture the details of neural population activation in the brain and generate novel, neural predictions (Bastian, Schöner, & Riehle, 2003; Markounikau et al., 2010). Thus, the neural grounding of DFT extends beyond mere analogy. Rather, DFT implements a set of formal hypotheses about how the brain works that can be directly tested using neuroscience methods. It was the success of this framework at capturing the details of neural population dynamics in the brain that encouraged us to consider the mapping between neural population dynamics and the BOLD signal measured with fMRI. The integrative cognitive neuroscience approach detailed here is a critical step in this new direction.

3. Introduction to the case study

To illustrate the model-based approach to fMRI using DFT, we have to select a specific case study. This anchors the modeling approach to a specific task, a specific set of behaviors, and a specific fMRI data set. Here, we use as case study the neural and behavioral dynamics that underlie response selection. Response selection has been studied using DFT for almost two decades at both behavioral (Christopoulos, Bonaiuto, & Andersen, 2015; Erlhagen & Schöner, 2002; Klaes, Schneegans, Schöner, & Gail, 2012; McDowell, Jeka, Schöner, & Hatfield, 1998, 2002; Schutte & Spencer, 2007) and neural levels (Bastian et al., 1998; Erlhagen et al., 1999; McDowell et al., 2002). Thus, there is a rich history to build on. Furthermore, the last decade has seen an explosion of research examining the behavioral and neural bases for response selection and inhibition using fMRI. This stems, in part, from the clinical relevance of this topic: poor performance on response selection tasks has been linked to performance deficits in atypical populations (Kaladjian et al., 2011; Monterosso et al., 2005; Pliszka, Liotti & Woldorff, 2000).

In a recent paper (Wijeakumar et al., 2015), we contributed to this fMRI literature by examining whether response selection and inhibition areas in the brain are active primarily on inhibitory trials as some researchers have claimed (Aron, Robbins, & Poldrack, 2014), or, alternatively, whether response selection and inhibition areas are active when salient events occur, regardless of whether these events require inhibition per se (Erika-Florence, Leech, & Hampshire, 2014; Hampshire & Sharp, 2015). To contrast these views, we had participants complete a set of classic inhibitory control tasks in an MRI scanner. We varied whether events were excitatory (i.e., required a motor response) or inhibitory, and whether events were frequent or infrequent. We were particularly interested in the brain response on infrequent, excitatory trials. The inhibitory network view suggests that key areas of a fronto-cortical-striatal network should show a weak response on these trials because no inhibition is required. The salience network view suggests the opposite--that there should be a robust fronto-cortical-striatal network response because infrequent events stand out as salient.

We used the data from Wijeakumar et al. (2015) as our case study in the present report. We do this for two reasons. First, this is a convenient choice because we have the full dataset, we are aware of all the processing details, and so on. Second, although there are numerous other studies we could have picked, this one has some unique features. Most notably, the study of Wijeakumar et al. has parametrically manipulated several factors in the same task. This is good fodder to probe the potential of our model-based approach because there is a lot of systematic patterning in the data to capture.

In the present report, we focus on data from one of the tasks from Wijeakumar et al. (2015)--a Go/Nogo (GnG) task. Participants were asked to press a button (Go) when they saw some stimuli and withhold (Nogo) their response when another set of stimuli were presented. Stimuli varied in color but not in shape. Go colors were separated from Nogo colors by 60 degrees in a uniform hue space such that directly adjacent colors were associated with different response types.

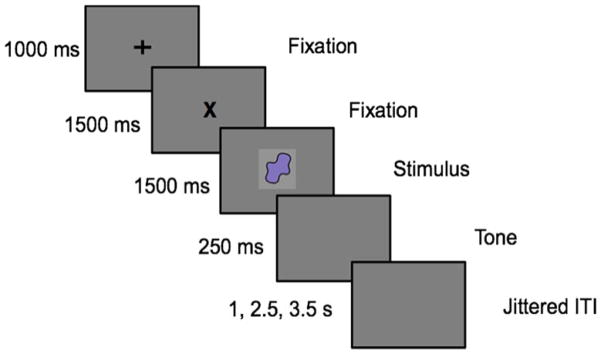
Each trial started with a fixation cross presented at the center of the screen for 2500 ms, followed by the stimulus presentation at the center of the screen for 1500 ms (see Figure 1). The participants were advised to respond to the visual stimuli as fast as possible. If a response was not detected on the Go trials, then a message saying ‘No Response Detected’ was presented on the screen for 250 ms. Inter-trial intervals were jittered between 1000, 2500 or 3500 ms presented on 50%, 25% or 25% of the trials respectively.

Figure 1.

Experimental design for the GnG task.

Two parametric manipulations were carried out – a Proportion manipulation and a Load manipulation. For the Proportion manipulation (at Load 4), the number of Go and Nogo trials were varied as follows. In the 25% condition, 25% of the trials were Go trials and 75% of the trials were Nogo trials. In the 50% condition, 50% of the trials were Go trials and 50% of the trials were Nogo trials. In the 75% condition, 75% of the trials were Go trials and 25% of the trials were Nogo trials.

For the Load manipulation, 50% of the trials were Go trials and the rest were Nogo trials. In the Load 2 condition, one stimulus (color) was associated with a Go response and another with the Nogo response. In the Load 4 condition, two stimuli were associated with a Go stimulus and two other stimuli with a Nogo response. In the Load 6 condition, three stimuli were associated with the Go response and three stimuli with a Nogo response. Participants completed five runs in the fMRI experiment: Load 2, Load 4 (also called Proportion 50), Load 6, Proportion 25 and Proportion 75. Each run had a total of 144 trials. The order of the runs was randomized.

fMRI data were collected using a 3T Siemens TIM Trio magnetic resonance imaging system with a 12-channel head coil. An MP-RAGE sequence was used to collect anatomical T1-weighted volumes. Functional BOLD imaging was acquired using an axial 2D echo-planar gradient echo sequence with the following parameters: TE=30 ms, TR=2000 ms, flip angle= 70°, FOV=240Å~240 mm, matrix=64Å~64, slice thickness/gap=4.0/1.0 mm, and bandwidth=1920 Hz/pixel.

The task was presented to the participant inside the scanner through a high-resolution projection system connected to a PC using E-prime software. The timing of the stimuli being presented was synchronized to the MRI scanner’s trigger pulse. Head movement was prevented by inserting foam padding between the particpants’ heads and the head coil. Participants’ responses were obtained through a manipulandam strapped to the participants’ hand.

Data were analyzed using Analysis of Functional NeuroImages (AFNI) software (http://afni.nimh.nih.gov/afni). DICOM images were converted to NIFTI images. Voxels containing non-brain tissue were stripped from the T1 structural image. The T1 structural image was aligned to the Talaraich space. Then, EPI data was transformed to align with the T1 structural scan in the subject-space. Transformation matrices across both these steps were concatenated and applied to the EPI data to move it from subject-space to Talaraich space. Six parameters for head movement were estimated X, Y, Z, pitch, roll, and yaw directions) for use as regressors to account for variance in the BOLD signal associated with motion. Spatial smoothing was performed on the functional data using a Gaussian function of 8mm full-width half-maximum.

Results showed a robust neural response in key areas of the fronto-cortical-striatal network on infrequent trials regardless of the need for inhibition (Wijeakumar et al., 2015). Interestingly, the number of stimulus-response (SR) mappings modulated the neural signal across multiple brain areas, with a reduction in the BOLD signal as the number of SR mappings increased. We suggested that this might reflect competition among associative memories of the SR mappings as the SR load increased, consistent with recent proposals (Cisek, 2012) and modeling work by Erlhagen and colleagues (Erlhagen & Schöner, 2002).

In the next section, we present an overview of a dynamic neural field model designed to capture both the behavioral and neural dynamics that underlie performance in this study. Note that we use the model primarily in a tutorial fashion--to illustrate the model-based fMRI approach using dynamic neural fields. Critically, we make no claims that this is an optimal model of response selection. There are other more comprehensive models of inhibitory control in the literature. For instance, Wiecki and Frank’s model of response inhibition unifies many findings from the inhibitory control literature and has simulated key aspects of neural data from both neurophysiology and evoked-response potentials (Wiecki & Frank, 2013). We think our model has some interesting strengths relative to Wiecki and Frank’s model that we highlight below, but it also has some interesting limitations that we also highlight. These strengths and limitations are useful in a tutorial style paper like this to illustrate the range of issues one must consider when pursuing an integrative cognitive neuroscience model.

4. A dynamic neural field model of response selection

A key question one must ask when modeling even the most basic of tasks is what perceptual, cognitive, and motor processes one should try to capture in the model and what aspects should be left out in the interest of simplicity. In mathematical psychology, such issues are central given that model simplicity versus complexity--often indexed by the number of free parameters--is a key dimension along which models are compared. The GnG task is relatively simple; thus, we can articulate the set of possibilities. One could consider modeling the following: (1) the early visual processes that perceive and encode colors presented in the visual field; (2) the attentional processes that selectively attend to the presented color; (3) the memory and visual comparison processes that identify whether the presented color is from the Go or Nogo set; (4) the response selection processes that compete to drive a Go or Nogo decision; (5) the motor planning processes that are activated, either partially or wholly by the response selection system; and (6) the motor control processes that do the job of pushing the response button in the event of a Go decision (whether correct or not).

In cognitive modeling of the GnG task, models typically focus on the heart of this list--the response selection processes. Classic race-horse models (Boucher, Palmeri, Logan, & Schall, 2007; Logan, Yamaguchi, Schall, & Palmeri, 2015), for instance, capture many aspects of reaction time (RT) distributions from the GnG task using an elegant set of simple equations. These models have also generated interesting neural predictions. More complex models have also considered aspects of the memory and visual comparison processes that underlie performance in this task (Wiecki & Frank, 2013). The Wiecki and Frank model, for instance, used a set of SR associations in a complex neural network to implement these memory and visual comparison processes. This added complexity was justified because their goal was to mimic properties of the neural systems that underlie response selection.

Our goal in the present report was to build a neural dynamic model of response selection that captures the processes that underlie the GnG task from perception to decision--to create an integrated neural architecture to capture processes 1–4 in the list above. (Links to motor planning and control systems have been studied extensively with DFT, but we opted for simplicity on this front; for discussion, see Schöner et al., 2015; Bicho & Schöner, 1997.) We did this for two central reasons. First, we have proposed and tested models that capture the full sweep of processes 1–4 in the domain of VWM; thus, we wanted to examine whether the processes that underlie performance in VWM tasks might also play a role in response selection. This is important theoretically, because it probes the generality of a theory--can a theory instantiated in a particular architecture and designed to capture data from one domain, quantitatively capture data from a different domain of study? If so, this suggests that the model has the potential to integrate findings across domains provided, of course, that the model is constrained and unable to capture findings that are not present in those domains. Note that answering this question requires deep study of the theory in question. We do not do that work here; rather, the present paper is merely a first step in this direction.

The second reason stems from Buss et al. (2013) where we used a dynamic neural field model to simulate fMRI data from a dual-task paradigm. In that project, we discovered that non-neural inputs to the model--for instance, a perceptual input applied directly to a higher-level processing area--often dominated the neural activation patterns, thereby dominating the model-based MRI signals as well. This suggests that it is important to embed the neural processes of interest within a fully neural system if you want to capture neural dynamics in a reasonable way. Concretely, this means that we had a priori reasons for simulating early perceptual and attentional processes in the model, even though most models do not do this in the interest of simplicity.

4.1 Conceptual overview and model architecture

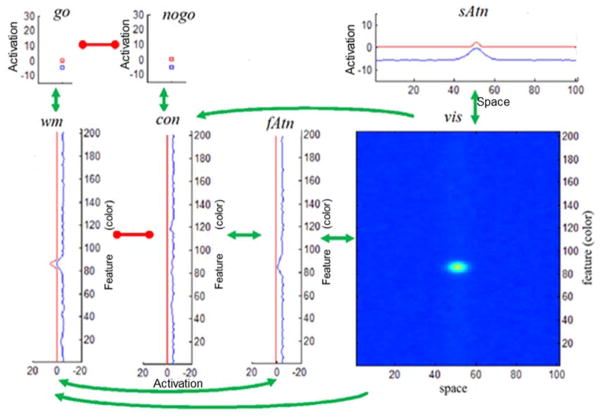
With that background in mind, Figure 2 shows the architecture of the model. This model is an integration of several models developed to simulate findings from VWM tasks (Johnson et al., 2009; Johnson et al., 2009; Schneegans et al., 2014; Schöner et al., 2015), consistent with our goal of asking whether a model of VWM can generalize to a response selection task. We describe the architecture in detail below, pointing out links to prior work to justify why we have used this particular architecture here. Note that each element in Figure 2 is a dynamic neural field. We provide the full mathematical specification of a dynamic neural field in the next section.

Figure 2.

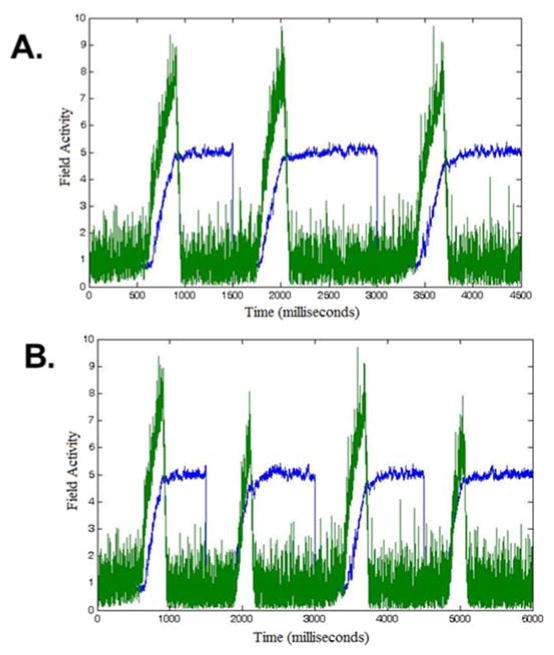
Architecture of the GnG DNF model. Seven sub-networks are included: (i) the visual field, vis; (ii) the spatial attention field, sAtn; (iii) the feature attention, fAtn; (iv) the contrast field, con; (v) the working memory field; wm; (vi) the go and (vii) nogo nodes. The neural fields are coupled by uni- or bi- directional excitatory (green) or inhibitory (red) connections. Within each field, the activation variable u(x,t) at a given time instance t = t̃ is plotted in blue. Field output g(u(x,t)) at t = f is in red. The range [−20,20] (horizontal axis for fAtn, con, wm), or [−15,15], [−15,30] (vertical axis for sAtn, go, Nogo) show values taken by activations and field outputs. Feature (color) and space dimensions have a span of 204 units (vertical axes in the lower panels) and 101 units (horizontal axes in upper and lower right panels) respectively.

The model has a visual field in the lower right panel that mimics properties of early visual cortical fields (Markounikau, Igel, Grinvald & Jancke, 2008). The visual field is composed of neural sites receptive to both color (hue) and spatial position. Inputs into this field build localized ‘peaks’ of activation in the two-dimensional field that specify the color of the stimulus and where it is located. These peaks, in turn, drive activation--in parallel--in the fields along a ventral feature pathway shown in the bottom row of Figure 2 (see fAtn, con, wm) and in a dorsal pathway in the top right panel (see sAtn). Two of these fields are ‘winner-take-all’ attentional fields that selectively attend to the color of the presented item (feature attention or fAtn) or its spatial position (spatial attention or sAtn). These fields do not have much to do in the GnG task because only a single item is presented centrally in the visual field; they are included here for continuity with previous models (Schneegans et al., 2014; Schöner et al., 2015) and to pass neurally-realistic inputs to the other cortical fields.

The more interesting fields are ‘higher up’ in the ventral pathway, where the model must decide whether the presented color is from the Go set or the Nogo set. This requires some form of memory--the system has to remember the details of the Go and Nogo set (see Logan et al., 2015 for evidence that the Nogo set is remembered)--and some form of visual comparison--the system has to visually compare the hue value of the presented color to the memorized options. The reciprocally inhibitory architecture instantiated in the working memory (wm) and contrast (con) fields implements this visual comparison process (see Johnson et al., 2009; Johnson et al., 2009). This piece of the architecture has been tested in several previous studies including tests of novel behavioral predictions (see Johnson et al., 2009). Moreover, this core approach to visual comparison has been generalized to visual comparison tasks in infancy as well (Perone & Spencer, 2013; Perone & Spencer, 2013, 2014). To this, we add a memory trace mechanism that remembers the colors previously consolidated in working memory (mem_wm) and the colors previously identified as ‘contrasting’ with the go set in the contrast field (mem_con) (Lipinski, Schneegans, Sandamirskaya, Spencer, & Schöner, 2012; Perone, Simmering, & Spencer, 2011; Schutte & Spencer, 2002).

The final piece of the architecture implements the decision process. Here, we have implemented two dynamical nodes--localized neural populations (Schöner et al., 2015) -- that compete in a winner-take-all manner to make a Go or a Nogo decision. The go node receives the summed activation from the working memory layer. Conceptually, if the working memory layer detects a match between the remembered set of Go colors (in the memory trace) and the current color detected in the feature attention and visual fields, this layer will build a peak of activation, consolidating the item in working memory and passing strong activation to the go node (Figure 3A). Alternatively, if the contrast layer detects a match between the remembered set of Nogo colors--the items that contrast with the Go set--and the current color detected in the feature attention and visual fields, this layer will build a peak of activation and send strong activation to the nogo node (Figure 3B). Conceptually, the winner in the race between Go and nogo nodes would then drive activation in the motor system (which we do not implement here).

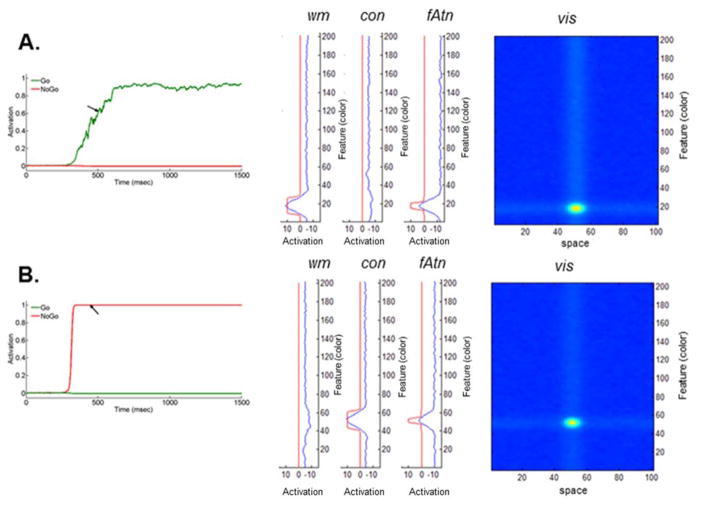
Figure 3.

Network state of the DNF model at time instance t̃ approximately 500 ms after stimulus onset, during: (A) Go task and (B) Nogo task (only vis, fAtn, con, wm are shown). Time evolution of the output of go (in green) and Nogo (in red; left panel) nodes is also shown. Time t̃ is indicated by the black arrow. Simulations used parameters from Appendix A (see Model 1 and Load 2 condition).

In the section below, we provide a more formal treatment of the dynamic neural field model. We also walk through an example to illustrate the neural population dynamics in the model that give rise to an in-the-moment decision to make a Go decision or to inhibit responding via a Nogo decision.

4.2 Formal specification of the model and exemplary simulations

The model consists of several dynamic neural fields (DNFs) that compute neural population dynamics u_j according to the following equation (Amari, 1977; Ermentrout, 1998):

$${\tau }_e{\stackrel{.}{u}}_j(x,t)=-u_j(x,t)+h_j+[c_j\ast g_j(u_j)](x,t)+\sum _k[c_{jk}\ast g_k(u_k)](x,t)+{\eta }_j(x,t)+s_j(x).$$ (4.1)

The activation u_j of each component is modeled at high temporal resolution (millisecond timescale) with time constant τ_e. It assumes a resting level h_j and depends on lateral (within the field) and longer range (between different fields) excitatory and inhibitory interactions, c_j * g_j(u_j) and c_jk * g_k(u_k) respectively. These are implemented by convolutions between field outputs g(u(x,t)) and connectivity kernels c(x) with the latter defined either as a Gaussian function or as the difference of two Gaussians (“Mexican hat” shape). The temporal dynamics of the neural activity is also influenced by external inputs s_j and it is non-deterministic due to noise η_j

The activation u(x,t) is distributed continuously over an appropriate feature space x such as color or spatial position (Figure 2 – blue curves). Then the field output, g(u(x,t)), is computed by the sigmoid (logistic) function g(u) = 1/(1 + Exp[−βu]) with threshold set to zero and steepness parameter β (Figure 2 – red curves). Therefore, g(u) remains near zero for low activations; it rises as activation reaches a soft threshold; and it saturates at a value of one for high activations. Excitatory and inhibitory coupling, both within fields and among them, promote the formation of localized peaks of activation in response to external stimulation. In our model, any above-the-threshold activation peak is interpreted as an experimentally detectable (via neural recordings) response of that particular neural field to a stimulus.

The architecture of the dynamic neural field model includes the seven fields shown in Figure 2. (For details on field equations and parameter values, see Appendix A.) A time snapshot of the dynamics of the DNF model during a Go/Nogo task is shown in Figure 3. (The time instance t̃ is approximately 500 ms after stimulus onset, and it is indicated on the graph by a black arrow).

Figure 3A illustrates the network state of the DNF model at time t̃ during the Go task. The parameter values used in simulations are listed in Appendix A (Model 1 for Load 2 condition). Shortly, when a Go color is presented (duration of stimulus is 1500 ms), an activation peak is built in the visual field, vis. This induces a peak in the working memory field, wm, and a weak peak in the feature attention field, fAtn (curves in blue). Then, the peak in wm leads to an increase in activation of the go node (Figure 3A; in green). In addition, due to inhibition from wm that dominates excitation received from vis, the activity of the contrast field, con, is lowered at the location of the Go color. At some time between 400 and 500 milliseconds after stimulus onset, the activity of the go node crosses the threshold, that is, its output function is greater than 0.5 (see left panel; in green). This is caused by the formation of a strong peak in wm. In addition, the peak in fAtn becomes stronger and a sub-threshold hill forms in con as well. In the interval of time between the response (reaction time RT~ 450 ms) and end of the trial (1500 ms), the activity peaks in vis, fAtn, con and wm stabilize. Importantly, the hill in con remains sub-threshold. Also, note that the activity of the go node reaches saturation.

Figure 3B shows the network state of the DNF model at time t̃ during the Nogo task. In this case, the Nogo color induces activation of the visual field, vis. This, in turn, increases activation in the contrast field, con, at the corresponding color coordinate along the feature space. A sub-threshold hill in fAtn forms as well, and wm is locally inhibited. Then, later during the trial (e.g. at time t̃), the activation of the nogo node has crossed its threshold. The peak in con becomes stronger and stabilizes, and field fAtn shows supra-threshold activity. At the Nogo color location in wm, the activity is inhibited. Approaching the end of the trial, the activity stabilizes in vis, fAtn, con and wm, the peak in wm remaining sub-threshold. Note that the nogo node stays ‘on’, while the go node remains inactive.

5. Simulating behavior with the dynamic neural field model

When contrasted with cognitive models, the dynamic neural field model in Figure 2 is complex. Each field has several parameters that need to be ‘tuned’ appropriately to get the model to perform in a manner that is consistent with our hypotheses about how response selection works. When contrasted with biophysical neural network models, however, the dynamic neural field model is relatively simple--there are fewer neural sites and far fewer free parameters. Along this dimension of complexity, therefore, DFT sits somewhere in the middle. That is by design. We contend that using neural process models is critical in psychology and neuroscience because this opens the door to important constraints for theory from both behavioral and neural measures--constraints readily apparent when one tries to construct integrative cognitive neuroscience models. In our view, these constraints justify the complexity. At the same time, we think it is important to add just the right amount of complexity. Data from neurophysiology suggest to us that perception, cognition, and action planning live at the level of neural population dynamics, and not at the biophysical level per se (for discussion, see (Gregor Schöner et al., 2015). Thus, we contend that the added detail from biophysical models is not critical if the goal is to bridge the gap between brain and behavior.

Of course, the downside to the added complexity introduced by dynamic neural field models is that fitting data to behavioral and neural data becomes harder and a bit more subjective in nature. This is not to say that DFT cannot achieve quantitative fits--that is certainly still a goal. Rather, the subjective sense of DFT comes from the fact that it is rarely possible to search the full parameter space of a dynamic neural field model. Consequently, many of the issues that are central to mathematical psychology and many of the tools that are used to evaluate model fits (Turner et al., 2016) are difficult, if not impossible, to apply to dynamic neural field models (Samuelson et al., 2015).

Critically, however, fitting dynamic neural field models to data is not an unconstrained free-for-all. Rather, constraints come from multiple sources. First, the neural dynamics in the model must reflect our understanding of how brains work. Thus, we would rule out parameters that give rise to pathological neural states. For instance, if excitatory neural interaction strengths in one of the cortical fields are too strong, input to the field will build a peak that grows out of control--the model has a seizure. By contrast, if excitatory neural interaction strengths are too weak, no peaks will build--the model will remain in a sub-threshold state.

Second, parameters must be tuned such that the neural dynamics reflect our conceptual theory of how the model should behave in the task. Concretely, this means that the right sequence of peaks emerges during the course of a trial to give rise to the right type of behavior (in this case, the generation of a Go or Nogo decision). Formally, this means that the sequence of bifurcations in the model must be correct. For instance, the following should hold: (1) peaks in the working memory and contrast fields should not build spontaneously from a memory trace; (2) peaks in the working memory and contrast fields should be influenced by the formation of peaks in feature attention (that is, the parallel input from the visual field should not be too strong); and (3) the Go and Nogo competition should be influenced by sub-threshold activation in the working memory and contrast fields as decision-making unfolds.

The third category of constraint comes, of course, from the details of behavioral data. In the GnG task, these constraints are relatively modest since the participant only responds on Go trials. Nevertheless, if one considers RT distributions rather than just means, this can be relatively constraining. For instance, Erlhagen and Schoner fit the details of response distributions from several response selection paradigms (Erlhagen & Schöner, 2002). This is possible with dynamic neural field models because such models are stochastic, and they generate measurable behaviors on every trial (e.g., the formation of a stable Go or Nogo decision). Moreover, relatively complex models as the one used here generate complex non-linear patterns through time--for instance, a sequence of peak states across fields, which can amplify stochastic fluctuations leading to macroscopic behavioral differences across conditions. Further behavioral constraints emerge when one considers response distributions from multiple studies. Here, the goal would be to capture the quantitative details of behavioral responses from multiple studies, ideally without any modification to model parameters. This has been achieved in several notable cases (Buss & Spencer, 2014; Erlhagen & Schöner, 2002; A.R. Schutte & Spencer, 2002).

Here, our goals were more modest--we did not optimize the quantitative fit to the behavioral data. Rather, we pursued a more iterative parameter fitting approach. First, we fit the mean reaction times with the dynamic neural field model, and made sure the variance in the model was in the right ballpark. We refer to this as Model 1 (see Appendix A). As readers will see, our fits to the standard deviations could have been better; however, we did not optimize the model on this front. Rather, we pushed forward to evaluate the quantitative fMRI fits first. Data from these fits revealed that Model 1 did not quite outperform the quantitative fit provided by a Standard GLM analysis -- the ‘gold standard’ statistical model we set a priori. We then examined the model’s neural data, focusing on the ways in which the model’s neural dynamics differed from the neural dynamics evident in the fMRI data (see Wijeakumar et al., 2015). This led to new insights into how we had the model parameters ‘tuned’ and prompted a second round of behavioral fits targeting more competitive neural interactions. This resulted in a second set of parameters--Model 2 (see Appendix A)--that fit the behavioral data relatively well and fit the fMRI data better than Model 1. This illustrates how an interactive cognitive neuroscience approach can be used in practice to bridge the gap between brain and behavior.

5.1 Simulation methods

Before turning to the details of the behavioral fits, we provide a few more details about the simulation method. All numerical simulations were performed using the COSIVINA simulation package (available at www.dynamicfieldtheory.org). This package allows one to construct dynamic neural field architectures relatively quickly, along with a graphic user interface that enables evaluation and ‘tuning’ of the model in real time (see Figures 2–3). The same simulator can then be run in ‘batch’ mode to iterate the model across many trials, recording responses that can be evaluated relative to empirical data. The COSIVINA package also includes a new toolbox for generating local field potentials directly from the model at the same time that the model is simulating the experimental task. Thus, the model is truly an integrative cognitive neuroscience model, generating behavioral and neural data (with millisecond precision) simultaneously.

5.1.1 Parameter fitting in Model 1

We adopted the following approach when tuning model parameters to arrive at Model 1. First, we made a simplification of the model. Initial simulations with a dynamic memory trace in both the working memory and contrast fields showed that the memory trace dynamics conformed to expectations based on previous work (Buss et al., 2013; Erlhagen & Schöner, 2002; Lipinski et al., 2010). In particular, memory traces were stronger in the Load 2 condition and weaker in the Load 6 condition. This occurs because each color is presented more often over trials in Load 2. Similarly, memory traces were stronger for Go stimuli in the Proportion 75% condition and weaker in the 25% condition. Again, this mimics the frequency of stimulus presentation. Although these memory trace--or learning--dynamics are fundamentally interesting, they also make simulation work more complex because one must simulate a variety of stimulus presentation orders to obtain robust estimates of learning effects. Given that such learning effects--in both behavioral and fMRI data--were central to our previous work using an interactive model-based fMRI approach (Buss et al., 2013), we opted to simplify the learning dynamics here. Thus, instead of simulating memory traces dynamically over trials, we used static memory traces, that is, the memory trace inputs were fixed for each condition to reflect the properties revealed by these initial simulations (see equation A.17 and Table A.4.1 in Appendix A, for details).

The next objective was to find a set of parameters that quantitatively captured data from the Load 2 condition. We started with parameters from Schöner, Spencer and the DFT Research Group (2015; Chapter 8), and adjusted the model parameters to approximate the right behavior from the Load 2 condition. For instance, connection strengths between the go node and wm field and nogo node and con field were tuned. The strength of the memory trace inputs into the wm and con fields for Go and Nogo trials respectively, were tuned as well.

Once the model captured the reaction times for Go trials at Load 2, the next step was to capture reaction times for the Load 4 and Load 6 conditions. Here, we hypothesized that increasing the Load in the task would increase competition among memory traces, slowing down the time it takes to build a peak in the working memory and contrast fields and yielding slower reaction times (Erlhagen & Schöner, 2002), Hence, we adjusted the strength of the memory trace inputs in both wm and con fields without modifying any other parameters. (See Table A.4.1 in Appendix A; third column shows how the strength of the memory trace inputs for wm and con is varied across different conditions.) We then tested whether the model was able to capture the increase in reaction times observed as memory Load increased.

For the Proportion manipulation, Proportion 50% corresponded to Load 4 and so its parameters were used as an anchor to fit the reaction times from Proportion 25% and Proportion 75%. Here, we hypothesized that as the number of Go trials increased, the strength of the memory trace for Go trials would also increase. Likewise, as the number of Go trials decreased, the strength of these memory traces would decrease. (Table A.4.1 in Appendix A).

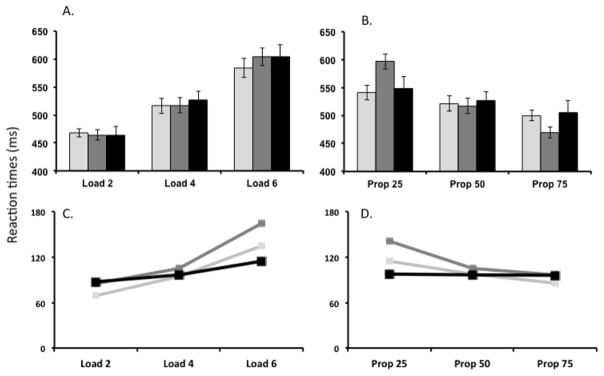
To generate quantitative data from the model, we ran 144 trials per model and 20 identical models (to reflect the number of participants in the original study) for each of the Load and Proportion manipulations. Mean and standard deviations were calculated across reaction times and compared to the empirical data (Figure 4).

Figure 4.

(A–B) Mean reaction times computed for the DNF model (Model 1 shown in light grey and Model 2 shown in dark grey) and behavioral data (shown in black) for the manipulation of the (A) Load and (B) Proportion. (C–D) Mean standard deviations of reaction times across simulations for the (Model 1 shown in light grey and Model 2 shown in dark grey) and behavioral data (shown in black) for the manipulation of (C) Load and (D) Proportion.

5.1.2 Parameter fitting in Model 2

To identify parameters for Model 2, we proceeded as follows. After discovering that Model 1 did not meet our quantitative criterion for fits to the fMRI data, we examined the neural predictions from the model across conditions relative to fMRI results from Wijeakumar et al. (2015). A central effect in Wijeakumar et al. was that regions of the fronto-cortical-striatal network showed greater activation on infrequent trials, regardless of whether an infrequent stimulus appeared on a Go or Nogo trial (Wijeakumar et al., 2015). For instance, brain areas responded strongly on infrequent Go trials. Quantitative fMRI predictions from Model 1 did not show this pattern. Given that local field potentials are positively influenced by both excitatory and inhibitory interactions, we hypothesized that a strong response on infrequent Go trials might be most likely to occur when there is a strong memory of frequent Nogo responses and strong competition between the working memory and contrast fields (and vice versa on infrequent Nogo trials). To examine this possibility, we added a new element to the model--a memory trace to the go and nogo nodes (implemented by modulating the gain on self-excitation across conditions, see Table A.2.1 in Appendix A) and we increased competition between the wm and con fields (Table A.3.1). We also balanced the parameters across the go and Nogo systems, setting the reciprocal connections between nogo node and con field so they were equal to the parameters connecting go node and wm field (Table A.3.1).

Our examination of the model’s neural dynamics also revealed that differences across conditions were relatively modest. We realized that this was influenced by the trial duration we were simulating. Decisions in the model--and decisions by participants--occur within the first 500ms; for the remaining 1000ms, the model simply sits in a neural attractor state, maintaining peaks across all fields (because the stimulus remains ‘on’). Because the BOLD signal reflects the slow blood flow response to all of these events, the ‘final’ attractor states of the model dominate the hemodynamic predictions and the more interesting cognitive processes--the neural interactions leading to the decision--have relatively less impact. This does not accurately reflect neural systems; rather, neurophysiological data suggest that neural attractor states stabilize, but are then suppressed once a stable decision has been made (Annette Bastian et al., 2003). To implement this, we added a ‘condition of satisfaction’ node (CoS), building off recent work by Sandamirskaya and colleagues (Sandamirskaya & Schöner, 2008; Sandamirskaya, Zibner, Schneegans, & Schöner, 2013; Gregor Schöner et al., 2015). This node receives input from both the go and nogo nodes. When either becomes active, the ‘CoS’ node becomes active, signalling that the conditions for a stable decision have been satisfied. The CoS node then suppresses the working memory and contrast fields, globally inhibiting these fields. Consequently, the stable decision made by the go or nogo node remains active throughout the 1500ms trial, but peaks in the wm and con fields are suppressed once the decision is made. Conceptually, this frees up these systems to move on to other interesting events that might (but don’t) occur in the visual field.

5.2 Quantitative behavioral results

Here, we present the results of the behavioral fits for Models 1 and 2 alongside the reaction times from the actual behavioral data. Both DNF models provide reasonable fits to the trends in reaction times shown by the behavioral data in response to manipulating Proportion and Load (see Figure 4A and 4B). Root Mean Squared Error (RMSE) for reaction times for Model 1 with respect to the Standard GLM analysis = 10.58ms and RMSE for reaction times for Model 2 with respect to the Standard GLM analysis = 27.02ms. For the Load manipulation, reaction times increased as the number of SR mappings increased. For the Proportion manipulation, increasing the frequency of Go trials from 25% to 75% resulted in a decrease in reaction times. Although there were some variations in the standard deviations across the 20 simulations for both models (as shown in Figure 4C and 4D), the trends across the conditions were qualitatively correct.

6. Generating local field potentials and hemodynamics from the DNF model

To simulate the hemodynamics for this study, we adapted the model-based fMRI approach from Deco et al. (2004). Specifically, we created an LFP measure for each component of the model during each condition and tracked the LFPs in real time as the model simulated behavioral data. Then, we convolved the simulated LFPs with a gamma impulse response function to generate simulated hemodynamics, and as a result, regressors for each component and condition.

6.1. Definition of the DNF model-based LFP

To illustrate the procedure, we explain below the computation of the LFP for the contrast field neural population (con field in Figures 2–3). The LFPs for all other neural fields in the GnG DNF model (e.g. Model 1; see Figure 1) follow an identical approach.

Consider the dynamic field equation (4.1) with appropriate input neural fields and connections that contribute to the dynamics of the neural population in the con field. This equation is defined by (A.4) in Appendix A or, more explicitly, by

$$\begin{array}{l}{\tau }_e{\stackrel{.}{u}}_{\mathit{con}}(y,t)=-u_{\mathit{con}}(y,t)+h_{\mathit{con}}+s_{\mathit{con}}(y)+c_{\mathit{con},,\mathit{noise}}\ast \xi (y,t)\\ +\left((c_{\mathit{con},E}-c_{\mathit{con},I})\ast g_{\mathit{con}}(u_{\mathit{con}})\right)(y,t)+\sum _{j=\mathit{vis},\mathit{fAtn},wm}{c}_{\mathit{con},j}\ast g_j\left(u_j\right)(y,t)\\ +a_{\mathit{con},\mathit{nogo}}{g}_{\mathit{nogo}}(u_{\mathit{nogo}}(t))\end{array}$$

where f * h denotes the convolution f * h(y,t) = ∫f(y − y′)h(y′,t)dy′.

Here s_con(y) specifies the stationary sub-threshold stimulus to the con field (“the memory trace”), spatially tuned to Nogo colors. The spatially correlated noise η_con is obtained by convolution between kernel c_con,noise and vector ξ of white noise. Local connections include both excitatory and inhibitory components, C_con = C_con,E − C_con,I. All kernels are Gaussian functions of the form $c(y-y^{\prime })=a\mathit{Exp}\left[-\frac{{(y-y^{\prime })}^2}{2{\sigma }^2}\right]$ with positive parameters a except a_con,wm < 0. Note that, whenever Model 2 is used in simulations, an additional term associated with feedback projections from the condition of satisfaction node (CoS) appears in u_con.

To generate an LFP for the contrast field, we sum the absolute value of all terms contributing to the rate of change of activation within the field, excluding the stability term, −u_con(y,t), and the neuronal resting level, h_con. The resulting LFP equation for the con field is given by:

$$\begin{array}{c}{\mathit{LFP}}_{\mathit{con}}(t)=\frac{1}{n}\int \mid s_{\mathit{con}}(y)\mid +|c_{\mathit{con},\mathit{noise}}\ast \xi (y,t)|dy\\ +\frac{1}{n}\int |c_{\mathit{con},E}\ast g_{\mathit{con}}(u_{\mathit{con}})(y,t)|+|c_{\mathit{con},I}\ast g_{\mathit{con}}(u_{\mathit{con}})(y,t)|dy+\\ +\frac{1}{n}\int |c_{\mathit{con},\mathit{fAtn}}\ast g_{\mathit{fAtn}}(u_{\mathit{fAtn}})(y,t)|+|c_{\mathit{con},wm}\ast g_{wm}(u_{wm})(y,t)|\\ +\frac{1}{n\times m}\int |c_{\mathit{con},\mathit{vis}}\ast g_{\mathit{vis}}(u_{\mathit{vis}})(y,t)|dy+\\ +\left|a_{\mathit{con},\mathit{nogo}}{g}_{\mathit{nogo}}\left(u_{\mathit{nogo}}(t)\right)\right|\end{array}$$ (6.1)

Several observations about this calculation need to be made. First, since both excitatory and inhibitory communication require active neurons and, biophysically, generate positive ion flow, we need to sum both in a positive way toward predictions of local activity; thus, we take the absolute value of all excitatory and inhibitory contributions. Second, given that field activities in the calculation of the LFP measure may span different dimensions, we normalize them. In this way, we can maintain a balance among their contributions. We do that by dividing each field contribution by the number of units in it (e.g., in equation (6.1) certain field contributions were divided by n or n ×m where n is the feature dimension and rn is the space dimension). Third, due to correlated noise in each field of the model, small-scale variations in the signal occur (especially evident in the second component), as well as overall variation in reaction times. Indeed, for same initial conditions, the DNF model yields relatively different LFP measures (see Figure 5A).

Figure 5.

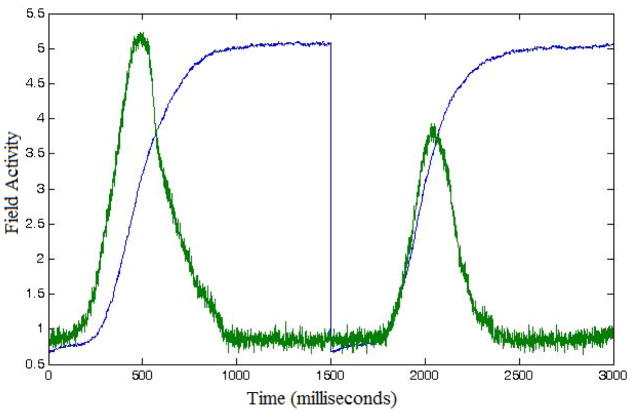
DNF-model-based LFPs computed for two fields in Model 2: feature attention (fAtn; in blue) and go node (green). Different fields drive different response patterns. They are computed under the following conditions: (A) Three repetitions (1500ms long each) of Load 4, Go trials, and (B) Sequence of four trials at Load 4 with order Go-Nogo-Go-Nogo. The variance between the repetitions is a consequence of the stochastic nature of the model.

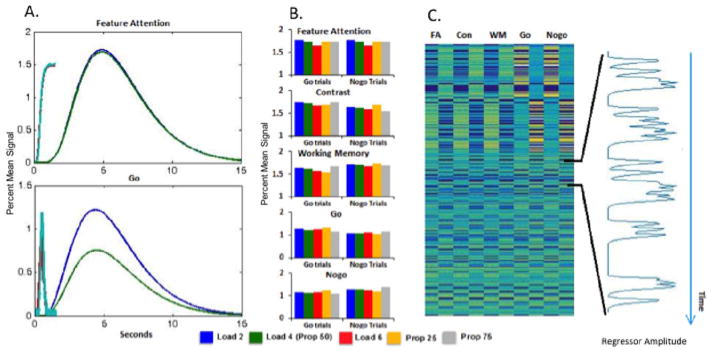
Each component in the model has a different network of interactions that drives a different response pattern. Consequently, individual LFP measures are created for each model component, that is, for each of the 7 fields shown in Figure 2. Figures 5A and 5B depict LFP simulations from fAtn and go node in Model 2, over three and four trials, respectively.

6.2. Canonical predicted LFPs per experimental condition

Note that, in some components, the LFP level is similar across conditions with minor differences in timing (fAtn). In others (go node), different conditions (Go trial versus Nogo trial) lead to larger differences in the LFP (Figure 5B). This contrast is key to the model-based approach because it allows components to have unique signatures on both the scale of the individual trial as well as larger scale signatures across task conditions.

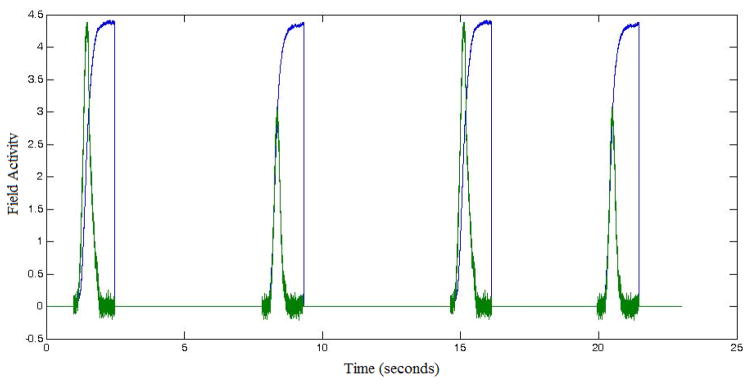
To account for this variance, we run many repetitions of each condition (i.e. we start from same initial values in the model; therefore, the variability will be a direct consequence of noise only). The number of repetitions is chosen usually to reflect the number of trials undertaken by the subjects in the actual experiment. (For example, if in the experiment, each of 20 subjects underwent 72 Go trials for Load 4, we will run 20 sets of 72 repetitions (simulations) of Model 2 with the corresponding parameters for stimulus strength from Table A.4.1.) We then average the generated LFP time series over repetitions of the same condition to determine what we call the canonical predicted LFP signal per condition. Figure 6 depicts examples of such canonical LFP predictions for two fields, fAtn (in blue) and go-node (in green). The first 1500 ms in Figure 6 shows the canonical LFP predictions for Load 4, Go trials (e.g., as seen repeated in Figure 5A). The last 1500 ms shows the canonical LFP predictions for Load 4 Nogo trials.

Figure 6.

Canonical predicted LFPs computed for two fields in Model 2: feature attention (fAtn; in blue) and go node (green). Different fields drive different response patterns. They are computed under the following conditions: (left; first 1500 ms) Load 4, Go trials, and (right, last 1500 ms) Load 4, Nogo trials.

6.3. Construction of the long-form LFP template

Another concern that we aimed to address was placing the simulated canonical LFP values in an appropriate context. Much like the measurement of fMRI data, we take a baseline measurement from the model as follows. We use the same LFP calculations as described above, but we compute a “resting level” by simulating the model in the absence of external stimuli. We average these readings (across all time points and repetitions) to obtain an average resting value. Then, this value is subtracted out of our predictions to express the change in LFP activity relative to the resting value.

Once we have calculated a canonical baselined LFP for each model component and condition type, we proceed to construct long-form, averaged LFP templates. The latter are long-scale (tens of minutes) model-generated LFP predictions for each subject in the experiment. The structure of the long-form LFP templates, for all components of the DNF model, is determined by the order and timing of trials that particular subject experienced during the experimental block(s).

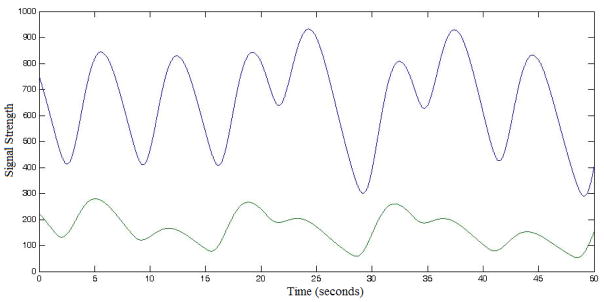
To do this, we first create a zero-valued time series the length of the entire experiment (i.e. a zero-valued long-form LFP template). We then use trial onset timings from the experiment to anchor the trial canonical baselined LFP prediction, for each corresponding trial type. For example, if a trial of a certain condition (e.g. Load 4, Nogo trial) has an onset time of 7500ms after the start of the experiment, then the canonical LFP for that trial is inserted to the long-form template-LFP starting at the same onset time (see Figure 7). Once this iterative process is completed (across all trials) and the algorithm is applied to all DNF model components, we have constructed experiment-based, subject-specific LFP time series for each component of the DNF architecture. These time series reflect predicted differences in neural activation based on the processes at work within each field.

Figure 7.

Excerpted long-form LFP templates computed for two fields in Model 2: fAtn (blue) and go node (green). Depicted is an experimental block of four trials at Load 4, presented to a particular subject in the ordered sequence Go-Nogo-Go-Nogo.

6.4. Generating hemodynamics from the DNF model

fMRI data does not measure neural activity directly. It measures changes in blood flow as the neurovascular system responds to resource demands of active neurons. Consequently, there is a delay between neural activity and the measured BOLD signal. To account for this, we use a standard hemodynamic response function,

$$\mathit{HRF}(t)=\frac{t^{n-1}}{{\lambda }^n(n-1)!}\mathit{Exp}\left(-\frac{t}{\lambda }\right),\lambda =1.3s,n=4,$$

to describe the expected response pattern in the BOLD signal, for a given amount a neural activity. By convolving HRF(t) with the long-form LFP templates ( $\widehat{\mathit{LFP}}(t)$), we are able to generate predicted BOLD activity patterns that are directly comparable to the measured data.

Note that time variable in HRF(t) and $\widehat{\mathit{LFP}}(t)$ has different units, seconds (former) and milliseconds (latter). Also, note that we used a mapping of 1 model time-step to 1 ms in the experiment to simulate the details of each trial. Thus, care should be taken to bring these time units on the same scale, before the convolution $\mathit{BOLD}(t)=(\mathit{HRF}\ast \widehat{\mathit{LFP}})(t)$ is computed. Figure 8 shows two examples of BOLD predictions obtained as described above.

Figure 8.

Excerpted BOLD predictions computed for two fields in Model 2: fAtn (blue) and go node (green). Same starting time point as in Figure 7 was used. Depicted is a sequence of seven trials at Load 4 with order Go-Nogo-Go-Nogo-Go-Nogo-Nogo.

Next, we address the question of comparing model units for the numerically generated BOLD signal to those derived from the fMRI data. We again take guidance from the treatment of fMRI data: we normalize each predicted BOLD signal by its average value over time across the entire experiment-length time series. This takes us away from model-based units to an abstract percentage scale relative to the mean.

Then we turn these normalized BOLD signal predictions into regressors for the statistical analysis of the fMRI data. Care should be taken at this step, again, given that the calculations require matching the sampling rate of the time series to that of the data (down sampling to match the temporal resolution (TR) from the fMRI data). Figure 9 shows the normalized BOLD signals resulting from those shown in Figure 8, as well as the discrete sequence of points retained from the numerically generated BOLD signal after down sampling.

Figure 9.

Excerpted normalized and downsampled BOLD predictions computed for two fields in Model 2: fAtn (blue) and go node (green). Circles indicate the 2-second resolution used to match the fMRI TR. The time range is the same as in Figure 8.

Note that in the analysis of the GnG task, we decided to create split regressors for Go and Nogo trials (see following section for details). To split the trials, two long-form LFPs (again, for each subject and each component) were created based on only Go or Nogo trial onsets instead of all trials together. The proceeding steps from long-form LFP to regressor follow identically.

7. Testing model-based predictions with GLM

In the previous section, we generated a linking hypothesis that allows us to specify a local-field potential for each field in a dynamic neural field model. We also detailed the steps required to transform these LFPs into hemodynamic predictions that are tailored to each individual participant. The next step is to evaluate whether these individually-tailored hemodynamic predictions are, in fact, good predictions relative to the fMRI data from each individual.

We used GLM to evaluate this question. In particular, we used the individually-tailored hemodynamic predictions described above as regressors in a GLM for each individual participant’s fMRI data. This provides quantitative metrics with which we can evaluate the model’s goodness of fit. In particular, we examined the following metrics from each individual GLM: (1) the number of voxels where the model-based GLM captured a significant proportion of variance, and (2) the average R² value across all significant voxels. Note that, because the R² values were not normally distributed, we z-transformed the data. An average z-value was calculated across the mask of voxels that were significant. The z-transformation was then undone using R = atanh(z), where z is the average z-value. Finally, the R-value was adjusted using

$$\mathit{adjR}=1-\frac{(1-R)(N-1)}{N-p-1}$$

where N = number of time points across runs and p =1.

Although the GLM approach gives us quantitative metrics, we need a way to assess whether the fit of the model is any good. As Turner et al. discuss, the optimal approach here would be to quantitatively compare the fit of the DNF model relative to a competing model (Turner et al., 2016). For instance, in Buss et al., they compared hemodynamic predictions of the DNF model to hemodynamic predictions of ACT-R (A. T. Buss et al., 2013). Here, we pursue an alternative approach that was motivated by a recent model-based fMRI study of VWM. In that study, we did not have a second cognitive model from which to generate competing fMRI predictions. Instead, we compared the GLM-based fit of a DNF model to Standard GLM fMRI analyses. This is useful because, at present, Standard GLM fMRI analyses are the gold standard in the functional neuroimaging literature and such analyses can be performed in all cases. Thus, we can treat the Standard GLM analysis as a baseline and ask whether the DNF-based GLM quantitatively outperforms this baseline.

The next question is, of course, which metric to use. One option is to analyze voxel counts; however, several studies have highlighted the limitations of this approach (Bennett & Miller, 2010; Cohen & DuBois, 1999). An alternative is to compare the mean R² values across models. The problem here is that the DNF-based GLM might capture significant variance in some voxels, while the Standard GLM analysis might capture significant variance in different voxels. The overall mean R² value does not take this into effect. Thus, we used an alternative approach: we created an intersection mask that defined voxels where the DNF-based GLM and the Standard GLM analysis both captured a significant proportion of variance and then statistically compared these intersection R² values. This provides a direct head-to-head comparison of the two models in the same voxels, asking which model does a better job fitting the brain data. Our objective was to see whether we could tune the DNF model parameters such that it significantly outperformed the Standard GLM analysis on this comparison metric.

We struggled with two final issues. First, the degrees of freedom of the DNF-based GLM and Standard GLM analysis were not the same. The Standard GLM analysis of data from Wijeakumar et al. (2015) had 10 regressors: 5 conditions (Proportion 75%, Proportion 25%, Load 2, Load 4, Load 6) × 2 trial types (Go, Nogo). By contrast, the DNF model had 7 regressors--one for each component (vis, sAtn, fAtn, con, wm, go, nogo; see, for instance, Figure 9) – see section 6 for the steps leading up to the creation of regressors from the DNF components. Second, we discovered when running the DNF-based GLM that several regressors were collinear which can make beta estimates unstable. This was not terribly surprising: the most collinear fields were vis, sAtn, and fAtn, and all three fields basically serve the same function in the GnG task.

To resolve both issues, we created a 10-regressor DNF-based GLM model by (1) reducing the number of model components to the 5 least collinear fields (fAtn, con, wm, go, nogo), and (2) including separate model-based regressor for Go and Nogo trials.

Figure 10 illustrates the DNF-based GLM approach with numerical results from Model 2. Figure 10A shows examples of HDRs and LFPs for Load 4 Go and Nogo trials in the fAtn field and go node--the same fields used for illustration in Figures 5–9. As above, differences in the HDR amplitude between Go and Nogo trials are evident in the go node but not in the fAtn field. Maximum HDRs across the five DNF components included in the GLM (fAtn, con, wm, go, nogo) and across Load and Proportion manipulations are displayed in Figure 10B. These bars reveal differences in the model-based predictions across components and conditions. Note, for instance, that fAtn shows comparable hemodynamic predictions across go and nogo trials, while the go and nogo nodes show different patterns with, for instance, greater activation in the Prop25 condition on go trials, and greater activation in the Prop75 condition on nogo trials. This reflects one of the key hemodynamic patterns evident in the fMRI data: some brain areas showed a strong response on infrequent trials, regardless of whether those trials required inhibition (a nogo trial in the Prop75 condition) or not (a go trial in the Prop25 condition).

Figure 10.

Testing DNF model predictions with GLM (numerical results using Model 2): (A) Average HDR and LFP for Go (blue/cyan) and Nogo (green/red) Load 4 trials for the fAtn field and go node. (B) Predictions for five components of DNF model (fAtn, con, wm, go, nogo) across Load and Proportion manipulations; bars show signal change. (C) DNF regressors of a single subject and a sampling of the nogo node’s time course (at right).

Figure 10C shows go and Nogo trial regressors for each component of the model, constructed by inserting the condition-specific HDR at the onset of each trial in the same order that was presented to each participant. An example predictor for one participant – a regressor in the GLM model – is shown in the inset in Figure 10C. This time course was created by inserting the predicted hemodynamic time course from the Nogo component (similar to those from Figure 10A) for each trial type at the appropriate start time in the time series and then summing these predictions. If there is a brain region involved in the generation of a Nogo decision, the model predicts that this brain area should show the particular pattern of BOLD changes over time shown in the inset. The GLM results can be used to statistically evaluate such predictions.

8. Model evaluation: Individual-level GLMs

We ran 3 sets of GLM models (using afni_proc in AFNI) for each participant: a 10-regressor DNF-based GLM for Model 1; a 10-regressor DNF-based GLM for Model 2; and a 10-regressor Standard GLM analysis. All GLM analysis also included regressors for motion and drifts in baseline. Figure 11 shows portions of the 10 regressor design matrices from the three models we investigated. Note in particular that the Standard GLM analysis employs a separate regressor for each trial type and condition. In contrast, the DNF model-based method only separates trials based on trial type (go and Nogo trials). For this reason, the model-based method generates more constrained predictions because the relationship between trial conditions (variations in Load and Proportion) is determined a priori and not allowed to vary independently as with the Standard GLM analysis method. As well, the model-based method employs different predictions for each model component, allowing us to identify effects indicative of specific functions.

Figure 11.

Excerpts from the 10-regressor design matrices for one subject from the three GLMs from the project. The excerpts are taken from part of the Load 6 and Load 4 experimental blocks for the given subject. Note that differences exist in the model regressors between components, but they are difficult to appreciate at this scale/resolution.

In each case, we report the total number of significant voxels and the mean R² value across those voxels (see below). We then intersected the images as per the model pairs and identified voxels that were significant for both Model 1 and the Standard GLM analysis, and voxels that were significant for both Model 2 and the Standard GLM analysis. Then, we calculated the mean intersection R² value for each model for each participant and compared these values using a paired-samples t-test.

Overall voxel counts across models were the following: Model 1 = 3964 voxels, Model 2 = 4762, Standard GLM analysis = 3978 voxels. Overall, both models were comparable but Model 2 captured significant variance in more voxels. The overall R² values were the following: Model 1 = 0.139, Model 2 = 0.135, Standard GLM analysis = 0.130, so both DNF models captured more variance, though neither represents a significant improvement relative to the Standard GLM analysis when we compare the average values computed across all voxels (p=0.20 and p=0.43, respectively).

The important metric in this evaluation between the DNF-based GLM and the Standard GLM analysis is the intersection R² values across model pairs. The intersection R² was 0.153 for Model 1 and 0.141 for the Standard GLM analysis across 1616 intersected voxels; Model 1 performed better than the Standard GLM analysis but this effect did not reach significance (t(19) = 0.199, p=0.086). On the other hand, the intersection R² was 0.150 for Model 2 and 0.131 for the Standard GLM analysis across 1507 intersected voxels, with Model 2 performing significantly better than the Standard GLM analysis (t(19) = 0.427, p=.006). When both DNF models were compared against each other, intersection R² values across 1615 intersected voxels were not significantly different, but Model 2 performed quantitatively better than Model 1 (Model 1 = 0.148 and Model 2 = 0.149, t = 0.01, p=0.18). In summary, Model 2 significantly outperforms the Standard GLM analysis and quantitatively performs better than Model 1. Thus, at the group level analysis, we only compared results between Model 2 and the Standard GLM analysis.

9. Model evaluation: Group-level GLMs

9.1 Overview of the approach

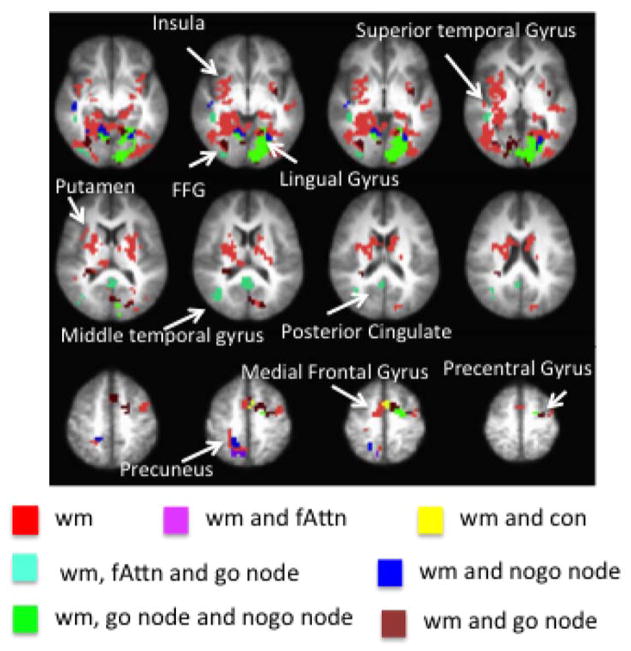
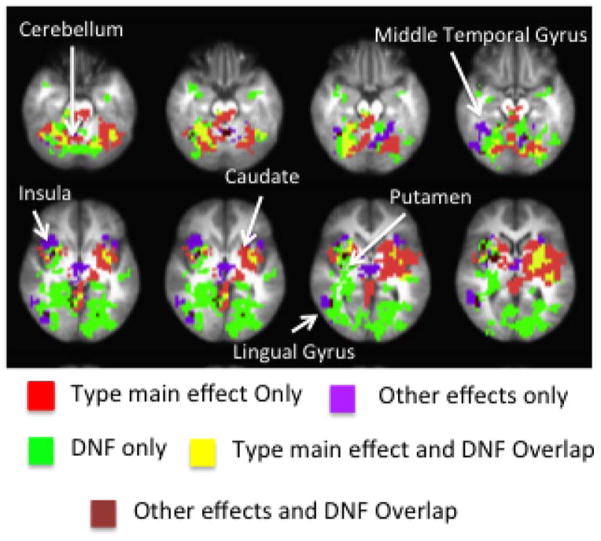
The betamaps from the Standard GLM analysis were input into two 2-factor ANOVAs, a Load ANOVA and a Proportion ANOVA (run using 3dMVM). The Load ANOVA consisted of Type and Load as factors and the Proportion ANOVA consisted of Type and Proportion as factors. The main effect and interaction maps from both sets of ANOVAs were thresholded and clustered based on family-wise corrections obtained from 3dClustSim (α = .05). The main effect of Type from the Proportion and Load ANOVAs were pooled together and called the ‘Type main effect’ image. The ‘Other effects’ image consisted of the pooled effects from the Load main effect, Proportion main effect, Load × Type interaction, and Proportion × Type interaction.

The DNF-based GLM (Model 2 only) also yielded betamaps for each of the ten regressors. These betamaps were input into an ANOVA with regressor as the only factor. The main effect of regressor obtained from this ANOVA was corrected for family wise errors using 3dClustSim as described above. A one-sample t-test was conducted within the spatial constraints of this clustered main effect image to ascertain the contribution of each regressor to the main effect. These t-test results for each regressor were corrected for family wise errors again, identifying which model components were significant predictors for each voxel. At this point, we collapsed effects across trial type for each regressor. For instance, voxels that showed an effect of the wm field for Go trials and/or for Nogo trials were pooled together as wm areas. Consequently, the final image consisted of voxels that showed unique and combined contributions from five fields in the DNF model -- fAtn, con, wm, go node and nogo node. This map was intersected with the Type effect and Other Effects maps from the Standard GLM analysis to establish whether the two GLM analyses identified similar brain regions and whether effects in each cluster were comparable.

It is important to note that the DNF-based approach not only identifies where the brain responded in a way predicted by the model, but also which function(s) operates within that brain region. Thus, in the section that follows, we examine the functional networks identified by the DNF model and then compare the spatial overlap between the DNF-based GLM and the Standard GLM analysis.

9.2 Group-level Results

Figure 12 shows those DNF model predictors that produced statistically significant clusters within the brain regions showing a main effect of component. Overall, the DNF-based GLM revealed patterns of activation consistent with the model-based predictions in cortical and sub-cortical networks of the brain that included the cerebellum, putamen, insula, caudate, supplementary motor area (SMA), as well as parts of the occipital cortex and the cingulate cortex.

Figure 12.

Functional maps generated by DNF model. Colored regions represent cortical areas where a main effect of component was present.

Unique contributions from the wm field recruited the largest numbers of regions (accounting for 1738 voxels). Critically, key parts of the insular-thalamic-putamen network were assigned to a working memory function, consistent with claims by Hampshire and colleagues (Erika-Florence et al., 2014) that working memory and attention processes may underlie response selection. Clusters that showed combined effects from more than one component accounted for 965 voxels. Importantly, all of these voxels included a common wm component. Looking at the model predictions from Figure 10B, two patterns likely explain the predominance of the wm field predictions: (1) there is a reduction in wm activation as Load was increased, and (2) there is a larger modulation of wm activation across the Proportion manipulation on Go trials relative to Nogo trials. As discussed in Wijeakumar et al. (2015), both patterns were pervasive in the fMRI data.

The DNF-based GLM approach also identified regions that laid outside of the network obtained from the Standard GLM analyses approach. The wm field recruited parts of the left fusiform gyrus, left cuneus and left superior temporal gyrus. The lingual gyrus and fusiform gyrus also reflected neural predictions of a combination of the wm, go, and nogo fields. This is consistent with previous findings suggesting that the lingual gyrus plays a role in visual memory as well as visual classification decisions (Mechelli, Humphreys, Mayall, Olson, & Price, 2000). Our results also assign the same functional role to the fusiform gyrus which is functionally connected to the lingual gyrus and plays a central role in visual processing and visual comparison (Mechelli et al., 2000). Another result is the recruitment of parts of the left middle frontal gyrus (not shown) by the wm field and a combination of the wm field and go and nogo nodes (Johnson, Hollingworth, & Luck, 2008; Johnson, Spencer, Luck, & Schöner, 2009; Simmering, Peterson, Darling, & Spencer, 2008). The wm field plays a very important role of maintaining memory traces in the DNF model of VWM in adulthood and development. Furthermore, the middle frontal gyrus has been implicated to be involved in maintenance of goals and abstract representations during VWM processing (Aoki et al., 2011; Barbey, Koenigs, & Grafman, 2013; Haxby, Petit, Ungerleider, & Courtney, 2000; Jonides et al., 1998; Munk et al., 2002; Pessoa, Gutierrez, Bandettini, & Ungerleider, 2002; Pessoa & Ungerleider, 2004).

The next question we examined was how these results from the DNF-based GLM overlapped with results from the Standard GLM analysis. Table 1 shows voxel counts for common and unique effects between these GLM results. Figure 13 shows the spatial distribution of these clusters for the unique and common effects. The Type main effect from the Standard GLM analysis overlapped with 534 voxels that were also significant in the DNF-based GLM (Figure 13; yellow). In addition, the ‘Other effects’ from the Standard GLM analysis overlapped with 116 voxels that were also significant in the DNF-based GLM (shown in brown in Figure 13). We focus on these overlapping effects below because they provide a way to evaluate our model-based fMRI results relative to findings discussed in Wijeakumar et al. (2015).

Table 1.

Voxel count of unique and common effects between the DNF-based GLM and Standard GLM analysis activation maps.

	Voxel Count
Type Main Effect only	2610
Other Effects only	414
DNF Components only	2053
DNF Components and Type Main Effects	494
DNF Components and Other Effects	97

Figure 13.

Overlap between DNF and the Standard GLM analysiss.

Tables 2 and 3 show clusters that overlapped between the DNF-based GLM and the Type main effect and Other effects respectively. For each overlapping cluster, we identify the fields that were significant in the DNF-based GLM.

Table 2.

Spatial overlap between DNF model and the Type main effect from the Standard GLM analysis.

Components	Intersected with	Region	Hemi	Volume (mm3)	Center of Mass
					X	Y	Z
WM	Type ME	Putamen	L	4502	22.6	3.1	10.8
	Type ME	Cerebellum	L	1458	2.6	66.5	−30.4
	Type ME	Cerebellum	R	1158	−15.6	47.7	−33.8
	Type ME	Caudate Nucleus	R	943	−21.2	7.8	18.3
	Type ME	Superior Temporal Gyrus	L	858	37.8	24.4	6.8
	Type ME	Putamen	R	686	−23.2	−9.1	4.5
	Type ME	Cerebellum	L	514	17.5	56.1	−40.2
	Type ME	Cerebellum	R	429	−28.0	64.0	−14.2
	Type ME	Cerebellum	R	386	−34.8	51.2	−25.8
	Type ME	Cerebellum	R	386	−17.3	53.9	−22.7
	Type ME	Thalamus	R	343	−9.2	23.3	14.4
	Type ME	Cingulate Gyrus	R	343	6.1	21.1	33.6
	Type ME	SMA	R	257	−3.5	5.1	54.9
	Type ME	Cerebellum	L	214	25.6	72.4	−11.0
	Type ME	Cerebellum	L	172	24.5	51.8	−46.0
	Type ME	Insula	R	172	−36.8	1.9	3.0
	Type ME	Cerebellum	-	172	0.0	44.8	0.5
	Type ME	Cerebellum	R	129	−30.9	43.0	−33.2
	Type ME	Cerebellum	R	129	−20.4	60.5	−12.2
	Type ME	Caudate Nucleus	R	129	−11.1	−3.7	20.5
	Type ME	Posterior Cingulate Cortex	L	129	5.2	27,8	26.3
	Type ME	Cerebellum	L	86	10.5	64.0	−35.5
	Type ME	Cerebellum	R	86	−8.8	43.0	−5.8
	Type ME	Cerebellum	R	86	−3.5	53.5	−7.5
	Type ME	Thalamus	R	86	−19.2	6.2	3.0
WM and fAtn	Type ME	Cerebellum	L	129	7.6	69.8	−11.0
WM, Go node and Nogo node	Type ME	Fusiform Gyrus	L	86	24.5	74,5	−7.5
	Type ME	SMA	L	86	12.2	6.2	55.5
WM and Con	Type ME	SMA	L	86	1.8	1.0	53.8
WM and Go node	Type ME	Cerebellum	L	514	35.0	50.0	−21.5
	Type ME	Putamen	L	514	22.8	14.1	8.2
	Type ME	Putamen	L	429	32.2	4.8	3.0
	Type ME	Cerebellum	R	257	−24.5	71.0	−13.3
	Type ME	Cerebellum	R	129	−41.4	51.2	−21.5
WM and Nogo node	Type ME	Cerebellum	R	2187	−25.6	48.9	−17.1
	Type ME	Cerebellum	L	686	17.7	59.6	−22.2
	Type ME	Cerebellum	R	557	−7.7	62.4	−30.9
	Type ME	Cerebellum	R	514	−9.3	25.5	−19.5
	Type ME	Cerebellum	R	343	−16.6	53.9	−42.1
	Type ME	Cerebellum	R	214	−13.7	50.0	−6.8
	Type ME	Cerebellum	L	172	41.1	51.8	−18.9
	Type ME	Cerebellum	L	172	24.5	58.8	−11.0
	Type ME	Cerebellum	R	129	−18.1	34.8	−21.5
	Type ME	Cerebellum	L	86	−12.2	64.0	−19.8

Table 3.

Spatial overlap between the DNF model and the Other effects from the Standard GLM analysis.

Components	Intersected with	Region	Hemi	Volume (mm3)	Center of Mass
					X	Y	Z
WM	Other Effects	Inferior Occipital Gyrus	R	943	−39.8	69.1	−6.2
	Other Effects	Cerebellum	R	557	−18.4	54	−28
	Other Effects	Putamen	R	557	−26	−0.3	4.9
	Other Effects	Middle Temporal Gyrus	R	386	−44.1	51.2	6.1
	Other Effects	Cerebellum	L	300	7.8	50	−8.5
	Other Effects	Cerebellum	L	257	1.8	48.2	−18
	Other Effects	Insula	R	172	−36.8	−12.1	6.5
	Other Effects	Fu5iform Gyrus	R	129	−35.6	50	−15.7
	Other Effects	Putamen	R	86	−28	−9.5	−4
	Other Effects	Insula	R	86	−33.2	−18.2	6.5
	Other Effects	Caudate Nucleus	L	86	8.8	4.5	15.2
WM, fAtn and Go node	Other Effects	Inferior Occipital Gyrus	R	86	−38.5	74.5	−4
WM, Go node and Nogo node	Other Effects	Lingual Gyrus	L	172	13.1	64	−4
	Other Effects	Cerebellum	L	86	17.5	67.5	−7.5
WM and Go node	Other Effects	Fusiform Gyrus	R	86	−26.2	65.8	−4
WM and Nogo node	Other Effects	Cerebellum	R	86	−14	64	−25
	Other Effects	Cerebellum	R	86	−8.8	55.2	−0.5

Critically, there was overlap between the areas recruited by the wm field and the Type main effect in parts of the insular-thalamic-putamen network. As noted above, this is consistent with claims by Hampshire and colleagues that working memory plays a central role in response selection via activation of anterior insular and frontal operculum network (Erika-Florence et al., 2014; Hampshire & Sharp, 2015). Overlap between combinations of the wm field and other components and the Type main effect was also observed in parts of the cerebellum and SMA. It is interesting that activation elicited by the DNF components seemed more localized as compared to the activation from the Type main effect (see yellow regions embedded in red regions in Figure 13). This is an encouraging sign for future work, suggesting that the DNF model might identify functional networks that are more precisely localized than what is typically revealed by Standard GLM analyses.

The Other effects activation maps contained the effects of Proportion and Load and interactions of these two manipulations with Type of trial. Once again, the greatest degree of overlap was with the wm field, including portions of the cerebellar regions and also the insula and putamen. In our previous work, this insular network has been implicated in detecting salient or infrequent events (Wijeakumar et al., 2015). In the model, the wm field is responsible for associating and retrieving the appropriate SR mappings to both frequent or non-salient and as well as infrequent, salient events. As noted above, the wm field showed two key effects that were pervasive in the Standard GLM analysis results: a reduction in activation over Load and a larger modulation of wm activation across the Proportion manipulation on Go trials relative to Nogo trials. This likely explains the overlap between predictions from the wm field and the Other effects.

10. General Discussion

The objective of the current paper was to formalize an integrative cognitive neuroscience approach using DFT. To this effect, we adopted a tutorial-style approach wherein we first introduced DFT and its applications to readers who might be less familiar with this modeling approach. Then, we used data from a response selection paradigm as an exemplar case study to explain the steps and rationale involved in building DNF models that could capture behavioral and neural data and the challenges in bridging brain and behavior using these methods. The central goal of this approach was to generate hemodynamic predictions from DNF models and evaluate these predictions at the individual and group levels using GLM by making comparisons to Standard GLM analyses.

Two DNF models captured behavioral data from the task reasonably well; however, only one of the DNF models outperformed the Standard GLM analysis when comparing adjusted R² values within the same regions of the brain. Interestingly, this model architecture was developed by tuning the first model parameters to capture competitive neural interactions first and then simultaneously capturing behavioral data as well. This suggests that iterative modeling using this approach might be most effective. Model 2 was then advanced to the group level analyses to look at spatial distributions of DNF components and how these distributions overlapped with effects observed in the Standard GLM analysis from our previous work.

The DNF model engaged a large cortico-sub-cortical network that included parts of the cerebellum, SMA, insula, putamen, thalamus, caudate and parts of the occipital cortex. In particular, unique contributions from the wm field accounted most of spatial distributions. The rest of the contributions were from a combination of effects between the wm field and other components in the DNF model. This finding is in line with Hampshire and colleagues who argue that response selection and inhibition is a property of spatially distributed functional networks that support a general class of working memory and attentional processes (Erika-Florence et al., 2014).

These spatial distributions also overlapped with effects from the Standard GLM analysis. Findings from the Cisek lab might provide some evidence that are in line with our findings on the recruitment of a host of cortical and sub-cortical regions by the wm field that overlapped with areas showing a difference between Go and Nogo responses in the Standard GLM analysis (Cisek, 2012). These authors presented evidence that action selection emerges through a distributed consensus across many levels of representation, which in the current case would represent multiple SR mappings. According to this theory, cortical and subcortical regions compete through inhibitory interactions when individuals are faced with multiple potential actions. So, it is possible that the BOLD signal reduction reported in our previous work is related to the inhibitory competition between the Go and Nogo responses.

The wm field also engaged regions in the occipital cortex, an insular ‘salience’ network, and the cerebellum. Collectively taken, we suggest that wm field is involved in processing visual information from the stimuli, to associating and retrieving the appropriate SR mappings to both frequent or non-salient and as well as salient events, before activating the motor planning and execution centers of the brain. These findings show a departure of our DNF model from typical integrative modeling approaches, as emphasized by Turner and colleagues (Turner et al., 2016). As these researchers underline, integrative models require a strong commitment to both the underlying cognitive process and where this process is executed in the brain. The DNF model does not fall into this category. The DNF model does show a strong commitment to specifying the cognitive and neural processes that underlie the behaviors in questions; however, our approach remains open to where in the brain these neural dynamics live. This is an important observation – remember, neurons do not always act like modules. Neurons can switch their allegiance, thus coding for multiple dimensions. So allowing for flexibility in the integrative modeling approach may be beneficial when mapping theories to cognitive processes in the brain. In the next section, we critically evaluate this modeling approach with an eye towards future efforts to optimize model performance and further DFT applications.

10.1 Evaluating the model-based approach

This tutorial has meticulously walked through explaining the background to DFT, previous applications, the rationale for developing DNF models, construction of the components of the fields of DNF models, and comparing quantitative fits to the behavioral and neural data to Standard GLM analyses. This raised several issues we summarize here in our efforts to formalize an integrative cognitive neuroscience approach.

Choosing parameters for DNF models

We obtained reasonable behavioral fits for both DNF models using parameters grounded by previous work (Erlhagen & Schöner, 2002) and our experience with learning dynamics. That said, it is possible that different sets of parameters could provide similar quantitative behavioral fits. Future work will be needed to explore a broader range of parameters, asking two key questions: (1) are there parameters that provide a better fit to the behavioral and neural data, and (2) do we see the same qualitative behavioral and neural outcomes from the model across a range of parameters, without dramatic violations of the behavioral and neural patterns. The former question examines the goodness-of-fit of the model; the latter question probes the generality of the model. We think an iterative approach to model exploration would be most fruitful here, stressing the important constraints gained by modeling two data sets simultaneously from a single neural process model.

Constraining the model

Despite not testing a multitude of parameters, there are still many points in this modeling approach where constraints have been placed. To begin, the architecture was heavily constrained by using components that have a history in explaining working memory processes (Johnson, Spencer, & Schöner, 2008; Johnson et al., 2009; Simmering & Spencer, 2007). This was done to place emphasis on the generalization of these components across different executive functions. Next, we constrained the model to account for both behavioral and neural data -- the key strength of adopting an integrative cognitive neuroscience approach. Concretely, constraints here come from the direct mapping of neural activation patterns in the model to LFPs to simulated BOLD data. Finally, in future work, constraints can also be applied when mapping from one model to the next with a goal to integrate across DNF architectures.

Model Complexity

When contrasted with other cognitive models, DNF models seem rather complex. They are composed of several fields and parameters that require fine-tuning to generate good fits to both behavioral and neural data. However, this added level of complexity is to be expected if one tries to bridge non-linear patterns of brain activity and macroscopic behavioral responses. We contend that bridging brain and behavior requires models that take into account how neural systems actually work. DFT does this by faithfully capturing many known properties of neural population dynamics and how neural populations are recurrently connected across multiple cortical fields to give rise to complex behaviors (Bastian, Riehle, Erlhagen, & Schöner, 1998; Bastian et al., 2003; Erlhagen et al., 1999).

That said, it is also important to note that DFT does not consider other known aspects of neural function such as the details of neurotransmitter action, the biophysical properties of individual neurons, and so on (Garagnani, Wennekers, & Pulvermüller, 2008; Markram et al., 2015). In this sense, DFT provides a limited view of neural function. To the extent that these details matter, even more complex biophysical models will be required if we want to bridge brain and behavior. Our claim, however, is that many of these low-level biophysical details are not necessary when capturing fMRI data because fMRI provides on a low-pass filter on neural activity. Future work will be needed to evaluate this conjecture. Critically, however, the approach described here facilitates that work by providing a formal method to test whether neural population dynamics are sufficient to capture the details inherent in fMRI.

Exploratory versus confirmatory modeling approaches

Turner et al. argue that integrative models are confirmatory by nature because fits to brain networks and behavioral patterns are constrained. We agree with this outlook (Turner et al., 2016). However, in the current case study, there is also an exploratory component. For instance, one of our central questions here was exploratory in nature: can components from previous working memory models capture brain and behavioral patterns in response selection? Once we have a model that does this, we can move into the confirmatory phase. A refined approach at this stage would be to design conditions in the task that de-correlate the fields of the DNF model. For instance, if we find that decreasing the proportion of go trials resulted in different LFP patterns in the wm field as compared to the go node, then a range of proportion of trials can be tested to determine the point at which collinearity between those two regressors would be at the lowest, whilst still preserving the integrity of the DNF model. Further, one could test the efficiency of multiple design matrices constructed from such regressors. After this confirmatory phase, one could optimally test the model across a range of scenarios. Indeed, the ideal scenario is one in which the confirmatory phase enables contrasts with other theories that make different predictions for both brain and behavior.

We note, however, that doing this requires having comparable theoretical approaches such as two integrative cognitive neuroscience models. At present, this is difficult given that there are relatively few integrative approaches (but see, Buss et al., 2013). One alternative is to contrast two different models from the same theoretical framework. We did a variant of this in the current study, contrasting Model 1 with Model 2. A more conceptually intriguing variant of this approach would be to contrast two different dynamic field architectures (rather than testing the same architecture under different parameter settings). When contrasted at the levels of both brain and behavior, this might enable one to eliminate candidate models based on the fit to data.

Difficulty of implementation

Developing a dynamic field model and fitting the model to data is a complex enterprise. However, the recent book from the DFT group unpacks this complexity, providing the background to DFT including the underlying rationale. The book also offers multiple examples of implemented models that can help foster the development of new models. Further, the COSIVINA simulation environment allows researchers to build entire DF models using a few lines of code making implementation easy. We note that we have added a neuroimaging toolbox to this framework; thus, creating the LFPs described herein is quite easy (see www.dynamicfieldtheory.org/software/).

Uncovering the ‘ground truth’ amongst models

An important issue to address in future work would be the nature of spatial neural patterns in the cortex that are revealed by the DNF-based approach relative to Standard GLM analyses. Most critically, when the two approaches disagree, which approach reveals the ‘ground truth’? One interesting avenue to explore this question would be to carefully introduce different types of synthetic data into an fMRI dataset. For instance, one could effectively insert neural patterns consistent with the DNF model, inconsistent with the model, or unbiased to either approach. One could then use Standard GLM analysis and DNF approaches to fish out these activation patterns. In this case, one knows the ‘ground truth’ and it is easier to evaluate which method outperforms the other. Then one could explore the overlap (or lack thereof) across spatial distributions between approaches to better understand the discrepancies.

Although future work in this direction will be needed, we note that compared to Standard GLM analyses, DNF models are grounded in a formal theory that specifies how neural populations dynamics give rise to behavioral patterns. In this sense, the fact that the DNF-based GLM reported here outperformed the Standard GLM analysis on key quantitative metrics is important. Nevertheless, we recognize that there is often an inherent mistrust with formal models and empirically-oriented researchers will likely gravitate toward Standard GLM analyses to provide the ‘ground truth’. This is certainly a reasonable approach until the DNF-based integrative cognitive neuroscience approach proves its worth across multiple projects.

Appendix A

A.1. Dynamic Field (DNF) Model for Go/Nogo Paradigm

The dynamic field (DNF) model for the Go/Nogo paradigm consists of 7 coupled neuronal sub-networks as illustrated in Figure 2: the visual field (vis); spatial attention field (sAtn); feature attention (fAtn); contrast field (con); working memory (wm); and the “decision system” consisting of two nodes (go and Nogo). The DNF Model 1 is therefore defined by a system of five integral-differential equations (A.1) – (A.5) and two ordinary differential equations (A.6) – (A.7), as listed below.

Each equation is described by a sum of several components. The first three terms correspond to the local field interactions, while local noise is modeled by the function η. All terms that depend on two distinct indices are associated with long-range, inter-field coupling. Applied stimulus, when appropriate, is given by function s. Excitatory coupling takes positive values, while inhibitory coupling is negative. The functional topography assumes local excitation and lateral inhibition, and it is modeled by a difference of two Gaussians resulting in a Mexican-hat connectivity. The dot in u̇ represents the derivative of neuronal activity u with respect to time t. Detailed definitions of each coupling term are included in Sections A.2–A.4, and the set of parameters used in the simulation of this DNF model are listed in Tables A.2.1, A.3.1 and A.4.1.

We start by describing the equation for the visual field. Besides local neuronal population interactions, the visual field receives excitatory connections from the spatial attention and the feature attention fields via convolutions c_vis,s,Atn * g_sAtn(u_sAtn) and c_vis,f,Atn * g_sAtn(u_fAtn). It is also subject to external stimulus s_vis(x,y).

$$\begin{array}{l}{\tau }_e{\stackrel{.}{u}}_{\mathit{vis}}(x,y,t)=-u_{\mathit{vis}}(x,y,t)+h_{\mathit{vis}}+\iint c_{\mathit{vis}}(x-x^{\prime },y-y^{\prime })g_{\mathit{vis}}\left(u_{\mathit{vis}}(x^{\prime },y^{\prime },t)\right){dx}^{\prime }{dy}^{\prime }\\ +\int c_{\mathit{vis},\mathit{sAtn}}(x-x^{\prime })g_{\mathit{sAtn}}\left(u_{\mathit{sAtn}}(x^{\prime },t)\right){dx}^{\prime }\\ +\int c_{\mathit{vis},\mathit{fAtn}}(y-y^{\prime })g_{\mathit{fAtn}}\left(u_{\mathit{fAtn}}(y^{\prime },t)\right){dy}^{\prime }+{\eta }_{\mathit{vis}}(x,y,t)+s_{\mathit{vis}}(x,y)\end{array}$$ (A.1)

The spatial attention field receives two excitatory inputs: projections c_sAtn,vis * g_sAtn(u_vis) from the visual field, and a sub-threshold bump activity s_sAtn(x). The latter is centered at the position of stimulus presentation and it simulates the response of the network during the fixation stage of the task.

$$\begin{array}{l}{\tau }_e{\stackrel{.}{u}}_{\mathit{sAtn}}(x,t)=-u_{\mathit{sAtn}}(x,t)+h_{\mathit{sAtn}}+\int c_{\mathit{sAtn}}(x-x^{\prime })g_{\mathit{sAtn}}\left(u_{\mathit{sAtn}}(x^{\prime },t)\right){dx}^{\prime }\\ +\iint c_{\mathit{sAtn},\mathit{vis}}(x-x^{\prime })g_{\mathit{vis}}\left(u_{\mathit{vis}}(x^{\prime },y^{\prime },t)\right){dy}^{\prime }{dx}^{\prime }+{\eta }_{\mathit{sAtn}}(x,t)+s_{\mathit{sAtn}}(x)\end{array}$$ (A.2)

The feature attention field receives excitatory inputs from the visual, contrast and working memory fields:

$$\begin{array}{l}{\tau }_e{\stackrel{.}{u}}_{\mathit{fAtn}}(y,t)=-u_{\mathit{fAtn}}(y,t)+h_{\mathit{fAtn}}+\int c_{\mathit{fAtn}}(y-y^{\prime })g_{\mathit{fAtn}}\left(u_{\mathit{fAtn}}(y^{\prime },t)\right){dy}^{\prime }\\ +\iint c_{\mathit{fAtn},\mathit{vis}}(y-y^{\prime })g_{\mathit{vis}}\left(u_{\mathit{vis}}(x^{\prime },y^{\prime },t)\right){dy}^{\prime }{dx}^{\prime }\\ +\int c_{\mathit{fAtn},\mathit{con}}(y-y^{\prime })g_{\mathit{con}}\left(u_{\mathit{con}}(y^{\prime },t)\right){dy}^{\prime }+\int c_{\mathit{fAtn},wm}(y-y^{\prime })g_{wm}\left(u_{wm}(y^{\prime },t)\right){dy}^{\prime }\\ +{\eta }_{\mathit{fAtn}}(y,t)\end{array}$$ (A.3)

The contrast field receives feedforward excitatory connections from the visual and feature attention fields; inhibitory connections from the working memory field; and excitatory feedback from the nogo node. To account for learning during the pre-task instruction step, a sub-threshold input s_con(y) with activity bumps localized at the Nogo colors is also included.

$$\begin{array}{l}{\tau }_e{\stackrel{.}{u}}_{\mathit{con}}(y,t)=-u_{\mathit{con}}(y,t)+h_{\mathit{con}}+\int c_{\mathit{con}}(y-y^{\prime })g_{\mathit{con}}\left(u_{\mathit{con}}(y^{\prime },t)\right){dy}^{\prime }\\ +\iint c_{\mathit{con},\mathit{vis}}(y-y^{\prime })g_{\mathit{vis}}\left(u_{\mathit{vis}}(x^{\prime },y^{\prime },t)\right){dy}^{\prime }{dx}^{\prime }+\int c_{\mathit{con},\mathit{fAtn}}(y-y^{\prime })g_{\mathit{fAtn}}\left(u_{\mathit{fAtn}}(y^{\prime },t)\right){dy}^{\prime }\\ +\int c_{\mathit{con},wm}(y-y^{\prime })g_{wm}\left(u_{wm}(y^{\prime },t)\right){dy}^{\prime }\\ +a_{\mathit{con},\mathit{nogo}}\times g_{\mathit{nogo}}\left(u_{\mathit{nogo}}(t)\right)+{\eta }_{\mathit{con}}(y,t)+s_{\mathit{con}}(y)\end{array}$$ (A.4)

Similarly, the working memory field receives feed-forward excitatory connections from the visual and feature attention fields; inhibitory connections from the contrast field; and excitatory feedback from the go node. In addition, we include a sub-threshold input s_wm(y) of activity bumps localized at the Go colors which simulates learning during the pre-task instruction step,

$$\begin{array}{l}{\tau }_e{\stackrel{.}{u}}_{wm}(y,t)=-u_{wm}(y,t)+h_{wm}+\int c_{wm}(y-y^{\prime })g_{wm}\left(u_{wm}(y^{\prime },t)\right){dy}^{\prime }\\ +\iint c_{wm,\mathit{vis}}(y-y^{\prime })g_{\mathit{vis}}\left(u_{\mathit{vis}}(x^{\prime },y^{\prime },t)\right){dy}^{\prime }{dx}^{\prime }\\ +\int c_{wm,\mathit{fAtn}}(y-y^{\prime })g_{\mathit{fAtn}}\left(u_{\mathit{fAtn}}(y^{\prime },t)\right){dy}^{\prime }\\ +\int c_{wm,\mathit{con}}(y-y^{\prime })g_{\mathit{con}}\left(u_{\mathit{con}}(y^{\prime },t)\right){dy}^{\prime }+a_{wm,go}\times g_{go}(u_{go}(t))+{\eta }_{wm}(y,t)\\ +s_{wm}(y)\end{array}$$ (A.5)

The go and nogo nodes are coupled by mutual inhibition. In addition, feed-forward excitation is projected from the working memory field to the go node, and from the contrast field to the nogo node respectively.

$$\begin{array}{c}{\tau }_e{\stackrel{.}{u}}_{go}(t)=-u_{go}(t)+h_{go}+a_{go}\times g_{go}\left(u_{go}(t)\right)\\ +a_{go,\mathit{nogo}}\times g_{\mathit{nogo}}\left(u_{\mathit{nogo}}(t)\right)+a_{go,wm}\times \int g_{wm}\left(u_{wm}(y^{\prime },t)\right){dy}^{\prime }+{\eta }_{go}(t)\end{array}$$ (A.6)

$$\begin{array}{c}{\tau }_e{\stackrel{.}{u}}_{\mathit{nogo}}(t)=-u_{\mathit{nogo}}(t)+h_{\mathit{nogo}}+a_{\mathit{nogo}}\times g_{\mathit{nogo}}\left(u_{\mathit{nogo}}(t)\right)\\ +a_{\mathit{nogo},go}\times g_{go}\left(u_{go}(t)\right)+a_{\mathit{nogo},\mathit{con}}\times \int g_{\mathit{con}}\left(u_{\mathit{con}}(y^{\prime },t)\right){dy}^{\prime }+{\eta }_{\mathit{nogo}}(t)\end{array}$$ (A.7)

A.2. Local Field Interactions

All parameters associated with local interactions in the DNF model above are listed in Table A.2.1.

The Gaussian interaction kernel that determines the spread of activation inside a given field to neighboring units (see parameters σ_j,E and σ_j,I in Table A.2.1) with strengths determined by the amplitude parameters a_j,E, a_j,I and a_j,global is defined by

$$c_j(z-z^{\prime })=a_{j,E}\mathit{Exp}\left[-\frac{{(z-z^{\prime })}^2}{2{\sigma }_{j,E}^2}\right]-a_{j,I}\mathit{Exp}\left[-\frac{{(z-z^{\prime })}^2}{2{\sigma }_{j,I}^2}\right]+a_{j,\mathit{global}}$$ (A.8)

Here the variable z = x or z = y spans either the spatial dimension (x ∈ S) or the feature (color) dimension (y ∈ F), while the index j ∈ {sAtn, fAtn, con, wm} corresponds to the neural field spatial attention, feature attention, contrast field or working memory, respectively. The gain output function g normalizes the field activation, and is assumed to be the sigmoidal

$$g(u)=\frac{1}{1+\text{Exp}[-\beta u]}$$ (A.9)

with threshold set to zero and steepness parameter β. Consequently, activation levels lower than the threshold contribute relatively little to neural interactions, while positive activation levels (higher than the threshold 0) contribute strongly to neural interactions.

Each neural network is subject to spatially correlated noise η_j(z,t) defined as the convolution between a Gaussian kernel and white noise ξ_j(z,t)

$${\eta }_j(z,t)=\int a_{j,\mathit{noise}}\mathit{Exp}\left[-\frac{{(z-z^{\prime })}^2}{2{\sigma }_{j,\mathit{noise}}^2}\right]\xi (z^{\prime },t)d{z}^{\prime }.$$ (A.10)

Note that the variable ξ_j(z,t) takes random values from a normal distribution with zero mean and unit standard deviation 𝒩(0,1) but has its strength scaled with $1/\sqrt{dt}$.

Similar definitions are given for the visual field (j = vis) which spans two coordinates, the spatial and color representations. In this case, the convolution c_vis * g_vis(u_vis) and the noise η_vis are two-dimensional functions so the Gaussian interaction kernel and the spatially correlated noise are defined by

$$\begin{array}{l}{c}_j(x-x^{\prime },y-y^{\prime })=a_{j,E}\mathit{Exp}\left[-\frac{{(x-x^{\prime })}^2}{2{\sigma }_{j,E}^2}\right]\mathit{Exp}\left[-\frac{{(y-y^{\prime })}^2}{2{\sigma }_{j,E}^2}\right]\\ +a_{j,I}\mathit{Exp}\left[-\frac{{(x-x^{\prime })}^2}{2{\sigma }_{j,I}^2}\right]\mathit{Exp}\left[-\frac{{(y-y^{\prime })}^2}{2{\sigma }_{j,I}^2}\right]+a_{j,\mathit{global}}\end{array}$$ (A.11)

and

$${\eta }_j(x,y,t)=\iint a_{j,\mathit{noise}}\mathit{Exp}\left[-\frac{{(x-x^{\prime })}^2}{2{\sigma }_{j,\mathit{noise}}^2}\right]\mathit{Exp}\left[-\frac{{(y-y^{\prime })}^2}{2{\sigma }_{j,\mathit{noise}}^2}\right]\xi (x^{\prime },y^{\prime },t){dx}^{\prime }{dy}^{\prime }$$ (A.12)

On the other hand, the go and nogo nodes with index j ∈ {go, nogo} are assumed to have global connectivity. Then their local field interactions are simply the product

$$a_j\times g_j\left(u_j(t)\right)$$ (A.13)

between the gain function and constant aj. The noise function is defined by

$${\eta }_j(t)=a_{j,\mathit{noise}}\times \xi (t)$$ (A.14)

A.3. Long Range (Inter-Network) Coupling

The coupling between two distinct fields of the neural network is defined by a Gaussian kernel as well. Thus, if field k receives input from field j then the connectivity function is the convolution c_k,j(·) * g_j(u_j(·,t)) with kernel

$$c_{k,j}(z-z^{\prime })=a_{k,j}\mathit{Exp}\left[-\frac{{(z-z^{\prime })}^2}{2{\sigma }_{k,j}^2}\right]$$ (A.15)

In particular, if the coupling is a projection of the visual field (j = vis) into either of the fields spatial attention, feature attention, contrast or working memory (k), then the convolution is a double-integral over the two-dimensional set, S×F. The Gaussian kernel depends, however, only on one variable (for example, x) so the integration over the other variable (y) ultimately reduces to a summation of the output gain along the secondary dimension y.

If the coupling is a projection of the working memory (or contrast field) into the go (or nogo node), then the kernel of the convolution function reduces to a constant,

$$c_{k,j}=a_{k,j}$$ (A.16)

In addition, if the coupling is between the go and nogo nodes then the convolution is simply the product c_k,j × g_j(u_j(t)) and, again, c_k,j = a_k,j.

Table A.3.1 summarizes all parameter values associated with long range coupling in the DNF model.

A.4. Stimulus Functions

All parameters associated with stimuli in the DNF model appear in Table A.4.1. Stimuli s_j to field j are modeled by normalized Gaussian inputs centered at particular position Z_j,s in the neural field, and with spread parameter σ_j,s and amplitude a_j,s. In particular, stimuli applied to the spatial attention, contrast and working memory fields induce local sub-threshold bump(s) of activity in the absence of the external stimulus s_vis(x,y).

$$\begin{array}{c}{s}_{\mathit{vis}}(x,y)=a_{\mathit{vis},s}\times \frac{1}{2\pi {\sigma }_{\mathit{vis},s}^2}\mathit{Exp}\left[-\frac{{(x-x_{\mathit{vis},s})}^2}{2{\sigma }_{\mathit{vis},s}^2}\right]\mathit{Exp}\left[-\frac{{(y-y_{\mathit{vis},s})}^2}{2{\sigma }_{\mathit{vis},s}^2}\right]\\ s_{\mathit{sAtn}}(x)=a_{\mathit{sAtn},s}\times \frac{1}{\sqrt{2\pi }{\sigma }_{\mathit{sAtn},s}}\mathit{Exp}\left[-\frac{{(x-x_{\mathit{sAtn},s})}^2}{2{\sigma }_{\mathit{sAtn},s}^2}\right]\\ s_{\mathit{con}}(y)=a_{\mathit{con},s}\times \frac{1}{\sqrt{2\pi }{\sigma }_{\mathit{con},s}}\sum _{l=1}^{\mathit{load}/2}\mathit{Exp}\left[-\frac{{(y-y_{\mathit{con},s}^l)}^2}{2{\sigma }_{\mathit{con},s}^2}\right]\\ s_{wm}(y)=a_{wm,s}\times \frac{1}{\sqrt{2\pi }{\sigma }_{wm,s}}\sum _{l=1}^{\mathit{load}/2}\mathit{Exp}\left[-\frac{{(y-y_{wm,s}^l)}^2}{2{\sigma }_{wm,s}^2}\right]\end{array}$$ (A.17)

The sub-threshold activity bump in the spatial attention field is assumed to form during the fixation stage and prior to application of the Go/Nogo stimulus s_vis(x,y). Similarly, sub-threshold activity bumps in the contrast and working memory fields are assumed to form during the instruction stage when the subject learns the Go and Nogo colors, and again prior to application of the external stimulus s_vis(x,y). For example, Load 4 requires learning of two Go colors and other two Nogo colors. Therefore, during the numerical simulation time, two sub-threshold activity bumps centered at the Go colors are placed in the working memory field, and two sub-threshold activity bumps centered at the Nogo colors are placed in the contrast field.

Table A.2.1.

Local field interactions: parameter values used in the simulation of the DNF model. See also Eqs. (A.1)–(A.5) and (A.8)–(A.14). Differences in parameter values between Model 2 (shown in the table) and Model 1 are highlighted in red and should be read as follows: Model 1 does not include any “condition of satisfaction” so, for it, last column in the table should be ignored. In addition, in Model 1, the amplitude a_j of all-to-all coupling for go and nogo nodes is fixed to a_Go = 1 and a_NoGo = 3 (see columns 8 and 9 in the table).

Symbol	Meaning	Parameter values for particular neural field j
		Visual Field j = vis	Spatial Attention j = sAtn	Feature Attention j = fAtn	Contrast Field j = con	Working Memory j = wm	Go j = go	NoGo j = nogo	Cond. of Satis. j = CoS
τe	Timescale	20	20	20	20	20	20	20	20
hj	Neuronal resting level	−5	−5	−5	−5	−5	−5	−5	−5
aj,E	Amplitude of lateral excitation	0.44	0.64	0.80	1.20	1.20
aj,I	Amplitude of lateral inhibition	−0.12	0	0	−0.32	−0.32
σj,E	Spread of lateral excitation	5	5	5	5	5
σj.I	Spread of lateral inhibition	10	10	10	10	10
aj, global	Amplitude of global inhibition	−0.002	−1	−1	0	0
aj	Amplitude all-to-all coupling						2, 1 or 3*	2,3 or 1*	2
βj	Steepness of the gain function	2	2	4	2	2	1	1	1
aj,noise	Amplitude of correlated noise	0.40	0.40	1.60	1.60	1.60	1	1
σj,noise	Spread of noise	1	1	1	1	1
x,x′ ∈ S	Field size forspatial dimension S	101	101
y,y′ ∈ F	Field size forfeature (color) dimension F	204		204	204	204

^*First value in Load 2/4/6, Second value in prop 25, Third value in Prop 75 (Model 2)

Table A.3.1.

Long range (inter-network) coupling: parameter values used in the simulation of the DNF model. For all existing connections j to k where it makes sense, the spread of activation takes the value σ_k,j = 5. See also Eqs. (A.6)–(A.7) and (A.15)–(A.16). Differences in parameter values between Model 2 (shown in the table) and Model 1 are highlighted in red and should be read as follows: Model 1 does not include any “condition of satisfaction” so, for it, last row and last column in the table should be ignored. In addition, in Model 1, the bi-directional coupling between wm and con is a_con,wm = a_wm,con = −0.56 and the bi-directional coupling between con and Nogo is a_con,nogo = a_nogo,con = 1.

Svmbol/Meaning		Neural Fields		Input layer, j
				vis	sAtn	fAtn	con	wm	go	nogo	CoS
ak,j	Amplitude of the coupling from field j into field k	Output Layer k	vis		0.24	0.08
			sAtn	0.16
			fAtn	0.32			0.16	0 16
			con	0 16		0.16		−0.60		0.27	−10
			wm	0 16		0.16	−0.60		0.27		−10
			go					0.28		−6
			nogo				0.28		−6
			CoS						4	4

^*Width/spread of all field → field connections is 5, except inhibitory wm ↔ con connections have width 60.

Table A.4.1.

Stimulus functions: parameter values used in the simulation of the DNF model. See also Eqs. (A.1), (A.2), (A.4), (A.5) and (A.17).

Condition	Neural Field j	Stimulus strength aj,s	Spread of stimulation σj.s	Spatial coordinate(s) at the center of stimulus xj.s	Feature (color) coordinate(s) at the center of stimulus yj,s
Load 2	vis	5.4	3	51	Either of 18 or 52
	sAtn	3	3	51
	con	1.97	3		52
	wm	1.97	3		18
Load 4	vis	5.4	3	51	Either of 18, 52, 86 or 120
	sAtn	3	3	51
	con	1.87	3		52 and 120
	wm	1.87	3		18 and 86
Load 6	vis	5.4	3	51	Either of 18, 52, 86, 120, 154 or 188
	sAtn	3	3	51
	con	1.78	3		52 and 120 and 188
	wm	1.78	3		18 and 86 and 154
Load 4 proportion 25/75 Go/NoGo	vis	5.4	3	51	Either of 18, 52, 86 or 120
	sAtn	3	3	51
	con	1.90	3		52 and 120
	wm	1.84	3		18 and 86
Load 4 proportion 75/25 Go/NoGo	vis	5.4	3	51	Either of 18, 52, 86 or 120
	sAtn	3	3	51
	con	1.84	3		52 and 120
	wm	1.90	3		18 and 86