Functional dissection of signal and noise in MT and LIP during decision-making

Abstract

During perceptual decision making, responses in the middle temporal (MT) and lateral intraparietal (LIP) areas appear to map onto theoretically defined quantities, with MT representing instantaneous motion evidence and LIP reflecting the accumulated evidence. However, several aspects of the transformation between the two areas have not been empirically tested. We therefore performed multi-stage systems identification analyses of the simultaneous activity of MT and LIP during individual decisions. We found that monkeys based their choices on evidence presented in early epochs of the motion stimulus, and that substantial early weighting of motion was present in MT responses. LIP’s responses recapitulated MT’s early weighting and contained a choice-dependent buildup that was distinguishable from motion integration. Furthermore, trial-by-trial variability in LIP did not depend on MT activity. These results identify important deviations from the idealizations of MT and LIP and motivate inquiry into sensorimotor computations that may intervene between MT and LIP.

Introduction

Area MT plays a critical role in representing the motion information used for direction discrimination^2,3 and neurons in LIP have spike rates that resemble the time course of decision formation^4,5. These observations have been synthesized in the form of a two-stage computational model. In this simple and elegant framework, MT represents instantaneous motion evidence, and LIP integrates MT’s output up to a decision bound, thereby instantiating a neural correlate of an evolving decision variable^5,6,7,8,9.

Although many studies invoke MT-to-LIP integration to explain behavioral and neurophysiological phenomena during perceptual decision making^7,8,9,10, it remains unknown how closely LIP activity reflects the integration of sensory evidence from MT and how direct their relationship is. Indeed, several studies have reported weak and/or nonmonotonic dependencies of LIP’s ramping responses on motion strength^4,11,12,13. Other studies have identified components of LIP firing rates that are not linked to the integration of motion, such as simple visual input^14,15, urgency¹⁶, prior probability^13,17, and subjective value¹⁸. Additionally, several studies have identified the presence of substantial pre-saccadic response components present during the deliberation phase of direction discrimination and other paradigms^19,20,21.

We therefore sought to more directly evaluate the basic tenets of the integrator model of LIP by assessing how the single-trial dynamics of MT responses propagate to LIP. To accomplish this, we developed a reverse-correlation motion-discrimination task that allowed us to control the time course of visual motion on each trial and to disambiguate the influence of various task variables, thus statistically resolving multiple response components. Monkeys to performed this direction discrimination task while we recorded neural activity in both MT and LIP. The combination of these approaches allowed us to use a single-trial statistical model to characterize how the stimulus, perceptual decisions, and the responses of MT and LIP neurons relate to one another.

This approach provided several new insights into the relationship between MT and LIP. We found that both MT and LIP, as well as the behavioral decisions, depended most strongly on motion early in the trial. MT contained a temporally re-weighted representation of the stimulus that itself was sufficient to explain a large portion of the strongly time-varying stimulus weighting evident in both behavior and in LIP responses, implying that a substantial part the early weighting in decisions and their neural correlates may be inherited from MT output. Similar to prior reports²², LIP’s responses to brief pulses of motion were sustained over many hundreds of milliseconds, consistent with the notion of temporal integration underlying the transformation of MT responses to a decision variable. However, LIP responses were not completely explained by the integration of MT output, and instead required the addition of large ramping signals that signified the eventual choice on that trial, but which were statistically decoupled from the time-varying motion signal. Finally, LIP’s decision-related responses were not better explained by incorporating simultaneously-measured MT activity, consistent with the idea that a significant number of stages intervene between the two areas^6,23.

Taken together, this constellation of results provides refinement of the MT-LIP integration framework. Our single-trial analyses identified dynamics in MT that likely contribute substantially to the temporal weighting seen in other brain areas and in decisions. They also cast LIP as an area with time-varying average activity that can be decomposed to reveal separate stimulus-driven activity and time-varying premotor buildup. Although both the stimulus-driven and motor-related activity are of course correlated with decision formation, this functional dissection suggests that sensory weighting and the preparation of response are encoded in distinct signals that may evolve in parallel and be mixed at the level of individual spike trains.

Results

Behavior and physiology in a reverse-correlation direction discrimination task

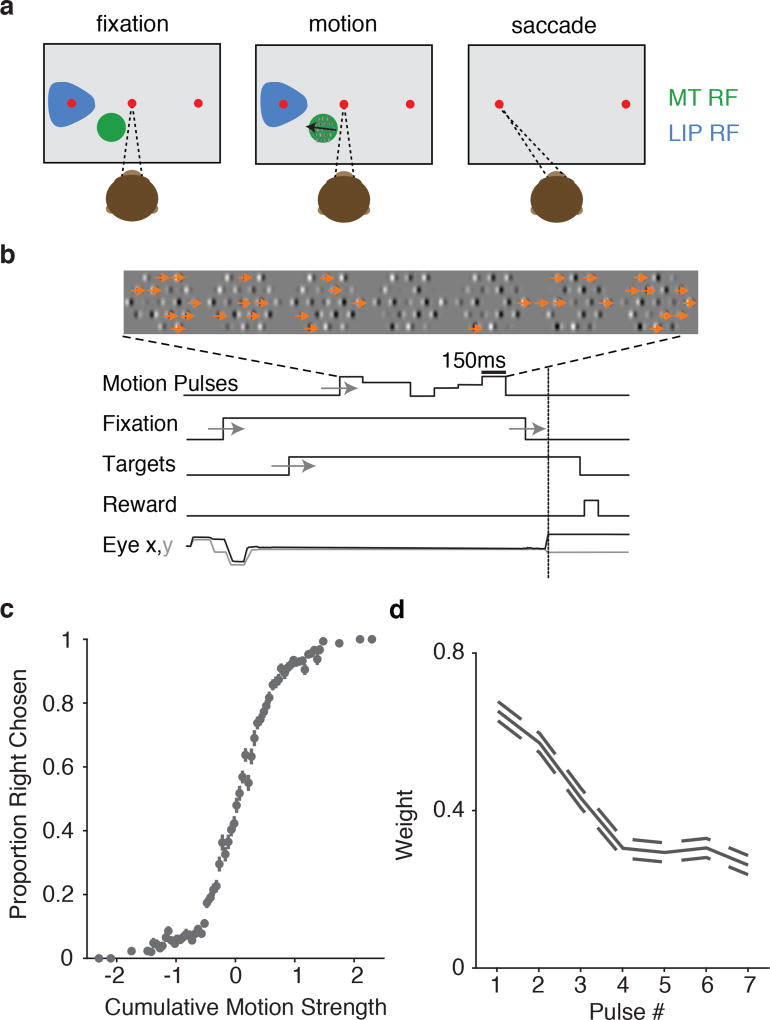
MT and LIP responses have vastly different temporal dynamics, which are thought to support their distinct roles in decision-making⁵. To characterize the response properties of both areas, as well as the psychophysical performance of the monkeys, we developed a motion discrimination task amenable to single-trial statistical analysis. Similar to an often-used moving-dot direction discrimination task, monkeys viewed a field of dynamic (flickering and drifting) elements (Gabor patches), and indicated their choice about the net direction of motion with an eye movement to one of two choice targets (Figure 1a). The strength of motion was controlled by manipulating the proportion of drifting Gabors (Figure 1b). Importantly, on each trial, the time course of directional information was manipulated across seven consecutive “motion pulses” (Figure 1c). The direction and strength of each pulse was drawn randomly so that we could correlate each pulse with the behavior and neural responses. Decisions exhibited a conventional sigmoidal dependence on the net motion strength (i.e., the integral of the motion pulses; Figure 1d), and early pulses contributed more to behavior than late pulses (Figure 1e; Supplemental Figure 1); this is similar to temporal weighting inferred from the classic moving-dot experiments^22,12,24,9.

Figure 1.

Experimental setup: Motion discrimination task, basic psychophysical performance, and geometry of task with respect to physiology. (a) Monkeys indicate their choice about the net direction of motion (in an array of drifting and flickering Gabor patches) with a saccadic eye movement. One target is place in the LIP RFs (blue). The motion stimulus is placed within the RFs of MT neurons (green). (b) The motion strength at any given time is manipulated by changing the proportion of drifting vs. flickering Gabor elements. Each motion stimulus presentation is separated into 7 consecutive motion “pulses”; each pulse has a random, signed, motion strength and lasts 150ms. (c) Trial timings: Motion consists of seven separate pulse epochs on each trial. The monkey must wait for the fixation point to extinguish before making a saccade to one of the two choice targets. Timings of experimenter-controlled task variables are jittered according to a uniform distribution (depicted by gray arrows). (d) Average dependence of choices on the cumulative motion strength and direction (n=22,838 trials) (e) Psychophysical kernel from behavioral data during electrophysiological recordings shows early weighting, with earlier pulses affecting decisions more than later pulses, as measured with logistic regression (dashed lines indicate ±1 s.e.m.).

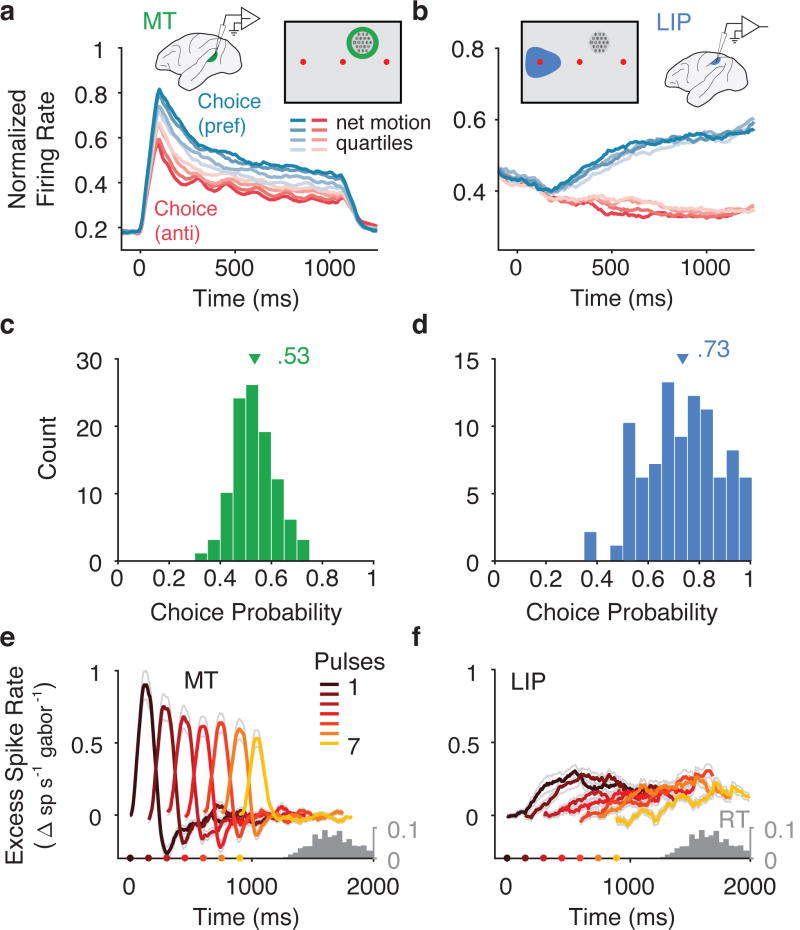
We recorded from 157 MT and 200 LIP single- and multi- unit clusters (hereafter “units”) across 42 sessions. Keeping with standard practice, we placed the motion stimulus in the receptive fields (RFs) of one or more MT units, and one of the choice targets in the RFs of the LIP units. MT units that were well-targeted by the motion stimulus (n=113, MT units with |d′| > 0.2) had robust responses during motion that increased rapidly after motion onset and decayed to a plateau(Figure 2a), similar to responses to classic moving-dot stimuli at low coherences²⁵. Well-targeted LIP units (n=104, LIP units |d′| > 0.2) had average firing rates that ramped up preceding choices into the RF, where the slope of the ramp was modulated by the net motion strength (Figure 2b). The particular steepness of the ramping relative to motion strength matched prior reports when plotted using matching conventions (Supplemental Figure 2).

Figure 2.

Population responses from MT and LIP. (a) Average firing rates for MT (n=113), sorted by choice and motion strength. Responses were sorted by choices in the preferred direction (blue) and anti-preferred direction (red) and the cumulative motion strength on each trial was divided into quartiles (shaded levels). Insets depict the recording setup and the geometry of the task with respect to the receptive field locations. (b) Same as in a except for LIP (n=104). (c) Choice probability (CP) for MT units calculated using repeated trials (with frozen random seeds). Triangle indicates mean, 0.53 (n=104 MT units with > 20 repeat trials). (d) CP for LIP units calculated with frozen repeat trials. Triangle indicates mean, 0.73 (n=91 LIP units with > 20 repeat trials). Units were only included if they had > 20 frozen repeat trials. (e) Average effect of a pulse in the preferred direction on firing rate in MT (scaled by the number of Gabors pulsing) across the population (n=113). Color indicates pulse number. Thin gray lines reflect ± s.e.m. across neurons. Gray histogram reflects the distribution of saccade times. (f) same as in e for LIP (n=104).

We also quantified the relationship between spiking activity and choices on repeats of identical trials (i.e., “frozen noise”) using choice probability (CP)¹. CP in MT was conventionally small but significantly greater than chance (Figure 2c; mean=0.53, p=1.36×10^-4, Student’s t test, two-sided, t(103)=3.963, n=104 well-targeted MT units with sufficient repeated trials). In LIP, the correlation with choice was much larger (Figure 2d; mean=.73, p=2.9×10^-26, Student’s t test, two-sided, t(90)=15, n=91 well-targeted LIP units with sufficient repeated trials). Given that both the psychophysical behavior and physiological responses in MT and LIP were reconcilable with prior literature, we then used our framework to precisely characterize how the time-course of motion integration evolves from the stimulus to MT, and from MT to LIP.

Motion responses in MT decrease over time, consistent with behavior

We first sought to directly characterize MT’s representation of the motion stimulus, instead of assuming a temporally stationary representation^7,5,8,9. Our motion paradigm was designed for direct reverse-correlation analysis, such that there were many trials on which the direction of motion was uncorrelated across the seven pulse epochs. This allowed us to measure the change in spike rate that resulted from a pulse in the preferred direction of the neuron, similar to the measurement of the psychophysical weighting described previously.

To describe the temporal dependence of MT and LIP responses on the motion pulses, we calculated a pulse-triggered average (PTA) separately for each of the seven pulses (Figure 2e,f). The PTA depicts the change in spike rate resulting from a single Gabor pulsing in the preferred direction of the neuron, assuming a linear scaling with motion strength (Methods). Although all seven of the pulses exerted strong and fairly transient effects on MT spike rate, early pulses affected MT considerably more than later pulses (Figure 2e). This effect was large, with pulses in the seventh (final) epoch generating only 63 ± 12% (mean and s.e.m., n=113, well-targeted MT units) of the (net) spike count of pulses in the first epoch. Thus, contrary to the simplifying assumption of a flat and faithful representation of direction evidence, MT emitted a time-varying representation of direction.

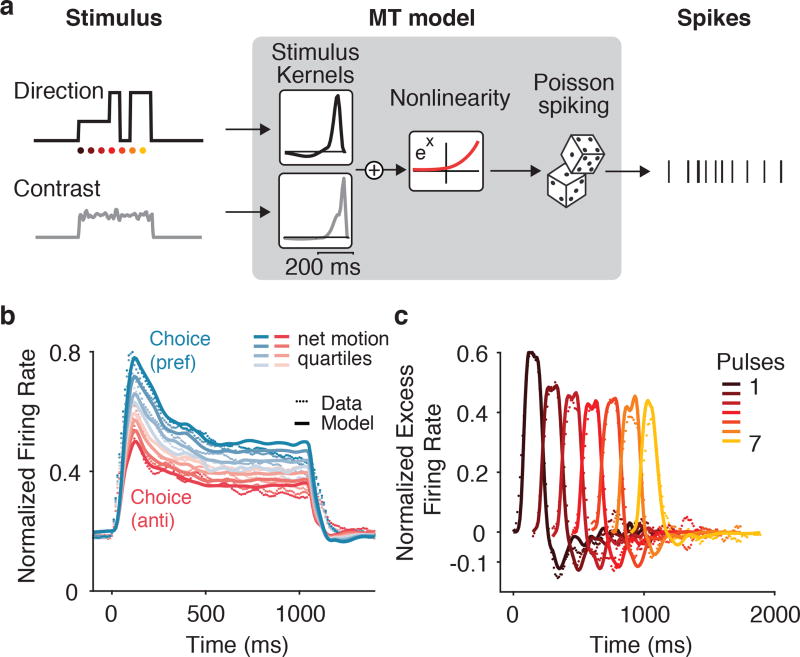
We investigated whether MT’s temporal pattern of response was well explained by a simple encoding model given by a Poisson generalized linear model (GLM)^26,15. This model is defined by three stages: (1) a linear stage that filters each stimulus component; (2) an exponential nonlinearity that converts the summed filter outputs into a spike rate; and (3) conditionally Poisson spiking. This “stimulus-to-MT” model included time-varying stimulus inputs for the direction and strength of the motion pulses, the spatially averaged contrast of the Gabors, the onset of the choice targets, and the time of the saccadic eye movement on each trial (Figure 3a; targets and saccade not shown).

Figure 3.

MT temporal weighting explained by linear-nonlinear (LN) model. (a) Schematic of modeling approach. The contrast and direction of each Gabor are summed spatially and form two temporal inputs to a Generalized Linear Model (GLM). The recovered population average temporal filters for contrast and direction (insets in diagram) show brief integration of these inputs. The filtered output is then passed through an exponential nonlinearity to generate the rate of a conditionally –Poisson spiking process. (b) Population (n = 113) PSTH for MT (dotted lines) superimposed with model prediction (solid lines). (c) Population (n = 113) average PTA (dotted lines) superimposed with model PTA (solid lines).

The stimulus-to-MT model reproduced the average stimulus-dependent responses for MT (Figure 3b), capturing 78% ± 1.56 (mean and s.e.m., n=113, well-targeted MT units) of the variance of the PSTH for each unit. Additionally, the model produced time-varying pulse responses that matched the decay in the MT data (Figure 3c). This analysis suggests that a substantial component of the time-varying stimulus representation could be sensory in nature, and is parsimoniously explained by a conventional linear-nonlinear (LN) framework. The stimulus-to-MT model captures the falloff in direction-selectivity over time in a manner similar to gain control. The “contrast” term— which was necessary to capture the onset transient and response plateau during visual stimulation of the RF— scales the response to direction by moving the output of the direction filters to a steeper or shallower part of the nonlinearity. Although our model is simply a statistical description of MT responses, a similar mechanism has been proposed to explain enhancements in other contexts²⁷.

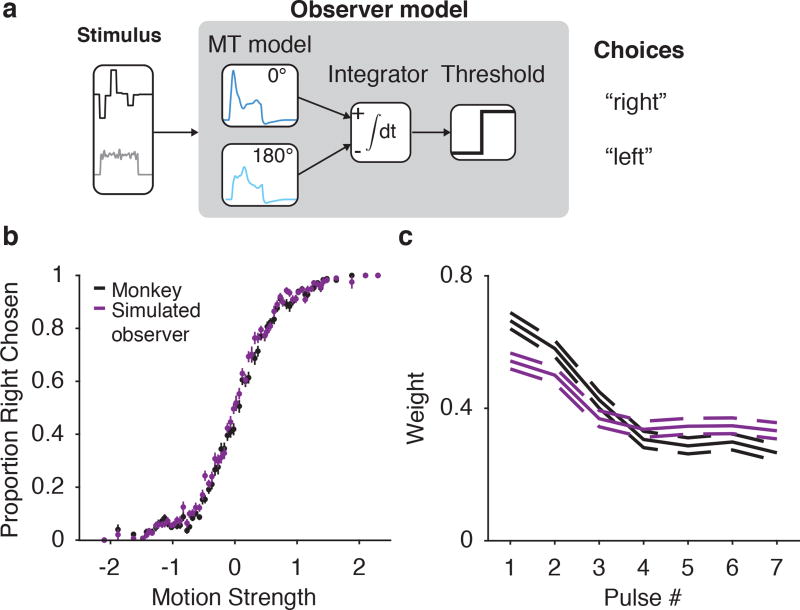
Given that the falloff in MT response was captured by a simple model, we then tested how this MT weighting might affect the time-varying dynamics of psychophysical weighting (and, later, how it might affect LIP responses). We used the stimulus-to-MT model to simulate two pools of realistic MT responses (i.e., generated from fits to our data) to every exact stimulus the animal was shown, and generated predicted psychophysical responses by comparing the time-integrated responses of the two MT pools (Figure 4a). We matched the sensitivity of the model observer to the actual psychophysics by adding noise to the pools before integrating. After adjusting this noise level with a single-parameter fit to the overall accuracy of the monkeys, the resulting psychophysical kernel exhibited a decay in weighting, commensurate with the decay in the MT responses (Figure 4b,c). Thus, the time-varying sensory representation itself enforces a stronger relation between stimulus direction and choices early during motion viewing. Because our decision model was a simple linear integrator, it provides a conservative account of the magnitude of the time-varying MT signal on the time-varying impact of each pulse on choices; downstream nonlinearities (either in sensory processing or decision mechanisms) could quantitatively alter this relation. The key point here is simply that a substantially time-varying representation is already contained in the sensory signals available from MT– which in turn constrains interpretations of the source of both time-varying psychophysical weighting and LIP responses.

Figure 4.

Early weighting in MT impacts psychophysical weighting. (a) Schematic of a model psychophysical observer based on model MT input. The stimulus is converted into model MT outputs for two pools of MT neurons, which are then integrated and compared to predict choices. (b) Psychometric function for the model observer (purple) overlaid with the data (black) (n=22,838 trials). Error bars are ± s.e.m. (c) Temporal weighting for an observer based on perfect integration of simulated realistic MT neurons (purple) overlaid with the data (black). Dashed lines indicate ±1 s.e.m.

LIP responses reflect more than the integration of MT signals

LIP’s motion-dependent ramping spike rates have long been interpreted as a reflection of the integration of MT responses⁷. Moreover, LIP firing rates have been shown to exhibit sustained deviations in response to single motion pulses, as measured relative to trials matched for choice and (unperturbed) motion strength²². Using our reverse-correlation paradigm, we measured how LIP firing rates reflect both the motion evidence and the upcoming choice. The LIP pulse-triggered average revealed considerably more complex responses than we observed in MT. First, as expected, the response to motion was delayed relative to MT, and sustained over many hundreds of milliseconds (Figure 2f). Second, responses to later pulses were not simply of lower amplitude, but instead increased much later relative to pulse onset. We reasoned that these delayed dynamics were likely dominated by buildup activity preceding the saccadic eye movements (Figure 2f), as the choices indicated by those saccades were correlated with the preceding motion pulses. This was confirmed coarsely by calculating a choice-corrected PTA (Supplemental Figure 3), but here we apply our GLM framework for a more principled dissection of the partially correlated variables that drive LIP. Importantly, because the individual motion pulses on each trial were not perfectly correlated with the choice, the GLM can resolve which aspects of the stimulus and task offer the best statistical explanation of the single-trial spike trains.

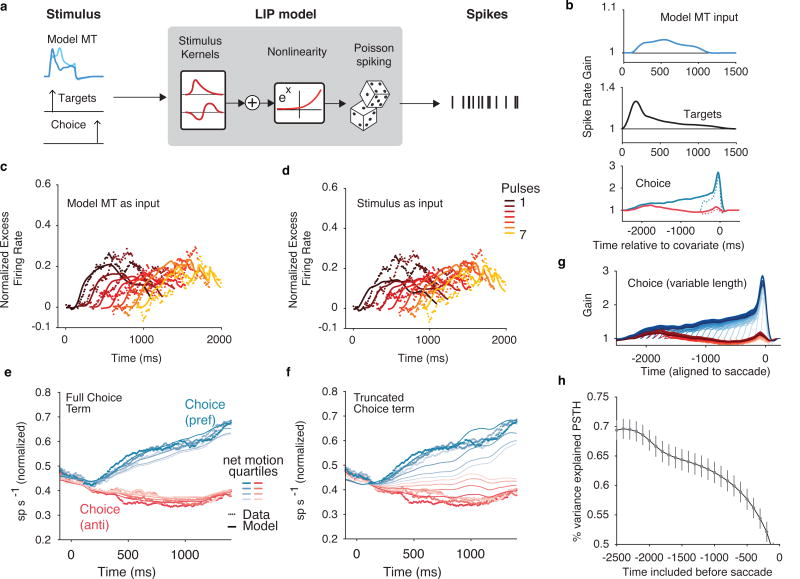
Given that the integration of MT is a fundamental component of many models of LIP^7,5,8, we first tested whether the integration of MT was sufficient to explain the LIP responses. We used the data-informed descriptive model of MT responses described above (“stimulus-to-MT”) as the temporal input to a GLM fit to LIP spike trains (Figure 5a). Additionally, we included terms to capture the well-documented responses to the onset of targets in the RF²⁸ and premotor preparatory activity preceding saccadic eye movements into the RF²⁹. This model builds off the parameterization of previous applications of the GLM¹⁵, with two critical extensions: First, the motion term was represented either by the reverse correlation motion-pulse stimulus itself (as in the stimulus-to-MT model), or by our data-informed model MT that contained realistic temporal weighting (Figure 5a). Second, we considered a range of parameterizations of the pre-saccadic choice: an unconstrained one that extended for 2.5 seconds before the saccade (as in¹⁵), and others that were truncated to shorter time spans, including one that enforced the premotor component did not overlap with the motion-viewing epoch.

Figure 5.

LIP encoding model requires choice terms to capture response dynamics. (a) LIP model schematic. Simulated MT, target onset, and saccade times are passed in as temporal signals to a GLM fit to LIP spike trains. (b) Population (n=104) average temporal kernels expressed as impulse response (in units of spike rate gain) by exponentiating the filter outputs. (Top) Spike rate gain in response to an early pulse in the preferred direction of the LIP neuron. (Middle) response to the onset of the targets. (bottom) acausal response to choices into the RF (blue) and out of the RF (red). Dashed lines represent the temporally truncated terms that generate the PSTH in panel f. (c) Pulse-triggered average (PTA) of the data (dots) compared to the model (lines) using realistic stimulated MT for each of the seven pulses (n=104). (d) Same as in c for an LIP model that receives the stimulus as input. The failure of this model in accounting for LIP’s responses to early pulses highlights the importance of MT’s response dynamics. (e) PSTH for the data (dots) superimposed with the model (lines) including the full choice terms in b. (f) PSTH for the data (dots) superimposed with the model (lines) using truncated choice terms. (g) Choice kernels truncated at 100ms steps shows that there are still nonzero weights even 2 seconds before the saccade on each trial. (h) PSTH variance explained for different length choice kernels (shown in g). Error bars indicate ±1 s.e.m.

We compared the “MT-to-LIP” model (which received a filtered motion representation from our realistic MT model) with one that operated directly on the (unfiltered) stimulus (“stimulus-to-LIP”). The more realistic MT-to-LIP model provided a better account of LIP’s responses than the stimulus-to-LIP model (3% higher likelihood per trial on test data, mean difference, p=9.8×10^-5, Wilcoxon signed rank test, n=104, well-targeted LIP units). Additionally, the MT-to-LIP model inherited the early weighting from MT (Figure 5c,d), which provided a better description of the population than the stimulus-to-LIP model (21 ± 8% more variance explained, population average, bootstrapped 68% confidence intervals, n=104). The recovered kernels (Figure 5b) confirmed that LIP was driven by the onset of targets and the direction of the stimulus (as represented by simulated MT) for a sustained period of time.

Despite the observation of sustained temporal kernels in our model-based (i.e. MT-to-LIP) explanation of the time-varying dynamics of LIP’s response to individual motion pulses, such motion integration by itself failed to capture the average LIP responses during motion viewing (Figure 5e,f). Instead, the fits required a premotor term, which extended many hundreds of milliseconds before the saccade (Figure 5b), and was critical for explaining the majority of the ramping responses (14% more variance of the PSTH on test data explained, p=9.6×10^-19, Wilcoxon signed rank test, n=104, well-targeted LIP units) and was a better description of single-trial activity than a model without choice-dependent terms (1.34 times higher likelihood per trial on test data than without choice terms, p=1.6×10^-10, Wilcoxon signed rank test, n=104, well-targeted LIP units). If we truncated these terms to only a few hundred milliseconds before the saccade, as is often asserted to be the premotor epoch of LIP responses by various analyses⁷, these modified models (which rely solely on motion integration to explain dynamics during motion viewing) could not capture even the average responses (Figure 5f). Specifically, no model based solely on integrated motion signals (modeled either as the stimulus or as the MT output) could capture the relatively steep slopes of the ramps for low coherence.

The stochastic time-varying nature of our stimulus allowed us to separate choice dependence and motion dependence in LIP spike rates. To test this systematically, we assessed a family of model fits that truncated the pre-saccadic choice kernels at different durations (Figure 5g). Longer choice kernels continued to improve the model fit for at least 2 seconds preceding the saccade (Figure 5h). The addition of long premotor choice terms was not necessary when we applied the same GLM to a simulated neuron that exclusively integrated MT signals (Supplemental math note), validating the model-based decomposition that pointed to a substantial choice-dependent premotor term in the real data. Thus, the ramping responses in LIP, even early in motion viewing, are probabilistically linked to the future eye movement, although they also carry a lower-amplitude contribution related to the integration of motion.

Up to this point, we have primarily considered how simple models explain the responses of the MT population average with respect to the stimulus, and how the average LIP response relates to that MT population average. In addition to the population-level insight that LIP responses could not be completely explained by an appeal to integrated MT responses, at the level of individual neurons, we noted that one third of LIP units had little if any motion-direction response component (36/104 units, test log-likelihood ratio per trial < 0, comparing model without direction filter to model with direction filter, n=104 well-targeted LIP units), and instead their ramping was accounted for by the premotor component and the timing of the motion onset, without the inclusion of any directional information. This finer-grained observation bolsters the dissociation between LIP (as a whole) and the integration of MT outputs, and motivates a final analysis in which we focused on the single-trial co-fluctuations of individual MT and LIP neurons.

Single-trial correlations between MT and LIP

Recent work has confirmed that MT is required for performance of this task²³, and it is likely that the motion signals in LIP originate there, regardless of the number of intervening stages⁶ or whether LIP is causally involved²³. If the mechanism that produces LIP’s motion-dependent responses was governed by a direct MT-LIP pathway, the trial-by-trial variation in MT activity should be predictive of LIP activity. To further investigate the relationship between MT and LIP, we turned to our simultaneous recordings from both areas to ask whether trial-by-trial fluctuations in MT activity were predictive of fluctuations in LIP.

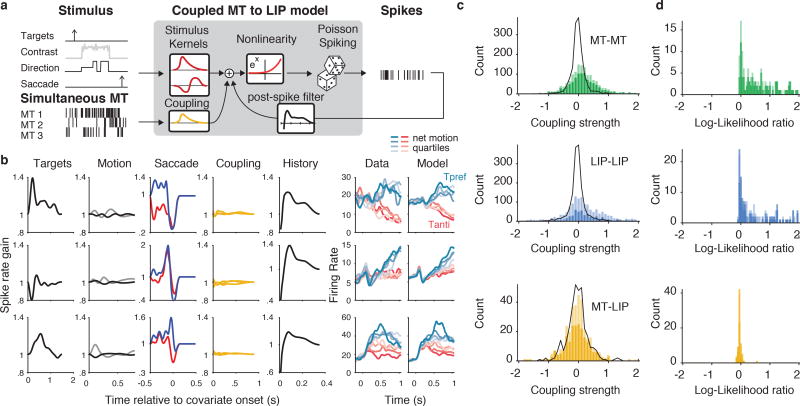
We successfully recorded from both areas simultaneously on 18 of the sessions, yielding 100 MT units, 67 LIP units, and 323 MT-LIP pairs. We extended the GLM to capture dependencies between neurons by incorporating coupling terms, which take spikes from simultaneously recorded units to help predict the spike trains of the unit being modeled (Figure 6a). Figure 6b shows coupling analyses in the “fully-coupled MT-to-LIP model” applied to example LIP units for which we had simultaneously recorded from multiple MT units. These coupling filters are similar in spirit to the positive lags of cross-correlations, except that they can be fit directionally and only measure variance that is not already explained by the stimulus and task variables (including the autocorrelation / spike-history dependencies of individual units). What is immediately apparent is that the kernels related to the targets, the saccade, and the cell’s own spike history are large, the motion-related kernel is relatively small, and the presence of the MT-to-LIP coupling filters is difficult to discern.

Figure 6.

Model-based explanation of LIP is not improved by adding coupling to simultaneously-recorded MT. (a) Schematic of the coupled MT-to-LIP model. The stimulus covariates and simultaneously-recorded MT spikes are passed into the GLM as a temporal signal; the neuron’s own spike history is also used to capture the autocorrelation. (b) Example fits: each row is an example LIP unit. Each column represents a separate covariate, expressed as spike-rate gain. “Motion” depicts both the direction kernel (black) and the contrast kernel (gray). “Saccade” depicts truncated choice terms for choices into the RF (blue) and choices out of the RF (red). On the right, the data PSTH and model PSTH are shown. (c) Strength of coupling compared to null model. The sum of each coupling filter is plotted as a histogram for different coupling types: MT intra area (green; n=1,474, MT-MT coupling filters), LIP intra area (blue; n=1,484, LIP-LIP coupling filters), and MT-to-LIP (yellow; n=333, MT-to-LIP coupling filters). Dark colors reflect coupling from units that were well targeted (n=1051 MT-MT, n=689 LIP-LIP, n=227 MT-LIP, from units with |d′| > 0.2 that were included in analyses for figures 2,3,5). Light color reflects coupling filters from poorly targeted units (n=423 MT-MT, n=793 LIP-LIP, n=106 MT-LIP). Black lines show the null distribution of coupling filter strengths. MT-MT and LIP-LIP coupling filters were significantly different than the null distribution for all selection criteria (p=1.7×10^-40, KS test, n=1474 MT-MT filters, p=1.5×10^-15, KS test, n=1482 LIP-LIP filters). MT-LIP coupling filters were not significantly different than the null (p=.29, KS test, n=333 MT-LIP filters). (d) Cross-validated model comparison of coupled to uncoupled model for different coupling types (log-likelihood ratio per trial; same color scheme as in c). MT-MT (n=156 MT units with simultaneous MT, n=112 with |d′| > 0.2) and LIP-LIP (n=197 LIP units with simultaneous LIP, n=101 with |d′| > 0.2). Model comparison for MT-LIP coupling. Inter-areal coupling did not significantly improve fit (p=0.99, Wilcoxon signed-rank test, one-sided, n=67 LIP units with simultaneous MT, p=0.91, Wilcoxon signed-rank test, one-sided, n=25 LIP units with |d′| > 0.2, dark yellow).

To more quantitatively interpret the MT-to-LIP coupling terms, we also characterized intra-area (MT-MT and LIP-LIP) coupling as a point of comparison. Across all experiments, we recorded from 737 MT pairs and 741 LIP pairs. In contrast to the cross-area coupling, the contribution of within area coupling was strong and easy to observe. On average, the GLM fits with added intra-area coupling were 3.67 times higher likelihood per trial on test data than the uncoupled model for MT (Figure 6c green, p=1.8×10^-26, Wilcoxon signed rank test, n=156, MT units with simultaneously recorded MT units) and 16.4 times higher for LIP (Figure 6c blue, p=7.6×10^-20, Wilcoxon signed rank test, n=197, LIP units with simultaneously recorded LIP units), demonstrating that within-area activity reflected strong coupling between neurons. To establish whether the measured MT-LIP coupling filters (Figure 6b; yellow) were strong enough to be meaningful, we first tested whether the size of observed coupling was larger than expected if the units were conditionally independent. We simulated responses from independent Poisson neurons based on the fits from the stimulus-to-MT and MT-to-LIP models described above. We then fit the fully-coupled GLM to this surrogate population to obtain a null distribution of coupling strengths. The within-area coupling filters from the real data were significantly larger than this null distribution (Figure 6c yellow), but the MT-to-LIP coupling filters did not differ significantly from the null (independent Poisson) population (p=0.29, Kolmogorov–Smirnov test, n=333, MT-to-LIP coupling filters). More importantly, we compared the predictive power of the fully coupled model to the uncoupled model on withheld data and observed no benefit for the inclusion of coupling (Figure 6d yellow; p = 0.99, one-sided Wilcoxon signed rank test, n=67, LIP units with simultaneously recorded MT). We did observe a small number of LIP units that depended on MT on single trials (8/67; test log-likelihood ratio per trial > 0), but these pairs involved neurons with unusual response dynamics in either MT or LIP (Supplemental Figures 4,5,6). In summary, single-trial correlations from MT to LIP did not provide support for a direct MT-to-LIP integration mechanism, although simulations with inter-areal coupling (as well as the small number of coupling observations between non-canonical neurons) suggest that it was possible to detect these in principle under many reasonable conditions (Supplementary math note).

Discussion

MT and LIP are two brain areas with long-standing hypothesized roles in perceptual decision-making⁵. Using a reverse correlation psychophysical paradigm, simultaneous multi-neuron / multi-area recordings, and single-trial generalized linear model analysis, we uncovered several revealing components of how activity in MT and LIP relate to the stimulus, behavior, and each other. First, we observed attenuating responses to motion, not just in LIP and behavior, but also in MT. MT’s response attenuation could be largely explained with a simple feedforward model, in which its response to directional motion was modulated by a decaying contrast gain component. The observed level of attenuation of the representation of direction at the sensory level likely has substantial downstream effects on psychophysical weighting and LIP responses. Second, spikes in LIP could not be explained by linear integration of motion signals, but required a term more directly linked to the upcoming saccade. Third, coupling analyses revealed strong statistical dependencies between LIP neurons, but no meaningful noise correlations (or coupling) between MT and LIP.

Our MT data suggest that interpretations of psychophysical weighting, as measured with reverse correlation, are likely affected by dynamics that are present in the sensory representation (as opposed to solely reflecting the decision mechanisms). Although we have shown the observed decay in MT response can be explained with a feedforward model, further experimental manipulations would be necessary to explore the possibility that the early weighting in MT results from top-down (i.e., strategy-driven) feedback. In fact, similar decreases in sensitivity over time can be expected from models that feed back the decision to sensory areas, which also produce early psychophysical weighting⁹. Early psychophysical weighting has been widely observed in nonhuman primates^12,24,30, although rodent studies, and some human studies have observed flat psychophysical weighting^31,32,33. It is unclear whether differences in the stimuli across experiments, combined with our feedforward explanation, are sufficient to explain these differences in findings. Neural recordings during systematic manipulations of sensory adaptation and/or psychophysical strategy will be needed to isolate these two sources.

Although our LIP neurons, which had the choice targets in their RFs, contained a signature of motion integration, their responses were not easily accounted for with the integrated output of MT. Instead, our decomposition analyses suggest a small motion integration term rides on top of a large and conventional premotor buildup^29,21,34. As this premotor buildup was choice dependent, it did not correspond to the canonical “urgency signal”¹⁶ (Supplemental Figure 7). Similar buildup activity is present before task training¹¹, and in other tasks²¹. This choice-dependent (but coherence-independent) buildup might be interpretable as a dynamic bias signal or as the addition of a neural representation of motor-related hazard rate³⁵. However, given that our experiment did not systematically manipulate bias and because the ensuing motor response was well after the end of the fixed duration motion stimulus, the simplest interpretation of the large ramping term is that LIP carries a signal correlated with the timing (and/or likelihood) of upcoming saccades that is distinguishable from motion integration.

In contrast to the clear statistical decomposition of the task-variables driving MT and LIP, we did not detect meaningful single-trial coupling between areas. It is possible that by sampling relatively small subpopulations of MT and LIP neurons, we were not able to resolve feedforward connectivity that indeed exists anatomically³⁶—although studies with similar sample sizes have found coupling between different areas in similar paradigms³⁷. However, our results are parsimoniously explained if the signature of motion–integration in LIP emerges from an indirect pathway. Of course, the notion of intervening processing between MT and LIP is not new⁶. Comparisons between the two areas during the classical moving dots task reveal roughly 100 msec between MT and LIP responses to motion¹². Furthermore, the flexible spatial mapping between visual motion (which drives MT neurons) and saccadic choice targets (used to drive LIP neurons) is also consistent with substantial intervening processing to establish the sensorimotor routing between the two areas. The lack of measurable noise correlations in this paradigm is therefore distinct from investigations that typically focus on measuring inter-areal co-fluctuations between neurons with overlapping receptive fields³⁸, although we did not see differences for LIP units with motion in their RFs (Supplemental Figure 8).

Taken together, our electrophysiological findings support a more nuanced and positive conclusion than recent null results of LIP inactivation²³; namely, that the decision-correlated activity in LIP reflects a record of the evolving response plan that emerges in parallel with the integration of perceptual evidence. Complemented by recent experimental manipulations of sensory-motor mappings¹⁹, this distillation of motor preparation from motion integration refines simpler mechanistic interpretations of LIP’s trial-averaged ramps as uniquely reflecting the accumulation of evidence. The response-related component we identified may correspond to other time-varying signals posited to contribute to decision making^39,40, but given that LIP responses are not causally required for this task²³, we posit that this signal is not part of the decision computation itself and more simply reflects the evolving prospect of a particular response²⁹. Thus the ramping activity seen in LIP may not provide a direct and/or unitary window onto the neural basis of psychological evidence accumulation, and the constellation of physiology and psychophysics may benefit from considering a wider class of models^41,42,43 – and likewise, how mixtures of sensory and motor variables can combine to generate ramping activity^{44,32,43,39,45}. Furthermore, the mixture of multiple decision-relevant and –irrelevant factors driving LIP constitute a complex representation that, if used to perform certain tasks, will either produce behavior that depends on multiple factors⁴⁶, or which requires a read-out scheme that de-multiplexes this complex signal¹⁵. In summary, these techniques (simultaneous recordings of multiple neurons in two areas, coupled generalized linear models, and an integrated reverse-correlation framework) have provided the basis for a more detailed understanding of the computations in MT and LIP. The application of these techniques to other parts of this circuit (e.g.,^47,48) is particularly motivated by our results, which suggest that a substantial component of decision-making occurs somewhere between MT and LIP.

Online Methods

Stimulus apparatus

All stimuli were presented using the Psychophysics Toolbox^49,50 with Matlab (The Mathworks) using a Datapixx I/O box (Vpixx) for precise temporal registration⁵¹. Monkeys sat in a primate chair (Crist Instruments) and faced a 55 inch LCD (LG) display (resolution = 1920 × 1080p, refresh rate = 60Hz, background luminance − 26.49 cd/m²) that was corrected to have a linear gamma function. Monkeys viewed the stimulus from a distance of 118cm such that the screen subtended 100 degrees of visual angle. Eye position was tracked using an Eyelink 1000 video eye tracker (SR Research), sampled at 1kHz. Reward was delivered through a computer-controlled solenoid.

Preparation and Electrophysiology

Data were recorded from two adult rhesus macaque monkeys (one male and one female, referred to as P and N hereafter), aged 14 and 10, weighting 10 and 7.7kg, respectively. All procedures were performed in accordance with US National Institutes of Health guidelines and approved by The University of Texas at Austin Institutional Animal Care and Use Committee and have been described previously²³. Extracellular recordings were accomplished using a combination of single electrodes (glass-coated tungsten; Alpha Omega; 8 sessions) and multisite linear-electrode arrays (U-probe or V-probe, Plexon; 50–150µm spacing; 35 sessions). Both areas were targeted using cranial landmarks or structural MRI. MT and LIP were identified using electrode depths, sulcal anatomy (identified with gray/white boundaries during recording) and functional mapping. Functionally, MT was identified based on receptive field size and a preponderance of directionally selective cells⁵². LIP was identified by spatially selective visual and saccadic activity with delay period activity during a memory-guided saccade task²⁸. The data have been described previously²³.

Recording from microelectrode arrays gave us a wide sample of units from MT and LIP (200 LIP, 157 MT). As such, we employed a set of inclusion criterion for our different analyses. The window of analysis was restricted to the largest region where all units had stable firing rates during the Gabor task (127 – 774 trials; median 426). For analyses of stimulus selectivity, we included all units that were sensitive to the net direction of the stimulus during the motion epoch by calculating a |d′| > 0.2. Although we targeted LIP neurons by placing the targets within the RFs of the units on our recording arrays, we noted that some LIP neurons that passed our inclusion criterion reflected onset transients to the Gabor stimulus, suggesting that at least part of their RF overlapped the motion stimulus. We excluded these units (n=11) from the main analyses and consider them separately (Supplemental Figure 8). Our results do not depend critically on the inclusion or exclusion of these units.

Gabor stimulus

The stimulus consisted of a hexagonal grid (5–7° across, scaled by eccentricity) of Gabor patches (0.9 cyc/deg). The spatial frequency was selected to roughly match the peak selectivity of MT neurons⁵³. The inter-element spacing and spatial standard deviation of each Gabor element were scaled by 10% of the eccentricity of the center of the aperture to match the average RF size of a v1 neuron at that eccentricity⁵⁴. This ensured that all of the Gabors were non-overlapping. The temporal frequency of the Gabors was 7Hz (Monkey P) or 5Hz (Monkey N), yielding speeds of 7.78 and 5.55°/s respectively. Subjects were trained to report the net direction of motion in a field of drifting and flickering Gabor elements with an eye movement to one of two targets.

Each trial’s motion stimulus consisted of seven consecutive motion pulses, each lasting 9 or 10 video frames (150ms or 166ms; pulse duration did not vary within a session), with no interruptions or gaps between the pulses. The strength of each pulse, X_i, was set by a draw from a Gaussian rounded to the nearest integer value: Z_i ~ 𝒩(μ, ν), X_i = round(Z_i), where μ and ν were fixed on each trial. For monkey P, pulse strengths, X, were discretized to a subset of possible integer values. On pulse i, |X_i| Gabors were randomly assigned to pulse and all would drift their carrier cosine-wave in the same direction (sign (X_i)) at their specified temporal frequency. The remaining Gabors underwent counter-phase flicker. The initial phase of each Gabor was assigned randomly to minimize grouping of flicker. The difficulty on each trial was modulated by manipulating both μ and ν. The monkey was rewarded based on the empirical stimulus, not the stimulus distribution. That is, for motion discriminated on a horizontal axis, the monkey was rewarded for making a choice to the target on the right if the sum of the seven pulses was greater than zero, and for making a saccade to the target on the left if the sum was less than zero. On trials that summed to exactly zero, the monkey was rewarded at random with probability 0.5. 10% of trials consisted of a fixed, frozen seed.

MT and LIP mapping

After hand-mapping the retinotopic location and direction selectivity of MT using drifting dot stimuli, MT selectivity was refined and quantified using a pair of protocols. For 59 units, we used a dynamic flow field to measure the direction preference and spatial RF^55,56. Spatial velocity fields were estimated using the spike-triggered average velocity at all spatial locations. This allowed us to measure the direction preference at each spatial location in the RF. For 122 MT units, we measured the tuning function by presenting drifting 100% coherence dots in 12 evenly spaced directions and counting spikes. Tuning was estimated by least-squares fitting of a von Mises function to the spike rate. 28 MT units were mapped using both methods.

LIP was mapped using a memory-guided saccade task²⁸. LIP response fields were estimated by counting spikes between target onset and saccade onset, and then using linear regression between the spatial location of the target and the spike rate on each trial. These maps were used for online guiding of the stimulus geometry, and offline confirmation of neural selectivity, however they did not guide our inclusion criterion for the main results.

Behavior

To measure the contribution of each pulse to the monkey’s choice on each trial, we used logistic regression, where the log-likelihood is given by

$$\text{log}ℒ(\mathrm{w};\mathrm{X},\mathrm{Y})={\mathbf{Y}}^{\mathrm{T}}\mathbf{X}\mathrm{w}-\sum \text{log}(1+\text{exp}(\mathbf{X}\mathrm{w}))$$

where Y ∈ {0,1} is a vector of the choice on each trial, X is a matrix, where each row is the seven pulses on that trial, augmented by a column of ones to capture the bias. The strength of the pulses was normalized by the standard deviation of all pulse values shown. The psychophysical performance (Figure 1d) was measured by calculating the proportion of rightward choices as a function of the net motion on each trial (sum of normalized pulse strength). The net motion strengths from all trials were divided into 30 equal quantiles to form the bins in Figure 1d.

Neural Analysis

To measure the relationship between the time-varying pulse strength and the spike rate, we measured the cross-correlation between pulses and the spike rate. The pulse-triggered average (PTA) effectively measures the excess spike rate that would result from a pulse at a particular time of unit strength. To compute the PTA, we binned the pulse stimulus and spike counts at 10ms resolutions. Let x(t) denote the value of the motion stimulus at time t, and y(t) the spike rate (spike count divided by the bin size). All trials were concatenated such that the stimulus vector, x⃗, is a vector of length T, the total time, and is zero everywhere except at the time of pulse onsets. For a pulse at time t, x(t) is the number of Gabors pulsing, with x(t) > 0 for pulses in the preferred direction and x(t) < 0 for pulses in the anti-preferred direction. To compute the temporal lags of the PTA, we build a design matrix, D, where D(i, j) is the stimulus, x⃗, at the i-th bin, at the j-th lag. We computed a separate D for each of the seven pulses and concatenated them to obtain a design matrix for all seven pulses X = [D₁, D₂, …, D₇] and estimated the PTA with ordinary least squares:

$$\mathit{\text{PTA}}={(X^{\mathrm{T}}X)}^{-1}(X^{\mathrm{T}}y)$$

This formulation of the PTA, which whitens the data, allowed us to include all trials, including trials with modest temporal correlation across pulses, increasing our statistical power. To calculate the motion- and choice-dependent Peri-Stimulus Time Histogram (PSTH), spike trains were smoothed by a 100ms boxcar and binned at 10ms. Pulse sequences were summed on each trial and these sums were divided into four equal quartiles for each choice. Choice probability was analyzed using stimuli generated from frozen random seeds (as described in ref 23).

Encoding Model

We compared multiple encoding models of single-trial spike trains to describe MT and LIP unit activity. All models were different variants of a GLM^57,58. We discretized time into 10ms bins (Δ=0.010 s). The log-likelihood for a single neuron is (up to an additive constant)

$$\text{log}ℒ(\mathrm{\lambda };\mathbf{r})=\sum _t\mathbf{r}(t)\text{ log}(\mathrm{\Delta }\lambda (t))-\mathrm{\Delta }\lambda (t)$$

where the conditional intensity (instantaneous spike rate) of the fully-coupled GLM, λ, at time t is given by

$$\lambda (t)=\text{exp}(\mathbf{k}·\mathbf{x}(\mathrm{t})+\mathbf{h}·\mathbf{r}(\mathrm{t}-1)+\mathbf{c}·\mathbf{s}(\mathrm{t})+\mathbf{b})$$

where k is the weights on the stimulus covariates, x; h is the post-spike weights that integrate the neuron’s own spiking history, r(t − 1); c is coupling weights on simultaneously recorded spikes s, and b is a constant offset to capture the neuron’s baseline firing rate. k comprises of a set of n_i weights for each of the m stimulus covariates and k·x is shorthand for ${\sum }_{i=1}^m{\sum }_{j=1}^{n_i}{\mathbf{k}}_{\mathit{\text{ij}}}{f}_j({\mathbf{x}}_i(t-\tau :t))$, where f_j are temporal basis functions – nonlinearly time-scaled raised cosine functions²⁶. To avoid overfitting, weights were fit with maximum a posteriori estimation of θ = {k, h, c} penalized with α(‖k‖₂ + ‖h‖₂ + ‖c‖₂).

The models we considered varied in their parameterization of the stimulus kernels, k, and their inclusion of coupling, c, and spike-history, h, terms. In the stimulus-to-MT model, the stimulus consisted of two temporal signals: the instantaneous signed pulse strength and the contrast of the motion stimulus. The contrast was the spatially averaged Michelson contrast of the Gabors on each frame.

The stimulus-to-LIP model had the same contrast and direction inputs as the stimulus-to-MT model, but also included the onset of the targets, and the choices as temporal inputs. In the MT-to-LIP model, we replaced the directional signal from the stimulus-to-LIP model with simulated average MT rates for two oppositely-tuned pools, using the model fits from the stimulus-to-MT model for each monkey’s respective population of MT units. To simulate MT in the anti-preferred direction, we flipped the sign of the direction filter, but kept the contrast filter identical (Figure 3a). We used these simulated rates in place of the direction to recover LIP’s “MT kernels” (Figure 5b).

For the fully-coupled MT-to-LIP model, we extended the stimulus-to-LIP model to included coupling filters, c, and spike-history, h. We compared this to an “uncoupled” model that had a spike-history filter, but no coupling filters. To evaluate the GLM fits, we used 5-fold cross-validation. We compared the test-likelihood normalized by the number of trials for each model. For coupled models, the model spike rate was estimated using spike input from the data. Goodness-of-fit (r²) was computed on test data by stitching across cross-validation folds to generate a PSTH.

Psychophysical observer based on simulated MT

To simulate psychophysical responses based on model MT, we simulated from the stimulus-to-MT model and averaged output to generate two oppositely-tuned pools (as described above). We simulated average spike counts with Poisson-like noise by adding Gaussian random noise with variance that was scaled by the mean rate. The rightward and leftward preferring pools had independent noise. The simulated observer perfectly integrated the MT counts and reported right whenever the sum of the rightward pool was greater than the sum of the leftward pool. We fit the standard deviation of the Gaussian noise by minimizing the squared error between the accuracy of the simulated observer and the monkey for each session and then pooled sessions to measure the psychophysical weights as described above. The results did not depend on the choice of noise and were similar for simulated downstream noise, Poisson-like noise, or Gaussian noise.

Statistics

No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications (ref 6,12,37). For parametric statistical tests (Student’s t test for difference of mean CP from 0.5), distributional assumptions were not tested. All other statistical hypothesis tests were nonparametric. To evaluate whether recovered coupling filters were of a magnitude greater than expected by chance, we simulated surrogate neural data for MT and LIP using the Stimulus-to-MT and Stimulus-to-LIP (with choice terms) models and then fit the fully coupled model to those surrogate units. Stimuli were generated at random. Analyses were not performed blind to the conditions of the experiments. More information is available in the Life Sciences Reporting Summary.