Local Genetic Correlation Gives Insights into the Shared Genetic Architecture of Complex Traits

Abstract

Although genetic correlations between complex traits provide valuable insights into epidemiological and etiological studies, a precise quantification of which genomic regions disproportionately contribute to the genome-wide correlation is currently lacking. Here, we introduce ρ-HESS, a technique to quantify the correlation between pairs of traits due to genetic variation at a small region in the genome. Our approach requires GWAS summary data only and makes no distributional assumption on the causal variant effect sizes while accounting for linkage disequilibrium (LD) and overlapping GWAS samples. We analyzed large-scale GWAS summary data across 36 quantitative traits, and identified 25 genomic regions that contribute significantly to the genetic correlation among these traits. Notably, we find 6 genomic regions that contribute to the genetic correlation of 10 pairs of traits that show negligible genome-wide correlation, further showcasing the power of local genetic correlation analyses. Finally, we report the distribution of local genetic correlations across the genome for 55 pairs of traits that show putative causal relationships.

Introduction

Genomic regions that harbor variants contributing to multiple traits provide valuable insights into the underlying biological mechanisms with which genetic variation impacts complex traits.^{1, 2, 3, 4, 5, 6, 7} Therefore, both de novo discovery of such regions as well as the quantification of the correlation in effect sizes at known shared regions are important to epidemiological and etiological studies. For example, genetic variants associated with multiple traits in genome-wide associations studies (GWASs) can be used as instrumental variables in Mendelian randomization analyses to suggest causal relationships among complex traits.^{7, 8, 9, 10} Unfortunately, many risk variants are left undetected by existing GWASs due to a combination of high polygenicity (i.e., many variants of small effects) and sample sizes which limits the power to detect genetic variants of small effect.¹¹ To improve accuracy at sub-GWAS significant regions, recent works^{1, 2} proposed to utilize the posterior probability of two traits sharing a causal variant at a given risk region to detect genetic overlap. Although powerful in detecting shared genetic risk variants, the posterior probability does not convey the direction or magnitude of the genetic effect at the overlapped genomic regions.^{1, 2} Alternative approaches have used genetic correlation (i.e., correlation of the genetic components of two traits), that summarizes both direction and magnitude of effects, to gain insights into genetic overlap of complex traits.^{12, 13, 14} Traditional methods to estimate genetic correlation are hindered by the lack of availability of large-scale individual-level data due to privacy concerns as they require individual genotype and trait measurements on the same set of individuals.^{12, 14, 15} More recent works have shown that GWAS summary data (i.e., effect sizes and standard errors at all variants typed in the study) are sufficient to estimate genome-wide genetic correlation under a polygenic trait architecture by aggregating information across all typed variants in the study.^{16, 17}

In this work, we investigate the correlation between traits due to typed genetic variants from a small region in the genome (i.e., local genetic correlation) as means to identify genomic regions that contribute disproportionately to the genetic sharing between traits. We introduce methods that estimate the local genetic correlation from GWAS summary data while allowing for overlapping GWAS samples and linkage disequilibrium (LD) among variants. We partition the genome-wide genetic sharing across approximately independent LD regions of 1.6 Mb in width on average.¹⁸ To allow for a broad range of causal effect sizes, our approach makes no distributional assumptions on the causal effect sizes by treating them as fixed quantities. Our method can be viewed as a natural extension to pairs of traits of recently proposed methods that quantify local SNP heritability from GWAS summary data under a fixed-effect model.¹⁹

We illustrate the utility of local genetic correlation through an analysis of GWAS summary data of 36 quantitative complex traits. We identify 25 genomic regions that show significant local genetic correlation across 27 pairs of traits; e.g., region chr2: 21M–23M that harbors APOB (MIM: 107730) shows a significant genetic correlation for the pair of traits high-density lipoprotein (HDL) and triglycerides (TG). Notably, 6 (out of the 25) regions show significant local genetic correlation although the genome-wide genetic correlation is not significantly different from 0; e.g., region chr6: 134M–136M shows a significant in local genetic correlation for mean cell volume (MCV) and platelet count (PLT) although the genome-wide genetic correlation MCV-PLT is negligible (0.02, 95% CI [−0.04, 0.07]). This shows that these traits are correlated at a local level (e.g., due to pleiotropy and/or shared pathways) that are not reflected in the genome-wide correlation (due to balancing effect of other loci; e.g., positive correlation partially canceling a negative correlation, see Figure 1). Regions with significant local genetic correlations can also be used to identify new risk loci. For example, although the region chr8: 9.2M–9.6M shows a significant local genetic correlation between HDL and LDL, it does not harbor GWAS variant for HDL and LDL. Finally, we explore putative causal relations between all the 36 studied traits using a recently proposed approach² and report 55 instances of pairs with putative causality. For most of these pairs, we show that the local genetic correlation ascertained for GWAS signals specific to each trait is consistent with the putative causal relation while providing a directly interpretable quantity of the magnitude of effect.

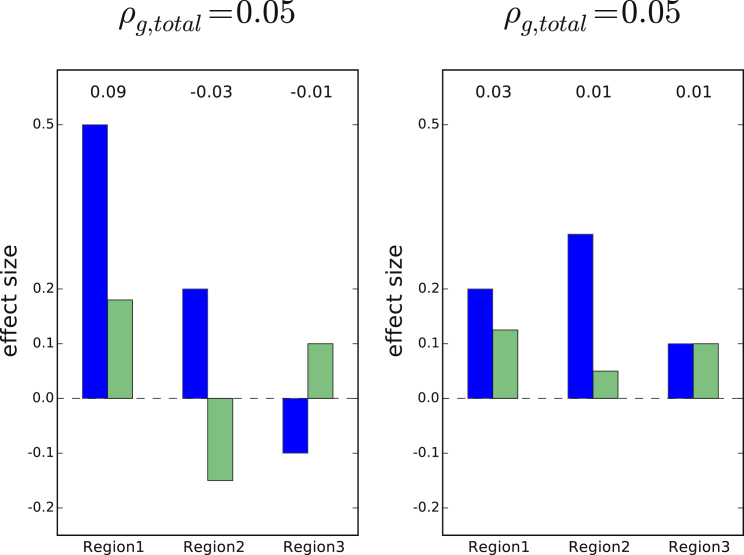
Figure 1.

Examples of Two Different Distributions of Local Genetic Covariances that Result in the Same Total Genetic Covariance

Covariances shown at the top of each bar; total genetic covariance (${\rho }_{g,total}$ = 0.05). In the left example, the total genetic covariance is a summation of a large positive local genetic covariance at region 1 and two smaller negative local genetic covariances at region 2 and region 3 (e.g., regions 2 and 3 impact traits through a different pathway than region 1). In the right example, the total genetic covariance is a summation of small positive local genetic covariances (e.g., all three regions impact both traits through the same pathway). Positive local genetic covariance can be interpreted as a locus driving a pathway that regulates two traits in the same direction, and negative local genetic covariance the opposite direction.

Material and Methods

Overview of Methods

Genetic covariance measures the similarity between a pair of traits driven by genetic variations and enjoys wide applications in understanding relations between complex traits.^{13, 20, 21} Genetic covariance is traditionally estimated as a single measure across the entire genome to capture the genome-wide contribution of genetic variations to the correlation between phenotypes. Here, we introduce local genetic covariance, the similarity between pairs of traits driven by genetic variations localized at a specific region in the genome (e.g., one LD block), as a principled way to partition the shared genetic risk between traits. For example, a high genome-wide genetic covariance can be driven by one genomic region containing a shared risk variant or by a large number of regions, each with a small contribution reflecting putative causal relations (where all risk variants for one trait are risk variants for the other trait) and/or pleiotropy (risk variants contributing to both traits through shared pathways) (see Figure 1). Whereas genetic covariance quantifies the magnitude of co-variation of the genetic components of two traits in their original scale, genetic correlation quantifies co-variation in a standardized scale and is therefore comparable across pairs of traits and/or genomic regions for which magnitude of effect size may differ. As a motivating example, consider two traits modeled by $\varphi =x_1{\beta }_1+x_2{\beta }_2+\mathit{ϵ}$ and $\psi =x_1{\gamma }_1+x_2{\gamma }_2+\delta$, where x₁ and x₂ represent two independent SNPs. In the special case where $\mathit{\gamma }$ is proportional to $\mathit{\beta }$ by a factor of α, i.e., $\mathit{\gamma }=\alpha \mathit{\beta }$, the genetic covariance between the two traits is $\alpha \left({\beta }_1^2+{\beta }_2^2\right)$ and is governed by α. However, the genetic correlation between the two traits is always 1 for positive α (−1 for negative α) regardless of the magnitude of α.

We start by defining local genetic covariance under the fixed effect model, making a distinction between genetic covariance and covariance of the causal effects, $\mathit{\beta }$ and $\mathit{\gamma }$ (see below). We then describe methods to estimate genetic covariance followed by an approach to standardize the local genetic covariance to estimate local genetic correlation.

Local Genetic Covariance under Fixed-Effect Model

Let $\varphi ={\mathit{x}}^{\mathrm{⊺}}\mathit{\beta }+\mathit{ϵ}$ and $\psi ={\mathit{x}}^{\mathrm{⊺}}\mathit{\gamma }+\delta$ be two traits measured at an individual, standardized so that $\text{E}\left[\varphi \right]=\text{E}\left[\psi \right]=0$ and $\text{Var}\left[\varphi \right]=\text{Var}\left[\psi \right]=1$, where $\mathit{\beta },\mathit{\gamma }\in {\mathbb{R}}^p$ are the fixed effect size vectors for the two traits; $\mathit{x}\in {\mathbb{R}}^p$, the genotype vector of the individual at p SNPs, standardized so that $\text{E}\left[\mathit{x}\right]=0$, and $\text{Var}\left[\mathit{x}\right]=\mathit{V}$, the LD matrix; and $\mathit{ϵ},\delta$, random environmental effects independent of $\mathit{x}$, $\mathit{\beta }$, $\mathit{\gamma }$, with $\text{E}\left[\mathit{ϵ}\right]=\text{E}\left[\delta \right]=0$, $\text{Var}\left[\mathit{ϵ}\right]={\sigma }_{\mathit{ϵ}}^2$, $\text{Var}\left[\delta \right]={\sigma }_{\delta }^2$, and $\text{Cov}\left[\mathit{ϵ},\delta \right]={\rho }_e$. Under these assumptions, one can decompose the phenotypic covariance, ρ, between ϕ and ψ into a summation of genetic covariance and environmental covariance, as

$$\begin{array}{c}\rho =\text{Cov}\left[\varphi ,\psi \right]=\text{E}\left[\varphi \psi \right]-\text{E}\left[\varphi \right]\text{E}\left[\psi \right]=\text{E}\left[\left({\mathit{x}}^{\mathrm{⊺}}\mathit{\beta }+\mathit{ϵ}\right){\left({\mathit{x}}^{\mathrm{⊺}}\mathit{\gamma }+\delta \right)}^{\mathrm{⊺}}\right]\\ =\text{E}\left[\left({\mathit{x}}^{\mathrm{⊺}}\mathit{\beta }\right)\left({\mathit{x}}^{\mathrm{⊺}}\mathit{\gamma }\right)\right]+\text{E}\left[\mathit{ϵ}\delta \right]=Cov\left[{\mathit{x}}^{\mathrm{⊺}}\mathit{\beta },{\mathit{x}}^{\mathrm{⊺}}\mathit{\gamma }\right]+\text{Cov}\left[\mathit{ϵ},\delta \right]\\ ={\mathit{\beta }}^{\mathrm{⊺}}\text{E}\left[\mathit{x}{\mathit{x}}^{\mathrm{⊺}}\right]\mathit{\gamma }+\text{Cov}\left[\mathit{ϵ},\delta \right]={\mathit{\beta }}^{\mathrm{⊺}}\mathit{V\gamma }+{\rho }_e,\end{array}$$ (Equation 1)

where ${\rho }_g=\text{Cov}\left[{\mathit{x}}^{\mathrm{⊺}}\mathit{\beta },{\mathit{x}}^{\mathrm{⊺}}\mathit{\gamma }\right]={\mathit{\beta }}^{\mathrm{⊺}}\mathit{V\gamma }$ is the genetic covariance between the two traits (i.e., covariance between the genetic components of the two traits, ${\mathit{x}}^{\mathrm{⊺}}\mathit{\beta }$ and ${\mathit{x}}^{\mathrm{⊺}}\mathit{\gamma }$), and ρ_e the environmental covariance (i.e., covariance between the environmental effects of two traits, ϵ and δ). The magnitude and sign of local genetic covariance can be interpreted as the effect and direction of the local genetic component of one trait on that of the other. Thus, given the true effect size vectors, $\mathit{\beta }$, $\mathit{\gamma }$, and the LD matrix $\mathit{V}$, one can obtain ρ_g by plugging in these quantities.

Genetic Covariance versus Covariance of the Causal Effects

An alternative approach to the covariance of the genetic components of the traits is to quantify the covariance of the causal effects (i.e., ${\rho }_{g,causal}={\mathit{\beta }}^{\mathrm{⊺}}\mathit{\gamma }$). In the special case where there is no LD (i.e., $\mathit{V}=\mathit{I}$, the identity matrix), genetic covariance and covariance of the causal effects coincide, ${\rho }_g={\mathit{\beta }}^{\mathrm{⊺}}\mathit{V\gamma }={\mathit{\beta }}^{\mathrm{⊺}}\mathit{I\gamma }={\mathit{\beta }}^{\mathrm{⊺}}\mathit{\gamma }={\rho }_{g,causal}$. However, in general genetic covariance is different from covariance of the causal effects as function of the LD between the causal variants. More importantly, high local genetic covariance does not necessarily imply high covariance of the causal effects. In fact, high genetic covariance can be attained even when causal variants are different between the traits. To illustrate the difference, consider an example involving two SNPs. Let $\mathit{\beta }=\left(\mathrm{1,0}\right)$ and $\mathit{\gamma }=\left(\mathrm{0,1}\right)$ be the causal effect vectors of the two traits, i.e., the two traits have two distinct set of causal variants. And let

$$\mathit{V}=\left[\begin{array}{cc}1.0& 0.9\\ 0.9& 1.0\end{array}\right]$$

be the LD matrix between the SNPs. In this example, the covariance of the causal effects is ${\rho }_{g,causal}={\mathit{\beta }}^{\mathrm{⊺}}\mathit{\gamma }=0$, whereas the genetic covariance is ${\rho }_g={\mathit{\beta }}^{\mathrm{⊺}}\mathit{V\gamma }=0.9$. Thus, at a region where the causal variants are distinct for the two traits, covariance of the causal effects is always zero, whereas genetic covariance may be non-zero depending on the LD (see Figure 2). The two definitions measure genetic sharing at different levels of resolution. Local genetic covariance measures sharing at regional level, giving a measure of how similar the regional genetic components are between the two traits, and has applications in predicting the regional genetic component of one trait from that of the other. In contrast, local causal effect covariance measures sharing at an individual SNP level, giving a measure of how similar the causal effects are between the two traits. Consider a scenario where two traits are each driven locally by a different SNP in the same gene. In this case, the local causal effect covariance is zero since the two traits share no causal SNP. However, the local genetic covariance is non-zero if the two SNPs are in LD, which induces similarity in the genetic component of the two traits and is an indication of the gene being shared across the two traits. Although in this work we focus on genetic covariance, for completeness we discuss an estimator for covariance of the causal effects (${\rho }_{g,causal}$) in Appendix A.

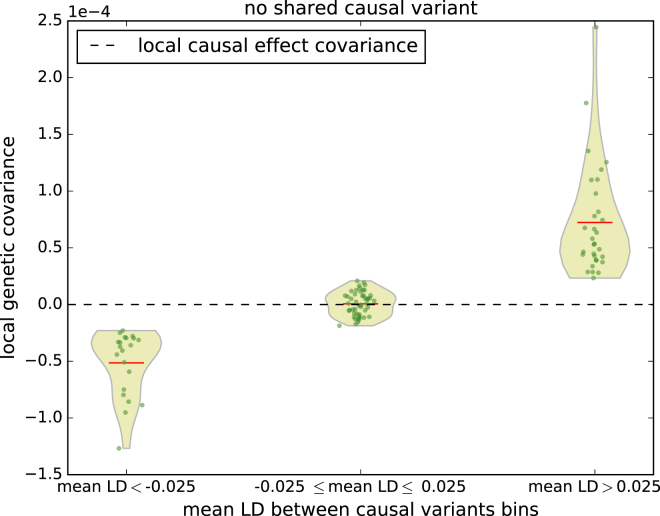
Figure 2.

Distribution of Simulated Genetic Covariance and Causal Effect Covariance across 100 LD-Independent Regions on Chromosome 1 Binned by Average LD between Causal Variants

The red lines represent the average local genetic covariance in each bin. For each region, we simulated 2 traits, each with 3 causal variants with effect sizes set to 0.01, and with no shared causal variants (see Figure S1 for the case where the two traits share causal variants). Genetic covariance varies with respect to LD whereas causal effect covariance is always 0 (horizontal dotted line). Since genetic covariance can be thought as an upper bound of prediction accuracy using causal effects from one trait to another, a positive genetic covariance indicates that non-zero prediction accuracy could be attained by virtue of LD tagging.

Estimating Local Genetic Covariance from GWAS Summary Data

In two GWASs involving n₁ individuals for trait 1 ($\varphi$), n₂ individuals for trait 2 ($\mathit{\psi }$), and n_s shared individuals, we assume

$$\left[\begin{array}{c}\varphi \\ {\varphi }_s\end{array}\right]=\left[\begin{array}{c}\mathit{Y}\\ {\mathit{X}}_s\end{array}\right]\mathit{\beta }+\left[\begin{array}{c}\mathrm{ϵ}\\ {\mathrm{ϵ}}_s\end{array}\right],\left[\begin{array}{c}\mathit{\psi }\\ {\mathit{\psi }}_s\end{array}\right]=\left[\begin{array}{c}\mathit{Z}\\ \mathit{X}{\text{'}}_s\end{array}\right]\mathit{\gamma }+\left[\begin{array}{c}\mathit{\delta }\\ {\mathit{\delta }}_s\end{array}\right],$$ (Equation 2)

where $\left(\varphi ,{\varphi }_s\right)\in {\mathbb{R}}^{n_1}$ and $\left(\mathit{\psi },{\mathit{\psi }}_s\right)\in {\mathbb{R}}^{n_2}$ are the standardized trait values of all individuals in each GWAS; $\left(\mathit{Y},{\mathit{X}}_s\right)\in {\mathbb{R}}^{n_1\times p}$ and $\left(\mathit{Z},\mathit{X}{\text{'}}_s\right)\in {\mathbb{R}}^{n_2\times p}$, column standardized genotype matrices of all individuals in each GWAS, where ${\mathit{X}}_s$ and $\mathit{X}{\text{'}}_s$ represent the genotype matrices for the same set of individuals and SNPs but standardized differently in each GWAS; and $\left(\mathrm{ϵ},{\mathrm{ϵ}}_s\right)\in {\mathbb{R}}^{n_1}$ and $\left(\mathit{\delta },{\mathit{\delta }}_s\right)\in {\mathbb{R}}^{n_2}$ are environmental effects of all individuals in each GWAS. We use the subscript s to represent individuals shared by both GWASs. We further assume that $\text{E}\left[\mathrm{ϵ}\right]=\text{E}\left[\mathit{\delta }\right]=\text{E}\left[{\mathrm{ϵ}}_s\right]=\text{E}\left[{\mathit{\delta }}_s\right]=0$, $\text{Var}\left[\mathrm{ϵ}\right]=\text{Var}\left[{\mathrm{ϵ}}_s\right]={\sigma }_{\mathit{ϵ}}^2\mathit{I}$, $\text{Var}\left[\mathit{\delta }\right]=\text{Var}\left[{\mathit{\delta }}_s\right]={\sigma }_{\delta }^2\mathit{I}$, $\text{Cov}\left[\mathrm{ϵ},\mathit{\delta }\right]=0$, and $\text{Cov}\left[{\mathrm{ϵ}}_s,{\mathit{\delta }}_s\right]={\rho }_e\mathit{I}$.

In a traditional GWAS, we obtain marginal effect size estimates, ${\hat{\mathit{\beta }}}_{gwas}$ and ${\hat{\mathit{\gamma }}}_{gwas}$, as

$$\begin{array}{c}{\hat{\mathit{\beta }}}_{gwas}=\frac{1}{n_1}\left[{\mathit{Y}}^{\mathrm{⊺}}{\mathit{X}}_s^{\mathrm{⊺}}\right]\left[\begin{array}{c}\varphi \\ {\varphi }_s\end{array}\right]=\frac{1}{n_1}\left({\mathit{Y}}^{\mathrm{⊺}}\mathit{Y}+{\mathit{X}}_s^{\mathrm{⊺}}{\mathit{X}}_s\right)\mathit{\beta }+\frac{1}{n_1}\left({\mathit{Y}}^{\mathrm{⊺}}\mathrm{ϵ}+{\mathit{X}}_s^{\mathrm{⊺}}{\mathrm{ϵ}}_s\right)\\ {\hat{\mathit{\gamma }}}_{gwas}=\frac{1}{n_2}\left[{\mathit{Z}}^{\mathrm{⊺}}\mathit{X}{\text{'}}_s^{\mathrm{⊺}}\right]\left[\begin{array}{c}\mathit{\psi }\\ {\mathit{\psi }}_s\end{array}\right]=\frac{1}{n_2}\left({\mathit{Z}}^{\mathrm{⊺}}\mathit{Z}+\mathit{X}{\text{'}}_s^{\mathrm{⊺}}\mathit{X}{\text{'}}_s\right)\mathit{\gamma }+\frac{1}{n_2}\left({\mathit{Z}}^{\mathrm{⊺}}\mathit{\delta }+\mathit{X}{\text{'}}_s^{\mathrm{⊺}}{\mathit{\delta }}_s\right).\end{array}$$ (Equation 3)

Assuming individuals in both GWASs are drawn from the same population with LD matrix $\mathit{V}$, we have ${\hat{\mathit{\beta }}}_{gwas}\sim N\left(\mathit{V\beta },\frac{{\sigma }_{\mathit{ϵ}}^2}{n_1}\mathit{V}\right)$, ${\hat{\mathit{\gamma }}}_{gwas}\sim N\left(\mathit{V\gamma },\frac{{\sigma }_{\delta }^2}{n_2}\mathit{V}\right)$. We also find

$$\text{Cov}\left[{\hat{\mathit{\beta }}}_{gwas},{\hat{\mathit{\gamma }}}_{gwas}\right]=\text{E}\left[{\hat{\mathit{\beta }}}_{gwas}{\hat{\mathit{\gamma }}}_{gwas}^{\mathrm{⊺}}\right]-\left(\mathit{V\beta }\right){\left(\mathit{V\gamma }\right)}^{\mathrm{⊺}}=\frac{{\rho }_e}{n_1{n}_2}\text{E}\left[{\mathit{X}}_s^{\mathrm{⊺}}{\mathit{X}}_s^{\prime }\right]=\frac{{\rho }_e{n}_s}{n_1{n}_2}\mathit{V},$$ (Equation 4)

where the last equality follows from Isserlis’ theorem.²²

Under infinite sample sizes, $\text{Var}\left[{\hat{\mathit{\beta }}}_{gwas}\right]=\text{Var}\left[{\hat{\mathit{\gamma }}}_{gwas}\right]=\text{Cov}\left[{\hat{\mathit{\beta }}}_{gwas},{\hat{\mathit{\gamma }}}_{gwas}\right]=0$, and we have $\mathit{\beta }={\mathit{V}}^{-1}{\hat{\mathit{\beta }}}_{gwas}$, $\mathit{\gamma }={\mathit{V}}^{-1}{\hat{\mathit{\gamma }}}_{gwas}$. Thus, local genetic covariance, ${\rho }_{g,local}$, can be computed as

$${\rho }_{g,local}=\left({\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-1}\right)\mathit{V}\left({\mathit{V}}^{-1}{\hat{\mathit{\gamma }}}_{gwas}\right)={\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-1}{\hat{\mathit{\gamma }}}_{gwas}.$$ (Equation 5)

However, when sample sizes are finite, from bilinear form theory,²³ the covariance between ${\hat{\mathit{\beta }}}_{gwas}$ and ${\hat{\mathit{\gamma }}}_{gwas}$ creates bias, resulting in

$$\text{E}\left[{\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-1}{\hat{\mathit{\gamma }}}_{gwas}\right]={\mathit{\beta }}^{\mathrm{⊺}}\mathit{V\gamma }+\frac{{\rho }_e}{n_1{n}_2}\text{tr}\left(\mathit{V}\right)={\mathit{\beta }}^{\mathrm{⊺}}\mathit{V\gamma }+\frac{p\left(\rho -{\rho }_{g,local}\right)n_s}{n_1{n}_2}.$$ (Equation 6)

Correcting for bias, we arrive at the unbiased estimator

$${\hat{\rho }}_{g,local}=\frac{n_1{n}_2{\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-1}{\hat{\mathit{\gamma }}}_{gwas}-n_{s}p\rho }{n_1{n}_2-n_{s}p}.$$ (Equation 7)

For rank-deficient LD matrix $\mathit{V}$, one replaces ${\mathit{V}}^{-1}$ with the pseudo-inverse (${\mathit{V}}^{†}$) and p with $q=\text{rank}\left(\mathit{V}\right)$, yielding the unbiased estimator

$${\hat{\rho }}_{g,local}=\frac{n_1{n}_2{\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{†}{\mathit{\gamma }}_{gwas}-n_{s}q\rho }{n_1{n}_2-n_{s}q}.$$ (Equation 8)

Thus, in order to obtain an unbiased estimate of genetic covariance between a pair of traits, one needs to know their phenotypic covariance. When phenotypic covariance is not available, one can obtain an estimate from genome-wide summary association data using cross-trait LD Score regression,¹⁶

$$\text{E}\left[z_{\varphi ,j}{z}_{\psi ,j}|l_j\right]=\frac{\sqrt{n_1{n}_2}{\rho }_g}{p}{l}_j+\frac{\rho n_s}{\sqrt{n_1{n}_2}},$$ (Equation 9)

where $z_{\varphi ,j}$ and $z_{\psi ,j}$ are the Z-scores of SNP j in the two traits, and l_j the LD score of SNP j. Cross-trait LD Score regression regresses the product of Z-scores at each SNP against its LD score, l_j, and accounts for bias generated by overlapping samples through the intercept term, $\frac{\rho n_s}{\sqrt{n_1{n}_2}}$,¹⁶ from which one can obtain an estimate of phenotypic covariance, ρ.

In the special case when ${\hat{\mathit{\beta }}}_{gwas}$ and ${\hat{\mathit{\gamma }}}_{gwas}$ are obtained for the same trait on the same set of individuals (i.e., ${\hat{\mathit{\beta }}}_{gwas}={\hat{\mathit{\gamma }}}_{gwas}$, n₁ = n₂ = n_s, $\rho =1$), Equation 7 reduces to the local SNP-heritability estimator.¹⁹ When n_s = 0 (i.e., no shared individuals between the GWASs), the unbiased estimator is simply ${\hat{\rho }}_{g,local}={\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-1}{\hat{\mathit{\gamma }}}_{gwas}$. An interpretation for this simple formula is that in the absence of sample overlap, the covariance in the noise, ϵ and δ, is 0 and does thus not introduce bias into the estimate of ${\rho }_{g,local}$.

Following bilinear form theory,²³ we can estimate the variance for ${\hat{\rho }}_{g,local}$ as

$$\text{Var}\left[{\hat{\rho }}_{g,local}\right]={\left(\frac{n_1{n}_2}{n_1{n}_2-n_{s}p}\right)}^2\left[{\left(\frac{p{\rho }_e{n}_s}{n_1{n}_2}\right)}^2+\frac{{\sigma }_{\mathit{ϵ}}^2{\sigma }_{\delta }^{2}p}{n_1{n}_2}+\frac{{\sigma }_{\delta }^2{h}_{g\varphi ,local}^2}{n_2}+\frac{{\sigma }_{\mathit{ϵ}}^2{h}_{g\psi ,local}^2}{n_1}+2\frac{n_s{\rho }_e{\rho }_{g,local}}{n_1{n}_2}\right].$$ (Equation 10)

For rank deficient LD matrix with $\text{rank}\left(\mathit{V}\right)=q$, one replaces p with q in Equation 10.

Accounting for Statistical Noise in LD Estimates

Limited sample size of external reference panels creates statistical noise in the estimated LD matrix that biases our estimates. Following our previous work,¹⁹ we apply truncated-SVD regularization²⁴ to remove noise in external reference LD. We note that ${\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{†}{\hat{\mathit{\gamma }}}_{gwas}={\sum }_{i=1}^q{s}_i={\sum }_{i=1}^q\frac{1}{w_i}\left({\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{u}}_i\right)\left({\hat{\mathit{\gamma }}}_{gwas}^{\mathrm{⊺}}{\mathit{u}}_i\right)$, where $w_i$ and ${\mathit{u}}_i$ are the eigenvalues and eigenvectors of the LD matrix $\mathit{V}$ and $q=\text{rank}\left(\mathit{V}\right)$. We use ${\hat{s}}_i=\frac{1}{{\hat{w}}_i}\left({\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\hat{\mathit{u}}}_i\right)\left({\hat{\mathit{\gamma }}}_{gwas}^{\mathrm{⊺}}{\hat{\mathit{u}}}_i\right)$ to denote the counterpart obtained from external reference LD matrix $\hat{\mathit{V}}$. We show through simulations that the bulk of ${\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{†}{\hat{\mathit{\gamma }}}_{gwas}$ comes from s_i where $i\ll q$ and that $s_i\approx {\hat{s}}_i$ for $i\ll q$, thus justifying truncated-SVD as an appropriate regularization method when only external reference LD ($\hat{\mathit{V}}$) is available.

Let $g\left({\hat{\mathit{\beta }}}_{gwas},{\hat{\mathit{\gamma }}}_{gwas},k\right)={\sum }_{i=1}^k{\hat{s}}_i={\sum }_{i=1}^k\frac{1}{{\hat{w}}_i}\left({\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\hat{\mathit{u}}}_i\right)\left({\hat{\mathit{\gamma }}}_{gwas}^{\mathrm{⊺}}{\hat{\mathit{u}}}_i\right)$ be the truncated-SVD regularized estimates for ${\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{†}{\hat{\mathit{\gamma }}}_{gwas}$, then it can be shown that

$$\text{E}\left[g\left({\hat{\mathit{\beta }}}_{gwas},{\hat{\mathit{\gamma }}}_{gwas},k\right)\right]=\frac{n_{s}k\left(\rho -{\rho }_g\right)}{n_1{n}_2}+\sum _{i=1}^k{\hat{w}}_i\left({\mathit{\beta }}^{\mathrm{⊺}}{\hat{\mathit{u}}}_i\right)\left({\mathit{\gamma }}^{\mathrm{⊺}}{\hat{\mathit{u}}}_i\right).$$ (Equation 11)

Assuming ${\hat{w}}_i=w_i$ and ${\hat{\mathit{u}}}_i={\mathit{u}}_i$ for $i\ll k$, Equation 11 is a biased approximation of ${\rho }_{g,local}$, with bias $\frac{n_{s}k\left(\rho -{\rho }_g\right)}{n_1{n}_2}$. Correcting for the bias, we arrive at the estimator

$${\hat{\rho }}_{g,local}=\frac{n_1{n}_{2}g\left({\hat{\mathit{\beta }}}_{gwas},{\hat{\mathit{\gamma }}}_{gwas},k\right)-n_s\rho k}{n_1{n}_2-n_{s}k},$$ (Equation 12)

which has variance

$$\text{Var}\left[{\hat{\rho }}_{g,local}\right]={\left(\frac{n_1{n}_2}{n_1{n}_2-n_{s}k}\right)}^2\left[{\left(\frac{k{\rho }_e{n}_s}{n_1{n}_2}\right)}^2+\frac{{\sigma }_{\mathit{ϵ}}^2{\sigma }_{\delta }^{2}k}{n_1{n}_2}+\frac{{\sigma }_{\delta }^2{h}_{g\varphi ,local}^2}{n_2}+\frac{{\sigma }_{\mathit{ϵ}}^2{h}_{g\psi ,local}^2}{n_1}+2\frac{n_s{\rho }_e{\rho }_{g,local}}{n_1{n}_2}\right].$$ (Equation 13)

Extension to Multiple Independent Regions

For genome partitioned into m regions, let

$$\begin{array}{c}\varphi ={\mathit{x}}_1^{\mathrm{⊺}}{\mathit{\beta }}_1+\cdots +{\mathit{x}}_m^{\mathrm{⊺}}{\mathit{\beta }}_m+\mathit{ϵ}\\ \psi ={\mathit{x}}_1^{\mathrm{⊺}}{\mathit{\gamma }}_1+\cdots +{\mathit{x}}_m^{\mathrm{⊺}}{\mathit{\gamma }}_m+\delta \end{array}$$ (Equation 14)

denote the phenotype measurements of two traits at an individuals, where we assume that SNPs in different pairs of regions are independent, i.e., $\text{E}\left[{\mathit{x}}_{ik}{\mathit{x}}_{il}\right]=0$ for all $i\ne j$, $k\in \left\{1,\cdots ,p_i\right\}$, and $l\in \left\{1,\cdots ,p_j\right\}$, where p_i and p_j are the number of SNPs in region i and j. Under these assumptions, we decompose the phenotypic covariance, ρ, between ϕ and ψ, into a summation of per-region genetic covariance and environmental covariance

$$\begin{array}{c}\rho =\text{Cov}\left[\varphi ,\psi \right]=\text{E}\left[\left({\mathit{x}}_1^{\mathrm{⊺}}{\mathit{\beta }}_1+\cdots +{\mathit{x}}_m^{\mathrm{⊺}}{\mathit{\beta }}_m+\mathit{ϵ}\right){\left({\mathit{x}}_1^{\mathrm{⊺}}{\mathit{\gamma }}_1+\cdots +{\mathit{x}}_m^{\mathrm{⊺}}{\mathit{\gamma }}_m+\delta \right)}^{\mathrm{⊺}}\right]\\ =\text{E}\left[\left({\mathit{x}}_1^{\mathrm{⊺}}{\mathit{\beta }}_1\right)\left({\mathit{x}}_1^{\mathrm{⊺}}{\mathit{\gamma }}_1\right)\right]+\cdots +\text{E}\left[\left({\mathit{x}}_m^{\mathrm{⊺}}{\mathit{\beta }}_m\right)\left({\mathit{x}}_m^{\mathrm{⊺}}{\mathit{\gamma }}_m\right)\right]+\text{E}\left[\mathit{ϵ}\delta \right]\\ =\sum _{i=1}^m\text{Cov}\left[{\mathit{x}}_i^{\mathrm{⊺}}{\mathit{\beta }}_i,{\mathit{x}}_i^{\mathrm{⊺}}{\mathit{\gamma }}_i\right]+\text{Cov}\left[\mathit{ϵ},\delta \right]=\sum _{i=1}^m{\mathit{\beta }}_i^{\mathrm{⊺}}{\mathit{V}}_i{\mathit{\gamma }}_i+{\rho }_e\end{array},$$ (Equation 15)

where ${\rho }_{g,local,i}=\text{Cov}\left[{\mathit{x}}_i^{\mathrm{⊺}}{\mathit{\beta }}_i,{\mathit{x}}_i^{\mathrm{⊺}}{\mathit{\gamma }}_i\right]={\mathit{\beta }}_i^{\mathrm{⊺}}{\mathit{V}}_i{\mathit{\gamma }}_i$ is the local genetic covariance between the pair of traits attributed to genetic variants at region i. Following strategies outlined in previous sections, we arrive at the estimator for genetic covariance at the i^th region,

$${\hat{\rho }}_{g,local,i}=\frac{n_1{n}_{2}g\left({\hat{\mathit{\beta }}}_{gwas,i},{\hat{\mathit{\gamma }}}_{gwas,i},k\right)-n_s\left(\rho -{\sum }_{j=1,j\ne i}^m{\hat{\rho }}_{g,local,j}\right)k_i}{n_1{n}_2-n_s{k}_i},$$ (Equation 16)

which defines a system of linear equation involving m unknown variables and m equations. Following bilinear form theory, we obtain variance estimate for ${\hat{\rho }}_{g,local,i}$ as

$$\begin{array}{c}\text{Var}\left[{\hat{\rho }}_{g,local,i}\right]={\left(\frac{n_1{n}_2}{n_1{n}_2-n_s{k}_i}\right)}^2\left[{\left(\frac{k_i{\rho }_e{n}_s}{n_1{n}_2}\right)}^2+\frac{{\sigma }_{\mathit{ϵ}}^2{\sigma }_{\delta }^2{k}_i}{n_1{n}_2}+\frac{{\sigma }_{\delta }^2{h}_{g\varphi ,local,i}^2}{n_2}+\frac{{\sigma }_{\mathit{ϵ}}^2{h}_{g\psi ,local,i}^2}{n_1}+2\frac{n_s{\rho }_e{\rho }_{g,local,i}}{n_1{n}_2}\right]\\ +\sum _{j=1,j\ne i}^m{\left(\frac{n_s{k}_j}{n_1{n}_2-n_s{k}_i}\right)}^2\text{Var}\left[{\hat{\rho }}_{g,local,j}\right]\end{array},$$ (Equation 17)

which also defines a system of linear equations with m equations and m variables. In the special case where there is no sample overlap (n_s = 0), ${\hat{\rho }}_{g,local,i}$ reduces to $g\left({\hat{\mathit{\beta }}}_{gwas},{\hat{\mathit{\gamma }}}_{gwas},k\right)$ with $\text{Var}\left[{\hat{\rho }}_{g,local,i}\right]=\frac{{\sigma }_{\mathit{ϵ}}^2{\sigma }_{\delta }^2{k}_i}{n_1{n}_2}+\frac{{\sigma }_{\delta }^2{h}_{g\varphi ,local,i}^2}{n_2}+\frac{{\sigma }_{\mathit{ϵ}}^2{h}_{g\psi ,local,i}^2}{n_1}\approx \frac{{\sigma }_{\mathit{ϵ}}^2{\sigma }_{\delta }^2{k}_i}{n_1{n}_2}$, i.e., both the local genetic covariance and its variance can be estimated independent of all other windows.

When $k_1=\cdots =k_m=k$, i.e., all regions use the same number of eigenvectors in the truncated-SVD regularization, summing over i on both sides of Equation 16 yields

$$\begin{array}{c}{\hat{\rho }}_g=\sum _{i=1}{\hat{\rho }}_{g,local,i}=\frac{n_1{n}_2}{n_1{n}_2-n_{s}k}\sum _{i=1}^{m}g\left({\hat{\mathit{\beta }}}_{gwas,i},{\hat{\mathit{\gamma }}}_{gwas,i},k\right)-\frac{k{n}_s}{n_1{n}_2-n_{s}k}\sum _{i=1}^m\left(\rho -\sum _{j=1,j\ne i}^m{\hat{\rho }}_{g,local,j}\right)\\ =\frac{n_1{n}_2}{n_1{n}_2-n_{s}k}\sum _{i=1}^{m}g\left({\hat{\mathit{\beta }}}_{gwas,i},{\hat{\mathit{\gamma }}}_{gwas,i},k\right)-\frac{k{n}_s}{n_1{n}_2-n_{s}k}\sum _{i=1}^m\left(\rho -{\hat{\rho }}_g+{\hat{\rho }}_{g,local,i}\right)\\ =\frac{n_1{n}_2}{n_1{n}_2-n_{s}k}\sum _{i=1}^{m}g\left({\hat{\mathit{\beta }}}_{gwas,i},{\hat{\mathit{\gamma }}}_{gwas,i},k\right)+\frac{k{n}_{s}m-k{n}_s}{n_1{n}_2-n_{s}k}{\hat{\rho }}_g-\frac{k{n}_{s}m\rho }{n_1{n}_2-n_{s}k}.\end{array}$$ (Equation 18)

Solving for ${\hat{\rho }}_g$ yields

$${\hat{\rho }}_g=\frac{n_1{n}_2{\sum }_{i=1}^{m}g\left({\hat{\mathit{\beta }}}_{gwas,i},{\hat{\mathit{\gamma }}}_{gwas,i},k\right)-k{n}_{s}m\rho }{n_1{n}_2-k{n}_{s}m},$$ (Equation 19)

which has variance

$$\text{Var}\left[{\hat{\rho }}_g\right]={\left(\frac{n_1{n}_2}{n_1{n}_2-k{n}_{s}m}\right)}^2\sum _{i=1}^m\text{Var}\left[g\left({\hat{\mathit{\beta }}}_{gwas,i},{\hat{\mathit{\gamma }}}_{gwas,i},k\right)\right].$$ (Equation 20)

Thus, if k is chosen such that $\left(n_1{n}_2-k{n}_{s}m\right)$ is small (i.e., $\frac{n_1{n}_2}{n_1{n}_2-k{n}_{s}m}$ large), the estimate of total genetic covariance will have large standard error. To reduce standard error in the estimates (at the cost of some bias), we recommend choosing k such that $\frac{n_1{n}_2}{n_1{n}_2-k{n}_{s}m}$ is less than 2. When testing for statistical significance, we assume that the estimates of local and genome-wide genetic covariance and correlation follow a normal distribution.

Standardizing Local Genetic Covariance

We estimate the local genetic correlation for the i^th region as

$${\hat{r}}_{g,local,i}=\frac{{\hat{\rho }}_{g,local,i}}{\sqrt{{\hat{h}}_{g\varphi ,local,i}^2}\sqrt{{\hat{h}}_{g\psi ,local,i}^2}},$$ (Equation 21)

where ${\hat{h}}_{g\varphi ,local,i}^2$ and ${\hat{h}}_{g\psi ,local,i}^2$ denote the local SNP heritability of trait ϕ and ψ at the i^th region. In some cases, this estimator of local genetic correlation may yield an estimate with magnitude greater than 1, and we cap the estimate at −1 or 1. In simulations, we show that ${\hat{r}}_{g,local,i}$ is approximately unbiased when both traits are heritable at the i^th region. In practice, however, the terms ${\hat{h}}_{g\varphi ,local,i}^2$ and ${\hat{h}}_{g\psi ,local,i}^2$ can be close to zero, greatly inflating the standard error of ${\hat{r}}_{g,local,i}$. Thus, we recommend estimating local genetic correlation only at regions with significant local SNP heritability. One can also estimate local genetic correlation at a set of regions. For example, to estimate genetic correlation at regions indexed by the index set $\mathit{C}$, one applies the formula

$${\hat{r}}_{g,\mathit{C}}=\frac{{\sum }_{i\in \mathit{C}}{\hat{\rho }}_{g,local,i}}{\sqrt{{\sum }_{i\in \mathit{C}}{\hat{h}}_{\varphi ,g,local,i}^2}\sqrt{{\sum }_{i\in \mathit{C}}{\hat{h}}_{\psi ,g,local,i}^2}}.$$ (Equation 22)

We estimate standard error of local genetic correlation at a single region through a parametric bootstrap approach²⁵ and local genetic correlation at a set of regions through jackknife.

Simulation Framework

Starting from half (202 individuals) of the EUR reference panel from the 1000 Genomes Project,²⁶ we simulated genotype data for 50,000 individuals at HapMap3²⁷ SNPs with minor allele frequency (MAF) greater than 5% in 100 randomly selected LD-independent regions defined in Berisa and Pickrell¹⁸ on chromosome 1 using HAPGEN2.²⁷ We used the other half of the EUR reference panel (203 individuals) to obtain external reference LD matrices.

We simulated phenotypes from the genotypes according to the linear model $\varphi =\mathit{X\beta }+\mathrm{ϵ}$ and $\mathit{\psi }=\mathit{X\gamma }+\mathit{\delta }$, where $\mathit{X}$ is the column-standardized genotype matrix. We drew the effects of causal SNPs (${\mathit{\beta }}_C$, ${\mathit{\gamma }}_C$) from the distribution

$$N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}\frac{h_{g\varphi }^2}{\left|C\right|}\mathit{I}& \frac{{\rho }_g}{\left|C\right|}\mathit{I}\\ \frac{{\rho }_g}{\left|C\right|}\mathit{I}& \frac{h_{g\psi }^2}{\left|C\right|}\mathit{I}\end{array}\right]\right),$$ (Equation 23)

where C is the index set of causal SNPs, and set the effects of all other SNPs to be zero. We then drew ($\mathrm{ϵ}$, $\mathit{\delta }$) from the distribution

$$N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}\left(1-h_{g\varphi }^2\right)\mathit{I}& {\rho }_e\mathit{I}\\ {\rho }_e\mathit{I}& \left(1-h_{g\psi }^2\right)\mathit{I}\end{array}\right]\right).$$ (Equation 24)

Finally, we simulated GWAS summary statistics using methods outlined in previous sections. For each $\mathit{\beta }$ and $\mathit{\gamma }$ drawn from the normal distribution, we simulated 1,000 sets of summary statistics by varying $\mathrm{ϵ}$ and $\mathit{\delta }$ and applied ρ-HESS to estimate genetic covariance and genetic correlation for each set of the simulated summary statistics.

Empirical Datasets

We obtained GWAS summary data for 36 quantitative complex traits and diseases from 15 GWAS consortia or institutions (see Table 1), all of which are based on individuals of European ancestry and have sample size greater than 20,000. We used approximately independent genomic regions previously defined¹⁸ to partition the genome and restricted our analyses on HapMap3 SNPs with minor allele frequency (MAF) greater than 5% in the European population in the 1000 Genomes data.²⁶ We also removed stand-ambiguous SNPs prior to our analyses. We follow the method previously outlined¹⁹ to estimate and re-inflate ${\lambda }_{gc}$ and to choose the number of eigenvectors to include in estimating local genetic covariance and SNP heritability.

Table 1.

A Summary of the 36 GWAS Summary Datasets Analyzed

Trait Name	Abbreviation	Consortium	# Gen Corr All Consortium	# Gen Corr outside Consortium	Approx. Sample Size
Age at menarche28	AM	REPROGEN	21 (4)	21 (4)	133K
Body mass index29	BMI	GIANT	27 (17)	23 (14)	231K
Height30	HEIGHT	GIANT	17 (2)	13 (1)	241K
Hip circumference31	HIP	GIANT	23 (14)	19 (10)	144K
Waist circumference31	WC	GIANT	26 (18)	22 (15)	153K
Waist-to-hip ratio31	WHR	GIANT	27 (19)	23 (16)	143K
Haemoglobin32	HB	HAEMGEN	21 (10)	18 (8)	51K
Mean cell haemoglobin32	MCH	HAEMGEN	9 (1)	8 (1)	44K
MCH concentration32	MCHC	HAEMGEN	6 (4)	2 (1)	47K
Mean cell volume32	MCV	HAEMGEN	12 (3)	10 (1)	49K
Packed cell volume32	PCV	HAEMGEN	18 (11)	14 (8)	45K
Red blood cell count32	RBC	HAEMGEN	20 (10)	17 (8)	46K
Number of platelets33	PLT	HAEMGEN	9 (1)	6 (1)	67K
Fasting glucose34	FG	MAGIC	19 (9)	16 (8)	46K
Fasting insulin34	FI	MAGIC	20 (12)	18 (12)	46K
HBA1C35	HBA1C	MAGIC	19 (14)	18 (13)	46K
HOMA-B34	HOMA-B	MAGIC	17 (11)	15 (11)	46K
HOMA-IR34	HOMA-IR	MAGIC	21 (12)	21 (12)	46K
High-density lipoprotein36	HDL	GLGC	23 (12)	21 (11)	96K
Low-density lipoprotein36	LDL	GLGC	19 (6)	17 (4)	91K
Total cholesterol36	TC	GLGC	18 (3)	15 (1)	96K
Triglycerides36	TG	GLGC	26 (14)	23 (11)	92K
Forearm BMD37	FA	GEFOS	4 (1)	2 (0)	53K
Femoral neck BMD37	FN	GEFOS	4 (2)	2 (0)	53K
Lumbar spine BMD37	LS	GEFOS	7 (1)	5 (0)	53K
Education years38	EY	SSGAC	26 (5)	24 (4)	294K
Neuroticism39	NEURO	SSGAC	5 (2)	3 (0)	171K
Subjective well-being39	SWB	SSGAC	4 (1)	2 (0)	298K
Age first birth40	AFB	BIOS	23 (5)	23 (5)	251K
Birth weight41	BW	EGG	13 (1)	13 (1)	68K
Urinary albumin-to-creatinine ratio42	UACR	DCCT-EDIC	11 (1)	11 (1)	53K
Rest heart rate43	HR	EPPINGA	14 (0)	14 (0)	265K
Serum urate concentrations44	URATE	GUGC	25 (14)	25 (14)	107K
Body fat45	BF	Lu et al.	26 (17)	26 (17)	58K
Extra-glomerular filtration rate of creatinin46	CRN	CKDGEN	10 (1)	10 (1)	133K
Age at menopause47	MP	BCAC	6 (0)	6 (0)	70K

We list the total number of traits with significant non-zero genome-wide genetic correlation (two-tailed p < 0.05/630) and the total number of traits outside the consortium with significant non-zero genome-wide genetic correlation in the fourth and fifth column, respectively. Number of traits for which the magnitude of genetic correlation is both significantly non-zero and greater than 0.2 is shown in parentheses.

Local Genetic Correlation at Regions Ascertained for GWAS Signals

Recent works leverage the difference in correlations of Z-scores at genomic regions ascertained for GWAS signals specific to each trait to prioritize putative causal models between pairs of complex traits.^{2, 3} We evaluated the local genetic correlation at regions harboring GWAS signals specific to each trait across all 298 pairs of traits exhibiting significant genome-wide genetic correlation. We estimate local genetic correlations only for pairs of traits for which the number of loci harboring GWAS hits specific to each trait is greater than 10. The confidence intervals (1.96 times jackknife standard error on each side) of the ascertained local genetic correlations (${\hat{r}}_{g,local,trait1}$ and ${\hat{r}}_{g,local,trait2}$) do not overlap; one of the confidence intervals overlap with 0 and the other does not.

Results

Local Genetic Correlation Estimation in Simulations

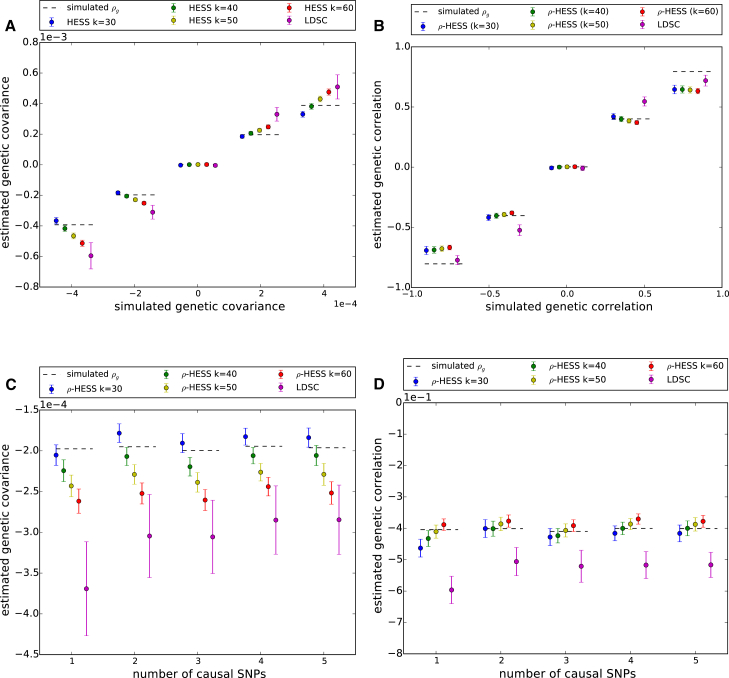
We evaluated the performance of our approach (ρ-HESS) through simulations across a wide range of disease architectures. We included cross-trait LDSC,¹⁶ an approach that assumes a random-effect model, in the comparison for completeness purposes. When LD is estimated in-sample, ρ-HESS provides an unbiased estimate of local genetic covariance and nearly unbiased estimates of genetic correlation (i.e., genetic covariance divided by the square root of local SNP heritability, see Material and Methods) (Figure S2). Next, we quantified the performance in the more realistic case when in-sample LD is unavailable and needs to be estimated from external reference panels. Although both cross-trait LDSC and ρ-HESS provide accurate estimates of genetic correlation, we observe superior accuracy with higher precision for ρ-HESS (Figures 3, S4, S6, and S7). We attribute the lower standard error of ρ-HESS to the truncated-SVD regularization of the LD matrix which effectively reduces the degree of freedom of the bi-linear form in Equation 7 (Figure S10). Different genomic regions vary in their total amount of LD and we observed that the accuracy of genetic correlation estimation decreases with the total amount of regional LD (Figure S11). This is expected as high LD regions lead to high rank deficiencies in the LD matrix and small eigenvalues, thus increasing the level of statistical noise in the estimation. We also evaluated the performance of local genetic correlation estimation in simulations where we varied the number of causal variants in each region. Overall, we observe that our estimator of genetic covariance and correlation is not sensitive to the underlying polygenicity (i.e., number of causal SNPs) (Figures 3, S5, S8, and S9). Finally, we also evaluated the performance of the estimator when causal variants are all drawn from DHS regions⁴⁸ and observed that the performance is not sensitive to the uneven distribution of causal variants (Figure S3).

Figure 3.

Performance of ρ-HESS and Cross-trait LDSC using External Reference LD across 100 LD-Independent Regions, with Each Region Having 1,000 Simulations

Here, each dot represents the mean (more than 100 regions) of the average performance (more than 1,000 simulations per region), with error bars representing 1.96 times the standard error on both sides. Overall, ρ-HESS provides approximately unbiased estimates of local genetic covariance (A) and correlation (B) and is not sensitive to the underlying genetic architectures (covariance in C and correlation in D). We also observe that ρ-HESS is less biased, is more consistent, and has smaller standard error than cross-trait LDSC.

Local Genetic Correlation across 36 Quantitative Traits

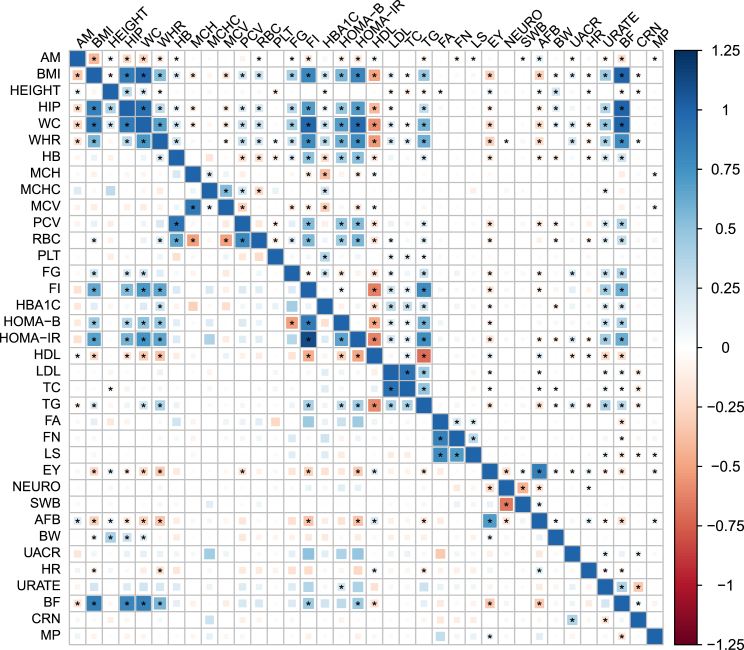
We analyzed GWAS summary data from 36 complex traits to obtain local genetic correlations at 1,703 approximately LD-independent regions in the genome (∼1.6 Mb in width on average).¹⁸ First, as a quality control step, we aggregated the local estimates into genome-wide estimates of genetic correlation (see Material and Methods) and compared to the cross-trait LDSC estimates. Reassuringly, we find a high degree of consistency with genetic correlations estimated by cross-trait LDSC regression (R = 0.77; Figures 4 and S13). Our estimator provides lower standard errors as compared to cross-trait LDSC (likely due to the truncated-SVD regularization procedure) and yields consistently lower estimates for pairs of traits from the same consortium where we conservatively assume full sample overlap (see Discussion). Overall, we identify 298 pairs of traits with significant genome-wide genetic correlation (p < 0.05/630). These include previously reported correlations, e.g., body mass index (BMI) and triglyceride (TG), as well as complex traits that have not been studied before using genetic correlation, e.g., red blood cell count (RBC) and fasting insulin (FI) (Figure 4).

Figure 4.

Genetic Correlation across the 36 Complex Traits Obtained by ρ-HESS and Cross-trait LDSC¹⁷

The magnitude of the correlation is represented by the color and the size of the square. Among the 630 pairs of traits, ρ-HESS (top half) (cross-trait LDSC [bottom half]) identified 298 (115) pairs showing significant genetic correlation (marked with dots).

Next, we searched for genomic regions that disproportionately contribute to the genetic correlation of the 36 analyzed traits; we excluded the HLA region due to complex LD patterns. We identify 25 genomic regions that show both significant local genetic correlation (two-tailed p < 0.05/1,703) as well as significant local SNP heritability (one-tailed p < 0.05/1703) (see Table 2, Figures S14–S16). For example, the estimate of local genetic correlation between HDL and TG at chr11: 116–117 Mb is −0.82 (95% CI [−0.95, −0.69]), suggesting highly shared genetic architecture at this region for HDL and TG. Indeed, the region chr11: 116M–117M harbors APOA1 (MIM: 107680), which is known to be associated with multiple lipid traits.³⁶ Interestingly, 4 out of the 25 regions do not contain GWAS-significant SNPs (p < 5 × 10⁻⁸) for either one or both traits and can be viewed as new risk regions for these traits.

Table 2.

Loci that Show Significant Local Genetic Covariance (Two-Tailed p < 0.05/1,703) and Local SNP Heritability (One-Tailed p < 0.05/1,703) for Both Traits

Trait1	Trait2	Locus	${\mathbf{h}}_{\mathbf{g},\mathbf{l}\mathbf{o}\mathbf{c}\mathbf{a}\mathbf{l},\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{t}1}^2$	${\mathbf{h}}_{\mathbf{g},\mathbf{l}\mathbf{o}\mathbf{c}\mathbf{a}\mathbf{l},\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{t}2}^2$	${\mathbf{r}}_{\mathbf{g},\mathbf{l}\mathbf{o}\mathbf{c}\mathbf{a}\mathbf{l}}$
AM	HEIGHT	chr9: 107M–109M	0.15 (0.02)	0.05 (0.01)	0.61 ([0.34,0.87])
BMI	HIP	chr16: 53M–55M	0.22 (0.02)	0.19 (0.03)	0.99 ([0.76,1.00])
BMI	HIP	chr18: 57M–59M	0.14 (0.02)	0.13 (0.02)	0.99 ([0.71,1.00])
BMI	WC	chr16: 53M–55M	0.22 (0.02)	0.21 (0.03)	1.00 ([0.78,1.00])
BMI	WC	chr18: 57M–59M	0.14 (0.02)	0.13 (0.02)	1.00 ([0.72,1.00])
BW	HEIGHT	chr12: 65M–67M	0.14 (0.02)	0.23 (0.02)	0.93 ([0.70,1.00])
HDL	TG	chr2: 21M–23M	0.16 (0.03)	0.22 (0.03)	−0.94 ([−1.00, −0.65])
HDL	TG	chr8: 19M–20M	0.65 (0.04)	0.82 (0.04)	−1.00 ([−1.00, −0.91])
HDL	TG	chr11: 116M–117M	0.40 (0.04)	1.27 (0.06)	−0.82 ([−0.95,-0.69])
HDL	TG	chr15: 58M–59M	1.18 (0.06)	0.18 (0.03)	0.89 ([0.68,1.00])
HEIGHT	HIP	chr16: 4M–5M	0.06 (0.01)	0.10 (0.02)	0.73 ([0.41,1.00])
HIP	WC	chr16: 53M–55M	0.19 (0.03)	0.21 (0.03)	0.99 ([0.73,1.00])
HIP	WC	chr18: 57M–59M	0.13 (0.02)	0.13 (0.02)	1.00 ([0.69,1.00])
LDL	TG	chr1: 61M–63M	0.14 (0.03)	0.28 (0.03)	0.98 ([0.67,1.00])
LDL	TG	chr2: 21M–23M	0.84 (0.05)	0.22 (0.03)	0.62 ([0.46,0.78])
LDL	TG	chr8: 126M–128M	0.16 (0.03)	0.32 (0.04)	0.94 ([0.63,1.00])
LDL	TG	chr19: 18M–19M	0.18 (0.03)	0.21 (0.03)	0.99 ([0.72,1.00])
PLT	RBC	chr6: 134M–136M	0.26 (0.05)	0.66 (0.09)	−0.99 ([−1.00, −0.69])
HDL	HEIGHT	chr11: 47M–49M	0.17 (0.02)	0.07 (0.01)	0.61 ([0.42,0.80])
HDL	LDL	chr2: 21M–23M	0.16 (0.03)	0.84 (0.05)	−0.56 ([−0.74, −0.39])
HDL	LDL	chr8: 9M–9M	0.14 (0.02)	0.12 (0.02)	0.99 ([0.70,1.00])
MCH	MCV	chr6: 24M–25M	0.49 (0.07)	0.37 (0.06)	0.97 ([0.67,1.00])
MCH	MCV	chr6: 134M–136M	0.86 (0.09)	0.70 (0.08)	0.98 ([0.76,1.00])
MCH	PLT	chr6: 134M–136M	0.86 (0.09)	0.26 (0.05)	1.00 ([0.72,1.00])
MCH	RBC	chr6: 134M–136M	0.86 (0.09)	0.66 (0.09)	−0.98 ([−1.00, −0.75])
MCV	PLT	chr6: 134M–136M	0.70 (0.08)	0.26 (0.05)	1.00 ([0.72,1.00])
MCV	RBC	chr6: 134M–136M	0.70 (0.08)	0.66 (0.09)	−0.98 ([−1.00, −0.74])
MP	HEIGHT	chr5: 175M–177M	0.31 (0.04)	0.10 (0.01)	−0.63 ([−0.82, −0.45])
URATE	MCH	chr6: 24M–25M	0.13 (0.02)	0.53 (0.07)	0.56 ([0.33,0.79])
URATE	MCV	chr6: 24M–25M	0.13 (0.02)	0.41 (0.06)	0.66 ([0.39,0.92])

We list pairs of traits for which the genome-wide genetic correlation is significant (two-tailed p < 0.05/630) and negligible in top and bottom half of this table, respectively. Here, we focus only on the pairs of traits excluding TC (see Table S1 for pairs of traits involving TC). Numbers in parentheses represent standard errors for local SNP heritability estimates and 95% confidence intervals for local genetic correlation estimates.

Since genetic correlation is an aggregation of local genetic covariance, for pairs of traits with highly positive or negative genetic correlation, we expect the distribution of local genetic covariances to be shifted toward the positive or negative side (see Figure S17), whereas for pairs of traits with low genetic correlation, we expect the distribution of local genetic covariances to be centered around zero (see Figures 5 and6). Indeed, pairs of traits with higher genome-wide genetic correlation tend to harbor more loci with significant local genetic covariance (see Figure S14). For instance, only one region exhibits significant local genetic covariance for the pair of traits age at menarche (AM) and height (r_g = 0.13, 95% CI [0.10, 0.13]), whereas four loci show significant local genetic covariance for the pair of traits LDL and TG (r_g = 0.45, 95% CI [0.42, 0.49]).

Figure 5.

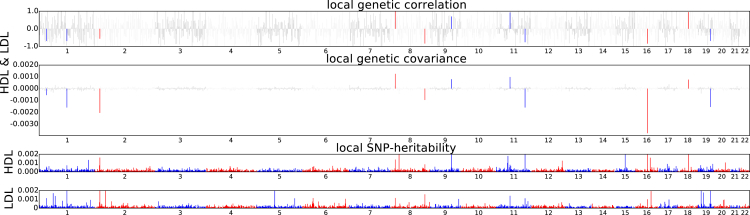
Manhattan-Style Plots Showing the Estimates of Local Genetic Covariance for the Pairs of Traits HDL and LDL

Although the genome-wide genetic correlation between HDL and LDL does not reach the significance level (p < 0.05/630), 11 loci exhibit significant local genetic covariance.

Figure 6.

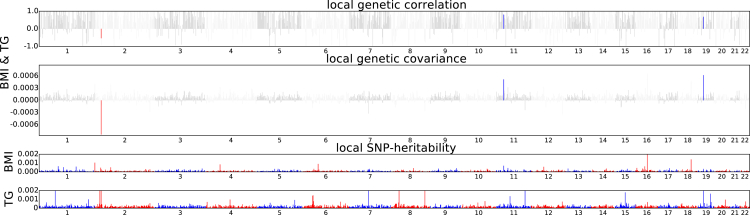
Manhattan-Style Plots Showing the Estimates of Local Genetic Covariance for the Pairs of Traits BMI and TG

That the local genetic covariance between BMI and TG is mostly one-sided implies plausible causal relationship between the two traits.

Local Correlations for Pairs of Traits with Negligible Genome-wide Correlation

Several pairs of traits show negligible genome-wide genetic correlation although they share GWAS risk regions. For example HDL and LDL share several GWAS risk loci³⁶ but the genome-wide genetic correlation is negligible (−0.05, 95% CI [−0.09, −0.01]).¹⁶ The absence of significant genome-wide genetic correlation between these pairs of traits can be attributed to either symmetric distribution of local genetic covariance (positive local genetic covariance cancels out negative local genetic covariance, see Figure 1) and/or lack of power to declare significance for genome-wide genetic correlation. Thus, we hypothesize that at the region-specific level, many loci may manifest significant local genetic covariance even if the genome-wide genetic correlation between a pair of traits is not significant. Indeed, 11 genomic regions show significant local genetic correlation (two-tailed p < 0.05/1,703) for HDL and LDL (see Figure 5). Some of these loci, e.g., chr2: 21M–23M, chr11: 116M–117M, and chr19: 44M–46M, harbor APOB, APOA1, and APOE (MIM: 107741), respectively, which are known to be involved in lipid genetics.^{36, 49, 50} Across all pairs of traits with non-significant genome-wide correlation, we identify 6 regions across 10 pairs of traits with significant local genetic correlation (two-tailed p < 0.05/1,703) and local SNP heritability (one-tailed p < 0.05/1,703) (see Table 2, Figure S16). For example, the region chr6: 134M–136M harbors the HBS1L (MIM: 612450)^{32, 51} and contributes to local genetic covariance across many blood traits (MCH, MCV, RBC, and PLT).

Genetic Correlation Ascertained for GWAS Risk Loci

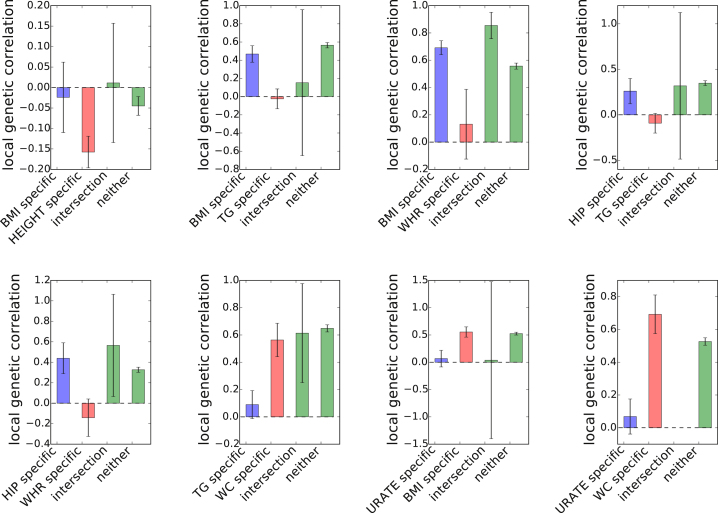
Assessing the correlation in the effects at genomic regions ascertained for trait-specific GWAS regions can be used to prioritize putative causal models between complex traits. We utilized a recently proposed approach² to assign putative causal relation to 55 pairs of traits. Restricting to 40 of the 55 pairs of traits that contain at least 10 regions with trait-specific GWAS signals (see Material and Methods), we quantified the local genetic correlation at genomic regions containing GWAS loci specific to each trait (see Table S2, Figure 7). Overall, the local genetic correlation is highly consistent with the putative causal relationships inferred by correlating the top signals at these loci.² For example, when considering body mass index (BMI) and triglyceride levels (TG), the correlation at BMI-specific regions is significantly greater than TG-specific loci (${\hat{r}}_{g,local,BM}=0.47$ 95% CI [0.37, 0.57] versus ${\hat{r}}_{g,local,TG}=-0.02$ 95% [−0.14, 0.10]), indicating that loci that increase BMI tend to consistently increase TG, whereas loci that increase TG do not consistently affect BMI, consistent with the putative model that BMI causally increases TG (see Figure 6).^{2, 3} We also observe correlations consistent with a model in which years of education (EY) consistently decreases hemoglobin level (HB), LDL, and TG (see Table S2), in line with previous conclusions on the effect of education on health.^{52, 53} However, we note that education attainment (or other studied traits) may be confounded by other factors such as social status and that one should exercise caution when inferring causality from genetic data. Finally, we also report pairs of traits in which the genetic correlation approach attains different results from bi-directional regression on the top signals.² For example, when considering body mass index (BMI) and age at menarche (AM), the local correlation approach do not yield different estimates ($r_{g,local,BMI}=-0.49$ 95% CI [−0.63, −0.35] versus $r_{g,local,AM}=-0.47$ 95% CI [−0.59, −0.35]), whereas the approach of Joseph et al.² suggests a putative causal relation. This discrepancy can be due to different model assumptions, e.g., single causal variant versus allelic heterogeneity, with further investigations needed to assign causality from these data.

Figure 7.

Estimates of Local Genetic Correlation at Loci Ascertained for GWAS Risk Variants for Eight Example Pairs of Traits that Show Plausible Causal Relationship

We obtained standard error using a jackknife approach. Error bars represent 1.96 times the standard error on each side.

Discussion

We have described ρ-HESS, a method to estimate local genetic correlation from GWAS summary association data. Through extensive simulations, we demonstrated that our method is approximately unbiased and provides consistent results irrespective of causal architecture. We analyzed large-scale GWAS summary association data of 36 quantitative traits. Compared with cross-trait LDSC, our methods identified considerably more pairs of traits displaying significant genome-wide genetic correlation likely because of the truncated-SVD regularization of the LD matrix, which decreases the standard error of the estimates. We identify genomic regions that are significantly correlated across pairs of traits regardless of the significance of genome-wide correlation. Finally, we performed bi-directional analyses over the local genetic correlations to identify putative causal relationships, and report local genetic correlations at loci harboring GWAS signal specific to each trait.

We conclude with several limitations highlighting areas for future work. First, our estimator requires phenotype correlation between two traits, as well as the number of shared individuals between the two GWASs. We estimate the phenotype correlation through cross-trait LDSC assuming full sample overlap between GWAS within the same consortium and no sample overlap between GWAS across two consortia. Second, we note that our bi-directional analyses over local genetic correlation can be further extrapolated to infer putative causal models between complex traits. We refrain from making conclusive causal inferences from the bi-directional analyses because exact inference of causal relations is largely complicated by unobserved confounders such as socioeconomic status, population stratification, and/or biological pathways. Furthermore, most of the GWAS summary association data are adjusted for covariates such as age and gender to increase statistical power,⁵⁴ and previous works have shown that adjusting for covariates can potentially lead to false positives.⁵⁵ Third, in our real data analyses, we made the assumption that the loci are independent of each other. In reality, however, correlations may exist across adjacent loci due to long-range LD and can lead to biased estimates. Nevertheless, we note that previous works have indicated the effect of LD leakage to be minimal,^{19, 56} and we conjecture that this statement still holds in estimating local genetic correlation. Lastly, we use truncated-SVD to regularize LD matrix and to reduce standard error in the estimates of local genetic correlation, at the cost of introducing bias. Currently, we use a fixed number of eigenvectors in the truncated-SVD regularization, across all the loci. However, this approach may not be optimal for genomic regions with different LD structure and leave a principled approach of estimating the number of eigenvectors as future work.

Published: November 2, 2017

Appendix A

Quantifying Shared Genetics via Covariance of the Causal Effects

An alternative measure of shared genetics is the covariance of the causal effects ($\mathit{\beta }$ and $\mathit{\gamma }$) of the two traits. Under the fixed-effect model, we define covariance of the causal effects, ${\rho }_{g,causal}$, as the dot product between the causal effect size vectors of the two traits,

$${\rho }_{g,causal}={\mathit{\beta }}^{\mathrm{⊺}}\mathit{\gamma }.$$ (Equation A1)

Here, we make the assumption that the average effect size of each SNP is 0.

The definition of covariance of the causal effects in Equation A1 coincides with genetic covariance under the random-effect model. As shown in the supplementary data of Bulik-Sullivan et al.,¹⁶ if one assumes that $\mathit{\beta }$ and $\mathit{\gamma }$ have zero mean and

$$\text{Var}\left[\left(\mathit{\beta },\mathit{\gamma }\right)\right]=\frac{1}{p}\left[\begin{array}{cc}{h}_{g\varphi }^2& {\rho }_g\\ {\rho }_g& h_{g\psi }^2\end{array}\right],$$ (Equation A2)

then it can be shown that the genetic covariance between two traits is

$$\text{Cov}\left[{\mathit{x}}^{\mathrm{⊺}}\mathit{\beta },{\mathit{x}}^{\mathrm{⊺}}\mathit{\gamma }\right]=\sum _{i=1}^p\sum _{j=1}^p\text{E}\left[{\mathit{x}}_i{\mathit{x}}_j{\mathit{\beta }}_i{\mathit{\gamma }}_j\right]=\sum _{i=1}^p\text{E}\left[{\mathit{x}}_i^2{\mathit{\beta }}_i{\mathit{\gamma }}_i\right]=\sum _{i=1}^p\text{E}\left[{\mathit{x}}_i^2\right]\text{E}\left[{\mathit{\beta }}_i{\mathit{\gamma }}_i\right]={\rho }_g.$$ (Equation A3)

The random-effect model makes the implicit assumption that many SNPs are causal, which is appropriate for genome-wide analysis but not for local analysis, where few SNPs are likely to be causal.

Estimating Covariance of the Causal Effects from GWAS Summary Data

For completeness, we derive an estimator for ${\rho }_{g,causal}$. We assume a linear model for the two traits (see Material and Methods). The effect size estimates from GWAS, ${\hat{\mathit{\beta }}}_{gwas}$ and ${\hat{\mathit{\gamma }}}_{gwas}$, follow ${\hat{\mathit{\beta }}}_{gwas}\sim N\left(\mathit{V\beta },\frac{1-h_{\varphi }^2}{n_1}\mathit{V}\right)$ and ${\hat{\mathit{\gamma }}}_{gwas}\sim N\left(\mathit{V\gamma },\frac{1-h_{\psi }^2}{n_2}\mathit{V}\right)$, with $\text{Cov}\left[{\hat{\mathit{\beta }}}_{gwas},{\hat{\mathit{\gamma }}}_{gwas}\right]=\frac{{\rho }_e{n}_s}{n_1{n}_2}\mathit{V}$, where n₁ and n₂ are the sample size for the two GWASs and n_s is the number of shared samples (see Material and Methods).

As the sample size, n₁ and n₂, of the two GWASs go to infinity, we have ${\mathit{\beta }}_{gwas}={\text{lim}}_{n\to \infty }{\hat{\mathit{\beta }}}_{gwas}=\mathit{V\beta }$ and ${\mathit{\gamma }}_{gwas}={\text{lim}}_{n\to \infty }{\hat{\mathit{\gamma }}}_{gwas}=\mathit{V\gamma }$, which implies $\mathit{\beta }={\mathit{V}}^{-1}{\mathit{\beta }}_{gwas}$ and $\mathit{\gamma }={\mathit{V}}^{-1}{\mathit{\gamma }}_{gwas}$, suggesting the following estimator for covariance of the causal effects,

$${\rho }_{g,causal}={\mathit{\beta }}^{\mathrm{⊺}}\mathit{\gamma }={\mathit{\beta }}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-2}{\mathit{\gamma }}_{gwas}.$$ (Equation A4)

In reality, however, finite sample sizes of GWAS results in noise in the estimates of $\mathit{\beta }$ and $\mathit{\gamma }$, creating bias in the estimate of ${\rho }_{g,causal}$. From bilinear form theory, it can be shown that

$$\text{E}\left[{\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-2}{\hat{\mathit{\gamma }}}_{gwas}\right]={\mathit{\beta }}^{\mathrm{⊺}}\mathit{\gamma }+\frac{{\rho }_e}{n}\text{tr}\left({\mathit{V}}^{-2}\mathit{V}\right)={\mathit{\beta }}^{\mathrm{⊺}}\mathit{\gamma }+\frac{{\rho }_e}{n}\text{tr}\left({\mathit{V}}^{-1}\right),$$ (Equation A5)

suggesting the unbiased estimator of ${\rho }_{g,causal}$,

$${\hat{\rho }}_{g,causal}={\hat{\mathit{\beta }}}_{gwas}^{\mathrm{⊺}}{\mathit{V}}^{-2}{\hat{\mathit{\gamma }}}_{gwas}-\frac{n_s{\rho }_e}{n_1{n}_2}\text{tr}\left({\mathit{V}}^{-1}\right),$$ (Equation A6)

where the environmental covariance can be estimated through cross-trait LD Score regression.¹⁶

Web Resources

• European Genome-phenome Archive (EGA) (accession number EGAS00000000132), https://www.ebi.ac.uk/ega

• GEFOS consortium, http://www.gefos.org/?q=content/data-release-2015

• GIANT consortium, https://www.broadinstitute.org/collaboration/giant/index.php/GIANT_consortium_data_files

• GLGC consortium, http://csg.sph.umich.edu//abecasis/public/lipids2013/

• HESS and ρ-HESS, http://bogdan.bioinformatics.ucla.edu/software/hess/

• LDSC, https://github.com/bulik/ldsc

• MAGIC, https://www.magicinvestigators.org/downloads/

• OMIM, http://www.omim.org/

• Psychiatric Genomics Consortium, https://www.med.unc.edu/pgc/acl_users/credentials_cookie_auth/require_login?came_from=http%3A//www.med.unc.edu/pgc/old-pages/downloads

• ReproGen, http://www.reprogen.org/

• SSGAC, https://www.thessgac.org/data