Abstract
Objective
Osteoporosis diagnosis using multidetector CT (MDCT) is limited to relatively high radiation exposure. We investigated the effect of simulated ultra-low-dose protocols on in-vivo bone mineral density (BMD) and quantitative trabecular bone assessment.
Materials and methods
Institutional review board approval was obtained. Twelve subjects with osteoporotic vertebral fractures and 12 age- and gender-matched controls undergoing routine thoracic and abdominal MDCT were included (average effective dose: 10 mSv). Ultra-low radiation examinations were achieved by simulating lower tube currents and sparse samplings at 50%, 25% and 10% of the original dose. BMD and trabecular bone parameters were extracted in T10–L5.
Results
Except for BMD measurements in sparse sampling data, absolute values of all parameters derived from ultra-low-dose data were significantly different from those derived from original dose images (p<0.05). BMD, apparent bone fraction and trabecular thickness were still consistently lower in subjects with than in those without fractures (p<0.05).
Conclusion
In ultra-low-dose scans, BMD and microstructure parameters were able to differentiate subjects with and without vertebral fractures, suggesting osteoporosis diagnosis is feasible. However, absolute values differed from original values. BMD from sparse sampling appeared to be more robust. This dose-dependency of parameters should be considered for future clinical use.
Key Points
• BMD and quantitative bone parameters are assessable in ultra-low-dose in vivo MDCT scans.
• Bone mineral density does not change significantly when sparse sampling is applied.
• Quantitative trabecular bone microstructure measurements are sensitive to dose reduction.
• Osteoporosis subjects could be differentiated even at 10% of original dose.
• Radiation exposure should be considered when comparing quantitative bone parameters.
Electronic supplementary material
The online version of this article (doi:10.1007/s00330-017-4904-y) contains supplementary material, which is available to authorized users.
Keywords: Computed tomography, Radiation dose, Sparse sampling, Osteoporosis, Trabecular microstructure
Introduction
Osteoporosis is a skeletal disorder, leading to an increased risk for fragility fractures [1]. The loss of bone mineral density (BMD) and the deterioration of bone microstructure is typically unnoticed until actual fractures occur. Osteoporotic fractures do not only reduce quality of life, but are also associated with increased mortality [2]. The prevalence of osteoporotic fractures is increasing in our aging society and causing a large burden to healthcare systems [3]. In order to prevent the occurrence of osteoporotic fractures, it is of great importance that patients at risk are identified in order to receive proper treatment in a timely manner.
The current clinical standard method to measure BMD is via dual-energy X-ray absorptiometry (DXA). However, it is partly insufficient in identifying subjects at high risk for osteoporotic fractures: Studies have shown that over half of all non-vertebral fractures occurred in patients with non-pathological BMD values [4, 5]. Quantitative BMD and trabecular bone microstructure analysis based on high-resolution multidetector computer tomography (MDCT) improves the prediction of biomechanical bone strength and fracture risk beyond BMD [6–8]. However, the currently applied radiation dose is clinically not acceptable, particularly for longitudinal assessment of fracture risk and therapy monitoring [9].
Several parameters contribute to the radiation dose of a conventional MDCT, namely tube current, peak kilovoltage (kVp), pitch and gantry cycle time [10]. In this study we considered two approaches to reduce the radiation dose. The first approach was to reduce the X-ray tube current, which can currently be realized with a commercial scanner. Due to the nature of commercially available detectors, lowering the tube current linearly decreases radiation dose, but causes a much lowered signal-to-noise ratio (SNR) at the detector, which reduces the diagnostic quality of the images. The second approach was to acquire fewer projections during the scan, which we refer to as sparse sampling. With the future development of X-ray generator units, it will be possible to switch off the X-ray source in MDCT scanners at certain angles and provide shorter X-ray pulses, thus keeping the SNR but lowering the total radiation dose in practice.
With a reduced radiation dose, it is still possible to generate images with relatively high diagnostic quality by applying advanced reconstruction algorithms, e.g. statistical iterative reconstruction (SIR). The performance of SIR under lower tube current [11–15] or fewer projection angles [16] has been validated. To reduce the resulting noise and artefacts, SIR uses a regularization term to produce smoother images.
The aims of our study were: (i) to assess the feasibility of BMD and trabecular bone microstructure parameter measurements in MDCT examinations when tube current is ultra-low or data is sparsely sampled, (ii) to compare their values with those derived from the original imaging data, and (iii) to investigate the possibility of differentiating subjects with and without prevalent vertebral fractures with the acquired quantitative measurements.
Materials and methods
Subjects and multidetector CT (MDCT) scanning
Institutional review board approval was obtained for this retrospective study. Twelve subjects with osteoporotic vertebral fractures and 12 age- and gender-matched subjects without fractures who all underwent routine thoracic and abdominal MDCT were retrospectively identified and included in this study. The presence of actual fractures was determined by radiologists. Collected scans had no original purpose for osteoporotic screening.
MDCT scans were acquired using a 256-row scanner (iCT, Philips Healthcare, Best, The Netherlands). Clinical thoracic/abdominal protocols after standardized intravenous contrast agent application were used in all subjects. For calibration purposes, a reference phantom (Mindways Osteoporosis Phantom, Austin, TX, USA [17]) was placed in the scanner mat beneath the subjects. The helical pitch was set as 0.91 in 18 subjects and 0.75 in four subjects. The tube voltage was 120 kVp in all cases. Maximum tube currents of the 24 scans ranged between 200 mA and 400 mA, while exact tube current during each scan was modulated implicitly by the scanner. The average of the exposure values recorded in all 24 dose reports was 109 mAs (min: 33 mAs, max: 188 mAs).
Tube current simulation and sparse sampling
For all subjects, we used a simulation tool to generate lower tube current scans. The simulation algorithm was based on raw projection data, as described in detail previously [18]. System parameters of the CT scanner, such as detector gain, were taken into consideration to properly account for electronic noise. Therefore, the result was accurate especially for ultra-low tube current [19]. Low-dose simulations at 50%, 25% and 10% of the original tube current were generated.
Sparse sampling was applied at levels of 50%, 25% and 10% of the original projection data. This was done by only reading every second, fourth and tenth projection angle and deleting the remaining projections in the sinogram. Thus, only the number of projections per full rotation was reduced, whereas other parameters, such as projection geometry and patient location, were kept the same.
Table 1 provides the average radiation exposure of all scans in this study. Original exposure (mAs) and CT Dose Index (CTDIvol, mGy) were extracted from the radiation dose report. Effective radiation dose (mSv) was approximated [28] for a female shoulder to middle thigh. Both sparse sampling and lowering tube current reduced the radiation dose linearly.
Table 1.
Mean radiation exposure, estimated effective dose, signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) of images under different simulated levels of the original scan
| Mean exposure (mAs) | Mean CDTIVol(mGy) | Effective dose (mSv) | SNR | CNR | |
|---|---|---|---|---|---|
| Original | 109 | 7.5 | 10 | 32.802 | 13.682 |
| Proj50 | 55 | 3.8 | 5 | 21.483 | 8.597 |
| Proj25 | 27 | 1.9 | 3 | 16.193 | 6.336 |
| Proj10 | 11 | 0.8 | 1 | 14.208 | 5.619 |
| Tube50 | 55 | 3.8 | 5 | 18.552 | 7.234 |
| Tube25 | 27 | 1.9 | 3 | 9.524 | 3.794 |
| Tube10 | 11 | 0.8 | 1 | 2.858 | 1.146 |
Proj50, Proj25 and Proj10 represent 50%, 25% and 10% of the sparse sampling, respectively
Tube50, Tube25 and Tube10 represent 50%, 25% and 10% of the simulated lower tube current, respectively
Effective dose was estimated for a female from the shoulder to the middle of the thigh
SNR was estimated within a homogenous region of the material of the highest density in the phantom
CNR was estimated between the homogenous regions of the materials of the highest and lowest density in the phantom
Statistical iterative reconstruction
Collected subjects were all reconstructed anew with statistical iterative reconstruction (SIR) in a much denser grid focusing on the spine. SIR was applied on the full dose data, the simulated projection data at 50%, 25% and 10% as well as the sparse sampling data at levels of 50%, 25% and 10%. SIR was performed with ordered-subset separable paraboloidal surrogate [20] combining a momentum-based accelerating approach [21].
The objective function of SIR consisted of a likelihood term and a regularization term. The likelihood term was computed with log-converted projection data. A Gaussian noise model was applied. We assumed the reconstruction with a helical path can converge with the selected solver. The iterative reconstruction stopped at a manually given number of iterations. Each small update of image u was made with a subset of projection data. This required one forward projection and one back projection. The forward and back projectors were implemented with a highly parallel framework [22].
For a non-sparse-sampling scan, the scanner acquired 2,400 projections per full rotation (PPR) and we chose a subset size of 100 projection images in one full rotation. The total number of iterations was 15, which yielded 360 subset updates. For 50%, 25% and 10% sparse sampling data, we kept the subset size as 100 projection images per PPR and increased the iteration number to be 30, 60 and 150, respectively. The selection of projection images was made randomly for each subset.
Regularization was applied between updates of the subsets. The regularization term was based on a Huber penalty. In order to preserve the trabecular bone microstructure as much as possible, regularization with a limited influence was selected [23].
All image slices were reconstructed as 1,152 × 1,152 pixels with a field of view of 450 × 450 mm2. All parts of the patient and the table were included in the field of view. Reconstruction slice interval was 0.3 mm. The resulting images had voxel spacing of 0.39, 0.39 and 0.3 mm in three dimensions. The exact voxel size was limited to the collimator width at the detector. Voxel intensities (linear attenuation coefficients) were translated to Hounsfield units (HU) using air/water information from the calibration of the scanner. Patient position and table height were incorporated so that all images for each individual were automatically registered.
Bone mineral density and trabecular microstructure analysis
Hounsfield units inside the vertebrae were calibrated to BMD values by using the reference phantom [17]. The phantom consisted of five rods of basic materials with known equivalent water and K2HPO4 densities. Transferring coefficients were thus calculated in a least squares manner with all five rods for each subject independently. To eliminate the effect of the intravascular contrast agent, a conversion equation was applied empirically as described previously [24].
Mean BMD and standard deviation were calculated inside regions of interest (ROIs) within the trabecular part of the vertebral bodies of each subject. ROIs were placed inside the ventral part, within the central third of the height of the thoracic vertebrae T10–T12 and lumbar vertebrae L1–L5 similar to standard QCT measurements. All ROIs were cylinders with a diameter of 14–16 mm and a height of 4–6 mm, depending on the individual’s vertebrae size. The same ROIs were applied for original dose images, sparsely-sampled and simulated lower-current images. Vertebrae with fractures were excluded from the ROI selection.
Trabecular bone microstructure within the ROIs was analysed with an in-house developed program based on IDL (Interactive Display Language; ITT Visual Information Solutions, Boulder, CO, USA). Similar to previous studies [25], voxels in ROIs were binarized to be either bone or marrow. A global threshold was chosen as 200 mg/cm3 equivalent K2HPO4, which was optimized visually for the microstructure analysis of the subjects [26]. Four morphometric parameters were estimated: bone volume over total volume as bone fraction (BF), trabecular number (TbN, mm-1), trabecular separation (TbSp, mm) and trabecular thickness (TbTh, mm) [9]. Parameters were labeled as apparent (app.) due to the limited spatial resolution. One texture parameter of the trabecular bone microstructure (fractal dimension, FD) was determined using a box counting algorithm [27].
Statistical analysis
The statistical analysis was performed with SPSS software package (SPSS, Chicago, IL, USA). All tests were done using a two-sided 0.05 level of significance. Mean and standard deviation of BMD and trabecular bone microstructure parameters were calculated. The Kolmogorov-Smirnov test showed for most parameters no significant difference from normal distribution (p < 0.05). Therefore, paired t-tests were used to evaluate the differences between BMD and trabecular bone microstructure parameters derived from the different sparse sampled and low-dose simulated data in all subjects. Differences in BMD and trabecular bone microstructure parameters derived from the different sparse sampled and low-dose simulated data between the matched groups of subjects with and without osteoporotic vertebral fractures were evaluated with paired tests and area under the receiver-operating characteristic (ROC) curves.
Results
At 10% of the original dose, estimated SNR and CNR were five times better with sparse sampling than with simulated lower tube current images (Table 1). For sparsely sampled data, artefact patterns slowly became obvious when fewer projections were used. For simulated lower tube current images, streaking artefacts emerged with the decrease of tube current and image quality dropped rapidly. A representative matched subject pair with and without osteoporotic vertebral fracture at original dose is depicted in Fig. 1. Sparse sampling and simulated lower current images are depicted in Figs. 2, 3 and 4 and in the Appendix in Figs. A1 and A2.
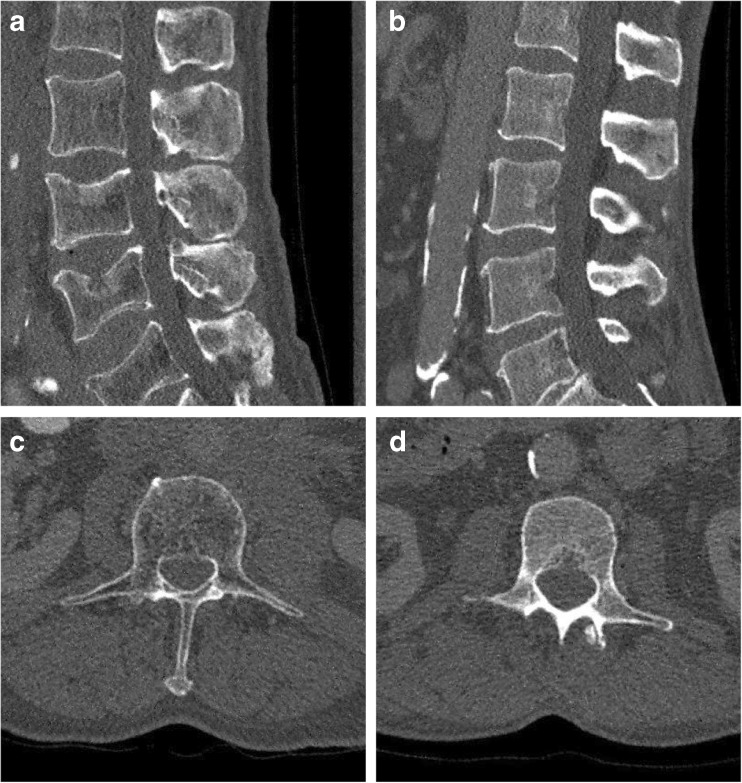
Fig. 1.
Representative reconstructions of the lumbar spine (L1–L5) of in-vivo spine multidetector CT (MDCT) data at the original dose. The left column depicts a subject with a fracture; the right column displays the matched healthy subject with regard to age and gender. The original dose was at 120 kV, 107 mAs (left) and 114 mAs (right) (exact tube current was modulated). Window level was 300 HU and width was 1,500 HU. Field of view was 180 × 153 mm2 for (a) and (b), and 156 × 156 mm2 for (c) and (d)
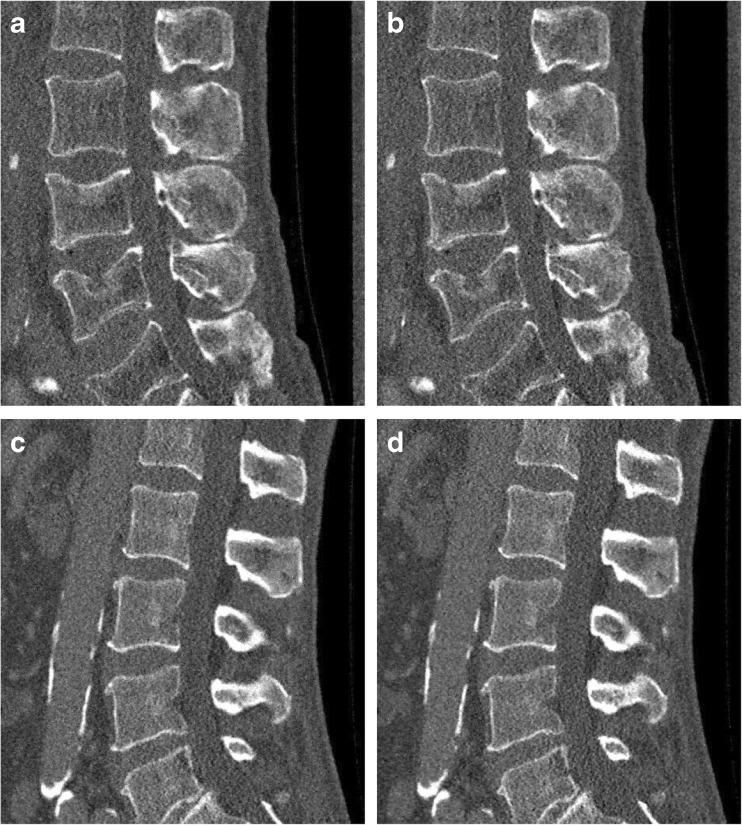
Fig. 2.
Representative sagittal reconstructions at 50% of the original dose level. The images depict the corresponding results for Fig. 1a and Fig. 1b. (a) and (c) represent the statistical iterative reconstruction (SIR) reconstructed image with 50% sparsely sampled projection. (b) and (d) show the SIR reconstructed images with the simulated 50% of the original tube current. Window level was 300 HU and width was 1,500 HU. Field of view was 180 × 153 mm2
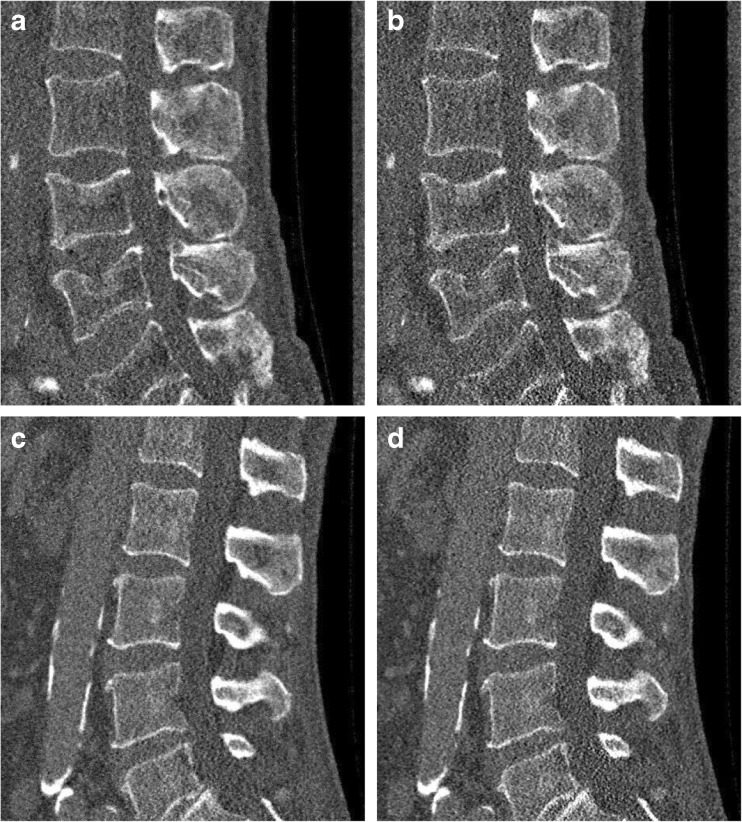
Fig. 3.
Representative sagittal reconstructions at 25% of the original dose level. The images depict the corresponding results for Fig. 1a and Fig. 1b. (a) and (c) represent the statistical iterative reconstruction (SIR) reconstructed image with 25% sparsely sampled projection. (b) and (d) show the SIR reconstructed images with the simulated 25% of the original tube current. Window level was 300 HU and width was 1,500 HU. Field of view was 180 × 153 mm2
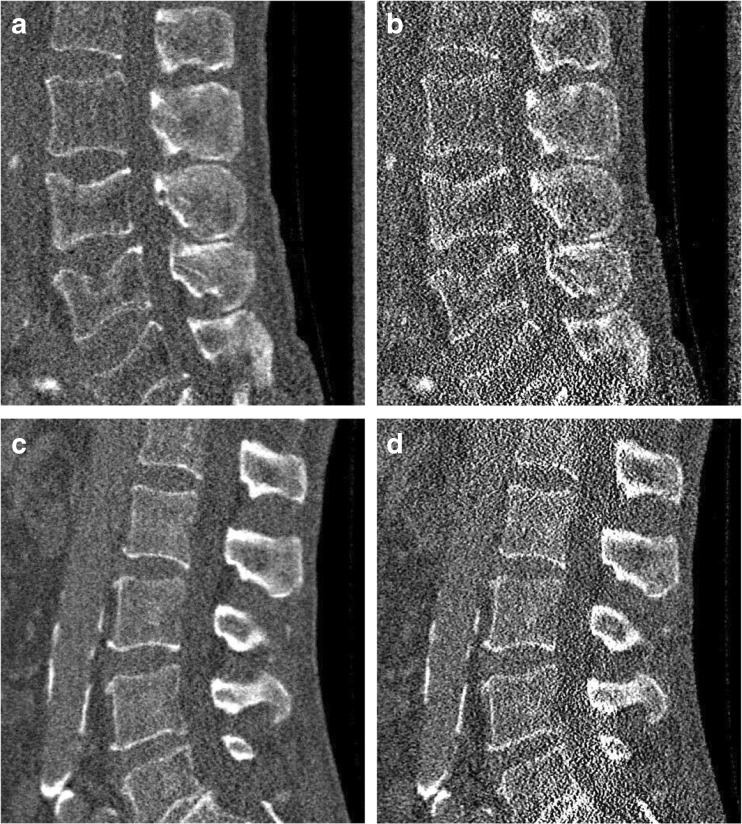
Fig. 4.
Representative sagittal reconstructions at 10% of the original dose level. The images depict the corresponding results for Fig. 1a and Fig. 1b. (a) and (c) represent the statistical iterative reconstruction (SIR) reconstructed image with 10% sparsely sampled projection. (b) and (d) show the SIR reconstructed images with the simulated 10% of the original tube current. Window level was 300 HU and width was 1,500 HU. Field of view was 180 × 153 mm2.
We observed no significant change in BMD when analysing the reduced projections even at 10% sampling rate (p > 0.05), whereas lowering tube current to 10% resulted in on average 38% higher BMD values (Fig. 5). For all trabecular parameters, both sparse sampling and lowering tube current affected the measurements in various degrees. BF, TbN and FD tended to increase when dose was lowered, while TbSp and TbTh decreased. TbN and TbSp were most sensitive to the dose reduction (p < 0.001) around changes of 20–40% (Fig. 6). All changes in BMD and trabecular bone microstructure parameters from the different reconstructions are shown in Table 2 and in the Appendix in Fig. A3 and Table A1.
Fig. 5.
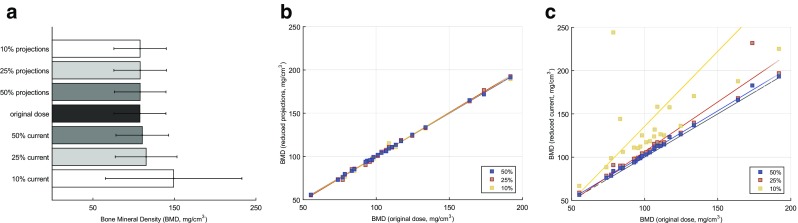
Bone mineral density (BMD) extracted from different image reconstructions. (a) The mean and standard deviations of all 24 subjects (mg/cm3). (b) The scatter plot of the measurements from sparse sampling images versus the original dose image. (c) The scatter plot of the measurements from the reduced tube current versus the original dose. The original dose is along the x-axis. Ultra-low-dose measurements at 50%, 25% and 10% are along the y-axis. The regression line is drawn in colour. The grey line depicts the centre line
Fig. 6.
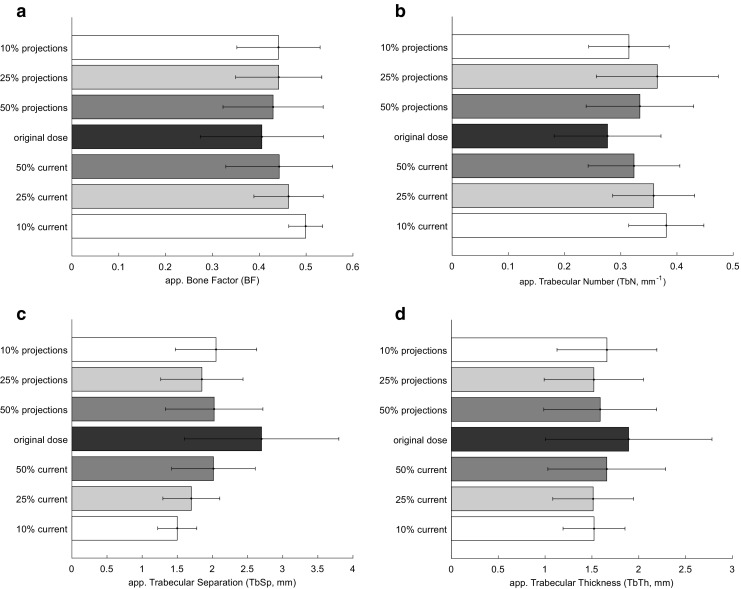
Trabecular parameters extracted from the different image reconstructions
Table 2.
Changes in bone mineral density (BMD) and trabecular bone microstructure parameters at reduced dose levels
| BMD, mg/cm-3 | Mean | SD | p-value | App. BF | Mean | SD | p-value |
|---|---|---|---|---|---|---|---|
| vs. original dose | vs. original dose | ||||||
| Proj50 | +0.216 | 0.797 | .197 | Proj50 | +0.024 | 0.034 | .002 |
| Proj25 | +0.145 | 1.547 | .650 | Proj25 | +0.036 | 0.052 | .003 |
| Proj10 | +0.233 | 1.978 | .569 | Proj10 | +0.035 | 0.055 | .004 |
| Tube50 | +2.900 | 1.863 | .000 | Tube50 | +0.037 | 0.032 | .000 |
| Tube25 | +7.546 | 11.040 | .003 | Tube25 | +0.057 | 0.072 | .001 |
| Tube10 | +41.32 | 67.131 | .006 | Tube10 | +0.094 | 0.120 | .001 |
| App. TbN, mm-1 | Mean | SD | p-value | App. TbSp, mm | Mean | SD | p-value |
| vs. original dose | vs. original dose | ||||||
| Proj50 | +0.058 | 0.025 | .000 | Proj50 | -0.675 | 0.555 | .000 |
| Proj25 | +0.089 | 0.066 | .000 | Proj25 | -0.849 | 0.690 | .000 |
| Proj10 | +0.038 | 0.047 | .001 | Proj10 | -0.648 | 0.678 | .000 |
| Tube50 | +0.046 | 0.027 | .000 | Tube50 | -0.685 | 0.650 | .000 |
| Tube25 | +0.082 | 0.048 | .000 | Tube25 | -1.000 | 0.865 | .000 |
| Tube10 | +0.104 | 0.091 | .000 | Tube10 | -1.200 | 1.119 | .000 |
| App. TbTh, mm | Mean | SD | p-value | FD | Mean | SD | p-value |
| vs. original dose | vs. original dose | ||||||
| Proj50 | -0.304 | 0.402 | .001 | Proj50 | +0.059 | 0.045 | .000 |
| Proj25 | -0.372 | 0.520 | .002 | Proj25 | +0.081 | 0.062 | .000 |
| Proj10 | -0.232 | 0.527 | .042 | Proj10 | +0.067 | 0.061 | .000 |
| Tube50 | -0.234 | 0.377 | .006 | Tube50 | +0.063 | 0.051 | .000 |
| Tube25 | -0.379 | 0.642 | .008 | Tube25 | +0.103 | 0.083 | .000 |
| Tube10 | -0.370 | 0.797 | .033 | Tube10 | +0.137 | 0.133 | .000 |
Values are shown as compared to the original dose in all subjects (n=24) with respective p-values
Proj50, Proj25 and Proj10 indicate sparse sampling of 50%, 25% and 10% projection data, respectively
Tube50, Tube25 and Tube10 indicate simulation of 50%, 25% and 10% of the original tube current, respectively
Displayed means and standard deviations (SD) are given in absolute values
App. apparent, BF bone fraction, BMD bone mineral density, FD fractal dimension, TbN trabecular number, TbSp trabecular separation, TbTh trabecular thickness
For BMD, BF and TbTh, subjects without osteoporotic fractures still had greater values as compared to the matched subjects with osteoporotic fractures in both dose-reducing approaches. The two groups could still be differentiated, as differences were statistically significant (p < 0.05) even at 10% of the original dose level. For TbSp and FD, the differences between the two groups were significant only when the original dose was used, but was not significant when either data were sparsely sampled or tube current was reduced (p > 0.05). The differences in TbN between the two groups was not significant at any dose level. The mean, standard deviation, p-value and area under ROC curves of all parameters for differentiating the two groups are listed separately in Tables 3 and 4.
Table 3.
Mean and standard deviation of bone mineral density (BMD) and trabecular bone microstructure
| Fracture | No fracture | Fracture | No fracture | ||||||
|---|---|---|---|---|---|---|---|---|---|
| BMD | Mean | SD | Mean | SD | App. BF | Mean | SD | Mean | SD |
| SIR | 90.236 | 17.455 | 125.228 | 33.868 | SIR | 0.311 | 0.095 | 0.500 | 0.160 |
| Proj50 | 90.447 | 17.668 | 125.449 | 33.404 | Proj50 | 0.356 | 0.082 | 0.503 | 0.127 |
| Proj25 | 89.671 | 17.477 | 126.083 | 34.116 | Proj25 | 0.378 | 0.074 | 0.505 | 0.107 |
| Proj10 | 90.189 | 17.262 | 125.742 | 33.951 | Proj10 | 0.375 | 0.072 | 0.507 | 0.103 |
| Tube50 | 92.439 | 17.513 | 128.824 | 34.078 | Tube50 | 0.362 | 0.083 | 0.523 | 0.138 |
| Tube25 | 94.938 | 17.883 | 135.619 | 42.176 | Tube25 | 0.406 | 0.065 | 0.519 | 0.082 |
| Tube10 | 110.210 | 21.069 | 187.904 | 104.438 | Tube10 | 0.472 | 0.035 | 0.526 | 0.037 |
| App. TbN | Mean | SD | Mean | SD | App. TbSp | Mean | SD | Mean | SD |
| SIR | 0.284 | 0.108 | 0.269 | 0.080 | SIR | 3.127 | 1.178 | 2.272 | 1.015 |
| Proj50 | 0.352 | 0.106 | 0.316 | 0.084 | Proj50 | 2.148 | 0.605 | 1.901 | 0.773 |
| Proj25 | 0.377 | 0.108 | 0.353 | 0.109 | Proj25 | 1.896 | 0.495 | 1.804 | 0.664 |
| Proj10 | 0.331 | 0.074 | 0.298 | 0.069 | Proj10 | 2.145 | 0.483 | 1.958 | 0.662 |
| Tube50 | 0.341 | 0.091 | 0.306 | 0.071 | Tube50 | 2.158 | 0.515 | 1.871 | 0.665 |
| Tube25 | 0.378 | 0.080 | 0.339 | 0.065 | Tube25 | 1.752 | 0.356 | 1.647 | 0.448 |
| Tube10 | 0.412 | 0.073 | 0.350 | 0.060 | Tube10 | 1.416 | 0.256 | 1.583 | 0.298 |
| App. TbTh | Mean | SD | Mean | SD | FD | Mean | SD | Mean | SD |
| SIR | 1.301 | 0.609 | 2.483 | 1.100 | SIR | 1.119 | 0.163 | 1.225 | 0.147 |
| Proj50 | 1.171 | 0.477 | 2.006 | 0.706 | Proj50 | 1.207 | 0.145 | 1.254 | 0.134 |
| Proj25 | 1.165 | 0.477 | 1.876 | 0.579 | Proj25 | 1.241 | 0.146 | 1.264 | 0.126 |
| Proj10 | 1.282 | 0.441 | 2.038 | 0.611 | Proj10 | 1.219 | 0.140 | 1.259 | 0.135 |
| Tube50 | 1.234 | 0.510 | 2.083 | 0.728 | Tube50 | 1.211 | 0.146 | 1.259 | 0.126 |
| Tube25 | 1.218 | 0.369 | 1.808 | 0.485 | Tube25 | 1.269 | 0.142 | 1.282 | 0.112 |
| Tube10 | 1.284 | 0.308 | 1.761 | 0.352 | Tube10 | 1.331 | 0.145 | 1.287 | 0.110 |
Parameters are shown as matched groups with (n=12) and without vertebral fracture (n=12) for the different dose levels
SIR indicates iterative reconstruction of the original dose
Proj50, Proj25 and Proj10 indicate sparse sampling of 50%, 25% and 10% projection data, respectively
Tube50, Tube25 and Tube10 indicate simulation of 50%, 25% and 10% of the original tube current, respectively
App. apparent, BF bone fraction, BMD bone mineral density, FD fractal dimension, TbN trabecular number, TbSp trabecular separation, TbTh trabecular thickness
Table 4.
P-values and area under the receiver-operating characteristic (ROC) curve for the fracture and no-fracture groups, observed at different dose levels
| BMD | p-value | ROC | App. BF | p-value | ROC |
|---|---|---|---|---|---|
| SIR | .002* | .875 | SIR | .002* | .861 |
| Proj50 | .002* | .875 | Proj50 | .002* | .840 |
| Proj25 | .002* | .875 | Proj25 | .002* | .833 |
| Proj10 | .002* | .868 | Proj10 | .001* | .854 |
| Tube50 | .002* | .875 | Tube50 | .003* | .878 |
| Tube25 | .002* | .882 | Tube25 | .001* | .868 |
| Tube10 | .023* | .896 | Tube10 | .001* | .878 |
| App. TbN | p-value | ROC | App. TbSp | p-value | ROC |
| SIR | .699 | .458 | SIR | .028* | .319 |
| Proj50 | .371 | .375 | Proj50 | .279 | .396 |
| Proj25 | .601 | .417 | Proj25 | .640 | .458 |
| Proj10 | .285 | .368 | Proj10 | .347 | .417 |
| Tube50 | .351 | .372 | Tube50 | .201 | .382 |
| Tube25 | .253 | .361 | Tube25 | .459 | .424 |
| Tube10 | .033* | .236 | Tube10 | .079 | .656 |
| App. TbTh | p-value | ROC | FD | p-value | ROC |
| SIR | .004* | .861 | SIR | .087 | .694 |
| Proj50 | .003* | .854 | Proj50 | .385 | .618 |
| Proj25 | .005* | .861 | Proj25 | .650 | .587 |
| Proj10 | .004* | .896 | Proj10 | .447 | .597 |
| Tube50 | .006* | .868 | Tube50 | .378 | .618 |
| Tube25 | .010* | .875 | Tube25 | .808 | .556 |
| Tube10 | .002* | .833 | Tube10 | .381 | .417 |
Parameters are shown as matched groups with (n=12) and without vertebral fracture (n=12) for the different dose levels
ROC denotes area under the ROC curve
SIR indicates iterative reconstruction of the original dose
Proj50, Proj25 and Proj10 indicate sparse sampling of 50%, 25% and 10% projection data
Tube50, Tube25 and Tube10 indicate simulation of 50%, 25% and 10% of the original tube current
* indicates p-values with statistically significant differences between the two groups (p<0.05)
App. apparent, BF bone fraction, BMD bone mineral density, FD fractal dimension, TbN trabecular number, TbSp trabecular separation, TbTh trabecular thickness
Discussion
To the best of our knowledge, this is the very first study of in-vivo data comparing reduced tube current and projection angles with statistical iterative reconstruction with regard to BMD and trabecular bone microstructure analysis. Our results demonstrated that it is computationally possible to assess the bone microstructure quantitatively with half or less of the dose in non-dedicated routine MDCT. BMD, BF and TbTh, were robust to dose changes and still differentiated between subjects with and without osteoporotic vertebral fractures, while TbSp and FD were dose-sensitive.
For sparse sampling, we observed that vertebral BMD did not change on a statistically significant level when less projection angles (down to only 10%) were used. This may allow BMD measurements with much lower radiation exposure in the future. However, it is not yet possible to apply sparse sampling to lower radiation exposure at commercial CT scanners. In current systems, the X-ray source is constantly delivering X-rays during the entire examination. However, precise and fast grid-switching units are reported to be introduced to control the X-ray source on and off in the future. On the other hand, tube current reduction, or modulation, is relatively easy to realize and has been intensively studied [10]. Current detectors are more suspended to electronic noise, especially when the tube current is lowered. Electronic noise can destroy the signal or can cause a bias to R1.4quantitative values. For this reason, we observed significant changes in absolute BMD values when tube current was lowered, compared to the data from sparse sampling. This suggests that values from sparse sampling seem to be more robust than values from lower tube currents for BMD measurement. However, the computed parameters at ultra-low-dose levels from both approaches still adequately differentiated subjects with and without osteoporotic fractures.
In our study, the mean CTDIvol value was 7.5 mGy (max. 13.7 mGy, min. 5.1 mGy, among abdomen scans) in the original scans. The approximated effective dose was about 2.6 mSv per person (estimation of T12–L5 coverage [28]). Our results showed that further dose reduction was still adequate to approximate quantitative bone parameters; this was actually much lower than previously reported (1.5 mSv for L1 and L2 only [29]).
We used statistical iterative reconstruction (SIR) in this study. Compared to the reconstruction process based on traditional methods like FBP, an iterative-based algorithm is considered more suitable handling noise and streaking artefacts, because it integrates physics modeling, providing better performances for missing data, irregular sampling and tube current reduction [30]. A higher level of the modelling provides greater image quality improvement, but also at a greater price of computational complexity. Because the image quality generated by traditional algorithms is still acceptable for most diagnostic purposes, additional algorithms with higher modelling complexity are often used in academics and avoided by manufacturers for clinical routine [31]. However, with the vast development of graphic units and computational power, SIR will become much more widely available [32]. The image noise in SIR is mainly handled with a regularization term. A previous study [23] investigated the effect of different models of regularization on trabecular bone microstructure at the spine in-vitro. These investigators observed that a minimum of regularization is best suited for quantitative bone microstructure analysis. For this reason, we also used a low regularization term in this study.
Admittedly our study had limitations. Firstly, the number of the investigated subjects was relatively small due to the pilot character of this study. Secondly, the decisions of osteoporotic or control subjects were determined merely by the presentation of actual vertebral fractures. Thirdly, MDCT imaging was performed with application of an intravenous contrast agent due to the clinical indication of the examinations, which affects quantitative bone measurements. However, a BMD conversion equation was applied as reported previously [24]. Lastly, low-dose scans in this study were simulated retrospectively and were not acquired prospectively due to radiation protection regulations. However, the validity of the low-dose simulation tool has been demonstrated previously both by the industrial manufacturers’ laboratory [18] and clinical research institution [19]. Further studies have to be performed in the future to validate the potential of dose reduction approaches for CT-based osteoporosis diagnostics and therapy monitoring.
In conclusion, we investigated the effect of sparse sampling and simulated lower tube current in non-dedicated MDCT scans combined with SIR on BMD and quantitative bone microstructure assessment. Our findings indicate that BMD and trabecular bone microstructure are still assessable at ultra-low dose levels. BMD, apparent bone factor and trabecular thickness were able to differentiate between subjects with and without osteoporotic fractures based on both approaches for dose reduction, sparse sampling and lower tube currents. This suggests that fracture risk prediction with low-dose protocols is feasible. However, absolute parameter values at reduced dose levels significantly differed from original values. BMD measurements derived from sparse sampling showing less changes compared to values acquired with lower tube currents, suggesting sparse sampling to be a more robust dose reduction approach for BMD measurements. These changes in parameters should be considered for future studies and clinical use.
Electronic supplementary material
Below is the link to the electronic supplementary material.
(DOCX 1716 kb)
Abbreviations
- app
Apparent
- BF
Bone fraction
- BMD
Bone mineral density
- CNR
Contrast-to-noise ratio
- DXA
Dual-energy X-ray absorptiometry
- FD
Fractal dimension
- MDCT
Multidetector computed tomography
- PPR
Projections per full rotation
- QCT
Quantitative computed tomography
- ROC
Receiver operating characteristic
- ROI
Region of interest
- SIR
Statistical iterative reconstruction
- SNR
Signal-to-noise ratio
- TbN
Trabecular number
- TbSp
Trabecular separation
- TbTh
Trabecular thickness
Compliance with ethical standards
Guarantor
The scientific guarantor of this publication is Dr Peter B. Noël.
Conflict of interest
The authors of this manuscript declare relationships with Philips Research Hamburg.
We thank Philips for providing data exportation and dose simulation tools.
Co-authors from Philips, Rolf Bippus and Thomas Köhler have provided great scientific and technical support for this study. They had no access to and were not involved in the collection or analysis of the data in this study.
Funding
This study has received funding by the European Research Council (ERC Starting Grant Stg-2014 637164 iBack), by Deutsche Forschungsgemeinschaft (DFG BA 4085/2-1 and BA 4906/1-1), by the German Department of Education and Research (BMBF) under grant IMEDO (13GW0072C) and by TUM Faculty of Medicine KKF grant H01.
Statistics and biometry
No complex statistical methods were necessary for this paper.
Informed consent
Written informed consent was obtained from all subjects (patients) in this study.
Ethical approval
Institutional Review Board approval was obtained.
Methodology
• retrospective
• retrospective
• case-control study
• performed at one institution
Footnotes
Electronic supplementary material
The online version of this article (doi:10.1007/s00330-017-4904-y) contains supplementary material, which is available to authorized users.
References
- 1.Consensus NI. Development panel on osteoporosis: prevention, diagnosis and therapy. Jama. 2001;285(6):785–795. doi: 10.1001/jama.285.6.785. [DOI] [PubMed] [Google Scholar]
- 2.Ioannidis G, Papaioannou A, Hopman WM, et al. Relation between fractures and mortality: results from the Canadian Multicentre Osteoporosis Study. CMAJ. 2009;181(5):265–271. doi: 10.1503/cmaj.081720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Burge R, Dawson-Hughes B, Solomon DH, et al. Incidence and economic burden of osteoporosis‐related fractures in the United States, 2005–2025. J Bone Miner Res. 2007;22(3):465–475. doi: 10.1359/jbmr.061113. [DOI] [PubMed] [Google Scholar]
- 4.Schuit SC, Van der Klift M, Weel AE, et al. Fracture incidence and association with bone mineral density in elderly men and women: the Rotterdam Study. Bone. 2004;34(1):195–202. doi: 10.1016/j.bone.2003.10.001. [DOI] [PubMed] [Google Scholar]
- 5.Siris ES, Chen YT, Abbott TA, et al. Bone mineral density thresholds for pharmacological intervention to prevent fractures. Arch Intern Med. 2004;164(10):1108–1112. doi: 10.1001/archinte.164.10.1108. [DOI] [PubMed] [Google Scholar]
- 6.Ito M, Ikeda K, Nishiguchi M, et al. Multi‐detector row CT imaging of vertebral microstructure for evaluation of fracture risk. J Bone Miner Res. 2005;20(10):1828–1836. doi: 10.1359/JBMR.050610. [DOI] [PubMed] [Google Scholar]
- 7.Link TM. Osteoporosis imaging: state of the art and advanced imaging. Radiology. 2012;263(1):3–17. doi: 10.1148/radiol.12110462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Baum T. C Karampinos D, Liebl H, et al. High-resolution bone imaging for osteoporosis diagnostics and therapy monitoring using clinical MDCT and MRI. Curr Med Chem. 2013;20(38):4844–4852. doi: 10.2174/09298673113206660279. [DOI] [PubMed] [Google Scholar]
- 9.Graeff C, Timm W, Nickelsen TN, et al. Monitoring Teriparatide‐Associated Changes in Vertebral Microstructure by High‐Resolution CT In Vivo: Results From the EUROFORS Study. J Bone Miner Res. 2007;22(9):1426–1433. doi: 10.1359/jbmr.070603. [DOI] [PubMed] [Google Scholar]
- 10.Coursey CA, Frush DP. CT and radiation: What radiologists should know. Appl Radiol. 2008;37(3):22. [Google Scholar]
- 11.Noël PB, Fingerle AA, Renger B, et al. Initial performance characterization of a clinical noise–suppressing reconstruction algorithm for mdct. Am J Roentgenol. 2011;197(6):1404–1409. doi: 10.2214/AJR.11.6907. [DOI] [PubMed] [Google Scholar]
- 12.Noël PB, Renger B, Fiebich M, et al. Does iterative reconstruction lower CT radiation dose: evaluation of 15,000 examinations. PLoS One. 2013;8(11):e81141. doi: 10.1371/journal.pone.0081141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sauter A, Koehler T, Fingerle AA, et al. Ultra low dose CT pulmonary angiography with iterative reconstruction. PLoS One. 2016;11(9):e0162716. doi: 10.1371/journal.pone.0162716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Marin D, Nelson RC, Schindera ST, et al. Low-tube-voltage, high-tube-current multidetector abdominal ct: Improved image quality and decreased radiation dose with adaptive statistical iterative reconstruction algorithm—initial clinical experience 1. Radiology. 2009;254(1):145–153. doi: 10.1148/radiol.09090094. [DOI] [PubMed] [Google Scholar]
- 15.Hara AK, Paden RG, Silva AC, et al. Iterative reconstruction technique for reducing body radiation dose at CT: feasibility study. Am J Roentgenol. 2009;193(3):764–771. doi: 10.2214/AJR.09.2397. [DOI] [PubMed] [Google Scholar]
- 16.Sidky EY, Kao CM, Pan X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J Xray Sci Technol. 2006;14(2):119–139. [Google Scholar]
- 17.QCT Pro Bone Mineral Densitometry Software, Phantom Module. Version 4.0, Mindways Software, 2005.
- 18.Žabić S, Wang Q, Morton T, et al. A low dose simulation tool for CT systems with energy integrating detectors. Med Phys. 2013;40(3). [DOI] [PubMed]
- 19.Muenzel D, Koehler T, Brown K, et al. Validation of a low dose simulation technique for computed tomography images. PLoS One. 2014;9(9):e107843. doi: 10.1371/journal.pone.0107843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fessler JA. Statistical image reconstruction methods for transmission tomography. Handb Med Imaging. 2000;2:1–70. [Google Scholar]
- 21.Kim D, Ramani S, Fessler JA. Combining ordered subsets and momentum for accelerated X-ray CT image reconstruction. IEEE Trans Med Imaging. 2015;34(1):167–178. doi: 10.1109/TMI.2014.2350962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Fehringer A, Lasser T, Zanette I, et al. A versatile tomographic forward- and back-projection approach on multi-GPUs. SPIE Medical Imaging 2014. International Society for Optics and Photonics.
- 23.Kopp FK, Holzapfel K, Baum T, et al. Effect of low-dose MDCT and iterative reconstruction on trabecular bone microstructure assessment. PLoS One. 2016;11(7):e0159903. doi: 10.1371/journal.pone.0159903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baum T, Müller D, Dobritz M, et al. BMD measurements of the spine derived from sagittal reformations of contrast-enhanced MDCT without dedicated software. EJR. 2011;80(2):e140–e145. doi: 10.1016/j.ejrad.2010.08.034. [DOI] [PubMed] [Google Scholar]
- 25.Baum T, Gräbeldinger M, Räth C, et al. Trabecular bone structure analysis of the spine using clinical MDCT: can it predict vertebral bone strength? J Bone Miner Metab. 2014;32(1):56–64. doi: 10.1007/s00774-013-0465-6. [DOI] [PubMed] [Google Scholar]
- 26.Baum T, Carballido-Gamio J, Huber MB, et al. Automated 3D trabecular bone structure analysis of the proximal femur—prediction of biomechanical strength by CT and DXA. Osteoporos Int. 2010;21(9):1553–1564. doi: 10.1007/s00198-009-1090-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Majumdar S, Genant HK, Grampp S, et al. Correlation of trabecular bone structure with age, bone mineral density, and osteoporotic status: in vivo studies in the distal radius using high resolution magnetic resonance imaging. J Bone Miner Res. 1997;12(1):111–118. doi: 10.1359/jbmr.1997.12.1.111. [DOI] [PubMed] [Google Scholar]
- 28.Stamm G, Nagel HD. CT-expo--a novel program for dose evaluation in CT. RoFo. Fortschr Geb Rontgenstr Nuklearmed. 2002;174(12):1570–1576. doi: 10.1055/s-2002-35937. [DOI] [PubMed] [Google Scholar]
- 29.Damilakis J, Adams JE, Guglielmi G, et al. Radiation exposure in X-ray-based imaging techniques used in osteoporosis. Euro Radiol. 2010;20(11):2707–2714. doi: 10.1007/s00330-010-1845-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Beister M, Kolditz D, Kalender WA. Iterative reconstruction methods in X-ray CT. Phys Med. 2012;28(2):94–108. doi: 10.1016/j.ejmp.2012.01.003. [DOI] [PubMed] [Google Scholar]
- 31.Pan X, Sidky EY, Vannier M. Why do commercial CT scanners still employ traditional, filtered back-projection for image reconstruction? Inverse Prob. 2009;25(12):123009. doi: 10.1088/0266-5611/25/12/123009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Eklund A, Dufort P, Forsberg D, et al. Medical image processing on the GPU–Past, present and future. Med Image Anal. 2013;17(8):1073–1094. doi: 10.1016/j.media.2013.05.008. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX 1716 kb)