Models of spatial and temporal dimensions of memory

Abstract

Episodic memory involves coding of the spatial location and time of individual events. Coding of space and time is also relevant to working memory, spatial navigation, and the disambiguation of overlapping memory representations. Neurophysiological data demonstrate that neuronal activity codes the current, past and future location of an animal as well as temporal intervals within a task. Models have addressed how neural coding of space and time for memory function could arise, with both dimensions coded by the same neurons. Neural coding could depend upon network oscillatory and attractor dynamics as well as modulation of neuronal intrinsic properties. These models are relevant to the coding of space and time involving structures including the hippocampus, entorhinal cortex, retrosplenial cortex, striatum and parahippocampal gyrus, which have been implicated in both animal and human studies.

Introduction

The coding of space and time is essential for a number of different memory phenomena, including episodic memory, which by definition involves coding of where and when an event occurs. Studies in humans have analyzed memory in humans for spatial trajectories to goal locations [1–3], and the spatial location of objects and landmarks [4–6]. Performance of spatial memory tasks involves interactions of neural activity in structures including the hippocampus, paraphippocampal gyrus, retrosplenial cortex and prefrontal cortex [1–5]. Studies have also analyzed memory for the temporal order of events in episodic memory [6–8], showing involvement of the hippocampus and parahippocampal gyrus. Research has also examined the disambiguation of overlapping spatial and non-spatial representations in both humans and animals [1,7,9].

Consistent with the patterns of activity observed in humans using fMRI, neurophysiological studies have demonstrated neurons that respond on the basis of spatial location of an animal in foraging tasks or tasks that require a specific memory of spatial location such as spatial alternation. Neurons in the hippocampus fire as place cells coding location [10,11] or time cells coding the time interval during a behavioral task [12–14]. Neurons in the entorhinal cortex code spatial features including location in the environment [15–18], distance to an environmental boundary [10,19], allocentric direction [10,17], and running speed [20,21]. Neurons with more complex firing patterns incorporating location and head direction appear in structures such as the basal forebrain [22], retrosplenial cortex [23], and parietal cortex [24]. For many years, computational models have attempted to describe the mechanisms and functional role of coding of space and time in these structures and their potential role in behavior. This review will provide an overview of recent work addressing the coding of space and time in these structures.

Modeling of spatial memory (grid cells, place cells and splitter cells)

Models have addressed the neural coding of spatial dimensions relevant to spatial memory. This includes models of spatial coding in foraging tasks. Foraging tasks may not be considered traditional memory tasks, but the capacity of neurons to respond in a stable manner across different trials requires memory of the overall configuration of cues in an environment. Models have also addressed the memory of specific behaviorally relevant locations within an environment.

Modeling neural responses based on spatial location

Many studies have addressed the response of place cells and grid cells to spatial location [25,26]. Models have addressed the generation of place cells and grid cells by both path integration or the angle of visual cues. This includes sophisticated models of physiological mechanisms for grid cells based on path integration. These models use different mechanisms that include interactions of oscillatory dynamics as initially proposed by Burgess, Barry and O’Keefe [27–29] or based on attractor dynamics as proposed by researchers such as McNaughton or Fiete [30,31]. Many properties of these two model classes are compatible, so features of these models can be combined [27]. Other models have addressed the response of grid cells based on self-organization of input from place cells [32] or as a result of a probabilistic learning process [33] or the eigenvectors of the normalized graph Laplacian [34].

The loss of grid cell spatial selectivity with the inactivation of input that provides coding of heading direction [17] supports models that use path integration in generation of grid cell responses. Extensive data supports a role for attractor dynamics in generation of grid cell firing, including the modular properties of distinct populations of grid cells that share properties such as spacing and orientation and the ellipsoid shape of firing fields [15,18], and the change in correlation of grid cell firing with different anatomical distances between grid cells [35]. The role of oscillatory dynamics in coding of grid cells is supported by evidence that the intrinsic rhythmicity of entorhinal neurons differs with spatial scale [36] and shifts with running speed [20,36], and that inactivation of the medial septum causes loss of grid cell firing properties [37]. The effects of medial septum inactivation could be due to loss of GABAergic input that can drive network theta rhythm activity [38], or to loss of the cellular effects of cholinergic modulation that normally shift network dynamics from sharp-wave spiking to theta rhythm dynamics [38,39] and normally enhance the influence of external sensory input [40]. The loss of spatial coding could also be due to the loss of glutamatergic input from the medial septum that contributes to coding of running speed in the hippocampus [41,42].

Modeling the influence of boundaries

Physiological studies in animals demonstrate that place cell firing depends on the position of environmental boundaries [11]. This led to models that coded location based on selective firing of boundary cells [10,43]. This prediction was later supported by experimental evidence of boundary cells [19,44]. Modeling demonstrated how egocentric visual input about boundaries could be transformed to code allocentric spatial location [45]. These models demonstrate how place cells can be driven without grid cell input, since inactivation of grid cells does not abolish place cell firing [46].

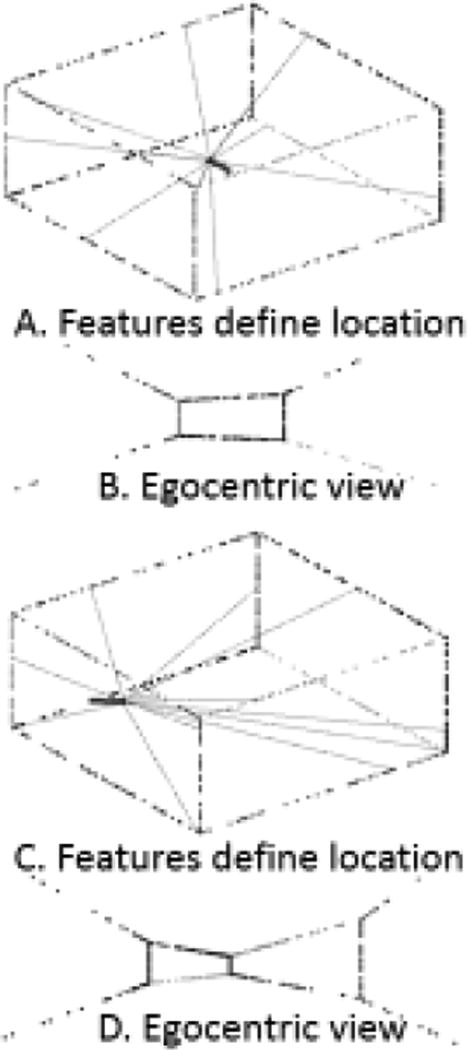
Alterations of visual boundaries also influence the location of grid cell firing fields. The spacing of grid cell firing fields is compressed or expanded by movements of the environment walls [18], and this change may be specific to grid cells with larger spacing while sparing smaller spacing [15] though the earlier study showed compression of cells with small spacing [18]. The response of grid cells to barrier movement has been modeled based on selective influences of the angle and optic flow of visual cues from different parts of the visual field [47]. The computation of location from visual angle is shown in Figure 1. The regular pattern of grid cell fields is lost when shifting from a rectangular environment to a trapezoid environment [16], and this has been modeled based on field boundary effects [48] or the normalized graph Laplacian [34].

Figure 1.

A. Computation of the location of an animal in a square environment with barriers can be determined from the angle and distance to visual features [47]. Movement of barriers has been shown to shift neurophysiological codes for location [15,18]. B. Figure showing the egocentric view of visual features at location in A. C–D. Same as A–B for a different location.

Grid cells, head direction and boundary cells have all been shown to fire in a stable manner when an animal is removed from the environment and then returned to the environment. This requires anchoring of the neural responses to features in the environment, as utilized in models showing how sensory cues observed when re-entering an environment can allow the accurate firing of grid cells [27,45,47] and head direction cells [49]. Consistent with this, grid cells exhibit greater consistency in the location of spatial firing near an environment boundary, and poorer consistency at greater distances from the boundary [50].

Modeling the encoding and retrieval of sequences

Models have also addressed the encoding and retrieval of sequences. In an influential model developed by Lisman and Jensen, the initial storage of a sequence of locations has been modeled using after-depolarization potentials triggered by high levels of cholinergic modulation [51,52]. This model includes separation of different elements of a sequence on different gamma cycles that are phase amplitude coupled with theta rhythm [52]. Considerable data supports this model, including evidence that different sequence positions exhibit greater gamma power at distinct phases of theta [8], and this segregation is related to successful temporal order memory. The maintenance of spiking activity associated with a sequence of locations allows strengthening of connections between place cells that can mediate later sequential replay of the sequence. This sequential replay of place cells occurs during sharp wave ripple activity observed in the local field potential in the hippocampus [53,54]. This sharp wave replay occurs during the low levels of cholinergic modulation that occur in quiet waking or slow wave sleep [51,55,56]. These replay events could mediate the consolidation of previously encoded information during periods of quiet waking or slow-wave sleep [6,38,53,54,57]. These replay events may correspond to information packets that form the basis of cortical cognitive processing [58]. Such information packets could use codes such as the residue number system suggested for grid cell coding [59].

Modeling of context-dependent disambiguation

Models have addresssed how the retrieval of spatial memory representations can be used to guide future decisions. This includes models in which retrieval of sequences guides spatial alternation and the selective retrieval of overlapping trajectories [56,60]. Models that allow selective retrieval of one out of many individual sequences can generate context-dependent neuronal activity [61,62]. These models can simulate the firing of splitter cells, that selectively respond on overlapping track segments based on the future or past turning response of a rat [9,63]. These circuit level mechanisms also allow simulation of the disambiguation of overlapping sequences in human subjects [1,64].

Modeling of goal-directed navigation

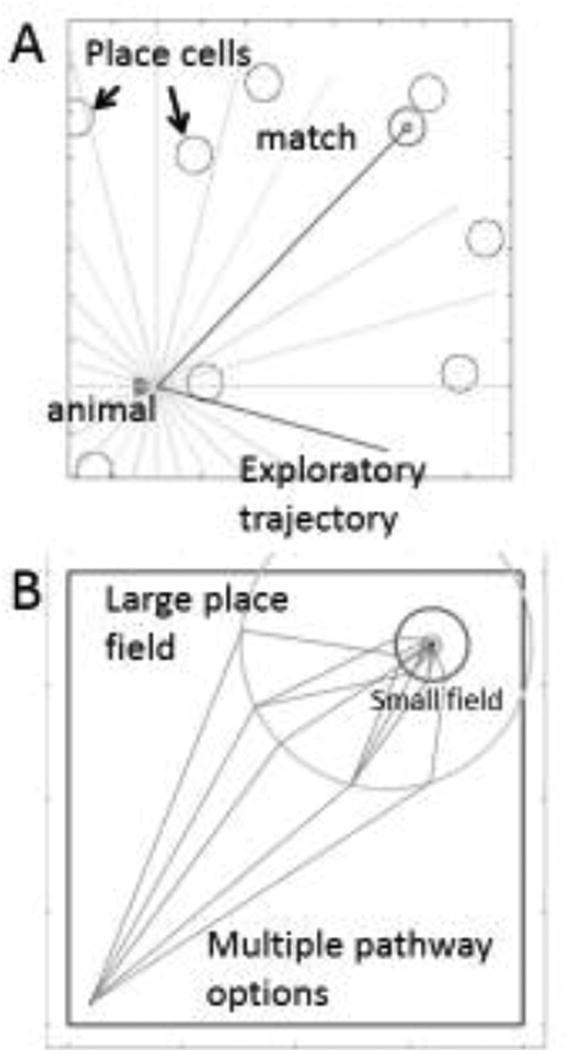
Models also address how the forward read-out of locations based on grid cell firing patterns allow selection of either the direct vector to a goal location [65–68] or a pathway dependent upon obstacles [67,69] as shown in Figure 2. These models are supported by experimental data indicating the replay of place cell sequences associated with goal-directed navigation [70–72]. The models are also supported by fMRI data in humans demonstrating hippocampal and parahippocampal activity at the start of a trajectory when a subject retrieves a previously learned overlapping trajectory [1,64]. Subsequent work showed that retrieval of a planned trajectory involves reactivation of intermediate locations on the trajectory [2]. Studies show coding of navigationally relevant information in fMRI activity, with hippocampus coding path length and entorhinal cortex coding the Euclidean distance to the goal [3,73]. Modeling shows how interaction of brain regions can allow performance based on semantic memory for the allocentric position of landmarks translated to the egocentric position of landmarks [45]. These models and other work on the influence of visual cues [47] are relevant to data showing the interaction of regions coding visual cues such as optic flow and feature angle with regions involved in navigation [73,74].

Figure 2.

A. Model for goal-directed behavior based on linear forward trajectory planning [68]. Circles represent the location where previous place cell firing took place. Triangle indicates animal location. Light gray lines indicate sequential sampling of forward trajectories through the environment. Darker line ending in circle indicates the trajectory that overlaps with the previously visited place cell firing field that was associated with a goal location, allowing selection of this trajectory. B. Different trajectories obtained by sampling at multiple spatial scales, allowing initial selection of trajectories to the large place cell firing field, followed by selection of trajectories to smaller place cell firing fields.

Modeling working memory for spatial location

Many spatial tasks require working memory for spatial location of an object either in allocentric or egocentric coordinates [75]. This has been modeled using attractor dynamics in which recurrent synaptic connections maintain a bump of activity representing the location of an object in a scene. Most models of attractor dynamics have focused on maintaining sustained activity in a full population of neurons for the full delay period. However, models show how activity might shift between different minicolumns [76]. The addition of inhibitory interneurons to the earlier model generates bursts of gamma frequency oscillations [77]. Experimental data on gamma oscillations [78] indicates that the pattern of neural activity during delay periods shows brief bursts of high frequency gamma oscillations similar to the model, in contrast to a background state of lower frequency beta oscillations.

Modeling of temporal memory (time cells)

As noted above, neurophysiological data indicates that neurons in a number of different structures including hippocampus and entorhinal cortex respond selectively at specific temporal intervals within behavioral tasks [12–14]. In particular, the neural activity occurring at specific intervals during delay periods of behavioral tasks have been described as time cells. These temporal interval phenomena have been modeled in a number of different ways which could be tested experimentally by evaluating the relative contribution of synaptic properties, intrinsic neuronal properties or oscillatory dynamics.

Temporal intervals coded by synaptic interactions

The sequence of neural activity observed in some tasks can be modeled by complex synaptic interactions. Sequence retrieval based on the fast time constants of glutamatergic synaptic potentials would cause fast sequence retrieval such as that observed during brief sharp-wave ripple events observed in the hippocampal EEG [53,54,57], in contrast to the slow transitions of time cells [12]. Therefore, models of the slow transitions between different cells over a time scale of seconds require complex network dynamics, such as the slow activation of different attractors referred to as context cells [79,80]. Similarly, slow transitions between active time cells can be obtained by modeling different dynamics of synaptic influences within recurrent neural network models [81]. A number of mechanisms have been proposed for coding position within a sequence, which includes addressing data on the verbal memory for serial order lists [80]

Temporal intervals coded by intrinsic properties

Another mechanism for obtaining slow transitions between neuronal populations is to utilize intrinsic conductances with slower time constants. For example, models have replicated time cells using exponential decay with slow time constants [82,83], and have shown how this could arise from slow decay of a calcium-activated non-specific cation current [55,84] or a change in spiking threshold due to the calcium activated potassium current [83]. These models could be tested by altering the level of neuromodulators such as acetylcholine that regulate these intrinsic properties.

Temporal coding by oscillatory interactions

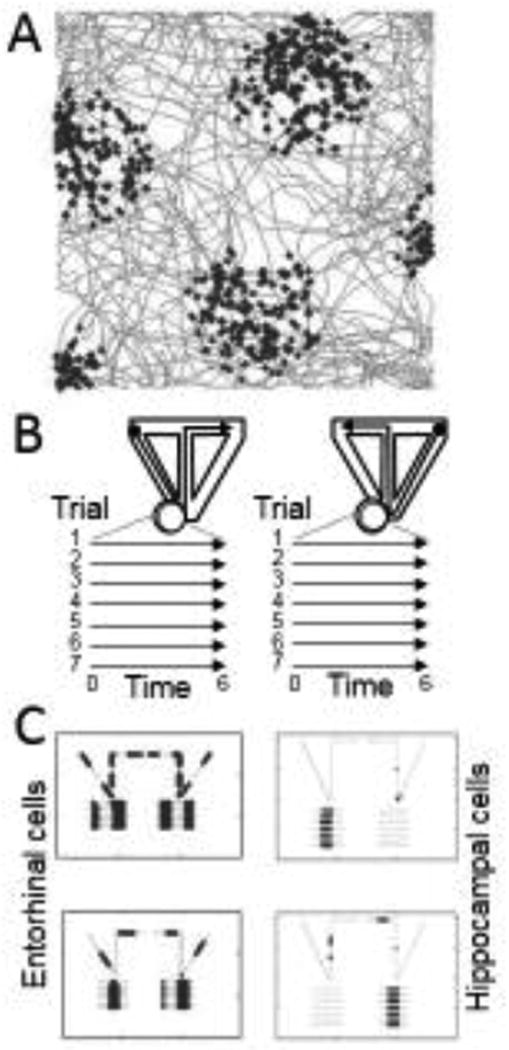
Models have also shown how temporal intervals can be coded by oscillatory interactions. This includes models in which the discrete temporal order of stimuli is coded by the position of gamma frequency oscillations within a theta frequency oscillation [52], which has been supported by recent data showing phase specificity of gamma oscillations related to stimulus order [8]. Another set of models show that a continuous representation of temporal interval can be coded by interference between different oscillations [60,85,86]. Simulations using these models demonstrated the same oscillatory dynamics that generate grid cell firing patterns could also generate time cell firing patterns [60] as shown in Figure 3. These models generated predictions of multiple time cell firing fields that are supported by experimental data [87]. The models that depend upon oscillatory interactions for coding of both space and time are supported by data showing that the inactivation of the medial septum causes loss of both grid cell firing in the entorhinal cortex [37] and the loss of time cell firing in the hippocampus [88]. However, further studies must determine whether these effects are due to loss of oscillatory input or loss of cholinergic modulation arising from the medial septum.

Figure 3.

Coding of space and time by the oscillatory interference model [29,60]. A. The model simulates grid cell firing as a simulated rat runs on a foraging trajectory (gray lines). Black dots show the location of the simulated rat each time the grid cell model generates a spike. B. The same model addresses activity during spatial alternation on a T-maze (top) with a period of running on a running wheel during the delay period between choices (lines on bottom). C. The same model shows location dependent firing on the T-maze (dark segments in top plot) as well as consistent firing at specific intervals of time or distance during running on the running wheel (dark segments on bottom lines).

Temporal coding between episodes

Note that most of the models described here focus on the timing of events within specific episodes, rather than the temporal order between different episodes, which requires larger scales of temporal coding. Modeling studies have proposed that neurogenesis within the dentate gyrus could provide different populations of granule cells allowing contextual coding between memories on a much larger temporal scale [89]. Work in humans suggests that adult neurogenesis additionally impacts the entorhinal cortex [90].

Conclusions

In summary, models have demonstrated potential mechanisms for a range of different spatial and temporal coding properties within cortical structures, and experimental data supports aspects of these different mechanisms. In particular, some classes of models can account for both the coding of spatial location in an environment as well as the coding of time during running in one location on a treadmill, including the oscillatory interference models [27,29,60], attractor dynamic models [83,91] and models using Laplace transforms [82]. These models have inspired and guided many experiments testing physiological mechanisms of spatial and temporal coding [13,15,17,18,20,21,87,88]. Modeling also demonstrates how coding of spatial location and time can form a framework to form the associations necessary to link events to the spatiotemporal trajectory of an episodic memory [56,82]. Modeling of episodic memories as trajectories has inspired experimental tests of the coding of memory in humans [1–3,69,73]. However, a full understanding of the network dynamics for coding space and time in episodic memory will require both more sophisticated and detailed models as well as more explicit experimental tests of the different mechanistic components of these computational models.

Highlights.

• Neurons show coding of time and spatial location in memory-guided tasks

• Models demonstrate how spatial coding could arise from integration of self-motion

• Models show how spatial coding could depend on angle and distance of visual stimuli.

• Models show how the same neuron can code both location and time interval.