Experimental and DFT Investigations Reveal the Influence of the Outer Coordination Sphere on the Vibrational Spectra of Nickel-Substituted Rubredoxin, a Model Hydrogenase Enzyme

Abstract

Nickel-substituted rubredoxin (NiRd) is a functional enzyme mimic of hydrogenase, highly active for electrocatalytic and solution-phase hydrogen generation. Spectroscopic methods can provide valuable insight into the catalytic mechanism, provided the appropriate technique is used. In this study, we have employed multi-wavelength resonance Raman spectroscopy coupled with DFT calculations on an extended active-site model of NiRd to probe the electronic and geometric structures of the resting state of this system. Excellent agreement between experiment and theory is observed, allowing normal mode assignments to be made on the basis of frequency and intensity analyses. Both metal-ligand and ligand-centered vibrational modes are enhanced in the resonance Raman spectra. The latter provide information about the hydrogen bonding network and structural distortions due to perturbations in the secondary coordination sphere. To reproduce the resonance enhancement patterns seen for high-frequency vibrational modes, the secondary coordination sphere must be included in the computational model. The structure and reduction potential of the Ni^IIIRd state have also been investigated both experimentally and computationally. This work begins to establish a foundation for computational resonance Raman spectroscopy to serve in a predictive fashion for investigating catalytic intermediates of NiRd.

TOC image

The electronic and geometric structures of nickel-substituted rubredoxin, a highly active enzyme mimic of hydrogenase, were investigated using multi-wavelength resonance Raman spectroscopy. DFT calculations on an extended active site model showed excellent agreement with experiment only when the full secondary coordination environment was considered, emphasizing the importance of outer sphere interactions. Validation of this model across multiple oxidation states establishes a foundation for using calculations synergistically with experiment to examine enzymatic intermediates during hydrogen evolution.

Introduction

Hydrogen is an energy-dense, clean-burning fuel that has long been touted as an ideal energy storage medium for either direct use or for the generation of secondary transport fuels.^1,2 Because of its industrial value, great effort has been aimed at developing sustainable methods for hydrogen generation and processing, with significant advances made on diverse fronts, from engineering hydrogen storage materials to developing efficient catalysts. In nature, hydrogen production and oxidation is carried out through the use of specialized metalloenzymes called hydrogenases (H₂ases).³ These large, multicofactor systems contain either di-iron ([FeFe]) or heterobimetallic nickel-iron ([NiFe]) active sites and feature earth-abundant metals, high turnover frequencies, activity under mild reaction conditions in aqueous solutions, and, notably, very high thermodynamic efficiencies for H₂ conversion reactions.^3,4 These favorable characteristics have motivated diverse spectroscopic investigations to arrive at a general understanding of the enzymatic mechanism (Figure 1).^3–10 The negligible catalytic overpotential renders the enzymes bidirectional, with important consequences both in vivo and in vitro.^11–13 However, H₂ases are relatively fragile, costly proteins, and as such, are generally poorly suited for large-scale application.^14–16 Alternative methods for sustainable hydrogen generation are needed.

Figure 1.

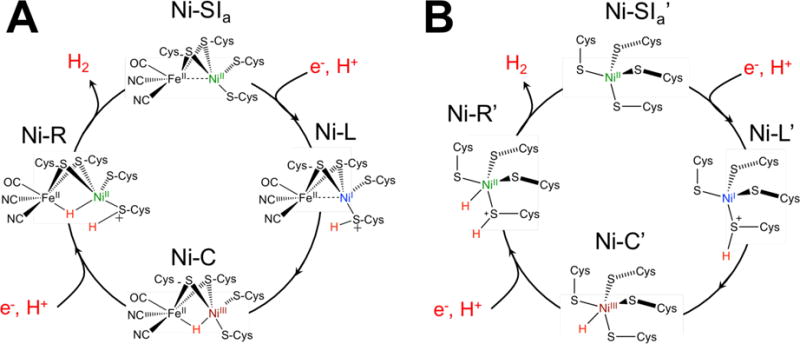
Proposed catalytic mechanisms for hydrogen generation by (A) [NiFe] hydrogenases and (B) NiRd.

Extensive research in the synthetic inorganic community aims to develop molecular catalysts that reproduce the advantages of the protein systems. A number of important advances have been made in recent years, including the use of first-row transition metals, low catalytic overpotentials that lead to bidirectionality, activity in aqueous solutions under mild conditions, electrocatalytic turnover frequencies that exceed solution-phase enzymatic rates, and incorporation of protein-like elements in the secondary coordination sphere.^17–20 Many excellent reviews describing these compounds and highlighting progress towards increased activity have been written in recent years.^21–26 However, no single catalyst has been able to incorporate all of the unique features of the native H₂ase enzymes.

We have elected to address this challenge by developing protein-based models of the [NiFe] hydrogenases. Using rubredoxin (Rd), a small, iron-containing electron transfer protein, as a scaffold, we have replaced the native metal center with nickel to generate a monomeric, tetrathiolate-coordinated nickel(II) active site (NiRd). This system serves as a basic structural model of the native enzyme as it directly mimics the primary atomic coordination sphere of the redox-active metal in the [NiFe] H₂ases. Further illustrating the relevance of this model protein system, we have recently been able to show high levels of solution-phase and electrochemical hydrogen evolution by NiRd, with electrocatalytic rates approaching that of the native enzyme and a modest overpotential of 540 mV.²⁷ Nickel-substituted rubredoxin (NiRd) shows great promise as an artificial hydrogenase; unlike the native H₂ases, it is easily generated, chemically and thermally robust, and highly tunable to enable catalyst optimization. The simplicity of the system also provides an opportunity to better understand the native [NiFe] hydrogenases, including investigation into the role that the Fe^II(CN)₂CO fragment plays during catalysis and identifying the impact of having two bridging cysteines rather than four terminal ones, as found in NiRd. Towards this end, we are very interested in understanding the mechanism of catalytic hydrogen evolution by NiRd.

A preliminary mechanism for NiRd based on the current model for the [NiFe] hydrogenases is proposed in Figure 1. Like the [NiFe] hydrogenases, at least one nickel-hydride species is likely involved in catalysis.^9,28,29 Additionally, while this is a controversial point in the native [NiFe] enzymes,^6,28 the thiolate ligands in NiRd likely serve as the basic site for protonation (Ni-L’ and Ni-R’), showcasing the chemical competence of nickel-bound thiolates for intramolecular proton transfer. The mechanisms of the protein-based systems differ from the well-studied DuBois-type nickel-phosphine systems, which rely on intramolecular proton transfer from an amine group in the outer coordination sphere and proceed through distinct reduction and protonation steps, with Ni⁰ intermediates identified during the catalytic process.^30,31 As with the model compounds and the native systems, detailed spectroscopic studies will be of great utility to characterize NiRd intermediates and identify mechanistic details, particularly when considering short-lived or reactive species.

Vibrational techniques are ideally suited to address questions of structure and bonding. However, conventional infrared (IR) spectroscopy is limited by the large absorption of water, and both IR and Raman spectroscopies suffer from a lack of selectivity, which is detrimental in the case of proteins. By contrast, resonance Raman (RR) spectroscopy is a highly selective and sensitive method that has been extensively applied to the study of metalloprotein active sites and a number of model compounds, including those related to hydrogenases.^32–37 This scattering technique uses laser excitation wavelengths that are resonant with an electronic transition of a chromophore, resulting in significant intensity increases exclusively for vibrations coupled to that electronic transition.^38,39 Because the enhancement mechanism relies on coupling between the electronic and vibrational excited states, RR spectroscopy provides information on both electronic and geometric structure.³⁹ Use of multiple excitation wavelengths can access different transitions, which gives distinct RR intensity patterns that report on the nature of the excited states.^40,41

In conjunction with experimental methods, theoretical calculations can be an invaluable aid for the interpretation of spectroscopic results. Computational methods are also increasingly employed to guide experimental design, which can preserve resources and accelerate progress.⁴² Prior to being used in a predictive fashion, however, a structural model must be developed and validated with respect to the computational methodology and available experimental data.^43,44 Because the costs of computing an entire protein at the density functional theory (DFT) or ab initio levels would be prohibitive, this step is particularly important in theoretical studies on enzymes to ensure an appropriate level of truncation was applied.^45,46

In this work, we have used multiple excitation wavelengths to obtain resonance Raman spectra of NiRd across different excited states to fully characterize the electronic and vibrational structure of the resting state of the enzyme. Isotope experiments were used to distinguish modes that are sensitive to hydrogen bonding within the active site, which will report on perturbations to this network during catalysis. In parallel, DFT studies were performed on models of the NiRd active site that varied in size to probe the importance of the outer coordination sphere. Structural, spectroscopic, and redox properties of these active-site models were calculated and compared to experimental data. Excellent agreement was obtained between the observed RR spectra and predicted vibrational frequencies and intensity patterns for the extended model, indicating that the calculations accurately reflect the electronic structure of the NiRd active site. Together, these results provide a foundation upon which to investigate the mechanism of hydrogen evolution by NiRd using resonance Raman spectroscopy synergistically with DFT calculations.

Materials and Methods

Sample Preparation

Expression, purification, and metal substitution of rubredoxin was carried out as previously described with minor modifications.²⁷ Briefly, an additional purification step was included. The protein was run on a size-exclusion column (5 mL Superdex-75, prep-grade, Sigma-Aldrich) in 50 mM Tris buffer, pH 8.0, following the trichloroacetic acid precipitation and metal exchange to ensure complete purity of all protein samples. Isotopic substitution experiments were prepared by exchanging protein samples into 15 mM phosphate-buffered D₂O (99.9% isotopic purity, Sigma-Aldrich) at pH 8.0 by centrifugal filtration (Millipore Centricons, 3.5 kDa MWCO). Solvent equilibration was allowed to proceed at 4 ˚C for at least 12 hrs prior to data collection.

Electrochemistry

All electrochemical experiments were carried out on a WaveNow potentiostat (Pine Research Instrumentation, Durham, NC) inside a nitrogen atmosphere glovebox, O₂ <10 ppm (Vigor Technologies). Solution-phase electrochemical studies of NiRd were performed using 150 μL of sample contained within a 10 mm ID borosilicate tube. A glassy carbon working electrode (CH Instruments) was used in a conventional three-electrode set-up, with a miniature Ag/AgCl reference electrode (Pine Research Instrumentation) and a platinum wire as the counter electrode. The reported potentials against NHE were calculated by the addition of +198 mV to the experimentally measured potentials.⁴⁷

Spectrophotometric Titrations

Potentiometric titrations were performed using a Shimadzu UV-2600 Spectrophotometer to monitor changes in the UV-visible absorbance spectrum of NiRd. Aliquots of potassium ferricyanide (Sigma-Aldrich) were added to a solution of Ni^IIRd in the indicated buffer and allowed to equilibrate for 15 minutes prior to recording the solution potential and optical spectrum. Potential measurements were made using a digital multimeter with a platinum working electrode and a Ag/AgCl reference electrode. As the optical absorption of K₃[Fe^III(CN)₆] overlaps with the NiRd charge transfer transitions, the absorbance values at 740 nm reflecting the Ni^II d-d transitions were monitored to obtain the concentration of Ni^IIRd as a function of solution potential for the Nernstian curves shown in Figures 7B and S21.

Figure 7.

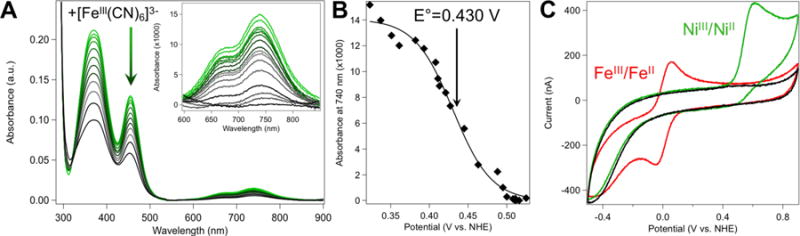
(A) Representative absorbance spectra showing the potentiometric titration of Ni^IIRd with potassium ferricyanide (40 μM NiRd, 50 mM Tris-buffer, pH 8.0; spectra shown reflect up to 1 equiv. ferricyanide added). (B) Absorbance of NiRd at 740 nm as increasing amounts of ferricyanide are added (50 mM Tris, pH 8.0). The line shown represents a least-squares fit of the data to the Nernst equation (E° = 0.430 V vs. NHE). (C) Cyclic voltammogram of NiRd (green), FeRd (red) and the blank glassy carbon electrode (black) in 100 mM KCl, 50 mM acetate buffer, pH 4.5 (ν = 10 mV/s).

Resonance Raman Spectroscopy

Resonance Raman (RR) spectroscopy was performed at room temperature with samples contained within a flame-sealed sodium borosilicate capillary tube (~1 mm ID). A mixed gas Kr-Ar laser (Coherent Innova Spectrum 70-C, Laser Innovations) provided excitation at 458 nm and 488 nm. The spectra obtained with 364 nm and 407 nm excitation employed a tunable titanium: sapphire laser (Spectra-Physics Tsunami) pumped by a 25 W DPSS laser (Spectra-Physics Millennia eV) and configured with a 10-ps Gires-Tournais interferometer, similar to the system described by Doig and coworkers.⁴⁸ The ~4.0 W fundamental beam at 728 nm or 814 nm was focused into a β-barium borate (BBO) crystal (Eksma Optics) for second-harmonic generation, and the ~20 mW of 364 nm or ~10 mW of 407 nm light was separated from the fundamental with a Pellin-Broca prism and a dichroic mirror. The excitation beam of ~20 mW, ~10 mW, 25–30 mW, and 25–30 mW at 364 nm, 407 nm, 458 nm, and 407 nm, respectively was focused onto the sample using a 100 mm RFL, 90° off-axis parabolic mirror (Thorlabs). Scattered light was collected at a 135° backscattering geometry by a 55 mm FD f/1.2 mounted camera lens (Canon, 458 nm and 488 nm excitation) or a 50 mm FD f/0.8 UV fused silica aspheric lens (Edmund Optics, 364 nm and 407 nm excitation) and focused onto the 100 μm entrance slit of a spectrograph using a 50 mm, f/4 achromatic lens (Newport Corporation, 458 nm and 488 nm excitation) or a 50 mm, f/4.6 uncoated UV fused silica lens (CVI Optics, 364 nm and 407 nm excitation). Rayleigh scattering was rejected by the appropriate long-pass edge filter (Semrock RazorEdge). Raman scattered light was dispersed in an f/4.6, 0.32 m imaging spectrograph (Princeton Instruments, IsoPlane SCT 320) equipped with an 1800 gr/mm (407 nm, 458 nm, and 488 nm excitation) or 3600 gr/mm (364 nm excitation) holographic grating and imaged onto a Peltier-cooled CCD detector (Princeton Instruments, Pixis 100B).

Raman signal intensity was optimized and calibrated using known bands from a 1:1 v/v mixture of toluene and acetonitrile.⁴⁹ The band pass and accuracy were found to be 9 cm⁻¹ and +/− 1 cm⁻¹, respectively. One-minute signal integrations were summed up over two hours for each sample to obtain accumulated spectra of NiRd and ZnRd as well as their respective protiated and deuterated buffers. Controls were performed at varying powers (0.7 – 115 mW) to ensure experiments were carried out under conditions of linear response (Figure S1). Single-pixel spikes due to cosmic rays impinging upon the detector were removed manually. The raw data is shown in Figure S2. Features from the appropriate buffer were subtracted from the spectra of NiRd (typically in a 0.6 –1 ratio to account for self-absorption), and a spline was drawn along the baseline of the resulting spectrum and subtracted to remove a broad fluorescent background; this process is shown in Figure S2, inset.^50,51 Intensity normalization was performed using the non-resonant Raman phenylalanine peak at 1004 cm⁻¹.⁵² The summed raw ZnRd spectra were subtracted from the raw NiRd spectra to obtain better signal-to-noise ratios and clearly identify bands attributed to the nickel-thiolate chromophore; these spectra were then baseline-corrected and scaled to the appropriate, Phenormalized, buffer-subtracted spectra using the remaining peaks (Figure S3). Peak positions of overlapping bands were resolved by Gaussian decomposition of the corrected NiRd spectra (Figure S4).

Construction of the Active-Site Model

The nickel-substituted rubredoxin (NiRd) computational model was constructed using the UCSF Chimera visualization software⁵³ starting from the X-ray crystal structure of oxidized iron rubredoxin from Desulfovibrio desulfuricans (Dd) ATCC 27774 (PDB Code: 6RXN).⁵⁴ Amino acid numbering refers to the Dd Rd. For the full model ([Ni^II(CNVC)(CPVC)]²⁻), the complete side chains of the C₆N₇V₈C₉ and C₃₂P₃₃V₃₄C₃₅ loops were retained (where C₆ refers to cysteine, the 6^th residue in the polypeptide chain), and the metal center was changed to a nickel ion. To model the secondary coordination sphere and retain natural hydrogen bonding networks, G₁₀, G₃₆, and V₃₇ were also included.⁵⁵ The loops were terminated with N-acetylation and C-amidation for charge neutrality. All other atoms were removed. For the backbone-only model ([Ni^II(CGGC)(CPGC)]²⁻), all side chains other than the coordinating cysteines and the proline residue were replaced by glycine residues, with G₁₀, G₃₆, and “G”₃₇ still included. These loops were also capped with N-terminal acetylation and C-terminal amidation. The [Ni^II(NACA)₄]²⁻ model included only the cysteine residues capped with N- and C-terminal acetylation for charge neutrality. The Ni^IIRd and Ni^IIIRd structures were optimized with charges of −2 and −1 and multiplicities of 3 and 2, respectively. The complete geometry-optimized structures of the three active-site models are shown in the Supporting Information (Figure S5).

Calculations

All calculations were carried out using the ORCA computational chemistry program^56–58 at the Ohio Supercomputer Center.⁵⁹ Geometry optimizations were performed at the density functional theory (DFT) level of computation employing the BP86^60,61 functional with the RI approximation⁶² followed by the B3LYP^63,64 functional employing the RIJCOSX approximation in the gas phase.⁶⁵ The C_α atoms of each amino acid were constrained in space to retain the fold of the protein without restricting the flexibility of the active-site nickel and ligands.^66–68 In the absence of these constraints, distortion of the protein backbone (Figure S6) and slight differences in the TD-DFT calculations were observed (Figure S7), and significantly higher computational costs were incurred. The def2-SVP basis set was used for all atoms except the cysteine sulfur atoms and the nickel center, for which the def2-TZVPP basis set was used.⁶⁹ The basis sets were benchmarked and the active site geometries optimized using both the TZVP and def2-TZVPP basis sets on all non-coordinating atoms, with few changes seen (Figure S8 and Table S1). Given the size of these models and resource constraints, the use of different basis sets for the primary and outer coordination spheres is necessary and is often used when considering extended models of metalloprotein active sites.^44,66,67,70 Scalar relativistic effects were corrected for using the all-electron zero-order-relativistic-approximation (ZORA) applied to all atoms, and dispersion interactions were treated with the DFT-D3 atom-pairwise correction as implemented in ORCA.^71–74

The absorption spectra of the geometry-optimized Ni^IIRd structures were calculated using time-dependent density functional theory (TD-DFT) calculations. The Tamm-Dancoff approximation was performed for the first 80 roots using the B3LYP functional.^75–77 Vertical excitation energies and molar extinction coefficients for TD-DFT transitions were calculated using the ORCA_MAPSPC module to give the transitions shown in Figure 3. The transitions were convolved with a Gaussian linewidth of 2500 cm⁻¹ to generate the absorption spectra in Figures S7 and S9. Vibrational frequencies were calculated using two-sided numerical differentiation. Resonance Raman intensities for each relevant electronic transition were obtained within the independent mode displaced harmonic oscillator (IMDHO) model using the gradient of the excited state energy at the ground state equilibrium geometry to calculate the dimensionless normal coordinate displacements (Δs) for each of the normal modes.⁷⁸ The program ORCA_ASA was used to simulate the RR spectra for the first-order vibrational transitions.^41,78,79 Normal modes were assigned by comparison to experimental spectra on the basis of similar frequencies and intensities. We note that absolute RR cross-sections are not calculated with this method. Instead, the theoretical spectral intensities were kept constant relative to each other and scaled collectively for comparison to experiment.

Figure 3.

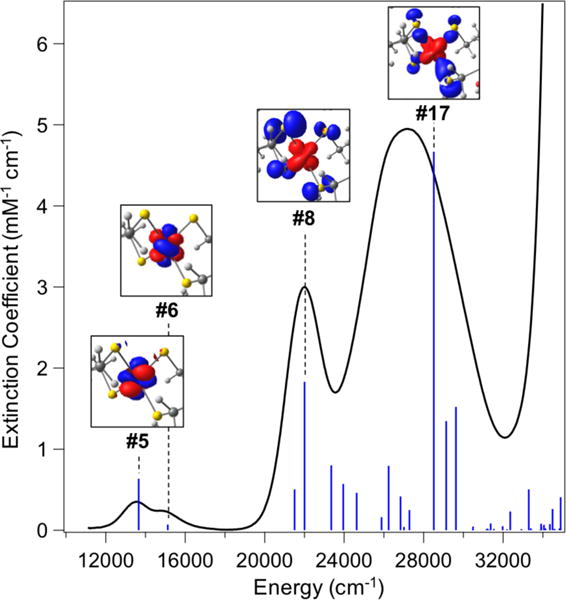
Optical absorption spectrum (black) of Ni^IIRd overlaid with TD-DFT-calculated optical transitions for the full model of Ni^IIRd (blue sticks). (Inset) Electron difference densities for the dominant transitions in the visible and near-UV region of the spectrum; blue lobes reflect loss of electron density, while red lobes reflect increased electron density in the transition. Difference density figures are labeled according to the energy-ordered number of that transition.

The reduction potential of the Ni^IIIRd/Ni^IIRd one-electron couple was calculated using a thermodynamic cycle as in Ref. 79 (for a detailed description, see the Supporting Information, Scheme S1).⁸⁰ Solvation free energies were computed at the optimized gas phase geometries using the conductor-like screening model (COSMO) with the dielectric constant of ε = 80.4 for water.⁸¹ This dielectric constant was chosen because the full computational model represents a highly surface-exposed portion of the protein (Figure S10). Additional calculations showed only a weak dependence of reduction potential on dielectric constant above ε~10 (Figure S11). The relative reduction potential was calculated with respect to the calculated SHE value of 4.281 V.⁸² The reduction potential of ferrocene (D_5d symmetry) was also calculated to estimate the accuracy of the computational method and compared to experimental data with respect to the SCE reference electrode (+0.241 V vs. SHE).⁸³

Results

DFT-Optimized Model Geometries

The full computational model of Ni^IIRd includes the complete side chains of both CXXC loops as well as an extended backbone with N-terminal acetylation and C-terminal amidation to more accurately mimic the protein environment. For structural validation, the DFT-optimized geometry of the model was compared to the crystal structure of the Ni^II-substituted rubredoxin from Clostridium pasteurinum (Figure 2A and Table 1), which is the only nickel-substituted rubredoxin that has been crystallographically characterized.⁸⁴ The protein backbone imposes a tetrahedral configuration at the metal center, which, for nickel(II), results in a high-spin, S=1 configuration that undergoes Jahn-Teller distortion to a tetragonally elongated pseudo-D_2d symmetry; a semi-quantitative molecular orbital diagram for the nickel-based d-orbitals is shown in the Supporting Information (Figure S12). While these general trends are also observed crystallographically, the experimental structure shows a slightly higher level of distortion at the active site, with different cysteines participating in the longer nickel-sulfur bonds. Specifically, the Cp Ni^IIRd structure shows elongation by almost 0.2 Å of the Ni-S(Cys₉) and Ni-S(Cys₃₂) bond lengths, while the optimized DFT model shows only 0.05 Å elongation along the Ni-S(Cys₆) and Ni-S(Cys₃₂) bonds. However, the reported structure of the Cp Ni^IIRd is of relatively low resolution (2.0 Å) with a B-factor of 38.4 Ų for the metal ion, which limits the extent to which the calculated and experimental active site geometries can be compared. In the secondary coordination sphere, the close hydrogen bonding network that has been noted in both the NMR and x-ray diffraction structures of iron- and nickel-substituted Rds is preserved, with distances of ~3.4 – 3.7 Å between the amide nitrogen and cysteine sulfur atoms (Figure 2A).^55,84,85

Figure 2.

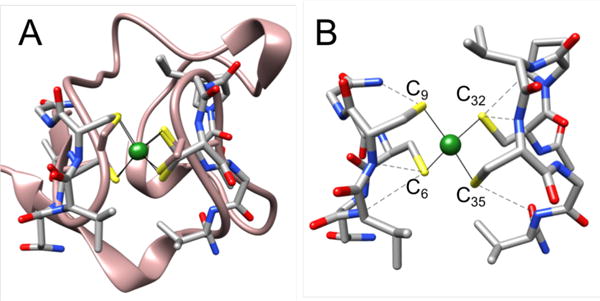
DFT-optimized geometry of full Ni^IIRd model (gray) (A) overlaid with the crystal structure of Cp Ni^IIRd (pink, PDB ID 1R0J) and (B) with the hydrogen-bonding network indicated with dashed lines. The full sidechains that are included in the model are shown; hydrogen atoms are omitted for clarity.

Table 1.

Selected bond distances of the geometry optimized NiRd models.

	X-Ray 1R0J.pdb	Full NiIIRd	Backbone NiIIRd	[NiII(NACA)4]2−	Full NiIII Rd	Backbone NiIIIRd
Bond Lengths (Å)
Ni-S6a	2.254	2.345	2.335	2.318	2.234	2.227
Ni-S9	2.381	2.282	2.294	2.297	2.204	2.212
Ni-S32	2.477	2.332	2.359	2.318	2.217	2.234
Ni-S35	2.134	2.287	2.285	2.290	2.198	2.209
Hydrogen Bonding Network Distancesb (Å)
Cys6-Val8	3.629	3.557	3.449	—	3.614	3.585
Cys6-Cys9	3.672	3.676	3.609	3.399	3.521	3.595
Cys9-Tyr11	3.543	3.314	3.437	—	3.393	3.367
Cys32-Val34	3.513	3.436	3.345	—	3.471	3.361
Cys32- Cys35	3.580	3.493	3.496	3.522	3.364	3.352
Cys35-Val37	4.077	3.649	3.536	—	3.510	3.441

^aS_n refers to the sulfur atom on the n^th cysteine.

^bHydrogen bonding values shown as distances between heavy atoms, i.e., d(S-N).

Truncated models of the NiRd active site were constructed and compared to the full model to investigate the role of the outer coordination sphere (Table 1). The simplest “[Ni^II(NACA₄)]²⁻” model includes only the coordinating cysteine residues terminated with N- and C-terminal acetylation. This model is highly symmetric yet retains the pattern of two long and two short Ni-S bonds (Figure S13). A larger “backbone” model was also developed that retains the full CXXC loops and extended backbone atoms but replaces the non-cysteine side chains with glycine residues. The effects of this truncation on the structure of the active site are minor, as shown in Table 1 and Supporting Information, Table S1 and Figure S14. However, as discussed below, these changes had notable effects on the predicted spectroscopic properties of the nickel center.

A computational model for the experimentally-accessible oxidized Ni^IIIRd was also constructed.^86,87 The Ni^IIIRd structure was obtained by starting with the optimized Ni^IIRd geometry for the full model, removing an electron, and re-optimizing the coordinates of the oxidized species. As expected, the nickel-thiolate bonds contract upon oxidation, and the Jahn-Teller distortion is lifted to give a near-ideal tetrahedral geometry for the d⁷ configuration (Table 1 and Figure S15). The hydrogen-bonding network is only slightly perturbed. While no crystal structure exists of the Ni^IIIRd species, experimental support for the DFT-optimized structure was gained by comparison to spectroscopic properties and the thermodynamic reduction potential (vide infra).

Absorption spectroscopy

Nickel-substituted rubredoxin exhibits strong absorption bands in the visible region of the spectrum, owing to the tetrahedral geometry and orbital overlap between the metal center and sulfur thiolates.^88–90 To validate the computational model of NiRd beyond structural markers, predicted spectroscopic properties were compared to experimental values. The optical absorption spectrum of Ni^IIRd is overlaid with the calculated absorption spectrum of the full Ni^IIRd model in Figure 3. Across the visible and near-UV wavelength range, there is good agreement for both the energies and intensities of the transitions. Notably, no energy offset or correction was needed for the direct comparison of the experimental and calculated absorption spectrum. The low-energy transitions at 13,654 cm⁻¹ (ε = 636 M⁻¹ cm⁻¹) and 15,118 cm⁻¹ (ε = 70 M⁻¹ cm⁻¹) had previously been assigned to d-d transitions on the basis of ligand field theory.^88,90 The calculations agree with this assignment, with the majority of the electron difference density for States 5 and 6 arising from metal-based electron rearrangement from the d_xy to the d_x2-y2 orbital (Figure 3, inset). At 22,001 cm⁻¹, State 8 can largely be ascribed to a ligand-to-metal charge-transfer transition in the sulfur p-π manifold; this is in good agreement, again, with ligand-field arguments and early MCD experiments on a related NiRd and nickel thiolate model compounds.^88,91 Finally, in the near-UV region of the spectrum, charge transfer transitions from the sulfur p-σ orbitals to nickel are observed at 28,508 cm⁻¹, as shown in the difference density plot for State 17. Similar energies and transition difference densities are obtained with TD-DFT calculations on the backbone Ni^IIRd model (Table S2 and Figure S16), though State 8 from the full model is split from one intense band into two similar, near-degenerate transitions in the backbone Ni^IIRd model. In the [Ni^II(NACA)₄]²⁻ model, however, much poorer agreement is seen between experiment and theory (Figure S9). Instead of two dominant charge-transfer transitions, many weak electronic excitations are seen, giving rise to a broad, featureless absorption spectrum. A single-point TD-DFT calculation using the x-ray diffraction structure of Cp NiRd also gave relatively poor agreement between experiment and theory (Figure S17).

Resonance Raman spectroscopy

The excellent agreement between the experimental and calculated optical absorption spectrum supports the use of this computational model to predict more sophisticated spectroscopic properties, such as resonance Raman (RR) intensities.³⁹ While resonance enhancement from excitation into d-d transitions is known to be weak due to the low associated nuclear displacements,⁹² the multiple ligand-to-metal charge transfer bands in the visible and near-UV region of the spectrum are well-suited for RR investigations. Resonance Raman spectra of NiRd were obtained with excitation wavelengths of 488 nm, 458 nm, 407 nm, and 364 nm. Subtraction of ZnRd control samples was performed to ensure that all bands observed in Figure 4 can be attributed to the resonantly enhanced nickel-thiolate chromophore. Corresponding theoretical resonance Raman spectra were calculated for the full NiRd model considering excitation into State 8 at 20,000 cm⁻¹ and 25,000 cm⁻¹ and State 17 at 25,000 cm⁻¹ and 30,000 cm⁻¹ to simulate the experimental spectra obtained at 488 nm, 458 nm, 407 nm, and 364 nm, respectively. The direct comparison between experiment and theory is shown in Figure 4.

Figure 4.

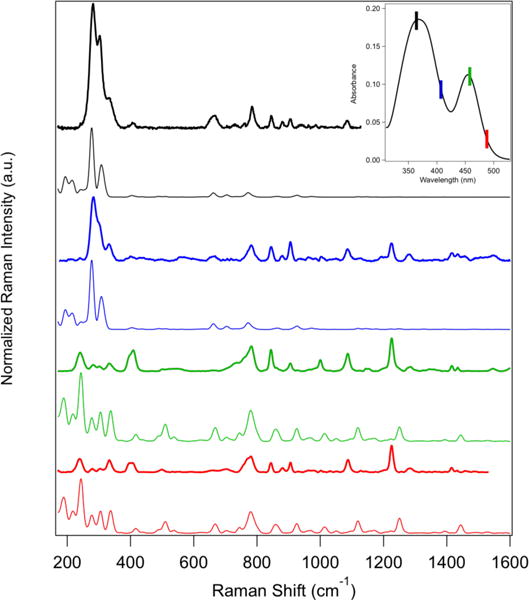
Experimental (thick lines, top) and calculated (thin lines, bottom) resonance Raman spectra of nickel-substituted rubredoxin at excitation wavelengths of 364 nm (black), 407 nm (blue), 458 nm (green), and 488 nm (red). (Inset) UV-vis absorption spectrum of NiRd with corresponding excitation wavelengths indicated.

The RR spectrum obtained with 364 nm excitation is dominated by three low-frequency modes at 282 cm⁻¹, 303 cm⁻¹, and 334 cm⁻¹. Additional bands from ~650–900 cm⁻¹ and ~1000–1100 cm⁻¹, typical frequency ranges for sulfur-carbon and carbon-carbon stretching modes, respectively, are observed with approximately 10-fold lower intensities. The calculated RR spectrum of the full NiRd model using excitation directly into State 17 shows similar trends, with three large bands predicted in the low-frequency region of the spectrum and bands of significantly lower intensity in the high-frequency region. While the spectra are generally similar, a slightly different enhancement pattern is seen with excitation at 407 nm. Specifically, the low frequency modes are less enhanced relative to the high frequency modes. This change in intensity across the spectrum is also predicted in the RR calculations.

With excitation into the principal visible transition at 458 nm and 488 nm, the relative intensities of the low frequency peaks are approximately reversed. At these wavelengths, the most intense bands occur at 241 cm⁻¹, 394 cm⁻¹, and 409 cm⁻¹. Additionally, the vibrational modes at higher frequencies are increasingly enhanced, with the most prominent high frequency peaks occurring at 783 cm⁻¹, 844 cm⁻¹, 1087 cm⁻¹, and 1226 cm⁻¹. These bands ultimately dominate the spectrum measured at 488 nm, though lower absolute intensities (when normalized to the Phe band) are seen. Analogous changes are seen in the calculated spectra.

Vibrational mode assignments

The vibrational frequencies of the RR bands seen at low energies are consistent with those expected for nickel-sulfur stretching and bending modes and can be qualitatively assigned on that basis. A more quantitative approach to vibrational mode assignments was carried out using the DFT-calculated vibrational frequencies in conjunction with predicted intensities (Table S3), which is necessary due to the high density of vibrational states found in such a large active-site model. To facilitate mode assignments, experimental and theoretical RR spectra were normalized to the intensity of the highest band at each wavelength for direct comparison (Figure 5).

Figure 5.

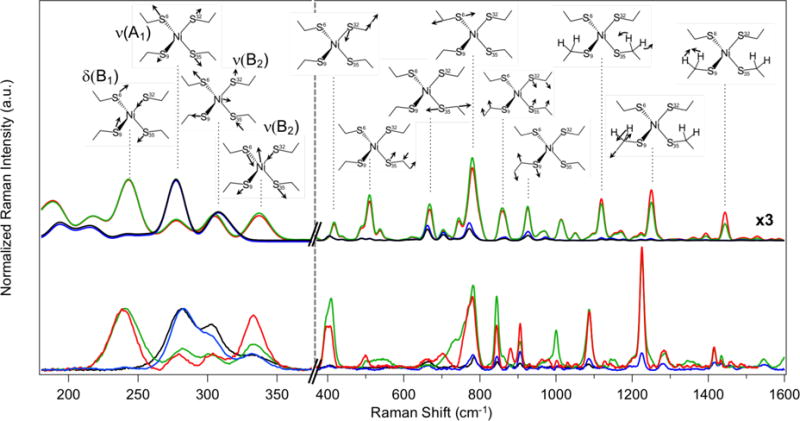
Intensity-normalized resonance Raman spectra of NiRd showing relative peak intensities across the four excitation wavelengths. Experimental (bottom) and calculated (top) spectra at 364 nm (black) and 407 nm (blue) were normalized to the 282 cm⁻¹ peak, while the 458 nm (green) and 488 nm (red) spectra were normalized to the 241 cm⁻¹ band to facilitate relative intensity comparisons. The high frequency region of the spectra is shown on a different abscissa, and the intensities of the calculated spectra in that region were scaled three-fold to better visualize the peaks. (Inset) Vector diagrams and approximate symmetry labels of the vibrational modes associated with the calculated spectra.

The low-frequency vibrations are dominated by metal-ligand normal modes. As discussed below, the vibrational modes were considered in a D_2d framework, in which the tetrahedral (T_d) T₂-symmetric metal-ligand stretches and E and T₂ bending modes are split into B₂ + E stretching and A₁ + B₂ and B₂ + E bending modes, respectively. The band calculated at 244 cm⁻¹ corresponds to the δ(B₁) S-Ni-S bend and has been assigned to the experimental band at 241 cm⁻¹. The totally¹ symmetric ν(A₁) Ni-S stretch is calculated at 277 cm⁻¹, in good agreement with the experimental band at 282 cm⁻¹. The two medium-intensity bands at 308 cm⁻¹ and 336 cm⁻¹ correspond to the ν(B₂) Ni-S anti-symmetric stretching modes, assigned to the experimental bands at 303 cm⁻¹ and 334 cm⁻¹. As mentioned above, the Jahn-Teller distortion at the active site results in longer Ni-S₆ and Ni-S₃₂ bonds than those of Ni-S₉ and Ni-S₃₅. As a result, the Ni-S anti-symmetric stretching modes occur at two different energies. The lower energy band at 308 cm⁻¹ reflects the normal mode of the longer Ni-S bonds, while the higher energy band at 339 cm⁻¹ reflects that of the shorter Ni-S bonds. The different nuclear displacement vectors for each of the modes are shown as insets in Figure 5. The bands calculated at 416 cm⁻¹ and 418 cm⁻¹ also show some ν(B₂) Ni-S anti-symmetric stretching character; however, these modes are coupled into the Ni-S₆-C bend and Ni-S₃₂-C bend, respectively, resulting in increased frequencies relative to what would be anticipated for pure metal-ligand vibrational modes. These higher energy modes are assigned to the experimental bands at 394 cm⁻¹ and 408 cm⁻¹.

At higher frequencies, the vibrational bands are dominated by sulfur-carbon and carbon-carbon stretching modes, with some mixing into C-H stretching and bending motion as well. Again, owing to the asymmetry of the active site, two different vibrational frequencies are seen for the sulfur-carbon stretching modes. The bands at 661 cm⁻¹ and 664 cm⁻¹ represent the ν(S₃₅-C) and ν(S₉-C) modes, respectively. These cysteine residues exhibit shorter Ni-S bonds and, accordingly, S-C bonds that are longer by an average of 0.01 Å. The bands calculated at 743 cm⁻¹ and 779 cm⁻¹ are attributed to the ν(S₆-C) and ν(S₃₂-C) modes, respectively, which correspond to the two cysteine ligands featuring longer Ni-S bonds and thus shorter S-C bond lengths. These modes are closer in frequency to typical carbon-carbon bond vibrations and, as a result, some C-C wagging motion is mixed into the mode, causing increased frequencies relative to standard S-C stretching modes. The intense, narrow bands calculated at 926 cm⁻¹ and 928 cm⁻¹ represent the Cys₉ C-C-C and Cys₃₅ C-C-C bending modes, respectively, while the bands at 1011 cm⁻¹ and 1019 cm⁻¹ correspond to the Cys₃₅ C-C and Cys₉ C-C stretches. Above 1000 cm⁻¹, significant proton motion is mixed into the heavy atom displacements, with the 1119 cm⁻¹ and 1246 cm⁻¹ bands assigned to the Cys₃₅ H_β-C-H_β twist and Cys₉ H_β-C-H_β twist coupled to ν(C_α-N) stretching motions, respectively. Finally, the calculated bands at 1443 cm⁻¹ and 1447 cm⁻¹ reflect the Cys₉ δ(H-C₉-H) and Cys₃₅ δ(H-C₃₅-H) bending modes. Calculated vibrational modes were assigned to experimental bands on the basis of visual correspondence in both intensity and frequency owing to the qualitative agreement between the intensity-normalized spectra, as is further described in Figure S18 and Table S3.

Isotope Shifts

Rubredoxin proteins are known to have a conserved set of hydrogen bonds between the backbone amide groups and the cysteine thiolate ligands that modulate structure and reduction potential.^55,85 Short N_amide - S distances of 3.4 – 3.7 Å were retained in the DFT-optimized geometry of Ni^IIRd (Table 1), with principal hydrogen-bonding interactions shown in Figure 2B. To probe this hydrogen-bonding network and identify vibrational modes that are coupled to the amide backbone, hydrogen/deuterium exchange experiments were performed. Resonance Raman spectra were obtained at all four excitation wavelengths for Ni^IIRd in protiated and deuterated buffer; representative spectra for both isotopes as well as the difference spectrum using 458 nm excitation are shown in Figure 6.

Figure 6.

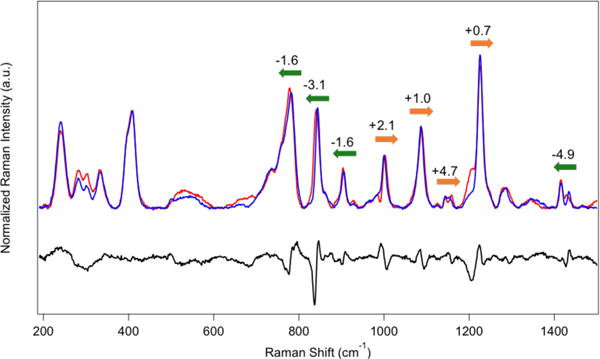
Resonance Raman spectra of NiRd (458 nm excitation) in buffered H₂O (blue), D₂O (red), and the corresponding difference spectrum (H – D, black). Frequency shifts indicated with colored arrows.

A number of modes are seen to shift experimentally upon isotopic exchange. In the low frequency region, where metal-ligand stretching and bending vibrations are prevalent, only minor changes in intensity are seen for the deuterated sample; vibrational frequencies of those modes generally remain constant. At higher frequencies, more pronounced changes are observed. Many bands shift to lower frequencies, including the S-C stretching mode at 780 cm⁻¹ and C-C-C backbone wag at 840 cm⁻¹; those modes are also calculated to shift in that direction (Table S3). However, the bands at 1000 cm⁻¹, 1087 cm⁻¹, 1153 cm⁻¹, and 1225 cm⁻¹, assigned to the backbone C-C stretching, Cys_9/35 H_β-C-H_β twisting motion, and Cys_6/32 H_β-C-H_β twisting motions, respectively, shift to higher frequencies in the presence of the heavier isotope. The calculated isotope shifts for these modes are also predicted to be positive, in support of the normal mode assignments. The increase in frequency can be attributed to coupling of N-H bending motion into the C-H torsional displacement. These amide protons are involved in strong hydrogen bonds to the coordinating cysteine residues. Owing to differences in mass, the vibrational coupling between the hydrogen-bonded amide backbone and the rest of the peptide will change upon isotopic substitution. This normal mode redistribution results in apparent frequency increases when deuterium is used. The same experimental frequency shifts are seen for analogous bands at different excitation wavelengths, albeit with different relative intensities (Figure S19). Because energy redistribution among normal modes upon isotopic substitution affects the calculated intensities significantly, some calculated shifts are overemphasized in the theoretical spectrum (Table S3 and Figure S20).

Ni^IIIRd

Spectrophotometric titrations using potassium ferricyanide (K₃[Fe(CN)₆], E˚’ = +420 mV vs. NHE at pH 7)⁹³ were carried out by monitoring the Ni^IIRd charge transfer and d-d absorption bands (Figure 7A) as a function of solution potential. These data were fit to a standard Nernst equation to obtain a solution-phase reduction potential for the Ni^III/II couple of +430 mV vs. NHE at pH 8 (Figure 7B). This potential was found to be pH-dependent, with an approximate −30 mV/pH unit shift from pH 4.5 to pH 10 (Figure S21). Protein film and solution-phase cyclic voltammetry experiments were also performed to directly measure the reduction potential. While the protein film experiments showed no electrochemical transition on the timescale of an experimentally accessible scan, possibly indicating slow electron transfer or film desorption, a quasi-reversible couple was observed using solution-phase electrochemistry, with an anodic peak potential of +610 mV at pH 4.5 (Figure 7C). This value is similar to that seen in the potentiometric titrations at pH 4.5, while the irreversibility of the transition is consistent with the lack of any signal in protein film voltammetry.

Using a thermodynamic square scheme, the reduction potential was calculated using DFT methods. To benchmark the level of theory and the accuracy of the computational methods, the reduction potential of the [FeCp₂]^0/+ couple was first examined in acetonitrile. The absolute reduction potential obtained by considering the change in the Gibbs free energy for the reduced and oxidized states was calculated to be +5.00 V. To convert this potential into a relevant reference frame, accepted values for the absolute potential of the standard hydrogen electrode (SHE) of +4.281 V and the standard calomel electrode (SCE) of +0.241 V vs. SHE were used.⁴⁷ With this, the reduction potential for the [FeCp₂]^0/+ couple was calculated to be +0.44 V vs. SCE, in good agreement with experimental values of approximately +0.38 V vs. SCE.⁴⁷ Analogous methods were employed for NiRd. The calculated reduction potential of the full Ni^III/IIRd model was found to be +0.106 V vs. SHE, in modest agreement with the experimental values observed in the potentiometric and electrochemical measurements. The absolute reduction potentials and electronic energies of the [FeCp₂]^0/+ and Ni^III/IIRd couples are presented in the Supporting Information (Tables S4–S5).

Because of the instability of the Ni^IIIRd species, no distinctive absorption peaks could be identified for the oxidized species. However, at low temperatures, EPR spectra of Ni^IIIRd were obtained (Figure S22). The spectral features are similar to those previously seen in the oxidized Ni^IIIRd from Pyrococcus furiosus,⁸⁶ with g-values of g_z = 2.27, g_y = 2.09, and g_x = 2.06 (g_iso = 2.14; Δg_xy = 0.03). Given the known propensity of DFT to underestimate experimental g-tensor shifts,⁹⁴ the calculated g-values are in satisfactory agreement with experiment at g_z = 2.19, g_y = 2.13, and g_y = 2.10 (g_iso = 2.14; Δg_xy = 0.03). The singly occupied molecular orbital (SOMO) represents a combination of the nickel d_yz orbital and significant π* involvement from the sulfur p_x and p_y orbitals, with the spin density almost entirely localized on the metal center (Figure S22, inset).

Discussion

Comparison between experiment and theory

Developing accurate theoretical models for enzyme active sites presents a significant challenge across fields. Even with the rapidly increasing advances in computational power, it remains generally intractable to treat all of the atoms in an entire protein quantum mechanically. Conversely, considering only the active-site atoms can be a faulty approach, as many key markers for energetics and structure are incorrectly predicted.^44,45 From an experimental standpoint, a similar argument can be made: Recreating an entire enzyme poses great biochemical difficulties, but generating a synthetic model that includes only the metal center and the primary coordination sphere typically fails to reproduce the reactivity of the enzyme.^26,95 It is clear that, on both fronts, an intermediate approach is necessary.

The Ni^IIRd theoretical model developed in this work incorporates the dominant secondary sphere interactions within the CXXC loops and preserves the general structure imposed by the protein backbone.^55,84 The model is moderately sized, containing 77 heavy atoms and 149 atoms total, and is readily processed with modest use of supercomputer resources.⁵⁹ Importantly, with this level of the outer coordination environment included, we are able to accurately reproduce the geometric and electronic structures of Ni^IIRd. This is evident when considering the TD-DFT-predicted absorption spectrum, which shows excellent agreement with experimental results when considering both energetics and intensities of the transitions. As the electronic absorption spectrum of a system is highly sensitive to coordination environment and symmetry around the metal center,^96–98 this high level of correspondence suggests the distortions predicted by the DFT optimization reflect the solution-phase geometry.

Further validation of the computational model is found in the predicted resonance Raman spectra. Resonance Raman spectroscopy relies on the coupling between electronic and vibrational states, with intensities governed by the displacement of the electronic excited state with respect to the ground state for each mode. The ground state vibrational frequencies that are measured in the experiment reflect bond length (bond order) and interatomic angles. Thus, RR spectroscopy is a direct probe of the electronic and geometric structures of a system.^39,99

It is straightforward to calculate the vibrational frequencies for a given geometry; these parameters are directly related to each normal coordinate force constant, which is the second derivative of the potential energy surface.⁴² To predict the resonance Raman spectrum, the absorption cross-section must be coupled into the dimensionless displacements of each normal mode, which requires more sophisticated methods of computation.³⁹ Traditionally, excited-state geometry optimizations must be performed and the excited state normal mode displacement is obtained by projecting the change in the mass-weighted Cartesian coordinates for each mode onto the excited-state normal coordinates.^100–102 This process is quite cumbersome and virtually impossible to perform for large models of protein active sites. However, assuming harmonic potentials, the excited-state gradient can be used to predict the displacement along each normal mode. This method has been efficiently implemented in the ORCA_ASA program,^75,78,103 developed by Petrenko and Neese, and integrated within the ORCA quantum chemistry software package.

To calculate the resonance Raman spectra of Ni^IIRd, the ORCA_ASA program was used within the IMDHO model considering only Albrecht A-term enhancement.¹⁰³ Because the effects of overlapping excited states can introduce significant complications,¹⁰⁴ a simplistic approach was taken in which RR intensities were calculated for only one excited state at a time, using a range of theoretical excitation energies, and the lower intensity transitions were ignored. Even with this primitive approach, notably good correspondence is seen between the experimental and predicted RR spectra, suggesting this approximation is valid. Considering that the relative intensity patterns of vibrational modes reflect the nature of the electronic transition probed, the spectra effectively serve as a “fingerprint” for the excited state.

Better agreement between experiment and theory is seen for the low frequency, metal-ligand-based modes relative to the higher energy, ligand-coupled modes, which has been seen previously in RR spectra of model inorganic compounds.³⁷ The discrepancy at higher energies is ascribed to the fact that RR intensities are proportional to ν²Δ², which causes increased enhancement for high frequency modes even in the case of smaller dimensionless displacements. For example, the calculated maximum Δs for the metal-ligand modes at 244 cm⁻¹ and 277 cm⁻¹ are approximately 1, while the corresponding Δs for the ligand-centered NiRd modes at 1000, 1200, and 1400 cm⁻¹ are approximately only 0.05–0.1 (Table S3), approaching the accuracy limit of the methodology. As a result, the intensities of the higher energy vibrational transitions are often underestimated. Nevertheless, when this region of the spectrum is scaled appropriately and compared to experiment (Figure 5, right hand side), similar trends are observed between the calculated and measured spectral intensities.

Effects of the outer coordination sphere on the calculated spectroscopic properties

To assess the impact and necessity of including the CXXC side chains in the computational model, two smaller models were generated and analogous calculations performed. In the simplest [Ni^II(NACA)₄]²⁻ model, only the four cysteine amino acids were included, giving a symmetric active site without any contribution from the protein backbone or the outer coordination sphere. The optimized structure retained the tetragonal elongation, with two long nickel-sulfur bonds and two short ones, that would be expected for a high-spin Ni(II) system, illustrating the electronic rather than steric origin of this distortion. However, the [Ni^II(NACA)₄]²⁻ model poorly reproduced both the experimental absorption and resonance Raman spectra of NiRd, as shown in the Supporting Information (Figures S9 and S23).

As a next step, a minimal “backbone” model was also developed and analyzed. In this system, the CXXC binding loops with the peptide backbone were included, but all of the non-cysteine side chains were replaced by glycine. This model is significantly smaller, with only 64 heavy atoms and 115 total atoms. As such, it requires fewer resources for computational analysis and therefore could be a desirable replacement for the full model in future studies. Examining structural properties, only minor differences are observed between the optimized active-site geometries of the two models for both the Ni^IIRd and Ni^IIIRd redox states. In addition, the predicted energies, intensities, and nature of the electronic transitions are also very similar. Slight frequency shifts (<10 cm⁻¹) were observed for the calculated vibrational bands, though the nuclear displacements of equivalent normal modes remained comparable. The same calculated g-tensor was obtained upon oxidation of the backbone model, further confirming the similarity in active-site electronic structure. On this basis, it would be reasonable to assume that the truncated backbone model accurately represents the NiRd active site.

However, important distinctions between the models become evident in the calculated resonance Raman intensities (Figure S23). While the calculated RR spectra of both models are dominated to some extent by the low frequency metal-ligand vibrations, greater intensity is transferred to the higher frequency, ligand-centered modes when the full side chains are included. The higher mode intensities can be attributed to increased coupling between the peptide backbone and side chains and the active site. The increased intensities thus reflect experimentally relevant contributions to the electronic excited state from the outer coordination sphere. This is reminiscent of the extended vibrational couplings seen between the heme group and the axial methionine ligand in cytochrome c and illustrates the potential relevance of these motions for modulating reactivity.¹⁰⁵ The backbone model underestimates the intensity of those bands by approximately an order of magnitude when compared to experiment (Figure S23). In the full model, these bands are still slightly underestimated relative to the low frequency modes (Figure 5); however, it is important to note that the intensities scale as ν²Δ², so smaller errors in calculated dimensionless displacements (Δs) result in larger deviations. Because a primary objective of this study is to develop and validate an accurate model of the NiRd active site for use in predicting RR features, reproducing the intensities and overall “fingerprint” across the entire vibrational spectrum is an important criterion. From this analysis, it seems necessary to use the full model of NiRd in future computational studies.

Using calculated RR spectra for mode assignments

In addition to providing a direct probe of the electronic transitions, the calculated resonance Raman spectra offer a convenient method for performing vibrational mode assignments. The traditional method for normal mode assignments typically requires systematic isotopic substitution and comparison to both calculated frequencies and frequency shifts. However, within a protein system, selective isotopic replacement can be prohibitively expensive and is often problematic. Further complicating analysis, substitution of heavy metals and sulfur-derived ligands only results in minor shifts (often <1 cm⁻¹) that may fall within the resolution of the experiment and produce ambiguous assignments (Figure S24).¹⁰⁶ By combining frequency and intensity analyses, as we have done in this study, robust vibrational mode assignments can be made.³⁷

A visual depiction of how vibrational modes were assigned is shown in Figure S18, with the assignments and normal mode character given in Table S3 and expanded active-site displacements shown in Figure S25. Under an idealized tetrahedral geometry, the nickel thiolate core should have ν(A₁) and ν(T₂) stretching modes and δ(T₂) and δ(E) sets of bending modes.¹⁰⁶ Distortion to a D_2d geometry lowers the symmetry and splits the T₂ sets into a B₂ + E set and the δ(E) modes into A₁ + B₁ modes (Figure S26). Briefly, considering the different enhancement patterns across the multiple excitation wavelengths employed, these fundamental normal modes were assigned in a pseudo-D_2d framework (using the D_2d point group symmetry labels). The totally symmetric ν(A₁) stretching mode is calculated at 277 cm⁻¹ and assigned to the band at 282 cm⁻¹. This mode is particularly intense at the high-energy excitation wavelengths, as would be expected for enhancement with State 17, a sulfur-to-nickel σ* charge transfer transition (Figure 3, inset). At lower frequencies, the δ(E) set is split into two bands, with a B₁ component observed at 244 cm⁻¹, and the bands at 307 cm⁻¹ and 335 cm⁻¹ can be assigned to components of the ν(T₂) set. This assignment is consistent with the ordering expected for a tetragonally elongated distortion, as seen in the DFT-optimized structure. Owing to vibrational coupling between the electronic and vibrational states, these typically weak normal modes are strongly enhanced with excitation into the lower energy, sulfur-to-nickel π* charge transfer transition. The bands at 394 cm⁻¹ and 408 cm⁻¹, previously attributed by Johnson and coworkers to cysteine deformation modes,¹⁰⁶ have also been assigned here to Ni-S-C bending modes, with different frequencies attributed to the different cysteine thiolates.

The enhancement of high frequency bands (400 – 1500 cm⁻¹) in the RR spectra arises because of mixing between metal-ligand modes and ligand-based vibrations and reflects coupling between the normal modes of the metal-ligand core and the protein backbone. Because of this vibrational mixing, RR spectroscopy can be used to monitor geometry and distortions beyond the metal-thiolate center. These modes provide information on local changes that arise from minor perturbations to the active site, for example, as a result of secondary sphere mutations. Additionally, we would expect significant frequency changes as a result of thiolate ligand protonation, which is involved in the proposed mechanism for hydrogen evolution. Assignment of these bands in the resting state will facilitate identification of changes in the ligand structure during catalysis.

Validation of the model across different oxidation states

In addition to obtaining a complete electronic and geometric description of the resting-state of the Ni^IIRd enzyme, we are interested in ultimately probing structures of catalytic intermediates. While Ni^IIIRd is not necessarily a proposed intermediate in the NiRd-catalyzed hydrogen evolution pathway, prior work by our lab and others have shown that this species can be generated near quantitatively and characterized,^86,90 which renders it an ideal system for initial study and validation. The calculated EPR g-tensor, while of similar magnitude, is somewhat underestimated when compared to experiment. These systematic deviations have been reported previously for nickel-containing proteins.^{42,94,107,108} The Ni^III/II reduction potential is also slightly underestimated by the calculations, though within the level of error seen for other calculated reduction potentials of metalloproteins;¹⁰⁹ further, the pH effects noted experimentally are neglected in the computational model, which could account for the modest differences seen. These results provide proof-of-concept evidence that, with the moderately sized computational model developed here, other oxidation states of the system can be accurately described by density functional theory. Ultimately, these calculations may be able to serve in a predictive as well as interpretive role.

Conclusions

Resonance Raman spectroscopy is a powerful technique for selective investigation of the electronic and geometric structure of a molecule, which, ultimately, reflects the reactivity of the system. We have obtained a detailed description of the electronic structure of nickel-substituted rubredoxin, which is a highly active hydrogenase mimic, using resonance Raman spectroscopy across multiple excitation wavelengths coupled to DFT calculations on an extended active site model. Inclusion of the complete outer coordination sphere in the computational model is necessary to reproduce experimentally observed spectroscopic properties, such as optical absorption and resonance Raman intensities. In this way, vibrational mode assignments and a quantitative description of the electronic excited states have been obtained. Additionally, spectroscopic markers indicating active site distortion and ligand-based vibrational modes were identified. The excellent agreement between experiment and theory for the resting state of Ni^IIRd and the one-electron-oxidized Ni^IIIRd highlights the potential utility of this method to characterize the structures of catalytic intermediates and obtain insight into the mechanism of NiRd-catalyzed hydrogen evolution.

ABBREVIATIONS

RR

resonance Raman

NiRd

nickel-substituted rubredoxin

NACA

N- and C-acetylated cysteinate

EPR

electron paramagnetic resonance; standard single-letter abbreviations used for all amino acids