Alpha-Band Oscillations Enable Spatially and Temporally Resolved Tracking of Covert Spatial Attention

Abstract

Covert spatial attention is essential for humans’ ability to direct limited processing resources to the relevant aspects of visual scenes. A growing body of evidence suggests that rhythmic neural activity in the alpha frequency band (8–12 Hz) tracks the spatial locus of covert attention, which suggests that alpha activity is integral to spatial attention. However, extant work has not provided a compelling test of another key prediction: that alpha activity tracks the temporal dynamics of covert spatial orienting. In the current study, we examined the time course of spatially specific alpha activity after central cues and during visual search. Critically, the time course of this activity tracked trial-by-trial variations in orienting latency during visual search. These findings provide important new evidence for the link between rhythmic brain activity and covert spatial attention, and they highlight a powerful approach for tracking the spatial and temporal dynamics of this core cognitive process.

A typical visual scene contains more information than an observer can process at once. Therefore, the observer must focus limited processing resources on the most relevant aspects of the environment. Spatial attention plays a central role in this effort, enhancing the quality and speed of processing at attended locations (Carrasco & McElree, 2000; Eriksen & Hoffman, 1974; Posner, 1980; for review, see Carrasco, 2011). Because spatial attention is essential for normal perceptual function, there is great interest in understanding the neural basis of this process. One promising approach has been to examine the links between attentional states and rhythmic brain activity. A growing body of evidence suggests that oscillatory activity in the alpha frequency band (8–12 Hz) is integral to covert spatial attention. Measurements of the topographic distribution of alpha power across the scalp have revealed that alpha power is reduced contralateral to an attended location (e.g., Kelly, Lalor, Reilly, & Foxe, 2006; Sauseng et al., 2005; Thut, Nietzel, Brandt, & Pascual-Leone, 2006). Further work has shown that the topography of alpha power tracks not just the hemifield but also the specific location that an observer is attending (e.g., Bahramisharif, Van Gerven, Heskes, & Jensen, 2010; Rihs, Michel, & Thut, 2007; Worden, Foxe, Wang, & Simpson, 2000). These findings suggest that spatially specific alpha-band activity directly tracks the deployment of spatial attention (Foxe & Snyder, 2011; Jensen & Mazaheri, 2010).

Nevertheless, the hypothesis that alpha-band activity is integral to spatial attention makes a clear prediction that remains untested: The topography of alpha-band activity should track not only the spatial locus of attention but also the time course of covert orienting. Extant studies have not provided a rigorous analysis of the time course of spatially specific alpha activity or examined whether the time course of this activity tracks variations in the latency of covert spatial orienting. Thus, our goal was to determine whether dynamic changes in alpha-band activity provide a sensitive index of the speed of covert spatial orienting.

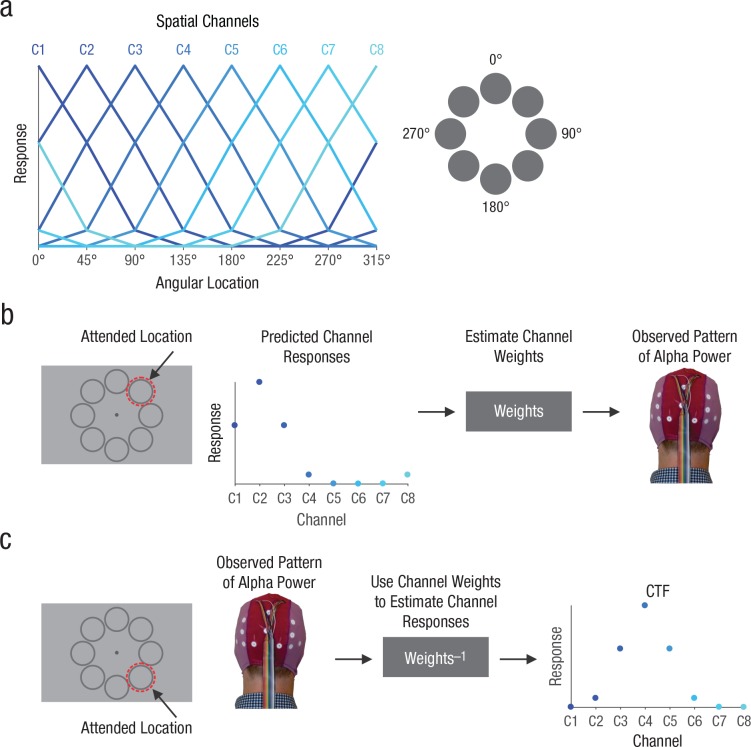
To this end, we used electroencephalography (EEG) recordings and an inverted encoding model (IEM; Brouwer & Heeger, 2009; Sprague & Serences, 2013; for review, see Sprague, Saproo, & Serences, 2015) to examine the time course of spatially specific alpha-band activity. This approach assumes that the topographic pattern of alpha power across the scalp reflects the activity of a number of underlying spatially tuned channels (or neuronal populations; Fig. 1a). By first estimating the relative contributions of these channels to each electrode on the scalp (Fig. 1b), the model can then be inverted so that the underlying response of these spatial channels can be estimated from the pattern of alpha power across the scalp (Fig. 1c). The resulting profile of responses across the spatial channels (termed channel-tuning functions, or CTFs) reflects the spatial tuning of population-level alpha power, as measured with EEG. Thus, the IEM approach enables a straightforward quantification of spatially selective activity from a higher-dimensional pattern of alpha power on the scalp. By performing this analysis across separate points in time, we were able to examine the temporal dynamics of spatially selective alpha-band activity (also see Foster, Sutterer, Serences, Vogel, & Awh, 2016; Samaha, Sprague, & Postle, 2016).

Fig. 1.

Illustration of the inverted encoding method for reconstructing spatial channel-tuning functions (CTFs) from the pattern of alpha-band power across the scalp. We modeled alpha power measured at each electrode as the weighted sum of eight spatially tuned channels (C1–C8). Each curve in (a) shows the predicted response of one of the channels across eight possible attended angular locations (the locations shown here were used in Experiment 1; in Experiment 2, we used 22.5°, 67.5°, 112.5°, etc.). The gray circles on the right indicate how locations were labeled. In the training phase (b), we used predicted channel responses to estimate a set of channel weights that characterized the relative contribution of each of the spatial channels to the response measured at each of the scalp electrodes. The example shown here is for an attended location at 45°. In the test phase (c), using an independent set of data, we used the channel weights determined from the training data to estimate the channel responses from the observed pattern of alpha power on the scalp. The resulting CTF reflects the spatial selectivity of population-level alpha power, as measured by electroencephalography (EEG). The example shown here is for an attended location at 135°. For more details, see the Inverted Encoding Model section.

In two experiments, we tested whether the topographic distribution of alpha-band activity tracks the time course of covert orienting. In Experiment 1, subjects performed a spatial-cueing task, which allowed us to examine the time course of alpha-band CTFs as subjects shifted covert attention to the cued location following an attention-directing cue. In Experiment 2, subjects performed a visual search task, in which we manipulated the latency of covert orienting toward the target by varying search difficulty. This design allowed us to directly test whether the time course of alpha-band CTFs tracked differences in the latency of target selection across different levels of search difficulty and as a function of within-subject variations in orienting latency across trials, as indexed by reaction times.

General Method

Subjects

Fifty volunteers (20 in Experiment 1, 30 in Experiment 2¹) participated in the experiments for monetary compensation ($10 per hr). Subjects were between 18 and 35 years old, reported normal or corrected-to-normal visual acuity, and provided informed consent according to procedures approved by the institutional review board at the University of Oregon.

In Experiment 1, we did not analyze data from subjects who provided fewer than 700 artifact-free trials (i.e., trials that were not contaminated by recording or ocular artifacts). This exclusion criterion was set during data collection and was chosen on the basis of our work using the IEM method to track locations stored in working memory (Foster et al., 2016). Two subjects were excluded because of excessive artifacts, and 2 subjects were excluded because of an error with stimulus presentation. Thus, the final sample included a total of 16 subjects.² All subjects in the final sample provided data for at least 700 artifact-free trials (M = 1,165, SD = 173).

In Experiment 2, we did not analyze data from subjects who provided fewer than 600 artifact-free trials (with correct responses) for each condition. We relaxed the exclusion criterion in Experiment 2 because we obtained fewer trials per condition, because Experiment 2 included two conditions rather than one. The exclusion criterion was determined during the course of data collection but before the data were analyzed. Seven subjects were excluded because of excessive artifacts, which left a total of 23 subjects.³ All subjects in the final sample provided data for at least 600 trials per search condition (M = 772, SD = 79) after artifacts and incorrect responses were discarded.

Apparatus and stimuli

We tested the subjects in a dimly lit, electrically shielded chamber. Stimuli were generated using MATLAB (The Mathworks, Natick, MA) and the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997) and were presented on a 17-in. CRT monitor (refresh rate = 60 Hz) at a viewing distance of approximately 100 cm. Stimuli were rendered in dark gray against a medium-gray background.

Procedure

After providing informed consent, the subjects were fitted with a cap embedded with 20 scalp electrodes before completing the experimental task. Including preparation time and experimental time, Experiment 1 took approximately 3 hr to complete, and Experiment 2 took approximately 3.5 hr to complete.

Experiment 1: spatial-cuing task

Subjects in Experiment 1 completed a spatial-cuing task in which they were required to identify a target digit among distractor letters (Fig. 2a). Subjects initiated each trial by pressing the space bar. Each trial began with a central fixation point (0.24° in diameter), surrounded by equally spaced placeholder rings (1.7° in diameter, with a border of 0.08°). Each placeholder was centered 2.4° from the fixation point. The exact angular position of the placeholders were jittered on each trial within a 45° wedge. Thus, the position of the first placeholder varied between −22.5° and 22.5°, the second varied between 22.5° and 67.5°, and so on. This jitter was not necessary for the IEM analysis.

Fig. 2.

Task and results from Experiment 1. In the spatial-cuing task (a), a central cross (cue) with three arms of one color and one arm of a different color directed the subjects to attend one of eight placeholders. After a 1,000-ms delay, the target digit was displayed among distractor letters and then masked with a pound sign. The graph in (b) shows target-discrimination accuracy (proportion correct) separately for trials with valid and invalid cues. The top graph in (c) shows the average alpha-band channel-tuning function (CTF) across time for all eight locations. The yellow band shows the peak channel response. The eight graphs below that show the average CTF for each of the eight cued locations separately. In (d), the graph shows the average slope of the alpha-band CTF as a function of time. The red marker indicates the area of reliable CTF selectivity. The shaded areas indicate ±1 bootstrapped SEM. The graphs in (e) show the channel-response profile recovered using the standard graded basis function (left) and a nongraded basis function (right). The shaded areas indicate ±1 bootstrapped SEM. The slopes of the CTFs reconstructed from the topographic distribution of oscillatory power across a broad range of frequencies (4–50 Hz, in increments of 1 Hz) are plotted in (f). Points at which the CTF slope was not reliably above zero as determined by a permutation test are set to zero (dark blue).

After a variable interval between 800 and 1,500 ms, a central cue (87.5% valid), presented for 250 ms, indicated the likely location of a subsequent target. The cue was a small cross (0.6° wide; arms were 0.08° thick) with three green arms and one blue arm (or vice versa, counterbalanced across subjects). The uniquely colored arm of the cue pointed toward the cued placeholder. In a target display presented 1,250 ms after cue onset, each placeholder was occupied by a letter or digit. The display included one target (a digit between 1 and 9) among distractors (uppercase letters). Digits and letters were approximately 0.9° tall and 0.8° wide. The distractor letters were randomly selected without replacement from all possible letters (except for “I,” “S,” and “Z” because of their similarity to the digits “1,” “5,” and “2,” respectively). The target was backward-masked with a pound symbol (“#”) presented for 400 ms. Following the mask, the subjects reported the target identity using the number pad on a standard keyboard; there was no time limit. The reported digit appeared ~1° above the fixation point, and the subjects could correct their response if they pressed a wrong key. Finally, the subjects confirmed their response by pressing the space bar.

To encourage the subjects to attend the cued location in advance of the target display, we adjusted the duration of the target display for each subject using a staircase procedure. Subjects completed one or two blocks (72 trials per block) of this procedure at the start of the session. During the staircase procedure, the cue was valid on all trials, and the subjects were instructed to attend the cued location. Exposure duration was decreased by 16.7 ms (i.e., one refresh cycle at 60 Hz) when the subjects made a correct response or increased by 33.3 ms (i.e., two refresh cycles at 60 Hz) when the subjects made an incorrect response, until performance reached an asymptote. The resulting duration of the target display varied between 33.3 ms and 66.7 ms across subjects. This staircase procedure was somewhat coarse because changing exposure duration by 16.7 ms had a considerable effect on task difficulty. Nevertheless, this procedure ensured that target identification was adequately difficult for all the subjects: Target identification accuracy ranged be-tween 65.7% and 97.0% (M = 83.5%, SD = 9.5) on trials with valid cues, and all subjects showed a large spatial-cuing effect, which ranged between 26.6% and 69.8% (M = 46.6%, SD = 13.0).

After the staircase procedure, the subjects completed as many blocks of the spatial-cuing task as time permitted, but the goal was 20 blocks. Each block contained 72 trials, and all subjects completed at least 13 blocks. Each of the eight placeholders was cued equally often within each block of trials.

Experiment 2: visual search task

Subjects in Experiment 2 performed a visual search task in which they searched for a target (a vertical or horizontal bar) among distractors (Fig. 3a). Each item in the search display consisted of a dark gray bar (1.5° × 0.2°) superimposed on a gray circle (2.1° in diameter). The items were equally spaced in a circle around a dark gray fixation point (0.2° in diameter). Each item was centered 3° from the fixation point. Stimulus positions were not jittered in Experiment 2.

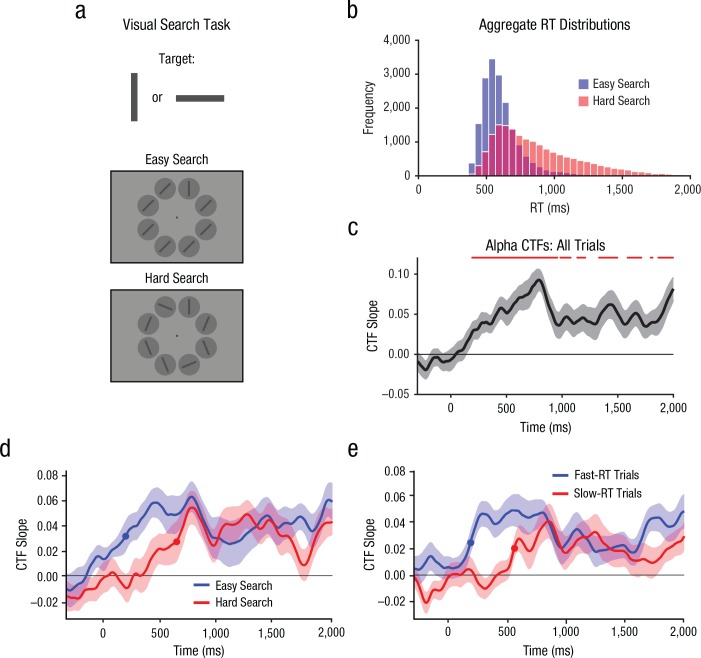
Fig. 3.

Task and results from Experiment 2. Subjects searched for a target (a vertical or horizontal bar) among distractors and reported the target’s orientation (a). The histogram in (b) shows the distributions of response times (RT) for easy and hard search. In (c), the plot shows the selectivity of the average target-related alpha-band channel-tuning function (CTF) across time, collapsed across the search conditions (easy and hard). Time points at which CTF selectivity was reliable are indicated by the red marker. The plots on the right show the average target-related CTF slope across time (d) for easy and hard search and (e) for fast- and slow-RT trials (regardless of search condition). The filled circles mark the points at which the target-related CTF reached the onset criterion (50% of maximum amplitude). The shaded areas in (c), (d), and (e) represent ±1 bootstrapped SEM.

We varied the difficulty of visual search by manipulating both distractor variability (i.e., distractor orientation was uniform or varied) and target-distractor similarity (i.e., the extent to which the distractors resembled the target). In the easy-search condition, all distractors were identical and were rotated 45° clockwise or counter clockwise from the possible target orientations (Fig. 3a). Thus, distractor variability and target-distractor similarity were low. In the hard-search condition, the distractors were heterogeneous and were rotated 22.5° from the possible target orientations (Fig. 3a). Thus, distractor variability and target-distractor similarity were higher than in the easy-search condition, resulting in a more difficult search (Duncan & Humphreys, 1989).

Each search array was presented for 2 s, separated by a variable intertrial interval between 1.8 and 2.3 s, during which only the fixation point remained visible. Subjects reported whether the target was vertical or horizontal by pressing the “z” key (left index finger) or “/” key (right index finger), respectively. Subjects were instructed to respond as quickly and as accurately as possible. Feedback (mean response time, or RT, and accuracy) was provided at the end of each block of trials. To minimize artifacts during the stimulus display and a 300-ms prestimulus baseline period, the subjects were instructed to maintain fixation throughout each block of the search task and to blink (if necessary) immediately after the offset of the search array.

The subjects completed 30 blocks of 64 trials each. The search conditions (easy or hard) were blocked, and the blocks alternated between conditions. The order of the conditions (easy first or hard first) was counterbalanced across subjects. Before beginning the session, the subjects completed two blocks of practice trials (easy search followed by hard search).

The subjects also completed a short practice session the day before the EEG session to familiarize themselves with the visual search task. During this session, the subjects completed three blocks of the easy-search condition followed by three blocks of the hard-search condition.

Electrophysiology

EEG was recorded using 20 tin electrodes mounted in an elastic cap (Electro-Cap International, Eaton, OH). We recorded from International 10/20 sites F3, FZ, F4, T3, C3, CZ, C4, T4, P3, PZ, P4, T5, T6, O1, and O2, along with five nonstandard sites: OL midway between T5 and O1, OR midway between T6 and O2, PO3 midway between P3 and OL, PO4 midway between P4 and OR, and POz midway between PO3 and PO4. All sites were recorded with the left mastoid as a reference; they were rereferenced off-line to the algebraic average of the left and right mastoids. To detect horizontal eye movements, we used horizontal electrooculography (EOG) recorded from electrodes placed approximately 1 cm from the external canthus of each eye. To detect blinks and vertical eye movements, we recorded vertical EOG from an electrode placed below the right eye and referenced to the left mastoid. The EEG and EOG were amplified using an SA Instrumentation (San Diego, CA) amplifier with a band-pass filter of 0.01 to 80 Hz and were digitized at 250 Hz using LabVIEW 6.1 (National Instruments, Austin, TX) running on a PC. Trials were visually inspected for artifacts, and we discarded trials (both EEG and behavioral data) contaminated by blocking (i.e., amplifier saturation), blinks, detectable eye movements, excessive muscle noise, or skin potentials. Removal of ocular artifacts was effective: Variation in the grand-averaged horizontal EOG waveforms by cued and target locations was less than 3 µV. Given that eye movements of about 1° of visual angle produce a deflection in the horizontal EOG of approximately 16 µV (Lins, Picton, Berg, & Scherg, 1993), the residual variation in the average horizontal EOG corresponds to variations in eye position of less than 0.2° of visual angle (i.e., smaller than the size of the fixation point).

Time-frequency analysis

Time-frequency analyses were performed using the Signal Processing toolbox and EEGLAB toolbox (Delorme & Makeig, 2004) for MATLAB (The Mathworks, Natick, MA). To isolate frequency-specific activity, we band-pass-filtered the raw EEG signal using a two-way least-squares finite-impulse-response filter (“eegfilt.m” from EEGLAB Toolbox; Delorme & Makeig, 2004). This filtering method uses a zero-phase forward and reverse operation, which ensures that phase values are not distorted, as can occur with forward-only filtering methods. A Hilbert transform (MATLAB Signal Processing Toolbox) was applied to the band-pass-filtered data, producing the complex analytic signal, z(t), of the filtered EEG, f (t):

$$z\left(t\right)=f\left(t\right)+i\stackrel{\sim }{f}\left(t\right),$$

where $i\stackrel{\sim }{f}\left(t\right)$ is the Hilbert transform of f (t), and $i=\sqrt{-1}$. The complex analytic signal was extracted for each electrode using the following MATLAB syntax:

$$\mathrm{hilbert}\left(\mathrm{eegfilt}\left(\mathrm{data},\mathrm{F},\mathrm{f}1,\mathrm{f}2\right)\prime \right)\prime$$

In this syntax, data is a 2-D matrix of raw EEG (number of trials × number of samples), F is the sampling frequency (250 Hz), f 1 is the lower bound of the filtered frequency band, and f 2 is the upper bound of the filtered frequency band. For alpha-band analyses, we used an 8- to 12-Hz band-pass filter; thus, f 1 and f 2 were 8 and 12, respectively. For the time-frequency analysis, we searched a broad range of frequencies (4–50 Hz, in increments of 1 Hz with a 1-Hz band pass). For these analyses, f 1 and f 2 were 4 and 5 to isolate 4- to 5-Hz activity, 5 and 6 to isolate 5- to 6-Hz activity, and so forth. Instantaneous power was computed by squaring the complex magnitude of the complex analytic signal.

Inverted encoding model

In keeping with our previous work on spatial working memory (Foster et al., 2016), we used an IEM to reconstruct location-selective CTFs from the topographic distribution of oscillatory power across electrodes. We assumed that power measured at each electrode reflected the weighted sum of eight spatial channels (i.e., neuronal populations), each tuned for a different angular location (see Brouwer & Heeger, 2009; Sprague & Serences, 2013). We modeled the response profile of each spatial channel across angular locations as a half sinusoid raised to the seventh power:

$$R=\sin {(0.5\theta )}^7,$$

where θ is angular location (ranging from 0° to 359°) and R is the response of the spatial channel in arbitrary units. This response profile was shifted circularly for each channel such that the peak response of each spatial channel was centered over one of the eight locations (corresponding to the cued locations 0°, 45°, 90°, etc., for Experiment 1 and the target locations 22.5°, 67.5°, 112.5°, etc., for Experiment 2; see Fig. 1a).

An IEM routine was applied to each time point in the alpha-band analyses and each time-frequency point in the time-frequency analysis.⁴ We partitioned our data into independent sets of training data and test data (for details, see the Training and Test Data section). The routine proceeded in two stages (training and test). In the training stage (Fig. 1b), the training data (B₁) were used to estimate weights that approximated the relative contributions of the eight spatial channels to the observed response (i.e., oscillatory power) measured at each electrode. We define B₁ (m electrodes × n₁ measurements) as a matrix of the power at each electrode for each measurement in the training set, C₁ (k channels × n₁ measurements) as a matrix of the predicted response of each spatial channel (specified by the basis function for that channel) for each measurement, and W (m electrodes × k channels) as a weight matrix that characterizes a linear mapping from channel space to electrode space. The relationships among B₁, C₁, and W can be described by a general linear model of the following form:

$$B_1=W{C}_1$$

The weight matrix was obtained via least squares estimation was as follows:

$$\widehat{W}=B_1{C_1}^T{\left(C_1{C_1}^T\right)}^{-1}$$

In the test stage (Fig. 1c), we inverted the model to transform the test data, B₂ (m electrodes × n₂ measurements), into estimated channel responses, $\widehat{C_2}$ (k channels × n₂ measurements), using the estimated weight matrix, $\widehat{W}$, that we obtained in the training phase:

$$\widehat{C_2}={\left({\widehat{W}}^T\widehat{W}\right)}^{-1}{\widehat{W}}^T{B}_2$$

Each estimated channel-response function was circularly shifted to a common center, so that the center channel was the channel tuned for the cued or target location (i.e., 0° on the channel offset axes of Figs. 2c and 2e). We then averaged these shifted channel-response functions to obtain the CTF averaged across the eight cued (or target) locations. The IEM routine was performed separately for each time point.

Finally, because the exact contributions of the spatial channels to electrode responses (i.e., the channel weights, W ) were expected to vary by subject, the IEM routine was applied separately for each subject, and statistical analyses were performed on the reconstructed CTFs. This approach allowed us to disregard differences in how location-selective activity was mapped to scalp-distributed patterns of power across subjects and instead focus on the profile of activity in the common stimulus, or information, space (Foster et al., 2016; Sprague et al., 2015).

Training and test data

For the IEM procedure, we partitioned artifact-free trials for each subject into independent sets of training data and test data. Specifically, we divided the trials into three sets. For each of these sets, we averaged power across trials for each cued location (Experiment 1) or target location (Experiment 2), which resulted in three 20 (electrodes) × 8 (locations) matrices of power values, one for each set. We used a leave-one-out cross-validation routine such that two of these matrices served as the training data (B₁, 20 electrodes × 16 measurements), and the remaining matrix served as the test data (B₂, 20 electrodes × 8 measurements). Because no trial belonged to more than one of the three sets, the training and test data were always independent. We applied the IEM routine using each of the three matrices as the test data, and the remaining two matrices as the training data. The resulting CTFs were averaged across the three test sets.

When we partitioned the trials into three sets, we constrained the assignment of trials to the sets so that all eight locations in all three sets had the same number of trials. To that end, we determined the minimum number of trials per subject for any location, n, and assigned n/3 trials for each location to each set. For example, if n was 100, we assigned 33 trials for each location to each set. Because of this constraint, some excess trials did not belong to any block. In Experiment 2, we compared CTFs across search conditions (easy or hard) and across trials with fast and slow RTs. To obtain a CTF for each condition separately, we partitioned each condition into three sets of data as described, which resulted in six sets in total (three for each condition). We constrained the assignment of trials as in Experiment 1. Note that this ensured that the same number of trials was used for each of the conditions.

We used an iterative approach to make use of all available trials. For each iteration, we randomly partitioned the trials into three sets (as just described) and performed the IEM routine on the resulting training and test data. We repeated this process of partitioning trials into sets multiple times (5 times for the full time-frequency analyses, 10 times for the alpha-band analyses, and 100 times for the latency analyses in Experiment 2). For each iteration, the subset of trials that were assigned to blocks was randomly selected. Therefore, the trials that were not included in any block were different for each iteration. We averaged the resulting channel-response profiles across iterations. This iterative approach reduced noise in the resulting CTFs by minimizing the influence of idiosyncrasies that were specific to any given assignment of trials to blocks.

Statistical analysis

Quantifying CTF selectivity

To quantify the location selectivity of CTFs, we used linear regression to estimate CTF slope (i.e., slope of channel response as a function of location channels after collapsing across channels that were equidistant from the channel tuned to the location of the evoking stimulus). Higher CTF slope indicates greater location selectivity.

Permutation test

In Experiment 1, to test whether CTF selectivity was reliably above chance, we tested whether CTF slope was greater than zero using a one-sample t test. Because mean CTF slope may not be normally distributed under the null hypothesis, we used a Monte Carlo randomization procedure to empirically approximate the null distribution of the t statistic. Specifically, we implemented the IEM as described earlier but randomized the location labels within each block so that the labels were random with respect to the observed responses in each electrode. This randomization procedure was repeated 1,000 times to obtain a null distribution of t statistics. To test whether the observed CTF selectivity was reliably above chance, we calculated the probability of obtaining (from the surrogate null distribution) a t statistic that was greater than or equal to the observed t statistic (i.e., the probability of a Type I error). Our permutation test was therefore a one-tailed test. CTF selectivity was deemed reliably above chance if the probability of a Type I error was less than .01. This testing procedure was applied to each time-frequency point in the time-frequency analyses and to each time point in the alpha-band analyses.

Jackknife test for latency differences

In Experiment 2, we tested for differences in CTF onset latency between easy-search and hard-search trials and between trials with fast RTs and trials with slow RTs. We used a jackknife-based procedure (Miller, Patterson, & Ulrich, 1998) to test for latency difference in CTF onset. CTF onset latency was measured as the earliest time at which CTF slope reached 50% of its maximum amplitude. The latency difference between conditions, D, was measured as the difference in onset latency between conditions in the time courses of the CTF slopes averaged across subjects. We used a jackknife procedure (Miller et al., 1998) to estimate the standard error of the latency difference, $S{E}_D$, from the latency differences obtained for subsamples that included all but one subject. Specifically, the latency differences, $D_{-i}$ (for i = 1, . . ., N, where N is the sample size), were calculated where $D_{-i}$ was the latency difference for the sample with all subjects except for subject i. The jackknife estimate of the $S{E}_D$ was calculated as

$$S{E}_D=\sqrt{\frac{N-1}{N}{\displaystyle {\sum }_{i=1}^N{\left(D_{-i}-\overline{J}\right)}^2}},$$

where $\overline{J}$ is the mean of the differences obtained for all subsamples (i.e., $\overline{J}={\displaystyle \sum D_{-i}/N}$).

A jackknifed t statistic, t_j, was then calculated as

$$t_j=\frac{D}{S{E}_D},$$

which follows an approximate t distribution with N – 1 degrees of freedom under the null hypothesis. Our jackknife tests for latency differences in CTF onsets were one-tailed because we had clear directional hypotheses: that CTF onset would be delayed for hard search compared with easy search and for trials with slow RTs compared with trials with fast RTs. The jackknife approach to testing for latency differences between conditions circumvents the need to calculate latency differences for individual subjects, which are often noisy because of the low signal-to-noise ratio of EEG data (Miller et al., 1998).

Experiment 1

Subjects in Experiment 1 performed a spatial-cuing task in which they identified a target digit among distractor letters (Fig. 2a). A central cue indicated the likely location of the target (valid on 87.5% of trials). We observed a robust spatial-cuing effect in the accuracy of target discrimination (Fig. 2b): Target-discrimination accuracy was higher on trials with a valid cue (M = 83.5%, SD = 9.5) than on those with an invalid cue (M = 36.9%, SD = 18.2), t(15) = 14.33, p < .001, Cohen’s dz $d_z$= 3.58.

Having established that the subjects attended the cued location, we tested whether the topography of alpha-band activity tracked shifts of covert attention to the cued location (collapsing across trials with valid and invalid cues). Using an IEM, we reconstructed spatial CTFs from the scalp distribution of alpha power. A spatially selective CTF emerged several hundred milliseconds after cue onset and was sustained until the search array was presented (Fig. 2c, top). Figure 2d shows CTF selectivity across time (quantified as CTF slope; see General Method). A permutation test revealed that CTF selectivity was reliably above chance beginning 304 ms after cue onset. Therefore, covert attention must have been shifted to the cued location by this time at the latest. The time course of the attention-related CTF dovetails with past behavioral work, which has shown that endogenously cued shifts of attention typically take 200 to 400 milliseconds to execute (Cheal & Lyon, 1991; Eriksen & Collins, 1969; Liu, Stevens, & Carrasco, 2007; H. J. Müller & Rabbitt, 1998; Nakayama & Mackeben, 1989; for review, see Egeth & Yantis, 1997).

Next, we examined whether alpha-band activity tracked the specific location that was attended. The alpha-band CTFs that we have reported so far reflected channel response profiles that were averaged across all possible cued locations. We did observe reliable spatial selectivity in the averaged CTF. Nevertheless, it is possible that the spatial selectivity of the averaged CTF reflects selectivity for some locations but not others, which leads to reliable spatial selectivity on average (Foster et al., 2016). Thus, we inspected the alpha-band CTFs for each cued location separately (Fig. 2c, bottom). For each location, the CTF peaked at the channel tuned for the cued location (i.e., a channel offset of 0°) starting approximately 300 ms after cue onset, which demonstrated that time-resolved alpha-band CTFs tracked which of the eight locations was attended. Thus, alpha-band activity tracks the locus of covert attention in a spatially precise fashion.

Alpha-band CTFs showed a graded response profile: The strongest response was in the channel tuned for the cued location, and responses steadily decreased across channels tuned for other locations (Fig. 2e, left). However, our standard set of basis functions (the basis set) specified a graded channel-response profile across locations. Therefore, the graded profile of alpha-band CTFs might be imposed by the graded basis function rather than reflecting truly graded spatially selective activity. To test this possibility, we reconstructed CTFs with the IEM again, with a basis set of Kronecker delta functions (stick functions; Foster et al., 2016). These basis functions do not specify a graded channel-response profile. Thus, a graded CTF profile seen when using this modified basis set necessarily reflects graded activity in the data itself rather than a pattern imposed by the basis function. Alternatively, if spatially selective alpha activity does not follow a graded format, then we should recover a peak in the channel tuned for the attended location and uniform responses across the other channels. Using this modified basis set, we found that alpha-band CTFs (averaged from 300 through 1,250 ms) showed a graded profile across channels (Fig. 2e, right), which demonstrated that the graded profile of alpha-band CTFs reflects the underlying spatial selectivity of covert spatial attention.

Having established that the topographic distribution of alpha power tracked the spatial locus of covert attention, we tested whether such spatially selective activity was specific to the alpha band (8–12 Hz). We used the IEM to search a range of frequencies (4–50 Hz, in increments of 1 Hz) across time to identify the frequency bands in which the topographic distribution of power carried information about the attended location (Fig. 2f). We found that spatially selective oscillatory activity was largely restricted to the alpha band.

Experiment 2

In Experiment 1, we showed that spatially selective CTFs can be reconstructed from the topographic distribution of alpha power after a central, attention-directing cue. This spatially selective activity emerged several hundred milliseconds after cue onset, so that it dovetailed with behavioral estimates of the time course of endogenous shifts of spatial attention (e.g., H. J. Müller & Rabbitt, 1998). Although this finding suggests that alpha-band CTFs track spatial attention in a temporally resolved fashion, a direct test requires a manipulation of covert orienting speed. Thus, in Experiment 2, we manipulated the speed of target selection during visual search. Subjects performed a visual search task in which they searched for a target (a horizontal or vertical bar) among distractors (Fig. 3a). We varied the difficulty of search by manipulating both distractor variability and target-distractor similarity (Duncan & Humphreys, 1989), and we measured reaction time to obtain a trial-by-trial estimate of the time taken to attend the target. This approach allowed us to test whether the time course of alpha-based CTFs tracked differences in the latency of target selection across different levels of search difficulty and as a function of within-subject differences in orienting latency across trials.

Figure 3b shows the aggregate RT distributions for easy and hard search. Our manipulation of search difficulty was effective: Median RTs were slower for hard search (M = 829 ms, SD = 153) than for easy search (M = 593 ms, SD = 71), t(22) = 12.31, p < .001, Cohen’s $d_z$dz = 2.57, and accuracy was lower for hard search (M = 91.7%, SD = 4.4) than for easy search (M = 97.0%, SD = 2.4), t(22) = 6.09, p < .001, Cohen’s $d_z$ = 1.27. We first tested whether alpha-band CTFs tracked orienting to the target location during the visual search task. As in Experiment 1, we quantified the spatial selectivity of alpha-band CTFs as CTF slope (see General Method). A spatially selective alpha-band CTF emerged soon after onset of the search array (Fig. 3c). A permutation test revealed that CTF selectivity was reliably above chance starting 196 ms after cue onset. Thus, alpha-band CTFs tracked covert orienting to the target’s location during visual search. To test whether alpha-band CTFs track the latency of covert orienting to the search target, we compared the onset latency of target-related CTFs between the easy- and hard-search conditions. To measure the difference in onset latency of target-related CTF between the search conditions, we used a jackknife-based procedure with a 50% maximum amplitude criterion (Miller et al., 1998; see General Method). The filled circles in Figure 3d mark the CTF onset estimates during easy and hard search. We found that the target-related CTF onset was 440 ms later for hard-search trials than for easy-search trials, t(22) = 2.48, p = .011, Cohen’s $d_z$dz = 0.52 (one-tailed test). Thus, the onset latency of the target-related CTF was delayed in hard search compared with easy search, which demonstrated that alpha-based CTFs revealed the difference in the latency of orienting attention to the target between the search conditions.

Although RTs were generally slower for the hard-search condition than for the easy-search condition, there was also considerable overlap in RTs between the easy- and hard-search conditions (Fig. 3b). This overlap was expected because target selection should sometimes occur very quickly during hard search, when the target happens to be one of the initial items to be selected. Given the overlap in RTs between conditions, we examined the onset latency of target-related CTFs split by RT, comparing the 50% of trials with the fastest RTs (fast trials) with the 50% of trials with the slowest RTs (slow trials), regardless of search condition (Fig. 3e). If alpha-band CTFs reveal the latency of target selection, CTF latency should covary with trial-by-trial reaction times. Indeed, we found that the target-related CTF onset was 372 ms later for slow trials than for fast trials, t(22) = 7.22, p < .001, Cohen’s $d_z$ = 1.51 (one-tailed test), which provides further evidence that the onset of target-related CTFs tracks the latency of covert orienting to the target item during visual search.

Discussion

The central role of covert spatial attention in visual cognition has motivated a sustained effort to elucidate the neural mechanisms that underpin this process. One productive avenue has been to examine the links between oscillatory alpha-band activity and spatial attention. A growing body of evidence has shown that the topographic distribution of alpha power tracks the locus of spatial attention (e.g., Kelly et al., 2006; Rihs et al., 2007; Thut et al., 2006; Worden et al., 2000), which suggests that alpha oscillations play a role in biasing visual processing toward attended locations (Foxe & Snyder, 2011; Jensen & Mazaheri, 2010). According to this view, the topographic distribution of alpha power should track the temporal dynamics of covert spatial attention. However, this prediction has not previously been subjected to a rigorous test.

Our findings provide a compelling confirmation of this prediction. In Experiment 1, we showed that variations in scalp distribution of alpha power enabled the reconstruction of spatially specific response profiles (i.e., CTFs) that track the endogenous orienting of spatial attention after a central cue. These alpha-band CTFs precisely discriminated the attended position beginning approximately 300 ms after the onset of the central cue, consistent with past estimates of the time taken to endogenously shift attention (e.g., H. J. Müller & Rabbitt, 1998; Nakayama & Mackeben, 1989; for review, see Egeth & Yantis, 1997). Critically, Experiment 2 extended this finding by showing that dynamic changes in alpha topography tracked the latency of covert orienting during visual search. The onset of alpha-band CTFs was delayed during difficult search compared with easy search and for trials with slow responses compared with trials with fast responses. Together these findings demonstrate that moment-by-moment changes in the topography of alpha-band activity track the temporal dynamics of covert spatial attention, which closes a significant gap in the evidence linking alpha activity with covert spatial orienting.

Experiment 2 also provides important evidence that spatially specific alpha-band activity plays a role in covert spatial attention in a range of paradigms. It has long been thought that covert spatial orienting plays a central role in visual search (e.g., Kim & Cave, 1995; Luck, Fan, & Hillyard, 1993). However, evidence linking alpha-band activity to covert orienting during visual search has been lacking because studies that have linked alpha-band activity with spatial attention have relied almost exclusively on spatial-cuing tasks (e.g., Thut et al., 2006; Worden et al., 2000). Our finding that alpha-band CTFs tracked the latency of orienting to a target during visual search provides clear evidence for the role of alpha-band activity in visual search. Thus, spatially specific alpha-band activity plays a general role in covert orienting in a range of paradigms.

Our findings also have important methodological implications for a field that has had a long-standing interest in the spatial and temporal dynamics of covert orienting (Egeth & Yantis, 1997). Early work relied on overt behavioral responses to probe these dynamics (e.g., Downing, 1988; H. J. Müller & Rabbitt, 1998). More recently, however, neural signals that track the allocation of attention have played a central role in this endeavor, in part because they circumvent the need for overt behavioral responses. Functional magnetic resonance imaging (fMRI) precisely tracks the spatial locus of covert attention (e.g., Brefczynski & DeYoe, 1999; Tootell et al., 1998) but provides little information about the time course of attention because of the slow hemodynamic response. Thus, researchers have relied on electrophysiological signals to examine the temporal dynamics of attention (e.g., Garcia, Srinivasan, & Serences, 2013; M. M. Müller, Teder-Sälejärvi, & Hillyard, 1998).

One productive approach has been to measure the consequences of spatial attention by examining stimulus-evoked potentials rather than directly measuring endogenous, attention-related activity. Sensory components that are amplified by spatial attention (e.g., the P1 component; Hillyard, Vogel, & Luck, 1998) have allowed researchers to probe the spatial allocation of attention. For example, Hopfinger and Mangun (1998) showed that the P1 response evoked by a probe stimulus was amplified after an exogenous spatial cue, which means that exogenous orienting shapes early stages of visual processing. However, although this approach has provided important insights into how and when attention modulates evoked visual responses, it does not reveal the time course of covert orienting before the evoking stimulus. To overcome this limitation, some studies have focused on the rhythmic brain activity—called a steady-state visual evoked potential—evoked by a flickering stimulus; this activity is amplified by spatial attention (Morgan, Hansen, & Hillyard, 1996). Thus, by examining the time course of amplitude modulations, it has been possible to measure the latency of orienting toward a flickering target (e.g., M. M. Müller et al., 1998). Nevertheless, stimulus-evoked approaches are not without limitations. Note that because these approaches rely on stimulus-evoked activity, they cannot be used to track attention to empty locations, which restricts the kinds of questions that can be addressed with these methods. Thus, there is much to be gained from a temporally resolved signal that tracks spatial attention in the absence stimulus-evoked activity.

Our findings suggest that spatially specific alpha-band activity provides such an opportunity. Alpha-band CTFs tracked the locus of covert spatial attention in balanced visual displays and in the absence of transient evoked activity, suggesting that spatially specific alpha-band activity reflects endogenous shifts of spatial attention rather than stimulus-evoked activity. Thus, given its spatial and temporal precision, this method provides a promising approach for obtaining a moment-by-moment index of the locus of covert attention across a broad range of paradigms.

Conclusions

In the current study, we showed that the topographic distribution of alpha-band activity tracked the spatial locus of covert attention after attention-directing cues and during visual search. These results demonstrate that alpha-band activity plays a central role in covert orienting in a range of paradigms. Critically, the time course of spatially specific alpha activity tracked trial-by-trial variations in the speed of covert orienting during visual search. Our results provide critical new evidence for the link between alpha-band activity and covert spatial attention.