Dichroism in Helicoidal Crystals

Abstract

Accounting for the interactions of light with heterogeneous, anisotropic, absorbing, optically active media is part of the characterization of complex, transparent materials. Stained biological structures in thin tissue sections share many of these features, but systematic optical analyses beyond the employ of the simple petrographic microscopes have not be established. Here, this accounting is made for polycrystalline, spherulitic bundles of twisted D-mannitol lamellae grown from melts containing light-absorbing molecules. It has long been known that a significant percentage of molecular crystals readily grow as helicoidal ribbons with mesoscale pitches, but a general appreciation of the commonality of these non-classical crystal forms has been lost. Helicoidal crystal twisting was typically assayed by analyzing refractivity modulation in the petrographic microscope. However, by growing twisted crystals from melts in the presence of dissolved, light-absorbing molecules, crystal twisting can be assayed by analyzing the dichroism, both linear and circular. The term “helicoidal dichroism” is used here to describe the optical consequences of anisotropic absorbers precessing around radii of twisted crystalline fibrils or lamellae. D-Mannitol twists in two polymorphic forms, α and δ. The two polymorphs, when grown from supercooled melts in the presence of a variety of histochemical stains and textile dyes, are strongly dichroic in linearly polarized white light. The bis-azo dye Chicago sky blue is modeled because it is most absorbing when parallel and perpendicular to the radial axes in the respective spherulitic polymorphs. Optical properties were measured using Mueller matrix imaging polarimetry and simulated by taking into account the microstructure of the lamellae. The optical analysis of the dyed, patterned polycrystals clarifies aspects of the mesostructure that can be difficult to extract from bundles of tightly packed fibrils.

Graphical Abstract

INTRODUCTION

The selective staining of cells with coal tar dyes is one of the great collective exercises in supramolecular chemistry.^1,2 However, stains used to diagnose disease were not often reduced to detailed understandings of non-covalent interactions, for which a prerequisite is a full accounting of the optical properties of materials that are typically anisotropic, absorbing, optically active, and heterogeneous both in the sample plane and along the direction of light propagation. Such an accounting can be complicated.³ Congo red stained amyloid plaques associated with Alzheimer’s disease are such structures that we have studied in the past.^4,5 They are anisotropic with a radial, spherulitic organization composed of twisted fibrils of laminated peptide sheets. Indeed, they fulfill the conditions of anisotropy, absorption, optical activity, and heterogeneity, but their characterization rarely⁶ goes beyond the declaration of their “apple-green birefringence”, a misnomer in any case. Here, we engineer a polycrystalline system with many of the features of the amyloid plaque, albeit on different length scales, and endeavor to characterize its light–matter interactions as completely as we are able. This work may be a starting point for comparable studie of pathological formations.

In fact, a great variety of crystals can be made to twist as they grow.^7,8 Among these are polycrystalline spherulites of the reduced hexose, D-mannitol,^9,10 composed of twisted lamellar fibrils. Here, we add light-absorbing molecules to the growth medium to add dichroism to the intrinsic optical complexity. Impurities or additives in crystals are critical for actualizing twisting in many cases.¹¹ Here, we evaluate additives that do not affect twisting but serve to assay the twisting. If helicoidal crystals are doped during growth with dye molecules^12–15 that are responsive to the crystal morphology, the anisotropy of the dye adsorption should give evidence of crystallographic twisting as the transition electric dipoles of the dye molecules precess around the twisting axes in spherulites composed of innumerable, radially oriented helicoids. We call the polarization dependence of dye absorption in twisted crystals helicoidal dichroism, and we analyze this phenomenon herein.

The study of twisted crystals in spherulitic aggregates began in the mineralogical literature.¹⁶ Wallerant was keen to bring the study of such dissymmetric crystals out of the ground and into the laboratory. In so doing, he pioneered the study of twisted molecular crystals including resorcinol, hydroquinone, glycolic acid, and malonamide grown from the melt.^17–19 Gaubert extended this work,^20–23 while adding dyes to the melts.^24–26 While he undoubtedly saw what we describe here as helicoidal dichroism, he did not have the wherewithal at that time to analyze the optics in detail.

RESULTS

Dyed Mannitol

We already had established that many dyes are highly soluble in molten D-sorbitol and that they can be oriented during crystallization from the melt.²⁷ As a result, the absorption was highly polarization dependent in the absorption band of the dye.

D-Mannitol is a stereoisomer of D-sorbitol with opposite configuration at C5. Three polymorphs have been characterized: α, β, and δ. Only α and δ grow from the melt. α- and δ-mannitol crystallize in the space groups P2₁2₁2₁ and P2₁, respectively (Figure 1).²⁸

Figure 1.

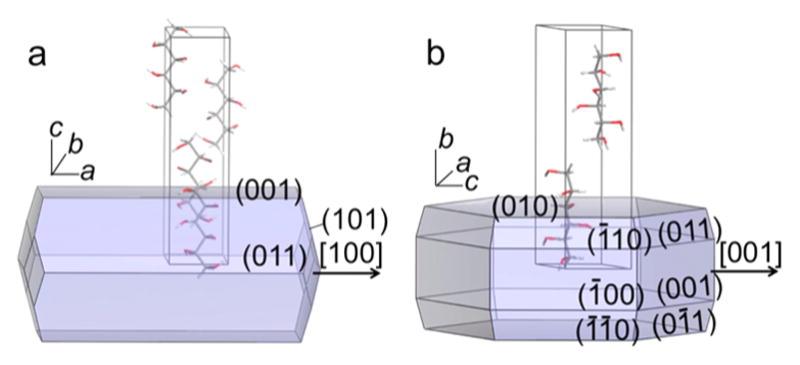
Predicted Bravais–Friedel–Donnay–Harker (BFDH) morphologies and unit cells of (a) α-mannitol and (b) δ-mannitol. The arrows indicate the radial directions in spherulties not shown here. α lattice constants at 100 K: a = 4.8653(10) Å, b = 8.873(2) Å, c = 18.739(5) Å. δ lattice constants at 100 K: a = 4.899(2) Å, b = 18.268(2) Å, c = 5.043(2) Å, and β = 118.39(2)°.²⁸

The α and δ phases of D-mannitol grow as spherulites in the presence of additives (e.g., polyvinylpyrrolidone (PVP)¹⁰ or even D-sorbitol⁹) with concentric bands of optical contrast in the petrographic microscope. This is a telltale sign of twisting along the spherulite radii, a consequence of the precession of the optical indicatrix. Previously we observed that thin lamellae alternate between edge-on and flat-on orientations.⁹ The refractive indices of α- and δ-mannitol single crystals at 589 nm are as follows: (α) N_X = 1.526, N_Y = 1.536, N_Z = 1.540 and (δ) N_X = 1.548, N_Y = 1.545, N_Z = 1.550.²⁹ α-Spherulites direct the refractive index N_Y radially (〈100〉), with {001} as the flat-on orientation, N_X||〈010〉. δ-Mannitol spherulites direct N_Z radially (〈001〉) with {010} as the flat-on orientation, N_Y||〈010〉 (Figure 1).

Mannitol, like sorbitol, forms homogeneous, highly colored melts when admixed with a variety of histochemical stains and textile dyes. Dyes were premixed with PVP (15 wt% with respect to mannitol) powder by evaporation of ethanol solution droplets. The dyed PVP powders were mixed with mannitol (85 wt%) by grinding in a ceramic mortar and pestle for ca. 2 min. Several milligrams of a mixed powder of D-mannitol with 15 wt% PVP and <1 wt% of a dye was melted on a glass slide beneath a cover glass at 180 °C. Melts of the mixtures were quenched at 90–105 °C to yield banded spherulites of the α-polymorph, or at 95–110 °C to give the δ-polymorph. Periodic radial oscillations (half-pitch) of α- and δ-mannitol were 30 μm for α and 10 μm for δ with the corresponding radii about 0.2–4.0 mm for α and 0.1–0.8 mm for δ grown at 100 °C. The dyes included 0.5 wt% of DAM⁺I⁻ (4-[2-(4-dimethylaminophenyl)-vinyl]-1-methyl-pyridinium iodide, CAS Registry No. 959-81-9) and MB⁺Cl⁻ (methylene blue chloride, CI# 52015). Like sorbitol, the resulting spherulites are invariably linearly dichroic (Figure 2). Each spherulite is composed of bundles of twisted lamellae. When pressed between glass slides the spherulites become flattened and disk-like, with helicoids oriented radially. The schematic structure of a spherulite is shown in Figure 2d. Dyes that formed colored, linearly dichroic mannitol spherulites are listed in the Supporting Information (SI), Table S1. In almost all cases, the transition moments of the dye molecules are radial as was seen for dyed sorbitol spherulites.²⁷ However, CSB⁴⁻4Na⁺ (Chicago sky blue 6B tetrasodium salt, CAS Registry No. 2610-05-1, CI# 24410) is intriguing because the transition moment of the chromophore, essentially parallel to the long molecular axis,³⁰ is radial in α- and tangential in δ-mannitol. This difference is shown schematically in Figure 3. For this reason, CSB (from here out we drop the charges for notational simplicity) embodies the full range of optical phenomenology and is thereby analyzed in detail.

Figure 2.

Plane view of dyed, banded mannitol spherulites with 0.5 wt % (a) DAM, (b) MB and (c) CSB in α- and δ-polymorphs of _D-mannitol in horizontally polarized (double arrow) white light. (d) Scheme of a banded spherulite. The dotted arrows represent the radial growth directions from the dot in the center of the spherulite, the site of nucleation. The dotted circle is the growth front of the spherulite, with the tangential direction labeled as a double arrow.

Figure 3.

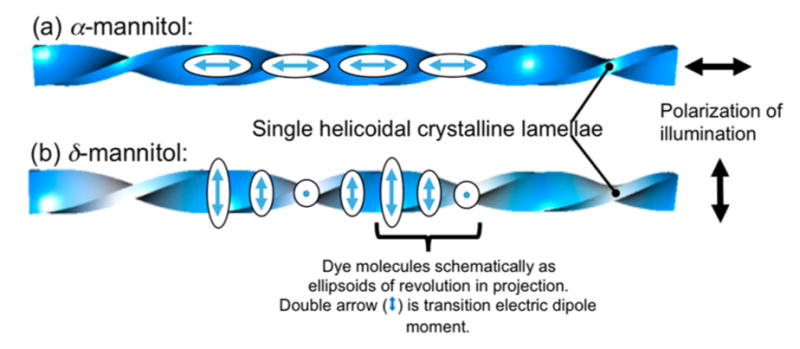
Dyed helicoidal lamellae and/or bundles of lamellae viewed normal to the long axes with (a) radially and (b) tangentially aligned dye molecules along helicoids with horizontal and vertical polarized light (double arrows on the right), respectively. Here, tangential is in reference to the spherulite growth front (see Figure 2d). The projections of the transition electric dipoles (long ellipsoid axes) are superimposed onto the corresponding regions of the dyed lamellae. The color of the helicoids qualitatively represents the observed color in the corresponding regions with aligned dye molecules in (a) horizontally and (b) vertically polarized light. In (a) there will be a slight modulation of the dye orientation at the edges of the helicoid, but not along the spine. In this schematic we are emphasizing the spine.

The radial vs tangential polarization can be used to readily distinguish the polymorphs from one another in linearly polarized illumination. Interactions between dyes and crystals have been used previously to distinguish polymorphs.³¹ CSB has a λ_max of 620 nm in mannitol/PVP melts. Ring-banded mannitol spherulites dyed with CSB absorb at lower energy (1.952 eV (635 nm) in α, 1.937 eV (640 nm) in δ). δ-Mannitol tends to promote dye dimerization as compared with melts or α-mannitol (SI, Figure S1). Typically the δ-polymorph forms first but eventually nucleates α, which produces a corona (Figure 2).^10,32,33

Mueller Matrix Polarimetry

“Complete polarimetry” refers to techniques for measuring the entire 16 element polarization transfer matrix, also known as the Mueller matrix. It is delivered in the application of Stokes–Mueller calculus to optical systems.^34,35 Unlike the Jones calculus, the Stokes–Mueller method is better adapted to imperfect complex crystalline samples.

The four-element Stokes vector, S, can describe any arbitrary time-averaged polarization state of light. A transformation of the polarization state by interaction with a specimen can be written as S_out = MS_in, where M is the 4×4 Mueller matrix associated with a specific wavelength distribution of light propagating in a particular direction through the specimen. As S is a time-averaged quantity, it can describe light that is not completely polarized (having some degree of random polarization). If M leaves the degree of polarization unchanged, M is said to be non-depolarizing, and the 16 independent parameters of M usually reduce to only seven.³⁶ The seven parameters populate the elements of the so-called generating matrix L,^37,38 which is connected to M by the matrix exponential, M = exp L, where

$$\mathbf{L}=\left[\begin{array}{llll}{L}_7& L_1& L_2& L_3\\ L_1& L_7& L_4& -L_5\\ L_2& -L_4& L_7& L_6\\ L_3& L_5& -L_6& L_7\end{array}\right]$$ (1)

For the special case of a homogeneous medium (i.e., a crystal) with plane-parallel interfaces measured at normal incidence, the elements of L are directly related to projections of the complex refractive indices of the crystal. The parameters take the names linear dichroism (LD and LD′), linear birefringence (LB and LB′), circular dichroism (CD), and circular birefringence (CB), defined as follows:

$$\begin{gathered} L_1\equiv -\text{LD}=-k({\kappa }_{0°}-{\kappa }_{90°}) \\ {L}_2\equiv -\mathrm{L}{\mathrm{D}}^{\prime }=-k({\kappa }_{45°}-{\kappa }_{135°}) \\ {L}_3\equiv \text{CD}=k({\kappa }_{\mathrm{L}}-{\kappa }_{\mathrm{R}}) \\ {L}_4\equiv -\text{CB}=k(n_{\mathrm{L}}-n_{\mathrm{R}}) \\ {L}_5\equiv -\mathrm{L}{\mathrm{B}}^{\prime }=-k(n_{45°}-n_{135°}) \\ {L}_6\equiv -\text{LB}=-k(n_{0°}-n_{90°}) \\ {L}_7\equiv -A=-\sqrt{{\text{LD}}^2+{\mathrm{L}{\mathrm{D}}^{\prime }}^2+{\text{CD}}^2}-k{\kappa }_{\text{iso}} \end{gathered}$$ (2)

where k = 2πd/λ is the propagation constant in terms of the path length (d) and wavelength of light (λ). Variables n and κ are, respectively, refractive indices and extinction coefficients experienced by the states of polarization denoted in subscripts; numerical values refer to the azimuthal angle of a linearly polarized wave measured counterclockwise from the horizon, while L and R refer to left- and right-circularly polarized waves. The last equation gives the total absorption of the medium, which has been written as the sum of the total anisotropic absorption and the isotropic absorption (κ_iso).

All 16 elements of M were measured simultaneously using home-built polarimeters described previously.^39–41 Measurements were performed at different wavelengths with light normally incident on the substrate. We observed negligible depolarization, thus permitting a reduction of M to a matrix L having the form in eq 1. Because spherulites are heterogeneous along the light path, the seven parameters of this generating matrix do not correspond to the definitions in eq 2 for homogeneous media, nonetheless, the parameters are a convenient basis for the optical effects of the ensemble. Exactness of definitions notwithstanding, we will use the labels CD, CB, LD, and LB for the elements of L to be consistent with our prior reports on spherulites. We will also make use of the polar expressions of the linear pairs, namely,

$$\begin{array}{ll}\hfill \mid \text{LB}\mid =\sqrt{{\text{LB}}^2+{\mathrm{L}{\mathrm{B}}^{\prime }}^2},& {\text{LB}}_{\text{angle}}=\frac{1}{2}\text{atan}2(\mathrm{L}{\mathrm{B}}^{\prime },\text{LB})\hfill \\ \hfill \mid \text{LD}\mid =\sqrt{{\text{LD}}^2+{\mathrm{L}{\mathrm{D}}^{\prime }}^2},& {\text{LD}}_{\text{angle}}=\frac{1}{2}\text{atan}2(\mathrm{L}{\mathrm{D}}^{\prime },\text{LD})\hfill \end{array}$$ (3)

where atan2 refers to the four-quadrant arctangent function.

Recently, we introduced Mueller matrix polarimetry^35,42,43 to the study of banded spherulites because it can simultaneously measure all of the aforementioned optical effects.^9,44 In banded spherulites, the concentric rings of oscillating LB have been well studied and are generally recognized as a result of helical twisting of crystalline fibers with anisotropic refraction.⁴⁵ We have shown that many such systems also show oscillating CB.⁴⁶ This is not natural optical activity as it occurs even in centric crystal systems. Rather, is a distinct feature of misoriented anisotropic lamellae, a phenomenon that originates from twisting under confinement.⁴⁶ It is a characteristic of the mesoscale organization of anisotropic components. Such artificial optical activity has also been observed in polylactide spherulites when the light path is inhomogeneous with stacked, misoriented lamellae⁴⁷ or in rhythmic deposits of phthalic acid.⁴⁸

The intensity and orientation of LD is different for the two polymorphs: |LD| is typically stronger in α-mannitol with the transition electric dipole moments nearly parallel to the radial direction of the twisted fibers rather than perpendicular. The similar |LD|_max in the two polymorphs indicates the same maximum projection in the two polymorphs, as we quantitatively analyzed in later sections (see Figure 7). The eye-catching difference in |LD| in different polymorphs is mainly due to the averaged difference in the projection of dye molecules: the projection is always close to maximum in α-mannitol, while oscillating between the maximum and near zero in δ-mannitol (Figure 3). Regardless, the orientation of dye molecules, oscillating |LB|, |LD|, CB and CD were observed for CSB in α- and δ-mannitol (Figure 4).

Figure 7.

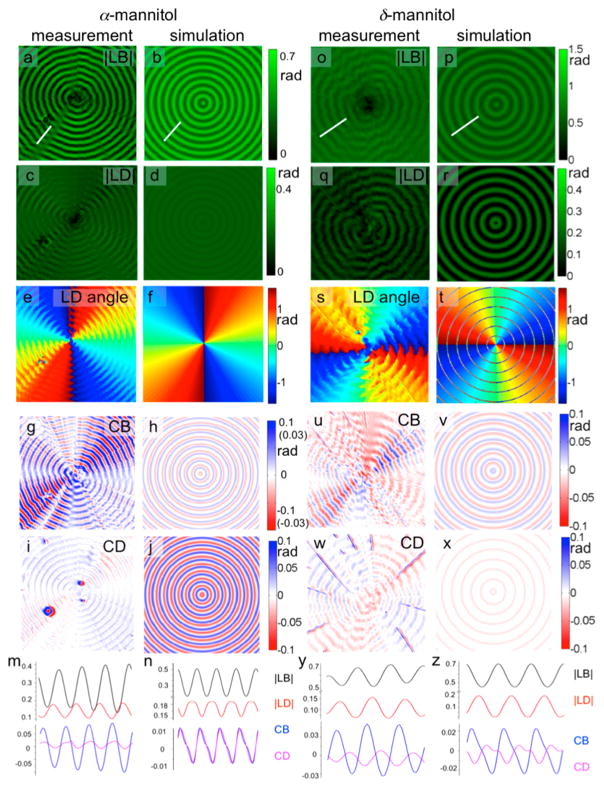
Experimental and simulated optical results of CSB dyed banded α- and δ-mannitol (c_PVP = 15 wt%, c_CSB = 0.5 wt%, T_crystal = 95 °C (α-) and 110 °C (δ-), λ = 630 nm): measured |LB| (a,o) |LD| (c,q), LD angle (e,s), CB (g,u), CD (i,w), and the extracted optical properties along the white lines in the |LB| image for α- and δ-mannitol and the corresponding simulation results on their right. All the units are in radians. Parameters used in the simulation for α-mannitol: N = 9, B = −i0.022, Φ_dye = ±10°, Θ_dye = ±80°, Ψ = 15°; and for δ-mannitol: N = 9, B = −i0.025, Φ_dye = ±70°, Θ_dye = ± 20°, Ψ = 15°. The measured CB and CD are not azimuthally invariant. We expect them to be. The deviations from circular symmetry are more pronounced in Mueller matrix element M₄₁ than in M₁₄. We do not understand this aspect of the images at present.

Figure 4.

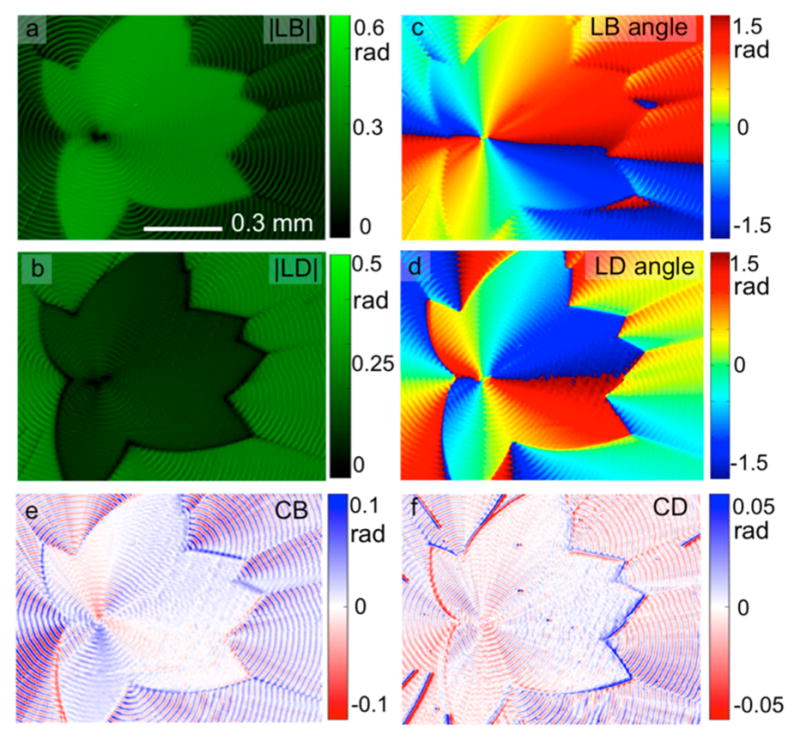
Images derived from the matrix L for CSB (c_CSB = 0.5 wt %)-dyed mannitol spherulites (c_PVP = 15 wt%, crystallize at 100 °C) at 630 nm: (a) |LB|, (b) |LD|, (c) LB angle (measured counterclockwise from + x), (d) LD angle, (e) CB and (f) CD images. The inner part is the δ-polymorph, and the outer part is the α-polymorph.

Dichroism in undoped spherulites comprised of transparent crystals is usually a consequence of scattering that can be thought to arise from Fresnel reflection amplified at many interfaces. This scattering is best thought of phenomenologically as extinction rather than absorption. In former times, dichroism in colorless polycrystalline media was called pseudopolychroism.⁴⁹ (SI, Figures S2 and S3) In dyed mannitol spherulites, the oscillating birefringence (LB and CB) is comparable to undyed spherulites, however, the dichroism (LD and CD) is obviously much higher; the maximum |LD| increased from 0.02–0.04 rad to 0.15–0.20 rad, and the maximum CD increased from 0.003–0.005 rad to 0.01–0.02 rad after the incorporation of CSB (Figure 4 and SI, Figures S2 and S3). The highly aligned transition electric dipole moments of CSB molecules contribute to the increased |LD| while the CD likewise must arise in the main in the added dyes (see below).

DISCUSSION

Simulation of Optical Properties

The measured optical properties are related to the mesostructures of banded spherulites, albeit this relationship is not straightforward. Thus, matching the measured optical properties with the expectations of a particular structural model is necessary to fit the data. Spherulite growth can be remarkably regular in its totality but it is locally stochastic with small angle branching and nucleation of new fibrils that are far from deterministic. We cannot consider geometrical models based on precise parameters, we can only consider average values. We have constructed a simple model based on only two mean geometrical parameters, ω and φ (see Figure 5). The parameter ω gives the mean twist angle as a function of the distance from the core, r, as ω = 2πr/l, where l is the average distance between bands (the parameter ω is the same quantity as the parameter α in ref 46). The second parameter φ gives the splay of the lamella, defined as the average azimuthal rotation of a lamella from the mean radii along which it grows. It is a function of ω, and the depth in the spherulite.

Figure 5.

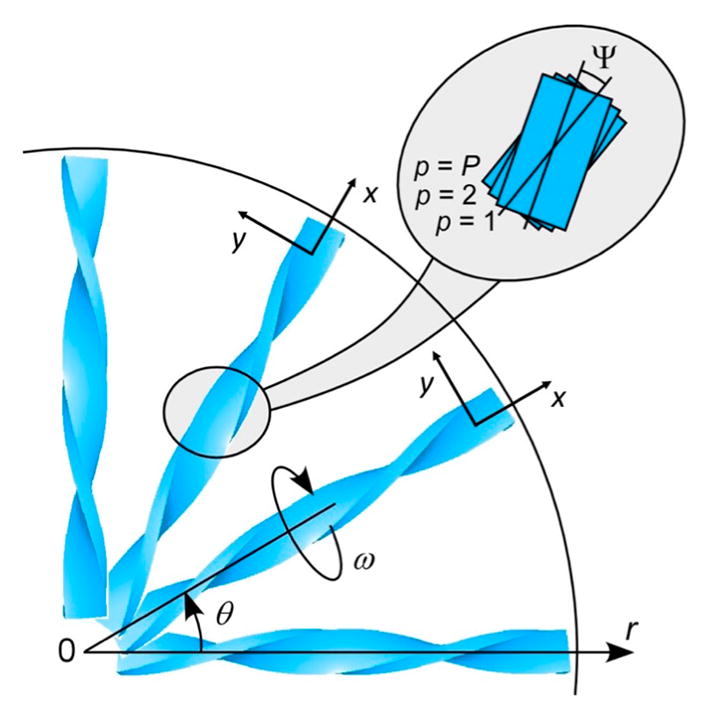
Scheme of one-quarter of a banded spherulite in polar (r,θ) coordinates. Each helicoid represent a bundle of thinner ribbons. In reality, the fibrils branch and nucleated new crystallites, filling the open spaces. The enlarged region highlights the misalignment of P layers of lamellae in each bundle with Ψ.

At edge-on and flat-on crystal orientations, growth directions of neighboring lamellae are precisely collinear and the splay is zero, but at intermediate positions, space limitations force lamellae to move away from each another, inducing splay. If we split the medium into P layers, the average splay φ in layer p is modeled as

$${\phi }_p=sin(2\omega )\mathrm{\Psi }\left(\frac{p-1}{P-1}-\frac{1}{2}\right)$$ (4)

for the maximum misorientation angle Ψ.⁴⁶ Light is considered to pass through layers in the order p = 1, 2, …, P

We set each bundle of lamellae in its own Cartesian coordinate system where the x-axis is along its radial direction and the z-axis is pointing out of paper. The electric permittivity tensor of layer p in the radial direction having angle θ from the x-axis is

$$\begin{gathered} {\mathbf{\epsilon }}_p={\mathbf{R}}_p\left(\left[\begin{array}{lll}{n_x}^2\hfill & 0\hfill & 0\hfill \\ 0\hfill & {n_y}^2\hfill & 0\hfill \\ 0\hfill & 0\hfill & {n_z}^2\hfill \end{array}\right]+\sum _q{[B(\mathit{u}\otimes \mathit{u})]}_q\right){\mathbf{R}}_p^{\mathrm{T}} \\ {\mathbf{R}}_p={\mathbf{R}}_z(\theta +{\phi }_p){\mathbf{R}}_x(\omega ) \end{gathered}$$ (5)

where n_x, n_y, and n_z refer to ambient refractive indices of undyed material in the calculation coordinate system at ω = 0. The term summed over q represents contributions from q uncoupled oscillators that represent the dye inclusion. Each oscillator is oriented by u, a unit-vector parallel to the transition electric dipole moment of the oscillator, and each contributes a dyadic tensor, defined by the outer product ⊗, to the total permittivity that is scaled by B, a wavelength dependent complex valued oscillator amplitude. B(u⊗u) gives rise to the differential Mueller matrix parameters L₁ (LD), L₂ (LD′), and L₃ (CD) in eq 2. The effect of extinction due to scattering is small in comparison. In our simulations, we neglect effects from the interfaces, as methods that are more exact⁵⁰ did not significantly change the features of our simulations. Matrices R_r(t) denote passive Euler rotations around the axis r by an angle t. Our sign convention requires that the imaginary part of B, which is related to absorption, should be given as a negative number. The real part of B is a contribution to dispersion; it is usually small at the wavelength corresponding to the maximum absorbance of a dye that has only a single dominant electronic transition as for CSB.

To describe the effect of bulk propagation in a single layer on the incident wave-vector k along the z-axis, we construct the Jones matrix

$${\mathbf{J}}_p=\left[\begin{array}{cc}{\mathrm{\epsilon }}_{1,1}-{\mathrm{\epsilon }}_{2,3}^2/{\mathrm{\epsilon }}_{3,3}& {\mathrm{\epsilon }}_{1,2}-{\mathrm{\epsilon }}_{1,3}{\mathrm{\epsilon }}_{2,3}/{\mathrm{\epsilon }}_{3,3}\\ {\mathrm{\epsilon }}_{1,2}-{\mathrm{\epsilon }}_{1,3}{\mathrm{\epsilon }}_{2,3}/{\mathrm{\epsilon }}_{3,3}& {\mathrm{\epsilon }}_{2,2}-{\mathrm{\epsilon }}_{2,3}^2/{\mathrm{\epsilon }}_{3,3}\end{array}\right]$$ (6)

from the elements of the tensor ε.⁵¹ This matrix can be written as the eigen decomposition:

$${\mathbf{J}}_p=\mathbf{V}\left[\begin{array}{cc}exp(-\mathit{ikd}\sqrt{{\mathrm{\Lambda }}_1})& 0\\ 0& exp(-\mathit{ikd}\sqrt{{\mathrm{\Lambda }}_2})\end{array}\right]{\mathbf{V}}^{-1}$$ (7)

where V is the eigenvector matrix of J_p, with corresponding eigenvalues Λ₁ and Λ₂. Again, k is the propagation constant, and d is the path length. The refractive indices experienced by the two forward propagating eigenwaves in a layer are given by $n_1=\sqrt{{\mathrm{\Lambda }}_1}$ and $n_2=\sqrt{{\mathrm{\Lambda }}_2}$. The overall Jones matrix is the ordered product J = ∏_pJ_p, where J_p is the Jones matrix of the pth lamella in a group. The transformation,

$$\begin{gathered} \mathbf{M}=\mathbf{A}(\mathbf{J}\otimes \mathbf{J}){\mathbf{A}}^{†} \\ \mathbf{A}=\frac{1}{\sqrt{2}}\left[\begin{array}{cccc}1& 0& 0& 1\\ 1& 0& 0& -1\\ 0& 1& 1& 0\\ 0& i& -i& 0\end{array}\right] \end{gathered}$$ (8)

converts a Jones matrix to a Mueller matrix, where † denotes the conjugate transpose. The overall M for any location on the spherulite can be reduced to a seven-parameter generating matrix L either numerically, using L = ln M, or using analytic equations.⁵²

We can now simulate two extreme situations corresponding to the two CSB polymorphs: u is radial or tangential (SI, Figure S7). The simulations parameters for α-mannitol with CSB were P = 9, Ψ = 5°, [n_x, n_y, n_z] = [1.540, 1.526,1.536], k = 29.92, u = [1,0,0], B = 0.01 − i0.05; those for δ-mannitol with CSB differed in [n_x, n_y, n_z] = [1.550, 1.548,1.545], u = [0,1,0]. The Mueller matrices M are given in the SI, Figures S5 and S6. The summation of elements M₁₁ and M₁₂ gives the total transmission of an absorbing medium under a horizontal polarizer. When the transition moment of dye is aligned radially (SI, Figure S5), this sum simulates what is seen in a CSB-dyed α-mannitol spherulite (Figure 2c) in horizontally polarized light. The banding is still evident even along the horizontal, which means there must be a small component of u that is non-radial either from intrinsic twisting of helicoids or dye misorientation. The simulated transmission images of spherulites with different dye orientations are available in SI, Figure S8.

The differential Mueller matrix (eqs 1 and 2) is analyzed in detail. For the spherulite where the transition electric dipole moment of dye molecules is tangential, the absorbance oscillates maximally along the fiber growth direction (SI, Figure S7a). The radial oscillation of LB is the result of the rotations of fibers, while the oscillation of LD is from the rotation of aligned dye molecules. CB in banded spherulites originates from the systematic misalignment between adjacent birefringent fibers in confined space as discussed above.⁴⁶ For the misaligned fibers with strong intrinsic LD, there is also an oscillation of the CD as was seen previously.³⁹

In the extreme case of radial alignment, it is not surprising that the resulting LD in the simulated matrix L is constant along radii (Figure S7b). However, due to misalignment, there is still a small radial oscillation in the resulting LD (albeit not discernible in L₁₂, L₁₃ in Figure S7b at the scale of reproduction, see SI, Figure S9). Oscillating LB, CB and CD are also observed. Thus, regardless of the orientation of aligned dye molecules, oscillating birefringences and dichroisms are distinct features in dyed banded spherulites.

Comparison with Experimental Results

Polarized light micrographs of CSB in mannitol crystallites were simulated for both α- and δ-mannitol (Figure 6). In α- and δ-D-mannitol, best fits between observations in polarized light and simulations of micrographs were achieved with small offsets of ca. 10° and 20° respectively in both Φ_dye and Θ_dye in the flat-on orientations (Figure 6). Angles refer to an expression of u in a spherical coordinate system (R,Θ,Φ), where

Figure 6.

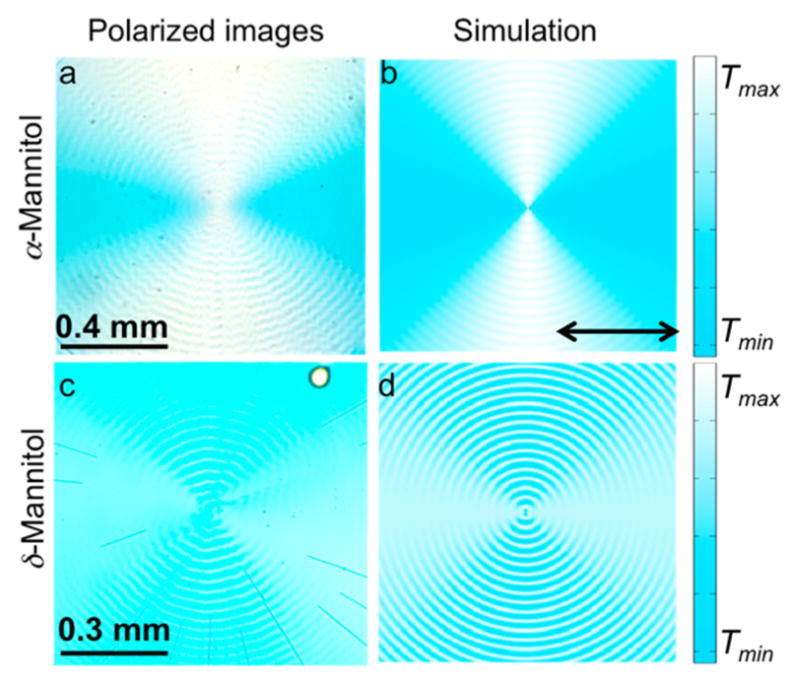
Images in horizontal linearly polarized light of (a) banded α-mannitol spherulites and (c) banded δ-mannitol spherulites containing 0.5 wt% CSB, 15 wt% PVP grown at 100 °C and the simulated transmission images with dyes oriented at (b) Φ_dye = ±10° and Θ_dye = ±80° and (d) Φ_dye = ±70° and Θ_dye = ±20°. T = normalized transmittance. The color in the simulations was chosen to match what is observed by the eye.

$$\begin{gathered} u_x=cos{\mathrm{\Phi }}_{\text{dye}}sin{\mathrm{\Theta }}_{\text{dye}} \\ {u}_y=sin{\mathrm{\Phi }}_{\text{dye}}sin{\mathrm{\Theta }}_{\text{dye}} \\ {u}_z=cos{\mathrm{\Theta }}_{\text{dye}} \end{gathered}$$ (9)

The parameter Θ_dye also accounts for the fact that the orientations of dyes in the radial case (Figure 3a) vary from the spine of a helicoid to the edges. Likewise, the parameter Φ_dye takes into account intrinsic variance in inclination (Figure 3b). These modulations are not indicated in the schematic Figure 3. Both of these intrinsic modulations of dye orientation induced by twisting, as well as imperfect dye alignments or multiple dye orientations, will give some ellipticity to the absorbance of any one helicoid at any point along the helix axis. The simulations are indifferent to the origin of this elliptical absorption.

In banded spherulites, the |LB| for each crystalline fiber, as well as the misalignment angle between adjacent fibers, are required for simulating the CB.⁴⁶ LD and CD additionally require specification of the parameters related to the dye (B, Φ_dye, and Θ_dye).

CSB-dyed α- and δ-mannitol was simulated under the assumption of nine lamellae, a judgment drawn from AFM and SEM data.⁹ For α-mannitol, the helicoidally twisted crystals are simulated with P = 9, k = 29.92, total misalignment Ψ = 15°, [n_x, n_y, n_z] = [1.540,1.526,1.536], B = −i0.022, Φ_dye = ±10° and Θ_dye = ±80°. The parameters in δ-mannitol are the same as for [n_x, n_y, n_z] = [1.550,1.548,1.545], B = −i0.025, Φ_dye = ±70°, and Θ_dye = ±20°.

Oscillating |LB|, |LD|, CB and CD with same period are observed in both experiment and simulation of CSB in α- and δ-mannitol. The twisting period and phase of the oscillating |LB| and CB were in accord with other banded spherulites.⁴⁶ The oscillation in |LD| was well matched by simulation (Figure 7m and n; y and z) for both nearly radial and tangential CSB alignment. In δ-mannitol, u is predominantly tangential, irrespective of where in the twist period we sit, except for sharp bands that given rings of opposite orientations in Figure 7t (but only in the simulation which has perfect coherence between crystallites). Albeit, at present we can not say with confidence what aspects of the molecular recognition events give rise to near orthogonal CSB orientations when the mannitol molecules are normal to the radii in both polymorphs.

CB and CD are in phase in α-mannitol and out of phase in δ-mannitol, which has also been observed in simulation (Figure 7g–j and u–x). Simulated CD resembles the measured CD in intensity, phase and twisting period in both polymorphs. In sum, the helicoidal dichroism (LD and CD) in such complicated polycrystalline ensembles can be recovered by the optical analysis described herein.

OUTLOOK

The brilliant interference colors for which the petrographic microscope famously produces images that routinely win scientific art contests is less well adapted to identifying properties of complex media whose effects on the polarization state of light are convolved. Mueller matrix imaging polarimetry is a tool for the analysis of the light–matter interactions of complex, anisotropic, heterogeneous, optically active, absorbing chemical systems by virtue of its ability to separate various influences from one another. Many stained, thin film biological preparations (e.g. tissue sections that are a mainstay of pathology) have these characteristics. The crystals that we designed or engineered for this study were intended to mimic stained, anisotropic, helicoidally twisted ribbons that compose biopathological amyloid plaques.^4,5

Here, differential polarization imaging was used to assay the microstructure of bundles of thin crystalline lamellae in mats of twisted crystallites. The optical properties of the helicoidal crystals with dye molecules precessing along and around the growth directions are used to assay microstructure by simulation on the basis of informed structural models. Herein, the helicoidal dichroism turns out to be a general consequence of the systematic misoriented dichroic crystallites in banded spherulites.

In addition to mannitol,⁹ previously we have studied the process of crystal twisting at length in hippuric acid,^44,53 resorcinol,^11,54 and aspirin,⁵⁵ among other systems, in transparent spectral regions.⁴⁶ It is well known that twisting in spherulites is a common feature of high-polymer crystallization, and it has been most well studied for macromolecules.^56–58 The spherulites composed of twisted fibrils of these materials can likewise be colored, and similar phenomena arise, illustrating that our model for bundles of twisted lamellae has general features that provide insights into non-classical crystal morphologies and growth mechanisms generally speaking. Dichroism in its fullest manifestation can be an incisive probe of complex morphologies.