Links Between Causal Effects and Causal Association for Surrogacy Evaluation in a Gaussian Setting

Abstract

Two paradigms for the evaluation of surrogate markers in randomized clinical trials have been proposed: the causal effects (CE) paradigm and the causal association (CA) paradigm [1]. Each of these paradigms rely on assumptions that must be made in order to proceed with estimation and to validate a candidate surrogate marker (S) for the true outcome of interest (T). We consider the setting in which S and T are Gaussian and are generated from structural models that include an unobserved confounder. Under the assumed structural models, we relate the quantities used to evaluate surrogacy within both the CE and CA frameworks. We review some of the common assumptions made in order to aid in estimating these quantities and show that assumptions made within one framework can imply strong assumptions within the alternative framework. We demonstrate that there is a similarity, but not exact correspondence between the quantities used to evaluate surrogacy within each framework and show that the conditions for identifiability of the surrogacy parameters are different from the conditions which lead to a correspondence of these quantities.

1. Introduction

The validation of an intermediate marker (S) as a surrogate marker for the true outcome of interest (T) in clinical trials has attracted much attention [2–4]. An intermediate marker shown to be a valid surrogate would allow trials to be run more cheaply and quickly by basing analyses on the earlier or more cheaply measured surrogate. To use an example we will refer to throughout this paper, in a clinical trial assessing the efficacy of a new therapy on lengthening overall survival (OS) time in ovarian cancer, the duration of the trial could be reduced if the treatment effect on progression free survival (PFS) time could be used to infer a treatment effect on OS time. However, in practice demonstrating the validity of a surrogate marker has proven challenging, possibly due to the disease process affecting T through pathways not mediated through the surrogate, or due to unobserved confounders, U, of S and T [5]. For instance, suppose PFS time (S) is being assessed as a surrogate marker for OS time (T) in ovarian cancer patients in a trial with a binary treatment (Z), where Z = 0 is standard of care and Z = 1 is a new treatment. If patients experiencing longer PFS are also more likely to eat a healthy diet (U) which is also associated with longer OS, a treatment that prolonged PFS would also appear to prolong OS, indicating PFS as a potentially valid surrogate marker even though the survival benefit was not due to the induced treatment effect on PFS.

Several causal frameworks have been explored to identify intermediate markers as valid surrogates. Joffe and Greene [1] group these frameworks into two paradigms. The first, termed the “causal-effects” (CE) paradigm, attempts to separate the direct effect of the treatment (Z) on T from the effect of Z on T that is mediated through S. The second paradigm, termed the “causal-association” (CA) paradigm, focuses on the association of the treatment effect on the surrogate and the treatment effect on the true endpoint. VanderWeele [6] argued that conceptually the CA paradigm is more appealing when assessing surrogacy, although that may not be universally accepted. Each of the approaches to surrogacy assessment rely on certain assumptions that one must be willing to make in order to proceed with estimation and the evaluation of S as a surrogate. Ten Have and Joffe [7] and Ensor et al. [8] provide a comprehensive reviews of the estimation methods used and the assumptions made within both the CE and CA paradigms. Here, we explore the connections between some of the typical assumptions made within each paradigm, and examine the implications of these assumptions on the quantities used to determine the validity of S as a surrogate marker within each of the CE and CA paradigms.

The consideration of surrogacy from a causal perspective has some similarities to causal considerations of compliance and mediation, which can both be considered as intermediate variables between an intervention or exposure and an outcome. A number of the assumptions we consider originate in the compliance and mediation literature [7, 9–12].

The CE paradigm can be represented as a structural model in which one can explicitly change the values of Z or S or both, and the model specifies how the outcome T would then change. The indirect effect of Z on T is then the part of the effect of Z that is explained by changes in S holding Z constant, and the direct effect is the part of the effect of Z on T when the value of S is held constant. If S is a good surrogate for T, the direct effect of Z on T should be zero for all values of S. The Prentice [2] criteria for assessing surrogacy can be considered to be in the CE paradigm. These criteria require that S and T be correlated, that S be affected by Z, and that T and Z be conditionally independent given S. If the coefficient of Z is zero in the regression model for T|Z, S, then S would be considered a valid surrogate. Since this model conditions on the post randomization variable S, it will in general not have a causal interpretation. For the Prentice criteria to be valid from a causal perspective requires the assumption of no unmeasured confounders of S and T. This assumption is often unlikely to hold in the surrogate marker setting, where S and T are frequently involved in the same disease process. In general, the parameters in the CE paradigm are not estimable without assumptions, of which no unmeasured confounders is an example. In the PFS and OS example in ovarian cancer, this would preclude the possibility of a healthy diet affecting both PFS and OS. Assumptions weaker than no unmeasured confounders have been suggested in the literature, and these will be considered below.

The assessment of surrogacy within the CA paradigm includes methods based on principal stratification [13], which consider the distribution of the potential outcomes of T conditional on principal strata based on the values of the potential outcomes of S. In this framework, each subject has two potential outcomes (in the case of a binary treatment), one under Z = 0 and one under Z = 1, for each of the surrogate and the final outcome. Measures of surrogacy are derived from the distribution of the potential outcomes of T conditional on principal strata based on the potential values of the outcomes of S. S is considered to be a valid principal surrogate if there is no expected treatment effect on T within the principal stratum where there is no treatment effect on S. As the potential outcomes of S are pre-randomization variables, they can be regarded as baseline covariates, thereby avoiding the issue of potential unobserved confounding between the post randomization observed values of S and T. However, as only two of the four potential outcomes of S and T are observed for each person, assumptions must be made to aid in the estimation of unidentifiable parameters. Common assumptions often involve restrictions or assumptions on certain model parameters through the use of prior distributional assumptions [14], or conditional independence assumptions between certain counterfactual outcomes [15–17] or concepts of monotonicity, under which negative effects of the treatment on the surrogate marker or outcome are precluded [18]. For the ovarian cancer example, the potential outcomes for S are the two PFS times that would have arisen under each of the treatment arms, and the potential outcomes for T are the two OS times that would have arisen under the two treatments. The CE paradigm additionally requires consideration of what the OS time would be if the PFS time could be externally manipulated. While it is hard to specify how that could be achieved, it is never the less part of the conceptual framework of the CE paradigm.

The CE paradigm is consistent with a mechanistic view of causality as it describes how the output will change if the inputs are separately manipulated. By allowing the manipulation of S for fixed values of Z, this framework represents a larger, more general model. By considering the potential outcomes of S and T under each treatment arm, the CA framework does not require manipulations of S, as it is concerned with how the causal treatment effect on S is associated with the causal treatment effect on T and not with the effect of S on T. Pearl [19] invited a discussion on the uses and limitations of estimating effects using potential outcomes. A common argument against the use of potential outcomes and the principal stratification approach is the unidentifiability of the principal strata. It is argued that this lack of identifiability makes it difficult to make progress in estimation within this framework. However, estimation methods within the CE framework also rely on untestable assumptions and on conceiving of interventions on S, which may not always be possible [6, 20].

In this paper, in order to illustrate the connections between the CE and CA frameworks, we consider the setting in which S and T are Gaussian. While the relationship between the CE and CA frameworks has been considered previously in a general setting [1, 21], restricting to the Gaussian setting facilitates consideration of a larger number of different assumptions and also allows algebraic development, providing a more clear and concrete understanding of the relationship between these two frameworks. We assume that S and T are generated from structural models that include an unobserved confounder. This model is detailed in Section 2. In Section 3, we explore the relationship between the parameters of the assumed Gaussian structural model and the model parameters in the principal surrogacy framework, and relate the structural model parameters to the parameters used to evaluate surrogacy within both the CE and CA frameworks. In Section 4, we briefly explore the role of baseline covariates in aiding in parameter estimation and in surrogacy evaluation. In Section 5, we review some of the common assumptions made within the CE framework to achieve identifiability and consider the impact of these assumptions on the parameters and quantities used to evaluate surrogacy in the CA framework. Section 6 explores some of the assumptions used to aid in estimation within the CA framework and their impact on the parameters within the CE framework. Section 7 presents a numerical study of the correspondence between the metrics of surrogacy under the various assumptions described in sections 5 and 6. Section 8 briefly outlines estimation methods for the parameters that are typically made in the two frameworks and explores how the explicit expressions derived for the relationship between the parameters and identifying assumptions of the two frameworks could aid in the estimation of surrogacy evaluation quantities. We conclude with a discussion in Section 9.

2. The structural model

Throughout the paper we will assume that the truth is a fairly general structural model, which is a model within the CE framework. We assume that both the surrogate marker S and the true endpoint T are continuous. We assume that the observed S_i is generated from a structural model which depends on the treatment, Z_i (Z_i = 0 or 1), and on an unobserved confounder, U_i, for each subject i, i = 1, ..., n. The observed value of T_i is also generated from a structural model that depends on Z_i, U_i and on S_i. Figure 1 provides a graphical representation of the assumed model.

Figure 1.

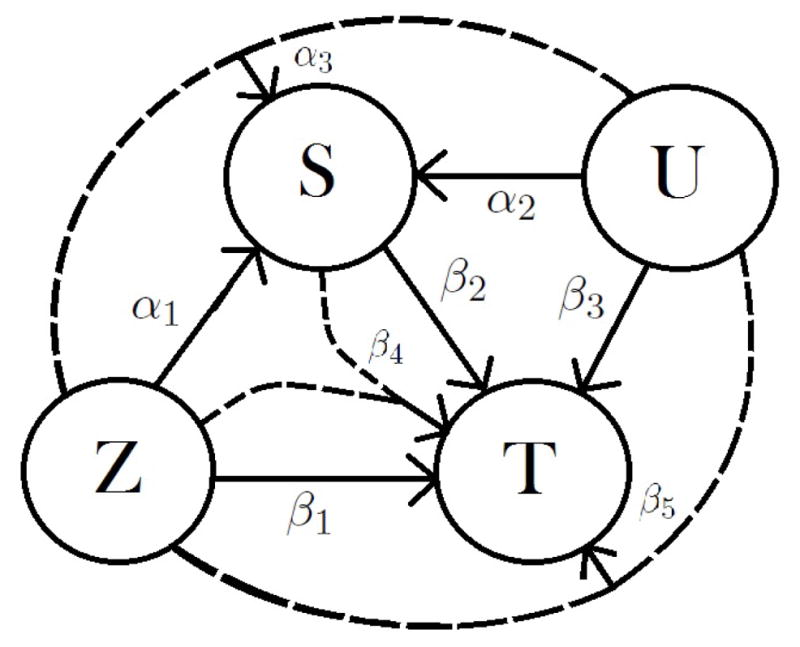
Causal graph for the intervention (Z), the surrogate (S) and the final outcome (T) with an unmeasured confounder (U).

We use the potential outcomes framework, and assume no interference, i.e. the potential outcomes of individual i are unaffected by the treatment and surrogate value of all other individuals. The assumed structural models for S_i and T_i are given by:

$$S_i(Z_i)={\alpha }_0+{\alpha }_1{Z}_i+{\alpha }_2{U}_i+{\alpha }_3{U}_i{Z}_i+e^{S_i(Z_i)}$$ (1)

$$T_i(Z_i,s)={\beta }_0+{\beta }_1{Z}_i+{\beta }_{2}s+{\beta }_3{U}_i+{\beta }_{4}s{Z}_i+{\beta }_5{U}_i{Z}_i+e^{T_i(Z_i)}$$ (2)

where U_i ~ N(0, 1), $e^{S_i(0)}~N(0,{\delta }_{S0}^2),e^{S_i(1)}~N(0,{\delta }_{S1}^2),e^{T_i(0)}~N(0,{\delta }_{T0}^2),e^{T_i(1)}~N(0,{\delta }_{T1}^2)$ and U_i, e^{S_i (0)}, e^{S_i (1)}, e^{T_i (0)}, e^{T_i (1)} are all uncorrelated. Note that the model is quite general in the sense that it does allow the outcome to depend on interactions between Z and U and between Z and S. To preclude having non Gaussian error terms, the model for T_i(Z_i, S_i) does not include any interactions between U_i and S_i. Additionally, while the error associated with the potential outcome of T_i(Z_i, S_i) changes with Z, there is no additional measurement error associated with S beyond that induced by the error of the selected S(z), only a location shift for T(Z, S(z)) conditional on e^S(z). Also note that the model does not include any other baseline covariates except for the intervention, which we assume to be randomly assigned. The situation with baseline covariates will be discussed later.

From the structural model we have the following for the four potential outcomes:

• S_i(0) = α₀ + α₂U_i + e^{S_i (0)}

• S_i(1) = α₀ + α₁ + (α₂ + α₃)U_i + e^{S_i (1)}

• T_i(0) = T_i(0, S_i(0)) = β₀ + β₂α₀ + (β₂α₂ + β₃)U_i + β₂e^{S_i (0)} + e^{T_i (0)}

• T_i(1) = T_i(1, S_i(1)) = β₀ + β₁ + (β₂ + β₄)(α₀ + α₁) + [(β₂ + β₄)(α₂ + α₃) + (β₃ + β₅)]U_i + (β₂ + β₄)e^{S_i (1)} + e^{T_i (1)}

In addition to no interference, the structural model (2) assumes consistency, T_i = T_i(z, s) if Z_i = z, S_i = s, which allows the observed outcome to be related to the potential outcome; and positivity, P(Z_i = z | U_i = u) > 0, P(S_i(z) = s | Z_i = z,U_i = u) > 0 for all z, u ∈ 𝒰, and s ∈ 𝒮. This implies that all treatments can be observed at all levels of potential confounders and that all levels of the surrogate marker are observable at all levels of potential confounders for all levels of treatment. The first part of the positivity assumption is trivially satisfied in the setting of a randomized trial.

The structural model described above has 14 parameters, which is the same number of parameters as the principal surrogacy model described in the following section. For the data that can be collected in a randomized trial, under the assumption that S and T are Gaussian, there are ten estimable quantities corresponding to the means and variances of S(0), S(1), T(0) and T(1) and the correlations of (S(0), T(0)) and (S(1), T(1)). While the structural model is a mechanistic model, the parameters still cannot all be estimated without untestable assumptions. Similarly, in the principal surrogacy model, there are ten estimable parameters; in the following section, we explicitly link the parameters of these two models. When there are no unmeasured confounders in the structural model, (i.e. α₂ = α₃ = 0 or β₃ = β₅ = 0 or both), then all of the remaining parameters of this model are identifiable, as are the parameters of the principal surrogacy framework. In Sections 4 and 5, we explore some of the common assumptions made within the CE and CA frameworks and the impact of these assumptions on the quantities used to evaluate S as a surrogate marker.

3. The CA and CE frameworks

3.1. The causal association model

The CA paradigm of surrogacy evaluation includes methods based on the “principal surrogacy” framework of Frangakis and Rubin [13]. This framework focuses on the distribution of the potential outcomes of T conditional on principal strata defined by the values of the potential outcomes of S. Let S_i(z) and T_i(z) denote the potential outcomes of S_i and T_i, respectively, for subject i under treatment assignment Z_i = z. We assume the joint distribution of (S_i(0), S_i(1), T_i(0), T_i(1)) is multivariate normal [14] with mean μ and covariance matrix Σ, and has the following distribution:

$$\left(\begin{array}{c}{S}_i(0)\\ S_i(1)\\ T_i(0)\\ T_i(1)\end{array}\right)~N\left(\left(\begin{array}{c}{\mu }_{S_0}\\ {\mu }_{S_1}\\ {\mu }_{T_0}\\ {\mu }_{T_1}\end{array}\right),\left(\begin{array}{cccc}{\sigma }_{S_0}^2& {\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}& {\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}& {\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}\\ & {\sigma }_{S_1}^2& {\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}& {\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}\\ & & {\sigma }_{T_0}^2& {\rho }_t{\sigma }_{T_1}{\sigma }_{T_0}\\ & & & {\sigma }_{T_1}^2\end{array}\right)\right)$$ (3)

The mean μ and the variances corresponding to the diagonal elements of Σ, as well as the correlation parameters ρ₀₀ and ρ₁₁ are fully identifiable from the observed data. However, because only one of the counterfactual pairs of outcomes is observed for each subject, the correlation parameters ρ_s, ρ₀₁, ρ₁₀, and ρ_t are not identifiable from data. The parameters of the structural model detailed in Section 2 can be directly related to the principal surrogacy model when the joint distribution of the potential outcomes of S and T is multivariate normal. The formulas for all the μs, σs and ρs in terms of the αs, βs and δs are given in Appendix A.

While there is a direct mapping of the 14 parameters of the structural model to the 14 parameters of the principal surrogacy model, there is not an explicit formula to map the parameters of the principal surrogacy model back to the structural model parameters. For some combinations of parameters within the parameter space of the principal surrogacy model no parameter combinations within the parameter space of the structural model exist.

3.1.1. Measures of surrogacy

To evaluate S as a surrogate marker within the principal surrogacy framework, Gilbert and Hudgens [15] proposed two properties that a good surrogate should possess, “average causal necessity” (ACN) and “average causal sufficiency” (ACS). ACN requires that there be no conditional treatment effect on T within the principal stratum where there is no treatment effect on S, while ACS requires a non-zero conditional treatment effect on T within principal strata where there is a non-zero treatment effect on S. For the ovarian cancer trial example with PFS as a potential surrogate for OS, ACN would be met if patients who would experience the same PFS under either treatment arm would on average experience the same OS under either treatment. ACS would be met if patients who would experience greater PFS in one treatment arm would on average experience greater OS under this treatment arm. The primary quantities of interest from the multivariate normal model used to evaluate surrogacy can be derived from the conditional distribution of (T(1) − T(0) | S(1) − S(0) = s), which in the joint Gaussian setting is normal with mean given by E[T(1) − T(0)|S(1) − S(0) = s] = γ₀ + γ₁s, where:

$${\gamma }_0=({\mu }_{T_1}-{\mu }_{T_0})-\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right)({\mu }_{S_1}-{\mu }_{S_0})$$ (4)

$${\gamma }_1=\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right).$$ (5)

ACN is then satisfied if γ₀ = 0 and ACS is satisfied if γ₁ ≠ 0. We note that neither γ₀ nor γ₁ depend on ρ_t, however, the variance of [T(1) − T(0)|S(1) − S(0) = s] does depend on ρ_t.

Based on the mapping of the parameters, the surrogacy quantities of interest in the CA framework γ₀ and γ₁ can be rewritten as:

$${\gamma }_0={\beta }_1+{\beta }_4({\alpha }_0+{\alpha }_1)-{\alpha }_1\left(\frac{{\beta }_4({\alpha }_3^2+{\alpha }_3{\alpha }_2+{\delta }_{S1}^2)+{\beta }_5{\alpha }_3}{{\delta }_{S0}^2+{\delta }_{S1}^2+{\alpha }_3^2}\right)$$ (6)

and

$${\gamma }_1={\beta }_2+\frac{{\beta }_4({\alpha }_3^2+{\alpha }_3{\alpha }_2+{\delta }_{S1}^2)+{\beta }_5{\alpha }_3}{{\delta }_{S0}^2+{\delta }_{S1}^2+{\alpha }_3^2}.$$ (7)

The principal surrogacy criteria requiring that γ₀ = 0 and γ₁ ≠ 0 will be met if ${\beta }_1+{\beta }_4({\alpha }_0+{\alpha }_1)={\alpha }_1\left(\frac{{\beta }_4({\alpha }_3^2+{\alpha }_2{\alpha }_3+{\delta }_{S0}^2)+{\beta }_5{\alpha }_3}{{\delta }_{S0}^2+{\delta }_{S1}^2+{\alpha }_3^2}\right)$ and these quantities are greater than −β₂α₁ for γ₁ > 0 and less than −β₂α₁ for γ₁ < 0. Thus the requirements of the structural model within the CE framework for achieving principal surrogacy under the CA framework are not simple.

3.2. The causal effects model

3.2.1. Direct and indirect effects

The causal effects framework for surrogacy evaluation attempts to quantify the direct effect of Z on T, and the indirect effect of Z on T that is mediated through S. The notions of direct and indirect effects [22, 23] are defined by the counterfactual outcomes S_i(z) and T_i(z, s), where S_i(z) is the value of S for subject i under treatment assignment Z_i = z and T_i(z, s) is the counterfactual outcome of T for subject i when Z_i is set to z and S_i is set to s. Robins and Greenland [22] and Pearl [23] provide definitions of the natural direct effect (NDE(z)), natural indirect effect (NIE(z)) and total effect (TE). The NDE(z) measures the effect of Z on T when S is set to its potential value under treatment assignment z. The NIE(z) measures the effect on T when Z is set to z and S is changed to what it would have been if Z were set to 1 compared to what it would have been if Z were set to 0. Finally, the TE of Z on T is equal to the sum of the NIE(1) and NDE(0) or to the sum of NIE(0) and NDE(1). Imai, Keele and Yamamoto [11] focus on the average causal effects of NDE(z), NIE(z) and TE defined by E[NDE(z)], E[NIE(z)], E[TE] respectively. From the assumed structural model, these average causal effects are given in Table 1. The average causal effects correspond to the relevant component parameters in the structural model. For example, E[NDE(0)] equals the direct effects of Z on T plus the effect of Z on S brought through the interaction between S and Z on T. Since U ~ N(0, 1), the expected effects in Table 1 do not depend on the parameters associated with the unmeasured confounders. An additional notion to measure the direct effect of Z on T is the controlled direct effect [22, 23]. It measures the effect of a treatment on an outcome after intervening to fix the value of the surrogate S to the same value s for the whole population; in the context of the ovarian cancer example, this would correspond to an intervention that sets the PFS time to be equal across the population before estimating the treatment effect on OS. In terms of the counterfactuals, we can define it as CDE = E[T(1, s) − T(0, s)] = β₁ + β₄s.

Table 1.

Expressions for direct, indirect and average causal effects

E[NDE(0)]:	E[T(1, S(0)) − T(0, S(0))] = β1 + α0β4
E[NDE(1)]:	E[T(1, S(1)) − T(0, S(1))] = β1 + β4(α0 + α1)
E[NIE(0)]:	E[T(0, S(1)) − T(0, S(0))] = α1β2
E[NIE(1)]:	E[T(1, S(1)) − T(1, S(0))] = α1(β2 + β4)
E[TE]:	E[T(1, S(1)) − T(0, S(0))] = β1 + β2α1 + β4(α0 + α1)

Note that if there is no interaction between the surrogate and the treatment in the structural model, then the CDE and the NDE coincide. However, the total effects decomposes into the sum of the NDE and the NIE, but such decomposition is not available when using the CDE, so we shall not consider the CDE any further in this paper.

3.2.2. Measures of surrogacy

A measure of surrogacy in the CE framework is the ratio of the indirect effect to the total effect, denoted by PE(Z), which can also be interpreted as the proportion of treatment effect on T explained by S. From the assumed structural model, PE(z) is given by:

$$PE(0)=\frac{E[T(0,S(1))-T(0,S(0))]}{E[T(1,S(1))-T(0,S(0))]}=\frac{{\alpha }_1{\beta }_2}{{\beta }_1+{\beta }_2{\alpha }_1+{\beta }_4({\alpha }_0+{\alpha }_1)}$$ (8)

and

$$PE(1)=\frac{E[T(1,S(1))-T(1,S(0))]}{E[T(1,S(1))-T(0,S(0))]}=\frac{{\alpha }_1({\beta }_2+{\beta }_4)}{{\beta }_1+{\beta }_2{\alpha }_1+{\beta }_4({\alpha }_0+{\alpha }_1)}.$$ (9)

For S to be considered a perfect surrogate marker, E[NDE(z)] should be zero and E[NIE(z)] should be non-zero, indicating that all of the effect of Z on T is mediated through S. The PE(z) provides a measure of the proportion of treatment effect on T that is explained by S, and should be large for good surrogate markers and equal to one for a perfect surrogate. In the ovarian cancer example, an E[NDE(z)] of zero would imply that the treatment only effects OS time through its effect on PFS time and a non-zero E[NIE(z)] would be the effect on OS time due to the treatment effect induced on PFS time, net of any treatment effect.

3.2.3. Relationship to Prentice criteria

Special cases of the direct and indirect effects approach to determine surrogacy are the Prentice [2] criteria and the closely related mediation methods proposed by Baron and Kenny [9]. The Prentice criteria considers the regression model

$$E[T\mid S,Z]={\theta }_0+{\theta }_{1}Z+{\theta }_{2}S+{\theta }_{3}SZ,$$

and S is considered a perfect surrogate if θ₁ = θ₃ = 0. From the structural model it can be shown that,

$${\theta }_1={\beta }_1-{\beta }_3\frac{{\delta }_{S0}^2({\alpha }_1+{\alpha }_0)({\alpha }_2+{\alpha }_3)+{\alpha }_2^2({\alpha }_2{\alpha }_1+{\alpha }_1{\alpha }_3-{\alpha }_0{\alpha }_3)-{\alpha }_0{\alpha }_2({\alpha }_3^2+{\delta }_{S1}^2)}{({\alpha }_2^2+{\delta }_{S0}^2)({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)}-{\beta }_5\frac{({\alpha }_1+{\alpha }_0)({\alpha }_2+{\alpha }_3)}{{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2}$$

and

$${\theta }_3={\beta }_4-{\beta }_3\frac{{\alpha }_2^2{\alpha }_3+{\alpha }_2({\alpha }_3^2+{\delta }_{S1}^2)-{\delta }_{S0}^2({\alpha }_2+{\alpha }_3)}{({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)({\alpha }_2^2+{\delta }_{S0}^2)}+{\beta }_5\frac{({\alpha }_2+{\alpha }_3)}{{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2}.$$

The coefficients of the Prentice model (θ₀, θ₁, θ₂, θ₃) depend on the coefficients of the confounding variables in equations 1 and 2 (i.e. they depend on α₂, α₃, β₃, β₅). Therefore, for the assessment of surrogacy using the Prentice criteria to be a valid causal assessment of surrogacy, there must be no confounders of S (α₂ = α₃ = 0) or no confounders of T (β₃ = β₅ = 0) so that we have θ₁ = β₁ and θ₃ = β₄. In the absence of confounders, S will be considered a perfect surrogate marker for T based on the Prentice criteria if α₁ ≠ 0, β₂ ≠ 0, β₁ = 0 and β₄ = 0 and subsequently θ₁ = θ₃ = 0. In this case, the direct effect of Z on T will be zero and all of the treatment effect will be completely mediated through S. The methods of Baron and Kenny [9] also require no unobserved confounders and additionally require there to be no interaction of Z and S (β₄ = 0). Then, if α₁ and β₂ are non-zero, α₁β₂ can be interpreted as the mediation effect, or the effect of Z that is explained by S.

In the absence of unobserved confounders and no interaction effect of S and Z, Freedman, Graubard, and Schatzkin [3] proposed a quantity to measure the proportion of treatment effect explained by S, derived from the ratio of treatment effects estimated from two regression models for T, one with no adjustment for S and the other adjusting for S. Freedman’s proportion explained is one minus this ratio, given by $p=1-\frac{{\beta }_1}{{\beta }_1+{\alpha }_1{\beta }_2}$, where p = 1 corresponds to a perfect surrogate. Wang and Taylor [24] proposed an estimate of the proportion of treatment effect explained by S that can be estimated from the observed data in the presence of an interaction of S and Z. For the structural model assumed here, this quantity is equivalent to PE(z) in equations 8 and 9.

3.3. Correspondence between the CA and CE models

Within the CE framework, S will be considered a valid surrogate when the natural direct effects are zero, corresponding to β₁ = 0 and β₄ = 0 and the natural indirect effects are non-zero (α₁ and β₂ are non-zero). Within the CA framework, S is considered a valid surrogate if γ₀ = 0 and γ₁ ≠ 0. VanderWeele [21] referred to the expected treatment effect on T within principal strata where there is no treatment effect on S, here corresponding to γ₀, as the “principal strata direct effect” and the expected treatment effect on T within principal strata where there is a treatment effect on S, here corresponding to γ₁, as the “principal strata indirect effect”. Working at the individual level, VanderWeele [21] showed that when the natural direct effects are zero for all subjects, corresponding to the assumption β₁ = β₄ = β₅ = 0 and ${\delta }_{S0}^2={\delta }_{S1}^2={\delta }_{T0}^2={\delta }_{T1}^2=0$, there is no principal strata direct effect, corresponding to γ₀ = 0, therefore meeting the CA surrogacy criteria. In our case, where we are interested in the expected natural direct effects, which are zero when β₁ = 0 and β₄ = 0, the surrogacy quantities of the CA model will be ${\gamma }_0=-\frac{{\alpha }_1{\beta }_5{\alpha }_3}{{\delta }_{S0}^2+{\delta }_{S1}^2+{\alpha }_3^2}$ and ${\gamma }_1={\beta }_2+\frac{{\beta }_5{\alpha }_3}{{\delta }_{S0}^2+{\delta }_{S1}^2+{\alpha }_3^2}$ when the expected natural direct effects are zero. Therefore, when the criteria for surrogacy are met within the CE framework, the criteria within the CA framework will not always be satisfied, but will be met if either α₃ = 0 or β₅ = 0, i.e. if either of the U_iZ_i interactions in Equation 1 or Equation 2 are zero.

When there is no interaction effect between S and Z on T (β₄ = 0), and no interaction between the unmeasured confounder U and Z for either the outcome (β₅ = 0) or the surrogate marker (α₃ = 0), then there is a simple relationship between the proportion explained (PE(z)) measure in the CE framework and the ACN and ACS parameters γ₀ and γ₁ in the CA framework. In particular, β₄ = 0 implies NDE(0) = NDE(1) = NDE = β₁, α₃ = 0 implies E(s) = E(S(1)) − E(S(0)) = α₁, while β₄ = 0 and β₅ = 0 together imply that γ₀ = β₁ and γ₁ = β₂. Thus

$$PE(0)=PE(1)=PE=1-\frac{\mathit{NDE}}{TE}=\frac{{\gamma }_{1}E(s)}{{\gamma }_0+{\gamma }_{1}E(s)}=1-\frac{{\gamma }_0}{{\gamma }_0+{\gamma }_{1}E(s)}.$$

Thus γ₀ can only be treated as analogous to the direct effect in the CE framework if there is no interaction effect of S and Z on T and there is no treatment interaction with the unobserved confounder on either the outcome or the surrogate marker.

3.3.1. Simulation experiments

The above algebra showed that the metrics of surrogacy in the CE framework (NDE(Z), NIE(Z) and PE(Z)) do not correspond to the metrics of surrogacy in the CA framework (γ₀ and γ₁) unless special conditions are met. To further understand the magnitude of the differences between the parameters and measures of surrogacy in the CE model and the CA model, we undertook a simulation experiment. We simulated a broad range of reasonable parameter combinations in the structural model. Additionally, the average total effect (β₁ + β₂α₁ + β₄(α₀ + α₁)) was constrained to be positive. Drawing the CE parameters in this way ensured that α₁ > 0, β₂ > 0 and (β₂ + β₄) > 0, which is a reasonable assumption in the surrogate marker setting where any S being considered as a potential surrogate for T would be known to have an association with the treatment and with T. Additionally, under the distributional assumptions, the magnitude of the coefficients of the confounding variable on S and on T must be less than the magnitude of the coefficient of α₁ and β₂, respectively, and ${\delta }_{S0}^2$ and ${\delta }_{S1}^2$ are constrained to have the same values, as are ${\delta }_{T0}^2$ and ${\delta }_{T1}^2$. Restricting the average total effect to be greater than zero ensures that PE(z) is greater than zero. For each parameter set, we calculated the corresponding parameters in the CA model and also the measures of surrogacy in both frameworks. Details of the distributions used to generate parameters for the simulations are provided in Appendix B. The range of R² values for regression models of T|Z, T|S and T|U is also shown in Appendix B, and demonstrates that the way in which the parameters were simulated was not overly restrictive and leads to a wide spectrum of scenarios. We explored the sensitivity of the simulation results to the chosen distributions and found that the results appear generalizable to parameters arising from different distributions.

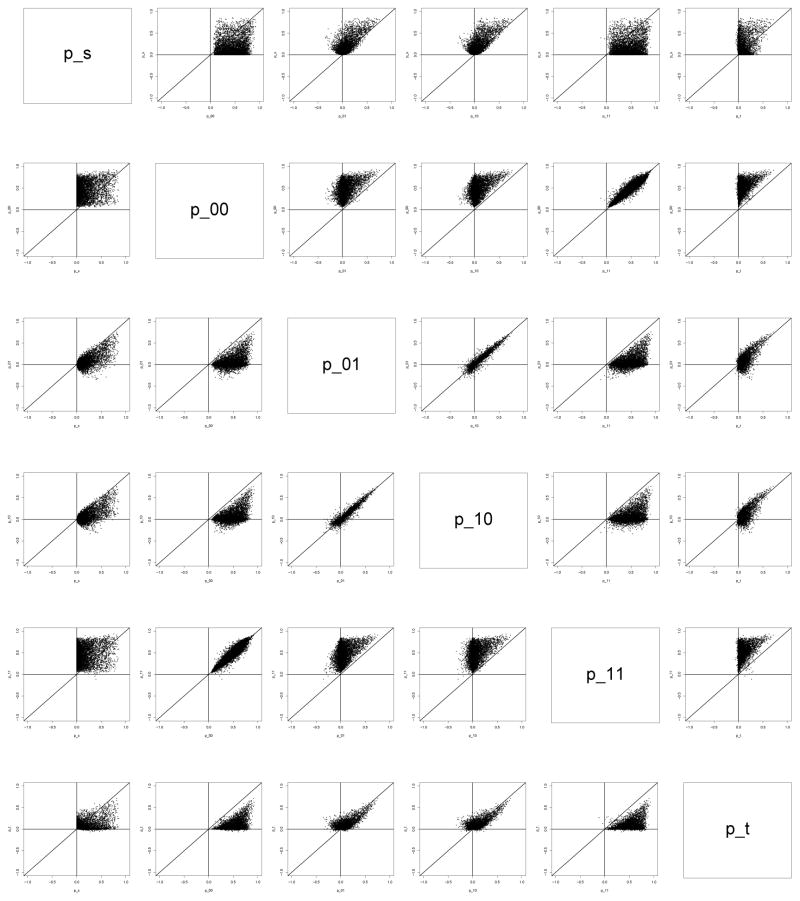
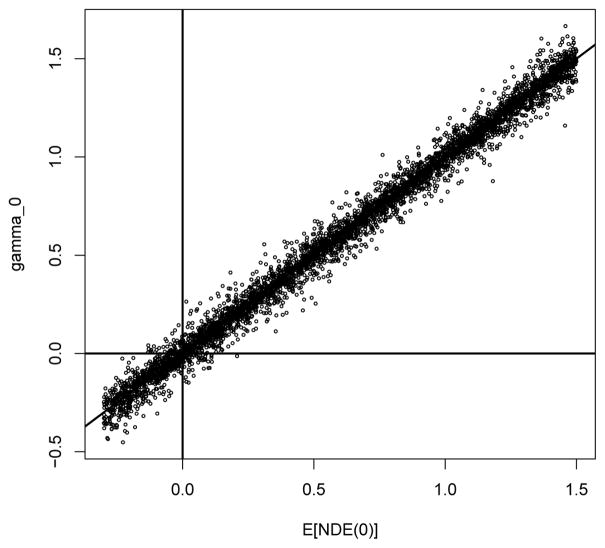
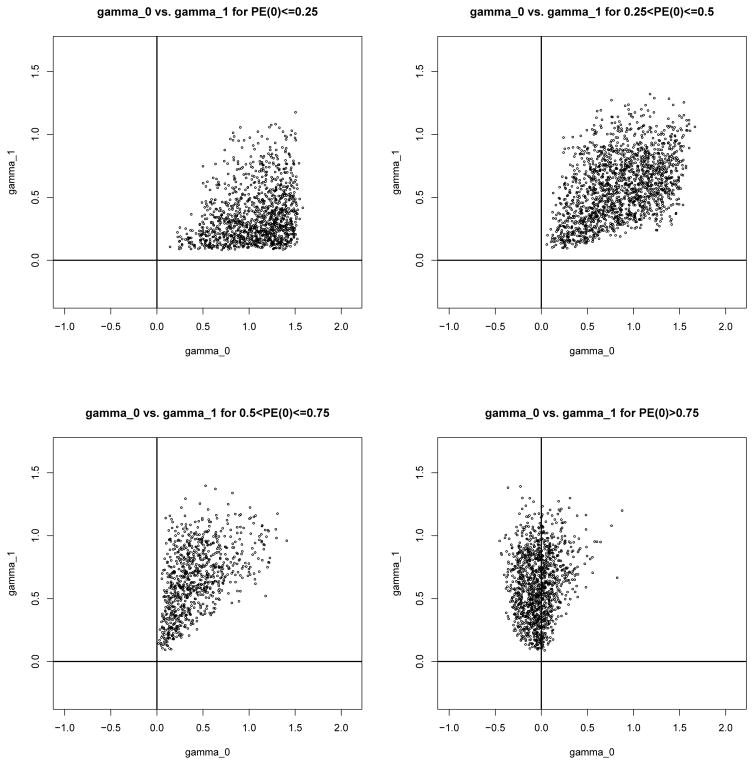
Figure 2 provides scatter plots of the correlation parameters of the CA model for the simulated CE model parameters. The plots show that ρ_s, ρ_t, ρ₀₀ and ρ₁₁ are almost always positive, that ρ₀₀ and ρ₁₁ are generally larger than the other four correlation parameters and that ρ_s and ρ_t are generally larger than ρ₀₁ and ρ₁₀. Figure 3 provides a scatter plot of E[NDE(0)] versus γ₀. We see that there is a close correspondence between the direct effects and γ₀. Figure 4 provides plots of γ₀ vs. γ₁ for different values of PE. When PE is small, γ₀ tends to be greater than zero. As PE increases, the distribution of γ₀ becomes more centered around zero. The plots show that although there is not a perfect concordance between the surrogacy measures in the two frameworks, similar conclusions regarding the validity of S as a surrogate marker will often be drawn from the two frameworks.

Figure 2.

CA model parameters for a range of plausible values from the assumed structural model.

Figure 3.

Correspondence between NDE and γ₀ for a range of plausible values from the assumed structural model.

Figure 4.

Correspondence between CA surrogacy measures (γ₀ and γ₁) and CE surrogacy measures (PE(0)) for a range of plausible values from the assumed structural model.

The above figures represent the degree of agreement between the two concepts of surrogacy, as if the joint distribution of all the counterfactual outcomes were known, that is all the parameters in Equations 1 and 2 were known. In practice the parameters would have to be estimated from observed data.

4. Baseline Covariates

In many settings, observed baseline covariates (X) are available that may explain some of the dependence between S and T, and explain some of the effect of Z on S and T. Often baseline covariates are sought that will control for any confounding of S and T. If X is a binary or categorical covariate, the models and assumptions within both the CE and CA frameworks could be made within strata defined by X. If X is a continuous covariate or a continuous linear combination of covariates, additional parameters could be added to the structural model to give:

$$\begin{array}{c}{S}_i(Z_i)={\alpha }_0+{\alpha }_1{Z}_i+{\alpha }_2{U}_i+{\alpha }_3{U}_i{Z}_i+{\psi }_1{X}_i+{\psi }_2{X}_i{Z}_i+e^{S_i(Z_i)}\\ T_i(Z_i,S_i)={\beta }_0+{\beta }_1{Z}_i+{\beta }_2{S}_i+{\beta }_3{U}_i+{\beta }_4{S}_i{Z}_i+{\beta }_5{U}_i{Z}_i+{\omega }_1{X}_i+{\omega }_2{X}_i{Z}_i+e^{T_i(Z_i)}.\end{array}$$

This model now has 18 parameters to estimate and leads to a new CA model given by: $\left(\begin{array}{c}{S}_i(0)\\ S_i(1)\\ T_i(0)\\ T_i(1)\end{array}\right)~N\left(\left(\begin{array}{c}{\mu }_{S_0}+{\psi }_1{X}_i\\ {\mu }_{S_1}+({\psi }_1+{\psi }_2)X_i\\ {\mu }_{T_0}+{\omega }_1{X}_i\\ {\mu }_{T_i}+({\omega }_1+{\omega }_2)X_i\end{array}\right),\left(\begin{array}{cccc}{\sigma }_{S_0}^2& {\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}& {\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}& {\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}\\ & {\sigma }_{S_1}^2& {\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}& {\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}\\ & & {\sigma }_{T_0}^2& {\rho }_t{\sigma }_{T_1}{\sigma }_{T_0}\\ & & & {\sigma }_{T_1}^2\end{array}\right)\right)$. The mean parameters of this model are estimable and, as the covariance matrix does not change with the addition of baseline covariates, there are still four correlation parameters that are not estimable. Full development of the structural model given in Equations 1 and 2 can be assumed to be conditional on X, making the common assumptions of conditional independence and sequential ignorability discussed in the next section more plausible. In Appendix D we describe the consequence of including additional covariates on the natural direct and indirect effects, on the Prentice criteria and on γ₀ and γ₁.

5. Assumptions made within the CE framework

The structural model assumed in Section 2 is not identifiable from the observed data. Therefore, assumptions must be made in order to aid in the estimation of the parameters and identification of the direct and indirect effects. We review some of the common identifying assumptions made within the CE framework and explore the implications of these assumptions on the parameters of the principal surrogacy model. The no interference assumption is expanded to mean that the treatment level of one individual has no effect on the surrogate of another, and we require generalized consistency, namely S(z) = S, and T(z, S(z)) = T when Z = z.

5.1. No unmeasured confounders

A critical assumption to identification within the causal effects framework is that there are no unobserved confounders driving the association between the outcome and the treatment or between the surrogate marker and the outcome. In the ovarian cancer example, the assumption of no unobserved confounders between the outcome and the treatment will be met because it is a randomized clinical trial. The assumption of no unobserved confounders between the surrogate marker and the outcome precludes the possibility that diet affects both PFS time and OS time, and therefore would only be a reasonable assumption to make in this context if diet was not thought to be associated with both of these outcomes, or if covariate information was available to be included in the model to sufficiently control for this association. Different versions of the no unmeasured confounders assumption are made in the literature.

Let X denote a set of measured covariates. Pearl [23] required conditional exchangeability, meaning that conditional on measured covariates X, treatment Z is “random”, and that once we stratify according to Z and X, their level of S is also essentially random. More formally,

$$\begin{array}{lll}\hfill T_i(z)& \perp \hfill & Z\mid X_i=x\hfill \\ \hfill T_i(z^{\prime },s)& \perp \hfill & S_i(z)\mid Z_i=z,X_i=x\hfill \end{array}$$

for all z, z′ and x = 𝒳, implying no Z − T confounding conditionally on observed covariates X, and no S − T confounding conditionally on observed covariates X and Z. The first assumption is automatically satisfied in randomized trials.

The conditional exchangeability assumption is replaced by Imai, Keele, and Yamamoto [11] by sequential ignorability, defined as

$$\begin{array}{c}{T}_i(z^{\prime },s),S_i(z)\perp Z_i\mid X_i=x\\ T_i(z^{\prime },s)\perp S_i(z)\mid Z_i=z,X_i=x\end{array}$$

for all z, z′ and x ∈ 𝒳. Again, the first assumption is automatically satisfied in randomized trials; the second is stronger, especially in the setting we have here without covariates.

Under our assumption of randomized treatment, Pearl and Imai, Keele, and Yamamoto correspond. Under the structural model (2) without covariates, sequential ignorability implies Pearl’s conditions for identification.

Petersen, Sinsi, and van der Laan [25] replace the assumption T_i(z′, s), S_i(z) ⊥ Z_i | X_i = x of Imai, Keele, and Yamamoto with the weaker assumption that the outcome rather than the joint distribution of the surrogate and the outcomes is independent of treatment: T_i(z′, s) ⊥ Z_i | X_i = x, but require the additional assumption that the magnitude of the direct effect is independent of the potential values of the surrogate marker conditional on observed covariates:

$$E_{S(z)}[Y_i(1,s)-Y_i(0,s)\mid S_i(z)=s,X=x]=E_{S(z)}[Y_i(1,s)-Y_i(0,s)\mid X=x].$$

As with the assumptions of Pearl [23], the Petersen, Sinsi, and van der Laan requirements match those of sequential ignorability in a randomized trial setting.

While these identification assumptions hold without further parametric assumptions, we can translate them into our parametric structural model by noting

$$\begin{array}{c}{S}_i(0)={\alpha }_0+{\alpha }_2{U}_i+e_i^{S(0)}\\ S_i(1)={\alpha }_0+{\alpha }_1+({\alpha }_2+{\alpha }_3)U_i+e_i^{S(0)}\\ T_i(0,s)={\beta }_0+{\beta }_{2}s+{\beta }_3{U}_i+e_i^{T(0)}\\ T_i(1,s)={\beta }_0+({\beta }_2+{\beta }_4)s+({\beta }_3+{\beta }_5)U_i+e_i^{T(0)}.\end{array}$$

The requirement that T_i(z′, s) ⊥ S_i(z) | Z_i = z,X_i = x implies α₂ = 0 or β₃ = 0 when Z = 0, and α₂ + α₃ = 0 or β₃ + β₅ = 0 when Z = 1, or, more concisely, α₂ = α₃ = 0 or β₃ = β₅ = 0, so that either S(Z_i) or T(Z_i, S_i) is independent of U_i and thus U_i no longer confounds the surrograte marker and the outcome.

5.2. No interaction

Recent work by VanderWeele [26] has highlighted the important role of interactions in mediation analysis. Baron and Kenny [9] propose methods for mediation analysis based on solving a system of linear equations. In order to obtain causal interpretations of the parameters of their models, an assumption of no unmeasured confounders as well as no interaction is necessary. This leads to the structural model of Section 2 with α₂ = α₃ = 0 or β₃ = β₅ = 0 and β₄ = 0. Then, E[NDE(0)] = E[NDE(1)] = β₁, E[NIE(1)] = E[NIE(0)] = α₁β₂ and E[TE] = β₁ + β₂α₁. Under these assumptions we have ρ_s = ρ₀₁ = ρ₁₀ = ρ_t = 0, and if ${\delta }_{S0}^2={\delta }_{S1}^2$ and ${\delta }_{T0}^2={\delta }_{T1}^2$ then ρ₀₀ = ρ₁₁. For our data example in ovarian cancer, these assumptions imply that diet does not affect both PFS time and OS time and OS time changes with PFS time to the same degree under both treatment arms. This assumption may therefore be reasonable to make if there is clinical knowledge to support the notion that longer (shorter) PFS times will result in similarly longer (shorter) OS times, regardless of treatment given. Under these assumptions, γ₀ is equal to the natural direct effect (E[NDE(0)] = E[NDE(1)] = γ₀ = β₁) and γ₁ = β₂, leading to exact correspondence between the CE and CA measures of surrogacy. Therefore, if β₁ = 0and β₂ ≠ 0, S will be a valid surrogate for T from both the CE or CA model perspective.

5.3. Conditional independence assumption

Daniels et al. [12] work under the assumption of conditional independence between potential outcomes which assumes that T(1, S(1)), T(1, S(0)) and T(0, S(0)) are conditionally independent given S(0) and S(1). In the ovarian cancer example, this assumption implies that given two PFS times, s₀ and s₁, under Z = 0 and Z = 1, respectively, amongst the set of people who have potential outcomes s₀ and s₁, the OS times under Z = 0 and the OS times under Z = 1 are independent, and also independent of the OS time under Z = 1 for PFS time s₀. They note that this assumption is not necessary to estimate the direct and indirect effects, however, in their Bayesian estimation strategy for estimating NDE and NIE, these assumptions are needed to estimate features of the posterior distribution of these quantities, such as the posterior variance. The conditional covariances of these three outcomes from the structural model of Section 2 are as follows:

$$\begin{array}{ll}\text{Cov}[T(0,S(0)),T(1,S(1))\mid S(0),S(1)]& =\frac{{\beta }_3({\beta }_3+{\beta }_5){\delta }_{S_0}^2{\delta }_{S_1}^2}{{\delta }_{S_0}^2{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S_1}^2({\alpha }_2^2+{\delta }_{S_0}^2)},\\ \text{Cov}[T(0,S(0)),T(1,S(0))\mid S(0),S(1)]& =\frac{{\beta }_3({\beta }_3+{\beta }_5){\delta }_{S_0}^2{\delta }_{S_1}^2}{{\delta }_{S_0}^2{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S_1}^2({\alpha }_2^2+{\delta }_{S_0}^2)},\text{and}\\ \text{Cov}[T(1,S(1)),T(1,S(0))\mid S(0),S(1)]& =\frac{{\delta }_{S_0}^2{\delta }_{S_1}^2{({\beta }_3+{\beta }_5)}^2+{\delta }_{S_0}^2{\delta }_{T_1}^2{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S_1}^2{\delta }_{T_1}^2({\alpha }_2^2+{\delta }_{S_0}^2)}{{\delta }_{S_0}^2{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S_1}^2({\alpha }_2^2+{\delta }_{S_0}^2)}\end{array}$$

In order for the three conditional independence assumptions to hold, in the structural model we must have (β₃ + β₅) = 0 and the possibly unrealistic assumption that ${\delta }_{T_1}^2=0$, making this assumption difficult to satisfy in most scenarios. In terms of the parameters of the causal association model, this assumption does not change the correlation parameters ρ_s, ρ₀₀ and ρ₁₀, and only slightly alters ρ_t, ρ₁₁ and ρ₀₁. The surrogacy quantities of interest, γ₀ and γ₁, are unchanged by this assumption.

5.4. Exclusion restriction

Many of the assumptions discussed so far required no unobserved confounding. The instrumental variable approach does not make assumptions about S–T confounding, but instead assumes that all of the effect of Z on the outcome is mediated by the intermediate variable S_i, i.e. that the direct effect of Z is zero, i.e. T_i(1, s) = T_i(0, s). This assumption is called exclusion restriction. More specifically, in the setting where the intermediate variable is binary (e.g. binary mediator or binary indicator of compliance to treatment), the exclusion restriction assumption requires that the distribution of the potential outcomes of T be independent of treatment assignment in the principal strata defined by the potential intermediate variable. So for the never-takers, (S_i(0) = S_i(1) = 0), and the always-takers (S_i(0) = S_i(1) = 1), this implies T_i(1, s) = T_i(0, s) = β₀ + β₂s + β₃U_i [31], and thus β₁ = β₄ = β₅ = 0. In the continuous setting, Holland [32] and Sobel [33] have a similar requirement for identifiability, requiring that β₁ + β₄s + β₅U = 0. While in the compliance literature, it is often reasonable to assume that the treatment has no direct effect on the outcome, we note that the exclusion restriction is not compatible with the goals of surrogacy evaluation, as it assumes that the direct effect of treatment on the outcome is zero, which in turn assumes that S is a valid surrogate marker [7], and would therefore never be a reasonable assumption to make in this setting.

6. Assumptions made within the CA framework

As in the CE setting, some parameters of the principal surrogacy model are unidentifiable from the data, requiring assumptions to be made to aid in estimation. The assumptions that are typically made vary based on the setting being explored and on the quantities of interest. In some settings, baseline covariate information is available that can aid in estimating the missing potential outcomes of S, or a “constant biomarker” assumption can be made about the potential outcomes of S in the control arm [15, 27]. Outside of these settings, assumptions must be placed on certain model parameters or on certain relationships between potential outcomes in order to proceed with estimation. While there is not a one-to-one mapping of the principal surrogacy model parameters to the structural model parameters as there is from the structural model parameters to the principal surrogacy model parameters, the assumptions made in the principal surrogacy setting have implicit effects on the parameters of the structural model.

6.1. Prior assumptions on correlation parameters

Within the setting of multivariate normally distributed outcomes of S(0), S(1), T(0), and T(1), Conlon, Taylor and Elliott [14] used a Bayesian estimation strategy and placed different plausible prior assumptions on the unidentified correlation parameters. These assumptions, along with the positive definite restriction of the covariance matrix aided in estimation. The assumptions made include restricting the correlation parameters to be positive and a restriction with respect to the ordering of the magnitudes of the correlations. These assumptions are reasonable in many surrogate marker settings, where the surrogate marker and the final outcome are often part of the same disease process. In the context of the ovarian cancer example, it would be reasonable to assume that the correlation parameters are positive, especially if the observed correlations between PFS time and OS time within each treatment arm are positive. It may also be reasonable to assume that the correlation between PFS time and OS time within the same treatment arm, the correlation between PFS times across treatment arms and the correlation between OS times across treatment arms are larger than the correlations between PFS time and OS time in opposite treatment arms. The implications of these assumptions on the parameters of the CE model are explored below.

6.1.1. Positivity of correlations

One assumption made by Conlon, Taylor and Elliott [14] restricts all of the correlation parameters to be positive. This assumption is motivated by the fact that S and T are usually scientifically or biologically related, and therefore if a person has an inherent frailty then this will result in both S and T being higher (or lower) irrespective of the treatment that they receive. In terms of the structural model, if we assume that (β₂ + β₄) ≥ 0, which would be expected in any setting where S is being considered as a potential surrogate marker, restricting the correlation parameters to be positive requires one of the following two settings: (1) α₂ > 0, (α₂ + α₃) > 0, (β₂α₂ + β₃) > 0 and (β₃ + β₅) + (β₂ + β₄)(α₂ + α₃) > 0 or (2) α₂ < 0, (α₂ + α₃) < 0, (β₂α₂ + β₃) < 0 and (β₃ + β₅) + (β₂ + β₄)(α₂ + α₃) < 0. These settings imply that the effect of U must act in the same direction on both S and T. In our ovarian cancer data example, this implies that healthy diets are associated with both longer PFS time and longer OS time and would not be associated with a longer PFS time combined with a shorter OS time or vice versa. Figure 3 provides scatter plots from the simulation experiment of the correlation parameters of the CA model for the simulated CE model parameters. The scatter plots show that under the assumed structural model, all six of the correlations are greater than zero a majority of the time, with ρ₀₀ and ρ₁₁ nearly always positive and ρ_s and ρ_t usually positive, indicating that the positivity assumption, at least for ρ_s, ρ_t, ρ₀₀ and ρ₁₁, would be reasonable in this setting.

6.1.2. Ordering of correlations

Another assumption explored by Conlon, Taylor and Elliott [14] restricts all of the correlation parameters to be positive and also restricts ρ₁₀ and ρ₀₁ to be less than the other four correlation parameters. This constraint is reasonable as ρ₁₀ and ρ₀₁ are measures of the correlation between S and T in opposite treatment arms, which is unlikely to be larger than the correlation between the S and T within the same treatment arm, or the correlation between the surrogate responses or final treatment responses across treatment arms. As not all combinations of parameter values of the principal surrogacy model are possible under the assumed structural model, it can be shown that one such set of parameters arises under the restriction of positivity and ordering of the correlations. If only the assumption about the ordering of the correlations is imposed and positivity is not assumed, then one of the following two settings is implied in terms of the structural model: (1) α₂ > 0, (α₂ + α₃) > 0, (β₂α₂ + β₃) < 0, and (β₂ + β₄)(α₂ + α₃) + (β₃ + β₅) < 0 or (2) α₂ < 0, (α₂ + α₃) < 0, (β₂α₂ + β₃) > 0, and (β₂ + β₄)(α₂ + α₃) + (β₃ + β₅) > 0. These settings imply that the effect of U on S must be in the same direction for Z = 0 and Z = 1 and the effect of U on T must be in the opposite direction as that of U on S, but the effect of U on T must be in the same direction for Z = 0 and Z = 1. In terms of the ovarian cancer example, this would imply that patients with healthy diets have longer (shorter) PFS time, regardless of their treatment assignment, but shorter (longer) OS time in either treatment arm. The scatter plots in Figure 3 show that under the assumed structural model, the assumption that ρ₀₀ and ρ₁₁ are greater than ρ₁₀ and ρ₀₁ appears to hold nearly all the time, and the assumption that ρ_s is greater than ρ₁₀ and ρ₀₁ holds the majority of the time. However, the assumption that ρ_t is greater than ρ₁₀ and ρ₀₁ holds only about half of the time

6.2. Conditional independence assumptions

Another approach to estimation in this framework involves reducing the number of unidentified parameters that must be estimated through assumptions about conditional independences. One common conditional independence assumption that has been considered is that of conditional independence of T(0) and T(1) given S(0) and S(1) [15, 16, 28, 29]. This assumption reduces the number of unidentified parameters by one, as ρ_t becomes a function of the other five correlation parameters. Specifically, this implies that ${\rho }_t=\frac{{\rho }_{11}{\rho }_{10}+{\rho }_{01}{\rho }_{00}-{\rho }_s({\rho }_{01}{\rho }_{10}+{\rho }_{11}{\rho }_{00})}{(1-{\rho }_s^2)}$. In terms of the structural model, conditional independence of T(0, S(0)) and T(1, S(1)) given S(0) and S(1) implies that β₃(β₃ + β₅) = 0. Therefore, in order for this conditional independence assumption to hold we must have either β₃ = 0 or (β₃ + β₅) = 0, i.e. there is zero effect of the unmeasured confounder in one of the treatment arms on the outcome T. This would imply in the ovarian cancer trial example that patients with healthy diets have similar OS times to those with unhealthy diets in at least one of the treatment arms, and would therefore only be reasonable to make if diet is not thought to be associated with both OS time and PFS time.

A different conditional independence assumption was made by Parast, McDermott and Tian [17] who assumed S(0) and T(1) were conditionally independent given S(1) and that S(1) and T(0) were conditionally independent given S(0), implying in the ovarian cancer example that given knowledge of PFS time under one treatment arm, OS time in the same treatment arm and PFS in the opposite treatment arm are independent. The consequence of these assumptions is the following

$$\frac{{\rho }_{01}}{{\rho }_{11}}=\frac{{\rho }_{10}}{{\rho }_{00}}={\rho }_s.$$

The consequence if this, derived from the equations in Appendix C, requires α₂ = α₃ = β₂ = β₄ = 0 and also holds for selected other parameter combinations.

A similar, but weaker, conditional independence assumption [30] is that S(0) and T(1) were conditionally independent given S(1) and T(0) and that S(1) and T(0) were conditionally independent given S(0) and T(1), implying in the ovarian cancer example that given knowledge of both PFS time under one treatment arm and OS time in the opposite treatment arm, OS time and PFS in the other treatment arms are independent. The consequence of these assumptions are the following:

• assuming S(0) ⊥ T(1)|S(1), T(0) gives

  $$\frac{{\rho }_S{\rho }_{11}-{\rho }_{00}{\rho }_{10}{\rho }_{11}+{\rho }_T{\rho }_{00}-{\rho }_S{\rho }_T{\rho }_{10}}{{\rho }_{01}(1-{\rho }_{10}^2)}=\frac{{\sigma }_{S_0}^2{\sigma }_{T_1}^2}{{\sigma }_{S_1}^2{\sigma }_{T_0}^2}$$
  and assuming S(1) ⊥ T(0)|S(0), T(1) gives

  $$\frac{{\rho }_S{\rho }_{00}-{\rho }_{11}{\rho }_{01}{\rho }_{00}+{\rho }_T{\rho }_{11}-{\rho }_S{\rho }_T{\rho }_{01}}{{\rho }_{10}(1-{\rho }_{01}^2)}=\frac{{\sigma }_{S_1}^2{\sigma }_{T_0}^2}{{\sigma }_{S_0}^2{\sigma }_{T_1}^2}$$

6.3. Monotonicity assumption

Within the setting of a binary surrogate and final outcome, Li, Taylor and Elliott [18] impose a monotonicity assumption to aid in the problem of non-identifiability. Specifically, they require that S_i(1) ≥ S_i(0) and T_i(1) ≥ T_i(0) for all i. In terms of the structural model, this requires that α₁ + α₃U_i + e^{S_i (1)} ≥ e^{S_i (0)} and β₁ + β₄(α₀ + α₁) + β₂α₁ + [β₄(α₂ + α₃) + β₂α₃ + β₅]U_i + (β₂ + β₄)e^{S_i (1)} + e^{T_i (1)} ≥ β₂e^{S_i (0)} + e^{T_i (0)}, which cannot be satisfied with Gaussian random variables. If monotonicity is only required to hold in expectation so that E[S_i(1)] ≥ E[S_i(0)] and E[T_i(1)] ≥ E[T_i(0)], this reduces to α₁ ≥ 0 and β₁ + β₄(α₀ + α₁) + β₂α₁ ≥ 0. As α₁ and β₂ are assumed to be positive within the surrogate marker setting, this assumption will hold as long as the average total effect of Z on T is positive. In the ovarian cancer setting, this holds if on average the combined effect of treatment and PFS time in the Z = 1 arm on OS time is greater than this combined effect on OS time in the Z = 0 arm, and would be reasonable to assume in this scenario for a treatment thought to improve OS time, as PFS time is known to be positively associated with the OS time.

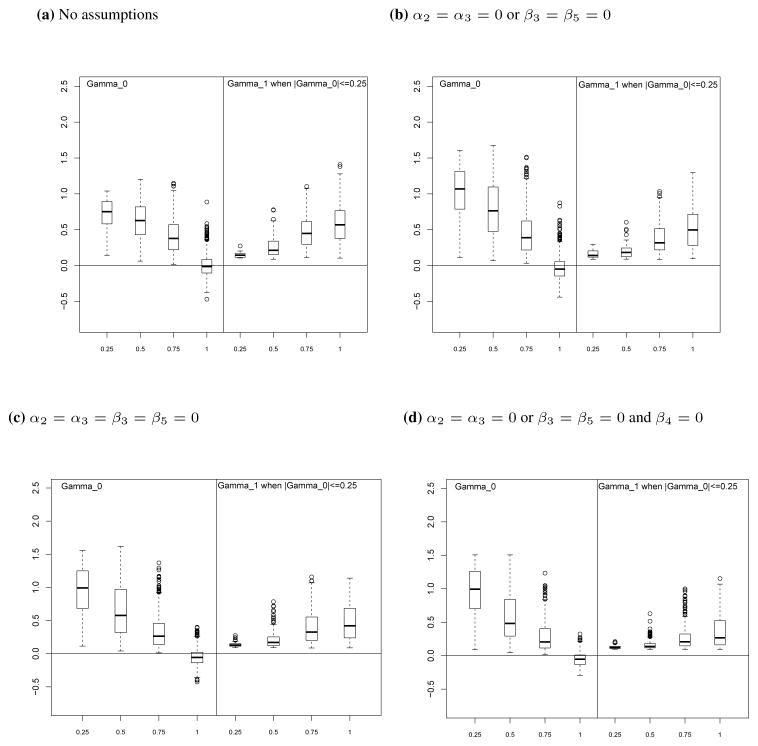
7. Numerical study of impact of assumptions on correspondence between the CE and CA metrics of surrogacy

The assumptions described in the previous sections are made either because they are reasonable in the scientific context or because they aid in estimation of quantities of interest. In this section we evaluate whether making these assumptions also leads to closer correspondence between the metrics of surrogacy in the two frameworks. Using the simulation experiment described in Section 3.3.1, we plot the distribution of γ₀ and of γ₁ when |γ₀| ≤ 0.25 for different ranges of PE(0). We note that the conditional independence assumption made by Daniels et al. [12] is not included, as the condition cannot be met under the parameter distributions used in our simulations. In the simulation experiment, for each assumption we only retain the draws of the parameters that either exactly or approximately satisfy the assumption.

7.1. Ordering of correlations assumption in CA framework

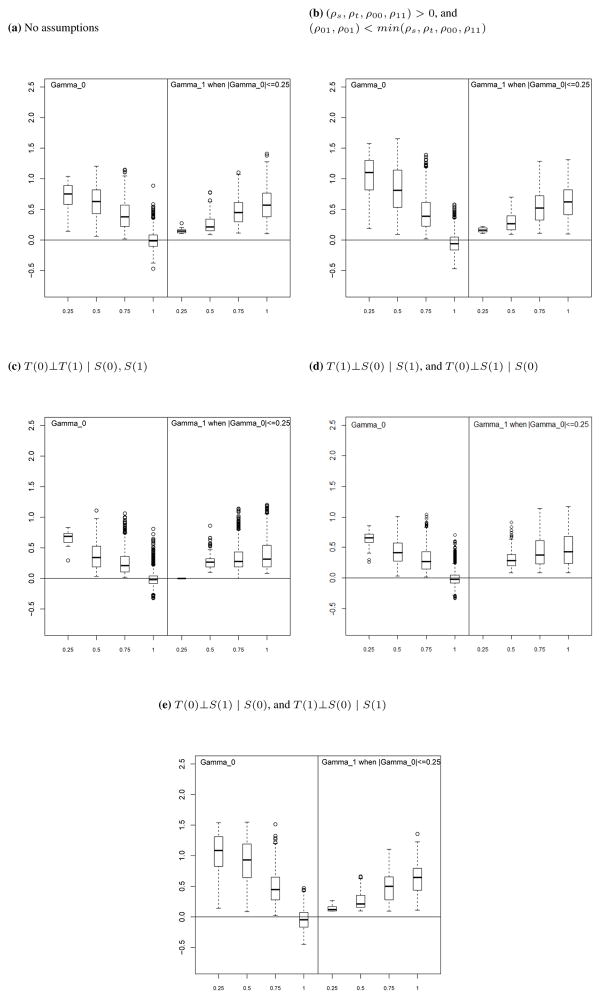
Under the assumption of Section 5.1.2 that ρ_s, ρ_t, ρ₀₀ and ρ₁₁ are all positive and that ρ₀₁ < min(ρ_s, ρ_t, ρ₀₀, ρ₁₁) and ρ₁₀ < min(ρ_s, ρ_t, ρ₀₀, ρ₁₁) the boxplots in Figure 5(b) show that the correspondence between the measures of surrogacy in the CE and CA frameworks is slightly improved as compared to the model without parameter restrictions (boxplot shown in Figure 5(a)). There is an increase in concordance between γ₀ and PE(0), with γ₀ decreasing as PE(0) increases.

Figure 5.

Correspondence between CA surrogacy measures (γ₀ and γ₁ shown on vertical axis) and CE surrogacy measure (PE(0) shown on horizontal axis) under assumptions made in the CA framework

7.2. Conditional independence assumptions in CA framework

The first conditional independence assumption of Section 5.2 is that T(0) and T(1) are independent given (S(0), S(1)). The second conditional independence assumption of Section 5.2 is that T(0) and S(1) are independent given S(0) and that T(1) and S(0) are independent given S(1) and the third conditional independence assumption of Section 5.2 is that T(1) and S(0) are independent given S(1) and that T(0) and S(1) independent given S(0).

Under the first two assumptions, the boxplots in Figures 5(c) and 5(d) show that the relationship between γ₀ and PE(0) is brought into slightly higher concordance by making these assumptions. In our simulations there were no cases where |γ₀| ≤ 0.25 when PE(0)= 0.25, indicating that when S is a poor surrogate, the CA framework and the CE framework would always agree. However, the relationship between γ₁ and PE(0) is in somewhat less concordance compared to the model with no parameter restrictions, with very little increase in γ₁ as PE(0) increases. Under the third conditional independence assumption, the boxplots in Figures 5(e) also show an increased concordance between the CE and CA measures of surrogacy, with γ₁ increasing as PE(0) increases but with slightly less concordance of γ₀ and PE(0) as compared to the first and second conditional independence assumptions.

7.3. Sequential ignorability assumptions in CE framework

Under the assumption of Section 4.1 that α₂ = α₃ = 0 or β₃ = β₅ = 0 the boxplots in Figure 6(b) and Figure 6(c) show some increase in the concordance between γ₀ and PE(0), with γ₀ larger when PE(0) is small and moving toward 0 as PE(0) increases, but little additional concordance between γ₁ and PE(0) is achieved by making this assumption.

Figure 6.

Correspondence between CA surrogacy measures (γ₀ and γ₁) and CE surrogacy measure (PE(0)) under assumptions made in the CE framework

7.4. Sequential ignorability and no interaction assumptions in CE framework

The sequential ignorability assumption of Section 4.3 together with the no interaction assumption of Section 4.4 is (i) β₄ = 0 and (ii) α₂ = α₃ = 0 or β₃ = β₅ = 0. For the combined sequential ignorability and no interaction assumption, the boxplot in Figure 6(d) shows a similar relationship between the CE and CA measures of surrogacy as with the sequential ignorability assumption alone, with some increase in the concordance between γ₀ and PE(0), but little additional concordance of γ₁ with PE(0) as compared to the model with no parameter restrictions.

8. Estimation and Sensitivity Analyses

8.1. Estimation

In the CA framework, the approach to estimation of the parameters in the multivariate normal model (Equation 3) is relatively straightforward. Either equality types of assumptions are made to make the model identifiable and likelihood based methods are used, or inequality types of constraints can be expressed in the form of prior distributions and a Bayesian approach can be taken using MCMC methods. From the estimates, inference about γ₀ and γ₁ is easy either from the delta method or directly from the MCMC draws. The Bayesian approach for not fully identified models is not without its challenges [34], especially if non-informative or only very weakly informative priors are used. In our experience [18], MCMC algorithms can be slow to converge, and from a frequentist perspective the coverage rates of 95% credible intervals can deviate from the desired level. In the CE framework, estimation of the direct and indirect effects derived from the parameters in Equations 1 and 2 usually proceeds by making identifying assumptions, such as sequential ignorability, and then non-parametrically estimating the direct and indirect effects [7,11,35,36].

Since the parameters in the CA framework are a direct function of the parameters in the CE framework, a different approach to estimation of γ₀ and γ₁ is to undertake estimation of the CE parameters in Equations 1 and 2 using a Bayesian approach, making assumptions that are appropriate for the context, and then mapping these directly to the CA parameters to obtain γ₀ and γ₁. It may even be possible to make reasonable, but not strong assumptions in both frameworks simultaneously using prior distributions, and then undertake Bayesian estimation to obtain inference for γ₀ and γ₁. For example, one might assume approximate sequential ignorability (as in Section 4.2) and approximate conditional independence (as in Section 5.2) and make inequality assumptions (as in Section 5.1).

8.2. Sensitivity Analyses

The estimation methods presented here for the CE approach assume no unobserved confounding. In the context of a randomized treatment, as is the case here, this assumption translates to “no unobserved confounding” of the surrogate-outcome relationship. Many sensitivity analyses to this unobserved confounding have been proposed, but the strategy to follow will depend on whether there is an interaction between the treatment and the surrogate and the type of the outcome (i.e. continuous or binary). In the absence of a treatment-surrogate interaction, the NDE and the CDE coincide, and thus simpler sensitivity analysis techniques, which are available for the CDE, can be employed. VanderWeele [37] develops an approach for binary confounders that computes bias in the CDE as the product of the expected difference in the outcome at the two levels of the confounder conditional on treatment and the expected difference in the confounder at the two levels of treatment. Imai et al. [11] propose a sensitivity analysis that fits more closely with the structural model proposed here, by introducing a correlation between the error terms in the structural equations for T and S. Beginning with equations analogous to Equations (1) and (2), we have,

$$S_i={\alpha }_0+{\alpha }_1{Z}_i+{\psi }_1{X}_i+e_S$$ (10)

$$T_i={\beta }_0+{\beta }_1{Z}_i+{\beta }_{2}s+{\omega }_1{X}_i+{\beta }_{4}s{Z}_i+e_T$$ (11)

Where X₁ is a measured baseline confounder and allow for the error terms e_S and e_T to be correlated. The correlation between these error terms, ρ, thus becomes the sensitivity parameter that the user must specify. Imai et al. [11] then give expressions for the NDE and the NIE in terms of the correlation term, and other parameters that can be estimated from the observed data. This method works for both continuous and binary outcomes, and has been implemented in the command medsens, as part of the R software package mediation. In the context of Equations (1) and (2), if we assume no confounder treatment interaction then the correlation between e_S and e_T is proportional to α₂β₃. Thus a sensitivity analysis could consist of estimation with this product held fixed.

An alternative approach within the CE framework, not yet attempted to our knowledge, would be to study the sensitivity to departures from the identification assumptions by using prior distributions with small variances. For example, instead of sequential ignorability assumption 1 in Table 2 that α₂ = α₃ = 0 or β₃ = β₅ = 0 set ${\alpha }_2~N(0,{\sigma }_{{\alpha }_2}^2),{\alpha }_3~N(0,{\sigma }_{{\alpha }_3}^2)$ and ${\beta }_3~N(0,{\sigma }_{{\beta }_3}^2),{\beta }_5~N(0,{\sigma }_{{\beta }_5}^2)$ where ${\sigma }_{{\alpha }_2}^2,{\sigma }_{{\alpha }_3}^2,{\sigma }_{{\beta }_3}^2$ and ${\sigma }_{{\beta }_5}^2$ are all small. For other parameters less informative priors would be used. Then proceed with Bayesian estimation.

Table 2.

Consequence of the sequential ignorability and no interaction assumptions on parameters within the CA framework.

	Assumption
	1. α2 = α3 = 0	2. β3 = β5 = 0
	No unmeasured confounders for S	No unmeasured confounders for T
ρs	0	$\frac{{\alpha }_2({\alpha }_2+{\alpha }_3)}{\sqrt{({\alpha }_2^2+{\delta }_{S0}^2)({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)}}$
ρ00	$\frac{{\beta }_2{\delta }_{S0}^2}{\sqrt{{\delta }_{S0}^2({\beta }_3^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)}}$	$\frac{{\beta }_2({\alpha }_2^2+{\delta }_{S0}^2)}{\sqrt{({\alpha }_2^2+{\delta }_{S0}^2)({({\beta }_2{\alpha }_2)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)}}$
ρ01	0	$\frac{{\alpha }_2({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)}{\sqrt{({\alpha }_2^2+{\delta }_{S0}^2)({[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)]}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$
ρ10	0	$\frac{({\alpha }_2+{\alpha }_3){\beta }_2{\alpha }_2}{\sqrt{({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)({({\beta }_2{\alpha }_2)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)}}$
ρ11	$\frac{({\beta }_2+{\beta }_4){\delta }_{S1}^2}{\sqrt{{\delta }_{S1}^2({({\beta }_3+{\beta }_5)}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$	$\frac{({\beta }_2+{\beta }_4)({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)}{\sqrt{({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)({[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)]}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$
ρt	$\frac{{\beta }_3({\beta }_3+{\beta }_5)}{\sqrt{({\beta }_3^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)({({\beta }_3+{\beta }_5)}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$	$\frac{{\beta }_2{\alpha }_2({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)}{\sqrt{({({\beta }_2{\alpha }_2)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)({[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)]}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$
γ0	$({\beta }_1+{\beta }_4({\alpha }_0+{\alpha }_1))-{\alpha }_1{\beta }_4\left(\frac{{\delta }_{S1}^2}{{\delta }_{S0}^2+{\delta }_{S1}^2}\right)$	$({\beta }_1+{\beta }_4({\alpha }_0+{\alpha }_1))-{\alpha }_1{\beta }_4\left(\frac{{\alpha }_3^2+{\alpha }_3{\alpha }_2+{\delta }_{S1}^2}{{\alpha }_3^2+{\delta }_{S0}^2+{\delta }_{S1}^2}\right)$
γ1	${\beta }_2+{\beta }_4\left(\frac{{\delta }_{S1}^2}{{\delta }_{S0}^2+{\delta }_{S1}^2}\right)$	${\beta }_2+{\beta }_4\left(\frac{{\alpha }_3^2+{\alpha }_3{\alpha }_2+{\delta }_{S1}^2}{{\alpha }_3^2+{\delta }_{S0}^2+{\delta }_{S1}^2}\right)$
	Assumption
	3. β4 = α2 = α3 = 0	4. β4 = β3 = β5 = 0
	No interaction, no unmeasured confounders for S	No interaction, no unmeasured confounders for T
ρs	0	$\frac{{\alpha }_2({\alpha }_2+{\alpha }_3)}{\sqrt{({\alpha }_2^2+{\delta }_{S0}^2)({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)}}$
ρ00	$\frac{{\beta }_2{\delta }_{S0}^2}{\sqrt{{\delta }_{S0}^2({\beta }_3^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)}}$	$\frac{{\beta }_2({\alpha }_2^2+{\delta }_{S0}^2)}{\sqrt{({\alpha }_2^2+{\delta }_{S0}^2)({({\beta }_2{\alpha }_2)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)}}$
ρ01	0	$\frac{{\alpha }_2{\beta }_2({\alpha }_2+{\alpha }_3)}{\sqrt{({\alpha }_2^2+{\delta }_{S0}^2)({[{\beta }_2({\alpha }_2+{\alpha }_3)]}^2+{\beta }_2^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$
ρ10	0	$\frac{({\alpha }_2+{\alpha }_3){\beta }_2{\alpha }_2}{\sqrt{({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)({({\beta }_2{\alpha }_2)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)}}$
ρ11	$\frac{{\beta }_2{\delta }_{S1}^2}{\sqrt{{\delta }_{S1}^2({({\beta }_3+{\beta }_5)}^2+{\beta }_2^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$	$\frac{{\beta }_2({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)}{\sqrt{({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)({[{\beta }_2({\alpha }_2+{\alpha }_3)]}^2+{\beta }_2^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$
ρt	$\frac{{\beta }_3({\beta }_3+{\beta }_5)}{\sqrt{({\beta }_3^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)({({\beta }_3+{\beta }_5)}^2+{\beta }_2^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$	$\frac{{\alpha }_2{\beta }_2^2({\alpha }_2+{\alpha }_3)}{\sqrt{({({\beta }_2{\alpha }_2)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2)({[{\beta }_2({\alpha }_2+{\alpha }_3)]}^2+{\beta }_2^2{\delta }_{S1}^2+{\delta }_{T1}^2)}}$
γ0	β1	β1
γ1	β2	β2

9. Discussion

Within the setting of Gaussian surrogate and final outcome variables, we have explored the connection between the quantities used to evaluate surrogacy within the CE framework of surrogacy assessment and the CA framework of surrogacy assessment. Under the assumed structural models for S and T, there is a direct mapping of the 14 parameters of these models to the 14 parameters of a Gaussian principal stratification model. Not all of these 14 parameters can be identified from the observed data alone, and therefore assumptions must be made in order to proceed with estimation. We have reviewed some of the common assumptions made within the CE and the CA frameworks, and explored the consequences of these assumptions on model parameters and quantities used to determine surrogacy. With parameter values from the assumed structural model that are reasonable in the surrogate marker setting, there is a close correspondence between the natural direct effect and average causal necessity. Under the assumptions of Baron and Kenny [9] of no interaction (β₄ = 0) and no unobserved confounding (α₂ = α₃ = 0 or β₃ = β₅ = 0) the surrogacy evaluation quantities in the CE and CA framework are equivalent, with E[NDE(0)] = E[NDE(1)] = γ₀ = β₁. This equivalence also holds under slightly weaker conditions of β₄ = 0 and either α₃ = 0 or β₅ = 0, however these conditions do not lead to identifiability. With the exception of the assumptions made by Baron and Kenny [9], the assumptions made within the CE or the CA framework that aid in estimation do not aid in bringing the surrogacy evaluation quantities in closer alignment.

Most estimation methods within the CE framework rely on assumptions about the absence of post-treatment unobserved confounders of S and T. This assumption is untestable and may be unlikely to hold in the surrogate marker setting, where S and T are usually involved in the same disease process. In contrast, the CA framework does not require assumptions about the absence of post-treatment confounders, as it focuses on the potential outcomes of S, which can be treated as baseline covariates. However, due to unobserved potential outcomes, assumptions must be made to aid in the estimation of unidentified parameters. If baseline covariate information is available, this may aid in the estimation of the unobserved principal strata of S. Baseline covariate information can also be used within the CE framework to relax assumptions about post-treatment confounding. However, estimation methods in this case require the presence of a baseline covariate that has an interaction effect with Z on S [1, 38], and we have shown in Appendix C that when such interactions exist, S will not be a valid surrogate within the CA framework.

The CE and CA frameworks have tradeoffs in terms of assumptions, bias in parameter estimation and variability [39]. Estimation methods within the CA framework have been shown to have less bias, but more variability than standard methods within the CE framework [40]. As the parameters of the proposed structural model have a direct mapping to the parameters of the CA model, these models offer the potential for assumptions that are reasonable to make in one framework to aid in informing the parameter values within the alternative framework. In this way, both the CE and CA models could be employed with reasonable, but not especially strong assumptions made in the evaluation of S as a surrogate marker. While the research in this paper has focused on the situation of surrogate markers, the frameworks of CA and CE have also been considered in mediation analysis. It would be of interest to evaluate the correspondence between the metrics of mediation in this setting too. We have focused on Gaussian variables and linear models and have shown a certain degree of correspondence for evaluating the surrogates, and the degree of correspondence increasing if certain assumptions are made. For non-Gaussian variables we hypothesize we might expect broadly similar findings, but with possibly a lower degree of correspondence, due to the nonlinear link functions in the models.

A. Relationship of CE and CA model parameters

The parameters of the principal surrogacy model (Equation 3) relate to those of the assumed structural model (Equations 1 and 2) assuming U ~ N(0, 1) in the following way:

• μ_S0 = α₀

• μ_S1 = α₀ + α₁

• μ_T0 = β₀ + β₂α₀

• μ_T1 = β₀ + β₁ + (β₂ + β₄)(α₀ + α₁)

• ${\sigma }_{S_0}^2={\alpha }_2^2+{\delta }_{S0}^2$

• ${\sigma }_{S_1}^2={({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2$

• ${\sigma }_{T_0}^2={({\beta }_2{\alpha }_2+{\beta }_3)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2$

• ${\sigma }_{T_1}^2={[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2$

• ${\rho }_s=\frac{{\alpha }_2({\alpha }_2+{\alpha }_3)}{\sqrt{{\alpha }_2^2+{\delta }_{S0}^2}\sqrt{{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2}}$

• ${\rho }_{00}=\frac{{\alpha }_2({\beta }_2{\alpha }_2+{\beta }_3)+{\beta }_2{\delta }_{S0}^2}{\sqrt{{\alpha }_2^2+{\delta }_{S0}^2}\sqrt{{({\beta }_2{\alpha }_2+{\beta }_3)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2}}$

• ${\rho }_{01}=\frac{{\alpha }_2[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]}{\sqrt{{\alpha }_2^2+{\delta }_{S0}^2}\sqrt{{[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2}}$

• ${\rho }_{10}=\frac{({\alpha }_2+{\alpha }_3)({\beta }_2{\alpha }_2+{\beta }_3)}{\sqrt{{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2}\sqrt{{({\beta }_2{\alpha }_2+{\beta }_3)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2}}$

• ${\rho }_{11}=\frac{({\alpha }_2+{\alpha }_3)[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]+({\beta }_2+{\beta }_4){\delta }_{S1}^2}{\sqrt{{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2}\sqrt{{[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2}}$

• ${\rho }_t=\frac{({\beta }_2{\alpha }_2+{\beta }_3)[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]}{\sqrt{{({\beta }_2{\alpha }_2+{\beta }_3)}^2+{\beta }_2^2{\delta }_{S0}^2+{\delta }_{T0}^2}\sqrt{{[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]}^2+{({\beta }_2+{\beta }_4)}^2{\delta }_{S1}^2+{\delta }_{T1}^2}}$.

B. Parameter distributions and R² values for regression models of T|Z, T|S and T|U from simulation experiment

For the simulation experiment, the CE model parameters were generated such that

• α₀, β₀ = 0,

• α₁ ~ U(0.25, 1.5),

• α₂ ~ U(max(−0.5,min(−α₁ + 0.05, α₁ − 0.05)),max(−α₁ + 0.05, α₁ −0.05)),

• α₃ ~ U(min(−α₂/2, α₂/2),max(−α₂/2, α₂/2)),

• β₁ ~ U(−0.3, 1.5),

• β₂ ~ U(0.1, 1.5),

• β₃ ~ U(max(−0.5,min(−β₂ + 0.05, β₂ − 0.05)),max(−β₂ + 0.05, β₂ − 0.05)),

• β₄ ~ U(min(−β₂/3, β₂/3),max(−β₂/3, β₂/3)),

• β₅ ~ U(min(−β₃/2, β₃/2),max(−β₃/2, β₃/2)),

• ${\delta }_{S0}^2,{\delta }_{T0}^2~U(0.3,1)$,

• ${\delta }_{S1}^2={\delta }_{S0}^2$,

• ${\delta }_{T1}^2={\delta }_{T0}^2$.

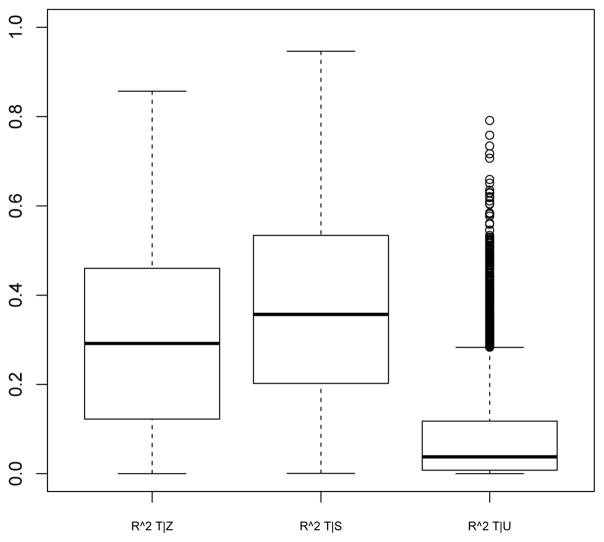
Figure B.1 below provides boxplots of the R² values across all of the parameter draws for regression models of T|Z, T|S and T|U, where S and T are 10,000 random samples from each set of parameter draws. The plots show that the simulated parameters lead to a broad range of R² values, indicating that the way in which the parameters were simulated was not overly restrictive and leads to a wide spectrum of scenarios.

Figure B.1.

Proportion of variance of T explained by Z, S and U for a range of plausible values from the assumed structural model.

C. Consequence of conditional independence assumptions in the CA framework on parameters in the CE model

In terms of the structural model, the assumptions that S(0) and T(1) are conditionally independent given S(1) and that S(1) and T(0) are conditionally independent given S(0) requires the following

$$\begin{array}{l}\frac{({\beta }_2{\alpha }_2+{\beta }_3)({\alpha }_2+{\alpha }_3)({\alpha }_2^2+{\delta }_{S0}^2)-{\alpha }_2^2{({\alpha }_2+{\alpha }_3)}^2-{({\alpha }_2({\beta }_2{\alpha }_2+{\beta }_3)+{\beta }_2{\delta }_{S0}^2)}^2}{{\alpha }_2^2+{\delta }_{S0}^2}=\\ \frac{{\alpha }_2[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]({({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2)-{\alpha }_2^2{({\alpha }_2+{\alpha }_3)}^2-{([({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]({\alpha }_2+{\alpha }_3)+({\beta }_2+{\beta }_4){\delta }_{S1}^2)}^2}{{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2}=0.\end{array}$$

D. Baseline covariates

Under the structural model with covariates, the direct and indirect effects of the CE framework become: E[NDE(0)|X = x] = β₁ + α₀β₄ + (β₄ψ₁ + ω₂)x, E[NDE(1)|X = x] = β₁ + β₄(α₀ + α₁) + (β₄(ψ₁ + ψ₂) + ω₂) x, E[NIE(0)|X = x] = β₂(α₁ + ψ₂x), E[NIE(1)|X = x] = (β₂ + β₄)(α₁ + ψ₂x), and E[TE|X = x] = (β₂ + β₄)α₁ + α₀β₄ + β₁ + ((β₂ + β₄)ψ₂ + β₄ψ₁ + ω₂) x. If there is no interaction effect of X and Z on S (ψ₂ = 0), then the indirect effect will not be changed by the presence of baseline covariates. Under the assumption of sequential ignorability, estimates of the direct and indirect effects in the presence of a baseline covariate can be obtained non-parametrically by integrating over the distribution of X. The Prentice model in the presence of baseline confounders becomes: E[T|S,Z] = θ₀ + θ₁Z + θ₂S + θ₃SZ + θ₄X + θ₅XZ, where θ₁ and θ₃ are as in Section 3.2 and ${\theta }_4={\omega }_1-\left(\frac{{\alpha }_2({\beta }_2{\alpha }_2+{\beta }_3)+{\beta }_2{\delta }_{S0}^2}{{\alpha }_2^2+{\delta }_{S0}^2}\right){\psi }_1$ and ${\theta }_5={\omega }_2+\left(\frac{{\alpha }_2({\beta }_2{\alpha }_2+{\beta }_3)+{\beta }_2{\delta }_{S0}^2}{{\alpha }_2^2+{\delta }_{S0}^2}\right){\psi }_1-\left(\frac{({\alpha }_2+{\alpha }_3)[({\beta }_2+{\beta }_4)({\alpha }_2+{\alpha }_3)+({\beta }_3+{\beta }_5)]+({\beta }_2+{\beta }_4){\delta }_{S1}^2}{{({\alpha }_2+{\alpha }_3)}^2+{\delta }_{S1}^2}\right)({\psi }_1+{\psi }_2)$. Therefore, if there are no unmeasured confounders, the Prentice criteria will be a valid measure of surrogacy (θ₁ = θ₃ = θ₅ = 0) if there is no interaction effect of X and Z on either S or T (ω₂ = ψ₂ = 0) and additionally if either ψ₁ or β₄ is zero. In this case, the baseline covariate information aids in estimation and does not affect the ability to determine surrogacy. Under certain conditions, it is possible to relax the sequential ignorability assumption when baseline covariates are available. For example, when sequential ignorability cannot be assumed and baseline covariates are available for which E[S(1) | X] − E[S(0) | X] varies with X (i.e. ψ₂ ≠ 0), and there is no interaction effect of either Z and S on T or of Z and X on T (i.e. β₄ = ω₂ = 0), Joffe and Greene [1] showed that a two-stage least squares procedure can be used to estimate the direct and indirect effects. Ten Have et al. [38] estimate the direct and indirect effects under the same conditions as Joffe and Greene [1] by assuming the following rank preserving model for T: T(z, s) = g(x) + γ_Zz + γ_Ss + ε and using a G-estimation procedure. Within the CA framework, if baseline covariates are present, the surrogacy quantities of interest become: $E[T(1)-T(0)\mid S(1)-S(0)=s,X=x]=({\mu }_{T_1}-{\mu }_{T_0})-\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right)({\mu }_{S_1}-{\mu }_{S_0})+\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right)s+\left({\omega }_2-\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right){\psi }_2\right)x={\gamma }_0+{\gamma }_{1}s+\left({\omega }_2-\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right){\psi }_2\right)x$. When there is no interaction of X and Z on either S or T (ψ₂ = ω₂ = 0), neither γ₀ nor γ₁ are affected by the presence of baseline covariates. In this case, controlling for X is helpful in explaining some of the variance of the potential outcomes and does not affect the ability to estimate γ₀ or γ₁. When there is an interaction of X and Z on either S or T, γ₁ is not affected but γ₀ becomes a function of x: ${\gamma }_0=({\mu }_{T_1}-{\mu }_{T_0})-\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right)({\mu }_{S_1}-{\mu }_{S_0})+\left({\omega }_2-\left(\frac{{\rho }_{11}{\sigma }_{S_1}{\sigma }_{T_1}-{\rho }_{10}{\sigma }_{S_1}{\sigma }_{T_0}-{\rho }_{01}{\sigma }_{S_0}{\sigma }_{T_1}+{\rho }_{00}{\sigma }_{S_0}{\sigma }_{T_0}}{{\sigma }_{S_0}^2+{\sigma }_{S_1}^2-2{\rho }_s{\sigma }_{S_0}{\sigma }_{S_1}}\right){\psi }_2\right)x$. In this case, when there is no treatment effect on S, the expected treatment effect on T depends on the baseline covariate, implying that S may only be a valid principal surrogate for T within certain subgroups defined by X. In order for ACN to be met and S to be considered a valid principal surrogate, we would need to have γ₀ = 0 for all X, requiring ∫_x E[T(1) − T(0) | S(1) − S(0) = 0,X = x]f(X | S(1) − S(0) = 0)dx be equal to zero, which is unlikely to hold. Therefore, in order for S to be considered a valid principal surrogate, there can be no interaction of the baseline covariate X with Z, so that both ψ₂ and ω₂ are equal to zero. In the CA framework, baseline covariates have also been used to aid in estimating the principal strata of S. For example, a model for f(S(1) | X,Z = 1) can be estimated using the surrogate response values in the Z = 1 arm and a model for f(S(0) | X,Z = 0) can be estimated using the surrogate response values in the Z = 0 arm. These models can then be used to impute missing S(1) values in patients in the Z = 0 arm and missing S(0) values in patients in the Z = 1 arm, respectively [15,16]. Implicit in this assumption is that [S(1) | X, S(0)] = [S(1) | X], requiring that ρ_s = 0, i.e. that either α₂ = 0 or α₂ + α₃ = 0.