Accelerated non-contrast enhanced 4-dimensional intracranial MR angiography using golden-angle stack-of-stars trajectory and compressed sensing with magnitude subtraction

Abstract

Purpose

To evaluate the feasibility and performance of compressed sensing (CS) with magnitude subtraction regularization in accelerating non-contrast enhanced dynamic intracranial MR angiography (NCE-dMRA).

Methods

A CS algorithm was introduced in NCE-dMRA by exploiting the sparsity of the magnitude difference of the control and label images. NCE-dMRA data were acquired using golden-angle stack-of-stars trajectory on six healthy volunteers and one patient with arteriovenous fistula. Images were reconstructed using 1) the proposed magnitude-subtraction CS (MS-CS); 2) complex-subtraction CS (CS-CS); 3) independent CS (iCS); and 4) view sharing with k-space weighted image contrast (KWIC). DMRA image quality was compared across the four reconstruction strategies. The proposed MS-CS method was further compared with KWIC for temporal fidelity of depicting dynamic flow.

Results

The proposed MS-CS method was able to reconstruct NCE-dMRA images with detailed vascular structures and clean background. It provided better subjective image quality than the other two CS strategies (p<0.05). Compared with KWIC, MS-CS showed similar image quality, but reduced temporal blurring in delineating fine distal arteries.

Conclusions

The MS-CS method is a promising CS technique for accelerating NCE-dMRA acquisition without compromising image quality and temporal fidelity.

Introduction

The detailed characterization of dynamic flow patterns is important in the diagnosis of cerebrovascular diseases, such as arteriovenous malformation (AVM), arteriovenous fistula (AVF), and intracranial aneurysm (1). Non-contrast enhanced dynamic MR Angiography (NCE-dMRA) (2-6) has become a promising approach due to its completely non-invasive nature and lack of ionizing radiation, compared to digital subtraction angiography (DSA) and dynamic contrast-enhanced MRA (DCE-MRA) (7). The conventional intracranial NCE-dMRA technique combines arterial spin labeling (ASL) with multi-phase k-space segmented balanced steady-state free precession (bSSFP) sequence, and is able to provide dynamic information with high spatial (~1mm³) and temporal (~100ms) resolution for the evaluation of cerebral malformations (5,8-10) and steno-occlusive diseases (11). However, the segmented cine acquisition usually requires a relatively long scan time to achieve sufficient spatiotemporal resolution and spatial coverage (8,9), which potentially hampers the application of NCE-dMRA in clinical practice.

Golden angle radial acquisition (12) in conjunction with k-space weighted image contrast (KWIC) reconstruction (13,14) was proposed to accelerate the NCE-dMRA acquisition by up to threefold (15). KWIC is a projection view-sharing technique based on radial k-space sampling (13,14). KWIC applies a spatiotemporal filter by using progressively more radial projection views towards outer k-space so that the image series can be reconstructed at a relative high temporal resolution without introducing severe streaking artifacts. However, a potential drawback of view-sharing techniques such as KWIC is temporal smoothing of rapidly changing events in vessels and at vessel boundaries (16,17).

Recent developments in applying compressed sensing (CS) theory to MRI have revealed new ways of accelerating image acquisition (18). By exploiting the signal sparsity in a transformation domain, CS could reconstruct MRI images from randomly under-sampled k-space by optimizing a non-linear function. It has been successfully applied in cardiac cine imaging (19), phase-contrast flow imaging (20), and dynamic contrast-enhanced body imaging applications (21). However, to date, very few studies have attempted to apply CS in ASL based applications due to the inherently low SNR of ASL signal. Han et al. (22) utilized the complex image subtraction sparsity between control and label images to reconstruct under-sampled perfusion ASL data. Similarly, Zhao et al. (23) enforced sparsity of image under a perfusion model after the complex k-space subtraction of control and label acquisitions and applied it for cerebral ASL perfusion reconstruction. Although complex subtraction sparsity is theoretically sound, it is, in practice, sensitive to phase errors caused by motion and other sources of off-resonance (24,25), especially in the case of bSSFP readout.

A CS algorithm has recently been developed, which takes advantage of the sparsity of the magnitude subtraction (MS) between the pre- and post-contrast images in thoracic DCE-MRA (26). Since the same subtraction sparsity may be applied to ASL-based MRA between the control and label images, we hypothesized that the magnitude-subtraction CS (MS-CS) method could be used to accelerate the acquisition of NCE-dMRA with high spatial and temporal resolutions. In this study, we focused on (1) investigation of the feasibility of using MS-CS to reconstruct highly under-sampled golden-angle stack-of-stars (SOS) NCE-dMRA data set; (2) comparison of the MS-CS method with the conventional independent CS (iCS) and complex-subtraction CS (CS-CS) methods (24,25) for image quality; and (3) comparison of MS-CS with KWIC in terms of temporal fidelity for depicting dynamic blood flow.

Methods

Similar to a previous work (26), the NCE-dMRA control and label data were reconstructed by optimizing Eq.1 for each temporal frame.

$$\mathrm{MS}­\mathrm{CS}:(m_1,m_2)=\mathit{argmin}\left(\begin{array}{c}{{\sum }_{i=1}^N\Vert \mathit{NUFFT}(S_i{m}_1)-y_1^i\Vert }^2+\lambda {\Vert W{m}_1\Vert }_1+\mu {\Vert m_1\mid -\mid m_2\Vert }_1\\ \begin{array}{c}{{\sum }_{i=1}^N\Vert \mathit{NUFFT}(S_i{m}_2)-y_2^i\Vert }^2+\lambda {\Vert W{m}_2\Vert }_1+\mu {\Vert m_1\mid -\mid m_2\Vert }_1\\ \end{array}\end{array}\right)$$ (Eq.1)

where $y_1^i$ and $y_2^i$ are acquired single coil (i^th coil) k-space data for control and label acquisitions in one frame; m₁ and m₂ are corresponding coil combined control and label images to be recovered jointly, NUFFT(·) is the non-uniform fast Fourier transform (27) that transforms image to radial k-space data; S_i is the sensitivity map of the i^th coil; W is the randomized shifting Daubechies spatial wavelets transform; ║m₁| − |m₂║₁ is the L1 norm of the pixel-wise magnitude difference between the control and label images; and λ and μ are regularization parameters.

To demonstrate the effectiveness of magnitude subtraction regularization, the conventional iCS and CS-CS reconstructions were also performed using the following equations:

$$\mathrm{iCS}:\{\begin{array}{c}{m}_1=\mathit{argmin}{{\sum }_{i=1}^N\Vert \mathit{NUFFT}(S_i{m}_1)-y_1^i\Vert }^2+\lambda {\Vert W{m}_1\Vert }_1\\ \begin{array}{c}{m}_2=\mathit{argmin}{{\sum }_{i=1}^N\Vert \mathit{NUFFT}(S_i{m}_2)-y_2^i\Vert }^2+\lambda {\Vert W{m}_2\Vert }_1\\ \end{array}\end{array}$$ (Eq.2)

$$\mathrm{CS}­\mathrm{CS}:I=\mathit{argmin}{\sum }_{i=1}^N{\Vert \mathit{NUFFT}(S_{i}I)-(y_1^i-y_2^i)\Vert }^2+\lambda {\Vert I\Vert }_1$$ (Eq.3)

where I is the final complex subtracted image and ║I║₁ is the L1-norm in the image domain.

MRI experiments

Six healthy volunteers (aged 28-32 years, 4 male) and one patient (23 y.o., male) with AVF were included in this study, after obtaining Institutional Review Board (IRB) approval and informed consent. All subjects were scanned on a 3T scanner (PRISMA, Siemens Healthcare, Erlangen, Germany) using a 20-channel head coil. NCE-dMRA data were collected using the previously proposed golden-angle SOS NCE-dMRA sequence (15) with the following parameters: spatial resolution=1×1×1.5 mm³; FOV=256×256×48 mm³, TE/TR=2.43/4.86ms, FA=25° (due to specific absorption rate constraint), BW=814Hz/pixel, 500 views per shot, one shot per slice, acquisition time: 3min. The sequence diagram for the 3D golden-angle SOS acquisition is illustrated in Figure 1. A 6-min 3D Cartesian NCE-dMRA scan without view-sharing (2) was performed as the gold standard for dynamic information. The spatial resolution and imaging coverage were identical to those of the 3D SOS scan. A total of 25 phases with a temporal resolution of 100ms were collected in the Cartesian acquisition. The sequence diagrams for the 3D Cartesian acquisition is illustrated in Supporting Figure S1. In order to minimize the potential off-resonance artifacts near the sinuses, the imaging slab of both 3D SOS and Cartesian acquisitions was tilted to avoid these regions. This is done on 3 out of 7 subjects. In addition, time-of-flight (TOF) MRA images were acquired as a reference for the anatomical information.

Figure 1.

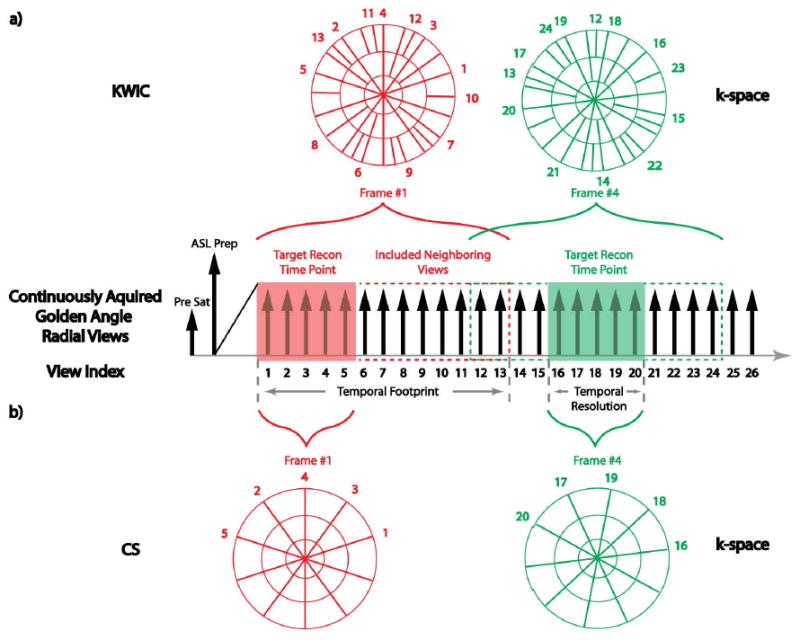
Sequence diagram of 3D SOS NCE-dMRA, which combines ASL with a continuous golden-angle bSSFP readout. An example of data binning with KWIC filtering and CS reconstruction is also shown in a) and b), respectively. In KWIC, K-space is divided into 3 regions, with 5 views (size of the target reconstruction time point) in the center region, 8 views in the middle region, and a total of 13 views in the outer region. For frame #1, included neighboring views (8 views) all reside on one side. For frame #4, included neighboring views symmetrically reside on both sides. In CS reconstructions, neighboring views are not included. Each frame only contains 5 views without overlapping with each other.

Image reconstruction

Each golden-angle SOS NCE-dMRA dataset was binned into 20 views per frame, i.e., a temporal resolution of 97ms, and reconstructed with the aforementioned three CS strategies respectively: MS-CS (Eq.1), iCS (Eq.2), and CS-CS (Eq.3). For demonstration purpose, one dataset was binned to 10, 20, and 30 views per frame separately and reconstructed with the MS-CS algorithm. The radials views in this demonstration reconstruction were aligned in such a way that the 10 views in the 10-view reconstruction corresponded to the middle 10 views of the 20-view reconstruction, and the 20 views in the 20-view reconstruction corresponded to the middle 20 views of the 30-view reconstruction. In addition, each dataset was binned using the KWIC method and reconstructed with the standard gridding reconstruction (28) with a k-space temporal filter described in (14), to reduce possible temporal blurring effect. The specific parameters of KWIC reconstruction were chosen based on the previous study (15): 20 views at the k-space center, 40 more views were added in each outward adjacent annular ring region, with a total of 5 rings and 160 views per frame for the outer-most ring.

All CS image reconstruction algorithms were implemented based on the Berkeley Advanced Reconstruction Toolbox (29,30). The regularization parameters were determined based on a pilot study on two volunteers for parameter optimization. Specifically, we normalized the data sets prior to reconstruction and varied the regularization parameter(s) in each method from 0.05 to 1.0 in a step size of 0.05 to identify the optimal value(s) that would provide the best image quality by visual assessment among the reconstructed images for each method. Selected regularization parameter(s) for the three CS reconstructions were: λ = 0.1, μ = 0.4 for MS-CS; λ = 0.4 for iCS; and λ = 0.2 for CS-CS. After the reconstruction of all image slices, label and control images were subtracted (except for CS-CS method in which the subtracted image is directly reconstructed) and maximum-intensity-projection (MIP) images along axial, coronal, and sagittal planes were generated.

Image evaluation

The image quality of the three CS as well as the KWIC reconstructions were subjectively graded independently by two reviewers (both are MRI experts with over seven years of experience). Images were evaluated in terms of vessel delineation and artifacts/noise on a 4-point scale: 1. Poor delineation of all-sized arteries, with severe streaking artifact and noise leading to nondiagnostic images; 2. Confident delineation of large arteries (M1, P1/2), but with considerable artifacts and noise that compromise the evaluation of intermediate and small arteries (M2,3,4 and P3,4); 3. Confident delineation of large and intermediate arteries (M1,2, and P1,2), with little artifacts and low noise level that only impairs the definition of the fine structures of small vessels (M3,4 and P3,4); 4. Confident delineation of all-size arteries (M1,2,3,4 and P1,2,3,4) with minimal artifacts and noise.

To evaluate the performance of the proposed MS-CS method on the temporal delineation of dynamic blood flow, we defined a weighted arrival time (wAT) as follows (31):

$$\mathit{wAT}=\frac{{\sum }_{t}I(t)\ast t}{{\sum }_{t}I(t)}$$ (Eq.4)

where I(t) is the signal intensity at time t. Quantitative wAT maps were calculated from MS-CS and KWIC reconstructions as well as the reference Cartesian acquisition. Five regions of interest (ROIs) encompassing different vascular regions (M1, M2, M3/4, P1/2, P3) were manually drawn on the calculated wAT maps, from which average wAT values were measured using the following method: An intensity threshold was set for each region such that the intensity of the smallest visible vessels within the region were above the threshold. The threshold was then used as a mask to exclude pixels with signal intensity below the threshold. wAT values from the remaining pixels were then averaged and reported as the final wAT value for the region.

Signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) were also calculated for MS-CS, KWIC and Cartesian reconstructed images, using the approach previously described (15). Specifically, a 16×16 square ROI was drawn on the M1 vessel and adjacent background from a MIP image that corresponds to the signal peak in each time series. All pixels were then averaged to determine the mean signal. Average noise level was calculated by taking the standard deviation of a background ROI placed far away from brain to avoid any motion or reconstruction related artifacts. SNR was then calculated as the ratio of the mean signal to the standard deviation of background noise. As for CNR measurement, the M1 signal used in SNR measurement were subtracted by the brain tissue signal that measured from a ROI placed between the middle and posterior cerebral arteries where vessels were absent. The resulting signal difference was then divided by the standard deviation of background noise to calculate CNR.

Statistical analysis

For subjective image quality scores, a Friedman test was performed among the four reconstructions to detect statistically significant differences. Post-hoc analyses with Wilcoxon signed-rank test were subsequently conducted to detect pairwise differences. For wAT, statistical significance for each ROI was determined between the three reconstructions using a repeated-measures analysis of variance (ANOVA) followed by a post-hoc paired t-test for the pairwise comparisons. In all the statistical pairwise comparisons, the null hypothesis was that there was no significant difference in image quality scores or wAT values between the two techniques. A two-tailed P<0.05 was considered statistically significant. The weighted kappa coefficient was used to evaluate the inter-observer agreement for the quality score. All statistical analyses were conducted using R software (version 3.3.1).

Results

All scans were successfully performed. The Cartesian dMRA images were directly reconstructed using the vendor-provided program. The MS-CS, iCS, CS-CS and KWIC reconstructions of the golden-angle SOS data took on average 4.7 minutes, 2 minutes, 1.3 minutes and 30s for the calculation of each temporal frame, respectively.

Figure 2 demonstrates the effects of different regularization terms on the proposed MS-CS method. The image reconstructed without any regularization (lower right), which is equivalent to the SENSE reconstruction, has the lowest SNR and inferior vessel delineation. Adding one regularization term was able to improve the image quality; however, the image with magnitude subtraction alone (lower left) had fewer streaking artifacts and lower noise level than the one with wavelets alone (upper right). Combing both regularization terms (upper left) further improved vessel delineation especially of fine structures.

Figure 2.

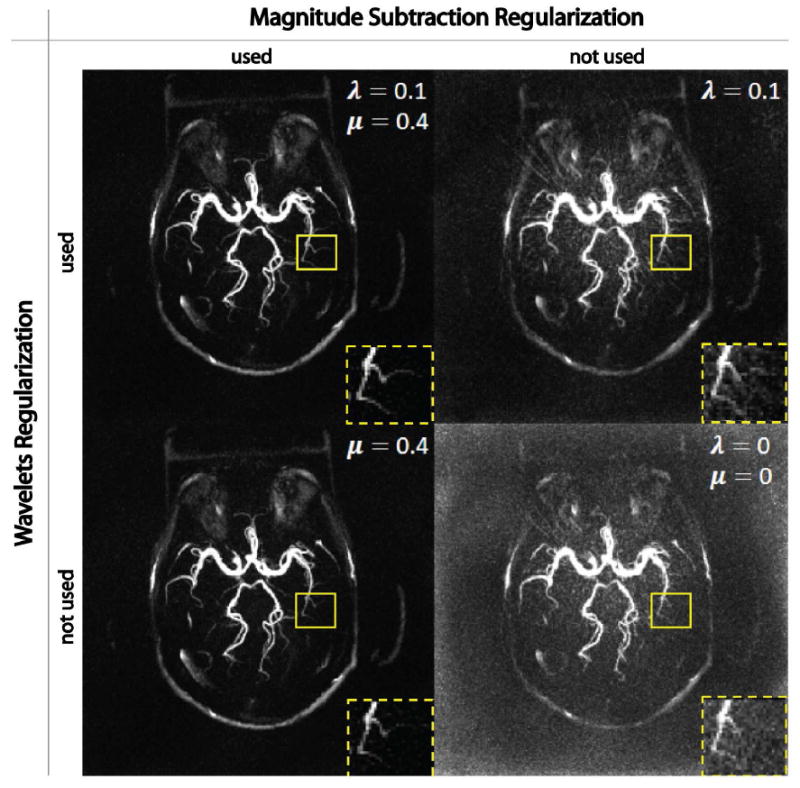
Demonstration of the contributions of magnitude subtraction regularization and wavelets regularization in the proposed MS-CS method. Without any regularization (lower right), reconstructed image has high noise level and suffers the loss of fine structures. By adding a single regularization term, image quality is significantly improved, although using magnitude subtraction (lower left) shows more improvement than wavelets (upper right). Combining the two regularizations provides the best image quality among all combinations. All images were normalized by its maximum intensity and displayed at the same window level.

Figure 3 illustrates four selected temporal frames of dMRA reconstructed with three different number of views per frame using the proposed MS-CS reconstruction. With 10 views per frame, the reconstructed images show residual streaking artifacts (red arrows) and increased background noise that precludes the visualization of small-sized vessels (yellow arrows). With 20 views per frame, the reconstructed images provide good image quality with sufficient SNR and adequate delineation of different vessels. With 30 views per frame, the reconstructed images demonstrate even better SNR that provides detailed delineation of all sizes of vessels. However, a wider reconstruction window would result in lower temporal resolution that may not capture sufficient temporal information. Based on visual inspection, the choice of 20 views per frame represents a good balance between image quality and temporal sampling rate.

Figure 3.

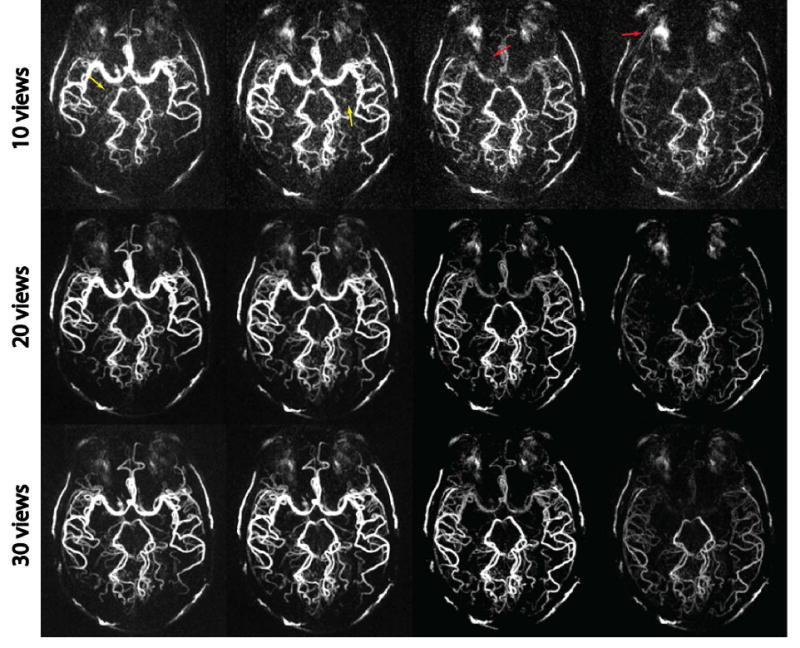
MIP images of a golden-angle SOS acquisition reconstructed with the MS-CS method using 10 views, 20 views and 30 views per frame. With 10 views per frame, increased noise (yellow arrow) and residual streaking artifacts (red arrow) are noted in the images. With 20 views per frame, reconstructed images provide adequate delineation of different sizes of vessels. With 30 views per frame, the reconstructed images have even better SNR, but a wider reconstruction window potentially results in a reduced temporal resolution. The use of 20 views represents a good balance between image quality and temporal resolution.

Figure 4 compares the three CS reconstruction strategies on one volunteer at four temporal frames. The conventional iCS reconstruction (middle row) shows residual streaking artifacts (yellow arrow) and fails to recover fine structures (red arrows), as it does not benefit from the subtraction sparsity. This is also reflected in the subjective quality scores in Table 1, where iCS had the lowest score (2.75±0.62) among all reconstruction strategies. The CS-CS reconstruction uses the additional information in complex subtraction regularization, and this indeed reduced the streaking artifact, with a slightly higher score (2.83±0.57), although no statistical significance was reached (P=0.38). However, due to the increased sensitivity to phase errors in complex subtraction, the CS-CS reconstruction suffers from loss of SNR, resulting in slightly increased noise level that submerged fine anatomical details (green arrows). The proposed MS-CS reconstruction was able to reconstruct images with clean background, sharp contrast, and adequate details. This improvement was confirmed by a significant higher score (3.83±0.38 vs. 2.75±0.62 vs. 2.83±0.57, P<0.05) when compared with both iCS and CS-CS. The MS-CS image quality scores were comparable to that of KWIC reconstruction (3.83±0.38 vs. 3.78±0.39, p=0.21). Scores from the two raters had moderate to excellent agreement, depending on the imaging and reconstruction techniques.

Figure 4.

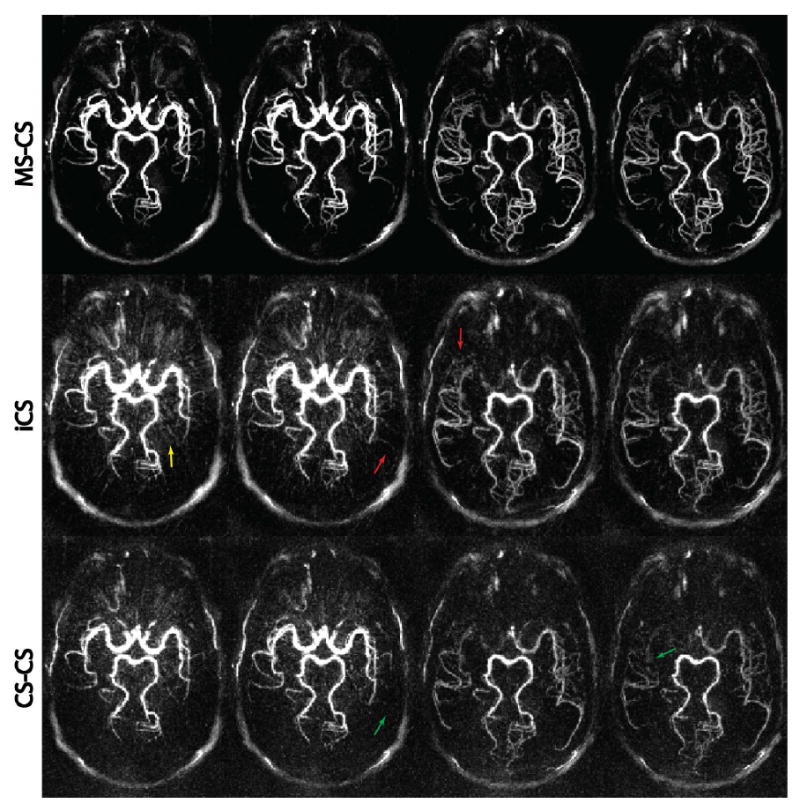
Comparison of the three CS reconstruction strategies. From top to bottom, each row represents axial MIP images at four time frames reconstructed with MS-CS, iCS, and CS-CS, respectively. Severe streaking artifacts and high noise level are clearly visible on the iCS and CS-CS reconstructions, while the proposed MS-CS reconstruction provides cleaner and sharper images. All images were normalized by its maximum intensity and displayed at the same window level.

Table 1.

Subjective image quality scores and weighted kappa coefficients к for different imaging techniques.

	MS-CS	iCS	CS-CS	KWIC
	1	2	3	4
Image Quality	3.83±0.38a	2.75±0.62	2.83±0.57	3.78±0.39b
к	0.83	0.92	0.85	0.82

^ap<0.05 (compared with iCS and CS-CS);

^bp<0.05 (compared with iCS and CS-CS). No significance was detected between MS-CS and KWIC, and between iCS and CS-CS.

Figure 5 shows the comparison of KWIC and MS-CS reconstruction, as well as the reference Cartesian acquisition. Overall, good to excellent dMRA image quality was achieved with both KWIC and MS-CS reconstructions. However, differences were evident in the dynamics of blood flow in certain regions between the two reconstructions. KWIC reconstruction showed early filling of distal branches of middle cerebral artery (MCA) (M3,4) and posterior cerebral artery (PCA) (P3) (yellow arrows) at the first two frames. It also had a delayed drainage of middle branches of MCA (M2) and PCA (P1/2) (green arrows) at the last two frames. At the corresponding positions mentioned above (red and blue arrows), the presence of arteries in MS-CS reconstruction matched well with the reference Cartesian acquisition. The average SNR (±standard deviation) and CNR of the MS-CS reconstruction of all healthy volunteers were 61.5(±3.3) and 53.9(±4.5), respectively, 63.2(±5.2) and 56.4(±3.8) for KWIC reconstruction, and those of Cartesian were 89.6(±4.6) and 82.3(±5.7).

Figure 5.

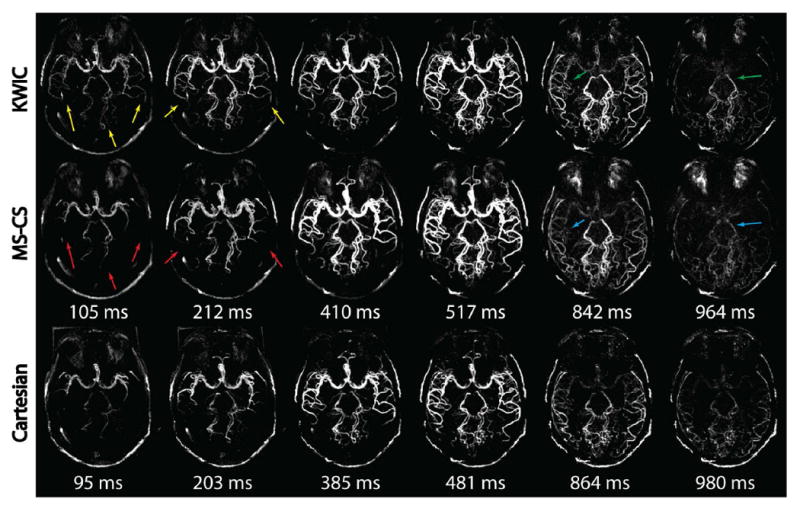
MIP images of KWIC reconstruction, MS-CS reconstruction and Cartesian reference acquisition at six frames. Comparable image quality without visible streaking artifacts was obtained by KWIC and CS-CS reconstructions. However, the view-sharing in KWIC caused early filling (yellow arrows) and late drainge (green arrows) of small vessels at different regions, while the proposed method provided improved temporal delineation (red and blue arrows) comparable to Cartesian acquisition.

Figure 6 shows comparisons of temporal MIP (tMIP) as well as the wAT maps for KWIC and MS-CS reconstructions and Cartesian acquisition from one representative volunteer. The tMIP images showed similar spatial information of vascular structures across the three techniques. However, the wAT maps exhibited visible differences in intermediate to distal MCA (blue arrow) and the entire PCA (green arrow) regions. ANOVA tests confirmed this observation with P<0.05 in M2, M3/4, P1/2 and P3 regions, but P=0.13 in M1 region. The wAT values for different ROIs and reconstructions, as well as the P values for pairwise comparisons are listed in Table 2. This result suggests that view-sharing in KWIC affects medium- to small-sized vessels (M2, M3/4, P1/2 and P3) and large-sized vessels (M1) in different ways.

Figure 6.

tMIP and wAT maps of Cartesian acquisition, KWIC reconstruction and MS-CS reconstruction from one volunteer. Anterior cerebral arteries were not visualized due to the tilting of the imaging slab. tMIP confirms minimal image quality difference between the three techniques. However, the wAT maps show significant differences in the MCA and PCA regions (blue and green arrows) between KWIC and the proposed method, while the proposed method generated comparable results with the reference Cartesian acquisition.

Table 2.

wAT values for different vessel segments and imaging techniques. Unit of wAT is millisecond (ms).

Vessel Segments	Cartesian	KWIC	MS-CS
	1	2	3
M1	1056.3	1048.2	1051.5
M2	977.7	1039.2a	978.2
M3/4	1095.6	1135.6a	1089.7
P1/2	1100.1	1180.2a	1097.5
P3	1138.3	1202.9a	1136.1

^ap<0.05 (compared with Cartesian and MS-CS). (MCA segments: M1, from the origin to bifurcation/trifurcation; M2, insular segment, from bi(tri)furcation to circular sulcus of insula; M3/4: opercular and cortical segment; M4: cortical segment. PCA segments: P1: from it origin at the termination of the basilar artery to posterior communicating artery (PCOM), P2: from the PCOM around the mid-brain; P3: quadrigeminal segment; P4: cortical segment.)

Figure 7 demonstrates NCE-dMRA acquired on an AVF patient with the proposed MS-CS and KWIC reconstructions, respectively. TOF and DSA images are also displayed as a reference. A left dural AVF was detected, where blood flows directly from the feeding artery (anterior branch of middle meningeal artery) into the transverse sinus bypassing the capillaries at a high flow velocity. MS-CS sequentially showed feeding artery (red arrow), fistula site (green arrow) and drainage into sinus (blue arrow), while such temporal information was lost in KWIC images and all the lesion components are displayed simultaneously. The signal intensity curves derived at three regions of interest (ROIs), shown in Supporting Figure S2 also support this observation: KWIC reconstruction generated wider curves at two ROIs with fast flow, while at the other ROI with relative slow flow, shape and peak position of the signal intensity curves from KWIC and MS-CS were similar.

Figure 7.

a). Example NCE-dMRA images of a AVF patient. From top to bottom, each row represents five frames of dynamic images reconstructed with KWIC and MS-CS, respectively. Anterior cerebral arteries were not visualized due to the tilting of the imaging slab. Images from MS-CS reconstruction sequentially display feeding artery (red arrow), fistula site (green arrow) and drainage into sinus (blue arrow). Such dynamic information is not as obvious in the KWIC reconstruction. b, c). Reference TOF and DSA images.

Since our radial acquisition took only half of the scan time of Cartesian acquisition, it allowed doubling of the spatial coverage within the same scan time. Figure 8 displays five frames of a 64-slice 3D SOS acquisition with 1×1×1mm³ isotropic resolution, which enabled high quality MIP images in sagittal, coronal, and axial views. The detailed vascular structure is also displayed as a reference by TOF. One can appreciate the cleaner dynamic information provided by the high-quality MS-CS reconstruction compared with KWIC reconstruction.

Figure 8.

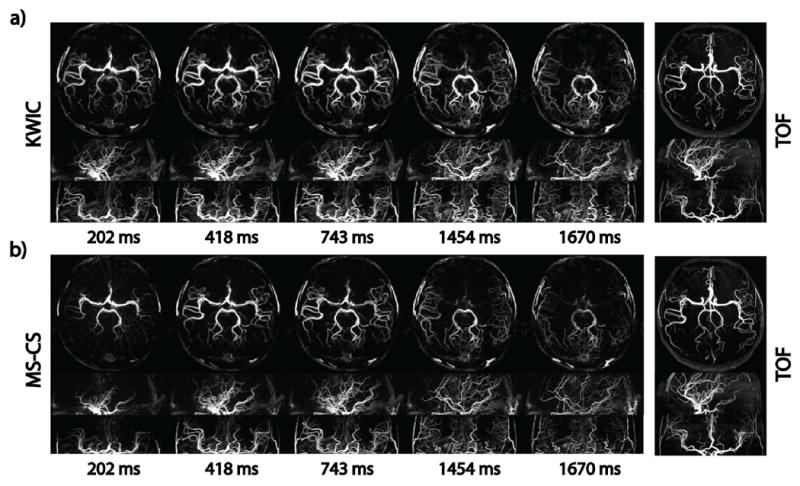
Example images of a 64 slices golden-angle SOS acquisition reconstructed with KWIC (a) and the proposed MS-CS method (b) in sagittal, coronal and axial views. Static TOF image is shown as an anatomical reference. The 1×1×1mm³ isotropic resolution allows high quality MIP images in all three views to be reconstructed with KWIC and MS-CS methods. However, temporal smoothing of distal arteries can also be observed in all three planes in KWIC reconstruction, while the proposed method showed reduced temporal blurring and improved delineation of signal evolution in small arteries.

Discussion

Our work demonstrates the feasibility of applying MS-CS to accelerate NCE-dMRA with golden-angle stack-of-stars trajectory. Compared with the previous Cartesian acquisition (2-5, 8-11), SOS NCE-dMRA was already shown to achieve a shorter scan time. By taking advantage of the magnitude subtraction sparsity of control and label images, the MS-CS method allows high spatial (~1mm³) and temporal (~100ms) resolution NCE-dMRA within a short scan time (~3min). We further demonstrated the MS-CS reconstruction is superior to both iCS and CS-CS strategies in NCE-dMRA. Comparison with the previously proposed KWIC method was also performed. Our results suggest MS-CS is capable of providing high temporal resolution images by reducing the number of radial spokes for each temporal frame without using view-sharing.

Compared to the conventional iCS reconstruction, where the control and label images are reconstructed independently before subtraction, the proposed method reconstructs both images in a joint optimization. Since the final dMRA image is generated by the subtraction between control and label acquisitions in ASL based MRA, the incorporation of magnitude subtraction in image reconstruction will highlight the labeled blood signal and effectively suppress the background signal including artifacts. On the other hand, from an algorithm perspective, the use of such an additional regularizer can further reduce the solution space and allow a higher likelihood to converge to an optimal solution (i.e. clean and sharp image). As another choice, complex subtraction in k-space between control and label acquisitions can be used to enhance the subtraction sparsity. However, we have shown in our work that this CS-CS method is inferior to the proposed MS-CS method for NCE-dMRA, due to the following two reasons: 1). Direct complex subtraction imposes signal to noise ratio (SNR) penalty and causes noise amplification; 2). MRA is based on the blood magnitude enhancement but complex subtraction partly depends on phase variation, and therefore, is sensitive to phase errors that come from system imperfection induced gradient delay, off-resonance effects raised from field inhomogeneity, as well as subtle motion between label and control acquisitions. Compared with the conventional Cartesian trajectory, the use of radial trajectory in our study also increases the sensitivity of data acquisition to these phase errors.

A previous study has successfully implemented KWIC reconstruction in NCE-dMRA with golden angle radial acquisition (15). With k-space view-sharing of adjacent temporal frames, reconstructed image series have both high spatial and apparent temporal resolution. As demonstrated in this work, both proposed MS-CS method and KWIC showed good image quality without apparent streaking artifacts. However, view-sharing in KWIC can potentially lead to temporal smoothing of underlying flow dynamics at certain locations, such as vessels with fast flow. This would be a limiting factor in certain clinical applications. For instance, it will be difficult to capture the flow dynamics in feeding arteries with fast flow or distinguish between feeding arteries and cortical venous reflux needed for Borden classification (32) in arteriovenous fistula (AVF). As illustrated in the AVF case (Figure 7), in which abnormally fast flow appears in a small-size fistula site, KWIC failed to capture the full passage of blood flow from the feeding artery into the fistula and vein. This is due to the fact that small structures are mainly represented by high spatial frequencies in k-space, which are heavily shared between neighboring frames in KWIC reconstruction. On the contrary, the proposed MS-CS requires no view-sharing, and therefore preserves the temporal information. In addition, a phantom experiment (Figure S3 in online supporting material) was also carried out to reproduce the scenario of imaging vessels with fast flow. One can appreciate the improved temporal delineation of fast flow using the proposed MS-CS reconstruction, compared to KWIC reconstruction. Overall, both patient and phantom data indicate that the accelerated MS-CS NCE-dMRA could be a promising alternative dMRA technique in clinical applications, in particular for the depiction of fast flow.

In terms of SNR and CNR measurements, the proposed MS-CS approach has a similar performance compared with KWIC reconstruction. However, both radial-based reconstructions had significantly lower SNR and CNR compared with Cartesian acquisition. This matches our previous result (15). Aside from the reason mentioned in (15), which ascribed the difference to a k-space apodizing filter along the slice encoding direction for Cartesian online reconstruction, it is also well-known that radial acquisition has intrinsically low SNR efficiency compared with Cartesian acquisition (33). Considering that the acquisition time for the 3D SOS radial sequence is only half of that of the 3D Cartesian sequence, such difference is expected. Another thing to notice is that since CS reconstruction is always an iterative nonlinear process, artificially high SNR and CNR can be created by manipulating regularization parameters. Therefore, care should be taken for the interpretation and evaluation of the SNR and CNR measured from MS-CS approach.

In the proposed reconstruction algorithm, the widely-used Wavelet regularization and application-tailored magnitude subtraction regularization are incorporated (26). We note that an inappropriate use of wavelets could lead to blurring of fine structures, due to the suppression of high frequency component in wavelets domain during the denoising (i.e. soft-thresholding) process. On the other hand, the magnitude subtraction regularization does not specifically penalize the high frequency component, since denoising is carried out in image domain and only signals with low amplitude are removed. To balance the two terms and prevent over-smoothing or insufficient artifact removal, we carefully tuned the associated regularization parameters. We found that both regularization terms contribute to final high quality images, although the majority of regularization comes from the proposed magnitude subtraction term whereas the wavelet term offered incremental improvement in image quality. We also note that our acquisition uses high under-sampling factor and has limited SNR. Under such circumstance, parallel imaging (PI) alone cannot guarantee to recover high quality image due to the ill-condition of the inverse problem in PI (34,35). Therefore, we included additional regularization terms in our optimization problem, although this came at a price of much longer reconstruction time and higher computation burden due to the iterative reconstruction.

Magnitude subtraction was originally introduced in the reconstruction of under-sampled CE-dMRA data sets (26). To apply it on SNR-limited ASL based NCE-dMRA, several optimizations were performed to compensate for the SNR difference. First, parallel imaging was incorporated in the image reconstruction to utilize the dense coil arrays, e.g. 20 channels were used in this study. Second, a non-Cartesian radial trajectory was chosen to maximize the incoherence of artifacts when k-space is highly under-sampled. The intrinsic variable density sampling feature of radial-sampling also benefits the performance of CS algorithms. Third, the regularization parameters were carefully tuned using several NCE-dMRA data sets in a pilot optimization study. They are drastically different than the ones used in (26), reflecting the signal level difference between these two studies.

In order to further improve temporal resolution, aside from investigating various advanced reconstruction strategies that allows further reduction of the number of spokes used per phase, an alternative solution is to sample the 3D k-space more efficiently with the SOS acquisition. In the current implementation, the angle of radial spokes does not vary in the partition direction. Several previously proposed methods such as SOS-CAIPIRINHA (36) and rotated stack-of-stacks (37) vary the angles of the radial spokes in the partition direction and demonstrated improved result. By varying the angle distribution along the partition direction and combining the proposed MS-CS reconstruction, it is possible to further push temporal resolution without sacrificing spatial resolution.

Balanced SSFP (bSSFP) has been successfully used for 4D NCE-dMRA data acquisition (2,3,13) by providing high SNR and imaging efficiency. However, it is intrinsically prone to off-resonance artifacts especially near sinuses. To minimize the off-resonance artifacts, a pre-saturation pulse was applied before the image acquisition to suppress the background tissue signal as well as the off-resonance induced artifacts. Furthermore, the ASL-based dMRA technique benefits from the subtraction between control and label images, which can effectively remove the off-resonance artifacts in subtracted dMRA images. Meanwhile, a tilted axial acquisition slab was carefully placed to avoid covering most of the sinuses, which further reduced the off-resonance artifacts. Therefore, the off-resonance artifact was not an issue in the current study. However, we have to note that the tilting of the acquisition slab may result in some arteries not being visualized.

Our study has limitations. First, our main goal was to demonstrate the feasibility of applying CS on ASL and evaluate its effect on reducing view-sharing, we did not perform any SNR and CNR analysis and comparison. This is particularly important for calculating hemodynamic parameters such as cerebral blood flow (CBF), and cerebral blood volume (CBV). A systematic evaluation needs to be developed in the future. Second, the proposed method was only evaluated on limited number of patients. Future evaluation of the clinical utility of NCE-dMRA with MS-CS reconstruction in a large cohort of patients is warranted. In addition, developing an online reconstruction pipeline (38) assembled with faster imaging reconstruction is needed to facilitate its clinical utility.

Conclusion

In conclusion, by taking advantage of magnitude-subtraction sparsity of the ASL based MRA, a CS algorithm has been successfully implemented and evaluated in golden-angle stack-of-stars NCE-dMRA. Better image quality was achieved using the proposed MS-CS than the conventional iCS and CS-CS methods. Compared to the previous KWIC method, the proposed MS-CS strategy allows more accurate temporal depiction of cerebral flow patterns without view-sharing, which may become a useful approach in clinical applications.

Supplementary Material

Supplementary Material

Figure S1. Sequence diagram of 3D Cartesian NCE-dMRA, which applies an ASL preparation pulse followed by a segmented multi-phase balanced steady-state free precession (bSSFP) readout. A pre-saturation pulse is applied before the ASL preparation pulse to saturate the background signal in the imaging slab. Segmented k-space is acquired in each repetition time, and the temporal resolution depends on the number of lines per segment.

Figure S2. Intensities of signal at three ROIs, shown in the upper left sub-figure, are plotted against time for the KWIC and MS-CS reconstructions. For ROIs 1 and 2, which contain vessels with fast flow, view-sharing of KWIC reconstruction causes early filling and late drainage. For ROI 3 that contains the main branch with relative slow flow, both reconstructions have similar signal intensity curves.

Figure S3. a): Overview of experiment setup. b): Four selected temporal frames of Cartesian acquisition (top row), KWIC reconstruction (middle row) and MS-CS reconstruction (bottom row). Each panel consists of one MIP image (lower right) of control-labeling subtracted image, and one fused image (upper left) of the structure overview and corresponding MIP image. Due to view-sharing, temporal smoothing with fast flow was observed in KWIC reconstruction. The proposed MS-CS algorithm, however, recovered artifact-free images without any temporal blurring. c): The intensity of signal at the red cross point in a) is plotted against time for three reconstructions.