Laboratory-scale photoredox catalysis using hydrated electrons sustainably generated with a single green laser

A combined photokinetical approach helped develop and optimize a green-light driven photoredox catalytic system that generates a “super-reductant” with simple instrumentation, consumes only a bioavailable donor, and provides very high turnover numbers.

Abstract

The ruthenium-tris-bipyridyl dication as catalyst combined with the ascorbate dianion as bioavailable sacrificial donor provides the first regenerative source of hydrated electrons for chemical syntheses on millimolar scales. This electron generator is operated simply by illumination with a frequency-doubled Nd:YAG laser (532 nm) running at its normal repetition rate. Much more detailed information than by product studies alone was obtained by photokinetical characterization from submicroseconds (time-resolved laser flash photolysis) up to one hour (preparative photolysis). The experiments on short timescales established a reaction mechanism more complex than previously thought, and proved the catalytic action by unchanged concentration traces of the key transients over a number of flashes so large that the accumulated electron total surpassed the catalyst concentration many times. Preparative photolyses revealed that the sacrificial donor greatly enhances the catalyst stability through quenching the initial metal-to-ligand charge-transfer state before destructive dd states can be populated from it, such that the efficiency of this electron generator is no longer limited by catalyst decomposition but by electron scavenging by the accumulating oxidation products of the ascorbate. Applications covered dechlorinations of selected aliphatic and aromatic chlorides and the reduction of a model ketone. All these substrates are impervious to photoredox catalysts exhibiting lower reducing power than the hydrated electron, but the combination of an extremely negative standard potential and a long unquenched life allowed turnover numbers up to 1400 with our method.

1. Introduction

Photoredox catalysis with visible light^1–7 is probably the most promising branch of current synthetic photochemistry considering the fact that all the fossil fuels on our planet, i.e., the most important raw materials for chemical syntheses, have originated in that way. It is based on storing, and possibly pooling,^8–15 photon energy in a catalyst molecule, utilizing that energy to activate a substrate through direct or relayed¹⁶ electron transfer, and finally recovering the starting form of the catalyst by a complementary electron donor or acceptor, which might also be a sacrificial additive. In consequence, the four key characteristics of a photoredox catalytic system are its operating wavelength, the oxidative or reductive power its activating state possesses, the lifetime of that state, and the susceptibility to catalyst-destroying parasitic reactions.

Regarding the first criterion, green light — the maximum of the terrestrial solar spectrum — is intuitively appealing; but in view of the fact that artificial radiation sources are so readily available, its main advantage is freedom from absorption by the substrate because the overwhelming majority of organic chemicals is transparent in the green.^17,18 The present work explores a photoredox catalytic cycle driven with 532 nm, a wavelength routinely obtainable with a frequency doubled Nd:YAG laser. Although these devices are expensive, their durability reduces the initial cost to a secondary issue; and their main asset is the easy access to two-photon processes through their extraordinarily high photon fluxes. Here, we exploit this to achieve photon pooling within a single laser flash, which greatly simplifies the instrumentation because two pulse-schemes on the required timescale (typically, microseconds) would demand two independently triggered lasers,^12,13 whereas in our case a single inexpensive laser running at its normal repetition rate (typically, 10 Hz) suffices.

The second and third criterion ultimately determine the bandwidth of chemical applications. On one hand, the larger the absolute redox potential of the activating species, the broader the range of substrates it can induce to react; on the other hand, the longer the intrinsic lifetime of that species, the lower the substrate concentration needed to quench it. In this study, we employ the hydrated electron e_aq˙^– as the activating species in reductive photoredox catalysis. By virtue of its standard potential of –2.9 V (ref. 19) it qualifies as a super-reductant; yet, its natural lifetime of hundreds of microseconds,²⁰ although typically reduced to less than one microsecond under actual operating conditions,^12–15,21 compares very favourably with that of excited states of very high reductive power currently available for photoredox catalysis.^{8–11,22–24} The fourth criterion primarily includes processes inherent to the catalytic system itself, mainly photochemical side reactions and intrinsic chemical irreversibility, which the present work addresses; beyond this, extrinsic processes such as a poisoning of the catalyst by the substrate or reaction products are conceivable, but need to be investigated on a case by case basis for each application.

Owing to the low photon energy (2.33 eV at 532 nm), e_aq˙^– generation with green light has to rely on a two-photon process. We have already reported catalytic cycles of such photoionizations that consume a sacrificial donor and are based on an acceptor as the catalyst.^12,13 Fig. 1 displays the mechanism for the catalytic system employed in this work. It is built around the popular photosensitizer ruthenium-tris-bipyridyl Rubpy.²⁵ A green photon suffices to transform the ground state GS into the long-lived metal-to-ligand charge-transfer excited state ³MLCT, which contains a localized radical anion of the ligand; reduction of the metal centre by the ascorbate dianion Asc^2– then affords the very persistent one-electron reduced form OER; and green-light monophotonic ionization of the radical-anion moiety still “hidden” in OER finally releases e_aq˙^– and closes the cycle. Attractive features of this system are the highly photostable catalyst and the consumption of a bioavailable sacrificial donor (in addition to the two green photons) only, which justifies the epithet sustainable.

Fig. 1. Cyclic mechanism (acceptor cycle) of the green-light (532 nm) ionization of Rubpy, as established by two-pulse laser flash photolysis.¹² The colour code of this figure is used throughout this work for the Rubpy-derived species (ground state GS, metal-to-ligand charge-transfer excited state ³MLCT, one-electron reduced form OER; formulas included at the right of the mechanism), the hydrated electron e_aq˙^–, and the ascorbate dianion Asc^2– serving as sacrificial donor.

In a previous communication, we have used two-pulse experiments to establish the mechanism of Fig. 1.¹² In this work, we first extend the photokinetic investigation to cover photoionization during a single laser flash; second, we study the intrinsic stability of this catalytic system under conditions of preparative laser irradiation; and third, we present a number of chemical applications, with NMR determinations of the turnover number (TON) and selectivity complemented by transient absorption measurements of the e_aq˙^– capture by the substrates. All experimental details have been relegated to ESI-1.† Our integrated approach to the effects of the catalyst, sacrificial donor, and substrate concentrations gives a much deeper insight into the reactions than simple product analysis could. It will facilitate systematic optimizations of bench-scale procedures^17,26 that are based on this high-TON source of the super-reductant e_aq˙^– for photoredox catalysis.

2. Results and discussion

2.1. The system Rubpy/Asc^2– as a single-pulse driven electron source

Photoexcitation of GS produces ³MLCT quantitatively (φ _MLCT = 1) and instantaneously (within less than 1 ps).²⁵ Fast reductive quenching of ³MLCT is thus the only kinetic prerequisite for generating e_aq˙^– through the catalytic cycle of Fig. 1 with a single green laser flash (typical duration with an inexpensive solid-state laser, about 5 ns) of sufficient intensity. Stern–Volmer experiments with Asc^2– at room temperature (compare, ESI-2.1†) gave a redetermined¹² quenching rate constant of 5.1 × 10⁹ M^–1 s^–1 and efficiency η of OER formation of 0.48. Hence an Asc^2– concentration in excess of some 10 mM ensures that an appreciable amount of OER is present during the pulse.

The ascorbate monoanion AscH^– quenches ³MLCT so much slower as to be negligible²⁷ but scavenges e_aq˙^–.²⁸ For given ascorbate total, a variation of the relative amounts of Asc^2– and AscH^– thus influences the performance of the catalytic system in a two-fold way, through the efficiency of dianion-assisted e_aq˙^– formation as well as through the partitioning of e_aq˙^– between the substrate and the monoanion. However, some systems require AscH^– as hydrogen donor in substantial amounts for terminating the intermediate radicals before they can attack the catalyst (Sections 2.3.2 and 2.3.3). To decouple the dianion-dependent process from the monoanion-dependent ones in these cases, we controlled the absolute concentrations of Asc^2– and AscH^– through varying the pH from its standard value in our experiments, (12.65; pK _a of AscH^–, 11.74 (ref. 29)) simultaneously with the weight-in concentration of the sacrificial donor.

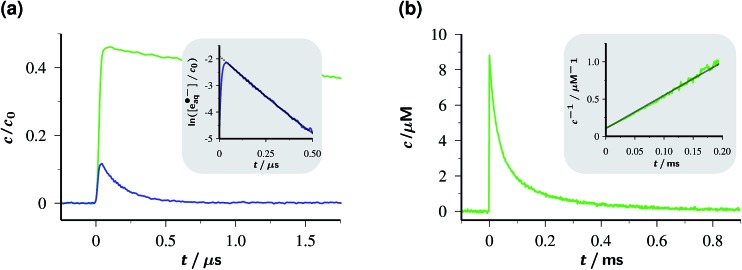
The concentration traces in Fig. 2a demonstrate that single-flash ionization with our 532 nm laser is indeed feasible in that system (all spectra and protocols for extracting the species concentrations have been compiled in ESI-1.2.†). With the standard composition of the catalytic system used in this work (50 µM Rubpy and 45 mM Asc^2–, after taking into account the pH-dependence) about 15% of the metal complex are ionized at the maximum laser intensity.

Fig. 2. Decay traces of the key species OER and e_aq˙^– in the Rubpy/Asc^2– catalytic system. Graph (a), OER (top) and e_aq˙^– (bottom) concentrations c relative to the starting Rubpy concentration c ₀ for the standard composition of the system in this work (c ₀, 50 µM; 50 mM sodium ascorbate in 100 mM NaOH, pH 12.65) on a µs timescale following a single green pulse of intensity 760 mJ cm^–2. Inset, log-linear plot of the e_aq˙^– trace demonstrating the first-order decay over 3.5 half lifes and the back-extrapolation (dotted part of the gray fit curve) to obtain the true e_aq˙^– concentration immediately after the flash despite the rounding of the tip (see, main plot) by the fast decay. Graph (b), second-order OER decay on a ms timescale, with the usual linearization over the first 2.5 half lifes as the inset. Same concentrations as in (a); laser intensity, 94 mJ cm^–2. For further explanation, see text.

Under these conditions, e_aq˙^– decays monoexponentially with a lifetime of 165 ns, corresponding to a decay rate of 6.1 × 10⁶ s^–1. At the high ionic strength of our solutions, e_aq˙^– capture by residual GS to give OER is decelerated so much (rate constant at zero ionic strength, 8.2 × 10¹⁰ M^–1 s^–1;³⁰ reduction factor estimated with the Brønsted–Bjerrum equation for this reaction between an anion and a dication, about 8)³¹ that it only accounts for about 5% of this rate, given the low GS concentration that can be extracted from Fig. 2a. Instead, the e_aq˙^– decay is predominantly due to scavenging by AscH^– present in its equilibrium concentration (about 11% of the weight-in concentration at the pH of Fig. 2a) to give an ascorbate-derived radical anion of uncertain structure.²⁸ The bimolecular rate constant of this reaction is 1.1 × 10⁹ M^–1 s^–1 at the ionic strength of our experiments, as determined using a Stern–Volmer type procedure with variation of the AscH^– concentration; our result is almost 3 times the literature value,²⁸ which is consistent with expectation when the ionic strength is taken into account.

The significant shortening of the e_aq˙^– lifetime compared to that with another green-light driven electron source recently reported by us (1–2 µs)¹⁴ does not constitute a true limitation with respect to an application. Owing to its extraordinary standard potential (–2.9 V, comparable to metallic potassium), e_aq˙^– reacts nearly diffusion controlled with an overwhelming number of substrates;¹⁹ hence, millimolar concentrations of these substrates already suffice to capture at least half the number of electrons, i.e., utilize them for the desired purpose. We also emphasize that the lifetime of e_aq˙^– in our system by far exceeds that of the recently reported triplet of hexachloro cerate (22 ns), whose reductive power in photoredox catalysis approaches but still falls short of that of e_aq˙^–.²⁴

As opposed to e_aq˙^–, OER vanishes by pure second-order kinetics, as is evidenced by Fig. 2b, where the laser intensity was reduced so much as to remove any direct or indirect kinetic interference by e_aq˙^–. This process (rate constant, 4.5 × 10⁹ M^–1 s^–1) must, therefore, be ascribed to the recombination with Asc˙^– by reverse electron transfer recovering the starting materials Rubpy and Asc^2–. The low concentrations of Asc˙^– compared to Asc^2– shift the timescale of this decay by two orders of magnitude towards the millisecond range. As the essentially complete disappearance of OER indicates, the complex secondary chemistry of Asc˙^– and its subsequent products²⁹ plays no discernible role in single-flash experiments on our system.

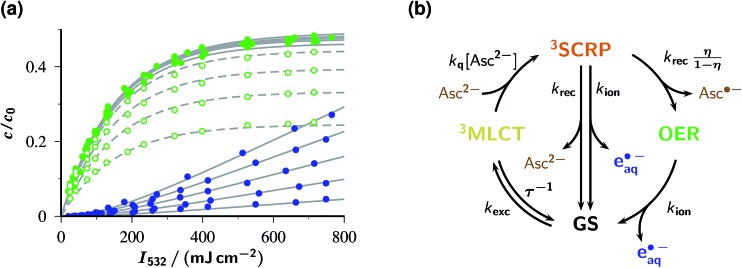
Fig. 3a visualizes the influences of the laser intensity and the Asc^2– concentration on the yields of OER and e_aq˙^– immediately after the laser flash, with the detected OER also including the amount formed by post-flash quenching of ³MLCT. The intensity dependences exhibit the saturation behaviour for OER and upward curvature for e_aq˙^– that are expected for catalytic photoionization through the acceptor cycle of Fig. 1.³² (Closed-form expressions are derived in ESI–2.2.†) Inexplicable by that simple model, however, is the dependence on [Asc^2–] in the high-concentration range (see the filled symbols and solid fit curves in the figure), namely, convergence of the OER plateau on the above-mentioned value of η, 0.48, as opposed to an unbounded rise of e_aq˙^– with increasing [Asc^2–]. With the mechanism of Fig. 1 under conditions of rapid ³MLCT quenching, the photostationary concentration of OER is c ₀ ε _GS φ _MLCT/(ε _GS φ _MLCT + ε _OER φ _ion);³² on the basis of the known extinction coefficients and photoionization quantum yield φ _ion,¹² the limiting OER yield would have to be almost twice as large as observed. Expectedly, the best fit for this scenario (see ESI Fig. 4a†) compensates this by unrealistic kinetic constants and still does not acceptably represent the data.

Fig. 3. Response of the catalytic system to the laser intensity and the concentration of the sacrificial donor. Graph (a), initial post-flash concentrations c relative to the starting Rubpy concentration c ₀ (50 µM) for OER (green) and e_aq˙^– (blue) as functions of the intensity I ₅₃₂ of a single green laser flash with the Asc^2– concentration as parameter. The gray curves represent a global fit for the kinetic scheme shown in (b); best-fit parameters with the effective laser pulse duration T and with the intensities I ₅₃₂ specified in mJ cm^–2, k _exc T = 6.6 × 10^–3 I ₅₃₂, T/τ = 1.7 × 10^–2, k _q T = 42 M^–1, k _rec T = 0.94, η = 0.48, k _ion T = 6.0 × 10^–4 I ₅₃₂. The ascorbate weight-in concentrations, in ascending order of the curves for each observed species, are 0.5 mM, 1 mM, 2 mM, 5 mM (open symbols and dashed curves, OER only; for clarity, the data and fit curves for e_aq˙^– have been omitted) and 10 mM, 20 mM, 50 mM, 100 mM, 250 mM (filled symbols and solid curves). Experimental temperature, 303 K. Graph (b), enhanced kinetic model used for the global fit, with ³SCRP being the spin-correlated radical pair 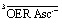. For further explanation, see text.

In contrast, the experimental observations of Fig. 3a are consistently explained by the enhanced reaction scheme of Fig. 3b. Its difference to Fig. 1 is the intermediacy of a spin-correlated radical pair ³SCRP produced by the quenching step. Spin conservation demands this pair to be born in a triplet state, 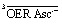, so immediate recombination of its two radicals is precluded. As is well known, what holds a radical pair together is not a mobility restriction; instead, its two radicals undergo diffusive excursions during which they are completely separated in space but remain an entity exclusively through their spin correlation.³³ During such an excursion, intersystem crossing is effected by differential precession of the electron spins of the two radicals, and upon a reencounter a chemical reaction differentiates between the singlet and triplet state of the pair. In our case, a geminate reaction (i.e., back electron transfer to give GS and Asc^2–) is only possible for the singlet multiplicity. A pair that has remained in the triplet state embarks on another diffusive excursion. In this chain of events, the spin correlation is eventually lost, so the components OER and Asc˙^– become free radicals; the parameter η is the probability of this outcome.

The described radical-pair mechanism has two important consequences for the system under study. First, the geminate reaction of 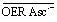does not obey second-order kinetics, only the reaction between free OER and free Asc˙^– (compare, Fig. 2b) does. Second, the photophysical and photochemical properties of OER contained in ³SCRP and of free OER are identical; in particular, both species can be ionized by a green photon with the same probability.

Evidently, the mechanism of Fig. 3b is kinetically indistinguishable from that of Fig. 1 if the radical pairs ³SCRP are short-lived on the timescale of the laser flash. If they are long-lived, however, they provide a catalytic source of e_aq˙^– as long as the flash lasts, but afterwards yield free OER with probability η only; hence, the contradiction to experimental observation is removed. For this limit, easy-to-use closed-form expressions can again be derived, and are given in ESI-2.2.† They represent the data much better (see ESI Fig. 4b†). However, remaining small but systematic deviations for OER indicate that the experiments of this work fall into the intermediate range of Fig. 3b where ³SCRP is neither very short-lived nor very long-lived on the timescale of the laser flashes.

Even for this case, closed-form integrated rate laws can in principle be formulated in a straightforward way. Owing to the identity [GS] + [³MLCT] + [³SCRP] + [OER] = c ₀, their form is A _i exp(–at) + B _i exp(–bt) + C _i exp(–ct) + D _i with A _i, B _i, C _i and D _i specific for the species i considered, but a, b and c independent of it; all their parameters are composed of the kinetic constants listed in the figure. The e_aq˙^– concentration follows from integrating the expressions for [³SCRP] and [OER], which does not introduce an additional exponential. However, these closed forms are extremely cumbersome to handle and computationally inefficient because a, b and c are the solutions of a cubic equation. Numerically solving the system of differential equations not only is faster, but also has a further advantage: the two rate “constants” k _exc and k _ion are actually time dependent, namely, proportional to the envelope of the laser flash; and the numerical solution can incorporate a realistic (i.e., Gaussian) shape with very little additional effort whereas the closed-from solution is only available for a rectangular shape.

As can be seen in Fig. 3a, a perfect global fit is obtained on the basis of the enhanced reaction scheme of Fig. 3b, with a lifetime of ³SCRP slightly shorter than 10 ns. Owing to the elevated experimental temperature, the best-fit kinetic constants deviate slightly from those determined at room temperature, but in no case by more than a factor of 2. The pulse shape was found to have a negligible effect, which provides a posteriori justification of the closed-form treatments in ESI-2.2.† The excellent simultaneous representation of 14 data sets spanning a two-species basis of observables, a concentration variation of the sacrificial donor by a factor of 500, and a very large intensity range must be considered very strong evidence that this single-flash source of e_aq˙^– operates according to the mechanism of Fig. 3b.

Despite the complex mechanism, all intensity dependences for one species can be made to coincide by scaling them with a multiplicative constant that depends on the Asc^2– concentration. This leads to hardly discernible deviations between the scaled curves in the case of OER and even to visual indistinguishability in the case of e_aq˙^–. For OER, the scaling factor virtually equals {1 – (k _q[Asc^2–]τ)^–1} × η, which is the fraction of ³MLCT quenched by Asc^2– and transferred to OER either within the pulse or afterwards. For e_aq˙^–, the scaling factor exhibits excellent proportionality to 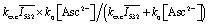with the average excitation intensity 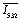, in other words, to the apparent rate constant for the transfer from GS to ³SCRP when the steady-state approximation for ³MLCT is used.³⁴

As has emerged from this section, single-pulse photoionization in this system is thus feasible and well-characterized photokinetically.

2.2. Intrinsic photochemical stability of the catalyst

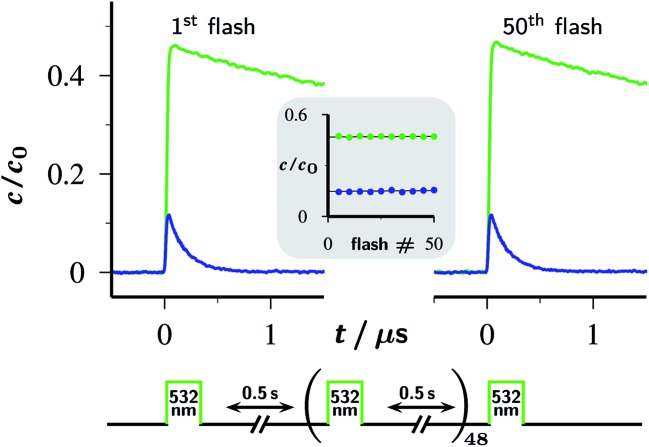
The absence of detectable catalyst-destroying side reactions in the single-flash experiments of Fig. 2 boded well for the usability of the Rubpy/Asc^2– system. Therefore, as a more stringent test of its suitability as a cyclic e_aq˙^– source, we repetitively flashed the same volume — i.e., without replacement of the solution between the flashes — of the standard catalyst composition specified in Section 2.1, and after each flash recorded concentration traces in the same way as in Fig. 2a.

The outcome of this experiment for 50 successive flashes is summarized by Fig. 4. As is evident, the decay traces of the key species OER and e_aq˙^– are indistinguishable between the first and the last flash; in particular, their amplitudes remain perfectly the same. For the laser intensity and Asc^2– concentration employed, the e_aq˙^– yield from a single flash is 15% of the starting Rubpy concentration. Accumulated over the 50 flashes, the system has thus delivered a total e_aq˙^– concentration equal to 7.5 times the catalyst concentration, without any sign of depletion or deterioration.

Fig. 4. Fifty-fold repetition of the experiment of Fig. 2a with the timing diagram (duration of the laser flashes not drawn to scale) shown below the plotted first and last set of concentration traces for OER (upper trace, green) and e_aq˙^– (lower trace, blue). The inset displays the concentrations of these two species immediately after each fifth flash as functions of the flash number, using the same colour code as in the traces. Experimental conditions are given in the caption of Fig. 2a; for further information, see text.

For further elucidation of the influence of the sacrificial donor Asc^2– on the catalytic system under illumination and as ultimate test of the catalyst stability under field conditions, we flashed the solutions in a cuvette at the maximum laser repetition rate (10 Hz) for up to 30 min. The high energy densities required by the two-photon ionization can only be retained through keeping the size of the laser beam comparably small to that in the experiments on short timescales (Fig. 2–4), in other words, through illuminating only a fraction of the cuvette; but under continuous, vigorous stirring the only consequence of this unavoidable size mismatch is an apparent reduction of the repetition rate by the ratio of illuminated volume to total solution volume. A related effect is caused by our method of analysis, which consisted of removing constant aliquots from the solution at constant time intervals; the result is an apparent stepwise increase of the repetition rate, or lengthening of the subsequent illumination period, after each sampling pause.

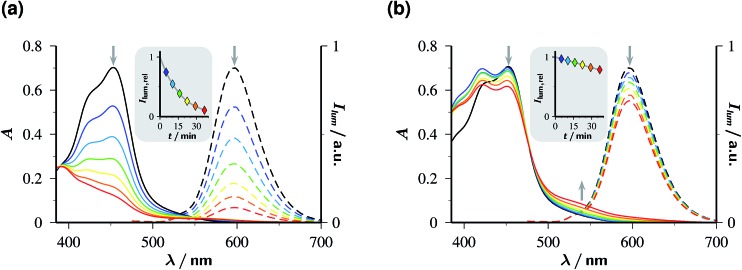
Fig. 5 juxtaposes the experimental findings without and with the sacrificial donor Asc^2–, using absorption and luminescence as observables. Based on the arguments of the preceding paragraph, the accumulated radiation dose absorbed per total volume during the experiment is estimated to exceed 3600 flashes of the original high energy density, or about 250 J.

Fig. 5. Stability of 50 µM Rubpy at pH 12.65 under continuous flashing with 532 nm at 10 Hz; intensity per flash, 352 mJ cm^–2. Graph (a), without Asc^2–; graph (b), with 45 mM Asc^2– in the solutions. Solid lines, absorption spectra; dashed lines, emission spectra (excitation wavelength, 453 nm; filter effects and quenching avoided by 15-fold dilution and acidification to pH 1, compare ESI-1.1†). Colour code and illumination time in minutes (values corrected for aliquot removal in brackets) for all spectra: black, 0 (0); blue, 5 (5); cyan, 10 (10.35); green, 15 (16.11); yellow, 20 (22.34); orange, 25 (29.12); red, 30 (36.58). The insets give the normalized luminescence intensities as functions of the irradiation duration; the solid lines are smoothing spline fits to guide the eye.

When the sacrificial donor is omitted (Fig. 5a), both the characteristic charge-transfer absorption of Rubpy with its peak at 453 nm (ref. 35) and the luminescence of ³MLCT rapidly disappear under the illumination; both effects are seen to parallel each other quantitatively and to lead to a reduction by more than 90% within the experiment duration. The slower absorption decay in the range below 425 nm and an isosbestic point at 390 nm reflect the buildup of a product, and the unchanged shape of the emission band reveals that product to be nonluminescent under excitation at 453 nm.

In the presence of the sacrificial donor Asc^2– at its standard concentration (Fig. 5b), photochemical degradation of the catalyst is slower by about one order of magnitude. The changes of the absorption spectrum at shorter wavelengths are more involved, and a new band appears at 530 nm; however, the constant shape of the emission spectrum again shows that luminescence detection upon 453 nm excitation captures only the remaining catalyst.

When we photolysed the catalyst as in Fig. 5a, i.e., without Asc^2–, and added this sacrificial donor only afterwards, the 530 nm absorption of Fig. 5b also arose (for details, see ESI-2.3†). This strongly supports its assignment to the product of a secondary thermal reaction between Asc^2– and a photoproduct of the catalyst with the solvent in both experiments, regardless of whether Asc^2– was present or absent during the illumination. Irradiated Rubpy is known to undergo stepwise ligand loss through thermal population of ³dd states that lie in close proximity to ³MLCT.^36–39 Hence, the nonemissive species absorbing at 530 nm most likely is a photosubstitution product of Rubpy with one of the bipyridyl ligands first replaced by water and then by Asc^2–.⁴⁰ This reasoning furthermore identifies the stabilizing effect of Asc^2– on the catalyst as the lifetime reduction of ³MLCT by the quenching; the faster this occurs, i.e., the higher the Asc^2– concentration is, the less likely is the population of the destructive ³dd states. To the best of our knowledge, this is the first experimental verification of that concept suggested decades ago.⁴¹

The significant protection of Rubpy against high-intensity illumination by the addition of large amounts of Asc^2– thus paves the way for employing this catalytic system as a regenerative source of the super-reductant e_aq˙^– in photochemistry.

2.3. Applications of the system

For synthetic photochemists less familiar with lasers as light sources, we emphasize that all the transformations of the following sections are carried out with an unmodified Nd:YAG laser at a current price of about 25 k€, which already includes the frequency-doubling unit to 532 nm. Running costs are basically determined by the replacement, after about 600 h of continuous operation, of the flash lamps within the laser, and amount to about 0.7 € h^–1. Neither additional lenses nor other optical elements are required. In particular, there is no necessity for external electronics because the laser is triggered by its internal timebase; it thus runs unattended, and operator interference is restricted to switching it on and off.

2.3.1. Detoxification of chloroacetic acid

Our first application example is the dechlorination of chloroacetate ClAcA. This compound serves as our reference to compare the usefulness of different e_aq˙^– generators for a two-fold reason.^13,42 First, in homogeneous solution to date no photochemically generated reductant other than e_aq˙^– has been shown to cleave aliphatic carbon–chlorine bonds lacking specific activation.^42,43 Second, ClAcA is an accepted model compound⁴³ for chlorinated organic waste, which poses severe ecological problems through the combination of high toxicity on one hand and extreme persistence on the other.

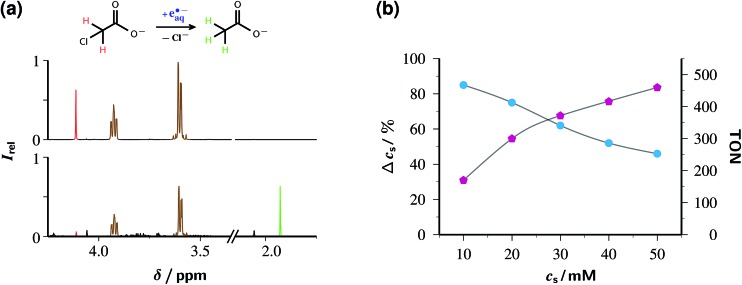
Fig. 6a provides experimental proof that the catalytic system of this work efficiently detoxifies ClAcA with green light. That end is achieved by simply adding ClAcA to the argon-saturated — because e_aq˙^– reacts with oxygen¹⁹ — catalyst solution and flashing the mixture with 532 nm laser pulses for some while under continuous stirring. Details of the experimental setup can be found in ESI-1.1.† The chloro-organic compound rapidly captures e_aq˙^– (rate constant, 1.29 × 10⁹ M^–1 s^–1)⁴² in a dissociative electron transfer according to eqn (1), with the resulting carbon-centered radical then abstracting a hydrogen, e.g., from the ascorbate monoanion AscH^– present to some extent even at the very basic pH of our solutions, to give acetate (AcA), as displayed in eqn (2).

Cl—CH₂COO^– + e_aq˙^– → Cl^– + ˙CH₂COO^– 1

˙CH₂COO^– + AscH^– → CH₃COO^– + Asc˙^– 2

Fig. 6. Detoxification of chloroacetate ClAcA with the green-light driven catalytic system of this work. Graph (a) depicts the gross reaction above the ¹H-NMR spectra before (upper trace) and after (lower trace) laser irradiation (532 nm, 600 mJ cm^–2, 10 Hz repetition rate, 1 h illumination time) of an aqueous solution (pH 12.65) of 50 µM Rubpy and 45 mM of Asc^2– (after correction for residual AscH^–) initially also containing 10 mM ClAcA. Both spectra were recorded after acidic workup (pH 1), and their vertical scales are identical. Signal assignment and colour code: chloroacetic acid, 4.11 ppm (s), red; acetic acid, 1.93 ppm (s), green; ascorbic acid, 3.93 ppm (m) and 3.60 ppm (m), brown. Graph (b) displays the outcome of a series of such experiments with identical illumination conditions, pH and catalyst concentration as in (a) but 89 mM Asc^2– (corrected) and the ClAcA concentration c _S as the independent variable. Workup and detection as in (a). Circles, cyan, left vertical scale, relative substrate consumption Δc _S; pentagons, magenta, right vertical scale, TON. The gray lines are spline fits to guide the eye. For further details, see text.

The disappearance of the substrate ClAcA and the sacrificial donor ascorbate as well as the buildup of the reaction product AcA are most conveniently monitored by ¹H-NMR spectroscopy. Because our workup (see, ESI-1.1†) includes acidifying the samples to pH 1, secondary loss of Asc^2– through reaction with molecular oxygen diffusing into the NMR tubes as well as exchange of the α protons of ClAcA and AcA with D₂O added for shimming and locking are safely avoided, and all relevant signals in the observed conjugated acids of ClAcA and AcA are well separated.

As the analysis of the NMR spectra in Fig. 6a shows, ClAcA is eradicated almost quantitatively (91%) by one hour of green-light illumination under the conditions of the figure, where the catalytic system was used in its standard composition. This corresponds to a turnover number (TON) of 186, which already is the highest for a green-light driven e_aq˙^– source reported to date, and demonstrates that side reactions destroying the catalyst are largely absent.

Nevertheless, the system can be further optimized for a much higher TON by increasing the substrate concentration; but this is only possible at the expense of a lower degree of substrate consumption. Fig. 6b illustrates that interdependence. To ensure that the reaction is not limited by the depletion of the sacrificial donor, we doubled the ascorbate weight-in concentration relative to that in Fig. 6a and simultaneously adjusted the NaOH concentration to keep the pH at its previous value. This choice was guided by the following considerations. The relationship between substrate consumption and ascorbate consumption in exhaustive photolysis is hopelessly complex because the destruction of ascorbate through electron transfer (in the catalytic e_aq˙^– source itself), attack by e_aq˙^– on the monoanion (which is wasteful, hence precludes raising the ascorbate concentration by more than strictly necessary),²⁸ and hydrogen abstraction by the substrate radicals (eqn (1)), is partly compensated by regeneration through disproportionation of Asc˙^–; none of these processes has a constant stoichiometric relationship to any of the others; and the rich secondary chemistry of dihydroascorbate adds to the difficulty.²⁹ Empirically, the sacrificial donor decreased between 1.5 and 1.7 times as fast as the substrate; therefore, we employed an ascorbate concentration twice as high as the highest substrate concentration.

The fractional substrate decomposition exhibits a minor, roughly linear decrease with increasing substrate concentration, by about 10% per 10 mM under the experimental conditions of Fig. 6b. This is thought to reflect a self-limitation by the accumulation of ascorbate oxidation products, such as ketogulonic acid,²⁹ which scavenge e_aq˙^– much more efficiently than does ClAcA.¹⁹ Corroboration is provided by luminescence measurements as in Fig. 5, which reveal that in the exhausted samples a noticeable amount of catalyst is still present, meaning that e_aq˙^– are still generated but no longer scavenged productively.

Even though the relative substrate decomposition is roughly halved at the highest substrate concentration in Fig. 6b, the absolute amount of decomposed substrate, and thus the TON, becomes 2.6 times higher under these conditions. Keeping the catalyst concentration at 50 µM and further increasing the concentrations of the substrate and the sacrificial donor to 150 mM and 200 mM (weight-in concentration), which also necessitates an increase of the base concentration to 250 mM, epitomizes the trade-off between relative turnover and TON: this experiment removes only 47% of ClAcA — although regarded by itself this is an impressive reduction, by 70.5 mM — but gives a TON as high as 1410.

The main reaction product is the completely nontoxic AcA, which was identified by comparison with an authentic reference. In Fig. 6 as well as in the example optimized for the highest TON, AcA accounted for about 85% of the substrate destroyed. Conspicuous in both examples is the virtual absence (≤3%) of succinic acid, the combination product of two acetyl radicals. The green-light driven system of this work thus exhibits a much higher selectivity than do the UV-driven pure ascorbate⁴² or sulfite⁴³ systems. As both acetic acid and succinic acid originate from the same carbon-centered radical (eqn (1)), the former through hydrogen abstraction from a suitable donor, the latter through dimerization, the product distribution is determined by the relative reaction rates, which in turn depend on the concentrations of the hydrogen donor and the radicals. The substantial concentration of AscH^– (about 11% of the total ascorbate content at our standard pH of 12.65) and the low concentration of e_aq˙^– per pulse (which is a direct consequence of the low catalyst concentration) thus provide an explanation for the high selectivity. Although selectivity is not of any concern with the detoxification investigated here, it becomes an issue when e_aq˙^– is to be used for syntheses, as in the following sections.

2.3.2. Selective dechlorination of arenes

Currently, there is a surge of interest in photoredox catalytic dehalogenations of aryl halides, aiming at their defunctionalization in the presence of hydrogen donors^8,11,24,44 on one hand, and at coupling the intermediate aryl radicals with reaction partners such as heteroarenes^6,8,9,45 on the other. Until very recently, the choice of the precursor to the aryl radicals was basically limited to iodo- and bromoarenes or chloroarenes activated by electron withdrawing substituents. Although the orchestra of catalysts has now been expanded by the super-reducing triplet excited state of hexachloro cerate,²⁴ this addition needs UV-light for its operation and consumes a heavy metal in near-stoichiometric quantities, as the maximum TON did not exceed 6. Metal consumption in the newly reported visible-light driven lanthanide-assisted rhodamine-6G system, which moreover requires super-dry conditions and glove-box handling, appears to be similar.⁴⁴ This prompted us to employ the Rubpy/Asc^2– catalytic source of e_aq˙^– for that purpose.

As model compounds, we selected 4-chlorobenzoic acid (ClPhA) and 4-chlorophenyl acetic acid (ClPhAcA). Their reductive dehalogenation occurs via an initial radical anion that is sufficiently long-lived to be detectable as an intermediate (lifetime, about 25 ns in the case of ClPhA);⁴⁶ in other respects, the reaction is completely analogous to that for ClAcA, eqn (1). With ClPhA, the carboxylate function provides sufficient activation for an almost diffusion-controlled primary electron capture (rate constant, 6.0 × 10⁹ M^–1 s^–1).⁴⁶ In contrast, ClPhAcA reacts more slowly by an order of magnitude (5.0 × 10⁸ M^–1 s^–1), as determined by the Stern–Volmer analysis of ESI-3.1.† This clearly indicates that the inserted methylene group completely removes the activation of the arene by the carboxylate function, as the obtained value is very similar to that for e_aq˙^– capture by 4-chlorotoluene (4.5 × 10⁸ M^–1 s^–1).¹⁹

A potential mechanistic complication arises in these systems from the propensity of the aryl radicals to add to aromatic systems (rate constant, 10⁷ M^–1 s^–1 for ClPhA),⁴⁷ which would decrease the product selectivity or destroy the catalyst if it occurred with surplus substrate or with the bipyridine ligand. However, these processes are suppressed in favour of the dehalogenation by sufficiently high concentrations of hydrogen donors. The addition of isopropanol for that purpose proved detrimental to the catalyst life, presumably because the resulting ketyl radicals attack the complex (compare, next section). Therefore, we instead increased the concentration of the hydrogen-donating monoanion AscH^– by a factor of approximately twenty through decreasing the pH by one unit, to 11.6, and concomitantly doubling the weight-in amount, which practically restores the concentration of the catalyst-reducing dianion Asc^2– to its standard value. As a further advantage, this keeps the chemical system as simple as possible.

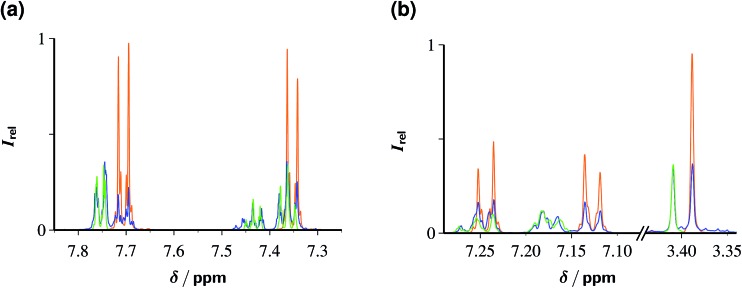
Fig. 7 displays the outcome of these experiments on ClPhA and ClPhAcA, as analyzed by ¹H-NMR. In both cases, irradiation for 1 h sufficed to convert between two-thirds and one-half of the starting material into benzoic acid or phenylacetic acid, with the yield of this specific product, relative to the substrate decrease, being 92% (ClPhA) and 100% (ClPhAcA). When we doubled the substrate concentrations, maximum TON were 130 (ClPhA) and 35 (ClPhAcA). The rather low fractional substrate consumption compared to the preceding section, especially in the case of ClPhAcA, is the reason why we doubled the Rubpy concentration in the experiments of Fig. 7.

Fig. 7. Dechlorination of 5 mM ClPhA (a) and 5 mM ClPhAcA (b) with e_aq˙^– generated from an aqueous solution of 100 µM Rubpy and 100 mM Asc^2– at pH 11.6 by illumination with 532 nm laser flashes (intensity, 600 mJ cm^–2; repetition rate, 10 Hz) for 1 h each. The ¹H-NMR spectra before the illumination (orange) and those after illumination (blue) have been superimposed with identical vertical scales, and overlaid with the spectra (green) of authentic reference samples of the products benzoic acid (a) and phenyl acetic acid (b). Further explanation, see text.

We did not find any evidence for secondary reactions arising from electron capture by the primary products benzoic acid and phenylacetic acid (rate constants, 3.2 × 10⁹ M^–1 s^–1 and 1.8 × 10⁷ M^–1 s^–1),¹⁹ such as the Birch reduction. In the case of ClPhAcA, the inefficiency of the secondary e_aq˙^– scavenger clearly accounts for this; but in the case of ClPhA, this is slightly surprising because during the experiment of Fig. 7b the average concentration ratio of benzoate and ClPhA exceeds 1 : 5, and the ratio of rate constants is larger than 1 : 2, so e_aq˙^– is expected to partition between benzoate and ClPhA in a ratio of at least 1 : 10. We tentatively suggest back electron transfer of the relatively long-lived (tens of microseconds in deaerated aqueous solution)⁴² π-type benzoate radical anion — as opposed to the short-lived σ-type radical afforded by the dissociative electron transfer to the substrate ClPhA — as an explanation for the absence of the respective side products.

We ascribe the lower TON for these aromatic substrates compared to the aliphatic one of the preceding section to the increased parasitic scavenging of e_aq˙^– by the higher concentration of the monoanion AscH^–, which was required to ensure termination of the intermediate aryl radicals through accepting a hydrogen. Still, the catalytic system of this work clearly outperforms the only other systems shown to dechlorinate nonactivated chloroarenes^24,44 as far as metal consumption — and to some extent also ease of handling — are concerned, with a TON improvement by up to a factor of 20.

2.3.3. Carbonyl reduction

To demonstrate that the photoredox catalytic system of this work is not limited to dehalogenations, we present the reduction of a ketone in this section. Considerable effort has been devoted to visible-light induced conversions of strongly activated carbonyl compounds, such as aryl aldehydes or aryl ketones, into their corresponding alcohols or their dimers (diols).^48–51 Here, we have selected 3,3-dimethyl-2-butanone (tert-butylmethylketone TBMK) as a typical representative of nonactivated ketones, illustrating that the high reductive power of e_aq˙^– extends the applicability such as to include also that class of substrates.

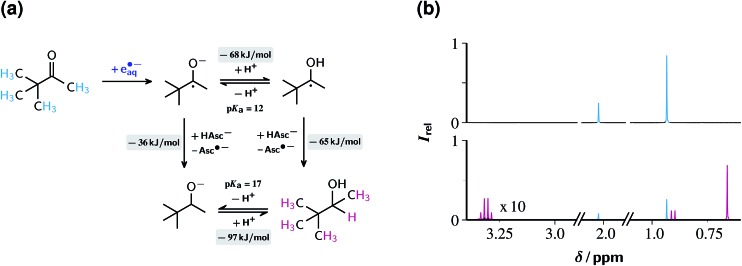
Fig. 8a displays the reaction scheme. Initially, TBMK captures e_aq˙^– to afford the radical anion, which exists in an equilibrium with its protonated form, the ketyl radical (for the close structural analogue acetone, pK _a = 12.03).⁵² By Stern–Volmer experiments completely analogous to those for ClPhAcA (see, ESI-3.1†) we determined the rate constant of e_aq˙^– scavenging by TBMK to be 2.1 × 10⁹ M^–1 s^–1. This is three times slower than in the case of acetone;¹⁹ hence, the unknown reduction potential of TBMK must be slightly more negative than that of acetone (–2.5 V vs. normal hydrogen electrode),³⁰ indicating the challenge that the reduction of TBMK poses.

Fig. 8. Reduction of the ketone TBMK with e_aq˙^–. Graph (a), reaction scheme, with pertaining reaction energies underlayed with gray, and the observed protons of the substrate and the product colour coded. Graph (b), ¹H-NMR spectra before (top) and after (bottom) illumination with 532 nm and 600 mJ cm^–2 at 10 Hz for 30 min of a 10 mM aqueous TBMK solution at pH 11.6 also containing 50 µM Rubpy and 100 mM ascorbate (weight-in concentration). Spectra recorded after acidic workup, see ESI-1.1.† Signal assignment and colour code; TBMK, 2.02 ppm (s) and 0.93 ppm, cyan; 3,3-dimethyl-2-butanol, 3.31 ppm (q), 0.91 ppm (d) and 0.66 ppm (s), magenta. Further explanation, see text.

Two pathways lead from the radical stage to the final product 3,3-dimethyl-2-butanol DMB. Both involve hydrogen atom transfer from the monoanion AscH^–. For the ketyl radical, the rate constant of that process has been reported (1.2 × 10⁶ M^–1 s^–1),⁵³ and from the difference in the bond dissociation energies of DMB (373 kJ mol^–1, taking isopropanol as model compound)⁵⁴ and AscH^– (308 kJ mol^–1)⁵⁵ that reaction is calculated to be exergonic by 65 kJ mol^–1. In the case of the radical anion, where the rate constant is unavailable, an ensuing protonation of the resulting alcoholate yields the final product. Although our experimental data do not allow a distinction between the two pathways, we presume that hydrogen abstraction by the ketyl radical dominates on the following grounds. First, the radical anion experiences a coulombic repulsion by the negatively charged AscH^– whereas the ketyl radical does not. Second, the difference by 5 pK _a units between the more acidic ketyl radical and the alcohol (value for isopropanol, pK _a = 17)⁵⁶ almost halves the driving force, to 36 kJ mol^–1 (owing to the structural similarities, the replacement of the unavailable thermodynamic data for DMB by those for isopropanol should incur a negligible error).

At the usual very basic pH of our experiments (12.65), not only the less favourable radical anion is present in higher concentration as the ketyl radical but also the hydrogen donor AscH^– is largely absent owing to its deprotonation, so the efficiency of the overall reaction is expected to be drastically reduced by the competition with back electron transfer to residual Rubpy (rate constant for the radical anion, 3.1 × 10⁹ M^–1 s^–1).⁵² This is borne out by very low product yields under these circumstances. However, decreasing the pH to 11.6 accompanied by doubling the ascorbate weight-in concentration, in the same way as in the preceding section, reduces both hurdles so much as to provide a rapid ketone reduction.

¹H NMR is again well suited for monitoring the progress and selectivity of the reaction, because the intense singlet of the non-coupled tert-butyl moieties in reactants and products allows a reliable quantification of ketone decrease and alcohol buildup on one hand and a sensitive detection of side products on the other. Fig. 8b shows that the irradiation of a 10 mM solution of TBMK in the presence of the catalytic electron source converted 74% of the substrate into the alcohol rapidly (within 30 minutes) and completely selectively (without any indication of side products). This corresponds to a TON of 148 in the example. Consistent with the results of Section 2.3.1, this TON can be significantly increased (to 221) by doubling the TBMK concentration, but only at the expense of reducing the relative TBMK decrease to 55%. This general trend for all our substrates supports the hypothesis that the Rubpy/Asc^2– catalytic source of e_aq˙^– is predominantly limited not by catalyst loss but by gradual self-poisoning caused by the oxidation products of the sacrificial donor.

3. Conclusions

As we have established, the Rubpy/Asc^2– system is capable of operating with single laser pulses and sustainably delivers the super-reductant e_aq˙^– in amounts well suited for laboratory-scale reactions; for this, concentrations of the sacrificial donor above some 10 mM already suffice.

The combination of photokinetic experiments on short timescales with studies of the intrinsic catalyst stability and substrate turnover in exhaustive photolysis have provided detailed answers on efficiency-limiting factors; in particular, that the quenching by Asc^2– greatly enhances the catalyst stability through reducing the probability of nonradiative transitions from ³MLCT to destructive dd states, and that the turnover numbers (TON) of these electron sources are not limited by substrate-derived products poisoning the catalyst but by accumulating oxidation products of the sacrificial donor scavenging more and more of the liberated electrons.

The setup is extremely simple, as it merely involves illuminating part of a well-stirred solution with an affordable frequency-doubled Nd:YAG laser running at its normal repetition rate; no accessory equipment is necessary. Upscaling is thus evidently possible by irradiating a larger volume for a proportionally longer time. Within the illuminated volume, the e_aq˙^– concentrations per laser flash are on the order of 10 µM, which is comparable to what can typically be reached by pulse radiolysis.¹⁹

The operating wavelength, superb reducing power, and high catalyst stability are clear assets of the method. Parasitic absorptions of the green light are completely absent for all our examples, and also not to be expected for typical reactants and products; nonactivated aliphatic and aromatic chlorides as well as carbonyl compounds pose no problems for the super-reductant e_aq˙^–; and TON of up to 1400 clearly provide an optimistic outlook for a broader application of the system in reductive photoredox catalysis. This low consumption of the metal catalyst, in conjunction with the bioavailable sacrificial donor and the green operating wavelength clearly warrant calling our procedure sustainable.

Conflicts of interest

There are no conflicts to declare.