Inference of Distribution of Fitness Effects and Proportion of Adaptive Substitutions from Polymorphism Data

Abstract

The distribution of fitness effects (DFE) encompasses the fraction of deleterious, neutral, and beneficial mutations. It conditions the evolutionary trajectory of populations, as well as the rate of adaptive molecular evolution (α). Inferring DFE and α from patterns of polymorphism, as given through the site frequency spectrum (SFS) and divergence data, has been a longstanding goal of evolutionary genetics. A widespread assumption shared by previous inference methods is that beneficial mutations only contribute negligibly to the polymorphism data. Hence, a DFE comprising only deleterious mutations tends to be estimated from SFS data, and α is then predicted by contrasting the SFS with divergence data from an outgroup. We develop a hierarchical probabilistic framework that extends previous methods to infer DFE and α from polymorphism data alone. We use extensive simulations to examine the performance of our method. While an outgroup is still needed to obtain an unfolded SFS, we show that both a DFE, comprising both deleterious and beneficial mutations, and α can be inferred without using divergence data. We also show that not accounting for the contribution of beneficial mutations to polymorphism data leads to substantially biased estimates of the DFE and α. We compare our framework with one of the most widely used inference methods available and apply it on a recently published chimpanzee exome data set.

NEW mutations are the ultimate source of heritable variation. Their fitness properties determine the possible evolutionary trajectories that a population can follow (Bataillon and Bailey 2014). For instance, supply rate and fitness effects of beneficial mutations determine the expected rate of adaptation of a population (Lourenço et al. 2011), while the proportion of deleterious mutations conditions the expected drift load of a population (Kimura et al. 1963). Even a few beneficial mutations with large effects can quickly move a population toward its fitness optimum, while the fitness can be reduced through the accumulation of multiple deleterious mutations with small effects that occasionally escape selection. Genome-wide rates and effects of new mutations influence, among others, the evolutionary advantage of sex (Otto and Lenormand 2002), the expected degree of parallel evolution (Chevin et al. 2010b), the maintenance of variation on quantitative traits (Hill 2010), and the evolutionary potential and capacity of populations to respond to novel environments (Chevin et al. 2010a; Hoffmann and Sgrò 2011).

Effects of new mutations on fitness are typically modeled as independent draws from an underlying distribution of fitness effects (DFE) which spans deleterious, neutral, and beneficial mutations. There has been considerable focus on estimating the DFE of new nonsynonymous mutations to learn more about factors governing the rate of adaptive molecular evolution, commonly defined as the proportion of fixed adaptive mutations among all nonsynonymous substitutions, denoted α. Therefore, inferring the DFE, both from experimental (Halligan and Keightley 2009; Bataillon et al. 2011; Sousa et al. 2012; Jacquier et al. 2013; Bataillon and Bailey 2014), and from polymorphism and divergence data (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007, 2012; Boyko et al. 2008; Eyre-Walker and Keightley 2009; Galtier 2016), has been a long-standing goal of evolutionary genetics.

The McDonald–Kreitman test (McDonald et al. 1991) was one of the first attempts to use DNA data to measure the amount of selection experienced by genes. It compares the amount of variation within a species (ingroup) to the variation between species. The test contrasts the amount of variation found at synonymous and nonsynonymous sites, where synonymous sites are assumed to be neutrally evolving. Smith and Eyre-Walker (2002) further developed this test to infer α and the amount of purifying selection, defined as the proportion of strongly deleterious mutations [see also Fay and Wu (2000) and Welch (2006) for a maximum-likelihood approach]. Building on the Poisson random field (PRF) theory (Sawyer and Hartl 1992; Sethupathy and Hannenhalli 2008) and arising as extensions to the classic McDonald–Kreitman test, a series of methods have been developed to not only characterize the amount of selection, but also the DFE (Bustamante et al. 2003; Piganeau and Eyre-Walker 2003; Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007, 2010; Boyko et al. 2008; Gronau et al. 2013; Kousathanas and Keightley 2013; Racimo and Schraiber 2014), using it as a building block to estimate α (Loewe et al. 2006; Eyre-Walker and Keightley 2009; Schneider et al. 2011; Keightley and Eyre-Walker 2012; Galtier 2016).

Assuming that sites are independent, new mutations arise as a Poisson process and always occur at new sites, these methods then either model the observed variation using a Poisson distribution or a binomial distribution conditioned on the total number of observed mutations (as in Keightley and Eyre-Walker 2007). Patterns of nucleotide variation within the ingroup can be summarized via the polymorphism counts occurring in each frequency class and form the site frequency spectrum (SFS), while variation between the ingroup and outgroup is measured by fixed mutations as divergence counts (Figure 1). The means of each entry of the SFS and divergence counts are calculated as a function of the DFE and other parameters. Selection is assumed to be weak ($s\ll 1,$ but note that $4N_{\mathrm{e}}s$ can still be large) and the DFE to be constant in time and the same in both the ingroup and outgroup.

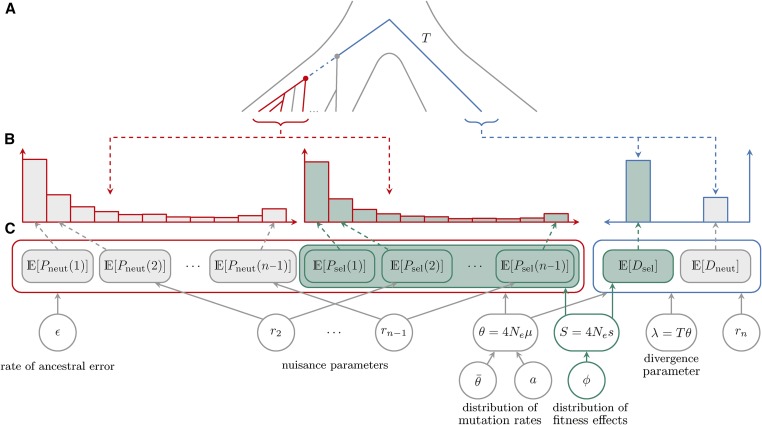
Figure 1.

Schematic of data and the hierarchical model assumed in the inference method. Throughout the figure, gray and blue fill indicates sites that are assumed to be evolving neutrally or potentially under selection, respectively; while red and blue outlines indicates polymorphism and divergence data (expectations), respectively. (A) The history and coalescent tree of two populations: the ingroup (on the left side), for which polymorphism data are collected, and the outgroup (on the right side), for which divergence counts are obtained. A total of n sequences are sampled from the ingroup (marked in red), with the MRCA marked with a red circle. The MRCA of the whole ingroup population is marked with a gray circle. From the outgroup we typically have access to one sequence (marked in blue). The total evolutionary time between the MRCA of the sample (red circle) and the sampled outgroup sequence can be divided into the time from the MRCA of the sample to the MRCA of the whole ingroup population (blue dot–dash line) and T, the time from the ingroup MRCA to the sampled outgroup sequence (blue solid line). (B) Observed SFS and divergence counts [$p_z\left(i\right)$ and $d_z,$ with $z\in \left\{\text{neut, sel}\right\}$ and $1\le i<n$]. (C) Expected counts [$\mathbb{E}\left[P_z\left(i\right)\right]$ and $\mathbb{E}\left[D_z\right],$ with $z\in \left\{\text{neut, sel}\right\}$ and $1\le i<n$], model parameters, and relations between parameters, expectations, and data. The dashed gray and blue ↓’s connect observed counts from (B) with matching expected counts from (C).

To disentangle selection from demography and other forces (Nielsen 2005), the sequenced sites are divided into two classes of neutrally evolving and selected sites. The DFE is then inferred by contrasting the SFS counts for the neutral and selected sites, by assuming that demography and other forces equally affect the two classes.

Ideally, a full demographic model should be jointly inferred with the DFE parameters from the data. This can be computationally very demanding and instead a simplified demography can be often assumed, where a few population size changes are allowed (Keightley and Eyre-Walker 2007; Eyre-Walker and Keightley 2009; Kousathanas and Keightley 2013), or a somewhat more complex model is inferred (Boyko et al. 2008). Alternatively, the explicit inference of demography can be avoided altogether by introducing a series of nuisance parameters that account for demographic and other effects. These parameters account for distortions of the polymorphism counts relative to neutral expectations in an equilibrium Wright–Fisher population (Eyre-Walker et al. 2006; Galtier 2016). The approach of Eyre-Walker et al. (2006) can potentially be more robust for estimating a DFE than putting a lot of faith in a simplified demographic scenario, especially when demography cannot be simply summarized by a few changes in population size. However, this approach will only be accurate for modeling the SFS in the limit of weak selection, as neutral and selected sites will increasingly have experienced different histories.

The proportion of adaptive substitutions, α, is typically obtained as a ratio between an estimate of the number of adaptive substitutions and the observed selected divergence counts (Loewe et al. 2006; Eyre-Walker and Keightley 2009; Keightley and Eyre-Walker 2012; Galtier 2016). The number of adaptive substitutions is calculated by subtracting the expected counts accrued by fixation of deleterious and neutral mutations from the observed divergence counts at selected sites. These expected counts are calculated from an inferred DFE of deleterious mutations (henceforth denoted deleterious DFE). The deleterious DFE is most often inferred from the SFS data under the assumption that all mutations at selected sites are deleterious. This approach for estimating α heavily relies on the assumption that the ingroup and outgroup species share the same DFE, or more accurately, the same distribution of scaled selection coefficients $S=4N_{\mathrm{e}}s.$ Unfortunately, this assumption of invariance might not often be met in practice, because the DFE might change, or simply because it is unlikely that both the ingroup and outgroup lineages evolved with the same population size.

There has been great focus on developing methods inferring a deleterious DFE from polymorphism data alone (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Kousathanas and Keightley 2013; Racimo and Schraiber 2014). These methods rely on a crucial assumption: beneficial mutations contribute negligibly to polymorphism and are not modeled. The reasoning behind this assumption is that strongly selected beneficial mutations will fix very quickly and that “at most an advantageous mutation will contribute twice as much heterozygosity during its lifetime as a neutral variant” (Smith and Eyre-Walker 2002), which is backed by one study (Keightley and Eyre-Walker 2010). We note that there is no sharp difference in the expected contribution to SFS and divergence counts between beneficial and deleterious mutations when their selection coefficients are small ($\left|N_{\mathrm{e}}s\right|<1$) (Charlesworth and Eyre-Walker 2007; Eyre-Walker and Keightley 2007). Hence, there is scope for weakly selected deleterious and beneficial mutations to contribute to both polymorphism and divergence data.

We develop a hierarchical probabilistic model that combines and extends previous methods, and that can infer both the full DFE and α from polymorphism data alone. While some DFE methods do model a full DFE encompassing both deleterious and beneficial mutations (Bustamante et al. 2003; Piganeau and Eyre-Walker 2003; Boyko et al. 2008; Schneider et al. 2011; Gronau et al. 2013; Galtier 2016), the majority of them do not estimate α [but see Schneider et al. (2011), who estimate related quantities]. We note that an outgroup is still needed to obtain an unfolded SFS, but our inference method does not have to assume invariance of the DFE in the ingroup and outgroup lineages. We show that the assumption that beneficial mutations make negligible contribution to SFS data are unfounded and that a full DFE can also be inferred from polymorphism data alone. Using the estimated full DFE, we show how α can be inferred without relying on divergence data. Performing inference on polymorphism data alone is desirable when assumptions regarding outgroup evolution (for example, invariance of the DFE) are unlikely to be met. We also demonstrate that when the contribution of beneficial mutations to SFS data is ignored, both the inferred deleterious DFE and α can be heavily biased. This point was also made by Messer and Petrov (2013) in the context of studies relying on McDonald–Kreitman tests. We compare our method and illustrate the resulting bias using the most widely used inference method, dfe-alpha (Keightley and Eyre-Walker 2007, 2012; Eyre-Walker and Keightley 2009; Schneider et al. 2011). We also investigate the impact of misidentifying the ancestral state on inference, and illustrate our method by reanalyzing a recently published exome data set, containing both polymorphism and divergence counts for three chimpanzee subspecies (Bataillon et al. 2015).

Method

Hierarchical Model for Inference of DFE and α

Based on PRF theory, we build a hierarchical model to infer the DFE from polymorphism (SFS) and divergence counts. Our model combines and extends features from different approaches. Figure 1 shows a schematic of the model. We offer below a summary of the assumptions and theory underlying our approach. Further details on the likelihood function, its implementation, and numerical optimization can be found in the Supplemental Material, File S1.

Notations and assumptions

The data are divided into sites that are assumed to be either evolving neutrally (henceforth marked by the subscript neut), or those bearing mutations with fitness consequences for which the DFE is estimated (henceforth marked by the subscript sel). Let the observed SFS be given through $p_z\left(i\right),$ where $p_z\left(i\right)$ is the count of polymorphic sites that contain the derived allele i times ($1\le i<n$) and $l_z$ the total number of sites surveyed, where n is the sample size and $z\in \left\{\text{neut, sel}\right\}.$ We denote by $P_z\left(i\right)$ the corresponding random variable per site, defined as the random number of sites that contain the derived allele i times, normalized by $l_z.$ From PRF theory, $p_z\left(i\right)$ follows a Poisson distribution with mean $l_z\mathbb{E}\left[P_z\left(i\right)|\theta ,\phi \right],$ where $\theta =4N_{\mathrm{e}}\mu$ is the scaled mutation rate per site per generation, and φ is a parametric DFE (Figure 1, B and C). A specific example of φ will be given in the Results and Discussion section. We assume additive selection and we define the selection coefficient s as the difference in fitness between the heterozygote for the derived allele and the homozygote for the ancestral allele, leading to fitness of 1, $1+s,$ and $1+2s$ for the ancestral homozygote, heterozygote, and derived homozygote genotypes, respectively.

Expected SFS

From PRF theory (Sawyer and Hartl 1992; Sethupathy and Hannenhalli 2008),

$$\begin{array}{c}\mathbb{E}\left[P_{\text{neut}}\left(i\right)|\theta \right]=\frac{\theta }{i},\\ \mathbb{E}\left[P_{\text{sel}}\left(i\right)|\theta ,S\right]=\theta {\displaystyle {\int }_0^{1}B\left(i,n,x\right)H\left(S,x\right)dx},\end{array}$$ (1)

where

$$B\left(i,n,x\right)=\left(\begin{array}{c}n\\ i\end{array}\right)x^i{\left(1-x\right)}^{n-i}$$

is the binomial probability of observing i derived alleles in a sample of size n when the true allele frequency is x, and

$$H\left(S,x\right)=\frac{1-e^{-S\left(1-x\right)}}{x\left(1-x\right)\left(1-e^{-S}\right)}.$$

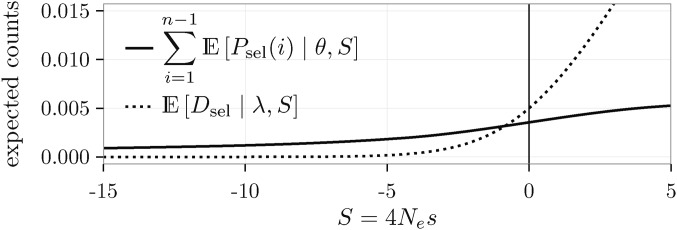
Note that due to our scaling of the mutation rate, $H\left(s,x\right)$ is proportional (with a factor of $1/2$) to the mean time a new semidominant mutation of scaled selection coefficient $S=4N_{\mathrm{e}}s$ spends between x and $x+dx$ (Wright 1938). Figure 2 shows the expectations from Equation 1 as a function of S.

Figure 2.

Expected counts per site as a function of S, for $\theta =0.001$ and $\lambda =\mathrm{0.005.}$

To obtain $\mathbb{E}\left[P_{\text{sel}}\left(i\right)|\theta ,\phi \right],$ we integrate over the DFE,

$$\mathbb{E}\left[P_{\text{sel}}\left(i\right)|\theta ,\phi \right]={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathbb{E}\left[P_{\text{sel}}\left(i\right)|\theta ,S\right]\phi \left(S\right)dS}.$$ (2)

Relative to the expected SFS of independent sites under a Wright–Fisher constant population (Equations 1 and 2), the observed SFS can be distorted due to demography, ascertainment bias, nonrandom sampling, and linkage. We account for such distortions that affect both the neutral and selected sites to a similar extent by using the approach of Eyre-Walker et al. (2006) and introduce nuisance parameters $r_i,$ $1\le i<n,$ that scale the expected SFS, for $z\in \left\{\text{neut},\text{sel}\right\},$

$$\mathbb{E}\left[P_z\left(i\right)|\theta ,r_i,\phi \right]=r_i\hspace{0.17em}\mathbb{E}\left[P_z\left(i\right)|\theta ,\phi \right].$$ (3)

To avoid identifiability issues, we set $r_1=1.$

Full DFE and divergence counts

Unlike methods that infer only a strictly deleterious DFE, we can incorporate a full DFE that includes both deleterious and beneficial mutations. We optionally model divergence counts $d_z$ as a Poisson distribution with mean $l_z^d\mathbb{E}\left[D_z|\lambda ,\theta ,\phi \right]$. Here, $l_z^d$ is the number of sites used for divergence counts, and can possibly be different from $l_z.$ We have that

$$\begin{array}{c}\mathbb{E}\left[D_{\text{neut}}|\lambda \right]=\lambda ,\\ \mathbb{E}\left[D_{\text{sel}}|\lambda ,S\right]=\lambda \frac{S}{1-e^{-S}},\end{array}$$ (4)

where $\lambda =T\theta$ is a composite divergence parameter that accounts for the number of neutral mutations that go to fixation during the divergence time T from the most recent common ancestor (MRCA) of the ingroup population to the outgroup (blue full line in Figure 1A). The term $S/\left(1-e^{-S}\right)$ accounts for the fixation of a mutation with scaled selection coefficient S, and can be obtained as ${\lim }_{x\to 1}H\left(S,x\right).$ Figure 2 shows the expectations for the divergence counts at selected sites from Equation 4 as a function of S.

As divergence counts are calculated by comparing the outgroup sequence to the sample of sequences from the ingroup, polymorphism may be misattributed as divergence, i.e., mutations that are polymorphic in the ingroup population but fixed in the sample are counted as divergence. This is the case for mutations that occur between the MRCAs of the sample and ingroup (blue dot–dash line in Figure 1A). Misattributed polymorphism can lead to biased inference of α (Keightley and Eyre-Walker 2012). To account for this issue, we adjust the above means to also incorporate the misattributed polymorphism by increasing the expectations with the contributions coming from mutations present in all n sampled individuals,

$$\begin{array}{c}\mathbb{E}\left[D_{\text{neut}}|\lambda ,\theta ,r_n\right]=\mathbb{E}\left[D_{\text{neut}}|\lambda \right]+\theta r_n\frac{1}{n},\\ \mathbb{E}\left[D_{\text{sel}}|\lambda ,\theta ,r_n,S\right]=\mathbb{E}\left[D_{\text{sel}}|\lambda ,S\right]+\theta r_n{\displaystyle {\int }_0^{1}B\left(n,n,x\right)H\left(S,x\right)dx}.\end{array}$$ (5)

Assuming that the ingroup and outgroup share the same DFE, we integrate over it to obtain

$$\mathbb{E}\left[D_{\text{sel}}|\lambda ,\theta ,r_n,\phi \right]={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathbb{E}\left[D_{\text{sel}}|\lambda ,\theta ,r_n,S\right]\phi \left(S\right)dS}.$$ (6)

Unfolded SFS and ancestral misidentification

When only a deleterious DFE is inferred, the folded SFS is typically used, where only sums of the form $p_z\left(i\right)+p_z\left(n-i\right)$ are modeled. This is sufficient for inference of a deleterious DFE (Keightley and Eyre-Walker 2007). However, the unfolded SFS contains valuable information for inference of the full DFE, as beneficial mutations are expected to be present in high frequencies (Fay and Wu 2000; Durrett 2008). To obtain an unfolded SFS, the ancestral state needs to be identified, and this is prone to polarization errors (Hernandez et al. 2007). Error rates can be reduced by relying on more than one outgroup population, as described by Keightley et al. (2016). Even for potentially well-identified ancestral states, polarization errors can remain, for instance at hypermutable CpG sites in mammals. We use the approach of Williamson et al. (2005), Boyko et al. (2008), and Glémin et al. (2015), which has proved efficient to correct for this problem (Glémin et al. 2015). We model the mean of $P_z\left(i\right),$ $z\in \left\{\text{neut},\text{sel}\right\},$ as a mixture of sites whose ancestral states were correctly identified (with probability $1-\mathit{ϵ}$), or misidentified (with probability ϵ),

$$\mathbb{E}\left[P_z\left(i\right)|\theta ,r_i,\mathit{ϵ},\phi \right]=\left(1-\mathit{ϵ}\right)\mathbb{E}\left[P_z\left(i\right)|\theta ,r_i,\phi \right]+\mathit{ϵ}\mathbb{E}\left[P_z\left(n-i\right)|\theta ,r_i,\phi \right].$$ (7)

Mutation variability

There is substantial evidence that both substitution and mutation rates vary along the genome (Golding 1983; Yang 1996; Arndt et al. 2005; Hodgkinson and Eyre-Walker 2011; Francioli et al. 2015), with a long tradition of modeling this variability in phylogenetic inferences as a gamma distribution (Golding 1983; Yang 1996). A few DFE inference methods allow for mutation rates to vary in a nonparametric fashion (Bustamante et al. 2003; Gronau et al. 2013). We model mutation variability by assuming that mutation rates follow a gamma distribution with mean $\overline{\theta }$ and shape a. This is motivated by the phylogenetic approaches, but also by mathematical convenience: if the mean of a Poisson distribution follows a gamma distribution, the resulting distribution is a negative binomial. We assume that the data are divided into m nonoverlapping fragments of lengths $l_{\text{neut}}^j+l_{\text{sel}}^j,$ $1\le j\le m;$ for each fragment j, we have the SFS $p_z^j\left(i\right),$ $1\le i<n.$ We can also include an additional $m^d$ fragments of lengths $l_{\text{neut}}^{d,j}+l_{\text{sel}}^{d,j}$ for which we have the divergence counts, $d_z^j.$ We assume that each fragment has a constant mutation rate θ, and mutation rates can vary between fragments. Given the mutation rate ${\theta }_j$ of the fragment j, then $p_z^j\left(i\right)$ and $d_z^j$ follow the Poisson distributions with means $l_z^j\mathbb{E}\left[P_z\left(i\right)|{\theta }_j,r_i,\mathit{ϵ},\phi \right]$ and $l_z^{d,j}\mathbb{E}\left[D_z|\lambda ,{\theta }_j,r_n,\phi \right],$ given by Equations 1–6. Integrating over the distribution of mutation rates, we obtain that $p_z^j\left(i\right)$ and $d_z^j$ have a negative binomial distribution with shape a and means $l_z^j\mathbb{E}\left[P_z\left(i\right)|\overline{\theta },r_i,\mathit{ϵ},\phi \right]$ and $l_z^{d,j}\mathbb{E}\left[D_z|\lambda ,\overline{\theta },r_n,\phi \right],$ respectively.

Inferring α using divergence or polymorphism data alone

Once the DFE is estimated, α can be calculated from the observed divergence counts as follows (Eyre-Walker and Keightley 2009):

$$\alpha \approx \frac{d_{\text{sel}}-\frac{l_{\text{sel}}^d}{l_{\text{neut}}^d}{d}_{\text{neut}}{\displaystyle {\int }_{-\mathrm{\infty }}^0\frac{S}{1-e^{-S}}\phi \left(S\right)dS}}{d_{\text{sel}}},$$ (8)

where the numerator represents the estimated number of adaptive substitutions, obtained by subtracting the expected deleterious and neutral substitutions from the total observed divergence counts at selected sites. Keightley and Eyre-Walker (2012) extended Equation 8 to account for misattributed polymorphism. We correct for it by removing the expected number of mutations that are in fact polymorphic from $d_{\text{sel}}$ and $d_{\text{neut}}.$ These expectations can be readily obtained from Equation 5 by setting $\lambda =0.$ The new estimate of α is obtained as in Equation 8, where $d_{\text{sel}}$ and $d_{\text{neut}}$ are replaced with the readjusted divergence counts $d_{\text{sel}}^{\ast }$ and $d_{\text{neut}}^{\text{*}}$ given by

$$\begin{array}{c}{d}_{\text{neut}}^{\ast }=d_{\text{neut}}-l_{\text{neut}}^d\mathbb{E}\left[D_{\text{neut}}|\lambda =0,\theta ,r_n\right],\\ d_{\text{sel}}^{\ast }=d_{\text{sel}}-l_{\text{sel}}^d\mathbb{E}\left[D_{\text{sel}}|\lambda =0,\theta ,r_n,\phi \right].\end{array}$$ (9)

This approach to calculate α relies heavily on the assumption that the ingroup and outgroup share the same scaled DFE. However, if one has access to an estimated full DFE purely from polymorphism data, α can still be estimated by replacing the observed divergence counts with the expected counts from Equation 4. As λ will cancel out in the resulting fraction, α can be obtained by setting $\lambda =1.$ Then,

$$\alpha \approx \frac{{\displaystyle {\int }_0^{\mathrm{\infty }}\mathbb{E}\left[D_{\text{sel}}|\lambda =1,S\right]\phi \left(S\right)dS}}{{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\mathbb{E}\left[D_{\text{sel}}|\lambda =1,S\right]\phi \left(S\right)dS}}.$$ (10)

In the following, we refer to the two above estimates of α as ${\alpha }_{\text{div}}$ and ${\alpha }_{\text{dfe}}$, respectively, to distinguish more clearly the type of information used.

Likelihood estimation and comparison of models

The framework described above allows maximum-likelihood estimation of both evolutionary (mutation rates and DFE parameters) and nuisance parameters, as well as the error in the ancestral states, ϵ. Details about the implementation and optimization of the likelihood function are given in File S1. Note that in our implementation, likelihood ratio tests (LRTs) can be used to rigorously test whether polymorphism data provide evidence for a full DFE, or if a strictly deleterious DFE is sufficient. This framework also allows for deciding whether including nuisance parameters and/or ancestral error provides a better fit to the data. The reported P-values for the LRT are obtained by assuming that the likelihood ratio under the null hypothesis (reduced model is correct) follows a ${\chi }^2$ distribution.

Data availability

The source code implementing the maximum-likelihood framework presented here is freely available from https://github.com/paula-tataru/polyDFE/.

Results and Discussion

To investigate the statistical performance of our method to infer the DFE, α, and test hypothesis regarding the contribution of beneficial mutations to patterns of polymorphism, we performed extensive simulations using SFS_CODE (Hernandez 2008). We generated exome-like data, where a 10.8-Mb genetic segment was simulated per data set, containing multiple independent fragments (typically of 216 sites) for which recombination took place. We sampled 20 sequences (10 diploid individuals) from the ingroup, and one sequence from the outgroup. We explored a wide range of simulated DFEs (12 full and 5 deleterious, Table 1), chosen such that the simulated α had one of four possible values ($0\text{,}$ $20\text{,}$ $50$, and $80\text{\%,}$ Figure 3A). Most simulations were performed using a constant population size and without error in the identification of the ancestral state. Results are shown for this case unless stated otherwise. These assumptions were later relaxed. For each considered simulation scenario (one given DFE, demographic, linkage, and misidentification of the ancestral state), we simulated 100 replicate data sets. For more details on the simulated data, see File S1.

Table 1. Simulated DFEs.

	DFE type	DFE abbreviation	$S_d$	b	$p_b$	$S_b$	α
Full DFEs	Low α, low $S_d$	LALSD	−10	0.4	0.02	4	0.21
	Low α, low b	LALB	−400	0.15	0.02	4	0.21
	Low α, low $p_b$	LALPB	−400	0.4	0.005	4	0.21
	Low α, low $S_b$	LALSB	−400	0.4	0.02	0.1	0.22
	Medium α, medium $S_d$	MAMSD	−400	0.4	0.02	4	0.53
	Medium α, low $p_b$	MALPB	−400	0.65	0.005	4	0.50
	Medium α, low $S_b$	MALSB	−400	0.4	0.07	0.1	0.50
	Medium α, high $S_b$	MAHSB	−400	0.4	0.005	16	0.51
	High α, high $S_d$	HAHSD	−10,000	0.4	0.02	4	0.80
	High α, high b	HAHB	−400	0.65	0.02	4	0.80
	High α, high $p_b$	HAHPB	−400	0.4	0.07	4	0.81
	High α, high $S_b$	HAHSB	−400	0.4	0.02	16	0.81
	High $S_b$	HSB	−400	0.4	0.02	800	0.99
Deleterious DFEs	Low $S_d$	DelLSD	−10	0.4	0	—	0
	Low b	DelLB	−400	0.15	0	—	0
	Medium $S_d$	DelMSD	−400	0.4	0	—	0
	High $S_d$	DelHSD	−10,000	0.4	0	—	0
	High b	DelHB	−400	0.65	0	—	0

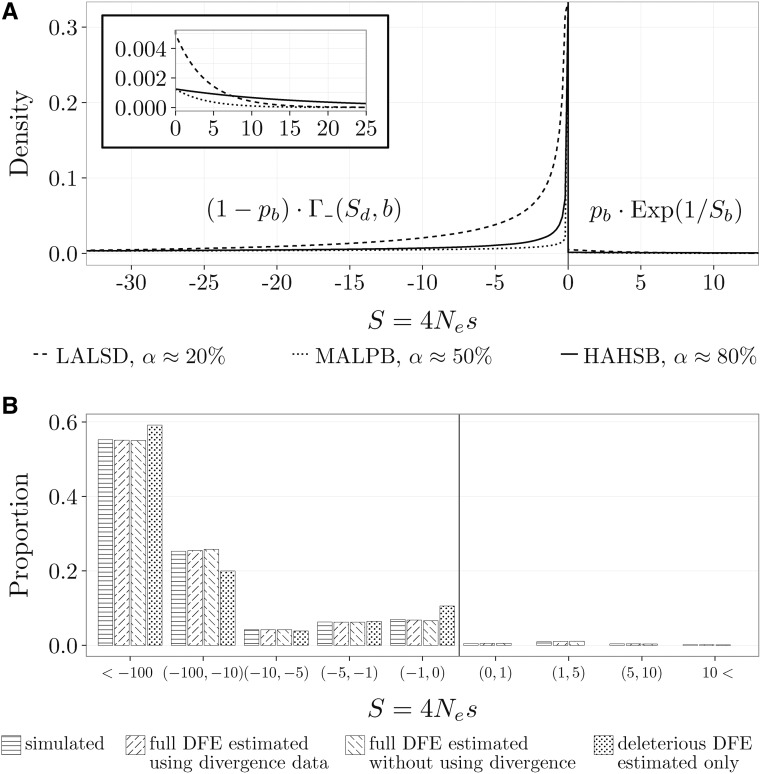
The DFE consists of a mixture between gamma and exponential distributions: a new mutation is deleterious with probability $1-p_b,$ and has a selection coefficient drawn from a reflected gamma distribution with mean $S_d<0$ and shape b; a new mutation is beneficial with probability $p_b,$ and has a selection coefficient drawn from an exponential distribution with mean $S_b>0.$

Figure 3.

Example of simulated and inferred mixture of gamma and exponential DFEs. (A) Three of the simulated DFEs (Table 1) with different α values (proportion of beneficial substitutions). The DFEs are parameterized by $S_d$ (mean selection coefficient of deleterious mutations), b (shape of distribution of deleterious DFE), $p_b$ (proportion of beneficial mutations), and $S_b$ (mean selection coefficient of beneficial mutations). The inset shows a zoom-in of the beneficial part of the DFE. (B) Simulated discretized DFE (corresponding to MAMSD from Table 1), together with the mean (over the 100 replicates) inferred discretized DFE using both polymorphism and divergence data and only polymorphism data, where a full DFE and a deleterious DFE was inferred.

The general shape of the DFE is not agreed upon (Welch et al. 2008; Bataillon and Bailey 2014). The DFE has been modeled using a wide range of functional continuous forms (Boyko et al. 2008; Kousathanas and Keightley 2013; Galtier 2016), but also as a discrete distribution (Keightley and Eyre-Walker 2010; Gronau et al. 2013; Kousathanas and Keightley 2013). We use a DFE consisting of a mixture between gamma and exponential distributions, which model deleterious and beneficial mutations, respectively. With probability $1-p_b,$ a new mutation is deleterious and its selection coefficient comes from a reflected gamma distribution with mean $S_d<0$ and shape b; while with probability $p_b,$ a new mutation is beneficial and its selection coefficient comes from an exponential distribution with mean $S_b>0$ (Figure 3A). We do not explore alternative parametric DFE families, but they could easily be incorporated within this framework. For such studies see Welch et al. (2008) and Kousathanas and Keightley (2013).

We inferred the DFE and α parameters using three different models: a full DFE was inferred from both polymorphism and divergence data, a full DFE was inferred from polymorphism data alone, or a deleterious-only DFE was inferred from polymorphism data alone. We calculated ${\alpha }_{\text{dfe}}$ and ${\alpha }_{\text{div}}$ from the inferred DFEs; ${\alpha }_{\text{dfe}}$ is always 0 for inference assuming only a deleterious DFE, so here we only calculated ${\alpha }_{\text{div}}.$ Distortion parameters r were always estimated, while the ancestral misidentification error ϵ was fixed at 0, unless otherwise specified.

Reporting inference quality

We report inference performance using ${\log }_2\left(\text{estim}/\text{sim}\right)$ on a log-modulus scale. Here, estim is the estimated value, while sim is the simulated value. Unlike the relative error, defined as $1-\left(\text{estim}/\text{sim}\right),$ this log ratio gives equal weight to both overestimation and underestimation of the parameters. For example, the log ratios of 1 and −1 correspond to the estimated value being double or half the simulated value, respectively. When sim equals estim, the ratio is equal to 0.

Where applicable, we report ${\log }_2\left(\text{estim}/\text{sim}\right)$ for the DFE parameters, α and ϵ in File S1. The remaining parameters ($\overline{\theta },$ a, λ, $r_i$) are also estimated but are not of interest here, and we do not investigate how well they are recovered (but see File S1 for details). For the sake of clarity, the figures in the main text do not cover all simulated DFEs, but illustrate the main results and overall trends. Where applicable, we also report in File S1 the P-values for different LRTs.

Inference of deleterious DFE

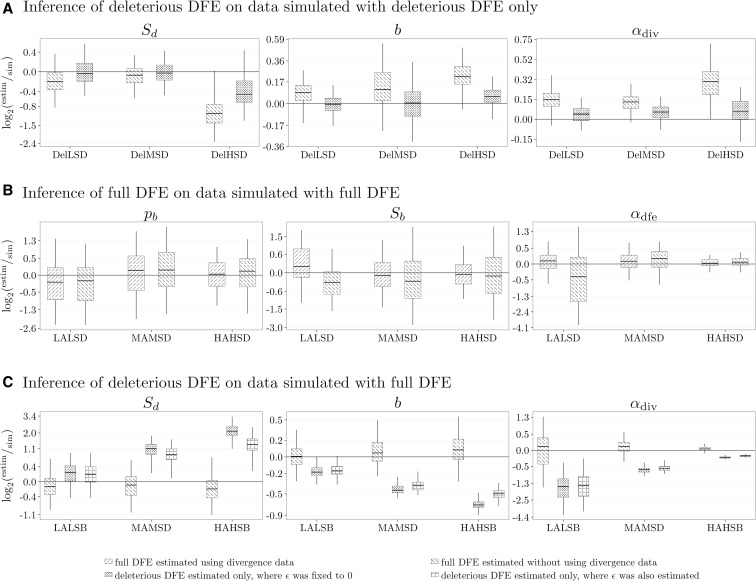
Using simulations that did not contain any beneficial mutations in the polymorphism data, we investigated how well we can infer the deleterious DFE and if our method can recover the fact that all polymorphic mutations are deleterious. We observed that the two parameters determining the deleterious DFE, $S_d$ and b, and α are accurately inferred when only a deleterious DFE was estimated (Figure 4A and Figure S1 in File S1). When, instead, a full DFE was inferred from the polymorphism data alone, the parameters showed different amounts of bias (Figure 4A and Figure S1 in File S1). When using an LRT to compare the relative goodness of fit on simulated data, virtually all data sets rejected the full DFE model in favor of the reduced model (Figure S2 in File S1). This indicates that our method can accurately detect if there is no empirical evidence for the presence of beneficial mutations in the SFS. So in principle, one can perform estimation under both the full and deleterious DFE models and use the LRT to decide which model is most appropriate for the data.

Figure 4.

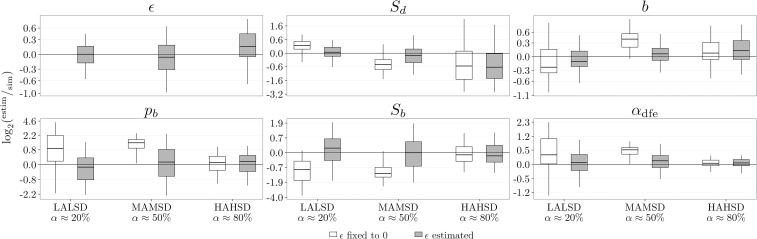
Inference of α (proportion of beneficial substitutions) and DFE parameters: $S_d$ (mean selection coefficient of deleterious mutations), b (shape of distribution of deleterious DFE), $p_b$ (proportion of beneficial mutations), and $S_b$ (mean selection coefficient of beneficial mutations). (A) Quality for inference performed on polymorphism data alone, for three simulated deleterious DFEs (Table 1) with different S_d’s. The DFE parameters are inferred using only polymorphism data assuming a full and deleterious DFE. (B) Quality for inference performed on polymorphism and divergence data, for three simulated DFEs with different α values (Table 1). The DFEs differ only in the simulated value of $S_d.$ The DFE parameters are inferred using polymorphism and divergence or only polymorphism data. (C) Quality for inference performed on polymorphism data alone, for three simulated DFEs with different α values (Table 1). The DFEs differ only in the simulated value of $S_b.$ Only polymorphism data are used and the DFE parameters are inferred assuming a full DFE, where ϵ is set to zero and is not estimated, and a deleterious DFE, where ϵ is set to zero and is not estimated, or is estimated. The data were simulated with $\mathit{ϵ}=0.$

Inference of full DFE

From the expected contribution of mutations to polymorphism and divergence data, as a function of S (Figure 2), it is evident that if beneficial mutations occur at any appreciable rate, they should have a nonnegligible impact in the polymorphism data. This suggests that it should be possible to infer the full DFE from polymorphism data alone. We investigated this using data generated under a full DFE. As expected, the deleterious DFE parameters were inferred equally well, regardless of whether the divergence data were used or not (Figure S3 in File S1). The variance of the estimates seems to be somewhat larger when divergence data are not used, but this is most likely due to the inference using less data. The parameters of the beneficial part of the DFE and α were inferred with different levels of accuracy (Figure 4B and Figure S3 in File S1). As beneficial mutations become more common or of stronger effects, they dominate the divergence counts and also make substantial contribution to SFS counts, which alone can allow reliable estimation of the beneficial fraction of the DFE and α. For $\alpha \approx 20\text{\%,}$ the use of divergence data provides more accurate estimates than when relying on polymorphism data alone. This could be explained by the fact that the polymorphism data are dominated by deleterious mutations and it is more difficult to tell apart the amount of beneficial selection from polymorphism data alone. However, as α increases, the differences in performance between the inference with and without divergence diminishes, strongly indicating that divergence data are not necessarily needed for accurate inference.

Similar to Schneider et al. (2011), we observe a strong negative correlation between the proportion of beneficial mutations $p_b$ and their scaled selection coefficient $S_b$ (Figure S4 in File S1). This illustrates the fact that $p_b$ and $S_b$ are difficult to estimate separately, but their product, which largely determines α, is more accurately estimated. This can be seen in Figure S3 in File S1, where even though $p_b$ and $S_b$ might be slightly biased, α is more accurately inferred. Schneider et al. (2011) reported that the estimation of $p_b$ and $S_b$ improves as more sites are included. We used a fixed number of sites in simulations, but we do observe that $p_b,$ $S_b,$ and α are better estimated as α increases.

When inferring a full DFE, we can calculate both ${\alpha }_{\text{div}}$ and ${\alpha }_{\text{dfe}},$ which should both be good predictors of the true simulated α. We generally found very good correlation between the two estimated values (Figure S5 in File S1).

We note here that Schneider et al. (2011) is the only method that we are aware of that can estimate both a full DFE and α from polymorphism data alone, though the authors did not investigate the power to infer α, but rather the product $p_b{S}_b,$ which is taken as a proxy for α. Additionally, they did not consider different deleterious DFEs in their simulations. Our simulated DFEs were chosen such that they cover cases with the same simulated $p_b$ and $S_b,$ but generate different α values. The differences in α can be driven by the amount of beneficial mutations, but also by the intensity of purifying selection, as reflected in the properties of the deleterious fraction of the DFE. These simulations revealed that the amount and strength of positive selection is not the only determinant of how accurately $p_b$ and $S_b$ are inferred. For example, the results in Figure 4B are given for simulated DFEs that differ only in the value of $S_d$ and we find a clear difference in the inference performance.

Biases arising from not inferring the full DFE

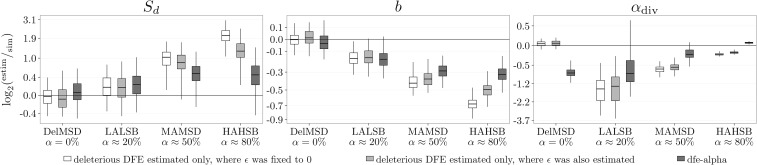
Divergence data are clearly not necessary for reliably estimating the full DFE. This raises the question: what happens when inference methods ignore the presence of beneficial mutations in the polymorphism data? Using simulated data generated assuming full DFEs, we performed inference only on polymorphism data where we inferred either a full DFE or under a reduced model restricted to only a deleterious DFE. The reduced model corresponds to the common approach for empirical studies of DFE from population genomics data, which tends to assume an exclusively deleterious DFE (Slotte et al. 2010; Strasburg et al. 2011; Halligan et al. 2013; Racimo and Schraiber 2014; Arunkumar et al. 2015; Bataillon et al. 2015; Charlesworth 2015; Castellano et al. 2016; Harris and Nielsen 2016), even though methods exist to infer a full DFE from the SFS data (Schneider et al. 2011).

As α increased, the inferred $S_d$ and b were increasingly biased (Figure 4C and Figure S6 in File S1). The mean $S_d$ was estimated to be more negative, while the shape b was estimated to be closer to 0: the inferred deleterious DFEs were getting much more leptokurtic than the parametric DFE used for simulations. This resulted in inferring DFEs with more probability mass accumulating close to zero. A straightforward interpretation is that the inference method attempted to fit the SFS counts, contributed by the weakly beneficial mutations, by fitting a DFE that comprised a sizable amount of weakly deleterious mutations (the best proxy for beneficial mutations). A comparison of the simulated and inferred discretized DFEs (Figure 3B and Figure S7 in File S1) illustrates this point: the inference with only deleterious DFE overestimated the amount of mutations which experience weak negative selection [simulated DFE, 0.07; deleterious DFE, 0.11 in the range $\left(-1,0\right)$].

We can test for the presence of beneficial mutations in the polymorphism data by comparing the inferences with a full or deleterious DFE using an LRT (Figure S8 in File S1). We observed that there exists a stronger preference for the full DFE model for larger α. Even for relatively large α, if the mean effect of beneficial selection was very low (Figure S8 in File S1, MALSB where $S_b=0.1$), the LRT indicated that there were no beneficial mutations in the polymorphism data. These mutations can pass as weakly deleterious mutations when fitting the data. When a deleterious-only DFE is inferred, the LRT favored the model with $\mathit{ϵ}\ne 0.$ This is because ϵ can partly mimic expected patterns contributed by weakly beneficial mutations to polymorphism data.

Inferring only a deleterious DFE also leads to a consistent bias in α. This bias is not well correlated with simulated α values, but it is apparent that a higher α leads to a smaller bias (Figure S6 in File S1). To obtain α from a deleterious DFE, we need to rely on the divergence data. Yet, for large α, the signal of positive selection in the divergence data are sufficiently strong that it overrides the bias in $S_d$ and b, so α is estimated more accurately.

The assumption of negligible contribution of beneficial mutations to SFS counts can be traced back to Smith and Eyre-Walker (2002). To support the claim, the authors stated that “if advantageous mutations, with an advantage of $N_{\mathrm{e}}s=25$ occur at 100th the rate of neutral mutations, they will account for 50% of substitutions, but account for just 2% of heterozygosity.” Our simulated $S_b$ (which is scaled by $4N_{\mathrm{e}}$) was typically 4. To investigate what happens when selection is much stronger, we simulated a full DFE with $S_b=800$ such that only $10\text{\%}$ of beneficial mutations ($0.2\text{\%}$ of all mutations) had a selection coefficient of 100 or less. Here, the simulated α was nearly $100\text{\%}$ and one would expect that most mutations would fix quickly. While the DFE parameters could not be recovered as accurately (Figure S9 in File S1), the estimated α was very precise, regardless of the model used for inference. Hence, even with very strong positive selection, there is sufficient information in polymorphism data to estimate α without relying on divergence data. The bias in $S_d,$ b, α (Figure S9 in File S1), and LRT (Figure S10 in File S1) from inference with only deleterious DFE followed the same trend as before. However, even though α was large, $p_b$ and $S_b$ were not that well estimated. This is most likely because when $S_b$ is getting very large, the expected counts from Equation 1 become independent of S, since $H\left(S,x\right)\approx 1/x\left(1-x\right)$ for large S (Figure 1D). This explains why the inference method will have trouble finding precise values of $S_b.$

Keightley and Eyre-Walker (2010) investigated if the presence of beneficial mutations in the polymorphism data could potentially affect the inference when assuming only a deleterious DFE. For this, they simulated data using a partially reflected gamma distribution, given by

$$\phi \left(S;S_d,b\right)=\frac{1}{1+e^S}\mathrm{\Gamma }\left(\left|S\right|;-S_d,b\right),$$

where $\mathrm{\Gamma }\left(x;m,s\right)$ is the density of a gamma distribution with mean m and shape s. This distribution arises from the assumption that the absolute strength of selection is gamma distributed and that each site can be occupied by either an advantageous or a deleterious allele, both having the same absolute selection strength $\left|s\right|.$ Keightley and Eyre-Walker (2010) simulated data with $\left|S_d\right|=400$ and $b=\mathrm{0.5.}$ Due to the chosen distribution, the simulated proportion of beneficial selection was $p_b=0.0214,$ while the mean selection coefficient of beneficial mutations was only $S_b=0.014$ ($p_b{S}_b=0.00029$). These values are close to one of our own simulated DFEs with $\alpha \approx 20\text{\%}$ (LALSB, Table 1), with the difference being that we simulated an $S_b$ that was approximately seven times larger. For this simulation scenario we did, indeed, find little bias in $S_d$ and b when inferring only a deleterious DFE (Figures S6 and S7 in File S1). However, arguably, this strength of beneficial mutations is extremely low. For example, Schneider et al. (2011) inferred the strength of beneficial mutations from Drosophila and found $p_b{S}_b$ to be two to three orders of magnitude higher: $p_b=0.0096$ and $S_b=18$ ($p_b{S}_b=0.1728$).

Impact of ancestral error on inference

The results presented above were based on simulations where the true ancestral state was used. To investigate the consequences of misidentification of the ancestral state, we first added errors to the simulated data using one unique error rate ϵ (set to $5\text{\%}$) for both neutral and selected sites (see File S1 for details). Inferring a full DFE using divergence data, we found that we can properly account for the rate of misidentification, and the error ϵ is accurately recovered (Figure 5 and Figure S11 in File S1). As expected, the inference of the DFE and α is biased when the misidentification is not accounted for. An LRT for $\mathit{ϵ}\ne 0$ (Figure S14 in File S1) supported the use of a model including the joint estimation of ϵ and DFE parameters for the data with errors, but rejected the more complex model for the data without errors.

Figure 5.

Inference of α (proportion of beneficial substitutions), ϵ (rate of ancestral error), and DFE parameters: $S_d$ (mean selection coefficient of deleterious mutations), b (shape of distribution of deleterious DFE), $p_b$ (proportion of beneficial mutations), and $S_b$ (mean selection coefficient of beneficial mutations). The figure shows the inference quality for three simulated DFEs (Table 1) with different α values. The DFEs differ only in the simulated value of $S_d.$ A full DFE is inferred from both polymorphism and divergence data, and ϵ is set to zero and is not estimated, or is estimated. The data were simulated with $\mathit{ϵ}=\mathrm{0.05.}$

Galtier (2016), who also used distortion parameters $r_i$ when inferring the DFE, stated that these parameters are “expected to capture any departure from the expected SFS as soon as it is shared by synonymous and nonsynonymous sites.” Our results indicate that the misidentification of the ancestral state cannot be accurately accounted for by the $r_i$ parameters (Figure 5 and Figure S11 in File S1). However, we did find that the resulting bias decreased with α and that the preference (as measured by an LRT) for models inferring $\mathit{ϵ}\ne 0$ also decreased for data sets with higher α (Figure S14 in File S1). For data simulations with $\alpha \approx 80\text{\%,}$ the inference was just as good when ϵ was set to zero. To investigate this in more detail, we also ran the inference with $r_i=1$ (i.e., no distortion correction) and $\mathit{ϵ}=0$ on those simulated DFEs. The results showed a large bias in the DFE parameters and α when $r_i=1$ (Figure S12 in File S1), and an LRT favored the estimation of $r_i$ values (Figure S15 in File S1). Merely using the $r_i$ parameters without explicitly accounting for misidentification of the ancestral state is not always accurate and can bias inference of DFE and α.

Both the presence of beneficial mutations and $\mathit{ϵ}\ne 0$ create similar patterns in the polymorphism data, as the frequency of common derived alleles increases. We have seen that ϵ can account for some of the positive selection in the data (Figure 4C and Figures S6 and S7 in File S1). Similarly, we observed that positive selection can account for some of the misidentification of ancestral states. For simulations with a deleterious DFE and incorrect ancestral states, we found that when assuming $\mathit{ϵ}=0,$ the parameters inferred using a full DFE are generally more accurate than when only a deleterious DFE is inferred (Figure S13 in File S1). An LRT also supported the use of a full DFE (Figure S16 in File S1). Comparing the inferred $S_b$ when ϵ is inferred or not (Figure S13 in File S1) showed that this parameter is higher when $\mathit{ϵ}=0,$ further indicating that it captured some of the ancestral misidentification errors. Therefore, if the data contain sites that have the ancestral state misidentified, which is virtually always the case in empirical data sets, ancestral misidentification will be wrongly interpreted as positive selection if the misidentification is not accounted for. If ϵ is inferred jointly with the DFE parameters, an LRT comparing models with full DFE or only deleterious DFE can correctly detect that the polymorphism data do not contain any beneficial mutations (Figure S16 in File S1).

Our approach to modeling misidentification of ancestral states assumes identical errors at both neutral and selected sites. To investigate how different error rates for neutral and selected sites affected our inference, we simulated data using two different error rates, ${\mathit{ϵ}}_{\text{neut}}$ and ${\mathit{ϵ}}_{\text{sel}},$ for the neutral and selected sites, respectively, and assumed one unique ϵ during inference. We simulated data using ${\mathit{ϵ}}_{\text{neut}}=5\text{\%}$ and ${\mathit{ϵ}}_{\text{sel}}=10\text{\%,}$ and ${\mathit{ϵ}}_{\text{neut}}=10\text{\%}$ and ${\mathit{ϵ}}_{\text{sel}}=5\text{\%}.$ Inferring a full DFE using divergence data, we found that the two different error rates create biases in the estimated parameters (Figure S17 in File S1), though this bias was reduced when the error rate ϵ was estimated. We observed a lower bias when ${\mathit{ϵ}}_{\text{sel}}<{\mathit{ϵ}}_{\text{neut}},$ which is the more realistic scenario as selected sites are expected to be less prone to homoplasy when purifying selection predominates. An LRT for $\mathit{ϵ}\ne 0$ (Figure S18 in File S1) showed a notable difference between the two different simulations: when ${\mathit{ϵ}}_{\text{neut}}=5\text{\%}$ and ${\mathit{ϵ}}_{\text{sel}}=10\text{\%,}$ the LRT generally supported the estimation of ϵ at ∼$10\text{\%}$ (Figure S17 in File S1); while for ${\mathit{ϵ}}_{\text{neut}}=10\text{\%}$ and ${\mathit{ϵ}}_{\text{sel}}=5\text{\%,}$ the LRT supported $\mathit{ϵ}=0.$ The distortions created in the data were instead captured by the $r_i$ parameters (Figure S19 in File S1), which greatly deviated from 1 when ϵ was not estimated.

Our simulation results illustrated that systematically incorporating the rate of ancestral error is crucial for a reliable inference of DFE parameters and α, and an LRT can be used to avoid model overfitting when the $r_i$ parameters are sufficient for correcting departures from the expected SFS.

Distortions of the SFS by linkage and demography

It has previously been suggested that correcting for demography by using the observed SFS at neutral sites can also reduce some of the bias introduced by linkage (Kousathanas and Keightley 2013; Messer and Petrov 2013). We explored this possibility by simulating different levels of linkage (see File S1 for details). We found that, indeed, the $r_i$ parameters could partially correct for the presence of linkage (Figure S20 in File S1), with the most pronounced effect on $S_d$ and b. An LRT for $r_i\ne 1$ (Figure S21 in File S1) increasingly favored models fitting $r_i$ as the level of linkage increased.

For the previous simulations we used a constant population size. To check that the $r_i$ parameters can also correct for demography, we simulated data using different demography scenarios (see File S1 for details). When population size varies in time, $N_{\mathrm{e}}$ is typically taken to be the harmonic mean of the different sizes (Kliman et al. 2008). While this approximation may be valid for neutral sites, those under selection experience a different $N_{\mathrm{e}},$ which depends on the strength of selection S (Otto and Whitlock 1997). Therefore, for these simulations, we do not have a priori knowledge of the $N_{\mathrm{e}}$ that accurately captures the interaction between selection and demography. We could only compare b and $p_b,$ which are independent of $N_{\mathrm{e}},$ and α, for which a value can be obtained by tracking the proportion of adaptive mutations contributing to divergence in forward simulations. As before, we first simulated a deleterious DFE, similar to previous studies (Eyre-Walker et al. 2006; Keightley and Eyre-Walker 2007; Boyko et al. 2008; Eyre-Walker and Keightley 2009). We found that an LRT correctly detected that $r_i\ne 1$ (Figure S23 in File S1), but that parameters can only partially correct for demography (Figure S22 in File S1). The b parameter was accurately inferred when $r_i$ parameters were estimated. However, the estimated α was still biased (Figure S22 in File S1). As no full DFE was inferred, α was calculated from the divergence data, assuming the same DFE in the ingroup and outgroup. However, as the ingroup underwent variable population size, its $N_{\mathrm{e}}$ was different from the constant-sized $N_{\mathrm{e}}$ of the outgroup, and therefore the two populations had different scaled DFEs. This difference could explain the observed bias in α. Eyre-Walker and Keightley (2009) noticed the same effect and proposed a correction for α. However, their correction requires the ratio of the N_e’s of the two populations, which is typically unknown.

We then investigated if the $r_i$ parameters could also correct for demography when a full DFE was simulated (Figure S24 in File S1). The LRT (Figure S25 in File S1) showed a clear preference for $r_i\ne 1.$ When inferring the DFE from both polymorphism and divergence data, we observed a bias in b and $p_b.$ As before, this was caused by the incorrect assumption of a shared DFE between the ingroup and outgroup. When only polymorphism data were used for inference, the $r_i$ parameters could accurately correct the estimation of $p_b$ and b, but the inferred α (estimated via ${\alpha }_{\text{dfe}}$) was still slightly biased. To investigate if this bias was caused by linkage, we also ran simulations with reduced linkage (Figure S24 in File S1), but the bias remained.

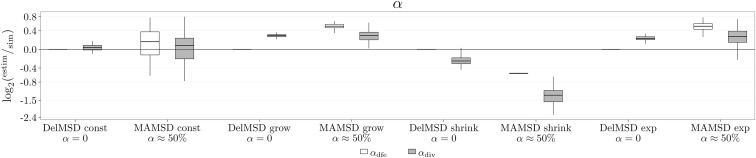
We investigated if the full or deleterious DFE model is preferred for the data simulated under variable population size. We found that an LRT consistently preferred the full DFE model when the SFS contained beneficial mutations (Figure S26 in File S1). Under demographic simulations, the estimated ${\alpha }_{\text{dfe}}$ and ${\alpha }_{\text{div}}$ could differ considerably (Figure 6). When only a deleterious DFE was simulated, relying on divergence data to estimate α can lead to heavily biased estimates. Note that when the population size was halved and a full DFE was simulated, the LRT favored the incorrect deleterious DFE model. In this simulation, the incorrect model choice can be explained by the extra deleterious load incurred by the population shrinkage.

Figure 6.

Inference of α (proportion of beneficial substitutions) for different demographic scenarios. The figure shows the inference quality for ${\alpha }_{\text{dfe}}$ (inferred from DFE alone) and ${\alpha }_{\text{div}}$ (inferred from DFE and divergence data) for four simulated demographic scenarios (const: population of constant size, grow: population that grows in size once; shrink: population that shrinks in size once; exp: population that undergoes an exponential growth; see details in File S1) and a deleterious DFE only or a full DFE (Table 1). For all inference, only SFS data were used and an LRT was performed to compare the full and deleterious-only DFE models. The estimated value of α was obtained from the model preferred by the LRT.

The simulated demographics were the same for both deleterious and full DFE simulations, and therefore the inferred $r_i$ parameters on the deleterious and full DFE data should be highly correlated, which we detected (Figure S27 in File S1). One of the simulations showed no correlation in $r_i$ and the LRT preferred the less complex model with $r_i=1$ (Figures S23 and S25 in File S1). The change in population size for this simulation was most likely not strong enough for it to leave an appreciable footprint in the data.

Galtier (2016) is the only study we are aware of that tested if demography can be accurately accounted for when a full DFE was simulated. While the estimated α values from Galtier (2016) were somewhat more accurate than what we found, there are critical differences between these studies. While we simulated a continuous full DFE, Galtier (2016) assumed that all beneficial mutations had the same selection coefficient $S_b.$ Nevertheless, Galtier (2016) inferred a continuous full DFE and used Equation 8 for calculating α, where the integration limit was set to some $S_{\text{adv}}>0$ instead of 0. The reasoning behind this is that mutations with a selection coefficient $S>0$ that is not very large should not be considered advantageous mutations. Galtier (2016) used an arbitrary cutoff at $S_{\text{adv}}=5.$ Note that a different cutoff value of $S_{\text{adv}}$ would lead to different α values: the smaller $S_{\text{adv}},$ the larger the estimated α.

Inference of mutation variability

Our framework provides means for estimating mutation variability, and this has been applied for all inferences performed. The shape parameter a of the gamma distribution governing the mutation rate was recovered accurately (data not shown). However, not modeling the mutation rate variability does not bias the remaining parameters. This is explained by the fact that the expected values of the SFS and divergence counts depend only on the average mutation rate and are independent of mutation variability.

Comparison with the dfe-alpha method

We compared our method with dfe-alpha, one of the most widely used inference methods for DFE and α. dfe-alpha was originally developed to infer a deleterious DFE (Keightley and Eyre-Walker 2007), and it was subsequently extended to estimate α (Eyre-Walker and Keightley 2009), model a full DFE (Schneider et al. 2011), and correct α for misattributed polymorphism (Keightley and Eyre-Walker 2012). For simplicity, and as we showed that accounting for errors in the identification of the ancestral state is crucial for accurate inference (Figure 5 and Figure S11 in File S1), we chose to run dfe-alpha with a folded SFS, where only a deleterious DFE can be estimated. We then compared with our method when only a deleterious DFE was inferred, where ϵ was either set to zero or estimated. Although these comparisons are quite limited in scope, we found that, for simulations with only a deleterious DFE, our method provided better estimates and with lower variance than dfe-alpha (Figure 7 and Figure S28 in File S1). For these simulations we also found that, sometimes, dfe-alpha estimated an α that was very large, both on the negative and positive side (Figure S28 in File S1, DelHB simulation). This seemed to be the result of the correction for the misattributed polymorphism introduced in Keightley and Eyre-Walker (2012), as the uncorrected α was much closer to the true value (data not shown). This most likely explains the general differences observed between the estimated α from dfe-alpha and our method. When the inference was performed on data simulated with a full DFE, we observed the same type of bias in $S_d$ and b as described before (Figure 7 and Figure S28 in File S1). When demography and a strictly deleterious DFE were simulated, the estimation was, again, comparable (Figure S29 in File S1). However, when demography was simulated on top of a full DFE, the bias of b differed between dfe-alpha and our method. This could be explained by the differences between the two methods for accounting for demography: while we used the nuisance parameters $r_i,$ dfe-alpha only allows the population to undergo a few size changes in the past.

Figure 7.

Comparison to dfe-alpha of inference of α (proportion of beneficial substitutions) and deleterious DFE parameters: $S_d$ (mean selection coefficient of deleterious mutations) and b (shape of distribution of deleterious DFE), for four simulated DFEs (Table 1) with different α values. The DFE parameters are inferred using only polymorphism data, assuming a deleterious DFE, where ɛ is set to zero and is not estimated, or is estimated. The data were simulated with $\mathit{ϵ}=0.$

Analysis of chimpanzee data

To illustrate the use of our method, we reanalyzed a recently published chimpanzee exome data set (Table 2) covering the central, eastern, and western chimpanzee subspecies (Bataillon et al. 2015). We assumed that the synonymous SNPs are neutrally evolving and we estimated the DFE and α from the nonsynonymous SNPs.

Table 2. Summary of chimpanzee exome data.

	Central	Eastern	Western
Autosome 20-Mb sites
Sample size	24	22	12
No. synonymous SNPs	33,941	21,871	10,217
No. nonsynonymous SNPs	25,290	16,664	8,567
X chromosome 0.89-Mb sites
Sample size	21	19	9
No. synonymous SNPs	684	492	202
No. nonsynonymous SNPs	471	323	150

The summary of chimpanzee exome data from Bataillon et al. (2015) is shown. As some of the sequenced chimpanzees were males, the sample size (number of haploid chromosomes sequenced) varies between the autosomes and X chromosomes. The number of sites represents the number of sequenced sites where SNPs where potentially called. The orientation of SNPs was inferred via parsimony using the human reference genome, as well as the orangutan reference genome. Further details on the SNP, divergence calling, and SNP orientation are available in Hvilsom et al. (2012).

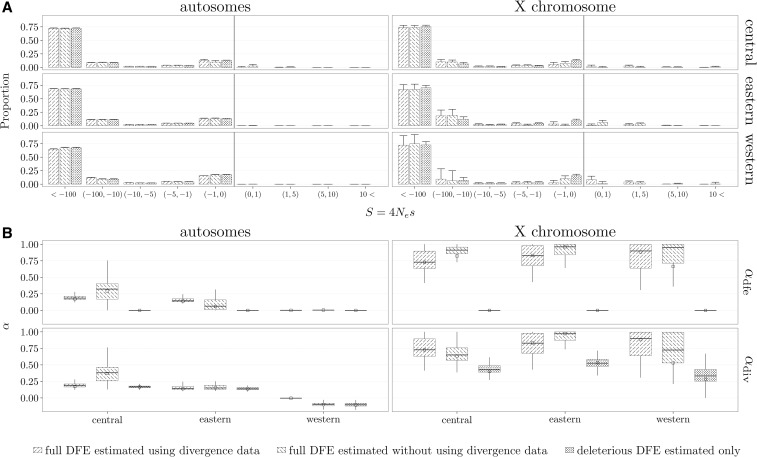
Bataillon et al. (2015) inferred a deleterious-only DFE from the SFS, using the method of Eyre-Walker et al. (2006), and the presence and strength of positive selection by relying on a variety of summary statistics. They found that the larger the effective population size, the stronger the purifying selection, and that autosomal regions have undergone less positive selection than the X chromosome. We analyzed the data by inferring both a deleterious and a full DFE, while relying or not on the divergence counts (Figure 8A), where both ϵ and the nuisance parameters r were estimated. From the inferred DFEs, we also estimated ${\alpha }_{\text{div}}$ and ${\alpha }_{\text{dfe}}$ (Figure 8B). The variability of parameter estimates was obtained by using 100 bootstrapped data sets.

Figure 8.

Inference of DFE and α (proportion of beneficial substitutions) on three chimpanzee subspecies. A full DFE was inferred from both polymorphism and divergence data, while also both a full DFE and deleterious DFE were inferred from polymorphism data only. (A) Inferred discretized DFE. The error bars indicate 1 SD obtained from the inferred discretized DFEs from 100 bootstrap data sets. (B) Box plot of inferred ${\alpha }_{\text{dfe}}$ and ${\alpha }_{\text{div}}$ from the 100 bootstrap data sets. The values of α inferred on the original data sets are given as empty squares. Note that when inferring a deleterious DFE only, ${\alpha }_{\text{dfe}}$ is zero.

We found that, for the autosomes, the central chimpanzees (the subspecies with the largest effective size) experienced the strongest purifying selection; while the western chimpanzees (with the smallest effective population size) had the most relaxed purifying selection (Figure 8A). These results are in accordance with the original study and hold regardless of the type of the DFE assumed and type of data used. The consistency of the inferred DFE is also supported by an LRT, which indicates that there is little evidence for the presence of beneficial mutations in the polymorphism data (Figure S30 in File S1). Even when divergence data are used, very little positive selection is found on the autosomes. When analyzing the X chromosome, the overall picture changes. While the smaller amount of data (Table 2) leads to a larger variance in the estimates, there is considerable difference between the estimated DFEs (Figure 8A). This is also supported by the LRT (Figure S30 in File S1), which shows more evidence for beneficial mutations in the polymorphism data for the X chromosomes than for the autosomes. Although the P-values obtained on the original data are not significant, the bootstrapped data point to the presence of beneficial mutations in the X-linked SFS from the central chimpanzees. The stronger evidence found in the central chimpanzee could be a result of the higher proportion of beneficial mutations with $S>10,$ the larger sample size, and, therefore, the higher amount of polymorphism data (Table 2). We would expect that support for the presence of beneficial mutations in the SFS data would be stronger if the number of sequenced individuals would have been larger. Our findings of more evidence for positive selection on the X chromosome than on the autosomes is also in line with the original study (Hvilsom et al. 2012; Bataillon et al. 2015). While for the autosomes, the type of DFE (full or deleterious only) assumed and the type of data used did not affect drastically the inferred discretized DFE (Figure 8A), the same cannot be said for the X chromosome; further indicating that care needs to be taken when making assumptions of no presence of beneficial mutations in the polymorphism data, or about the invariance of the DFE in the ingroup and outgroup species used. We also observed the same trend in the inferred discretized DFE for the chimpanzee subspecies previously noted for the simulated data: the estimated proportion for $S\in \left(-1,0\right)$ is considerably larger when only a deleterious DFE is estimated (Figure 8A).

While for the autosomes the inferred discretized DFE is very similar across assumptions, the same cannot be said about the inferred α; where the type of inferred DFE and type of data used does leave a clear impact (Figure 8B). In line with the observations from the discretized DFE, the estimated α is larger for the X chromosome than the autosomes.

A visual comparison of the observed SFS and divergence counts with the expected counts given the fitted DFEs (Figure S31 in File S1) reveals that autosomal patterns of polymorphism and divergence are generally well fitted. Consistent with the LRTs, the models using a full DFE do not further improve the fit of data. For the X chromosome, the data are intrinsically noisier, but using a full DFE yields expectations that are closer to the observed data.

Conclusion

We have presented a new method to infer the DFE and proportion of advantageous substitutions, α, from polymorphism and divergence data. We demonstrated that inference can be performed using polymorphism data alone, without relying on the assumption that the DFE is shared between the ingroup and the outgroup. We additionally illustrated that, when the effects of beneficial mutations on polymorphism data were not modeled, the inferred deleterious DFE was biased. This bias arises from an increase of mutations at selected sites that segregate at high frequencies. Methods ignoring the contribution of the beneficial fraction to SFS counts will tend to infer DFEs that have a larger amount of slightly deleterious mutations, as this is the best way to account for the observed data. Therefore, the estimated deleterious DFE had a much larger mass close to zero compared to the simulated deleterious DFE. This, in turn, could be achieved by a larger (more negative) $S_d$ and a lower b of the gamma distribution used here for the deleterious DFE. In cases where polymorphism data did not contain any beneficial mutations, the inference was much more accurate under a reduced model positing only a deleterious DFE. The use of an LRT comparing a model featuring a full DFE and a deleterious DFE would accurately select the reduced model and allow precise inference of the deleterious DFE. This is an important result, as it suggests that using a full DFE for inference from SFS data does not come with a cost when no beneficial mutations contributed to the SFS counts, and that the method does not spuriously infer presence of beneficial mutations.

To correct for demography and other forces that can distort the SFS data, such as linkage, we used the nuisance parameters $r_i.$ These parameters have the potential of accounting for more complex scenarios without directly modeling the underlying changes in population size and, potentially, other events such as migration and admixture. This correction could prove more robust than just allowing for a few population size changes, as dfe-alpha assumes. However, we did not test the behavior of our method under these more complex scenarios and the extent of bias in α they might generate.

To infer the full DFE, we used the unfolded SFS. This requires the identification of the ancestral state, which is prone to errors. These errors can be accounted for by using a probabilistic modeling of the ancestral state (Schneider et al. 2011; Gronau et al. 2013; Keightley et al. 2016). We assumed that the polymorphism data are comprised of a mixture of sites with correctly inferred ancestral state and sites with incorrect ancestral state. This approach has proved to be efficient for unbiased estimation of GC-biased gene conversion (Glémin et al. 2015), a weak selection-like process. We also showed that we could capture the errors in the identification of ancestral state and, as opposed to the expectations of Galtier (2016), that the $r_i$ parameters are not sufficient to correct for misidentification of ancestral state. The inferred parameters were biased when the neutral and selected sites did not share the error rate of the ancestral state identification.

When using the divergence data in the inference, we corrected for mutations that were fixed in the sample but that were, in fact, polymorphic in the population. These mutations would incorrectly be counted into the divergence data. Our correction is different from the one used by Keightley and Eyre-Walker (2012), which is implemented in dfe-alpha. We found that this correction can sometimes lead dfe-alpha to predict extreme positive or negative values of α. Our approach showed a much more consistent behavior throughout the simulations.

Similar to the $r_i$ parameters, both our approach and methods that use probabilistic modeling to account for the identification of ancestral state rely on that the same process applies to both neutral and selected sites. This is probably not the case, as one could expect that the error in the identification of the ancestral state is different for the sites that are under selection. Theoretically, the neutral and selected sites could both be modeled with their own ϵ, but this would not be easily identifiable. Additionally, error rates might vary with strength of selection, with some selected sites being more prone to misidentification of ancestral state (Keightley et al. 2016). To correct for variable error rates and rates that are not shared by neutral and selected sites, DFE inference will benefit by using maximum-likelihood methods for inference of ancestral states (Hernandez et al. 2007; Wilson et al. 2011; Keightley et al. 2016). This reduces the errors, but does not necessary remove them completely (Glémin et al. 2015). Combining accurate ancestral state inference and models including errors is thus an efficient strategy. In particular, separate inference of neutral and selected ancestral states by maximum likelihood (Keightley et al. 2016) should make the residual errors similar between both sites, making our method more accurate.

Throughout this article, we used LRTs for model testing. However, inferences with or without divergence data are not comparable through LRT, the Akaike information criterion, or any other similar method (as the data used are different). Using a recently published chimpanzee exome data set (Bataillon et al. 2015), we showed that care needs to be taken when choosing the type of data analyzed and the type of DFE assumed. To make an informed choice about whether or not to include the divergence data in the inference of the DFE and α, a goodness-of-fit test could be developed that investigates how closely the predicted SFS matches the observed one.

Our general approach can be applied to a wide range of species where the amount and impact of beneficial mutations on patterns of polymorphism and divergence varies widely [as uncovered by Galtier (2016)]. Our method allows for accurate detection of whether beneficial mutations are present in the data, and an LRT can be used to decide if a full or strictly deleterious DFE should be inferred. Importantly, we also show that estimating a full DFE, and thus learning about the property of beneficial mutations and expected amounts of adaptive substitution, is possible without relying on divergence data. We also note that alternative statistics with different properties for measuring molecular adaptation, such as ${\omega }_A$ (the rate of adaptive evolution relative to the mutation rate) and $K_{a^{+}}$ (the rate of adaptive amino acid substitution), can be used (Gossmann et al. 2010; Castellano et al. 2016). These might be better suited for studying various aspects of adaptation (Castellano et al. 2016). It remains to be investigated how reliably they can be estimated using our framework.

Supplementary Material

Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.117.300323/-/DC1.