3D-MB-MUSE: A robust 3D multi-slab, multi-band and multi-shot reconstruction approach for ultrahigh resolution Diffusion MRI

Abstract

Recent advances in achieving ultrahigh spatial resolution (e.g. sub-millimeter) diffusion MRI (dMRI) data have proven highly beneficial in characterizing tissue microstructures in organs such as the brain. However, the routine acquisition of in-vivo dMRI data at such high spatial resolutions has been largely prohibited by factors that include prolonged acquisition times, motion induced artifacts, and low SNR. To overcome these limitations, we present here a framework for acquiring and reconstructing 3D multi-slab, multi-band and interleaved multi-shot EPI data, termed 3D-MB-MUSE. Through multi-band excitations, the simultaneous acquisition of multiple 3D slabs enables whole brain dMRI volumes to be acquired in-vivo on a 3 Tesla clinical MRI scanner at high spatial resolution within a reasonably short amount of time. Representing a true 3D model, 3D-MB-MUSE reconstructs an entire 3D multi-band, multi-shot dMRI slab at once while simultaneously accounting for coil sensitivity variations across the slab as well as motion induced artifacts commonly associated with both 3D and multi-shot diffusion imaging. Such a reconstruction fully preserves the SNR advantages of both 3D and multi-shot acquisitions in high resolution dMRI images by removing both motion and aliasing artifacts across multiple dimensions. By enabling ultrahigh resolution dMRI for routine use, the 3D-MB-MUSE framework presented here may prove highly valuable in both clinical and research applications.

Introduction

The sensitivity of diffusion magnetic resonance imaging (dMRI) to the underlying diffusion processes of water offers the potential to provide detailed characterization of tissue microstructure. Through dMRI and fiber tractography derived from diffusion tensor imaging (DTI) (Mori et al., 1999; Tuch et al., 2002; LeBihan et al., 1986; Basser et al., 1994), neuronal microstructures in the brain are observed in-vivo and used to map the disruption of structural brain connectivity linked to psychiatric and neurological disorders such as schizophrenia, epilepsy and dementia (Zhang et al., 2011; Quan et al., 2013; Lo et al., 2010; Richardson et al., 2012; Vu et al., 2015). In recent years, advances in achieving ultrahigh spatial resolution diffusion images, which provide exquisite anatomical details of important organs (such as the human brain), have proven to be highly beneficial (Miller at al., 2011; Heidemann et al., 2012; Setsompop et al., 2013; Sotiropoulos et al., 2013).

Despite many significant efforts, the ability to achieve high spatial resolutions in dMRI has been limited by prolonged scan times and the attainable signal-to-noise ratio (SNR). While many dMRI studies use single-shot echo planar imaging (ss-EPI) pulse sequences (Turner et al., 1991) to prevent severe motion-induced artifacts (Anderson and Gore, 1994), geometric distortions that result from signal decay throughout a ss-EPI acquisition place limitations on the achievable spatial resolution. With parallel MRI techniques (Roemer et al., 1990; Pruessmann et al., 1999, Griswold et al., 2002), the severity of these distortions can be minimized by accelerating data acquisition through a sub-sampling of spatial frequencies. Although highly accelerated data offers the lowest level of distortion, the SNR of sub-sampled data is decreased proportionally to the sampling acceleration factor, and thus limitations remain on the achievable spatial resolution of dMRI images. The SNR loss of highly accelerated dMRI data can, however, be recovered by combining multiple sub-sampled data sets acquired with an interleaved multi-shot EPI (ms-EPI) pulse sequence (Holdsworth et al., 2009; Jeong et al., 2013; Chen et al., 2013). Through techniques such as multiplexed sensitivity encoding (MUSE) (Chen et al., 2013), the motion-induced artifacts associated with ms-EPI can be inherently accounted for to generate images with high spatial resolution, sufficient SNR to perform reliable fiber tracking (Landman et al., 2007), and minimal geometric distortions.

In recent studies (Frank et al., 2010; Engstrom et al., 2013; Engstrom et al., 2015; Frost et al., 2015), it has been shown that an additional SNR advantage can be gained over conventional 2D imaging by phase encoding the slice dimension of a thick slab with a 3D acquisition. In single-shot 3D data, motion artifacts arise from bulk through plane movement throughout the acquisition of slice-encoding planes (kz-planes) in a slab. Such artifacts are typically accounted for by removing phase variations estimated from low resolution navigator images that are acquired at kz=0 following the acquisition of each kz-plane in the 3D slab (Engstrom et al., 2013). To further increase the spatial resolution of dMRI data, the SNR advantages of ms-EPI and 3D imaging were recently combined by applying the original 2D MUSE model to the individual kz-planes of multi-shot 3D data (Chang et al., 2015; Song et al., 2014). In this application, inter-shot phase variations were estimated from the low resolution navigator images to account for motion in each kz-plane of a slab individually before a 1D Fourier transform converted the 3D encoded slab into slice images along the z dimension. Despite the apparent SNR gains of 3D ms-EPI, such an application is limited for three reasons: First, the acquisition of whole brain dMRI data with single-band 3D ms-EPI can be very time consuming (~7–10min/volume), rendering the application impractical for routine use. Second, motion artifacts in multi-shot 3D data stem from a combination of in-plane and through-plane movement. As through-plane motion can occur throughout the acquisition of all shots, applying the 2D MUSE algorithm to individual kz-planes does not directly account for phase variations across both shots/kz-planes. Third, using 2D MUSE to reconstruct each kz-plane requires coil sensitivities to be derived from either a collapsed slab (such as the low resolution navigator images at kz=0) or from thinner slabs acquired using a 2D acquisition. In either case, a sub-optimal variation of coil sensitivities across the slab may result in a high g-factor (Pruessmann et al., 1999), and reconstructed slice images will consequently experience amplified noise levels and potential aliasing artifacts, particularly in slices towards the outer edges of the 3D slab.

To address each of these technical challenges, we present a novel technique for acquiring and reconstructing 3D multi-slab, multi-band, and multi-shot dMRI data, termed 3D-MB-MUSE. With multi-band imaging, multiple 3D slabs are excited and acquired concurrently with custom 3D RF pulses, allowing whole brain acquisition times to be as short as ~1 min/volume for sub-millimeter resolutions. To account for both in-plane and through-plane motion artifacts, 3D-MB-MUSE represents a unified framework that reconstructs all shots in all kz-planes of all simultaneously excited 3D slabs at once. Such a framework also enables the use of coil sensitivities that vary across the entire slab, thereby reducing noise amplification and potential aliasing artifacts. By combining 3D multi-slab imaging with multi-band excitation and interleaved multi-shot acquisition into a single model, 3D-MB-MUSE enables ultra-high spatial resolution dMRI data to be acquired in minimal time with sufficient SNR and fidelity to achieve reliable fiber tractography.

Theory

To best outline a framework for reconstructing data acquired with 3D ms-EPI, the SENSE reconstruction (Pruessmann et al., 1999) of multi-band and multi-shot data is first represented through a linear isomorphism of matrix operators (Rowe et al., 2007; Nencka et al., 2009; Bruce et al., 2011). In a ms-EPI acquisition, each of N_S interleaved shot segments sub-samples spatial frequencies in the phase encoding direction (PE) by a factor of N_L. Typically, ms-EPI acquisitions are performed with N_L=N_S, however it is possible to acquire ms-EPI data with N_L>N_S, and thus a generalized acquisition is described here. This sub-sampling results in reduced FOV aliased coil images for each shot that can be reconstructed into full FOV images through models such as SENSE. In the single-band SENSE model, a vector of measurements in voxel v from each of the N_C aliased coil images, a_v, is ideally a coil sensitivity weighted combination of N_L true un-aliased voxel values in vector z_v by

$$a_v=S_v{z}_v,$$ (1)

where matrix S_v contains sensitivity values from N_C coils in the N_L locations that are aliased into voxel v. If a multi-band excitation is used, the SENSE model in Eq. (1) is expanded to perform un-aliasing across the N_L aliased locations in each of N_B slice bands by

$$a_v=[S_{v,b1},S_{v,b2},\dots S_{v,N_B}]\left[\begin{array}{c}\hfill z_{v,b1}\hfill \\ \hfill z_{v,b2}\hfill \\ \hfill ⋮\hfill \\ \hfill z_{v,N_B}\hfill \end{array}\right].$$ (2)

As all shots in ms-EPI ideally acquire the same sensitivity weighted combination of un-aliased voxels in z_v, an isomorphism can be formed to reconstruct all N_S shots at once (with inter-shot phase variations to be added later) by expanding the multi-band SENSE model in Eq. (2) by

$$\begin{array}{ccc}\hfill a_v=\hfill & \hfill S_v\hfill & \hfill z_v\hfill \\ \hfill \left[\begin{array}{c}\hfill a_{v,1}\hfill \\ \hfill a_{v,2}\hfill \\ \hfill ⋮\hfill \\ \hfill a_v,N_S\hfill \end{array}\right]=\hfill & \hfill j_{N_S}\otimes [S_{v,b_1},S_{v,b2},\dots S_{v,N_B}]\hfill & \hfill \left[\begin{array}{c}\hfill z_v,b_1\hfill \\ \hfill z_v,b_2\hfill \\ \hfill ⋮\hfill \\ \hfill z_v,N_B\hfill \end{array}\right]\hfill \end{array},$$ (3)

where j_NS is an N_S×1 vector of ones, and ⊗ is a Kronecker product that multiplies each element in j_NS by the entire matrix of sensitivities. When N_Z multi-band slices are acquired with ms-EPI, all N_Z acquired slices can be reconstructed with Eq. (3) at once by

$$\begin{array}{ccc}\hfill a=\hfill & \hfill S\hfill & \hfill z\hfill \\ \hfill \left[\begin{array}{c}\hfill a_1\hfill \\ \hfill a_2\hfill \\ \hfill ⋮\hfill \\ \hfill a_{N_Z}\hfill \end{array}\right]=\hfill & \hfill \left[\begin{array}{cccc}\hfill S_1\hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill S_2\hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill S_{N_Z}\hfill \end{array}\right]\hfill & \hfill \left[\begin{array}{c}\hfill z_1\hfill \\ \hfill z_2\hfill \\ \hfill ⋮\hfill \\ \hfill z_{N_Z}\hfill \end{array}\right],\hfill \end{array}$$ (4)

where S is a block diagonal matrix comprised of slice-specific coil sensitivity matrices.

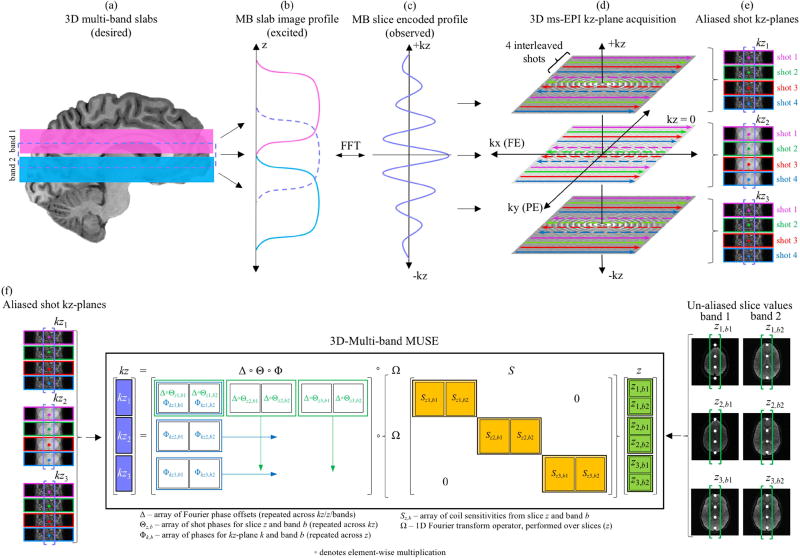
Expanding the SENSE model in Eq. (1) into the multi-band, multi-shot and multi-slice formulation in Eq. (4) provides the foundation for a model that can reconstruct data acquired with 3D ms-EPI. Consider N_B=2 thick slabs (pink and blue) in Fig. 1a, simultaneously excited with a 3D multi-band pulse to form a multi-band slab (purple). While the profiles in Fig. 1b represent the slabs excited along z, the slice-encoded profile in Fig. 1c is observed and sampled along kz. In a 3D ss-EPI acquisition, a single kz-plane is encoded and acquired in all excited slabs within a single TR before the next kz-plane is encoded. Once all kz-planes are acquired, slice images along z can be derived through a 1D Fourier transform performed across kz. In 3D ms-EPI, however, the same encoded kz-plane in all excited slabs is sequentially sub-sampled by all shots (one shot per TR) before the next kz-plane is encoded. As illustrated for a single slab with N_KZ=3 kz-planes and N_S=4 interleaved shots in Fig. 1d, this results in a reduced FOV aliased image for each shot in each kz-plane, as shown in Fig. 1e.

Fig. 1.

3D multi-band ms-EPI acquisition and 3D-MB-MUSE model. When (a) two slabs (pink and blue) are simultaneously excited to form a multi-band slab (purple), the excited slab profiles in z (b) are encoded into a slice-encoded profile in kz (c). In 3D ms-EPI, each of three kz-planes is sub-sampled by four interleaved shots (d), resulting in a reduced-FOV aliased kz-plane image acquired for each shot (e). For a given aliased voxel in all aliased shot images in all kz-planes, the 3D-MB-MUSE model (f) incorporates phase variations across both shots and kz-planes as well as slice specific coil sensitivities to produce full FOV un-aliased images for all three slices in both excited bands that are free of shot-to-shot and through-plane motion artifacts associated with 3D ms-EPI acquisitions.

If the aliased coil measurements for a voxel v in all N_S shots from all N_KZ kz-planes in Fig. 1e are stored in a vector kz_true (assuming no phase variations between shots or kz-planes), then the relationship between the vector a in Eq. (4) and kz_true is

$${\mathit{\text{kz}}}_{\mathit{\text{true}}}=\mathrm{\Omega }a=\mathrm{\Omega }\mathit{\text{Sz}},$$ (5)

where Ω is a matrix operator that performs a 1D Fourier transform over the slices in the slab (Rowe et al., 2007). While the relationship in Eq. (5) represents an ideal acquisition in which no noise or motion artifacts are considered, a series of phase adjustments can be incorporated into Eq. (5) to account for the various motion artifacts that arise in 3D multi-band ms-EPI. If in-plane phase encoding for shot m=[1,…,N_S] begins on row k_y=m, then the first necessary phase adjustment involves a Fourier offset at each location n=[1,…,N_L] aliased into the reduced FOV images of shot m of the form

$$\delta (m,n)=e^{i\frac{\pi }{2}(m-1)(n-1)}.$$

As δ is applied to shot measurements from all coils and all kz-planes, the phase matrix

$$\mathrm{\Delta }=(J_{N_Z}\otimes \delta )\otimes j_{N_C},$$

is applied directly to the Fourier-encoded coil sensitivities on the right had side of Eq. (5) by

$$O=\mathrm{\Delta }◦\mathrm{\Omega }S,$$ (6)

where J_NZ and j_NC are N_Z×N_Z and N_C×1 arrays of ones respectively, and ◦ represents a Hadamard (element-wise) product.

The second necessary phase adjustment in 3D ms-EPI stems from in-plane aliasing artifacts induced by motion between shots, particularly in the presence of strong diffusion gradients. To account for these artifacts, the reduced FOV aliased kz-planes in Fig. 1e are reconstructed into full FOV slice images for each shot through a 3D multi-band SENSE reconstruction (achieved by defining N_S=1 in Eqs. (3)–(5)). By spatially filtering the N_S reconstructed shot images for slice z, a matrix of low frequency phase variations, θ_z, can be formed with elements θ_z,(m,n) corresponding to the phase in each un-aliased location n in shot m. To account for these phase variations in the reconstruction, the inter-shot phase estimates from each of the N_Z slices are applied directly to the Fourier-encoded sensitivities from all N_C coils and all N_KZ kz-planes. This is achieved by incorporating a shot-phase adjustment matrix,

$$\mathrm{\Theta }=j_{N_{\mathit{\text{KZ}}}}\otimes ([{\theta }_1,{\theta }_2,\dots {\theta }_{N_Z}]\otimes j_{N_C}),$$

into the reconstruction operators in Eq. (6) by

$$O=\mathrm{\Delta }◦\mathrm{\Theta }◦\mathrm{\Omega }S.$$ (7)

The final necessary phase adjustment in 3D ms-EPI accounts for through-plane movement throughout the acquisition of kz-planes in 3D imaging. In 3D ss-EPI, these artifacts are typically accounted for by estimating phase fluctuations from low resolution navigator images acquired at kz=0 following the acquisition of each kz-plane (Engstrom et al., 2013). Although the navigator phase adjustment accounts for most bulk through-plane motion artifacts when applied to the individual shots of 3D ms-EPI, the time between acquiring the first shot in the first kz-plane and the final shot in the last kz-plane can be extensive, leaving residual phase variations that span all shots and kz-planes. To account for these variations, the 3D SENSE reconstructed slice images for each shot are converted into kz-planes through a 1D Fourier transform and spatially filtered. For each kz-plane k, low frequency phase differences (relative to an arbitrary reference kz-plane) are estimated at each un-aliased location n in shot m, ϕ_k,(m,n), and inserted into a slice-encoding phase matrix for the entire slab,

$$\mathrm{\Phi }={j_{N_Z}}^T\otimes (\text{vec}({\varphi }_1,{\varphi }_2,\dots {\varphi }_{N_{\mathit{\text{KZ}}}})\otimes j_{N_C}),$$

where vec(•) forms a column vector of its arguments. Together with the Fourier offset phase matrix, Δ, and the shot phase adjustment matrix, Θ, the slice-encoding phase matrix Φ is applied directly to the Fourier-encoded coil sensitivities in Eq. (7) to create the complete 3D-MB-MUSE operator,

$$M=\mathrm{\Delta }◦\mathrm{\Theta }◦\mathrm{\Phi }◦\mathrm{\Omega }S.$$ (8)

Eq. (8) forms a direct relationship between a vector of 3D slice-encoded, multi-band, multi-shot aliased coil measurements, kz, and the vector of true un-aliased slice measurements, z, in Eq. (4),

$$\mathit{\text{kz}}=M_z.$$ (9)

The formulation in Eq. (9) is visualized in Fig. 1f with N_B=2 bands, N_S=4 shots and N_KZ=3 kz-planes. When solved, the vector kz in Eq. (9) is reconstructed into un-aliased voxel values in all slices of all simultaneously excited slabs with both shot-to-shot and slab-encoding motion artifacts accounted for. It is of note that the 2D multi-band MUSE model (Chang et al., 2015b) is derived from Eq. (8) if N_Z=N_KZ=1, and the original 2D MUSE model (Chen et al., 2013) is derived when both N_Z=N_KZ=1 and N_B=1.

Methods

Acquisition of dMRI data

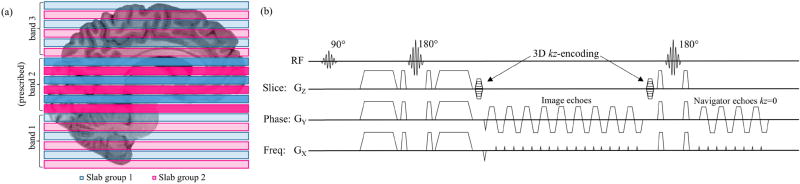
Two diffusion weighted data sets were acquired from healthy volunteers on a 3 Tesla MRI scanner (General Electric, Waukesha, WI) using a 32-channel head coil. Informed consent was obtained from all human subjects, in accordance with the Duke University Medical Center IRB. In each data set, one b=0 volume and twelve dMRI volumes were acquired with b=800s/mm² in the first scan and b=2500s/mm² in the second scan. To achieve full brain coverage, slabs from three bands (spaced 48mm apart) were simultaneously excited in each of the six prescribed slabs in Fig. 2a using custom 3D multi-band RF pulses and the 3D ms-EPI pulse sequence in Fig. 2b. For each 10mm thick slab, a 25.6mm FOV_xy was acquired in a 256×256 sampling matrix with 12 kz-planes, 20% oversampling in z, and a 20% overlap with neighboring slabs. This resulted in volumes with 1.0mm isotropic voxels. Using the 3D ms-EPI pulse sequence in Fig. 2b, each of four interleaved shots sub-sampled the same slice-encoded kz-plane in all prescribed slabs before the next kz-plane was encoded. In each shot, low resolution navigator images were acquired in a 96×96 matrix at kz=0, immediately following the acquisition of each kz-plane. Both kz-planes and navigator images were acquired with 65% partial Fourier sampling in ky. Shown to be optimal for SNR per unit time in 3D imaging (Frost et al., 2013), a 1.5 sec TR was used with a flip angle of 77°, and TE for the b=800s/mm² and b=2500s/mm² scans were 62 ms and 75 ms respectively.

Fig. 2.

Multi-band slab placement and 3D ms-EPI pulse sequence. (a) With six slabs excited using a 3-band RF pulse, a total of eighteen slabs provide full brain coverage in z. Odd (blue) and even (pink) slabs are acquired sequentially in two separate groups to avoid T1 cross-talk artifacts. 3D slice-encoding is performed with a spin echo pulse sequence (b) in which kz-encoding gradients are applied before and after slice imaging echoes. A second spin echo is used to acquire low resolution navigator images at kz=0.

Traditionally, all six multi-band slabs would be acquired in an interleaved fashion within the same 1.5 sec TR, resulting in an imaging time of 1 min 12 sec per volume, or 15 min 36 sec overall. Such an acquisition, however, requires an ideal square RF excitation profile to minimize cross-talk artifacts between adjacent slabs. As the main focus of this study is to demonstrate the effectiveness of the 3D-MB-MUSE reconstruction algorithm, the odd and even slabs were acquired in separate TRs, illustrated in Fig. 2a, which doubled the overall scan time to 31 min 12 sec. This approach was used to 1) remove any confounding cross-talk artifacts between slabs and 2) provide redundant data in the overlapping region between slabs that can be used to improve slab stitching and minimize banding artifacts.

Image reconstruction

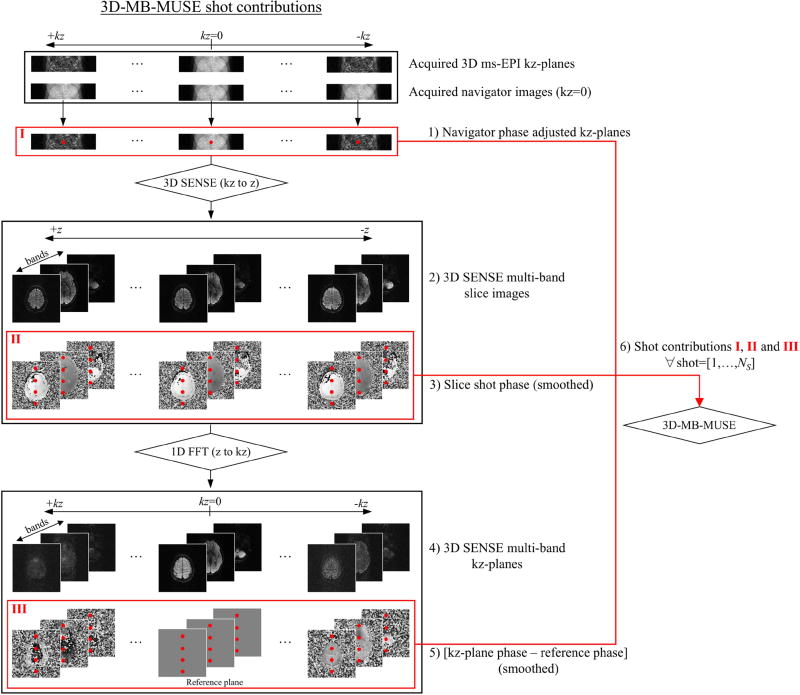
Before being inserted into the 3D-MB-MUSE model for final image reconstruction, the 3D multi-band slab data for each shot was individually processed and reconstructed in the five steps outlined in Fig. 3: 1) To remove bulk movement throughout the acquisition of kz-planes within a shot, the phase of each reduced FOV kz-plane was adjusted by adding phase variations estimated from the corresponding navigator image. The phase adjusted, reduced FOV kz-planes from each shot in step 1 are labeled I in Fig. 3. 2) Using coil sensitivities from a separately acquired single-band b=0 volume (with 12 kz-planes in each of the 18 slabs in Fig. 2a), the phase adjusted, reduced FOV kz-planes in I were reconstructed into full FOV slice images in each band through a 3D multi-band SENSE reconstruction. 3) Phase maps from the slice images generated in step 2 were spatially filtered to produce the low frequency shot-to-shot phase variations, labeled II in Fig. 3, that are stored in Θ in Eq. (8). 4) The slice images generated in step 2 were converted into full FOV kz-planes through a 1D Fourier transform performed across z. 5) Relative to an arbitrary reference kz-plane, spatially filtered phase difference maps were generated for each kz-plane from step 4 to provide slice-encoding phase variations, labeled III in Fig. 3, that are stored in Φ in Eq. (8). 6) Upon completion of these five steps for all four shots, the navigator phase adjusted, reduced FOV kz-planes in I, the shot-to-shot phase maps generated for each slice in II, and the slice-encoding phase difference maps generated in III were inserted into the 3D-MB-MUSE reconstruction model.

Fig. 3.

Flow chart for the processing of all kz-planes in each shot of a 3D multi-band ms-EPI acquisition. From each of N_S shots, reduced FOV navigator phase adjusted kz-planes (I), shot phase maps for each slice (II), and slice-encoding phase variations across kz-planes (III) are generated and inserted into the 3D-MB-MUSE model for reconstruction.

For comparative purposes, two additional reconstructions were performed with conventional 2D reconstruction models that use coil sensitivities collapsed over the slab. In the first data set, all shots in each kz-plane of the acquired 3D ms-EPI data were individually reconstructed with SENSE and combined through a complex average performed over shots. In the second data set, all kz-planes of the acquired 3D ms-EPI data were individually reconstructed with the 2D MUSE model, as in (Chang et al., 2015b). Finally, the kz-planes generated by both the SENSE and 2D MUSE reconstructions were converted to slice images through a 1D Fourier transform performed across kz.

Post processing

After reconstruction, slabs appear shifted off-center in z by an amount proportional to their distance from the iso-center, and thus a Fourier shift is applied to re-center each slab. To reduce banding artifacts when stitching the reconstructed slabs together, slab profiles were normalized before profile encoding (PEN) (Van et al., 2015) was performed using a slab profile derived through the Bloch equations. With a 20% overlap between adjacent slabs, the 18 reconstructed slabs were stitched together to produce 144mm of brain coverage in z. Image registration and eddy current corrections were performed on each volume using DTIPrep (Oguz et al., 2014), followed by a bias-field correction using FSL (Woolrich et al., 2009; Smith et al., 2004; Jenkinson et al., 2012.). Finally, fractional anisotropy (FA) maps were estimated using FSL and a deterministic streamline tracking procedure was carried out using TrackVis (www.trackvis.org).

Results

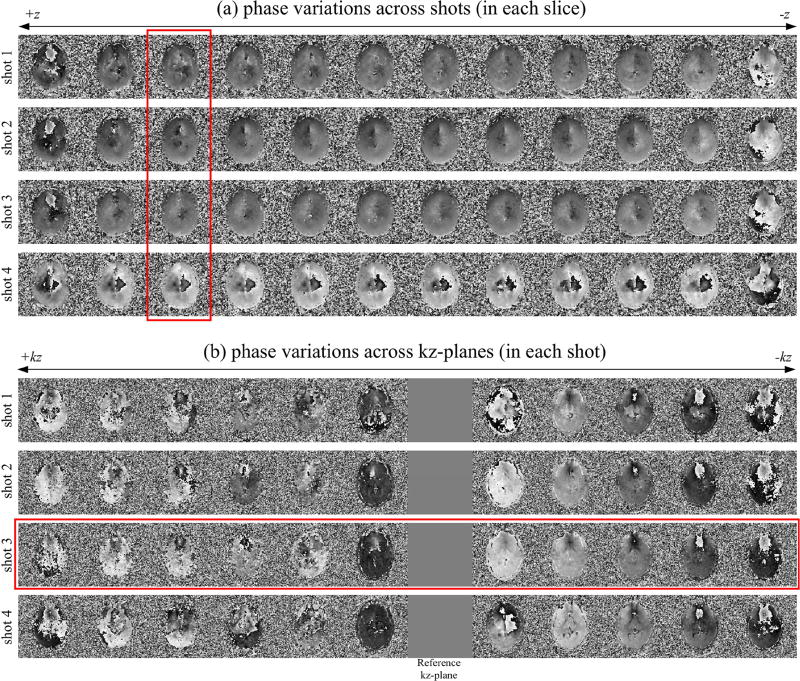
The shot-to-shot phase variations estimated in step 3 of Fig. 3 are presented for all twelve slices of the central band in Fig. 4a. Upon observation of the third slice, marked by the vertical red box in Fig. 4a, the first three shots exhibit strong similarities in their phase maps, suggesting minimal subject motion, while a phase variation noted in the fourth shot signifies more severe subject motion. Using the seventh kz-plane as a reference, phase variations estimated throughout the acquisition of kz-planes in step 5 of Fig. 3 are presented for all four shots in Fig. 4b. Upon initial observation, all four shots exhibit a similar overall trend in phase variation across kz. However, it is of note that while minimal phase variations are present between the first three shots within a slice in Fig. 4a, differences can be noted between the phase maps across kz from the first two shots and that of the third shot, highlighted by the horizontal red box in Fig. 4b.

Fig. 4.

Phase variations in 3D ms-EPI data. Subject motion estimated across shots (a) is noted through phase variations within a slice (highlighted by a vertical red box) between the fourth shot and that of the first three shots. Treating the seventh kz-plane (arbitrarily chosen) as a reference, subject motion is noted throughout the acquisition of kz-planes within each shot (b). Phase variations across kz in the third shot (horizontal red box) show differences with those in other shots.

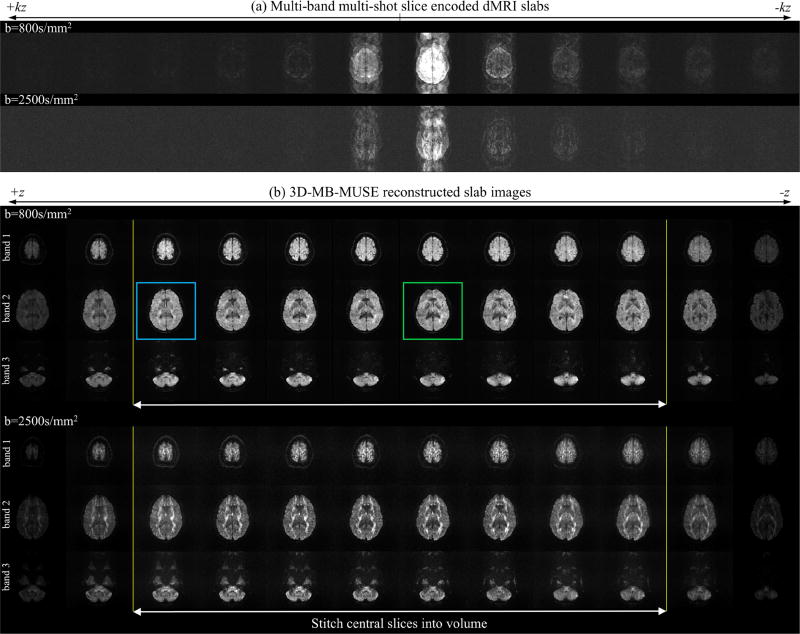
Fig. 5a presents slice-encoded dMRI slabs with 12 kz-planes acquired at both b=800s/mm² and b=2500s/mm² using the 3D multi-band ms-EPI pulse sequence in Fig. 2a. In the presence of strong diffusion gradients, subject movement throughout the acquisition of all shots and kz-planes takes the form of notable aliasing in the PE direction (anterior/posterior). With 3D-MB-MUSE, all twelve kz-planes from each data set in Fig. 5a are reconstructed at once with Eq. (9) to produce the un-aliased slab images in Fig. 5b for each of the three excited bands. By incorporating phase variations across both shots and kz-planes into 3D-MB-MUSE, the motion artifacts noted in the PE direction in Fig. 5a are almost entirely removed in Fig. 5b. Furthermore, the use of slice-specific coil sensitivity profiles that vary across the slab results in slab images with minimal aliasing artifacts. To compare noise properties in slices towards the edge (blue) and center (green) of the slab in band two of Fig. 5b, slice images of 3D ms-EPI data reconstructed with SENSE, 2D MUSE and 3D-MB-MUSE are presented in Fig. 6.

Fig. 5.

3D-MB-MUSE reconstructed slabs. Multi-band, multi-shot slice-encoded dMRI slabs acquired with 12 kz-planes, 3 bands and 4 interleaved shots (a) are reconstructed with 3D-MB-MUSE to produce slab images (b) that are free of motion artifacts. Noise properties in edge (blue) and central (green) slices from the b=800s/mm² reconstruction are inspected in Fig. 6.

Fig. 6.

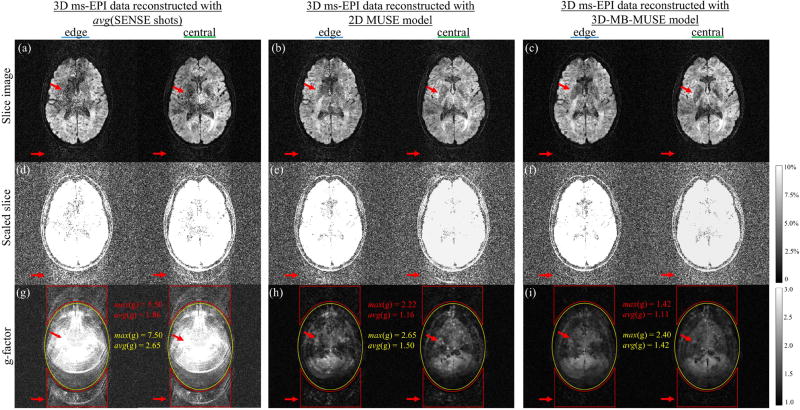
Noise properties of SENSE, 2D MUSE and 3D-MB-MUSE. As highlighted by red arrows both within the brain and in space, edge and central slice images of 3D ms-EPI data reconstructed by SENSE (a) and 2D MUSE (b) show elevated noise levels compared to a 3D-MB-MUSE reconstruction (c). Slice images in (a–c) scaled to 10% maximum magnitude (d–f) and g-factor maps (g–i) highlight noise amplifications (and SNR losses) both within the brain (yellow) and in space across the PE dimension (red) for SENSE and 2D MUSE that are minimized with 3D-MB-MUSE.

To un-alias accelerated 3D slab data, coil sensitivities are often derived from either additional calibration scans, where a single 2D slice is acquired at the center of the slab, or from a collapsed 3D slab, such as the low resolution navigator images acquired at kz=0. For thin slabs, minimal variations in either anatomical structure or coil sensitivities across the slab allow for a straightforward reconstruction of multi-band and/or sub-sampled 3D data with SENSE or 2D MUSE. For thicker slabs (e.g. ≥10mm), however, these variations can be more significant due to the increased spatial coverage in z. Whether acquired with 2D or 3D RF pulses, the use of sensitivities derived from a single 2D slice will always benefit slices towards the center of the slab, with greater potential for aliasing and SNR loss in slices towards the slab edges.

Using coil sensitivities from a collapsed slab, the edge and central slice images of 3D ms-EPI data reconstructed with SENSE in Fig.6a and 2D MUSE in Fig. 6b both exhibit elevated noise levels distributed across the PE direction when compared with a 3D-MB-MUSE reconstruction in Fig. 6c, where coil sensitivities vary across the slab. To highlight and quantify this distribution of noise, the slice images in Figs. 6a–6c are scaled to a maximum of 10% in Figs. 6d–6f respectively, and g-factor maps are presented for each model in Figs. 6g–6i. In parallel MRI, the g-factor represents the condition number of a reconstruction model’s aliasing matrix, measuring noise amplifications due to the way in which overlapping coil sensitivities are applied (Pruessmann et al., 1999). With SNR directly proportional to 1/g-factor, the bright regions of the g-factor maps in Figs. 6g–6i therefore indicate areas with the greatest loss in SNR. As each of the acquired aliased shot images represents a twelve-fold acceleration (4× in-plane and 3× through-plane), the SENSE aliasing matrix in Eq. (2) (with a 32-channel head coil) is 32×12 in dimension. It is the challenge of inverting the poorly conditioned SENSE matrix in Eq. (2) that results in the noisy slice images in Fig. 6a, with the greatest g-factor for any model both within the brain (yellow) and along the PE dimension in space (red) in Fig. 6g. For 2D MUSE, the aliasing matrix is of the form in Eq. (3) (with added inter-shot phase variations), and thus for four shots is 128×12 in dimension. While the 2D MUSE aliasing matrix is easier to invert than that of SENSE, offering an improved g-factor map in 6h, noise in 2D MUSE remains amplified across the PE dimension in Figs. 6b, 6e and 6h due to a sub-par use of collapsed coil sensitivities and residual through-plane motion artifacts. By accounting for phase variations across all slices/kz-planes and incorporating slice-specific coil sensitivities into 3D-MB-MUSE, the g-factor map in Fig. 6i shows noise amplification to be constrained to within the brain itself, with the lowest maximum and average g-factor values across the entire image. This demonstrates the ability of 3D-MB-MUSE to more fully realize the SNR inherent in 3D multi-band ms-EPI data than that of either SENSE or 2D MUSE. Additionally, the improved SNR achieved through 3D-MB-MUSE could be further enhanced by adapting controlled aliasing techniques such as blipped-CAIPI (Setsompop et al., 2012) for use in 3D ms-EPI acquisitions.

The final diffusion weighted slabs, reconstructed by both 2D MUSE and 3D-MB-MUSE, are stitched into volumes and presented together with trace weighted volumes and color FA maps in Fig. 7. While in-plane motion artifacts appear largely removed in the axial images of Fig. 7a, where the 3D ms-EPI data with b=800s/mm² is reconstructed using the 2D MUSE model, failure to account for motion throughout the slice-encoding process results in through-plane striping artifacts observed in both coronal and sagittal views. By comparison, both in-plane and through-plane artifacts appear to be removed through the 3D-MB-MUSE reconstruction in Fig. 7b, where high fidelity images exhibit minimal striping artifacts. The improved motion correction achieved through 3D-MB-MUSE extends to the FA maps in Fig. 7b, where superior anatomical detail is noted when compared to FA maps produced by 2D MUSE in Fig. 7a.

Fig. 7.

3D ms-EPI diffusion data reconstructed with 2D MUSE and 3D-MB-MUSE. Axial, coronal, and sagittal images with 1.0mm isotropic voxels are presented for diffusion weighted (DWI), trace weighted and color fractional anisotropy (FA) volumes generated from 3D ms-EPI dMRI data reconstructed by the 2D MUSE model (a) and 3D-MB-MUSE (b) with b=800s/mm², and by the respective models with b=2500s/mm2 in (c) and (d). Differences between the 2D MUSE and 3D-MB-MUSE reconstructions are highlighted in trace weighted images with red arrows, while regions exhibiting differences in FA between the two models are highlighted by yellow arrows in enlarged images.

When acquired with b=2500s/mm², the prolonged application of diffusion gradients results in low SNR images that are subject to increased motion. Under these conditions, the motion induced artifacts noted in the 2D MUSE reconstruction in Fig. 7a appear amplified in both diffusion and trace weighted volumes in Fig. 7c. While SNR remains low at b=2500s/mm², volumes reconstructed by 3D-MB-MUSE in Fig. 7d exhibit minimal motion artifacts, with improved fidelity when compared to their 2D MUSE counterparts in Fig. 7c. Similar to the FA comparison made between Figs. 7a and 7b, the anatomical detail achieved in FA maps produced from b=2500s/mm² data using 3D-MB-MUSE in Fig. 7d remains superior to that of 2D MUSE in Fig. 7c. The FA degradation in Fig. 7d stems primarily from a reduction in SNR at b=2500s/mm², which is further reduced by the g-factor in Fig. 6i. The FA in Fig. 7d would thus be improved if 1) the g-factor is reduced with controlled aliasing techniques, and/or 2) the increased b-factor is complimented by an angular resolution greater than the twelve diffusion directions used here.

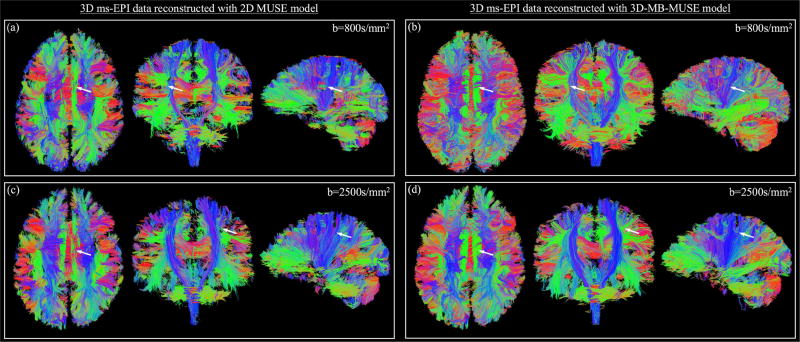
Streamline fiber tracts generated from b=800s/mm² dMRI data reconstructed with 2D MUSE and 3D-MB-MUSE are presented in Figs. 8a and 8b respectively. As demonstrated in Fig. 7a, the 2D MUSE model is incapable of appropriately accounting for motion induced throughout a 3D ms-EPI acquisition, and thus fiber bundles such as the superior longitudinal fasciculus and cortical spinal tract in Fig. 8a appear segmented. By comparison, the ability to account for both in-plane and through-plane motion artifacts with 3D-MB-MUSE results in fiber bundles shown in Fig. 8b that exhibit minimal segmentation. This comparison remains true when observing fibers generated by b=2500s/mm² dMRI data reconstructed with 2D MUSE in Fig. 8c and with 3D-MB-MUSE in Fig. 8d.

Fig. 8.

Fiber tractography comparison. Streamline fiber tract images generated from 3D ms-EPI dMRI data reconstructed by the 2D MUSE model (a) and 3D-MB-MUSE (b) with b=800s/mm², and by the respective models with b=2500s/mm² in (c) and (d). Differences of note between the 2D MUSE and 3D-MB-MUSE reconstructions are highlighted by white arrows.

In studies with low spatial resolution (~2.0mm voxels), the accurate delineation of crossing fiber bundles is a known challenge that is typically overcome by acquiring data with high angular resolutions (Frank, 2001; Anderson, 2005). Despite being derived from only 12 diffusion directions, the fibers in Figs. 8b and 8c exhibit a clear delineation between crossing fiber bundles as they are estimated from images with high spatial resolution (1.0mm isotropic voxels) and fidelity. An additional advantage of high spatial resolution dMRI is the ability for high curvature inter-gyral association fibers to be resolved. At the 2.0mm spatial resolution commonly used in dMRI studies, a 3–5mm fiber could perform an entire 180° turn within the volume of a single voxel, and would thus fail to be resolved regardless of the angular resolution. With voxels on the order of 1.0mm or smaller, such as those in Figs. 7 and 8, these tightly curved fibers are more accurately resolved and could ultimately improve the accuracy of structural connectomes derived through fiber tracking.

Discussion and Conclusion

In this study, it has been demonstrated that ultrahigh (e.g. submillimeter) spatial resolution dMRI can be achieved with sufficient SNR and temporal throughput for routine use by employing a 3D multi-slab, multi-band, and multi-shot acquisition strategy. Through a new model, termed 3D-MB-MUSE, image quality is ensured by reconstructing 3D ms-EPI data while simultaneously accounting for motion artifacts induced across different dimensions (in-plane and through-plane) throughout the acquisition of shots and kz-planes. In comparison, using the traditional 2D MUSE approach to reconstruct high-resolution 3D multi-shot dMRI data (Chang et al., 2015b) fails to appropriately account for both motion artifacts and coil sensitivity variations across the slice dimension of a relatively thin 3D slab (e.g. 10mm used in this report). It is anticipated that our framework for acquiring and reconstructing 3D ms-EPI data will be broadly applicable in ultrahigh resolution dMRI studies, which are experiencing greatly increased utility in neuroscience (Sporns et al., 2005; Hagmann et al., 2008; Hagmann et al., 2010).

As alluded to in earlier sections, the acquisition and reconstruction framework presented here can be expanded upon to further increase both SNR and imaging speed. In addition to optimizing the TR for the highest achievable SNR and throughput per unit time, an effective approach for minimizing SNR loss in multi-band acquisitions is through controlled aliasing techniques. In controlled aliasing, FOV offsets are performed in each excited band to minimize the overlap of brain regions aliased into the acquired multi-band images (Breuer et al., 2005; Breuer et al., 2006). This can be accomplished in one of two ways: First, slabs from each band can be excited by separate RF pulses (Chang et al., 2015) that are applied sequentially with different phase modulations. While implementing this approach is straightforward, the extended duration of sequential 3D RF pulses (~30ms for 3 bands) would significantly increase TE, ultimately limiting SNR gains due to greater signal dephasing. In the second approach, techniques such as blipped-CAIPI (Setsompop et al., 2012) apply FOV offsetting gradients concurrently with phase encoding gradients. While this approach only requires a single 3D multi-band RF pulse, thereby maintaining a short TE, the cyclical pattern in which the FOV offsetting gradients are applied is typically designed for ss-EPI, with no in-plane acceleration. With 3D ms-EPI, the interleaved sub-sampling of each kz-plane requires gradient blip amplitudes to account for acquisitions with high in-plane acceleration (such as the fourfold acceleration of each shot in this report). The development of a protocol that incorporates these SNR enhancements into 3D ms-EPI is currently underway.

For dMRI studies focused on a particular region, and thus not requiring whole-brain coverage, great increases in SNR can be achieved when a thicker slab is acquired with multiple kz-planes, as SNR is directly proportional to $\sqrt{N_{\mathit{\text{KZ}}}}$ in 3D imaging. As the acquisition of a thick slab with a large number of kz-planes (e.g. ~20 kz-planes) with ms-EPI can be lengthy, an optimal combination of a shortened TR and increased NKZ needs to be derived. Additionally, it is to be expected that coil sensitivities will vary greatly across a thick slab (e.g. ≥20mm) and motion induced artifacts will be more severe across an increased number of shots/kz-planes. However, it is with such an acquisition that the true reconstruction power of the 3D-MUSE model presented here can be realized, as no 2D ms-EPI model would be able to account for either significant sensitivity variations across the slab or motion artifacts spanning the entire acquisition. Furthermore, a more accurate estimation of through-plane motion artifacts across thick slabs could be achieved by acquiring a 3D navigator volume after each kz-plane (Chang et al., 2017). A 3D phase map for each shot/kz-plane could be incorporated into the 3D-MB-MUSE model by appropriately adjusting the slice-encoding phase matrix Φ in Eq. 8.

Imaging speed can be further increased with improved RF pulse design, as optimizing the acquired slab profiles can directly influence the cross-talk artifacts between adjacent slabs, and thus the number of slabs that can be acquired in the same TR. In conventional 2D multi-band imaging, the thin slice profile necessary for high resolution dMRI allows for a large number of slices (in ~8 bands) to be simultaneously excited by a relatively short RF pulse (<10ms). To achieve an ultra-sharp slab profile in 3D imaging, however, an RF pulse requires a high time-bandwidth product (TBW) in its design (e.g. >5–8). When modulated to as few as three bands, such pulses can exceed 15–20ms in duration to avoid exceeding maximum SAR limits, thereby reducing the achievable SNR through an extended TE. Thus, 3D multi-band RF pulse design needs to be optimized to generate pulses with a short pulse width, high TBW and minimal SAR. The development of more optimal 3D multi-band pulses using techniques such as PINS (Noris et al., 2011) or VERSE (Conolly et al., 1988; Hargreaves et al., 2004) is currently underway.

Another means of increasing imaging speed in 3D ms-EPI is through improved gradient and RF coils. While a reduction in overall scan time can be achieved with a short TR (<1.0 sec), the corresponding loss in SNR can be compensated for through high-powered gradient coils. By increasing the amplitude of diffusion gradients and reducing their duration, the SNR and achievable throughput are increased through a reduction in TE. Additional increases in SNR can be achieved through optimized RF coil design, effectively reducing both the g-factor and magnetic field inhomogeneities. By designing RF coil arrays with multiple tiers of coils along z and a minimal overlap of in-plane sensitivities, more bands can be simultaneously acquired in ms-EPI without incurring a significant g-factor penalty. Furthermore, the geometric distortions induced by B-field inhomogeneities (particularly near regions such as the sinus) can be greatly reduced through localized shimming techniques such as iPRES (Han et al., 2013; Truong et al., 2014. Darnell et al., 2016). With localized B-field shimming performed throughout the brain, the acquired 3D slab profiles will be more rectangular in shape, ultimately enabling more slabs to be acquired in each TR, and banding artifacts will be greatly minimized when stitching the reconstructed slabs into a volume.

In conclusion, the 3D-MB-MUSE model presented here offers a unified framework to appropriately reconstruct and process 3D multi-band ms-EPI data. With such a model, it has been shown that whole brain in-vivo dMRI data can be acquired in a clinical 3T MRI scanner at high spatial resolution with high SNR in minimal time. Using a shortened TR (~1.0sec) together with further optimizations to RF pulse design, the incorporation of controlled aliasing techniques, and improvements to both RF and gradient coil hardware, the reduced scan times would enable whole-brain volumes with sub-millimeter isotropic spatial resolutions (~0.85mm) to be achieved together with increased angular resolutions (25 directions) within an imaging time practical for routine use (20min). The development of such a target protocol is currently underway, and its use would greatly improve the ability to delineate neuronal microstructures.