Shape Up: An Eye-Tracking Study of Preschoolers’ Shape Name Processing and Spatial Development

Abstract

Learning the names of geometric shapes is at the intersection of early spatial, mathematical, and language skills, all important for school-readiness and predictors of later abilities in science, technology, engineering, and mathematics (STEM). We investigated whether socioeconomic status (SES) influenced children’s processing of shape names and whether differences in processing were predictive of later spatial skills. 3-year-olds (N = 79) with mothers of varying education levels participated in an eye-tracking task that required them to look at named shapes. Lower-SES children took longer to fixate target shapes and spent less time looking at them than higher-SES children. Gaze variables measured at age 3 were predictive of spatial skills measured at age 5 even though the spatial measures did not require shape-related vocabulary. Early efficiency in the processing of shape names may contribute to the development of a foundation for spatial learning in the preschool years.

Early geometry and spatial skills predict success in school, especially in the so-called STEM subjects (science, technology, engineering, and mathematics) (Mix & Cheng, 2012; Wai, Lubinski, Benbow, & Steiger, 2010). The term spatial skills refers to the encoding and mental manipulation of information about the configuration of objects and their location in our environment (Uttal et al., 2013). With recent changes in early curricula, learning about shapes and spatial skills both play a major role in school readiness for mathematics (e.g., Common Core State Standards Initiative, 2010; Office of Head Start, 2011). Understanding early STEM-related learning is, therefore, critical for improving school readiness and increasing later STEM achievement, and may be essential for minimizing socioeconomic status (SES) achievement gaps in STEM-related domains (e.g., citation removed for blinding).

This study investigated 3-year-old children’s processing of shape names in a mixed-SES sample. The same children were then given tests of spatial skills over two more years to investigate connections between shape name processing and later spatial skills. The study had two main goals: 1) to assess whether differences in maternal education influence the time course of the identification of named shapes; and 2) to determine whether individual differences in shape name processing predict future spatial skills.

Early Language Experience

Differences in early experiences can have important implications for both vocabulary acquisition and language processing speed. For example, children from lower-SES households appear to have difficulty quickly learning new words (citation removed; but see Horton-Ikard & Weismer, 2007). One explanation is that children in lower-SES households receive less and lower quality language input than those from higher-SES families (e.g., Hart & Risley, 2003; Hirsh-Pasek et al., 2015). Additionally, children from lower-SES families often attend lower quality childcare programs where language development is not emphasized compared to those attended by children from higher-SES families (Magnuson, Meyers, Ruhm, & Waldfogel, 2004). These differences in early experience may contribute to the SES gap in language development.

The amount and complexity of parental language input at 18 months can predict not only children’s vocabulary size at 24 months, but also the speed with which they resolve word meaning (Hurtado, Marchman, & Fernald, 2008). Differences in processing speed are important because they are likely to influence comprehension broadly. Understanding the speech stream requires listeners to continuously process language at multiple levels (e.g., from phonemes to phrases to clauses), and to integrate acoustic information with linguistic and conceptual knowledge to interpret language as it unfolds (Fernald & Weisleder, 2011). Children who are slower in understanding speech may need to exert more effort in trying to keep up with the speech stream, effectively limiting the cognitive resources left to comprehend less-familiar words. The effects of slower language processing may not be evident in everyday contexts in which children are processing familiar words and structures in rich environmental contexts. However, they may be magnified in contexts like STEM learning, in which children are likely to encounter unfamiliar words that would be expected to take more time to process and more cognitive resources to comprehend.

Preschool Shape Learning

Shape categories are differentiated by their spatial or mathematical properties, e.g., the number of sides, sizes of sides or angles, symmetry. To quickly identify a shape after hearing its name, children must not only be able to recall some mental representation that shares the shape’s defining spatial and numerical properties, but also to process the shape name quickly and map it onto the mental representation.

Young children begin to show interest in shapes while they are still quite young (Shutts, Örnkloo, von Hofsten, Keen, & Spelke, 2009) and begin to accurately label them during the preschool years, with some variation across shapes and understanding of shapes’ defining properties (e.g., Satlow & Newcombe, 1998; citation removed). Between 25 and 30 months, children begin identifying standard versions of common shapes (citation removed). By 3 years of age, over 60% of children can name basic shapes like circle, square, and triangle (Fuson & Murray, 1978) and those numbers climb near 80% by age 5 (Klein, Starkey, & Wakeley, 1999). Indeed, many parents of preschoolers would claim that their child “knows” their shapes. However, studies on early shape labeling have primarily used the most often encountered, equilateral versions and none that we are aware of have investigated speed in identifying shapes.

Opportunities to learn the range of exemplars in each shape category appear to also be relatively limited. Most children’s toys focus on a small set of shapes (citation removed) that are mostly canonical. That is, they include prototypical versions which are especially salient even for adults (e.g., Rosch, 1973) and are usually equilateral or have some preferred ratio of side lengths (e.g., a “golden rectangle” with side ratios of approximately 1:1.62; Benjafield, 1976). In schools, educators infrequently use shape names (Rudd, Lambert, Satterwhite, & Zaier, 2008; Sarama & DiBiase, 2004), and rarely describe their properties when they do (Sarama & Clements, 2004). Research suggests that exposure to varied exemplars of a category is necessary to separate defining from incidental features (e.g., Rakison & Oakes, 2003). Given the relatively infrequent exposure to varied exemplars and the lack of description of their properties, it is perhaps not surprising that children need years of exposure to understand the features that define shapes (Satlow & Newcombe, 1998). At 30 months, children begin to extend shape labels to less standard versions, but they are not adept at doing so (citation removed).

The ability to identify shapes has been directly related to experience with shapes before formal instruction (e.g., Clements, Swaminathan, Hannibal, & Sarama, 1999). In addition, there is reason to believe that children’s shape identification will be related to their language skills. It is well known that shape plays a role in early word learning. For example, children show a “shape bias” in learning object labels (Landau, Smith, & Jones, 1988) and, as they learn more object categories, they use shape to recognize stylized three-dimensional caricatures of known and novel objects (Smith, 2003). Given variability in how much and what kind of exposure children receive to shapes early in life, there may be individual differences in how efficiently they can process shape terms. These processing differences may be indicative of prior experience with shapes and instruction on their defining spatial properties, and may affect children’s ability to learn about the spatial properties of shapes. For example, for children with good language skills and much experience with shapes and their names, some shapes may be identified quickly using lower-level, perceptual processes, regardless of changes in color or context. On the other hand, children with lower language skills and less experience with shapes and their names may experience processing bottlenecks that make it more difficult to identify shapes. In turn, these bottlenecks might make it more difficult to attend to new information about shapes, including considering their spatial properties. If this cascade of effects is accurate, the time course of children’s identification of a set of prompted shapes should predict later spatial skills, even after accounting for the size of a child’s vocabulary. Prior work does show that early experiences and exposure to language can influence spatial skills (Pruden, Levine, & Huttenlocher, 2011). Do children who are better at processing shape names also have better spatial skills?

The Current Study

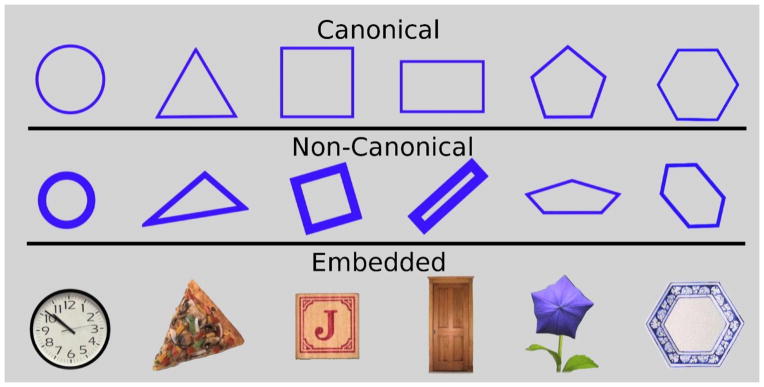
Our Shape Fixation Task (SFT) incorporated an eye-tracker to observe the locus of children’s attention as they processed shape labels for six categories of common geometric shapes (circle, triangle, square, rectangle, pentagon, and hexagon –Figure 1). With the SFT we explicitly measure children’s ability to look to shapes in response to verbal prompts. Both the percent of time spent looking at targets and the speed with which they are selected are potentially meaningful indicators of how children process geometric language. Across trials, looking consistently more at target shapes than non-target shapes requires some understanding of shape category labels and of the shared properties of shapes within a category. Prior work (citation removed) with 30-month-olds using an untimed comprehension test indicates that most children of this age would be at or near ceiling performance on the presented shapes. Our priority was to go beyond a simple accuracy task to assess the speed with which participants looked to named target shapes, as a measure of processing.

Figure 1.

Stimuli used in the study.

Adapted in part with permission from “The Shape of Things: The Origin of Young Children’s Knowledge of the Names and Properties of Geometric Forms,” by B.N. Verdine, K.R. Lucca, R.M. Golinkoff, K. Hirsh-Pasek & N.S. Newcombe, 2016, Journal of Cognition and Development, 17, p. 146. Copyright 2016 by Routledge.

Six categories of common geometric shapes were selected to provide a spectrum of difficulty based on performance in other studies (Fuson & Murray, 1978; Klein et al., 1999; Satlow & Newcombe, 1998; citation removed). Three variants of each of the six shape categories were selected to also alter difficulty across trials within the same category. The three variants included typical, monochromatic versions of shapes children were likely to have seen before, such as an equilateral triangle, referred to as canonical. Other versions of each shape, such as a scalene triangle, and shapes represented by everyday objects (e.g., a triangular slice of pizza), were also included and referred to as non-canonical and embedded shapes, respectively. Inclusion of these shape types was meant to challenge children’s understanding of shape names. The design also reduces the use of simple visual-matching strategies or incorrect assumptions about shapes (e.g., that shapes can only be represented by line drawings).

Hypotheses

A longitudinal design allowed us to determine whether shape processing is modulated by SES-related factors like maternal education and whether it predicts later spatial skills. We expected to find individual differences in children’s looking to the shape targets such that children with less educated mothers would take more time to locate targets and spend less time looking at them. We also expected that aspects of shape processing would predict later spatial skills.

Method

Participants

Participants were 79 typically developing 3-year-old children (M = 3 yrs; 7.7 mos, SD = 2.46 mos, range = 3 yrs; 1.7 mos to 3 yrs; 11.4 mos; males = 45, females = 34; higher-SES = 43, lower-SES = 36) which were also assessed approximately one (12.8 months; SD = 1.6) and two years later (25.8 months; SD = 1.6) at ages 4 (56.3 months; SD = 2.8) and 5 (69.2 months; SD = 3.4). Children were native monolingual English speakers from diverse preschools in a medium-sized mid-Atlantic U.S. city: private preschools (N = 29; 1 lower-SES), Head Starts (N = 30; 1 higher-SES), and a University-related preschool (N = 19; 6 lower- and 13 higher-SES).

Throughout this report we used highest level of maternal education as a proxy for socioeconomic status. Hoff (2013) argued that mother’s education is a critical SES component for development. In our sample, maternal education was typically related to income; all but one child from a Head Start was characterized as lower-SES and all but one child in the private preschools was characterized as higher-SES. Mothers who completed a 4-year college degree or higher are referred to as the higher-SES group (bachelor’s, N = 15; graduate, N = 28) and those who had less than a 4-year degree are referred to as the lower-SES group (some high school, N = 3; high school diploma or equivalent, N = 15; trade qualification or 2-year associates degree, N = 15). Survey data from three children in Head Start facilities were not returned; they were characterized as lower-SES.

A total of 102 children were consented. Ten children (5 higher-SES; 5 lower-SES) were excluded due to uncooperativeness during the eye-tracker calibration procedure or before data collection started and 13 were excluded for track loss (see Data Analysis section). Attrition was about 20% per year of the study; 63 of the 79 participants at age 3 participated at age 4 and 50 participated at age 5. As is typical, attrition over the 2 years was higher in the lower-SES group (N = 19 vs. 10). In year 2, one participant was excluded for speech problems and one was excluded because the child refused to participate. All other year 2 attrition was due to an inability to locate the participants. In year 3 most participants matriculated to other schools and had to consent to be in the study again. All attrition was due to being unable to contact them (N = 12) or unwillingness to be re-consented (N = 4). Three participants that were not located in year 2 were found during our year 3 search and tested. According to a series of t-tests, those that started the study but dropped out and those that completed the study performed similarly on all tests except for the Test of Spatial Assembly (TOSA); those that completed the study scored higher [M_sample = .24(SD = .91)] than those that did not [M_drops = −.16(SD = .62); t = 2.07; df = 76; p = .042]. There were SES differences in most measures (citation removed) and it is likely this effect resulted at least partially from differences in attrition by SES.

Apparatus and Stimuli

The Shape Fixation Task (SFT) was conducted using a Tobii T60XL with a 1920 × 1200 pixel resolution monitor (75.3 × 20.8 cm) run with Tobii Studio 2.2.4 operating at a 60 Hz sampling rate. The screen was divided into left and right halves, each with a centered shape occupying approximately 9% of the screen (roughly 12 × 12 cm). The task used 18 stimuli (Figure 1).

To select the shapes, nine variations of each shape were generated by varying vertex angles, side lengths, orientation, or line weights. The canonical representations were unanimously picked by eight adults as representing prototypical versions. They had equilateral features or a typical ratio of sizes for the sides and matched those likely encountered in books, touchscreen apps, and shape sorters (citation removed). Non-canonical representations were neither typical, nor highly atypical. To select these, five versions of each shape were posted to a survey site where their typicality was rated by 73 adults on a 7-point Likert scale. The shape rating nearest the category average was selected. Highly atypical shapes were not used to avoid floor effects (Satlow & Newcombe, 1998). Certain forms such as the circle and square, by definition, had to retain properties that made them more similar to the canonical versions. Lastly, embedded shapes were photographs of everyday objects with shapes similar to the canonical forms (e.g., a rectangular door), although some were not “perfect” representations of their categories. Pizza, for example, traditionally has a rounded crust (though not in the version used) and the pentagonal flower does not have perfectly straight sides. Object selection was guided by examples in children’s books, which frequently contain imperfections. In a forced-choice paradigm, these imperfections should not greatly impact recognition if children understand even basic features of a shape.

Procedure

All testing (apart from one child who was tested in the lab) was done individually in preschools in a quiet room. The SFT in which the eye-tracker was used was administered as part of a larger longitudinal study, presented in (citation removed). Participants sat in a chair approximately 66 cm from the monitor within the tracking range of the device (35°). After a standard 5-point calibration, children were told they were going to watch a movie and that they should look where the movie tells them, stay in their chair, and not touch the screen. Participants were presented with two practice trials and one familiarization trial (Supplemental Figure 1). Practice trials presented two stimuli children were expected to know (e.g., a cupcake, a tiger) and prompted them to look at one, allowing us to determine whether children understood the instructions. All participants followed these initial prompts. The familiarization trial provided a baseline of exposure to all shapes and consisted of six canonical shapes labeled in random order and presented simultaneously. Next came two blocks of nine test trials divided by a break (18 total), and four intermingled filler trials. Filler trials used the same stimuli as the practice trials and were easy trials to maintain attention (one after trial 5, two for reorientation after the break, and one after trial 14).

The 18 test trials presented pairs of shapes in 3 quasi-random orders with the following constraints: 1) The same shape was not allowed to be the target on back-to-back trials; 2) the stimuli were always paired within representation category (e.g., only canonical shapes with canonical shapes); and 3) squares and rectangles were never paired. Each of the 18 stimuli appeared once as a target and once as a distractor. The four randomly selected prompts were recordings of either a male (for familiar object trials) or a female (for test trials) native English speaker using child-directed speech: 1) Gosh! Check out the [target]! Check out the [target]!; 2) Hey! Watch the [target]! Watch the [target]!; 3) Oh look! Look at the [target]! Look at the [target]!; or 4) Wow! See the [target]! See the [target]!). The shape name prompt was repeated to reduce looking away from the target toward the end of a trial.

Each of the practice, test, and filler trials began with a 3-s video of a laughing baby or a dancing feather with a rattling sound, to center the child’s gaze. An approximately 2.5-s time came next during which the target and non-target shapes were visible on screen but no directions were given. Then the auditory prompt was given, and the child had approximately 3.5 s to look at the display before the fixation image for the next trial. Actual trials were 6 s; the length of time before and after a prompt varied slightly depending on the prompt (2042–2455 ms before and 3535–3948 ms after). All timing reported is relative to the onset of the first shape name (i.e., “[target]”) within the prompts. For analyses, only eye-tracker samples from 4000 ms of the trials were used –the 1000 ms period before the shape prompt (Salience phase) and the 3000 ms period after onset of the prompt word (Test phase). This period provides enough data to account for baseline looking prior to the prompt and a reasonable amount of time to respond. The full procedure was approximately 4 minutes.

Dependent variables

Areas of interest (AOIs) were the two halves of the screen with the target and the distractor. Most data are reported as the percent of eye-tracker samples (sampling rate = 60 Hz) children fixated on the target AOI versus the non-target AOI. We refer to the amount of target looking as Percent Looking to Target or PLT (i.e., [samples on target AOI /(samples on target AOI + samples on non-target AOI)] * 100). For most analyses, PLT was calculated for each of 16 windows 250 ms in length: SalienceWin-1 through SalienceWin-4 in the Salience phase and TestWin-1 through TestWin-12 in the Test phase. Test windows of 250 ms were selected to allow comparison of the SES groups at smaller time intervals than just the overall trial. The 250-ms test windows we selected allowed us to take some advantage of the rich time course information in our data while avoiding the statistical and reporting problems associated with the number of comparisons necessary to use smaller time units.

Note that average PLT is consistently computed across trials and we expected, a priori, that speed in locating the targets would vary on different trials. For an individual participant or group, that variance created a response curve similar to that seen in Figure 2, computed from underlying data that are inherently binary. Whether an individual child actually knows the right answer cannot be taken for granted, let alone that they will quickly arrive at that answer and consistently fixate the target without glancing, perhaps multiple times, to the distractor. Because responses to some trials take more time or are more inconsistent at first, PLT averaged across trials takes time to rise above chance and achieve a maximum. That maximum is inherently limited by the number of trials on which children know the answer and consistently fixate the target. Thinking about the answer before responding, visually scanning back-and-forth to determine the answer, simply not knowing the answer in the provided timeframe (i.e., chance looking), or being systematically wrong (i.e., PLT significantly less than .5) will all lower the average PLT for a given time window even when children are accurately responding to other trials. This is how it is possible that PLT can remain well below 100% and yet still reflect valid responding. This is also why any discussion of a “response” to the target should be assumed to be referring to the point at which PLT exceeds chance based on an average across different trials; visual behavior in any individual trial could vary significantly from the average. When this variable is included prior to processing speed in regressions, it may help to control for factors that would otherwise influence processing speed but are not directly related to it (e.g., shape familiarity, overall interest in shapes, attention to the task, etc.).

Figure 2.

Percent looking to target (PLT) by SES group on the Shape Fixation Task (SFT) across all trials for each 250 ms Salience and Test window.

Note: The black vertical bars with circles show test windows in which the SES groups are significantly different from one another. The black square markers note the test window in which each group’s PLT first statistically exceeds chance (50%).

Longitudinal assessments

Tests of spatial skills and vocabulary were administered in the same session as the SFT at age 3 and at ages 4 and 5. All tests were untimed and did not rely on knowledge of shapes or any geometric knowledge. Though some of these tests may differentially tap certain spatial skill domains, they were combined into z-scored variables that take advantage of multiple measurements of the same construct to create more stable measurements of omnibus spatial skills. This approach helps address one of the challenges of assessing young participants, whose scores on any one test are more likely than older children and adults to be influenced by factors unrelated to the tested construct (e.g., the order of tests within a session).

Age 3 assessments

The Peabody Picture Vocabulary Test – 4th Ed. (PPVT; Dunn & Dunn, 2007), a measure of receptive vocabulary and also related to general intelligence (Hodapp & Gerken, 1999), asks children to point to the depiction of a prompted word from four possible images. Thus, the PPVT was used as a covariate in a number of analyses because it is a strong control for early language skills and likely also controls for some other domain-general skills that may influence performance on both tests but are not directly related to their content (e.g., inhibition control).

The Test of Spatial Assembly (TOSA) was given as an early, omnibus test of spatial skills (citation removed). Designed for 3-year-old children, the TOSA is composed of 2- and 3-dimensional (2-D and 3-D) trials (six of each; see Supplemental Figure 2). Trials use two to four pieces (flat magnetic foam geometric shapes or interlocking construction blocks) which children arranged to match an always visible target design. Scores for the 2-D and 3-D trials were calculated separately, then z-scored, and those scores were averaged to create the overall TOSA scores. This measure has good reported reliability (Chronbach’s α = .747) and validity, correlating with other established or standardized spatial measures (r = .44 to .60; citation removed).

Age 4 assessments

Overall age 4 spatial scores (Z age 4) were calculated by averaging the z-scores from the two tests given at age 4: 1) The Woodcock-Johnson III: Spatial Relations Subtest (WJ-III; Woodcock, McGrew, & Mather, 2001) and 2) the Wechsler Preschool and Primary Scale of Intelligence III: Block Design Subtest (WPPSI; Wechsler, 2002). The WJ-III taps understanding of spatial relations by showing a design on the left side of the page with possible component pieces to the right. A point was awarded for each correctly identified component piece (33 trials; 81 possible points). The WPPSI Block Design Subtest was administered as per the standardized instructions. Items require participants to use 3-D blocks with red and white colored patterns to create specific target designs from 2-D images.

Age 5 assessments

Overall age 5 spatial scores (Z age 5) were calculated by averaging the z-scores from the two tests given at age 5: 1) The WJ-III and 2) the Children’s Mental Transformation Task (CMTT; Levine, Huttenlocher, Taylor, & Langrock, 1999; Levine, Ratliff, Huttenlocher, & Cannon, 2012). The WJ-III was the same at ages 4 and 5. The CMTT is a 32-item test that measures mental rotation and translation by asking children to select an image from among four choices that together comprise a target design.

Track Loss

Track loss occurs when the eye-tracker fails to register the child’s eyes, often because the child looks away or moves. A total of 271 trials out of 1,656 (16.4%) administered to the initial 92 participants had more than 50% track loss and were removed. Individuals with seven or more excluded trials were removed from analysis (N = 11) and two participants with six dropped trials were excluded for missing more than three trials from a single representation type.

Results

Group-Level Analysis of Eye Gaze Patterns

Figure 2 shows the time course of looking to the target as a percent of gazes directed at the target versus the non-target for each SES group. As the figure portrays, and as expected, during the salience windows preceding the prompt, both higher- and lower-SES children were near chance (50%). However, as the test windows proceed, both groups begin to rise above chance and reach a maximum PLT before looking to the target begins to decline for both groups.

To investigate group-level differences in these patterns, the group-level analyses probed for effects of SES and shape type on the timing and magnitude of responses to the shape prompts separately for each of the 16 analysis windows (4 salience and 12 test). Elogit transformations were used to reduce the dependency caused by eye gaze location not being independent from one sample to the next (Barr, 2008). Trends were tested using multi-level mixed logit modeling with crossed random intercepts for Participants and Items (after Baayen, Davidson, & Bates, 2008). Due to concerns over attention, participants were given one trial for each stimulus. This trial limitation prompted two analyses to assess the magnitude of the group-level response: one with Shape Category (i.e., rows in Figure 1) as a fixed factor and Representation Type (i.e., columns in Figure 1) as a random effect, and another with Representation Type as a fixed factor and Shape Category as a random effectⁱ. Preliminary analyses showed no sex differences, so that variable was excluded from further analyses. As reported in Table 13 of Verdine, Golinkoff, Hirsh-Pasek, and Newcombe (2017), the spatial measures given at ages 3, 4, and 5 all demonstrate significant, medium to large effect size SES differences (Hedges g = .60 to 1.69), so group-level analyses focus exclusively on SFT data in this report.

Group PLT for shape and representation categories

In the test for effects of Shape Category, Participant and Representation Type were entered as crossed random intercepts and Shape and SES were first-level predictors. When not perfectly correlated with random intercepts, Shape was entered as a random slope in the Participant effects structure, and Shape, SES, and an SES × Shape interaction were entered as random slopes in the Representation Type effects structure. Higher-SES children had higher PLT (Table 1) in TestWin-7 (1500–1750 ms; p < 0.05) and TestWin-8 (1750–2000 ms; p < 0.01). These significant comparisons are shown in Figure 2 with vertical bars.

Table 1.

Statistically Significant Effects of SES from the Best-Fitting Multilevel Linear Models of PLT by Analysis Window

Effect	Estimate	SE	t
TestWin-7 (1500–1750 ms after prompt)
Intercept	1.22	0.21	5.95
Higher-SES vs. Lower-SES	−0.41	0.17	−2.38
TestWin-8 (1750–2000 ms after prompt)
Intercept	0.98	0.13	7.52
Higher-SES vs. Lower-SES	−0.55	0.19	−2.87

The models presented are the best-fitting model for each time window; when effects or interactions do not appear, it is because adding them to the models did not reliably improve the fit. Formula in R – TestWin-7: DepVar ~ SES + Shape + (1 + Shape | Subject) + (1 | Rep Type); TestWin-8: DepVar ~ SES + (1 | Subject) + (1 | Rep Type). For the remaining 14 analysis windows, no models tested provided a better fit than an empty model with no fixed effects.

There was a main effect of Shape for SalienceWin-1 (−1000 to −750 ms; p < 0.01) and effects of shape during TestWin-4 (750–1000 ms; p < 0.05), TestWin-6 (1250–1500 ms; p < 0.01) and TestWin-7 (1500–1750 ms; p < 0.05; the best-fitting model for TestWin-7 included effects of SES and Shape). There were no other effects of SES or Shape and no interactions. Analysis of the specific shape effects are presented in the online-only materials.

A similar multi-level mixed model to that above tested for effects of Representation Type. SES effects mirrored the previous analysis, appearing in TestWin 7 and 8. The only significant effect of Representation type was in TestWin 12 and appears to result from eye gaze wandering away from canonical targets near the end of a trial, likely due to stimulus familiarity.

Group reaction time: Comparison of eye gaze patterns to chance performance by SES group

To assess group-level reaction time to targets, we used “correct” trials only. A trial was considered correct if more than 55.56% of the eyetracker samples in that 1500 ms timeframe were directed toward the target. That timeframe was selected because it allowed adequate response time, even for slow responders, encompassed the peak PLT for both SES groups, and excluded the end of the trial when some children may start wandering away from the target. Assuming that a child was paying attention to the prompt, knew the name of the shape, and was responding appropriately to a trial, their looking to the target in this timeframe should be above chance. The 55.56% chance threshold was calculated by determining the lowest k value with a probability (i.e., P = p-value) below 0.05. $P(k\mathit{successes}inn\mathit{samples})=\frac{n!}{k!(n-k)!}{p}^k{q}^{n-k}$, where n = eye-tracker samples in the time window (i.e., 60 samples/s × 1.5 s = 90); k = on-target samples; p = probability of success (chance = 0.5); and q = 1 − p = probability of failure. P drops below 0.05 with 50 on-target samples out of 90 (55.56%; actual probability = 0.048).

Speed analyses for the group and individual analyses were focused on these correct trials to remove the influence of trials on which children were inattentive or for some reason did not look very much at the target shape (i.e., low PLT trials). This was a valid concern since the higher-SES group had a higher proportion of correct trials than the lower-SES group for non-canonical targets [M_high = .62(SD = .21); M_low = .51(SD = .24); t(77) = 2.25; p = .027] and squares [M_high = .69(SD = .35); M_low = .52(SD = .31); t(77) = 2.16; p = .034], with a trend toward more correct overall [M_high = .62(SD = .16); M_low = .55(SD = .15); t(77) = 1.89; p = .062]. Practically, it would be odd to measure the speed of responses that did not appear to actually identify the target.

Percent Looking to Target [PLT = (target looks/(target looks + non-target looks)) * 100)] in the sixteen 250 ms windows was compared to chance by assessing the t-values of the intercepts of empty models with no fixed factors. Elogit-transformed PLT was modeled for each SES group for each window using multi-level mixed elogit modeling with Participant and Representation Type as crossed random intercepts. Higher-SES children were faster than lower-SES children, first demonstrating above chance PLT in TestWin-5 (1000–1250 ms; t = 2.39, p < 0.05) rather than TestWin-6 (1250–1500 ms; t = 4.90, p < 0.05). Therefore, the higher-SES group looked more to the targets and were faster in shifting attention to them. The SES difference in speed is unlikely due to differences in the groups’ ability to look to the correct targets since only correct trials were used.

Individual-Level Analyses of Shape Processing

Individual PLT and speed variables

A PLT score for each child was calculated by determining average PLT across all eye-tracker samples in all test windows for all trials. Creating the speed variable for each individual required identifying how long each child took, on average, to respond to targets for correct trials. This was operationalized by identifying the window in which each child, on average, tended to move their gaze most toward the target compared to the previous test window. An average PLT was calculated across all correct trials for each of the twelve 250 ms Test phase windows for each participant. The consecutive window pair with the largest positive slope between them was selected as the average “response” to the target for each child (i.e., the pair where PLT for the second window minus PLT for the first window was highest). Once selected, the number for the second test window of the pair was assigned as the speed of the child’s response, representing the time where the participant moved most from off- or non-target looking to looking at the target. TestWin-1 and 2 (0–500 ms) were not assigned speed values as Fernald and Marchman (2012) indicated that looks that fast do not reflect reactions to the prompt. Thus, speed values were whole numbers from 3 to 12; those having lower numbers were faster responders.ⁱⁱ

Individual-level analyses using PLT and speed as predictors

PPVT scores were correlated with PLT (r = .26, p = .022; df = 76). PPVT scores were used in individual-level analyses as a covariate for receptive vocabulary and domain general skill. Participant age was not significantly correlated with scores on any of the measures except the TOSA (r = .40, p < .001; df = 76). However, since the age range of the sample was approximately one year, age was entered as a covariate.

The speed variable used only correct trials, in part to allow Speed and PLT to vary independently, and indeed they were not correlated (r = −.12; n.s.) even after partialling out PPVT scores (pr = −11; n.s.). Correlations between the SFT variables and all of the other tests are reported in Table 2. Scatterplots showing the PLT and speed variables from the SFT with z-score combined spatial scores at age 5 appear in Figure 3. Table 2 shows that PLT at age 3 was related to performance on the age 3 spatial measure (the TOSA), even after accounting for PPVT scores and age. PLT was not related to WJ-III scores at ages 4 or age 5, but PLT was marginally related to WPPSI scores at age 4 and significantly related to CMTT scores at age 5. With respect to speed, our data hint that the relation between speed at age 3 and spatial skills gets stronger over time; speed was not related to spatial ability at age 3 (r = −.06); there were mixed results at age 4 (r = −.22 to −.29); and there were significant correlations with both spatial measures and the z-scored spatial measure at age 5 (r = −.33 to −.41). According to Fisher r-to-z transformations, the correlations between speed and the spatial measure at age 3 (TOSA) and speed and the age 5 z-score combined spatial measure are significantly different (z = −1.98; p = .048). Though the correlations between speed with spatial skill and other variables from age 3 to age 4 and age 4 to age 5 were not significant, there was a consistent pattern: the apparent magnitude of longer-term correlations were higher. Even the correlations of speed with the WJ-III follow this pattern (r_Age4 = −.22; r_Age5 = −.39). As it is unusual for correlations over increasingly large timeframes to appear to increase, this pattern might be explored in future work.

Table 2.

Correlations and Partial Correlations Controlling for PPVT and Age

Age	df†	Measure		Age 3				Age 4			Age 5			Age†††
				Shape Task		Spatial	Vocab	Spatial			Spatial
				Acc	Speed	TOSA	PPVT	Z††	WJ-III	WPPSI	Z††	WJ-III	CMTT
				Zero-Order Pearson Correlations
3	76	Shape Task	PLT	----	−.12	.36**	.26*	.24	.10	.32	.40**	.23	.46**	−.02
			Speed	−.12	----	−.06	−.02	−.29*	−.22	−.29*	−.41**	−.39**	−.33*	−.01
		Spatial	TOSA	.36**	−.06	----	.40**	.58**	.46**	.54**	.68**	.58**	.60**	.40**
		Vocab	PPVT	.26*	−.02	.40**	----	.48**	.41**	.41**	.59**	.46**	.56**	.19
4	61	Spatial	Z††	.24	−.29*	.58**	.48**	----	.86**	.87**	.80**	.67**	.74**	.09
			WJ-III	.10	−.22	.46**	.41**	.86**	----	.48**	.71**	.62**	.63**	.05
			WPPSI	.32*	−.29*	.54**	.41**	.87**	.48**	----	.69**	.55**	.66**	.10
5	48	Spatial	Z††	.40**	−.41**	.68**	.59**	.80**	.71**	.69**	----	.87**	.88**	.08
			WJ-III	.23	−.39**	.58**	.46**	.67**	.62**	.55**	.87**	----	.52**	.12
			CMTT	.46**	−.33*	.60**	.56**	.74**	.63**	.66**	.88**	.52**	----	.02
			Age†††	−.02	−.01	.40**	.19	.09	.05	.10	.08	.12	.02	----
				Partial Correlations Controlling for PPVT and Age at Time of Test
3	74	Shape Task	PLT	----	−.11	.34**	----	.14	−.01	.24	.31*	.13	.39**	----
			Speed	−.11	----	−.06	----	−.32*	−.23	−.31*	−.49**	−.43**	−.38**	----
		Spatial	TOSA	.34**	−.06	----	----	.52**	.40**	.47**	.66**	.51**	.58**	----
4	59	Spatial	Z age 4†	.14	−.32*	.52**	----	----	.82**	.84**	.73**	.57**	.66**	----
			WJ-III	−.01	−.23	.40**	----	.82**	----	.38**	.63**	.53**	.53**	----
			WPPSI	.24	−.31*	.47**	----	.84**	.38**	----	.61**	.44**	.58**	----
5	46	Spatial	Z age 5†	.31*	−.49**	.66**	----	.73**	.63**	.61**	----	.83**	.82**	----
			WJ-III	.13	−.43**	.51**	----	.57**	.53**	.44**	.83**	----	.36*	----
			CMTT	.39**	−.38**	.58**	----	.66**	.53**	.58**	.82**	.36*	----	----

Notes:

^*p < .05;

^**p < .01

^†Degrees of freedom apply pairwise and are limited by the variable with the lowest degrees of freedom (e.g., all zero-order CMTT correlations df = 48)

^††The “Z” variables are summary variables averaging z-scores from the two individual spatial tests listed below them (WJ-III and WPPSI at age 4; WJ-III and CMTT at age 5). The score provides a stronger measure of the construct by collapsing across multiple theoretically-related tests within a time point.

^†††Age = age in months at the time of the age 3 testing session.

Figure 3.

Scatterplots with linear trend lines showing the relation between spatial scores at age 5 and the SFT variables (PLT and Speed).

To understand how PLT and speed are related to spatial ability after accounting for other covariates and earlier spatial skills, regressions were run predicting age 5 spatial skills from the other variables in the study (Table 3). Our approach to presenting these regressions was to start with the simplest model using only our PLT and speed variables, to understand how well they would predict later spatial skills if the SFT was the only measure given. We then systematically added groups of variables to control for and understand their influence. The second model adds individual difference variables that we thought were likely to influence performance broadly and represents a parsimonious and reasonably controlled model for predicting later spatial skills. The third model controlled for age 3 and 4 spatial skills before adding the PLT and speed variables. We did this to see if the PLT and speed variables are just proxy measures of spatial skill. If true, neither variable should be significant in Model 3 even if they are strong predictors in Models 1 and 2.

Table 3.

Results of Hierarchical Multiple Regressions for Predicting Spatial Scores^† at Age 5

	Step	Variable	ΔF††	df	adj. R2	Δ adj. R2	Unstandardized Coefficients		Standardized Coefficients			Partial r
							B	SE	β	t	p
Model 1		Constant					−1.49	1.11		−1.34	.186
	1	PLT	8.91**	1,48	.139	.139	5.13	1.80	.353	2.86	.006	.385
	2	Speed	9.74**	2,47	.263	.124	−0.20	0.07	−.372	−3.01	.004	−.402
Model 2		Constant					−3.35	1.90		−1.77	.084
	1	SES	12.46***	3,46	.412	.412	0.57	0.22	.315	2.61	.012	.366
		PPVT					0.02	0.01	.340	2.77	.008	.385
		Age					0.02	0.04	.060	0.60	.554	.089
	2	PLT	5.03*	4,45	.460	.048	3.04	1.44	.060	2.12	.040	.304
	3	Speed	11.47**	5,44	.562	.102	0.05	0.05	−.328	−3.39	.002	−.412
Model 3		Constant					1.21	1.56		0.78	.442
	1	SES	11.65***	3,43	.410	.410	0.21	0.16	.118	1.38	.176	.215
		PPVT					0.01	0.00	.207	2.40	.021	.359
		Age					−0.04	0.03	−.118	−1.50	.141	−.234
	2	TOSA	26.05***	4,42	.627	.217	0.38	0.10	.352	3.71	.001	.511
	3	Z age 4†	22.44	5,41	.753	.126	0.37	0.09	.363	4.01	.000	.541
	4	PLT	1.73	6,40	.757	.004	1.05	1.03	.072	1.02	.315	.161
	5	Speed	13.33***	7,39	.815	.058	−0.13	0.04	−.252	−3.65	.001	−.505

Notes:

^†The “Z age 4” variable is a summary variable calculated by taking the average z-score from the WJ-III and WPPSI given at age 4.

^††Asterisks in this column indicate the p-value of the change in F for a given step of the regression -

^*p < .05;

^**p < .01,

^***p < .001

When entered into a regression without covariates, PLT and speed account for 26.3% of the variability in spatial skills two years later at age 5 (Model 1). The two variables have similar standardized beta weights in the model (PLT = .353; speed = −.372) and account for similar variability in age 5 spatial skills (adj. R² PLT = .139; speed = .124). As suggested by the low correlation of PLT with speed, order of entry had negligible effects and we present all of the models entering PLT first. Both variables showed important and independent contributions to the prediction of later spatial skills when no control variables were used.

Model 2 entered SES, PPVT scores, and Age in Step 1 to account for individual differences related to parent education, participant vocabulary, and age-related maturation. These variables accounted for significant variability in age 5 spatial scores (Adj. R² = .412), but both PLT and speed remained significant predictors in Model 2 (Δ Adj. R² = .048 and .102, respectively). Model 3 added scores from the TOSA in Step 2 and the z-score combined average of the WJ-III and WPPSI in Step 3, to account for individual differences in spatial skills at ages 3 and 4. The overall model accounted for over 81% of the variability in age 5 spatial skills (Adj. R² = .815). Notably, the inclusion of either the TOSA or the age 4 spatial measures caused PLT to lose prediction potency. This indicates a significant overlap in the amount of variability in age 5 spatial skills explained by earlier spatial skills and PLT. This finding comportss with our hypothesis that identifying named shapes is related to spatial development. However, speed remained a significant predictor in this model, accounting for about 5.8% of the variability in spatial skills assessed two years later. Thus, speed in processing shape names is not only an important predictor of spatial skills but has a unique influence not explained by receptive vocabulary or spatial skills measured with untimed tests, or even the amount of looking to target shapes within the same task.

Discussion

A recent emphasis on teaching early geometry in preschool and kindergarten (Common Core State Standards, 2010; Office of Head Start, 2011) and evidence suggesting the importance of early spatial skills in long-term STEM outcomes (e.g., Wai et al., 2010) prompted this study. Young children’s speed of processing familiar, everyday words (e.g., Hurtado et al., 2008) inspired us to probe the speed with which preschoolers identify named geometric shapes. There are some differences in response to different shapes types but there were no effects of representation type, which we expected especially for non-canonical shapes. It seems likely that children were able to bootstrap their knowledge of canonical shapes to identify them (e.g., the non-canonical triangle still looks more like a triangle than the non-canonical rectangle), whether or not they really understood the defining features of the shapes (Satlow & Newcombe, 1998). Aside from these findings, this study was primarily aimed at exploring whether differences in maternal education influence shape identification and how individual differences in identifying shapes predict later spatial skills.

Does SES Influence Shape Identification?

The present data confirm that even when language is from a specific content area appearing with relatively low frequency in speech (i.e., geometric shape terms; Rudd et al., 2008; Sarama & DiBiase, 2004), higher-SES children have an advantage. They move more quickly to targets than the lower-SES group, rising above chance looking to target in test window 5 rather than test window 6 (approximately 250 ms), indicating that they are processing the language more quickly. They also look more at target shapes than the lower-SES group, on average, in test windows 7 and 8.

A long history of research suggests that SES factors influence the amount and type of language children hear (e.g., Hart & Risley, 1995) and that these experiences influence vocabulary size and processing speed (Weisleder & Fernald, 2013; Hurtado et al., 2008). Hurtado and colleagues (2008) showed that the amount of language low-income parents direct to their children influences their children’s processing speed at 24 months. For children whose parents used more words during a play session, they found an approximately 200 ms advantage in children’s reaction time to familiar nouns. Analogously, we found that participants with more educated mothers, who we know tend to hear more language (Hart & Risley, 2003; Hoff, 2013), respond one 250 ms window faster than peers with less educated mothers. Thus, the speed difference potentially lends additional credence to those earlier findings.

It appears then that lower-SES children are at a disadvantage in processing the names of geometric shapes compared to their higher-SES peers. Assuming these differences remain relatively constant and that shape identification predicts later spatial skills, this may have the unfortunate consequence of impeding STEM learning for lower-SES children.

Do Individual Differences in Shape Processing Predict Future Spatial Skills?

A delay of approximately 250 ms in processing and responding to prompted shape words at age 3 might seem unlikely to have practical, long-term impacts on learning. However, research has documented long-term impacts of similar sized delays in the recognition of everyday words (e.g., Fernald & Marchman, 2012; Fernald, Perfors, & Marchman, 2006; Marchman & Fernald, 2008). Our individual-level analyses suggest that processing speed for shape names relates to the learning of spatial skills over the ensuing two years and helps substantiate the conclusion that speed is consequential over-and-above simply identifying word targets. Speed was not related to concurrent spatial skills at age 3 but was a unique predictor of later spatial skills. Furthermore, speed as a predictor of age 5 spatial skills was affected little by the inclusion of a wide range of controls.

On the other hand, the variance explained by PLT, our measure of attention, was especially influenced by the inclusion of scores from early spatial tests. The impact of entering spatial scores into the model on the predictive power of PLT indicates that there is a substantial degree of overlap between PLT and the spatial variables. Thus, both looking to the target shapes and identifying them quickly appear to be notable independent predictors of later spatial skills. However, though PLT from our shape fixation task has some merit as an early test of spatial skill and does predict later spatial skills, it offers little for prediction of later spatial skills above-and-beyond other available spatial measures. A strong overlap of this sort would be expected if shape identification relies on or helps build spatial skills and, thus, these results align with our suggestion that the SFT has a spatial component. Speed, on the other hand, predicts unique variability not accounted for by a host of other controls, which points to the speed variable being associated with a cause not controlled for in our models.

Many of the domain-general explanations for the link between speed and later spatial skills were controlled for by our covariates (vocabulary knowledge, SES, and Age). Though we cannot rule out that the speed variable simply tapped into general language processing speed (e.g., Fernald, Marchman, & Weisleder, 2013), it is likely that including vocabulary and SES among our predictors controlled for much of that variability. Nonetheless, we are unable to determine from our correlational design whether response speed in the SFT is an index of general speed of processing, language-specific speed of processing, speed of processing shape terms specifically, or perhaps even the result of some other cognitive factor like executive function. Certainly the SFT requires processing of language other than just shape terms. There is a possibility that factors influencing language processing in general could play some role in quickly reacting to the SFT and later spatial tasks. For example, response speed to general nouns is related to later working memory (Marchman & Fernald, 2008) and working memory may be a factor in the tasks used here. However, aside from the controls used, the fact that language and spatial ability are usually not strongly related also makes it unlikely that general language processing skills could be the proximal cause of the observed link between speed and spatial skills. Most standardized tests treat language and spatial domains as separable and research on working memory seems to indicate largely separable systems for processing language and visual-spatial information (Shah & Miyake, 1996), except perhaps with written language which is inherently spatial (Baddeley, 2003).

Though we have argued that it is unlikely that the speed link to later spatial skills is explained by general language speed advantages alone, it seems rather unlikely that the link we have observed is so specific that it only applies to speed in identifying a handful of geometric shapes; the link with speed may generalize in response to other spatial or number words. It is also conceivable that differences in things like how children deploy their attention could result in slower responses and that the observed outcomes in this and other studies are not related to specific or general language processing at all. For example, a child who anticipates the prompt and has their attention focused may be faster to respond than a child whose attention wanders at the start of a trial. More work will be needed to untangle the extent to which the link between speed and later spatial skills is specific to shape terms or language. Nonetheless, this work shows significant links between shape processing, measured either with percent or speed of looking to targets, and later spatial skills.

A long-term relation of individual differences in speed at age 3 and spatial skills at age 5, but an absence of a short-term relation between speed and spatial skills at age 3 may seem surprising. However, this pattern could be expected if fluency in using geometric and spatial terms creates a foundation for future learning; children who process these words faster may use that skill to understand more spatial language and better build their spatial skills over the ensuing two years. For example, if a parent is describing the spatial properties of a shape but the child is processing all language more slowly including shape names, the child may fail to actually think about the spatial properties the parent is highlighting. Over time, this might be expected to slow a child’s mastery of spatial language and skills. Such a mechanism is speculative and requires more study.

Differences in the length of time it takes to process spatial language, as opposed to differences in accuracy, may have important down-stream implications for success in STEM-specific content areas. While children are resolving spatial or geometric language, they are using cognitive resources that might be better deployed for assimilating new knowledge (e.g., Just & Carpenter, 1980). Novel, challenging, and technical information is often encountered in STEM subjects so these deficits may have important long-term implications for STEM success.

Limitations

The preferential looking method, despite its advantages for observing the time course of responses while keeping task requirements low, has some limitations for 3-year-old children. For example, children could fixate the target briefly and then begin exploring the visual scene. In doing so, some children could move off target, despite having responded to the prompt, and lower their group’s PLT. Though this is a concern in any looking time study, it is mitigated by the use of a second prompt during the trial, which redirected children to the target. Further, the effect of this is more likely to have reduced group differences that may have otherwise been observed at the end of the trial than it is to have created any of the group differences noted near the beginning; the observed SES differences appear shortly after the prompt on the upswing of each group’s response.

Track loss also resulted in some children (3 higher-SES; 10 lower-SES) being dropped from the study and these drops do not appear to be entirely random. These participants had raw PPVT scores that were about half of a standard deviation below the analyzed sample (M_{Track Loss} = 59.9, SD = 21.3; M_{Full Sample} = 68.1; SD = 21.1) and tended to be concentrated on both ends of the range of PPVT scores. Of the dropped participants 10 had PPVT standard scores below the analyzed sample average of 109.1 (SD = 19.9). All of the remaining 3 participants had high PPVT scores more than one standard deviation above the population mean (121, 127, and 142). Though dropping these children was necessary, the drops likely impact how representative the sample is of the overall population. Nonetheless, the analyzed sample was still diverse relative to most laboratory-based research.

Conclusions

Unfortunately, this study joins other literature demonstrating that 3-year-old children from lower-SES backgrounds are already behind in language processing (Hart & Risley, 2003) and spatial skills (Levine, Vasilyeva, Lourenco, Newcombe, & Huttenlocher, 2005). We now know that processing speed differences exist in both general vocabulary (Fernald et al., 2013) and geometric terms (this study). However, this paper uniquely links processing speed in a particular domain of language (shape terms) to long-term outcomes in a related, yet quite different domain (spatial skills). As preschool skills in understanding and describing shapes claim a more important place in early education (Common Core State Standards Initiative, 2010; Office of Head Start, 2011), largely due to their short- and long-term implications for STEM success (citation removed; Wai, Lubinski, & Benbow, 2009), this work should be taken as a call for further study of whether these relationships are causal and how best to leverage them if they are.