Stress Analysis-Driven Design of Bilayered Scaffolds for Tissue-Engineered Vascular Grafts

Abstract

Continuing advances in the fabrication of scaffolds for tissue-engineered vascular grafts (TEVGs) are greatly expanding the scope of potential designs. Increasing recognition of the importance of local biomechanical cues for cell-mediated neotissue formation, neovessel growth, and subsequent remodeling is similarly influencing the design process. This study examines directly the potential effects of different combinations of key geometric and material properties of polymeric scaffolds on the initial mechanical state of an implanted graft into which cells are seeded or migrate. Toward this end, we developed a bilayered computational model that accounts for layer-specific thickness and stiffness as well as the potential to be residually stressed during fabrication or to swell during implantation. We found that, for realistic ranges of parameter values, the circumferential stress that would be presented to seeded or infiltrating cells is typically much lower than ideal, often by an order of magnitude. Indeed, accounting for layer-specific intrinsic swelling resulting from hydrophilicity or residual stresses not relieved via annealing revealed potentially large compressive stresses, which could lead to unintended cell phenotypes and associated maladaptive growth or, in extreme cases, graft failure. Metrics of global hemodynamics were also found to be inversely related to markers of a favorable local mechanobiological environment, suggesting a tradeoff in designs that seek mechanical homeostasis at a single scale. These findings highlight the importance of the initial mechanical state in tissue engineering scaffold design and the utility of computational modeling in reducing the experimental search space for future graft development and testing.

1. Introduction

First-in-human reports demonstrate that implantable, biodegradable, polymeric scaffolds can promote neotissue formation and generate living autologous neovessels that have an ability to grow and remodel, thereby establishing tissue-engineered vascular grafts (TEVGs) as the first vascular conduits with growth potential [1]. These grafts have been used to treat congenital heart defects in children and thus have been implanted within the low-pressure caval-pulmonary circulation. Attempts to use similar scaffolds in the higher pressure arterial system have presented a greater challenge, however, with pressure-induced dilatation and/or rupture possible. There is, therefore, a pressing need for improvements in the design of biodegradable scaffolds for use as arterial replacements.

Recent studies using bilayered polymeric designs show promise as a tissue-engineered scaffold for the arterial system [2–4]. The basic design combines a rapidly degrading, highly porous, compliant core with a slower degrading, stiffer, protective sheath. Although such a bilayered design seems reminiscent of the native arterial structure—characterized by a compliant media surrounded by a stiff adventitia—the differential load-bearing of the two polymeric layers is designed to be very different from native. In a native large artery, the normal media bears much of the load under physiologic conditions, whereas the normal adventitia serves mainly as a sheath to protect the medial smooth muscle cells and elastic fibers from damage in cases of severe acute increases in blood pressure [5]. In contrast, the core of current bilayered TEVGs is meant to serve as a permissive environment for cellular infiltration while the outer sheath limits pressure-induced over-distension or rupture at physiological pressures. Such a design can stress-shield the core, however, where we note that stress-shielding of the media in native arteries can lead to atrophic remodeling, as in the Glagov phenomena [6]. We should thus consider carefully the potential effects of stress-shielding in developing neovessels.

In this paper, we present a parametric study of possible bilayered scaffold designs based on a nonlinear stress analysis. Mechanical stress is a fundamental design parameter in TEVGs for two primary reasons: first, vessels can fail catastrophically if stress exceeds strength at any time during the natural history of neovessel development and, second, stress is a strong stimulus for mechanobiological control of cellular function and thus extracellular matrix integrity [7]. We show that different ratios of layer thickness and material stiffness can affect the predicted stress distributions in nonintuitive ways, particularly when one includes swelling of the core or fabrication-induced residual stresses in the sheath.

In particular, hydrophilic polymers typically swell upon implantation, thus leading to a change in graft geometry and load carrying or even buckling or delamination of the scaffold in extreme cases [8]. Such swelling can also lead to circumferential compression [9,10], which may adversely affect mechanobiological outcomes especially if nascent cells are undergoing phenotypic modulation. Additionally, the fabrication process can impart residual stresses in constructs as solubilized polymers harden or fibers are woven together under tension [11]. These effects can modify the stresses experienced by both layers of the scaffold depending on the layer in which they exist and the bulk material properties. For this reason, we simulated effects of swelling of the core and residually stressing the sheath on overall stress distributions in model grafts under simulated physiologic loading.

While local mechanical stress is of paramount mechanobiological importance to neovessel formation, the implanted scaffold also interacts with native vascular and perivascular tissue, notably the adjacent vessels, flowing blood, and surrounding tissues. The material and geometry of the graft determine its structural compliance, which in turn can directly affect the surrounding tissue. Compliance mismatch has been shown to adversely affect patency rates by changing vessel hemodynamics and remodeling of the adjacent vessels [12]. Moreover, the geometry of the graft can modulate the thrombotic response of the blood by affecting the blood flow field [13]. Thus, we also consider effects of design parameters on graft compliance and geometry to better characterize the broader mechanical effects. By comparing parametric effects on these properties with effects on local metrics (e.g., transmural circumferential stress), we are better able to understand potential tradeoffs for matching homeostatic values locally or globally.

2. Methods

Analysis of mechanical stress within a finitely deformed bilayered cylindrical vessel is a well-posed equilibrium problem [14], thus we simply specialize this general solution for the class of tissue-engineered constructs of interest. In particular, we describe the elastomeric core as a Hart-Smith material that can swell when hydrated, as seen for previously used core materials [8,15,16]. Swelling of an otherwise incompressible material can be modeled by imposing a constraint on the volume change once swollen [9]. Conversely, we describe the stiffer sheath as a neo-Hookean material that can be residually stressed during fabrication, as noted previously [11,17]. We model the residual stress using the concept of an opening-angle associated deformation [18]. In all the cases, we satisfy overall radial and axial equilibrium under the assumption of an axisymmetric geometry and loading, namely,

$$P={\int }_{r_{\mathrm{i}}}^{r_{\mathrm{I}}}\frac{(t_{\theta \theta }-t_{\mathit{r}\mathit{r}})}{r}dr+{\int }_{r_{\mathrm{I}}}^{r_{\mathrm{o}}}\frac{(t_{\theta \theta }-t_{\mathit{r}\mathit{r}})}{r}dr$$ (1)

where $P$ is the distending pressure, and

$$L=\pi {\int }_{r_{\mathrm{i}}}^{r_{\mathrm{I}}}(2t_{\mathit{z}\mathit{z}}-t_{\mathit{r}\mathit{r}}-t_{\theta \theta })rdr+{\int }_{r_{\mathrm{I}}}^{r_{\mathrm{o}}}(2t_{\mathit{z}\mathit{z}}-t_{\mathit{r}\mathit{r}}-t_{\theta \theta })rdr+P\pi r_{\mathrm{i}}^2$$ (2)

where $L$ is the applied axial load, with the core delimited by the inner and interfacial radii $r\in [r_{\mathrm{i}},r_{\mathrm{I}}]$ and the sheath by the interfacial and outer radii $r\in (r_{\mathrm{I}},r_{\mathrm{o}}]$. The general constitutive relation for Cauchy stress is, as usual

$$\mathbf{t}=-p\mathbf{I}+\frac{2}{\text{det}\mathbf{F}}\mathbf{F}\frac{\partial W}{\partial \mathbf{C}}{\mathbf{F}}^{\mathrm{T}}$$ (3)

where $\mathbf{C}={\mathbf{F}}^{\mathrm{T}}\mathbf{F}$ is the right Cauchy-Green tensor and $\mathbf{F}$ is the deformation gradient tensor; $p(r)$ is a scalar Lagrange multiplier that enforces incompressibility during transient motions, which can be calculated using the radial equilibrium equation, by integrating from $r_{\mathrm{i}}$ to any value $r$ within the wall, and boundary conditions. Once swollen, nearly incompressible behavior is expected given the bulk stiffness of the polymers.

Specifically, let the layer-specific stored energy function $W$ be given by

$$\begin{array}{c}{W}_{\mathrm{c}}=\frac{{\mu }_{\mathrm{c}}}{2}{\int }^{\hspace{0.17em}}\hspace{0.17em}\text{exp}\left(c_2{(I_1-3)}^2\right)d{I}_1{W}_{\mathrm{s}}=\frac{{\mu }_{\mathrm{s}}}{2}(I_1-3)\end{array}$$ (4)

where $W_{\mathrm{c}}$ is a Hart-Smith model for the core, with ${\mu }_{\mathrm{c}}$ as the shear modulus and $c_2$ modulating the material nonlinearity, and $I_1=tr\mathit{C}$ is the first invariant of the right Cauchy-Green tensor. $W_{\mathrm{s}}$ is the neo-Hookean model for the sheath, with ${\mu }_{\mathrm{s}}$ as the shear modulus. For an isotropic material that undergoes swelling, the stored energy function may be modified as [9]

$$W^{*}=m({\upsilon }^{*})W({\upsilon }^{*-1/3}\mathbf{F})$$ (5)

where ${\upsilon }^{*}=\text{det}\mathbf{F}$ is the volume change of the material due to swelling. If the material behavior further depends on $I_1$ alone, we have

$$W^{*}=m({\upsilon }^{*})W({\upsilon }^{*-2/3}{I}_1)$$ (6)

A convenient form for $m({\upsilon }^{*})$ is ${\upsilon }^{*q}$ with $q\in [0,1]$. Such an assumption (with q = 2/3) recovers Treloar's postulated form for a swelling neo-Hookean material based on statistical arguments and fits well with experimental data [19]. The Hart-Smith material can thus be modified to include swelling as

$$W_{\mathrm{c}}^{*}=\frac{{\mu }_{\mathrm{c}}{\upsilon }^{*2/3}}{2}\int \hspace{0.17em}\text{exp}\left(c_2{({\upsilon }^{*-2/3}{I}_1-3)}^2\right)d{I}_1$$ (7)

The deformation gradient $\mathbf{F}$ is visualized in Fig. 1 for each of the assumed motions, which remain continuous from layer to layer (i.e., no delamination considered) during the sequence of motions: opening angle, pressurization, and swelling related.

Fig. 1.

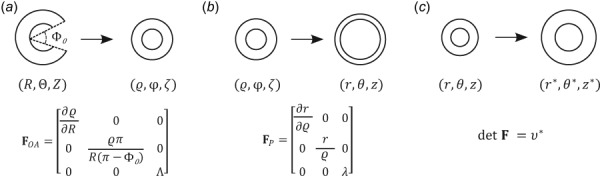
(a) Deformation to induce residual stresses, where ${\Phi }_{\mathrm{o}}$ is the prescribed opening angle and $\Lambda$ an associated axial stretch; $(R,\Theta ,Z)$ are coordinates in the stress-free configuration and $(\varrho ,\phi ,\zeta )$ are coordinates in the traction-free but residually stressed configuration. (b) Pressure-induced deformation where $\lambda$ is a prescribed axial stretch; $(r,\theta ,z)$ are coordinates in the residually stressed and loaded configuration. (c) Volumetric swelling constraint where ${\upsilon }^{*}$ is a prescribed swelling ratio; $(r^{*},{\theta }^{*},z^{*})$ are coordinates in the swollen and loaded configuration.

Specifically, the deformation of the core was calculated from the prescribed swelling-induced volumetric deformation and a pressure-driven deformation according to

$${\mathbf{F}}_{\mathrm{c}}=\left[\begin{array}{ccc}\frac{{\upsilon }^{*}R}{\lambda r^{*}}& 0& 0\\ 0& \frac{r^{*}}{R}& 0\\ 0& 0& \lambda \end{array}\right]$$ (8)

This swelling in the core was assumed to be homogeneous with a negligible “opening-angle induced deformation,” thus coordinates in the stress-free configuration match those in the unloaded configuration: $R=\varrho$, $\Theta =\phi$, and $\mathrm{Z}=\zeta$. Radial locations in the undeformed configuration are mapped to the deformed configuration via

$$r^{*}=\sqrt{\frac{{\upsilon }^{*}}{\lambda }\left(R^2-R_{\mathrm{i}}^2\right)+{r_{\mathrm{i}}^{*}}^2}\hspace{1em}\forall r\in [r_{\mathrm{i}}^{*},r_{\mathrm{I}}^{*}]$$ (9)

The deformation for the sheath was calculated using the incompressibility constraint ($\text{det}{\mathbf{F}}_{\mathrm{s}}=1)$ and a multiplicative combination of an opening angle (${\Phi }_{\mathrm{o}}$) induced and pressure-induced deformation, namely,

$${\mathbf{F}}_{\mathrm{s}}=\left[\begin{array}{ccc}\frac{(\pi -{\Phi }_{\mathrm{o}})R}{\pi r\Lambda \lambda }& 0& 0\\ 0& \frac{\pi r}{(\pi -{\Phi }_{\mathrm{o}})R}& 0\\ 0& 0& \Lambda \lambda \end{array}\right]$$ (10)

The fabrication-induced opening angle in the sheath was assumed to be homogeneous; it was also assumed that the sheath did not swell. Axial stretch $\Lambda$, caused by the opening-angle related deformation, was calculated from the axial equilibrium equation in the traction-free configuration. Radial locations in the sheath were found via integration to give

$$r=\sqrt{\frac{(\pi -{\Phi }_{\mathrm{o}})}{\pi \Lambda \lambda }\left(R^2-R_{\mathrm{I}}^2\right)+{r_{\mathrm{I}}^{*}}^2} \forall r\in (r_{\mathrm{I}}^{*},r_{\mathrm{o}}]$$ (11)

The equations of interest were nondimensionalized using the Buckingham-Pi method. Scales for length, mass, and time were taken as

$$L_{\mathrm{s}}=R_{\mathrm{D}},M_{\mathrm{s}}=\rho R_{\mathrm{D}}^3,M_{\mathrm{s}}=\rho R_{\mathrm{D}}^3$$ (12)

where $R_{\mathrm{D}}$ is the inner radius of the native (host) vessel at diastole (D), $\rho$ is the mass density of native tissue, and $P_{\mathrm{D}}$ is the native blood pressure at diastole. Table 1 lists values for these normalizing scales.

Table 1.

Listed relevant scales (for nondimensionalization), parameters (both fixed and varied), and metrics along with their prescribed values or simulated ranges. Normalized values are used in the computations and thus figures; actual (dimensional) values are listed for comparison.

Scales	Name	Normalized	Actual baseline
$R_{\mathrm{D}}$	Native inner diastolic radius	1	320 μm
$P_{\mathrm{D}}$	Diastolic pressure	1	10 kPa

Fixed	Name	Normalized	Actual baseline
$R_{\mathrm{i}}$	Unloaded inner radius	1	320 μm
$\Lambda$	Axial stretch from opening angle	<1.01	<1.01
$\lambda$	Axial stretch from pressurization	1	1
${\mu }_{\mathrm{s}}$	Sheath shear modulus	100	1 MPa
$c_2$	Core nonlinearity parameter	0.02	0.02
$P$	Distending pressure	1	10 kPa
$q$	Swelling parameter	2/3	2/3

Varied	Name	Range	Actual range
$H_{\mathrm{c}}$	Unloaded core thickness	[0.2, 1.0]	[64, 320] μm
$H_{\mathrm{s}}$	Unloaded sheath thickness	[0.025, 0.4]	[8, 128] μm
${\mu }_{\mathrm{c}}$	Core shear modulus	[1, 50]	[10, 500] kPa
${\upsilon }^{*}$	Core swelling ratio	[1.0, 1.4]	[1.0, 1.4]
${\Phi }_{\mathrm{o}}$	Sheath opening angle	—	[0, 40] deg

Metrics	Name	Normalized native	Actual native
$t_{\mathrm{c}}^{\text{avg}}$	Average circumferential core stress	20	200 kPa
$t_{\theta \theta }^{\mathrm{c}}$	Core stress distribution	—	See Ref. [5]
$t_{\theta \theta }^{\mathrm{s}}$	Sheath stress distribution	—	See Ref. [5]
$\Delta r_{\mathrm{i}}^{*}/\Delta P$	Radial compliance	0.5	3 μm/mm Hg
$r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$	Diastolic internal radius	1	320 μm
$h/H$	Thickness ratio	2.5	2.5

Parametric studies examined five parameters in the equilibrium solution: shear modulus of the core ${\mu }_{\mathrm{c}}$, undeformed thickness of the core and sheath $H_{\mathrm{c}}=R_{\mathrm{I}}-R_{\mathrm{i}}$ and $H_{\mathrm{s}}=R_{\mathrm{o}}-R_{\mathrm{I}}$, respectively, swelling ratio for the core ${\upsilon }^{*}$, and opening angle for the sheath ${\Phi }_{\mathrm{o}}$. Values for ${\mu }_{\mathrm{c}}$, ${\upsilon }^{*}$, and ${\Phi }_{\mathrm{o}}$ encompassed normal ranges for polymers and tissues, as reported in the literature, and allowed the examination of potentially coupled nonlinear behaviors. Ranges for thickness for each layer reflected those used in past bilayered graft experiments in mice [4]. The shear modulus of the sheath ${\mu }_{\mathrm{s}}$ was held at a high constant value to simulate the stiffness required to resist arterial pressure and limit strains, as in prior designs. Due to previous experimental results in rubberlike materials, $q$ was set to a single value (=2/3). Because strains in the core were limited by the stiffness of the sheath, a fixed value for the core nonlinearity parameter $c_2$ was prescribed for all the simulations based on prior bilayer scaffold data. Similarly, the high stiffness of the sheath typically leads to minimal axial stretch of the graft upon implantation [20]. Hence, axial stretch was assumed to be unity for all the simulations, and effects of parametric variation on axial force are not shown. Table 1 also lists the range of values for each simulated parameter. Finally, simulations included variations in both ${\upsilon }^{*}$ and ${\Phi }_{\mathrm{o}}$ to illustrate their combined effects.

To examine effects of these parameters on model outputs of clinical interest, six key metrics were selected as representative of graft performance. At the functional biomechanical scale, we calculated the average transmural stress in the core, $t_{\mathrm{c}}^{\text{avg}}$, the pointwise stress in the core, $t_{\theta \theta }^{\mathrm{c}}$, and the pointwise stress in the sheath, $t_{\theta \theta }^{\mathrm{s}}$. On the gross hemodynamics scale, we considered the diastolic luminal radius, $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$, and the radial compliance of the graft from diastole to systole, $\Delta r_{\mathrm{i}}^{*}/\Delta P$. Also, to account for structural effects of core swelling and sheath residual stresses, the ratio of overall deformed to undeformed thickness, $h/H$, was calculated for these motions. Native values for these metrics are included or referenced in Table 1. Figure 2 schematically illustrates the input parameters and calculated metrics.

Fig. 2.

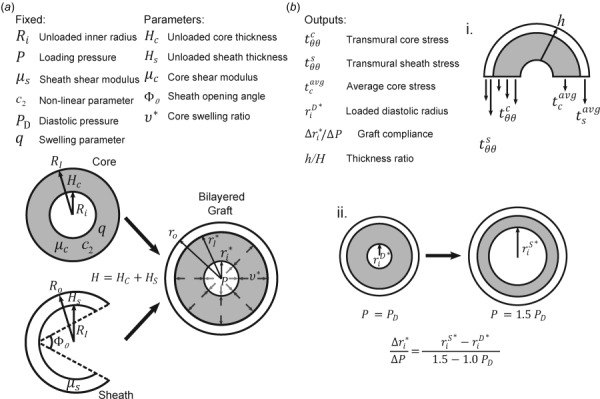
(a) List of fixed and varied parameters and their corresponding physical representations on the scaffold. (b) List of model outputs and their representations: (i) illustrative stresses that are calculated based in part on deformations in Fig. 1 and (ii) radial compliance and the method of calculation.

3. Results

3.1. Effects of Core Shear Modulus.

Generally, for a single layered neo-Hookean cylinder, a simple stress analysis reveals that increasing the stiffness of the material results in less distension at a fixed value of pressure and axial stretch and, thus, lower wall stress. Intuition may similarly suggest that increasing the shear modulus of the core ${\mu }_{\mathrm{c}}$ in a bilayered cylinder would lead to a lower mean stress within the core, but one must consider relative effects of stiffness and thickness in the core and sheath. Indeed, given a high ${\mu }_{\mathrm{s}}$ (fixed at a normalized value of 100), increases in ${\mu }_{\mathrm{c}}$ from a normalized value of 1–50 increase the share of the load borne by the core and, therefore, increase $t_{\mathrm{c}}^{\text{avg}}$ (Fig. 3(a)). This behavior holds over a wide range of relative thicknesses and moduli, only reversing for very thin sheaths ($H_{\mathrm{s}}/H_{\mathrm{c}}<0.025$ ; not shown) and values of ${\mu }_{\mathrm{c}}$ approaching those of the sheath (${\mu }_{\mathrm{c}}/{\mu }_{\mathrm{s}}>0.95$ ; not shown). Although the pressurized graft remains stretched circumferentially for all the values of modulus and thickness considered, the average circumferential stresses in the core can become negative when the relative structural stiffness of the sheath is significantly higher than that of the core. These negative values result from what is essentially a confined compression of an incompressible core since axial length was assumed to remain constant while the stiff sheath distended minimally.

Fig. 3.

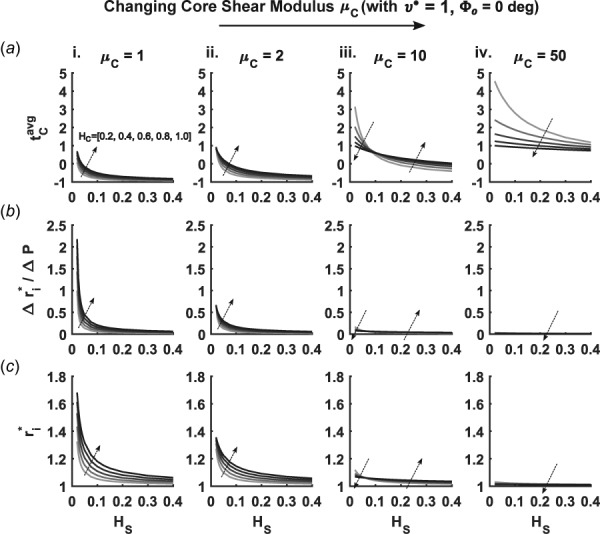
Combinatorial parametric study of the effects of three scaffold parameters—normalized core shear modulus ${\mu }_{\mathrm{c}}$ (subpanels i–iv), core thickness $H_{\mathrm{c}}$ (families of curves in each subpanel, with larger values denoted by darker curves and the local arrows), and varying sheath thickness $H_{\mathrm{s}}$ (abscissa for each subpanel)—on three important characteristics of scaffold behavior: (a) average core stress $t_{\mathrm{c}}^{\text{avg}}$, (b) radial compliance $\Delta r_{\mathrm{i}}^{*}/\Delta P$, and (c) diastolic radius $r_{\mathrm{i}}^{*}$. Note the absence of core swelling and sheath residual stress.

Increases in sheath thickness $H_{\mathrm{s}}$ decrease $t_{\mathrm{c}}^{\text{avg}}$, as would be expected when increasing the overall structural stiffness of the graft. Therefore, increases in core thickness $H_{\mathrm{c}}$, which would typically be thought to increase the structural stiffness of the graft, could lower the stress in both layers. Yet, the effect of $H_{\mathrm{c}}$ depends on both ${\mu }_{\mathrm{c}}$ and $H_{\mathrm{s}}$, whereby increases in $H_{\mathrm{c}}$ with low ${\mu }_{\mathrm{c}}$ actually increase $t_{\mathrm{c}}^{\text{avg}}$. This finding was supported further by the increasing value of diastolic radius $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ experienced with increasing $H_{\mathrm{c}}$ (Fig. 3(c)—i and ii). The opposite effect was seen for the highest value of ${\mu }_{\mathrm{c}}$, such that an increase in $H_{\mathrm{c}}$ decreases $t_{\mathrm{c}}^{\text{avg}}$ at any $H_{\mathrm{s}}$. At intermediate values of ${\mu }_{\mathrm{c}}$, $t_{\mathrm{c}}^{\text{avg}}$ increases and decreases depending on the value of $H_{\mathrm{s}}$, which created transition points in Fig. 3(a)—ii and iii. While these transitions were also seen in graft compliance $\Delta r_{\mathrm{i}}^{*}/\Delta P$ and diastolic radius $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ (Figs. 3(b) and 3(c)—iii), the major effects of increasing ${\mu }_{\mathrm{c}}$ on these metrics were a marked decrease in magnitude and attenuation of thickness dependence.

3.2. Effects of Core Swelling.

Previous work on swelling in cylindrical models focused on single layered constructs [9,10]. For a swelling core and nonswelling stiff sheath, simulations revealed lower values of $t_{\mathrm{c}}^{\text{avg}}$ with increases in swelling (Fig. 4(a)). Furthermore, the compressive stresses in the core were amplified by increases in $H_{\mathrm{s}}$. Depending on the degree of amplification, changes in $H_{\mathrm{c}}$ raised or lowered the value of $t_{\mathrm{c}}^{\text{avg}}$. At low values of ${\upsilon }^{*}$, increasing $H_{\mathrm{c}}$ led to increased values of $t_{\mathrm{c}}^{\text{avg}}$ if $H_{\mathrm{s}}$ was low enough to allow the sheath to dilate as the core swelled. With higher values of ${\upsilon }^{*}$, increasing $H_{\mathrm{c}}$ actually decreased $t_{\mathrm{c}}^{\text{avg}}$ for a wide range of $H_{\mathrm{s}}$. These transitions seen with ${\upsilon }^{*}$ were similar to those identified with changes in core shear modulus ${\mu }_{\mathrm{c}}$.

Fig. 4.

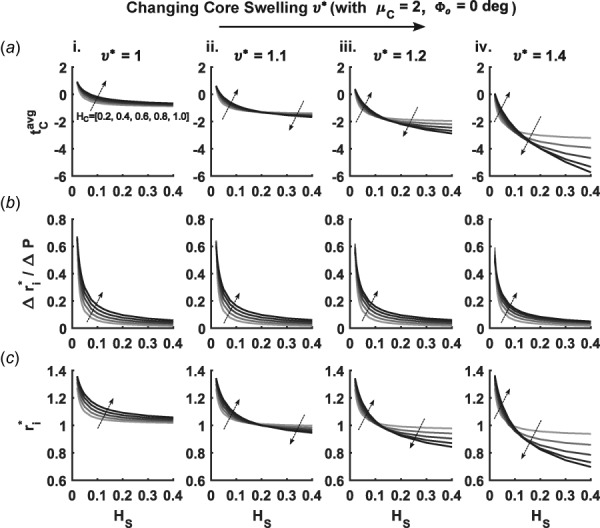
Similar to Fig. 3 except for different core swelling ratios ${\upsilon }^{*}$ (i)–(iv) for a fixed core shear modulus. Each subpanel again varies core thickness $H_{\mathrm{c}}$ (represented by progressively darker shading on the curves and local arrows) and sheath thickness $H_{\mathrm{s}}$ (abscissa) and shows (a) average core stress $t_{\mathrm{c}}^{\text{avg}}$, (b) radial compliance $\Delta r_{\mathrm{i}}^{*}/\Delta P$, and (c) diastolic radius $r_{\mathrm{i}}^{*}$. Note the absence of residual stress in the sheath.

The radial compliance of the graft decreased slightly with swelling of the core (Fig. 4(b)). This suggests that distension upon pressurization is reduced by increasing the hydration of the core. Swelling of the core in the presence of a stiff or thick sheath led to a decrease in $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ (Fig. 4(c)), that is, the swelling was inward, which in a clinical setting could be interpreted as stenosis. The effects of both thickness parameters on diastolic radius were qualitatively similar to effects on average core stress. Another important geometric effect arising with swelling was a progressive increase in thickness ratio $h/H$ with increasing ${\upsilon }^{*}$ (Figs. 5(a) and 5(b)). Despite this intuitive thickening, changes in $H_{\mathrm{s}}$ at high fixed values of ${\upsilon }^{*}$ actually decreased $h/H$ in sufficiently thin cores (Fig. 5(b)—ii and iii). Such behavior can be ascribed to a balance between circumferential compression and thickening, where less stress is induced in the graft by distending and thinning rather than protruding further into the lumen.

Fig. 5.

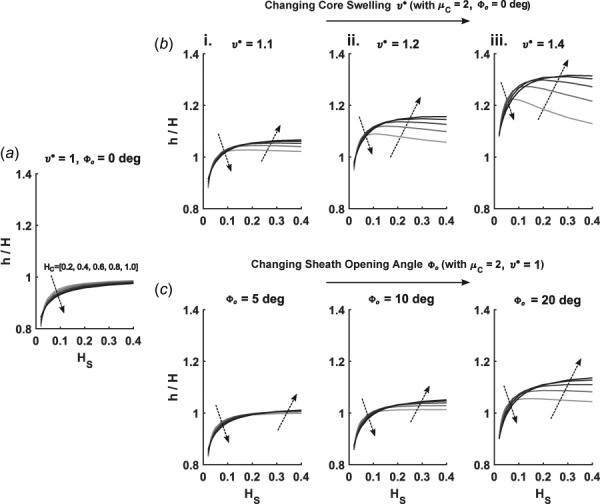
Changes in thickness ratio $h/H$ (deformed/undeformed) for various values of core swelling ${\upsilon }^{*}$ and sheath residual stress (prescribed by opening angles ${\Phi }_{\mathrm{o}}$) from (i)–(iii). Each subpanel shows changes as a function of increasing core thickness $H_{\mathrm{c}}$ (represented by darker shading on the plotted curves and local arrows) and varying sheath thickness $H_{\mathrm{s}}$ (along the abscissa) for (a) a control case with no swelling or residual stress, (b) varying core swelling (${\upsilon }^{*}$), and (c) varying sheath residual stress (opening angles ${\Phi }_{\mathrm{o}}$).

3.3. Effects of Sheath Residual Stress.

Similar to results in Sec. 3.2, increasing ${\Phi }_{\mathrm{o}}$ (i.e., sheath residual stress) led to dramatic decreases in $t_{\mathrm{c}}^{\text{avg}}$, particularly with high values of $H_{\mathrm{s}}$ (Fig. 6(a)). While residual stress in the sheath produced similar effects on $t_{\mathrm{c}}^{\text{avg}}$ as did swelling in the core, a few key differences emerged. Radial compliance decreased, relative to values for both the swelling and the control cases, with increasing ${\Phi }_{\mathrm{o}}$ (Fig. 6(b)). Furthermore, at low values of $H_{\mathrm{s}}$, Fig. 6(c) shows that $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ decreased with increasing values of opening angle, whereas $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ increased for this range of $H_{\mathrm{s}}$ for increasing ${\upsilon }^{*}$. Opening angles also had less of an effect on the thickening of the scaffold when compared to swelling of the core, as seen by the lower magnitude of the thickness ratio for increasing opening angles (Fig. 5(c)). The pronounced decreases in $h/H$ seen with high swelling ratios and thin cores were also absent from opening-angle simulations. These effects can likely be attributed to the volume conserving nature of the assumed opening-angle induced deformation, while swelling fundamentally assumes an increase in volume.

Fig. 6.

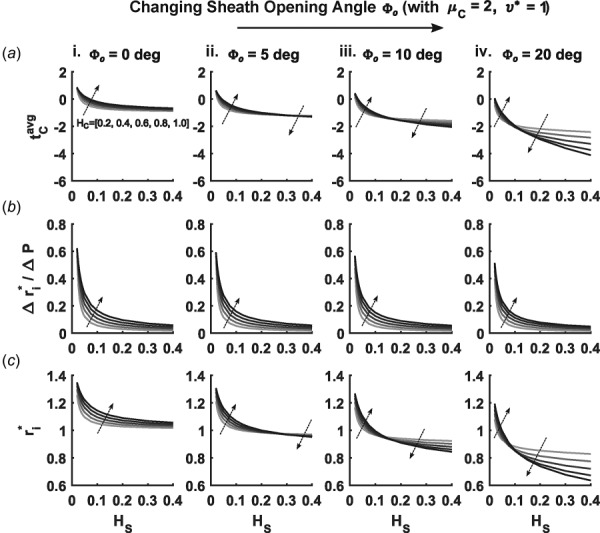
Similar to Figs. 3 and 4 except for different sheath opening angles ${\Phi }_{\mathrm{o}}$ (i)–(iv) for a fixed core shear modulus. Each subpanel again varies core thickness $H_{\mathrm{c}}$ (represented by progressively darker shading on the curves and local arrows) and sheath thickness $H_{\mathrm{s}}$ (abscissa) and shows (a) average core stress $t_{\mathrm{c}}^{\text{avg}}$, (b) radial compliance $\Delta r_{\mathrm{i}}^{*}/\Delta P$, and (c) diastolic radius $r_{\mathrm{i}}^{*}$. Note the absences of swelling of the core.

3.4. Coupled Effects of Core Swelling and Sheath Residual Stress.

Together, core swelling and sheath residual stresses synergistically reduce $t_{\mathrm{c}}^{\text{avg}}$ to a greater degree than either effect individually. Decreases in $\Delta r_{\mathrm{i}}^{*}/\Delta P$ were seen at low values of $H_{\mathrm{s}}$ due to the effects of ${\Phi }_{\mathrm{o}}$, but little change was evident in the higher range of sheath thickness. At low values of $H_{\mathrm{s}}$, the reduction in diastolic radius $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ due to increasing ${\Phi }_{\mathrm{o}}$ was averaged with the increase of $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ seen with increasing ${\upsilon }^{*}$ such that the diastolic radius changed minimally when both motions were included. For higher sheath thicknesses, $r_{\mathrm{i}}^{{\mathrm{D}}^{*}}$ behaved similarly to $t_{\mathrm{c}}^{\text{avg}}$ and was lower than for either motion alone.

3.5. Pointwise Stress Comparisons.

In all the cases considered thus far, it is immediately apparent that values of sheath stress $t_{\theta \theta }^{\mathrm{s}}$ were much higher than values of core stress $t_{\theta \theta }^{\mathrm{c}}$ (Fig. 7). These results stem from the relatively high value of sheath modulus (1 MPa) and confirm that stress-shielding is largely a function of material property imbalance, though relative values of thickness of the layers also plays a role. Increases in ${\mu }_{\mathrm{c}}$ raise $t_{\theta \theta }^{\mathrm{c}}$ while decreasing $t_{\theta \theta }^{\mathrm{s}}$. Increases in $H_{\mathrm{s}}$ reduce $t_{\theta \theta }$ for both the core and the sheath. Yet, an increase in $H_{\mathrm{c}}$ decreases $t_{\theta \theta }^{\mathrm{c}}$ slightly while having a differential effect on $t_{\theta \theta }^{\mathrm{s}}$ depending on the value of ${\mu }_{\mathrm{c}}$. With low ${\mu }_{\mathrm{c}}$, an increase in $H_{\mathrm{c}}$ increases $t_{\theta \theta }^{\mathrm{s}}$ (Fig. 7(a)—i and iii). This trend holds for an increase in $H_{\mathrm{c}}$ at a higher value of $H_{\mathrm{s}}$ (Fig. 7(a)—iii and iv). As typically calculated for nonresidually stressed cylinders experiencing a pressure load, stresses were slightly higher at the innermost radial location for each layer and decreased with increasing radius.

Fig. 7.

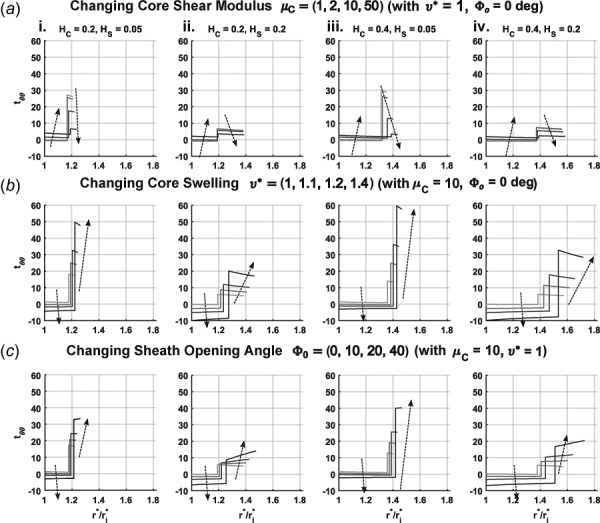
Transmural values of circumferential stress for the core and the sheath, $t_{\theta \theta }^{\mathrm{c}}$ and $t_{\theta \theta }^{\mathrm{s}}$, respectively, as a function of normalized radial position $r^{*}/r_{\mathrm{i}}^{*}$ ; $t_{\theta \theta }^{\mathrm{c}}$ is represented by the leftmost portion of each curve while the section of the curve after the discontinuity represents $t_{\theta \theta }^{\mathrm{s}}$. Subpanels (i)–(iv) show various combinations of core thickness $H_{\mathrm{c}}$ and sheath thickness $H_{\mathrm{s}}$. Each panel shows a different parameter increasing using darkening curves: (a) normalized core shear modulus ${\mu }_{\mathrm{c}}$ from 1 to 2, 5, and 10, (b) core swelling ratio ${\upsilon }^{*}$ from 1 to 1.1, 1.2, and 1.4, (c) sheath opening angle ${\Phi }_{\mathrm{o}}$ from 0 to 10 deg, 20 deg, and 40 deg. Note that ${\mu }_{\mathrm{c}}=10$ (normalized) was used for (b) and (c) to better visualize the effects of swelling and opening angle.

With the addition of core swelling, increasing values of ${\upsilon }^{*}$ lower $t_{\theta \theta }^{\mathrm{c}}$ and raise $t_{\theta \theta }^{\mathrm{s}}$ (Fig. 7(b)). The increasingly negative values of $t_{\theta \theta }^{\mathrm{c}}$ highlighted a change in stress distribution when circumferential stretch becomes compressive. Swelling causes circumferential stretch to fall below 1, such that $t_{\theta \theta }^{\mathrm{c}}$ values at the luminal radial location become the most negative and $t_{\theta \theta }^{\mathrm{c}}$ increases toward the sheath. This effect does not change the distribution of stress in the sheath, which follows the trend from the nonswelling cases. Increasing $H_{\mathrm{s}}$ lowered $t_{\theta \theta }^{\mathrm{c}}$ and $t_{\theta \theta }^{\mathrm{s}}$ in all the swelling cases. Increasing $H_{\mathrm{c}}$ had differential effects on $t_{\theta \theta }^{\mathrm{c}}$ as predicted by average stress comparisons in Fig. 4, though $t_{\theta \theta }^{\mathrm{s}}$ was increased at each simulated ${\upsilon }^{*}$ value regardless of core thickness.

Changes in residual stress in the sheath resulted in similar effects as those for core swelling, that is, increases in ${\Phi }_{\mathrm{o}}$ generally reduce $t_{\theta \theta }^{\mathrm{c}}$ and raise $t_{\theta \theta }^{\mathrm{s}}$ (Fig. 7(c)). Also, changes in thickness led to similar trends in both cases. A major difference between the two motions was the change in radial dependence of $t_{\theta \theta }^{\mathrm{s}}$ with increasing ${\Phi }_{\mathrm{o}}$ and the thickness dependence of this change. As shown in Fig. 7(c)—i, $t_{\theta \theta }^{\mathrm{s}}$ tended to be highest at the layer interface in the absence of sheath residual stress, but increasing ${\Phi }_{\mathrm{o}}$ shifted the distribution such that the highest value of $t_{\theta \theta }^{\mathrm{s}}$ was at the outer surface. For a thicker sheath, the radial stress distributions for each corresponding ${\Phi }_{\mathrm{o}}$ had more positive slopes in comparison to the thinner sheath cases (Fig. 7(c)—ii). Thickening of the core had the opposite effect, where the slope of the stress distribution decreased with increasing $H_c$.

4. Discussion

A basic tenet of functional tissue engineering has been that one should design scaffolds so as to mimic the native tissue structure and material properties. For arteries, this implies that one should design multilayered constructs to mimic the native biomechanical properties of the medial and adventitial layers while ensuring a nonthrombogenic inner surface [21]. In this way, replacement of large (elastic) arteries should attempt to create vessels having a stress-bearing, energy-storing core (i.e., medialike structure) that is protected from acute pressure-induced over-distension by an initially less-loaded but nonlinearly stiffening, strong outer sheath (i.e., adventitialike structure). The primary energy-storing constituent within a large artery is the elastic fiber, consisting primarily of elastin (90%) and elastin-associated glycoproteins (10%) that are organized in a repeating lamellar fashion. Functional elastin is produced primarily during the perinatal period, however, its production and organization in tissue engineering remain a significant challenge [22]. The protective adventitia consists primarily of undulated type I collagen, oriented in multiple directions to endow the wall with necessary multiaxial strength while allowing normal distensibility.

The design of a tissue-engineered polymeric construct for implantation has necessarily been very different, however. The primary desire is to create a rapidly degrading porous environment that allows cells to infiltrate and synthesize native matrix as the scaffold degrades. Ideally, such synthesis and degradation should be balanced to enable the material and/or structural stiffness of the TEVG to continually mimic values of the distal and proximal host so as to not adversely disturb the (local) mechanobiology or the (global) pressure pulse wave [23–25]. Toward this end, the core material is often designed to serve as the permissive porous environment while the sheath is designed to ensure structural integrity until the neotissue has formed and is capable of bearing the in vivo loads. Issues of swelling and residual stress arise from the choice of materials and fabrication methods rather than a desire to mimic biological phenomenon. Yet, the presence of residual stresses in an implanted scaffold has been proposed to offer benefits (though without detailed mechanical analysis), such as smooth muscle cell alignment in the circumferential direction and additional strength [26,27]. Given the many different design parameters—materials, porosities, symmetries, geometry, and fabrication methods—and possible nonlinear couplings, it is difficult to intuit potentially beneficial effects.

In this paper, we showed that even if a compliant core material (e.g., poly(glycerol sebacate)) is modeled by an elastomeric Hart-Smith strain energy function, its ability to distend and act as a “media” is severely limited by the stiffness of the sheath, which must currently be nonelastomeric (e.g., poly(caprolactone)) to bear the majority of the magnitude of blood pressure loading without dilatation. Preliminary simulations showed minimal sensitivity to the degree of nonlinearity in the core, as represented by the parameter $c_2$. The lack of load bearing by the core contributes greatly to the low average stress values therein seen over the range of simulations. In comparison to native medial stresses, on the order of 100–200 kPa, core stresses were frequently an order of magnitude lower. Since the core is the primary site of infiltrating cells in most experimentally tested grafts, these cells may exhibit attenuated mechanostimulated matrix production while the sheath remains [2]. Given that the sheathing materials often have extended degradation times, this could both stress-shield the infiltrating cells for long periods and promote a long-term foreign body (inflammatory) response [28]. Indeed, the presence of stress-shielding suggests that much of the matrix production in the core would likely be immunomediated. Finally, when the sheathing materials eventually degrade, they often do so with a rapid loss of mechanical integrity [29]. If the core neotissue is not “preconditioned” with a significant chronic load, its capacity to suddenly bear the majority of the blood pressure induced load may be inadequate. Hence, potential stress-shielding of the core by a stiff sheath could lead to multiple problems.

Sudden rupture can arise whenever the stress experienced by the graft exceeds its strength. In the case of long-term failure noted earlier, unstressed neotissue can lack sufficient organization and crosslinking to bear normal arterial loads. Acute rupture can also occur due to a failure of the graft materials themselves shortly after implantation. The stiff polymers typically used as sheathing materials have moderate strain-at-break values, often below 20% [30]. Using a thin sheath may allow higher stresses in the core, but at an increased risk for rupture. Considering effects of either swelling in the core or fabrication-induced residual stresses in the sheath increases the stress experienced by the sheath, which could contribute to its failure. Residual stresses in the sheath were of particular importance due to the change in the stress distribution seen with thicker sheaths (Fig. 7(c)—ii and iv). In this case, the stress was highest at the outer edge of the graft. Experience in fabrication has shown that defects in the sheath, such as tears or holes, typically concentrate on the outer surface of the graft. With the highest value of stress at the outer surface of the graft, the effect of these stress concentrating defects could be amplified.

The large negative values of circumferential stress experienced by swollen and residually stressed grafts can similarly play a role in adverse outcomes. Compressive stresses have been associated with chondrocyte/osteocyte differentiation and proliferation [31]. If infiltrating cells experience compressive loads, the graft could become calcified. Local calcifications could serve as stress concentrations and promote failure; diffuse calcification could increase graft stiffness and adversely affect the mechanobiology and hemodynamics. Indeed, previous bilayered grafts have exhibited calcified regions in the core [4]. Furthermore, compressive circumferential stresses could lead to buckling of the graft. Extensive analysis of growing bilayered cylinders has shown that exceeding critical values of stress leads to collapse of the open lumen into a wrinkled geometry [32]. Such wrinkling would likely increase the thrombotic potential of the graft. In addition to thrombosis from collapse, the decrease in lumen diameter that comes with increased swelling or residual stress (cf. Figs. 4(c) and 6(c)) could contribute to stenosis or thrombosis at the proximal or distal anastomosis [13]. Finally, axial buckling from circumferentially constrained swelling can cause delamination or tearing of the scaffold, resulting in graft failure due to dissection or focal aneurysmal dilation and rupture.

Another important mechanobiological consideration is swelling alone, which increasingly thickens the graft (Fig. 5(b)). Thickening provides more wall volume for infiltrating cells to fill with inflammatory matrix [33], which may be difficult to resolve since the ability of over-thick vessels to reverse remodel appears to be minimal [34]. Implanted grafts are already typically much thicker than the native vessel to provide enough structural stiffness to bear the pressure load. A thicker graft at long time points could also affect the surrounding adjacent vessels by reducing the compliance of the construct.

Adjacent vessels anastomosed to the implanted graft are constrained to move with the ends of the construct. While area compliance of the graft can approach that of the native artery for thin sheaths and compliant cores, the strain associated with such deformations could exceed the safe limit for many stiff polymeric materials, including poly(caprolactone). Increasing the stiffness of the core seems to be a reasonable solution to the stress mismatch between the core and the sheath, but this can greatly reduce the compliance of the graft, even when the core is an order of magnitude less stiff than the sheath. Designing a successful implant will likely require a balancing act to prevent instabilities or acute rupture, to engender mechanobiological viability, and to promote normal hemodynamics. We submit that the present simulations represent another step toward the ultimate goal of identifying an optimal design.

The challenge of balance will likely need to be met by the increasing ability of material scientists to tailor microscale properties to a particular application. For example, aligning fibers circumferentially could allow increased core stresses while reducing the effect of radial compression [35]. Furthermore, residual stresses introduced into polymeric materials during fabrication can be relaxed by annealing. Such processing can also affect the crystallinity of the polymer chains, however, leading to changes in modulus and strain-at-break [36]. Understanding the microstructure and how fabrication techniques can affect the implant is critical. Due to the many possible scaffold designs, including different combinations of porosity, fiber diameter, anisotropy, and so forth, parametric studies involving more complex microstructural models may be essential in determining which designs hold promise without undue experimental burden. Herein, we used computational modeling to consider a subset of parameters and we were able to contrast over 1000 different design scenarios in a time- and cost-efficient manner.

We are not the first to use modeling to guide the design of a TEVG. For example, Harrison et al. [37] showed that the compliance of a (cross-linked gelatin/fibrinogen) graft could be predicted as a function of cross-linking time, thus enabling one to better match the compliance of the graft and host tissues. Compliance matching is important for avoiding adverse hemodynamic effects, but as we note throughout, there is also a need to consider intramural distributions of wall stress as possible mechanobiological stimuli, particularly in biodegradable grafts wherein cells are necessary for producing the neotissue. Our study appears to be the first in this regard. We also appear to be the first to note that there is a tradeoff between matching native mechanobiological cues for cells infiltrating the scaffold and preserving normal biomechanical cues to nearby tissues. Of course, the mechanobiological cues considered herein were static, that is, there was no consideration of the time-course of loading over a cardiac cycle. Efforts to identify effects of dynamic loading on cellular responses may be important for arterial TEVGs, particularly since there is a large difference in the loading rate between murine and human models.

Finally, the present study focused solely on the initial structure and properties of the scaffold, not any consideration of how these parameters evolve in vivo. Such studies can and should be pursued as well [24]. Nevertheless, we submit that “initial conditions” greatly influence subsequent growth and remodeling of an implanted TEVG and the present study provides important new insight into how a bilayered composition can be designed to interact initially with the native vasculature and infiltrating cells.

Funding Data

• National Institutes of Health (Grant Nos. R01 HL098228 and R01 HL128602).

• National Science Foundation Graduate Research Fellowship (Grant No. NSF DGE1122492).