Significance
The empirically observed transferability of functional groups is shown to follow from Kohn’s nearsightedness principle for electron density. To show this, we analytically calculated and analyzed the softness kernel for molecules. The relevance of this work touches on physics (the nearsightedness principle), molecular chemistry and materials science (chemical transferability and similarity), and computer science (machine-learning approaches for pharmaceutical and materials design).
Keywords: nearsightedness, electronic matter, linear response, chemical transferability, density functional theory
Abstract
We establish the physical origins of chemical transferability from the perspective of the nearsightedness of electronic matter. To do this, we explicitly evaluate the response of electron density to a change in the system, at constant chemical potential, by computing the softness kernel, . The softness kernel is nearsighted, indicating that under constant-chemical-potential conditions like dilute solutions changing the composition of the molecule at has only local effects and does not have any significant impact on the reactivity at positions far away from point . This locality principle elucidates the transferability of functional groups in chemistry.
One of the fundamental precepts of chemistry is that molecules are built from atoms and functional groups, which largely retain their chemical identity regardless of their molecular environment. This implies that the chemical properties of functional groups are largely transferable between molecules (1). As a corollary, chemical reactivity is nearsighted: Adding or changing a functional group in a molecule rarely affects its reactivity far away from where it was modified.
The physical origins of chemical transferability remain obscure but are clearly related to Kohn’s nearsightedness of electronic matter (NEM) principle. NEM has been used to explain the transferability of functional groups along with other concepts like Pauling’s concept of the chemical bond and the “divide and conquer” approach used in the linear scaling strategy to study large molecular systems (2–10). This principle states that for many-electron systems at constant electronic chemical potential the amount of change in electron density at , , induced by a perturbation in the external potential at position , , with outside a sphere with radius centered on , will always be smaller than a maximum value , no matter how large the perturbation. In other words, the electron density at cannot “see” any perturbation beyond with an accuracy greater than . Prodan and Kohn (8) showed that for 1D gapless model systems the decay of as a function of (i.e., upon increasing ) follows a power law. For “gapped” systems, that is, with a hardness greater than zero, this decay is exponential. This suggests that in the molecular world, where is always greater than zero, the electron density should only be sensitive to “nearby” changes in the external potential. One aim of this paper is to provide the first numerical confirmation of this “nearsightedness principle” for real 3D molecules. In addition, this paper aims at establishing the link between the basic physics encoded in the nearsightedness principle and the empirically observed transferability of functional groups, which is the basis for how chemists conceive organic and inorganic molecules as being built from fragments that largely retain their identity even after being combined to form a larger molecule. If a molecule is only sensitive to nearby changes in external potential, changing a functional group will only affect the reactivity of the molecule in the vicinity of the modification. Conversely, when adding/changing substituents on the molecular backbone, only the changes that are close to the functional group influence the reactivity of the functional group. The plausible link between “physical” and “chemical” nearsightedness was pointed out in 2008 by Richard Bader (10). Cárdenas et al. (11) followed Prodan and Kohn stating that in an open-system representation (at constant electronic chemical potential ) reactivity indicators that depend on more than one point, including the hardness kernel and Kohn–Sham dielectric response function, are nearsighted.
As mentioned, NEM is stated to be the fundamental principle underlying important concepts in (quantum) chemistry like the transferability of functional groups, Pauling’s concept of the chemical bond, linear scaling algorithms (3, 4, 6, 7), and the divide and conquer approach (12), but it can also be understood as the concept underlying the success of machine learning when applied to chemical problems. As such, demonstrating the principle for molecules is an important step in understanding the electronic structure of molecular systems.
The Softness Kernel
The nearsightedness principle is fundamentally a statement about the change in density, , in response to a change in external potential, . This suggests that nearsightedness should be related to the linear response function (13, 14). However, the nearsightedness principle only holds under constant-chemical-potential conditions, so the quantity that must be studied is , which is minus the softness kernel, , and is related to the linear response function by the identity (15)
| [1] |
Substituting the definitions of linear response function, softness kernel (15), local softness (16), and Fukui function (17) gives
| [2] |
Using the relationship between the local softness and the Fukui function, , and the relationship between the global softness and the chemical hardness, (16, 18), one obtains a somewhat more traditional form of the Berkowitz–Parr relation,
| [3] |
This is the main working equation in the present paper. In a recent contribution, Yang et al. (19) derived analytical expressions for the linear response function, Fukui function and hardness, based on coupled-perturbed Kohn–Sham theory. These expressions were implemented and combined to calculate the softness kernel using Eq. 3.
Keeping the chemical potential, instead of the number of electrons, constant might seem strange at first, but it is often a more realistic perspective when investigating the reactivity of a molecule. In practice, molecules are not isolated but instead are found in solution, where the chemical potential is fixed by the solvent, allowing (partial) charge transfer to or from the molecule while keeping its chemical potential constant. Moreover, the nearsightedness principle does not hold under constant- conditions, as is easily seen from a simple counterexample: If one adds a bare helium nucleus, , far away from a hydrogen atom placed at , then the electron density at changes dramatically no matter how far away the helium nucleus is.
Results and Discussion
The Atom-Condensed Softness Kernel.
The analysis of the six dimensional softness kernel is facilitated by dividing it into atomic contributions (20). To do this, we integrate and of the kernel over the domains of atoms and , represented by and , thereby defining an atom–atom condensed softness kernel:
| [4] |
In this contribution, the molecule is partitioned into (fuzzy) atoms using the iterative Hirshfeld method (21, 22).
1,3,5-Hexatriene.
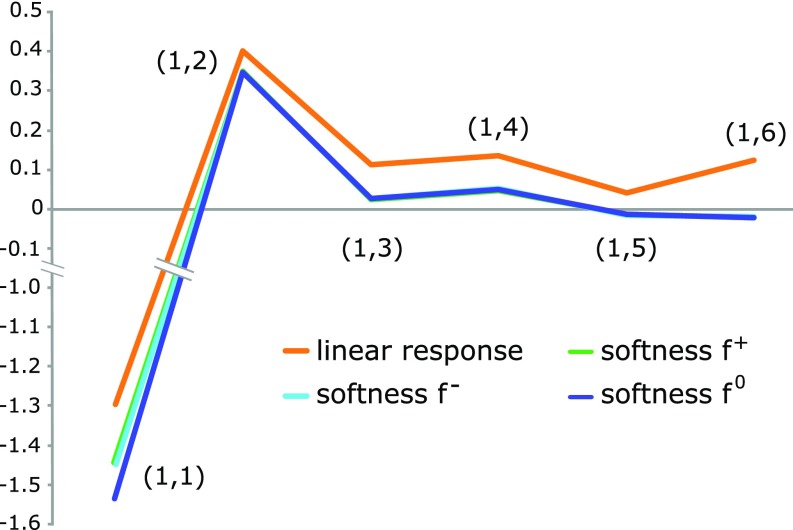
Fig. 1 shows the atom–atom condensed linear response and softness kernel between the carbon atoms of 1,3,5-hexatriene. In the case of polyenes the atom-condensed linear response function is known to show an alternating behavior with maxima between mesomeric active atoms (, , and ) and minima between mesomeric passive atoms (, , and ) (14, 23). Fig. 1 shows the softness kernel to be more nearsighted than the linear response kernel, with all values except the smaller in magnitude than the linear response. Moreover, and are very close to zero, indicating that changes in the external potential in the domain of carbon atom have, at least in the linear regime (discussed below), a negligible influence on the density of carbon atoms and , proving the nearsightedness of the softness kernel in this molecule. This observation is invariant to the choice of Fukui function (, , or ) used to calculate the softness kernel, proving the generality of the principle. Fig. 1 shows the values for the carbon atoms alone. The same conclusions hold when summing the hydrogen atoms into the domains of the carbon atoms (The Atom-Condensed Softness Kernel). The nearsighted character of should be ascribed to a cancellation of the nonnearsighted part of the linear response due to the second term in Eq. 3, which accounts for density change induced by charge transfer to/from the electron reservoir to keep the chemical potential constant. This second term thus serves as a rank-one correction to the linear response, making it nearsighted.
Fig. 1.
Atom-condensed linear response and softness kernel () of 1,3,5-hexatriene. The curves of the softness kernel using and are overlapping.
Heptatrienyl cation.
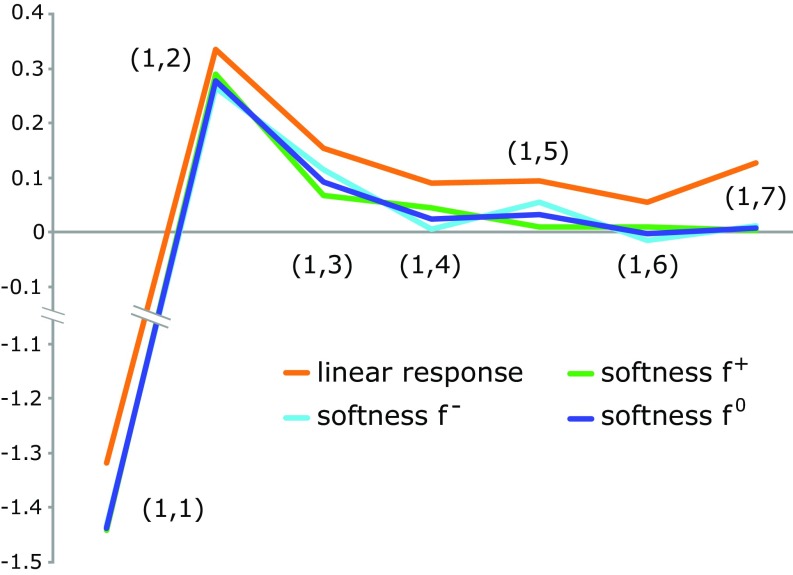
To assert the generality of the principle, the heptatrienyl cation was chosen as a test case where the nearsightedness of the softness kernel could become problematic. The Fukui function (especially and ) of this cation is more localized on the terminal carbon atoms, which, by inspection of Eq. 3, could potentially lead to a significant nonzero . Fig. 2, however, shows that the nearsightedness also holds for this molecule. Again, all values except are smaller in magnitude than the linear response counterpart and and are essentially zero. (The values calculated with and are nearly zero. The value calculated using , however, is somewhat larger, but still smaller than .)
Fig. 2.
Atom-condensed linear response and softness kernel () of the heptatrienyl cation.
“Alchemical” Changes.
The difference in density when changing one functional group to another can be obtained from the softness kernel using so-called alchemical derivatives (24, 25), that is, derivatives of the atomic or molecular density with respect to one or more nuclear charges:
| [5] |
In the following examples, these alchemical changes have been computed to probe the effect of replacing one functional group by another while keeping the electronic chemical potential constant. The chemical potential was chosen as the average of the energies of the highest-occupied molecular orbital (HOMO) and lowest-unoccupied molecular orbital (LUMO) (corresponding to ), to keep the chemical potential at the Fermi level of the molecule. We verified that nearly identical results are obtained when the chemical potential is set to the HOMO or LUMO energy (corresponding to or , respectively).
Functionalization of 1,3,5-Hexatriene.
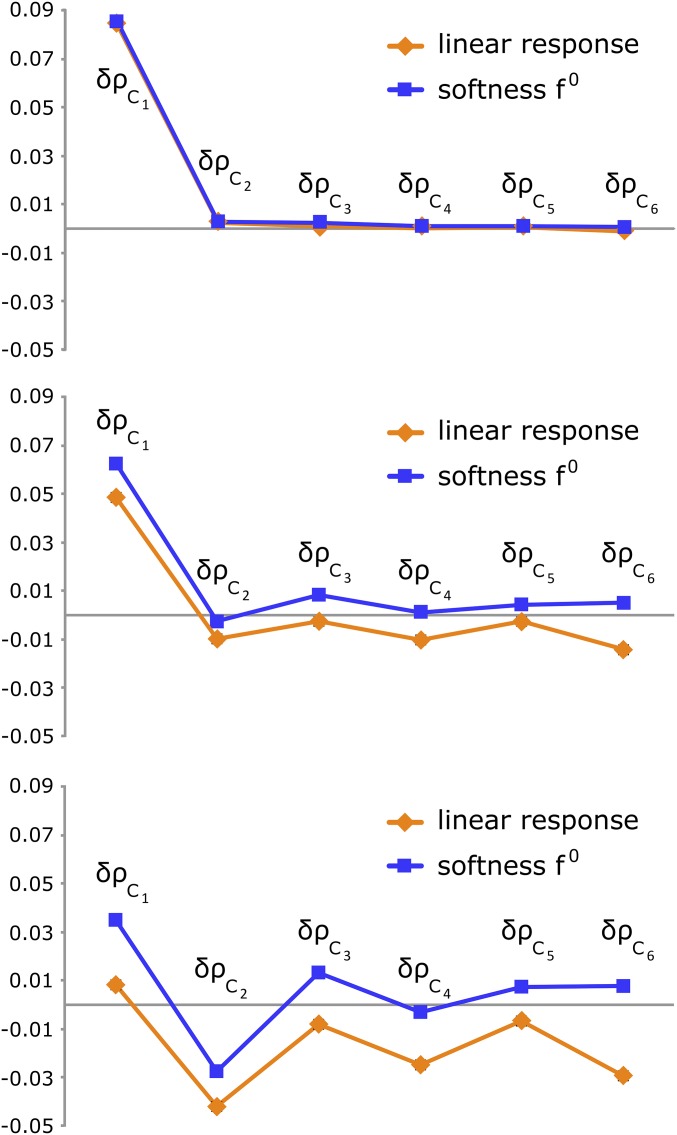
To study the effect of changing functional groups, the alchemical change in density of 1,3,5-heptatriene to 1,3,5-hexatrien-1-amine, 1,3,5-hexatrien-1-ol, and 1-fluoro-1,3,5-hexatriene at constant chemical potential was calculated using Eq. 5. The CH3 group was annihilated and replaced by a NH2, OH, or F group, respectively. The changes in the electron population of the carbon atoms in hexatriene, evaluated using the iterative Hirshfeld partitioning, are shown in Fig. 3 (corresponding to minus the change in the charge of the atoms). When changing the methyl group to an amino group, only the charge on the first carbon atom (the carbon connected to the functional group) is significantly affected, both at constant number of electrons (using the linear response) and at constant chemical potential (using the softness kernel). When changing the methyl group to a hydroxyl group or a fluorine atom the charges change more at constant number of electrons than at constant chemical potential. Specifically, the charges at carbon atoms , , and are only slightly affected by the functional group when using the softness kernel but change significantly when using the linear response. It should be emphasized that these alchemical changes perturb the potential by , extending beyond the domain of the methyl group, which explains why there are still small changes in the density of carbon atoms and when using the softness kernel, even though the value of is essentially zero when is located on the methyl group and is located on these carbon atoms.
Fig. 3.
Alchemical change in electron population using the linear response and softness kernel for 1,3,5-heptatriene to 1,3,5-hexatrien-1-amine (Top), 1,3,5-heptatriene to 1,3,5-hexatrien-1-ol (Middle), and 1,3,5-heptatriene to 1-fluoro-1,3,5-hexatriene (Bottom). The atom partitioning was done using the iterative Hirshfeld method.
Changing the methyl group to a hydroxyl group or fluorine atom at constant number of electrons withdraws electrons from hexatriene, making more positively charged. At constant chemical potential, the molecule accepts charge from the electron reservoir to compensate for this electron withdrawal (0.12 electrons for OH and 0.23 electrons for F). These results prove that changing the functional group at constant chemical potential only affects the atoms in the vicinity of the functional group. This observation, ubiquitous in organic chemistry, is the basis for the concept of the transferability of functional groups.
Heptatrienyl Cation.
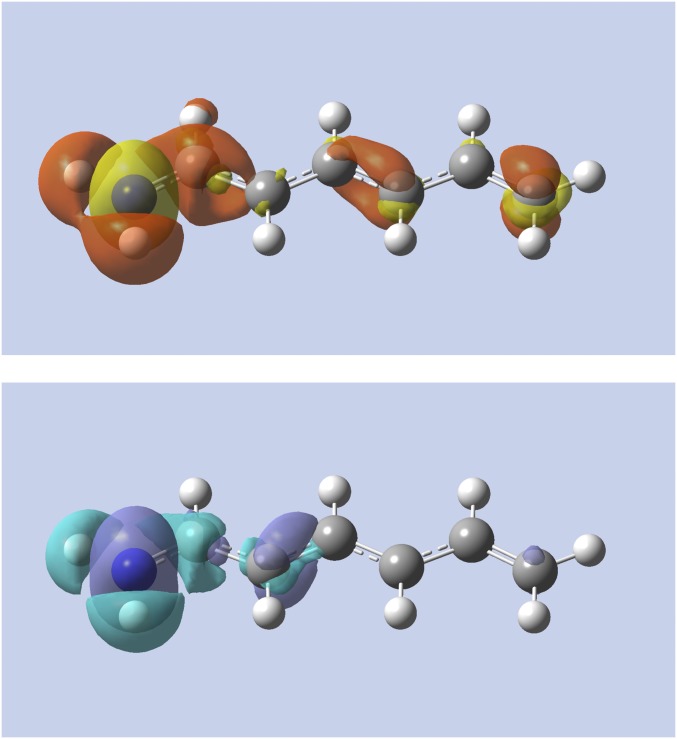
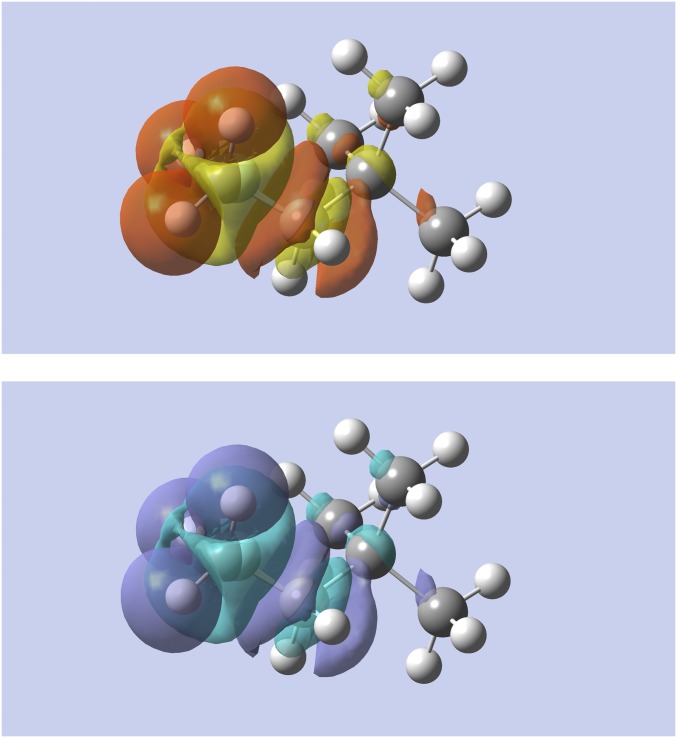
Fig. 4 shows the change in density when substituting one of the terminal carbon atoms in the heptatrienyl cation with a nitrogen atom to form 1,3,5-hexatrien-1-amine. (In the linear response case, this is an especially extreme change, resulting in the 1,3,5-hexatrien-1-amine dication.) The figure shows that, at constant number of electrons, the nitrogen withdraws electrons from the whole molecule, with an important depletion of the density at the opposite side of the molecule on carbon atom . However, at constant chemical potential, the results confirm that the change in electron density is nearsighted, with no change in density on to , as was already expected from Fig. 2. In this case, the molecule takes up 1.12 electrons using (1.10 electrons with and 1.14 electrons with ), and the net charge of 1,3,5-hexatrien-1-amine remains close to plus one.
Fig. 4.
Alchemical change in density using the linear response (Top) and softness kernel (Bottom) for the heptatrienyl cation to 1,3,5-hexatrien-1-amine. The left carbon atom is changed. Yellow (purple) indicates regions of density accumulation; red (light blue) indicates regions of density depletion.
Heptane.
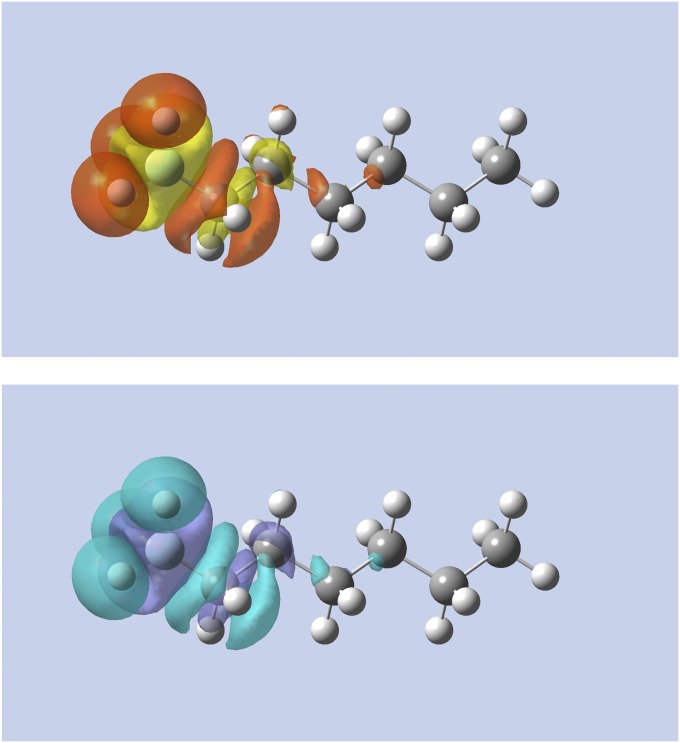
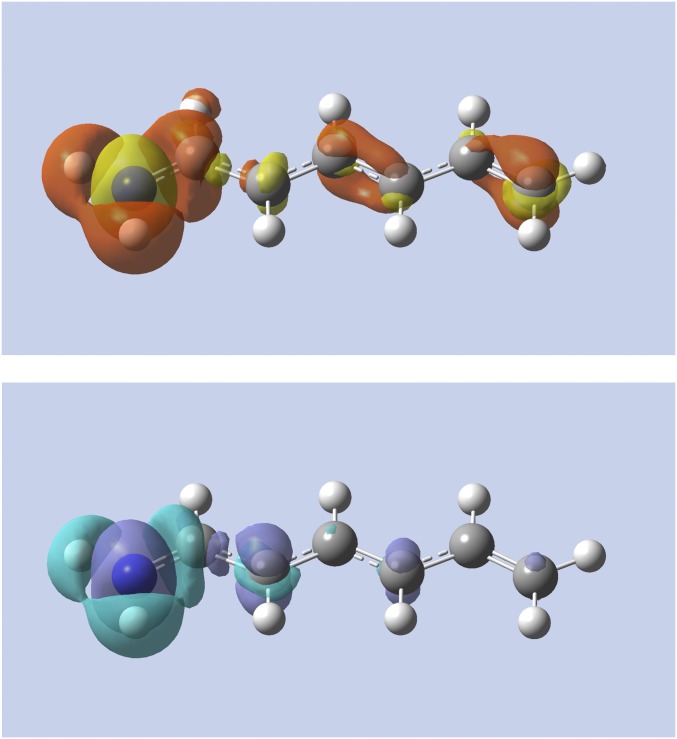
In saturated systems, is already nearsighted due to the lack of a conjugated system (14, 23). For the softness kernel to be likewise nearsighted, the second term in Eq. 3 should not counteract the nearsightedness of . To test this, we studied the alchemical change of the terminal methyl group to a fluorine atom in heptane, forming 1-fluorohexane. As shown in Fig. 5, the change in density evaluated by the linear response and the softness kernel are almost identical, with the latter being slightly more localized. This establishes that the second term of in Eq. 3 does not counteract the nearsightedness of in this saturated system.
Fig. 5.
Alchemical change in density using the linear response (Top) and softness kernel (Bottom) for heptane to 1-fluorohexane. The left carbon atom is changed (the annihilated H atoms are shown as reference). Yellow (purple) indicates regions of density accumulation; red (light blue) indicates regions of density depletion.
Three-Dimensional Systems.
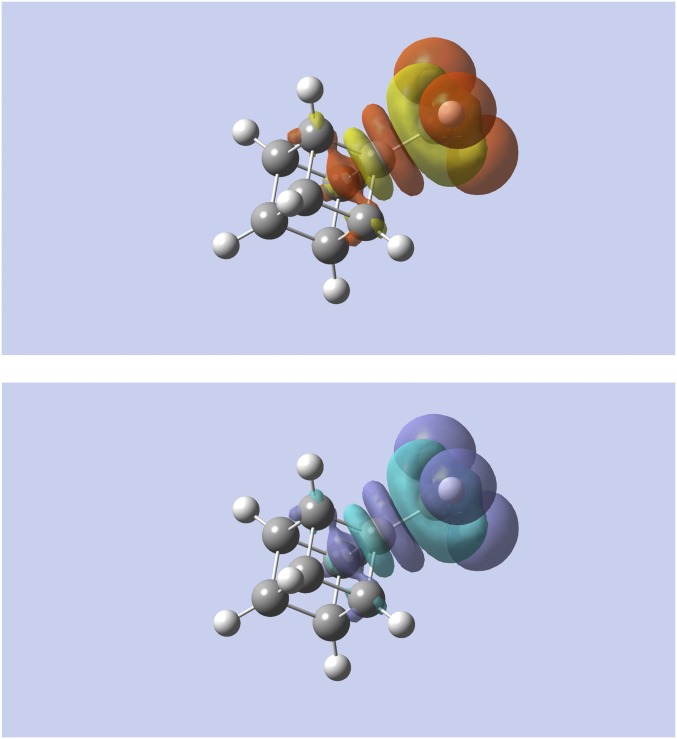
The examples considered until now are all linear hydrocarbons. To examine the nearsightedness in three dimensional structures, the alchemical change of methyl-cubane to fluoro-cubane was studied. The results are shown in Fig. 6. The changes in density evaluated by the linear response and the softness kernel are nearly identical and resemble the changes in density obtained for heptane. Numerically the change in density decays slightly faster at constant chemical potential than at constant number of electrons. These data, along with data for functionalized neopentane (where similar trends were observed), are included as Figs. S1 and S2. Our conclusions about the NEM and chemical transferability also hold, therefore, for 3D systems.
Fig. 6.
Alchemical change in density using the linear response (Top) and softness kernel (Bottom) for methylcubane to fluorocubane (the annihilated H atoms are shown as reference). Yellow (purple) indicates regions of density accumulation; red (light blue) indicates regions of density depletion.
Fig. S1.
Alchemical change in density using the linear response (Top) and softness kernel (Bottom) for 2,2-dimetylbutane to 1-fluoro-2,2-dimethylpropane. The left carbon atom is changed. Yellow (purple) indicates regions of density accumulation; red (light blue) indicates regions of density depletion.
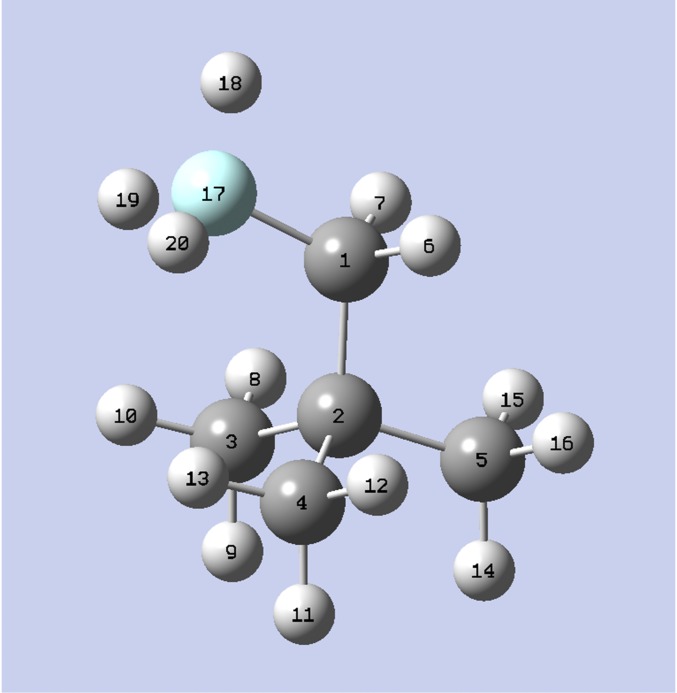
Fig. S2.
The numbering of the atoms for the change of 2,2-dimetylbutane to 1-fluoro-2,2-dimethylpropane. Atoms 17 to 20 are changed from CH3 to F.
Metals.
For gapless systems, has an asymptotic decay as a function of that is inverse-polynomial, in contrast to gapped systems, which have an exponential decay (8). To assess this computationally, we considered (equidistant) linear hydrogen chains, (H2),n (n = 5, 6, …10), as a model for this type of system, since they approach a conductor in the limit of infinitely large chains. For these chains, the data of which are included in Alchemical Changes, the condensed softness kernel is much more localized than the condensed linear response kernel, demonstrating that the NEM principle still holds when going toward a zero band gap.
The Applicability of Softness Kernel to Alchemical Changes.
In the previous section, the change in the electron density upon replacing one functional group by another was studied at constant number of electrons and constant chemical potential using the linear response function and softness kernel, respectively. Since the linear response function and softness kernel only provide first-order estimates of the change in the electron density when changing the external potential, this raises the question of whether higher-order contributions to the density are likewise nearsighted. There are mathematical reasons that the higher-order contributions should also be nearsighted (11, 26), but this has never been confirmed computationally. To assess this, we computed the change in density when the heptatrienyl cation was alchemically transformed to 1,3,5-hexatrien-1-amine. Fig. 7 shows the change in density at constant , obtained by subtracting the electron density of the heptatrienyl cation from the electron density of the 1,3,5-hexatrien-1-amine dication. This picture, which shows the exact change of the density, not only including the linear but also all higher-order terms, is remarkably similar to the first-order change estimated by the linear response (cf. Fig. 4), with an important depletion of density on the carbon atom far away from where the substitution took place. It seems that the first-order estimate by the linear response provides a plausible qualitative picture of the change in the density upon alchemical substitution. To determine the change in density at constant chemical potential, the number of electrons in 1,3,5-hexatrien-1-amine was increased in steps of 0.05 until the orbital energy of the partially filled orbital exceeded that of the LUMO in the heptatrienyl cation. Interpolation led to an estimate of 1.02 electrons being transferred from the reservoir to the molecule. This slightly differs from the value of 1.12 electrons found using the softness kernel. The difference of 0.1 electrons originates from the difference between the first-order estimate and the full self-consistent field calculation, showing that the first-order estimate recovers 90.2% of the change in number of electrons. When comparing the difference in electron density between the heptatrienyl cation and the 1,3,5-hexatrien-1-amine “+0.98” cation a picture similar to that of the softness kernel is obtained (cf. Fig. 7). Virtually no change in density can be observed on and , illustrating again the nearsightedness of the change in density at constant chemical potential.
Fig. 7.
The difference density obtained by subtracting the density of theheptatrienyl cation from the density of 1,3,5-hexatrien-1-amine at constant N (Top) or constant (Bottom). The left carbon atom is changed. Yellow (purple) indicates regions of density accumulation; red (light blue) indicates regions of density depletion. These figures can be compared with the first-order estimate in Fig. 4.
Implications.
The NEM was introduced by W. Kohn as the theoretical basis underlying the linear-scaling algorithms proposed in density functional theory. In these algorithms, the molecular system is divided into overlapping subsystems comprised of a group of atoms for which the Kohn–Sham equations are solved separately. Since each region is treated independently, this approach scales linearly with system size and can be easily parallelized. This insight justifies algorithms such as the fast multipole method (3), density-matrix-based linear scaling methods (4), the natural linear scaling coupled-cluster method (6, 7), and the divide-and-conquer method (12). The latter explicitly uses a common chemical potential to control the electron population and to allow fractional subsystem charges. The results presented in this paper provide numerical corroboration that the constant chemical potential in the divide-and-conquer method has, as a desirable side effect, the removal of possible nonlocal interactions between subsystems. This ensures that the molecular systems can be divided into locally interacting subgroups, allowing one to achieve linear computational scaling.
This paper also provides direct computational evidence for the transferability of functional groups: Under the constant-chemical-potential conditions that are typical for molecules in dilute solutions or on molecular surfaces, the effect of changing a molecular substituent decreases rapidly with distance and is essentially negligible for atoms that are separated by more than three chemical bonds from the site of functionalization. This quick decrease of the influence of functionalizing the molecular backbone by modifying a substituent/functional group supports chemists’ intuition that functional groups “operate” locally: They largely retain their identity and therefore act similarly independent of the backbone (i.e., functional groups are transferable entities). Although this paper studies the effect on the backbone when changing a functional group, the nearsightedness principle also holds in the reverse sense. Changes to the molecular backbone will only affect the functional group in a nonnegligible way if they occur in the vicinity of the group. This effect is well known in organic chemistry. Consider, for example, the evolution in the pKa on 2- ,3-, and 4-chlorobutanoic acid where, compared with the unsubstituted acid, the pKa decreases by 2.0, 0.7, and 0.3 units, respectively. The relevant functional group property (acidity) is retained throughout, but the strength of the effect, however, diminishes exponentially after the nearsighted region. The nearsightedness implies that molecular systems can be divided in subgroups, whose reactivity is affected only mildly by the other subgroups of the system. This “chemical” nearsightedness principle enables the chemical divide-and-conquer perspective of large molecules as assemblages of chemically transferable functional groups. This ensures that similar molecular subgroups have similar functionality and justifies the use of molecular similarity measures. This not only provides the theoretical basis for applying modern machine-learning approaches for chemical property prediction but also for traditional quantitative structure activity/property relationships (27–29). For example, it is popular to define a “distance” between molecules solely based on the identity and position of their constituent atoms [e.g., the Coulomb matrix measure (30)]. One can then use a machine-learning method like kernel-ridge regression to make a prediction for the properties of an unknown molecule, based on the idea that its properties will most closely resemble those of the structurally similar molecules.
The Atom-Condensed Softness Kernel
To calculate the atom-condensed linear response and softness kernel, Eqs. S1 to S6 were combined and partitioned using the iterative Hirshfeld method:
| [S8] |
The numerical data of the molecules discussed in the article are listed below.
Hexatriene.
One can also sum the contributions of the hydrogen atoms together with the heavy atoms, for which the following results are obtained. The conclusions remain the same; all values of the softness kernel, except the , are smaller in magnitude than the linear response ():
| HOMO | 0.1940 | |||||||
| LUMO | 0.1889 | |||||||
| Average | 0.1915 | |||||||
| X | ||||||||
| C1 | -1.2984 | 0.4016 | 0.1121 | 0.1355 | 0.0416 | 0.1256 | ||
| C2 | -1.0888 | 0.1381 | 0.0971 | 0.0206 | 0.0416 | |||
| C3 | -1.1663 | 0.3159 | 0.0971 | 0.1355 | ||||
| C4 | -1.1663 | 0.1381 | 0.1121 | |||||
| C5 | -1.0888 | 0.4016 | ||||||
| C6 | -1.2984 | |||||||
| X | ||||||||
| C1 | 0.0933 | 0.0951 | 0.1001 | 0.0564 | 0.0358 | 0.0307 | 0.0321 | 0.0385 |
| C2 | 0.0884 | 0.0897 | 0.1141 | 0.0343 | 0.0333 | 0.0767 | 0.0117 | 0.0104 |
| C3 | 0.0314 | 0.0172 | 0.0336 | 0.0968 | 0.0750 | 0.0472 | 0.0294 | 0.0369 |
| C4 | 0.0294 | 0.0369 | 0.0472 | 0.0750 | 0.0968 | 0.0336 | 0.0314 | 0.0172 |
| C5 | 0.0117 | 0.0104 | 0.0767 | 0.0333 | 0.0343 | 0.1141 | 0.0884 | 0.0897 |
| C6 | 0.0321 | 0.0385 | 0.0307 | 0.0358 | 0.0564 | 0.1001 | 0.0933 | 0.0951 |
| H7 | -0.4492 | 0.0607 | 0.0432 | 0.0227 | 0.0065 | 0.0114 | 0.0074 | 0.0108 |
| H8 | -0.4461 | 0.0410 | 0.0114 | 0.0137 | 0.0081 | 0.0108 | 0.0126 | |
| H9 | -0.4897 | 0.0285 | 0.0214 | 0.0028 | 0.0114 | 0.0081 | ||
| H10 | -0.4748 | 0.0390 | 0.0214 | 0.0065 | 0.0137 | |||
| H11 | -0.4748 | 0.0285 | 0.0227 | 0.0114 | ||||
| H12 | -0.4897 | 0.0432 | 0.0410 | |||||
| H13 | -0.4492 | 0.0607 | ||||||
| H14 | -0.4460 |
| X | |||||||
| C1 | -1.2984 | 0.1689 | 0.1647 | 0.1668 | 1.445470 | 1.4419 | 1.4419 |
| C2 | 0.4016 | 0.0610 | 0.0645 | 0.0628 | -0.348504 | -0.3454 | -0.3476 |
| C3 | 0.1121 | 0.1002 | 0.0959 | 0.0980 | -0.024868 | -0.0285 | -0.0277 |
| C4 | 0.1355 | 0.1002 | 0.0959 | 0.0980 | -0.048273 | -0.0519 | -0.0512 |
| C5 | 0.0416 | 0.0610 | 0.0645 | 0.0628 | 0.011539 | 0.0147 | 0.0124 |
| C6 | 0.1256 | 0.1689 | 0.1647 | 0.1668 | 0.021536 | 0.0180 | 0.0179 |
| H7 | 0.0933 | 0.0451 | 0.0464 | 0.0457 | -0.054086 | -0.0529 | -0.0540 |
| H8 | 0.0951 | 0.0525 | 0.0548 | 0.0537 | -0.049321 | -0.0473 | -0.0489 |
| H9 | 0.1001 | 0.0345 | 0.0357 | 0.0351 | -0.070054 | -0.0690 | -0.0699 |
| H10 | 0.0564 | 0.0378 | 0.0379 | 0.0379 | -0.023480 | -0.0233 | -0.0238 |
| H11 | 0.0358 | 0.0378 | 0.0379 | 0.0379 | -0.002922 | -0.0028 | -0.0033 |
| H12 | 0.0307 | 0.0345 | 0.0357 | 0.0351 | -0.000726 | 0.0004 | -0.0006 |
| H13 | 0.0321 | 0.0451 | 0.0464 | 0.0457 | 0.007184 | 0.0084 | 0.0073 |
| H14 | 0.0385 | 0.0525 | 0.0548 | 0.0537 | 0.007246 | 0.0093 | 0.0077 |
| X | |||||||
| C1 | -1.6954 | 0.2666 | 0.2659 | 0.2662 | 2.0616 | 2.0696 | 2.0656 |
| C2 | 0.7640 | 0.0955 | 0.1002 | 0.0978 | -0.6328 | -0.6229 | -0.6279 |
| C3 | 0.2511 | 0.1380 | 0.1339 | 0.1359 | -0.0616 | -0.0627 | -0.0621 |
| C4 | 0.2579 | 0.1380 | 0.1339 | 0.1359 | -0.0683 | -0.0695 | -0.0689 |
| C4 | 0.1140 | 0.0955 | 0.1002 | 0.0978 | 0.0172 | 0.0271 | 0.0221 |
| C5 | 0.3084 | 0.2666 | 0.2659 | 0.2662 | 0.0578 | 0.0658 | 0.0618 |
Heptatrienyl Cation.
With the hydrogen atoms summed together with the heavy atoms, the conclusions remain the same; all values of the softness kernel, except the , are smaller in magnitude than the linear response ():
| HOMO | 0.1834 | ||||||
| LUMO | 0.1788 | ||||||
| Average | 0.1811 | ||||||
| X | |||||||
| C1 | −1.3182 | 0.3348 | 0.1527 | 0.0899 | 0.0930 | 0.0548 | 0.1261 |
| C2 | -1.1512 | 0.1970 | 0.0929 | 0.0540 | 0.0275 | 0.0548 | |
| C3 | -1.2008 | 0.2400 | 0.1188 | 0.0540 | 0.0930 | ||
| C4 | -1.2032 | 0.2400 | 0.0929 | 0.0899 | |||
| C5 | -1.2008 | 0.1970 | 0.1527 | ||||
| C6 | -1.1512 | 0.3348 | |||||
| C7 | -1.3182 | ||||||
| X | |||||||
| C1 | 0.0923 | 0.0871 | 0.0729 | 0.0554 | 0.0278 | 0.0346 | 0.0250 |
| C2 | 0.0798 | 0.0765 | 0.0967 | 0.0456 | 0.0338 | 0.0138 | 0.0140 |
| C3 | 0.0213 | 0.0388 | 0.0409 | 0.0890 | 0.0490 | 0.0408 | 0.0169 |
| C4 | 0.0246 | 0.0188 | 0.0363 | 0.0558 | 0.0865 | 0.0558 | 0.0363 |
| C5 | 0.0229 | 0.0257 | 0.0169 | 0.0408 | 0.0490 | 0.0890 | 0.0409 |
| C6 | 0.0161 | 0.0139 | 0.0140 | 0.0138 | 0.0338 | 0.0456 | 0.0967 |
| C7 | 0.0371 | 0.0347 | 0.0250 | 0.0346 | 0.0278 | 0.0554 | 0.0729 |
| H8 | -0.4415 | 0.0537 | 0.0338 | 0.0107 | 0.0107 | 0.0087 | 0.0080 |
| H9 | -0.4487 | 0.0348 | 0.0210 | 0.0050 | 0.0126 | 0.0057 | |
| H10 | -0.4433 | 0.0272 | 0.0186 | 0.0037 | 0.0088 | ||
| H11 | -0.4666 | 0.0289 | 0.0190 | 0.0037 | |||
| H12 | -0.4338 | 0.0289 | 0.0186 | ||||
| H13 | -0.4666 | 0.0272 | |||||
| H14 | -0.4433 |
| X | ||
| C1 | 0.0347 | 0.0371 |
| C2 | 0.0139 | 0.0161 |
| C3 | 0.0257 | 0.0229 |
| C4 | 0.0188 | 0.0246 |
| C5 | 0.0388 | 0.0213 |
| C6 | 0.0765 | 0.0798 |
| C7 | 0.0871 | 0.0923 |
| H8 | 0.0101 | 0.0116 |
| H9 | 0.0104 | 0.0101 |
| H10 | 0.0057 | 0.0080 |
| H11 | 0.0126 | 0.0087 |
| H12 | 0.0050 | 0.0107 |
| H13 | 0.0210 | 0.0107 |
| H14 | 0.0348 | 0.0338 |
| H15 | -0.4487 | 0.0537 |
| H16 | -0.4415 |
| X | |||||||
| C1 | -1.3182 | 0.1454 | 0.1480 | 0.1467 | 1.4336 | 1.4407 | 1.4371 |
| C2 | 0.3348 | 0.0880 | 0.0541 | 0.0711 | -0.2650 | -0.2900 | -0.2772 |
| C3 | 0.1527 | 0.0488 | 0.1026 | 0.0757 | -0.1140 | -0.0677 | -0.0913 |
| C4 | 0.0899 | 0.1077 | 0.0545 | 0.0811 | -0.0045 | -0.0448 | -0.0242 |
| C5 | 0.0930 | 0.0488 | 0.1026 | 0.0757 | -0.0543 | -0.0081 | -0.0316 |
| C6 | 0.0548 | 0.0880 | 0.0541 | 0.0711 | 0.0151 | -0.0100 | 0.0028 |
| C7 | 0.1261 | 0.1454 | 0.1480 | 0.1467 | -0.0107 | -0.0036 | -0.0072 |
| H8 | 0.0923 | 0.0465 | 0.0488 | 0.0476 | -0.0555 | -0.0520 | -0.0538 |
| H9 | 0.0871 | 0.0410 | 0.0405 | 0.0408 | -0.0545 | -0.0536 | -0.0540 |
| H10 | 0.0729 | 0.0328 | 0.0298 | 0.0313 | -0.0469 | -0.0482 | -0.0475 |
| H11 | 0.0554 | 0.0270 | 0.0344 | 0.0307 | -0.0339 | -0.0269 | -0.0305 |
| H12 | 0.0278 | 0.0332 | 0.0291 | 0.0311 | -0.0015 | -0.0037 | -0.0026 |
| H13 | 0.0346 | 0.0270 | 0.0344 | 0.0307 | -0.0132 | -0.0062 | -0.0098 |
| H14 | 0.0250 | 0.0328 | 0.0298 | 0.0313 | 0.0010 | -0.0004 | 0.0003 |
| H15 | 0.0347 | 0.0410 | 0.0405 | 0.0408 | -0.0022 | -0.0012 | -0.0017 |
| H16 | 0.0371 | 0.0465 | 0.0488 | 0.0476 | -0.0002 | 0.0033 | 0.0015 |
| X | |||||||
| C1 | -1.7422 | 0.2329 | 0.2373 | 0.2351 | 2.0381 | 2.0571 | 2.0475 |
| C2 | 0.6326 | 0.1208 | 0.0839 | 0.1024 | -0.4792 | -0.5213 | -0.4997 |
| C3 | 0.2997 | 0.0758 | 0.1370 | 0.1064 | -0.2034 | -0.1180 | -0.1616 |
| C4 | 0.1768 | 0.1409 | 0.0836 | 0.1122 | 0.0021 | -0.0660 | -0.0312 |
| C5 | 0.1975 | 0.0758 | 0.1370 | 0.1064 | -0.1012 | -0.0158 | -0.0594 |
| C6 | 0.1236 | 0.1208 | 0.0839 | 0.1024 | 0.0299 | -0.0122 | 0.0093 |
| C7 | 0.3119 | 0.2329 | 0.2373 | 0.2351 | -0.0160 | 0.0029 | -0.0067 |
Alchemical Changes
The difference in density when changing one functional group to another can be obtained from the linear response, or the softness kernel using so-called alchemical derivatives (24, 25) (i.e., derivatives of the atomic or molecular density with respect to one or more nuclear charges):
| [S9] |
| [S10] |
This change in density was then partitioned using the iterative Hirshfeld method or visualized using a cube file.
Functionalization of 1,3,5-Hexatriene.
Changing 1,3,5-heptatriene to 1,3,5-hexatrien-1-amine (CH3 to NH3, FG indicates the functional group):
| X | ||
| FG | -0.0418 | 0.0401 |
| C1 | 0.0837 | -0.0850 |
| C2 | 0.0023 | -0.0029 |
| C3 | 0.0011 | -0.0021 |
| C4 | 0.0000 | -0.0010 |
| C5 | 0.0004 | -0.0011 |
| C6 | -0.0011 | -0.0007 |
| H7 | -0.0231 | 0.0226 |
| H8 | -0.0177 | 0.0174 |
| H9 | -0.0003 | -0.0001 |
| H10 | -0.0019 | 0.0015 |
| H11 | 0.0001 | -0.0005 |
| H12 | -0.0008 | 0.0002 |
| H13 | -0.0008 | 0.0002 |
Changing 1,3,5-heptatriene to 1,3,5-hexatrien-1-ol (CH3 to OH, FG indicates the functional group):
| X | ||
| FG | 0.1112 | -0.1282 |
| C1 | 0.0484 | -0.0623 |
| C2 | -0.0099 | 0.0025 |
| C3 | -0.0026 | -0.0083 |
| C4 | -0.0102 | -0.0010 |
| C5 | -0.0028 | -0.0043 |
| C6 | -0.0141 | -0.0049 |
| H7 | -0.0656 | 0.0607 |
| H8 | -0.0296 | 0.0260 |
| H9 | -0.0058 | 0.0015 |
| H1 | -0.0059 | 0.0017 |
| H11 | -0.0029 | -0.0010 |
| H12 | -0.0056 | -0.0005 |
| H13 | -0.0043 | -0.0008 |
Changing 1,3,5-heptatriene to 1-fluoro-1,3,5-hexatriene (CH3 to F, FG indicates the functional group):
| X | ||
| FG | 0.2924 | -0.3252 |
| C1 | 0.0082 | -0.0349 |
| C2 | -0.0416 | 0.0273 |
| C3 | -0.0078 | -0.0131 |
| C4 | -0.0245 | 0.0029 |
| C5 | -0.0065 | -0.0071 |
| C6 | −0.0290 | -0.0076 |
| H7 | −0.0929 | 0.0833 |
| H8 | −0.0522 | 0.0452 |
| H9 | −0.0084 | 0.0000 |
| H10 | −0.0123 | 0.0041 |
| H11 | −0.0057 | -0.0020 |
| H12 | −0.0105 | -0.0013 |
| H13 | −0.0088 | -0.0012 |
Three-Dimensional Systems.
Cubane.
Methyl-cubane to fluoro-cubane: The functional group is attached to C1. C2a, C2b and C2c are connected to C1; C3a, C3b and C3c are connected to C2a, C2b and C2c and C4 is the other side of the cube, connected to C3a, C3b and C3c. H1a is the hydrogen atom of C2a, H2a is the hydrogen atom of C3a, and so on.
Methyl-cubane to fluoro-cubane: The functional group is attached to C1. C2a, C2b and C2c are connected to C1; C3a, C3b and C3c are connected to C2a, C2b and C2c and C4 is the other side of the cube, connected to C3a, C3b and C3c. H1a is the hydrogen atom of C2a, H2a is the hydrogen atom of C3a, etc.
| X | ||
| FG | 0.2893 | -0.3032 |
| C1 | 0.0156 | -0.0184 |
| C2a | -0.0293 | 0.0251 |
| C2b | -0.0292 | 0.0254 |
| C2c | -0.0293 | 0.0250 |
| C3a | -0.0106 | 0.0073 |
| C3b | -0.0107 | 0.0071 |
| C3c | -0.0107 | 0.0071 |
| C4 | -0.0034 | 0.0009 |
| H1a | -0.0373 | 0.0332 |
| H1b | -0.0374 | 0.0343 |
| H1c | -0.0374 | 0.0331 |
| H2a | -0.0202 | 0.0173 |
| H2b | -0.0203 | 0.0162 |
| H2c | -0.0203 | 0.0164 |
| H3 | -0.0089 | 0.0060 |
Neopentane.
As a second example of a 3D system, the alchemical change of a functional group placed on the neopentane structure was studied. In Fig. S1, the alchemical change of the terminal methyl group of 2,2-dimetylbutane to a fluorine atom from to 1-fluoro-2,2-dimethylpropane is shown. The numerical values of the charges at constant chemical potential and constant number of electrons are listed below and are very close to each other, differing no more than 0.007 electron, with exception of the modified functional group. The changes in density evaluated by the linear response and the softness kernel are thus almost identical and have a remarkable resemblance to the changes in density obtained for heptane. The 3D structure thus has no effect on the NEM.
For the change of 2,2-dimetylbutane to 1-fluoro-2,2-dimethylpropane the atom numbering is shown in Fig. S2.
| X | ||
| FG | 0.3495 | 0.3308 |
| C1 | -0.0230 | 0.0222 |
| C2 | -0.0011 | 0.0008 |
| C3 | -0.0122 | 0.0115 |
| C4 | -0.0122 | 0.0115 |
| H5 | -0.0236 | 0.0231 |
| H6 | -0.0728 | 0.0722 |
| H7 | -0.0728 | 0.0722 |
| H8 | -0.0059 | 0.0054 |
| H9 | -0.0094 | 0.0088 |
| H10 | -0.0255 | 0.0251 |
| H11 | -0.0094 | 0.0088 |
| H12 | -0.0059 | 0.0054 |
| H13 | -0.0255 | 0.0251 |
| H14 | -0.0314 | 0.0309 |
| H15 | -0.0094 | 0.0090 |
| H16 | -0.0094 | 0.0090 |
Hydrogen Chains.
For conductors has an asymptotic decay as a function of that is inverse-polynomial, instead of exponential (like in the case of gapped systems). To assess the NEM for conductors computationally, we considered linear hydrogen chains, (H2), n (n = 5, 6, …10), which are a model for this type of system. When all of the hydrogen–hydrogen distances are the same, the system approaches a conductor in the limit of infinitely large chains. For these equidistant hydrogen chains, a bond length of 1.8 a.u. was chosen, corresponding to the equilibrium bond length of H50. The atom condensed linear response () and softness kernel () between the terminal hydrogen atoms are listed below, along with the changes in the electron density at one terminal hydrogen when alchemically changing the other terminal hydrogen atom to He+, both at constant number of electrons () and at constant chemical potential ():
| HOMO-LUMO gap (a.u.) | |||||
| H10 | 0.2028 | −0.0362 | −0.2224 | −0.0869 | 0.1210 |
| H12 | 0.1735 | −0.0307 | −0.1956 | −0.0731 | 0.1040 |
| H14 | 0.1521 | −0.0262 | −0.1750 | −0.0628 | 0.0911 |
| H16 | 0.1353 | −0.0229 | −0.1586 | −0.0549 | 0.0811 |
| H18 | 0.1221 | −0.0201 | −0.1452 | −0.0487 | 0.0731 |
| H20 | 0.1113 | −0.0180 | −0.1340 | −0.0437 | 0.0665 |
Chains with a bond-length alternation (with different inter-H2 and intra-H2 distances) are insulators. For these alternating system, bond lengths of 1.7 a.u. and 1.9 a.u. were chosen for the inter-H2 and intra-H2 distances, respectively. The following values for the atom condensed linear response (), softness kernel (), and changes in the electron density when alchemically changing one terminal hydrogen atom to He+ are obtained:
| HOMO-LUMO gap (a.u.) | |||||
| H10 | 0.1393 | −0.0662 | −0.1628 | −0.1142 | 0.1550 |
| H12 | 0.1116 | −0.0573 | −0.1351 | −0.0983 | 0.1387 |
| H14 | 0.0917 | −0.0506 | −0.1142 | −0.0865 | 0.1264 |
| H16 | 0.0766 | −0.0453 | −0.0978 | −0.0773 | 0.1168 |
| H18 | 0.0649 | −0.0410 | −0.0846 | −0.0700 | 0.1091 |
| H20 | 0.0555 | −0.0375 | −0.0738 | −0.0640 | 0.1029 |
For the equidistant H2 chain, the condensed softness kernel is much more localized than the condensed linear response kernel. The same is true for the atom-condensed change in the electron density; the values obtained using the softness kernel, , are more localized than the ones using the linear response kernel, . Interestingly, when the bond-length alternation is introduced the difference between the condensed linear-response kernel and the condensed linear-response kernel is reduced (possibly because the dominant long-range effect is no longer long-range electron transfer). In all cases, the change in electron density at constant chemical potential (using the softness kernel) decreases appropriately with increasing distance, reaffirming the nearsightedness and transferability principle.
Conclusions
The sensitivity of the electron density to changes in molecular structure, at constant chemical potential, was studied using the softness kernel. To do this, we first developed an analytical expression for the softness kernel based on the Berkowitz–Parr relation and then computed this quantity for a representative sequence of saturated and unsaturated organic molecules. The atom–atom condensed softness kernel shows that the effects of changing the external potential is negligible after about three bonds. The corresponding change in electron density at constant number of electrons is defined by the linear response function, where the effects of changing the external potential decay slowly and can be important even six or seven bonds away. By considering alchemical changes—where one functional group was changed to another at fixed chemical potential—the nearsightedness of the softness kernel has been confirmed numerically on molecules. This provides computational evidence for the transferability of functional groups: The molecular systems can be divided into locally interacting subgroups which retain a similar functionality and reactivity, which can only be influenced by changes in the direct environment of the functional group. This justifies what is colloquially known as the methyl-ethyl-propyl-butyl-futile rule: Changing a molecular substituent more than four carbons away does not lead to significant chemical effects.
Materials and Methods
The softness kernel was calculated using Eq. 3 together with the equations given in ref. 19. The geometries were optimized at PBE/cc-pVDZ using Gaussian 09 (31). The Kohn–Sham orbitals were obtained from the same software package at the same level of theory, and the values of the linear response function, Fukui function, and hardness were analytically calculated using our in-house program developed for this purpose. The necessary exchange-correlation functionals were also obtained from the Libxc library (32). Both the atoms-in-molecules partitioning and the calculations with fractional number of electrons were performed using the open source HORTON package (33). When performing alchemical changes, the functional groups where “grown” at the position of their corresponding optimized coordinates.
In the following Supporting Information an overview of the equations used in calculating the linear response and softness kernel is given and the numerical data obtained from them have been listed.
The Softness Kernel
In the present contribution, the softness kernel is obtained through the Berkowitz–Parr relation (15),
| [S1] |
in combination with the analytical expressions for the linear response function, Fukui function, and hardness, derived using coupled-perturbed Kohn–Sham perturbation theory by Yang et al. (19) The linear response function, , has been calculated as
| [S2] |
where are the Kohn–Sham orbitals, with labels , ,… for occupied and , , … for virtual orbitals. Greek letters are used for spin labels. The matrix is introduced which, using Kohn–Sham density functional theory, has the form
| [S3] |
where is defined as
| [S4] |
and as
| [S5] |
The Fukui function, , can be calculated analytically as
| [S6] |
where the lable indicates the frontier molecular orbital used in the expression. As such three Fukui functions can be calculated: for electron withdrawal using the HOMO orbital, for electron addition using the LUMO orbital, and , calculated as the average of and . Similarly, the hardness , can be calculated analytically as well:
| [S7] |
All molecules were optimized using Gaussian 09 (revision B.01) at PBE/cc-pVDZ. (31) Whenever alchemical changes in functional groups are considered, the molecule with the methyl group was optimized as a whole and subsequently the NH2, OH, and F groups were optimized while fixing the backbone of the molecule. For these alchemical changes, the basis functions of the target functional groups were added to eliminate basis set effects. The MO coefficients were read in from the formatted checkpoint files and Eqs. S2, S6, and S7 have been calculated using a program developed in-house. The Libxc library was used for the calculation of the second-order derivatives of the exchange correlation functional (Eq. S5) (32). The iterative Hirshfeld method was used for population analysis. (21, 22)
Acknowledgments
S.F. thanks the Research Foundation Flanders for financially supporting his postdoctoral research at the General Chemistry (ALGC) group. This work was supported by grants from the Natural Sciences and Engineering Research Council and Compute Canada (to P.W.A. and F.H.-Z.) and the Free University of Brussels through a Strategic Research Program grant to the ALGC group (to P.G.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1615053114/-/DCSupplemental.
References
- 1.McNaught AD, Wilkinson A, editors. IUPAC Compendium of Chemical Terminology. 2nd Ed Blackwell Science; Oxford: 1997. [Google Scholar]
- 2.Kohn W, Yaniv A. Locality principle in wave mechanics. Proc Natl Acad Sci USA. 1978;75:5270–5272. doi: 10.1073/pnas.75.11.5270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Greengard L, Rokhlin VI. A fast algorithm for particle simulations. J Comput Phys. 1987;73:325–348. [Google Scholar]
- 4.Li XP, Nunes RW, Vanderbilt D. Density-matrix electronic-structure method with linear system-size scaling. Phys Rev B. 1999;47:10891–10894. doi: 10.1103/physrevb.47.10891. [DOI] [PubMed] [Google Scholar]
- 5.Kohn W. Density functional and density matrix method scaling linearly with the number of atoms. Phys Rev Lett. 1996;76:3168–3171. doi: 10.1103/PhysRevLett.76.3168. [DOI] [PubMed] [Google Scholar]
- 6.Flocke N, Bartlett RJ. A natural linear scaling coupled-cluster method. J Chem Phys. 2004;121:10935–10944. doi: 10.1063/1.1811606. [DOI] [PubMed] [Google Scholar]
- 7.Hughes TF, Bartlet RJ. Transferability in the natural linear-scaled coupled-cluster effective Hamiltonian approach: Applications to dynamic polarizabilities and dispersion coefficients. J Chem Phys. 2008;129:054105. doi: 10.1063/1.2961037. [DOI] [PubMed] [Google Scholar]
- 8.Prodan E, Kohn W. Nearsightedness of electronic matter. Proc Natl Acad Sci USA. 2005;102:11635–11638. doi: 10.1073/pnas.0505436102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Prodan E, Kohn W. Nearsightedness of electronic matter in one dimension. Phys Rev B. 2006;73:085108. doi: 10.1073/pnas.0505436102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bader RFW. Nearsightedness of electronic matter as seen by a physicist and a chemist. J Phys Chem A. 2008;112:13717–13728. doi: 10.1021/jp806282j. [DOI] [PubMed] [Google Scholar]
- 11.Cárdenas C, et al. Chemical reactivity descriptors for ambiphilic reagents: Dual descriptor, local hypersoftness, and electrostatic potential. J Phys Chem A. 2009;113:8660–8667. doi: 10.1021/jp902792n. [DOI] [PubMed] [Google Scholar]
- 12.Yang W. Direct calculation of electron density in density-functional theory. Phys Rev Lett. 1991;66:1438–1441. doi: 10.1103/PhysRevLett.66.1438. [DOI] [PubMed] [Google Scholar]
- 13.Geerlings P, De Proft F, Langenaeker W. Conceptual density functional theory. Chem Rev. 2003;103:1793–1874. doi: 10.1021/cr990029p. [DOI] [PubMed] [Google Scholar]
- 14.Geerlings P, Fias S, Boisdenghien Z, De Proft F. Conceptual DFT: Chemistry from the linear response function. Chem Soc Rev. 2014;43:4989–5008. doi: 10.1039/c3cs60456j. [DOI] [PubMed] [Google Scholar]
- 15.Berkowitz M, Parr RG. Molecular hardness and softness, local hardness and softness, hardness and softness kernels, and relations among these quantities. J Chem Phys. 1988;88:2554–2557. [Google Scholar]
- 16.Yang W, Parr RG. Hardness, softness, and the Fukui function in the electron theory of metals and catalysis. Proc Natl Acad Sci USA. 1985;82:6723–6726. doi: 10.1073/pnas.82.20.6723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Parr RG, Yang W. Density functional approach to the frontier-electron theory of chemical reactivity. J Am Chem Soc. 1984;106:4049–4050. [Google Scholar]
- 18.Parr RG, Pearson RG. Absolute hardness: Companion parameter to absolute electronegativity. J Am Chem Soc. 1983;105:7512–7516. [Google Scholar]
- 19.Yang W, Cohen AJ, De Proft F, Geerlings P. Analytical evaluation of Fukui functions and real-space linear response function. J Chem Phys. 2012;136:144110. doi: 10.1063/1.3701562. [DOI] [PubMed] [Google Scholar]
- 20.Yang W, Mortier WJ. The use of global and local molecular parameters for the analysis of the gas-phase basicity of amines. J Am Chem Soc. 1986;108:5708–5711. doi: 10.1021/ja00279a008. [DOI] [PubMed] [Google Scholar]
- 21.Hirshfeld FL. Bonded-atom fragments for describing molecular charge densities. Theor Chim Acta. 1977;44:129–138. [Google Scholar]
- 22.Bultinck P, Van Alsenoy C, Ayers P, Carbó-Dorca R. Critical analysis and extension of the Hirshfeld atoms in molecules. J Chem Phys. 2007;126:144111. doi: 10.1063/1.2715563. [DOI] [PubMed] [Google Scholar]
- 23.Sablon N, De Proft F, Geerlings P. The linear response kernel: Inductive and resonance effects quantified. J Phys Chem Lett. 2010;1:1228–1234. [Google Scholar]
- 24.von Lilienfeld OA, Lins RD, Rothlisberger U. Variational particle number approach for rational compound design. Phys Rev Lett. 2005;95:153002. doi: 10.1103/PhysRevLett.95.153002. [DOI] [PubMed] [Google Scholar]
- 25.von Lilienfeld OA. First principles view on chemical compound space: Gaining rigorous atomistic control of molecular properties. Int J Quant Chem. 2013;113:1676–1689. [Google Scholar]
- 26.Cárdenas C, Echegaray E, Chakraborty D, Anderson JSM, Ayers PW. Relationships between the third-order reactivity indicators in chemical density-functional theory. J Chem Phys. 2009;130:244105. doi: 10.1063/1.3151599. [DOI] [PubMed] [Google Scholar]
- 27.Karelson M, Lobanov VS, Katritzky AR. Quantum-chemical descriptors in qsar/qspr studies. Chem Rev. 1996;96:1027–1043. doi: 10.1021/cr950202r. [DOI] [PubMed] [Google Scholar]
- 28.Bajorath J, et al. Navigating structure–activity landscapes. Drug Discov Today. 2009;14:698–705. doi: 10.1016/j.drudis.2009.04.003. [DOI] [PubMed] [Google Scholar]
- 29.Fujita T, Winkler D. Understanding the roles of the “two qsars”. J Chem Inf Model. 2016;56:269–274. doi: 10.1021/acs.jcim.5b00229. [DOI] [PubMed] [Google Scholar]
- 30.Rupp M, Tkatchenko A, Müller KR, von Lilienfeld OA. Fast and accurate modeling of molecular atomization energies with machine learning. Phys Rev Lett. 2012;108:058301. doi: 10.1103/PhysRevLett.108.058301. [DOI] [PubMed] [Google Scholar]
- 31.Frisch MJ, et al. 2010. Gaussian 09, revision b.01 Gaussian Inc., Wallingford, CT)
- 32.Marques MAL, Oliveira MJT, Burnus T. Libxc: A library of exchange and correlation functionals for density functional theory. Comput Phys Commun. 2012;183:2272–2281. [Google Scholar]
- 33.Verstraelen T, et al. 2016 Horton 2.0.1. Available at theochem.github.com/horton/. Accessed August 28, 2017.