In silico evidence for sequence-dependent nucleosome sliding

Significance

The dynamic compaction of DNA into chromatin is essential for gene expression. Errors during compaction are associated with numerous diseases. Several molecular factors are known to affect chromatin dynamics, but their relative importance and the interplay between them are poorly understood. A detailed molecular model is used here to examine chromatin dynamics at the level of its most fundamental building block, namely the nucleosome. Nucleosome dynamics are demonstrated to be encoded in the DNA sequence itself, and key fundamental factors are uncovered that can significantly alter these dynamics at the molecular level. The results serve to complete a hitherto unavailable description of nucleosome dynamics by introducing previously unappreciated molecular processes, with the potential to influence macroscopic chromatin structure and genetics.

Abstract

Nucleosomes represent the basic building block of chromatin and provide an important mechanism by which cellular processes are controlled. The locations of nucleosomes across the genome are not random but instead depend on both the underlying DNA sequence and the dynamic action of other proteins within the nucleus. These processes are central to cellular function, and the molecular details of the interplay between DNA sequence and nucleosome dynamics remain poorly understood. In this work, we investigate this interplay in detail by relying on a molecular model, which permits development of a comprehensive picture of the underlying free energy surfaces and the corresponding dynamics of nucleosome repositioning. The mechanism of nucleosome repositioning is shown to be strongly linked to DNA sequence and directly related to the binding energy of a given DNA sequence to the histone core. It is also demonstrated that chromatin remodelers can override DNA-sequence preferences by exerting torque, and the histone H4 tail is then identified as a key component by which DNA-sequence, histone modifications, and chromatin remodelers could in fact be coupled.

The basic building block of eukaryotic chromatin is the nucleosome, a DNA–protein complex containing 147 bp of DNA wrapped around a disk-like protein complex known as the histone octamer (1). Since nucleosomal DNA is inaccessible to other DNA-binding proteins, such as transcription factors and polymerases (2–4), the locations of nucleosomes represent an important mechanism by which cellular processes are controlled. Notably, nucleosome positions are dynamic, with changes in transcription levels, cellular state, and environmental factors resulting in different packagings of chromatin (5, 6). Proper packaging of genomic DNA is critical to cellular function, and a wide range of human diseases have been associated with defects in chromatin structure (7, 8). Understanding the molecular factors that control the locations of nucleosomes, and how they are dynamically modulated, therefore represents a central goal of molecular biology and biophysics.

It is now appreciated that the DNA sequence itself represents a key factor that governs the locations of nucleosomes. Different DNA sequences exhibit different affinities for the histone proteins, and as such, they form nucleosomes with probabilities that can differ by several orders of magnitude (9, 10). The dependence of nucleosome locations on DNA sequence originates from subtle differences in the intrinsic shape and flexibility of a specific DNA sequence, which lead to favorable electrostatic interactions between the DNA backbone and residues on the histone surface (11). In fact, this pronounced dependence on DNA sequence has led several authors to propose that a genetic code exists (12, 13) where the positions of 50% of nucleosomes in vivo are dictated by DNA sequence alone. Such a view, however, is not without controversy (14, 15), and a better understanding of the underlying processes must be developed.

Given that DNA sequence is largely constant throughout the life of a cell, other mechanisms must also be at play to achieve the dynamic nucleosome repositioning necessary for cellular function. One part of this dynamic regulation is accomplished by chromatin remodelers, ATP-dependent proteins within the nucleus that actively reposition nucleosomes along the genome (16). Chromatin remodelers can facilitate many different modifications to chromatin by positioning (17) or removing (18, 19) nucleosomes from promoters or by evenly spacing nucleosomes across sections of DNA (20–22). They are central to genetic compaction because, in their absence, nucleosome diffusion is extremely slow, typically on the time scale of hours (23–25). Chromatin remodelers accelerate the packaging of DNA by moving nucleosomes away from their sequence-directed binding locations into metastable positions. The mechanism by which these metastable nucleosomes relax back to their equilibrium locations represents an important process through which DNA sequence and chromatin dynamics are coupled.

Several studies have sought to elucidate the mechanism by which DNA repositions around the nucleosome. One group of studies has led researchers to propose a “loop propagation” model, where DNA loops are introduced into one side of the nucleosome and then move along the histone core in an inchworm-like manner (26–31). Another group of studies has led authors to propose a “twist diffusion” model, in which a twist defect in the natural helicity of nucleosomal DNA is first introduced and then diffuses around the nucleosome in a corkscrew-like motion (32–35). Several single-molecule measurements suggest a repositioning mechanism that cannot be classified into any of these models (36, 37). There is considerable evidence in support of each model, and it is likely that these repositioning mechanisms are not mutually exclusive but arise depending on other factors, including the DNA sequence (38). Because chromatin is inherently dynamic, elucidating the mechanisms by which nucleosomes are rearranged, both in the presence and absence of chromatin remodelers, is of considerable scientific interest.

Both sequence and dynamics do matter, but the relationship between these factors has been difficult to elucidate by relying exclusively on experiments. A major obstacle to developing a comprehensive picture of nucleosome repositioning is the lack of sequence-dependent studies on the mechanism of chromatin repositioning. Some of the effects of DNA sequence on nucleosome mobility have been explored (21, 36, 39). However, the vast majority of studies on nucleosome repositioning (22, 37, 40–44) have only considered the 601 positioning sequence (9), which exhibits a particularly strong affinity for histones. Such studies have led to valuable insights, but it remains unclear if or to what extent observations pertaining to the 601 sequence can be generalized to other, naturally occurring, nonsynthetic, DNA sequences. Note that the lack of sequence-dependent studies even extends to high-resolution crystal structures of the nucleosome, which are only available for several DNA sequences (45). Several models now assume that a bias exists toward nucleosome affinity depending on sequence, but little work (38, 46) has been done to understand the effects of sequence on the dynamics of nucleosome positions and how DNA sequence might impact the underlying mechanism of nucleosome rearrangement.

In this work, we investigate the interplay of DNA sequence and nucleosome repositioning dynamics in detail, by using a molecular model of the nucleosome. By relying on a variety of advanced simulation techniques, we characterize the effect of DNA sequence on both the free energies of nucleosome arrangement as well as the time scales over which they occur. Our results indicate that different DNA sequences do indeed rely on different mechanisms to reposition, through pathways reminiscent of both the loop propagation and twist diffusion models described above. However, our results demonstrate that the original formulation of these previously proposed mechanisms is incomplete and identify several molecular details of the histone surface that play crucial roles in repositioning. Lastly, we examine the effect of applied forces on nucleosomal dynamics and suggest that nucleosome remodelers can override certain sequence-based positioning preferences by applying torque to nucleosomal DNA. Taken together, our results serve to provide a more comprehensive picture of the effect of DNA sequence on nucleosome repositioning dynamics than was previously available and will help develop an understanding of the dynamic molecular processes that occur within chromatin.

Results

To examine nucleosome repositioning, we rely on a coarse-grained model of the nucleosome that combines the “3 Site Per Nucleotide” (3SPN) model of DNA with the “Atomic-Interaction-based Coarse-Grained” (AICG) model of proteins (47, 48). By combining detailed, fully validated models of DNA (49) and proteins (50), the 3SPN-AICG combination has been demonstrated to accurately reproduce experimental measurements of both the tension-dependent and sequence-dependent binding free energies of nucleosome formation without introducing adjustable parameters (48). Importantly, no information from the nucleosome crystal structure (51) or locations of DNA–histone contacts are rigidly fixed in our model; instead, all energies, conformations, and dynamics arise naturally from the DNA and protein force fields, which include explicit Coulombic interactions between the negatively charged DNA phosphate groups and the charged residues on the histone proteins (see Materials and Methods). As such, the 3SPN-AICG model can be viewed as truly predictive and is an appropriate choice for a molecular-level investigation of DNA repositioning.

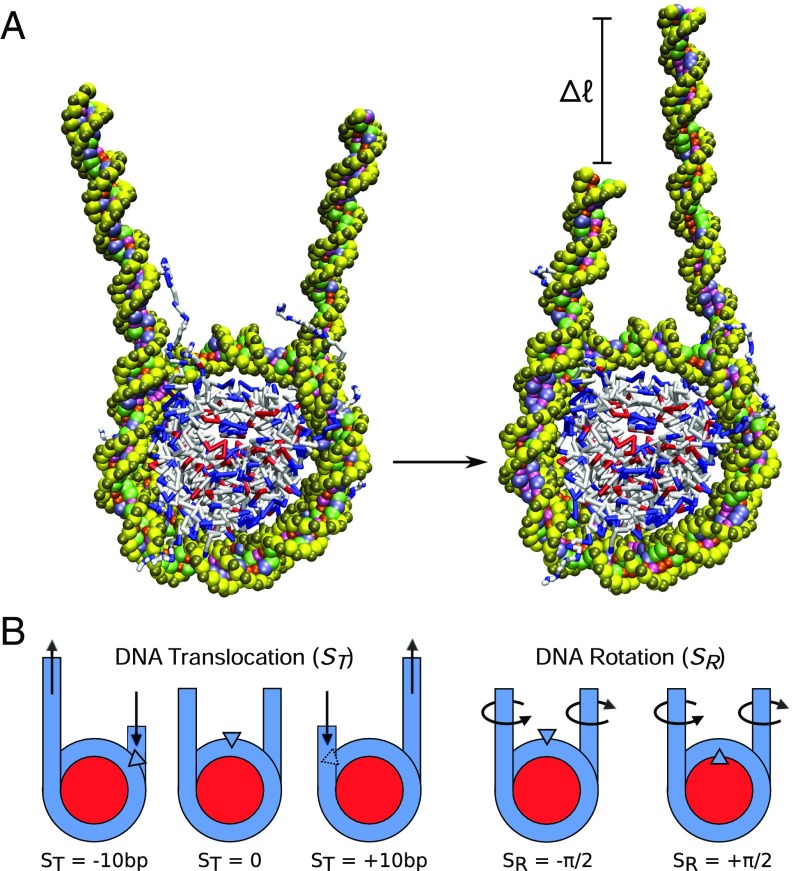
Two representative 3SPN-AICG molecular configurations of relevance to nucleosome sliding are shown in Fig. 1A. They contain 223 bp of DNA, of which 147 bp are initially incorporated into the nucleosome, with 38 flanking base pairs on each side. Since we are primarily concerned with the mechanism of small rearrangements of DNA ($<20$ bp), 38 flanking bases were used to minimize boundary effects that might arise from the free DNA ends. To characterize the degree of nucleosome sliding, an order parameter is defined, $S_T$, which represents the translocational position of the central base pair relative to the histone dyad (Fig. 1B and Materials and Methods). Here $S_T$ is given in units of base pairs (bp), with $S_T\approx \mathrm{\hspace{0.17em}0}$ bp corresponding to the native binding position of a DNA sequence and $S_T=\pm 10$ corresponding to a translocation of the DNA by one helical turn forward (+) or backward (−) relative to the histone dyad.

Fig. 1.

Molecular configurations of nucleosome repositioning. (A) Molecular representation of repositioning using coarse-grained nucleosome model. The chief aim of this study is to characterize the molecular mechanism by which this repositioning occurs. (B) Order parameters used to characterize DNA translocation, $S_T$, and rotational position, $S_R$, relative to the histone proteins.

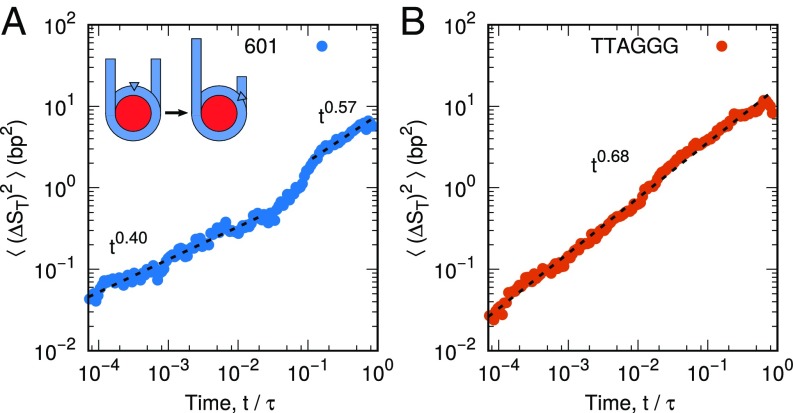
To characterize the time scales at play during nucleosome repositioning, we first compute the mean-squared displacement (over short to intermediate times), $⟨{\left(\mathrm{\Delta }{S}_T\right)}^2⟩$, of DNA around the histone core for two different DNA sequences (Fig. 2). In this analysis, time is reported in units of $\tau$, the characteristic time scale of DNA unwrapping (see Materials and Methods). The first sequence, denoted “601,” contains the strongly positioning 601 sequence discovered by Lowary and Widom (9). In contrast, the second sequence is a “TTAGGG” repeat, a sequence found in the telomeres of human chromosomes (52, 53) that positions nucleosomes poorly (39, 54). Both sequences are characterized by anomalous subdiffusion, with scaling exponents ranging from 0.4 to 0.69 for all time scales below $\tau$. Subdiffusion here was expected; entire nucleosomes are known to reposition on the time scale of minutes to hours (23–25) and would not be expected to exhibit diffusive motion ($⟨{\left(\mathrm{\Delta }{S}_T\right)}^2⟩\sim t$) on the time and length scales considered here.

Fig. 2.

Mean-squared displacement of nucleosomal DNA around histone proteins for (A) 601 positioning sequence and (B) TTAGGG repeat. Both DNA sequences exhibit anomalous diffusion, but the 601 positioning sequence contains two dynamic regimes, while the TTAGGG repeat only contains one. This difference suggests that DNA with different sequences might translate using different mechanisms. Averaging was performed over 100 independent molecular trajectories.

What was not expected, however, was the qualitative differences between the dynamics of the two different sequences. Whereas the TTAGGG repeat is characterized by a single dynamic regime (i.e., $\sim t^{0.68}$ for all times), the 601 sequence is observed to demonstrate two dynamic regimes: a strongly subdiffusive regime ($\sim t^{0.40}$) for short time scales $<{\mathrm{\hspace{0.17em}10}}^{-2}\tau$, and a weakly subdiffusive regime ($\sim t^{0.57}$) at longer times $>{\mathrm{\hspace{0.17em}10}}^{-1}\tau$. These results suggest that the 601 sequence might reposition via a slow mode at short times, characterized by little DNA motion, followed by a faster mode at longer times, where DNA repositions more rapidly. More generally, the fact that motion of the TTAGGG repeat exhibits one time scale, whereas the 601 sequence exhibits two, leads us to hypothesize that these two DNA sequences reposition via different mechanisms.

Sequence-Dependent Nucleosome Sliding

To explore this possibility, we focus on the free energy surface of DNA repositioning. An additional order parameter is introduced, $S_R$, which corresponds to the rotational position of DNA relative to the histone proteins. $S_R$ measures what side of the DNA double helix is facing the histone core, with $S_R=\pm \pi /2$ corresponding to the major groove (+) or the minor groove (−) facing the protein core (see Fig. 1B and Materials and Methods). Combined with $S_T$, which quantified the translocational position of DNA, these two order parameters provide a relatively complete description of the position of DNA wrapped around the histone core.

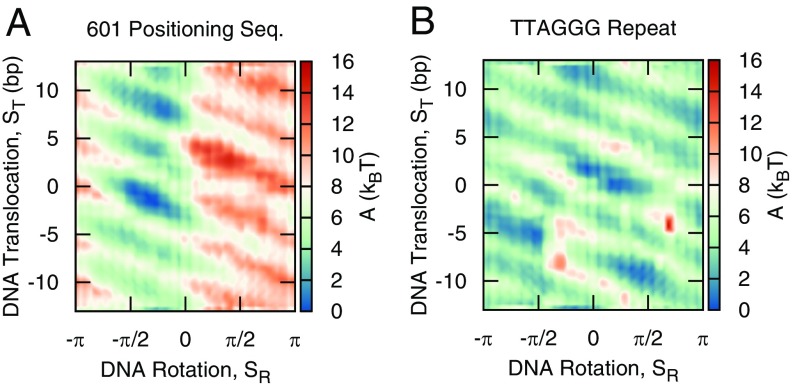
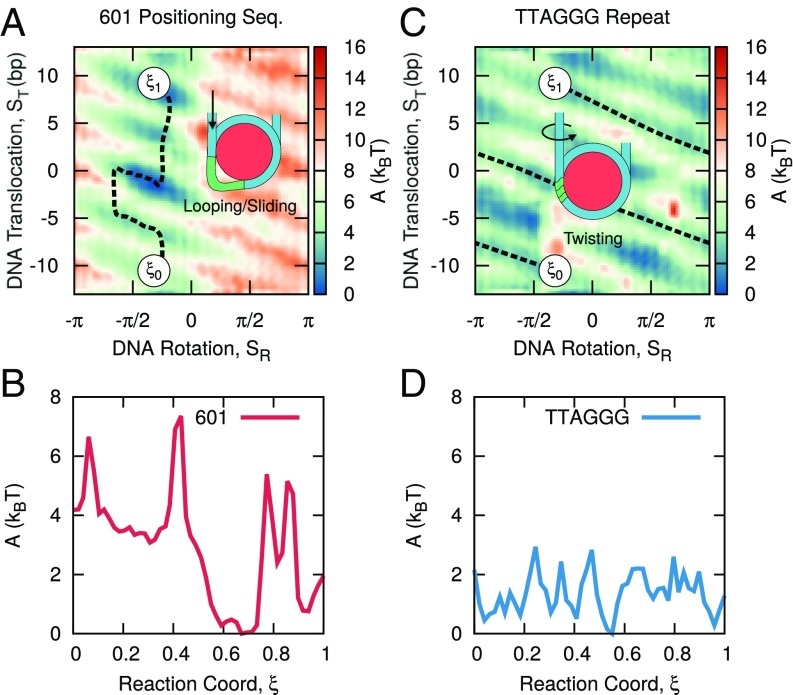
Fig. 3 shows the free energy surfaces as a function of $S_T$ and $S_R$ for the 601 sequence and the TTAGGG repeat. As with the mean-squared displacement measurements, the two free energy surfaces are considerably different. The free energy surface of the 601 sequence reveals a strong tendency for both translocational and rotational positioning. More specifically, the free energy minimum corresponds to translocational DNA positions with the 601 sequence centered on the nucleosome ($S_T\approx \mathrm{\hspace{0.17em}0}$) and with the minor groove facing the histone core ($-\pi /2>S_R>0$). DNA movement away from these strongly bound configurations leads to large free energy penalties. The location of this minimum corresponds well with the experimentally established position of the 601 sequence (55) (see Fig. S1) and serves as further validation that the 3SPN-AICG model can accurately capture DNA sequence effects within the nucleosome. The free energy surface of the TTAGGG repeat lacks the pronounced translocational and rotational positioning preferences of the 601 sequence and is characterized by a diffuse and relatively flat free energy surface.

Fig. 3.

Free energy surface of DNA repositioning for (A) 601 positioning sequence and (B) TTAGGG repeat. The 601 sequence demonstrates strong rotational, $S_R$, and translocational, $S_T$, positioning preferences, whereas the TTAGGG repeat does not.

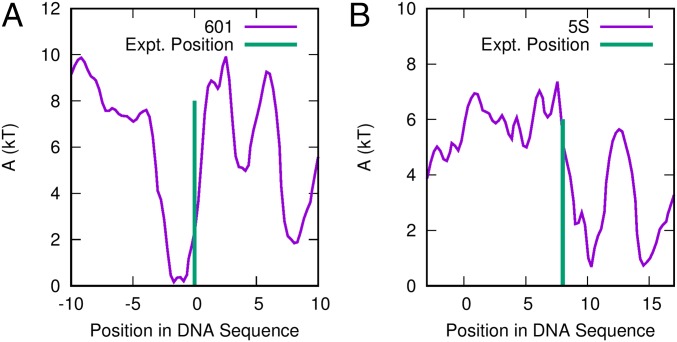
Fig. S1.

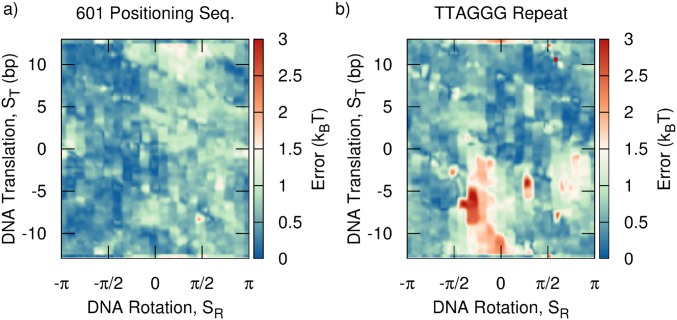
Sequence-dependent positioning free energies predicted by the model presented in this work. (A) The 601 positioning sequence of Lowary et al. (9) and (B) 5S positioning sequences. The experimental binding locations of these sequences are given by Morozov et al. (55) and Flaus et al. (76), respectively.

Given these differences, it is reasonable to anticipate that these two DNA sequences would reposition through different mechanisms. To infer such mechanisms from the free energy surfaces, we rely on the “String Method,” as implemented in the SSAGES package (see Materials and Methods), to calculate the minimum energy path corresponding to a 20 bp rearrangement from ${\xi }_0$ to ${\xi }_1$ (Fig. 4). Since this minimum-energy path corresponds to the most probable transition from ${\xi }_0$ to ${\xi }_1$, the resulting string can be used to infer the most likely mechanism of DNA rearrangement.

Fig. 4.

Minimum free energy path corresponding to 20 bp of DNA translocation for (A and B) 601 positioning sequence and (C and D) TTAGGG repeat. (A) The 601 sequence exhibits a minimum energy path similar to loop propagation, whereas (B) the TTAGGG repeat exhibits a path characteristic of twist diffusion. (C) The corresponding energy barriers along this path are large for the 601 positioning sequence and (D) relatively small for the TTAGGG repeat.

For the 601 sequence (Fig. 4A), we observe that the mechanism of DNA repositioning is almost independent of rotational position. The minimum energy path is characterized by two distinct modes: One is characterized by increasing $S_T$ at constant $S_R$, and the other is characterized by changing $S_R$ at near-constant $S_T$. Notably, these two modes alternate semiperiodically, with the first mode always followed by the second (and vice versa). The free energy along this path (Fig. 4B) indicates that the regions corresponding to this first mode are associated with large free energy barriers (e.g., $\xi =\mathrm{\hspace{0.17em}0.05},0.4,0.8$), whereas regions corresponding to the second mode have a flat free energy surface (e.g., $\xi =\mathrm{\hspace{0.17em}0.2},0.6$). This mechanism is consistent with the loop propagation model described above, where DNA translocation is achieved independently of DNA rotation.

In contrast, the minimum energy path for the TTAGGG repeat exhibits a strong coupling between DNA translocation, $S_T$, and DNA rotation, $S_R$ (Fig. 4C). In fact, the relationship between $S_T$ and $S_R$ observed here corresponds exactly to the 10 bp pitch of DNA: One complete rotation of DNA leads to a translocation of 10 bp. This translocation–rotation coupling is similar to the twist diffusion model, in which DNA repositions via a corkscrew-like motion, where DNA translocation is accompanied by DNA rotation to maintain minor-groove contacts with the histone protein. The energy surface corresponding to this mechanism is rough, with barriers $\approx \mathrm{\hspace{0.17em}2}{k}_{B}T$, but largely uniform, with no global translocational positioning preferences across the 20 bp region considered here (Fig. 4D).

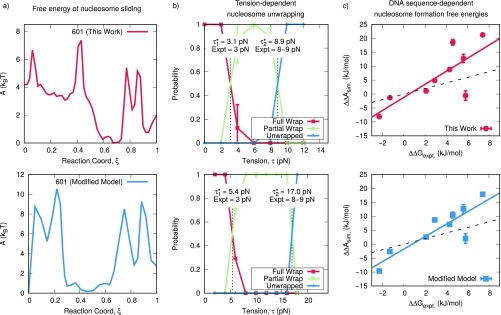
In previous work, Schiessel et al. estimated that the energy barriers of DNA loop formation are $\approx \mathrm{\hspace{0.17em}20}{k}_{B}T$ (26), whereas other work by Kulíc and Schiessel estimate the energy barriers of twist defects to be 1 to 2 $k_{B}T$ for some DNA sequences and $8-\mathrm{\hspace{0.17em}10}{k}_{B}T$ for others (27). Other work by Tolstorukov et al. has estimated barriers that are much higher at $\approx \mathrm{\hspace{0.17em}50}-\mathrm{\hspace{0.17em}100}{k}_{B}T$ (56). The energy barriers reported in our work are comparable to the predictions of refs. 26, 27 and are somewhat lower than those of ref. 56. We note that these past models rely heavily on nucleosome crystal structures to make assumptions about the locations of contacts between the DNA and histones. Our model makes no such assumptions about the locations of these DNA–histone contacts, and it incorporates them through explicit molecular interactions between the DNA and histone proteins. This feature permits our model to account for the effects of thermal fluctuations and the concomitant configurational sampling when determining the free energies of nucleosomal DNA. Additionally, our model simultaneously explains the free energies of sequence-dependent nucleosome formation (47), nucleosome unwrapping (48), and in this work, nucleosome repositioning (Fig. S2). Though previous models have examined these phenomena individually, a comprehensive view of the nucleosome requires that a wide range of experimental measurements are matched and explained simultaneously by a single model, as in our approach here.

Fig. S2.

Comparison of model presented in this work (Top) and a modified model (Bottom). The modified model contains stronger DNA–histone interactions and is described in detail in The Energies of Nucleosome Sliding are Not Independent from Other Biophysical Measurements. (A) Free energies of nucleosome sliding. Top is reproduced from Fig. 4B; Bottom is calculated using the modified model. (B) Tension-dependent nucleosome unwrapping. Top corresponds to figure 3B of ref. 48; Bottom corresponds to the modified model. ${\tau }_1^{\ast }$ and ${\tau }_2^{\ast }$ correspond to the unwrapping tensions of the outer and inner DNA turns, respectively. Experimental data are from Miharadja et al. (75). (C) Sequence-dependent nucleosome formation energies for the model used in this work (Top) and modified model (Bottom). The solid line corresponds to a linear fit; the dashed line corresponds to quantitative agreement. Detailed descriptions of the methods used in B and C can be found in ref. 48.

We should also note that the minimum energy paths observed in Fig. 4 are not strictly equivalent to the “loop diffusion” and “twist defect” mechanisms described in the Introduction. Since the order parameters $S_R$ and $S_T$ were defined to give the global translocational and rotational position of nucleosomal DNA, they do not resolve the detailed energies corresponding to the motion of a single twist or loop defect. Despite this, the sequence-dependent repositioning mechanism in Fig. 4 contains striking similarities to the loop diffusion and twist defect mechanisms proposed elsewhere in the literature.

The minimum free energy paths observed in Fig. 4 can also be used to explain the mean-squared displacement measurements shown in Fig. 2. The single dynamic regime observed for the TTAGGG repeat (Fig. 2B) is found to correspond to the uniform corkscrew-like motion of repositioning, which, from the minimum energy path, appears to be the dominant repositioning mode during DNA motion. The two dynamic regimes observed for the 601 sequence (Fig. 2A), however, correspond to the two modes of repositioning present in the minimum energy path. We can now interpret the slow repositioning mode ($\sim t^{0.57}$), as corresponding to the formation and propagation of DNA loops, where DNA is translated quickly. The fast repositioning mode ($\sim t^{0.40}$) then corresponds to the small events that proceed the formation of the subsequent DNA loop.

Taken together, the dynamic and thermodynamic (i.e., free energy) evidence indicates that the 601 sequence and the TTAGGG repeat do indeed reposition through different processes, which are reminiscent of the loop propagation or twist defect mechanism, respectively. Note, however, that the 601 sequence and the TTAGGG repeat represent the two extremes of the DNA sequence affinity for the nucleosome; the free energy difference between the two corresponding nucleosomes is $\approx \mathrm{\hspace{0.17em}20}$ kJ/mol (9, 54). It is therefore unclear whether this result can be generalized to other sequences, especially naturally occurring genomic sequences with intermediate affinities for the nucleosome.

To investigate whether a truly sequence-dependent mechanism of repositioning indeed exists, we generated a small library of sequences across the range of binding free energies for the histone core. Binding free energies are given by $\mathrm{\Delta }\mathrm{\Delta }G$, with smaller values of $\mathrm{\Delta }\mathrm{\Delta }G$ corresponding to stronger DNA–histone binding. These sequences range from strongly bound sequences based on the 601 positioning sequence (9, 12) (c1/601, c2, c3) to intermediately bound sequences (57) (TG, TRGC, TG-T) to weakly bound sequences based on other telomeric repeat sequences (TTAGGG in mamals, TGTGTGGG in Saccharomyces cerevisiae, TTGGGG in Tetrahymena) (54, 58). For each of these sequences, we simulated 100 independent and unbiased realizations of nucleosome repositioning by first initializing the system at $S_T\approx \mathrm{\hspace{0.17em}0}$ and then performing molecular dynamics until $S_T=\pm 10$. The mechanism of repositioning (i.e., looping or twisting) as well as the repositioning time were examined for each realization. By performing this analysis over an ensemble of trajectories, we were able to generate a probabilistic picture of the different repositioning mechanisms and time scales that are dominant for different DNA sequences.

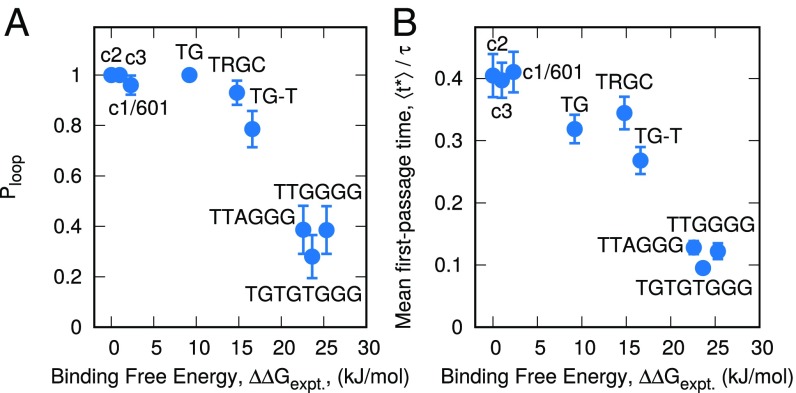
The mechanism of repositioning for our library of DNA sequences is illustrated in Fig. 5A. Consistent with our earlier results, it is strongly dependent on the binding free energy, $\mathrm{\Delta }\mathrm{\Delta }G$, of the DNA sequence. Strongly bound sequences (low $\mathrm{\Delta }\mathrm{\Delta }G$) are dominated by the loop propagation repositioning mechanism, with a looping probability, $P_{\text{loop}}\approx \mathrm{\hspace{0.17em}1}$. In contrast, weakly bound sequences, associated with high values of $\mathrm{\Delta }\mathrm{\Delta }G$, are dominated by DNA twisting. However, even though twisting dominates in these sequences, $P_{\text{loop}}=\mathrm{\hspace{0.17em}20}-\mathrm{\hspace{0.17em}40}\%$, indicating that DNA looping still occurs. Perhaps the most notable feature of Fig. 5A is that the transition between these two repositioning mechanisms is smooth, with intermediately binding sequences exhibiting both the looping and twisting mechanism. Importantly, this transition occurs over the range $\mathrm{\Delta }\mathrm{\Delta }G=\mathrm{\hspace{0.17em}10}-\mathrm{\hspace{0.17em}20}$ kJ/mol, which corresponds to almost all naturally occurring DNA sequences. In naturally occurring chromatin, our results therefore indicate that both twisting and looping mechanisms are present simultaneously.

Fig. 5.

Sequence-dependent nucleosome repositioning. (A) Probability of repositioning through a loop-like mechanism, $P_{\text{loop}}$, for different DNA sequences. Stronger binding sequences (low $\mathrm{\Delta }\mathrm{\Delta }G$) exhibit looping, whereas weaker binding sequences exhibit a twisting mechanism. (B) The mean first-passage time, $⟨{\tau }^{\ast }⟩$, of a 10-bp DNA translocation for a different DNA sequences. Despite the different repositioning mechanisms exhibited by these different sequences, $⟨{\tau }^{\ast }⟩$ displays a simple, near-linear decay with $\mathrm{\Delta }\mathrm{\Delta }G$.

We are not aware of other evidence suggesting that both mechanisms exist simultaneously for naturally occurring DNA sequences, and if correct, this result has important implications for the study of chromatin. Experimentally, it suggests that single-molecule experiments that rely on the 601 sequences may indeed be missing important physics that characterizes naturally occurring DNA sequences. More broadly, however, the simultaneous presence of both looping and twisting could represent an important mechanism for the coupling of DNA sequence and chromatin dynamics, with different combinations influencing the 3D structure of chromatin in both complementary and competing ways.

The time scale of repositioning as a function of DNA sequence can also be quantified from this ensemble of trajectories(Fig. 5B) by the mean first-passage time,$⟨{\tau }^{\ast }⟩$, corresponding to a transition from $S_T\approx \mathrm{\hspace{0.17em}0}$ to $S_T=\pm 10$. That time scale is found to be approximately linear with respect to $\mathrm{\Delta }\mathrm{\Delta }G$, even though the repositioning mechanism changes significantly over this range; $⟨{\tau }^{\ast }⟩$ appears to be largely independent of mechanism and is instead a simple function of the binding strength of the DNA to the histone surface.

A comment on the sheer magnitude of information contained within this ensemble of trajectories is in order. It consists of 100 independent simulations for 9 different DNA sequences, each of which encompasses at least 10 bp of DNA translocation. These trajectories consist of $350\tau$ of cumulative simulation time, whose spatial, near-Angstrom level resolution approaches that of fully atomistic representations. These trajectories are provided through our website (see Materials and Methods), and their analysis might yield additional insights into the structure and dynamics of the nucleosome with a spatial and temporal resolution that complements that of single-molecule experiments. In the section that follows, we further analyze this ensemble of trajectories to highlight additional details of pertaining to the loop propagation and twist diffusion repositioning events.

DNA Loops Are Distributed Unevenly on the Histone Surface.

Most theories suggest that, during loop propagation, DNA loops are first introduced in the outer wrap of the nucleosome, where the DNA is known to transiently disassociate from the histone core (59). Such theories suggest that these DNA loops then propagate deeper into the nucleosome, through the dyad, and then exit the nucleosome on the other side, thereby leading to a net DNA translocation (26). In this view, one might expect DNA loops to be, on average, evenly distributed across the histone surface, particularly since loops located at different regions in the nucleosome have comparable energies. However, by analyzing our ensemble of trajectories, we demonstrate that this traditional view of loop propagation is incomplete and that DNA loops are distributed unevenly on the histone surface.

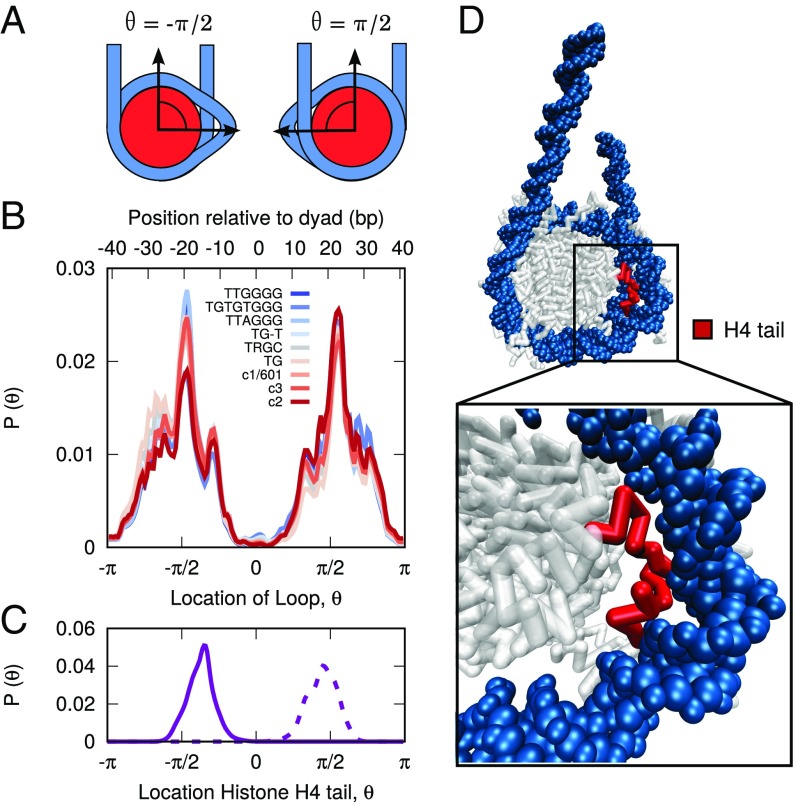
To quantify the position of loops in these trajectories, we first define a variable, $\theta$, that measures the location of loops on the histone surface (Fig. 6A; Materials and Methods). We then construct a histogram of the loop locations extracted from our trajectories, as shown in Fig. 6B. In contrast to the predictions of the loop diffusion model, we observe that loops are distributed in a highly uneven manner along the histone surface, with different regions on the histone either enhancing or inhibiting the formation of loops. Loops are rarely found at the histone dyad ($\theta =\mathrm{\hspace{0.17em}0}$) and are strongly favored at $\theta \approx \pm \pi /2$, a location $\pm 20$ bases from the dyad frequently referred to as SHL$\pm 2$. These loops are observed to be $\approx \mathrm{\hspace{0.17em}10}$ bp in size, and their locations are found to be insensitive to DNA sequence, with each of our nine DNA sequences exhibiting a similar histogram. This result was unexpected, since these different DNA sequences were observed to reposition by dramatically different mechanisms (cf Fig. 5A). This lead us to propose that the location of loops is dictated by a feature of the histone and not the DNA sequence.

Fig. 6.

Distribution of DNA loops on histone surface. (A) Diagram describing the relationship between $\theta$ and loops on the histone surface. (B) Distribution of loop positions for different DNA sequences. Loops are distributed unevenly on the histone surface, in a manner largely independent of DNA sequence. (C) Location of histone H4 tail. The H4 tail is colocalized with the location of DNA loops. (D) Molecular snapshot highlighting the role of the H4 tail in stabilizing DNA loops at $\theta \approx \pm \pi /2$, a position $\pm 20$ bp from the histone dyad.

One explanation for the observed distribution of loops could be the variable strength of different DNA–histone binding sites to DNA. Single-molecule experiments (40) have shown that certain regions of nucleosomal DNA are more strongly bound to the histone proteins than others (40). For the 601 sequence, these experiments identified three regions of strong DNA–histone binding, with the strongest binding observed at the histone dyad and two other regions at $\pm 40$ bp from the dyad. These three regions correspond exactly with regions in our calculations where looping is absent (Fig. 6B), implying that regions of strong DNA–histone binding suppress the formation of DNA loops. Additionally, the lack of sequence dependence in our results suggests that the strong binding regions observed in ref. 40 might be a general feature of nucleosome structure and not simply a specific feature of the 601 sequence used in the experiments.

The observed distribution of loops could also be related to the ability of histone tails to enhance the formation of loops at certain regions in the nucleosome. The location in the nucleosome where we observe the highest probability of loop formation ($\theta =\pm \pi /2$, SHL$\pm 2$) is also associated with the protrusion of the tail of histone H4 from the histone surface (1, 51). Our molecular trajectories show that the tail of histone H4 is strongly colocalized with the DNA loops, with the highest probability of being located at $\theta \approx \pm \pi /2$ (Fig. 6C). Beyond mere colocalization, however, our simulations suggest that the H4 tails are in fact critical for stabilizing the DNA loops present at $\theta =\pm \pi /2$. When molecular configurations that exhibit loops are visualized, the H4 tail is found to be bent backward toward the histone core and to be in contact with the in-facing side of the looped DNA (Fig. 6D). By adopting that orientation, the H4 tail stabilizes the formation of a loop by restoring the DNA–histone contacts that were originally disrupted. Through this process, the energy of loop formation at SHL$\pm 2$ is greatly reduced (and hence the high probability of finding loops at that position).

The H4 histone tail, and the DNA region at SHL$\pm 2$, is rapidly becoming a nexus for nucleosome repositioning phenomena. For many years, SHL$\pm 2$ has been known to exhibit increased structural variability in crystal structures (1, 60, 61) and is now associated with weak DNA–histone contacts (40). Furthermore, SHL$\pm 2$ is the site of DNA translocation inside the nucleosome (62) and is a known site where SWI/SNF and ISWI remodelers associate (63). Additionally, the H4 tail is now considered an integral component of chromatin remodeling, with H4 both facilitating remodeling at SHL$\pm 2$ (42) and playing a role in the mechanism by which ACF senses linker DNA length (41). Our results add to this chorus of results by identifying SHL$\pm 2$ as a location of prominent DNA looping, through a mechanism that is dependent on the H4 tail. Building on these previous studies, our results suggest a potential for cross-talk between the mechanism of repositioning, the H4 tail, and chromatin remodeler action.

The uneven distribution of loops also has important implications for the mechanism of DNA repositioning. Our observation that loops are rarely found at certain locations along the histone (i.e., $\theta =\mathrm{\hspace{0.17em}0},\pm \pi$) suggests that DNA loops do not slowly propagate across the histone surface as in the loop propagation model but instead rapidly localize to SHL$\pm$2. In this view, the H4 tail at SHL$\pm 2$ could function as a step-wise molecular ratchet, where a DNA loop is (1) pulled into the nucleosome and stored at SHL$\pm$2, (2) pulled across the dyad by the H4 tail on the other side at SHL$\mp$2), and finally (3) released from the nucleosome, thus leading to net nucleosome motion. Our simulations present evidence for this type of H4 tail-mediated repositioning event.

Nucleosome Mobility Can Be Enhanced Through an Applied Torque.

We now turn our attention to twist-diffusion repositioning. Since the results above indicate that DNA translocation and rotation are coupled in a corkscrew-like motion, chromatin remodelers could be expected to reposition nucleosomes through a “drill”-like mechanism. That is, a chromatin remodeler that applies a purely rotational torque to the DNA molecule could in fact facilitate translocational nucleosomal motion. It is also of interest to determine how DNA sequence, especially a sequence’s preference for looping or twisting, might influence this motion.

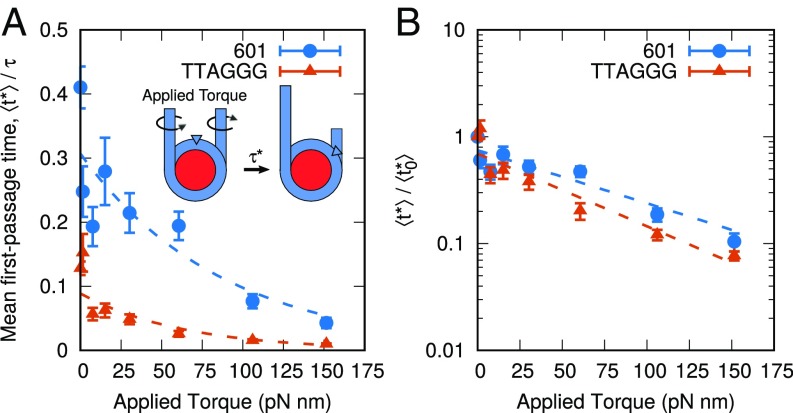
To examine this possibility, we applied a rotational torque to the DNA molecule (see Materials and Methods) and observed that a DNA can indeed be repositioned through a drill-like mechanism (Movie S1). This effect was then quantified by applying a range of rotational torques to the DNA molecule and measuring the effect on repositioning dynamics. The results are shown in Fig. 7. For both the TTAGGG repeat and the 601 sequences, repositioning times (as measured by $⟨{\tau }^{\ast }⟩$) are significantly reduced when torque is applied. Small torques, of $\approx \mathrm{\hspace{0.17em}8}$ pN nm, are sufficient to reduce the repositioning rate by more than 50%. For larger torques, the decay times follow a simple exponential form (dotted lines). It is of interest to note that when these results are normalized by the value corresponding to zero torque, ${\tau }_0^{\ast }$, both sequences collapse onto a single line (Fig. 7B). Since the TTAGGG repeat repositions through twisting, we had originally expected that its motion would be significantly enhanced when torque is applied. However, since the 601 sequence repositions through looping, an applied torque was not expected to have a large effect on the rate of repositioning. The fact that both sequences are affected equally by applied torque suggests that chromatin remodelers might in fact be able to overlook or bypass many sequence effects. By simply applying a torque, remodelers can override the sequence-dependent repositioning mechanisms (i.e., looping or twisting) and force DNA to reposition via a corkscrew-like motion. Further, even if the torques applied by these remodelers are small, the dynamics of nucleosomal DNA can be altered considerably.

Fig. 7.

Applied torque can mobilize nucleosomes. (A) Effect of applied torque on mean first-passage times, $⟨{\tau }^{\ast }⟩$, for 601 sequence and TTAGGG repeat. Small amounts of torque dramatically decrease $⟨{\tau }^{\ast }⟩$ with a dependence well fit by an exponential decay (dotted lines). (B) Upon renormalizing by the zero-torque value $⟨{\tau }_0^{\ast }⟩$, both sequences exhibit a similar dependence on applied torque. This suggests a mechanism by which chromatin remodelers override sequence-positioning preferences.

Conclusion

In this work, we present a coarse-grained molecular model that can simultaneously reproduce the free energies of sequence-dependent nucleosome formation, nucleosome unwrapping, and nucleosome repositioning. With this model, we provide in silico evidence that both the loop propagation and twist diffusion mechanisms can occur within the nucleosome. Our results indicate that such mechanisms depend on DNA sequence and that the binding free energy of a given DNA sequence is an excellent predictor of which is the dominant repositioning mechanism. The free energy is also correlated with the characteristic time scale corresponding to a particular repositioning event. It is found that for most naturally occurring DNA sequences, which exhibit a moderate binding energy, both looping and twisting repositioning mechanisms coexist. Importantly, a number of previously unknown features have been identified within the nucleosome as it repositions. These include an asymmetric distribution of DNA loops, a strong influence of the H4 tail in their formation, and the dominating effect of torques in the mobilization of nucleosomes.

One of the central findings of this work is that DNA sequence can lead to a wide range of mechanisms and dynamics of nucleosome positioning. However, we have also shown that certain features are not influenced by DNA sequence, including the locations of DNA loops, and the effect of torque on nucleosome mobility. Building on these findings, it will be important to pursue experimental studies that go beyond the 601 positioning sequence and toward naturally occurring, moderately binding DNA sequences. For cases where it is not possible to perform single-molecule experiments with genomic DNA sequences, the 3SPN-AICG model presented here can serve as a complementary tool to predict situations where sequence dependence might be important.

Materials and Methods

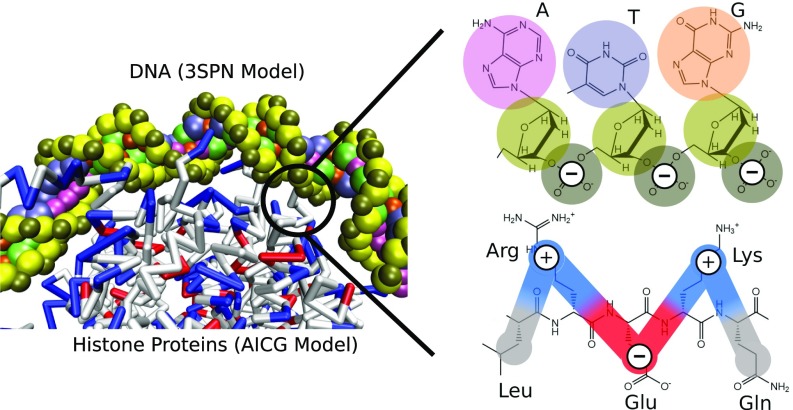
The model of the nucleosome is identical that that used previously (48), where DNA is represented by the 3SPN.2C model (63) and the histone proteins by the AICG model (50) (Fig. 8). The 3SPN.2C model is the latest version of the 3SPN model (64–66), where DNA is represented by three force sites, located at the center of mass of the phosphate, sugar, and base. The 3SPN.2 model has been parameterized to reproduce the melting of double-stranded to single-stranded DNA and correctly predicts the effects of DNA sequence and salt. Additionally, 3SPN.2C can reproduce the sequence-dependent curvature and sequence-dependent flexibility of DNA (63). The AICG used for the histone proteins represents each amino acid by a single site located at the center of mass of the side chain (50). Interactions between 3SPN.2C and AICG models are represented only by electrostatic and excluded volume effects as described previously (48). Electrostatic forces are introduced at the level of Debye–Hückel theory. All simulations were performed in the canonical ensemble using a Langevin thermostat and 150 mM ionic strength. The coarse-grained topology of the 3SPN-AICG model permits the simulation of very long time scales characteristic of nucleosome repositioning.

Fig. 8.

Description of coarse-grained nucleosome model. DNA is represented by the 3SPN.2C model (63), which represents each nucleotide by three sites located at the center-of-mass of the phosphate (brown), sugar (yellow), and base (pink, purple, orange, green). The histone proteins are represented by the AICG model (50), where each amino acid is represented by a single site, located at the center-of-mass of the amino acid side chain. Interactions between the DNA and histones are represented by Coulombic interactions at the level of Debye–Hückel theory. Phosphate sites of DNA are given a charge of −1, whereas protein sites are given a charge of −1, 0, +1 (red, white, and blue, respectively) corresponding to the charge of that amino acid under physiological pH. Nucleosome configurations and DNA–histone contacts in the 3SPN-AICG model arise naturally from a balance between these Coulombic interactions, with no bias toward the observed nucleosome crystal structure (51).

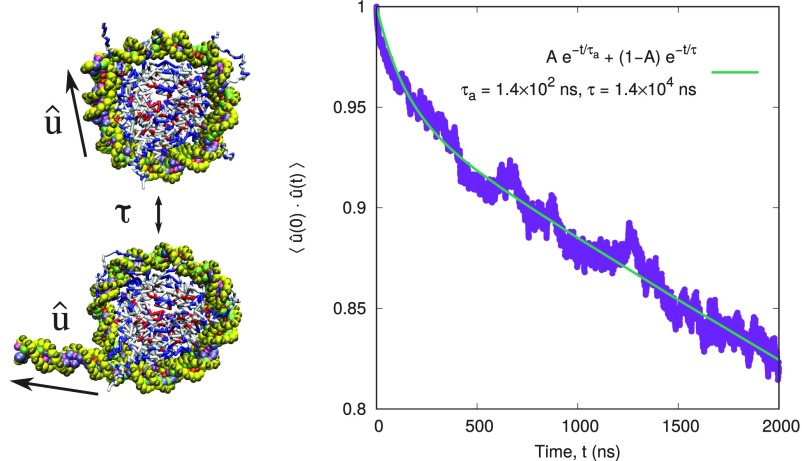
A Langevin thermostat represents the solvent implicitly, and the absolute magnitudes of the time scales predicted by this model are less informative than the relative ones. As a consequence, it is conventional to normalize the times in an implicit solvent simulation relative to some other time scale of interest, $\tau$. In this work, we define $\tau$ as the characteristic time scale of spontaneous nucleosomal DNA unwrapping as measured experimentally (59, 67). The details of the definition of $\tau$ and how it was computed are given in Fig. S3.

Fig. S3.

Timescale of nucleosome unwrapping. The time scale of nucleosome unwrapping is characterized by the autocorrelation function, $⟨\widehat{\text{𝒖}}(0)\widehat{\text{𝒖}}(t)⟩$, where $\widehat{\text{𝒖}}$ corresponds to the orientation of the 30 bp of entering nucleosomal DNA. The autocorrelation function is fit well to a two-exponential decay, $A{e}^{-t/{\tau }_a}+(1-A)e^{-t/\tau }$, where ${\tau }_a$ is a short time scale and $\tau$ is the time scale of interest.

We also note that the use of Debye–Hückel theory to represent the DNA–histone interactions in the 3SPN-AICG model neglects multivalent ions and water-mediated hydrogen bonds that have been suggested to mediate DNA–histone contacts (51). For this reason, the 3SPN-AICG model can only capture this complex electrostatic environment to the first order and may smooth out certain aspects of the nucleosome repositioning energy surface. Higher order approximations are available for the 3SPN model (68) but significantly limit the length and time scales that can be examined.

As an initial configuration to examine nucleosome repositioning, we use the 223 bp configuration used previously (48) based on the 1KX5 crystal structure (51) and a proposed structure of exiting nucleosomal DNA (69). We note that this configuration was only used as the initial configuration, and no information from either structure was directly encoded into the nucleosome model. For the c1/601, c2, c3, TG, TRGC, and TG-T sequences used, the 223 bp sequence was generated by taking the defined 147 bp sequence and periodically appending 38 bp on each side. Specifically, if $X_i$ denotes the identity of the $i$th base pair of a 147 bp DNA sequence, then the resulting 223 bp sequence would be $X_{109},X_{110},\mathrm{\dots },X_{147},X_1,\mathrm{\dots },X_{147},X_1,\mathrm{\dots },X_{38}$.

Order Parameters.

To characterize the movement of DNA around the histone proteins, we explicitly track the rotational and translocational position of the DNA relative to the protein dyad. To define the translocational position of the DNA molecule, we define an order parameter, $S_{\text{T}}$, defined as:

$$S_{\text{T}}=\frac{1}{\lambda }⟨\pm \text{arccos}\left(\frac{\text{𝑷}\cdot {\text{𝑷}}_0}{\parallel \text{𝑷}\parallel \parallel {\text{𝑷}}_0\parallel }\right)⟩,$$

where P is a vector from the center of a base step to the center of the protein, ${\text{𝑷}}_{\mathrm{𝟎}}$ is the value of P from the 1KX5 nucleosomal crystal structure (51), and the angle brackets denote an average over base steps at the −15, −5, +5, and +15 positions relative to the dyad. The positive sign is chosen if $\left(\text{𝑷}\times {\text{𝑷}}_0\right)\cdot \widehat{\text{𝒇}}\le \mathrm{\hspace{0.17em}0}$ (negative if $>0$), where $\widehat{\text{𝒇}}$ is a vector that points along the center of the nucleosomal DNA superhelix. Therefore, positive $S_{\text{T}}$ corresponds to “forward” translocation of DNA (toward 5’ end), whereas negative $S_{\text{T}}$ corresponds to “backward” motion (toward 3’ end) as shown in Fig. 1B. Lastly, $\lambda$ represents a conversion factor from radians to base pairs of DNA translocation and is defined as $\lambda =\mathrm{\hspace{0.17em}0.08}$ rad/bp. $\lambda$ is calculated by dividing the circumference of the histone proteins (1), $r\approx \mathrm{\hspace{0.17em}42}\text{Å}$, by $2\pi$ and the distance between adjacent base pairs, $3.3\text{Å}$.

The rotational position of DNA is defined by an order parameter, $S_{\text{R}}$, given by:

$$S_{\text{R}}=⟨\pm \text{arccos}\left(\frac{\text{𝑷}\cdot \text{𝑩}}{\parallel \text{𝑷}\parallel \parallel \text{𝑩}\parallel }\right)⟩,$$

where B is a vector from the center of a given base step on the sense strand to its complementary base step on the antisense strand and all other terms are the same as defined for $S_{\text{T}}$. The positive sign is chosen if $\left(\text{𝑷}\times \text{𝑩}\right)\cdot \text{𝑫}\le 0$ (negative if $>0$), where D is a vector in the 5’ to 3’ direction along the sense strand. Notably, when $S_{\text{R}}=-\pi /2$, the minor groove is oriented toward the protein core, and when $S_{\text{R}}=\pi /2$, it is oriented away from it (see Fig. 1B). The order parameter $S_{\text{R}}$ has been used previously to quantify the positioning preferences of different DNA sequences to the histone proteins (47).

To apply a torque to the DNA molecule, we simply applied a constant force along the $S_R$ order parameter. Since $S_R$ is defined as the average over four different DNA base steps, this applied torque is divided evenly among the base steps at −15, −5, +5, and +15 positions relative to the central base pair. By definition this force results in rotation of the DNA molecule around the histone proteins and can be converted to a torque using the diameter of the DNA.

Free Energy Methods.

Two-dimensional free energy surfaces (Fig. 3) were obtained along $S_{\text{T}}$ and $S_{\text{R}}$ using 2D umbrella sampling and WHAM (70, 71). Errors in these free energies were assessed by reconstructing three independent free energy surfaces and computing the SD. The majority of the free energy is found to be accurate to within $\pm 1k_{B}T$. The largest errors ($3k_{B}T$) correspond to large values of the free energy ($12k_{B}T$), leading to an acceptable relative error of $\approx \mathrm{\hspace{0.17em}25}\%$ (Fig. S4).

Fig. S4.

Error corresponding to free energy surfaces reported in Fig. 3. (A) 601 positioning sequence and (B) TTAGGG repeat. Errors were obtained from the SD of three independent free energy surfaces obtained by umbrella sampling, as described in the main text.

To determine probable reaction paths along these free energy surface (Fig. 4), we use the string method (72, 73), as implemented in the SSAGES package (miccomcodes.com). Rather than randomly guessing initial paths, we used a hybrid approach where the finite-temperature string method (73) was used at a high temperature to generate an ensemble of possible paths, which were then energy minimized using the zero-temperature string method (72). This hybrid approach was found to yield a much wider range of possible paths than the zero-temperature or finite-temperature string methods alone. Since the free energy surfaces used in the string method were obtained from a complex molecular system, they are expectedly rough, and many probable paths contained similar energies. Accordingly, the paths reported in Fig. 4 represent a representative minimum energy path chosen from an ensemble of possible paths predicted using the finite-temperature string.

Quantification of DNA Loop Locations.

To quantify the locations of DNA loops on the histone surface, it was necessary to first define an orthonormal basis to represent the rotational position of the histone proteins. This orthonormal basis consisted of three vectors, $\widehat{\text{𝒇}},\widehat{\text{𝒗}},\widehat{\text{𝒖}}$, where $\widehat{\text{𝒖}}$ points from the center of mass of the histone to the dyad, $\widehat{\text{𝒇}}$ (as defined above) points along the nucleosomal DNA superhelix, and $\widehat{\text{𝒖}}\times \widehat{\text{𝒇}}=\widehat{\text{𝒗}}$. After this basis was defined, the center of the DNA helical axis was calculated for each base pair using the Kahn method (74) as described previously (66). A vector was then constructed from the center of mass of the protein to the helical axis site of the $i$th base pair with orientation ${\widehat{\text{𝒘}}}_i^{\prime }$ and magnitude ${\mathrm{\ell }}_i=|{\text{𝒘}}_i^{\prime }|$. The vector rejection of ${\widehat{\text{𝒘}}}_i^{\prime }$ and $\widehat{\text{𝒇}}$, ${\widehat{\text{𝒘}}}_i={\widehat{\text{𝒘}}}_i^{\prime }-{\widehat{\text{𝒘}}}_i^{\prime }\cdot \widehat{\text{𝒇}}$ is computed, where ${\widehat{\text{𝒘}}}_i$ is the projection of ${\widehat{\text{𝒘}}}_i^{\prime }$ onto the plane containing $\widehat{\text{𝒗}}$ and $\widehat{\text{𝒖}}$, perpendicular to $\widehat{\text{𝒇}}$. The location of each base pair is then defined by the angle ${\theta }_i$, where ${\theta }_i=\text{arccos}({\widehat{\text{𝒘}}}_i\cdot \widehat{\text{𝒖}})$ (see Fig. 6A). This process characterizes each base pair of DNA by two values: ${\mathrm{\ell }}_i$ the distance of that base pair to the histone center of mass, and ${\theta }_i$ the location of the base pair relative to the dyad. Note that since DNA is dynamically repositioning, ${\theta }_i$ and ${\mathrm{\ell }}_i$ are not constant during a simulation. We therefore found it more useful to compute the average distances as a function of theta, $⟨\mathrm{\ell }(\theta )⟩$.

Next, to define whether a loop was present, we first construct a normalization curve, $⟨\overline{\mathrm{\ell }}(\theta )⟩$, which characterizes the average distance of a base pair at a given $\theta$ in the absence of loops. To ensure that loops did not form in this calculation, $⟨\overline{\mathrm{\ell }}(\theta )⟩$ was calculated at a very low salt for a strongly bound DNA sequence. $⟨\overline{\mathrm{\ell }}(\theta )⟩$ is then used to normalize $⟨\mathrm{\ell }(\theta )⟩$ to obtain $\mathrm{\Delta }\mathrm{\ell }(\theta )$, where $\mathrm{\Delta }\mathrm{\ell }(\theta )=⟨\mathrm{\ell }(\theta )⟩-⟨\overline{\mathrm{\ell }}(\theta )⟩$. Using this metric, in the absence of DNA loops, when DNA is in close contact with the histone surface, $\mathrm{\Delta }\mathrm{\ell }\approx \mathrm{\hspace{0.17em}0}$ for all $\theta$. However, when DNA loops form and DNA–histone contacts are disrupted, $\mathrm{\Delta }\mathrm{\ell }>\mathrm{\hspace{0.17em}0}$. We define loops as base pairs where $\mathrm{\Delta }\mathrm{\ell }(\theta )>\delta$, where $\delta$ is some predefined threshold. We choose $\delta =\mathrm{\hspace{0.17em}8}\text{Å}$, corresponding to the Debye length at 150 mM, the length at which the DNA–histone attraction has significantly decayed. Small variations in the value of $\delta$ had little effect on our results.

All simulation codes and results presented in this work are freely available from our website (datahub.uchicago.edu and miccomcodes.org).

Timescale of Nucleosome Unwrapping.

As stated in the main text, the 3SPN-AICG model uses Langevin dynamics, where the solvent is represented implicitly by a continuum. In Langevin dynamics, the time scale of a simulation is governed exclusively by $\zeta$, the drag coefficient of the solvent. By changing $\zeta$, the dynamics of a system can be scaled almost arbitrarily, and thus, the relative time scales are more important to consider than the absolute ones. For this reason, it is conventional to normalize all time Langevin dynamics calculations relative to a time scale of interest, $\tau$, to emphasize that relative time scales are important. In this work, we define $\tau$ as the characteristic time scale of spontaneous unwrapping of DNA from the histone core as measured experimentally (59, 67).

To calculate $\tau$, we first define a unit vector $\widehat{\text{𝒖}}$, which points from the center 30th DNA base pair within the nucleosome to the center of the first base pair entering it (see Fig. S3 snapshots). Because DNA is stiff over the 30 bp-length scales, $\widehat{\text{𝒖}}$ gives the orientation of the exiting 30 bp of nucleosomal DNA. We then calculate the autocorrelation $⟨\widehat{\text{𝒖}}(0)\widehat{\text{𝒖}}(t)⟩$ to characterize the time scale of DNA unwrapping (Fig. S3). We find that the autocorrelation function is fit well to a two-exponential decay, $A{e}^{-t/{\tau }_a}+(1-A)e^{-t/\tau }$, where ${\tau }_a$ is a fast time scale corresponding to local fluctuations in $\widehat{\text{𝒖}}$ and $\tau$ is the time scale of interest. Upon fitting, $\tau =\mathrm{\hspace{0.17em}1.4}\times {10}^4$ ns and is used to nondimensionalize the time scales in the main text. What emerges from this scaling is that the 10 bp repositioning times observed in our model are comparable to the timescale of unwrapping. This finding is consistent with the hypothesis by Widom and coworkers that spontaneous DNA unwrapping could be associated with nucleosome looping and remodeling (59).

Note that these calculations were performed using 147 bp of DNA, not the 223 bp of DNA used in the main text. We observed the time scales of unwrapping in the 223 bp system to be much slower and as a result were more challenging to estimate. From our preliminary calculations, $\tau \approx \mathrm{\hspace{0.17em}4.0}\times {10}^5$ ns for this 223 bp system. We also note that the histone proteins were prevented from rotating in these calculations so that the autocorrelation function of $\widehat{\text{𝒖}}$ was a true measure of DNA unwrapping and not nucleosome rotational diffusion.

Sequence-Dependent Positioning.

To further validate our nucleosome model, we have compared the nucleosome mapping locations predicted by our model with those measured experimentally for the 601 and 5S sequences (Fig. S1). These positioning free energy surfaces were obtained by first performing 2D umbrella sampling along order parameters $S_R$ and $S_T$ (as with Fig. 3) and then integrating out $S_R$ to get the free energy as a function of $S_T$ alone. Since these positioning maps involve calculating free energies (and not simple potential energies), they involved sampling a large region of configurational space for each sequence. This computational expense limited our calculations to nucleosome positions of $\pm 10$ bp relative to the known binding site. Nonetheless, for both sequences, our model predictions are within 2 bp from the experimentally measured binding locations—an accuracy comparable to that of positioning models published previously (55, 56).

The Energies of Nucleosome Sliding Are Not Independent from Other Biophysical Measurements.

As stated in the main text, the energy barriers of nucleosome repositioning are not an independent quantity and are strongly related to other biophysical processes within the nucleosome, such as tension-induced nucleosome unwrapping. To demonstrate this relationship, we performed additional calculations with a slight variant of our model that has stronger attractions between the DNA and histone proteins and therefore is expected to have higher energy barriers to repositioning (Fig. S2). Specifically, this modified model includes a Lennard–Jones interaction between all DNA and protein sites, as used in the original 3SPN-AICG model of Freeman et al. (47). The energy scale of this attraction was chosen to be very small (0.25 kJ/mol) and was included by Freeman et al. to represent the enhanced nucleosome stability due to water-mediated DNA–histone contacts and a spatially heterogeneous dielectric constant (47). Though subsequent work (48) showed that this Lennard–Jones interaction was unnecessary to achieve agreement with experimental measurements, we reintroduce the modified model here to illustrate how many biophysical processes within the nucleosome are coupled (Fig. S2).

When analyzing the free energy of repositioning, this modified model had higher repositioning energy barriers of 11 kT, compared with 7 kT in our original model (Fig. S2A). The modified model also correctly predicts the sequence-dependent formations energies of nucleosome formation (Fig. S2C). An unintended consequence of this modified model, however, was a dramatic increase in the tension-dependent unwrapping of the nucleosome, which would now be in conflict with experimental data (Fig. S2B). Whereas our model in this work demonstrates quantitative agreement with experimentally measured unwrapping forces (top row), this modified model predicts unwrapping forces that are twice as large (bottom row). Though it is tempting to fit one experimental metric at the expense of others, a comprehensive view of the nucleosome requires that a wide range of experimental measurements are matched and explained simultaneously by a single model. The approach presented in this work is, to our knowledge, the only such treatment where this is achieved and therefore represents important progress in our understanding of the nucleosome.