Increasing potential for intense tropical and subtropical thunderstorms under global warming

Significance

A substantial fraction of the world’s most intense thunderstorms occur in the tropics and subtropics, but the response of such storms to climate change remains uncertain. Here, we show that, in simulations of global warming, a measure of the energy available to thunderstorms increases robustly across the tropics and subtropics. Furthermore, we elucidate an important mechanism contributing to such increases in available energy, and we present observational evidence that this mechanism is present in Earth’s atmosphere. By combining theory, observations, and models, our results provide confidence in climate model projections of future intense thunderstorm potential; such model projections are shown to imply large future increases in the frequency of damaging thunderstorm environments in tropical and subtropical regions.

Abstract

Intense thunderstorms produce rapid cloud updrafts and may be associated with a range of destructive weather events. An important ingredient in measures of the potential for intense thunderstorms is the convective available potential energy (CAPE). Climate models project increases in summertime mean CAPE in the tropics and subtropics in response to global warming, but the physical mechanisms responsible for such increases and the implications for future thunderstorm activity remain uncertain. Here, we show that high percentiles of the CAPE distribution (CAPE extremes) also increase robustly with warming across the tropics and subtropics in an ensemble of state-of-the-art climate models, implying strong increases in the frequency of occurrence of environments conducive to intense thunderstorms in future climate projections. The increase in CAPE extremes is consistent with a recently proposed theoretical model in which CAPE depends on the influence of convective entrainment on the tropospheric lapse rate, and we demonstrate the importance of this influence for simulated CAPE extremes using a climate model in which the convective entrainment rate is varied. We further show that the theoretical model is able to account for the climatological relationship between CAPE and a measure of lower-tropospheric humidity in simulations and in observations. Our results provide a physical basis on which to understand projected future increases in intense thunderstorm potential, and they suggest that an important mechanism that contributes to such increases may be present in Earth’s atmosphere.

Intense thunderstorms, defined as those storms that produce the strongest cloud updrafts, are important for the initiation of wildfires through their production of lightning (1) and may be associated with destructive weather such as high winds, large hail, and flash floods. Potential future changes in the frequency and intensity of thunderstorms therefore represent an important societal impact of climate change. Predicting future thunderstorm activity directly is difficult, however, because global climate models (GCMs) typically do not resolve individual storms. Studies of future thunderstorms that use higher-resolution models capable of simulating thunderstorms explicitly are generally conducted in relatively small computational domains that either require GCM output to provide boundary conditions (2–4) or neglect large-scale dynamics entirely (5, 6).

An alternative approach is to use GCMs to project future changes in the frequency of large-scale environmental conditions conducive to intense thunderstorms. Recent studies have reported projected increases in such large-scale environments over the continental United States [e.g., refs. 7–10] and eastern Australia (11) under anthropogenic global warming. These increases are driven primarily by increases in the convective available potential energy (CAPE), a measure of the maximum kinetic energy obtainable by an air parcel lifted adiabatically from near the surface. CAPE is an important large-scale indicator for the potential for lightning (12), and, along with the lower-tropospheric wind shear, it is known to be important for thunderstorms that produce damaging winds and hail (13, 14).

In the tropics, where a substantial fraction of the world’s most intense thunderstorms occur (15), GCMs simulate increases in summertime mean CAPE in response to anthropogenic global warming (16, 17). However, the extent to which such increases in the mean imply increases in the largest CAPE values (CAPE extremes) that are most relevant to intense thunderstorms has not been elucidated. Moreover, the physical mechanisms that lead to increases in CAPE in GCM simulations of warmer climates remain unclear. Tropical lapse rates and CAPE are likely to be strongly influenced by motions associated with moist convection, including thunderstorms themselves (18, 19). Since such motions are typically not resolved in GCMs, it is reasonable to question the fidelity of GCM projections of increased tropical CAPE absent a physical understanding of this model response.

Here, we seek to document and understand projected changes in CAPE extremes across the tropics and subtropics in response to a warming climate. We show that tropical and subtropical CAPE extremes increase strongly with warming across an ensemble of GCMs participating in the fifth phase of the Coupled Model Intercomparison Project (CMIP5) (20) and in a “superparameterized” GCM that includes an explicit representation of moist convection within each grid column. These increases in CAPE extremes are associated with a large and robust increase in the frequency of days with values of CAPE and lower-tropospheric wind shear that are conducive to damaging thunderstorms (8, 13) in projections of a future warmer climate. Using a recently proposed theoretical model for CAPE (21), we argue that the simulated increase in CAPE extremes may be understood by considering the influence of convective entrainment on the lapse rate and how this influence varies with temperature. Furthermore, we present evidence from observations that this entrainment influence may be present in Earth’s tropical and subtropical atmosphere, thereby providing a potential link between the behavior of CAPE in GCMs and in the observed atmosphere.

Results

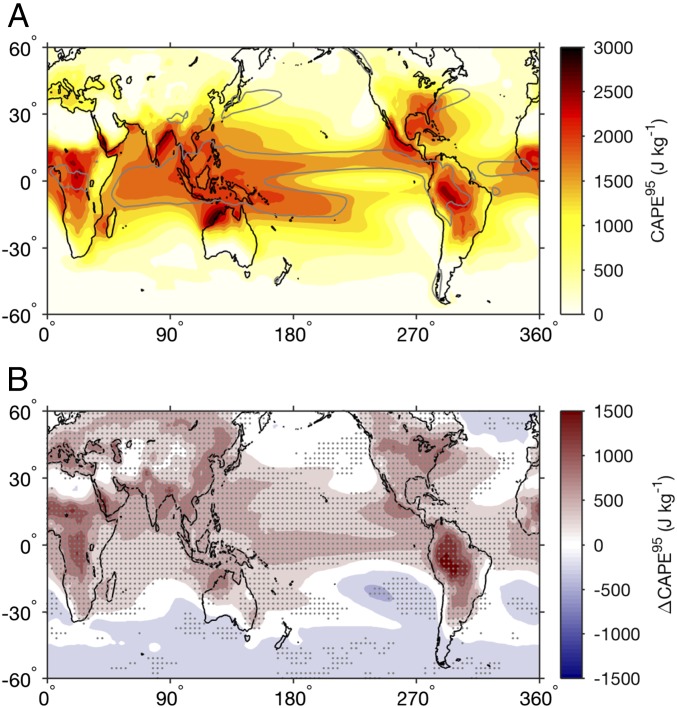
We begin by examining daily CAPE values in the current climate (1981–2000) and in the future climate (2081–2100) under the representative concentration pathway (RCP) highest concentration scenario (RCP8.5) in an ensemble of 12 CMIP5 GCMs. We calculate CAPE based on the buoyancy of a parcel lifted pseudoadiabatically from near the surface (Methods), and we focus on the 95th percentile of the daily mean CAPE distribution, denoted CAPE⁹⁵, as a measure of CAPE extremes. The ensemble mean climatology of CAPE⁹⁵ peaks in the tropics, with the largest values occurring in the tropical warm pool and over tropical continents (Fig. 1A). These features are common to the climatology of most individual models considered, but the peak value of the CAPE⁹⁵ distribution varies substantially across the ensemble (SI Appendix, Fig. S1). Additionally, some models show a substantial enhancement of CAPE⁹⁵ over land (e.g., ACCESS1-3), while, in other models, the largest CAPE⁹⁵ values occur over the ocean (e.g., IPSL-CM5B-LR).

Fig. 1.

(A) Ensemble mean of CAPE⁹⁵ (colors) and 5 mm$\cdot {\text{d}}^{-1}$ contour of time mean and ensemble mean precipitation (gray) based on 12 CMIP5 models for the period 1981–2000. (B) Change in the ensemble mean CAPE⁹⁵ from the current climate (1981–2000) to the future climate (2081–2100) under the RCP8.5 scenario. Stipling in B indicates regions where 11 of the 12 models agree on the sign of the response.

In the future warming scenario, the ensemble mean CAPE⁹⁵ increases across most of the tropics and subtropics and over almost all land regions (Fig. 1B). These increases are robust, occurring in every model analyzed (SI Appendix, Fig. S2), although the magnitude of the increase varies. The fractional rate of increase of CAPE⁹⁵ per unit surface warming in the region 36°S to 36°N ranges from 6 to 14% ${\text{K}}^{-1}$ across the ensemble (SI Appendix, Table S1).

Similar increases with warming are found in the frequency of large-scale environmental conditions conducive to damaging thunderstorms. Here we follow previous work (7, 8, 10, 11, 13, 22) and define damaging thunderstorm environment (DTE) days based on the occurrence of values of the product of CAPE and the magnitude of the vertical wind shear between the surface and 500 hPa (S500) that exceed a model-dependent threshold (Methods). The spatial distribution of the frequency of DTE days differs from that of CAPE⁹⁵ (SI Appendix, Fig. S3A), but, like CAPE⁹⁵, the frequency of DTE days increases robustly with warming across the tropics and subtropics (SI Appendix, Fig. S3B), with a rate of increase of 13 to 32% ${\text{K}}^{-1}$ in the region $36°$S to $36°$N among the models considered (SI Appendix, Table S1). This increase is primarily related to changes in the distribution of CAPE rather than changes in the distribution of lower-tropospheric wind shear (SI Appendix, Fig. S3C). Such large projected increases in the frequency of DTEs may have important implications for natural hazard risk assessment among vulnerable populations throughout tropical and subtropical regions.

Next we consider changes in CAPE extremes with warming in simulations of preindustrial and quadrupled CO₂ concentrations using a superparameterized GCM. Superparameterization involves replacing the moist convection parameterization within a GCM by a 2D high-resolution cloud model (Methods) (23), thereby allowing for a more faithful simulation of some aspects of moist convection [e.g., refs. 24 and 25]. The climatology of CAPE⁹⁵ produced by the superparameterized GCM is broadly similar to that of the CMIP5 ensemble mean, although, in the superparameterized case, the largest CAPE⁹⁵ values occur over the ocean rather than the land (SI Appendix, Fig. S4A). As for the CMIP5 ensemble, tropical and subtropical CAPE⁹⁵ increases substantially with warming in the superparameterized GCM simulations, particularly in regions where the climatological value of CAPE⁹⁵ is large (SI Appendix, Fig. S4B). The consistency of the results of the superparameterized GCM and of the CMIP5 ensemble suggests that the simulated increases in CAPE extremes with warming are independent of uncertain convection parameterizations.

A Simple Model for Tropical and Subtropical CAPE.

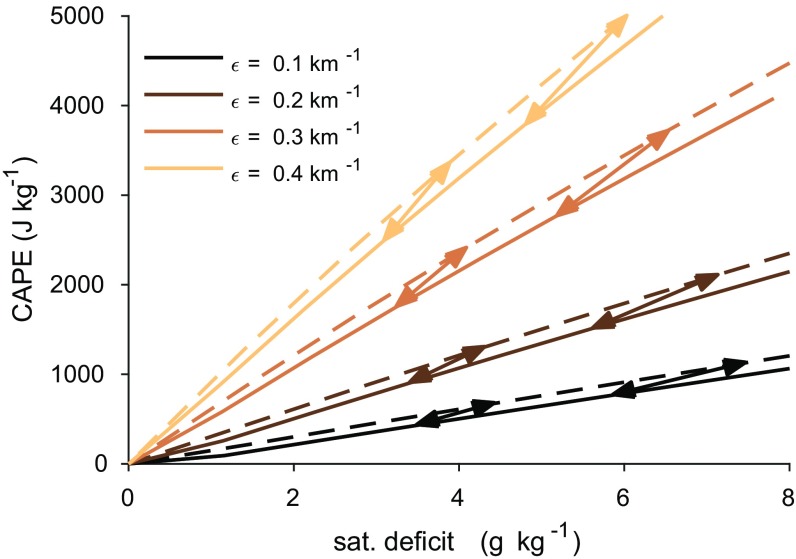
To better understand the physical mechanisms leading to the simulated increase in CAPE extremes, we consider a recently proposed theoretical model for CAPE that accounts for the influence of convective entrainment on the tropospheric lapse rate (21). The model consists of a single entraining plume representing an ensemble of convective clouds, and it assumes that the buoyancy of this plume relative to its environment is negligible. This assumption is consistent with idealized numerical simulations (5, 6, 21, 26) and observations of tropical oceanic clouds [e.g., refs. 27 and 28] in which typical cloud updrafts remain an order of magnitude weaker than the theoretical maximum obtained by converting all available CAPE into kinetic energy. According to this zero-buoyancy plume model, convective entrainment acts to alter the virtual temperature profile of the plume and its environment away from that of a moist adiabat, thereby producing a finite value of CAPE. As a result, the model predicts that CAPE increases with the convective entrainment rate and with the difference between the specific humidity and the saturation specific humidity, termed the saturation deficit, in the free troposphere. Assuming a fixed relative humidity, this saturation deficit increases with warming, implying that the influence of entrainment on the virtual temperature profile is larger in a warmer atmosphere. Indeed, the zero-buoyancy plume model predicts that CAPE increases with warming at a fractional rate of roughly 7% ${\text{K}}^{-1}$ (29), comparable to the rate of increase in CAPE⁹⁵ projected by the CMIP5 ensemble.

The zero-buoyancy plume model has been shown to account for variations in CAPE with surface temperature (21) and environmental relative humidity (30) in simulations of the idealized state of radiative–convective equilibrium. However, the entrainment mechanism described in the previous paragraph is only relevant if it may be assumed that moist convection provides a primary control on the tropospheric lapse rate; the extent to which the zero-buoyancy plume model is applicable to daily CAPE extremes across the tropics and subtropics remains unknown. We therefore seek to test the applicability of the zero-buoyancy plume model to the tropical and subtropical CAPE distribution in GCM simulations.

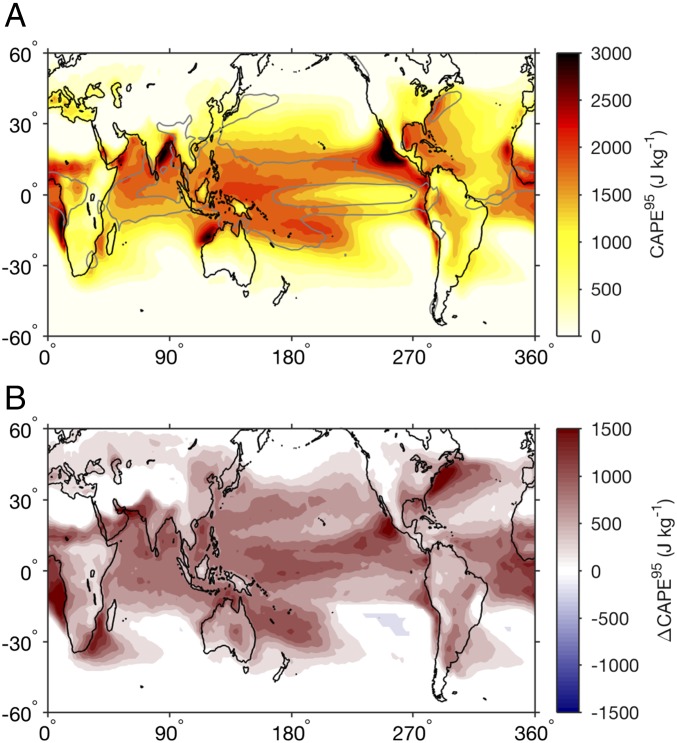
We examine a set of GCM simulations in which the convective entrainment rate is modified by varying a parameter $\alpha$ that is proportional to the minimum value of the entrainment rate allowed within the model’s moist convection parameterization (31) (Methods). As the entrainment parameter $\alpha$ is increased, the simulated CAPE⁹⁵ values increase substantially across the tropics and subtropics (SI Appendix, Table S2), particularly in regions where the climatological value of CAPE⁹⁵ is large (Fig. 2). This is consistent with the zero-buoyancy plume model, which predicts that CAPE is proportional to the convective entrainment rate, and it suggests that the entrainment effect embodied in the zero-buoyancy plume model may be important for simulated tropical and subtropical CAPE extremes.

Fig. 2.

(A) CAPE⁹⁵ (colors) and 5 mm$\cdot {\text{d}}^{-1}$ contour of time mean precipitation (gray) in simulations with modified entrainment for the control value of the entrainment parameter $\alpha =0.2$. (B) Difference in CAPE⁹⁵ for the case $\alpha =0.4$ compared with the case $\alpha =0.2$.

Next we examine the dependence of CAPE extremes on the lower-tropospheric saturation deficit. We consider the modified entrainment simulations along with the CMIP5 and superparameterized GCM simulations discussed above. To focus on regions where moist convection is likely to have a large influence on the tropospheric lapse rate, we consider only strongly precipitating regions, in which the grid column daily precipitation accumulation is greater than 5 mm, and we limit our analysis to the latitude band $36°$S to $36°$N. In the CMIP5 ensemble mean, 53% of tropical and subtropical CAPE extremes occur in strongly precipitating regions, and so this restriction captures the majority of the CAPE extreme events. We bin the CAPE in strongly precipitating regions by the lower-tropospheric saturation deficit $q_{\text{def}}$, taken here as the arithmetic mean of the saturation deficit at 850, 700, and 500 hPa, and we calculate the 95th percentile of CAPE in each bin, denoted ${\text{CAPE}}_p^{95}$.

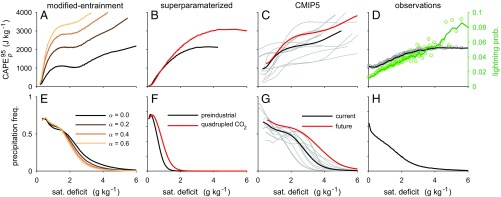
A number of aspects of the simulated ${\text{CAPE}}_p^{95}$ distributions are consistent with the behavior of CAPE according to the zero-buoyancy plume model. Firstly, ${\text{CAPE}}_p^{95}$ generally increases with $q_{\text{def}}$ in the GCM simulations considered, and, for the modified entrainment and superparameterized GCM simulations, the value of ${\text{CAPE}}_p^{95}$ approaches zero as the lower troposphere approaches saturation (Fig. 3 A–C). For low values of $q_{\text{def}}$, this increase in ${\text{CAPE}}_p^{95}$ occurs even when nonprecipitating points are also included in the analysis (SI Appendix, Fig. S5), and it occurs despite the fact that the frequency of strong precipitation peaks when the lower troposphere is close to saturation (Fig. 3 E–G) [cf. ref. 32]. Secondly, in the modified entrainment simulations, ${\text{CAPE}}_p^{95}$ increases with $q_{\text{def}}$ at a higher rate for larger values of the entrainment parameter $\alpha$. This is consistent with the relationship between CAPE, saturation deficit, and the entrainment rate in calculations performed based on the zero-buoyancy plume model (compare Figs. 3A and 4). Lastly, for low values of $q_{\text{def}}$, the relationship between ${\text{CAPE}}_p^{95}$ and $q_{\text{def}}$ is relatively unaffected by a warming of the climate, particularly in the superparameterized GCM simulations (Fig. 3 B and C). This is also consistent with the zero-buoyancy plume model, which predicts a weak sensitivity of CAPE to surface temperature for fixed values of $q_{\text{def}}$ (Fig. 4), and it implies that, in a warming climate, the tendency for the precipitation distribution to shift toward larger $q_{\text{def}}$ values (Fig. 3 F and G) results in a shift toward higher values of ${\text{CAPE}}_p^{95}$.

Fig. 3.

(A–D) The 95th percentile of CAPE in strongly precipitating regions (${\text{CAPE}}_p^{95}$; left axis) and (E–H) frequency (freq.) of daily precipitation exceeding 5 mm$\cdot {\text{d}}^{-1}$, as a function of the lower-tropospheric saturation (sat.) deficit $q_{\text{def}}$ for (A and E) modified entrainment simulations for different values of the entrainment parameter $\alpha$, (B and F) superparameterized GCM simulations of preindustrial climate (black) and quadrupled CO₂ concentration (red), (C and G) CMIP5 ensemble mean in the current climate (1981–2000; thick black; individual models shown in gray) and in the future climate under the RCP8.5 scenario (2081–2100; thick red), and (D and H) observations. Statistics are calculated using 100 bins, each containing roughly the same proportion of the available data. In D, lightning frequency in strongly precipitating regions is plotted as a function of lower-tropospheric saturation deficit (green, right axis), and lines are smoothed with a five-point Lowess filter, with symbols giving unsmoothed values.

Fig. 4.

CAPE as a function of lower-tropospheric saturation deficit $q_{\text{def}}$ calculated using the zero-buoyancy plume model. Calculations are performed with a surface relative humidity of 80% and surface temperatures of 300 K (solid) and 303 K (dashed) for values of the environmental relative humidity in the free troposphere varying between 20% and 100% and entrainment rates $ϵ$ as given in the legend. Arrows connect solutions with the same relative humidity for different surface temperatures.

There are also some differences between the simulated behavior of ${\text{CAPE}}_p^{95}$ and the behavior of CAPE according to the zero-buoyancy plume model, particularly for large values of the lower-tropospheric saturation deficit $q_{\text{def}}$ and in some individual models within the CMIP5 ensemble. These differences may arise because processes other than moist convection play a role in setting the lapse rate, even during strong precipitation. Nevertheless, the overall consistency between the GCM results and the predictions of the zero-buoyancy plume model supports the use of this theoretical model for understanding the simulated CAPE distribution, and it indicates that the entrainment mechanism identified may be an important contributor to the increases in CAPE⁹⁵ found in simulations of global warming.

Observational Support for the Simple Model.

We may also examine CAPE extremes and the relationship between ${\text{CAPE}}_p^{95}$ and $q_{\text{def}}$ in observations. We calculate CAPE and the lower-tropospheric saturation deficit using soundings taken from version 2 of the Integrated Global Radiosonde Archive (IGRA) (33) for the latitude band 36°S to 36°N, and we identify strongly precipitating regions using the Tropical Rainfall Measurement Mission (TRMM) 3B42 (v7) daily precipitation estimate (34) (Methods). The observed distribution of CAPE⁹⁵ has some similarities with the simulated distributions described previously (SI Appendix, Fig. S6A), even though the observed CAPE⁹⁵ values are calculated based on instantaneous measurements rather than daily means.

The observed values of ${\text{CAPE}}_p^{95}$ increase with $q_{\text{def}}$ (Fig. 3D), consistent with the GCM results and the zero-buoyancy plume model, and despite the fact that the frequency of observing strong precipitation is maximized when the lower troposphere is close to saturation (Fig. 3H). Similar relationships between measures of lower tropospheric instability and humidity have been noted in a number of previous observational studies (21, 35, 36). These results may be interpreted through the lens of the zero-buoyancy plume model as evidence for a role of entrainment in determining the observed distribution of CAPE in Earth’s tropics and subtropics.

The probability of lightning in strongly precipitating regions, estimated using the TRMM precipitation feature database (Methods), increases with $q_{\text{def}}$ in a similar way to ${\text{CAPE}}_p^{95}$ (Fig. 3D), and it also increases monotonically when binned by the CAPE itself (SI Appendix, Fig. S6B). Since the production of lightning is known to require strong updrafts, this suggests that high values of CAPE are associated with intense thunderstorms, despite the potential effects of entrainment limiting the cloud buoyancy within such storms.

It should be noted that the estimates of saturation deficit and CAPE in the observations are based on point measurements rather than an average over a grid box. As a result, the observed saturation deficit may not be representative of the large-scale environment for clouds. For instance, the sounding may sample the humidity within a cloud, thus underestimating the environmental saturation deficit, or it may sample a localized dry region with an anomalously high saturation deficit. One effect of such representation errors would be to reduce the gradient of ${\text{CAPE}}_p^{95}$ with respect to $q_{\text{def}}$, and this may help to explain why the increase in observed ${\text{CAPE}}_p^{95}$ with $q_{\text{def}}$ is weaker than in the GCMs, particularly compared with simulations conducted using the superparameterized GCM.

Conclusions

We have shown that tropical and subtropical CAPE extremes increase robustly with warming across an ensemble of GCMs, including a superparameterized GCM that incorporates an explicit representation of convection within each grid column. The zero-buoyancy plume model provides a physical explanation for such increases in CAPE based on the influence of convective entrainment on the tropospheric lapse rate, and we have shown that this influence is important for tropical and subtropical CAPE extremes in GCM simulations in which the convective entrainment rate is varied. The zero-buoyancy plume model also predicts that high values of CAPE occur preferentially in regions of large lower-tropospheric saturation deficit, and this is consistent with the behavior of CAPE in the simulations. Importantly, a similar relationship between CAPE and the lower-tropospheric saturation deficit is found in observations of the tropics and subtropics, suggesting the potential applicability of the zero-buoyancy plume model to Earth’s atmosphere.

An outstanding question not addressed in this study is the extent to which increases in CAPE extremes with warming may be realized as increases in actual thunderstorm intensity. The zero-buoyancy plume model suggests that entrainment acts to reduce the mean buoyancy of clouds to be small relative to that of an adiabatic parcel, and this would also have the effect of reducing the sensitivity of the mean cloud buoyancy to changes in CAPE. However, in idealized high-resolution simulations, the strongest updrafts appear to be less affected by entrainment than the average updraft, and, as a result, simulated updraft velocities increase along with CAPE under warming (5, 6) and with changes in environmental humidity (30). Indeed, the largest increases in updraft speeds with warming are found to occur in the strongest updrafts (37), although the fractional rate of increase may not be as large as implied by fractional changes in CAPE (4, 37). In Earth’s atmosphere, convective organization may further reduce the effect of entrainment on the most intense thunderstorms (38), allowing for a higher proportion of the CAPE to be attainable in strong, highly organized storms.

Future thunderstorm activity may also be affected by changes in convective initiation, and such changes may only be estimated using simulations that explicitly resolve thunderstorm initiation processes (4). Additionally, increases in CAPE extremes in a future climate may themselves be modulated by changes in the convective entrainment rate driven by, for example, changes in convective updraft velocities (39) or convective organization. Notwithstanding these caveats, our results provide a physical basis for understanding increases in the potential for intense thunderstorms in a warming atmosphere, and we have shown that such increases are a robust feature of future projections of tropical and subtropical climate.

Methods

GCM Simulations.

The 12 CMIP5 models used in the analysis are listed in SI Appendix, Table S1. For each model, the first ensemble member is used.

Simulations with the superparameterized GCM are conducted using a superparameterized version of the Community Earth System Model (CESM), and they are identical to those described in refs. 40 and 41. Briefly, the parent GCM is the CESM1.0.2, which includes an atmospheric model (Community Atmospheric Model version 5.0; CAM5.0) run with a finite-volume dynamical core on a $1.9°\times 2.5°$ horizontal grid and using CAM4 physics, and dynamical ocean (Parallel Ocean Program version 4) and sea ice [Los Alamos Sea Ice Model (CICE)] models. A 2D version of the System for Atmospheric Modeling (42) is embedded within each grid column of the atmospheric model to provide the subgrid convective tendencies. Simulations are initialized using multicentury integrations of a conventional (nonsuperparameterized) version of the model (40) and run for 16 y under preindustrial conditions and for 13 y for the quadrupled CO₂ case. Daily output from the final 10 y are used in our analysis.

Simulations with modified convective entrainment are conducted using CAM version 3.1 and are identical to those described in ref. 31. The model is run with a relaxed Arakawa–Schubert convection scheme (43) in which the convective ensemble is represented as a spectrum of entraining plumes with different entrainment rates. Following ref. 44, a minimum value of the entrainment rate of any plume ${ϵ}_{\text{min}}$ = $\alpha /D$ is enforced on the ensemble. The value of $D$ is fixed to 2,000 m in all simulations, and $\alpha$ is varied in the range 0.0 to 0.6. Simulations are forced by climatological sea surface temperatures and run for 27 y; daily data from the final 20 y are used in our analysis.

Calculation of CAPE.

CAPE is taken as the vertical integral of the positive buoyancy of a parcel lifted pseudoadiabatically from near the surface to the upper atmosphere. Freezing is treated using a mixed-phase range, with the fraction of ice increasing linearly from zero at 273.16 K to unity at 233.16 K. In the superparameterized and modified entrainment simulations, the parcel is initialized using the daily mean temperature and humidity at the lowest model level and the daily mean surface pressure, and parcel buoyancy is calculated relative to the daily mean temperature and humidity profiles at each model level. Model-level data and daily surface pressure data were not available for all CMIP5 models, and, in the CMIP5 simulations, the parcel is initialized using the daily mean surface air temperature and humidity and the monthly mean surface pressure, and parcel buoyancy is calculated relative to the daily mean temperature and humidity profiles at standard pressure levels. For the IPSL-CM5B-LR model, the use of model-level data rather than pressure-level data and of monthly surface pressure data rather than daily surface pressure data in the calculation of CAPE has some effect on the climatology of CAPE⁹⁵, but the response of CAPE⁹⁵ to future global warming is similar using either methodology (SI Appendix, Fig. S7).

The observed CAPE is calculated based on radiosonde observations contained in version 2 of the IGRA (33). We extract sounding measurements of pressure, temperature, and humidity at the surface and temperature and humidity at standard pressure levels (1,000, 850, 700, 500, 300, 200, 100, and 50 hPa). The parcel is initialized with surface properties or with the temperature and specific humidity at 1,000 hPa if there are no surface measurements available. Parcel buoyancy is calculated relative to the sounding virtual temperature profile. We consider soundings launched in the tropics and subtropics (36°S to 36°N) during the period of observation of the TRMM precipitation radar (1998–2015) that have no missing temperature or humidity data at levels above the surface and between 1,000 and 500 hPa inclusive. The parcel buoyancy is set to zero if there is missing data at pressures lower than 500 hPa. These criteria give a set of 3.2 million soundings from 576 stations within the tropics and subtropics that we use in the analysis.

Damaging Thunderstorm Environments.

We define days in which the large-scale environmental conditions are conducive to damaging thunderstorms as occurring when (i) the CAPE is greater than 100 J$\cdot$${\text{kg}}^{-1}$, (ii) the magnitude of the vector wind shear between the surface and 500 hPa, denoted $S500$, is greater than 5 m$\cdot$${\text{s}}^{-1}$, and (iii) the product $S500\times$CAPE exceeds a threshold value. In each model, this threshold is given by the 95th percentile of $S500\times$CAPE in the current climate, calculated based on all grid columns in the region $36°$S to $36°$N.

Zero-Buoyancy Plume Model.

In Fig. 4, CAPE is calculated based on the zero-buoyancy plume model using a method similar to that of ref. 21. First, the environmental density profile is calculated assuming that it is equal to that of an entraining plume with a given entrainment rate and experiencing a given environmental relative humidity in the free troposphere. The plume is initialized at the surface, which we take to be at 1,000 hPa, with a given temperature and relative humidity (which may differ from the free-tropospheric environmental relative humidity), and its vertical profile is calculated following ref. 21 under the assumption that all condensed water is immediately removed from the plume by precipitation processes. CAPE is then calculated as the vertical integral of the positive buoyancy of a parcel lifted pseudoadiabatically as outlined above, but with the parcel ascent taken from 1,000 hPa to the 220 K isotherm. The pseudoadiabatic parcel ascent is initialized identically to the plume.

Strongly Precipitating Regions.

Strongly precipitating regions are defined in the GCM simulations as grid columns in which the precipitation on a given day exceeds 5 mm. An observed sounding is considered to be in a strongly precipitating region if the accumulated precipitation in a 2° $\times$ 2° box centered on the sounding launch location exceeds 5 mm on the day on which the sounding was launched. The observed precipitation is estimated using the TRMM 3B42 (v7) daily precipitation estimate (34), which is provided on a 0.25° $\times$ 0.25° grid for the latitude band $50°$S to $50°$N and for the years 1998–2015.

Lightning Probability in Strongly Precipitating Regions.

Probability of lightning is estimated using the TRMM precipitation feature database (45), which gives the lightning flash rate associated with contiguous regions of precipitation [“radar precipitation features” (RPFs)] occurring in the latitude band $36°$S to $36°$N and defined based on estimates of the near-surface rainfall rate from the TRMM precipitation radar. We associate these lightning flash rate measurements with the sounding in the IGRA launched closest to the location of the RPF center, provided this sounding is within a $2°\times 2°$ box of the location of the RPF center and it was launched within 12 h of the RPF observation time. We further require that the sounding be within a strongly precipitating region as defined above. This process gives a set of 1.7 million measurements of lightning flash rate in strongly precipitating regions, collocated with measurements of CAPE and saturation deficit (note that a sounding may be collocated with more than one flash rate measurement). The lightning probability is defined to be the ratio of the number of RPFs with a lightning flash rate greater than zero to the total number of RPFs being considered.