Osteocyte calcium signals encode strain magnitude and loading frequency in vivo

Significance

Osteocytes are thought to be the major regulator of bone mechanosensation events. However, little is known about how osteocytes in vivo acutely respond to tissue-level mechanical loading. We report here a technique for the direct in vivo observation of osteocyte calcium signaling events with simultaneous whole bone loading. Our results demonstrate that osteocyte populations integrate mechanical signals by altering the number of responding cells and that this effect is dependent on loading frequency.

Abstract

Osteocytes are considered to be the major mechanosensory cells of bone, but how osteocytes in vivo process, perceive, and respond to mechanical loading remains poorly understood. Intracellular calcium (Ca²⁺) signaling resulting from mechanical stimulation has been widely studied in osteocytes in vitro and in bone explants, but has yet to be examined in vivo. This is achieved herein by using a three-point bending device which is capable of delivering well-defined mechanical loads to metatarsal bones of living mice while simultaneously monitoring the intracellular Ca²⁺ responses of individual osteocytes by using a genetically encoded fluorescent Ca²⁺ indicator. Osteocyte responses are imaged by using multiphoton fluorescence microscopy. We investigated the in vivo responses of osteocytes to strains ranging from 250 to 3,000 $𝝁\mathit{ϵ}$ and frequencies from 0.5 to 2 Hz, which are characteristic of physiological conditions reported for bone. At all loading frequencies examined, the number of responding osteocytes increased strongly with applied strain magnitude. However, Ca²⁺ intensity within responding osteocytes did not change significantly with physiological loading magnitudes. Our studies offer a glimpse into how these critical bone cells respond to mechanical load in vivo, as well as provide a technique to determine how the cells encode magnitude and frequency of loading.

Bone has a remarkable ability to sense mechanical load and adapt its structure in response. This mechanical adaptation ability is so prominent for bone that it was among the first organ systems to be recognized in this regard; indeed, the word “orthopedics,” first coined in the mid-1700s, derives from straightening the bones of children. The ability of bone to adapt its structure is essential for growing a skeleton appropriate to its mechanical demands and for maintaining the integrity of that skeleton throughout life. Osteoblasts and osteoclasts are the effector cells that carry out bone formation and resorption (respectively), and their dysfunction leads to growth defects and osteoporosis. However, it is increasingly recognized that osteocytes, buried within the bone matrix, are the major local orchestrators of diverse functions in bone. They produce soluble signaling factors that regulate both bone formation and resorption, local mineralization, and also calcium (Ca²⁺) and phosphate transport at the bone matrix level. They also function as endocrine cells, producing factors such as FGF23, that have an impact on renal functions. Among the most essential functions of osteocytes is sensing mechanical load to which bone is subjected and transducing this load into downstream signals, which regulate osteoblasts and osteoclasts.

Osteocytes in situ exist in a complex, 3D, highly interconnected array. Osteocyte cell bodies and processes reside in spaces (lacunae and canaliculi, respectively) within bone matrix and are surrounded in these spaces by a fluid-gel layer that fills the lacunar-canalicular space (LCS). This fluid layer, which moves when bones are mechanically loaded, transmits mechanical forces and determines much of how osteocytes experience their environment. It also accounts for solute transport to and from osteocytes, including metabolites as well as key osteocyte-produced signaling molecules such as sclerostin, RANKL, and OPG. Osteocyte expression of these key signaling molecules is sensitive to changes in mechanical load as well as other stimuli that initiate bone remodeling, such as changes in gonadal steroids and local tissue microdamage (1–4).

Mechanical loads at the bone tissue level are translated to fluid flow in the LCS (5–7). Indeed, a growing body of evidence indicates that fluid flow through the LCS dominates the local mechanical input to osteocytes in situ (8–11). Mechanical stimulation of osteocytes increases cytoplasmic Ca²⁺, a ubiquitous response to both mechanical and biochemical stimuli (12–15). In particular, Thi et al. demonstrated with cells that fluid forces acting on the ${\alpha }_{\text{v}}{\beta }_3$ integrin adhesion sites on osteocyte cell processes in vitro triggered Ca²⁺ responses that spread toward the cell body and then initiated a typical whole-cell Ca²⁺ signaling response like that seen in other cells (16). Finally, most studies of osteocyte Ca²⁺ signaling have been conducted either in 2D cell cultures or in explanted bones (10, 17), which have limitations. Cell cultures lack the LCS and attendant localized tissue architecture and fluid flow, while bone explants are subject to postmortem tissue changes, as well as fluid pressure loss in the LCS resulting from loss of in vivo vascular pressure (8, 18, 19).

In the present studies, we report an in vivo approach to explore osteocyte Ca²⁺ signaling in whole bone where the cells can be individually imaged during mechanical loading. We generated a mouse model with an osteocyte-targeted genetically encoded Ca²⁺ indicator (GECI) to study Ca²⁺ signaling in osteocytes in their authentic in vivo environment. We also created a bone loading approach for use in live mice while simultaneously observing the intracellular Ca²⁺ responses of individual osteocytes with multiphoton microscopy (MPM). We report how Ca²⁺ signaling of osteocytes in vivo, both individually and as networks, responds to mechanical loading. We used this approach to test the hypothesis that encoding of mechanical strain and frequency information by osteocytes in vivo is based on recruitment of responding cells (i.e., numerical encoding) rather than on graded Ca²⁺ responses by individual cells.

Results

Osteocyte GCaMP3 Expression.

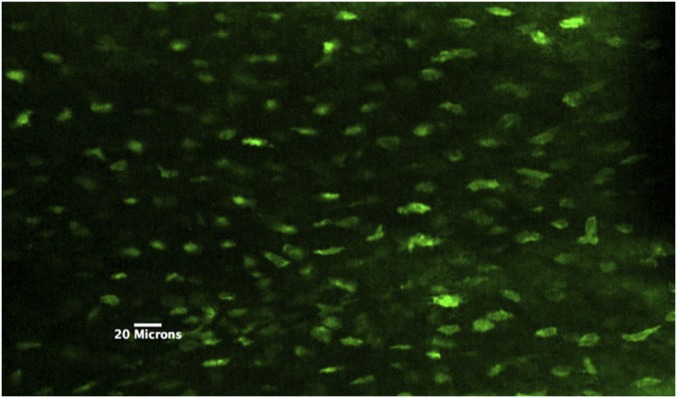
Mice expressing the osteocyte-targeted GECI GCaMP3, which are here termed OtGP3, were created. Baseline GCaMP3 fluorescence was visible in osteocytes throughout the diaphyseal cortex (Fig. 1). In pilot studies, we found that >95% of osteocytes in OtGP3 mice exhibited detectable fluorescence. Fluorescence intensity level varied among cells, and resting osteocytes exhibited low-level fluctuations in Ca²⁺ fluorescence intensity (Fig. 2).

Fig. 1.

Multiphoton z-stack image of OtGP3 MT3 osteocytes in vivo. Note that all cells in the field of view exhibit GCaMP3 signal, indicating highly efficient expression in osteocytes.

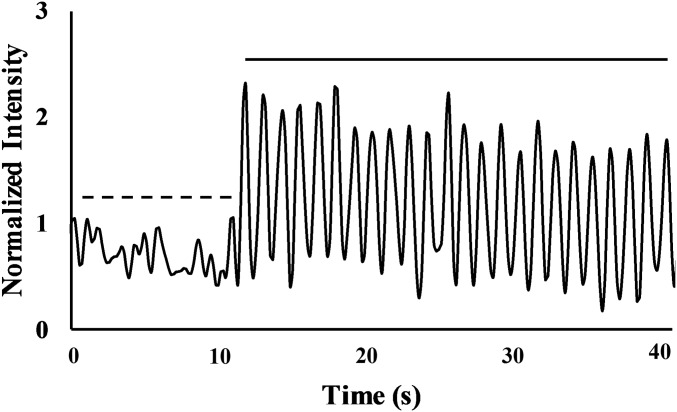
Fig. 2.

A representative Ca²⁺ trace for a single osteocyte before (dashed line) and after the start of cyclical loading (solid line) at 1 Hz to 3,000 $\mu ϵ$. Before mechanical loading, all osteocytes exhibited low-level Ca²⁺ fluctuations. Immediately following the start of mechanical loading, responsive cells showed cyclic increases in Ca²⁺ fluorescence intensity coinciding with the applied loading frequency.

Bone Structure in OtGP3 Mice.

Our studies used the third metatarsal (MT3) of the mouse foot. Previous studies in our group demonstrated that this bone is well-suited for direct visualization of cortical bone osteocytes in living animals by using MPM (20). Its tubular geometry lends itself to bending without creating off-axis stresses. MT3 bones from OtGP3 mice had larger cortical bone areas, but slightly lower tissue mineral density than WT bones (Table 1; P < 0.05), resulting in similar cross-sectional moduli and diaphyseal bending rigidities.

Table 1.

Bone structure, mineralization, stiffness, and osteocyte density in WT and OtGP3 MT3 bone

Parameter	B6-WT	OtGP3
Bone length, mm	7.75 $\pm$ 0.07	7.59 $\pm$ 0.14*
Total bone area, mm2	0.208 $\pm$ 0.25 E-2	0.205 $\pm$ 0.12 E-2
TMD, g/cm3	1.15 $\pm$ 0.02	1.05 $\pm$ 0.02*
Sectional stiffness, N/m	7.58 $\pm$ 0.36	7.82 $\pm$ 1.03
Ot.N, no./mm2	491 $\pm$ 38	448 $\pm$ 39*

Values are mean ± SD. n = 6 per group. Ot.N, osteocyte number; TMD, tissue mineral density. *P < 0.05.

Osteocyte Response to Mechanical Loading in Vivo.

We used a custom-designed device to deliver controlled mechanical strains to MT3 bones of living OtGP3 mice while simultaneously monitoring intracellular Ca²⁺ responses with MPM. Ca²⁺ fluorescence in responding cells increased very rapidly, within 200 ms of loading onset (Fig. 2), and oscillations followed the applied loading (Movie S1). Osteocytes were examined in bones loaded cyclically to habitual physiological strain magnitudes [250, 500, 1,000, and 2,000 microstrain($\mu ϵ$)] as well as a nonhabitual high strain level (3,000 $\mu ϵ$). Loading frequency effects were examined as well (0.5, 1, or 2 Hz; n = 6 animals per loading frequency group).

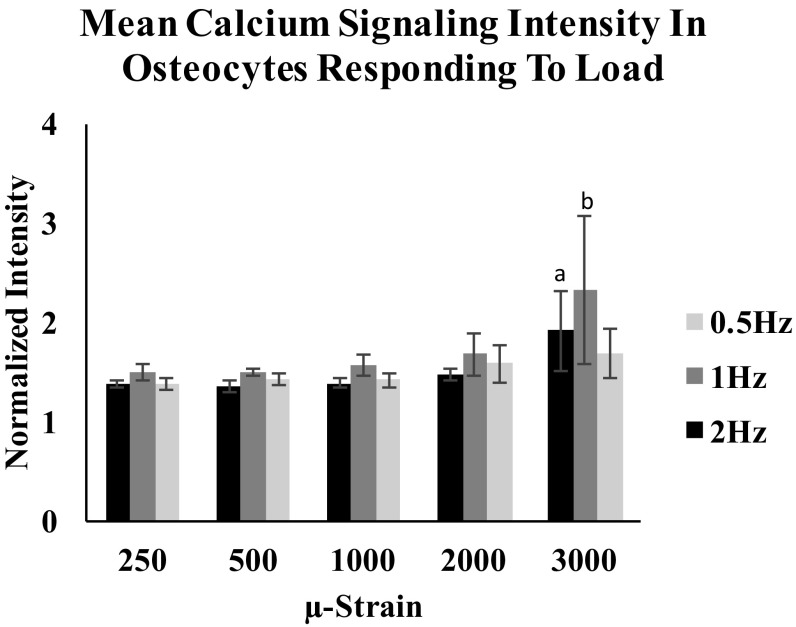
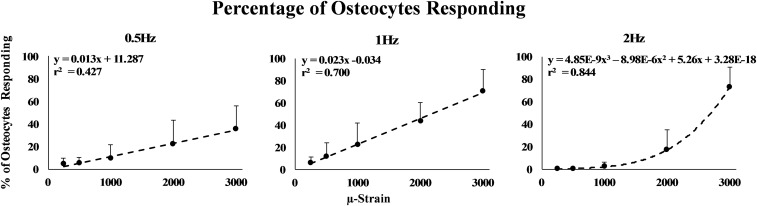
Once activated, Ca²⁺ response intensity remained consistent for each osteocyte for loading up to 2,000 $\mu ϵ$. Osteocyte Ca²⁺ intensity increased only with loading to 3,000 $\mu ϵ$ (Fig. 3; P < 0.05, ANOVA). In contrast, the number of Ca²⁺ responding osteocytes increased markedly with increasing strain magnitude for all loading frequencies tested (Fig. 4). At 0.5- and 1-Hz loading, the load–response curves (i.e., relationship between responding osteocytes and strain magnitude) were linear (P < 0.01). However, osteocyte “recruitment rate” (i.e., the number of responding osteocytes per strain level) was approximately twofold greater at 1- vs. 0.5-Hz loading (0.023 vs. 0.012; P < 0.001, analysis of covariance). The load–response curve was fundamentally different at 2 Hz. At this frequency, the number of Ca²⁺ responding osteocytes was near zero for strains of <1,000 $\mu ϵ$. Above this strain level, osteocyte recruitment increased steeply. The relationship between applied strain levels and responding osteocytes at 2-Hz loading appeared nominally exponential, but was better described by a polynomial relationship (r² = 0.55 vs. 0.85, respectively). Responding osteocytes were distributed within regions of interest (ROIs) without an apparent spatial pattern. We observed instances in which loading at a given strain level triggered a Ca²⁺ response in one osteocyte, but none in an adjacent osteocyte.

Fig. 3.

Intensity of Ca²⁺ signaling per osteocytes was not changed with increasing strain levels up to 2,000 $\mu ϵ$ in all loading rate groups. Increases in Ca²⁺ were noted at 3,000 $\mu ϵ$. (a) P $<$ 0.05; 2-Hz loading group; (b) P $<$ 0.05 1-Hz loading group. Error bars represent SD, n = 6 per group.

Fig. 4.

Shown is the percentage of responding osteocytes as a function of applied strain magnitude for 0.5-, 1-, and 2-Hz loading frequencies. All response curves increased with increasing strain and were effectively linear at 0.5- and 1-Hz loading. The 2-Hz loading response curve was nonlinear. Error bars represent SD. n = 6 per frequency group.

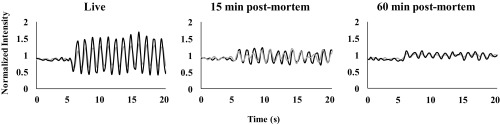
To address the importance of vascular pressure to maintaining the fluid pressure of the LCS, MT3s from an additional group of mice (n = 3) were cyclically loaded to a single test strain (2,000 $\mu ϵ$, 1 Hz) for 60 s while animals were alive and then again at 15 min postmortem (no vascular pressure but cells viable) and 60 min postmortem (severe mitochondrial stress) (20). Amplitude of osteocyte Ca²⁺ response was attenuated markedly at 15 min after death compared with in vivo loading (Fig. 5). These small Ca²⁺ oscillations in response to loading became irregular and did not track the applied loading frequency. The situation further decayed by 60 min.

Fig. 5.

Typical Ca²⁺ traces for two representative osteocytes before and after the onset of mechanical loading in live bone (Left) and at 15 min (Center) and 60 min (Right) postmortem. Osteocyte Ca²⁺ signal amplitude acutely after death was markedly attenuated compared with in vivo, although the Ca²⁺ signaling still tracked the applied loading frequency. In contrast, at 60 min postmortem, the response of osteocytes to loading was low and irregular, with Ca²⁺ signaling no longer consistent with the applied loading frequency. n = 3 per group.

Discussion

This study provides a report of in vivo osteocyte Ca²⁺ responses to mechanical loading of bone in living animals and provides critical information about how osteocyte Ca²⁺ transients encode mechanical strain and frequency information that govern bone adaptation to mechanical loading. Using a technology that permitted skeletal loading while simultaneously visualizing fluorescence signals from cortical bone osteocytes, we discovered that osteocytes loaded to strain magnitudes typical of habitual physiological activities respond in an all-or-none fashion (i.e., OFF–ON). In contrast, the number of osteocytes was strongly proportional to applied strain magnitude. Finally, the number of Ca²⁺ responding osteocytes was also strongly influenced by loading frequencies (Fig. 4).

We previously showed that mechanically stimulated Ca²⁺ elevation in osteocytes is triggered through stretch on a cell process integrin attachment that opens channels allowing ATP release (16). This ATP release then causes a Ca²⁺ influx to the osteocyte cell process that in turn triggers the cytoplasmic Ca²⁺ increase observed in the cell body (10, 12, 21, 22). Increased cytoplasmic Ca²⁺ in osteoblast and osteocyte in vitro (23, 24) is a well-established initial response to mechanical stimulation due to a range of mechanical challenges (12, 25–28). Moreover, this Ca²⁺ signaling is implicated in control of expression of PGE2, RANKL, and sclerostin, as well as Wnt, all critical regulators of bone formation and resorption (2, 29–33).

Our findings establish that within the habitual physiological strain range, intensity or magnitude of Ca²⁺ response for individual osteocytes to loading is effectively binary (i.e., all or none). Such “OFF–ON” responses are typical of Ca²⁺ signaling events in a range of cell types and networks, including glia and skeletal and cardiac muscles (34). Interestingly, we observed that some adjacent osteocytes experiencing identical tissue strains appeared to have different thresholds for mechanical activation. Such threshold differences may be intrinsic to the cells and indeed would be expected in a system where cell responses are binary. Alternatively, this could arise from local differences in fluid flow patterns through the LCS, such that adjacent osteocytes do not experience the same local mechanical stimuli (35, 36). Why Ca²⁺ signaling intensity was elevated at 3,000 $\mu ϵ$ remains obscure at this time and requires further investigation. It is worth noting that this high strain is the level at which bone formation switches from controlled lamellar bone apposition to a dysregulated woven bone formation—the “emergency” response system associated with rapid bone proliferation of poorly organized tissue as seen in fracture healing (37, 38). Thus, it seems reasonable to postulate that the change in osteocyte signaling at this high strain level reflects a transition in cell signaling as the bone moves from controlled to proliferative bone-formation response.

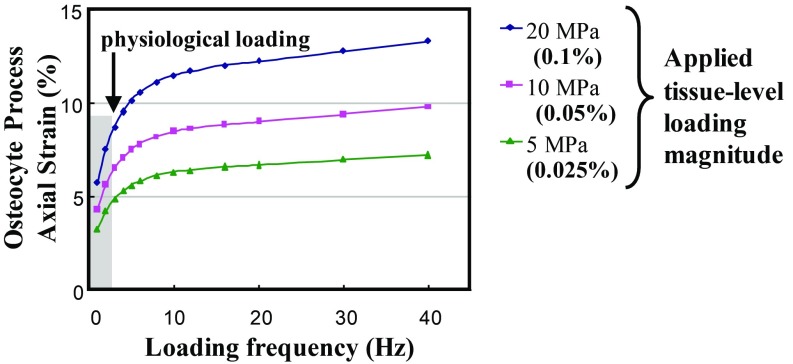
The present studies revealed a profound effect of loading frequency on osteocyte recruitment over the range of physiological frequencies examined. Bone formation and remodeling are known to depend strongly on loading rate and frequency, although the physiological basis for frequency effects remains unknown (37, 39–41). There are examples of ‘frequency-tuned’ excitatory cells in other systems such as the inner ear (42, 43), and osteocytes may be similar. Alternatively, we previously demonstrated that local fluid flow stresses on osteocyte processes in situ can increase sharply over the range of loading frequencies examined in this study, suggesting a way that loading frequency might directly influence what osteocytes experience mechanically (5, 8, 44). This is exemplified in Fig. 6, which shows theoretical predictions for axial strain in the cell membrane at an ${\alpha }_{\text{v}}{\beta }_3$ integrin attachment site on an osteocyte process (5). At loading frequencies <2 Hz, there is a roughly linear increase in axial membrane strain as the whole tissue strain is increased from 250 to 1,000 $\mu ϵ$. This behavior is consistent with our experimental results shown for 0.5 and 1 Hz. In contrast, there is no significant osteocyte response at 2 Hz for this same strain range. Cells are viscoelastic, meaning that they become stiffer as loading rate increases. A stiffer osteocyte would experience reduced membrane strains at mechanotransduction sites; thus, we can reasonably posit that, above some frequency/rate threshold, we would see reduced cell transduction that would be most evident at low loads, as is consistent with the results of this study (45).

Fig. 6.

Predicted axial strain at the transduction sites on the osteocyte process cell membrane as a function of loading frequency at various tissue-loading magnitudes [adapted from the mathematical model of Wang et al. (5)]. The shaded region has been added to highlight the exponential increases in focal membrane strains expected on osteocyte process over the physiological frequency range examined experimentally in the present studies.

A loose association between mechanical loading levels and number of responding osteocytes can be inferred from numerous studies showing strain-dependent changes in expression of molecular markers, including GP6DH activity, prostaglandin synthase, IGF-1, c-fos, and sclerostin (33, 46–48). Thus, an association between the number of Ca²⁺ responding osteocytes and strain magnitude we observed was not unexpected. However, we observed surprisingly high correlations between applied strain magnitudes and the number of Ca²⁺ responding osteocytes. Our results further indicated that osteocyte networks are remarkably precise in their encoding of mechanical frequency input. Tight coupling between input and transducer output signals are characteristic of precise measurement and control systems. Physiological examples include baroreceptors and muscle stretch receptors.

Pereira et al. recently reported a computational model to predict the response of mouse tibiae to anabolic loading based on osteocyte responses (49). They found that normal bone formation rates and predictions of bone adaptation could be achieved only when osteocytes functioned as binary responders (i.e., OFF or ON) above a given threshold strain level, while osteocyte recruitment number varied with load. Bone adaptation was dysregulated when osteocytes were allowed to vary response intensity in a strain-dependent manner, consistent with our experimental results. These results suggest that bone adaptation is regulated by recruiting more osteocytes to the signaling population rather than by modulation of individual cell responses. Both the Pereira model and our experimental results are consistent with the “set-point” concept put forth by Frost more than two decades ago (50). He posited that the then-unknown mechanosensor in bone (now known to be the osteocyte) had a mechanical strain set-point for activation, analogous to the set-point of a thermostat. Once the mechanosensor, or “mechanostat,” is turned on by the appropriate strain, it would signal actuator cells (osteoblasts or osteoclasts) to adapt bone.

A number of studies have examined osteocyte Ca²⁺ signaling in situ by using explanted bones (10, 17). Adachi et al. found that osteocytes in calvaria deformed by using a needle showed a rapid and prolonged increase of Ca²⁺ concentration (51). Jing et al. found that osteocytes in explanted mouse tibiae displayed repetitive Ca²⁺ spikes in response to cyclic loading, with spike frequency and magnitude dependent on load magnitude (10). They further reported that Ca²⁺ responses were dependent on purinergic signaling, consistent with the mechanism reported by Thi et al. for isolated osteocytes (16). Jing et al. found that Ca²⁺ peaks of mechanically loaded osteocytes in explants were of longer duration and at a much slower rate than the mechanical input stimulus (10). The results of our studies on osteocytes in vivo differ substantially. Why these differences occur is not yet clear, but contributing factors likely include removal of explant bone from its normal vascular environment, which will alter LCS fluid pressure (8, 18, 19), solute transport, and oxidative stresses on osteocytes (20). Indeed, in our study of in vivo vs. postmortem effects, we observed that osteocyte responses to mechanical loading change rapidly and markedly once vascular pressure is removed.

We report here information about real-time osteocyte Ca²⁺ responses in vivo. We found that number of osteocytes responding to load was strongly correlated to strain magnitude and that osteocyte load–response curves were also dependent upon loading frequency. These data indicate that tight coupling between loading and number of responding osteocytes is an essential feature of the control of bone mechanosensing and, ultimately, adaptation to mechanical loading. Indeed, having sensors or measurement systems that precisely track input is an indispensable feature of precision engineering controls systems. That osteocyte populations precisely track loading stimuli both in terms of magnitude and frequency also suggests parallels to sensory information encoding in the nervous system, where deviations from normal tightly coupled encoding behaviors are often typical of diseases. We speculate that hormonal or cell alterations that disrupt the couplings between osteocyte recruitment and mechanical input may be characteristic or even predictive of skeletal diseases such as osteoporosis.

Materials and Methods

Details regarding device development and study methods can be found in SI Materials and Methods.

Mice Expressing Osteocyte-Targeted GCaMP3.

Mice exhibiting osteocyte-targeted GCaMP3 (designated OtGP3) were obtained by mating Ai38 mice [B6;129S-Gt(ROSA)26Sortm38(CAG-GCaMP3)Hze/J; JAX Labs] with DMP1/Cre mice [B6N.FVB-Tg(Dmp1-cre)1Jqfe/BwdJ; JAX Labs], which possess Cre recombinase driven by a 10-kb fragment of the DMP1 promoter, which is dominantly expressed in osteocytes and odontoblasts (52). Mice were bred onto a C57BL/6 background. Studies used 16-wk-old female mice and all procedures were approved by the Institutional Animal Care and Use Committees at both Albert Einstein College of Medicine and City College of New York.

Structural and Material Properties of OtGP3 and B6 Metatarsal Bones.

Structural and mineralization studies were performed by using micro-CT ($\mu$CT) to assess OtGP3 vs. WT C57Bl/6 bones as detailed elsewhere (53) (n = 6 bones per genotype). Lamellar vs. woven bone area and osteocyte density (number per mm²) were measured at 400× magnification from 5-$\mu$m-thick middiaphyseal cross-sections, which were counterstained with toluidine blue.

In Vivo Mechanical Loading Apparatus.

We created a mechanical loading device for in vivo three-point bending of MT3 during simultaneous multiphoton imaging (Ultima; Bruker Instruments) of osteocytes in vivo. Loading apparatus details (Fig. S2) and strain calibrations data (Fig. S3) are presented in SI Materials and Methods. Osteocytes were visualized in middiaphyses between upper loading contact points (tensile region). Loading studies were performed under displacement control.

Fig. S2.

Angled (A) and frontal (B) views of custom device for in vivo loading studies. Actuator (i) and load cell (ii) are in series beneath the platform and rectangular water bath (iii) to contain the foot. Upper loading contacts for three-point bending are part of the arm bracket assembly (iv) that wraps around the water bath, and is pulled from below to apply loads to the dorsal bone surface. The red stick shown in the apparatus represents the positioning of the MT3 in the device (v). Mice are under anesthesia while on the platform (vi). The entire apparatus sits on the stage of a multiphoton microscope.

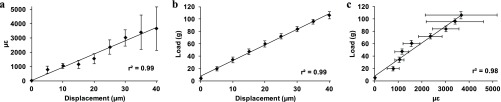
Fig. S3.

Calibration curves from MT3 bones showing strain vs. displacement (A), load vs. displacement (B), and load vs. strain (C). Error bars represent SD, n = 6.

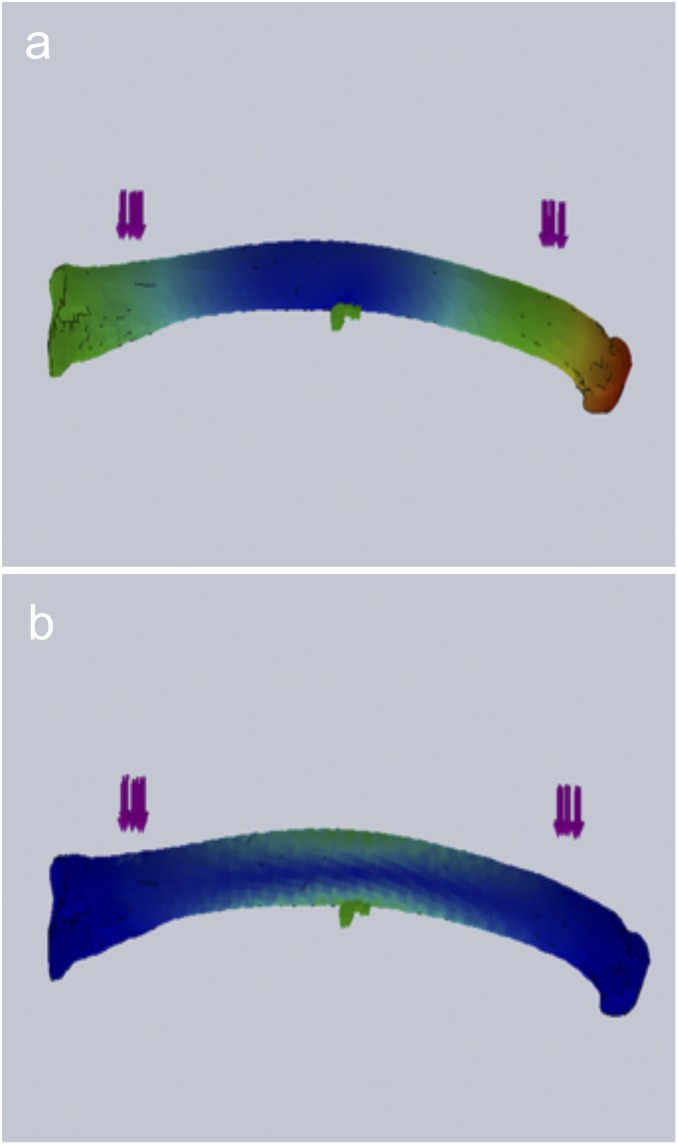
Fig. S1.

FEA modeling results with heat maps of total displacement (A) and von Mises strain (B). Note that the location of maximum strain coincides with the area showing little z axis displacement.

Osteocyte Response to Mechanical Loading in Vivo.

Under isoflurane anesthesia, the MT3 dorsal surface was accessed, and the foot was positioned in the loading apparatus. Isoflurane does not alter Ca²⁺ signaling (54). Bones were loaded cyclically to strain magnitudes of 250, 500, 1,000, 2,000, and 3,000 $\mu ϵ$. Strains up to $\sim$2,000 $\mu ϵ$ occur in diaphyses in vivo and are characteristic of normal physiological activities from moderate walking to running (55, 56). The highest strain level examined (3,000 $\mu ϵ$) is typical of extreme activities and approximates the threshold reported for turning on periosteal woven bone apposition (38). Loading frequency effects were examined as well, with groups tested at 0.5, 1, or 2 Hz (n = 6 per frequency). Images were acquired in two ROIs located immediately on either side of the middiaphysis. These ROIs were chosen because they had effectively no measurable strain gradients based on strain calibration studies (see SI Materials and Methods for details). Images were collected continuously for a 60-s loading period at each test strain. The bone was then unloaded and allowed to rest for 15 min, which exceeds the refractory period for bone cells (57). This procedure was repeated for each strain level, going from lowest to highest strain at one imaging site and then from highest to lowest strain at the adjacent imaging site to assess potential conditioning or offset in osteocyte response from loading sequence. No sequential effect was observed. Mice were euthanized at the end of the loading study.

In addition, we used this experimental system to assess whether vascular pressure contributes to osteocyte response in vivo. MT3 from additional mice (n = 3 males) were loaded to a single test strain (2,000 $\mu ϵ$), and osteocyte Ca²⁺ response was measured. Mice were then euthanized in place, and loading and imaging were repeated at 15 and 60 min after death; 60 min approximates incubation times reported in bone explant studies (10, 17, 58).

Imaging.

Osteocyte Ca²⁺ response in MT3 bones of OtGP3 mice during whole bone loading was visualized by using MPM. By using a 40× magnification water immersion objective, imaging was performed with 920-nm wavelength excitation and 490- to 560-nm bandpass filter acquisition at 6 frames per second. Osteocytes were imaged in a single optical plane located $\sim$20 $\mu$m below the periosteal surface to maintain uniform strain distribution within the ROI. Ca²⁺ intensity measurements from osteocytes observed were performed by postprocessing images using ImageJ (NIH). Fluorescence intensity for each cell was normalized to its mean intensity for a 30-s period before the start of loading. GCaMP3 and other GECIs have a lower signal-to-noise ratio than exogenous Ca²⁺ sensing dyes (5 vs. 12, respectively), and, thus, a lower potential fold change in fluorescent intensity (59, 60). Accordingly, osteocytes were considered as responding if they exhibited >25% increase in normalized fluorescence intensity during loading.

Statistical Analyses.

The $\mu$CT and histological difference between mouse strains were assessed by using the t test. Differences in osteocyte response vs. strain level among strain groups were examined by using either ANOVA with Fisher’s least squared difference for post hoc testing or regression analyses. Analyses were performed with SPSS (Version 20; IBM).

SI Materials and Methods

Mouse Model.

The GCaMP family of GECI mouse strains (61, 62) expresses a cytoplasmically localized calcium (Ca²⁺) indicator protein that consists of a 149–144 circularly permuted enhanced green fluorescent protein (EGFP) fused to calmodulin (CaM) at one end, and myosin-light chain kinase fragment M13 at the other. Binding of Ca²⁺ to CaM results in increased EGFP fluorescence (more than fivefold at 510 nm upon maximum Ca²⁺ binding) (63). The Ai38 mouse strain [B6; 129SGt(ROSA) 26Sortm38(CAG-GCaMP3)Hze/J; JAX Labs] contains a GCaMP3 gene positioned behind a floxed stop codon. We generated a mouse model with osteocyte (Ot)-targeted (via DMP-1) expression of the GECI GCaMP3 to study Ca²⁺ signaling in osteocytes in their authentic in vivo environment. We termed this model OtGP3. GCaMP3 expression was highly effective, with fluorescence visible in >95% of osteocytes throughout the diaphyseal cortex. GCaMP3 has a lower signal-to-noise ratio than exogenous calcium sensing dyes, and thus a lower potential fold change in fluorescent intensity (60). An example of baseline fluorescence and intensity increases with in vivo loading is demonstrated in Movie S1.

Structural and Material Properties of OtGP3 and B6 Metatarsal Bones.

Structural and mineralization studies were performed by using $\mu$CT to assess OtGP3 vs. WT (C57Bl/6) bone. The target bone for our studies was the mouse MT3 bone; this bone is subcutaneous, which allows easy surgical exposure, and is located away from the major blood vessels on the dorsum of the mouse foot. The MT3 diaphysis is tubular in shape, and, thus, when mechanically loaded in bending, it has a straightforward strain distribution. $\mu$CT scans were performed at a voxel resolution of 6.7 $\mu$m by using a Sky-Scan 1172 (Bruker), using a 10-MP digital detector, at 100 KV, 100 mA, and a 0.5-mm aluminum filter. Flat field calibration was performed before each scanning session. Image acquisition, exposure, reconstruction, postalignment compensation, and thresholding were detailed by us in Cheung et al. (53). Cortical bone area and tissue mineral density were determined at the middiaphysis. After $\mu$CT, bones were decalcified and processed for histology; 5-$\mu$m-thick cross-sections of MT3 were cut from middiaphyses and stained with toluidine blue for examination of tissue type (lamellar vs. woven bone) and osteocyte numbers (number per mm²).

Finite Element Analysis Evaluation of Loading Modes.

Finite element analysis (FEA) was used to evaluate potential loading modes (i.e., cantilever or three- or four-point bending) for optimal design of in vivo loading of the MT3. The design goal was to determine which loading configuration provided the best combination of load and minimal z axis displacement during loading; this latter requirement is essential for keeping osteocytes in the plane of focus during the in situ imaging studies of loaded bone described below. The $\mu$CT scans were imported to SolidWorks modeling software (Version 2013 x64 Edition SP3; Dassault Systemes SOLIDWORKS Corp.) and converted to curvature-based meshes with $\sim$10,000 tetrahedral elements and $\sim$150,000 nodes for FEA. Model material properties for diaphyseal for cortical bone were 15 GPa Young’s modulus for cortical bone, 0.3 Poisson’s ratio, and yield strength of 150 MPa (64). Contact patches were rectangular areas of 0.25 mm². Models were solved for displacement in the direction of loading and von Mises stress. A “reversed” three-point bending configuration (fulcrum fixed on volar surface, actuation applied at outer contact points at the dorsal surface of the bone) produced the best combination of minimal z-displacement with maximum strain at middiaphysis (<0.5 $\mu$m z-displacement at 3,500 $\mu \epsilon$; Fig. 1). Cantilever and four-point bending, in contrast, yielded larger z- displacements, on the order of 10–15 $\mu$m.

In Vivo Mechanical Loading Apparatus.

Based on this three-point bending model, we designed and constructed a mechanical loading device for in vivo bending of MT3 that can be used with simultaneous multiphoton imaging of osteocytes in situ in live bone. Osteocytes were visualized in the middiaphyseal cortex (tensile region) between upper loading contact points. The fixed center support was anchored beneath the middiaphysis. In the loading apparatus, a linear actuator (T-NA08A25-S; Zaber Technologies Inc.) and load cell (GSO-250; Transducer Techniques, LLC) were situated in series beneath the loading stage (Fig. 2). The actuating upper contact points were integrated into a rectangular hoop, which fastened to the linear actuator and wrapped around the loading stage to interface with the bone inside of a 37 °C PBS-filled bath, where the foot sat during experiments (Fig. 2). Loading contacts and the PBS bath were fabricated by direct 3D laser sintering of stainless steel (PH1 alloy, GPI Prototype & Manufacturing Services, Inc.) from the 3D SolidWorks STL files. Bone contact points were 1.25-mm-diameter cylinders with bending rigidity of 0.024 N/m², which is $\sim$150-fold greater than that of mouse metatarsals. The rest of the loading apparatus (e.g., platform, actuator housing) was fabricated out of 3/8” aluminum. Custom control and data acquisition programs were written in LabView (LabVIEW Full Development System, Version 10.0 32-bit; National Instruments). Studies were performed under displacement control. The apparatus was anchored onto the stage of a multiphoton microscope (Ultima; Bruker Instruments) equipped with a tunable Ti-sapphire laser light source for in vivo osteocyte imaging.

Displacement, Load, and Strain Calibration.

Calibration studies were performed by using the load cell, actuator displacement, and an optical extensometry approach. Metatarsal bone (MT3) was surgically exposed, and the periosteum was removed. The lower fulcrum pin of the three-point bending device was inserted immediately beneath the MT3 middiaphysis and placed in its anchor bracket within the PBS bath, thus functionally isolating the bone. Upper loading contacts were positioned on the dorsal bone surface. For strain calibration studies, a solution containing 45-$\mu$m-diameter fluorescent beads (Polysciences) was applied to the bone surface. MT3s were then loaded, and beads were imaged with fluorescence video microscopy by using a 5× magnification objective. Only beads that returned to their baseline positions with unloading were considered as adhered and used for measurement. Position changes in multiple clusters of three to five fluorescent beads under loads were then measured in the longitudinal and transverse directions by using an image correlation algorithm in MatLab (Version R2015a; MathWorks, Inc.), and these displacements were used to calculate diaphyseal surface strains. Displacement vs. strain and load vs. strain relationships were determined for eight bones, and resulting regressions were used to determine bone strain vs. load and strain vs. displacement based calibration curves used for the subsequent in vivo experiments (Fig. 3). Critically, it was found that, up to $\sim$3,800 $\mu \epsilon$, there was no measurable strain gradient along the diaphyseal cortex within 500 $\mu$m of either side of the middiaphyseal line, allowing us to treat this area as a uniform strain region for the purposes of our in vivo osteocyte response studies.

Osteocyte Response to Mechanical Loading in Vivo.

Under isoflurane anesthesia, the MT3 dorsal surface was accessed through a skin; the periosteum was left intact. The foot was then positioned in the loading apparatus as described above. Upper loading, contacts were positioned on the dorsal bone surface with a nominal tare strain ($\sim$100 $\mu \epsilon$) applied to prevent the bone from moving during loading. Bones were loaded cyclically by using a haversine waveform to strain magnitudes of 250, 500, 1,000, 2,000, and 3,000 $\mu \epsilon$. Strains ranging from a few hundred to $\sim$2,000 $\mu \epsilon$ have been measured on diaphyses from in vivo strain gage studies and are characteristic of normal physiological activities from moderate walking to running (55, 56). The highest strain level examined (3,000 $\mu \epsilon$) is more typical of extreme activities and approximates the strain threshold reported for turning on periosteal woven bone apposition characteristic of a high overload in bone (38). Loading frequency effects were examined as well, with groups tested at 0.5, 1, or 2 Hz (n = 6 animals per loading frequency). Osteocytes were imaged in two ROIs located immediately on either side of the middiaphysis. These ROIs were sampled, as the strain calibration studies revealed that they had no measurable strain gradients (i.e., uniform strain), thus eliminating a potentially confounding variable from the analyses of osteocyte responses. Each ROI captured 30–60 osteocytes.

Loading Protocol.

In each experiment, bones were cyclically loaded to the desired test strain level with osteocyte Ca²⁺ responses simultaneously imaged by using MPM. Images were collected continuously for a 60-s loading period. The bone was then unloaded and allowed to rest for 15 min, which exceeds the refractory period for bone cells (57). This procedure was repeated sequentially at each test strain levels until all strain levels were sampled. In addition, testing at one the first middiaphyseal imaging ROI was performed by going from lowest to highest strain levels; the opposite experimental loading sequence (from highest to lowest strain levels) was used at the adjacent imaging site. This allowed us to assess potential conditioning or offset in osteocyte response from loading sequence. Loading frequency studies was performed on different groups of mice following this experimental loading protocol. Mice were euthanized at the end of loading experiments without recovery from anesthesia.

Imaging.

Osteocyte Ca²⁺ signaling in the OtGP3 mice during whole bone loading was visualized by using MPM. Imaging was performed by using a 40× magnification water immersion objective (Olympus LUMPLFLN 40XW; NA = 0.8; working distance = 3.3 mm) focused at the middiaphysis, using 920-nm wavelength excitation and 490- to 560-nm bandpass filter detection for osteocyte data acquisition. Time series images were acquired at a rate of 6 frames per second, the maximum rate for full field imaging using this imaging platform. In addition, osteocytes were imaged in a single optical plane located $\sim$20 $\mu$m deep from the periosteal surface to maximize image acquisition rate. There was no significant truncation or clipping of signaling events at the 2- vs. 0.5-Hz loading, so aliasing of the Ca²⁺ fluorescence signal was not a concern. Each sample plane typically contained 15–30 osteocytes. Ca²⁺ intensity measurements from each osteocyte was performed by postprocessing MPM time series images using ImageJ (NIH). Individual osteocytes were traced, and mean pixel intensity values within these ROIs were collected in each frame before and during loading. Fluorescence intensities for each cell were normalized to mean intensity for that cell over a 30-s period before the start of cyclic loading. All osteocytes within the ROI were measured. GCaMP3 has a lower signal-to-noise ratio than exogenous calcium sensing dyes; thus, a lower range for fluorescent intensity fold change can be used than for exogenous calcium sensing dyes (63, 65). Accordingly, osteocytes were considered as responding if they exhibited >25% increase in normalized fluorescence intensity during loading. Number of responding osteocytes were counted and expressed as a percentage of total osteocyte number.