Significance
The bacterial flagellar motor is a rotary molecular motor responsible for swimming, swarming, and chemotaxis in many species of bacteria. It generates torque by interactions between a rotor 50 nm in diameter and multiple stator units. We overturn the prevailing understanding of how stator units interact with each other by showing that motor speed is dependent on the number of stator units even at high speed near zero torque. We describe a method to measure torque and speed that uses synthetic hybrid stators driven by different ion types and show that, with simple rescaling, a single torque–speed curve describes the motor over widely varying values of the membrane voltage, driving ion type and ionic chemical potential gradient.
Keywords: bacterial flagellar motor, molecular motor, hybrid fuel motor, Escherichia coli, motility
Abstract
The bacterial flagellar motor (BFM) rotates hundreds of times per second to propel bacteria driven by an electrochemical ion gradient. The motor consists of a rotor 50 nm in diameter surrounded by up to 11 ion-conducting stator units, which exchange between motors and a membrane-bound pool. Measurements of the torque–speed relationship guide the development of models of the motor mechanism. In contrast to previous reports that speed near zero torque is independent of the number of stator units, we observe multiple speeds that we attribute to different numbers of units near zero torque in both Na+- and H+-driven motors. We measure the full torque–speed relationship of one and two H+ units in Escherichia coli by selecting the number of H+ units and controlling the number of Na+ units in hybrid motors. These experiments confirm that speed near zero torque in H+-driven motors increases with the stator number. We also measured 75 torque–speed curves for Na+-driven chimeric motors at different ion-motive force and stator number. Torque and speed were proportional to ion-motive force and number of stator units at all loads, allowing all 77 measured torque–speed curves to be collapsed onto a single curve by simple rescaling.
At high load in Escherichia coli, each stator unit is exchanged every 30 s (1), and stator units leave the motor when the ion-motive force (IMF) is removed (2–4). Natural (5, 6) and artificial (7) hybrid fuel motors exist, in which H+ and Na+ stators are coexpressed. Bacterial flagellar motor (BFMs) combining the rotor of E. coli with chimeric Na+-driven stator units containing PomA from Vibrio alginolyticus and a fusion of MotB from E. coli and PomB from V. alginolyticus (8) have been used for many mechanistic studies. Measured torque in H+ and Na+ motors with various numbers of stator units (9–13) is nearly constant up to a so-called “knee” speed, falling more steeply to zero at higher speeds. Both the knee and zero-torque speeds increase with temperature, and at high sodium concentrations (85 mM), they are higher for Na+ than for H+ motors.
Extrapolations of torque–speed curves predicted that the speed of the H+-driven motor at zero load is independent of unit number (9). The observation of only one speed of gold nanoparticles attached to the hook of H+-driven motors lacking a flagellar filament at expression levels of stator proteins that give many units at high load appeared to support this prediction—under the assumption that these motors also contained many units (14). However, the recent discovery that motors contain fewer units at lower load (15, 16) invalidates this assumption. Furthermore, Na+-driven motors show multiple speeds at low load (13). These results reopen the question of how the zero-load speed depends on unit number and indicate that previous torque–speed measurements likely conflated properties of stator units with load-dependent stator recruitment.
Here, we show that speed at low load increases approximately linearly with the number of both Na+- and H+-driven stator units. We measure 75 torque–speed relationships for chimeric motors driven by one to three Na+ units and a wide range of electrical and chemical potentials. We also measure, in individual hybrid fuel motors, torque–speed curves for one and two H+ units by using Na+ stator units operating in their constant torque regime to push H+ units in the same motor up to and beyond their zero-torque speed. We rescale torque and speed, dividing each by IMF and stator number and further dividing speed by an empirical function of ion concentration, to obtain a single torque–speed curve that describes flagellar motors in E. coli at all 77 different measured combinations of driving ion, chemical and electrical potential, and number of stator units.
Results
Na+ Motor at Low Load.
Gold nanoparticles 100 nm in diameter were attached to hooks of Na+-driven chimeric motors lacking flagellar filaments. Motor speeds were monitored via backscattering dark-field microscopy (17). These recordings were combined with previous data acquired in the same manner (13). Fig. 1A shows a typical trace, where 85 mM Na+ was transiently removed ( s). The speed of the motor quickly dropped to zero with Na+ removal and increased in stepwise increments after Na+ was reintroduced, a typical signature of the removal and addition of torque-generating stator units (7, 18). Fig. 1 B–D shows examples of spontaneous stepwise speed changes in 85 mM Na+, similar to those previously observed with larger loads (13, 19), presumably corresponding to the loss or gain of a stator unit. Similar examples for other [Na+] are shown in Fig. S1. Each motor often showed zero or low speed, especially at low [Na+]. Fig. 2A shows histograms of motor speed driving 100-nm gold nanoparticles for five different [Na+] ranging from 1 to 85 mM. As observed previously (13), the speed histograms show clear multiple peaks, indicating multiple speed levels at very low load. Speed histograms were fit as a sum of Gaussians, with the peak of each Gaussian defining a speed level corresponding to a particular configuration of the motor. These configurations have always previously been assumed to correspond to different numbers of stator units (9, 14, 19–21), which is our starting assumption.
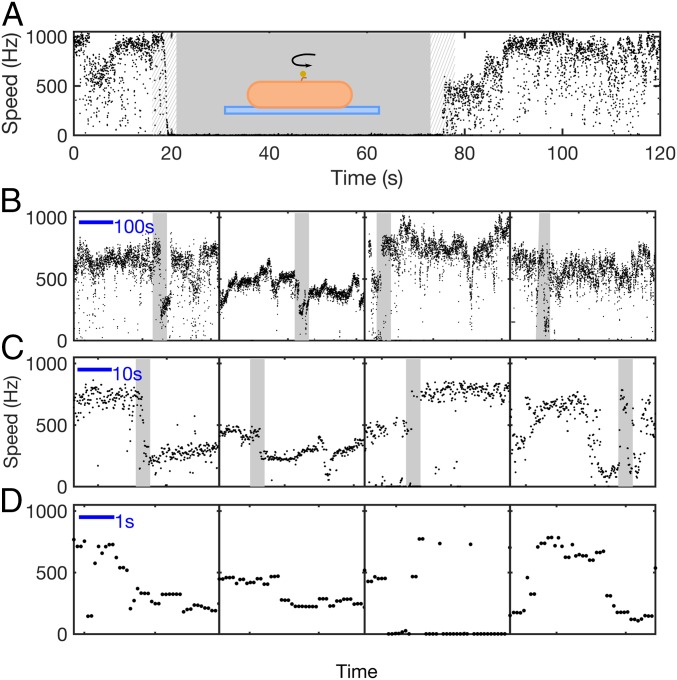
Fig. 1.
Discrete speed levels of the Na+-driven motor at low load. (A) Speed versus time for a 100-nm gold bead attached to the hook of a single Na+-driven chimeric flagellar motor. Na+ was removed between 20 and 75 s (shading). Inset shows a schematic of the experimental assay. (B–D) Typical speed time traces at pH 7 in 85 mM [Na+]. Transitions between distinct speed levels are seen on timescales ranging from seconds to minutes. Shaded portions in B and C are shown in C and D, respectively.
Fig. S1.
Four panels showing typical speed time traces for a 100-nm gold bead attached to the hook of single Na+-driven BFM at pH 7.0, where [Na+] is labeled at the top of each panel. Transitions between a characteristic set of distinct speed levels are seen on timescales ranging from seconds to minutes. Shaded portions in the top and middle rows of each panel are represented in the middle and bottom rows, respectively, of each panel.
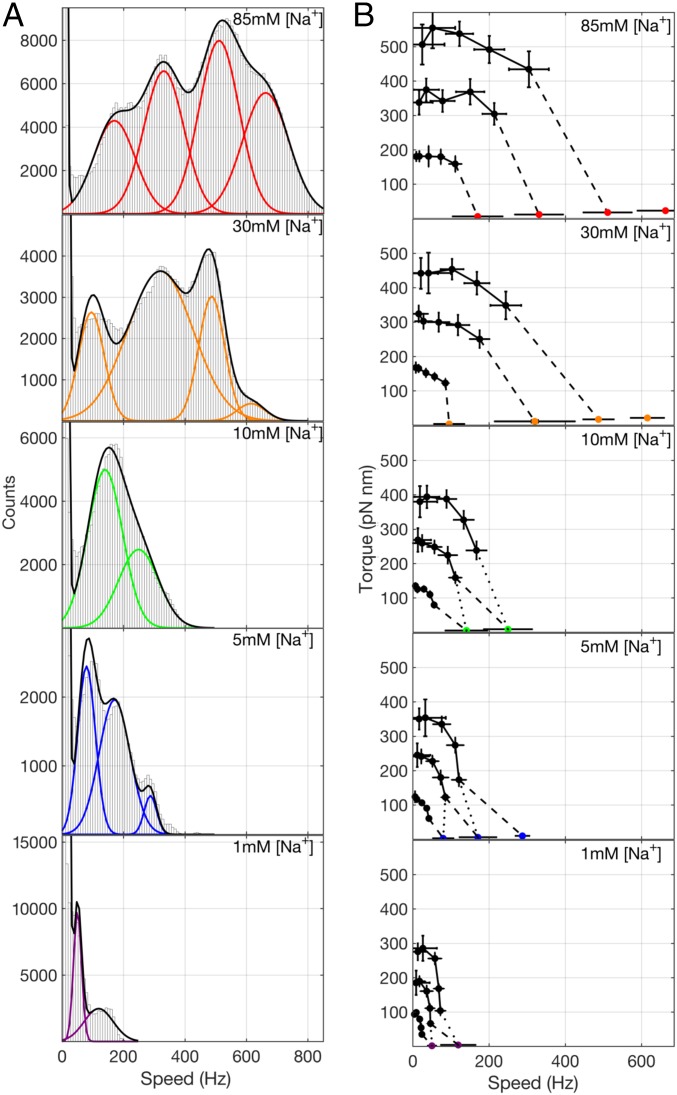
Fig. 2.
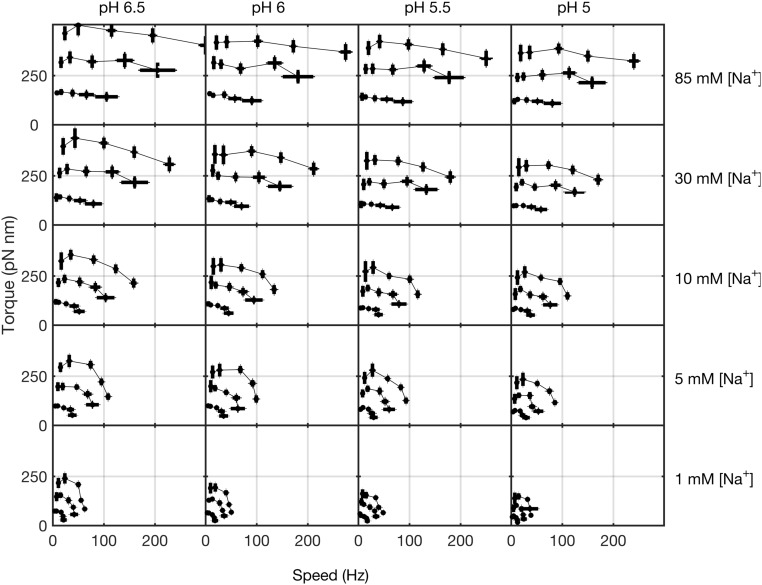
Torque and speed of the Na+-driven motor at pH 7 for varying [Na+]. (A) Histograms of speeds of 100-nm gold beads attached to Na+-driven motors from records such as those illustrated in Fig. 1 B–D. Distinct peaks in the histograms are fit (black lines) as a sum of Gaussians (colored lines). Speeds from 56, 44, 28, 40, and 51 different motors were combined for 85, 30, 10, 5, and 1 mM [Na+], respectively. (B) Torque–speed curves of Na+-driven motors with one to three stator units at pH 7.0 and varying [Na+]. Colored symbols show speeds from the Gaussian fits in A. Black symbols show previously published speeds of polystyrene beads on flagellar filaments (13). Black solid lines connect measurements of motors with the same presumed number of stators. Black dashed lines indicate an inference of the correspondence between numbers of stators in the polystyrene and gold bead data based on the assumption that the lowest speed corresponds to a single stator unit. Black dotted lines indicate an alternative inference based on the assumption that some speed levels have not been resolved in the gold bead data at 1, 5, and 10 mM [Na+]. Data points indicate means, and error bars indicate SDs.
Torque–Speed Curves of the Na+ Motor.
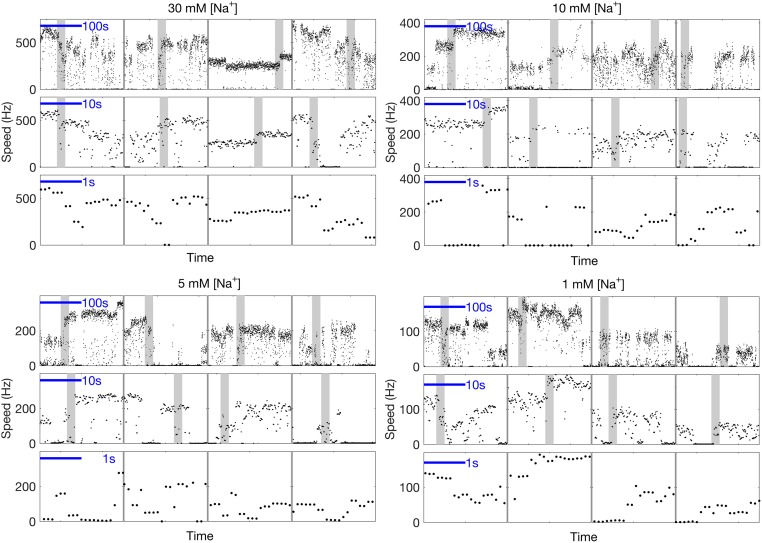
Fig. 2B shows torque–speed curves of the Na+-driven motor driven by one, two, or three stator units at pH 7 and the same values of [Na+] as Fig. 2A. Speeds correspond to Gaussian peaks in speed histograms (Fig. 2A) for motors driving gold beads (Fig. 2B, colored circles) and similarly, for motors driving polystyrene beads of diameters m attached to truncated filaments of the Na+-driven motor (13) (Fig. 2B, black circles). Torque was calculated as speed times the rotational frictional drag coefficient of each size of bead. The dataset of speeds of polystyrene beads was the same as that used by Lo et al. (13). Black dashed lines in Fig. 2B link the lowest speed levels observed with polystyrene and 100-nm gold beads at each [Na+]. The lowest speed levels observed with gold beads in 10, 5, and 1 mM Na+ were faster than expected for single stator units given the concave-down shape of the torque–speed curves for higher [Na+] and for polystyrene beads. Given the variance in speed for each speed level, we would not expect to resolve any level below 100 Hz, and the most likely explanation is that single-unit speed levels are not resolved by Gaussian fitting at low [Na+]. Dotted lines in Fig. 2B link gold to polystyrene data under the assumption that the lowest resolved speed levels with gold represent motors with two stator units at 10, 5, and 1 mM [Na+].
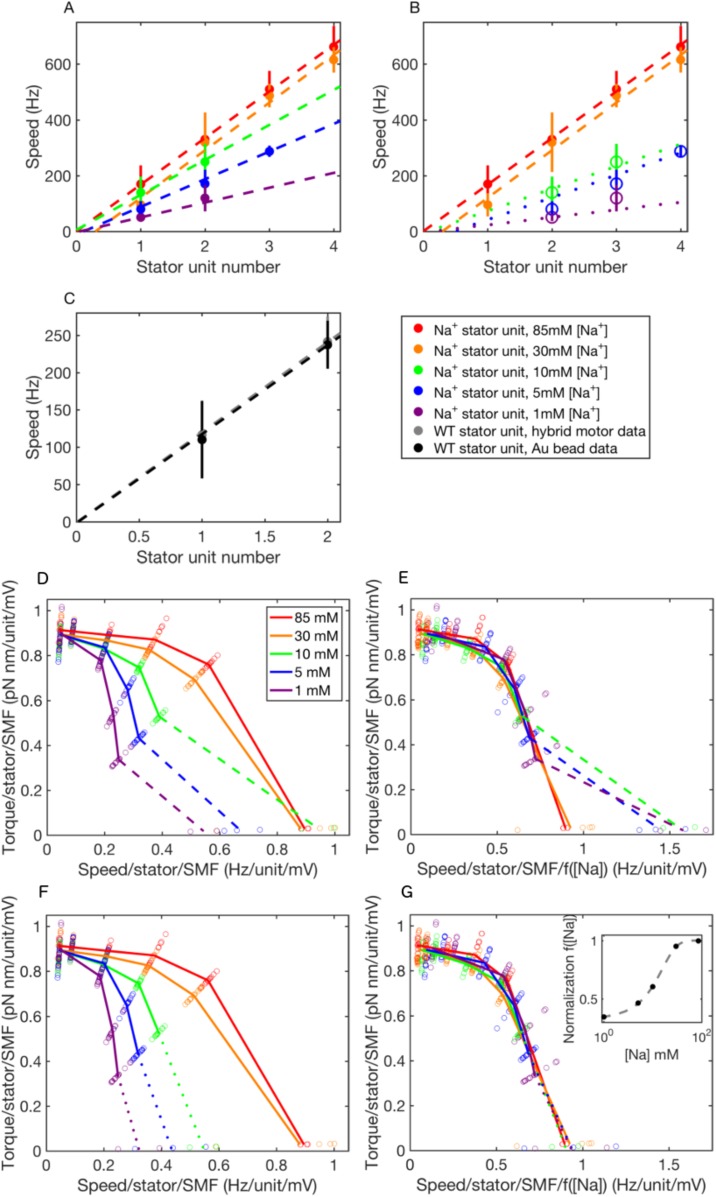
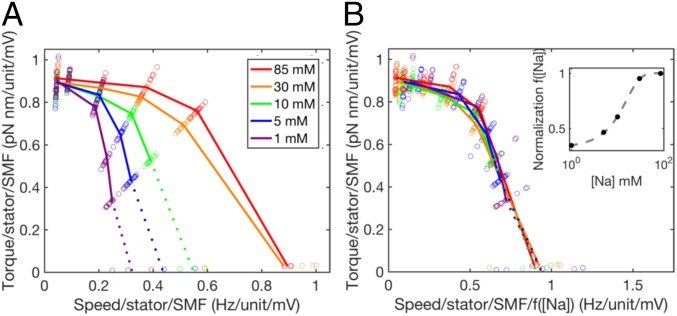
Under this assumption, the torque–speed curves for motors with one to three stator units all share the characteristic concave-down shape previously reported for motors with one (22) and many (9–12, 22–24) units. The zero-torque speed and the stall torque are both approximately proportional to unit number (Fig. S2). Torque–speed curves obtained similarly but with polystyrene beads only [at a range of pH values corresponding to a range of values of the membrane voltage (13, 25)] all showed the same qualitative features (Fig. S3). Fig. 3A combines all 75 chimeric motor torque–speed curves, composing a filled 5 × 5 × 3 matrix corresponding to five different values of membrane voltage, five different [Na+], and one to three stator units, normalized by dividing each torque and each speed by both the number of stator units and the sodium-motive force (SMF) (25). The same colors as in Fig. 2 are used to mark each value of [Na+], and lines show averages over membrane voltage and number of stator units. This shows that both torque and speed at each sodium concentration are proportional to both SMF and the number of units under all conditions and all viscous loads measured. Fig. 3B collapses all 75 curves onto a single torque–speed curve after further normalizing speed by dividing by an empirical function [Na+]) (Fig. 3B, Inset), with values at each measured [Na+] chosen by hand to maximize the overlap of the resulting curves. The empirical function represents the effect of [Na+] on motor speed over and above its effects via SMF. The observed saturating response is expected, as motor speed cannot increase indefinitely with [Na+]. Future modeling of the motor mechanism will be required to offer a mechanistic explanation for the shape of [Na+]). Fig. S2 D and E shows the alternative assignment of stator numbers to gold bead data.
Fig. S2.
Speed versus stator number and torque–speed curves. (A–C) Approximate linearity of BFM speed with stator unit number. Data points and error bars give averages and SDs, respectively, from the experiments listed. (A and B) Na+ stator units: filled symbols show assignments of stator unit number based on the assumption that the lowest resolved speed corresponds to a single stator unit (fit with dashed lines). Open symbols in B show alternative assignments of stator unit number at low [Na+] (fit with dotted lines) based on the assumption that speed levels for a single stator unit are not always resolved in the multiple Gaussian fits of Fig. 2A. (C) H+ stator units. Linear regression fits are weighted by the inverse of the variance in speed. (D–G) Normalized torque–speed curves of the Na+-driven motor. (D and F) Seventy-five individual torque–speed curves as shown in Fig. 2. Colored lines show averages for each [Na+] over numbers of stators and pH values. This plot combines data from this study and two previous studies (13, 25), showing average measurements from 396 combinations of bead size, [Na+], pH, and stator unit number. (E and G) The same as D and F but with speeds further divided by an empirical normalizing function [Na+] (G, Inset; fit by a logistic function; dashed) that collapses all 75 torque–speed curves onto a single curve. Dashed lines (D–E) assign gold bead stator number under the assumption that the lowest speed corresponds to a single stator, as in A. Dotted lines (F and G) assign gold bead stator number under the assumption that some speed levels are not resolved, as in B. Plots (F and G) are reproduced from Fig. 3.
Fig. S3.
Torque–speed curves of the Na+-driven motor calculated from previously published data showing one to three stator units obtained with polystyrene beads of diameters 0.2–1.0 m at a range of pH values (shown along the top and corresponding to columns) and [Na+] concentrations (shown at the right and corresponding to rows) (13, 25). All show the previously reported concave-down shape of a single stator (13).
Fig. 3.
Normalized torque–speed curves of the Na+-driven motor. (A) Seventy-five individual torque–speed curves similar to those of Fig. 2 but including data obtained at pH 5, 5.5, 6, 6.5, and 7 and with both torque and speed normalized by the number of stator units and the SMF, the latter estimated from pH and [Na+] as described (25). Colored lines (corresponding to Fig. 2) show averages for each [Na+] over stator number and pH. This plot combines data from this study and two previous studies (13, 25), showing average measurements from 396 combinations of bead size, [Na+], pH, and stator unit number. (B) The same as A but with speeds further divided by an empirical normalizing function [Na+] (Inset; fit by a logistic function; dashed line) that collapses all 75 torque–speed curves onto a single curve. Dotted lines assign gold bead stator number under the assumption that some speed levels are not resolved for 1, 5, and 10 mM [Na+].
H+ Motor at Low Load.
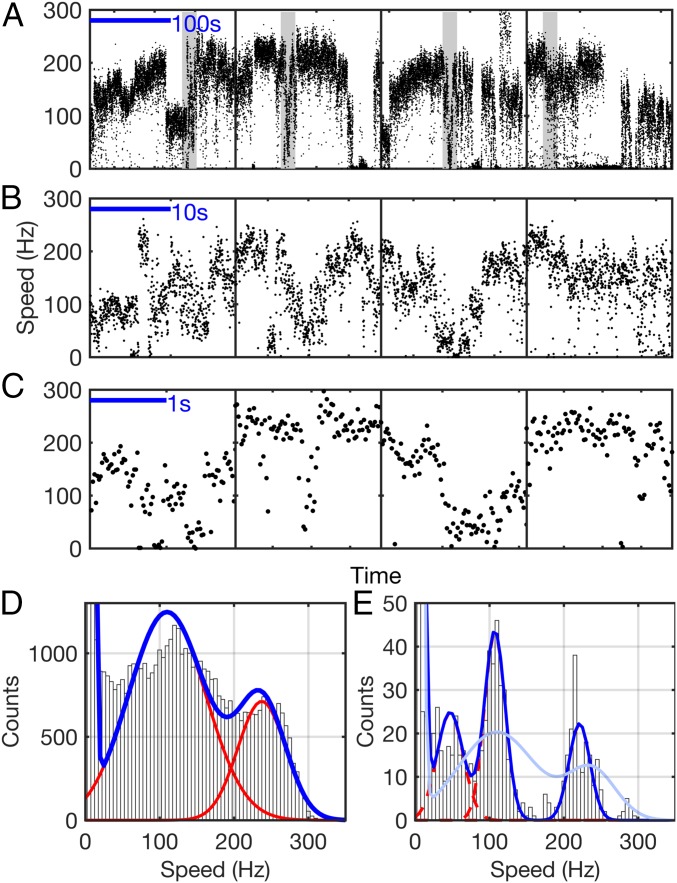
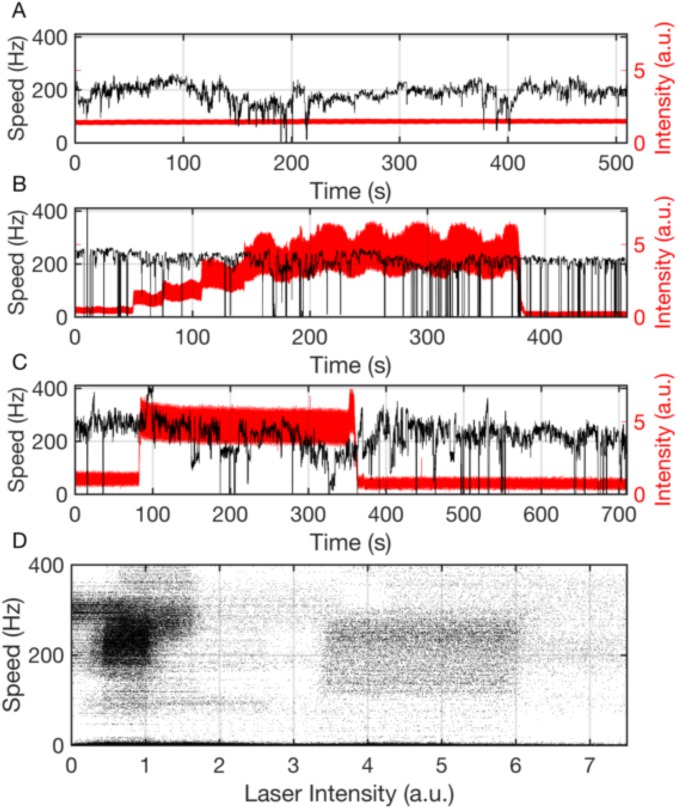
The speed of H+-driven motors in motility buffer near zero load was investigated in a manner similar to the Na+-driven motor experiments above. Fig. 4 A–C shows examples of spontaneous stepwise speed changes similar to those of the Na+ motor in Fig. 1, and Fig. 4D shows the histogram of all speeds recorded from 59 different motors driving 100-nm gold nanoparticles. As the distribution shows at least two evident peaks, we applied a two-Gaussian fit (blue line in Fig. 4D). The highest of these speed levels is similar to the single speeds previously reported in similar experiments (14, 26), while lower speeds have not previously been reported.
Fig. 4.
Discrete speed levels of the H+-driven motor at low load. (A–C) Typical speed time traces for 100-nm gold beads attached to the hook of single H+-driven (WT) flagellar motors. As with Na+ motors in Fig. 1 B–D, transitions between distinct speed levels are seen on timescales ranging from seconds to minutes. Data shown in A were acquired at 20 kHz, and shaded portions in A are shown in B. Separate traces, shown in C, were acquired at 109.5 kHz. (D) Histogram of speeds of 100-nm gold beads attached to H+-driven motors from records, such as those illustrated in A–C [8 cells (1,394 s) acquired at 20 kHz on the QPD and 51 cells (53 s) acquired at 109.5 kHz on a high-speed camera]. Distinct speed levels are seen as peaks in the histogram, and fit (blue line) is seen as a sum of Gaussians (red lines). (E) Histogram of the subset (96%, eight cells) of data in D that was acquired in continuous blocks longer than 9 s, down-sampled, and filtered to match the time resolution of previous low load data (14) (SI Results). The distribution was fit (blue line) as a sum of Gaussians (red lines). The scaled distribution of D is overlaid (light blue).
Torque–Speed Curves of H+-Driven Stator Units.
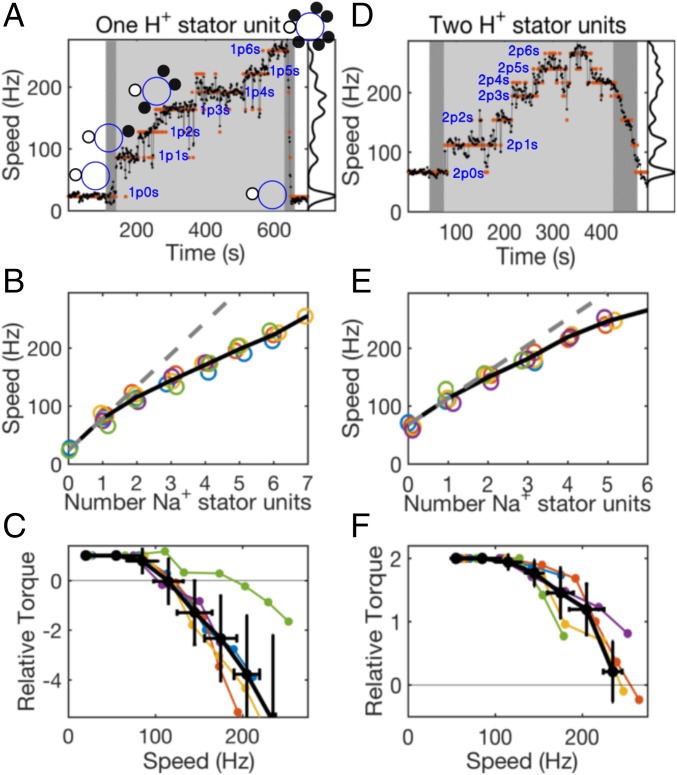
We took advantage of the hybrid fuel motor, in which the torques generated by Na+ and H+ stator units on a common rotor were found simply to sum (7), to measure the complete torque–speed curves of single or pairs of H+-driven stator units. Fig. 5A shows speed versus time of a 0.5-μm bead attached to the truncated filament of a hybrid fuel motor at pH 7 in a cell with low-level induction of H+ stator proteins, MotA/MotB, and high-level induction of Na+ stator proteins, PomA/PotB. Initially, the motility medium contained no sodium, guaranteeing that any rotating motors were driven only by H+ units (4, 18). Under these conditions, motor speeds have previously been determined to be about 30 Hz per H+ unit (9). We selected motors driven initially by either one (∼30 Hz) or two (∼60 Hz) H+ stator units and measured speeds while the sodium-free buffer was transiently replaced by 85 mM Na+ buffer. Fig. 5 A and D shows speed versus time for examples of one and two H+-unit motors, respectively, with shading in Fig. 5 A and D indicating the presence of sodium. Motor speed increased in stepwise increments on addition of sodium and decreased rapidly after the removal of sodium several minutes later, as seen in previous resurrection experiments with larger beads on the hybrid fuel motor (7). In 10 of 43 cases, the motor returned to the speed measured before the introduction of sodium buffer. We calculated torque–speed curves for these cases under the assumption that the same number of H+ stator units remained in these motors throughout.
Fig. 5.
Torque–speed curves for one and two H+ stator units measured in hybrid fuel motors. (A and D) Typical speed verus time traces of motors containing (A) one and (D) two H+ stator units, with a speed histogram on the right. Orange dots show the speed level of each data point assigned by k-means clustering. Light shading and dark shading indicate 85 mM [Na+] and transitions between 0 and 85 mM [Na+], respectively. Na+ stator units are recruited in 85 mM [Na+]: interpretations of the number and type of units engaged in the motor are shown, where ps indicates H+ units and Na+ units. (B and E) Speed versus the number of Na+ units for all motors that showed the same speed before and after addition of 85 mM [Na+] (five motors each). Each motor in each plot is shown in a different color; the motors from A and D are shown in orange. The black solid lines connect the mean speed of all of the motors for each number, and the black dashed lines are linear fits to the points of the first (B) three or (E) two units (those for which motor speed is less than 115 Hz, the approximate position of the knee of the torque–speed curve). (C and F) Calculated torque–speed curves for one and two H+ stator units. Colors match those in B and E. The black lines show average torque–speed curves (mean SD), with each point an average over speed bins of width 40 Hz.
Discrete speed levels were determined using k-means clustering, and orange dots in Fig. 5 A and D show the speed level assigned to each data point. The corresponding interpretations of the number and type of stator units engaged (one additional Na+ unit for each speed level) are also shown. It has previously been shown that the resurrection of Na+ units within a motor causes equal speed increments up to a speed of 400 Hz (12), indicating that there is no change in the torque generated per Na+ unit in this speed range. Fig. 5 B and E, by contrast, shows reducing speed increments with the addition of Na+ units at speeds above 115 Hz, consistent with the expected decrease in torque generated by the H+ unit(s) at higher speeds. Assuming that the total torque is the sum of independent contributions from H+ and Na+ stator units (denoted , ) and that each Na+ unit generates a constant torque at all speeds observed in these experiments, we may write the balance between motor torque and viscous drag as
| [1] |
where is the combined rotational drag coefficient of the filament stub and bead, is the measured speed, and is the torque generated by x stator units of type y. Assuming that, at low speeds, each H+ stator unit generates a constant torque (19), we divide Eq. 1 by the torque generated by a single H+ stator at low speeds:
| [2] |
where is the measured speed in the absence of Na+ stator units. This defines a relative H+ stator unit torque:
| [3] |
where is the difference between the lowest two speed levels determined by k-means clustering. The average values of were 57 10 and 46 5 Hz in one and two H+ stator unit motors, respectively, in agreement with previous measurements (13). Fig. 5 C and F shows versus for individual motors (colors in Fig. 5 C and F) and the corresponding average torque–speed curves (black in Fig. 5 C and F). By exploiting the higher characteristic speed of Na+ stator units at high sodium concentration, this method allows determination of torque–speed curves of a single or a pair of H+ unit(s) up to and beyond zero load without the need to apply external torque. The zero-torque speeds for one and two H+ stator units are 120 and 240 Hz, respectively, confirming our independent observation of multiple speed levels near zero load with gold nanospheres (Fig. 4).
Discussion
In this study, we have observed that both H+-and Na+-driven flagellar motors in E. coli show multiple speed levels near zero load. Thus, contrary to previous assumptions, the zero-torque speed of the BFM is not independent of stator unit number, requiring a reassessment of mechanistic models of the BFM. We have developed a method allowing measurement of the entire torque–speed curves of one and two H+-driven stator units in individual motors and obtained 77 different torque–speed curves for H+- and Na+-driven motors with a range of IMFs and numbers of stator units. Both torque and speed are approximately proportional to both IMF and number of stator units for all viscous loads measured, and with simple rescaling, all 77 torque–speed curves collapse onto a single curve (Fig. S4C) with the previously reported concave-down shape (9–13) characteristic of counterclockwise (CCW) rotation in E. coli.
Fig. S4.
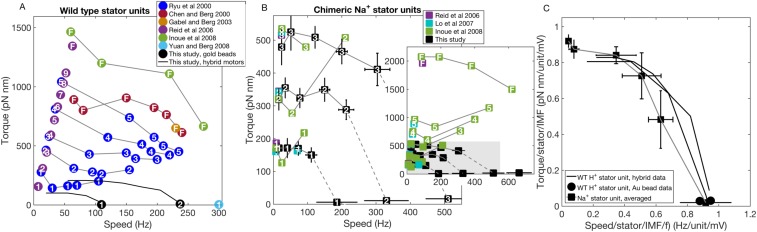
Torque versus speed curves. (A and B) Measurements derived from various studies, which measured the speed of a rotating bead stuck to the filament or hook of an immobilized cell. (A) WT E. coli BFMs and (B) E. coli BFMs with chimeric Na+ stator units (at 85 mM [Na+], pH 7.0). B is an enlarged copy of the region demarcated by the gray box in B, Inset. For consistency, we recalculated torque from previously published speeds using a single model for the viscous drag coefficient of beads of different sizes attached to hooks (26) or filament stubs (9, 11, 12, 19, 25, 48). Marker color denotes the data source, and the number within each marker shows the number of units previously assigned, some of which are incorrect in retrospect. Data from motors presumed to have a full complement of stator units are labeled F and likely represent variable numbers of units given the load dependence of stator units (15, 16). Where measurements were made over more than two viscous loads, a line connects data points from the same study. Details regarding the calculation of torque are given in SI Materials and Methods. (C) Normalized torque–speed curves for Na+ (black squares and gray line; average of the 75 curves from Fig. 3B; mean SD) and Na+ (black circles and black lines) motors. For normalization of the Na+ motor, we have used a PMF of –125 mV and an empirical normalization function ([Na+]) = 1. For pH 7.0, this value of ([Na+]) corresponds to the saturation value of ([Na+]) (Fig. 3B).
This is in contrast to the linear torque–speed curve reported for clockwise (CW) rotation (27). We speculate that the CCW torque–speed relationship may indicate selection pressure for high power output, as it combines high torque and high speed at viscous drag coefficients similar to those experienced in the bundle of a swimming E. coli cell. By contrast, the linear relationship seen in CW rotation is easier to achieve in mechanistic models and may represent a lack of selection pressure given that CW rotation is not typically used to propel swimming. If so, we predict that species in which both rotation directions are selected for swimming will show concave-down torque–speed curves in both directions.
If torque and speed are proportional to the number of units beyond three in other species, those with additional stator structures that are thought to maintain high numbers of stator units (28) are predicted to rotate above 1,000 Hz at low load. We note that the speed per unit per millivolt of IMF of the H+ motor at pH 7 is roughly the same as that of the chimeric motor at saturating [Na+], despite an approximately million-fold difference in ion concentration. This anomalously high rate of proton arrival presumably indicates some or all of following: enhanced proton mobility near the lipid membrane (29), diffusion by the Grotthuss mechanism (30), and delivery of protons to the motor by buffer species. If ion arrival is the rate-limiting step at low load, equal arrival rates for H+ and Na+ may simply be a coincidence. If ion transit or conformational changes in the motor are limiting, this may point to common mechanisms for these processes in both types of stator.
Our method of controlling hybrid motor speed with Na+ stator units avoids the problems of angular variation and mechanical or photodamage associated with previous measurements of the torque–speed relationship of a single motor using electrorotation (22, 24) or laser trapping of a bead duplex (31). Furthermore, because Na+ stator torque is applied directly to the rotor, potential artifacts caused by flexible hook interactions (32) are also avoided. This method measured zero-load speeds of about 120 and 240 Hz for one and two stator units, respectively, in good agreement with our data from gold beads, supporting the conclusion that the zero-load speed depends on the number of stator units in the H+ motor as well as in the Na+ motor.
This is the most striking discrepancy between our results and previous literature. Previously, it was reported that H+-driven motors jump suddenly between not rotating and rotating at a maximum speed between 250 and 300 Hz, with no intermediate speed levels (14). In our study, while some motors were observed to rotate continuously at a single speed over many seconds, similar to those reported previously (14), most showed extensive speed changes as shown in Fig. 4. The 4.6-fold difference in viscous drag coefficient between our 100-nm beads and the 60-nm beads used previously (14) (an upper limit, assuming rotation about a diameter) is unlikely to explain this discrepancy, as in both cases, the loads are very low. We tested several alternative hypotheses. Our data were acquired at 20 or 109.5 kHz, and speeds were calculated over 0.02-s intervals; those of the previous study (14) were at 3 kHz, and speeds were calculated over 1-s intervals and then median filtered, rank 4, to yield a time resolution of 9 s, 450 times slower than ours. Our high time resolution may explain the relatively noisy speed traces for both H+ and Na+ motors. Given the spatial and temporal resolutions of our measurements, this noise is representative of the motor rather than an artifact of measurement. Analysis of speed histograms, however, extracts discrete speed levels without loss of time resolution. Down-sampling and filtering a subset of our data traces (with sufficiently long duration) to match the procedures of the previous study (14) returned peaks at 107 14 and 215 47 Hz, similar to our original analysis, plus an additional peak at 47 18 Hz that might represent an average of switching between zero and the lowest level that is resolved at our original time resolution but not after down-sampling (Fig. 4E). We excluded the alternative possibility that lower speed levels in our experiments are a consequence of photodamage under the assumption that our laser intensity (100 W/cm−2) was greater than that used previously (14) by observing a lack of intensity dependence of rotation of gold beads attached to H+ motors over more than a fourfold range of laser intensities (Fig. S5).
Fig. S5.
Motor speed is independent of laser intensity. (A–C) Motor speed for gold beads attached to Na+ motors (black) and laser power (red) verus time, showing that the motor speed is not affected by the laser light on a timescale of minutes. For B and C, laser power was adjusted by hand by rotating a half-wave plate. Increasing laser power shows no obvious effect on motor speed. (D) Motor speed versus laser power measured over six motors, each recorded for 400–800 s, including the motors shown in B and C. The speed of an additional 25 motors was observed in real time but not recorded, as laser power was varied; these motors showed a similar independence of motor speed on laser power. Laser intensity was measured in arbitrary units (a.u.) via the voltage of the QPD; a laser intensity of ∼1 a.u. was used for low-load gold bead experiments.
The discrepancy between our results and previous results (14) remains unexplained. Given previous literature and our Na+ data, the simplest interpretation of our observation of the same two distinct speeds near zero torque in the H+ motor using two totally different methods (steady-state recording with gold beads and measurement of the torque–speed curve of the proton stator in the hybrid motor) is that the speed levels correspond to one and two stator units. Testing this interpretation with simultaneous determination of stator number by fluorescence microscopy is beyond our current experimental capabilities, and very low yields of rotating motors at low loads combined with short recording times in our high-speed setup prevent us from identifying single-unit motors using initial speed levels in “resurrection” experiments (19). We attempted to observe speed levels corresponding to three or more H+ units by overexpression of stator proteins. Induction with 1 M arabinose yielded zero spinning motors, while 10 M, 20 M, and 1 mM arabinose were indistinguishable in both yield and motor speed. We hypothesize that either the concentration of stator proteins is not limiting in our experiments or our expression system is saturated at 10 M arabinose; also, we hypothesize that either the affinity at low load or the expression level of sodium stator units is greater than those of the proton stator, allowing for observation of higher stator numbers. Without these tests, the possibility remains that Na+ and H+ stators are different at low load, and alternative interpretations of discrete speed levels in the H+ motor need to be considered. If a fully functional unit rotates at 240–300 Hz (14), lower speed levels might represent partially functional units. Speculations as to the possible nature of these include units attached to the peptidoglycan at suboptimal orientations or distances from the rotor and half-functional units with one channel blocked, misfolded, or otherwise misassembled.
The torque–speed relationships of motors driven by Na+ and H+ stators are very similar, indicating that the motor mechanism is shared by both ion types. To fit the previously held experimental constraint of zero-load speeds independent of stator unit number, mechanistic motor models have invoked three conditions: (i) compliant springs linking stator units to the cell wall, storing energy and allowing stator units to step independently (33, 34); (ii) high duty ratio, such that the stator units remain attached to the rotor most of the time (9); and (iii) load independence of rate constants for forward transitions of the motor, which are rate-limiting at low load (9). Our results lift this constraint. Lifting condition iii in a model where rotation and ion transit are tightly coupled and thus, the duty ratio is one causes the zero-load speed to increase with stator number (9), and with suitable parameters, it might be able to reproduce the observed approximate linear dependence for one to three stator units (Fig. S2). Loose coupling and low duty ratio also reproduce approximately linear dependence on stator number (9, 35). Loose coupling is one possible explanation for the discrepancy between observations of 26 steps per revolution with one stator unit (18) and an estimate that at least 37 ions pass through the Na+-driven motor per stator unit per revolution (13). Recent models have proposed loose coupling either where torque-generating conformational changes in a stator unit can be driven by either one or two ions (36) or where coupling between ions and stator unit conformation change is tight but the duty ratio is less than one at low load (35). Our data leave open the question of stator springs. Finally, we note the possibility that the observed 26 steps per revolution are a signature of a passive periodic structure in the motor rather than of the mechanochemical cycle (33).
Materials and Methods
Additional details regarding materials and methods are in SI Materials and Methods.
Bacteria and Culture.
E. coli strains (7, 8, 18, 21, 37–39) were grown and stator proteins were induced as described previously (7).
Speed Measurements.
Cells were immobilized on poly-l-lysine–coated glass coverslips in custom-made flow chambers. Particles were attached to the hook or truncated flagella as described previously (7, 14, 38). Beads were tracked using either back focal plane interferometry (7, 40) or back-scattering dark-field microscopy (17) and a quadrant photodiode (QPD) or high-speed camera (Photron). All experiments were performed at 23 °C in motility buffer (7).
Motor Speed Analysis.
Speeds were analyzed using custom Labview and MATLAB programs from power spectra of the (x, y) position of the bead, similar to that performed previously (9) (SI Materials and Methods). A multiple Gaussian fit was applied to speed histograms. For hybrid motor experiments, speeds were clustered using the k-means (41) and G-means (42) algorithms.
Torque Calculation.
Motor torque was calculated as , where is the angular velocity, and and are the rotational frictional drag coefficients of the attached bead and filament stub (where present), respectively (12).
One and Two H+ Stator Torque–Speed Curves.
In Fig. 5 A and C, the numbers of H+ stator units engaged before Na+ buffer addition and after Na+ buffer removal were assigned according to motor speed. The number of Na+ stators engaged was assigned by adding one for each speed level. In Fig. 5 C and F, each point in the average curve (black in Fig. 5 C and F) shows the mean and SD of all of the points from the individual curves (shown in colors in Fig. 5 C and F) falling within a bin width of 40 Hz.
SI Results
Speed Levels of the Na+-Driven Motor.
Fig. S1 shows examples of spontaneous stepwise speed changes at various [Na+], similar to Fig. 1.
Torque–Speed Curves of the Na+-Driven Motor at Different Membrane Voltages.
Fig. S3 shows previously published data (13, 25) of polystyrene beads driven by one to three stator units. These torque speed curves show the same concave-down shape as seen previously (13).
Speed Levels of the WT+-Driven Motor Down-Sampled and Filtered.
In the text, we compare the speed of the WT motor at low load (Fig. 4D) with previously published values (14). As noted, the speeds in the work by Yuan and Berg (14) were filtered to yield a time resolution of 9 s. Fig. 4E shows data from Fig. 4D, where the data have been down-sampled and filtered to match the resolution of Yuan and Berg (14). Not all of our traces were of sufficient length for this analysis; Fig. 4E contains data from eight cells (1,394 s) and is fit as described in SI Materials and Methods. The multiple Gaussian fit identifies three peaks at 47 18, 107 14, and 215 47 Hz. Both the distribution and the position of the Gaussians are not significantly different from Fig. 4D, suggesting that the multiple speeds at zero load identified in this study are a characteristic of the motor and that reduced time resolution is insufficient to explain why they were not observed previously.
Torque and Speed Versus Number of Stator Units Compiled from Multiple Studies.
Mechanistic models of torque generation in the BFM rely on measurements of the relationship between torque and speed. Fig. S4 A and B shows a compilation of such measurements over multiple studies. Where necessary, we have recalculated torques from published speeds using the method of Inoue et al. (12) to reflect subsequent refinements in analysis methods and to ensure consistency when comparing results from different studies. Stator unit numbers are those assigned by the individual studies before the knowledge that stator unit number was a function of load. Our data from this study are shown in black in Fig. S4 A and B, with solid black lines in Fig. S4 A and B for torque–speed curves in hybrid fuel motors.
Where ranges overlap, our data are in broad agreement with previous measurements with one to three stator units, with the exception of zero-torque speeds in WT motors. Fig. S4C combines the averaged normalized torque–speed curve for the chimeric motor (Fig. S4C, squares) with the data for one and two H+ stator units, showing that both types of motor share the same normalized curve under all conditions measured. Whether this holds for different values of proton-motive force (PMF) and for more than three stator units remains to be discovered. If so, we would predict that, if it were possible to maintain high stator numbers at low load, motor speeds as high as 1,000 Hz in WT and 2,000 Hz in chimeric motors would be observed at room temperature. Furthermore, if this curve applies to WT motors with more than two stators, Fig. S4A indicates that decreases in stator number with speed were indeed missed in previous studies.
SI Materials and Methods
Bacteria and Culture.
Escherichia coli strain YS1243 (37) [YS34 (CheY, fliC:Tn10, pilA, motAmotB)], transformed with plasmid pYS13 (18) [pomApotB (8), isopropyl -D-1-thiogalactopyranoside (IPTG) inducible, chloramphenicol resistance)], was used for Na+ motor gold nanoparticle experiments. E. coli strain MTB22 [CheY, FliC, pilA, motAmotB, RP437 (43) derivative], transformed with plasmid pDFB27 (21) (motAmotB, arabinose inducible, ampicilin resistance), was used for H+ motor gold nanoparticle experiments; the hook protein, FlgE, was replaced in this strain with an FlgE protein with an AviTag sequence, ensuring endogenous biotinylation of the hook (38). E. coli strain JHC36 (7) [CheY, pilA, motAmotB, FliC-sticky (39)], transformed with plasmids pYS13 and pDFB27, was used for hybrid motor polystyrene bead experiments. Cells were grown from frozen aliquots [0.1 mL, grown overnight in LB medium and stored at −80 °C with DMSO or glycerol, 10 or 25% (vol/vol), respectively] in 5 mL of T broth [1% Bacto tryptone (Difco), 0.5% NaCl] for 4.5–5.5 h with shaking at 30 °C. Cells were grown with appropriate antibiotics (chloramphenicol, 25 g/mL, and/or ampicillin, 50 g/mL) and inducers (IPTG, 2–30 M, and/or arabinose, 10 M). Stator proteins were induced at different levels as described previously (7).
Speed Measurements.
Cells were immobilized on poly-l-lysine–coated glass coverslips in custom-made flow chambers. For Na+ motor gold nanoparticle experiments, anti-rabbit IgG-modified gold particles of 100-nm diameter (BBInternational) were attached to hooks of strain YS1243 via anti-FlgE antibody as described previously (14). For H+ motor gold nanoparticle experiments, gold particles (100-nm diameter; BBInternational) were modified with streptavidin and attached to endogenously biotinylated hooks of strain MTB22 (38). Beads were tracked using back-scattering dark-field microscopy (17) and a QPD or high-speed camera (Photron). The acquisition rate was 2–4 kHz for Na+ motors and 20–109.5 kHz for H+ motors. For hybrid motor experiments, polystyrene beads (0.50-m diameter; Polysciences, Inc.) were attached to truncated flagellar filaments of strain JHC36 and tracked at 2 kHz using a QPD and back focal plane interferometry as described (7, 40). Experiments were performed in motility buffer [10 mM potassium phosphate, 0.1 mM EDTA, X mM sodium chloride, (85-X) mM potassium chloride, pH 7.0, where X = 0, 1, 5, 10, 30, 85]. Flow chambers with two input channels containing sodium concentrations of 0 and 85 mM were used for sodium resurrection and deresurrection experiments. All experiments were performed at 23 °C.
Motor Speed Analysis.
Speeds were analyzed using custom Labview and MATLAB programs. For Na+ and H+ motor experiments, motor speed was calculated from power spectra of the (x, y) position (9) of the bead after mapping to a circle via ellipse fitting (18) using continuous data windows of 0.02 s. With the assumption that the motor rotated at a single frequency during any window, data windows were padded to 1 s with zeros, and the peak of the resulting power spectrum was identified, yielding a speed resolution of 1 Hz. Zero padding allows the localization of an isolated spectral component with higher precision than the intrinsic resolution of the power spectrum of the unpadded data window, a process that is the equivalent in time to superresolution microscopy (44) in space, allowing simultaneously high time and frequency resolutions. Histograms of speeds were constructed using 8-Hz bins. A multiple Gaussian fit was applied to all speeds greater than 30 Hz to identify the speed of multiple peaks for each [Na+]. The optimal number of Gaussians was determined by Bayesian information criterion (45) of the fits. A separate Gaussian was fit with a center at 0 Hz.
For hybrid motor experiments, motor speed was defined by the largest peak in the power spectrum of the combined (x, y) bead position as measured by the QPD (9). Windows of length 1 s were used at 0.1-s intervals. Speeds were clustered using the k-means clustering algorithm (41), a center-based clustering algorithm, which partitions data into clusters to minimize the within-cluster sum of squares. The optimal number of clusters was determined using the G-means algorithm (42), which is based on the assumption that each cluster should follow a Gaussian distribution.
Torque–Speed Curve Compilation.
Fig. S4 combines data from seven previously published studies and this study to show the torque versus speed for BFMs with varying numbers of either WT or chimeric Na+ stator units. For each previous study, beads were attached to either a truncated filament or the hook of a BFM on an immobilized cell. The speed of the bead was measured, and in some studies, the viscous load was estimated to calculate the torque on the motor. Although the assay was consistent among the studies, the calculation of torque was not. In Fig. S4, we have used the speed data taken by eye from published figures and applied a consistent method of torque calculation based on that used in Inoue et al. (12) as described below. This allows for comparison among the various datasets.
The torque of the BFM can be estimated as
| [S1] |
where is the angular velocity, and and are the rotational frictional drag coefficients of the attached bead and filament (where present), respectively. The negligible drag of the hook is ignored; and are products of a geometric factor, or , respectively, and the viscosity of the medium, . Previous studies have varied the viscosity of the medium by adding various concentrations of Ficoll, a neutral, highly branched, high-mass, hydrophilic polysaccharide, which dissolves readily in aqueous solutions. The geometric factor of the attached bead can be estimated as
| [S2] |
where and are the radius and rotational eccentricity of the bead, respectively.
In Fig. S4, for beads attached to a truncated filament, we used an eccentricity radius of 0.20 m (19) and a geometric factor for filament drag of 1.29 × 108 nm3 (11). For beads attached directly to the hook of a BFM lacking a filament, the eccentricity radius was set to the length of the hook: 50 nm (46). For experiments in motility medium, was 9.86 × 10−10 pN s nm−2, and for experiments in Ficoll, viscosity values were taken from Chen and Berg (11). Details of how this analysis differed from the original torque calculation of each study are provided below.
In the work by Ryu et al. (9), torque of the BFM was estimated as
| [S3] |
where was the structural factor of the flagellar stub (47),
| [S4] |
the minor flagellar radius, , was 10 nm, the major radius, , was left as a free parameter for fitting, and the rotational radius of the flagellar stub, , was set to /2. Rotational eccentricity was 0.15 0.05 m. The drag for each bead size was then adjusted, such that the data points representing five stator units coincided with the torque–speed curve in the works by Berg and Turner (24) and Chen and Berg (11), scaled by 5/8, but with the same knee and zero-torque speeds. At the time, the maximum number of stator units within a motor was believed to be eight (21). The fitted truncated flagellar lengths were 1.22, 1.07. 0.95, 0.91, and 0.75 m for bead sizes 1.0, 0.54, 0.41, 0.36, and 0.30 m, respectively (9). The geometric factor of the filament in these studies was 15–60% of that used in the work by Inoue et al. (12). Speed measurements used in Fig. S4A were extracted from figure 3A of Ryu et al. (9).
The parent strain in the study by Chen and Berg (11) was KAF95. All other studies represented in Fig. S4A, with the exception of that of Gabel and Berg (48), used strains of either an motA mutant or motAmotB and induced the stator proteins on a plasmid. This study calculated only the relative torque of the BFM, equal to viscosity multiplied by speed. Rotational eccentricity was not measured. Speed and Ficoll solution values used in Fig. S4A were extracted from figure 4B of Chen and Berg (11). The bulk viscosity of the Ficoll solution was taken from table 1 of Chen and Berg (11). We note that it is unclear from the paper whether figure 4B of Chen and Berg (11) used beads of size 0.25 or 0.36 m. We have assumed the latter; if not, the torque values corresponding to this study in Fig. S4A should be reduced by a factor of 30%.
The parent strain in the study by Gabel and Berg (48) was KAF95. This study did not measure rotational eccentricity and did not calculate motor torque. The speed measurement used in Fig. S4A was extracted from figure 3B of Gabel and Berg (48).
The study by Reid et al. (19) measured speed as a function of stator unit number. The speed measurements used in Fig. S4 A and B were extracted from table 2 and figure 6B of Reid et al. (19). Torque was estimated ignoring the drag of the filament and using Eq. S2 for the geometric factor of the bead. The rotational eccentricity measured was 0.2 0.03 m.
The study by Lo et al. (25) measured speed, did not measure rotational eccentricity, and did not estimate BFM torque. The speed measurements used in Fig. S4B were extracted from figure 4 A, B, D, and E of Lo et al. (25).
The study by Inoue et al. (12) estimated the geometric factor of the filament stub to be 1.29 0.32 × 108 nm3 by equating the drag coefficients of smaller beads in Ficoll with those of 1-m beads spinning at the same speed without Ficoll, and it is the source of the estimate of filament drag for torques shown in Fig. S4. The rotational eccentricity of the beads measured in this study was not published. The bulk viscosity of the Ficoll solution was as reported in Chen and Berg (11). The speed measurements used in Fig. S4 A and B were extracted from figures 1 B and D and 3 A and B of Inoue et al. (12).
The study by Yuan and Berg (14) measured speed, and the speed measurement used in Fig. S4A was taken from figure 2A and the text of Yuan and Berg (14). The study calculated a range of motor torques depending on the rotational eccentricity, which was not measured.
The study by Lo et al. (13) estimated motor torque as in Inoue et al. (12), including the estimation of the geometric factor of the filament. The values of the geometric factor of the filament and the rotational eccentricity were not published. The speed measurements used in Fig. S4B were taken from figure 3A of Lo et al. (13).
Gabel and Berg (48) and Chen and Berg (11) were the only two studies represented in Fig. S4A to use strain KAF95. All other studies used strains of either an motA mutant or motAmotB and induced the stator proteins on a plasmid. The lower torques observed in these two studies may be because of an inherent difference in strain or because of a difference in copy number between genetically encoded and plasmid-encoded stator proteins. It is also possible that chosen beads showed a higher rotational eccentricity than in other studies, perhaps because of the method of detection; for these two studies to match the torque values of Inoue et al. (12), the rotational eccentricity would need to be about 60% larger than estimated.
Acknowledgments
We thank Howard C. Berg for the gift of anti-FlgE antibody. A.L.N. was supported by the Rhodes Trust, and Y.S. was supported by KAKENHI and the Japan Society for the Promotion of Science Abroad. This work was also supported by Biotechnology and Biological Sciences Research Council Grants BB/H01991X/1 and BB/E00458X/1. Centre de Biochimie Stucturale is a member of France-BioImaging and the French Infrastructure for Integrated Structural Biology, two national infrastructures supported by French National Research Agency Grants ANR-10-INBS-04-01 and ANR-10-INBS-05.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1708054114/-/DCSupplemental.
References
- 1.Leake MC, et al. Stoichiometry and turnover in single, functioning membrane protein complexes. Nature. 2006;443:355–358. doi: 10.1038/nature05135. [DOI] [PubMed] [Google Scholar]
- 2.Tipping MJ, Steel BC, Delalez NJ, Berry RM, Armitage JP. Quantification of flagellar motor stator dynamics through in vivo proton-motive force control. Mol Microbiol. 2013;87:338–347. doi: 10.1111/mmi.12098. [DOI] [PubMed] [Google Scholar]
- 3.Sowa Y, Berry RM. Bacterial flagellar motor. Q Rev Biophys. 2008;41:103–132. doi: 10.1017/S0033583508004691. [DOI] [PubMed] [Google Scholar]
- 4.Fukuoka H, Wada T, Kojima S, Ishijima A, Homma M. Sodium-dependent dynamic assembly of membrane complexes in sodium-driven flagellar motors. Mol Microbiol. 2009;71:825–835. doi: 10.1111/j.1365-2958.2008.06569.x. [DOI] [PubMed] [Google Scholar]
- 5.Paulick A, et al. Two different stator systems drive a single polar flagellum in Shewanella oneidensis mr-1. Mol Microbiol. 2009;71:836–850. doi: 10.1111/j.1365-2958.2008.06570.x. [DOI] [PubMed] [Google Scholar]
- 6.Paulick A, et al. Dual stator dynamics in the Shewanella oneidensis mr-1 flagellar motor. Mol Microbiol. 2015;96:993–1001. doi: 10.1111/mmi.12984. [DOI] [PubMed] [Google Scholar]
- 7.Sowa Y, Homma M, Ishijima A, Berry RM. Hybrid-fuel bacterial flagellar motors in Escherichia coli. Proc Natl Acad Sci USA. 2014;111:3436–3441. doi: 10.1073/pnas.1317741111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Asai Y, Yakushi T, Kawagishi I, Homma M. Ion-coupling determinants of Na+-driven and H+-driven flagellar motors. J Mol Biol. 2003;327:453–463. doi: 10.1016/s0022-2836(03)00096-2. [DOI] [PubMed] [Google Scholar]
- 9.Ryu WS, Berry RM, Berg HC. Torque-generating units of the flagellar motor of Escherichia coli have a high duty ratio. Nature. 2000;403:444–447. doi: 10.1038/35000233. [DOI] [PubMed] [Google Scholar]
- 10.Sowa Y, Hotta H, Homma M, Ishijima A. Torque-speed relationship of the Na+-driven flagellar motor of Vibrio alginolyticus. J Mol Biol. 2003;327:1043–1051. doi: 10.1016/s0022-2836(03)00176-1. [DOI] [PubMed] [Google Scholar]
- 11.Chen X, Berg HC. Torque-speed relationship of the flagellar rotary motor of Escherichia coli. Biophys J. 2000;78:1036–1041. doi: 10.1016/S0006-3495(00)76662-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Inoue Y, et al. Torque-speed relationships of Na+-driven chimeric flagellar motors in Escherichia coli. J Mol Biol. 2008;376:1251–1259. doi: 10.1016/j.jmb.2007.12.023. [DOI] [PubMed] [Google Scholar]
- 13.Lo CJ, Sowa Y, Pilizota T, Berry RM. Mechanism and kinetics of a sodium-driven bacterial flagellar motor. Proc Natl Acad Sci USA. 2013;28:E2544–E2551. doi: 10.1073/pnas.1301664110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yuan J, Berg HC. Resurrection of the flagellar rotary motor near zero load. Proc Natl Acad Sci USA. 2008;105:1182–1185. doi: 10.1073/pnas.0711539105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lele PP, Hosu BG, Berg HC. Dynamics of mechanosensing in the bacterial flagellar motor. Proc Natl Acad Sci USA. 2013;110:11839–11844. doi: 10.1073/pnas.1305885110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tipping MJ, Delalez NJ, Lim R, Berry RM, Armitage JP. Load-dependent assembly of the bacterial flagellar motor. MBio. 2013;4:e00551-13. doi: 10.1128/mBio.00551-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sowa Y, Steel BC, Berry RM. A simple backscattering microscope for fast tracking of biological molecules. Rev Sci Instrum. 2010;81:113704. doi: 10.1063/1.3495960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sowa Y, et al. Direct observation of steps in rotation of the bacterial flagellar motor. Nature. 2005;437:916–919. doi: 10.1038/nature04003. [DOI] [PubMed] [Google Scholar]
- 19.Reid SW, et al. The maximum number of torque-generating units in the flagellar motor of Escherichia coli is at least 11. Proc Natl Acad Sci USA. 2006;103:8066–8071. doi: 10.1073/pnas.0509932103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Block SM, Berg HC. Successive incorporation of force-generating units in the bacterial rotary motor. Nature. 1984;309:470–472. doi: 10.1038/309470a0. [DOI] [PubMed] [Google Scholar]
- 21.Blair DF, Berg HC. Restoration of torque in defective flagellar motors. Science. 1988;242:1678–1681. doi: 10.1126/science.2849208. [DOI] [PubMed] [Google Scholar]
- 22.Berry RM, Berg HC. Torque generated by the flagellar motor of Escherichia coli while driven backward. Biophys J. 1999;76:580–587. doi: 10.1016/S0006-3495(99)77226-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nakamura S, et al. Effect of intracellular pH on the torque–speed relationship of bacterial proton-driven flagellar motor. J Mol Biol. 2009;386:332–338. doi: 10.1016/j.jmb.2008.12.034. [DOI] [PubMed] [Google Scholar]
- 24.Berg HC, Turner L. Torque generated by the flagellar motor of Escherichia coli. Biophys J. 1993;65:2201–2216. doi: 10.1016/S0006-3495(93)81278-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lo CJ, Leake MC, Pilizota T, Berry RM. Nonequivalence of membrane voltage and ion-gradient as driving forces for the bacterial flagellar motor at low load. Biophys J. 2007;93:294–302. doi: 10.1529/biophysj.106.095265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yuan J, Berg HC. Thermal and solvent-isotope effects on the flagellar rotary motor near zero load. Biophys J. 2010;98:2121–2126. doi: 10.1016/j.bpj.2010.01.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yuan J, Fahrner KA, Turner L, Berg HC. Asymmetry in the clockwise and counterclockwise rotation of the bacterial flagellar motor. Proc Natl Acad Sci USA. 2010;107:12846–12849. doi: 10.1073/pnas.1007333107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Beeby M, et al. Diverse high-torque bacterial flagellar motors assemble wider stator rings using a conserved protein scaffold. Proc Natl Acad Sci USA. 2016;113:E1917–E1926. doi: 10.1073/pnas.1518952113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yoshinaga MY, Kellermann MY, Valentine DL, Valentine RC. Phospholipids and glycolipids mediate proton containment and circulation along the surface of energy-transducing membranes. Prog Lipid Res. 2016;64:1–15. doi: 10.1016/j.plipres.2016.07.001. [DOI] [PubMed] [Google Scholar]
- 30.Prats M, Teissié J, Tocanne JF. Lateral proton conduction at lipid-water interfaces and its implications for the chemiosmotic-coupling hypothesis. Nature. 1986;322:756–758. [Google Scholar]
- 31.Berry RM, Berg HC. Absence of a barrier to backwards rotation of the bacterial flagellar motor demonstrated with optical tweezers. Proc Natl Acad Sci USA. 1997;94:14433–14437. doi: 10.1073/pnas.94.26.14433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hashimoto M, Mashimo T, Hirano T, Yamaguchi S, Aizawa S. Functional roles of the hook in a rotating tethered cell. J Mol Biol. 2008;375:367–375. doi: 10.1016/j.jmb.2007.09.046. [DOI] [PubMed] [Google Scholar]
- 33.Mora T, Yu H, Wingreen NS. Modeling torque versus speed, shot noise, and rotational diffusion of the bacterial flagellar motor. Phys Rev Lett. 2009;103:248102. doi: 10.1103/PhysRevLett.103.248102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bai F, Lo CJ, Berry RM, Xing J. Model studies of the dynamics of bacterial flagellar motors. Biophys J. 2009;96:3154–3167. doi: 10.1016/j.bpj.2009.01.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nirody J, Berry R, Oster G. The limiting speed of the bacterial flagellar motor. Biophys J. 2016;111:557–564. doi: 10.1016/j.bpj.2016.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Boschert R, Adler FR, Blair DF. Loose coupling in the bacterial flagellar motor. Proc Natl Acad Sci USA. 2015;112:4755–4760. doi: 10.1073/pnas.1419955112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nord AL, Pedaci F, Berry RM. Transient pauses of the bacterial flagellar motor at low load. New J Phys. 2016;18:115002. [Google Scholar]
- 38.Brown MT, et al. Flagellar hook flexibility is essential for bundle formation in swimming Escherichia coli cells. J Bacteriol. 2012;194:3495–3501. doi: 10.1128/JB.00209-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Scharf BE, Fahrner KA, Turner L, Berg HC. Control of direction of flagellar rotation in bacterial chemotaxis. Proc Natl Acad Sci USA. 1998;95:201–216. doi: 10.1073/pnas.95.1.201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Rowe AD, Leake MC, Morgan H, Berry RM. Rapid rotation of micron and submicron dielectric particles measured using optical tweezers. J Mod Opt. 2003;50:1539–1554. [Google Scholar]
- 41.MacQueen J. Some methods for classification and analysis of multivariate observations. In: Le Cam LM, Neyman J, editors. Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability. Vol 1. Univ of California Press; Berkeley, CA: 1967. pp. 281–297. [Google Scholar]
- 42.Hamerly G, Elkan C. Learning the k in k-means. In: Thrun S, Saul LK, Scholkopf PB, editors. Advances in Neural Information Processing Systems 16. MIT Press; Cambridge, MA: 2003. pp. 281–288. [Google Scholar]
- 43.Parkinson JS. Complementation analysis and deletion mapping of Escherichia coli mutants defective in chemotaxis. J Bacteriol. 1978;135:45–53. doi: 10.1128/jb.135.1.45-53.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Betzig E, et al. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–1645. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 45.Schwarz G. Estimating the dimension of a model. Ann Stat. 1978;6:461–464. [Google Scholar]
- 46.Hirano T, Yamaguchi S, Oosawa K, Aizawa S. Roles of flik and flhb in determination of flagellar hook length in Salmonella typhimurium. J Bacteriol. 1994;176:5439–5449. doi: 10.1128/jb.176.17.5439-5449.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Happel J, Brenner H. Low Reynolds Number Hydrodynamics. Springer; Dordrecht, The Netherlands: 1991. [Google Scholar]
- 48.Gabel CV, Berg HC. The speed of the flagellar rotary motor of Escherichia coli varies linearly with protonmotive force. Proc Natl Acad Sci USA. 2003;100:8748–8751. doi: 10.1073/pnas.1533395100. [DOI] [PMC free article] [PubMed] [Google Scholar]