Evolution of stochastic demography with life history tradeoffs in density-dependent age-structured populations

Significance

We derive a univariate approximation for the growth of a density-dependent age-structured population in a fluctuating environment. Its accuracy is demonstrated by comparison with simulations of the age-structured model under assumptions applicable to many vertebrate populations. This facilitates extension to age-structured populations of recent theory on the evolution of stochastic population dynamics, showing that evolution tends to maximize a simple function of three key population parameters: the maximum population growth rate and carrying capacity in the average environment, $r_0$ and $K$, and the variance of population growth rate, ${\sigma }_e^2$. Regardless of the complexity of trade-offs among these parameters, for the classical logistic model of population growth, evolution in a fluctuating environment tends to maximize the average population size.

Abstract

We analyze the stochastic demography and evolution of a density-dependent age- (or stage-) structured population in a fluctuating environment. A positive linear combination of age classes (e.g., weighted by body mass) is assumed to act as the single variable of population size, $N$, exerting density dependence on age-specific vital rates through an increasing function of population size. The environment fluctuates in a stationary distribution with no autocorrelation. We show by analysis and simulation of age structure, under assumptions often met by vertebrate populations, that the stochastic dynamics of population size can be accurately approximated by a univariate model governed by three key demographic parameters: the intrinsic rate of increase and carrying capacity in the average environment, $r_0$ and $K$, and the environmental variance in population growth rate, ${\sigma }_e^2$. Allowing these parameters to be genetically variable and to evolve, but assuming that a fourth parameter, $\theta$, measuring the nonlinearity of density dependence, remains constant, the expected evolution maximizes $\text{E}[N^{\theta }]=[1-{\sigma }_e^2/(2r_0)]K^{\theta }$. This shows that the magnitude of environmental stochasticity governs the classical trade-off between selection for higher $r_0$ versus higher $K$. However, selection also acts to decrease ${\sigma }_e^2$, so the simple life-history trade-off between $r$- and $K$-selection may be obscured by additional trade-offs between them and ${\sigma }_e^2$. Under the classical logistic model of population growth with linear density dependence ($\theta =1$), life-history evolution in a fluctuating environment tends to maximize the average population size.

Classical population genetic models assuming a constant population size or density in a constant environment (1–5) show that evolution maximizes the mean fitness of individuals in the population. The ecological meaning of this result is that when population dynamics is density-dependent, but selection is not, evolution in a constant environment maximizes the intrinsic rate of population increase, $r_0$, the per capita population growth rate at low population density (ref. 6, chap. 1).

Density-dependent selection happens when the relative fitness of genotypes differs in response to change in population density. MacArthur (5) showed that density-dependent selection in a constant environment maximizes the equilibrium population size or carrying capacity, $K$. This result for density-dependent selection in a constant environment was extended to an age-structured population by Charlesworth (7) for the case where all density dependence in the life history is exerted by a single age or stage class (e.g., adults), showing that evolution maximizes the size of that class.

Contrasting conclusions for density-independent and density-dependent selection in a constant environment led to the conceptual theory of $r$- and $K$-selection, proposing a constraint or trade-off between these variables within populations, such that $K$-selection prevails in stable populations in nearly constant environments, while $r$-selection prevails in highly variable populations in strongly fluctuating environments (8–13). The dichotomous classification of species being either $r$- or $K$-selected lost popularity when more cognizance was taken that $r$ and $K$ are emergent properties of age-structured populations, with complex trade-offs between survival and fecundity among age classes. Furthermore, in every fluctuating population $r$- or $K$-selection prevails, respectively, when population density is low or high, corresponding on average to an increasing or decreasing population (7, 14).

Initial analytical investigations of evolution in fluctuating environments for populations without age structure were made by Dempster (15) for single-locus haploid or asexual inheritance, and by Haldane and Jayakar (16) for a single diallelic locus in an obligately sexual, randomly mating diploid population. They modeled random environmental fluctuations with a stationary distribution of fitnesses for each genotype, implicitly assuming density-independent selection, and found a simple condition that determines the final evolutionary outcome. For a haploid or asexual population, the genotype with the highest geometric mean fitness eventually becomes fixed. For a diallelic locus in a diploid randomly mating population, if a homozygote has the highest geometric mean fitness it eventually becomes fixed, but if the heterozygote has the highest mean fitness a genetic polymorphism is maintained by fluctuating selection (neglecting fixation by genetic drift in a finite population). These conclusions are especially interesting because the genotype with the highest geometric mean fitness may not be that with the highest arithmetic mean fitness, if the latter occasionally experiences very low fitness; thus, genotypes that are well-buffered against catastrophic loss of fitness in extreme environments may have a decisive long-term evolutionary advantage. For polygenic characters, fluctuating density-independent selection generally does not act to maintain genetic polymorphism except possibly at a single locus (17).

A common misinterpretation of these classical results on fluctuating selection still pervades the evolutionary and ecological literature, which is that the geometric mean fitness of a genotype in a fluctuating environment measures the selection on it. This interpretation is erroneous because fitness is supposed to predict short-term changes in gene frequencies over time spans on the order of one generation, whereas the geometric mean fitness only predicts the final outcome of selection. For density-independent selection in a fluctuating environment, the correct measure of the expected relative fitness of a genotype is its Malthusian fitness (the intrinsic rate of increase in the average environment) minus the covariance of its fitness with that of the population (17–19). A similar definition of expected mean fitness of a genotype also applies with density-dependent selection, with the Malthusian fitness conditioned on the current population density (20, 21).

In a constant environment, assuming constant genotypic fitnesses and approximate linkage equilibrium among loci, the log of mean fitness in a population, $\ln \hspace{0.17em}\overline{w}=r$, as a function of gene frequencies, describes an adaptive topography that governs both short-term and long-term evolution of gene frequencies by natural selection (3, 4, 22, 23). A similar adaptive topography has been derived for the evolution of mean phenotypes in quantitative characters (24, 25). The gradient of the adaptive topography (or selection gradient) at any given point, $\nabla r$, is a vector with elements that are the partial derivatives of the log mean fitness in the population with respect to gene frequencies or mean phenotypes. The gradient dynamics imply that evolution in a constant environment is a hill-climbing process, continually increasing the mean fitness of the population until a local maximum in mean fitness, an adaptive peak, is achieved.

In a fluctuating environment with a stationary distribution of environmental states and no autocorrelation, Lande (17, 18) showed that the long-run growth rate of the population, $r-{\sigma }_e^2/2$, provides an unchanging adaptive topography governing the expected evolution. From the theory of stochastic demography, the long-run growth rate of a density-independent population gives the expected (or asymptotic) rate of increase of $\ln \hspace{0.17em}N$, where $r$ is the expected growth rate in the average environment and ${\sigma }_e^2$ is the environmental variance in growth rate (26–30).

Density-dependent selection in a fluctuating environment presents the additional complication that stochastic evolution is coupled with the stochastic dynamics of population size. Lande et al. (20) and Engen et al. (21) analyzed density-dependent selection in a fluctuating environment for populations without age structure, respectively both for asexual inheritance and for quantitative (polygenic) characters in an obligately sexual population. Neglecting genetic drift and demographic stochasticity due to small population size, they showed that evolution tends to maximize the expected density dependence averaged over the distribution of population size, E[g(N)]. The density-dependence function $g(N)$ may often be nonlinear, as suggested by evidence from a variety of species (31, 32). For the $\theta$-logistic model of density dependence, $g(N)=N^{\theta }$ (33), evolution maximizes $\text{E}[N^{\theta }]=[1-{\sigma }_e^2/(2r)]K^{\theta }$. This simple result generalizes to stochastic environments MacArthur’s (5) finding that density-dependent selection in a constant environment maximizes the equilibrium population size, $K$. In a stochastic environment, genetic trade-offs can constrain adaptive evolution toward increasing $r$ and $K$ and decreasing ${\sigma }_e^2$. This incorporates the trade-offs most often considered in the literature on $r$- and $K$-selection, by including the environmental variance in population growth rate.

Explicit age or stage structure is essential for any theory of selection, inheritance, and evolution of life histories. Here we extend the recent results on the evolution of stochastic demography and life-history trade-offs (20, 21) by assuming that all density dependence in the life history is exerted through a single positive linear combination of age classes, defined as the population size or density. The age-specific vital rates are all affected by the same possibly nonlinear function of population density but may differ in their sensitivity to population density and environmental stochasticity. We obtain parallel results for asexual inheritance and polygenic inheritance of quantitative traits.

Stochastic Demography of Population Size

We analyze the stochastic density-dependent demography of an age- or stage-structured population that is genetically monomorphic, as in classical demographic theory neglecting genetic variation and evolution, to derive an approximation for the expected growth rate of the log of population size, $N$, as a function of its current size.

The dynamics of the age- (or stage-) vector $n$ are

$$n(t+1)=L(N,t)n(t),$$ [1a]

where the density-dependent projection matrix $L(N,t)$ has nonnegative elements, the vital rates of age- or stage-specific annual survival and reproduction

$$L_{ij}(N,t)=l_{ij}(g(N))+{ϵ}_{ij}(t)$$ [1b]

with stochastic terms having mean $\text{E}[{ϵ}_{ij}(t)]=0$ and covariance $C_{iji\prime j\prime }=\text{E}[{ϵ}_{ij}(t){ϵ}_{i\prime j\prime }(t)]$. Elements $l_{ij}(g(N))$ of the expected projection matrix $l(g(N))$ involve a density-dependent function $g(N)$, where $N={\sum }_i{b}_i{n}_i$ is a linear combination of the age or stage classes with nonnegative coefficients $b_i$. In some cases it will be convenient to set the largest coefficient to 1, so that the contributions of all age classes to the population density are scaled to this unit. If all coefficients are unity then $N$ is the total population size. All density dependence in the life history is therefore exerted by a single linear combination of age classes, weighted, for example, by body mass and/or metabolic rate, governing the utilization, and competition for, a limiting resource, acting through $g(N)$. Neglecting Allee effects at small population size or density $g(N)$ we assume that $g(0)=0$ at $N=0$ and that $g(N)$ increases with increasing $N$ such that nonzero elements of the expected projection matrix $l(g(N))$ decrease with increasing $g(N)$.

For most natural populations, and particularly for vertebrates with adult body weights above 1 kg and discrete annual intervals of reproduction, realized intrinsic rates of increase are usually below about 0.1 per year (34). This applies even for many species with potentially high fecundity, due to high (density-independent and nonselective) mortality of prereproductive life stages in the average environment (35, 36). Most species are therefore located in the region of parameter space with nonchaotic dynamics and smoothly damped responses to stochastic perturbations (37, 38).

The deterministic model in the average environment therefore is assumed to have a stable equilibrium at $N=K$, given by the dominant eigenvalue $\lambda (g(N))$ of the expected projection matrix $l(g(N))$ as the solution of $\lambda (g(K))=1$. For values of $g(N)$ in the neighborhood of $g(K)$ the first-order expansion of $r=\ln \hspace{0.17em}\lambda$ yields

$$r(g(N))=\sum _{ij}{v}_i{u}_j{\gamma }_{ij}[g(K)-g(N)],$$ [2a]

where ${\gamma }_{ij}=-\partial l_{ij}/\partial g$ evaluated at $g=g(K)$. The right and left eigenvectors $u$ and $v$ of the deterministic projection matrix with the dominant eigenvalue $\lambda =1$ are respectively the stable age distribution and reproductive values evaluated at $N=K$ and normalized so that ${\sum }_i{u}_i=1$ and ${\sum }_i{v}_i{u}_i=1$. The coefficient $v_i{u}_j$ is the elasticity of the population growth rate with respect to a small change in the ijth element of the deterministic projection matrix $\partial \ln \hspace{0.17em}\lambda /\partial \ln l_{ij}$ (ref. 30, p. 209 and ref. 39).

The expansion of population growth rate in Eq. 2a is linear in the function $g(N)$ rather than $N$ to preserve the possible nonlinearity of density dependence. For a small intrinsic rate of increase in the average environment (discussed in the Introduction), Eq. 2a can be extrapolated from $g(N)$ near $g(K)$ to $g(0)=0$. Defining $\gamma ={\sum }_{ij}{v}_i{u}_j{\gamma }_{ij}$, the deterministic intrinsic rate of increase, denoted as $r_0=r(0)$, is then $r_0=\gamma g(K)$, and substituting this in Eq. 2a yields

$$r(g(N))=r_0[1-g(N)/g(K)].$$ [2b]

This is a standard form for a one-dimensional population (lacking age structure) with nonlinear density dependence (29, 33).

The overall strength of density dependence in the life history is defined by the elasticity of $\lambda$ to a small change in population density, $-\partial \ln \hspace{0.17em}\lambda /\partial \ln \hspace{0.17em}N$ evaluated at $N=K$, which gives the expected rate of return to the equilibrium or average population size following a small perturbation (29, 40, 41). For the $\theta$-logistic model, $g(N)=N^{\theta }$ with $\theta >0$, the overall strength of density dependence is $\theta r_0$ (29). Thus, $r_0$ is an important parameter governing population fluctuations around the equilibrium or average size (29, 42).

In the stochastic model the environmental variance in population growth rate near the deterministic equilibrium is

$${\sigma }_e^2=\sum _{iji\prime j\prime }{v}_i{u}_{j}vi\prime u_{j\prime }\text{E}[{\xi }_{ij}(t){\xi }_{i\prime j\prime }(t)]$$ [2c]

(26–30, 43). We assume that the $l_{ij}(g(N))$ depends weakly on $g(N)$ so that ${\sigma }_e^2$ is nearly constant and independent of $N$.

The long-run growth rate of the population given the current population size is $r(g(N))-{\sigma }_e^2/2$. More accurately this gives the expected rate of increase of the log of population size (or any positive linear combination of age or stage classes) (26–30). The one-dimensional approximation for the stochastic dynamics of log population size in discrete time is, therefore,

$$\ln \hspace{0.17em}N(t+1)=\ln \hspace{0.17em}N(t)+r(g(N))-{\sigma }_e^2/2+{\sigma }_e\xi (t),$$ [3]

where $\xi (t)$ is a normally distributed random variable with mean $0$, variance $1$, and no autocorrelation and the population parameters $r_0$, $K$, and ${\sigma }_e^2$ are derived from the full matrix projection model for the age structure.

The continuous-time diffusion approximation to Eq. 3 has infinitesimal mean and variance $M_{\ln N}=r(g(N))-{\sigma }_e^2/2$ and $V_{\ln N}={\sigma }_e^2$, which can be used to find the stationary distribution of $\ln N$ or $N$ (29), as done for the $\theta$-logistic model with environmental stochasticity by Diserud and Engen (31). Neglecting demographic stochasticity and Allee effects at small population size, the stationary distribution exists when the stochastic intrinsic rate of increase is positive, $s=r_0-{\sigma }_e^2/2>0$. For the stochastic $\theta$-logistic model, the diffusion approximation for the stationary distribution of $N/K$, and its moments, depend only on $\theta$ and one composite parameter (Appendix),

$$a={\sigma }_e^2/(2r_0).$$ [4]

Stochastic simulations of the full age-structured model (Eqs. 1a and 1b) were compared with analytical formulas for the diffusion approximation (Appendix) for two different avian life histories representing a typical raptor and passerine species. Standard matrix projection methods were used for stochastic simulations of a stage-structured population composed of a number of juvenile (prereproductive) and immature age classes and a final stage class including all adults of a certain age or older. Assuming a prebreeding census, with the first age class being one-year-olds, the annual fecundities include a multiplicative factor of the probability of survival during the first year of life (30). Vital rates and their density dependence and environmental sensitivity can change with age until the final stage at which they become independent of age, neglecting senescence in the oldest individuals which usually are so rare as to be of little demographic importance (44–46). The vital rates of the youngest age classes are assumed to have both the highest environmental stochasticity (47–52) and to suffer the strongest density dependence (53, 54), which is exerted by a positive linear combination of stage classes with individuals weighted in proportion to their utilization of a limiting resource, such that weights generally increase with age and/or body size (Supporting Information).

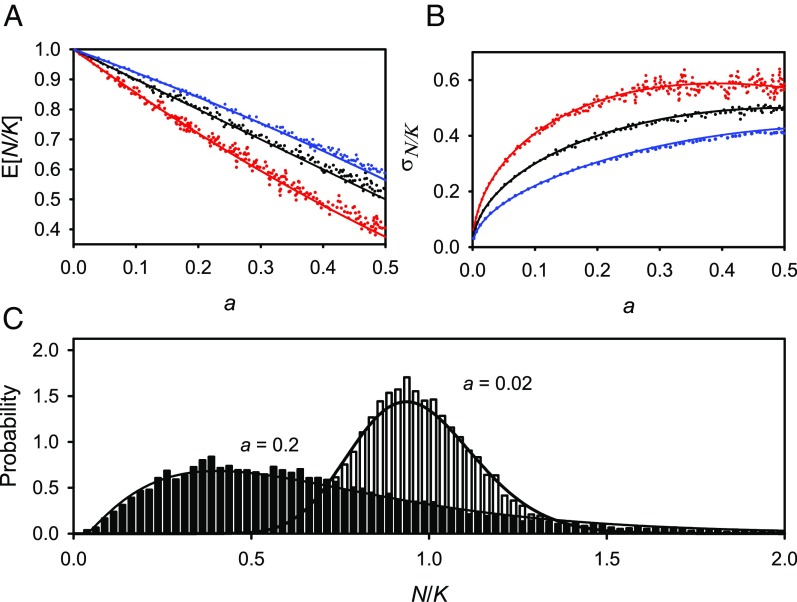
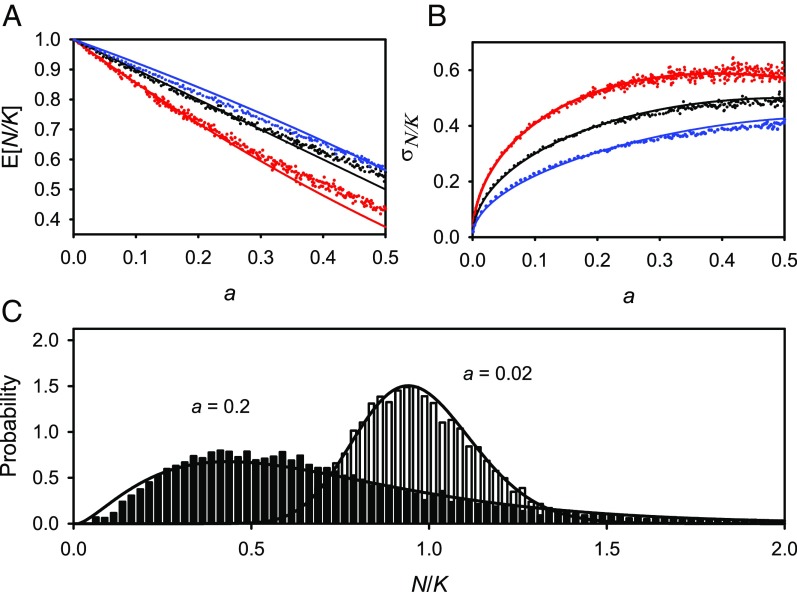
Fig. 1 and Fig. 2 compare the mean and SD of $N/K$ in the simulations with those from diffusion theory as functions of $a$ for different values of $\theta$, along with examples of the probability distribution of $N/K$ for two values of $a$ in the logistic model. The age-structure simulations show a remarkably good fit to the one-dimensional diffusion approximation for small values of $r_0\le 0.1$ (Figs. 1 and 2) and remain close for values of $a<0.5$, corresponding coefficients of variation in population size below one for the logistic model, ${\text{CV}}_N<1$ (Appendix). Excluding estimation error variance, most vertebrate populations with long time series have small or moderate coefficients of variation (30).

Fig. 1.

(A) Mean, $\text{E}[N/K]$, and (B) SD, ${\sigma }_{N/K}$, as functions of the composite parameter $a={\sigma }_e^2/(2r_0)$, in the stochastic $\theta$-logistic model of density dependence for $\theta =0.5$ (red), $1$ (black), and $2$ (blue). (C) Stationary probability distribution $\varphi (N/K)$ in the stochastic logistic model ($\theta =1$) for two values of $a$. Solid lines calculated from diffusion approximation (Appendix). Each point in A or B and each distribution in C gives statistics for a sample of ${10}^4$ observations from a stage-structured model of an avian raptor with age at first breeding of 4 y and $r_0=0.04$, simulated for ${10}^6$ y and recorded once every 100 y (Supporting Information).

Fig. 2.

The same as Fig. 1 but with simulations for a passerine bird life history with age at first breeding of 1 y and $r_0=0.1$.

Evolution of Stochastic Demography

Asexual Inheritance and Evolution.

For a genetically monomorphic population, such as a single asexual genotype, averaging both sides of Eq. 3 through time it can be seen that the expected long-run growth rate, averaged over the stationary distribution of population size, must equal zero, $E[r(g(N))]-{\sigma }_e^2/2=0$, and using Eq. 2b we find

$$\text{E}[g(N)]=[1-{\sigma }_e^2/(2r_0)]g(K),$$ [5a]

which for the $\theta$-logistic model is

$$\text{E}[N^{\theta }]=[1-{\sigma }_e^2/(2r_0)]K^{\theta }.$$ [5b]

The analytical formula for $\text{E}[N^{\theta }]$ derived from the diffusion approximation for the $\theta$-logistic model agrees with Eq. 5b (Appendix).

For competition between two asexual genotypes, the final outcome of evolution is determined by the long-run growth rates of the genotypes, so it is sufficient to analyze only the invasion of a rare genotype into a population of a common resident genotype. Following Lande et al. (20), consider a resident genotype with population dynamics parameters $r_{0R}$, $K_R$, and ${\sigma }_{eR}^2$ and a rare invader genotype similarly indexed by $I$. For a sufficiently rare invader the density regulation it experiences is exerted by the density of the resident genotype, so the long-run growth rate of the rare invader is $r_{0I}[1-g(N_R)/g(K_I)]-{\sigma }_{eI}^2/2$. Assuming weak selection, so that evolution occurs much more slowly than population fluctuations, the long-run growth rate of the invader, averaged over the stationary distribution of population size of the resident genotype, determines the condition for successful invasion. The rare invader increases in frequency if its expected long-run growth rate, found by inserting $\text{E}[g(N_R)]$ from Eq. 5a, is positive,

$$r_{0I}\left[1-\left(1-\frac{{\sigma }_{eR}^2}{2r_{0R}}\right)\frac{g(K_R)}{g(K_I)}\right]-{\sigma }_{eI}^2/2>0,$$

or

$$\left(1-\frac{{\sigma }_{eI}^2}{2r_{0I}}\right)g(K_I)>\left(1-\frac{{\sigma }_{eR}^2}{2r_{0R}}\right)g(K_R).$$ [6]

This demonstrates that single-locus haploid (or asexual) evolution in a fluctuating environment maximizes the quantity in Eq. 5a, or for the $\theta$-logistic model that in Eq. 5b, as in Lande et al. (20).

Inheritance and Evolution of Quantitative Characters.

For populations with various combinations of age structure, density dependence of population dynamics and selection, fluctuating environments, and for different mechanisms of inheritance, evolution has been shown to depend on the gradient of a suitable mean fitness function with respect to the evolutionary variables. For selection in a fluctuating environment with a stationary distribution of environmental states and no autocorrelation, the expected evolution depends on the gradient of the long-run (or expected) growth rate of the population, conditioned on its current genetic state, and on its current population density if selection is density-dependent (17, 18, 20, 21, 55, 56). We analyze the evolution of a vector of mean phenotypes, $\overline{z}$, of quantitative polygenic characters, such as measurements of morphology, behavior, and physiology. Discrete-time recursions apply to characters measured each unit of time before selection; ideally this is done in the youngest age or stage class, although some or all of the characters may be age- or stage-specific in their expression (e.g., body size as a function of age), or the characters may be parameters of individual growth trajectories (57).

Expected Population Growth Rate.

For a population without age structure, in a fluctuating environment with a stationary distribution of environmental states and no autocorrelation, the mean fitness function governing both the stochastic demography and evolution is the long-run growth rate, conditioned on the current population density if selection is density-dependent (17–21). Here we generalize this to age-structured populations using reproductive value weighting and then apply the gradient operator to derive the expected evolution of the mean phenotype.

The characters of individuals are assumed to be measured on scales such that their phenotypic and additive genetic (breeding) values follow multivariate normal distributions with constant variances and covariances independent of the mean phenotypes and population density (57–59). The vector of individual phenotypes, $z=x+e$, is determined by an additive genetic component (or breeding value), $x$, with covariance matrix $G$ plus a random microenvironmental effect (including developmental noise and nonadditive genetic effects from dominance and epistasis), $e$, with mean zero and covariance matrix $E$, so that $P=G+E$. The phenotype distribution $p(z)$ has mean $\overline{z}$, which can evolve under selection, and phenotypic covariance matrix $P$.

Each phenotype $z$ has a matrix of vital rates of survival and reproduction $L(z,N,t)$ with elements $L_{ij}(z,N,t)=l_{ij}(z,g(N))+{\xi }_{ij}(z,t)$, that may depend on $z$. Because the population is obligately sexual, a matrix of vital rates cannot be used to project a single genotype or phenotype alone. Instead, assuming weak selection, the average matrix of vital rates in the population, $\overline{L}(\overline{z},N,t)$, is used to approximately project the age- or stage-distribution in the population as a whole,

$$n(t+1)=\overline{L}(\overline{z},N,t)n(t)$$ [7]

with evolution of the mean phenotype determining changes in the frequency distribution of individual phenotypes (57). Each element of the population projection matrix is the sum of a deterministic component ${\overline{l}}_{ij}(\overline{z},g(N))=\int p(z)l_{ij}(z,g(N))dz$ and a stochastic component ${\overline{\xi }}_{ij}(\overline{z},t)=\int p(z){\xi }_{ij}(z,t)dz$.

The deterministic projection matrix for the population in the average environment, $\overline{l}(\overline{z},g(N))$, has dominant eigenvalue $\lambda (\overline{z},g(N))$ with associated left and right eigenvectors $v(\overline{z})$ and $u(\overline{z})$. The deterministic model is assumed to have a stable equilibrium at $N=K(\overline{z})$ obtained from the solution of $\lambda (\overline{z},g(K(\overline{z})))=1$. Expansion of the population growth rate, $r(\overline{z},g(N))=\ln \hspace{0.17em}\lambda (\overline{z},g(N))$, around the equilibrium at $N=K(\overline{z})$ gives

$$r(\overline{z},g(N))=\gamma (\overline{z})[g(K(\overline{z}))-g(N)],$$ [8a]

where

$$\gamma (\overline{z})=\sum _{ij}{v}_i(\overline{z})u_j(\overline{z}){\gamma }_{ij}(\overline{z})$$

and ${\gamma }_{ij}(\overline{z})=-\partial {\overline{l}}_{ij}(\overline{z},g(N))/\partial g$ evaluated at $g=g(K(\overline{z}))$.

For a small intrinsic rate of increase in the average environment, Eq. 8a can be extrapolated from $g(N)$ near $g(K(\overline{z}))$ to $g(0)=0$. The deterministic intrinsic rate of increase denoted as $r_0(\overline{z})=r(\overline{z},0)$ is then $r_0(\overline{z})=\gamma (\overline{z})g(K(\overline{z}))$, and substituting this in Eq. 8a yields

$$r(\overline{z},g(N))=r_0(\overline{z})[1-g(N)/g(K(\overline{z}))].$$ [8b]

In the stochastic model the environmental variance in population growth rate is

$${\sigma }_e^2(\overline{z})=\sum _{iji\prime j\prime }{v}_i(\overline{z})u_j(\overline{z})v_{i\prime }(\overline{z})u_{j\prime }(\overline{z})\text{E}[{\overline{\xi }}_{ij}(\overline{z},t){\overline{\xi }}_{i\prime j\prime }(\overline{z},t)].$$ [8c]

The stochastic demography of the population is therefore described by population parameters that are now functions of the mean phenotype, $r_0(\overline{z})$, $K(\overline{z})$, and ${\sigma }_e^2(\overline{z})$. The expected (or long-run) growth rate of the population, conditional on the mean phenotype and population density, is $r(\overline{z},g(N))-{\sigma }_e^2(\overline{z})/2$. Neglecting demographic stochasticity and Allee effects, and provided that the stochastic intrinsic rate of increase $s(\overline{z})=r_0(\overline{z})-{\sigma }_e^2(\overline{z})/2$ is positive, a stationary distribution of population size exists. For a population fluctuating around carrying capacity the expected growth rate through time equals zero, giving

$$\text{E}[g(N)]=\frac{s(\overline{z})}{r_0(\overline{z})}g(K(\overline{z}))=\left[1-\frac{{\sigma }_e^2(\overline{z})}{2r_0(\overline{z})}\right]g(K(\overline{z}))$$ [9a]

or, for the $\theta$-logistic model,

$$\text{E}[N^{\theta }]=\frac{s(\overline{z})}{r_0(\overline{z})}{[K(\overline{z})]}^{\theta }=\left[1-\frac{{\sigma }_e^2(\overline{z})}{2r_0(\overline{z})}\right]{[K(\overline{z})]}^{\theta },$$ [9b]

analogous to Eqs. 4a and 4b.

Expected Evolution of the Mean Phenotype.

Having reduced the age-structured population dynamics to the one-dimensional variable of population density, previous analyses (18, 21, 56) indicate that the expected evolutionary change in the mean phenotype vector per unit time, $\mathrm{\Delta }\overline{z}$ conditional on the mean phenotype and population density, is proportional to the additive genetic covariance matrix $G$ times the gradient with respect to $\overline{z}$ of the expected growth rate of the population as a function of $\overline{z}$ and $N$,

$$\text{E}[\mathrm{\Delta }\overline{z}|\overline{z},N]=\frac{G}{T}\nabla \{s(\overline{z})-r_0(\overline{z})\frac{g(N)}{g(K(\overline{z}))}\},$$ [10]

where $\nabla$ is the gradient operator with respect to the mean phenotypes, a column vector with ith element $\partial /\partial \overline{z_i}$. The generation time $T$ is the average age of mothers of newborn individuals when the population is at the stable age distribution in the average environment (29, 30); it accounts for overlapping generations when the (annual) demographic time unit (Eq. 1) differs from the generation time for inheritance (7, 57, 60). [The continuous-time models of Lande (18) and Engen et al. (21) implicitly use the time unit of generations.]

Again, we assume weak selection so that evolution is slow compared with population fluctuations, average both sides of Eq. 10 over the stationary distribution of population sizes, substitute for $E[g(N)]$ using Eq. 9a, and rearrange to yield

$$\text{E}[\mathrm{\Delta }\overline{z}|\overline{z}]=\frac{G}{T}\{\nabla s(\overline{z})-\text{E}[g(N)]\nabla \left[\frac{r_0(\overline{z})}{g(K(\overline{z}))}\right]\}=\frac{G}{T}s(\overline{z})\nabla \ln \left\{\frac{s(\overline{z})}{r_0(\overline{z})}g(K(\overline{z}))\right\}.$$ [11]

The expected evolution therefore maximizes the function in Eq. 9a, or for the $\theta$-logistic model that in Eq. 9b, as in Engen et al. (21). This result now allows interpretation of life-history trade-offs in $r$- and $K$-selection for age- and stage-structured populations.

Discussion

Evolutionary maximization of the expected mean fitness in Eqs. 5 and 9 describes the expectation of a stochastic process. For asexual inheritance this is realized by eventual fixation of the genotype with the highest value of the function, with large excursions and repeated reversals of gene frequency evolution (20). With sexual reproduction and polygenic inheritance of quantitative traits, in a model without age structure, Engen et al. (21) performed numerical simulations of the joint evolution of mean phenotype and population size. After an initial stochastic increase, sample paths of the expected mean fitness function in Eq. 9b fluctuated in a narrow range around the maximum, despite substantial fluctuations in population size. Deterministic approximations for the growth rate of an age- or stage-structured population using reproductive values, as in Eqs. 2a and 8a, have been shown quite accurate when the perturbations multiplied by their sensitivity coefficients are small (29, 30). Evidence from a variety of species shows that the age- or stage-specific vital rates subject to higher temporal variance have smaller sensitivity coefficients (47–50, 61), including both environmental stochasticity and density dependence operating through fluctuating population size. Recent studies separating these components of variance in vital rates indicate that the youngest and oldest age classes, which typically have the lowest sensitivity coefficients, are most subject to both environmental stochasticity and fluctuating density dependence (51, 53, 54).

Reproductive Value Weighting of Individuals.

For populations lacking age structure, with discrete nonoverlapping generations, the geometric mean fitness of a genotype through time determines the final outcome of selection, regardless of temporal autocorrelation in the fitnesses (62). Environmental stochasticity in an age-structured population causes transient fluctuations in age structure (associated with complex eigenvalues of the projection matrix) even when the environment is not autocorrelated; this creates temporal autocorrelation in the genetic and phenotypic composition of a population that complicates the measurement and analysis of phenotypic evolution. These complications can be largely overcome by weighting individuals of different ages by their reproductive values, as first suggested by Fisher (1, 2). Reproductive value weighting is often used in life-history theory (7, 14, 57, 63, 64) and has been shown numerically to act as an efficient filter for minimizing autocorrelated fluctuations in population size and gene frequency caused by transient dynamics of population size, genetic composition, selection, and evolution (7, 14, 55, 65–68). In the estimation of population parameters, particularly the expectation and environmental variance of population growth rate, reproductive value weighting, such as that in Eqs. 2a and 2c and 8a and 8c, removes the bias caused by transient fluctuations in age structure (68, 69). Our simulations show that this approach also provides accurate results for the dynamics of total size of density-dependent age-structured populations in a stochastic environment, provided that the fluctuations of population size around carrying capacity are not very large (Figs. 1 and 2). The present theory of life history evolution in density-dependent age-structured populations in a fluctuating environment is therefore likely to have good accuracy, given the basic assumptions of a small intrinsic rate of increase and weak selection.

Life History Trade-Offs and Evolution.

The expected mean fitness function that is maximized by long-term evolution in a fluctuating density-dependent population (Eqs. 5 and 9) involves three major components that are key parameters in stochastic population dynamics and life history: the intrinsic rate of increase in the average environment, $r_0$, the carrying capacity in the average environment, $K$, and the environmental variance, ${\sigma }_e^2$, all implicit functions of the primary phenotypic characters $\overline{z}$. Each of the major components of fitness is under consistent directional selection: $r_0$ and $K$ are always selected to increase, and ${\sigma }_e^2(\overline{z})$ is always selected to decrease, conditional on the other two (57, 70). An evolutionary equilibrium implies trade-offs among them are manifested as a negative genetic correlation between $r_0$ and $K$, and/or positive genetic correlations between these and ${\sigma }_e^2$. A genetic trade-off among the major components of fitness is expressed by a lack of expected response to selection; using their additive genetic covariance matrix $G$, operating on their selection gradient, $\nabla E[N^{\theta }]$ (where $\nabla ={(\partial /\partial r_0,\partial /\partial K,\partial /\partial {\sigma }_e^2)}^T$ and ^T indicates matrix transpose), such that $G\nabla E[N^{\theta }]=0$.

All populations fluctuate and are thus subject to alternating periods of $r$- and $K$-selection, when the population is at low or high density (7, 14, 57). For $\theta$-logistic density dependence (Eqs. 5b and 9b), it is especially clear that the resolution of the genetic trade-off between $r$- and $K$-selection depends on the magnitude of environmental stochasticity, ${\sigma }_e^2$, with $K$-selection prevailing under low environmental variance and $r$-selection prevailing under high environmental variance. This was illustrated by numerical simulations for the asexual inheritance without age structure by Lande et al. (20). However, this classical trade-off between $r$- and $K$-selection may be modified or obscured by positive genetic correlations between these parameters and ${\sigma }_e^2$. Under high environmental stochasticity, evolution to maximize $[1-{\sigma }_e^2/(2r_0)]K^{\theta }$ may occur more through reducing ${\sigma }_e^2$ rather than increasing $r_0$. An important mechanism for reducing ${\sigma }_e^2$, and therefore increasing the expected fitness of a population at any population size, is through the evolution of plasticity, discussed below.

Three considerations may thus help to explain the limited genetic and comparative evidence supporting a simple trade-off between $r$- and $K$-selection (12, 71, 72). First is the difficulty of measuring genetic variance and genetic correlations between $r$ and $K$ within populations (12). Second, as with any major components of fitness, the environmental components of $r_0$ and $K$ within and/or among populations may produce a positive phenotypic correlation between them (57, 59). Finally, selection to reduce ${\sigma }_e^2$ may be stronger than that to increase $r_0$ or $K$ so that the dominant trade-off becomes that between ${\sigma }_e^2$ and $r_0$ or $K$, rather than the traditional trade-off between $r_0$ and $K$.

Regardless of the complexity of genetic trade-offs among the three key population dynamics parameters, the simplest expression of our results for the $\theta$-logistic form of density dependence is that evolution in a fluctuating environment maximizes $\text{E}[N^{\theta }]$. This provides an elegant extension to the evolution of stochastic population dynamics of the classical finding of MacArthur (5) that evolution in a constant environment maximizes the equilibrium population size, $K$. The reason why a larger environmental variance shifts the trade-off from $K$-selection toward $r$-selection is that environmental stochasticity reduces the average size of a population below its carrying capacity. This is readily apparent for standard logistic density dependence, $\theta$ = 1, as can be seen from Eqs. 5b and 9b, but also holds for any positive value of $\theta$, as illustrated in Figs. 1 and 2.

Phenotypic Plasticity.

Phenotypic plasticity is described by the norm of reaction giving the expected phenotype of a genotype or population as a function of the environment in which it develops (73). Unmeasured microenvironmental variation among individuals affecting their phenotypic development and developmental noise contributes to the incomplete heritability of quantitative characters (58, 59). Measurable macroenvironmental effects such as temperature and precipitation often occur on a regional scale, producing parallel effects on the phenotypic development of all individuals in a population. Models of the evolution of phenotypic plasticity show that its evolution depends on the environmental predictability over developmental time lag between critical stages environmental influence on development and phenotypic selection (74–76).

The present model is based on discrete-time annual censuses at the reproductive season, assuming random environmental fluctuations with no autocorrelation between years. Critical development events occurring within years allow adaptive plasticity to evolve based on short-term environmental predictability within years. Simple models of phenotypic evolution in fluctuating environments with linear norms of reaction indicate that the main effect of adaptive plasticity is to reduce the intensity of fluctuating selection (18). The main conclusions of the present models should therefore still be applicable with a constant level of plasticity.

Limitations of the Model.

Our results are based on several assumptions, and relaxing them presents opportunities for future investigation.

Autocorrelated environments and complex life cycles.

In populations with no age structure the long-run growth does not depend on whether the environment is autocorrelated, but with age structure environmental autocorrelation does affect the long-run growth rate (30, 43, 77). Life history evolution in autocorrelated and cyclical environments is not well understood despite much biological attention especially for seasonal environments. Adaptation to such environments often involves complex life cycles, including morphological transformation and seasonal migration, with a major change in habitat, ecology, and density regulation at different life history stages (78–81). In such populations density dependence may not operate through a single variable of population size or a positive linear combination of age classes (51).

Sexual dimorphism.

In species with separate sexes, males and females may differ substantially in morphology and life history. This produces a disparity between ecological and evolutionary definitions of mean fitness. Nevertheless, it is generally possible to extend the basic results for monoecious populations to those with sexual dimorphism (e.g., refs. 60 and 82). Sexual selection typically causes selection on one sex (usually males) to be frequency-dependent, violating an assumption necessary for the evolutionary maximization of mean fitness (23, 82, 83). Frequency-dependent selection also arises for asymmetric density-dependent resource competition (84).

Genetic variance in the form of density dependence.

Genetic variance in the strength of density dependence on age-specific vital rates is allowed in the present theory but not in the functional form of density dependence. In the $\theta$-logistic model genetic variance in $\theta$, in combination with heritable variation in other population parameters, creates frequency-dependent selection which produces complications that have prevented any general conclusions about what evolution maximizes in stochastic density-dependent populations (85–87). For asexual inheritance, with other population parameters constant, ref. 20 showed that $\theta$ evolves to the interval $(1.781,2)$ corresponding to ${\sigma }_e^2$ in the range $(0,\mathrm{\infty })$.

Delayed density dependence.

Although chaotic population dynamics is precluded by realistic intrinsic rates of increase in the average environment, long time lags in density dependence interacting with environmental stochasticity can create a tendency for sustained oscillations. Multiyear time lags can arise from the life history of a population with high adult annual survival and/or high age at first reproduction (29). Multigenerational time lags can occur because of density-dependent interspecific interactions, especially predation (88).

Appendix

The stationary distribution of population size relative to carrying capacity, $N/K$, for the continuous-time stochastic $\theta$-logistic model without age structure, was derived using diffusion theory, neglecting demographic stochasticity and Allee effects at small population size,

$$\varphi (N/K)=\frac{\theta }{\mathrm{\Gamma }[(1/a-1)/\theta ]}{\left(\frac{1}{a\theta }\right)}^{(1/a-1)/\theta }{\left(\frac{N}{K}\right)}^{1/a-2}\times \exp \left\{-\frac{{(N/K)}^{\theta }}{a\theta }\right\}$$

where $a={\sigma }_e^2/(2r_0)$ (31). This distribution exists only if $0<a<1$, corresponding to a positive stochastic intrinsic rate of increase, $r_0-{\sigma }_e^2/2>0$ and has moments

$$\text{E}[{(N/K)}^b]=\frac{\mathrm{\Gamma }[(1/a-1+b)/\theta ]}{\mathrm{\Gamma }[(1/a-1)/\theta ]}{(a\theta )}^{b/\theta }$$

which when $b=\theta$ reduces to $\text{E}[{(N/K)}^{\theta }]=1-a$ as in Eqs. 4b and 8b.

The moments can be used to derive the mean $\text{E}[N/K]$, variance ${\sigma }_{N/K}^2$, and squared coefficient of variation ${\text{CV}}_N^2$, as illustrated in Figs. 1 and 2:

$$\text{E}[N/K]=\frac{\mathrm{\Gamma }[1/(a\theta )]}{\mathrm{\Gamma }[(1/a-1)/\theta ]}{(a\theta )}^{1/\theta },$$

$${\sigma }_{N/K}^2=\left\{\frac{\mathrm{\Gamma }[(1/a+1)/\theta ]}{\mathrm{\Gamma }[(1/a-1)/\theta ]}-{\left(\frac{\mathrm{\Gamma }[(1/a\theta )]}{\mathrm{\Gamma }[(1/a-1)/\theta ]}\right)}^2\right\}{(a\theta )}^{2/\theta },$$

$${\text{CV}}_N^2=\frac{{\sigma }_{N/K}^2}{{(\text{E}[N/K])}^2}=\frac{\mathrm{\Gamma }[(1/a+1)/\theta ]\mathrm{\Gamma }[(1/a-1)/\theta ]}{{(\mathrm{\Gamma }[1/(a\theta )])}^2}-1.$$

For the standard logistic model with $\theta =1$ these become

$$\text{E}[N/K]=1-a,\hspace{0.17em}{\sigma }_{N/K}^2=a(1-a),\hspace{0.17em}{\text{CV}}_N^2=\frac{a}{1-a}.$$

SI Text

In simulations of the full age-structured model we assume that elements of the projection matrix are linear in $g(N)$, $l_{ij}(g(N))=l_{ij}-{\gamma }_{ij}g(N)$, where $N=\sum b_i{n}_i$ with nonnegative weights $b_i\ge \mathrm{\hspace{0.17em}0}$. The matrix $l$ is constructed by adjusting the fecundities in an initial matrix by a common multiplicative factor to give a prescribed value of $r_0=\ln ({\lambda }_0)$. Similarly, the ${\gamma }_{ij}$ are adjusted by a common factor to give a prescribed value of $K$ so that the deterministic growth rate at $K$ is zero, or the dominant eigenvalue of $l(g(K))$ is 1.

Stochasticity is introduced by replacing $l_{ij}$ by $L_{ij}=l_{ij}{\mathrm{\Lambda }}_{ij}$ where the ${\mathrm{\Lambda }}_{ij}$ are lognormally distributed with expectation 1. Then ${\mathrm{\Lambda }}_{ij}=\exp ({\sigma }_{ij}{u}_{ij}-{\sigma }_{ij}^2/2)$, where the $u_{ij}$ are standard normal variates. The elements $l_{ij}$ chosen to be zero have no stochasticity so that ${\sigma }_{ij}^2=\mathrm{\hspace{0.17em}0}$. To reduce the number of parameters we have chosen the $u_{ij}$ equal, say $u_f$, for all nonzero fecundities, and similarly equal to $u_s$ for the survivals. Then $u_f$ and $u_s$ can be considered as environmental variables affecting fecundity and survival, respectively. The correlation $\rho$ between $u_f$ and $u_s$ is given a prescribed value. Then, the covariance between two nonzero fecundities $L_{1i}$ and $L_{1j}$ is $l_{1i}{l}_{1j}[\exp ({\sigma }_{1i}{\sigma }_{1j})-1]$ and similar expressions give the covariance between two nonzero survivals. The covariances between nonzero fecundities and survivals take the form $l_{1i}{l}_{(j+1)j}[\exp ({\sigma }_{1i}{\sigma }_{(j+1)j}\rho )-1]$.

Raptor Life History

The annual stage projection matrix for a raptor life history is

$$L=\left(\begin{array}{ccccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill f_3\hfill & \hfill f_4\hfill & \hfill f_5\hfill \\ \hfill s_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill s_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill s_3\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill s_4\hfill & \hfill s_5\hfill \end{array}\right)$$

with weight parameters $b=\{0.1,0.1,0.1,0.2,0.3\}$, deterministic carrying capacity $K={\mathrm{\hspace{0.17em}10}}^5$, and intrinsic rate of increase $r_0=\mathrm{\hspace{0.17em}0.04}$. Relative values for the expectations of parameters for the stochastic vital rates are as follows: fecundities $f=\{0,0,0,1,1.5\}$ and survivals $s=\{0.65,0.65,0.80,0.85,0.85\}$ at $N\approx \mathrm{\hspace{0.17em}0}$; coefficients of density dependence in fecundities ${\gamma }_f=\{0,0,0,0.2,0.2\}$ and survivals ${\gamma }_s=\{0.1,0.1,0.1,0.1,0.1\}$; coefficients of environmental variation in fecundities ${\text{CV}}_f=\{0,0,0,0.2,0.1\}$ and survivals ${\text{CV}}_s=\{0.3,0.2,0.1,0.1,0.1\}$; and environmental correlation between nonzero survivals and fecundities $\rho =0.6$.

Passerine Life History

The annual stage projection matrix for a passerine life history is

$$L=\left(\begin{array}{ccc}\hfill f_1\hfill & \hfill f_2\hfill & \hfill f_3\hfill \\ \hfill s_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill s_2\hfill & \hfill s_3\hfill \end{array}\right)$$

with weight parameters $b=\{0.7,0.9,0.9\}$, deterministic carrying capacity $K={\mathrm{\hspace{0.17em}10}}^5$, and intrinsic rate of increase $r_0=\mathrm{\hspace{0.17em}0.1}$. Relative values for the expectations of parameters for the stochastic vital rates are as follows: fecundities $f=\{0.8,\mathrm{1,1}\}$ and survivals $s=\{0.3,0.5,0.6\}$ at $N\approx \mathrm{\hspace{0.17em}0}$; coefficients of density dependence in fecundities ${\gamma }_f=\{0.3,0.2,0.1\}$ and survivals ${\gamma }_s=\{0.3,0.3,0.3\}$; coefficients of environmental variation in fecundities ${\text{CV}}_f=\{0.5,0.5,0.5\}$ and survivals ${\text{CV}}_s=\{0.3,0.2,0.1\}$; and environmental correlation between nonzero survivals and fecundities $\rho =\mathrm{\hspace{0.17em}0.2}$.